Abstract
Growth and remodeling in the heart is driven by a combination of mechanical and hormonal signals that produce different patterns of growth in response to exercise, pregnancy, and various pathologies. In particular, increases in afterload lead to concentric hypertrophy, a thickening of the walls that increases the contractile ability of the heart while reducing wall stress. In the current study, we constructed a multiscale model of cardiac hypertrophy that connects a finite-element model representing the mechanics of the growing left ventricle to a cell-level network model of hypertrophic signaling pathways that accounts for changes in both mechanics and hormones. We first tuned our model to capture published in vivo growth trends for isoproterenol infusion, which stimulates β-adrenergic signaling pathways without altering mechanics, and for transverse aortic constriction (TAC), which involves both elevated mechanics and altered hormone levels. We then predicted the attenuation of TAC-induced hypertrophy by two distinct genetic interventions (transgenic Gq-coupled receptor inhibitor overexpression and norepinephrine knock-out) and by two pharmacologic interventions (angiotensin receptor blocker losartan and β-blocker propranolol) and compared our predictions to published in vivo data for each intervention. Our multiscale model captured the experimental data trends reasonably well for all conditions simulated. We also found that when prescribing realistic changes in mechanics and hormones associated with TAC, the hormonal inputs were responsible for the majority of the growth predicted by the multiscale model and were necessary in order to capture the effect of the interventions for TAC.
Keywords: multiscale modeling, cardiac hypertrophy, transverse aortic constriction, finite-element modeling, signaling networks, systems biology
INTRODUCTION
Left ventricular hypertrophy is complex in nature and involves an array of mechanical and hormonal changes that stimulate growth and remodeling of the heart. In particular, both aortic stenosis and hypertension lead to an increase in afterload and subsequent left ventricular concentric hypertrophy, a thickening of the walls that increases the contractile ability of the heart and reduces wall stress (Lorell and Carabello 2000; Grossman, Jones, and McLaurin 1975). However, development of left ventricular hypertrophy is also associated with increased risk of further cardiovascular disease, heart failure, and mortality (Benjamin et al. 2018; Bruno and Taddei 2014; Cuspidi et al. 2010; Kawel-Boehm et al. 2019). Current treatment options for aortic stenosis and hypertension involve management of afterload and ideally a reduction in hypertrophy. For example, aortic stenosis is treated through surgical repair or replacement of the stenotic valves, which can lead to improved cardiac function and even reversal of hypertrophy. However, clinical decisions for aortic stenosis are not always straightforward, because the benefit of these interventions must be weighed against the risk of surgical complications on a patient-by-patient basis (Monrad et al. 1988; Gelsomino et al. 2001; Otto 2006; Nishimura et al. 2014). In the case of hypertension, current treatment options for most patients include lifestyle changes and drugs, such as β-blockers, angiotensin-converting enzyme (ACE) inhibitors, and angiotensin receptor blockers (ARBs), but given the prevalence of the disease there is still a need for identifying new therapies to treat or prevent the associated hypertrophy. The long-term goal of the work described here is to develop computational models that predict the progression of hypertrophy in the setting of increased afterload, altered hormonal levels, and the presence of pharmacological interventions, in order to better understand the underlying processes, develop new treatment strategies, and guide clinical decision making.
Several experimental methods, pharmacological and mechanical, are used to induce concentric hypertrophy in animals; here, we use data from two models to construct and validate growth models. Infusion of isoproterenol, an FDA-approved β-adrenergic receptor agonist normally used to treat bradycardia and heart block, induces cardiac hypertrophy and fibrosis through activation of the β-1 adrenergic receptor and subsequent increases in G-protein signaling and cAMP (Xiang 2011; Szymanski and Singh 2019). Because it is not present as an endogenous hormone, isoproterenol infusion provides a straightforward way to study the development of cardiac hypertrophy and specific interventions that can attenuate growth. By contrast, in transverse aortic constriction (TAC), a pressure overload is created by tying a suture around the aorta that constricts the vessel. The pressure overload caused by TAC induces concentric hypertrophy both directly through mechanical stimulation and indirectly through increases in circulating hormones such as endothelin-1 (ET-1) and norepinephrine (NE) and activation of the renin-angiotensin system, which leads to elevated levels of angiotensin II (Ang II) and atrial natriuretic peptide (ANP) (Swynghedauw 1999; Lorell and Carabello 2000; Yamazaki et al. 1995, 1996; Schunkert et al. 1990; Sugden 1999; Izumo, Nadal-Ginard, and Mahdavi 1988; Rapacciuolo et al. 2001; Lindpaintner, Lund, and Schmid 1987; Yoshida et al. 2015; Kamal et al. 2014; Liao et al. 2003). These hormones in turn activate pro-hypertrophic pathways in cardiomyocytes and further exacerbate the growth experienced by the heart. While TAC remains artificial in terms of its sudden onset, it recreates features of the complex hormonal and mechanical stimulation associated with diseases such as aortic stenosis and hypertension.
Computational growth modeling is an evolving area of biomechanics aimed at predicting the growth of biological tissues in response to their mechanical environment. Most computational growth models of the heart use phenomenologic equations to predict growth based on mechanical stimuli such as stretch and stress, and some of those models have proven successful at predicting the different patterns of myocyte thickening and lengthening that occur in response to both experimental volume overload and pressure overload (Kerckhoffs, Omens, and McCulloch 2012; Taber 1998; Arts et al. 2005). However, the main limitation of phenomenologic growth laws based on mechanical stimuli is that they are unable to predict how hormones and pharmacologic interventions will influence the amount of growth experienced by the heart. This limitation is especially problematic for models that aim to predict clinical outcomes, because nearly all patients with clinically significant cardiac disease receive drugs such as β-blockers, ACE inhibitors, and ARBs that can alter hypertrophic signaling. However, techniques from the field of systems biology now offer the possibility to model large signaling networks within a cell and predict how cell growth and gene expression are altered by specific perturbations. For example, Ryall et al. (Ryall et al. 2012) published a model of hypertrophic signaling within a single cardiomyocyte and used it to predict increases in cell area in response to both mechanical stretch and hormonal agonists and to identify key intracellular signaling hubs for this process. A more recent version of this model, published by Frank et al. (Frank, Sutcliffe, and Saucerman 2018), further refined and validated the network model against in vivo data from 52 transgenic mouse models.
The purpose of the current study was to construct a multiscale model of cardiac hypertrophy that connects a finite-element model (FEM) representing the mechanics of the growing left ventricle to a cell-level hypertrophy signaling network model. In the present work, we test the ability of the multiscale model to predict in vivo growth due to isoproterenol infusion (hormones only), TAC (mechanical overload and hormones), and different genetic and pharmacologic interventions that attenuate hypertrophy in TAC (mechanical overload, hormones, and hormonal perturbations).
METHODS
Finite-element model simulations
We used a previously published finite-element model of the left ventricle as the basis for our multiscale model of hypertrophy (Estrada et al. 2020). Briefly, the finite-element model was constructed from average endocardial and epicardial surface contours obtained by segmenting and averaging magnetic resonance (MRI) scans of a set of canine left ventricles from a previous study (Clarke et al. 2015). The mesh consisted of 9680 nodes and 7840 linear elements, including rigid-body rings of elements at the base and apex. The finite-element model had five transmural layers, with a fiber distribution of −60° to 60° from epicardium to endocardium. For this study the model used the compressible transversely isotropic Mooney-Rivlin (TIMR) material in FEBio 2.6.4 (febio.org), with growth capabilities added in a custom-built plugin, described below. We simulated full cardiac cycles by prescribing the time course of internal cavity pressure and a time-varying activation curve that represents the rise and fall of active tension generation in the myocardium due to calcium cycling (Estrada et al. 2020). We generated these input curves using a previously published compartmental model of canine pressure overload that included both ventricles and a closed-loop circulation (Witzenburg and Holmes 2018). We matched the left ventricular (LV) end-systolic and end-diastolic pressure-volume relationships in the compartmental model to the finite-element model, and then simulated both baseline and aortic constriction states in order to generate LV pressure-time and volume-time curves. We then optimized the activation curve for each condition in the finite-element model such that the input pressure-time curve would result in the corresponding volume-time output curve from the compartmental model. The basal rigid body ring was fixed in all directions, the basal-most nodes were fixed in the base-apex direction, and all other elements were allowed to move freely during the simulation. In the isoproterenol simulations, we used the baseline pressure-time and activation curves throughout the simulation, consistent with a previous study (Allwood et al. 2014) showing little difference in the pressure vs. time curves of sham and isoproterenol-induced mice at doses shown to result in hypertrophy. For all TAC simulations we instead used the aortic constriction pressure-time and activation curves. Changes to the hormonal activation during isoproterenol infusion and TAC were represented as global changes present throughout the simulation. All finite-element model simulations were run using the Pardiso solver in FEBio 2.6.4.
Growth implementation
To allow growth in the finite-element framework, we implemented the kinematic growth framework proposed by Rodriguez et al. (Rodriguez, Hoger, and McCulloch 1994) using a custom FEBio plugin that redefined the stress in the material to depend on the elastic deformation necessary to enforce compatibility after growth rather than total deformation experienced by the material. The plugin added a user-defined diagonal growth deformation tensor with fiber, cross-fiber, and radial components (Equation 1) and a user-defined radial direction vector in addition to a fiber direction already defined in the TIMR material. Using a multiplicative decomposition, we calculated the elastic deformation within the plugin from the total deformation applied to the model and the user-defined growth deformation tensor (Equation 2). We used the compressible TIMR material as the template for our growth plugin, and within its FEBio material file, we redefined the matrix, fiber, and dilatational components of the stress (Equation 3) to depend on our calculated elastic deformation (Felastic). Thus, stress became a function of the elastic deformation rather than the total deformation. The variables in Equations 1–3 are defined as follows: Fgrowth is the diagonal growth deformation tensor in the fiber (ff), cross-fiber (cc), and radial (rr) directions; Ftotal is the total deformation tensor; σmatrix is the isotropic Cauchy stress, Jelastic is the determinant of Felastic, Belastic the elastic left Cauchy-Green deformation tensor, Ielastic1 the trace of Belastic, and c1 and c2 as the Mooney-Rivlin parameters; σfiber corresponds to the Cauchy stress in the fiber direction, with Aelastic being the tensor that defines the fiber direction, λfiber the stretch in the fiber direction, c3 the linear fiber parameter, c4 the exponential fiber parameter, and T the time-varying active tension; and σdilatational is the volume penalty stress, with K corresponding to the bulk modulus of the material. The active tension (Equation 4) is the product of a time-varying normalized activation, e(t); an instantaneous length-dependent term, which depends on the maximum tension Tmax, the initial calcium concentration Ca0, the maximum calcium concentration Ca0,max, and the unloaded (l0) and reference (lr) sarcomere lengths; and a force-velocity dampening function Q that depends on the slow tension recovery rate constant α1 the slow tension weighing coefficient A1, and the force-velocity curvature parameter a.
| (1) |
| (2) |
| (3) |
| (4) |
Hypertrophy signaling network model
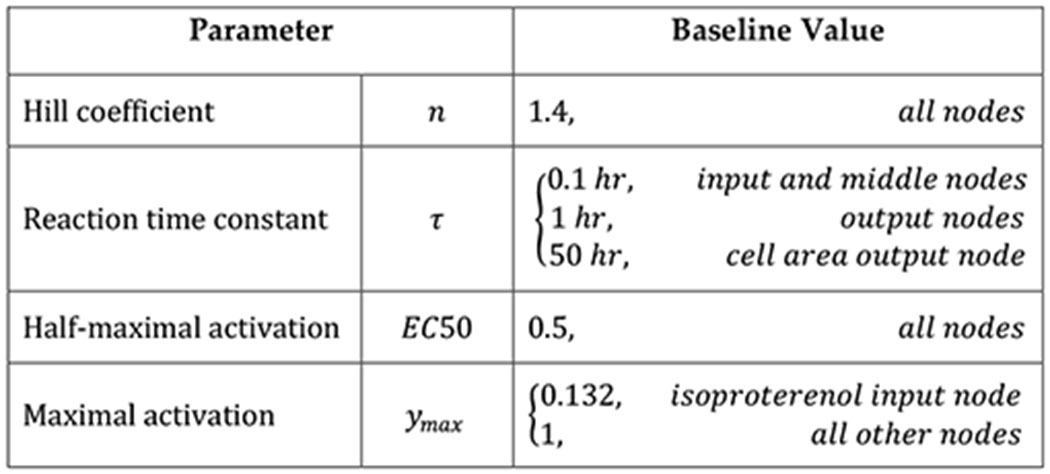
We used a previously published hypertrophy signaling network model (Ryall et al. 2012; Frank, Sutcliffe, and Saucerman 2018) to calculate predicted growth in response to stretch and hormonal inputs associated with pressure overload. The network model consisted of a system of normalized Hill-type ordinary differential equations with 107 species and 207 reactions that capture the intracellular signaling leading to increases in cell size and protein production necessary for hypertrophy. In this framework, the level of activation of every node (input, intermediate, or output) is represented as a value between 0 and 1, where 0 indicates no input, signaling activity, or output and 1 represents maximal levels of activation. We show examples of the differential equations for the model isoproterenol input node (ISO) and for the β-adrenergic receptor downstream node (βAR) in Equation 5 and in Equations 6–9, respectively. In these equations, W corresponds to the weight of the reaction, a measure of the extent to which the reaction can activate or inhibit its downstream nodes, and ymax to the maximum activation possible for each particular node. By default, all nodes used ymax = 1, Hill coefficient n = 1.4, and half-maximal activation EC50 = 0.5 in the Hill-type activation function fact(X) (Equation 7), as described in the original publications (Ryall et al. 2012; Frank, Sutcliffe, and Saucerman 2018). The model used a reaction time constant τ = 0.1 hrs for all nodes except for the outputs α-myosin heavy chain (aMHC), atrial natriuretic peptide (ANP), β-myosin heavy chain (bMHC), brain natriuretic peptide (BNP), skeletal α-actin (sACT), sarcoplasmic reticulum ATPase (SERCA), and input isoproterenol (ISO), which were set to 1 hr, and output Cell Area, which was set to 50 hrs. Default node weights were set to 0.06 for all inputs except isoproterenol, 0 for isoproterenol because it is an exogenous drug, and 1 for all downstream nodes. Table 1 summarizes the network model parameters.
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Table 1:
Signaling network model parameters
 |
 |
Coupling the network and mechanical models
We built the multiscale model of hypertrophy (Figure 1) by coupling the cardiomyocyte hypertrophy signaling network model and finite-element model of the left ventricle described above via MATLAB (R2014b, Mathworks). We coupled the two models by mapping key outputs of each model to inputs of the other model. Specifically, we used a linear transfer function to map strain from the finite-element model to the stretch input of the network model and a separate linear transfer function to map the cell area output of the network model to the growth deformation tensor applied to the finite-element model. We present these transfer functions and their rationale in more detail below.
Fig. 1.
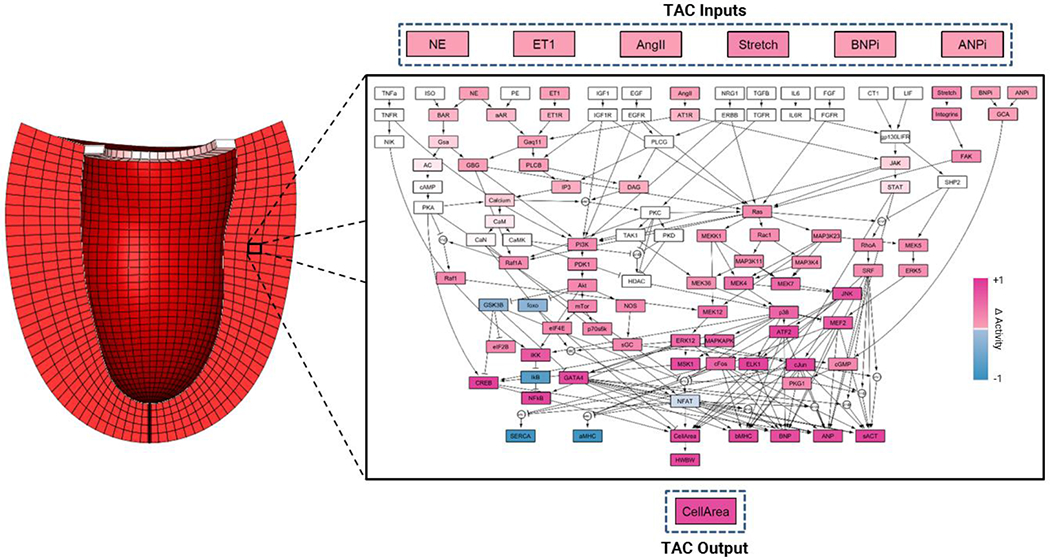
Schematic of the multiscale model of hypertrophy. A finite-element model of the left ventricle is coupled to a network model of intracellular hypertrophy signaling in cardiomyocytes. The network model shows the change in activation of each node in response to simulated transverse aortic constriction (TAC) compared to baseline activation. Increased activation is shown in pink and decreased activation is shown in blue
For each growth step in the multiscale model, we ran the network model to simulate 5 hours of real time, sampled the cell area output, and used it to drive an increase in mass in the FEM by updating the growth deformation tensor Fgrowth (Figure 2). For the simulations of concentric hypertrophy presented here, we assumed that all growth would occur in the radial direction; the potential limitations of this assumption are considered in the Discussion. We then sampled the elastic deformation from the FEM over the course of one simulated cardiac cycle and used it to update the stretch input to the network model, then iterated to the next growth step. To account for the differences in value ranges when coupling the model inputs and outputs, we defined linear transfer functions as described in the following section.
Fig. 2.
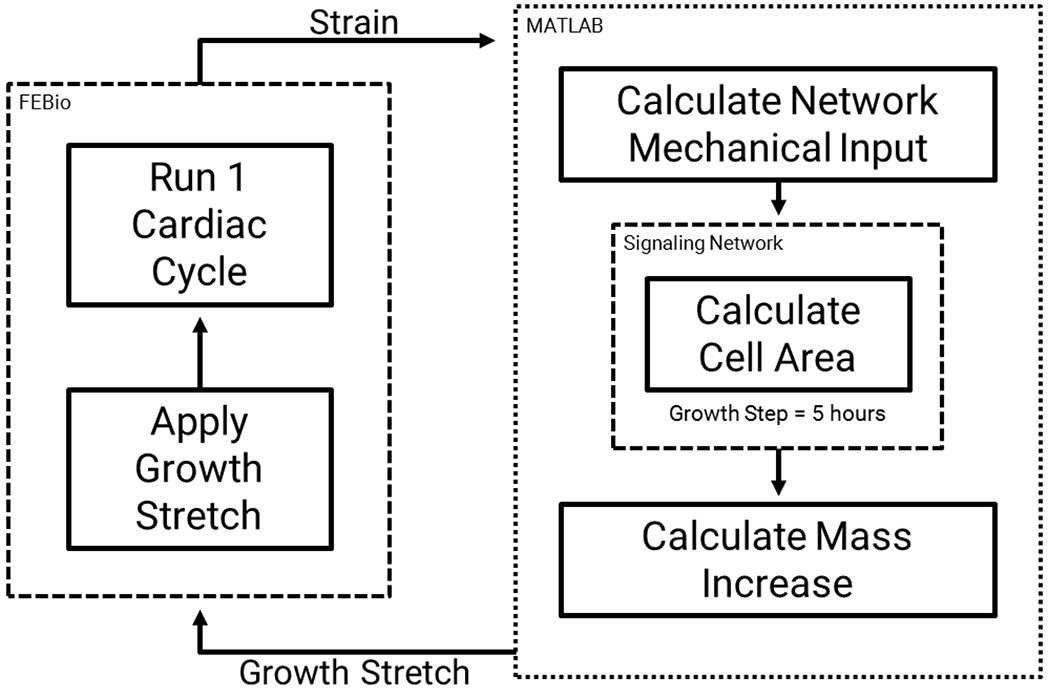
Multiscale model coupling process. We apply the growth stretch to the FEM in FEBio and run one cardiac cycle. We then parse the elastic deformation from the FEM in MATLAB and use it to calculate the network mechanical input. We run the network model for a simulated 5 hour growth step and sample the cell area, which we use to calculate the mass increase and growth stretch for the FEM
Our stretch transfer function coupled the mechanical behavior of the models by mapping a measure of strain from the FEM to the normalized stretch input in the network model. Because the signaling network incorporates a single generic stretch input that activates stretch-related intracellular pathways, this mapping required calculating a single strain metric from the FEM. We chose the minimum of the greatest principal cross-fiber strain (min(Ecross,max)) during the cardiac cycle, a metric successfully used by Kerckhoffs et al. (Kerckhoffs, Omens, and McCulloch 2012) to drive thickening of the myocardium in previous phenomenologic models of pressure overload and volume overload. Based on the fact that the pressure gradients imposed in the studies modeled here fell in the middle of the range of severities of TAC known to induce graded hypertrophic responses (Richards et al. 2019), we calibrated the mapping between min(Ecross,max) in the FEM and normalized stretch in the network so that the mechanical changes associated with TAC would stimulate a half-maximal increase in predicted cell area (Figure 3). We did this by averaging the min(Ecross,max) values across all finite elements in the FEM at baseline and during simulated aortic constriction, and mapping them to values of the network stretch input that trigger no growth (0.06) and a 50% increase in cell area in the network model when all other parameters are held constant. The resulting stretch transfer function is shown in Equation 10. In addition to the single-network simulations, we ran TAC simulations in which we averaged strains across each of five transmural layers of the FEM and coupled each layer to its own representative network. We used the same stretch transfer function but shifted along the strain axis, such that the average mechanical stimulus for each layer would be at its homeostatic point at baseline.
| (10) |
Fig. 3.
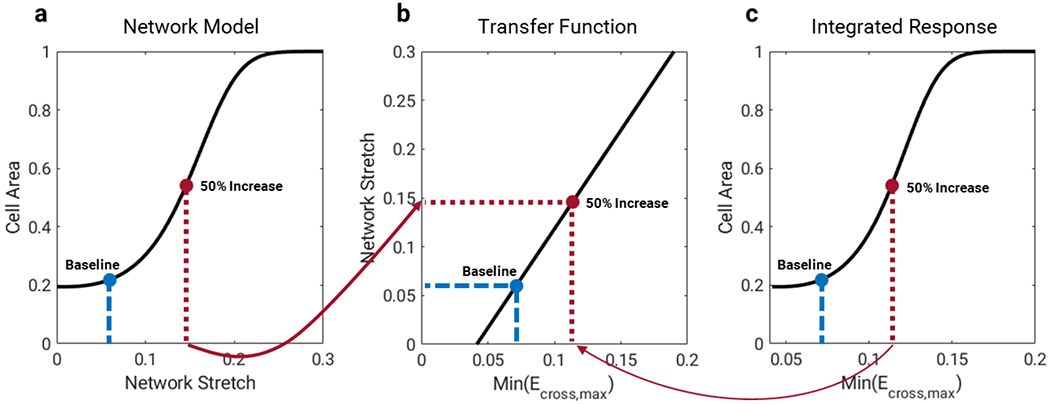
Mapping model inputs and outputs. a) Steady-state cell area response in the network model for different levels of normalized stretch input. b) Mechanical stimulus from the FEM (min(Ecross,max), see text for details), is mapped to the network model stretch input using a linear transfer function such that the baseline min(Ecross,max) corresponds to the baseline network stretch and values of min(Ecross,max) expected during TAC trigger half-maximal increases in cell area. c) Combining (a) and (b) yields an integrated response curve relating min(Ecross,max) directly to predicted steady-state cell area.
We also constructed a linear transfer function to map the predicted cell area output of the network model to the determinant, Jg, of the growth deformation tensor Fgrowth in the FEM. As described in more detail below, we calibrated this mapping so that the baseline cell area in the network model corresponds to Jg = 1 (no growth), and the cell area value in the network model after 2 weeks of simulated TAC corresponds to the average fold change in LV mass (Jg = 1.45) 2 weeks after TAC as reported in the literature. Because we assumed all growth to be in the radial direction, we assigned the diagonal components of the growth deformation tensor to be Fgrowth,rr = Jg and Fgrowth,ff = Fgrowth,cc = 1. The final growth transfer function is shown in Equation 11.
| (11) |
Model tuning: simulating isoproterenol infusion and TAC
We tuned the multiscale model by simulating two different conditions that stimulate concentric hypertrophy: isoproterenol infusion and TAC. We gathered mass fold increase data reported in the literature for both isoproterenol infusion and TAC (De Windt et al. 2001; Tuerdi et al. 2016; Allwood et al. 2014; Sucharov et al. 2013; Drews et al. 2010; Tshori et al. 2006; Zhang et al. 2016; Waters et al. 2013; Ryu et al. 2016; Jaehnig et al. 2006; Galindo et al. 2009; Liao et al. 2003; Akhter et al. 1998; Rapacciuolo et al. 2001; Huss et al. 2007; Choi et al. 1997; Ling et al. 2009; Rockman et al. 1994; Li et al. 2010; Wang et al. 2016; Patrizio et al. 2007) and used these data (Table 2) to tune the level of hormonal input to the network model and the growth transfer function as follows. Based on data showing that the doses of isoproterenol used in these studies did not significantly alter blood pressure (Allwood et al. 2014), we simulated isoproterenol infusion by maintaining baseline loading conditions for the FEM and increasing the activation level of the isoproterenol input node (ISO) in the network model, with all other hormonal inputs remaining at their baseline levels. Because the data showed that even maximal doses of isoproterenol produce a lower steady-state mass increase than TAC in murine experiments (De Windt et al. 2001; Tuerdi et al. 2016; Allwood et al. 2014; Sucharov et al. 2013; Drews et al. 2010; Tshori et al. 2006; Zhang et al. 2016; Waters et al. 2013; Ryu et al. 2016; Jaehnig et al. 2006; Galindo et al. 2009; Brooks and Conrad 2009), we set the maximum activation (ymax) of ISO to 0.132, which restricted maximal growth due to ISO to about two-thirds of the growth induced in our TAC simulations.
Table 2:
Data used to tune and validate the model
| Tuning: Isoproterenol Infusion | |||
|---|---|---|---|
| Study | Isoproterenol Dose (mg/kg BW/day) | Mass Fold Change ± Standard Deviation | Time point |
| De Windt et al. 2001 | 60 | 1.25 ± 0.05 | 14 days |
| Tuerdi et al. 2016 | 5 | 1.37 ± 0.03 | 7 days |
| Allwood et al. 2014 | 30 | 1.36 ± 0.03 | 14 days |
| Sucharov et al. 2013 | 30 | 1.20 ± 0.04 | 7 days |
| Drews et al. 2010 | 30 | 1.16 ±0.01 | 1 day |
| 30 | 1.53 ± 0.08 | 7 days | |
| Tshori et al. 2006 | 5 | 1.38 ± 0.14 | 7 days |
| Zhang et al. 2016 | 5 | 1.23 ± 0.01 | 7 days |
| Waters et al. 2013 | 47 | 1.27 ± 0.01 | 3 days |
| Ryu et al. 2016 | 25 | 1.31 ± 0.01 | 3 days |
| 25 | 1.24 ± 0.01 | 14 days | |
| Jaehnig et al. 2006 | 60 | 1.29 ± 0.02 | 10 days |
| Galindo et al. 2009 | 40 | 1.49 ± 0.13 | 10 days |
| Brooks and Conrad | 100 | 1.19 ± 0.01 | 14 days |
| Tuning: Transverse Aortic Constriction | |||
| Study | Mass Fold Change ± Standard Deviation | Time point | |
| Liao et al. 2003 | 1.50 ± 0.01 | 7 days | |
| Akhter et al. 1998 | 1.39 ± 0.13 | 7 days | |
| De Windt et al. 2001 | 1.22 ± 0.10 | 14 days | |
| Rapacciuolo et al. 2001 | 1.60 ± 0.23 | 7 days | |
| Huss et al. 2007 | 1.17 ± 0.03 | 7 days | |
| Choi et al. 1997 | 1.34 ± 0.20 | 7 days | |
| Ling et al. 2009 | 1.65 ± 0.02 | 14 days | |
| Rockman et al. 1994 | 1.20 ± 0.08 | 7 days | |
| Li et al. 2010 | 1.73 ± 0.21 | 14 days | |
| Wang et al. 2016 | 1.36 ± 0.06 | 14 days | |
| Patrizio et al. 2007 | 1.29 ± 0.02 | 14 days | |
| Validation: Transverse Aortic Constriction Plus Intervention | |||
| Study | Intervention | Mass Fold Change ± Standard Deviation | Time point |
| Akhter et al. 1998 | GqI | 1.15 ± 0.01 | 7 days |
| Rapacciuolo et al. 2001 | NE KO | 1.20 ± 0.03 | 7 days |
| Rockman et al. 1994 | Losartan | 0.96 ± 0.06 | 7 days |
| Li et al. 2010 | Losartan | 1.20 ± 0.01 | 14 days |
| Wang et al. 2016 | Losartan | 1.05 ± 0.07 | 14 days |
| Patrizio et al. 2007 | Propranolol | 1.15 ±0.07 | 14 days |
TAC alters both the level of hormonal stimulation and the mechanical load experienced by the heart. Based on data showing that beta-adrenergic pathways are activated but not saturated during TAC (Choi et al. 1997), we simulated the hormonal environment associated with TAC by increasing angiotensin II (AngII), endothelin-1 (ET1), norepinephrine (NE), atrial natriuretic peptide (ANPi), and brain natriuretic peptide (BNPi) inputs to levels (normalized inputs of 0.09 for each) that produced a half-maximal increase in cell area from baseline in the network model. Finally, we simulated TAC in the multiscale model by elevating these hormonal inputs in the network and applying pressure-overload loading conditions in the FEM, and tuned our growth transfer function (Equation 11) so that Jg matched the average reported fold mass increase two weeks following TAC (Liao et al. 2003; Akhter et al. 1998; De Windt et al. 2001; Rapacciuolo et al. 2001; Huss et al. 2007; Choi et al. 1997; Ling et al. 2009; Rockman et al. 1994; Li et al. 2010; Wang et al. 2016; Patrizio et al. 2007). Simulation conditions for isoproterenol infusion and TAC are summarized in Table 3.
Table 3:
Simulation conditions
| Simulation | Hemodynamic Condition | Elevated Input Nodes | Intervention Target Node ymax = 0 | |||||
|---|---|---|---|---|---|---|---|---|
| Baseline Pressure | Acute Pressure Overload | ISO | AngII, NE, ET1, ANPi, BNPi | Gαq11 | NE | AT1R | βAR | |
| Isoproterenol Infusion | ||||||||
| TAC | ||||||||
| GqI | ||||||||
| NE KO | ||||||||
| ARB | ||||||||
| β-blocker | ||||||||
Model validation: simulating interventions for TAC
We validated the multiscale model by simulating multiple genetic modifications (Akhter et al. 1998; Rapacciuolo et al. 2001) and pharmacologic interventions (Rockman et al. 1994; Li et al. 2010; Wang et al. 2016; Patrizio et al. 2007) shown to attenuate hypertrophy due to TAC. We used the same pressure loading conditions and hormonal activation levels as with TAC but with specific perturbations for each intervention. In order to simulate an inhibition, a knock-out, or a blockade in the network model, we set the maximum activation (ymax) of the node of interest to zero, thus preventing any level of activation. We simulated a transgenic Gq-coupled receptor inhibitor overexpression (GqI) that prevented activation of the Gαq11 network node (Akhter et al. 1998); an endogenous NE knock-out (NE KO) that eliminated the NE input (Rapacciuolo et al. 2001); the angiotensin II receptor blocker losartan (ARB), which blocked the AT1R network node (Rockman et al. 1994; Li et al. 2010; Wang et al. 2016); and the β-blocker propranolol, which blocked the βAR network node (Patrizio et al. 2007). The GqI and NE KO interventions each used a version of the network model with their respective modifications to obtain initial steady-state network conditions before TAC was simulated, since these genetic modifications were present throughout the life of the mice. The ARB and β-blocker interventions instead used the baseline network to obtain initial steady-state conditions and then applied the modifications once TAC was induced, consistent with the fact that these were administered following TAC in experiments. Simulation conditions for TAC interventions are summarized in Table 3.
RESULTS
Growth plugin validation
We wrote a custom plugin that implements directional volumetric growth in the FEBio framework. Our plugin is based on the compressible transversely isotropic Mooney-Rivlin (TIMR) material with the capability of active contraction. The TIMR growth plugin requires that users specify four new parameters: growth deformation in the fiber, cross-fiber, and radial directions (Fgrowth,ff, Fgrowth,cc, and Fgrowth,rr, respectively) and the radial direction vector for each element. The plugin rotates the diagonal growth deformation tensor from fiber coordinates into local coordinates and updates the stress and tangent calculations so that they depend on the elastic deformation only. We demonstrated the proper implementation of the plugin by prescribing growth in an unloaded single-element simulation for five distinct cases: fiber growth only, cross-fiber growth only, radial growth only, fiber and cross-fiber growth equally, and isotropic growth. In Figure 4a–c, we show the strain in Cartesian coordinates induced by each prescribed growth case with fibers at 0°, 45°, and 90° from the x axis. We then tested the effect of growth on the material stress by applying a prescribed stretch and hold in a one-element simulation. As shown in Figure 4d, the initial stretch increased the stress within the element, but as the element was allowed to grow, the stress decreased despite the sustained total stretch as growth reduced the elastic stretch.
Fig. 4.
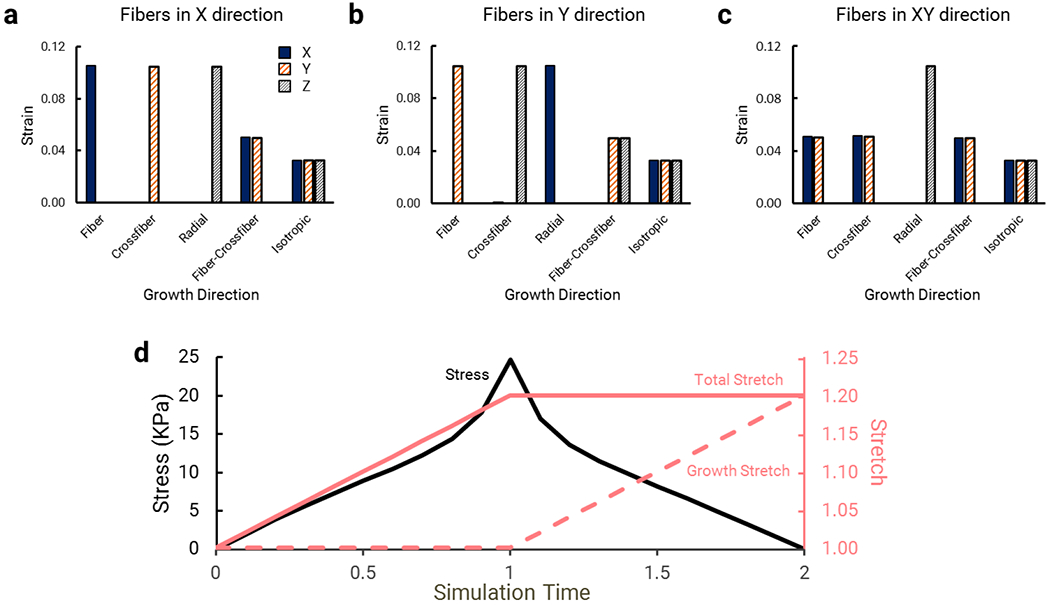
Strain in the X, Y, and Z directions in response to growth in the fiber direction, cross-fiber direction, radial direction, fiber and cross-fiber directions, and isotropically, in the following fiber directions: a) Fibers in the X direction; b) Fibers in the Y direction; c) Fibers at 45° between the X and Y directions. d) Growth reduces stress in a single-element simulation of constant applied stretch. A single finite element is initially stretched (solid pink line), causing an increase in stress (solid black line), and this stretch remains constant during the rest of the simulation. After the increase in stretch, the element is allowed to grow in the fiber direction (dashed pink line). The growth subsequently results in a decrease in stress, in spite of the constant total stretch.
Multiscale simulations of isoproterenol infusion and TAC
We simulated two weeks of isoproterenol infusion using the multiscale model by elevating the isoproterenol input to its maximum possible value of 1, maintaining all other hormonal inputs at their baseline values of 0.06, and allowing the stretch input to evolve in response to growth according to the coupling equations outlined under Methods. As seen in Figure 5a, the calibrated simulation predicted a steady-state mass increase of 1.33 fold with a time course consistent with published data from experimental studies of isoproterenol infusion in mice (De Windt et al. 2001; Tuerdi et al. 2016; Allwood et al. 2014; Sucharov et al. 2013; Drews et al. 2010; Tshori et al. 2006; Zhang et al. 2016; Waters et al. 2013; Ryu et al. 2016; Jaehnig et al. 2006; Galindo et al. 2009; Brooks and Conrad 2009). Figure 5b shows short-axis cross-sections of the baseline left ventricle and the left ventricle after two weeks of isoproterenol infusion, both at end diastole. These cross-sections show the substantial thickening of the left-ventricular walls, consistent with the growth patterns in concentric hypertrophy.
Fig. 5.
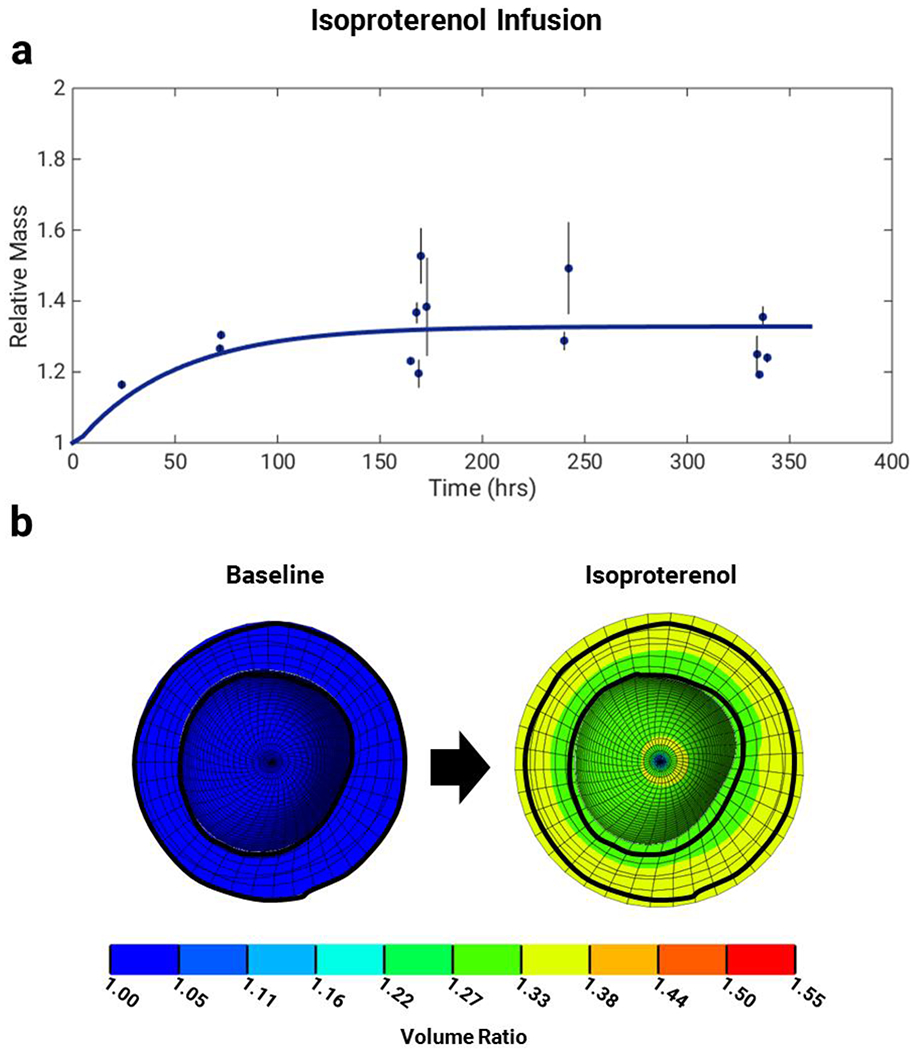
Simulations of isoproterenol infusion for two weeks. a) The multiscale model predicts a growth time course consistent with experimental data of isoproterenol infusion in mice (De Windt et al. 2001; Tuerdi et al. 2016; Allwood et al. 2014; Sucharov et al. 2013; Drews et al. 2010; Tshori et al. 2006; Zhang et al. 2016; Waters et al. 2013; Ryu et al. 2016; Jaehnig et al. 2006; Galindo et al. 2009; Brooks and Conrad 2009). Data are shown as mass fold change ratio relative to control ± standard deviation of ratio. b) Finite-element model short-axis cross-sections show volume ratios at end diastole for baseline (pre-growth) and after two weeks of isoproterenol infusion. Baseline outline is shown for clarity
We simulated transverse aortic constriction by imposing pressure-overload loading conditions and increasing input levels of AngII, ET1, NE, ANPi, and BNPi as described under Methods. Figure 6a shows the mass increase in the left ventricle over two weeks in response to the combined mechanical and hormonal stimulation induced by TAC. While there is substantial variability in the experimental data, our calibrated model predicts a 1.52 fold mass increase that falls near the average of the values reported in the literature (Liao et al. 2003; Akhter et al. 1998; De Windt et al. 2001; Rapacciuolo et al. 2001; Huss et al. 2007; Choi et al. 1997; Ling et al. 2009; Rockman et al. 1994; Li et al. 2010; Wang et al. 2016; Patrizio et al. 2007). Imposing pressure-overload loading conditions in the absence of elevated hormonal inputs produced much less growth than observed in our TAC simulation (Figure 6a, see Discussion). We also ran TAC simulations where a separate network model was coupled to each of the five transmural layers of the FEM. In this 5-layer model, the average mass fold increase was similar to that of the single-network simulation, but the dynamics were different (Figure 6b). During initial overload, the inner layers grew faster due to greater mechanical stimuli. However, the growth of the inner layers subsequently pushed the mechanical stimuli of the outer layers farther from their homeostatic point, thus leading to sustained growth.
Fig. 6.
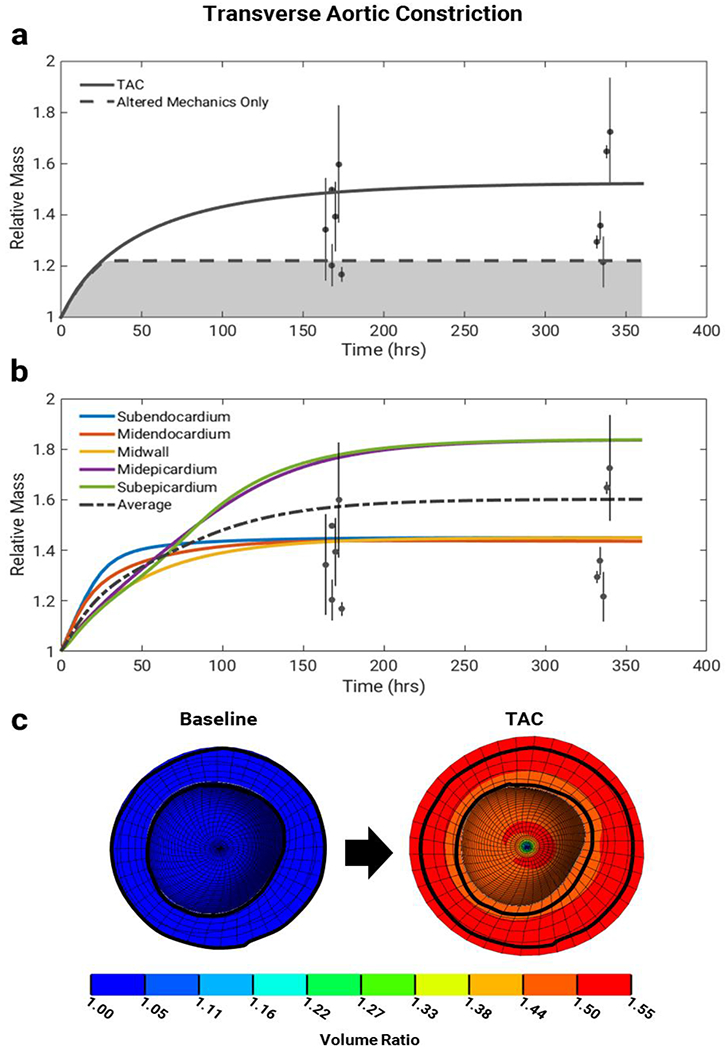
Simulations of transverse aortic constriction (TAC) for two weeks. a) When using both mechanical and hormonal stimulation (solid line), the multiscale model predicts a growth time course that follows experimental data trends of TAC in mice, from (Liao et al. 2003; Akhter et al. 1998; De Windt et al. 2001; Rapacciuolo et al. 2001; Huss et al. 2007; Choi et al. 1997; Ling et al. 2009; Rockman et al. 1994; Li et al. 2010; Wang et al. 2016; Patrizio et al. 2007). When stimulated using stretch alone, the multiscale model reaches a lower growth steady state than is seen in the TAC experimental data. The dashed line corresponds to the growth response obtained by stimulating the model with the maximum network input stretch (1), and the possible growth obtained when using the full range of network stretch inputs (0-1) is shown in the shaded region. Data are shown as mass fold change ratio relative to control ± standard deviation of ratio. b) When each transmural layer (subendocardium, midendocardium, midwall, midepicardium, and subepicardium; solid lines) of the FEM is coupled to its own representative network, the inner layers initially grow more rapidly, while the outer layers experience sustained growth. However, the average behavior (dashed line) is similar to that of the single-network simulation shown in (a). Data are shown as mass fold change ratio relative to control ± standard deviation of the ratio, c) Finite-element model short-axis cross-sections show volume ratios at end diastole for baseline (pre-growth) and after two weeks of TAC. Baseline outline is shown for clarity
Simulations of genetic and pharmacologic interventions for TAC
Finally, we simulated the effect of several interventions for attenuating the hypertrophy induced by TAC: a transgenic Gq-coupled receptor inhibitor (GqI) overexpression model, an endogenous norepinephrine genetic KO (NE KO), an angiotensin receptor blocker (ARB), and a β-adrenergic receptor blocker (β-blocker). We ran each of the intervention models using appropriate modifications to the signaling network model and the same mechanical loading conditions as TAC. As shown in Figure 7a–c, all interventions attenuated hypertrophy compared to TAC and to an extent that was broadly consistent with reported data (Akhter et al. 1998; Rapacciuolo et al. 2001; Rockman et al. 1994; Li et al. 2010; Wang et al. 2016; Patrizio et al. 2007). The differences in growth attenuation among the interventions can be attributed to the influence of the target nodes on the network. For example, removing activation of the Gαq11 node decreases the effect of the activation of inputs AngII, ET-1, and NE, while removing the NE node does not directly reduce the influence of the other hormonal inputs (Figure 1). Similarly, blocking the AT1R node prevents activation of JAK and Gαq11 by AngII, while blocking the βAR node only partly reduces the influence of NE, because NE also activates the αAR node, thus bypassing the block.
Fig. 7.
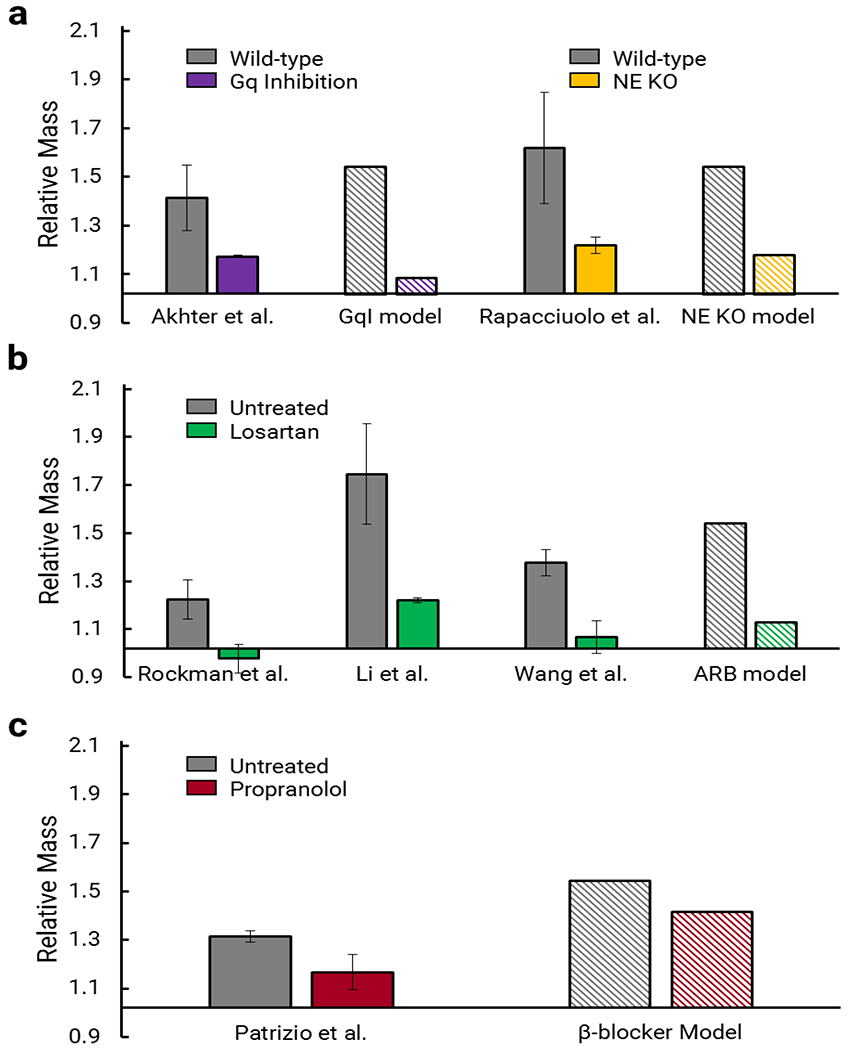
Simulations of transverse aortic constriction (TAC) interventions compared to experimental data. The multiscale model simulations of TAC interventions attenuate growth at two weeks in a manner consistent with experimental trends for a) genetic interventions GqI (Akhter et al. 1998) and NE KO (Rapacciuolo et al. 2001), b) ARB therapy (Rockman et al. 1994; Li et al. 2010; Wang et al. 2016) and c) β-blocker therapy (Patrizio et al. 2007),respectively. Data are shown as mass fold change ratio relative to control ± standard deviation of ratio
DISCUSSION
We present here a multiscale model of cardiac hypertrophy that connects a detailed model of intracellular cardiomyocyte signaling with a finite-element model of organ-level mechanics. We simulated concentric growth due to isoproterenol infusion, transverse aortic constriction (TAC), and TAC plus genetic or pharmacologic intervention, and our model captured the experimental trends for all conditions reasonably well (Figures 5–7). The most striking finding from our study was that despite the fact that we attempted to simulate realistic levels of elevated stretch and hormonal stimulation associated with TAC, the hormonal inputs were responsible for the majority of the growth predicted by the multiscale model (Figure 6a).
In order to better understand this result, we explored the impact of each choice we made when constructing the model that could affect the relative impact of stretch vs. hormonal inputs in driving hypertrophy in the multiscale model. The most important choice was how to map physical variables such as stretch and circulating hormone concentrations into normalized (0-1) inputs in the signaling network model. We increased the level of several hormones as part of our simulation of TAC based on experimental data showing that they are elevated (Swynghedauw 1999; Lorell and Carabello 2000; Yamazaki et al. 1995, 1996; Schunkert et al. 1990; Sugden 1999; Izumo, Nadal-Ginard, and Mahdavi 1988; Rapacciuolo et al. 2001; Lindpaintner, Lund, and Schmid 1987; Yoshida et al. 2015; Kamal et al. 2014; Liao et al. 2003). We chose to increase them to levels which would trigger a half-maximal hypertrophy response in the network model, based on data showing that even after TAC animals mount a significant additional hemodynamic response to agonists of some of these pathways (Choi et al. 1997). Experimental data has shown that levels of these circulating hormones will remain elevated and even increase over time as hypertrophy progresses towards heart failure (Sergeeva and Christoffels 2013; Iwanaga et al. 2001). However, some receptors, such as the β-adrenergic and AT1 receptors, have been shown to be downregulated due to long-standing hypertrophy (Lorell and Carabello 2000). While we did not include receptor desensitization in our simulations, this is an effect that could be incorporated in future versions of these multiscale models looking at longer time periods of hypertrophy. We tested higher and lower levels of hormone activation but found that these activation levels failed to properly capture the growth attenuation of all TAC interventions considered here. If we wanted to more precisely match the intervention data shown here, or to match a wider array of experimental data, we could certainly tune each of the individual hormonal input levels further in our TAC simulation, but given the high variability in the available experimental data on both hormone levels and growth following TAC, we did not feel that additional fine-tuning could be appropriately supported by data.
With regard to mapping stretch, we assumed that aortic constriction induced an initial stretch that – if maintained – would also induce half-maximal hypertrophy, based on data showing that the TAC models used in most of the studies simulated here fell in the middle of the range of severities of TAC capable of induce graded hypertrophic responses (Richards et al. 2019). However, due to the nature of the volumetric growth framework, as growth progressed it reduced elastic stretches in the finite-element model, returning the stretch input transmitted to the network model to its baseline (homeostatic) value within the first 2-3 days of simulated time. To determine if this response depended on the specific choice of stretch mapping, we ran additional simulations where strains during aortic constriction were mapped to network stretch inputs ranging from 0 to 1, five times the value normally required to achieve maximal growth in the network, and found that none of these mappings could produce even half the growth observed in our TAC simulation (shaded region, Figure 6a). As discussed further below, this aspect of the volumetric growth modeling approach may not be the best representation of the underlying biology, and the model could certainly be altered in various ways to prolong or accentuate the effects of mechanical stretch on growth. However, the fact that multiple interventions that disrupt hormonal signaling can nearly abolish TAC-induced hypertrophy experimentally (Figure 7) suggests that the balance between mechanically- and hormonally-driven hypertrophy in our multiscale model of TAC is reasonable.
Incorporating hormonal effects into a growth framework has significant advantages over using a phenomenologic growth law driven by mechanics alone. Our multiscale model separates the effects of mechanical overload from hormonal changes, and it uses a fundamentally different approach for predicting growth than traditional phenomenologic laws. In our model, the amount of growth that occurs depends on the signaling network intermediate nodes reaching new steady-state levels. In contrast, the phenomenologic laws drive growth based on the differences between a mechanical stimulus such as stress or strain and its homeostatic value, so that the growth will only increase until the homeostatic value is reached. Both approaches can be used to capture the growth due to an initial mechanical perturbation, such as pressure overload (Kerckhoffs, Omens, and McCulloch 2012; Lin and Taber 1995; Göktepe et al. 2010; Taber 1998; Arts et al. 2005), and the phenomenologic laws can be parameterized to account for elevated hormones. However, any subsequent changes to the hormone levels or addition of drugs would require re-fitting the phenomenologic laws. Accounting for hormones in addition to mechanics through their known signaling pathways has the potential to extend the predictive capabilities of the multiscale model. Incorporating hormonal and pharmacologic effects will likely be necessary for properly predicting cardiac hypertrophy in individual patients, who receive individualized drug regimens for their specific conditions. Additionally, our multiscale model may prove useful in identifying new therapeutic targets or intervention strategies for attenuating growth, be it for concentric hypertrophy more broadly or for patient-specific situations.
We simulated growth in our multiscale model using a volumetric growth framework. This choice assumes that the reference state for growth remains constant throughout the simulation and that the stress depends solely on the elastic deformation required to enforce compatibility in the grown tissue. In order to implement this framework in the multiscale model, we mapped the network cell area output – a single measure of mass increase – to the determinant of the growth deformation tensor Fgrowth, assuming that changes in cell area for the in vivo model correspond to changes in cell volume. However, other growth frameworks, such as the constrained mixture approach, could also be used to relate the predicted network hypertrophy to organ-level changes. Constrained mixture approaches implement growth via turnover of individual constituents within a single material, allowing for the reference state to evolve and accounting for differences in loading for each constituent (Humphrey and Rajagopal 2002). The hypertrophy network model also outputs gene expression levels for specific proteins associated with sarcomere formation and contractile function: α-myosin heavy chain (aMHC) and β-myosin heavy chain (bMHC), which form the thick filaments of sarcomeres; sarcoplasmic reticulum ATPase (SERCA), a critical channel involved in calcium cycling; and skeletal α-actin (sACT), which contributes to thin filament formation. These outputs could be incorporated into a constrained mixture growth approach either directly or within a function that determines addition of new constituents.
While our multiscale model provides a new method for predicting concentric growth, it currently has some limitations. First, the simulations included in this study assume spatially uniform concentric growth throughout the left ventricle. The multiscale model framework can be modified to incorporate different signaling networks with different signaling states for each individual finite element, but doing so would lead to substantially longer computation times. We ran additional simulations with separate signaling networks for each of the five transmural layers of the FEM and found that, while there are differences in the layer-specific growth, the average growth time course was comparable to that of the single-network simulation. Additionally, the data used for tuning and validation in our study corresponds to fold changes in mass but does not include regional differences in growth. Second, the current network model cell area output can be interpreted as an increase in mass, but it does not account for directional differences in growth. We assumed that all growth would occur in the radial direction in our simulations of conditions that cause concentric hypertrophy. Thus, the multiscale model presented here could not correctly capture both concentric growth as demonstrated here and eccentric growth patterns as observed during volume overload. More work is needed to understand the signaling events controlling myocyte shape and incorporate them into a multiscale model that can account for both thickening and lengthening of muscle fibers. Lastly, the model presented here mixes information across species: mechanical loading was simulated using an average canine left ventricle, the network model was constructed primarily from data on cultured neonatal rat ventricular myocytes, and comparison data comes from mouse experiments. While subsequent versions of the model could use a finite-element model based on a mouse left ventricle, the results from this study show that hormones are more important in reproducing observed growth following TAC than mechanics, indicating that the exact choice of geometry is probably not critical for matching qualitative trends such as whether an intervention will attenuate or accentuate hypertrophy. In spite of these limitations, our multiscale model demonstrates a promising strategy for predicting cardiac hypertrophy by integrating mechanics and biology.
ACKNOWLEDGEMENTS
This study was funded by the National Institutes of Health (NIH) grant U01 HL127654 and American Heart Association (AHA) grant 16PRE30250007.
Footnotes
DECLARATIONS
Conflicts of interest: None
Ethics approval: Not applicable
Consent to participate: Not applicable
Consent for publication: Not applicable
Availability of data and material: Not applicable
Code availability: FEBio Growth Plugin code will be uploaded to the FEBio Plugins page (https://febio.org/plugins/) and to SimTK (https://simtk.org/) when the manuscript is published; Network model can be run independently through Netflux (https://github.com/saucermanlab/Netflux).
Contributor Information
Ana C. Estrada, University of Virginia, Charlottesville, Virginia, USA.
Kyoko Yoshida, University of Virginia, Charlottesville, Virginia, USA.
Jeffrey J. Saucerman, University of Virginia, Charlottesville, Virginia, USA.
Jeffrey W. Holmes, University of Virginia, Charlottesville, Virginia, USA.
REFERENCES
- Akhter Shahab A., Luttrell Louis M., Rockman Howard A., Iaccarino Guido, Lefkowitz Robert J., and Koch Walter J.. 1998. “Targeting the Receptor-G(q) Interface to Inhibit in Vivo Pressure Overload Myocardial Hypertrophy.” Science 280 (5363): 574–77. 10.1126/science.280.5363.574. [DOI] [PubMed] [Google Scholar]
- Allwood Melissa A, Kinobe Robert T, Ballantyne Laurel, Romanova Nadya, Melo Luis G, Ward Christopher A, Brunt Keith R, and Simpson Jeremy A. 2014. “Heme Oxygenase-1 Overexpression Exacerbates Heart Failure with Aging and Pressure Overload but Is Protective against Isoproterenol-Induced Cardiomyopathy in Mice.” Cardiovascular Pathology: The Official Journal of the Society for Cardiovascular Pathology 23 (4): 231–37. 10.1016/j.carpath.2014.03.007. [DOI] [PubMed] [Google Scholar]
- Arts Theo, Delhaas Tammo, Bovendeerd Peter, Verbeek Xander, and Prinzen Frits W.. 2005. “Adaptation to Mechanical Load Determines Shape and Properties of Heart and Circulation: The CircAdapt Model.” American Journal of Physiology - Heart and Circulatory Physiology 288 (4 57-4). 10.1152/ajpheart.00444.2004. [DOI] [PubMed] [Google Scholar]
- Benjamin Emelia J., Virani Salim S., Callaway Clifton W., Chang Alexander R., Cheng Susan, Chiuve Stephanie E., Cushman Mary, et al. 2018. Heart Disease and Stroke Statistics—2018 Update: A Report From the American Heart Association. Circulation. 10.1161/CIR.0000000000000558. [DOI] [PubMed] [Google Scholar]
- Brooks Wesley W, and Conrad Chester H. 2009. “Isoproterenol-Induced Myocardial Injury and Diastolic Dysfunction in Mice: Structural and Functional Correlates.” Comparative Medicine 59 (4): 339–43. http://www.ncbi.nlm.nih.gov/pubmed/19712573. [PMC free article] [PubMed] [Google Scholar]
- Bruno RM, and Taddei S. 2014. “Renal Denervation and Regression of Left Ventricular Hypertrophy.” European Heart Journal 35 (33): 2205–7. 10.1093/eurheartj/ehu127. [DOI] [PubMed] [Google Scholar]
- Choi Dong Ju, Koch Walter J., Hunter John J., and Rockman Howard A.. 1997. “Mechanism of β-Adrenergic Receptor Desensitization in Cardiac Hypertrophy Is Increased β-Adrenergic Receptor Kinase.” Journal of Biological Chemistry 272 (27): 17223–29. 10.1074/jbc.272.27.17223. [DOI] [PubMed] [Google Scholar]
- Clarke Samantha A., Goodman Norman C., Ailawadi Gorav, and Holmes Jeffrey W.. 2015. “Effect of Scar Compaction on the Therapeutic Efficacy of Anisotropic Reinforcement Following Myocardial Infarction in the Dog.” Journal of Cardiovascular Translational Research 8 (6): 353–61. 10.1007/s12265-015-9637-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuspidi Cesare, Vaccarella Alvaro, Negri Francesca, and Sala Carla. 2010. “Resistant Hypertension and Left Ventricular Hypertrophy: An Overview.” Journal of the American Society of Hypertension 4 (6): 319–24. 10.1016/J.JASH.2010.10.003. [DOI] [PubMed] [Google Scholar]
- Drews Oliver, Tsukamoto Osamu, Liem David, Streicher John, Wang Yibin, and Ping Peipei. 2010. “Differential Regulation of Proteasome Function in Isoproterenol-Induced Cardiac Hypertrophy.” Circulation Research 107 (9): 1094–1101. 10.1161/CIRCRESAHA.110.222364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estrada Ana Cristina, Yoshida Kyoko, Clarke Samantha A., and Holmes Jeffrey W.. 2020. “Longitudinal Reinforcement of Acute Myocardial Infarcts Improves Function by Transmurally Redistributing Stretch and Stress.” Journal of Biomechanical Engineering 142 (2). 10.1115/1.4044030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank Deborah U., Sutcliffe Matthew D., and Saucerman Jeffrey J.. 2018. “Network-Based Predictions of in Vivo Cardiac Hypertrophy.” Journal of Molecular and Cellular Cardiology 121 (August): 180–89. 10.1016/j.yjmcc.2018.07.243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galindo Cristi L., Skinner Michael A., Errami Mounir, Danielle Olson L, Watson David A., Li Jing, McCormick John F., et al. 2009. “Transcriptional Profile of Isoproterenol-Induced Cardiomyopathy and Comparison to Exercise-Induced Cardiac Hypertrophy and Human Cardiac Failure.” BMC Physiology 9 (1): 23 10.1186/1472-6793-9-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelsomino Sandro, Frassani Romeo, Morocutti Giorgio, Nucifora Rosario, Paolo Da Col Giorgio Minen, Morelli Angelo, and Livi Ugolino. 2001. “Time Course of Left Ventricular Remodeling after Stentless Aortic Valve Replacement.” American Heart Journal 142 (3): 556–62. 10.1067/mhj.2001.117777. [DOI] [PubMed] [Google Scholar]
- Göktepe Serdar, Oscar John Abilez Kevin Kit Parker, and Kuhl Ellen. 2010. “A Multiscale Model for Eccentric and Concentric Cardiac Growth through Sarcomerogenesis.” Journal of Theoretical Biology 265 (3): 433–42. 10.1016/j.jtbi.2010.04.023. [DOI] [PubMed] [Google Scholar]
- Grossman W, Jones D, and McLaurin LP. 1975. “Wall Stress and Patterns of Hypertrophy in the Human Left Ventricle.” Journal of Clinical Investigation 56 (1): 56–64. 10.1172/JCI108079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey JD, and Rajagopal KR. 2002. “A Constrained Mixture Model for Growth and Remodeling in Soft Tissues.” Mathematical Models and Methods in Applied Sciences 12 (3): 407–30. 10.1142/S0218202502001714. [DOI] [Google Scholar]
- Huss Janice M., Imahashi Ken-ichi, Du four Catherine R., Weinheimer Carla J., Courtois Michael, Kovacs Atilla, Giguère Vincent, Murphy Elizabeth, and Kelly Daniel P.. 2007. “The Nuclear Receptor ERRα Is Required for the Bioenergetic and Functional Adaptation to Cardiac Pressure Overload.” Cell Metabolism 6 (1): 25–37. 10.1016/j.cmet.2007.06.005. [DOI] [PubMed] [Google Scholar]
- Iwanaga Yoshitaka, Kihara Yasuki, Inagaki Koichi, Onozawa Yoko, Yoneda Takeshi, Kataoka Kazuaki, and Sasayama Shigetake. 2001. “Differential Effects of Angiotensin II Versus Endothelin-1 Inhibitions in Hypertrophic Left Ventricular Myocardium During Transition to Heart Failure.” Circulation 104 (5): 606–12. 10.1161/hc3101.092201. [DOI] [PubMed] [Google Scholar]
- Izumo S, Nadal-Ginard B, and Mahdavi V. 1988. “Protooncogene Induction and Reprogramming of Cardiac Gene Expression Produced by Pressure Overload.” Proceedings of the National Academy of Sciences of the United States of America 85 (2): 339–43. 10.1073/pnas.85.2.339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaehnig Eric J., Heidt Analeah B., Greene Stephanie B., Cornelissen Ivo, and Black Brian L.. 2006. “Increased Susceptibility to Isoproterenol-Induced Cardiac Hypertrophy and Impaired Weight Gain in Mice Lacking the Histidine-Rich Calcium-Binding Protein.” Molecular and Cellular Biology 26 (24): 9315–26. 10.1128/MCB.00482-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamal Fadia A., Mickelsen Deanne M., Wegman Katherine M., Travers Joshua G., Moalem Jacob, Hammes Stephen R., Smrcka Alan V., and Blaxall Burns C.. 2014. “Simultaneous Adrenal and Cardiac G-Protein-Coupled Receptor-Gβγ Inhibition Halts Heart Failure Progression.” Journal of the American College of Cardiology 63 (23): 2549–57. 10.1016/j.jacc.2014.02.587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawel-Boehm Nadine, Kronmal Richard, Eng John, Folsom Aaron, Burke Gregory, Jeffrey Carr J, Shea Steven, Lima João A.C., and Bluemke David A.. 2019. “Left Ventricular Mass at MRI and Long-Term Risk of Cardiovascular Events: The Multi-Ethnic Study of Atherosclerosis (MESA).” Radiology 293 (1): 107–14. 10.1148/radiol.2019182871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerckhoffs Roy C. P., Omens Jeffrey H., and McCulloch Andrew D.. 2012. “A Single Strain-Based Growth Law Predicts Concentric and Eccentric Cardiac Growth during Pressure and Volume Overload.” Mechanics Research Communications 42: 40–50. 10.1016/j.mechrescom.2011.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Lei, Zhou Ning, Gong Hui, Wu Jian, Lin Li, Komuro Issei, Ge Junbo, and Zou Yunzeng. 2010. “Comparison of Angiotensin II Type 1-Receptor Blockers to Regress Pressure Overload-Induced Cardiac Hypertrophy in Mice.” Hypertension Research 33 (12): 1289–97. 10.1038/hr.2010.182. [DOI] [PubMed] [Google Scholar]
- Liao Yulin, Takashima Seiji, Asano Yoshihiro, Asakura Masanori, Ogai Akiko, Shintani Yasunori, Minamino Tetsuo, et al. 2003. “Activation of Adenosine A1 Receptor Attenuates Cardiac Hypertrophy and Prevents Heart Failure in Murine Left Ventricular Pressure-Overload Model.” Circulation Research 93 (8): 759–66. 10.1161/01.RES.0000094744.88220.62. [DOI] [PubMed] [Google Scholar]
- Lin I-En, and Taber LA. 1995. “A Model for Stress-Induced Growth in the Developing Heart.” Journal of Biomechanical Engineering 117 (3): 343–49. 10.1115/1.2794190. [DOI] [PubMed] [Google Scholar]
- Lindpaintner K, Lund DD, and Schmid PG. 1987. “Effects of Chronic Progressive Myocardial Hypertrophy on Indexes of Cardiac Autonomic Innervation.” Circulation Research 61 (1): 55–62. 10.1161/01.RES.61.1.55. [DOI] [PubMed] [Google Scholar]
- Ling Haiyun, Zhang Tong, Pereira Laetitia, Christopher Kable Means Hongqiang Cheng, Gu Yusu, Dalton Nancy D., et al. 2009. “Requirement for Ca2+/Calmodulin-Dependent Kinase II in the Transition from Pressure Overload-Induced Cardiac Hypertrophy to Heart Failure in Mice.” Journal of Clinical Investigation 119 (5): 1230–40. 10.1172/JCI38022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorell Beverly H., and Carabello Blase A.. 2000. “Left Ventricular Hypertrophy.” Circulation 102 (4): 470–79. 10.1161/01.CIR.102.4.470. [DOI] [PubMed] [Google Scholar]
- Monrad ES, Hess ΟM, Murakami T, Nonogi H, Corin WJ, and Krayenbuehl ΗP. 1988. “Time Course of Regression of Left Ventricular Hypertrophy after Aortic Valve Replacement.” Circulation 77 (6): 1345–55. 10.1161/01.cir.77.6.1345. [DOI] [PubMed] [Google Scholar]
- Nishimura Rick A., Otto Catherine M., Bonow Robert O., Carabello Blase A., Erwin John P., Guyton Robert A., O’Gara Patrick T., et al. 2014. “2014 AHA/ACC Guideline for the Management of Patients with Valvular Heart Disease: Executive Summary: A Report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines.” Journal of the American College of Cardiology 63 (22): 2438–88. 10.1016/j.jacc.2014.02.537. [DOI] [PubMed] [Google Scholar]
- Otto Catherine M. 2006. “Valvular Aortic Stenosis. Disease Severity and Timing of Intervention.” Journal of the American College of Cardiology 47 (11): 2141–51. 10.1016/j.jacc.2006.03.002. [DOI] [PubMed] [Google Scholar]
- Patrizio Μ, Musumeci M, Stati T, Fasanaro P, Palazzesi S, Catalano L, and Marano G. 2007. “Propranolol Causes a Paradoxical Enhancement of Cardiomyocyte Foetal Gene Response to Hypertrophic Stimuli.” British Journal of Pharmacology 152 (2): 216–22. 10.1038/sj.bjp.0707350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rapacciuolo Antonio, Esposito Giovanni, Caron Kathleen, Mao Lan, Thomas Steven A., and Rockman Howard A.. 2001. “Important Role of Endogenous Norepinephrine and Epinephrine in the Development of in Vivo Pressure-Overload Cardiac Hypertrophy.” Journal of the American College of Cardiology 38 (3): 876–82. 10.1016/S0735-1097(01)01433-4. [DOI] [PubMed] [Google Scholar]
- Richards Daniel A., Aronovitz Mark J., Calamaras Timothy D., Tam Kelly, Martin Gregory L., Liu Peiwen, Bowditch Heather K., Zhang Phyllis, Huggins Gordon S., and Blanton Robert M.. 2019. “Distinct Phenotypes Induced by Three Degrees of Transverse Aortic Constriction in Mice.” Scientific Reports 9 (1): 1–15. 10.1038/s41598-019-42209-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockman HA, Wachhorst SP, Mao L, and Ross J. 1994. “ANG II Receptor Blockade Prevents Ventricular Hypertrophy and ANF Gene Expression with Pressure Overload in Mice.” The American Journal of Physiology 266 (6 Pt 2): H2468–75. 10.1152/ajpheart.1994.266.6.H2468. [DOI] [PubMed] [Google Scholar]
- Rodriguez EK, Hoger A, and McCulloch AD. 1994. “Stress-Dependent Finite-Growth in Soft Elastic Tissues.” Journal of Biomechanics 27 (4): 455–67. [DOI] [PubMed] [Google Scholar]
- Ryall Karen A., Holland David O., Delaney Kyle A., Kraeutler Matthew J., Parker Audrey J., and Saucerman Jeffrey J.. 2012. “Network Reconstruction and Systems Analysis of Cardiac Myocyte Hypertrophy Signaling.” The Journal of Biological Chemistry 287 (50): 42259–68. 10.1074/jbc.M112.382937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryu Yuhee, Li Jin, Hae Jin Kee, Zhe Hao Piao, Jae Yeong Cho, Gwi Ran Kim, Sin Young Choi, Ming Quan Lin, and Myung Ho Jeong. 2016. “Gallic Acid Prevents Isoproterenol-Induced Cardiac Hypertrophy and Fibrosis through Regulation of JNK2 Signaling and Smad3 Binding Activity.” Scientific Reports 6 (1): 34790 10.1038/srep34790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schunkert Heribert, Dzau Victor J., Shiow Shin Tang, Hirsch Alan T., Apstein Carl S., and Lorell Beverly H.. 1990. “Increased Rat Cardiac Angiotensin Converting Enzyme Activity and MRNA Expression in Pressure Overload Left Ventricular Hypertrophy: Effects on Coronary Resistance, Contractility, and Relaxation.” Journal of Clinical Investigation 86 (6): 1913–20. 10.1172/JCI114924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sergeeva Irina A., and Christoffels Vincent M.. 2013. “Regulation of Expression of Atrial and Brain Natriuretic Peptide, Biomarkers for Heart Development and Disease” Biochimica et Biophysica Acta - Molecular Basis of Disease. Elsevier; 10.1016/j.bbadis.2013.07.003. [DOI] [PubMed] [Google Scholar]
- Sucharov Carmen C., Hijmans Jamie G., Sobus Rebecca D., Melhado William F. A., Miyamoto Shelley D., and Stauffer Brian L.. 2013. “β-Adrenergic Receptor Antagonism in Mice: A Model for Pediatric Heart Disease.” Journal of Applied Physiology (Bethesda, Md. : 1985) 115 (7): 979–87. 10.1152/japplphysiol.00627.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugden Peter H. 1999. “Signaling in Myocardial Hypertrophy: Life after Calcineurin?” Circulation Research 84 (6): 633–46. 10.1161/01.RES.84.6.633. [DOI] [PubMed] [Google Scholar]
- Swynghedauw Bernard. 1999. “Molecular Mechanisms of Myocardial Remodeling.” Physiological Reviews 79 (1): 215–62. 10.1152/physrev.1999.79.1.215. [DOI] [PubMed] [Google Scholar]
- Szymanski Michael W., and Singh Davinder P.. 2019. Isoproterenol StatPearls. StatPearls Publishing, http://www.ncbi.nlm.nih.gov/pubmed/30252298. [PubMed] [Google Scholar]
- Taber Larry A. 1998. “Biomechanical Growth Laws for Muscle Tissue.” Journal of Theoretical Biology, 10.1006/jtbi.1997.0618. [DOI] [PubMed] [Google Scholar]
- Tshori Sagi, Gilon Dan, Beeri Ronen, Nechushtan Hovav, Kaluzhny Dmitry, Pikarsky Eli, and Razin Ehud. 2006. “Transcription Factor MITF Regulates Cardiac Growth and Hypertrophy.” The Journal of Clinical Investigation 116 (10): 2673–81. 10.1172/JCI27643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuerdi Nuerbiye, Xu Lu, Zhu Baoling, Chen Cong, Cao Yini, Wang Yunan, Zhang Qiang, Li Zijian, and Qi Rong. 2016. “Preventive Effects of Simvastatin Nanoliposome on Isoproterenol-Induced Cardiac Remodeling in Mice.” Nanomedicine: Nanotechnology, Biology, and Medicine 12 (7): 1899–1907. 10.1016/j.nano.2016.05.002. [DOI] [PubMed] [Google Scholar]
- Wang Xingxu, Ye Yong, Gong Hui, Wu Jian, Yuan Jie, Wang Shijun, Yin Peipei, et al. 2016. “The Effects of Different Angiotensin II Type 1 Receptor Blockers on the Regulation of the ACE-AngII-ATl and ACE2-Ang(1–7)-Mas Axes in Pressure Overload-Induced Cardiac Remodeling in Male Mice.” Journal of Molecular and Cellular Cardiology 97 (August): 180–90. 10.1016/j.yjmcc.2016.05.012. [DOI] [PubMed] [Google Scholar]
- Waters Steve B., Diak Douglass M., Zuckermann Matthew, Goldspink Paul H., Leoni Lara, and Roman Brian B.. 2013. “Genetic Background Influences Adaptation to Cardiac Hypertrophy and Ca2+ Handling Gene Expression.” Frontiers in Physiology 4: 11 10.3389/fphys.2013.00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Windt LJ De HW. Lim OF. Bueno Q. Liang U. Delling JC. Braz BJ. Glascock, et al. 2001. “Targeted Inhibition of Calcineurin Attenuates Cardiac Hypertrophy in Vivo.” Proceedings of the National Academy of Sciences 98 (6): 3322–27. 10.1073/pnas.031371998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witzenburg Colleen M., and Holmes Jeffrey W.. 2018. “Predicting the Time Course of Ventricular Dilation and Thickening Using a Rapid Compartmental Model.” Journal of Cardiovascular Translational Research 11 (2): 109–22. 10.1007/s12265-018-9793-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang Yang K. 2011. “Compartmentalization of β-Adrenergic Signals in Cardiomyocytes.” Circulation Research 109 (2): 231–44. 10.1161/CIRCRESAHA.110.231340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamazaki Tsutomu, Komuro Issei, Kudoh Sumiyo, Zou Yunzeng, Shiojima Ichiro,Hiroi Yukio, Mizuno Takehiko, et al. 1996. “Endothelin-1 Is Involved in Mechanical Stress-Induced Cardiomyocyte Hypertrophy.” Journal of Biological Chemistry 271 (6): 3221–28. 10.1074/jbc.271.6.3221. [DOI] [PubMed] [Google Scholar]
- Yamazaki Tsutomu, Komuro Issei, Kudoh Sumiyo, Zou Yunzeng, Shiojima Ichiro, Mizuno Takehiko, Takano Hiroyuki, et al. 1995. “Angiotensin II Partly Mediates Mechanical Stress–Induced Cardiac Hypertrophy.” Circulation Research 77 (2): 258–65. 10.1161/01.RES.77.2.258. [DOI] [PubMed] [Google Scholar]
- Yoshida Yohko, Shimizu Ippei, Katsuumi Goro, Jiao Shuang, Suda Masayoshi, Hayashi Yuka, and Minamino Tohru. 2015. “Journal of Molecular and Cellular Cardiology P53-Induced in F1 Ammation Exacerbates Cardiac Dysfunction during Pressure Overload” 85: 183–98. [DOI] [PubMed] [Google Scholar]
- Zhang Yaxing, Xu Jingting, Long Zhiyuan, Wang Chen, Wang Ling, Sun Peng, Li Ping, and Wang Tinghuai. 2016. “Hydrogen (H2) Inhibits Isoproterenol-Induced Cardiac Hypertrophy via Antioxidative Pathways.” Frontiers in Pharmacology 7 (October): 392 10.3389/fphar.2016.00392. [DOI] [PMC free article] [PubMed] [Google Scholar]


