Extracting the dynamics of behavior in sensory decision-making experiments

Abstract

Decision-making strategies evolve during training, and can continue to vary even in well-trained animals. However, studies of sensory decision-making tend to characterize behavior in terms of a fixed psychometric function, fit after training is complete. Here we present PsyTrack, a flexible method for inferring the trajectory of sensory decision-making strategies from choice data. We apply PsyTrack to training data from mice, rats, and human subjects learning to perform auditory and visual decision-making tasks, and show that it successfully captures trial-to-trial fluctuations in the weighting of sensory stimuli, bias, and task-irrelevant covariates such as choice and stimulus history. This analysis reveals dramatic differences in learning across mice, and rapid adaptation to changes in task statistics. PsyTrack scales easily to large datasets and offers a powerful tool for quantifying time-varying behavior in a wide variety of animals and tasks.

eTOC:

Roy et al. present a method for inferring the time course of behavioral strategies in sensory decision-making tasks, which they use to analyze how behavior evolves during training in rats, mice, & humans.

Introduction

The behavior of well-trained animals in carefully designed tasks is a pillar of modern neuroscience research (Carandini, 2012; Krakauer et al., 2017; Niv, 2020). In sensory decision-making experiments, animals must learn to integrate relevant sensory signals while ignoring a large number task-irrelevant covariates (Gold and Shadlen, 2007; Brunton et al., 2013; Hanks and Summerfield, 2017). However, the sensory decision-making literature has tended to focus on characterizing the decision-making behavior of fully trained animals in terms of fixed strategies, such as signal detection theory (Green and Swets, 1966) or the drift-diffusion model (Ratcliff and Rouder, 1998). This approach neglects the dynamics of decision-making behavior, which may be essential for understanding learning, exploration, adaptation to task statistics, and other forms of non-stationary behavior (Usher et al., 2013; Pisupati et al., 2019; Brunton et al., 2013; Piet et al., 2018).

Characterizing the dynamics of sensory decision-making behavior is challenging due to the fact that decisions may depend on a large number of task covariates, including the sensory stimuli, an animal’s choice bias, past stimuli, past choices, and past rewards. Detecting and disentangling the influence of these variables on a single choice is an ill-posed problem due to fact that we have many unknowns (the weights on each variable) and a single observation (the animal’s choice). As a result, it is common to assume that an animal’s decision-making rule, or strategy, is fixed over some reasonably large number of trials. However, this assumption is at odds with the fact that decision-making strategies may change on a trial-to-trial basis, and may evolve rapidly during training when animals are learning a new task (Carandini and Churchland, 2013).

Understanding what drives changes in decision-making behavior has long been the domain of reinforcement learning (RL) (Sutton and Barto, 2018; Sutton, 1988). In this paradigm, behavioral dynamics are examined through the lens of the rewards and punishments that may accompany each decision. RL models are normative, meaning they describe changes in behavior as resulting from the optimization of some measure of future reward (Niv, 2009; Daw et al., 2011; Niv et al., 2015; Samejima et al., 2004; Daw and Courville, 2008; Ashwood et al., 2020). By contrast, descriptive modeling approaches seek only to infer time-varying changes in strategy from an animal’s observed choices, without attributing such changes to any notion of optimality. Previous studies in this tradition include Smith et al. (2004); Suzuki and Brown (2005), which focused on identifying the time at which an untrained animal had begun to learn. Other work from Kattner et al. (2017) extended the standard psychometric curve to allow its parameters to vary continuously across trials.

Here we present PsyTrack, a descriptive modeling approach for inferring the trajectory of an animal’s decision-making strategy across trials, building on ideas developed in (Bak et al., 2016; Roy et al., 2018a). Our model describes decision-making behavior at the resolution of single trials, allowing for visualization and analysis of psychophysical weight trajectories both during and after training. Moreover, it contains interpretable hyperparameters governing the rates of change of different weights, allowing us to quantify how rapidly different weights evolve between trials and between sessions. We apply PsyTrack to behavioral data collected during training in two different experiments (auditory and visual decision-making) and three different species (mouse, rat, and human). After validating the method on simulated data, we use it to analyze an example mouse that learns to track block structure in a non-stationary visual decision-making task (IBL et al., 2020). We then examine the influence of trial-history on rat (but not human) decisions during early training on an auditory parametric working memory task (Akrami et al., 2018). To facilitate application to new datasets, we provide a publicly available software implementation in Python, along with a Google Colab notebook that precisely reproduces all figures in this paper directly from publicly available raw data (see STAR Methods).

Results

Our primary contribution is a method for characterizing the evolution of animal decision-making behavior on a trial-to-trial basis. Our approach consists of a dynamic Bernoulli generalized linear model (GLM), defined by a set of smoothly evolving psychophysical weights. These weights characterize the animal’s decision-making strategy at each trial in terms of a linear combination of available task variables. The larger the magnitude of a particular weight, the more the animal’s decision relies on the corresponding task variable. Learning to perform a new task therefore involves driving the weights on “relevant” variables (e.g., sensory stimuli) to large values, while driving weights on irrelevant variables (e.g., bias, choice history) toward zero. However, classical modeling approaches require that weights remain constant over long blocks of trials, which precludes tracking of trial-to-trial behavioral changes that arise during learning and in non-stationary task environments. Below, we describe our modeling approach in more detail.

Dynamic Psychophysical Model for Decision-Making Tasks

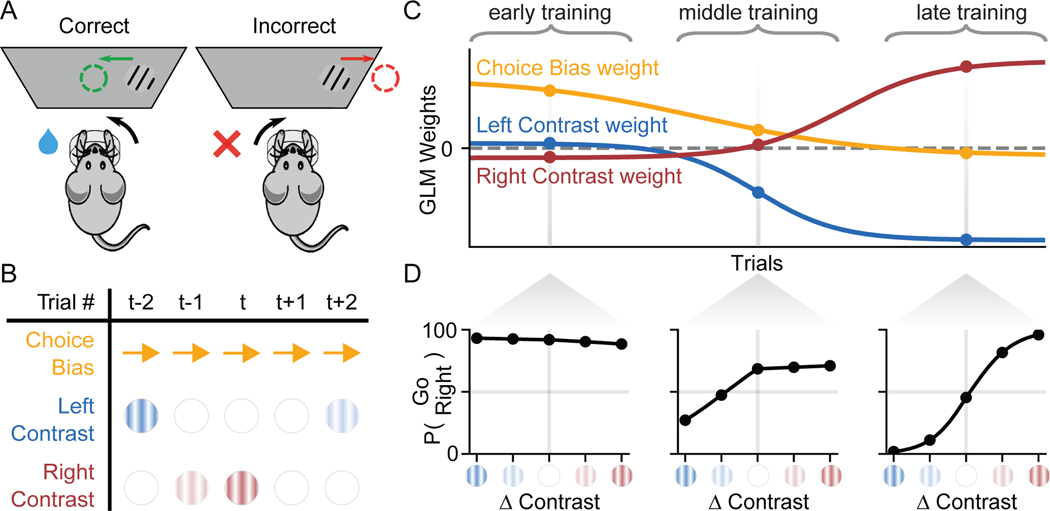
Although PsyTrack is applicable to any binary decision-making task, for concreteness we introduce our method in the context of the task used by the International Brain Lab (IBL) (illustrated in Figure 1A) (IBL et al., 2020). In this visual detection task, a mouse is positioned in front of a screen and a wheel. On each trial, a sinusoidal grating (with contrast values between 0 and 100%) appears on either the left or right side of the screen. The mouse must report the side of the grating by turning the wheel (left or right) in order to receive a water reward (see STAR Methods for more details).

Figure 1:

Schematic of Binary Decision-Making Task and Dynamic Psychophysical Model

(A) A schematic of the IBL sensory decision-making task. On each trial, a sinusoidal grating (with contrast values between 0 and 100%) appears on either the left or right side of the screen. Mice must report the side of the grating by turning a wheel (left or right) in order to receive a water reward (see ar]STAR Methods for details) (IBL et al., 2020).

(B) An example table of the task variables X assumed to govern behavior for a subset of trials {t − 2,…, t + 2}, consisting here of a choice bias (a constant rightward bias, encoded as “+1” on each trial), the contrast value of the left grating, and the contrast value of the right grating.

(C) Hypothetical time-course of a set of psychophysical weights W, which evolve smoothly over the course of training. Each weight corresponds to one of the K = 3 variables comprising x_t, such that a weight’s value at trial t indicates how strongly the corresponding variable is affecting choice behavior.

(D) Psychometric curves defined by the psychophysical weights w_t on particular trials in early, middle, and late training periods, as defined in (C). Initial behavior is highly biased and insensitive to stimuli (“early training”). Over the course of training, behavior evolves toward unbiased, high-accuracy performance consistent with a steep psychometric function (“late training”).

Our modeling approach assumes that on each trial the animal receives an input x_t and makes a binary decision $y_t\in \{0,1\}$. Here, x_t is a K-element vector containing the task variables that may affect an animal’s decision on trial $t\in \{1,\dots ,T\}$, where X = [x₁,…, x_T]. For the IBL task, x_t could include the contrast values of left and right gratings, as well as stimulus history, a bias term, and other covariates available to the animal during the current trial (Figure 1B). We model the animal’s decision-making process with a Bernoulli generalized linear model (GLM), also known as the logistic regression model. This model characterizes the animal’s strategy on each trial t with a set of K linear weights w_t, where W = [w₁,…,w_T]. Each w_t describes how the different components of the K-element input vector x_t affect the animal’s choice on trial t. The probability of a rightward decision (y_t = 1) is given by

$$p\left(y_t=1\mid {\mathbf{x}}_t,{\mathbf{w}}_t\right)=\varphi \left({\mathbf{x}}_t\cdot {\mathbf{w}}_t\right),$$ (Equation 1)

where $\varphi (\cdot )$ denotes the logistic function. Unlike standard psychophysical models, which assume that weights are constant across time, we instead assume that the weights evolve gradually over time (Figure 1C). Specifically, we model the weight change after each trial with a Gaussian distribution (Bak et al., 2016; Roy et al., 2018a):

$${\mathbf{w}}_{t+1}={\mathbf{w}}_t+{\mathit{\eta }}_t,{\eta }_{t,k}\sim \mathcal{N}\left(0,{\sigma }_k^2\right),$$ (Equation 2)

here η_t is the vector of weight changes on trial t, and ${\sigma }_k^2$ denotes the variance of the changes in the k^th weight. The rate of change of the K different weights in w_t is thus governed by a vector of smoothness hyperparameters $\theta =\left\{{\sigma }_1,\dots ,{\sigma }_K\right\}$. A larger σ_k means larger trial-to-trial changes in the k^th weight. Note that if ${\sigma }_k=0$ for all k, the weights are constant, and we recover the classic psychophysical model with a fixed set of weights for the entire dataset.

Learning to perform a new task can be formalized under this model by a dynamic trajectory in weight space. Figure 1C-D shows a schematic example of such learning in the context of the IBL task. Here, the hypothetical mouse’s behavior is governed by three weights: a Left Contrast weight, a Right Contrast weight, and a (Choice) Bias weight. The first two weights capture how sensitive the animal’s choice is to left and right gratings, respectively, whereas the bias weight captures an independent, additional bias towards leftward or rightward choices.

In this hypothetical example, the weights evolve over the course of training as the animal learns the task. Initially, during “early training”, the left and right contrast weights are close to zero and the bias weight is large and positive, indicating that the animal pays little attention to the left and right contrasts and exhibits a strong rightward choice bias. As training proceeds, the contrast weights diverge from zero and separate, indicating that the animal learns to compute a difference between right and left contrast. By the “late training” period, left and right contrast weights have grown to equal and opposite values, while the bias weight has shrunk to nearly zero, indicating unbiased, highly accurate performance of the task.

Although we have arbitrarily divided the data into three different periods—designated “early,” “middle,” and “late training”—the three weights change gradually after each trial, providing a fully dynamic description of the animal’s decision-making strategy as it evolves during learning. To better understand this approach, we can compute an “instantaneous psychometric curve” from the weight values at any particular trial (Figure 1D). These curves describe how the mouse converts the visual stimuli to a probability over choice on any trial. Together, the weights in this example illustrate the gradual evolution from strongly right-biased strategy (Figure 1D, left) toward a high-accuracy strategy (Figure 1D, right). Of course, by incorporating weights on additional task covariates (e.g. choice and reward history), the model can characterize time-varying strategies that are more complex than those captured by a psychometric curve.

Inferring Weight Trajectories from Data

The goal of PsyTrack is to infer the full time-course of an animal’s decision-making strategy from the observed sequence of stimuli and choices over the course of an experiment. To do so, we estimate the animal’s time-varying weights W using the dynamic psychophysical model defined above (Equation 1 and Equation 2), where T is the total number of trials in the dataset. Each of the K rows of W represents the trajectory of a single weight across trials, while each column provides the vector of weights governing decision-making on a single trial. Our method therefore involves inferring K × T weights from only T binary decision variables.

To estimate W from data, we use a two-step procedure called empirical Bayes (Bishop, 2006). First, we estimate θ, the hyperparameters governing the smoothness of the different weight trajectories, by maximizing evidence, which is the probability of choice data given the inputs (with W integrated out). Second, we compute the maximum a posteriori (MAP) estimate for W given the choice data and the estimated hyperparameters $\widehat{\theta }$. Although this optimization problem is computationally demanding, we have developed fast approximate methods that allow us to model datasets with tens of thousands of trials within minutes on a desktop computer (see STAR Methods for details; see also Figure S1) (Roy et al., 2018a).

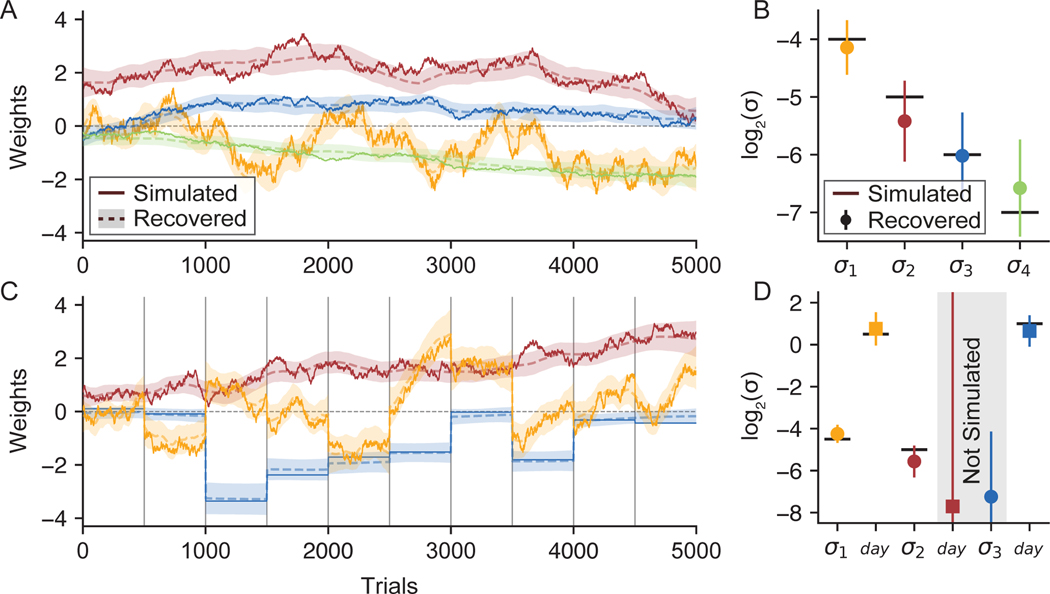
To validate the method, we generated a dataset from a simulated observer with K = 4 weights that evolved according to a Gaussian random walk over T = 5000 trials (Figure 2A). Each random walk had a different standard deviation σ _k (Equation 2), producing weight trajectories with differing average rates of change. We sampled input vectors x_t for each trial from a standard normal distribution, then sampled the observer’s choices y according to Equation 1. We applied PsyTrack to this simulated dataset, which provided estimates of the 4 hyperparameters $\widehat{\theta }=\left\{{\widehat{\sigma }}_1,\dots ,{\widehat{\sigma }}_4\right\}$ and weight trajectories $\widehat{\mathbf{W}}$. Figure 2A-B shows that our method accurately recovered both the weights W and the hyperparameters θ.

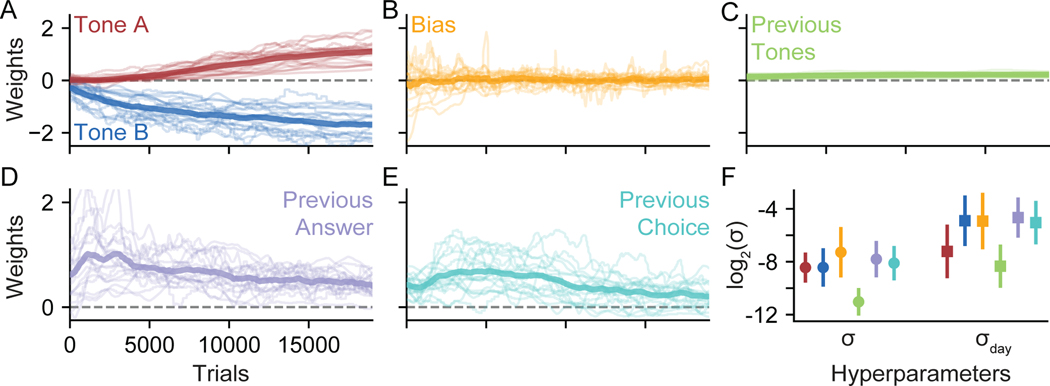
Figure 2:

Recovering Psychophysical Weights from Simulated Data

(A) To validate PsyTrack, we simulated a set of K = 4 weights $\widehat{\mathbf{w}}$ that evolved for T = 5000 trials (solid lines). We then use our method to recover weights W (dashed lines), surrounded with a shaded 95% credible interval. The full optimization takes less than one minute on a laptop, see Figure S1 for more information.

(B) In addition to recovering the weights W in (A), we also recovered the smoothness hyperparameter σ_k for each weight, also plotted with a 95% credible interval. True values ${\widehat{\sigma }}_k$ are plotted as solid black lines.

(C) We again simulated a set of weights as in (A), except now session boundaries have been introduced at 500 trial intervals (vertical black lines), breaking the 5000 trials into 10 sessions. The yellow weight is simulated with a σ_day hyperparameter much greater than its respective σ hyperparameter, allowing the weight to evolve trial-to-trial as well as “jump” at session boundaries. The blue weight has only a σ_day and no σ hyperparameter meaning the weight evolves only at session boundaries. The red weight does not have a σ_day hyperparameter, and so evolves like the weights in (A). See Figure S2 for weight trajectories recovered for this dataset without the use of any σ_day hyperparameters.

(D) We recovered the smoothness hyperparameters θ for the weights in (C). Though the simulation only has four hyperparameters, the model does not know this and so attempts to recover both a σ and a σ_day hyperparameter for all three weights. The model appropriately assigns low values to the two non-existent hyperparameters (gray shading).

Augmented Model for Capturing Changes Between Sessions

One limitation of the model described above is that it does not account for the fact that experiments are typically organized into sessions, each containing tens to hundreds of consecutive trials, with large gaps of time between them. Our basic model makes no allowance for the possibility that weights might change much more between sessions than between other pairs of consecutive trials. For example, if either forgetting or consolidation occurs overnight between sessions, the weights governing the animal’s strategy might change much more dramatically than is typically observed within sessions.

To overcome this limitation, we augmented the model to allow for larger weight changes between sessions. The augmented model has K additional hyperparameters, denoted (σ_day1,…,σ_day1), which specify the prior standard deviation over weight changes between sessions or “days”. A large value for σ_dayk means that the corresponding k’th weight can change by a large amount between sessions, regardless of how much it changes between other pairs of consecutive trials. The augmented model thus has 2 K hyperparameters, with a pair of hyperparameters (σ_k, σ_dayk) for each of the K weights in w_t.

We tested the performance of this augmented model using a second simulated dataset which includes session boundaries at 500 trial intervals (Figure 2C). We simulated K = 3 weights for T = 5000 trials, with the input vector x_t and choices y_t on each trial sampled as in the first dataset. The red weight was simulated like the red weight in Figure 2A, that is, using only the standard σ and no σ_day hyperparameter. Conversely, the blue weight was simulated using only a σ_day hyperparameter, such that the weight is constant within each session, but can “jump” at session boundaries. The yellow weight was simulated with both types of smoothness hyperparameter, allowing it to smoothly evolve within a session as well as evolve more dramatically at session boundaries. Once again, we can see that the recovered weights closely agree with the true weights.

Figure 2D shows the hyperparameters recovered from the second dataset. While the simulated weights had only four hyperparameters (a σ for the yellow and red weights, and a σ_day for the yellow and blue weights), our method inferred both a σ and σ_day hyperparameter for each of the three weights. Thus two of the hyperparameters recovered by the model were not simulated, as indicated by the gray shading. In practice, recovering a value for these unsimulated hyperparameters that is low relative to other hyperparameters will result in an accurate recovery of weights. Thus, the two unsimulated hyperparameters were accurately recovered, as were the four simulated hyperparameters. All subsequent models are fit with σ_day hyperparameters unless otherwise indicated.

We can also consider a situation in which behavior changes suddenly at some arbitrary point within a session, in which case σ_day will be of limited use. Trying to capture a large “step” change in behaviour with our smoothly evolving weights usually results in the step being approximated by a sigmoid. The accuracy of the approximation is related to the slope of the sigmoid, which is in turn controlled by that weight’s σ value (higher σ allows for a steeper slope). Figure S2 shows PsyTrack’s recovery of the simulated dataset used in Figure 2C without the σ_day hyperparameter to capture the jumps at session boundaries.

Characterizing Learning Trajectories in the IBL Task

We now turn to real data, and show how PsyTrack can be used to characterize the detailed trajectories of learning in a large cohort of animals. We examined a dataset from the International Brain Lab (IBL) containing behavioral data from over 100 mice on a standardized sensory decision-making task (see task schematic in Figure 1A) (IBL et al., 2020).

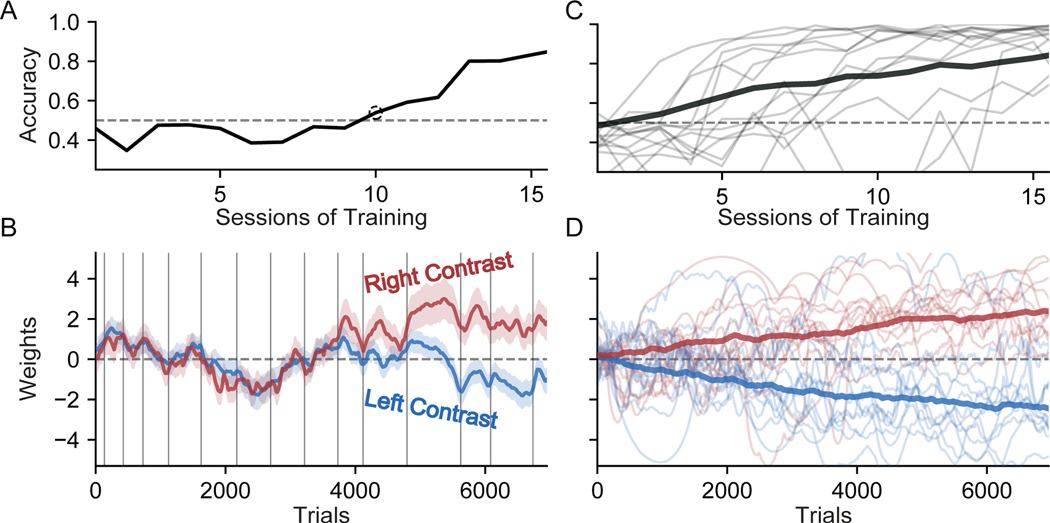
We began by analyzing choice data from the earliest sessions of training. Figure 3A shows the learning curve (defined as the fraction of correct choices per session) for an example mouse over the first several weeks of training. Early training sessions used “easy” stimuli (100% and 50% contrasts) only, with harder stimuli (25%, 12.5%, 6.25%, and 0% contrasts) introduced later as task accuracy improved. To keep the metric consistent, we calculated accuracy only from easy-contrast trials on all sessions.

Figure 3:

Visualization of Early Learning in IBL Mice

(A) The accuracy of an example mouse over the first 16 sessions of training on the IBL task. We calculated accuracy only from “easy” high-contrast (50% and 100%) trials, since lower-contrast stimuli were only introduced later in training. The first session above chance performance (50% accuracy) is marked with a dotted circle.

(B) Inferred weights for left (blue) and right (red) stimuli governing choice for the same example mouse and sessions shown in (A). Grey vertical lines indicate session boundaries. The black dotted line marks the start of the tenth session, when left and right weights first diverged, corresponding to the first rise in accuracy above chance performance (shown in (A)). See Figure S3 for models using additional weights.

(C) Accuracy on easy trials for a random subset of individual IBL mice (gray), as well as the average accuracy of the entire population (black).

(D) The psychophysical weights for left and right contrasts for the same subset of mice depicted in (C) (light red and blue), as well as the average psychophysical weights of the entire population (dark red and blue) (σ_day was omitted from these analyses for visual clarity).

Although traditional analyses provide coarse performance statistics like accuracy-per-session, our dynamic GLM offers a detailed characterization of the animal’s evolving behavioral strategy at the timescale of single trials. In Figure 3B, we used PsyTrack to extract time-varying weights on left contrast values (blue) and right-side contrast values (red). During the first nine sessions these two weights fluctuated together, indicating that the probability of making a rightward choice was the independent of whether the stimuli was presented on either the left or right side of the screen. Positive (negative) fluctuations in these weights corresponded to a bias toward rightward (leftward) choices. This movement in the weights indicated that the animal’s strategy was not constant across these sessions, even though accuracy remained at chance-level performance.

At the start of the tenth session, the two weights began to diverge. The positive value of the right contrast weight means that right contrasts led to rightward choices; the opposite is true of the negative value of the left contrast weight. Together, this diveregence corresponds to an increase in accuracy. This separation continued throughout the subsequent six sessions, gradually increasing performance to roughly 80% accuracy by the sixteenth session.

However, the learning trajectory of this example mouse was by no means characteristic of the entire cohort. Figure 3C-D shows the empirical learning curves (above) and inferred weight trajectories (below) from a dozen additional mice selected randomly from the IBL dataset. The light red and blue lines are the right and left contrast weights for individual mice, whereas the dark red and blue lines are the average weights calculated across the entire population. While we see a smooth and gradual separation of the contrast weights on average, there is great diversity in the dynamics of the contrast weights of individual mice.

Adaptive Bias Modulation in a Non-Stationary Task

Once training has progressed to include contrast levels of all difficulties, the IBL task introduces a final modification to the task. Instead of left and right contrasts appearing randomly with an equal 50:50 probability on each trial, trials are now grouped into alternating “left blocks” and “right blocks”. Within a left block, the ratio of left contrasts to right contrasts is 80:20, whereas the ratio is 20:80 within right blocks. The blocks are of variable length, and sessions sometimes begin with a 50:50 block for calibration purposes.

Using the same example mouse from Figure 3, we extend our view of its task accuracy (on “easy” high-contrast trials) to include the first fifty sessions of training in Figure 4A. The initial gray shaded region indicates training prior to the introduction of bias blocks. The pink outline designates a period of three sessions as “Early Bias Blocks” which includes the last session without blocks and the first two sessions with blocks. The purple outline looks at two arbitrary sessions several weeks of training later, a period designated as “Late Bias Blocks”. In Figure S5, we infer weight trajectories for an example session from each of these periods in training and validate that psychometric curves predicted from our model closely match curves generated directly from the behavioral data.

Figure 4:

Adaptation to Bias Blocks in an Example IBL Mouse

(A) An extension of Figure 3A to include the first months of training (accuracy is calculated only on “easy” high-contrast trials). Starting on session 17, our example mouse was introduced to alternating blocks of 80% right contrast trials (right blocks) and 80% left contrasts (left blocks). The sessions where these bias blocks were first introduced are outlined (pink), as are two sessions in later training where the mouse has adapted to the block structure (purple). Figure S5 validates model fits to sessions 10, 20, & 40 against psychometric curves generated directly from behavior.

(B) Three psychophysical weights evolving during the transition to bias blocks, with right (left) blocks in red (blue) shading. Weights correspond to contrasts presented on the left (blue) and right (red), as well as a weight on choice bias (yellow). See Figure S4 for models that parametrize contrast values differently.

(C) After several weeks of training on the bias blocks, the mouse learns to quickly adapt its behavior to the alternating block structure, as can be seen in the dramatic oscillations of the bias weight in sync with the blocks.

(D) The bias weight of our example mouse during the first three sessions of bias block, where the bias weight is chunked by block and each chunk is normalized to start at 0. Even during the initial sessions of bias blocks, the red (blue) lines show that a mild rightward (leftward) bias tended to evolve during right (left) blocks.

(E) Same as (D) for three sessions during the “Late Bias Blocks” period. Changes in bias weight became more dramatic, tracking stimulus statistics more rapidly, and indicating that the mouse had adapted its behavior to the block structure of the task. While some of the bias weight trajectories may appear to “anticipate” the start of the next block, this is largely an methodological artifact of the smoothing used in the model (see Figure S6).

(F) For the second session from the “Late Bias Blocks” shown in (C), we calculated an “optimal” bias weight (black) given the animal’s sensory stimulus weights and the ground truth block transition times (inaccessible to the mouse). This optimal bias closely matches the empirical bias weight recovered using our model (yellow), indicating that the animal’s strategy was approximately optimal for maximizing reward under the task structure.

In Figure 4B, we apply PsyTrack to three “Early Bias Blocks” sessions. Our left and right contrast weights are the same as in Figure 3B (though they now also characterize sensitivity to “hard” as well as “easy” contrast values). We also introduce a third psychophysical weight, in yellow, that tracks sensitivity to choice bias: when this weight is positive (negative), the animal prefers to choose right (left) independent of any other input variable. While task accuracy improves as the right contrast weight grows more positive and the left contrast weight grows more negative, the “optimal” value of the bias weight is naively 0 (no a priori preference for either side). However, this is only true when contrasts are presented with a 50:50 ratio and the two contrast weights are of equal and opposite size.

For this mouse, we see that on the last session before the introduction of bias blocks, the bias weight tends to drift around zero and the contrast weights have continued to grow in magnitude from Figure 3B. When the bias blocks commence on the next session, the bias weight does not seem to immediately reflect any change in the underlying stimulus ratio. In Figure 4C, however, we see a clear adaptation of behavior after several weeks of training with the bias block structure. Here the bias weight not only fluctuates more dramatically in magnitude, but is also synchronized with the block structure of the trials.

We examine this phenomenon more precisely in Figure 4D-F, which leverages the results of our method for further analysis. To better examine how our mouse’s choice behavior is changing within a bias block, we can chunk our bias weight according to the start and end of each block. Plotting the resulting chunk (normalized to start at 0) shows how the bias weight changes within a single block. In Figure 4D, we plot all the bias weight chunks from the first three sessions of bias blocks. Chunks of the bias weight that occurred during a left block are colored blue, while chunks occurring during a right block are colored red.

Viewed in this way, we can see that there is some adaptation to the bias blocks even within the first few sessions. Within only a few dozen trials, the mouse’s choice bias tends to slowly drift rightward during right blocks and leftward during left blocks. If we run the same analysis on three sessions near the “Late Bias Blocks” period, we see that this adaptation becomes more dramatic after training (Figure 4E). While it may appear that the animal proactively adjusts it’s choice bias in the opposite direction toward the end of the longer blocks, as if in anticipation of the coming block, this is largely an artifact of the smoothing in our model. Figure S6 explores this further and presents an easy tweak to PsyTrack that removes this methodological confound.

We can further analyze the animal’s choice bias in response to the bias blocks by returning to the notion of an “optimal” bias weight. As mentioned before, the naive “optimal” value of a bias weight is zero. However, a non-zero choice bias could improve accuracy if, say, the contrast weights are asymmetric (i.e., a left choice bias is useful if the animal is disproportionately sensitive to right contrasts). The introduction of bias blocks further increases the potential benefit of a non-zero bias weight. Suppose that the values of the two contrast weights are so great that the animal can perfectly detect and respond correctly to all contrasts. Even in this scenario, one-in-nine contrasts are 0% contrasts, meaning that (with a bias weight of zero) the animal’s accuracy maxes out at 94.4% (100% accuracy on 8/9 trials, 50% on 1/9). If instead the bias weight adapted perfectly with the bias blocks, the mouse could get the 0% contrasts trials correct with 80% accuracy instead of 50%, increasing the upper bound of its overall accuracy to 97.8%.

Whereas normative models might derive a notion of optimal behavior (Tajima et al., 2019), we can use our descriptive model to calculate what the “optimal” bias weight would be for each trial and compare it to the bias weight recovered from the data. Here we define an “optimal” bias weight on each trial as the value of the weight that maximizes expected accuracy assuming that (a) the left and right contrasts weights recovered from the data are considered fixed, (b) the precise timings of the block transitions are known, and (c) the distribution of contrast values within each block are known. Under those assumptions, we take the second session of data depicted in Figure 4C and re-plot the psychophysical weights in Figure 4F with the calculated optimal bias weight superimposed in black. Note that the optimal bias weight uses information inaccessible to a mouse in order to jump precisely at each block transition, but also adjusts subtly within a block to account for changes in the contrast weights. We see that, in most blocks, the empirical bias weight (in yellow) matches the optimal bias weight closely. In fact, we can calculate that the mouse would only increase its expected accuracy from 86.1% to 89.3% with the optimal bias weight instead of the empirical bias weight.

Trial History Dominates Early Behavior in Akrami Rats

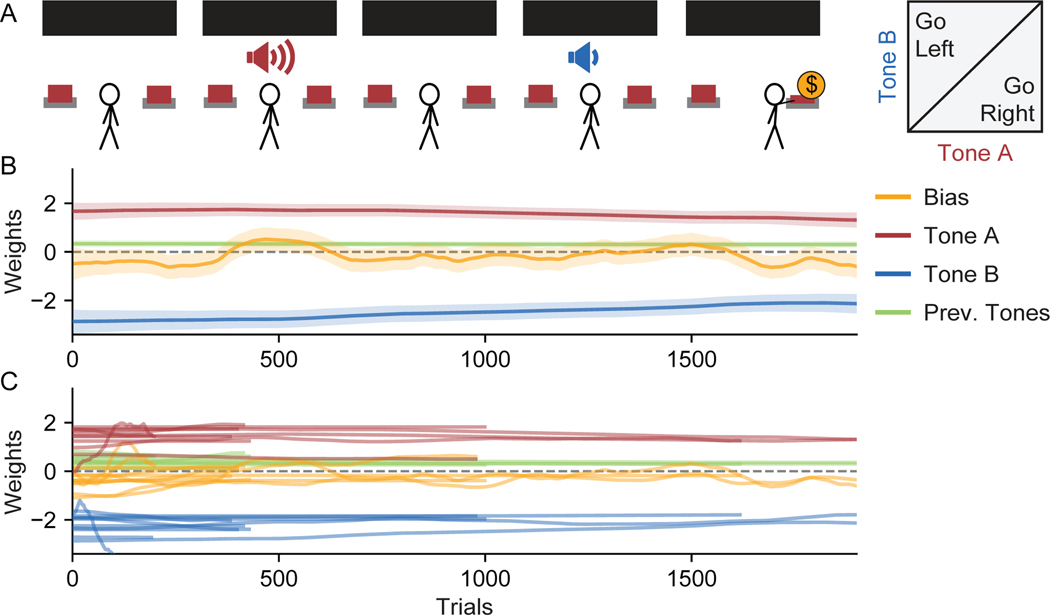
To further explore the capabilities of PsyTrack, we analyzed behavioral data from another binary decision-making task previously reported in Akrami et al. (2018), where both rats and human subjects were trained on versions of the task (referred to hereafter as “Akrami Rats” and “Akrami Humans”). This auditory parametric working memory task requires a rat to listen to two white noise tones, Tone A then Tone B, which have different amplitudes and are separated by a delay (Figure 5A). If Tone A is louder than Tone B, than the rat must nose poke right to receive a reward, and vice-versa.

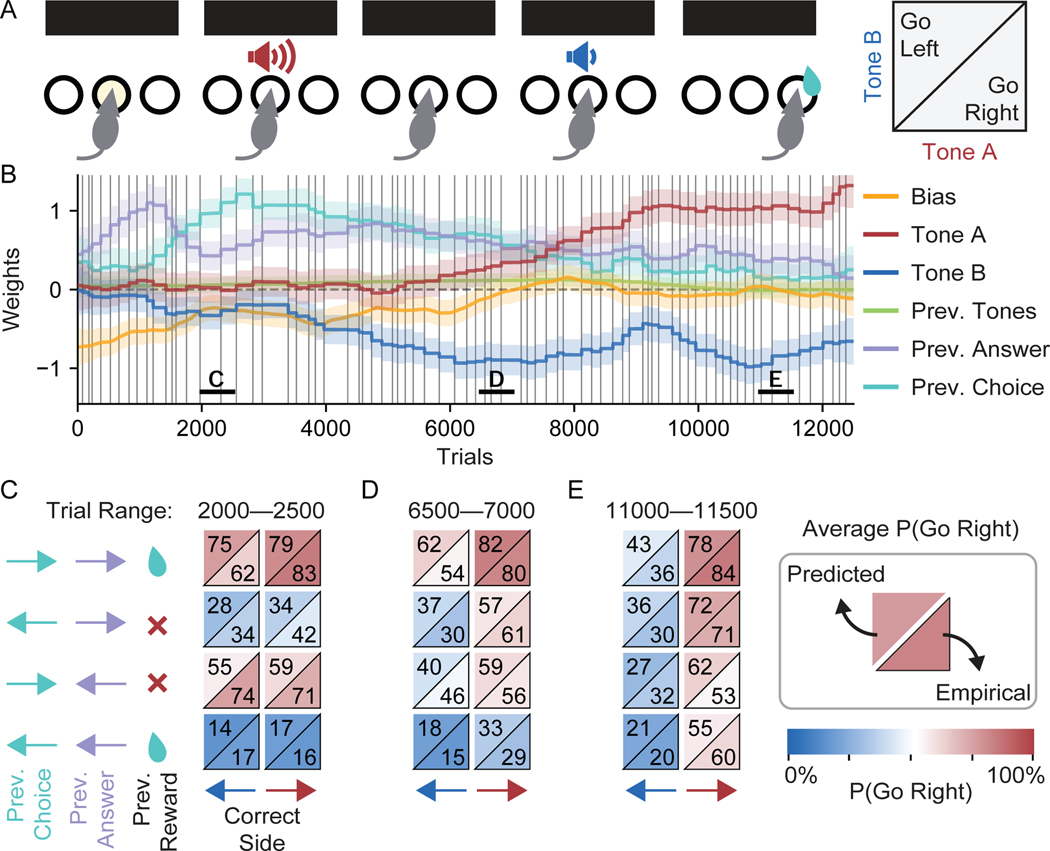
Figure 5:

Visualization of Learning in an Example Akrami Rat

(A) For this data from Akrami et al. (2018), a delayed response auditory discrimination task was used in which a rat experiences an auditory white noise stimulus of a particular amplitude (Tone A), a delay period, a second stimulus of a different amplitude (Tone B), and finally the choice to go either left or right. If Tone A was louder than Tone B, then a rightward choice triggers a reward, and vice-versa.

(B) The psychophysical weights recovered from the first 12,500 trials of an example rat. “Prev. Tones” is the average amplitude of Tones A and B presented on the previous trial; “Prev. Answer” is the rewarded (correct) side on the previous trial; “Prev. Choice” is the animal’s choice on the previous trial. Black vertical lines are session boundaries. Figure S7 reproduces the analyses of this figure using a model with no history regressors–the remaining three weights look qualitatively similar.

(C-E) Within 500 trial windows starting at trials 2000 (C), 6500 (D), and 11000 (E), trials are binned into one of eight conditions according to three variables: the Previous Choice, the Previous (Correct) Answer, and the Correct Side of the trial itself. For example, the bottom left square is for trials where the previous choice, the previous correct answer, and the current correct side are all left. The number in the bottom right of each square is the percent of rightward choices within that bin, calculated directly from the empirical behavior. The number in the top left is a prediction of that same percentage made using the cross-validated weights of the model. Close alignment of predicted and empirical values in each square indicate that the model is well-validated, which is the case for each of the three training periods.

In 5B, we apply our method to the first 12,500 trials of behavior from our example rat. Despite the new task and species, there are several similarities to the results from the IBL mice shown in 3 and 4. Tones A and B are the task-relevant variables (red and blue weights, respectively) treated similarly to the left and right contrast variables, while the choice bias (yellow weight) is the same weight used by the IBL mice. While at most one of the contrast weights was activated on a single trial in the IBL task, both the Tone A and B weights are activated on every trial in the Akrami task (the inputs are also parametrized differently, see STAR Methods).

The biggest difference in our application of the method to the Akrami rats is the inclusion of “history regressor” weights; that is, weights which carry information about the previous trial. The Previous Tones variable is the average of Tones A and B from the previous trial (green weight). The Previous (Correct) Answer variable indexes the rewarded side on the previous trial, tracking a categorical variable where {−1,0,+1} = {Left, N/A, Right} (purple weight). The Previous Choice variable indexes the chosen side on the previous trial, also a categorical variable where {−1,0,+1} = {Left, N/A, Right} (cyan weight). History weights are always irrelevant in this task. Despite this, the information of previous trials often influences animal choice behavior, especially early in training (for the impact of history regressors during early learning in an IBL mouse, see Figure S3A).

As can be seen clearly from our example rat, the set of task-irrelevant weights (the three history weights plus the bias weight) dominate behavior early in training. In contrast, the task-relevant weights (on Tones A and B) initialize at zero. However, as training progresses, the task-irrelevant weights shrink while the Tone A and B weights grow to be equal and opposite. Note that the weight on Tone B begins to evolve away from zero very early in training, while the weight on Tone A does not become positive until after tens of sessions. In context of the task, this makes intuitive sense: the association between a louder Tone B and reward on the left is comparatively easy since Tone B occurs immediately prior to the choice. Making the association between a louder Tone A and reward on the right is much more difficult to establish due to the delay period.

Furthermore, the positive value of all three history weights matches our intuitions. The positive value of the Previous (Correct) Answer weight indicates that the animal prefers to go right (left) when the correct answer on the previous trial was also right (left). This is a commonly observed behaviour known as a “win-stay/lose-switch” strategy, where an animal will repeat its choice from the previous trial if it was rewarded and will otherwise switch sides. The positive value of the Previous Choice weight indicates that the animal prefers to go right (left) when it also went right (left) on the previous trial. This is known as a “perseverance” behavior: the animal prefers to simply repeat the same choice it made on the previous trial, independent of reward or task stimuli. The slight positive value of the Previous Tones weight indicates that the animal is biased toward the right when the tones on the previous trial were louder than average, the same effect produced by Tone A. This corroborates an important finding from the original paper: the biases seen in choice behavior are consistent with the rat’s memory of Tone A contracting toward the stimulus mean (Akrami et al. (2018), though note that the analysis there was done on post-training behavior and uses the 20–50 most recent trials to calculate an average previous tones term; see also Papadimitriou et al. (2015); Lu et al. (1992)).

To validate our use of these history regressors, we first analyze the empirical choice behavior to verify that this strong dependence on the previous trial exists. Then, we can examine whether our model with history regressors effectively captures this dependence.

Figure 5C-E shows three different windows of 500 trials each, taken from different points during the training of our example rat. Within a particular window, the trials are binned according to three conditions: the choice on the previous trial (“Prev. Choice”), the correct answer of the previous trial (“Prev. Answer”), and the correct answer on the current trial (“Correct Side”). This gives 2 ³ = 8 conditions, represented by the eight boxes. For example, the box in the lower left corresponds to trials where the previous choice, previous answer, and current answer are all left. The two numbers within each box represent the percent of trials within that condition (and within that 500 trial window) where the rat chose to go right. The number in the bottom right of each square is calculated directly from the empirical behavior, whereas the number in the top left is calculated from the model. Specifically, for each trial the model weights on that trial can be combined with the inputs of that trial to calculate P(Go Right), according to Equation 1— these are then averaged for all trials within a particular box. The color of each half-box maps directly to its average P(Go Right) value, red for rightward and blue for leftward.

Focusing first on empirical data from early in training (the values in the bottom right of each square in Figure 5C), we can verify that behavior is indeed strongly dependent on the previous trial. In a well trained rat, the left column would all be blue and the right column would all be red, since choices would align with the correct answer on the current trial. Instead, the empirical behavior is almost entirely history dependent with the rat only going right on 16% of rightward trials if the previous choice and answer were both left (fourth row, right column). As the rat continues to train, we observe that the influence of the previous trial on choice behavior decreases, though it has not disappeared by trial 11000 (Figure 5E).

With the influence of the previous trial firmly established by the empirical behavior, we would like to compare these measurements against the predictions of our model. For almost all of the boxes in each of the trial windows, we observe that the model’s predictions align closely with the empirical choice behavior. In fact, only one predicted value exists outside the 95% confidence interval of our empirical measurement (third row, left column in Figure 5C). This is a strong validation that PsyTrack is accurately capturing potent features of the underlying behavior. We repeat the analyses done here in Figure S7 with a model that does not have history regressors and show that this alternative model is not able to capture any of the dependence on the previous trial evident in the empirical choice behavior.

It is not appropriate to calculate the model’s predicted P(Go Right) for a trial when that same trial was used during inference. To avoid this, we use a 10-fold cross-validation procedure. For each fold, the model is fit using 90% of trials and choice predictions are made for the remaining 10% of trials. For more details regarding this cross-validation procedure see the STAR Methods.

Behavioral Trends Are Shared Across the Population of Akrami Rats

By applying PsyTrack to the entire population of Akrami rats, we can uncover trends and points of variation in training. Figure 6 looks at the same set of weights used in Figure 5B. Here, trajectories are calculated for the first 20,000 trials of training for each rat. Each plot consists of the individual weight trajectories from the whole population of 19 rats as well as the average trajectory. Figure 6A shows the weights for both Tone A and Tone B. The observation from our example rat that Tone B grows before the Tone A weight appears to hold uniformly across the population. There is more extensive variation in the bias weights of the population as seen in Figure 6B, though the variation is greatest early in training and at all points averages out to approximately 0. The slight positive value of the Previous Tones weight is highly consistent across all rats and constant across training, seen in Figure 6C. The prevalence of both “win-stay/lose-switch” and “perseverance” behaviors across the population can be clearly seen in the positive values of the Previous (Correct) Answer and Choice weights in Figure 6D and E, though there is substantial variation in the dynamics of these history regressors.

Figure 6:

Population Psychophysical Weights from Akrami Rats

The psychophysical weights during the first T = 20000 trials of training, plotted for all rats in the population (light lines), plus the average weight (dark line): (A) Tone A and Tone B, (B) Bias, (C) Previous Tones, (D) Previous (Correct) Answer, and (E) Previous Choice. (F) Shows the average σ and σ_day for each weight (±1 SD), color coded to match the weight labels in (A-E).

Figure 6F shows the average σ and σ_day values for each weight (with weights specified by matching color). The similar average σ values of the Tones A and B weights (blue and red circles) indicate a comparable degree of variation within sessions, but Tone A is prone to far less variation between sessions as indicated by its relatively low σ_day average (red square). The individual bias weights in Figure 6B show the most variation, which is reflected by the bias weight having the highest average σ value (yellow circle). Despite having a similar average trajectory to the Bias weight, the Previous Tones weight in Figure 6C has almost no individual variation which is reflected in its markedly low average σ and σ_day values (green circle and square).

In Contrast to Rats, Human Behavior is Stable

In addition to training rats on a sensory discrimination task, Akrami et al. (2018) also adapted the same task for human subjects. The modified task also requires a human subject to discriminate two tones, though the human chooses with a button instead of a nose-poke and is rewarded with money (Figure 7A). The weights from an example human subject are shown in Figure 7B, whereas the weights from all the human subjects are shown together in Figure 7C.

Figure 7:

Population Psychophysical Weights from Akrami Human Subjects

(A) The same task used by the Akrami rats in Figure 5A, adapted for human subjects.

(B) The weights for an example human subject. Human behavior is not sensitive to the previous correct answer or previous choice, so corresponding weights are not included in the model (see Figure S8 for a model which includes these weights).

(C) The weights for the entire population of human subjects. Human behavior was evaluated in a single session of variable length.

It is useful to contrast the weights recovered from the Akrami human subjects to the weights recovered from the Akrami rats. Since the rules of the task are explained to human subjects, one would intuitively expect that human weights would initialize at “correct” values corresponding to high performance and would remain constant throughout training. These, however, are assumptions. An advantage of our method is that no such assumptions need to be made: the initial values and stability of the weights is determined entirely from the data. From Figure 7C, we see that the model does indeed confirm our intuitions without the need for us to impose them a priori. All four weights remain relatively stable throughout training, though choice bias does oscillate near zero for some subjects. Two of the history weights that dominated early behavior in rats, Previous (Correct) Answer and Choice, are not used by humans in the population and so are omitted here (see Figure S8). The slight positive weight on Previous Tones remains for all subjects, however, and there is a slight asymmetry in the magnitudes of the Tone A and Tone B weights in many subjects.

Including History Regressors Boosts Predictive Power

Just as we were able to leverage the results of our analysis of the IBL mice to examine the impact of the bias block structure on the choice bias of an example mouse in Figure 4, we can also extend our analysis of the Akrami rats to quantify the importance of history regressors in characterizing behavior. Using our example rat from Figure 5, we wish to quantify the difference between a model that includes the three history regressors and another model without them (one with weights for only Tone A, Tone B, and Bias). To do this, we calculate the model’s predicted accuracy at each trial. The predicted accuracy on a trial t can be defined as max (P(Go Right), P(Go Left)), calculated using Equation 1. Note that for the predictions to be valid, we determine predicted accuracy using weights produced from a cross-validation procedure (STAR Methods).

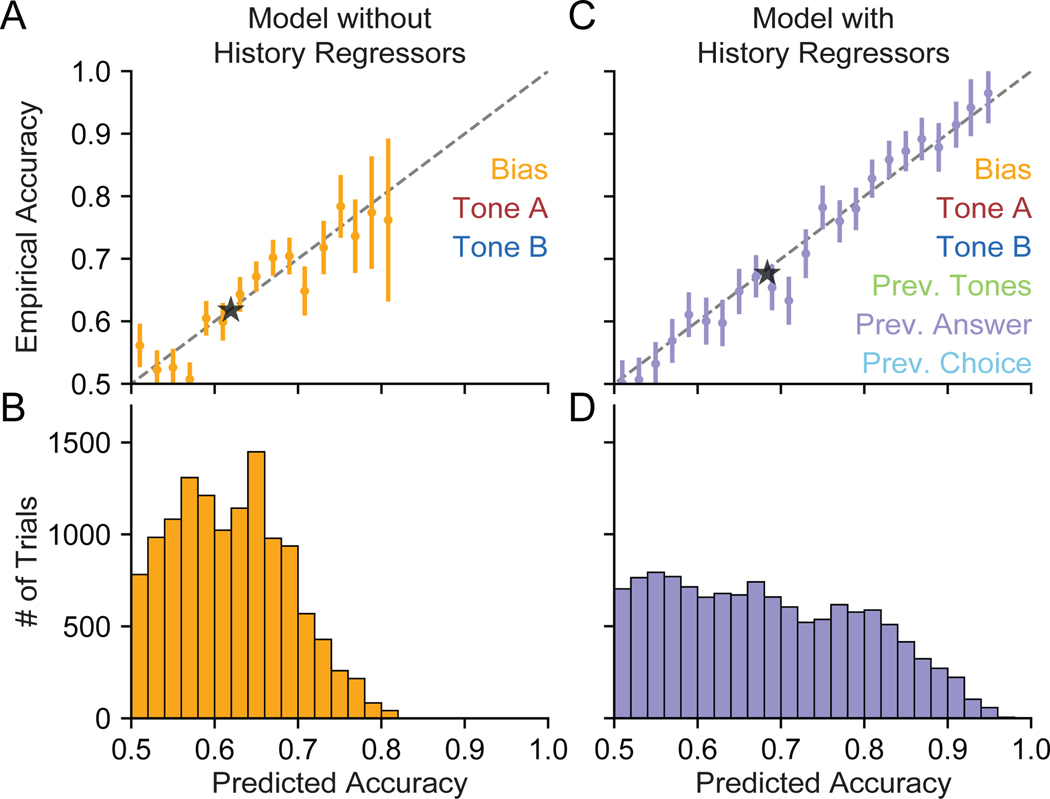
In Figure 8A, we refit a model to the same data shown in Figure 5B using only Bias, Tone A, and Tone B weights (shown in Figure S7). Next, we bin the trials according to the model’s predicted accuracy, as defined above. Finally, for the trials within each bin, we plot the average predicted accuracy on the x-axis and the empirical accuracy of the model (the fraction of trials in a bin where the prediction of the model matched the choice the animal made) on the y-axis. Points that lie below the dotted identity line represent over-confident predictions from the model, whereas points above the line indicate under-confidence. The fact that points (shown with 95% confidence intervals on their empirical accuracy) lie along the dotted line further validates the accuracy of the model.

Figure 8:

History Regressors Improve Model Accuracy for an Example Akrami Rat

(A) Using a model of our example rat that omits history regressors, we plot the empirical accuracy of the model’s choice predictions against the model’s cross-validated predicted accuracy. The black dashed line is the identity, where the predicted accuracy of the model exactly matches the empirical accuracy (i.e., points below the line are overconfident predictions). The animal’s choice is predicted with 61.9% confidence on the average trial, precisely matching the model’s empirical accuracy of 61.9% (black star). Each point represents data from the corresponding bin of trials seen in (B). Empirical accuracy is plotted with a 95% confidence interval. See ar]STAR Methods for more information on the cross-validation procedure.

(B) A histogram of trials binned according to the model’s predicted accuracy.

(C) Same as (A) but for a model that also includes three additional weights on history regressors: Previous Tones, Previous (Correct) Answer, and Previous Choice. We see that data for this model extends into regions of higher predicted and empirical accuracy, as the inclusion of history regressors allows the model to make stronger predictions. The animal’s choice is predicted with 68.4% confidence on the average trial, slightly overshooting the model’s empirically accuracy of 67.6% (black star).

(D) Same as (B), but for the model including history regressors.

The histogram in Figure 8B shows the number of trials in each of the bins used in Figure 8A. We can see that almost no choices are predicted with greater than 80% probability. The black star in Figure 8A shows the average predictive accuracy for this model (61.9%) and corresponding empirical accuracy (also 61.9%).

After adding the three trial-history weights, we first check if our model is still making valid predictions. Figure 8C shows that most of our data points still lie along the dotted identity line, meaning that the model’s predictions remain well-calibrated. The data points also extend further along the diagonal—accounting for the impact of the previous trial on choice behavior allows the model to make more-confident predictions. Figure 8D shows that a significant fraction of trials now have a predicted accuracy greater than the most confident predictions made by the model without history regressors. In fact, choices on some trials can be predicted with near certainty, with over 95% probability. As the black star in Figure 8C indicates, the inclusion of history regressors improves the predicted accuracy of the model to 68.4% (slightly overconfident relative to the average empirical accuracy of 67.6%).

Discussion

Sensory decision-making strategies evolve continuously over the course of training, driven by learning signals as well as noise. Even after training is complete, these strategies can continue to fluctuate, both within and across sessions. Tasks with non-stationary stimuli or rewards may require continual changes in strategy in order to maximize reward (Piet et al., 2018). However, standard methods for quantifying sensory decision-making behavior, such as learning curves (Figure 3A) and psychometric functions (Figure 1D, Figure S5), are not able to describe the evolution of complex decision-making strategies over time. To address this shortcoming, we developed PsyTrack, which parametrizes time-varying behavior using a dynamic generalized linear model with time-varying weights. The rates of change of these weights across trials and across sessions are governed by weight-specific hyperparameters, which we infer directly from data using evidence optimization. We have applied PsyTrack to data from two tasks and three species, and shown that it can characterize trial-to-trial fluctuations in decision-making behavior, and provides a quantitative foundation for more targeted analyses.

PsyTrack contributes to a growing literature on the quantitative analysis of time-varying behavior. An influential paper by Smith et al. (2004) introduced a change-point-detection approach for identifying the trial at which learning produced a significant departure from chance behavior in a decision-making task. We have extended this model by moving beyond change points in order to track detailed changes in behavior over the entire training period and beyond, and by adding regression weights for a wide variety of task covariates that may also influence choices. Previous work has shown that animals frequently adopt strategies that depend on previous choices and previous stimuli (Busse et al., 2011; Frund et al., 2014; Akrami et al., 2018), even when such strategies are sub-optimal. Our approach builds upon a state-space approach for dynamic tracking of behavior (Bak et al., 2016), utilizing the decoupled Laplace method (Wu et al., 2017; Roy et al., 2018a) to scale up analysis and make it practical for modern behavioral datasets (STAR Methods). In particular, the efficiency of our algorithm allows for routine analysis of large behavior datasets, with tens of thousands of trials, within minutes on a laptop (see Figure S1).

We anticipate a variety of use cases for PsyTrack. First, experimenters training animals on binary decision-making tasks can use PsyTrack to better understand the diverse range of behavioral strategies seen in early training (Cohen and Schneidman, 2013). This will facilitate the design and validation of new training strategies, which could ultimately open the door to more complex tasks and faster training times. Second, studies of learning will benefit from the ability to analyze behavioral data collected during training, which is often discarded and left unanalyzed. Third, the time-varying weights inferred under the PsyTrack model will lend themselves to downstream analyses. Specifically, our general method can enable more targeted investigations, acting as one step in a larger analysis pipeline (as in Figure 4 and Figure 8). To facilitate these uses, we have released our method as PsyTrack, a publicly available Python package (Roy et al., 2018b). The Google Colab notebook accompanying this work provides many flexible examples and we have included a guide in the STAR Methods devoted entirely to practical considerations.

The two assumptions of PsyTrack, that (i) decision-making behavior can be described by a set of GLM weights, and (ii) that these weights evolve smoothly over training, are well-validated in the datasets explored here. However, these assumptions may not be true for all datasets. Behaviors which change suddenly may not be well described by the smoothly evolving weights in our model (see Figure S2), though allowing for weights to evolve more dramatically between sessions can mitigate this model mismatch (as in Figure 2C). Determining which input variables to include can also be challenging. For example, task-irrelevant covariates of decision-making typically include the history of previous trials (Akrami et al., 2018; Frund et al., 2014; Corrado et al., 2005), which is not always clearly defined; depending on the task, the task-relevant feature may also be a pattern of multiple stimulus units (Murphy et al., 2008). We do not currently consider high-dimensional inputs to our model (e.g., images or complex natural signals), but incorporating an automatic relevance determination prior is an exciting future direction that would allow for model weights to be automatically pruned during inference (Tipping, 2001).

Furthermore, deciding how input variables ought to be parameterized can dramatically affect the accuracy of the model fit. For example, a transformation of the contrast levels used in our analysis of data from the IBL task allows the model to discount the impact of incorrect choices under extreme levels of perceptual evidence (e.g. 100% contrasts, see Figure S4) (Nassar and Frank, 2016). While many models discount the influence of such trials using a lapse rate, PsyTrack relies on a careful parametrization of the perceptual input in lieu of any explicit lapse (STAR Methods). This flexibility gives the model the ability to account for a wide variety of behavioral strategies.

In the face of these potential pitfalls, it is important to validate our results. Thus, we have provided comparisons to more conventional measures of behavior to help assess the accuracy of our model (see Figure 5, Figure 8, and Figure S5). Furthermore, the Bayesian setting of our modeling approach provides posterior credible intervals for both weights and hyperparameters, allowing for an evaluation of the uncertainty of our inferences about behavior.

The ability to quantify complex and dynamic behavior at a trial-by-trial resolution enables exciting future opportunities for animal training. The descriptive model underlying PsyTrack could be extended to incorporate an explicit model of learning that makes predictions about how strategy will change in response to different stimuli and rewards (Ashwood et al., 2020). Ultimately, this could guide the creation of automated optimal training paradigms where the stimuli predicted to maximize learning on each trial is presented (Bak et al., 2016). There are also opportunities to extend the model beyond binary decision-making tasks, so that multi-valued choices (or non-choices, e.g. interrupted or “violation” trials) could also be included in the model (Churchland et al., 2008; Bak and Pillow, 2018). Our work opens up the path toward a more rigorous understanding of the behavioral dynamics at play as animals learn. As researchers continue to ask challenging questions, new animal training tasks will grow in number and complexity. We expect PsyTrack will help guide those looking to better understand the dynamic behavior of their experimental subjects.

STAR★METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Nicholas A. Roy (nicholas.roy.42@gmail.com).

Materials Availability

This study did not generate any new materials.

Data and Code Availability

Each of the three datasets analyzed are publicly available. The mouse training data, from IBL et al. (2020): (https://doi.org/10.6084/m9.figshare.11636748.v7); the rat training data, from Akrami et al. (2018): (https://doi.org/10.6084/m9.figshare.12213671.v1); the humans subject training data, also from Akrami et al. (2018): (https://doi.org/10.6084/m9.figshare.12213671.v1)

Our code for fitting psychophysical weights to behavioral data is distributed as a GitHub repository (under a MIT license): https://github.com/nicholas-roy/PsyTrack. This code is also made easily accessible as a Python package, PsyTrack (installed via pip install PsyTrack). Our Python package relies on the standard SciPy scientific computing libraries as well as the Open Neurophysiology Environment produced by the IBL (Jones et al., 2001; Hunter, 2007; IBL et al., 2019).

We have assembled a Google Colab notebook (https://tinyurl.com/PsyTrack-colab) that will automatically download the raw data and precisely reproduce all figures from the paper. Our analyses can be easily extended to additional experimental subjects and act as a template for application of PsyTrack to new datasets.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Mouse Subjects

101 experimental subjects were all female and male C57BL/6J mice aged 3–7 months, obtained from either Jackson Laboratory or Charles River. All procedures and experiments were carried out in accordance with the local laws and following approval by the relevant institutions: the Animal Welfare Ethical Review Body of University College London; the Institutional Animal Care and Use Committees of Cold Spring Harbor Laboratory, Princeton University, and University of California at Berkeley; the University Animal Welfare Committee of New York University; and the Portuguese Veterinary General Board. This data was first reported in IBL et al. (2020).

Rat Subjects

19 experimental subjects were male Longâ Evans rats (Rattus norvegicus) between the ages of 6 and 24 months. Animal use procedures were approved by the Princeton University Institutional Animal Care and Use Committee and carried out in accordance with National Institutes of Health standards. This data was first reported in Akrami et al. (2018).

Human Subjects

11 human subjects (8 males and 3 females, aged 22â 40) were tested and all gave their informed consent. Participants were paid to be part of the study. The consent procedure and the rest of the protocol were approved by the Princeton University Institutional Review Board. This data was first reported in Akrami et al. (2018).

METHOD DETAILS

Optimization: Psychophysical Weights

Our method requires that weight trajectories be inferred from the response data collected over the course of an experiment. This amounts to a very high-dimensional optimization problem when we consider models with several weights and datasets with tens of thousands of trials. Moreover, we wish to learn the smoothness hyperparameters θ = {σ₁, …, σ _K } in order to determine how quickly each weight evolves across trials. The theoretical framework of our approach was first introduced in Bak et al. (2016). The statistical innovations facilitating application to large datasets, as well as the initial release of our Python implementation PsyTrack (Roy et al., 2018b), were first presented in Roy et al. (2018a).

We describe our full inference procedure in two steps. The first step is optimizing for weight trajectories W given a fixed set of hyperparameters, while the second step optimizes for the hyperparameters θ given a fixed set of weights. The full procedure involves alternating between the two steps until both weights and hyperparameters converge.

For now, let W denote the massive weight vector formed by concatenating all of the K individual length-T trajectory vectors, where T is the total number of trials. We then define η = Dw, where D is a block-diagonal matrix of K identical T × T difference matrices (i.e., 1 on the diagonal and −1 on the lower off-diagonal), such that η_t = w_t − w_t−1 for each trial t. Because the prior on η is simply $\mathcal{N}(0,\text{Σ})$, where Σ has each of the ${\sigma }_k^2$ stacked T times along the diagonal, the prior for w is $\mathcal{N}(0,C)\text{with}{C}^{-1}=D^{\top }{\text{Σ}}^{-1}D$. The log-likelihood is simply a sum of the log probability of the animal’s choice on each trial, $L=\sum _{t=1}^T\log p\left(y_t\mid {\mathbf{x}}_t,{\mathbf{w}}_t\right)$.

The log-posterior is then given by

$$\log p(\mathbf{w}\mid \mathcal{D})=\frac{1}{2}\left(\log \left|C^{-1}\right|-{\mathbf{w}}^{\top }{C}^{-1}\mathbf{w}\right)+\sum _{t=1}^T\log p\left(y_t\mid {\mathbf{x}}_t,{\mathbf{w}}_t\right)+const,$$ (Equation 3)

where $\mathcal{D}={\left\{\left({\mathbf{x}}_t,y_t\right)\right\}}_{t=1}^T$ is the set of user-defined input features (including the stimuli) and the animal’s choices, and const is independent of w.

Our goal is to find the w that maximizes this log-posterior; we refer to this maximum a posteriori (MAP) vector as w_MAP. With TK total parameters (potentially 100’s of thousands) in w, most procedures that perform a global optimization of all parameters at once (as done in Bak et al. (2016)) are not feasible; for example, related work has calculated trajectories by maximizing the likelihood using local approximations (Smith et al., 2004). Whereas the use of the Hessian matrix for second-order methods often provides dramatic speed-ups, a Hessian of (TK)² parameters is usually too large to fit in memory (let alone invert) for T > 1000 trials.

On the other hand, we observe that the Hessian of our log-posterior is sparse:

$$H=\frac{{\partial }^2}{\partial {\mathbf{w}}^2}\log p(\mathbf{w}\mid \mathcal{D})=C^{-1}+\frac{{\partial }^{2}L}{\partial {\mathbf{w}}^2}$$ (Equation 4)

where $C^{-1}$ is a sparse (banded) matrix, and ${\partial }^{2}L/\partial {\mathbf{w}}^2$ is a block-diagonal matrix. The block diagonal structure arises because the log-likelihood is additive over trials, and weights at one trial t do not affect the log-likelihood component from another trial t'.

We take advantage of this sparsity, using a variant of conjugate gradient optimization that only requires a function for computing the product of the Hessian matrix with an arbitrary vector (Nocedal and Wright, 2006). Since we can compute such a product using only sparse terms and sparse operations, we can utilize quasi-Newton optimization methods in SciPy to find a global optimum for w_MAP, even for very large T (Jones et al., 2001).

Optimization: Smoothness Hyperparameters

So far we have addressed the problem of finding a global optimum for w, w_MAP, given a specific hyperparameter setting θ; now we must also find the optimal hyperparameters. A common approach for selecting hyperparameters would be to optimize for cross-validated log-likelihood. Given the potential number of different smoothness hyperparameters and the computational expense of calculating w_MAP, this is not feasible. We turn instead to an optimization of the (approximate) marginal likelihood, or model evidence, called empirical Bayes (Bishop, 2006).

To select between models optimized with different θ, we use a Laplace approximation to the posterior, $p(\mathbf{w}\mid \mathcal{D},\theta )\approx \mathcal{N}\left(\mathbf{w}\mid {\mathbf{w}}_{\text{MAP}},-H^{-1}\right)$, to approximate the marginal likelihood as in (Sahani and Linden, 2003):

$$p(\mathbf{y}\mid \mathbf{x},\theta )=\frac{p(\mathbf{y}\mid \mathbf{x},\mathbf{w})p(\mathbf{w}\mid \theta )}{p(\mathbf{w}\mid \mathcal{D},\theta )}\approx \frac{\exp (L)\cdot \mathcal{N}(\mathbf{w}\mid 0,C)}{\mathcal{N}\left(\mathbf{w}\mid {\mathbf{w}}_{\text{MAP}},-H^{-1}\right)}.$$ (Equation 5)

Naive optimization of θ requires a re-optimization of w for every change in θ, strongly restricting the dimensionality of tractable θ. Under such a constraint, the simplest approach is to reduce all σ_k to a single σ, thus assuming that all weights have the same smoothness (as done in Bak et al. (2016)).

Here we use the decoupled Laplace method (Wu et al., 2017; Roy et al., 2018a) to avoid the need to re-optimize for our weight parameters after every update to our hyperparameters by making a Gaussian approximation to the likelihood of our model. This optimization is given in Algorithm 1. By circumventing the nested optimizations of θ and w, we can consider larger sets of hyperparameters and more complex priors over our weights (e.g. σ_day) within minutes on a laptop (see Figure S1). In practice, we also parametrize θ by fixing σ_k,t−0 = 16, an arbitrary large value that allows the likelihood to determine w₀ rather than forcing the weights to initialize near some predetermined value via the prior.

Algorithm 1.

Optimizing hyperparameters with the decoupled Laplace approximation

Require: inputs x, choices y
Require: initial hyperparameters θ0, subset of hyperparameters to be optimized θOPT
1:	tepeat
2:	Optimize for w given current θ → wMAP, Hessian of log-posterior Hθ, log-evidence E
3:	Determine Gaussian prior $\mathcal{N}\left(0,C_{\theta }\right)$ and Laplace appx. posterior $\mathcal{N}\left({\mathbf{w}}_{\text{MAP}},-H_{\theta }^{-1}\right)$
4:	Calculate Gaussian approximation to likelihood $\mathcal{N}\left({\mathbf{w}}_L,\text{Γ}\right)$ using product identity, where ${\text{Γ}}^{-1}=-\left(H_{\theta }+C_{\theta }^{-1}\right)\text{and}{\mathbf{w}}_L=-\text{Γ}{H}_{\theta }{\mathbf{w}}_{\text{MAP}}$
5:	Optimize E w.r.t. θOPT using closed form update (with sparse operations) ${\mathbf{w}}_{\text{MAP}}=-H_{\theta }^{-1}{\text{Γ}}^{-1}{\mathbf{w}}_L$
6:	Update best θ and corresponding best E
7:	until θ converges
8:	return wMAP and θ with best E

Selection of Input Variables

The variables that make up the model input x are entirely user-defined. The decision as to what variables to include when modeling a particular dataset can be determined using the approximate log-evidence (log of Equation 5). The model with the highest approximate log-evidence would be considered best, though this comparison could also be swapped for a more expensive comparison of cross-validated log-likelihood (using the cross-validation procedure discussed below).

Non-identifiability is another issue that should be taken into account when selecting the variables in the model. A non-identifiability in the model occurs if one variable in x is a linear combination of some subset of other variables, in which case there are infinite weight values that all correspond to a single identical model. Fortunately, the posterior credible intervals on the weights will help indicate that a model is in a non-identifiable regime — since the weights can take a wide range of values to represent the same model, the credible intervals will be extremely large on the weights contributing to the non-identifiability. See Figure S3B for an example and further explanation.

Parameterization of Input Variables

It is important that the variables used in X are standardized such that the magnitudes of different weights are comparable. For categorical variables, we constrain values to be {−1, 0, +1}. For example, the Previous Choice variable is coded as a − 1 if the choice on the previous trial was left, +1 if right, and 0 if there was no choice on the previous trial (e.g. on the first trial of a session). Additionally, variables depending on the previous trial can be set to 0 if the previous trial was a mistrial. Mistrials (instances where the animal did not complete a trial, e.g., by violating a “go” cue) are otherwise omitted from the analysis. The choice bias is fixed to be a constant +1.

Continuous variables can be more difficult to parameterize appropriately. In the Akrami task, each of the variables for Tone A, Tone B, and Previous Tones are standardized such that the mean is 0 and the standard deviation is 1. The left and right contrast values used in the IBL task present a more difficult normalization problem. Suppose the contrast values were used directly. This would imply that a mouse should be twice as sensitive to a 100% contrast than to a 50% contrast. Empirically, however, this is not the case: mice tend to have little difficulty distinguishing either and perform comparably on these “easy” contrast levels. Nonetheless, we used both contrast values as input to the same contrast weight, so the model always predicts a significant difference in behavior between 50% and 100% contrasts.

To improve accuracy of the model, we transformed the stimulus contrast values to better match the perceived contrasts of different stimuli, motivated by the fact that responses in the early visual system are not a linear function of physical contrast (Busse et al., 2011). For all mice, we used a fixed transformation of the contrast values used in the experiment (though this transformation could in principle be tuned separately for each mouse). The following tanh transformation of the contrasts x has a free parameter p which we set to p = 5 throughout the paper: ${\widehat{x}}_p$ = tanh(px)/tanh(p). Specifically, this maps the contrast values from [0, 0.0625, 0.125, 0.25, 0.5, 1] to [0, 0.302, 0.555, 0.848, 0.987, 1]. See Figure S4 for a worked example of why this parametrization is necessary.

More generally, this particular transformation of contrasts allows us to avoid the pressure exerted on our likelihood by the most extreme levels of perceptual evidence (e.g. 100% contrast levels). In many behavior fitting procedures, this issue is avoided by the inclusion of an explicit lapse rate which discounts the influence of incorrect choices despite strong perceptual evidence. Since our model does not include explicit lapse rates, transformations to limit the influence of the strongest stimuli may be necessary for robust fitting under many psychophysical conditions (Nassar and Frank, 2016).

IBL Task

Here we review the relevant features of the task and mouse training protocol from the International Brain Lab task (IBL task). Please refer to IBL et al. (2020) for further details.

Mice are trained to detect of a static visual grating of varying contrast (a Gabor patch) in either the left or right visual field (1A). The visual stimulus is coupled with the movements of a response wheel, and animals indicate their choices by turning the wheel left or right to bring the grating to the center of the screen (Burgess et al., 2017). The visual stimulus appears on the screen after an auditory “go cue” indicates the start of the trial and only if the animal holds the wheel for 0.2–0.5 sec. Correct decisions are rewarded with sweetened water (10% sucrose solution, Guo et al. (2014)), while incorrect decisions are indicated by a noise burst and are followed by a longer inter-trial interval (2 seconds).

Mice begin training on a “basic” version of the task, where the probability of a stimulus appearing on the left or the right is 50:50. Training begins with a set of “easy” contrasts (100% and 50%), and harder contrasts (25%, 12.5%, 6.25%, and 0%) are introduced progressively according to predefined performance criteria. After a mouse achieves a predefined performance criteria, a “biased” version of the task is introduced where probability switches in blocks of trials between 20:80 favoring the right and 80:20 favoring the left. The length of each block is sampled from an exponential distribution of mean 50 trials, with a minimum block length of 20 trials and a maximum block length of 100 trials.

Akrami Task

Here we review the relevant features of the task, as well as the rat and human subject training protocols from the Akrami task. Please refer to Akrami et al. (2018) for further details.

Rats were trained on an auditory delayed comparison task, adapted from a tactile version (Fassihi et al., 2014). Training occurred within three-port operant conditioning chambers, in which ports are arranged side-by-side along one wall, with two speakers placed above the left and right nose ports. Figure 5A shows the task structure. Rat subjects initiate a trial by inserting their nose into the centre port, and must keep their nose there (fixation period), until an auditory “go” cue plays. The subject can then withdraw and orient to one of the side ports in order to receive a reward of water. During the fixation period, two auditory stimuli, Tones A and B, separated by a variable delay, are played for 400 ms, with short delay periods of 250 ms inserted before Tone A and after Tone B. The stimuli consist of broadband noise (2,000–20,000 Hz), generated as a series of sound pressure level (SPL) values sampled from a zero-mean normal distribution. The overall mean intensity of sounds varies from 60– 92 dB. Rats should judge which out of the two stimuli, Tones A and B, had the greater SPL standard deviation. If Tone A > B, the correct action is to poke the nose into the right-hand nose port in order to collect the reward, and if Tone A < B, rats should orient to the left-hand nose port.

Trial durations are independently varied on a trial-by-trial basis, by varying the delay interval between the two stimuli, which can be as short as 2s or as long as 6s. Rats progressed through a series of shaping stages before the final version of the delayed comparison task, in which they learned to: associate light in the centre poke with the availability of trials; associate special sounds from the side pokes with reward; maintain their nose in the centre poke until they hear an auditory “go” signal; and compare the Tone A and B stimuli. Training began when rats were two months old, and typically required three to four months for rats to display stable performance on the complete version of the task.

In the human version of the task, similar auditory stimuli to those used for rats were used (see Figure 7A). Subjects received, in each trial, a pair of sounds played from ear-surrounding noise-cancelling headphones. The subject self-initiated each trial by pressing the space bar on the keyboard. Tone A was then presented together with a green square on the left side of a computer monitor in front of the subject. This was followed by a delay period, indicated by “WAIT!” on the screen, then Tone B was presented together with a red square on the right side of the screen. At the end of the second stimulus and after the go cue, subjects were required to compare the two sounds and decide which one was louder, then indicate their choice by pressing the “k” key with their right hand (Tone B was louder) or the “s” key with their left hand (Tone A was louder). Written feedback about the correctness of their response was provided on the screen, for individual trials as well as the average performance updated every ten trials.

A Practical Guide

In order to facilitate easy application of our model to new datasets, we have assembled a list of practical considerations. Many of these have already been addressed in the main text and in the STAR Methods, but we will provide a comprehensive list here for easy access. We divide these considerations into three sections. First, model specification for considerations that arise before attempting to apply PsyTrack to new behavioral data. Second, fitting and model-selection for considerations that occur when trying to obtain the best possible characterization of behavior with the model. And finally, post-modeling analysis which is concerned with the interpretation and validation of the model results.

Model specification

• Is the behavior appropriately described by a binary choice variable?

• The current method cannot handle more than two choices, though the extension to the multinomial setting is an exciting future direction that has already received some attention (Bak and Pillow, 2018).

• Early training in many tasks often results in a high proportion of “mistrials,” i.e. trials where the animal responded in an invalid (rather than incorrect) way. These mistrials are omitted in our model (though they can indirectly influence valid trials via history regressors).

• What sort of variability is expected from the behavior?

• If there is reason to believe that behavior is static (e.g. human behavior or behavior from the end of training), then PsyTrack may not offer anything beyond standard logistic regression. However, one major benefit is that PsyTrack will infer static behavior rather than assume it (see Figure 7).

• If behavior is expected to “jump” at known points in training (e.g. in-between sessions), consider using σ_day to accommodate that behavior (see Figure 2C, also Figure S6 for creative usage of σ_day).

• If behavior is expected to “jump”, but it’s uncertain when those sudden changes might occur, be aware of how the model makes a smooth approximation to a sudden change (Figure S2).

• What input variables should be tried?

• Relevant task stimuli should certainly be included. Choice bias is also a good bet.

• The irrelevant input variables can be harder to settle upon. It is often worth a preliminary analyses of the empirical data to see if certain dependencies are clearly present (e.g. Figure 5C-E verifies a behavioral dependence on the choice and correct answer of the previous trial).

Fitting and model-selection

• Which candidate input variables should ultimately be chosen?

• For models with the same number of hyperparameters, we use the model evidence (Equation 5) to perform model selection.

• For models with different numbers of hyperparameters, we can use the Bayesian Information Criterion (BIC), given by − 2E + KlogT, where E is the log-evidence, K is the number of hyperparameters, and T is the number of trials, and selecting the model with lowest BIC.

• Users may also perform model selection via cross-validation. This involves dividing the data into a training and test set, then selecting the model with highest cross-validated log-likelihood on the test set. This approach is more principled than the BIC but computationally more expensive.

• How should input variables be parametrized?

• The default option is {−1, 0, +1} for discrete variables and to standardize continuous variables (subtract mean and divide by standard deviation).

• If weights ever grow to be greater than 5 (or less than −5), this is generally a red flag. This often means that the corresponding variable should be reparametrized to discount the effect of extreme evidence (see Figure S4 and STAR Methods).

• Example alternate parametrizations in the current work include: (i) combining the left and right contrast weights in the IBL task into a single contrast weight (where left contrasts are encoded as negative values); (ii) increasing the number of history regressors in the Akrami task to capture more specific effects (e.g. a weight to capture the specific impact of previously choosing rightward on a leftward trial).

• Again, model evidence (Equation 5) can be used to decide between different parametrizations.

• Over what time frame should the model be applied?

• While the weights of the model vary smoothly, the hyperparameters do not. For example, if you apply the model to two consecutive sessions where a particular weight is static for the first session then highly variable for the second session, the model will settle on a compromise value for that weight’s σ. It may be preferred in this instance to apply the model to each session separately.

• If you are looking for fine-scale fluctuations (e.g. bias weight fluctuations in response to bias blocks in Figure 4), it is often better to look at shorter time frames, down to a single session.

Post-modeling analysis

• How should the weights of a model be interpreted?

• The credible intervals around the weights can help gauge the model’s uncertainty about that weight’s value at a particular point in training (and also alert you to non-identifiability in your input variables, see Figure S3).

• Keep in mind that the weights trajectories are conditioned on a point estimate (the MAP estimate) of the smoothness hyperparameters. Uncertainty in the σ values can also be calculated (Figure 2B+D).

• Remember that the model is not causal: information from future trials is free to affect the weight values at earlier points in training (see Figure S6).

• PsyTrack is a descriptive, not normative, model of behavior. There is no notion of what an animal ought to be doing; in fact, task rewards do not play a part in the model inference at all (though previous rewards could be included as an optional input variable).

• How should the results of a model be validated?

• The best way to validate a model is to compare model predictions (optimally using cross-validated weights) against empirical measure direct from the choice behavior.

• For example, Figure 5C-E validates that the added history regressors are indeed capturing a dependence on the previous trial (especially when compared to Figure S7C-E). Figure S5 validates the predictions of the model against to the standard psychometric curve.

QUANTIFICATION AND STATISTICAL ANALYSIS

Cross-validation Procedure

When making predictions about specific trials, the model should not be trained using those trials. We implement a 10-fold cross-validation procedure where the model is fit using a training set composed of a random 90% of trials at a time, and the remaining 10% is used for predicting and testing. We modify the prior Σ such that the gaps created by removing the 10% of test set trials are taken into account. For example, if trial t is in the test set and trials t − 1 and t + 1 are in the training set, then we modify the value on the diagonal of Σ corresponding to trial t − 1 from σ² to 2σ² to account for the missing entry in Σ created by omitting trial t from the training set.

To predict the animal’s choice at a test trial t, we first infer the weights for a training set of trials that excludes t, as described above. Then we approximate w_t by linearly interpolating from the nearest adjacent trials in the training set. We repeat this to obtain a set of predicted weights for each trial. Using the predicted weights w_t and the input vector x_t for that trial, we can calculate a predicted choice probability P(Go Right) (as in 5), and compare this to the actual choice y_t to calculate the predicted accuracy (as in 8; see below for more details). Using the predicted weights to calculate a cross-validated log-likelihood L can be used to choose between models in lieu of approximate log-evidence.

Calculation of Posterior Credible Intervals

In order to estimate the extent to which our recovered weights w are constrained by the data, we calculate a posterior credible interval over the time-varying weight trajectories (e.g., the shaded regions shown in 5B). Specifically, we approximate the 95% posterior credible interval by using 1.96 standard deviations. The standard deviation is calculated by taking the square-root of the diagonal of the covariance matrix at w_MAP.

The covariance matrix can be approximated by the inverse Hessian, but inversion of a large matrix can be challenging. Here we adapt a fast method for inverting block-tridiagonal matrices (Rybicki and Hummer, 1991), taking advantage of the fact that our Hessian (while extremely large) has a block-tridiagonal structure, and that we only need the diagonal of the inverse Hessian. If H is the Hessian matrix of our weights at the posterior peak w_MAP (also with the highest log-evidence, according to the optimization procedure in Algorithm 1), this method calculates a diagonal matrix,

$$A=\text{diag}(H^{-1}),$$ (Equation 6)

such that we can take $\sqrt{A}$ to estimate one standard deviation for each weight on each trial. The algorithm requires order TK³ scalar operations for calculating the central blocks of our inverse Hessian (for T trials and K weights).

To calculate the posterior credible intervals for our hyperparameters θ, we take the same approach of inverting the K × K hyperparameter Hessian matrix (or 2K × 2K if σ_day is used). The difficulty here is not in inverting this Hessian matrix, since it is much smaller, but in calculating the Hessian in the first place. We calculate each entry in our Hessian manually, numerically determining each of the Κ(K + 1)/2 unique entries with finite differencing. Once we have determined the Hessian matrix for the hyperparameters, it is straightforward to calculate the 95% posterior credible intervals for each hyperparameter, using the same procedure as in the case for the weights.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Human subject behavior dataset	Akrami et al., 2018	https://doi.org/10.6084/m9.figshare.12213671.v1
Mouse behavior dataset	IBL et al., 2020	https://doi.org/10.6084/m9.figshare.11636748.v7
Rat behavior dataset	Akrami et al., 2018	https://doi.org/10.6084/m9.figshare.12213671.v1
Software and Algorithms
IBL Python Library / ONE Light	Bonacchi et al., 2019	https://github.com/int-brain-lab/ibllib/tree/master/oneibl
PsyTrack	Roy et al., 2018	https://github.com/nicholas-roy/psytrack
SciPy ecosystem	Jones et al., 2001; Hunter, 2007	https://www.scipy.org/

Highlights:

• Dynamic model for time-varying sensory decision-making behavior

• Visualize changes in behavioral strategies of mice, rats, and humans across training

• Infer how quickly different parameters change, between trials and between sessions

• Colab notebook reproduces figures and analyses, facilitating application to new data