Abstract
Cryopreservation in a vitrified state has vast potential for long-term storage of tissues and organs that may be damaged by ice formation. However, the toxicity imparted by the high concentration of cryoprotectants (CPAs) required to vitrify these specimens remains a hurdle. To address this challenge, we previously developed a mathematical approach to design less toxic CPA equilibration methods based on the minimization of a toxicity cost function. This approach was used to design improved methods for equilibration of bovine pulmonary artery endothelial cells (BPAEC) with glycerol. To fully capitalize on the toxicity cost function approach, it is critical to describe the toxicity kinetics of additional CPAs, including multi-CPA mixtures that are commonly used for vitrification. In this work, we used automated liquid handling to characterize the toxicity kinetics of five of the most common CPAs (glycerol, dimethyl sulfoxide (DMSO), propylene glycol, ethylene glycol, and formamide), along with their binary and ternary mixtures for BPAEC. In doing so, we developed experimental methods that can be used to determine toxicity kinetics more quickly and accurately. Our results highlight some common CPA toxicity trends, including the relatively low toxicity of ethylene glycol and a general increase in toxicity as the CPA concentration increases. Our results also suggest potential new approaches to reduce toxicity, including a surprising toxicity neutralization effect of glycerol on formamide. In the future, this dataset will serve as the basis to expand our CPA toxicity model, enabling application of the toxicity cost function approach to vitrification solutions containing multiple CPAs.
Keywords: cryoprotectants, vitrification, toxicity, cell viability, automated liquid handling
1. INTRODUCTION
The ability to cryopreserve living biological samples has had far-reaching implications in many fields. For example, cryopreservation is routinely used to store bacterial and mammalian cells, making thousands of cell types available to the research community [4,12,47]. In addition, cryopreservation of gametes and embryos has dramatically improved animal breeding, and expanded options and improved outcomes for human assisted reproduction as well [34,53,55]. However, not all biological samples can be successfully cryopreserved. In particular, it remains a challenge to cryopreserve complex three-dimensional samples such as tissues and organs [22,23]. Breakthroughs in complex specimen cryopreservation would have far-reaching implications for medicine and public health including organ transplantation, banking tissues for research including drug discovery, and banking skin, blood vessels, and bone marrow for emergency preparedness [23,31,45].
Cryopreservation methods can be divided into two main categories: slow cooling and vitrification. Slow cooling involves formation of extracellular ice and is often successful for cryopreservation of suspension-phase cells. Vitrification is particularly promising for preserving specimens that are damaged by extracellular ice formation, such as adherent cells, tissues, and organs [24,38,49,59]. The main challenge with vitrification methods is that a high concentration of CPA(s) must be added to prevent ice formation. Exposure to high CPA concentrations can cause damage by two mechanisms: 1) mechanical (osmotic) damage from specimen volume excursions, and 2) chemical (toxicity) damage from unfavorable CPA interactions with the specimen [11,13,15,22,43]. Osmotic damage can be overcome by slowly adding and removing CPA to prevent excessive volume excursions [11,13,30,43,51]. However, toxicity is more challenging and is considered the single biggest hurdle to vitrification [2,21,22,37].
Before toxicity can be reduced, it first needs to be characterized. One of the biggest challenges with measuring toxicity is decoupling it from osmotic damage. Several previous studies involve direct exposure to high CPA concentrations [1,63]. This can cause osmotic damage, making it impossible to distinguish whether a corresponding loss of viability is due to toxicity or osmotic damage. Studies that have attempted to decouple toxicity from osmotic damage include the chondrocyte studies of Jomha et al [37], Almansoori et al [2], and Fahmy et al [13]. These studies provide an in-depth analysis of the toxicity of CPAs to chondrocytes, including development of a mathematical model that enables prediction of toxicity as a function of CPA mixture composition. However, the model does not allow prediction of CPA toxicity as a function of exposure time or temperature. The work of Fahy and colleagues [21] serves as another example of a large data repository that decouples osmotic damage from toxicity but for rabbit kidneys. They propose an interesting empirical relationship linking the toxicity of a vitrification solution to its composition, which may facilitate selection of less toxic compositions for vitrification, but again, the relationship lacks a time and temperature dependency. Overall, current data sets are lacking, and there is a need for a more comprehensive understanding of toxicity kinetics for design of CPA equilibration methods in which exposure time and temperature are varied.
The vast majority of previous efforts to reduce CPA toxicity have used an empirical approach. For example, Fahy and colleagues chose to iteratively exploit CPA solution compositions and the corresponding perfusion pressure, temperature, and duration as a way to overcome CPA toxicity, and thus to vitrify rabbit kidneys [14–19,22–27]. Others have explored the use of additives in an attempt to reduce CPA toxicity [52,65,66]. While these empirical approaches have led to some promising results, including the long-term survival of a lone rabbit kidney after vitrification [24], there are too many potential solution compositions and/or equilibration methods to exhaustively test experimentally.
Mathematical modeling can potentially address this limitation by exploring the range of possible CPA equilibration methods in silico and identifying promising approaches toward reducing CPA toxicity. A recent example is the use of diffusion predictions to design methods for equilibration of articular cartilage with CPAs [36,38,58]. The predictions were used to design a multistep vitrification protocol with the goal of reaching a desired minimum CPA concentration in the shortest amount of time [58]. Karlsson and colleagues also used mathematical modeling to minimize the duration of CPA equilibration in an attempt to reduce CPA toxicity [39]. However, minimizing CPA equilibration time does not necessarily correspond to minimizing toxicity [6]. Another example comes from Lawson et al [43] where heat and mass transfer were modeled as well as CPA toxicity. Lawson et al [43] used their model to predict cell viability for several protocols of interest, but they stopped short of using their model for optimization of CPA equilibration methods to minimize toxicity.
In previous studies, we sought to minimize toxicity through the development of a toxicity cost function [5,10,11]. This cost function approach enables the estimation of toxicity during CPA equilibration, making it possible to mathematically optimize methods that minimize toxicity. We implemented the toxicity cost function approach for adherent BPAEC and were able to predict a novel protocol for glycerol addition and removal that greatly improved cell viability compared to conventional equilibration protocols [11]. To date, the toxicity cost function approach has only been used to design methods involving a single CPA. However, many vitrification protocols use multi-CPA mixtures in an attempt to mitigate toxicity [22,38], highlighting the need for development of a toxicity model that can account for multiple CPAs. Without new experimental methods that ease the workload burden over previous manual methods [11], the task of conducting the large set of experiments needed to assess multi-CPA toxicity would be cumbersome and difficult.
In this work, we quantified the toxicity of five of the most common CPAs (glycerol, DMSO, propylene glycol, ethylene glycol, and formamide), as well as their binary and ternary mixtures, using BPAEC as a model system. For these CPA mixture types, we varied CPA concentration and exposure time at room temperature. In order to carry out these experiments, we developed methods leveraging automated liquid handling using a Hamilton Microlab STARlet system. The Hamilton system features a 96-channel head that can manipulate fluid in every well of a 96-well plate at the same time, and it has 8 independently moving channels that we used to prepare CPA solution reservoirs. As a result, automated liquid handling allowed us to randomize CPA treatment locations in the 96-well plate format, as well as improve the accuracy of our experiments and increase throughput when compared to our previous manual methods [11]. The resulting comprehensive toxicity data set provides a foundation for future expansion of the toxicity cost function approach to vitrification using CPA mixtures.
2. METHODS AND MATERIALS
2.1. Experimental Overview
This work is a direct extension of our previous work [11] where we measured the viability of an adherent monolayer of BPAEC after exposure to glycerol while varying exposure time, temperature, and glycerol concentration. By varying these experimental conditions, we were able to characterize the toxicity rate of glycerol as a function of concentration and temperature. In this work, we again seek to characterize CPA toxicity but for more CPA types and for mixtures containing multiple CPAs. Table 1 details the experimental conditions tested.
Table 1.
CPA exposure conditions tested.
| CPA Mixture Type | Single CPA | Binary Mixture | Ternary Mixture |
|---|---|---|---|
| CPAs | Glycerol, DMSO, propylene glycol, ethylene glycol, formamide | 10 binary combinations of the 5 CPAs | 10 ternary combinations of the 5 CPAs |
| Total CPA Concentrations (molal) | 1, 3, 5, 7, 10 | 1, 3, 5, 7, 10 (equi-molal split between CPAs) | 7 (equi-molal split between CPAs) |
| Times (min) | 5, 10, 30, 60 | ||
| Temperature (°C) | Room temperature (25 ± 2.1) | ||
Table 1 highlights that we tested a total of 340 experimental conditions. For each condition, multiple solution exchange steps are required, including washing the cells at the beginning and end of the protocol, as well as multi-step addition and removal of CPA to avoid osmotic damage. This results in thousands of pipetting operations, many of which need to be timed precisely. To facilitate these pipetting operations, we utilized an automated liquid handling instrument at the Oregon State University High Throughput Screening Services Laboratory. In our previous work, we conducted CPA exposure experiments manually, and we will discuss later on the benefits of moving to an automated liquid handling methodology.
Although we changed our liquid handling methodology, the core principles of the experiment remained the same. Namely, we cultured the BPAEC in 96-well plates, exposed the BPAEC to various solutions through repeated aspirate/dispense operations, and measured viability before and after CPA exposure using the PrestoBlue assay.
2.2. Cell Culture
BPAEC were purchased from Cell Applications, Inc. (San Diego, CA). The cells were received at passage 2 and subsequently expanded to passage 5 using culture methods described previously [11,29], at which point they were cryopreserved in 90% culture medium (Dulbecco’s Modified Eagle Medium augmented with 5% fetal bovine serum, 100 U/mL penicillin and 100 μg/mL streptomycin [11,29]) and 10% DMSO (Corning Inc., Corning, NY). These cryopreserved cells were used for all experiments. For each experiment, a vial of cells was thawed (~106 cells/vial), seeded into a T-75 flask containing 15 mL of culture medium, and cultured for 24-30 h, at which point the cells had reached about 80% confluency. At that time, the cells were harvested and seeded into black clear bottom 96-well plates (Greiner Bio-One, Monroe, NC) at a density of 1500 cells/well. The cells were cultured in the well plates for two days, at which point an initial PrestoBlue assay was performed. The cells were then treated with CPA solutions and cultured for an additional 20-24 h before performing the final PrestoBlue assay. This approach allowed us to maximize confluency to increase the signal in the PrestoBlue assay, while making sure that confluency did not reach 100% at the end of the experiment on the third day.
2.3. Experimental Solutions for CPA Addition and Removal
We employed multi-step CPA addition and removal to mitigate osmotic damage, as described in our previous study [11]. Table 2 shows the necessary steps for maximum CPA concentrations ranging between 1 and 10 molal, including the time the cells were exposed to each solution (see Appendix for how CPA addition and removal steps were designed). Solutions were prepared in a similar fashion to our previous work [11]. The following chemicals were used to prepare the buffer solutions: MgCl2·6H2O (VWR Chemicals BDH, Radnor, PA), CaCl2·2H2O (Fisher Chemical, Waltham, MA), NaCl (VWR Chemicals BDH, Radnor, PA), KCl (EMD Millipore, Burlington, MA), and HEPES (VWR Chemicals BDH, Radnor, PA). The following CPAs were used: glycerol (Macron Fine Chemicals, Radnor, PA), DMSO (Fisher Chemical, Waltham, MA), propylene glycol (VWR Chemicals BDH, Radnor, PA), ethylene glycol (Macron Fine Chemicals, Radnor, PA), and formamide (Sigma-Aldrich, St. Louis, MO).
Table 2.
Multi-step methods for CPA exposure. For each step, the solution composition is listed first followed by the exposure time in parentheses.
| Max CPA Conc. | Step 1 | Step 2 | Step 3 | Step 4 | Step 5 | Step 6 | Step 7 | Step 8 | Step 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 molal | Isotonic Buffer (2.5 min) | 1 molal CPA in Isotonic Buffer (Variable) | Hypertonic Buffer (3 min) | Isotonic Buffer (5 min) | Media (20-24 h) | ||||
| 3 molal | Isotonic Buffer (2.5 min) | 1 molal CPA in Isotonic Buffer (4 min) | 3 molal CPA in Isotonic Buffer (Variable) | 1 molal CPA in Hypertonic Buffer (4.5 min) | Hypertonic Buffer (4.5 min) | Isotonic Buffer (5 min) | Media (20-24 h) | ||
| 5 molal | Isotonic Buffer (2.5 min) | 1 molal CPA in Isotonic Buffer (4 min) | 3 molal CPA in Isotonic Buffer (2 min) | 5 molal CPA in Isotonic Buffer (Variable) | 3 molal CPA in Hypertonic Buffer (6.5 min) | 1 molal CPA in Hypertonic Buffer (4.5 min) | Hypertonic Buffer (4.5 min) | Isotonic Buffer (5 min) | Media (20-24 h) |
| 7 molal | Isotonic Buffer (2.5 min) | 1 molal CPA in Isotonic Buffer (4.5 min) | 3 molal CPA in Isotonic Buffer (4.5 min) | 7 molal CPA in Isotonic Buffer (Variable) | 3 molal CPA in Hypertonic Buffer (7 min) | 1 molal CPA in Hypertonic Buffer (7 min) | Hypertonic Buffer (5 min) | Isotonic Buffer (5 min) | Media (20-24 h) |
| 10 molal | Isotonic Buffer (2.5 min) | 1 molal CPA in Isotonic Buffer (4.5 min) | 3 molal CPA in Isotonic Buffer (10.5 min) | 10 molal CPA in Isotonic Buffer (Variable) | 3 molal CPA in Hypertonic Buffer (12.5 min) | 1 molal CPA in Hypertonic Buffer (7 min) | Hypertonic Buffer (5 min) | Isotonic Buffer (5 min) | Media (20-24 h) |
As shown in Table 2, CPA solutions were prepared in either isotonic or hypertonic buffer, at CPA concentrations ranging from 1 molal to 10 molal. This results in a total of 155 distinct CPA solutions. Rather than make 155 solutions from scratch, we prepared the solutions by diluting stock solutions as described in our previous work [11]. To make all of the 155 unique solutions, we only had to make 7 different stocks: isotonic HEPES buffered saline, hypertonic HEPES buffered saline, and 10 molal isotonic stocks of each of the 5 CPAs. All stock solutions were pH-adjusted to 7.3 ± 0.1 and sterile filtered.
Isotonic HEPES buffered saline was made as in our previous work [11]. The osmolality was measured to be within 2% of 300 mOsm on an Advanced Micro Osmometer Model 3300 (Advanced Instruments, Norwood, MA). The water mass concentration was determined by measuring the density of the solution and multiplying by the known water mass fraction, resulting in a value of 1 kg/L. The hypertonic HEPES buffered saline was made in the same way as its isotonic counterpart, but extra NaCl was added to bring the osmolality to 1200 mOsm, assuming a dissociation factor of 1.68 [11]. The measured osmolality was within 5% of 1200 mOsm. The water mass concentration of the hypertonic HEPES buffered saline was 0.97 kg/L.
For the CPA solutions in isotonic buffer, the concentration of nonpermeating solute was adjusted to ensure that the equilibrium cell volume was equal to the normal physiological volume. This nonpermeating solute concentration was calculated as before [11], and the 10 molal stocks were made by adding pure CPA to isotonic HEPES buffered saline with an additional amount of NaCl to reach the desired nonpermeating solute concentration. The necessary calculations for dilution of the stock solutions were made using their water mass concentrations, as described in our previous study [11]. The water mass concentrations of the 10 molal CPA stock solutions were measured to be 0.59 kg/L for glycerol, 0.60 kg/L for DMSO, 0.58 kg/L for propylene glycol, 0.66 kg/L for ethylene glycol, and 0.72 kg/L for formamide.
To make a CPA solution in isotonic buffer, 10 molal CPA stock solutions were diluted with isotonic HEPES buffered saline. The resulting CPA solution has a nonpermeating solute concentration that allows the cells to equilibrate at the normal physiological volume. For the CPA solutions in hypertonic buffer, the same dilution strategy was used but with hypertonic HEPES buffered saline. The hypertonic nature of the solution is not intended to allow the cell to equilibrate at its physiological volume but to counteract cell swelling during CPA removal.
2.4. Automated Liquid Handling
2.4.1. Overview
For the CPA exposure experiments, a Hamilton Microlab STARlet liquid handler (Hamilton Company, Reno, NV) was employed. The Hamilton system has both a 96-channel head and 8 independently moving channels that were used to conduct experiments. To carry out the experimental steps shown in Table 2, fluid was transferred from a source plate to the cell-seeded assay plate using the 96-channel head. Multiple source plates were needed that contained the necessary solutions for each step of the CPA addition and removal process. These source plates were prepared using the 8 independently moving channels. Figure 1 shows a picture of the Hamilton system and highlights its key features, along with demonstrating the fluid transfer scheme.
Figure 1.

Pictures showing the key features of the Hamilton Microlab STARlet liquid handler. The 8 independently moving channels were used to fill source plates (A), and the 96-channel head was used to transfer fluid from a source plate to an assay plate (B).
2.4.2. Treatment Layouts on a 96-Well Assay Plate
With the capabilities of the Hamilton system, we were able to randomize the experimental conditions on a well-by-well basis on the assay plate. Plate layout maps were generated with a custom MATLAB script. We included 5 replicates per experimental condition, allowing us to have a total of 19 experimental conditions on a plate. Fifteen experimental conditions were dedicated to different CPA treatments, with one treatment having a randomly assigned 6th replicate. The remaining four experimental conditions were used for a positive control, negative control, and two different background media controls (see Fig. 3 in Results and Discussion for a plate layout example).
Figure 3.
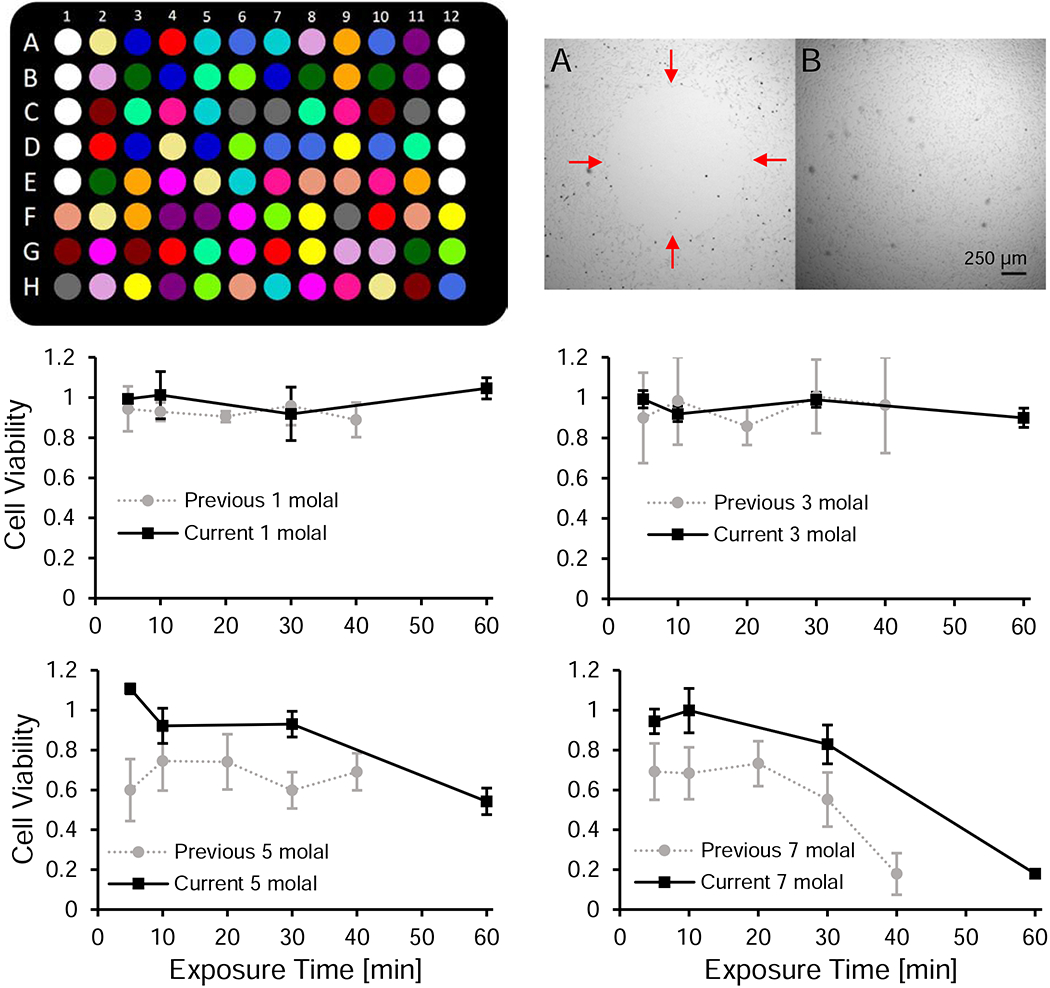
Automated liquid handling reduces experimental variability and enables high-throughput measurement of CPA toxicity. Top left panel: schematic of a randomized 96-well plate map. The cell-free media controls (white wells) are in A1-E1 and A12-E12. The remaining wells are seeded with cells and treatments are randomly distributed throughout the rest of the plate. These include the positive controls (dark green), negative controls (red), and CPA treatments (15 unique colors). Top right panel: side by side comparison of a cell monolayer before (A) and after (B) optimizing the pipetting settings. There is a distinct hole in the monolayer in the before image with red arrows indicating the boundary. The images were taken under different lighting conditions and have been contrast enhanced. Bottom panels: comparison of the cell viability data between our previous [11] and current work for exposure to 1, 3, 5, and 7 molal glycerol. Error bars represent the standard deviation. We subjected our previous data set to the outlier analysis described in the methods section of the current study.
The positive control was subjected to the same liquid handling as a CPA treatment, but the fluid used at every step was isotonic buffer, with the exception of the media wash in the final step. The negative control was washed with isotonic buffer during the first step and then had no liquid handling until the penultimate step, at which point 70% ethanol in water was introduced. The media control wells were not seeded with cells and were kept in the same position on every plate to streamline the seeding process. One media control was subjected to the same liquid handling as the positive control. The other media control was only subjected to a water wash, and fresh culture medium was only added right before the PrestoBlue assay was conducted. The first media control served as the background fluorescence to subtract off for the assay, and the second media control serves as a check for contamination. The Hamilton system is open to the atmosphere, and the experiment takes place in semi-sterile conditions. If contamination were an issue and a resazurin reducing contaminant was present, we would expect a difference in the fluorescence signal to be seen between the two media controls. In our experiments, we did not see any spikes in the fluorescence signal of the second media control when compared to the first, nor did we see any evidence of contamination from random well checks under the microscope.
2.4.3. Preparation of 96-Well Source Plates
To enable the appropriate solution to be dispensed into each well at each step of the CPA addition and removal process, deep well plates were prepared containing solutions that mapped to the randomized treatment conditions of the assay plate. We refer to these deep well plates as source plates. A separate source plate was needed for each step in the CPA addition and removal process. The wash steps that do not include a CPA have a simple enough layout to fill source plates by manual pipetting, which was done under sterile conditions. However, source plates that require a CPA solution are nearly impossible to fill by hand because 16 different solutions with 5-6 replicates each must be dispensed into a randomized well. To overcome this challenge, we used the Hamilton system to fill the source plates that contained CPA solutions. The Hamilton system has 8 channels that can move individually, allowing automated control of well-by-well filling, and the 8 channels provide the means to successfully execute an experiment with randomized treatment locations. A custom MATLAB script was written that takes a plate map and generates the necessary commands for the Hamilton to fill a randomized source plate.
2.4.4. Automated Addition and Removal of CPA
After the initial PrestoBlue assay, the assay plate was immediately moved to the Hamilton system to carry out the subsequent liquid handling steps. For every experimental step, the following core operations were performed for every well: 1) aspirate, 2) dispense 250 μL, 3) aspirate, and 4) dispense 250 μL. We optimized the settings on the Hamilton system to minimize the amount of dead volume after aspiration while not disturbing the cell monolayer, which resulted in using an aspirate and dispense flowrate of 20 μL/s and a tip height offset from the bottom of the well of 500 μm.
Due to the nature of automated liquid handling, the pipette tip has to approach normal to the bottom of the well, resulting in a larger dead volume when compared to manual pipetting where the user can tilt the plate and slide the pipette tip down the side of the well. We measured a high-end well dead volume of 40 μL after aspiration, with the majority of dead volumes falling in the range of 20-40 μL. Using the high-end dead volume, the cells are exposed to approximately 86% of the intended change in fluid composition (by volume) after the first dispense and approximately 98% after the second dispense. We recorded the time the cells were exposed to a given fluid as the time between the first dispense from one source plate to the first dispense from the subsequent source plate. In the final dispense step on the Hamilton system, we transferred 180 μL of media (rather than 250 μL). This was done to achieve a total media volume of about 200 μL, the desired volume for the PrestoBlue assay.
2.5. Cell Viability Assay
Cell viability was assessed using PrestoBlue (Invitrogen, Waltham, MA) right before CPA exposure and then 20-24 h after CPA exposure. The 20-24 h recovery period in culture before the second PrestoBlue assay was included to allow time for apoptosis induced by CPA exposure to occur [3,9]. The assay was conducted in 200 μL of culture medium and 20 μL of PrestoBlue reagent. We measured fluorescence on a Synergy 4 plate reader (BioTek, Winooski, VT) using excitation and emission filters of 528 nm and 600 nm, respectively. The plate reader was pre-heated to 37 °C and held at this temperature throughout the assay. PrestoBlue was first added to the assay plate at room temperature, and then the plate was transferred to the plate reader and given 5 min to reach 37 °C, at which point the fluorescence was measured. After an additional 20 min the fluorescence was measured again, giving a 20 min development time. As in our previous study [11], we defined the cell viability as the final fluorescence after CPA exposure divided by the initial fluorescence before CPA exposure, normalized to the average fluorescence ratio for the positive control:
| 1 |
where F is the background-corrected fluorescence signal from the plate reader, the subscripts i and f denote the initial and final PrestoBlue assays, and superscript P denotes the positive control.
2.6. Cell Viability Data Analysis
2.6.1. Determination of Toxicity Rates
As in our previous work [11], we used a first-order kinetic model for analysis of our viability data to determine the toxicity rate. In particular, we modeled the change in the number of viable cells N as follows:
| 2 |
where λ is the sum of growth and toxicity rates. From the initial time ti to the final time tf, we assumed a constant cell growth rate. The toxicity rate was assumed to vary depending on the CPA type and concentration. As an example of our data analysis method, consider an experiment with a maximum CPA concentration of 3 molal (see Fig. 2). This experiment involves exposure to a 1 molal CPA concentration during CPA addition and removal. Our data analysis method accounts for the different toxicity rates during exposure to each of these CPA concentrations.
Figure 2.
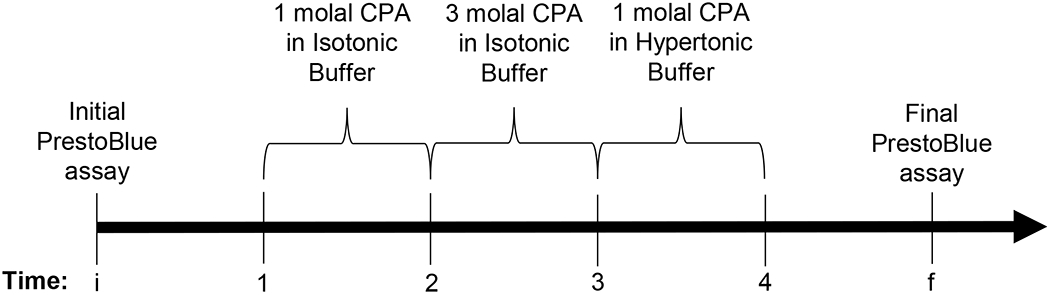
Timeline for an experiment with a maximum CPA concentration of 3 molal, showing the CPA addition and removal steps in relation to the PrestoBlue assays.
Figure 2 details that we have five distinct time periods, three of which are CPA exposure time periods. If we integrate Equation 2 for the five time periods with the convention ti = 0, we produce the following equations:
| 3a |
| 3b |
| 3c |
| 3d |
| 3e |
where α is the growth rate, k1 is the toxicity rate for 1 molal CPA exposure, and k3 is the toxicity rate for 3 molal CPA exposure. To isolate k3, we must first eliminate the growth rate. To do this, we can use the positive control, which is not exposed to CPA and hence does not exhibit CPA toxicity. For the positive control, we have from ti to tf:
| 4 |
If we multiply Equations 3a–3e and divide by Equation 4, we arrive at
| 5 |
The left-hand side of Equation 5 is equivalent to the cell viability as defined in Equation 1, since the fluorescence signal F is expected to be proportional to the number of viable cells N. The above equation includes two toxicity rates: k1 and k3. The value of k1 was first determined from experiments with a maximum CPA concentration of 1 molal (see Table 2), leaving k3 as the only unknown toxicity rate.
To find the toxicity rate k3, we performed non-linear regression in MATLAB utilizing a least squares approach. Specifically, Equation 6 was used for the regression, which is a rearrangement of Equation 5:
| 6 |
We refer to the quantity on the left-hand side of Equation 6 as the adjusted cell viability. The adjusted viability was plotted versus the duration of exposure to 3 molal CPA (i.e., t3 – t2), which we varied according to the exposure times of Table 1 (5, 10, 30, and 60 min). The adjusted cell viability is a convenient quantity for examining toxicity during exposure to the maximum CPA concentration, as its value always starts at 1.
For higher CPA concentration exposures (5, 7, and 10 molal), the same approach was used but the value of k3 in conjunction with k1 is needed to find the corresponding toxicity rate. For the most toxic CPA treatments, where cell viability was less than 1 % for even the 5 min CPA exposure, the toxicity rate could not be accurately determined.
In many cases, exposure to 1 molal or 3 molal CPA did not appreciably decrease cell viability, resulting in a best-fit toxicity rate that was not statistically different from zero. In these cases, we set the toxicity rate to zero for subsequent analysis. To assess this, we performed an F-test to estimate the p-value for the null hypothesis that the toxicity rate was equal to zero. Toxicity rates were only assumed significant for p ≤ 0.05.
2.6.2. Outlier Analysis
For outlier analysis, we employed Tukey’s (boxplot) method [61]. Outliers are identified if they are outside of the following range:
| 7 |
where Q1 is the first quartile, Q3 is the third quartile, IQR is the inter-quartile range which is the difference between the third and first quartiles, k is a constant, and x represents a specific sample value. Quartiles are found through the standard fourths method presented by Tukey. The value of k has been historically presented as 1.5 as a general rule of thumb. We opted to use of value of 2.5, which is more conservative and identifies less data points as outliers [7,28,35,61].
There are several samples in our data set that show ~0% average viability (e.g., exposure to 10 molal formamide). These samples are prone to erroneous identification of outliers. As such, we implemented outlier analysis only for samples that showed at least 1% average viability. If an outlier was identified in a positive control, the CPA treatments were normalized against the positive control sample excluding the outlier. Overall, 3.9% of the entire data set was labeled as outliers. This is comparable to the work of Hoaglin et al [35], which found approximately 8.6% of data to be labeled as outliers for k = 1.5 and 3.3% of data to be labeled as outliers for k = 3.
3. RESULTS AND DISCUSSION
3.1. Benefits of Automated Liquid Handling
The use of automated liquid handling afforded us several benefits over our past work [11] that utilized manual pipetting. These benefits can be broken down into three main categories: 1) consistency of pipetting, 2) increased throughput for faster data generation, and 3) the ability to increase the complexity of the experimental workflow, including randomization of the experimental groups within the well plate.
One of the biggest changes we made to our experimental setup was randomizing the locations of experimental conditions on a 96-well assay plate. This required preparation of multiple source plates containing appropriate wash solutions in randomized locations, a task that would have been very challenging to accomplish manually. Figure 3 (top left panel) shows a schematic of a representative 96-well plate where we tested 15 different CPA treatments. By randomizing locations on the well plate, we can distribute any systematic bias associated with location between treatments. Systematic bias has been reported due to higher rates of evaporation near the edges of the well-plate [46,64], and can also occur due to pipetting inconsistencies when using a multi-channel pipette. Overall, randomization of treatments within a well plate helps to improve results by mitigating location bias [41,42,50,57].
The automated liquid handling system also enables improved consistency compared to manual pipetting. Pipetting operations can yield erroneous results through accidental mechanical damage to cultured cells and/or imprecise aspirate/dispense volumes [33,44]. In some cases, there can even be doubt if the pipetting operation was carried out [48]. With the automated liquid handling system, we know the exact location of the pipette tip in relation to the cell monolayer, and the aspirate/dispense flowrate is precisely controlled. This enabled us to optimize settings to ensure that cells were not sheared from the surface during pipetting, as illustrated in Figure 3 (top right panel). In addition, there is a digital record that the pipetting operation was carried out, and the timing of each pipetting operation is controlled.
Taken together, plate randomization and improved pipetting consistency are expected to reduce variability and lead to more accurate results. These improvements are illustrated in the bottom panels of Figure 3, which compare viability data we obtained in the current work to the corresponding results from our previous work [11]. A noticeable difference can be seen in the error bars: the average standard deviation in our previous work was 12.9% [11], compared to 6.0% for our current work. In addition, we observed a more substantial decrease in viability after exposure to high glycerol concentrations in our previous work, especially at early time points [11]. One explanation for this difference is the removal of viable cells through manual pipetting, either due to accidental contact between the pipette tip and the culture surface or excessive aspirate/dispense rates. As a result, in our current work, we have measured toxicity rates for glycerol to be about one-half of those in our previous work [11]. Overall, increased pipetting consistency and the ability to randomize the location of treatments has allowed us to develop a more accurate methodology for measuring CPA toxicity.
As a final benefit of automated liquid handling over manual liquid handling, we not only can conduct more complicated experiments with higher precision, but we can conduct them more quickly resulting in higher throughput. As a simple comparison between the two liquid handling approaches, we can compare the number of pipetting operations between a manual 12-channel pipette and the 96-channel head of the Hamilton system. With the 96-channel head, we can perform about ~8x as many pipetting operations in the same amount of time as a 12-channel pipette, which by itself, would be expected to increase throughput ~8x. However, with manual pipetting, the user also has to manipulate the assay plate and source plates, perform multiple tip changes during a step, and manually keep track of pipetting operations and their timing—all of which takes more time than automated liquid handling. Over the course of an experimental day, we also have to consider an increase in user fatigue from having to carry out so many manual operations, which could further slow the process towards the latter part of a workday. In the end, automated liquid handling provides a platform to conduct CPA exposure experiments in a faster, more precise, and more robust manner when compared to manual pipetting.
3.2. Cell Viability Decreases after Exposure to CPA
The goal of this study was to quantify the toxicity of five of the most common CPAs: glycerol, DMSO, ethylene glycol, propylene glycol, and formamide. The bottom panels of Figure 3 show representative cell viability data after exposure to glycerol. Cell viability decreased as the glycerol concentration increased and as exposure time increased. Similar trends were observed for the other CPAs. While this loss of cell viability is consistent with CPA toxicity, there are other potential explanations, including cell detachment from the culture surface and osmotic damage.
3.3. Are Cell Losses Caused by Cell Detachment?
Although we have confirmed that negligible cell detachment from the culture surface occurs in the positive control wells, it is possible that exposure to CPA weakens cell adhesion leading to loss of viable cells into the wash solution during liquid handling. To test this, we collected the cells in the solution phase in each of the CPA removal steps after exposure to 7 molal CPA for 60 min. These cells were collected into a new well plate which mapped to the original assay plate containing the cultured cells. We refer to this new well plate as the solution plate. After each wash step, the recovered solution was added to the solution plate and centrifuged to pellet the cells, and the excess fluid was then removed before the fluid from the next step was added. This process ensures that the cells still received the intended CPA removal procedure (which was designed to prevent osmotic damage). After completing the CPA removal process, the pelleted cells in the solution plate were resuspended in media and placed alongside the original assay plate in the incubator for recovery in culture. Figure 4 shows that there is no viability signal for the solution plate for any treatment, whereas the viability of the original plate ranged from 0% to around 80%. We also examined the wells under the microscope, which revealed that cells were present in the solution plate. This indicates that cells were collected into the solution phase during the CPA removal process, but that the cells were not viable or the number of viable cells was below the detection threshold. Overall, our results show that cell losses after CPA exposure cannot be attributed to detachment of viable cells from the culture surface.
Figure 4.
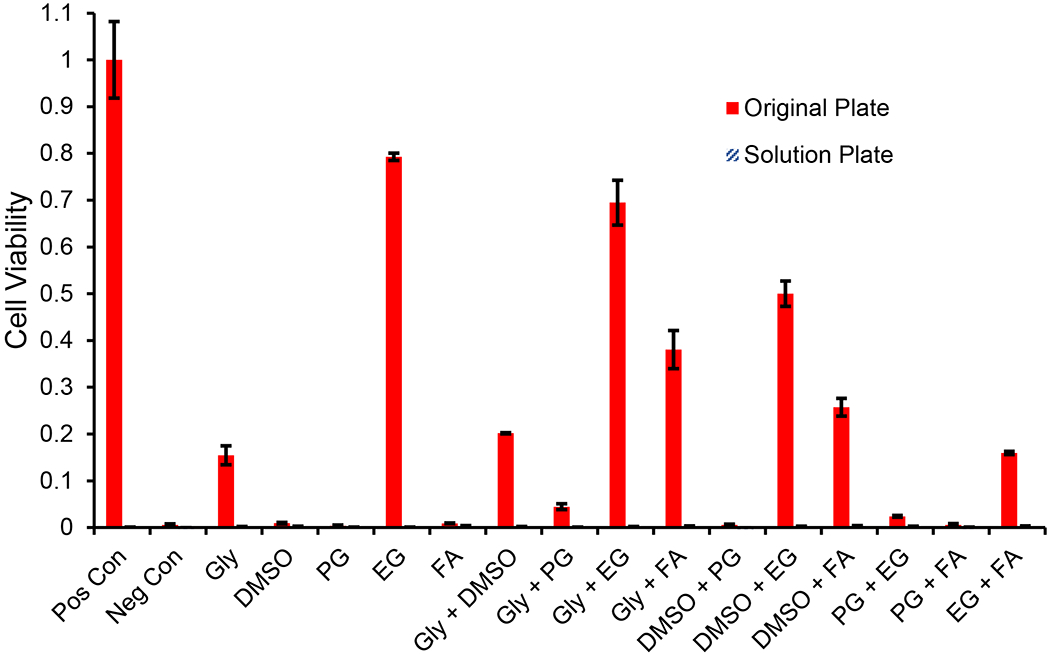
Comparison of viability between cells in the original well plate and those lost into the solution phase during CPA removal after exposure to 7 molal CPA solutions for 60 min. CPAs are abbreviated as follows: glycerol (Gly), propylene glycol (PG), ethylene glycol (EG), and formamide (FA). Solution from each wash step during CPA removal was collected into a new well plate (solution plate), which was cultured alongside the original plate for the assessment of viability. The viability of solution phase cells was negligible. Error bars represent the standard error of the mean.
3.4. Are Cell Losses Caused by Osmotic Damage?
CPA exposure can cause osmotic damage due to cell volume changes resulting from the flow of water and CPA across the cell membrane. Out of the five CPAs tested, glycerol has by far the lowest membrane permeability [29,32,54,56,62] and consequently is expected to cause the largest volume changes. As such, we designed our loading and removal procedures around cell volume predictions for glycerol. In particular, we designed multi-step procedures to ensure that the predicted cell volumes did not exceed the osmotic tolerance limits [11] (see Appendix for more details). We assessed the potential for osmotic damage in both the CPA loading and removal regimes from an experimental and theoretical point of view, as described below.
3.4.1. CPA Loading
CPA loading typically causes cell shrinkage because water leaves the cells faster than CPA can enter. In our experiments, the conditions most likely to result in osmotic damage during CPA loading are exposure to either 7 molal or 10 molal glycerol. Figure 5 shows the predicted cell volume response during each of the loading steps for maximum glycerol concentrations of 7 and 10 molal (solid lines of panels A and B, respectively). For both glycerol concentrations, the minimum predicted volume is about 30% of the physiological cell volume, which is well above the osmotic tolerance limit. Also shown in Figure 5 are conservative predictions using a glycerol permeability 2x lower than the published value (dashed lines) [29]. While more extensive shrinkage is predicted in this case, the minimum predicted volume still exceeds the osmotic tolerance limit. These theoretical predictions demonstrate that the CPA loading methods that we used in our experiments are not expected to cause osmotic damage.
Figure 5.
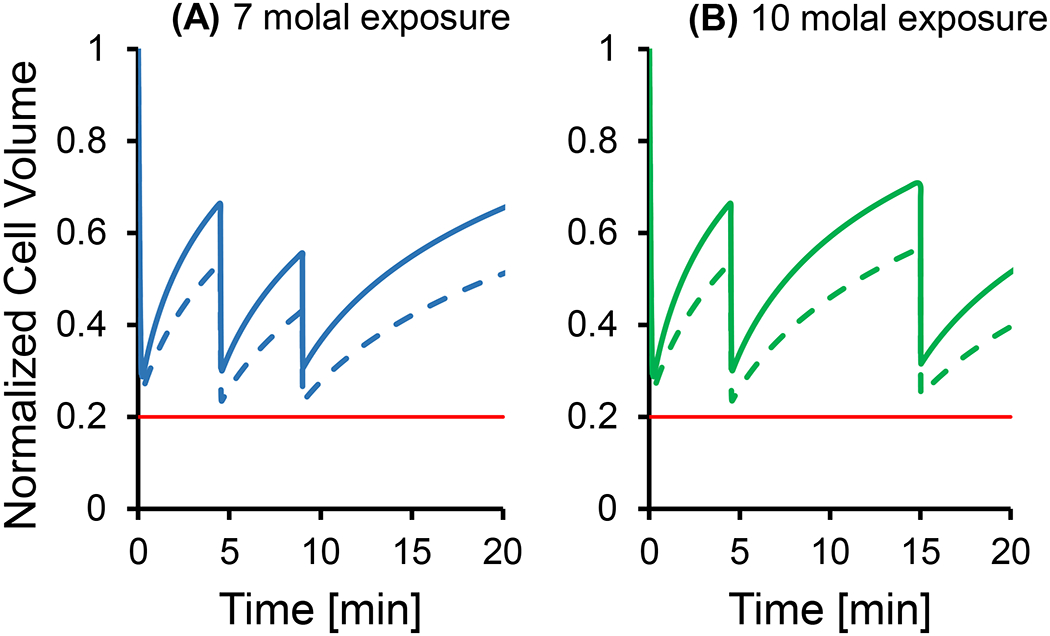
Cell volume predictions for multi-step glycerol loading procedures for exposure to 7 and 10 molal glycerol. Solid lines show predictions using published permeability values [29], while the dashed lines show predictions using a 2x lower glycerol permeability. The horizontal red line in both panels shows the lower osmotic tolerance limit [11]. In all simulations, a temperature of 25 °C was used.
Our experimental data also suggests that osmotic damage does not occur during CPA loading. Cell viability remained high (>87%) after exposure to 7 molal or 10 molal glycerol for up to 10 min, using the multi-step CPA addition processes depicted in Figure 5. Since the maximum cell shrinkage after exposure to 7 or 10 molal glycerol is predicted to occur in less than 1 min, osmotic damage from CPA loading should manifest itself in both 5 and 10 min exposures to glycerol. Therefore, the high cell viability observed for the 5 and 10 min glycerol exposures provides strong evidence that osmotic damage during CPA loading is negligible.
3.4.2. CPA Removal
During CPA removal, osmotic damage due to excessive cell swelling is the main concern. The potential for osmotic damage depends on the amount of CPA in the cell, which increases with the CPA concentration and exposure time. In our experiments, the condition most likely to cause osmotic damage during CPA removal is exposure to 10 molal glycerol for 60 min. This condition completely killed the cells, resulting in a viability of less than 1%. The condition next most likely to cause osmotic damage is exposure to 7 molal glycerol for 60 min, which resulted in a viability of 18%. In order to rule out osmotic damage as the main contributor to this loss in viability, we evaluated the 7 molal 60 min treatment using a more conservative CPA removal process in which the duration of each step was increased to 15 min (2-3 times longer than the standard procedure). As shown in Figure 6, the conservative CPA removal procedure is predicted to decrease the amount of cell swelling (panel B) compared to the standard procedure (panel A), which would be expected to reduce osmotic damage. However, the cell viability after CPA removal using the conservative method was only 15.5% ± 2%, which is nearly identical to the viability of 18.0% ± 0.7% obtained using the standard method (p-value of 0.27 for a two-sample t-test). This suggests that the loss of viability after 60 min exposure to 7 molal glycerol is due to toxicity and not osmotic damage.
Figure 6.
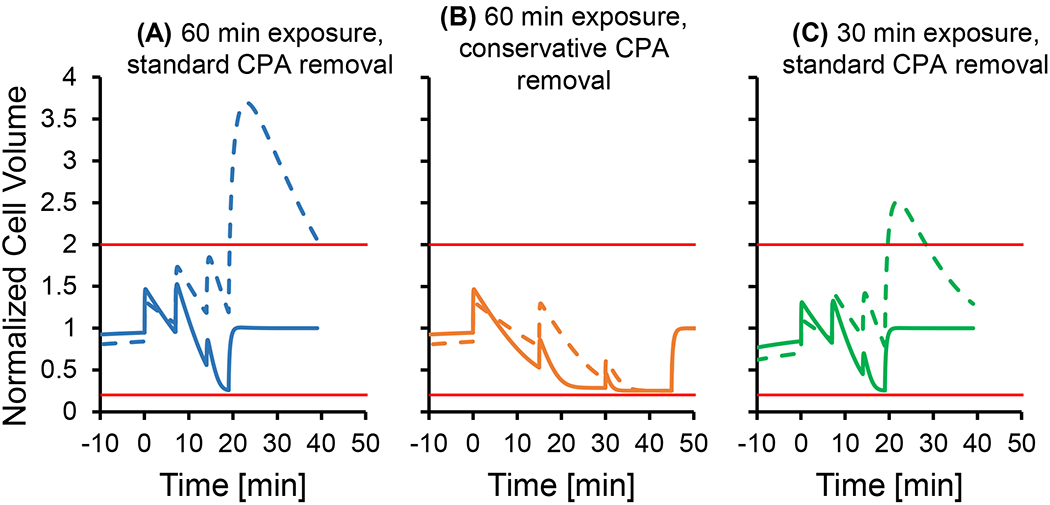
Cell volume predictions for multi-step CPA removal after exposure to 7 molal glycerol. Solid lines show predictions using published permeability values [29], while the dashed lines show predictions using a 2x lower glycerol permeability. Horizontal red lines show the osmotic tolerance limits [11]. Panel A shows the cell volume predictions after 60 min exposure to glycerol using standard hold times for each CPA removal step, while Panel B shows predictions when the step times are increased to 15 min each. In Panel C, cell volume predictions are shown after a 30 min exposure using standard hold times during CPA removal. In all simulations, a temperature of 25 °C was used.
Comparison of the results for 30 min and 60 min exposure to 7 molal glycerol provides further evidence that the observed cell losses cannot be attributed to osmotic damage. The viability was relatively high at 83% after a 30 min exposure to 7 molal glycerol but reduced to 18% after exposure to glycerol for 60 min. Cell volume predictions suggest that this reduction in viability is not caused by osmotic damage. As shown in Figure 6, the maximum predicted cell volume was actually higher after 30 min exposure to glycerol (using the standard CPA removal procedure) than after 60 min exposure using the more conservative CPA removal procedure. This indicates that 60 min exposure to glycerol is actually expected to result in less osmotic damage (when the conservative CPA removal process is used) and rules out osmotic damage as the cause of the lower viability.
The analysis above demonstrates that glycerol toxicity, rather than osmotic damage, is the most likely cause of the reduced cell viability after exposure to 7 molal glycerol for 60 min. Therefore, toxicity is likely the major cause of the reduced viability after exposure to 10 molal glycerol as well. To evaluate the potential for osmotic damage after exposure to 10 molal glycerol, we examined cell volume predictions during CPA removal (not shown). The maximum predicted cell volume after 30 min exposure to 10 molal glycerol is less than the maximum predicted cell volume after exposure to 7 molal glycerol for 60 min, which suggests that osmotic damage is negligible in this case. This only leaves the experimental group with 60 min exposure to 10 molal glycerol with potential osmotic damage. We cannot conclusively rule out osmotic damage in this case because the maximum predicted cell volume is higher than that for 60 min exposure to 7 molal glycerol. It is also difficult to experimentally assess osmotic damage after 60 min exposure to 10 molal glycerol because the resulting viability was very low (<1%), probably as a result of glycerol toxicity. Nonetheless, osmotic damage is unlikely because the glycerol removal process was designed to maintain cell volumes within the osmotic tolerance limits based on predictions using the published glycerol permeability [29]. Since the other CPAs have a much higher permeability than glycerol, osmotic damage is even less likely for the other CPAs.
3.5. Cell Losses are Caused by CPA Toxicity
Our results suggest that CPA toxicity is the main cause for the observed reduction in cell viability after exposure to CPA. We quantified toxicity by fitting a first-order kinetic model to the cell viability data, resulting in best-fit toxicity rates for each CPA mixture type at various concentrations. Figure 7 presents viability data and the corresponding toxicity rate fits for solutions containing a single CPA and for binary CPA mixtures (see Research Data section for the full data set). Overall, the fits are a reasonable match for the data, and the best-fit toxicity rate provides a convenient metric for comparing the toxicity of different CPA solutions.
Figure 7.
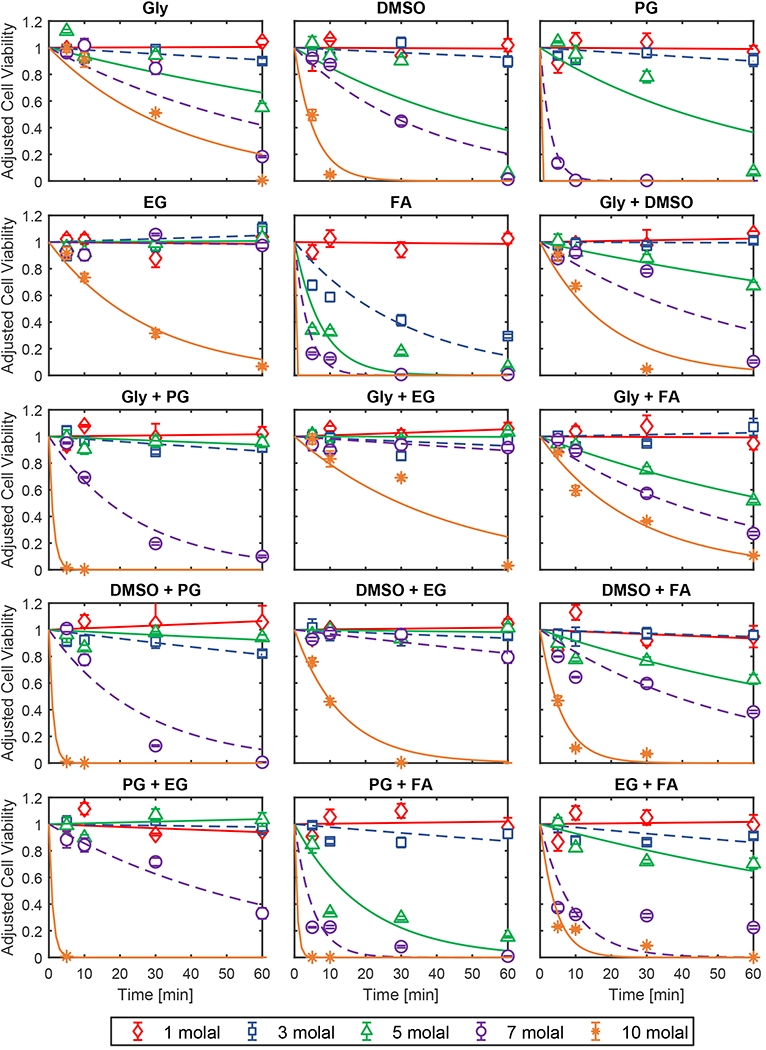
Cell viability after exposure to single CPA solutions and binary CPA mixtures. Lines show the best-fit toxicity rate models. Error bars represent the standard error of the mean. CPAs are abbreviated as follows: glycerol (Gly), propylene glycol (PG), ethylene glycol (EG), and formamide (FA). Viability was adjusted to account for toxicity during CPA addition and removal as described in the methods section (see Eq. 6).
From the toxicity rate data, some common trends in CPA toxicity can be seen. Figure 8 compares the toxicity rates for solutions containing a single CPA. Our results show that ethylene glycol is one of the least toxic CPAs and formamide is one of the most toxic, which are common findings in previous studies of CPA toxicity [2,8,13,37,63]. However, there is a strong concentration dependence of the toxicity rates that is more nuanced. Formamide is the most toxic CPA up to a concentration of 5 molal, but at higher concentrations, propylene glycol toxicity increases dramatically and actually exceeds that of formamide. High propylene glycol toxicity has been reported in the oocyte and chondrocyte studies of Szurek and Eroglu [60], Jomha et al [37], and Almansoori et al [2]. Comparison of our results for propylene glycol and formamide reveals differing effects of concentration on the toxicity rate, which may reflect different mechanisms of CPA toxicity.
Figure 8.
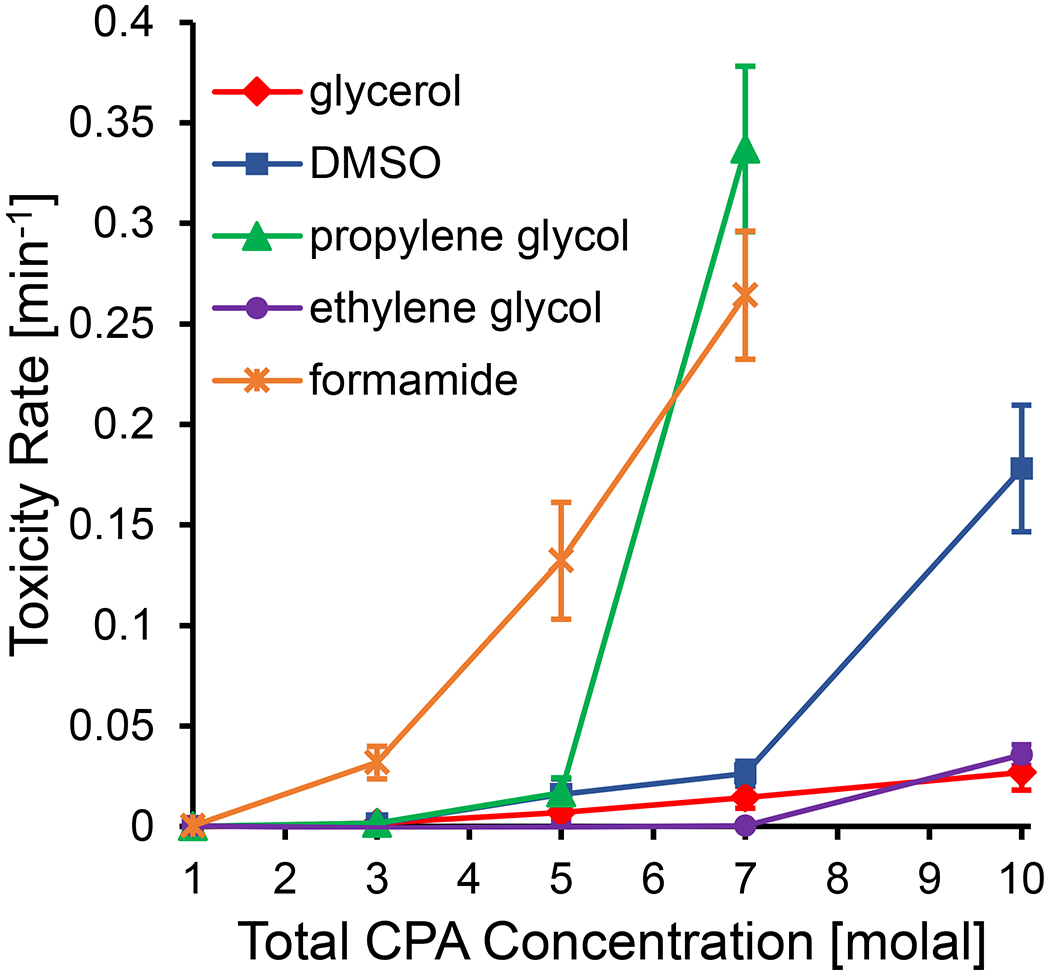
Best-fit toxicity rates for solutions containing a single CPA as a function of CPA concentration. It was not possible to measure a toxicity rate for propylene glycol or formamide at a concentration of 10 molal, as no viability was measured for any exposure time. Error bars represent the 95% confidence intervals of the best-fit toxicity rates.
Examination of the toxicity rates for the binary CPA mixtures also revealed some interesting trends, as shown in Figure 9. We split Figure 9 into two panels, with one panel showing all of the binary mixtures without propylene glycol and the other panel showing the mixtures with propylene glycol. The binary mixtures with propylene glycol exhibited a dramatic increase in toxicity at higher concentrations, similar to the spike in toxicity that was observed for propylene glycol on its own. In Almansoori et al [2], they also show that multi-CPA mixtures with propylene glycol are particularly toxic. Figure 9 also shows that glycerol + ethylene glycol is a favorable binary mixture, which has also been shown in Jomha et al [37].
Figure 9.
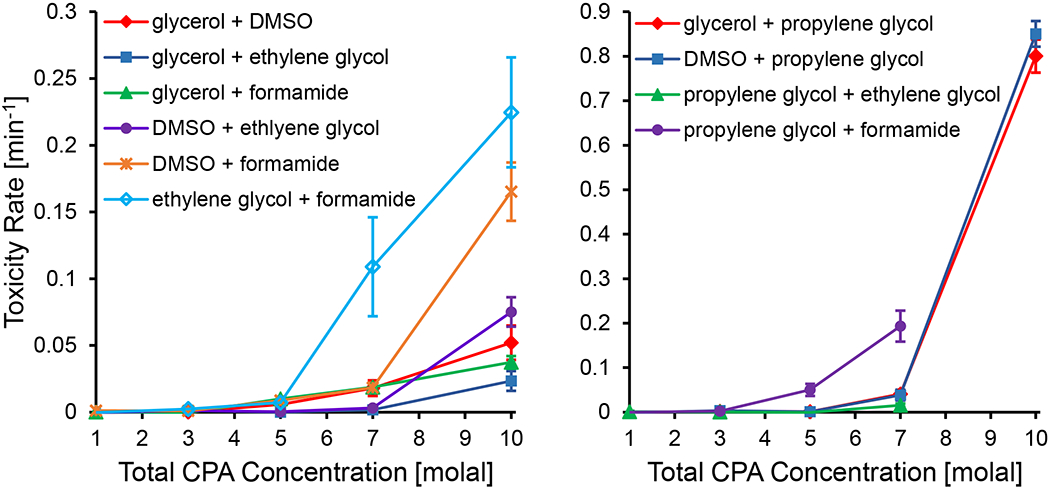
Best-fit toxicity rates for binary CPA mixtures. Left panel: binary CPA mixtures not containing propylene glycol. Right panel: binary CPA mixtures containing propylene glycol. Propylene glycol mixtures were the most toxic, and the toxicity rate axis scales are adjusted accordingly between the two panels. In the right panel, no viability was measured after exposure to 10 molal mixtures of propylene glycol + ethylene glycol and propylene glycol + formamide for any of the exposure times and therefore no toxicity rate could be measured. Error bars represent the 95% confidence intervals of the best-fit toxicity rates.
Figure 10 compares toxicity rates for single CPA solutions, binary mixtures, and ternary mixtures at a total CPA concentration of 7 molal. Our results highlight the general decrease in toxicity as more CPAs make up a mixture, as has been observed in several previous studies [1,2,21,22,25,37]. Figure 10 also showcases that some CPA interactions in a mixture are more beneficial than others. Within the ternary combinations shown in Figure 10, glycerol + DMSO + ethylene glycol was found to be the least toxic. This ternary CPA mixture was also found to be favorable in Jomha et al [37] and Almansoori et al [2].
Figure 10.
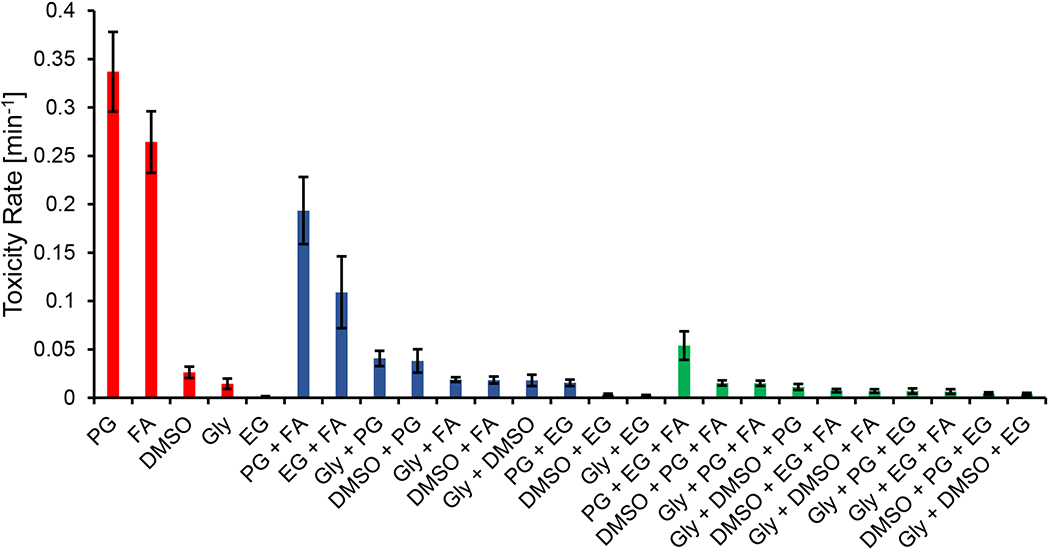
Best-fit toxicity rates for single CPA solutions, binary mixtures, and ternary mixtures at a total CPA concentration of 7 molal. CPAs are abbreviated as follows: glycerol (Gly), propylene glycol (PG), ethylene glycol (EG), and formamide (FA). To determine the toxicity rates for the ternary solutions it was assumed that toxicity was negligible during exposure to 1 molal and 3 molal solutions during CPA addition and removal. This is a reasonable assumption considering that none of the 1 molal toxicity rates were found to be statistically significant in this study, and the majority of 3 molal toxicity rates for binary solutions were not statistically significant. Moreover, even in cases where the 3 molal toxicity rate was significant, there is a negligible decrease in cell viability for relatively short exposure times of ~10 min (see Fig. 7), which is the case for the total time of the 3 molal CPA addition and removal steps. Error bars represent the 95% confidence intervals of the best-fit toxicity rates.
We can further investigate toxicity in multi-CPA mixtures through the lens of toxicity neutralization, as described by Fahy. In particular, Fahy [20,25] has described the neutralization of formamide toxicity by DMSO. Fahy showed the neutralization of formamide toxicity in rabbit renal cortical slices by adding various concentrations of DMSO to fixed formamide concentrations. Even though the total CPA concentration was higher in the resulting mixtures, Fahy observed that the mixtures were less toxic than the original formamide solutions on their own. As shown in Figure 11, we observed the same phenomenon in DMSO + formamide mixtures at some concentrations, but we observed even more substantial toxicity neutralization in glycerol + formamide mixtures. In particular, Figure 11 shows that a mixture containing 5 molal formamide and 5 molal glycerol is much less toxic than a solution containing 5 molal formamide on its own. A favorable glycerol + formamide interaction can be inferred from the model fit of Jomha et al [37], but to our knowledge, we are the first to report such a comprehensive case of formamide toxicity neutralization by glycerol.
Figure 11.
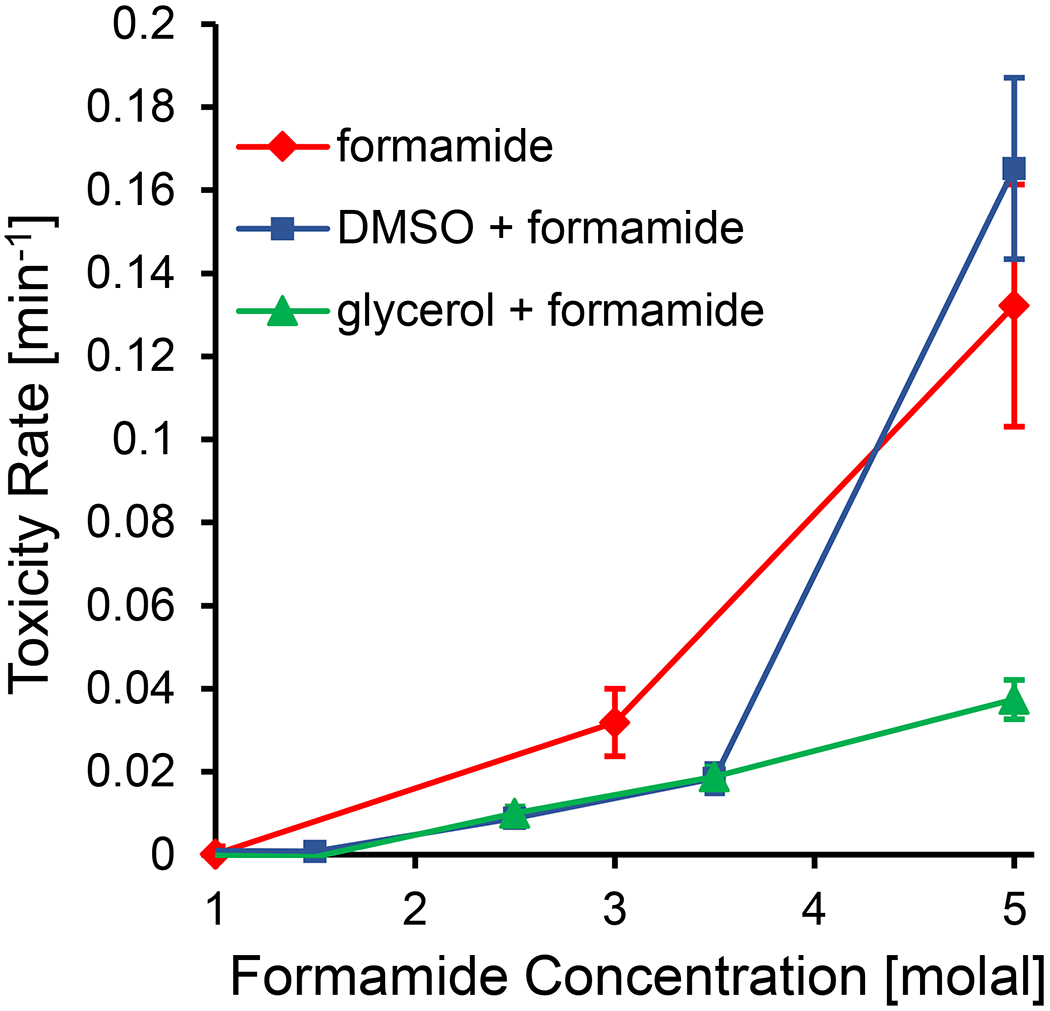
Synergistic effects of glycerol and DMSO on formamide toxicity. The toxicity rates for the three CPA compositions are plotted against formamide concentration. In the glycerol and DMSO mixtures, formamide makes up half the CPA concentration on a molal basis, resulting in a total CPA concentration that is twice what is reported on the x-axis. Error bars represent the 95% confidence intervals of the best-fit toxicity rates.
4. CONCLUSIONS AND FUTURE DIRECTIONS
In this work, we have established an automated liquid handling methodology for high-throughput measurement of CPA toxicity in a 96-well plate format. This new approach makes it possible to randomize treatment locations on the well plate and precisely control the aspirate/dispense flow rate and timing, resulting in less experimental variability and more accurate results. Automated liquid handling also enables much higher throughput compared to manual pipetting, enabling faster generation of CPA toxicity data sets.
Using this new high-throughput approach, we were able to rapidly test 340 unique experimental conditions, including CPA mixtures containing glycerol, DMSO, propylene glycol, ethylene glycol, and formamide at various concentrations. Our results are consistent with some commonly observed trends, including the observation that ethylene glycol and glycerol are relatively non-toxic CPAs, formamide is a relatively toxic CPA, and that overall toxicity decreases as the number of CPAs in the mixture increases. Our results also confirm previous observations that the toxicity of formamide can be neutralized by addition of DMSO to the solution. Surprisingly, we observed even more significant neutralization of formamide toxicity from glycerol.
In the end, our goal is to create a robust toxicity model for multi-CPA vitrification solutions that can be implemented in our toxicity cost function approach for designing minimally toxic CPA equilibration methods [11]. In future work, we plan to use the data presented here to develop a multi-CPA toxicity model that accounts for multiple mechanisms of toxicity, including toxicity neutralization. In addition, we plan to carry out experiments at various temperatures, which will allow us to account for the temperature-dependence of CPA toxicity. We are currently integrating third-party hardware with the automated liquid handling system in order to control the temperature of the assay and source plates. Overall, the novel high-throughput approach described here is expected to enable quantification of CPA toxicity over a wide range of conditions, leading to the development of a comprehensive toxicity model that can be used for design of less toxic cryopreservation methods.
Supplementary Material
ACKNOWLEDGEMENTS
This work was supported from funding from the Hirsch Foundation and the National Institutes of Health (R01 EB027203).
ABBREVIATIONS
- BPAEC
bovine pulmonary artery endothelial cells
- CPAs
cryoprotectants
- DMSO
dimethyl sulfoxide
- EG
ethylene glycol
- FA
formamide
- Gly
glycerol
- PG
propylene glycol
APPENDIX
CPA addition and removal steps were designed in order to stay within the osmotic tolerance limits as defined in our previous study [11]. The osmotic tolerance limits established in that study were conservatively set at a normalized osmotically active volume of 0.2 for the lower limit and 2 for the upper limit. In this study, we designed multi-step CPA equilibration methods using even more conservative limits for the lower and upper limit at 0.25 and 1.8, respectively. As such, we slightly modified the steps established in our previous work [11] to account for the more conservative limits. The time for each step (excluding the peak CPA exposure step) was minimized to the nearest 0.5 min while making sure that the osmotic tolerance limits were not crossed.
An osmotic tolerance limit refers to the normalized osmotically active volume of a cell that we do not want to cross, with the reference volume being that of the osmotically active volume of a cell in isotonic buffer. In order to calculate the normalized osmotically active volume of our cells through time, we used the classic two-parameter cell membrane transport model [11,40]:
| #A1 |
| #A2 |
| #A3 |
| #A4 |
where and are the normalized intracellular volumes of water and CPA, respectively, and the sum of the two gives the normalized osmotically active volume of a cell at time t. As such, we sought to satisfy the equation for all time. The effective water permeability (LpA/Vw0 = 4.36 x 10−8 [1/Pa/s]) and the effective glycerol permeability (PsA/Vw0 = 6.02 x 10−3 [1/s]) at 25 °C were found through a previous study [29]. Effective permeabilities were used for glycerol, as out of the five CPAs tested, glycerol has the lowest membrane permeability and causes the largest cell volume excursions. The remaining parameters in Equations A1–A4 are defined as follows: ρw = 1 kg/L is the density of water, R is the universal gas constant, T is the absolute temperature, M0 = 300 mOsm/kg is the isotonic reference osmolality, vs = 0.071 L/mol is the molar volume of glycerol, and M is osmolality with subscripts s and n referring to glycerol and the nonpermeating solute, respectively, and superscripts i and e referring to the intracellular and extracellular space, respectively.
RESEARCH DATA
The full data sets (cell viability and adjusted cell viability) are made available in two Excel files in the Supplementary Material.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
CONFLICTS OF INTEREST
The authors have no conflicts of interest.
REFERENCES
- [1].Ali J, and Shelton JN, Design of vitrification solutions for the cryopreservation of embryos. J Reprod Fertil 99 (1993) 471–7. [DOI] [PubMed] [Google Scholar]
- [2].Almansoori KA, Prasad V, Forbes JF, Law GK, McGann LE, Elliott JA, and Jomha NM, Cryoprotective agent toxicity interactions in human articular chondrocytes. Cryobiology 64 (2012) 185–91. [DOI] [PubMed] [Google Scholar]
- [3].Baust JM, Properties of Cells and Tissues Influencing Preservation Outcome: Molecular Basis of Preservation-Induced Cell Death in: Baust JG, and Baust JM, (Eds.), Advances in Biopreservation, CRC Press, Boca Raton, 2007, pp. 63–87. [Google Scholar]
- [4].Beier AF, Schulz JC, Dorr D, Katsen-Globa A, Sachinidis A, Hescheler J, and Zimmermann H, Effective surface-based cryopreservation of human embryonic stem cells by vitrification. Cryobiology 63 (2011) 175–85. [DOI] [PubMed] [Google Scholar]
- [5].Benson JD, Kearsley AJ, and Higgins AZ, Mathematical optimization of procedures for cryoprotectant equilibration using a toxicity cost function. Cryobiology 64 (2012) 144–151. [DOI] [PubMed] [Google Scholar]
- [6].Benson JD, Higgins AZ, Desai K, and Eroglu A, A toxicity cost function approach to optimal CPA equilibration in tissues. Cryobiology 80 (2018) 144–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Carling K, Resistant outlier rules and the non-Gaussian case. Computational Statistics & Data Analysis 33 (2000) 249–258. [Google Scholar]
- [8].Cordeiro RM, Stirling S, Fahy GM, and de Magalhaes JP, Insights on cryoprotectant toxicity from gene expression profiling of endothelial cells exposed to ethylene glycol. Cryobiology 71 (2015) 405–12. [DOI] [PubMed] [Google Scholar]
- [9].Corwin WL, Baust JM, Baust JG, and Van Buskirk RG, The unfolded protein response in human corneal endothelial cells following hypothermic storage: Implications of a novel stress pathway. Cryobiology 63 (2011) 46–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Davidson AF, Benson JD, and Higgins AZ, Mathematically optimized cryoprotectant equilibration procedures for cryopreservation of human oocytes. Theoretical Biology and Medical Modelling 11 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Davidson AF, Glasscock C, McClanahan DR, Benson JD, and Higgins AZ, Toxicity Minimized Cryoprotectant Addition and Removal Procedures for Adherent Endothelial Cells. PLoS One 10 (2015)e0142828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].El-Shewy HM, Kendall WF, Darrabie M, Collins BH, and Opara EC, Polyvinyl pyrrolidone: A novel cryoprotectant in islet cell cryopreservation. Cell Transplantation 13 (2004) 237–243. [DOI] [PubMed] [Google Scholar]
- [13].Fahmy MD, Almansoori KA, Laouar L, Prasad V, McGann LE, Elliott JA, and Jomha NM, Dose-injury relationships for cryoprotective agent injury to human chondrocytes. Cryobiology 68 (2014) 50–6. [DOI] [PubMed] [Google Scholar]
- [14].Fahy GM, and Macfarlane DR, Recent Progress toward Vitrification of Kidneys. Cryobiology 19 (1982) 668–669. [Google Scholar]
- [15].Fahy GM, Cryoprotectant Toxicity - Biochemical or Osmotic. Cryo-Letters 5 (1984) 79–90. [Google Scholar]
- [16].Fahy GM, MacFarlane DR, Angell CA, and Meryman HT, Vitrification as an approach to cryopreservation. Cryobiology 21 (1984) 407–26. [DOI] [PubMed] [Google Scholar]
- [17].Fahy GM, The Relevance of Cryoprotectant Toxicity to Cryobiology. Cryobiology 23 (1986) 1–13. [DOI] [PubMed] [Google Scholar]
- [18].Fahy GM, Lilley TH, Linsdell H, Douglas MS, and Meryman HT, Cryoprotectant toxicity and cryoprotectant toxicity reduction: in search of molecular mechanisms. Cryobiology 27 (1990) 247–68. [DOI] [PubMed] [Google Scholar]
- [19].Fahy GM, Saur J, and Williams RJ, Physical Problems with the Vitrification of Large Biological-Systems. Cryobiology 27 (1990) 492–510. [DOI] [PubMed] [Google Scholar]
- [20].Fahy GM, da Mouta C, Tsonev L, Khirabadi BS, Mehl P, and Meryman HT, Cellular Injury Associated with Organ Cryopreservation: Chemical Toxicity and Cooling Injury in: Lemasters JJ, and Oliver C, (Eds.), Cell Biology of Trauma, CRC Press, Boca Raton, 1995, pp. 333–356. [Google Scholar]
- [21].Fahy GM, Wowk B, Wu J, and Paynter S, Improved vitrification solutions based on the predictability of vitrification solution toxicity. Cryobiology 48 (2004) 22–35. [DOI] [PubMed] [Google Scholar]
- [22].Fahy GM, Wowk B, Wu J, Phan J, Rasch C, Chang A, and Zendejas E, Cryopreservation of organs by vitrification: perspectives and recent advances. Cryobiology 48 (2004) 157–178. [DOI] [PubMed] [Google Scholar]
- [23].Fahy GM, Wowk B, and Wu J, Cryopreservation of complex systems: The missing link in the regenerative medicine supply chain. Rejuvenation Research 9 (2006) 279–291. [DOI] [PubMed] [Google Scholar]
- [24].Fahy GM, Wowk B, Pagotan R, Chang A, Phan J, Thomson B, and Phan L, Physical and biological aspects of renal vitrification. Organogenesis 5 (2009) 167–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Fahy GM, Cryoprotectant toxicity neutralization. Cryobiology 60 (2010) S45–53. [DOI] [PubMed] [Google Scholar]
- [26].Fahy GM, and Wowk B, Principles of Cryopreservation by Vitrification in: Wolkers WF, and Oldenhof H, (Eds.), Cryopreservation and Freeze-Drying Protocols, Springer, 2015. [Google Scholar]
- [27].Fahy GM, Cooling injury in rabbit kidneys below −22°C. Cryobiology 81 (2018) 217–218. [Google Scholar]
- [28].Frigge M, Hoaglin DC, and Iglewicz B, Some Implementations of the Boxplot. American Statistician 43 (1989) 50–54. [Google Scholar]
- [29].Fry AK, and Higgins AZ, Measurement of Cryoprotectant Permeability in Adherent Endothelial Cells and Applications to Cryopreservation. Cellular and Molecular Bioengineering 5 (2012) 287–298. [Google Scholar]
- [30].Gao DY, Liu J, Liu C, Mcgann LE, Watson PF, Kleinhans FW, Mazur P, Critser ES, and Critser JK, Prevention of Osmotic Injury to Human Spermatozoa during Addition and Removal of Glycerol. Human Reproduction 10 (1995) 1109–1122. [DOI] [PubMed] [Google Scholar]
- [31].Giwa S, Lewis JK, Alvarez L, Langer R, Roth AE, Church GM, Markmann JF, Sachs DH, Chandraker A, Wertheim JA, Rothblatt M, Boyden ES, Eidbo E, Lee WPA, Pomahac B, Brandacher G, Weinstock DM, Elliott G, Nelson D, Acker JP, Uygun K, Schmalz B, Weegman BP, Tocchio A, Fahy GM, Storey KB, Rubinsky B, Bischof J, Elliott JAW, Woodruff TK, Morris GJ, Demirci U, Brockbank KGM, Woods EJ, Ben RN, Baust JG, Gao DY, Fuller B, Rabin Y, Kravitz DC, Taylor MJ, and Toner M, The promise of organ and tissue preservation to transform medicine. Nature Biotechnology 35 (2017) 530–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Glazar AI, Mullen SF, Liu J, Benson JD, Critser JK, Squires EL, and Graham JK, Osmotic tolerance limits and membrane permeability characteristics of stallion spermatozoa treated with cholesterol. Cryobiology 59 (2009) 201–6. [DOI] [PubMed] [Google Scholar]
- [33].Hanson SM, Ekins S, and Chodera JD, Modeling error in experimental assays using the bootstrap principle: understanding discrepancies between assays using different dispensing technologies. Journal of Computer-Aided Molecular Design 29 (2015) 1073–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Hezavehei M, Sharafi M, Kouchesfahani HM, Henkel R, Agarwal A, Esmaeili V, and Shahverdi A, Sperm cryopreservation: A review on current molecular cryobiology and advanced approaches. Reproductive Biomedicine Online 37 (2018) 327–339. [DOI] [PubMed] [Google Scholar]
- [35].Hoaglin DC, Iglewicz B, and Tukey JW, Performance of Some Resistant Rules for Outlier Labeling. Journal of the American Statistical Association 81 (1986) 991–999. [Google Scholar]
- [36].Jomha NM, Law GK, Abazari A, Rekieh K, Elliott JAW, and McGann LE, Permeation of several cryoprotectant agents into porcine articular cartilage. Cryobiology 58 (2009) 110–114. [DOI] [PubMed] [Google Scholar]
- [37].Jomha NM, Weiss AD, Fraser Forbes J, Law GK, Elliott JA, and McGann LE, Cryoprotectant agent toxicity in porcine articular chondrocytes. Cryobiology 61 (2010) 297–302. [DOI] [PubMed] [Google Scholar]
- [38].Jomha NM, Elliott JA, Law GK, Maghdoori B, Forbes JF, Abazari A, Adesida AB, Laouar L, Zhou X, and McGann LE, Vitrification of intact human articular cartilage. Biomaterials 33 (2012) 6061–8. [DOI] [PubMed] [Google Scholar]
- [39].Karlsson JOM, Younis AI, Chan AWS, Gould KG, and Eroglu A, Permeability of the Rhesus Monkey Oocyte Membrane to Water and Common Cryoprotectants. Molecular Reproduction and Development 76 (2009) 321–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Kleinhans FW, Membrane permeability modeling: Kedem-Katchalsky vs a two-parameter formalism. Cryobiology 37 (1998) 271–289. [DOI] [PubMed] [Google Scholar]
- [41].Lansky D, Validation of bioassays for quality control. Dev Biol Stand 97 (1999) 157–68. [PubMed] [Google Scholar]
- [42].Lansky D, Strip-plot designs, mixed models, and comparisons between linear and non-linear models for microtitre plate bioassays. Dev Biol (Basel) 107 (2002) 11–23. [PubMed] [Google Scholar]
- [43].Lawson A, Mukherjee IN, and Sambanis A, Mathematical modeling of cryoprotectant addition and removal for the cryopreservation of engineered or natural tissues. Cryobiology 64 (2012) 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Lee D, and Chang LC, Development of the pipetting error sensor. Sensors and Actuators B-Chemical 119 (2006) 150–158. [Google Scholar]
- [45].Lewis JK, Bischof JC, Braslavsky I, Brockbank KGM, Fahy GM, Fuller BJ, Rabin Y, Tocchio A, Woods EJ, Wowk BG, Acker JP, and Giwa S, The Grand Challenges of Organ Banking: Proceedings from the first global summit on complex tissue cryopreservation. Cryobiology 72 (2016) 169–182. [DOI] [PubMed] [Google Scholar]
- [46].Lundholt BK, Scudder KM, and Pagliaro L, A simple technique for reducing edge effect in cell-based assays. J Biomol Screen 8 (2003) 566–70. [DOI] [PubMed] [Google Scholar]
- [47].Lusianti RE, and Higgins AZ, Continuous removal of glycerol from frozen-thawed red blood cells in a microfluidic membrane device. Biomicrofluidics 8 (2014) 054124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Lyman K, Fisher D, Han Y, and Chetkovich DM, A Novel Method for Reducing Human Pipetting Errors. Journal of Medical Laboratory and Diagnosis 6 (2015) 36–40. [Google Scholar]
- [49].Malpique R, Tostoes R, Beier AF, Serra M, Brito C, Schulz JC, Bjorquist P, Zimmermann H, and Alves PM, Surface-based cryopreservation strategies for human embryonic stem cells: a comparative study. Biotechnol Prog 28 (2012) 1079–87. [DOI] [PubMed] [Google Scholar]
- [50].MireSluis AR, Gerrard T, Das RG, Padilla A, and Thorpe R, Biological assays: Their role in the development and quality control of recombinant biological medicinal products. Biologicals 24 (1996) 351–362. [DOI] [PubMed] [Google Scholar]
- [51].Mukherjee IN, Song YC, and Sambanis A, Cryoprotectant delivery and removal from murine insulinomas at vitrification-relevant concentrations. Cryobiology 55 (2007) 10–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Pero ME, Zullo G, Esposito L, Iannuzzi A, Lombardi P, De Canditiis C, Neglia G, and Gasparrini B, Inhibition of apoptosis by caspase inhibitor Z-VAD-FMK improves cryotolerance of in vitro derived bovine embryos. Theriogenology 108 (2018) 127–135. [DOI] [PubMed] [Google Scholar]
- [53].Porcu E, Ciotti P, and Venturoli S, Handbook of Human Oocyte Cryopreservation, Cambridge University Press, Cambridge, United Kingdom, 2012. [Google Scholar]
- [54].Rivers RL, McAteer JA, Clendenon JL, Connors BA, Evan AP, and Williams JC Jr., Apical membrane permeability of MDCK cells. Am J Physiol 271 (1996) C226–34. [DOI] [PubMed] [Google Scholar]
- [55].Saragusty J, and Arav A, Current progress in oocyte and embryo cryopreservation by slow freezing and vitrification. Reproduction 141 (2011) 1–19. [DOI] [PubMed] [Google Scholar]
- [56].Savitz D, and Solomon AK, Tracer determinations of human red cell membrane permeability to small nonelectrolytes. J Gen Physiol 58 (1971) 259–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Schlain B, Jethwa HS, Subramanyam M, Moulder K, Bhatt B, and Molloy M, Designs for bioassays with plate location effects. Biopharm-the Applied Technologies of Biopharmaceutical Development 14 (2001) 40–44. [Google Scholar]
- [58].Shardt N, Al-Abbasi KK, Yu H, Jomha NM, McGann LE, and Elliott JAW, Cryoprotectant kinetic analysis of a human articular cartilage vitrification protocol. Cryobiology 73 (2016) 80–92. [DOI] [PubMed] [Google Scholar]
- [59].Song YC, Khirabadi BS, Lightfoot F, Brockbank KGM, and Taylor MJ, Vitreous cryopreservation maintains the function of vascular grafts. Nature Biotechnology 18 (2000) 296–299. [DOI] [PubMed] [Google Scholar]
- [60].Szurek EA, and Eroglu A, Comparison and avoidance of toxicity of penetrating cryoprotectants. PLoS ONE 6 (2011) e27604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Tukey JW, Exploratory Data Analysis, Addison-Wesley, Reading, MA, 1977. [Google Scholar]
- [62].Vian AM, and Higgins AZ, Membrane permeability of the human granulocyte to water, dimethyl sulfoxide, glycerol, propylene glycol and ethylene glycol. Cryobiology 68 (2014) 35–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Vuthiphandchai V, Pengpun B, and Nimrat S, Effects of cryoprotectant toxicity and temperature sensitivity on the embryos of black tiger shrimp (Penaeus monodon). Aquaculture 246 (2005) 275–284. [Google Scholar]
- [64].Walzl A, Kramer N, Mazza G, Rosner M, Falkenhagen D, Hengstschlager M, Schwanzer-Pfeiffer D, and Dolznig H, A Simple and Cost Efficient Method to Avoid Unequal Evaporation in Cellular Screening Assays, Which Restores Cellular Metabolic Activity. International Journal for Applied Science and Technology 2 (2012) 17–25. [Google Scholar]
- [65].Wu KZ, Laouar L, Dong R, Elliott JAW, and Jomha NM, Evaluation of five additives to mitigate toxicity of cryoprotective agents on porcine chondrocytes. Cryobiology 88 (2019) 98–105. [DOI] [PubMed] [Google Scholar]
- [66].Wusteman M, Rauen U, Simmonds J, Hunds N, and Pegg DE, Reduction of cryoprotectant toxicity in cells in suspension by use of a sodium-free vehicle solution. Cryobiology 56 (2008) 72–79. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


