Abstract
Prostate cancer is one of the most prevalent cancers in men, with increasing incidence worldwide. This public health concern has inspired considerable effort to study various aspects of prostate cancer treatment using dynamical models, especially in clinical settings. The standard of care for metastatic prostate cancer is hormonal therapy, which reduces the production of androgen that fuels the growth of prostate tumor cells prior to treatment resistance. Existing population models often use patientsâĂŹ prostate-specific antigen levels as a biomarker for model validation and for finding optimal treatment schedules; however, the synergistic effects of drugs used in hormonal therapy have not been well-examined. This paper describes the first mathematical model that explicitly incorporates the synergistic effects of two drugs used to inhibit androgen production in hormonal therapy. The drugs are cyproterone acetate, representing the drug family of anti-androgens that affect luteinizing hormones, and leuprolide acetate, representing the drug family of gonadotropin-releasing hormone analogs. By fitting the model to clinical data, we show that the proposed model can capture the dynamics of serum androgen levels during intermittent hormonal therapy better than previously published models. Our results highlight the importance of considering the synergistic effects of drugs in cancer treatment, thus suggesting that the dynamics of the drugs should be taken into account in optimal treatment studies, particularly for adaptive therapy. Otherwise, an unrealistic treatment schedule may be prescribed and render the treatment less effective. Furthermore, the drug dynamics allow our model to explain the delay in the relapse of androgen the moment a patient is taken off treatment, which supports that this delay is due to the residual effects of the drugs.
Keywords: prostate cancer modeling, hormonal therapy, intermittent androgen deprivation therapy, adaptive therapy, optimal treatment schedule, drug effects, androgen dynamics, pharmacokinetics
1. Introduction
1.1. Background
Prostate cancer is a significant public health concern. Among men in the U.S., it is the most common non-skin cancer and is responsible for approximately 20 percent of all new cancer cases [1]. Although most common in men over 50, prostate cancer can start to develop in men in their 20s and take decades to progress before symptoms appear [2]. The overall 5-, 10-, and 15-year survival rates for prostate cancer are among the highest of all localized malignancies, but once prostate cancer has metastasized, the 5-year relative survival rate drops to about 30 percent. Prostate cancer is the second deadliest cancer in men and is projected to become the deadliest cancer in men in the next decade [1]. Globally, the incidence of prostate cancer is steadily increasing, especially in developing nations, making it one of the deadliest cancers in men worldwide [3].
Androgens (male hormones) are produced mainly by the testes and in small amounts by the adrenal glands. Androgens bind to receptors on both healthy and cancerous prostate cells, leading to the transcription of genes that enhance proliferation and inhibit apoptosis [4]. Because the level of androgens in the body plays a crucial role in the maintenance of prostate cells, androgen deprivation therapy (ADT) has become the standard of care for prostate cancer that has spread beyond the prostate gland [5]. ADT is effective when, as is initially the case, most of the prostate cancer cells are androgen dependent; however, selective pressures promote the evolution of androgen-independent cells, and the therapy eventually becomes ineffective [6, 7].
Androgen deprivation therapy dramatically reduces blood levels of testosterone, which can cause potentially serious side effects, including depression, osteoporosis, impotence, and an increased risk of dementia [8]. Intermittent ADT has been investigated to mitigate the side effects and forestall treatment resistance. During intermittent therapy, the patient takes androgen-suppression medication until his serum level of prostate-specific antigen (PSA) falls below some predetermined threshold (e.g., below the detectable threshold of 0.1 μg/L). Then the patient goes off of treatment until his PSA level rises above another predetermined threshold (usually ~ 10 μg/L). The cycle continues until the cancer evolves resistance [9].
Cyproterone acetate (CPA) and leuprolide acetate (LEU) are examples of two classes of medications that are commonly used for androgen suppression therapy. CPA is taken daily in pill form but LEU must be injected, usually on a monthly basis. Although LEU is a long-lasting drug, it causes a temporary increase in androgen production by the testes shortly after administration, as explained in more detail below. To counter this effect, patients often start CPA therapy about a month prior to initial LEU injection. Figure 3 shows time series of the estimated effect on androgen production by each medication for a representative patient.
Figure 3:
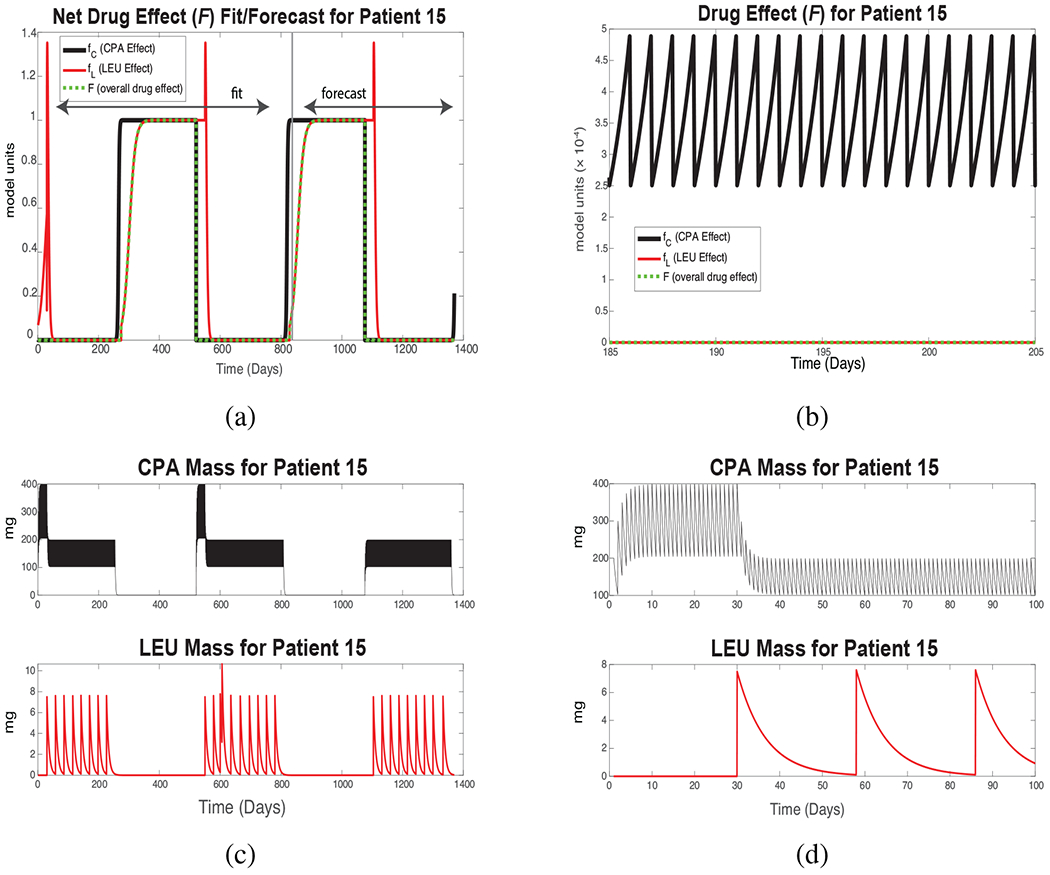
New Androgen Model results for Patient 15. (a) Black curve: simulated CPA effect fC, Eq. (12). Red curve: simulated LEU effect fL, Eq. (15). Green curve: the combined drug effect F, Eq. (11). Values 0 < F < 1 correspond to reductions in the androgen production rate in the testes; smaller values denote more potent effects. (b) Zoomed-in version of (a) over an initial 20-day treatment period. (c) Total serum mass of each drug, Eqs. (9) and (10). The spike in LEU mass at Day 606 reflects an additional injection. CPA therapy begins before LEU injection in each successive treatment cycle. (d) Intake and clearance of each drug for a portion of a single drug cycle. CPA is taken daily with rapid degradation; LEU, monthly with slow degradation. These daily fluctuations are present but not visible in subsequent plots.
1.2. Prior Work
A comprehensive review of existing modeling work for prostate cancer is presented by Phan et al. [10]. An in-depth mathematical treatment of various mathematical models pertaining to prostate cancer can also be found in chapters 5 and 6 in the book by Kuang et al. [11]. Here, we describe only work that directly relates to the development of our modeling formulation.
The first clinically motivated mathematical model for prostate cancer was proposed and studied by Jackson in 2004 [12, 13]. The model takes the form of a partial differential equation under radial symmetry to approximate cancer progression under continuous androgen deprivation therapy. However, imaging technology has played a limited role in the clinical management of prostate cancer [14], and the relative lack of spatial information has motivated the development of dynamical models based on systems of ordinary differential equations (ODEs).
ODE models generally use the PSA level over time as a biomarker for treatment response and cancer progression, because patient-specific time series of PSA level data usually are available from clinical trials. Hirata et al. [15] suggested a piecewise-linear system of ODEs to model the effects of intermittent treatment and eventual resistance. The model supposes that prostate tumors can be divided into three sub-populations of androgen-dependent, reversibly androgen-independent, and irreversibly androgen-independent cells (also called castration sensitive, and reversibly and irreversibly castration resistant, respectively). The growth rates of the three subpopulations depend linearly on their present sizes, with separate sets of rate coefficients for the on- and off-treatment periods. Although rate parameters can be found that reproduce clinical time series of PSA in individual patient cases with reasonable accuracy, the parameters are not identifiable from such time series data alone, which complicates efforts to quantify uncertainties in the parameters and model outputs [16].
Barton and Andersen in 1998 [17] developed a mathematical model for pharmacokinetics as an initial framework to help understand the hormonal regulatory processes. Their model attempts to simulate the physiological feedback between testosterone, luteinizing hormone, and follicle stimulating hormone using adult male rat data. Potter et al. [18] extended the work of Barton and Andersen and developed a model that describes the interaction between testosterone, 5-α dihydrotestosterone, and luteinizing hormone. Model validation was also carried out with experimental data.
Portz et al. [19] developed the first clinically validated dynamical model for prostate cancer, insofar as sets of parameters could be determined, using an optimization procedure, to approximate the observed PSA level in each of seven patients in a clinical trial of intermittent androgen deprivation therapy. The model assumes that intracellular levels of androgen are the growth-limiting resource for the cancer cells. A modified model by Baez and Kuang [20] (the BK Model) used a simplified tumor population structure and incorporated a dynamical model for androgen production. Their model was able to provide consistent prediction of PSA dynamics but has some limitations when directly incorporating clinical data. To address this issue, Phan et al. [21] developed the Improved BK Model to incorporate logistic-type dynamics for the recovery of blood androgen levels following the cessation of hormone therapy The Improved BK Model outperforms the BK Model in terms of replicating observed time series of PSA levels. However, neither model accurately captures the initial increase (decrease) in serum androgen levels immediately following the cessation (re-initiation) of hormone therapy. One potential explanation is that the models fail to account for residual effects of the drugs on the endocrine system, which is the focus of our new model.
1.3. New Androgen Model
Despite the current development and studies of various promising treatments for prostate cancer, such as immunotherapy [22, 23], there is still no curative treatment for metastatic prostate cancer. Ongoing efforts have modeled immunotherapy treatment [24, 25, 26], combinations of chemotherapy and immunotherapy [27], and optimal scheduling of cyclical therapy to forestall resistance and continued growth of tumors [28, 29, 30, 31]. Typically, these models assume that the effects of intermittent androgen suppression therapy begin and end immediately upon initiation and cessation of therapy.
Our efforts focus on how the drugs interact with male hormones. Most prostate cancers, especially early in treatment, require androgen, particularly testosterone, for growth. Cyproterone acetate (CPA) is part of a family of drugs, called anti-androgens, that suppress the binding of androgen to androgen receptors on various cells, but for our purposes on prostate cancer cells. CPA typically is administered orally at daily intervals when used to treat prostate cancer [32, 33]. It is a steroidal anti-androgen (some newer drugs are non-steroidal anti-androgens). CPA also affects the overall serum androgen level by suppressing luteinizing hormones (LH) coming from gonadotropic cells in the pituitary gland [34, 35] LH induces the production of androgen in the testes.
Leuprolide acetate (LEU) is administered by injection, generally at monthly intervals [36]. LEU is a potent analog of gonadotropin-releasing hormone (GnRH), which triggers the pituitary gland to release gonadotropic cells carrying LH. LEU represents the GnRH analog or GnRH agonist family of drugs [37]. Clinical evidence suggests that LEU takes effect only when its concentration exceeds a certain threshold [38]. LEU is clinically proven to restrict LH production, but the precise biological pathway is unknown. However, an accepted overview of the process goes as follows. First, injection of LEU causes an increase in the production of gonadotropic cells carrying LH, which in turn increases the production of androgen in the testes. Eventually, the pituitary gland reaches a saturation point and is no longer sensitive to GnRH, the hormone for which LEU is an analog. Subsequently, the production of gonadotropic cells sharply drops, which causes the production of androgen in the testes to cease [33, 37, 38]. After the treatment is halted, the testes do not resume the production of androgen for about a month [36].
While several studies have explored androgen regulation of prostate growth within a pharmacokinetic framework using data from laboratory experiments on rats [17, 18], to our knowledge, no mathematical model has previously been developed to capture the dynamics of CPA, LEU, and androgen during intermittent suppression therapy. In this work, we develop a pharmacokinetic framework for the dynamics of androgen suppression therapy that is based on a population model approach.
A new type of treatment, adaptive therapy, aims to maintain a stable tumor burden by adjusting the treatment scheme based on the patient’s responses [39, 40, 41]. Current efforts seek to develop a quantitative framework that can be incorporated into the clinical decision-making process. We hope that our accounting for drug interactions will improve the predictive ability of future mathematical models of therapy.
2. Materials and Methods
In this section, we briefly describe the Improved BK Model [21]. (See [20, 21] for additional background.) Next, we introduce the New Androgen Model and combine them into the New PSA Model. Finally, we describe our parameter estimation method and sensitivity analysis using clinical data.
2.1. Improved BK Model
Phan et al. [21] introduced an improved version of the BK model by Baez and Kuang [20]. Similar to the BK Model, the Improved BK Model [21] has two sub-populations of cancer cells: androgen-dependent (AD) and androgen-independent (AI), denoted as x1 and x2, respectively. Q represents the intracellular androgen level, and P is the PSA level. However, unlike the BK Model, the Improved BK Model differentiates between the serum androgen and the intracellular androgen level. Consequently, the authors included the serum androgen level, A, as the fifth compartment. The Improved BK Model uses Eqs. (16)–(20), below, with Eq. (1) representing the serum androgen:
| (1) |
2.2. New Androgen Model Formulation
The New Androgen Moden replaces Eq. (1), the rate of change of androgen, as the sum of three production rates: a near-constant one, γ2, by the adrenal glands, a considerably larger (but non-constant) production rate from the testes, and a degradation rate:
| (2) |
The testes production rate takes the form of logistic growth, where Am is a patient-specific maximum androgen level. The coefficient F reflects the combined effect of ADT: F = 0 when the drugs block all androgen production from the testes, F = 1 when the drugs have no effect, and F > 1 when the drugs increase androgen production over the baseline. Androgen is degraded at a rate that is proportional to its present level. We assume that the treatment does not affect androgen production rates in the adrenal glands or the cancer cells; androgen produced by the latter is assumed not to affect the serum androgen level [42].
The total serum mass L(t) of LEU and of CPA, C(t), reflect their consumption by cells plus source terms reflecting intake (injection):
| (3) |
| (4) |
The source terms and reflect clinical protocols and are taken from the data set. In a clinical setting, represents the time at which CPA is orally ingested (normally daily) and represents the time at which LEU is injected (normally monthly). The New Androgen Model reflects the total serum mass—not the serum concentration—of the respective drugs.
The cumulative effect of the drugs is described by the factor F. As noted in the introduction, LEU temporarily increases androgen production. In the New Androgen Model formulation, we set F = fC · fL, where the factors fC and fL describe the effects of CPA and LEU, respectively. Generally, both drugs suppress the testes’ production of androgen. Similar multiplicative formulations have been used in control system models of cancer treatment [43] and other types of drug treatment models [44]. CPA and LEU inhibit androgen production only if the effect of one of the drugs is less than the inverse of that of the other. That is, if or , then F < 1, causing androgen production to drop. If LEU is administered alone, then F > 1 insofar as androgen production increases until desensitization of the pituitary gland occurs [37, 38]. We now discuss the chosen forms of fC and fL.
The effect of CPA takes the form of a Hill function:
| (5) |
where β is the half-effectiveness constant for CPA (a Hill equation is used to model the pharmacologic effect of many drugs [45].) Here fC → 1 as C → 0 and fC → 0 as C becomes large.
Because androgen-producing cells in the testes adjust their sensitivity to the level of hormonal stimulus, we assume that LEU exhibits a clinical effect only when its serum concentration exceeds some critical level, L* [38]. However, since we model the total serum mass, we convert this critical drug level concentration to a critical drug level mass by a factor whose range is given in Table 1.
Table 1:
Parameter definitions for the New PSA Model. Ranges are taken from the literature or estimated as described in the text. (*) We choose a − 5 ≤ Am ≤ a + 5, where a is the maximum androgen value from the data for each individual patient.
| Parameter | Description | Range | Unit | Source |
|---|---|---|---|---|
| α1 | LEU desensitization length | 0.1–0.45 | unitless | [36] |
| α2 | LEU spike amplitude | 0.1–0.3 | unitless | [36] |
| α3 | Shift for time LEU remains effective below L* | 0–102.5 | unitless | ad hoc |
| α4 | androgen production recovery rate | 0.1–0.4 | unitless | ad hoc |
| β | CPA effectiveness half-saturation constant | 0.005–0.01 | mg | ad hoc |
| δ | androgen degradation rate | 0.03–0.09 | day−1 | [47] |
| δC | decay for CPA | 0.3–0.7 | day−1 | [48] |
| δL | decay for LEU | 0.04–0.25 | day−1 | [38] |
| γ1 | testes’ androgen production rate | 0.9–7 | mg day−1 | [49] |
| γ2 | adrenal gland androgen production | 0.01–0.1 | mg day−1 | [49] |
| Am | maximum androgen | (*) | nmol L−1 | [50] |
| L* | critical drug level | 4.5-5.5 | μg | [38] |
| ω | rate for S1 and S2 | 30 | unitless | ad hoc |
The remaining terms in fL each represent a different biological process. When L ≥ L*, there is an initial spike in androgen production, followed by cessation. The equation
| (6) |
models the spike and desensitization effect of LEU, where the parameter α1 controls the time required to desensitize from LEU and α2 controls the spike amplitude. The rate of recovery of androgen production once the level of LEU falls below L* is unknown. The New Androgen Model assumes that the production of androgen recovers logistically according to
| (7) |
Here α3 is chosen to reflect times at which treatment is stopped, and α4 denotes the recovery rate back to normal androgen production levels. The model takes the form of logistic growth in lieu of a time-delay differential equation and is similar to prior efforts to model testosterone recovery [46]. The expressions for S1 and S2 that appear in Eqs. (6)–(7) are steep Hill equations and are defined in Eqs. (13)–(14) below. The parameter ω is chosen so that fL remains positive during a treatment interval. The parameter ta (respectively tb) corresponds to the value of fL obtained at the last time step that L has decreased below (increased above) L*. The terms ta and tb allow fL to be piecewise differentiable. Furthermore, the value of the time variable t in Eqs. (13)–(15) resets to 0 whenever L crosses L* in either direction.
The New Androgen Model is described by the following system of differential equations:
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
2.3. New PSA Model
The New PSA Model utilizes Eqs. (16)–(20) is based on the Improved BK Model but replaces Eq. (1), describing androgen production, with the New Androgen Model, Eqs. (8)–(15). Equation (19) models the production rate of PSA. The New PSA Model is described by Eqs. (16)–(20):
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
The value of A in Eq. (18 comes from the New Androgen Model, Eqs. (8)–(15). Descriptions of the parameter values and their ranges are given in Table 1; details about how they are estimated for each patient are given below.
2.4. Data
The data for this study come from a clinical trial at the Vancouver Prostate Center, which consisted of patients with high serum PSA levels and no evidence of distant metastasis prior to intermittent androgen suppression therapy [50]. Several drugs were used for hormonal therapy in this study; however, all patients initially were put on a combination of LEU and CPA and were changed to different drugs only when a problem occurred.
We have selected the 20 patients with the most complete set of observations. Each patient received more than 2.5 cycles of therapy, had at least 20 clinical measurements of serum androgen, and were on CPA and LEU consistently. Unlike previous approaches that focus on the use of PSA measurements for model validation, the New PSA Model uses androgen data as well, which more directly reflects the effects of therapy. Figure 1 shows a time series of the serum androgen level of a representative patient over the course of treatment.
Figure 1:
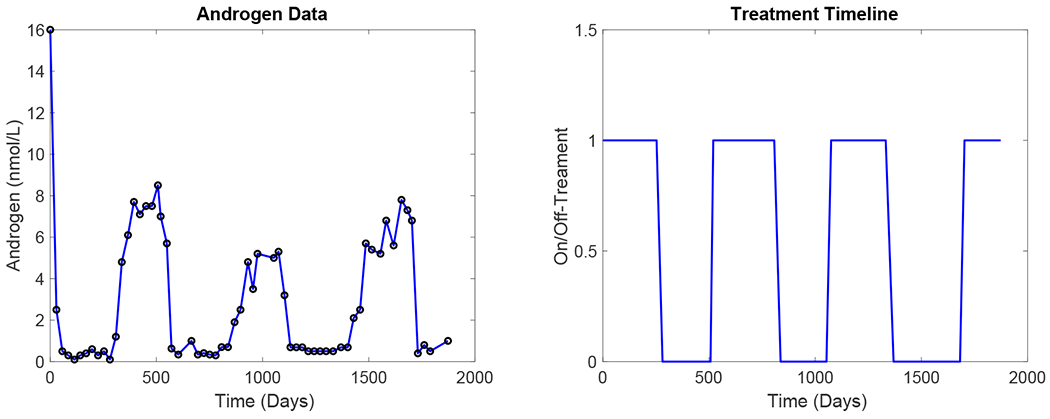
(a) Time series of serum androgen levels in a representative patient (Patient 15). (b) Corresponding on- and off-treatment timeline.
2.5. Data Uncertainty
The methods for measuring both PSA and serum androgen levels have several sources of error. We do not know what method was used, but two procedures, the double antibody RIA and the polyclonal RIA method, were commonly used during the time that the clinical data in this paper were collected (late 1990’s to early 2000’s). The main type of androgen that is measured is testosterone, although biologically, dihydrotestosterone (DHT) also plays a role in androgen receptor binding. In general, serum testosterone levels measured using commercially available kits have a high degree of between-kit variability [51]. Compared to more modern testing methods, such as liquid chromatography-tandem mass spectrometry (LC-MSMS), all serum testosterone measurements for this study typically have over 60 percent of samples (with T levels within the adult male range) within ±20% of levels measured using LC-MSMS. However, all the methods typically used during the period of data collection have poor accuracy and precision at low serum testosterone concentrations (< 100 ng/dL or 3.47 nmol/L) [52].
Likewise, we do not know the exact method used to measure PSA [50]. The likely largest source of error arises when assays of total serum PSA do not recognize the free and ACT-bound species of PSA equivalently [53, 54]. The ratios of the two types of PSA can vary in a single patient through different stages of prostate cancer. Therefore, even if the measurement method for PSA stays consistent throughout the study, the errors can be biased in either direction. Generally speaking, the proportion of free PSA is higher in patients without cancer. The molar response of skewed-response assays for free PSA is usually higher than that for PSA-ACT [55].
Both biomarkers vary diurnally within patients. One study [56] finds that “serum PSA measurements fluctuate unpredictably over the course of a day in patients with and without prostatic disease.” Another study [57] concludes that there is “significant variability between PSA measurements obtained within a short-time interval, which is due to chance alone.” The largest differences noted in the latter study were −5.3 and +7.5 ng/mL. For androgen, levels of testosterone can vary by 20–25 percent depending on the hour at which the measurements are taken, likely as a result of the normal diurnal cycle [58].
2.6. Parameter Estimation
To optimize parameters for each patient, we use the MATLAB (R2019b) built-in function fmincon [59], which implements an interior point algorithm, to minimize an appropriate sum of squares, subject to prescribed constraints on the parameters. First, we use the clinical data from the first 1.5 cycles of treatment, i.e., the first full cycle of treatment plus the next on-treatment period, to find the parameter vector in the New Androgen Model such that
| (21) |
where and denote the modeled and observed values of serum androgen level, respectively, at the ith time point during the fitting interval, i = 1, …, N. Table 1 lists the components of qA and the set QA of admissible values. Then the components of qA are fixed and substituted into the New PSA Model; the remaining components of are determined from
| (22) |
where QP is the set of admissible values for the remaining parameters of the New PSA Model (see Table 5). The modeled and observed values of PSA at the ith time point, respectively, are and . We repeat this process for every patient.
The ranges for several of the New Androgen Model parameters, including α1, α2, δ, δC, δL, γ1, and γ2, are derived empirically. LEU causes levels of luteinizing hormone (LH) and follicle stimulating hormone (FSH) to drop within two to four weeks of initiation [36]. In the New Androgen Model framework, a 2- to 4-week drop corresponds to a range of 0.1–0.45 for α1. LEU administration initially increases levels of serum testosterone increases by 50% or more above baseline during the first week of treatment, depending on dosage [36]; we choose 0.1 ≤ α2 ≤ 0.3 to replicate this clinical finding. No clinical estimates are available for α3, α4, and β. The lowest allowed value of α4 and the highestallowed value of α3 imply that the effect of LEU, measured by the parameter fL, does not last beyond 100 days. At day 100, the values α3 = 102.5 and α4 = 0.1 yield fL = 0.986, which is close to the value fL = 1 that corresponds to no LEU effect on androgen production. Thus, these upper and lower bounds for α3 and α4 were deemed suitable. The lower bound for α3 = 0 is necessary to make fL continuous and to allow for the situation in which the amount of LEU dips below L* before fL comes off the spike and goes below 1. The upper bound α4 = 0.4 is set to limit the LEU recovery period to 14 days, consistent with the pharmacokinetics [38]. Initial parameter fittings resulted in values of β between 0.005 and 0.01 for all patients, so we use this parameter range for the simulations discussed in this paper. The values of S1, S2, and ω in Eq. (13) and Eq. (14) should allow for a shift of fL when the critical drug level is crossed, but otherwise S1 and S2 should have to only have a negligible effect on fL. Setting ω = 30 causes the fL function to stay positive throughout any reasonable treatment interval, assuming that all other parameters stay within their respective ranges. Based on published pharmacokinetics [38], the critical drug level, L*, is 1 μg/L. This quantity is converted to a net mass (μg) using an average human serum volume range of 4.5 to 5.5 L [60], to have units consistent with Eq. (10).
The degradation rates of CPA and LEU are estimated from their respective serum concentration half-lives, as reported in descriptions of their pharmacokinetics [38, 48]. However, the estimated degradation rates do not correspond to a standard one-parameter exponential decay. For example, Humpel et al. [48] report that CPA reaches a maximum concentration after 4 hours; however, the first half-concentration is reported at 3 ± 1.3 hours, while the second half-concentration is 2 ± 0.4 days. Analogous measures are reported for LEU, which is injected at monthly (or longer) intervals. Instead of using the ranges derived from the clinical measurements, we determine parameter ranges that fit the data while also satisfying suitable constraints, such as the drug should stay above a critical threshold within a certain time frame. The constraints are considered in the context of the outlook for total serum mass. Therefore, we use 0.3 ≤ δC ≤ 0.7 for the degradation rate of CPA and 0.04 ≤ δL ≤ 0.16 for LEU.
Wang et al. [47] show that, in rats, the half-life of dihydrotestosterone (DHT), a form of androgen, is greater than 6 hours. Since DHT is the most relevant androgen for prostate cancer growth, we take their measurement as a base value. To account for uncertainty and physiological differences, we choose 0.03 ≤ δ ≤ 0.09 for the androgen degradation coefficient in Eq. (2).
2.7. Quantitative Assessment of the New Models
To evaluate the performance of the New Androgen Model and the New PSA Model as formulated in this paper, we compare fitting and forecasting results to those of the Improved BK model [21]. In this application, we define the error in terms of the mean of squared differences (mean-squared error, MSE) between the observed and predicted values of serum androgen (likewise PSA) levels at each of N measurement time points:
| (23) |
where and are, respectively, the estimated and the observed values of serum androgen (or PSA) at the ith time point. We carry out fitting on 1.5 cycles for each patient to obtain a set of parameters, within the set of admissible values for the New Androgen and New PSA models, that minimizes Eq. (23). Next, we use the parameters to forecast the next cycle. Finally, we evaluate the MSE over the forecast period to quantify the models’ predictive ability.
3. Results
We show that the New Androgen Model is able to capture the expected dynamics of the drugs, their effectiveness, and the androgen level. Next, we compare the data fitting and forecasting performance of the New PSA Model against the Improved BK Model. Finally, we consider the basic properties of the New Androgen Model to validate its biological plausibility.
3.1. Simulation of the New Androgen Model
Figure 2 shows the results of a simulation (blue curve) of the New Androgen Model, Eqs. (8)–(15), and corresponding serum androgen measurements (circles) for a representative patient. The timing and dosages of the drugs used during each treatment cycle are taken from clinical data [50]. The model parameters are selected to minimize the mean-squared error, Eq. (21), between observed and simulated serum androgen levels using the fitting procedure described above. The minimization is done over the first 1.5 treatment cycles (i.e., the fitting interval is Days 1–837 in the case of this patient); then, using the model state vector at Day 837 as the initial condition, the integration is continued to the end of the treatment course at Day 1369 (the forecast interval). Table 2 lists the parameter values used in this simulation.
Figure 2:
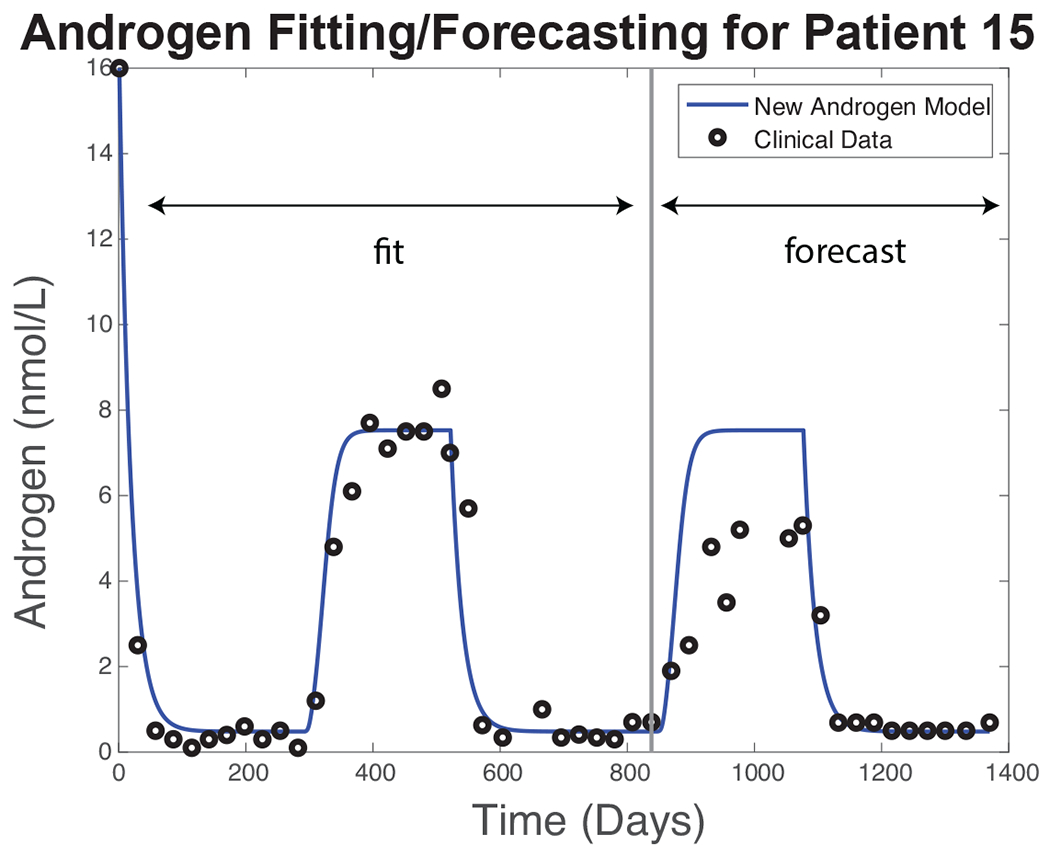
Simulation results for Patient 15. Blue curve: serum androgen level simulated by the New Androgen Model using a parameter vector obtained by minimizing Eq. (21) with clinical data (black circles) for the first 837 days of treatment. The simulation is continued to Day 1369 using the same parameters and the Day 837 state vector as the initial condition.
Table 2:
Parameter values for Patient 15 using the estimation procedure described above. Bounds for the parameters in Eqs. (16)–(20) are taken from Phan at al. [21].
| Param | Description | Value | Unit |
|---|---|---|---|
| α1 | LEU desensitization length | 0.4474 | unitless |
| α2 | LEU spike amplitude | 0.2973 | unitless |
| α3 | hift for time LEU remains effective below L* | 101.1756 | unitless |
| α4 | androgen production recovery rate | 0.1000 | unitless |
| β | half-saturation constant of effectiveness in CPA | 0.0500 | mg |
| δ | androgen degradation rate | 0.0541 | day−1 |
| δC | decay for CPA | 0.6995 | day−1 |
| δL | decay for LEU | 0.1507 | day−1 |
| γ1 | testes’ androgen production rate | 0.9000 | mg day−1 |
| γ2 | androgen production from adrenal gland | 0.0263 | mg day−1 |
| Am | maximum androgen | 13.0413 | nmol·L−1 |
| L* | critical drug level | 5.5 | μg |
| ω | maximum logistic rate for S1 and S2 | 30 | unitless |
| — | Parameters below are for Eqs.(16)–(20) | — | — |
| μ1 | max proliferation rate (AD cells) | 0.0806 | day−1 |
| μ2 | max proliferation rate (AI cells) | 0.0900 | day−1 |
| q1 | min AD cell quota | 0.4435 | nmol·day−1 |
| q2 | min AI cell quota | 0.0100 | nmol·day−1 |
| b | baseline PSA production rate | 0.0018 | μg·nmol−1·day−1 |
| σ | tumor PSA production rate | 1.0000 | μg·nmol−1·L−1·day−1 |
| ε | PSA clearance rate | 0.05610 | day−1 |
| d1 | max AD cell death rate | 0.0900 | day−1 |
| d2 | max AI cell death rate | 0.0010 | day−1 |
| δ1 | density death rate | 1.0000 | L−1·day−1 |
| δ2 | density death rate | 3.0602 | L−1·day−1 |
| R1 | AD death rate half-saturation | 0.4872 | nmol·L−1 |
| R2 | AI death rate half-saturation | 5.9961 | nmol·L−1 |
| c | maximum mutation rate | 0.0001 | day−1 |
| k | mutation rate half-saturation level | 1.6537 | nmol·day−1 |
| m | diffusion rate from A to Q | 0.9000 | day−1 |
Figure 3 shows simulated serum drug levels and their treatment effect over the same fitting and forecast intervals. For this patient, each on- and off-treatment interval is approximately 200 days. As mentioned above, the patient takes CPA daily in pill form; LEU is injected monthly by a medical professional (with the occasional exception, as around Day 606), and the first injection does not occur until about 30 days after CPA therapy is initiated. Figure 3(a) shows the estimated treatment effect of each drug (fC and fL, the black and red curves, respectively) and the combined treatment effect, F (green), over the entirety of the clinical course; Figure 3(b) shows a 20-day magnification to make apparent the daily fluctuations in CPA.
Figure 3(c) shows simulated time series of the serum masses of CPA and LEU, and Fig. 3(d) shows a magnification of the timeline to make apparent their respective daily and monthly dosing. Brief enhancement of androgen production (F > 1) is reflected in the “spikes” shortly following each LEU injection. Figure 3(a) shows that the drug effect is nearly a step function; however, serum androgen levels (Fig. 2) respond more slowly, insofar as testosterone production by the adrenal glands (represented by γ2 in Eq. (8)) is assumed to be unaffected by the treatment.
Patients take CPA at home daily during each on-treatment interval. Our simulations assume that patients do not miss doses. LEU administration data are more trustworthy, as the dosages and injection times are recorded by medical professionals. Imperfect patient compliance is a potential source of error in the model results.
Figure 4 compares simulations of serum androgen against clinical data (black circles) using the Improved BK Model [21] (red curves) and the New PSA Model (blue) for Patients 6, 15, 29, and 77. The parameter fitting procedure is similar to that for Patient 15, except that the length of each fitting interval varies according to the length of the first 1.5 treatment cycles for each patient. The fitting intervals comprise the first 1140, 837, 1115, and 735 days of treatment for Patients 6, 15, 29, and 77, respectively.
Figure 4:
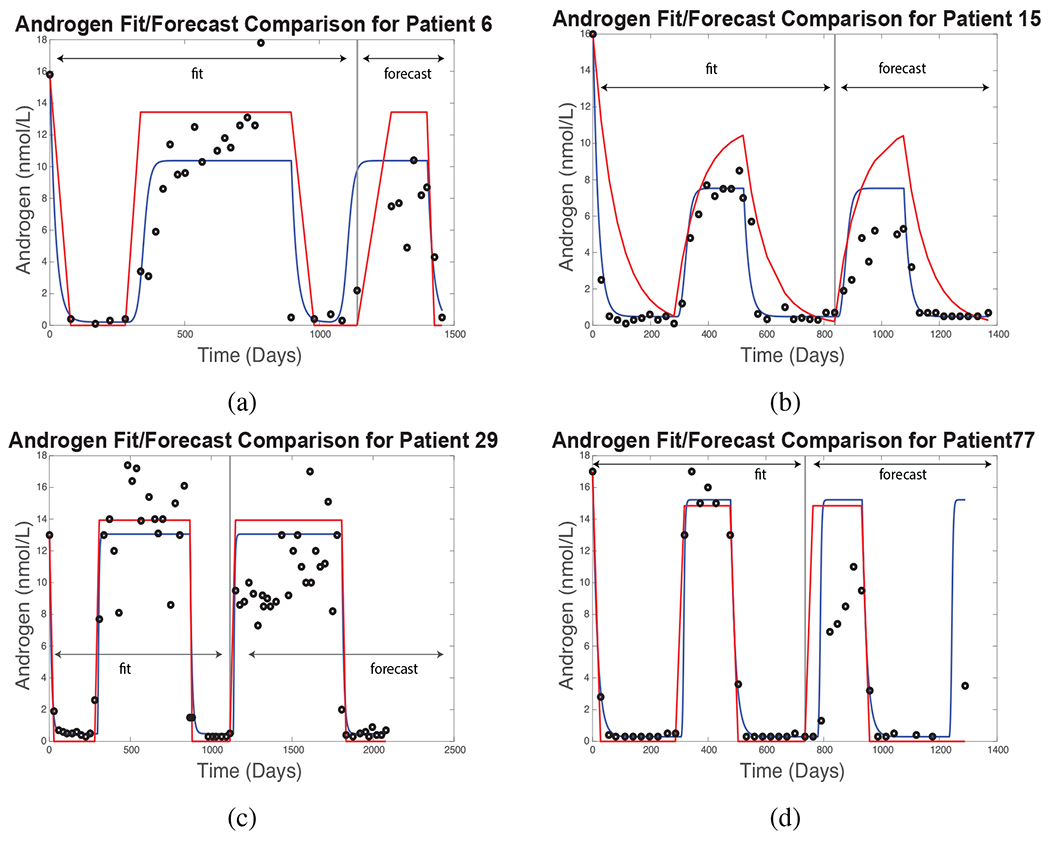
Androgen fitting and forecasting results for the Improved BK model (red curves) and New PSA Model (blue). Black circles denote clinical measurements for each patient. The fitting and forecasting procedure is similar for each patient, as described in the text.
3.2. Simulation of Prostate-Specific Antigen (PSA)
Prostate-specific antigen (PSA) is a crucial biomarker for clinical diagnosis and monitoring of prostate cancer. We use the New Androgen Model to drive the New PSA Model, Eqs. (16)–(20. Figure 5 shows the simulated PSA levels for four representative patients using the parameter fitting procedure describe above.
Figure 5:
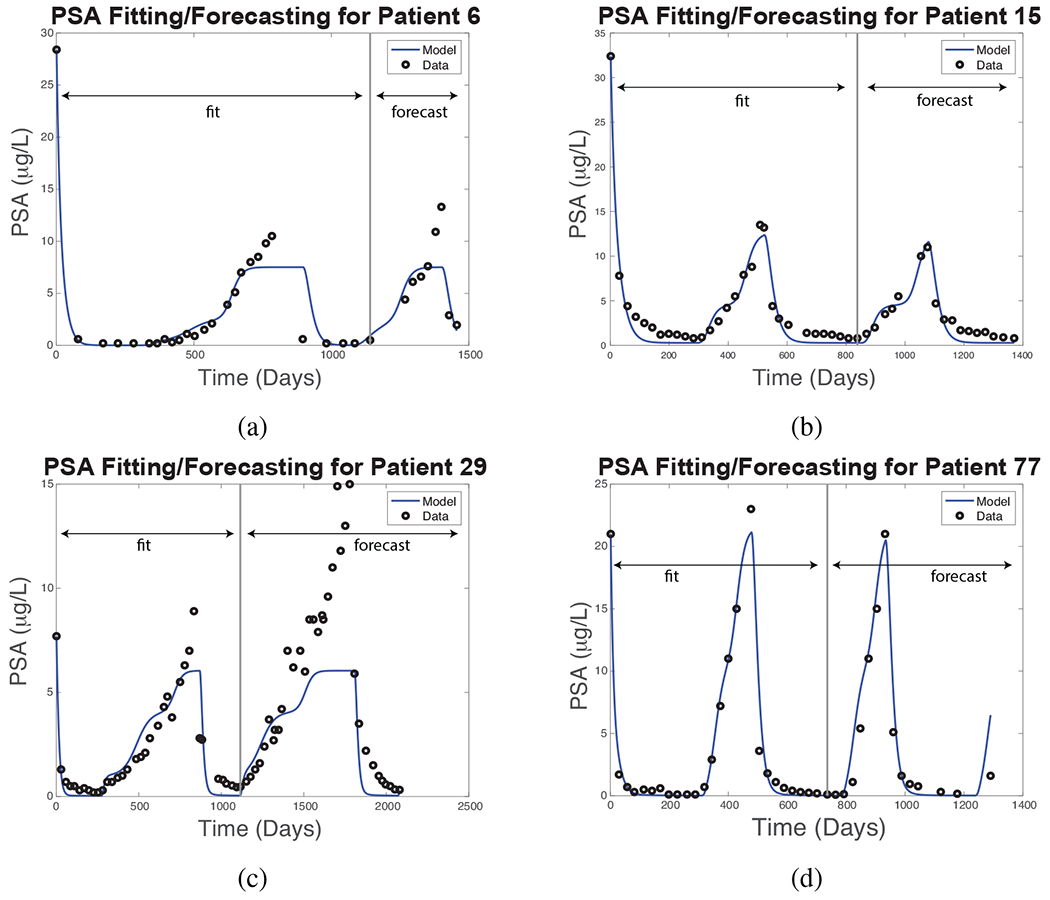
New PSA Model simulated (blue curves) and clinically measured (black circles) PSA levels for four representative patients. The parameter fitting and model forecast intervals are as indicated for each patient.
Although no curative treatment is possible at present, one goal of therapy is to help patients survive as long as possible. While there is debate as to the best way to achieve this goal, one consensus is to limit the growth of androgen-dependent (AD) cells without accelerating that of androgen-independent (AI) cells, so that androgen deprivation treatment (ADT) may remain viable as long as possible [13, 61, 62]; androgen-independent cells are resistant to ADT. Figure 6 shows simulations of the the effect of therapy on AD and AI cell populations for the same patients as in Fig. 5, using the New PSA Model. The results suggest that Patients 29 and 77 have large fractions of AI cells, but clinical records show that treatment was successful for another cycle in each case, and both survived for an extended period. No assay or biopsy data are available to evaluate these simulation results.
Figure 6:
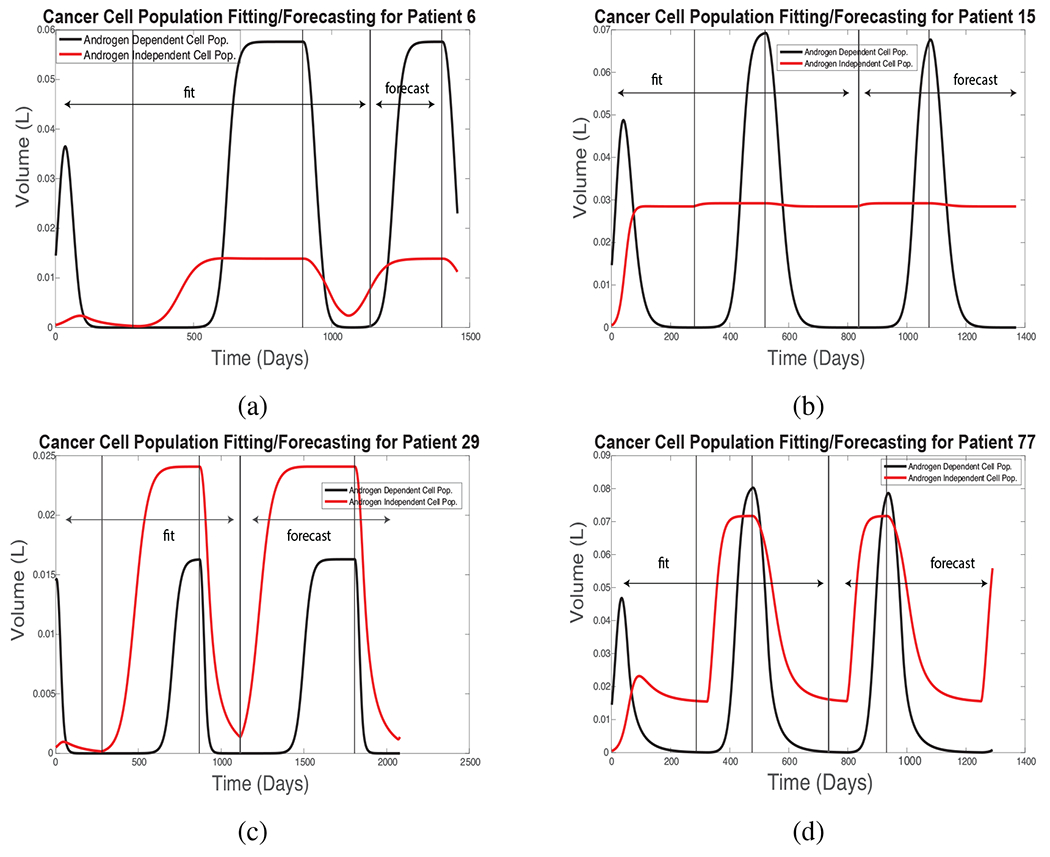
Simulated androgen-dependent and -independent cell populations using the same parameters and fitting intervals in the New PSA Model as in Fig. 5.
Analogous simulations of serum androgen and PSA levels were performed for each of the 20 patients with the most complete clinical data sets, as described in Section 2.4. Table 3 shows quartiles of the MSE between the simulated and measured values of serum androgen for the 20 patients evaluated in this study. Fitting errors are computed over the first 1.5 cycles of treatment and reflect the minimum MSE obtained by fmincon’s optimization algorithm. The model state vector at the end of each fitting interval is used as the initial condition for the forecasting interval. The New Androgen Model significantly reduces the simulation error, compared to the Improved BK Model [21], over both the fitting and forecasting intervals.
Table 3:
Androgen fitting and forecasting MSE comparison between the New Androgen Model, which is part of the New PSA Model, formulated here and the Improved BK model. Error results are based on data from 20 patients.
| Model | Androgen Fitting Error |
Androgen Forecasting Error |
||||
|---|---|---|---|---|---|---|
| Q1 | Median | Q3 | Q1 | Median | Q3 | |
| Improved BK model | 2.91 | 7.41 | 13.82 | 8.47 | 20.81 | 33.14 |
| New Androgen Model | 0.88 | 1.42 | 2.22 | 4.99 | 8.75 | 11.90 |
Table 4 shows analogous measures for PSA. The improvement of the New PSA Model over the Improved BK Model is modest. Additional results are given in the supplementary materials.
Table 4:
Prostate-specific antigen fitting and forecasting MSE comparison between the New PSA Model formulated here and the Improved BK model. Error results are based on data from 20 patients.
| Model | PSA Fitting Error |
PSA Forecasting Error |
||||
|---|---|---|---|---|---|---|
| Q1 | Median | Q3 | Q1 | Median | Q3 | |
| Improved BK model | 1.20 | 4.38 | 7.34 | 5.31 | 11.19 | 17.47 |
| New PSA Model | 1.77 | 3.28 | 9.92 | 5.65 | 10.80 | 16.39 |
3.3. Simulated Clinical Response Experiment
The simulation results presented above use the drug dosages that were prescribed for each patient in the Vancouver clinical trial. In this section, we use the New Androgen and New PSA Models to simulate the effect of a different drug administration protocol. Our goal is to illustrate how a validated mathematical model might be used to inform clinical practice, in this case, by asking whether reduced a dosage of CPA would have a deleterious effect on a particular patient’s outcome during the last cycle of treatment.
The oral drug CPA acts synergistically with the injected drug LEU to decrease the amount of luteinizing hormones in the serum and thereby suppress androgen production in the testes. As mentioned in the introduction, however, LEU paradoxically increases testosterone production by the testes for a short interval following initial administration, which daily doses of CPA counteract. We theorize that after counteracting this initial spike in androgen production, the effect of CPA otherwise is negligible.
During the Vancouver trial, CPA therapy in four patients (1, 26, 50, and 106) was halted at times due to negative side effects. During these periods, ranging from four days to 16 weeks, patients stayed at stable, low serum androgen levels, consistent with ranges observed during the ordinary administration of both drugs. The goal of this numerical experiment is to test the effect of cessation of CPU therapy shortly after the start of the third on-treatment interval. We use Patient 15 as a case study and consider the hypothetical situation in which CPA administration halts after Day 1140.
For this simulation, we suppose that the therapy proceeds for the initial 2.5 cycles of therapy (1140 days) exactly as documented in the clinical trial. The New Androgen and New PSA Models are run with the same parameters as in Table 2, and the results of the model simulation are as in Fig. 2 for the initial 1140 days.
In this experiment, LEU is injected at the same intervals and dosages as documented in the clinical trial. Next, we suppose that Patient 15 takes CPA only for the first 60 days of the last treatment cycle, as illustrated in Fig. 7(a). Using the same parameters as before, we run the models without CPA administration thereafter. Figure 7(c) suggests that the net effectiveness of the drugs is unchanged, and, as expected, the predicted levels of serum androgen and PSA, shown in Fig. 7(b) and (d), are nearly same as before (panel (f)). The models imply that the population of androgen-independent cells remains stable during this last treatment interval (panel (e)). Insofar as drug dosage probably correlates with severity of side effects in most patients, clinically validated models may be able to predict which patients will sustain a therapeutic response at reduced drug dosages.
Figure 7:
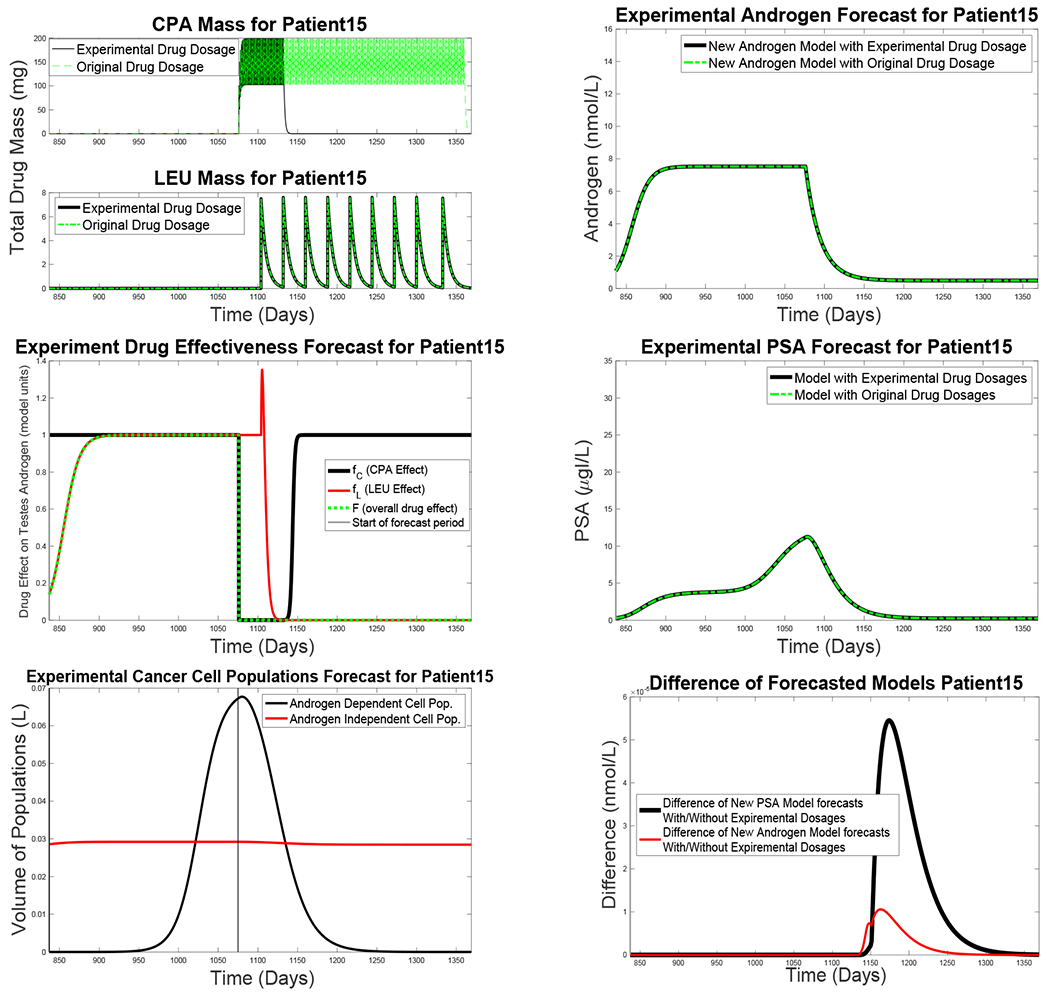
Simulation results of a hypothetical treatment regimen in which CPA therapy halts after Day 1140 for Patient 15. (a) Simulated serum masses of CPA and LEU; administration of the latter is assumed to continue as documented in the clinical record. (b) Simulated serum androgen levels, using the New Androgen Model, at the original (green curve) and reduced (black) CPA dosages. (c) Simulated effects of CPA (green) and LEU (black) at the new dosages. (d) Simulated PSA levels, using the New PSA Model, at the original (green curve) and reduced (black) CPA dosages. (e) Estimated androgen-dependent and -independent cell populations, by the New PSA model, under the reduced dosage regimen. (f) Absolute differences between the androgen and PSA levels for the New Androgen Model (red curve) and Improved BK Model (black) for the two treatment regimens.
3.4. Sensitivity Analysis
We focus our analysis here on the New Androgen Model, using parameters computed for a representative patient during both on- and off-treatment intervals, and consider the effect of perturbations of the parameter vector obtained by minimizing the sum of squares in Eq. (21) on the model output variables at each clinical measurement time during the initial fitting period (corresponding to 1.5 treatment cycles). We find that the results of our simulations are relatively insensitive to changes in all but four parameters.
We define the parameter sensitivity according to the normalized sensitivity equation from section 5.5 of [63]:
| (24) |
where p is the model parameter of interest and y(t) is the model variable under consideration at some time point of interest. Heuristically, one can think of Sp(y(t)) as measuring the relative change in y(t) for a given relative change in some component p of the model parameter vector .
In the results described here, we take the “baseline” parameter vector to be as determined in Section 2 for Patient 15 and define y0(t) to be the associated simulated time series of the model variable of interest. (For example, the serum androgen level, y0(t) = A0(t), is plotted in Fig. 2.) We alter one component, say p0, by a relative value of 1 percent to yield the perturbed value , and re-run the model to produce a new time series, say , of serum androgen levels (and similarly for other model variables). At the ith clinical observation time ti, we approximate the change in y(ti) given as
| (25) |
For each of the N clinical observation times within the parameter-fitting interval (837 days in the case of Patient 15), we compute Sp(y(ti)), i = 1, …, N, the mean , and the total sensitivity as the root-mean square
| (26) |
This procedure is performed for each of the first 10 parameter components listed in Table 2; the baseline values are those in the table and are obtained from the fitting procedure outlined in Section 2. Each component is perturbed by a relative amount of 1 percent from the baseline, and the corresponding sensitivity of serum androgen and total drug mass of CPA and LEU are calculated. In the latter case, we evaluate Tp only over the time points following the initial injection of LEU.
Figure 8 shows the total sensitivity of serum androgen (blue bars), CPA drug mass (red) and LEU drug mass (green) as a function of each of the first 10 parameters of the New Androgen Model given in Table 1. The serum androgen level, governed by Eq. (8), is most sensitive to the clearance rate parameter δ and secondarily to the production rate γ2 by the adrenal glands (whose hormone production is assumed to be unaffected by the therapy). The total masses of the drugs CPA and LEU, Eqs. (9) and (10), are most sensitive to their estimated degradation rates, δC and δL, respectively. Small perturbations of the remaining components of the parameter vector have negligible effects on the model outputs.
Figure 8:

Total sensitivity Tp, Eq. (25), for the New Androgen Model, Eqs. (8)–(15), for output model variables representing serum androgen levels (A, blue bars), total CPA drug mass (C. red), and total LEU drug mass (L, green), as a function of each of the first 10 components p of the parameter vector obtained for Patient 15 from the fitting procedure described in Section 2.
The simulated clinical response experiment discussed above suggests that the cessation of CPA therapy has little effect on serum androgen levels after LEU is injected during a subsequent cycle of therapy. To conclude this section, we consider scenarios in which dosages of the two drugs are varied and the subsequent effects on androgen production under the assumptions of the New Androgen Model. Among other questions, we explore the reduced dosage levels of the drugs that might be expected to have clinical effect.
Figure 9 shows simulated time series of serum androgen levels for Patient 15 over 1.5 cycles of therapy with varying values of CPA and LEU dosage: large, normal, and small dosage levels, using the parameters given in Table 2. The “large” doses simulated here are comparable to those used at the start of therapy; “normal” doses are representative of maintenance therapy and most closely approximate the doses that Patient 15 received. We also investigate the potential use of “small” doses that are 25 to 50 percent as large as “normal.” If the synergistic effect of the two drugs remains approximately multiplicative at these dosage levels, as assumed in Eq. (11), then “small” doses may be almost as effective as “normal” ones, although androgen production levels recover somewhat more quickly at the small dose than for the others. The minimum serum androgen level is independent of dosage (provided that LEU levels attain the critical level L*), because the adrenal glands are assumed to be unaffected by the treatment and continue to produce androgen at their usual rates. Heat maps of simulated net androgen production rates for various combinations of dosages over 0.5 cycles and 1.5 cycles are given in the supplementary materials.
Figure 9:
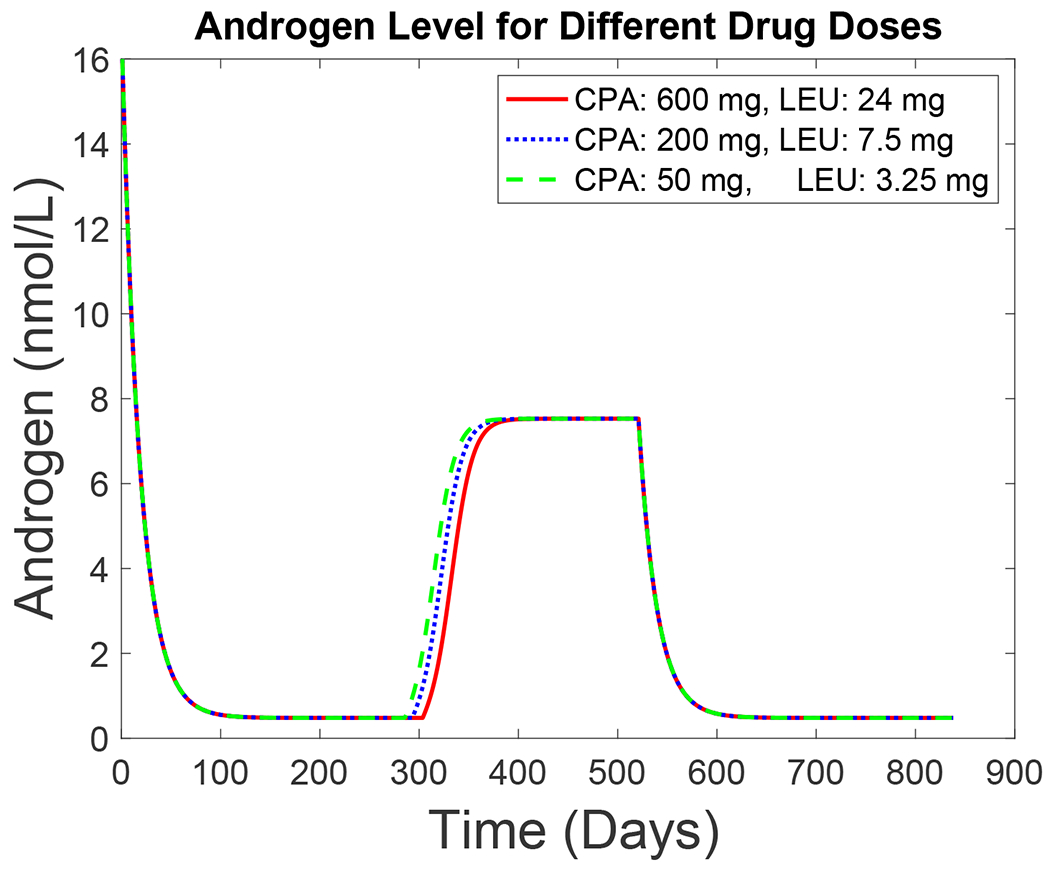
Simulated androgen levels, according to the New Androgen Model, for Patient 15 for three different CPA and LEU dosage levels over 1.5 cycles of therapy. Red curve: large doses (600 mg CPA daily and 24 mg LEU monthly). Blue curve: 200 mg CPA daily and 7.5 mg LEU monthly (closest to those actually given). Green curve: small doses (50 mg CPA daily and 3.25 mg LEU monthly).
4. Discussion and Conclusions
In this work, we have constructed and verified a framework that can qualitatively and quantitatively describe the dynamics of serum androgen and drugs in intermittent androgen suppression therapy. Our modeling framework may be useful as a basis for a more mechanistic serum androgen model, and our approach may be helpful for applications other than prostate cancer.
(A1) The New Androgen Model can replicate clinically observed serum levels of testosterone in a patient-specific manner using prespecified dosages of two anti-androgenic drugs. In particular, the New Androgen Model is the first (to our knowledge) that captures the delay of recovery in androgen production rates during intermittent androgen suppression therapy by incorporating residual treatment effects. Equations (11)–(15), which quantify the effect of the drugs on the testes’ androgren production rates, mostly follow logistic growth dynamics during recovery periods; therefore, serum androgen levels eventually reach a steady state independently of any drug-related parameters. Such parameter independence is reasonable, considering we expect the drug to eventually clear from the system and the function of androgen-producing organs to return to baseline levels. In some patients, however, androgen production rates may not return to pre-treatment levels following prolonged suspension; the effect may depend on the length of androgen suppression and/or the total drug dosages. Future refinements to the New Androgen Model may need to incorporate the details of key biological pathways, which besides improved data fitting may also allow the models to be applied to new types of androgen-suppression therapies.
(A2) Data from most patients show a decline in the peak serum androgen level after each subsequent drug treatment interval. While the reason for the decline is unknown, we speculate that there may be four possible causes: a change in the patient’s diet and behaviors, compounding residual drug effects over multiple treatment cycles, changes in the cancer cells’ uptake of serum androgen, and the inability of the body to recover full androgen production due to treatment-induced changes in gonadotropic-cell dynamics.
(A3) Treatment resistance always occurs, due to selective pressures from the therapy. The New PSA Model (and the Improved BK Model) postulate the existence of androgen-dependent and -independent cancer cell populations. However, in some cases (e.g., Fig. 6), the models create a large androgen-independent cell population in patients who responded well to repeated cycles of treatment and survived for several years. Unfortunately, there is no data to support or refute the simulated cell populations. Improved biological understanding and mathematical models of this crucial point are needed.
(A4) The parameter-fitting procedure in this paper uses data from the first 1.5 treatment cycles to predict the response to the last treatment cycle. Our methods do not account for potential changes to the drug dosages or administration protocol, nor for any observed decreases in maximum serum androgen levels, that may occur during the forecast period. A better approach may be to use an augmented Kalman filter that estimates changes in selected components of the model parameter and state vector at each clinical measurement time point.
(A5) Our primary focus in this paper is on the modeling of serum androgen levels in response to drug therapy, and the New Androgen Model outperforms its predecessor in terms of fitting the available clinical data. We have examined whether these improvements translate to better predictions of serum PSA levels, insofar as the serum androgen level is a forcing term in the New PSA Model. In this respect, the results are modest, as shown in Table 4. A better understanding of the dynamics of the androgen-dependent and -independent cell populations is needed.
(A6) In this study, we performed both local and global sensitivity analyses to investigate the influence of parameters on model outputs. Representative results for the local sensitivity analysis on the New Androgen Model are shown in Figure 8. (Additional sensitivity results for the New PSA Model are given in the Figures 11 and 12 in the supplementary materials.) The simulations of serum androgen are most sensitive to the assumed degradation rates of the drugs used for therapy and the assumed androgen-production rates by the adrenal glands (which are largely unaffected by therapy), and to degradation rates by metabolism and absorption. Simulated clinical experiments suggest that LEU has the most important androgen-suppressive effect and that patients may be able to stop daily CPA administration after awhile. The dynamics of serum PSA levels are assumed to depend on the relative size of androgen-dependent and -independent tumor cell populations. However, the simulated results suggest that large treatment-resistant cell populations develop right away in patients who are known to have responded well to therapy for extended periods. The meaning of these results is not clear, and the associated parameters cannot be identified from the clinical data that has been used for this study. Improved models of the tumor biology remain as future work.
To our knowledge, ours is the first modeling effort to focus on the dynamics of drugs used for intermittent androgen-suppression therapy for prostate cancer. Future investigations can consider the interactions between other multi-drug therapies for cancer and their optimization for individual patients.
After prostate cancer has metastasized, there is no cure. Selection pressures from hormonal treatment eventually lead to treatment resistance. Improved biological and mathematical understanding of the evolution of treatment resistance is needed. The advent of adaptive therapy [39, 40] for prostate cancer has created new opportunities for mathematical models to optimize treatment plans for individual patients.
Supplementary Material
Highlights.
Formulation of dynamical model that explicitly incorporates the synergistic properties of drugs commonly used in hormonal therapy.
Model is better at capturing the androgen dynamics under treatment than previously published models.
By improving the ability of the model to describe androgen dynamics, the model also shows improvement in fitting and forecasting the progression of prostate cancer.
Acknowledgments
The authors would like to thank the reviewers for their critical comments that help improve the manuscript significantly. Additionally, the authors would like to thank Professor Carlo C. Maley and his lab group at Arizona State University for insightful discussions about the scientific implications of this work and Professors Ralph Smith and Alen Alexanderian at North Carolina State University for their helpful comments regarding global sensitivity analysis.
Funding
Yang Kuang is partially supported by NSF grants DMS-1615879, DEB-1930728 and NIH grant 5R01GM131405-02. Kyle Nguyen was supported by NSF under grant DMS-1246991.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest
The authors declare no conflict of interest.
References
- [1].Siegel RL, Miller KD, and Jemal A, “Cancer statistics, 2020,” CA: A Cancer Journal for Clinicians, vol. 70, no. 1, pp. 7–30, 2020. [DOI] [PubMed] [Google Scholar]
- [2].Gupta S, Gupta A, Saini AK, Majumder K, Sinha K, and Chahal A, “Prostate cancer: How young is too young?,” Current Urology, vol. 9, no. 4, pp. 212–215, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Taitt HE, “Global trends and prostate cancer: A review of incidence, detection, and mortality as influenced by race, ethnicity, and geographic location,” American Journal of Men’s Health, vol. 12, no. 6, pp. 1807–1823, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Cherian MT, Wilson EM, and Shapiro DJ, “A competitive inhibitor that reduces recruitment of androgen receptor to androgen-responsive genes,” Journal of Biological Chemistry, vol. 287, no. 28, pp. 23368–23380, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Ekman P, “The prostate as an endocrine organ: Androgens and estrogens,” Prostate, vol. 45, no. S10, pp. 14–18, 2000. [PubMed] [Google Scholar]
- [6].Feldman BJ and Feldman D, “The development of androgen-independent prostate cancer,” Nature Reviews Cancer, vol. 1, no. 1, p. 34, 2001. [DOI] [PubMed] [Google Scholar]
- [7].Devlin HL and Mudryj M, “Progression of prostate cancer: Multiple pathways to androgen independence,” Cancer Letters, vol. 274, no. 2, pp. 177–186, 2009. [DOI] [PubMed] [Google Scholar]
- [8].Jayadevappa R, Sumedha Chhatre S, Malkowicz SB, Parikh RB, Guzzo T, and Wein AJ, “Association between androgen deprivation therapy use and diagnosis of dementia in men with prostate cancer,” JAMA Network Open, vol. 2, no. 7, p. e196562, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].“Prostate cancer,” American Cancer Society, pp. 4–18, 28,–29, 56–57, March 2016. [Google Scholar]
- [10].Phan T, Crook SM, Bryce AH, Maley CC, Kostelich EJ, and Kuang Y, “Mathematical modeling of prostate cancer and clinical application,” Applied Sciences, vol. 10, no. 8, p. 2721, 2020. [Google Scholar]
- [11].Kuang Y, Nagy JD, and Eikenberry SE, Introduction to mathematical oncology. CRC Press, 2018. [Google Scholar]
- [12].Jackson TL, “A mathematical investigation of the multiple pathways to recurrent prostate cancer: Comparison with experimental data,” Neoplasia, vol. 6, no. 6, pp. 697–704, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Jackson TL, “A mathematical model of prostate tumor growth and androgen-independent relapse,” Discrete & Continuous Dynamical Systems-B, vol. 4, no. 1, pp. 187–201, 2004. [Google Scholar]
- [14].Kelloff GJ, Choyke P, and Coffey DS, “Challenges in clinical prostate cancer: Role of imaging,” American Journal of Roentgenology, vol. 192, no. 6, pp. 1455–1470, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Hirata Y, Bruchovsky N, and Aihara K, “Development of a mathematical model that predicts the outcome of hormone therapy for prostate cancer,” Journal of Theoretical Biology, vol. 264, no. 2, pp. 517–527, 2010. [DOI] [PubMed] [Google Scholar]
- [16].Wu Z, Phan T, Baez J, Kuang Y, and Kostelich EJ, “Predictability and identifiability assessment of models for prostate cancer under androgen suppression therapy,” Mathematical Biosciences and Engineering, vol. 16, pp. 3512–3536, 2019. [DOI] [PubMed] [Google Scholar]
- [17].Barton HA and Andersen ME, “A model for pharmacokinetics and physiological feedback among hormones of the testicular-pituitary axis in adult male rats: a framework for evaluating effects of endocrine active compounds,” Toxicological Sciences, vol. 45, no. 2, pp. 174–187, 1998. [DOI] [PubMed] [Google Scholar]
- [18].Potter LK, Zager MG, and Barton HA, “Mathematical model for the androgenic regulation of the prostate in intact and castrated adult male rats,” American Journal of Physiology-Endocrinology and Metabolism, vol. 291, no. 5, pp. E952–E964, 2006. [DOI] [PubMed] [Google Scholar]
- [19].Portz T, Kuang Y, and Nagy JD, “A clinical data validated mathematical model of prostate cancer growth under intermittent androgen suppression therapy,” Aip Advances, vol. 2, no. 1, p. 011002, 2012. [Google Scholar]
- [20].Baez J and Kuang Y, “Mathematical models of androgen resistance in prostate cancer patients under intermittent androgen suppression therapy,” Applied Sciences, vol. 6, no. 11, p. 352, 2016. [Google Scholar]
- [21].Phan T, Nguyen K, Sharma P, and Kuang Y, “The impact of intermittent androgen suppression therapy in prostate cancer modeling,” Applied Sciences, vol. 9, no. 1, p. 36, 2019. [Google Scholar]
- [22].Drake CG, “Prostate cancer as a model for tumour immunotherapy,” Nature Reviews Immunology, vol. 10, no. 8, pp. 580–593, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Kantoff PW, Higano CS, Shore ND, Berger ER, Small EJ, Penson DF, Redfern CH, Ferrari AC, Dreicer R, Sims RB, et al. , “Sipuleucel-t immunotherapy for castration-resistant prostate cancer,” New England Journal of Medicine, vol. 363, no. 5, pp. 411–422, 2010. [DOI] [PubMed] [Google Scholar]
- [24].Rutter EM and Kuang Y, “Global dynamics of a model of joint hormone treatment with dendritic cell vaccine for pprostate cancer,” Discrete & Continuous Dynamical Systems-B, vol. 22, no. 3, p. 1001, 2017. [Google Scholar]
- [25].Coletti R, Leonardelli L, Parolo S, and Marchetti L, “A QSP model of prostate cancer immunotherapy to identify effective combination therapies,” Scientific Reports, vol. 10, no. 1, pp. 1–18, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Coletti R, Pugliese A, and Marchetti L, “Modeling the effect of immunotherapies on human castration-resistant prostate cancer,” Journal of Theoretical Biology, p. 110500, 2020. [DOI] [PubMed] [Google Scholar]
- [27].Valle PA, Coria LN, and Carballo KD, “Chemoimmunotherapy for the treatment of prostate cancer: Insights from mathematical modelling,” Applied Mathematical Modelling, 2020. [Google Scholar]
- [28].Hirata Y, Morino K, Akakura K, Higano CS, and Aihara K, “Personalizing androgen suppression for prostate cancer using mathematical modeling,” Scientific Reports, vol. 8, no. 1, p. 2673, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Nakanishi A and Hirata Y, “Practically scheduling hormone therapy for prostate cancer using a mathematical model,” Journal of Theoretical Biology, 2019. [DOI] [PubMed] [Google Scholar]
- [30].Fleck JL and Cassandras CG, “Optimal design of personalized prostate cancer therapy using infinitesimal perturbation analysis,” Nonlinear Analysis: Hybrid Systems, vol. 25, pp. 246–262, 2017. [Google Scholar]
- [31].Cunningham JJ, Brown JS, Gatenby RA, and Staňková K, “Optimal control to develop therapeutic strategies for metastatic castrate resistant prostate cancer,” Journal of Theoretical Biology, vol. 459, pp. 67–78, 2018. [DOI] [PubMed] [Google Scholar]
- [32].Kuhl H, “Pharmacology of estrogens and progestogens: Influence of different routes of administration,” Climacteric, vol. 8, no. sup1, pp. 3–63, 2005. [DOI] [PubMed] [Google Scholar]
- [33].Wishart DS, Feunang YD, Guo AC, Lo EJ, Marcu A, Grant JR, Sajed T, Johnson D, Li C, Sayeeda Z, et al. , “Drugbank 5.0: A major update to the Drugbank database for 2018,” Nucleic Acids Research, vol. 46, no. D1, pp. D1074–D1082, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Neumann F, “The antiandrogen cyproterone acetate: Discovery, chemistry, basic pharmacology, clinical use and tool in basic research,” Experimental and Clinical Endocrinology and Diabetes, vol. 102, no. 01, pp. 1–32, 1994. [DOI] [PubMed] [Google Scholar]
- [35].Donald RA, Espiner EA, Cowles RJ, and Fazackerley JE, “The effect of cyproterone acetate on the plasma gonadotrophin response to gonadotrophin releasing hormone,” European Journal of Endocrinology, vol. 81, no. 3, pp. 680–684, 1976. [DOI] [PubMed] [Google Scholar]
- [36].“Lupron depot 7.5 mg 1-month, 22.5 mg 3-month, 30 mg 4-month, 45 mg 6-month (leuprolide acetate) - full prescribing information,” Lupron Depot 7.5 mg 1-Month, 22.5 mg 3-Month, 30 mg 4-Month, 45 mg 6-Month | FULL Prescribing Information | PDR.net.
- [37].Wilson AC, Vadakkadath Meethal S, Bowen RL, and Atwood CS, “Leuprolide acetate: A drug of diverse clinical applications,” Expert Opinion on Investigational Drugs, vol. 16, no. 11, pp. 1851–1863, 2007. [DOI] [PubMed] [Google Scholar]
- [38].Periti P, Mazzei T, and Mini E, “Clinical pharmacokinetics of depot leuprorelin,” Clinical Pharmacokinetics, vol. 41, no. 7, pp. 485–504, 2002. [DOI] [PubMed] [Google Scholar]
- [39].Gatenby RA, Silva AS, Gillies RJ, and Frieden BR, “Adaptive therapy,” Cancer Research, vol. 69, no. 11, pp. 4894–4903, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Greaves M and Maley CC, “Clonal evolution in cancer,” Nature, vol. 481, no. 7381, p. 306, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Zhang J, Cunningham JJ, Brown JS, and Gatenby RA, “Integrating evolutionary dynamics into treatment of metastatic castrate-resistant prostate cancer,” Nature Communications, vol. 8, no. 1, pp. 1–9, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Dillard PR, Lin M-F, and Khan SA, “Androgen-independent prostate cancer cells acquire the complete cteroidogenic potential of synthesizing testosterone from cholesterol,” Molecular and Cellular Endocrinology, vol. 295, no. 1–2, pp. 115–120, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Bahrami K and Kim M, “Optimal control of multiplicative control systems aris-ing from cancer therapy,” IEEE Transactions on Automatic Control, vol. 20, no. 4, pp. 537–542, 1975. [Google Scholar]
- [44].Hayashida K.-i. and Eisenach JC, “Multiplicative interactions to enhance gabapentin to treat neuropathic pain,” European Journal of Pharmacology, vol. 598, no. 1–3, pp. 21–26, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Felmlee MA, Morris ME, and Mager DE, “Mechanism-based pharmacodynamic modeling,” in Computational Toxicology, pp. 583–600, Springer, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Nascimento B, Miranda EP, Jenkins LC, Benfante N, Schofield EA, and Mulhall JP, “Testosterone recovery profiles after cessation of androgen deprivation therapy for prostate cancer,” The journal of sexual medicine, vol. 16, no. 6, pp. 872–879, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Wang Z, Tufts R, Haleem R, and Cai X, “Genes regulated by androgen in the rat ventral prostate,” Proceedings of the National Academy of Sciences, vol. 94, no. 24, pp.12999–13004, 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Hümpel M, Wendt H, Schulze P-E, Dogs G, Weiss C, and Speck U, “Bioavailability and pharmacokinetics of cyproterone acetate after oral administration of 2.0 mg cyproterone acetate in combination with 50 μg ethinyloestradiol to 6 young women,” Contraception, vol. 15, no. 5, pp. 579–588, 1977. [DOI] [PubMed] [Google Scholar]
- [49].Becker KL, Principles and Practice of Endocrinology and Metabolism. Lippincott Williams & Wilkins, 2001. [Google Scholar]
- [50].Bruchovsky N, Klotz L, Crook J, Malone S, Ludgate C, Morris WJ, Gleave ME, and Goldenberg SL, “Final Results of the Canadian Prospective Phase II trial of Intermittent Androgen Suppression for Men in Biochemical Recurrence After Radiotherapy for Locally Advanced Prostate Cancer: Clinical parameters,” Cancer, vol. 107, no. 2, pp. 389–395, 2006. [DOI] [PubMed] [Google Scholar]
- [51].Boots LR, Potter S, Potter HD, and Azziz R, “Measurement of total serum testosterone levels using commercially available kits: High degree of between-kit variability,” Fertility and Sterility, vol. 69, no. 2, pp. 286–292, 1998. [DOI] [PubMed] [Google Scholar]
- [52].Wang C, Catlin DH, Demers LM, Starcevic B, and Swerdloff RS, “Measurement of total serum testosterone in adult men: Comparison of current laboratory methods versus liquid chromatography-tandem mass spectrometry,” Journal of Clinical Endocrinology and Metabolism, vol. 89, no. 2, pp. 534–543, 2004. [DOI] [PubMed] [Google Scholar]
- [53].Bankson DD, Lyon ME, Costales LV, and Haver VM, “The response of assays for total prostate specific antigen to changing proportions of âĂIJfreeâĂİ and α1-antichymotrypsin bound psa,” Clinical Chemistry, vol. 40, p. 1009, 1994. [Google Scholar]
- [54].Strobel S, Smith K, Wolfert R, and Rittenbouse H, “Role of free psa in discordance across commercial psa assays.,” Clinical Chemistry, vol. 42, no. 4, pp. 645–647, 1996. [PubMed] [Google Scholar]
- [55].Blase AB, Sokoloff RL, and Smith KM, “Five psa methods compared by assaying samples with defined psa ratios,” Clinical Chemistry, vol. 43, no. 5, pp. 843–845, 1997. [PubMed] [Google Scholar]
- [56].Dejter SW Jr., Martin JS, McPherson RA, and Lynch JH, “Daily variability in human serum prostate-specific antigen and prostatic acid phosphatase: A comparative evaluation,” Urology, vol. 32, no. 4, pp. 288–292, 1988. [DOI] [PubMed] [Google Scholar]
- [57].Roehrborn CG, Pickens GJ, and Carmody III T, “Variability of repeated serum prostate-specific antigen (psa) measurements within less than 90 days in a well-defined patient population,” Urology, vol. 47, no. 1, pp. 59–66, 1996. [DOI] [PubMed] [Google Scholar]
- [58].Brambilla DJ, Matsumoto AM, Araujo AB, and McKinlay JB, “The effect of diurnal variation on clinical measurement of serum testosterone and other sex hormone levels in men,” Journal of Clinical Endocrinology and Metabolism, vol. 94, no. 3, pp. 907–913, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].MATLAB, version R2019b. Natick, Massachusetts: MathWorks Inc., 2019. [Google Scholar]
- [60].Geggel L, “How much blood is in the human body?,” LiveScience, March 2016. [Google Scholar]
- [61].Sato N, Gleave ME, Bruchovsky N, Rennie PS, Goldenberg SL, Lange PH, and Sullivan LD, “Intermittent androgen suppression delays progression to androgen-independent regulation of prostate-specific antigen gene in the lncap prostate tumour model,” Journal of Steroid Biochemistry and Molecular Biology, vol. 58, no. 2, pp. 139–146, 1996. [DOI] [PubMed] [Google Scholar]
- [62].Craft N, Chhor C, Tran C, Belldegrun A, DeKernion J, Witte ON, Said J, Reiter RE, and Sawyers CL, “Evidence for clonal outgrowth of androgen-independent prostate cancer cells from androgen-dependent tumors through a two-step process,” Cancer Research, vol. 59, no. 19, pp. 5030–5036, 1999. [PubMed] [Google Scholar]
- [63].Saltelli A, Chan K, Scott EM, et al. , Sensitivity Analysis, vol. 1 Wiley New York, 2000. [Google Scholar]
- [64].Sobol IM, “Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates,” Mathematics and Computers in Simulation, vol. 55, no. 1–3, pp. 271–280, 2001. [Google Scholar]
- [65].Saltelli A, “Making best use of model evaluations to compute sensitivity indices,” Computer Physics Communications, vol. 145, no. 2, pp. 280–297, 2002. [Google Scholar]
- [66].Sobol I, Tarantola S, Gatelli D, Kucherenko S, and Mauntz W, “Estimating the approximation error when fixing unessential factors in global sensitivity analysis,” Reliability Engineering and System Safety, vol. 92, pp. 957–960, 07 2007. [Google Scholar]
- [67].Saltelli A, Annoni P, Azzini I, Campolongo F, Ratto M, and Tarantola S, “Variance based sensitivity analysis of model output. design and estimator for the total sensitivity index,” Computer Physics Communications, vol. 181, no. 2, pp. 259–270, 2010. [Google Scholar]
- [68].Wentworth MT, Smith RC, and Banks HT, “Parameter selection and verifycation techniques based on global sensitivity analysis illustrated for an hiv model,” SIAM/ASA Journal on Uncertainty Quantification, vol. 4, no. 1, pp. 266–297, 2016. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


