FLOW-MAP: a graph-based, force-directed layout algorithm for trajectory mapping in single-cell time course datasets

Abstract

High-dimensional single-cell technologies present new opportunities for biological discovery, but the complex nature of the resulting datasets makes it challenging to perform comprehensive analysis. One particular challenge is the analysis of single-cell time course datasets: how to identify unique cell populations and track how they change across time points. To facilitate this analysis, we developed FLOW-MAP, a graphical user interface (GUI)-based software tool that uses graph layout analysis with sequential time ordering to visualize cellular trajectories in high-dimensional single-cell datasets obtained from flow cytometry, mass cytometry or single-cell RNA sequencing (scRNAseq) experiments. Here we provide a detailed description of the FLOW-MAP algorithm and how to use the open-source R package FLOWMAPR via its GUI or with text-based commands. This approach can be applied to many dynamic processes, including in vitro stem cell differentiation, in vivo development, oncogenesis, the emergence of drug resistance and cell signaling dynamics. To demonstrate our approach, we perform a step-by-step analysis of a single-cell mass cytometry time course dataset from mouse embryonic stem cells differentiating into the three germ layers: endoderm, mesoderm and ectoderm. In addition, we demonstrate FLOW-MAP analysis of a previously published scRNAseq dataset. Using both synthetic and experimental datasets for comparison, we perform FLOW-MAP analysis side by side with other single-cell analysis methods, to illustrate when it is advantageous to use the FLOW-MAP approach. The protocol takes between 30 min and 1.5 h to complete.

Introduction

High-dimensional single-cell technologies allow for unprecedented profiling of complex biological processes at the cellular level^1,2. However, analyzing the resulting datasets remains challenging, as traditional methods for single-cell analysis such as 2D gating do not take advantage of the multi-dimensionality of this data, and do not scale easily for high-dimensional analysis. Therefore, computational tools are required to leverage these data and gain a comprehensive understanding of the underlying biological systems. Dimensionality reduction methods have gained favor in this area because they compress high-dimensional datasets into 2D space in a human-interpretable manner^3–27, but most of these approaches do not explicitly treat time as a variable for analysis. Toward this end, we have developed FLOW-MAP, a graph-based algorithm for visualizing high-dimensional single-cell datasets that can incorporate sequential time point information. This approach, previously applied to study the progression of cellular reprogramming²⁸, can be used to identify unique cell populations at a single time point or connect these populations across multiple time points.

In this manuscript, we demonstrate how to use the FLOW-MAP software interface to analyze single-cell time course datasets, and we demonstrate the applicability of this graph layout approach in multiple contexts. FLOW-MAP graphs can accommodate a static characterization of a system, but the algorithm can also be applied to multiple time points and conditions to compare trajectories on a single graph. In Anticipated results, we compare and contrast FLOW-MAP with other single-cell analysis methods, using a simple 2D synthetic dataset and a more complex mouse embryonic stem cell (mESC) differentiation time course collected via mass cytometry. Using these datasets for demonstration, we provide practical guidelines on how to use FLOW-MAP and choose optimal parameter settings for data exploration. Moreover, we show how the FLOW-MAP algorithm can be applied to other data such as single-cell RNA sequencing(scRNAseq), and we highlight several improvements over the previously described version of FLOW-MAP²⁸, including a graphical user interface (GUI).

Overview of the FLOW-MAP algorithm

FLOW-MAP is a dimensionality reduction tool with an easy-to-use software interface that allows researchers to explore patterns or rare phenomena in single-cell datasets from a single time point or over multiple time points obtained using flow cytometry, mass cytometry or scRNAseq experiments. The goal of these analyses is to identify relationships between cell types, visualize cellular trajectories and identify the molecular signatures associated with cell-state transitions. The FLOW-MAP algorithm builds single cells or cell clusters into a graph structure with similarity-based edge weights, and it allows for sequential time point ordering. After graph construction, the 2D layout is resolved by iterative force-directed layout with the ForceAtlas2 algorithm²⁹. In visualization plots, node size is used to indicate the number of cells from the initial dataset that are represented by each graph vertex, if clustered or downsampled. When downsampling is used, node size is determined by assigning removed cells to the nearest unremoved cell and sizing the node for the unremoved cell according to its number of assignments. Node color is used to indicate the properties of that cell type or cluster, such as marker expression level or condition type. Thus, FLOW-MAP summarizes diverse changes in multiple cell populations over time in a single 2D graph, facilitating the identification of cellular trajectories and branch points in a robust and reproducible manner. FLOW-MAP graphs can contain one or multiple experimental conditions simultaneously to allow comparison of trajectories. This analysis provides visualization of dynamic biological processes and the relationships between cell populations across time points, for hypothesis generation and testing.

After data preprocessing and cleanup that is performed before FLOW-MAP analysis, there are three major stages to the FLOW-MAP algorithm: data preprocessing within FLOW-MAP (Steps 1–3), graph building (Step 4) and graph layout for visualization (Steps 5–9). An overview of the FLOWMAPR software workflow and the program output is shown in Fig. 1, and the synthetic datasets used for this demonstration are described in Supplementary Fig. 1. Implementation tips are given in Boxes 1 and 2, and troubleshooting tips are given in Table 1. In the FLOWMAPR package, the function FLOWMAP implements the major steps of the algorithm from start to finish. Here we provide technical details for each of these steps for a single sample (Fig. 1a), multiple samples from a single time point (Fig. 1b), multiple time points from a single sample condition (Fig. 1c) and multiple time points with more than one condition at some or all time points (Fig. 1d).

Fig. 1 |. Conceptual overview of FLOWMAPR software.

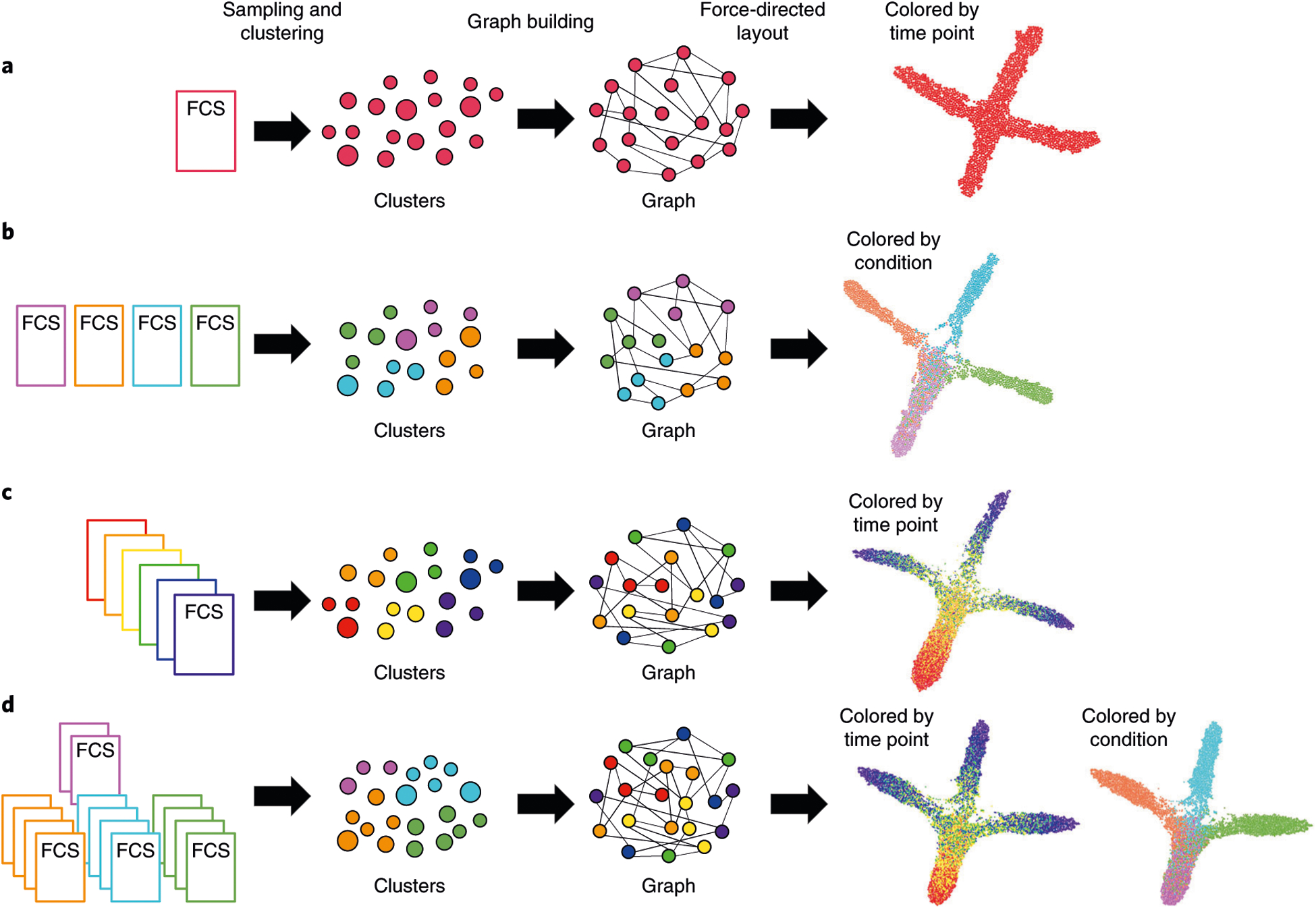
The FLOW-MAP algorithm has three major stages: data preprocessing, including optional subsampling or density-dependent downsampling and clustering (Steps 1–3); graph building between nodes from adjacent time points, allotting edges in a density-dependent manner (Step 4); and graph visualization after iterative force-directed layout and postprocessing (Steps 5–9). Workflow and example outputs are shown for the four available modes: a, single time point, single condition; b, single-time point, multiple conditions; c, multiple time points, single condition; and d, multiple-time points, multiple conditions. The default input for FLOW-MAP is an FCS file, but the tool can be applied to other formats. Example FLOW-MAPs are shown on synthetic 2D datasets.

Box 1 |. FLOWMAP function.

In this Box, we describe all the parameters you can set within the FLOWMAP() function, as well as some guidelines on what the default values are set to and how you can pick values for your given analysis.

• mode: this variable specifies what type of FLOW-MAP analysis you want to run.

• files: this variable specifies the input (cell data) for the FLOW-MAP run.

• var.remove: this variable designates any channels you want completely excluded from analysis.

• var.annotate: this variable can be used to rename channels as needed.

• clustering.var: this variable names the channels that should be used to influence the graph shape. Channels specified in this variable will be used to calculate the between-node distances.

• cluster.numbers: this variable specifies how many clusters to generate from each subsampled file. Setting this variable and the subsamples variable will dictate the cluster ratio (ratio of the cells subsampled to the number of clusters).

• distance.metric: this variable chooses the distance metric to use in all calculations.

• minimum: this variable specifies the minimum number of edges allotted based on the density in each density-dependent edge drawing step. Setting this variable and the maximum edge setting variable will affect the cohesiveness of the graph.

• maximum: this variable specifies the maximum number of edges allotted based on the density in each density-dependent edge drawing step. Setting this variable and the minimum edge setting variable will affect the cohesiveness of the graph.

• save.folder: this variable names the folder to which the output files will be saved.

• subsamples: this variable specifies how many cells to randomly subsample from each FCS file named in files. Setting this variable and the cluster. numbers variable will dictate the cluster ratio.

• name.sort: this variable toggles the option to sort user-inputted FCS files according to name in alphanumeric order.

• downsample: this variable toggles the option to use the SPADE density-dependent downsampling^11,12.

• seed.X: this variable is an integer that sets the seed and can be reused to reproduce FLOWMAPR results.

• savePDFs: this variable toggles the option to produce PDF files for all markers in the final graph.

• which.palette: this variable specifies what colors to use in the scale for each variable if the savePDFs option is set to TRUE.

Box 2 |. FLOW-MAP tips and troubleshooting.

In this Box, we provide some general guidelines on how to effectively navigate preprocessing, implementation, and troubleshooting of the FLOW-MAP algorithm ● Timing 5–8 h

Procedure

1. Analyze your dataset by some conventional means (i.e., heatmaps, histogram, dotplots and contour plots) to get an intuition for the following:

   • Any parameters that can be removed from the analysis, such as DNA staining or cell-event size parameters. These can be supplied using the variable var.remove to reduce the number of parameters carried through the analysis process.
   • Different subpopulations in your data, especially those of interest to your question(s). Knowledge of markers that define these populations can be used to choose channels to include in the variable clustering. var.
   • The relative abundance of different subpopulations. This knowledge can guide the choice of random subsampling or density-dependent downsampling and variables like subsamples, cluster.numbers and downsample. Users should choose the appropriate sampling process to ensure they do not lose rare populations, if relevant.
   • Which markers vary or change across the dataset. Expert knowledge of informative markers or markers revealed to be informative using other visualizations should be specified in the variable clustering.var.
   • If possible or relevant, any expected changes in different subpopulations over time. Knowledge of known trajectories in the dataset can be used to validate the results of FLOWMAPR analysis before identifying novel trajectories.

2. Install FLOWMAPR using instructions found in README and run GUI at https://github.com/zunderlab/FLOWMAP using default parameters. If comfortable working in R scripts, use run_FLOWMAPR.R file outputted in the results folder for fast iteration of parameters.

3. We recommend starting with a small number of clusters and generally keeping the cluster ratio smaller (subsample close to or equal to cluster.numbers). These settings will allow you to quickly iterate through different configurations of edge settings and different choices of markers for clustering.var. Try using ≤2,000 total nodes in the graph (clustering.numbers = 2,000/number of samples).

4. Several iterations of FLOWMAPR might be necessary to arrive at optimal settings for minimum, maximum and clustering.var. The order in which you proceed through the following steps (5 and 6) may depend on your results.

5. Try using the default edge settings for minimum and maximum with different options for clustering.var. These results will show how informative different sets of markers are. Once you narrow down to a particular marker set, you can refine the edge settings.

6. For a given clustering.var setting, you can change edge settings minimum and maximum to achieve maximal separation within your data. Users generally get the most utility from a graph that best resolves difference and allows for spread of different trajectories in the data. Here are some general rules for how to tweak the FLOWMAPR edge settings:

   • If the graph is too interconnected, reduce the value of maximum. You can reduce minimum to 1, but in most cases, we recommend keeping the minimum value to ≥2. Try setting maximum to being at most minimum +1.
   • If the graph is not interconnected enough, increase the value of minimum and/or maximum.
   • Graphs can essentially become tangled as they are resolved using a force-directed layout. Check for these tangles that can be resolved in Gephi. In addition, the force-directed layout step is a computationally intensive and time-consuming step that may not complete during the FLOWMAPR run. Graphs can be resolved to a stable shape in Gephi.

7. Once you arrive at a FLOW-MAP graph with the optimal settings, repeat the analysis with multiple settings of seed.X to produce ‘technical replicates’ of your analysis. Different settings of seed.X will show how the graph does or does not change with different random subsampling or random clustering of your data.

Most datasets produce interpretable results by setting minimum to 2 and maximum to any value between 5 and 20. Some datasets exhibit a ‘saturation point’, where more edges allotted (a higher value of maximum) do not significantly change the graph shape. If you need more cohesiveness, increase minimum. If you need less cohesiveness, reduce maximum.

Table 1 |.

Troubleshooting table

Step	Problem	Possible reason	Solution
4	In the FLOWMAPfromDF() function, the software does not recognize input	This error will appear if the provided input (the dataframe in R) does not match the mode specified by the user	We suggest double-checking that the mode of analysis is what you intended and also check that the input is one of the accepted inputs for that mode
	In the FLOWMAP() function, the software does not recognize input	This error will appear if the provided input (the full path of the folder or of the FCS files) does not match the mode specified by the user	We suggest that you double-check that the mode of analysis is what you intended and also check that the input is one of the accepted inputs for that mode
	The program crashes during clustering through Rclusterpp	These crashes originate during hierarchical clustering. The source of this bug is still unclear	We recommend trying to circumvent the error by changing the number of clusters/subsampled cells, the distance metric used and/or the seed of the FLOWMAPR analysis
	The program crashes during ForceAtlas2	These crashes originate during the ForceAtlas2 algorithm stage, which is programmed in C++ called from R. The source of this bug is still unclear	We recommend trying to circumvent the error by changing the seed of the FLOWMAPR analysis
7	The final FLOW-MAP graph is too interconnected (hairball-like)	Certain edge settings that lead to many edges with strong edge weights between the different nodes can result in too much pull during the force-directed layout step. As a result, differences between cell subsets or branching will be de-emphasized	Try reducing minimum to 1, but generally we recommend that minimum is ≥2. Try moving maximum to being at most minimum +1
	The final FLOW-MAP graph layout is amorphous, and/or the major cell trajectories are obscured by a broad network of interconnected low-density nodes	Rare outliers can have an outsized influence on graph structure. These can make independent branches of a graph appear to be more connected than they would seem otherwise. Density-dependent downsampling in particular will enrich for these low-density outliers	Perform more stringent preprocessing and include an outlier removal step. Great care must be exercised in determining which cells are outliers to be removed and which cells belong to rare populations of interest
	The final FLOW-MAP graph is not interconnected enough (spiky, single nodes radiating out)	Certain edge settings lead to too few edges between the different nodes. During the force-directed layout step, there are not enough connections to hold cell subsets together and visualize clear, cohesive trajectories	Try increasing the minimum and/or maximum
	The graph has one or more time points, showing up in the wrong ordering	Time labels are scraped from these file paths in the case of the FLOWMAP function or from columns in a data.frame object, if using the FLOWMAPfromDF function. These labels may then be sorted in R, which may organize the labels in a way that seems counterintuitive. For example, three FCS files named ‘20.fcs’, ‘3.fcs’ and ‘03.fcs’ would be sorted in order: ‘03.fcs’, ‘20.fcs’ and ‘3.fcs’ in R	Check ahead of time how the file names you use would be sorted in R and rename accordingly; if your files are named ‘5.fcs’, ‘10.fcs’ and ‘20.fcs’, then the first file should be renamed to ‘05.fcs’ before FLOW-MAP analysis
9	The graph from the graphml file or the PDFs have unexpected labels (especially for time or condition)	Condition and time names are scraped from these file paths in the case of the FLOWMAP function or from columns in a data.frame object if using the FLOWMAPfromDF function	If you are performing a FLOWMAPR run using the FLOWMAP function, check that your FCS files (and folders, if applicable) are named according to the acceptable naming convention. If you are performing a FLOWMAPR run using the FLOWMAPfromDF function, check that you correctly specify the names of the Condition and Time columns in the dataframe, and that the labels contained in those columns are correct

FLOW-MAP was originally developed and implemented as a series of R scripts and applied to a series of cellular reprogramming time course datasets²⁸. These scripts have been organized and compiled into the R package FLOWMAPR version 1.2.0, which is open source and freely available at https://github.com/zunderlab/FLOWMAP/. Graph and layout output from the FLOWMAPR package can be viewed or processed further using graph analysis software, such as Gephi³⁰, a free and open-source software tool for Windows, Mac OS X and Linux systems (https://gephi.org/).

Comparison of FLOWMAP to other high-dimensional single-cell visualization algorithms

FLOW-MAP is one of several algorithms designed and implemented for single-cell analysis. Other tools include implementations of dimensionality-reduction techniques like principal component analysis (PCA)^3,4 and t-distributed stochastic neighborhood embedding (t-SNE)^5–7 to project a high-dimensional manifold to an interpretable 2D pattern. These tools have been used largely to distinguish between patient samples, whether disease and normal, or cell types within a given sample. In a previous study by Amir et al.⁶, t-SNE was used to demonstrate the inter-patient variability of cancer using bone marrow taken from different acute lymphoblastic leukemia and acute myeloid leukemia patients. More recently, uniform manifold approximation and projection (UMAP) has gained popularity as an alternative method for dimensionality reduction of single-cell data^16,17. Some tools, such as SPRING³¹, instead summarize the data using graph-based visualizations. Generally, these methods aim to recreate a progression of cell types from static data, based on a single time point. For example, SPRING was used by Tusi et al.³² to identify fated hematopoietic stem cells (HSCs) from scRNAseq data of bone marrow. In contrast, FLOW-MAP aims to recreate one or more trajectories of cells undergoing processes over time from snapshots of time course data. Trajectory inference algorithms^33,34 determine pseudotime to assign temporal ordering to cell types in dynamic processes. This ordering is used to infer trajectories and branch points within these processes. FLOW-MAP does not calculate ordering or branch points but uses temporal input to generate a visualization that allows users to generate hypotheses about key points in the processes, as well as perform downstream graph-based analyses^35,36.

Limitations of FLOW-MAP

A major limitation of FLOW-MAP analysis that is inherent to all dimensionality reduction methods with real datasets is the lack of a known gold standard, or an objective function to calculate the accuracy and comprehensiveness of the cell populations and trajectories identified by the algorithm. Changing the FLOW-MAP parameters for marker choice, cluster number and edge density produces different output graph structures, and none of these are simply ‘correct’ or ‘incorrect’. Instead, they are all viewing the same high-dimensional dataset from different angles. Depending on the research question, some viewing angles may be more useful than others, and we propose that the best objective measure for the utility of a dimensionality-reduction method is its ability to predict cell trajectories and form testable hypotheses. Users may need to try many iterations of FLOW-MAP analysis with different settings to arrive at the most useful visualization to make population-level conclusions (see Anticipated results for examples).

General limitations of single-cell analysis methods also apply to the FLOW-MAP approach. On cell dissociation, all cell morphology and spatial information is lost. This limitation may be mitigated by new high-dimensional imaging methods, such as multiplexed error-robust fluorescence in situ hybridization³⁷ and multiplexed ion beam imaging³⁸, or imaging mass cytometry³⁹, although cell segmentation remains a challenging problem for these approaches. FLOW-MAP can identify unique cell populations in heterogeneous single-cell datasets and visualize the trajectories of these populations as they change over time. However, the algorithm cannot directly retrace the fates of individual cells, because it relies on destructive single-cell technologies that cannot take multiple measurements from the same cell over time. Therefore, cellular trajectories identified by FLOW-MAP analysis must be tested by alternative methods to draw any conclusion about causal relationships between the observed molecular and cellular transitions. In addition, a central assumption for time-resolved FLOW-MAP analysis is that each timed sample is collected with sufficient fine-grained resolution so that no intermediate stage cell types are missed. If the timed samples are collected too far apart, the underlying ground truth cell trajectory will have a gap in it, and the graph-building algorithm may not be able to properly connect these gapped trajectories. Using a weighted emphasis on time point adjacency rather than the rigid connectivity rules of FLOW-MAP may be well suited to samples with anticipated trajectory gaps^40,41. Along these lines, these destructive or ‘snapshot’ measurements present a caveat, which is specific for time course analysis in FLOWMAPR. Each time point will come from a separately collected sample, so sample variability and outliers will confound the analysis. For example, in setting up a cell differentiation time course, one of the collected samples may have followed a different course than all the other samples due to stochastic variability or experimental error. This outlier time point will have an outsize skewing effect on the FLOW-MAP graph. To protect against this behavior, it is recommended to use experimental replicates for all samples, adjusting the number of replicates based on the expected variability in the biological system of interest. In addition, a single culture may be used to collect multiple time points, if the cells of interest can be collected fractionally without disturbing the biological system, as is the case for suspension cell culture or blood draws.

Similar to identifying trajectories, branch point identification is not defined by the algorithm. User parameters will have a large role in the number of branches on a graph, with the potential for branches to become merged with too many edges, or the formation of spurious branches when graphs have few edges. Any conclusions drawn from FLOW-MAP analysis will require additional experimental validation.

Applications of the FLOW-MAP algorithm

We previously applied FLOW-MAP to cellular reprogramming to map the transition from mouse embryonic fibroblasts to induced pluripotent stem cells (iPSCs)²⁸. This approach identified heterogeneous expression of the reprogramming factors at the single-cell level, including an early Oct4^highKlf4^high stage that was followed by an intermediate stage, phenotypically similar to partially reprogrammed cell lines, a Lin28^high cell population that diverges from the mESC-like end stage and a Ki67^low branch that reverts to a mouse embryonic fibroblast-like phenotype. In addition to cellular reprogramming, FLOW-MAP can also be applied to study other dynamic cell processes assayed by single-cell measurement techniques, such as oncogenesis, metastasis, drug resistance, direct reprogramming, in vivo development and as described below, in vitro cell differentiation. In Anticipated Results, we demonstrate how the FLOW-MAP algorithm can be applied to other data such as single-cell transcriptomics, using a recently published scRNAseq dataset from Nestorowa et al.⁴².

Experimental design

Data preprocessing

Before FLOW-MAP analysis, data preprocessing and cleanup are performed using standard workflows (e.g., normalization, cleanup and cell-type gating) for the data type being analyzed. After loading the preprocessed dataset into R via the FLOW-MAP package, the dataset may be further preprocessed by applying an Arcsinh transform. The mESC dataset presented in this manuscript was Arcsinh transformed after dividing by five, a standard transform for mass cytometry datasets¹³. Additional preprocessing by downsampling and clustering may be applied to reduce the size of the FLOW-MAP graph. This reduction may be necessary to successfully perform and complete the FLOW-MAP analysis, depending on available processor speed and memory allocation, as discussed below in Timing. Three varieties of downsampling and clustering methods are available in the FLOW-MAP package: (i) density-dependent downsampling, which helps to preserve rare cell populations^11,12; (ii) random subsampling; and (iii) hierarchical clustering implemented in the Rclusterpp library as the hclust function (https://cran.r-project.org/web/packages/Rclusterpp/). These methods can be performed either individually or sequentially in combination. If downsampling or clustering is performed, FLOW-MAP performs best with an overclustering approach, rather than attempting to capture the true number of distinct populations in the dataset. As discussed in the following section, the graph structure and force-directed layout will draw these overclustered cells together to recapitulate the distinct underlying cell populations.

FLOW-MAP graph building

After the optional downsampling and clustering steps, FLOW-MAP computes the distance matrix for the dataset with either Euclidean or Manhattan city block distances. These distances are used to construct a graph containing all of the cells or cell clusters, with the number of edges per vertex determined by local density. Vertices with lower local density receive fewer edges, and vertices with higher local density receive more edges, with ‘Edge Min’ and ‘Edge Max’ set as user-defined parameters. If ‘Edge Min’ and ‘Edge Max’ are set equal to each other, a kNN graph would be built, where k is equal to the number of edges. Local density is estimated by counting the number of neighbors within a high-dimensional sphere, the radius of which is defined by a fixed quantile parameter derived from all edges in the distance matrix. Once the number of allotted edges per vertex (i.e., k) are determined, each vertex will have its corresponding number of edges drawn connecting that vertex to its k-nearest neighbors from the same or adjacent time point. In addition to these density-based edges, the edges of the minimum spanning tree are added to the graph to ensure that the final graph is connected to remain proximal during the force-directed layout step. For time course dataset graph building, the distance matrices, density calculation, edge selection and minimum spanning tree overlay are performed sequentially by pairs of time points n and n + 1. For example, FLOWMAPR will isolate the vertices from time point 1 and the vertices from time point 2 to calculate the distances between all vertices. This prevents connections between nonadjacent time points. As described above, edges will be drawn from each vertex to its k-nearest neighbors, where k is chosen for each vertex in a density-based manner according to the ‘Edge Min’ and ‘Edge Max’ edge parameters. The software proceeds in this manner until edges are drawn between nodes from the last two time points. After graph construction, the vertices are annotated with the single-cell measurement parameters. If the original dataset was downsampled or clustered, these are recorded as median values. Moreover, upsampling is performed using the starting dataset to record the percent of the total cells associated with each graph vertex. Annotations for sample time point, condition or name are also added if applicable. Edge weights in the graph are assigned by the inverse distance between the connected vertices.

FLOW-MAP graph layout and visualization

After graph construction and annotation are complete, the FLOWMAPR software first outputs a graph file in GRAPHML format without any layout information, and then applies the ForceAtlas2 layout algorithm²⁹ implemented in R to the graph for a defined number of iterations, to produce an x–y layout that is output as a second GRAPHML file. These graphml output files can be loaded into graph analysis software programs, such as Gephi (https://gephi.org/)³⁰ for interactive graph manipulation such as force-directed layout with manual perturbations, which can help to relieve overlapping branches that become trapped in local energy minima. Automated output of the final graph layout in PDF or PNG format from the FLOWMAPR package can be used to identify the characteristic marker expression patterns for every region of the graph.

Extending FLOW-MAP to scRNAseq

In addition to mass cytometry datasets, FLOW-MAP can also be applied to other single-cell data types, including scRNAseq datasets. We demonstrate this capability in Anticipated results using a publicly available dataset from Nestorowa et al.⁴², who performed scRNAseq analysis on lineage-depleted bone marrow to profile cell-type heterogeneity in early hematopoiesis. We recommend preprocessing data in Seurat⁴³ for quality control, normalization and PCA, determining an elbow point to decide on a number of principal components to analyze by FLOW-MAP.

Materials

Equipment

• Hardware. 32- and 64-bit computer with at least a 2.2-GHz processor running Windows or Mac OS X (10.11 systems); ≥4 GB of RAM (16 GB preferred). An internet connection is needed for downloading the R and FLOWMAPR packages from GitHub, as well as any prerequisite packages

• Data. Example datasets used in this paper include the 2D synthetic single-cell data (available as Supplementary Data 1 and on Cytobank: http://community.cytobank.org/cytobank/experiments/71954) and the mESC mass cytometry dataset (available as Supplementary Data 2 and on Cytobank: http://community.cytobank.org/cytobank/experiments/71953)

Software

• R. Users can install R by downloading the appropriate R-x.y.z.tar.gz file from http://www.r-project.org and following the system-specific instructions. The version of FLOWMAPR described in this manuscript was developed and tested on version 3.5.3 of R

• FLOWMAPR. FLOW-MAP R version 1.2.0 package, called FLOWMAPR, is free software available on GitHub (https://github.com/zunderlab/FLOWMAP/) and licensed under the MIT license (https://opensource.org/licenses/MIT), and it can be redistributed under the terms of that license. FLOWMAPR depends on R libraries: igraph, Rclusterpp, SDMTools, robustbase, shiny, tcltk, rhandsontable, spade and flowCore from Bioconductor, and scaffold published on the Nolan Lab GitHub^12,27. It runs on Windows and Mac OS X 10.11 systems

• Gephi. Gephi is a free, open-source program that can be used to change the aesthetics of the final FLOW-MAP graph. Users can download Gephi from http://www.gephi.org³⁰. We recommend using Gephi version ‘0.9.2-SNAPSHOT’, which is the most compatible with graphml files from the FLOWMAPR package

Equipment setup

FLOWMAPR installation

To install the FLOWMAPR package from GitHub, start R and enter the following:

> install.packages(“devtools”)
> library(devtools)
> install.packages(“SDMTools”)
> install.packages(“igraph”)
> install.packages(“robustbase”)
> install.packages(“shiny”)
> install.packages(“tcltk”)
> install.packages(“rhandsontable”)
> source(“http://bioconductor.org/biocLite.R“)
> biocLite(“flowCore”)
> library(devtools)
> install_github(“nolanlab/scaffold”)
> install_github(“nolanlab/Rclusterpp”)
> install_github(“nolanlab/spade”)
> install_github(“zunderlab/FLOWMAP”)

Procedure

Setting up files and specifying parameters for FLOW-MAP analysis ● Timing 1–5 min

▲ CRITICAL To run a FLOW-MAP analysis on a given dataset: the first critical step is to choose a FLOW-MAP mode that reflects the question the user intends to ask about the data.

• 1
  Choose the most applicable FLOW-MAP mode. The available modes and their purposes are as follows (also shown in Fig. 1):

  • OneFLOW-MAP visualizes a single time point. This mode can be useful for visualizing the heterogeneity and unique subpopulations present within a single sample (one time point, one condition).
  • OneFLOW-MAP has a special subcase, where you can visualize multiple conditions at a single time point.
  • SingleFLOW-MAP visualizes one time course. This mode is the core functionality of the FLOWMAPR package and is used to map trajectories of cells undergoing some process over time within a single condition.
  • MultiFLOW-MAP visualizes two or more different conditions. This mode can be useful for comparison of the effects of two or more treatments across time.
• 2
  Format the data so that it can be accessed and correctly parsed by the selected FLOWMAPR package. For the OneFLOW-MAP mode for a single sample or multiple conditions, follow option A or B, respectively. For SingleFLOW-MAP, follow option C, and for MultiFLOW-MAP, follow option D.

  1. OneFLOW-MAP mode (mode <- ‘one’)

     1. Name the flow cytometry standard (FCS) file as desired for outputted graphs and PDFs, but otherwise no precautions are necessary in file naming as no information is parsed from the FCS file in this mode.
  2. OneFLOW-MAP mode with multiple conditions (mode <- ‘one-special’)

     1. To properly label each condition, include the appropriate condition label as the first part of the FCS file name separated by ‘-’ or ‘.’ characters (e.g., ‘ConditionA-othertext.fcs’, where ‘ConditionA’ will be the condition label).
  3. SingleFLOW-MAP mode (mode <- ‘single’)

     1. Ensure that the FCS files include time labels that are named such that they can be properly sorted by labels (e.g., use time labels, such as ‘01.fcs’, ‘02.fcs’, ‘04.fcs’, ‘06.fcs’, and ‘10.fcs’ instead of ‘1.fcs’, ‘2.fcs’, ‘4.fcs’, ‘6.fcs’, and ‘10.fcs’: in R, these labels would sort ‘1.fcs’ and ‘10.fcs’ as the first two labels instead of ‘10.fcs’ last).
     2. Ensure that time labels in FCS file names use numeric characters, not alpha characters (e.g., use ‘01.fcs’ and not ‘one.fcs’). Note that when FCS files are loaded into FLOWMAPR, any ‘Time’ variables already in the data will be removed and overwritten with the time point of each FCS file.
  4. MultiFLOW-MAP mode (mode <- ‘multi’)

     1. If the file variable provided is a directory, then make sure that each subfolder in this directory contains samples from the same time point. If FCS files in the same subfolder appear to come from different time points (e.g., a folder containing ‘ConditionA-d01.fcs’ and ‘ConditionB-d02.fcs’), then FLOWMAPR will pick one time label arbitrarily.
     2. To properly label each condition within each time point, include the appropriate condition label as the first part of the FCS file name separated by ‘-’ or ‘.’ characters (e.g., ‘ConditionA-d01.fcs’, where ‘ConditionA’ will be the condition label and ‘01’ will be the time label).
     3. Do not use any numeric characters in the name of the FCS file unless they specify time. Change any labels for the conditions in the FCS file name to be alpha characters (e.g., ‘Condition1-t24.fcs’ should be renamed to ‘ConditionOne-t24.fcs’, or the time label will be incorrectly parsed as ‘124” instead of ‘24’ for this file).
• 3Establish variable names as shown in the example provided below. The variables that need to be assigned before running FLOWMAPR are described in more detail in Box 1, and tips for determining their values are detailed in Box 2.

> files <- “FLOW-MAP/inst/extdata/SingleFLOWMAP”
> mode <- “single”
> save.folder <- “/Users/mesako/Desktop”
> var.annotate <- list(“marker1” = “marker1”, “marker2” = “marker2”)
> var.remove <- c()
> minimum <- 2
> maximum <- 5
> distance.metric <- “manhattan”
> subsamples <- 200
> cluster.numbers <- 100
> seed.X <- 1
> clustering.var <- c(“marker1”, “marker2”)

▲ CRITICAL STEP Alternatively, you can take advantage of FLOWMAPR’s GUI if you are working with FCS files. Setting up the variables described above can instead be done in a series of windows that leverage the shiny R package. To launch the GUI, type:

> FLOWMAPR::LaunchGUI()

How to assign FLOWMAPR settings in the GUI is demonstrated in Fig. 2.

Fig. 2 |. FLOW-MAP software GUI interface.

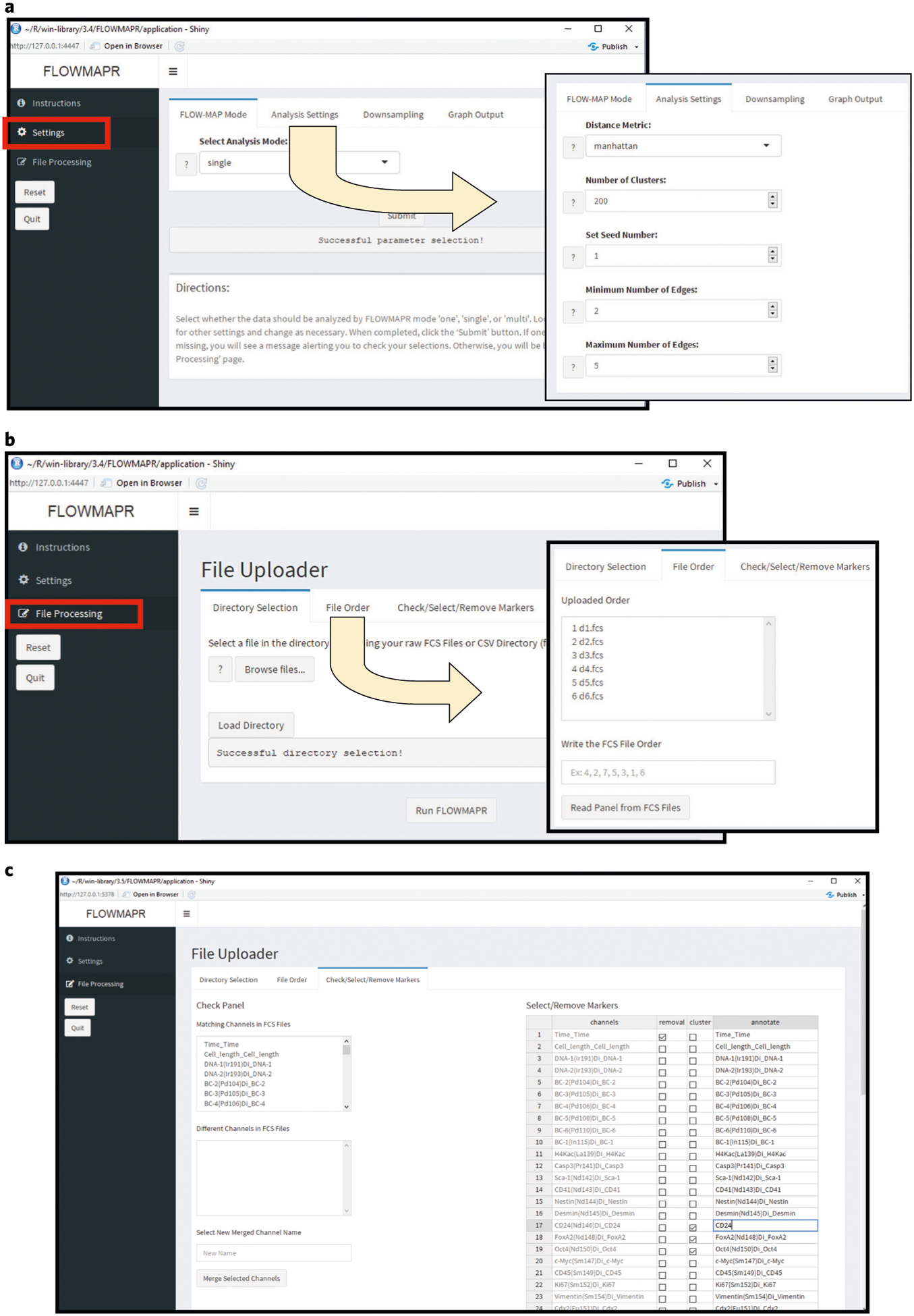
a, Initial interface and file selection for FLOWMAPR GUI. The user should first ensure that all FCS files to be analyzed are in one folder. Choose the FCS file directory and a separate directory for FLOWMAP results. Recommended defaults are: distance metric = Manhattan, FLOW-MAP mode = selection depends on data (see text) and color palette = blue and red. b, Parameter selection and running FLOWMAP in R Shiny. After completing steps detailed in a, FCS files in the selected folder will be listed here. Reorder FCS files if desired and then select ‘Generate Parameters’ to populate FCS file fields. c, Once files are selected, shared channels across FCS files will be under the ‘Similar Fields’ section, and any different channels across FCS files will be under the ‘Different Fields’ section. There is an option to merge different channels across FCS files under a user-generated merge name. For each channel in the FCS file(s), the user can rename, remove or specify its use as a clustering variable.

Running FLOW-MAP ● Timing 10–45 min

• 4
  Run the FLOWMAP() function with all specified input parameters. If running with all default settings, the user will only need to provide the correct mode, files for input and the clustering variables to use to cluster, as well as inform the shape of the FLOW-MAP graph.

  > FLOWMAP(mode = mode, files = files, clustering.var = clustering.var)
  

  If you have specified your own settings in Step 3, pass these variables to the FLOWMAP() function for customized analysis as shown:

  > FLOWMAP(mode = mode, seed.X = seed.X, files = files, var.remove = var. remove, var.annotate = var.annotate, clustering.var = clustering.var, cluster.numbers = cluster.numbers, subsamples = subsamples, distance. metric = distance.metric, minimum = minimum, maximum = maximum, save. folder = save.folder, name.sort = name.sort, downsample = downsample, savePDFs = savePDFs, which.palette = which.palette)
  

  If you have set up the run in the FLOWMAPR GUI, execute the FLOWMAP function by instead pressing the button labeled ‘Run FLOWMAPR’.

  When running data other than FCS files as a starting input, the FLOWMAPfromDF() function can be used. There are subtle differences between this function and the main FLOWMAP() function, especially in terms of available parameter settings, which are detailed in Box 3.

  Depending on the settings specified in Step 3, messages similar to the following output should appear on your R console:

  Seed set to 1
  check FALSE folder
  output.folder is 2018-01-01_12.30.00_SingleFLOWMAP_run
  Subsampling all files to: 200
  Reading FCS file data from: d00.fcs
  Subsampling d00.fcs to 200 cells
  Fixing channel names from: d00.fcs
  Removing unnecessary channel names from: d00.fcs
  Transforming data from: d00.fcs
  …
  IGRAPH 5904bd7 UNW- 600 1938 --
  + attr: marker1 (v/n), marker2 (v/n), timepoint (v/n), percent.total 
  | (v/n), name (v/n), size (v/n), x (v/n), y (v/n), weight (e/n),
  | label (e/c), sequence_assignment (e/n) + edges from 5904bd7 (vertex names):
  [1] 1-- 48 1-- 3 2-- 31 2-- 61 3-- 17 4--100 4-- 67 5-- 84 5—26
  [10] 6-- 54 6-- 16 7-- 8 1-- 7 7-- 20 8-- 55 8-- 10 8-- 52 9—69
  [19] 9-- 17 9-- 32 9-- 46 10-- 55 10-- 88 11-- 79 11-- 91 12-- 74 12—50
  [28] 13-- 37 13--100 14-- 22 14-- 36 15-- 33 15-- 19 15-- 44 16-- 54 3—16
  [37] 16-- 17 18-- 25 18-- 51 19-- 95 20-- 24 20-- 48 20-- 67 21-- 35 21—99
  [46] 21-- 80 22-- 36 22-- 49 23-- 52 23-- 43 23-- 72 23-- 76 23-- 26 24—67
  +… omitted several edges
  

Box 3 |. FLOWMAPfromDF function.

In this Box, we describe all the parameters you can set within the FLOWMAPfromDF() function, which can be used to apply the FLOW-MAP algorithm to any dataset formatted as a data.frame object in R. Notably, FLOWMAPfromDF() does not accept var.remove or var.annotate variables as data should be properly transformed and markers changed or removed before using the FLOW-MAP algorithm. Moreover, SPADE downsampling is not available in this mode and should be done before calling FLOWMAPR’s functions. Many of the variables and their usage are shared with the FLOWMAP() function, and only unique parameters are explained below:

• project.name: this variable specifies a text label that will be appended to some of the files generated in the results from the FLOW-MAP run.

• df: this variable contains your data as a data.frame format object, a list of data.frame objects or a list of lists of data.frame objects in R. If the latter, it is expected that the first level of each list corresponds to different time points and that sublists correspond to different conditions (if applicable).

• time.col.label: this required variable specifies which column (by name) should be used as the time label for each cell.

• condition.col.label: this optional variable is needed only in the case of MultiFLOW-MAP runs to distinguish cells from different conditions/treatments/time courses. The function will use the column with this name as the condition label for each cell.

• clustering: this variable specifies whether or not to cluster within each time point, in which case you will need to specify optional variable cluster.numbers.

This final output that prints an igraph graph object indicates that analysis is complete and that all results have been generated without error.

▲ CRITICAL STEP Note that the duration of this step will depend largely on your settings, as well as the number of computer cores available and the speed of your computer’s processor. More nodes in your graph, as determined by the number of individual cells or clusters of cells from each time point and condition (if relevant), will take longer to process, especially during the step that determines the force-directed layout of the graph.

▲ CRITICAL STEP You may get the warning message below in R, which can be ignored, as it will have no effect on the output of your run.

Warning messages:

1. In if (subsamples == FALSE) {:

   the condition has length >1 and only the first element will be used?

   ? TROUBLESHOOTING

Visualizing FLOW-MAP results ● Timing 5–20 min

▲ CRITICAL Though FLOWMAPR automatically generates PDF files of the final graph image, the user may find producing aesthetically pleasing graphs easier in Gephi. We recommend scanning through the resulting graphs in the FLOWMAPR output during the iteration process to arrive at the best settings. After doing so, we find that Gephi allows for greater customization of visual settings.

• 5Open one of the FLOW-MAP graphml files in Gephi. We recommend starting with the resulting graphml file that contains the substring ‘xy_orig_time’ in the file name as this graph has already been partially resolved with a force-directed layout.
• 6Set the node size in the FLOW-MAP graph. The nodes will need to be the intended size in the graph before running the force-directed layout. We recommend setting the node size to scale with the percent.total parameter, describing the relative size of each cluster, if relevant (Supplementary Fig. 2a).
• 7
  Resolve the FLOW-MAP graph further using Gephi’s ForceAtlas2 algorithm²⁹ (Supplementary Fig. 2b). If regions of the graph appear tangled while the ForceAtlas 2 algorithm is actively running, the user can move and manipulate the nodes to untangle the graph (Supplementary Fig. 2c). As ForceAtlas 2 does not have a stopping time, we recommend running the algorithm until there are no tangles and the graph stops changing. Steps to manipulating the final FLOW-MAP graph in Gephi are also shown in Supplementary Fig. 2. We recommend:

  • Trying to toggle on the ‘Dissuade Hubs’ option in ForceAtlas 2. This option can be helpful to resolve graphs that are less spread out (Supplementary Fig. 2d).
  • Toggling on the ‘Prevent Overlap’ option in ForceAtlas 2. This setting will spread the nodes to all be clearly visible as opposed to stacked on top of each other (Supplementary Fig. 2d).
    ? TROUBLESHOOTING
• 8(Optional) Following the force-directed layout step, color the final graph by the expression of different markers using the ‘Appearance’ pane in Gephi.
• 9Export final figures from the FLOW-MAP graph to PDFs or image files in the ‘Preview’ option within Gephi.

  ? TROUBLESHOOTING

Troubleshooting

Troubleshooting advice can be found in Table 1.

Timing

Steps 1–3, setting up files and specifying parameters for FLOW-MAP analysis: 1–5 min

Step 4, running FLOW-MAP: 10–45 min

Steps 5–9, visualizing FLOW-MAP results: 5–20 min

In a SingleFLOW-MAP with no downsampling (uses random subsampling), 1,200 total nodes take ~2 min to produce results (including PDFs) on a MacBook Pro (2.7 GHz Intel Core i5, 16 GB RAM). In comparison, 3,000 total nodes take ~6 min to produce all results, 6,000 total nodes take ~21 min and 12,000 total nodes take ~59 min on the same computer. These all ran with a subsample:cluster. numbers ratio of 2:1.

Anticipated results

The output of FLOWMAPR is a FLOW-MAP visualization, a 2D graph representation of high-dimensional single-cell time course data. The layout of this graph is resolved using a ForceAtlas 2 algorithm to produce a final graph that shows patterns of change across time across multiple markers, simultaneously.

To aid in data interpretation, FLOWMAPR creates a final graph where each node has the associated median expression level for each marker in the analysis, as well as what percentage of cells are represented in the node. With expert knowledge of the biological system, the user can use a FLOW-MAP graph to visualize relationships between cell states over time, as well as markers of interest that may regulate the process under study. Repeating the same FLOWMAPR analysis with multiple settings of seed.X can be used to produce ‘technical replicates’ and demonstrate the analysis’ reproducibility. This process can replicate FLOW-MAP graphs with different random subsampling from each FCS file to ensure that patterns are robust.

Specifying different FLOW-MAP settings

We demonstrate the effects of varying multiple FLOW-MAP parameters in Fig. 3, including the ratio of the cells subsampled to the number of clusters (i.e., ‘cluster ratio’ (Fig. 3b)) and edge density parameters (Fig. 3c). The resulting graphs from parameter testing can be found in Supplementary Data 1. Too few clusters for a given sample results in ‘averaging’ of the single-cell events and reduces separation, although too many clusters greatly increases computation time. Choice of edge parameters represents a balance between too few edges, which leads to a graph lacking cohesion, and too many edges, which restricts the branching separation of the graph. The choice of measurement parameters used in the clustering and graph-building steps can also have a dramatic effect on the final graph; using all available markers in a high-dimensional dataset is not recommended, because uninformative or confounding variables may dilute or even distort the underlying cell population trajectories.

Fig. 3 |. FLOW-MAP output with extreme parameter settings.

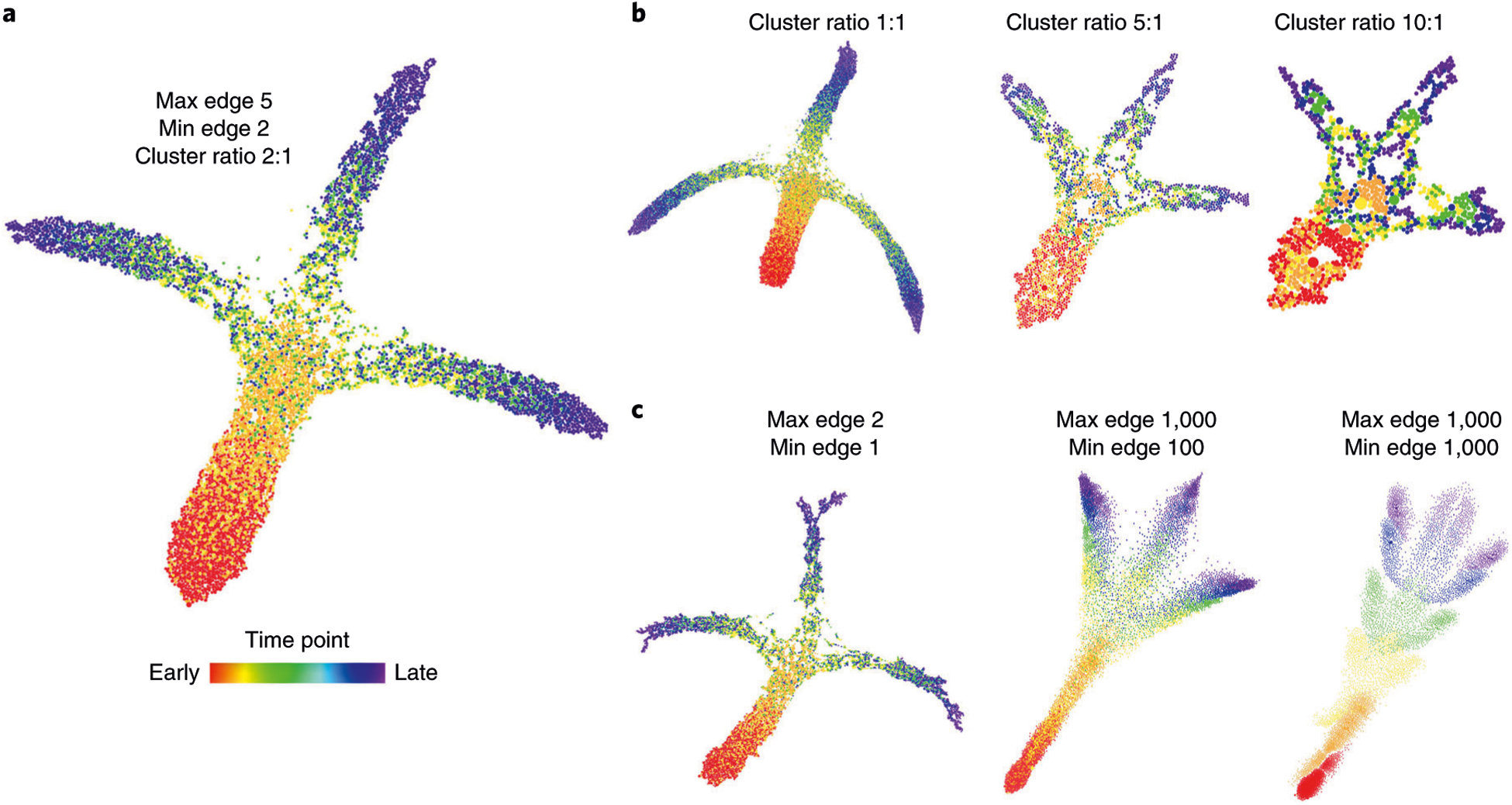
The effects of extreme parameter selection on global graph shape. a, FLOW-MAP analysis of a 2D synthetic time course dataset (Supplementary Data 2), with settings Min edge = 2, Max edge = 5 and Cluster ratio = 2:1. b, Changing Cluster ratio while holding Min edge and Max edge constant. c, Changing the Max edge and Min edge parameters while holding Cluster ratio constant.

Comparison of FLOW-MAP with other single-cell analysis methods

To compare the performance of FLOW-MAP for time course analysis with other single-cell dimensionality-reduction methods, we first applied each method to a 2D synthetic time course dataset. This dataset was created to mimic cell differentiation over time, with three diverging lineage branches that emerge from a single progenitor (Supplementary Fig. 1). Stripes were drawn on this dataset, and corresponding index values were assigned to evaluate the performance of the methods. Comparing FLOW-MAP to PCA, t-SNE, diffusion maps, SPADE, Monocle and UMAP shows the ability of all of these techniques to recapitulate the general structure of the synthetic dataset, placing assigned stripes on the correct branch in the correct order (Fig. 4a–g). A similar comparison on other datasets, including higher-dimensional versions of the synthetic dataset used, swissroll⁴⁴, spiral⁴⁵ and gaussian distributions, show some variation in the 2D layouts from the techniques, while mostly recapitulating the expected layout (Supplementary Figs. 3–8). The datasets and code used to generate the synthetic datasets can be found in Supplementary Data 2.

Fig. 4 |. Comparison of FLOW-MAP to other single-cell analysis tools.

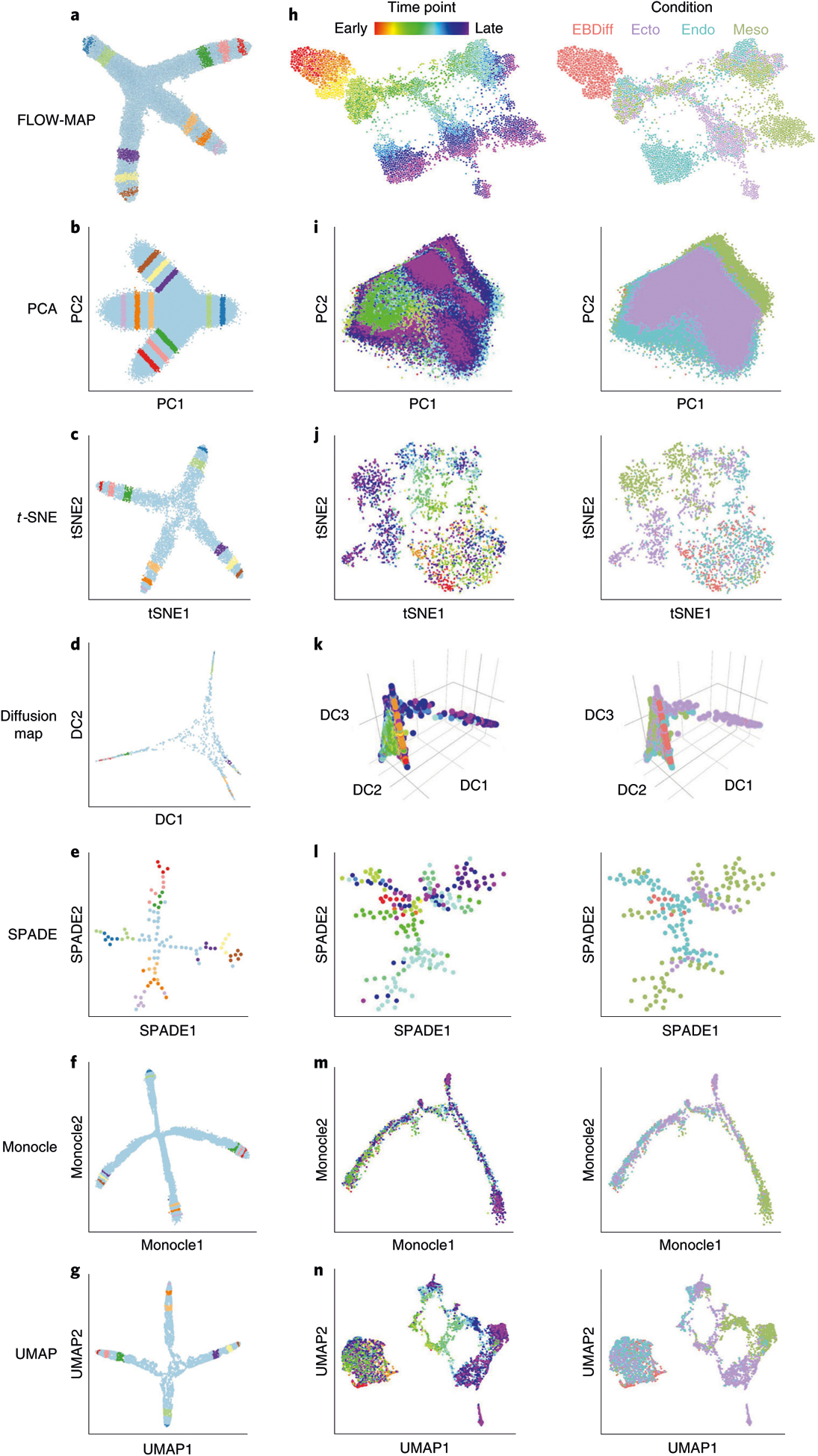
a, FLOW-MAP plot produced from a 2D synthetic time course dataset (Supplementary Data 2) with nodes colored by index values to denote the same points across different visualizations. The FLOW-MAP graph was generated from random subsampling to 800 cells each in the first two time points and 2,400 cells each in the remaining time points, followed by clustering to 400 clusters and 1,200 clusters, respectively, with edge settings of Min = 2 and Max = 5, using marker 1 and marker 2 as clustering variables. b, PCA results produced from a dataset containing all time points merged. c, t-SNE results produced from 5,000 cells randomly subsampled from merged time point files (perplexity = 250). d, Diffusion maps produced in destiny from 1,000 cells subsampled from a dataset containing all time points merged, using most informative axes DC1 and DC2. e, SPADE analysis from 2,000 cells after density-dependent downsampling of merged time point files with 100 target nodes. f, Monocle analysis of 50,000 cells randomly subsampled from merged time point files. Monocle analysis was produced using the Monocle package in R using transformed data assuming Gaussian-distributed expression. g, UMAP results produced from 10,000 cells randomly subsampled from merged time point files (n_neighbor = 500). All analyses were created using marker 1 and marker 2 as clustering/informative variables and colored by time point from which cells came. h, mESC differentiation measured by mass cytometry (Supplementary Data 3) and then analyzed by FLOW-MAP algorithm, colored by time point and condition. The FLOW-MAP graph was generated from random subsampling to 100 nodes (with no clustering) from each time point and condition, respectively, with edge settings of Min = 2 and Max = 100, using the following parameters for graph building: Nestin, FoxA2, Oct4, CD45, Vimentin, Cdx2, Nanog, Sox2, Flk1, Tuj1, PDGFRa, EpCAM, CD44, GATA4 and CCR9. i, PCA results produced from all conditions and time points merged. j, t-SNE results produced from 200 cells subsampled from each condition and time point (perplexity = 50). k, Diffusion maps produced in destiny from 100 cells subsampled from each condition and time point using the most informative axes DC2, DC3 and DC4. l, SPADE analysis from 50,000 cells after density-dependent downsampling of merged time point/condition files with 200 target nodes. m, Monocle analysis of 100 cells subsampled from each condition and time point. Monocle analysis in Monocle was produced with Gaussian family expression. n, t-SNE results produced from 200 cells subsampled from each condition and time point. Unless otherwise mentioned, default parameters were used for each analysis. All analyses were created using the same markers listed above for FLOW-MAP as clustering/informative variables and colored by time point and condition from which cells came.

FLOW-MAP analysis of mESC differentiation time course

To further compare the performance of FLOW-MAP against other single-cell dimensionality-reduction methods, we applied each method to a comprehensive mESC differentiation time course dataset measured by mass cytometry (Supplementary Data 3). The mESC differentiation experiment was performed using three separate culture conditions that favor differentiation into the endoderm lineage (with activin and epidermal growth factor (EGF))⁴⁶, mesoderm lineage (with BMP4)⁴⁷, or ectoderm lineage (N2B27 basal medium with no additional supplements)⁴⁸. Time course samples were collected every day over an 11-day period to capture the intermediate stages of cell differentiation toward the three germ layers in vitro (Supplementary Fig. 9a). Individual samples were collected as previously described²⁸. After sample barcoding⁴⁹, the pooled cell samples were stained with an antibody panel that covers markers of pluripotency and developmental regulators for the three germ layers (Supplementary Methods, Supplementary Table 1).

The data presented in this manuscript were collected by mass cytometry^13,50,51 before preprocessing for FLOW-MAP analysis with bead-based normalization (https://github.com/nolanlab/bead-normalization^52;] Supplementary Fig. 9b), sample debarcoding (https://github.com/zunderlab/single-cell-debarcoder^53;] Supplementary Fig. 9c) and sequential 2D cleanup gating on iridium intercalator × event length and histone/nuclear positivity to remove cell debris (Supplementary Fig. 9d; www.cytobank.org)^54,55. After sample preprocessing and cleanup, the mESC differentiation time course dataset was analyzed by FLOW-MAP, with three samples per time point after embryoid body plating at day 2.5. More details on data generation can be found in the Supplementary Methods. The resulting FLOW-MAP graph structure illustrates the cellular trajectories and lineage branching pattern that result from the three differentiation culture conditions (Fig. 4h). Data following cleanup gating and graphs used to generate figures for the stem cell time course can be found in Supplementary Data 3.

Further, we show a comparison of FLOW-MAP to alternative dimensionality-reduction methods (Fig. 4i–n). Building sequential time information into the graph provides a significant advantage for identifying cell trajectories, as demonstrated by the results obtained from withholding the time point information from FLOW-MAP analysis (Supplementary Fig. 10). Ultimately, the utility of this and other dimensionality-reduction methods will be determined by their ability to identify predictive models and testable hypotheses about cell populations and their behavior. This FLOW-MAP method was previously used to map the cellular trajectories of mouse iPSC reprogramming²⁸ and helped to identify a previously undescribed intermediate stage that is phenotypically similar to ‘partially reprogrammed’ cell lines⁵⁶.

Analysis of 2D dot plots can provide insight into cellular transitions (Fig. 5a and Supplementary Figs. 11–13), but FLOW-MAP analysis of the mESC differentiation time course dataset allows simultaneous comparison of differentiation to the three germ layers in a combined phenotypic space (Fig. 5b). Cell populations identified by the Louvain modularity method for community detection implemented in Gephi⁵⁷ enable violin plot expression profile visualization for different regions of the differentiation time course graph (Fig. 5c). Coloring each node by time point enables visualization of temporal progression for cell trajectories (Fig. 6a). Coloring each node by experimental condition reveals the contribution of each differentiation culture to the overall graph structure (Fig. 6b). Coloring each node by median values of the pluripotency and differentiation markers measured by mass cytometry reveals the underlying cell populations that contribute to the graph structure (Fig. 6c–j). Unexpectedly, SSEA1 expression was observed to increase in the initial stages of differentiation during embryoid body formation (Fig. 6c). This unanticipated result is likely because of SSEA1 repression during mESC monolayer culture, caused by supplementing the mESC growth medium with MEK and GSK3 inhibitors (2i)⁵⁸. On embryoid body suspension culture in differentiation medium without 2i, this inhibition is relieved, which we hypothesize to result in a transient spike of SSEA1 expression.

Fig. 5 |. FLOW-MAP analysis of combined mESC differentiation time course.

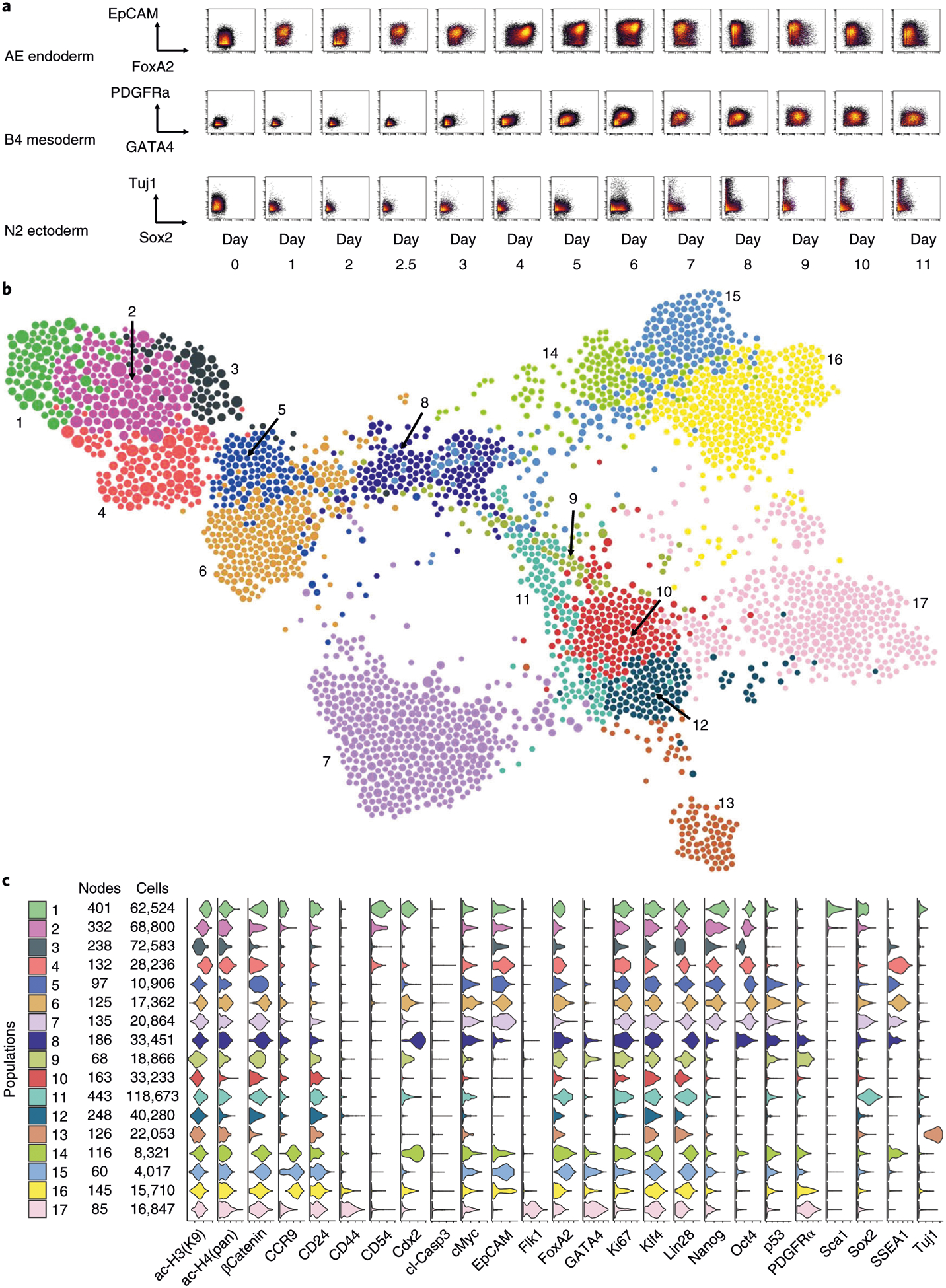
a, Representative biaxial plots across all time points: FoxA2 versus EpCAM for endoderm-promoting activin-EGF condition (AE), GATA4 versus PDFGFRα for mesoderm-promoting BMP4 condition (B4) and Sox2 versus Tuj1 for ectoderm-promoting N2B27 basal condition (N2). b, FLOW-MAP plot colored by distinct graph regions identified in Gephi through the Louvain Modularity community detection algorithm with the following settings: randomization on, use edge weights on and resolution = 1.0. The FLOW-MAP graph layout was generated using the same parameter settings described in Fig. 4h. c, Violin plots showing marker expression distributions in each separate graph region identified by Gephi community detection. The color code matches identified graph regions shown in b.

Fig. 6 |. Comparison of protein expression levels in combined mESC differentiation time course.

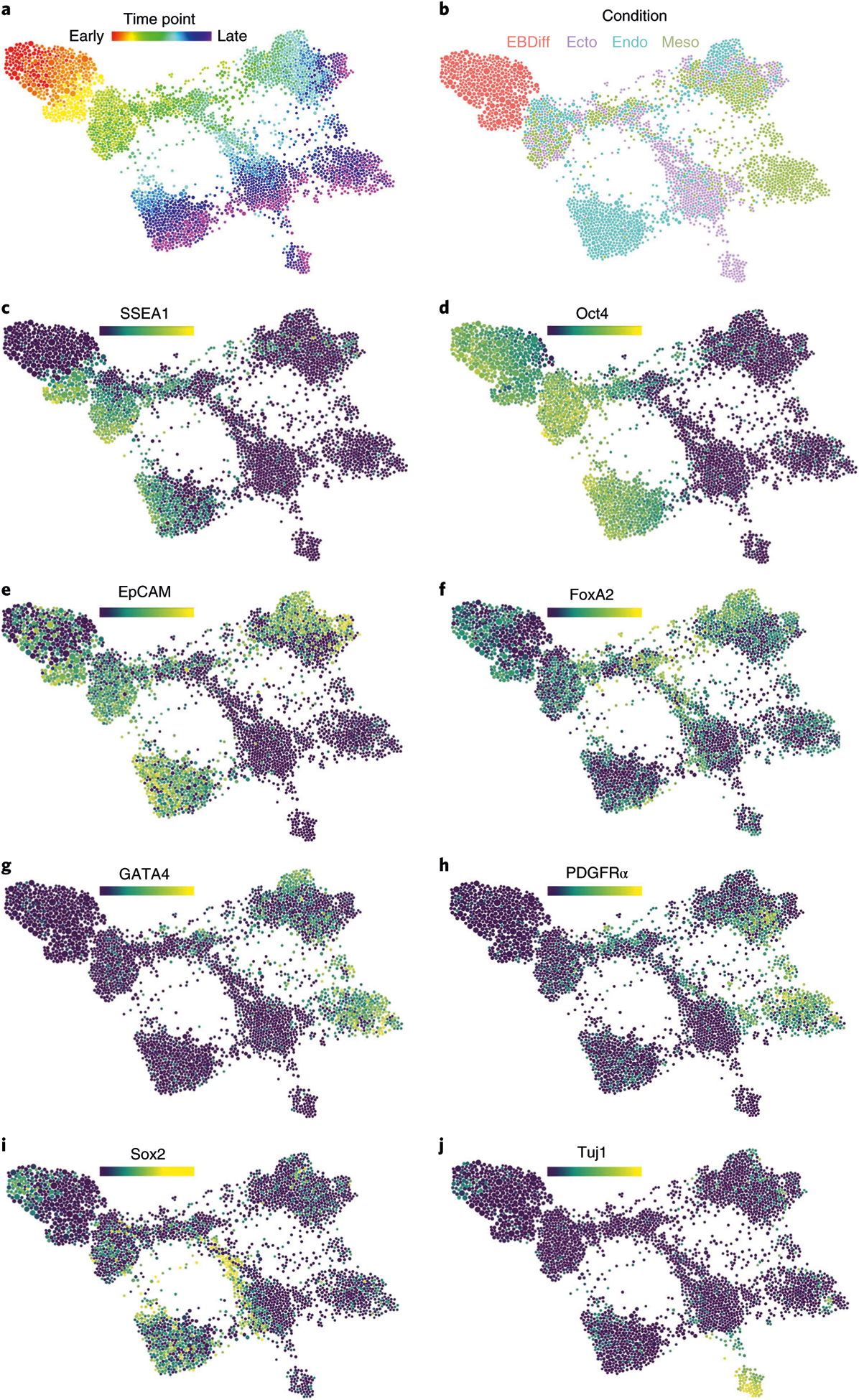
The same FLOW-MAP graph layout as in Figs. 4h and 5b, now colored by, time point (a), culture condition (b) and the median expression levels of SSEA1 (c), Oct4 (d), EpCAM (e), FoxA2 (f), GATA4 (g), PDGFRα (h), Sox2 (i) and Tuj1 (j).

After embryoid body plating on day 2.5, the cell molecular expression profiles transition along defined trajectories into phenotypes that indicate formation of endoderm, mesoderm and ectoderm lineages. In an unanticipated result, activin/EGF-supplemented culture resulted in an epiblast stem cell (EpiSC)-like phenotype, characterized by Oct4 and EpCAM expression (Fig. 6d,e), as well as the desired endoderm population, characterized by FoxA2 and Gata4 expression (Fig. 6f,g). This unexpected result is consistent with the fact that activin/fibroblast growth factor (FGF) is commonly used to maintain mouse EpiSCs^59,60, as well as the phenotypically similar human pluripotent stem cells, such as human embryonic stem cells⁶¹ and iPSCs⁶². The mesoderm cell population induced by BMP4-supplemented differentiation medium is characterized by Gata4 and PDGFR-α expression (Fig. 6g,h), while the neuroectoderm cell population induced by unsupplemented N2B27 culture medium is characterized by Sox2 expression at intermediate time points, followed by TuJ1 expression at later time points (Fig. 6i,j). The complete stem cell time course dataset is available for download and analysis at www.cytobank.org. FLOW-MAP plots colored by additional measurement parameters are shown in Supplementary Fig. 14. This combined FLOW-MAP analysis provides a global perspective on mESC differentiation into the three germ layers from separate culture conditions.

When FLOW-MAP analysis is performed on the three differentiation conditions individually rather than in combination, the molecular trajectory for the cell populations in each culture condition is derived without interference from the other conditions. Individual FLOW-MAP analysis of the ectoderm differentiation samples reveals three primary cell trajectories, with a TUJ1+ neuronal trajectory on the left side of the plot and CCR9-expressing and EpCAM-expressing trajectories on the right side of the plot (Fig. 7a). Differentiation of the mesoderm differentiation samples individually reveals a more uniform cellular trajectory, without distinct branch points, that appears to follow an Oct4/Klf4/Cdx2/CCR9/PDGFRα/Flk1/Gata4/CD44 progression from pluripotency to a mesoderm state (Fig. 7b). Individual FLOW-MAP analysis of the endoderm differentiation samples reveals a primary bifurcation in the graph structure between the FoxA2-expressing endoderm branch, which progresses to express EpCAM and CD24 at later time points, and the Oct4/Nanog/SSEA-expressing EpiSC-like branch (Fig. 7c). In the endoderm time course graph structure, we observe a relatively sparse, but still substantial, number of intermediate cell types bridging the phenotypic space between the two major branches. We hypothesize that this sparse intermediate phenotypic space is composed of cells differentiating from the EpiSC-like cells into the endoderm (FoxA2⁺) and neuroectoderm (Fig. 7b) lineages over the entire time course. The complete sets of FLOW-MAP plots for each separate condition colored by every measurement parameter are shown in Supplementary Figs. 15–17. This type of analysis by the FLOW-MAP algorithm provides an intuitive window into mass cytometry datasets, enabling the visualization of discrete cellular trajectories and their molecular determinants simultaneously.

Fig. 7 |. FLOW-MAP analysis of mESC differentiation by individual culture conditions.

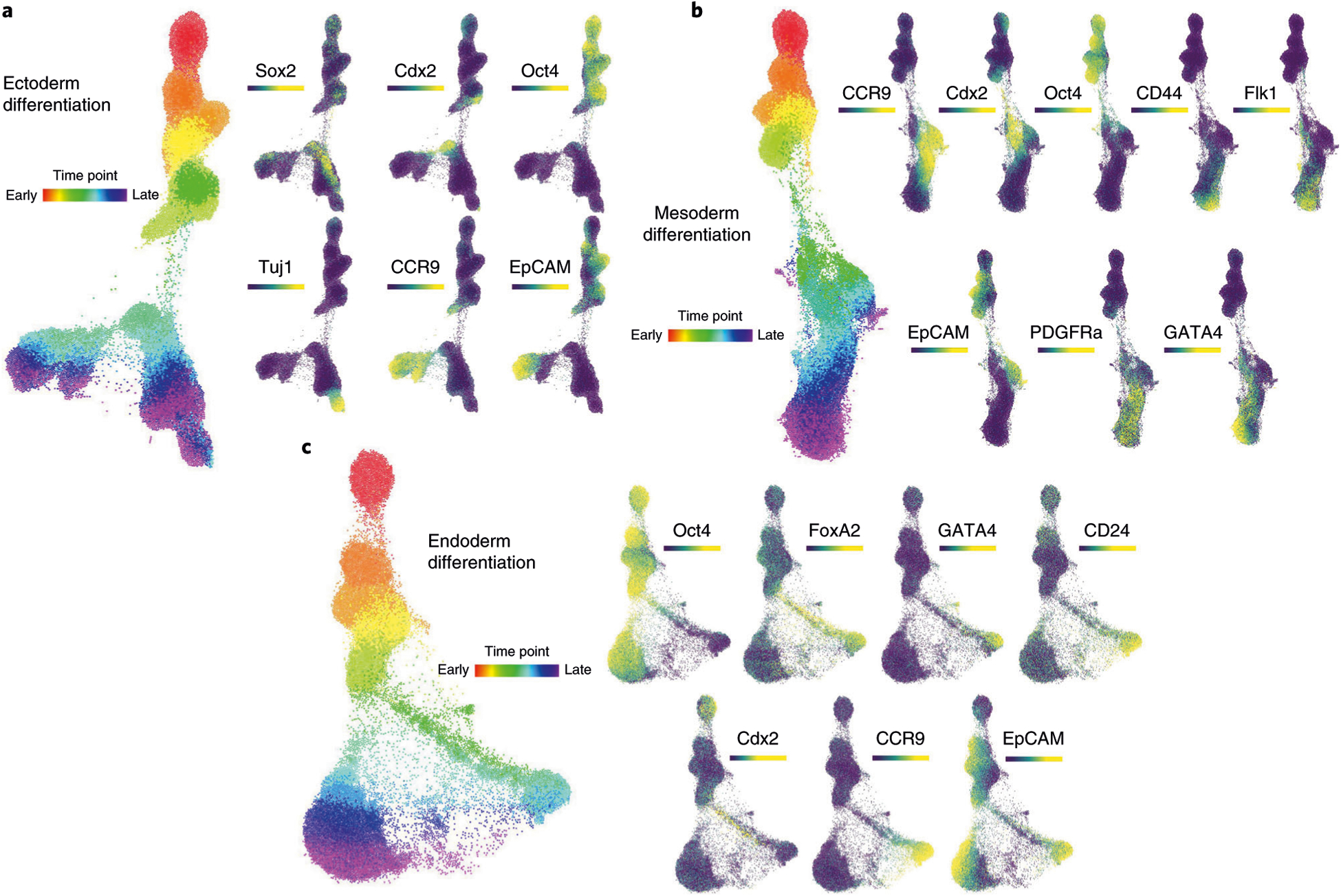
a, FLOW-MAP graph of ectoderm differentiation, generated from random subsampling and clustering to 2,000 cells and 1,000 clusters from each time point, with edge settings of Min = 2 and Max = 5, using the following set of clustering variables: Sca1, Nestin, FoxA2, Oct4, CD54, SSEA1, Lin28, Cdx2, CD45, Vimentin, Nanog, Sox2, Flk1, Tuj1, PDGFRa, EpCAM, CD44 and CCR9. b, FLOW-MAP graph of mesoderm differentiation, generated from random subsampling and clustering to 2,000 cells and 1,000 clusters from each time point, with edge settings of Min = 2 and Max = 5, using the following set of clustering variables: Sca1, Oct4, CD54, SSEA1, Lin28, Cdx2, CD45, Nanog, Sox2, Flk1, Tuj1, PDGFRa, EpCAM, CD44, CCR9 and GATA4. c, FLOW-MAP graph of endoderm differentiation, generated from random subsampling and clustering to 2,000 cells and 1,000 clusters from each time point, with edge settings of Min = 2 and Max = 20, using the following set of clustering variables: Sca1, FoxA2, Oct4, CD54, SSEA1, Lin28, Cdx2, CD45, Nanog, Sox2, Flk1, Tuj1, PDGFRa, EpCAM, CD44, CCR9 and GATA4.

Using FLOW-MAP to analyze scRNAseq data

To demonstrate the application of FLOW-MAP to analyze scRNAseq data, we used a scRNAseq dataset published by Nestorowa et al.⁴², who performed scRNAseq analysis on lineage-depleted bone marrow to profile cell-type heterogeneity in early hematopoiesis. Surface marker cell typing as provided in the original analysis showed grouping of HSCs and multipotent progenitors with one another. Other cell types mostly grouped together, but there was overlap between common myeloid progenitors and granulocyte-macrophage progenitors, as well as common myeloid progenitors and megakaryocyte-erythroid progenitors (MEPs; Fig. 8a).

Fig. 8 |. FLOW-MAP analysis of hematopoietic transitions in bone marrow measured by scRNAseq.

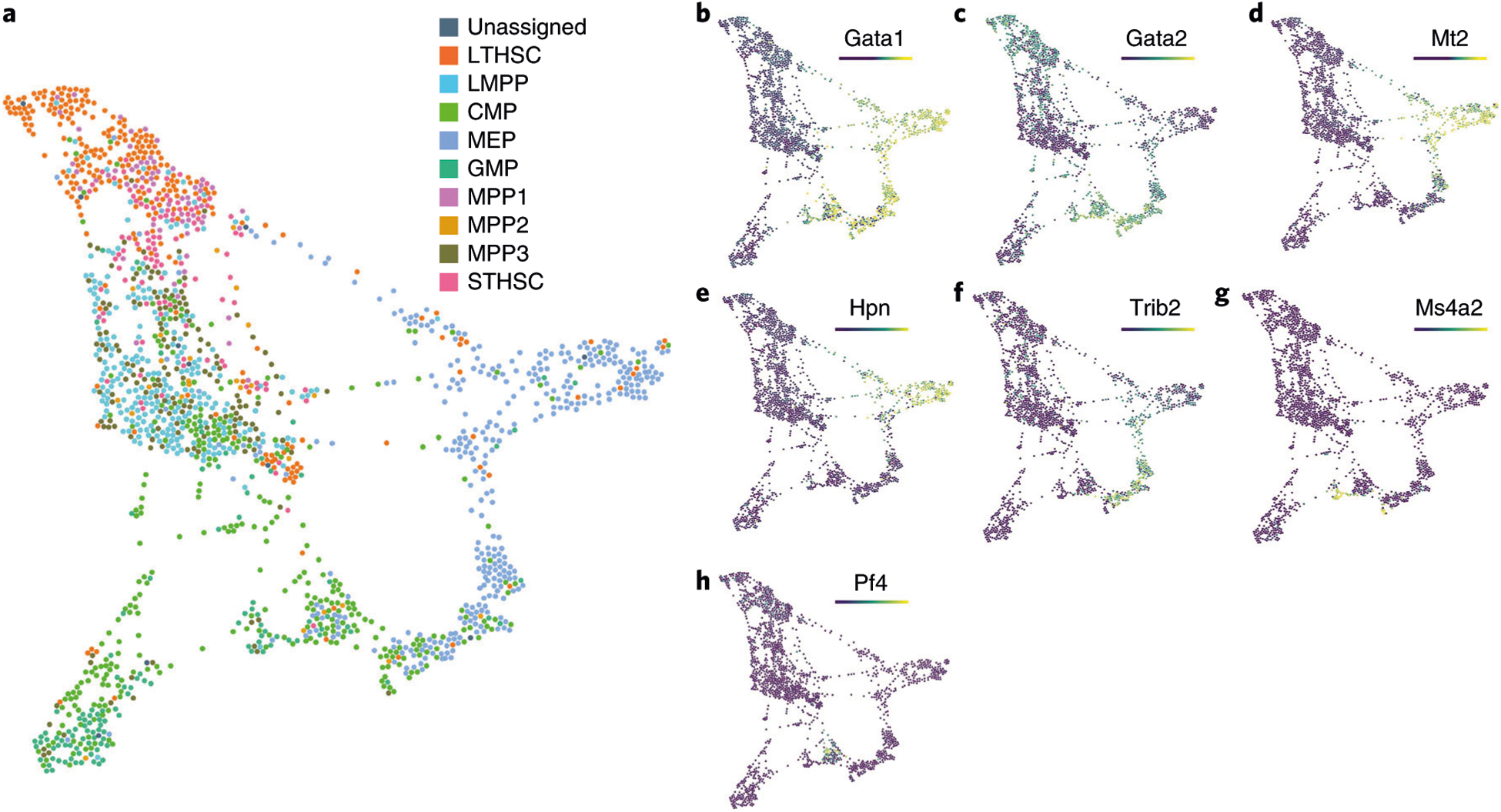
a, FLOW-MAP analysis of FACS-sorted human bone marrow populations, measured by scRNAseq⁴², with edge settings of Min = 2 and Max = 5. Coloring by cell types as defined by surface markers in Nestorowa et al.⁴² shows similar cell types grouped. Gata1 (b) and Gata2 (c) point to GATA factor switching in this dataset. Mt2 (d) and Hpn (e) as markers of erythroid-fated cells, Trib2 (f) as a marker of a pre-erythroid progenitor, Ms4a2 (g) as a marker of basophil-fated cells and Pf4 (h) as a marker of megakaryocyte fated cells as defined by Tusi et al.³². CMP, common myeloid progenitor; GMP, granulocyte-monocyte progenitor; LMPP, lymphoid multipotent progenitor; LTHSC, long-term hematopoietic stem cell; MPP, multipotent progenitor; STHSC, short-term hematopoietic stem cell.

For FLOW-MAP analysis of Nestorowa et al.⁴², the original quality control parameters were used to maintain analysis of the same genes and cells as the original analysis. Consistent with standard scRNAseq analysis, we performed PCA before further dimensionality reduction^32,63–65. Data normalization and PCA were performed using Seurat⁴³. The first five principal components were used for FLOW-MAP analysis. The data and code used to generate figures for the Nestorowa et al.⁴² scRNAseq dataset can be found in Supplemental Data 4.

Gata1 expression points to the rightmost group of MEPs as erythroid-fated cells (Fig. 8b), with decreasing Gata2 expression in the leftmost MEPs (Fig. 8c), representing canonical GATA factor switching⁶⁶. Using transcript signatures identified in a separate scRNAseq study by Tusi et al.⁶⁰, erythroid cells (Fig. 8d,e), cells in transition to erythroid (Fig. 8f), basophil-fated cells (Fig. 8g) and megakaryocyte-fated cells (Fig. 8h) were identified. Notably, Gata1, Mt2, and Hpn4 show a gradual transition from HSCs to the erythroid population, suggesting a potential non-canonical GATA2-independent differentiation trajectory.

Kee et al.⁶⁵ showed scRNAseq of mesencephalic dopamine neurons and subthalamic nucleus neurons at multiple time points in development, showing similarities in the trajectories. FLOW-MAP analysis recapitulated the major findings of that study (Supplementary Fig. 18 and Supplemental Data 5). By including FLOW-MAP in current scRNAseq analysis pipelines, differentiation trajectories can be better visualized from time course datasets.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

Mass cytometry datasets have been placed on Cytobank for the stem cell differentiation time course (http://community.cytobank.org/cytobank/experiments/71954) and synthetic 2D single-cell data (http://community.cytobank.org/cytobank/experiments/71953). Original scRNAseq data from Nestorowa et al.⁴² and Kee et al.⁶⁵ can be found on NCBI GEO (accession numbers GSE81782 and GSE87069, respectively).

Code availability

The code to run FLOW-MAP has been shared on Github (https://github.com/zunderlab/FLOWMAP/).