Parallel reaction pathways accelerate folding of a guanine quadruplex

Abstract

G-quadruplexes (G4s) are four-stranded, guanine-rich nucleic acid structures that can influence a variety of biological processes such as the transcription and translation of genes and DNA replication. In many cases, a single G4-forming nucleic acid sequence can adopt multiple different folded conformations that interconvert on biologically relevant timescales, entropically stabilizing the folded state. The coexistence of different folded conformations also suggests that there are multiple pathways leading from the unfolded to the folded state ensembles, potentially modulating the folding rate and biological activity. We have developed an experimental method for quantifying the contributions of individual pathways to the folding of conformationally heterogeneous G4s that is based on mutagenesis, thermal hysteresis kinetic experiments and global analysis, and validated our results using photocaged kinetic NMR experiments. We studied the regulatory Pu22 G4 from the c-myc oncogene promoter, which adopts at least four distinct folded isomers. We found that the presence of four parallel pathways leads to a 2.5-fold acceleration in folding; that is, the effective folding rate from the unfolded to folded ensembles is 2.5 times as large as the rate constant for the fastest individual pathway. Since many G4 sequences can adopt many more than four isomers, folding accelerations of more than an order of magnitude are possible via this mechanism.

INTRODUCTION

G-quadruplexes (G4s) are four-stranded, helical nucleic acid structures formed when guanine (G)-rich tracts in DNA or RNA come together to form G-tetrads, arrangements of four planar, Hoogsteen hydrogen-bonded Gs that are stacked to form the core G4 structure, with a cation (typically, Na⁺ or K⁺) coordinated between each pair of tetrads (Figure 1A,B) (1,2). G4s are typically associated with sequences following the pattern 5′-G_3–5N_1–7G_3–5N_1–7G_3–5N_1–7G_3–5-3′ (3,4), where three G-tetrads form the canonical core structure. However, divergent patterns are also sometimes observed that include G4s with bulges (5), vacant positions in their cores (6) and those formed with two or more than three G-tetrads (7,8). G4-forming sequences are found in genomes from all three domains of life (9–11) as well as in mitochondria (12) and viruses (13). G4s are implicated in the regulation of many biological processes such as DNA replication (14), transcription (15), mRNA translation (16), alternative splicing (17) and post-translational protein processing (18). Intriguingly, G4 sequences frequently adopt multiple folded conformations of similar free energy, leading to conformational ensembles of interconverting structures. For example, we have shown that many G4 sequences within the promoter regions of human genes contain G-tracts with nonidentical numbers of Gs (19). This type of sequence produces an ensemble of different strand-shifted conformations we term G-register (GR) isomers (3,19), where each structure incorporates a unique subset of the available Gs in the G4 core (Figure 1A). Previously, we have investigated the influence of adopting multiple GR isomers on the thermal stability of the c-myc Pu18, VEGFA and PIM1 G4s (19). Through mutational analysis, nuclear magnetic resonance (NMR) spectroscopy, thermal melting-based global fitting and computer simulations, we demonstrated that these G4s all populate an ensemble of GR isomers at equilibrium. The minimum number of GR isomers is given simply by the number of G-tract alignments afforded by their additional core dG residues. We found that for the PIM1 G4, GR isomers can also have different topologies such that G-tract shifting is accompanied by strand reversals, pointing to the existence of a complex conformational energy landscape. Remarkably, in all cases we found that these structural dynamics thermodynamically stabilize G4s by reducing the equilibrium entropy penalty for folding in a manner that correlates with the number of GR isomers populated by the sequence (19). Since G4 stability is known to have a direct influence on gene expression levels (20,21) and regulatory proteins can bind to different GR isomers (22), these dynamics offer an additional level of control. In another recent NMR folding kinetics study, we explored the kinetic mechanism of GR exchange dynamics (23). We demonstrated that the GR exchange mechanism can depend on the particular G4 sequence. For example, we found for the c-myc Pu18 and hTERT promoter G4s that GR isomers exchange with one another largely via the unfolded state in a three-state manner; that is, each GR isomer transits through the unfolded state without populating other structural intermediates. For the c-myc Pu-18, the exchange can also occur to some extent through direct G-tract sliding (23).

Figure 1.

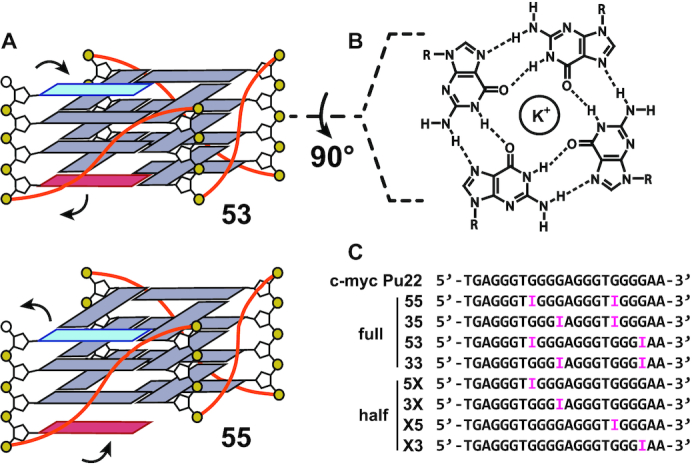
G4 structures and sequences were investigated in this study. (A) GR isomers with exchanging dG residues colored red and blue. (B) G-tetrad structure. (C) The WT c-myc Pu22 and trapped mutant sequences were investigated in this study. dG to dI mutations to the WT sequence are shown in pink. Full corresponds to the fully trapped sequences that contain dual mutations, whereas half indicates the half-trapped sequences with a single mutation that are capable of undergoing two-state GR exchange. Numbers indicate the direction that the G-tract is locked by mutation; for example, the 33 sequence has both exchanging G-tracts locked in the 3′ direction. The exchanging G-tract for the half-trapped sequences is denoted by X.

The roles of G4s in the cell have been rationalized in terms of thermodynamic equilibria between duplex and G4 forms of DNA (24). Yet, many of the processes that G4s help to control are fundamentally nonequilibrium and folding kinetics that could become highly influential (25,26). Several groups have studied G4 folding in a double-stranded DNA background where multiple folded G4 populations were observed in coexistence with the unfolded or duplex states (27,28), pointing to a rich dynamic repertoire that could help regulate biological function. For example, during transcription and replication, helicases actively unwind the stable DNA duplex, briefly offering single-stranded regions unique opportunities to fold. mRNA secondary structures are unwound by the ribosome with each round of translation. The relative rates of G4 formation versus other processes such as polymerase and ribosomal engagement and movement and interactions with binding proteins could represent decisive factors in G4 function. For instance, RNA Pol II generates a transcription bubble of roughly 18–25 unwound base pairs (29). The enzyme can spend several minutes at the site of initiation before achieving promoter escape (30) — it often pauses at promoter–proximal sites (31) — and the rates of polymerization can vary greatly even within the same gene, providing a highly variable and dynamic environment for single-stranded DNA to adopt the G4 fold. There is evidence that passage of RNA Pol II can promote G4 folding, block DNA replication and generate genome instability in yeast (15). In another example, synthesis of the lagging strand during DNA replication involves generating thousands of bases of single-stranded DNA, while the polymerase synthesizes the complementary strand through a backstitching mechanism (32). The DNA, thus exposed, is protected through interactions with replication protein A (RPA), which binds 30 single-stranded nucleotide stretches with sub-nanomolar affinity (33,34), preventing reannealing of the DNA and degradation by nucleases. A recent model of RPA function proposes that proteins bind individually to single-stranded DNA and then close the gaps between them by sliding to form a contiguous coating (33), potentially leading to brief and fluctuating opportunities for G4 formation. Finally, folding of mRNA into G4 structures has been reported to impede translation in both prokaryotes and eukaryotes in vitro and in vivo (26,35), although some aspects remain controversial (36). Secondary structures are absent from mRNAs immediately after they emerge from RNA Pol II or the ribosome. Therefore, translation inhibition by G4s depends on the balance between their folding rates and the delays between transcription and subsequent rounds of translation (37). An additional level of dynamic control can exist when the G4-forming region can adopt metastable alternative folds such as hairpin structures (26,38) or partly structured folding intermediates like three-stranded triplexes (39–41). Thus, characterizing G4 folding mechanisms and elucidating rules for how the primary nucleotide sequence influences folding rates are key to understanding how G4s function in the cell.

G4 folding has been studied by a variety of approaches such as rapid mixing with cations (23,42), thermal melting combined with singular value decomposition (43), atomic force microscopy (44) or single-molecule Förster resonance energy transfer (smFRET) (45,46). In general, folding studies of G4s have focused on quantifying the properties and populations of partly structured intermediates along the folding trajectory, though some G4s have been found to fold in a two-state manner (19). Here, we have investigated the possibility that conformational heterogeneity of the folded-state ensemble may be an important factor in controlling how quickly G4s are able to fold, and one that until now has been largely overlooked. We previously investigated how conformational heterogeneity influences thermodynamics, and how different folded conformers interconvert (19,23). However, the relationship between conformational heterogeneity and folding rates has been largely unexplored and is important for understanding G4 function. In essence, this relationship is based on the idea that the transition from the unfolded state to each conformational isomer making up the folded state can be considered a separate folding pathway, particularly when the exchange between folded isomers is slow (23). In principle, the existence of multiple parallel pathways accelerates biomolecular folding, since the apparent macroscopic folding rate constant is equal to the sum of the microscopic rate constants for the individual pathways (47). However, to our knowledge, this effect has never been quantified for G4s. Here, we investigate the relationship between pathway multiplicity and the folding kinetics of G4s for the regulatory c-myc oncogene promoter Pu22 G4, which we have found to adopt a minimum of four distinct GR isomers in the folded state with conserved parallel topologies. Consequently, the formation of this ensemble can be described by folding through four parallel pathways. This G4 controls 80–90% of the expression of the potent c-myc oncogene (48), with c-myc estimated to be deregulated in >50% of human cancers (49). Our approach combines mutagenesis, thermal hysteresis (TH) kinetics melting experiments (50,51) and a novel global fitting procedure to dissect the kinetic contributions of individual pathways to the overall folding rate. We find that folding of the Pu22 G4 is accelerated by roughly a factor of 2.5 due to the existence of four parallel pathways, with a macroscopic folding rate about 2.5 times as large as that of the most rapid individual route. Orthogonal kinetic experiments performed using NMR to monitor the folding of G4s following laser photolysis of caging groups gave results in good agreement with the thermal hysteresis analysis. Isothermal folding through multiple pathways leads to a transient conformational ensemble where the populations of folded isomers are controlled kinetically rather than thermodynamically; the equilibrium populations are then gradually reached via GR exchange. The principle of folding acceleration by parallel reaction pathways extends to more complex GR conformational ensembles that can have 20 or more distinct structural isomers, potentially giving an order of magnitude rate increases. Our TH-based approach is widely applicable to complex nucleic acid folding mechanisms and provides a simple and effective method for unraveling the contributions of parallel reaction pathways.

MATERIALS AND METHODS

Sample preparation

Oligonucleotide samples were purchased from the Yale Keck Oligonucleotide Synthesis facility (Yale University, USA) or were synthesized using a MerMade-12 Oligonucleotide Synthesizer with standard solid-phase phosphoramidite chemistry. Samples for TH and 1D NMR measurements were subjected to cartridge purification and analyzed by LC-mass spectrometry for purity. DNA strands were dissolved in MilliQ water and concentrations were calculated using nearest neighbor extinction coefficients (52). O6-(R)-NPE-dG phosphoramidites have been synthesized as described earlier (53). Incorporation of the photocaged nucleotides into the oligonucleotides was achieved via solid-state synthesis. Prior to usage, the DNAs were HPLC purified and desalted. All experiments were performed in TH buffer: 10 mM lithium phosphate, pH 7.0, supplemented with 2 mM KCl. The buffer pH was titrated using 1 M LiOH to avoid the further addition of stabilizing Na⁺ or K⁺ cations. Note that the samples employed in the circular dichroism (CD) and TH experiments had a 200-fold excess of K⁺ per G4 strand, whereas the NMR experiments had a minimum of 20-fold excess due to the higher G4 concentrations employed. Nevertheless, we expect the folded G4 strands to be fully coordinated with K⁺ ions in all experiments, since the cations are in great excess. Our reaction conditions employed 2 mM K⁺ ions, since higher concentrations (physiological is approximately 140 mM (54)) lead to much higher melting temperatures with undetectably small amounts of hysteresis and short or nonexistent unfolded baselines.

Circular dichroism spectroscopy

CD experiments were performed using a JASCO J-810 (JASCO, USA) spectropolarimeter with a cell path length of 0.1 cm. Spectra were recorded with 10 μM samples. The samples were scanned three times from 330 to 230 nm at 25 °C for signal averaging. The CD spectra were baseline corrected using a buffer blank.

Nuclear magnetic resonance spectroscopy

1D ¹H NMR spectra were collected at 25 °C using a 500 MHz Bruker AVIIIHD outfitted with a SampleXpress sample changer. Sample concentrations were 0.1 mM supplemented with 10% D₂O and referenced to 4,4-dimethyl-4-silapentane-1-sulfonic acid (DSS). Each spectrum was recorded using 512 transients. Spectra were processed with NMRPipe (55), visualized with the Python package nmrglue (56), and population-weighted average spectra were generated by an in-house Python script using the equilibrium populations of the four GR isomers calculated from the optimal TH global fit kinetic parameters (at 295 nm and k_ex = 0 min⁻¹, see below). For example, the WT 33+35+53+55 population-weighted average intensity was calculated according to 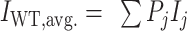, where P_j and I_j are the populations and NMR intensities of the four GR isomers (j ∈ (33,53,35,55)). Populations were calculated at 25 °C for comparison with the experimental data according to 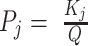, where 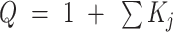, 1 represents the unfolded state, and 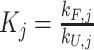is the folding equilibrium constant for the j_th isomer. Similar equations hold for the population-weighted averages of the half-trapped mutants, except their sums contain just two folded populations as these G4s fold into only two GR isomers. WT spectra were reconstructed from half-trapped data according to 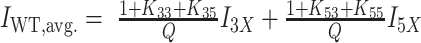for the 3X+5X spectrum and 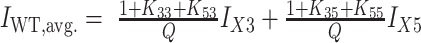for the X3+X5 spectrum.

NMR spectra of photocaged oligonucleotides were recorded on a Bruker AVIII HD 700 MHz spectrometer equipped with a 5 mm z-axis TXI-HCP cryogenic probe at 310 K using 0.05 mM DNA in TH buffer (given above) with 0.05 mM DSS and 10% D₂O. Water suppression was achieved using a jump-return-echo pulse scheme. Time-resolved NMR experiments were performed as reported previously (23) in a pseudo-2D experiment. Laser irradiation within the NMR tube was triggered via a TLL connection to a laser set up (Paladin Advanced 355−8000). Kinetics were recorded after 1.5 s of laser irradiation. Kinetic traces were generated by adding 8 FIDs per time point (giving approximately 9.24s spacing between points), processing these summed FIDs with an exponential window function, and integrating the signal intensity in the imino region. No baseline correction or solvent suppression was applied during processing in order to preserve the imino signals. The kinetic profiles were fitted to the monoexponential function 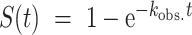where k_obs. is the effective rate constant governing the rate of the folding reaction upon laser irradiation.

Thermal hysteresis measurements

TH datasets were collected using a Cary Win-UV spectrophotometer (Agilent Technologies, USA) and cuvettes with a 1 cm path length. Absorbance profiles were measured as a function of temperature at 260 and 295 nm over the interval of 5–90 °C with 10 μM samples. Scan rates of ±2, ±3 and ±4 °C min⁻¹ were chosen to induce TH between the heating and cooling scans. The samples were equilibrated at high and low temperatures for 5 min. A layer of mineral oil was placed on top of the sample solution in the cuvettes to mitigate evaporation. Measurements were repeated in triplicate yielding a total of 27 datasets (3 replicates for each of the 9 G4 sequences studied herein). We applied temperature corrections to all datasets as described previously (51) to account for deviations between the true solution temperature and the block temperature reported by the instrument. TH datasets were collected in both 1 and 0.1 cm cuvettes to assess the influence of heat transfer in the two cell volumes at the rapid scanning rates employed here (Supplementary Figure S1). We measured nearly identical TH datasets using either cuvette, implying that heat transfer throughout the cell volume is efficient in both cases, even at very fast scanning rates. TH measurements collected in 1 cm cuvettes represent the primary dataset used below.

RESULTS

Trapping individual GR isomers by systematic mutation

We studied the c-myc Pu22 G4 sequence, 5′-TGAGGGTGGGGAGGGTGGGGAA-3′, which is derived from the promoter region of the human c-myc oncogene (57). This sequence contains four dG residues in its second and fourth G-tracts and three in the first and third (Figure 1C). Thus, there are two ways for both the second and fourth tract to align with respect to the first and third, giving rise to four GR isomers in total (Figure 1A) (19). The exchange between c-myc GR isomers takes place on the minutes timescale (∼2 × 10⁻² min⁻¹) at ambient temperatures (23); therefore, the transition from the unfolded state to each of the folded isomers can be considered a distinct folding pathway. In order to study each pathway separately, we used site-directed mutagenesis to trap the second and fourth G-tracts shifted in either the 5′ or 3′ direction with respect to the 3 G-tetrads of the G4 core. We substituted surplus dG residues in the second and fourth G-tracts with deoxyinosine (dG>dI) that lacks an N2 amino group but is otherwise identical to guanine. The hypoxanthine base can therefore closely mimic the physical properties of surplus guanines in loop positions, but cannot form the full complement of H-bonds in a G-tetrad and is therefore disfavored within the G4 core. In what follows, we refer to the c-myc Pu22 as wild-type (WT), sequences containing two dG>dI substitutions as fully trapped mutants, and those with a single dG>dI mutation as half-trapped mutants. We have previously shown that trapped mutants are excellent structural and thermodynamic mimics of the corresponding WT GR isomers (19). For instance, the Pu22 double mutant 5′-TGAGGGTIGGGAGGGTIGGGAA-3′ mimics the WT GR isomer in which both the second and fourth G-tracts are shifted in the 5′ direction, and we refer to this as the 55 fully trapped mutant. The Pu22 single mutant 5′-TGAGGGTGGGGAGGGTIGGGAA-3′ mimics the two WT GR isomers in which the fourth G-tract is shifted in the 5′ direction and the second G-tract can shift in either 3′ or 5′ directions, and we refer to this as the X5 half-trapped mutant. We systematically mutated positions 8, 11, 17 and 20 in the Pu22 G4 to generate a library of 4 fully trapped (55, 33, 35, 53) and 4 half-trapped (5X, 3X, X5, X3) mutants, in addition to the WT sequence.

Trapped mutants are structurally similar to the corresponding WT GR isomers

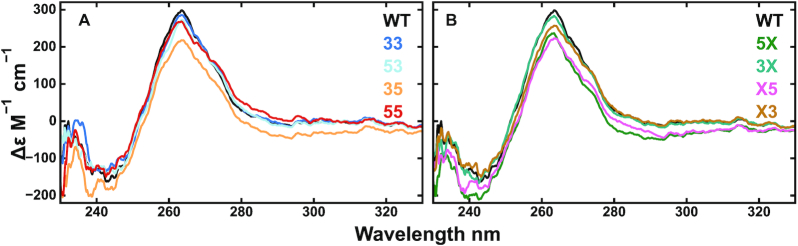
We evaluated the structures of the Pu22 WT and mutant G4s using CD and ¹H NMR spectroscopy. Typically, CD spectra of G4s with either parallel or antiparallel topologies contain positive signals at either 265 or 290 nm, respectively (58). CD spectra of the WT and all mutants closely overlay with strong peaks at about 265 nm and little signal at 290 nm, which is indicative of parallel G4 structures and suggests that the mutations have not altered the WT G4 topology (Figure 2A,B), as observed previously (59,60). To further test the idea that the trapping mutations do not alter the overall topology, we applied a recently developed analytical approach (58) to our CD data that gives the relative fractions of G-G glycosidic bond angle base steps in the G4 core (e.g. anti–anti, syn–anti or anti–syn), and indicates the type of G4 structure formed. The analysis showed that all 9 of our studied sequences contain 7–9 anti–anti base steps in their G4 cores, consistent with a three G-tetrad, parallel G4 structure (Supplementary Table S1). For the WT, this implies that the two well-populated GR isomers (33 and 53) both adopt 3-tetrad, parallel topologies, as do the 33 and 53 trapped mutants. The results of this analysis are also in very good agreement with those obtained for the c-myc Pu22 dT-trapped 33 mutant (8 anti–anti G-G steps) that has a parallel topology as shown by solution NMR (PDB structure: 1XAV) (57,58). Together, these metrics suggest that trapping mutations do not disrupt the G4 topology and that all Pu22 GR isomers adopt parallel folds.

Figure 2.

Structural characterization of the c-myc Pu22 G4 and trapped mutants by CD. The WT CD spectrum is shown overlaid with those for the fully trapped (A) and half-trapped (B) mutant structures.

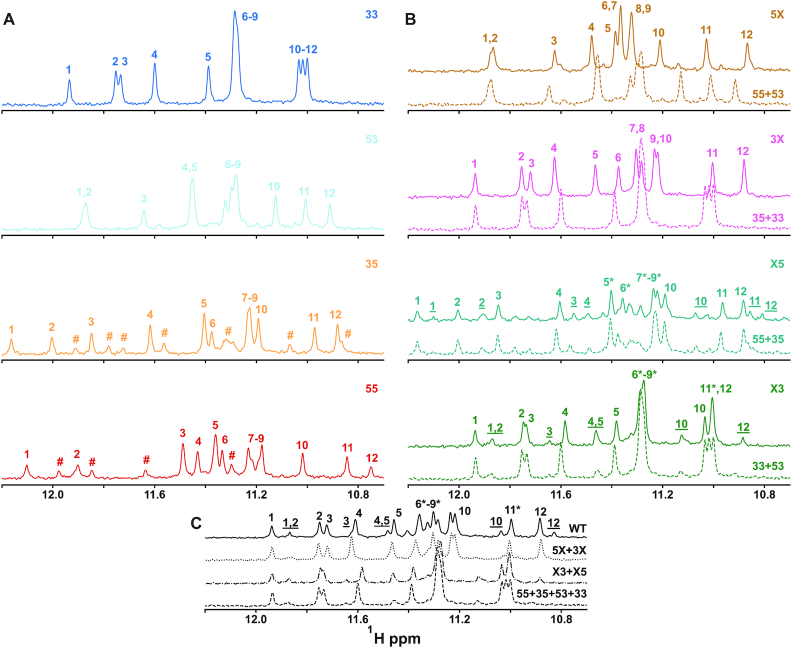
We further characterized the structures of the Pu22 WT and trapped mutant G4s using NMR spectroscopy. The portion of the ¹H NMR spectrum from about 10 to 12 ppm is the fingerprint region for G4 formation (Figure 3A) (61); each resonance corresponds to an imino ¹H located in one of the G-tetrads. For a canonical G4 with a single ground state conformation consisting of three G-tetrads, 12 well-resolved imino ¹H resonances are expected (indicated by numbers in Figure 3). We observed one dominant set of peaks for the 33 and 53 fully trapped mutants, suggesting these mutations lock the structures nearly completely (Figure 3A). The 35 and 55 fully trapped mutants contained, in addition to the set of major peaks, a set of low intensity peaks (indicated by #) which we attribute to the formation of a high energy (weakly populated) GR isomer in which a dI residue shifts into the G4 core. The chemical shifts for the minor set of peaks in the 35 and 55 spectra bear some similarity to those of the next most stable GR isomer (Table 1, thermal melting temperatures) that involves the least number of dI residues within the G4 core. For example, the next most stable GR isomer available to the 35 mutant is the 33 form, since this shift involves shifting the fourth G-tract by one position, introducing one dI residue into the core. Minor resonances resembling the 33 state are observed in the 35 spectrum (# symbols). A similar relationship holds for minor peaks resembling the 35 isomer in spectra of the 55 trapped state. Note that perfect agreement with the minor peaks would not be expected, since the G4 core would contain dI, which could affect the magnetic environment of nearby imino protons. It stands to reason that these minor isomers are observed for the two least stable trapped mutants. In these cases, the energetic penalty for shifting dI into the core is partially offset by adopting a more stable GR isomer. In contrast, for the more stable isomers, the penalty for shifting dI into the core is compounded by the transition to a less stable isomer. Thus, the minor peaks we observe in the 35 and 55 spectra do not likely correspond to alternate structures beyond the four GR isomers. The half-trapped sequences that we predicted to fold into GR isomers with highly skewed populations (see details below) showed just one major set of peaks (Figure 3B, 5X, 3X), as expected. The remaining half-trapped sequences, which in principle populate their two respective isomers to a similar extent, exhibited two sets of resonances resulting from the exchange between the two GR isomers that occurs slowly on the NMR timescale (Figure 3B, X5, X3). We recently measured the rate of exchange between GR isomers in a half-trapped c-myc G4 mutant to be on the order of 1 h⁻¹, using NMR photocaging experiments (23). Considering the X5 spectrum, the major (numbered peaks) and minor (underlined numbered peaks) state chemical shifts are well-represented by the corresponding shifts of the 35 and 55 mutant spectra, which are the two basis GR isomers for the X5 sequence. A similar result was obtained for the X3, 33 and 53 spectra. In addition, the Pu22 WT gave at least two sets of peaks with chemical shifts matching the predominant 33 and 53 isomers of the ensemble, reflecting slow exchange between these two states (Figure 3C). We note that the least populated isomers are not expected to show distinct peaks in the WT spectrum since they are populated at <5% at equilibrium. Interestingly, we observed a downfield imino ¹H resonance at ∼14 ppm for sequences harboring a dG>dI mutation at the 17th position (Supplementary Figure S2). This downfield signature has been observed for reverse Hoogsteen dT:dA basepairs that form capping motifs over the core structure of certain G4s (62), and alternatively for hydrogen-bonded dI residues (63). The intensity of this signal is comparable to the dG imino peaks for the dominant states of the 55 and 35 mutants. We tentatively assign it to the dI base residing in the third loop that likely participates in the stabilization of the 5′-TGA capping structure through some form of dI:dA or dI:dT wobble base pair (64,65).

Figure 3.

G4 structural analysis by proton NMR. Imino proton spectra for the fully trapped (A), half-trapped (B) and WT structures (C). Imino peaks for the 12 major resonances in each spectrum are numbered. Minor state peaks due to incomplete trapping of the 35 and 33 mutants are indicated with # symbols. The resonances for minor state GR isomers in the WT and X5 and X3 half-trapped mutants are labeled with underlined numbers. Numbers with asterisks indicate regions where the major and minor state GR isomer resonances are overlapped. In panels (B) and (C), the equilibrium population-weighted average spectra of the corresponding fully trapped mutants are shown as colored dashed lines, calculated from the extracted TH global fitting parameters (see ‘Materials and Methods’ section for details). The 5X, 3X, X5, X3 weighted average spectra are given by the weighted sums of the 55 + 53, 35 + 33, 55 + 35 and 53 + 33, respectively. The WT weighted average spectra are the weighted sums of the 5X + 3X, X3 + X5 and 33 + 53 + 35 + 33 spectra.

Table 1.

Kinetic parameters extracted from global fits to the c-myc Pu22 and trapped mutant TH datasets collected at 295 nm according to Scheme 1C with k_ex = 0 min⁻¹

GR isomer	E F (kJ mol−1)	k F (min−1)	E U (kJ mol−1)	k U (min−1)	T m (°C)
55	−36.0 ± 0.7	(387 ± 6) × 10−3	121 ± 1	(162 ± 3) × 10−3	43.23 ± 0.04
35	−47.9 ± 0.8	(572 ± 6) × 10−3	140.4 ± 0.8	(72.1 ± 0.9) × 10−3	47.48 ± 0.03
53	−54.6 ± 0.6	(917 ± 8) × 10−3	144.5 ± 0.4	(23.2 ± 0.2) × 10−3	53.27 ± 0.02
33	−54.4 ± 0.5	(1220 ± 9) × 10−3	164.3 ± 0.3	(7.2 ± 0.1) × 10−3	57.69 ± 0.03

Rate constants are reported at T₀ = 37 °C. Equilibrium T_m values were extracted from two-state fits of slow scanning (0.2 °C min⁻¹) thermal melts monitored at 295 nm (Supplementary Figure S10). Errors were calculated using a Monte-Carlo approach (87).

We can gain some insight into the effects of the trapping mutations on the structures of the G4s from comparisons of the ¹H NMR spectra. In principle, half-trapped spectra should be similar to the population-weighted sum of spectra for fully trapped mutants mimicking the two GR isomers, i.e. spectra for the 3X, 5X, X3 and X5 half-trapped mutants should be combinations of 33+35, 53+55, 33+53 and 35+55 spectra, respectively. We shall use the term ‘reconstructed’ spectra to simplify the discussion below, but we note that when populations are highly skewed (3X and 5X), the reconstructed spectrum is essentially just the spectrum of the more stable fully trapped mutant. The correspondence between the half-trapped and reconstructed spectra is clear in all cases (Figure 3B). Although the ppm values of many of the peaks do not line up exactly (many differences are on the order of 0.05 ppm), the peak distribution patterns are well reproduced, in terms of the relative locations of weak/intense and single/clusters of peaks. For the WT, there are a number of different possible reconstructions based on mutant spectra, including 5X+3X, X3+X5 and 55+35+53+33 (fully trapped) (Figure 3C). In this case, the 5X+3X reconstruction is extremely close to the WT spectrum over the entire 10.8–12.0 ppm window. The X3+X5 and fully trapped reconstructions are also quite close between about 11.4 and 12.0 ppm; however, they lack any major peaks upfield of about 11.0 ppm, whereas the WT and 5X+3X spectra have a strong peak at 10.85 ppm. The 33 and X3-trapped mutants contain dI in the 20th position and either dI or dG in 11th position, respectively. In the NMR-derived structure of the dT-trapped 33 mutant, residues 11 and 20 are both present on the same face of the G4 core, together with two dA residues from the 3′ terminus (57). Interestingly, the presence of dI at position 20 together with dI or dG at position 11 (i.e. the 33-trapped mutant and X3 major conformer respectively) is associated with the absence of a ¹H peak at 10.85 ppm, while the presence of a dG at position 20 together with a dI or dG at position 11 (i.e. the 3X and WT, respectively) is associated with the presence of a ¹H peak at 10.85 ppm, pointing to different NMR shielding environments depending on the identities of bases present in this location. We repeated this analysis for regions of the ¹H spectra associated with nucleobase aromatic protons (approximately 7.2–8.7 ppm; Supplementary Figure S3) and sugar protons (approximately 5.5–6.8 ppm; Supplementary Figure S4) and observed very much the same behavior: half-trapped and WT spectra show many similarities to the reconstructed spectra, but they are not identical. It must be noted that some spectral differences between the WT and mutant spectra are expected since dI residues are chemically distinct from dG, so protons near the sites of substitutions will necessarily experience slightly different magnetic shielding environments. As well, some structural rearrangements of the mutants compared to the WT GR isomers cannot be ruled out. However, many points of similarity between the WT, half-trapped and reconstructed ¹H spectra suggest that any such conformational perturbations are relatively subtle. Furthermore, small structural differences between trapped mutants and the corresponding WT GR isomers would not affect our analysis of parallel folding pathways. First, the folding rate of a given isomer is governed by how rapidly it can pass through the transition state on the way to the folded state. The precise packing geometry of bases in a G4 is almost certainly determined after the transition state has already been crossed. Second, folding rates are governed by the free energy difference between the unfolded state and the transition state, and not by the structures of the states, per se; isoenergetic transition states give identical folding rates, even if they have different structures. We have already shown that the folded states of trapped mutants have very similar thermodynamic stabilities to the corresponding GR isomers (19). It therefore seems a reasonable assumption that the stabilities of the transition states are also similar and that trapped mutants and corresponding GR isomers fold at comparable rates. The fact that neither CD nor NMR spectroscopy points to any major structural reorganization of the folded state as a result of the mutations is consistent with the idea that the stabilities of mutant folded and transition states are similar to those of the corresponding WT GR isomers.

Folding kinetics characterized by thermal hysteresis

We used TH measurements to characterize the folding kinetics and thermodynamic stabilities of the Pu22 WT G4 and trapped mutants. The TH approach is based on spectrophotometric detection of folding/unfolding as the temperature is varied, similarly to simple thermal melting experiments. In the case of TH, the temperature ramp rate is adjusted to be fast compared to the length of time required by the molecules to equilibrate such that populations of folded and unfolded states lag behind their equilibrium values. This causes the melting mid-point on the up-scan to occur at a higher temperature than the refolding mid-point on the down-scan. The gap between heating and cooling profiles increases with increasing scan rates and gives detailed information on the folding and unfolding rate constants of the system (51). The transition temperatures themselves are related to the thermodynamic stability of the system.

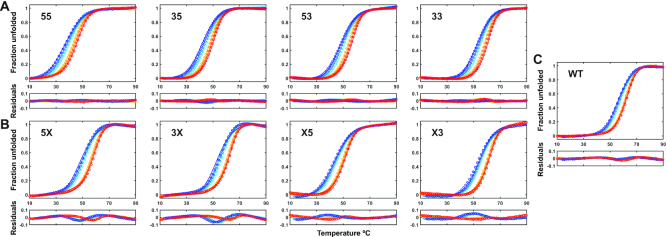
We measured TH datasets for the Pu22 WT G4 and trapped-mutant sequences at six temperature scan rates ranging from -4 to 4 °C min⁻¹ (Figure 4). The data were baseline (Supplementary Figure S5) and temperature corrected as described previously (51). TH absorbance thermograms were collected at both 260 and 295 nm for the fully trapped mutants to test whether folding is two-state, since the presence of well-populated intermediates such as triplexes can lead to large discrepancies between folding/unfolding curves collected at these two wavelengths (40). Data for the fully trapped mutants collected at the two wavelengths overlaid closely (Supplementary Figure S6), suggesting that partly structured folding intermediates with very different spectroscopic properties are not appreciably populated and the fully trapped mutant G4s fold in an effectively two-state manner. We further tested this assumption by comparing the kinetic parameters extracted from global fits (described below) to the TH datasets at both wavelengths, finding similar values in all cases (details are given below, Table 1; Supplementary Table S2 and Supplementary Figure S7), which further supports the idea that folding is effectively two-state for these mutants. Finally, CD spectra collected over a range of temperatures superimpose extremely closely, suggesting that alternative folded conformations are not populated as the folding transition is approached (Supplementary Figure S8). This agrees with several other studies of the Pu22 G4. For instance, mechanical unfolding measurements obtained using magnetic tweezers were consistent with a two-state transition (59). Similarly, a two-state kinetic model gave good agreement with TH measurements for dT-variants of the trapped mutants studied here (dG>dT instead of dG>dI substitutions) (66). Finally, it has been shown that under some circumstances, Pu22 folding can involve well-populated folding intermediates (60), but as we discuss below, this does not preclude the rigorous use of two-state equations to describe folding in the current study. Specifically, Gray et al. found that when folding of the dT-variant of the 33 fully trapped mutant (dT-33) is initiated by the rapid addition of K⁺ ions, antiparallel intermediates are formed early in the process, followed by slow conversion to the parallel topology ground state (60). Similarly, mass spectrometric analyses of K⁺-initiated G4 folding detected long-lived, incompletely K⁺-coordinated G4 folding intermediates (67). However, we have found that folding reactions starting from a K⁺-free unfolded state (i.e. K⁺-initiated) differ fundamentally and are slower by about two orders of magnitude, compared to reactions starting from a K⁺-equilibrated unfolded state, such as TH or photocaged NMR experiments (23). The folding intermediates detected in K⁺-initiated folding experiments likely represent kinetic traps that are not present when the unfolded state is allowed to equilibrate with K⁺ ions, as they do in this study. Gray et al. also analyzed circular dichroism thermal unfolding traces of the dT-33 fully trapped mutant using singular value decomposition. They found that unfolding involved three-states: folded (F), unfolded (U) and an intermediate (I). The difference in enthalpy between F and I was only 12% of the total enthalpy of unfolding, and the reconstructed parallel topology CD spectra of the F and I states were very similar. Therefore, the I state appears to involve a modest rearrangement or slight partial unfolding of the F state. We have tested whether folding under these conditions can be well approximated as a two-state process involving the U state and a F:I ensemble. As shown in Supplementary Figure S9, we fitted synthetic data generated with an F↔I↔U model to two-state folding equations and accounted for the F↔I transition with an adjustable linear premelting baseline. The extracted thermodynamic parameters closely reproduced the populations and folding enthalpy of an effective folded state comprising the F:I ensemble. Equilibrium melting and TH experiments for the fully trapped mutants had gently sloping folded baselines and were well fit by the two-state equations (Supplementary Figures S4, S5 and S10), similar to these simulations, giving us confidence that our analysis yields meaningful thermodynamic and kinetic parameters for the folded to unfolded transition.

Figure 4.

Global fits of a parallel pathways model to TH data for the WT and trapped-mutant G4s. TH datasets (295 nm) for the fully trapped (A), half-trapped (B) and WT (C) G4s. Fit residuals are shown in the subpanel below each dataset. Light to dark blue and orange to red indicate slowest to fastest annealing and melting scan rates, respectively. Experimental data are shown as colored circles, while optimized global fit data are colored lines.

Equilibrium melting temperatures (i.e. thermal stability) for the trapped mutants followed the order 55 < 35 < 53 < 33 (Table 1), which is consistent with equilibrium melting and differential scanning calorimetry experiments performed previously on fully trapped mutants of the slightly shorter c-myc Pu18 G4 (19). In general, the melting transitions occurred at higher temperatures for the half-trapped mutants than for the fully trapped ones, and the melting transitions for the WT occurred at the highest temperatures of all. We have previously shown that the Pu18 WT G4 melts at a higher temperature than any of its fully trapped mutants due to entropic stabilization of the folded state by GR exchange (19). We expect the situation is similar here as well, with the half-trapped and WT molecules able to adopt 2 and 4 GR isomers, respectively, compared to the fully trapped molecules that have only a single GR isomer available. Conformational entropy from GR exchange thus dictates that both the half-trapped and WT are more stable than the single most stable GR isomer within their conformational ensembles.

Visual inspection of the TH datasets indicates that all four potential pathways contribute to the effective folding rate of the Pu22 WT G4. The temperature gap between the apparent melting points on the heating and cooling scans (ΔT_m) decreases as the rates of folding and unfolding increase (note that at the equilibrium T_m these rates are equal). A mutation that decreases the folding rate but does not affect the unfolding rate will lead to a lower apparent melting temperature, slower kinetics and larger ΔT_m. Alternatively, a mutation that increases the unfolding rate will also lead to a lower apparent melting point, but with faster kinetics and a smaller ΔT_m (Supplementary Figure S11). Here, the ΔT_m for the WT is smaller than those of the half-trapped mutants, which in turn are smaller than those of the fully trapped mutants (Supplementary Table S3). This implies that the effective folding rate of the WT is greater than those of the half-trapped mutants, which are greater than those of the fully trapped mutants. Since each mutation reduces the number of folding pathways by a factor of 2, and in every case the apparent folding rate decreases, this implies that all four folding pathways makes non-negligible contributions to the overall folding rate of the WT.

Globally fitting a parallel pathways folding model

The qualitative analysis of ΔT_m values described above suggested that increasing numbers of folding pathways lead to increasing folding rates. In order to test this conclusion, we analyzed whether TH data for G4s with two and four possible pathways (half-trapped and WT) are quantitatively consistent with TH data for the fully trapped mutants, which approximate folding through each individual pathway. TH kinetic data have typically been analyzed assuming two-state folding behavior described by temperature-dependent folding k_F and unfolding k_U rate constants (Scheme 1A) (50). Briefly, in this approach the spectroscopic thermal melting data are used to estimate the fraction of folded (θ_F) and unfolded molecules (1 - θ_F) as a function of temperature, by applying appropriate folded and unfolded baselines. The shapes of the TH profiles are then given by the expressions:

(1)

and

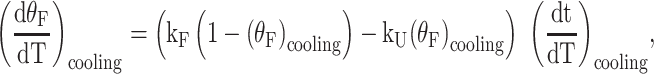(2)

where the values (θ_F)_{heating,cooling} and slopes (dθ_F/dT)_{heating,cooling} of the curves are obtained directly from the data and the inverses of the temperature ramp rates (dt/dT)_{heating,cooling} are set by the user. At any given temperature, this gives a system of two equations and two unknowns (k_F and k_U) that are obtained algebraically as a function of temperature. The temperature dependences of the rate constants can then be fitted to extract the activation energies from an Arrhenius plot. Examples of this type of classical analysis for the sequences studied here are shown in Supplementary Figure S12.

Scheme 1.

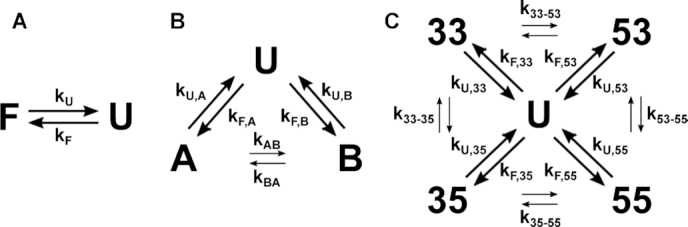
Folding mechanisms for the WT c-myc Pu22 ensemble and trapped mutants. (A) The fully trapped G4s adopt a single folded (F) conformation from the unfolded state (U). (B) The half-trapped G4s fold into two GR isomers (A and B) from the unfolded state, which can then slowly equilibrate by direct interconversion (indicated by small arrows) (23). (C) The WT c-myc Pu22 ensemble primarily folds by directly adopting the four GR isomers from U in parallel, with slow GR exchange between isomers.

The analysis of TH data for half-trapped and WT G4s quickly becomes more complicated, due to the existence of multiple GR isomers in the folded state ensemble, as visualized directly by NMR spectroscopy. For example, in the case of a half-trapped mutant whose folded state ensemble consists of the GR isomers A and B, the kinetics of the system is now described in terms of two folding rates, k_F,A and k_F,B, two unfolding rates, k_U,A and k_U,B, as well as the rates of GR exchange, k_AB and k_BA, for A→B and B→A, respectively (Scheme 1B). The fraction of folded molecules is the sum of fractions of A and B isomers, θ_F = θ_A + θ_B, and the shape of the TH profile is given by

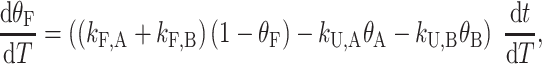(3)

where the relative amounts of the A and B isomers obey the equations

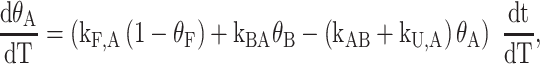(4)

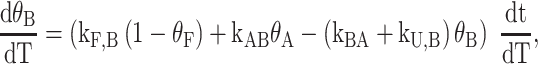(5)

and the principle of detailed balance (68) requires that

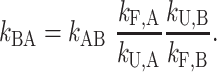(6)

In the case of the Pu22 WT G4, there are four folding rates, four unfolding rates, four GR exchange rates and 12 associated activation energies (Scheme 1C). Note that the half-trapped and WT datasets are very well fit by two-state folding models (Supplementary Figure S13). The apparent folding rates extracted from these fits match the ΔT_m analysis above, with each half-trapped mutant generally folding faster than their two corresponding fully trapped mutants, and the WT generally folding faster than the half-trapped mutants (Supplementary Table S4). However, this simple model does not capture the underlying equilibrium since the WT and half-trapped mutants contain multiple, slowly exchanging folded isomers. Clearly, data from the heating and cooling scans are insufficient to extract all of the half-trapped parameters algebraically, or even by nonlinear least squares fitting to a single dataset.

Although it is not possible to reliably extract all the relevant folding kinetic parameters for half-trapped and WT G4s from analyses of their individual TH datasets alone, we can still rigorously test whether their data are consistent with a parallel pathways folding mechanism by fitting the data for all sequence variants globally. We applied an extension of a global fitting approach we had developed previously to analyze the thermodynamics of GR exchange (19). We simultaneously analyzed the data for the Pu22 G4 WT and all fully trapped and half-trapped mutants with the assumption that the kinetic parameters for any folding or unfolding transition in the WT or half-trapped mutant are equal to those of the corresponding fully trapped mutant, and that all rate constants obey an Arrhenius temperature dependence (see Supplementary Methods). This produces a global fit where kinetic parameters for 12 independent transitions are extracted from data for 9 different sequence variants, which compare favorably to the simple two-state case where kinetic parameters for two transitions (folding and unfolding) are extracted from data for one sequence variant. The global fit provides a quantitative test of the parallel folding pathways model. Large systematic deviations between calculated and experimental TH profiles in the global fit would indicate that either the half-trapped or WT G4s do not follow a parallel pathways mechanism as depicted in Scheme 1C and/or the fully trapped G4 folding kinetics are not good measures of the individual pathways. However in actuality, we found that the parallel pathways model gave excellent simultaneous agreement with all nine datasets (Figure 4), providing validation for the model and justifying the use of fully trapped mutants to mimic the individual GR isomers. The sum of squared residuals from the global fit is only ∼3.8-fold greater than that obtained from fitting data for each sequence variant independently (Supplementary Figure S13), even though the global fit contains 20 fewer adjustable parameters overall (16 versus 36 kinetic parameters in the global and independent fits, respectively) and therefore represents the simpler model. Furthermore, the global fit yields rate constants and activation enthalpies for all folding and unfolding transitions of the WT (listed in Table 1), providing some insight into how the WT Pu22 c-myc G4 folds.

The rates of folding into each of the four GR isomers were similar at 37 °C, with only ∼5-fold variation between the different folding pathways. In contrast, the unfolding rates differed by up to 15-fold between the most- and least-stable GR isomer. This suggests that the specific molecular interactions that give the GR isomers different stabilities are largely formed after the G4 folding transition state. All of the activation energies for folding were negative on the order of -35 to -55 kJ mol⁻¹, implying that enthalpically favorable interactions are made in the transition states for folding, as have been observed previously for other G4s (69). The activation energies for unfolding were all large and positive (∼120–170 kJ mol⁻¹) and followed an identical order to the stabilities of the isomers at 37 °C and their melting temperatures, i.e. 55 < 35 < 53 < 33. Unlike the folding and unfolding transitions, the rates of direct GR exchange (i.e. transitions from one GR isomer to another without unfolding) were not precisely defined by the data. However, we could place limits on how rapidly these transitions might occur. We performed global fits fixing all four direct GR exchange rates (k_ex = k_AB + k_BA) to values between 1 × 10⁻⁶ and 1 × 10⁵ min⁻¹ while optimizing all other kinetic parameters (Supplementary Figure S14). We obtained optimal agreement with k_ex = 0.1 min⁻¹, i.e. on a similar timescale to the unfolding rate constants, and slightly worse fit qualities at k_ex below this value. Fixing k_ex to faster values resulted in substantially worse agreement with the data as evinced by larger residual sum of squared differences (RSS) between experimental and calculated values. This agrees well with a recent dynamic NMR study of GR exchange rates that found a Pu18 half-trapped mutant undergoes transitions between GR isomers on a timescale that is approximately 10-fold faster (k_ex ∼2 × 10⁻² min⁻¹) than global unfolding (k_U ∼2 × 10⁻³ min⁻¹) at 25 °C (23). Importantly, all k_F, k_U, E_F and E_U values were not at all sensitive to the particular value of k_ex (≤1 × 10³ min⁻¹), so all the values reported in Table 1 are well-defined by the fits. We further tested the robustness of the extracted global fit folding rate constants by generating pairwise parameter correlation surfaces (Supplementary Figure S15) that additionally show that the parameters are well-defined in the global fit. We note that this dataset was collected in 2 mM K⁺ to produce folding kinetics that was slow enough for TH and isothermal NMR folding measurements (see below). This is far below the biological K⁺ concentration of ∼140 mM (54), and therefore we collected an additional TH dataset for the fully trapped mutants at 5 mM K⁺ to test whether these results held at higher K⁺ concentrations. We found a strong linear correlation between rate constants in 2 and 5 mM K⁺, with approximately 2- to 3-fold faster folding and slower unfolding, respectively, in 5 mM K⁺ at 37 °C (Supplementary Figure S16). This suggests that the folding rates of the GR isomers in the Pu22 WT ensemble scale similarly with respect to K⁺ concentration, and the results of our model can be extrapolated to higher, more biologically relevant salt conditions. The extracted kinetic parameters from either the 2 or 5 mM K⁺ TH datasets reveal the extent to which parallel reaction pathways accelerate folding of the Pu22 WT G4. The effective rate constant for the transition from the unfolded state to the ensemble of folded conformations is given by the sum of folding rate constants for the four pathways leading to the four GR isomers,

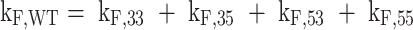(7)

giving a value of k_F,WT = 3.1 min⁻¹ in 2 mM K⁺. For comparison, the rate constant for the fastest folding and most stable GR isomer (33) is k_F,33 = 1.2 min⁻¹, meaning that folding is accelerated by at least a factor of 2.5 due to the presence of multiple pathways. It is worth noting that compared to the average rate constant, folding acceleration is always equal to the number of pathways, four in this case. In other words,

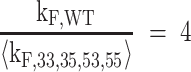(8)

where angled brackets indicate the mean value.

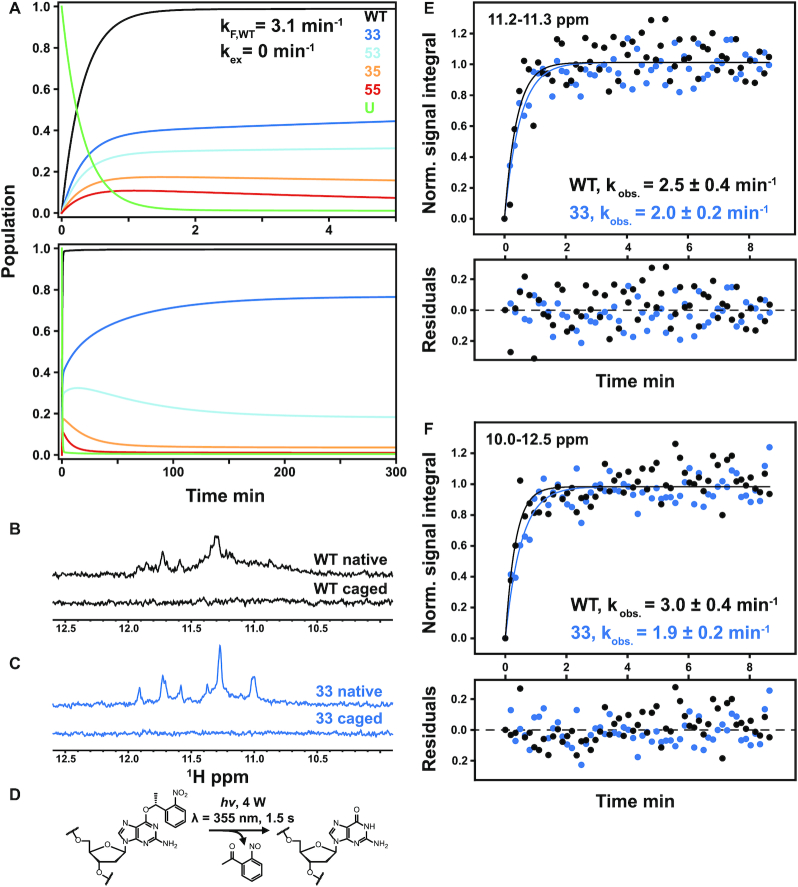
The different folding and unfolding rates for the four reaction pathways imply the existence of some interesting nonequilibrium behavior when an unfolded Pu22 WT chain is allowed to fold under ambient conditions. We performed a numerical simulation of the folding reaction using the measured kinetic constants (see Supplementary Methods) according to Scheme 1C with k_ex = 0 and the optimal value of 0.1 min⁻¹, and plotted the relative amounts of each GR isomer as a function of time (Figure 5A and Supplementary Figure S17). Interestingly, the populations of the 35 and 55 isomers built up relatively quickly to reach maxima near ∼1 min (Figure 5A, top) and then decreased by up to a factor of 10 at longer time points (Figure 5A, bottom). At very long times, the relative populations are thermodynamically controlled and the folded ensemble consists of 77%, 18%, 4% and 1% of the 33, 53, 35 and 55 GR isomers, respectively, in agreement with our previous studies of c-myc G4s (19). In contrast, at the early stages of folding, populations are determined by the rate rather than the equilibrium constants of folding and the ensemble consists of approximately 40%, 30%, 18% and 12% of the 33, 53, 35 and 55 GR isomers, respectively, which explains the transient buildup of the less stable 35 and 55 forms. Similar results were obtained for simulations including direct GR isomer exchange at the optimal value of k_ex (Supplementary Figure S17), with only slightly more rapid equilibration of the folded ensemble. Thus, the composition of the Pu22 G4 structural ensemble is different at short and long time-points following the initiation of folding. Furthermore, the effective rate constant for unfolding depends on the instantaneous populations of GR isomers according to

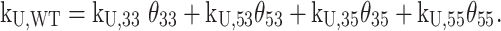(9)

Figure 5.

Theoretical prediction of folding acceleration in the c-myc Pu22 WT ensemble by TH and experimental validation by isothermal NMR folding experiments. (A) Short- and long-timescale isothermal population distributions predicted by TH are shown in the top and bottom plots, respectively. U (green) denotes the unfolded state, and the WT trace is the sum of the profiles for the four GR isomers (colors matching Figures 2 and 3). Isothermal simulations were performed according to Scheme 1C using the optimized parameters from Table 1 without direct GR isomer interconversion (37 °C and k_ex = 0 min⁻¹, see Supplementary Methods for details). (B and C) Imino proton region of the 1D ¹H spectra of 3x-NPE-caged and native (after irradiation) c-myc Pu22 oligonucleotides: WT (B) and 33 fully trapped mutant (C) at 37 °C. For the 3x-caged oligonucleotides, the absence of imino proton signals indicates an unfolded state with no stable Hoogsteen base-pair interactions. (D) Photolysis reaction for O6-(R)-NPE-caged dG with laser light at 355 nm. Folding is initiated after the caging group is released from the dG residue. (E and F) Normalized kinetic NMR data for the light-induced folding of photocaged c-myc Pu22 WT and 33 fully trapped G4s using imino proton signal integration limits of 11.2–11.3 and 10–12.5 ppm, respectively. Data (colored points) were fit to a monoexponential function 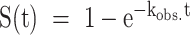(colored lines) with fit residuals shown underneath each panel. Extracted rate constants are indicated.

Initially, k_U,WT ≈ 0.043 min⁻¹ while at very long times, k_U,WT = 0.014 min⁻¹. Thus, the average lifetime of a folded G4 ( = 1/k_U,WT) is about 20 min in the ensemble of conformations that forms initially, but increases to over an hour as the populations of more stable GR isomers are enriched with time.

Measuring the Pu22 folding acceleration by salt-equilibrated isothermal NMR folding experiments

To directly measure the folding acceleration of the Pu22 WT as a result of adopting multiple GR isomers in parallel, we turned to isothermal NMR folding experiments. Our experiments incorporated site-specific photolabile caging groups into the WT and 33 mutant sequences (see Supplementary Methods and Supplementary Table S5) that completely abolish folding of the strand into the native structure as evidenced by flat imino region baselines in 1D ¹H NMR spectra (Figure 5B,C) (caged spectra). Once inside the NMR spectrometer, the caging groups can be released by irradiating the NMR sample with a laser (Figure 5D), and the folding reaction can be followed in real time via the increase in the imino ¹H signal intensities (Figure 5B,C native spectra). Both the WT and 33 mutant folded rapidly in the NMR measurements, with the process reaching completion within approximately 1–2 min after photolysis. By tracking the signal integral within the imino fingerprint region as a function of time, we obtained folding progress curves for the WT and 33 mutants that are shown in Figure 5E,F. We used two different limits of spectral integration to calculate folding rates. The first used the relatively narrow region of 11.2–11.3 ppm that contains the most intense cluster of peaks in both WT and 33 folded spectra. In the 33 mutant, these peaks correspond to imino resonances for a single GR isomer (i.e. the 33 isomer), whereas in the WT this region contains signals from several GR isomers. The second integration window extended from 10 to 12.5 ppm and captured all NMR imino signals for the folded WT and 33 structures. In all cases, progress curves were well-fit by single exponential build-up functions, suggesting that well-populated, long-lived, partly structured folding intermediates are not formed, in agreement with our tests of effective two-state folding described above and detailed in the TH models of Scheme 1. Fits to the 11.2–11.3 ppm integration data yielded observed folding rate constants (k_obs.) for the WT and 33 sequences of 2.5 ± 0.4 and 2.0 ± 0.2 min⁻¹, while those of the 10 to 12.5 ppm range gave 3.0 ± 0.4 and 1.9 ± 0.2 min⁻¹, respectively, in excellent agreement with the TH-derived values of 3.08 and 1.2 min⁻¹ (taking the WT folding rate to be the sum of all four pathways). The 1.25- to 1.6-fold folding acceleration detected by NMR is similar in magnitude to the 2.5-fold acceleration determined by TH analyses. We note that the NMR experiments were performed near the lower detection limit in terms of signal intensity, leading to somewhat noisy data in Figure 5E,F, and we have greater confidence in the TH-derived values. Nevertheless, the high level of quantitative agreement between two such different experimental approaches is remarkable, and strongly validates our findings.

DISCUSSION

A key question in this research is the extent to which conformational heterogeneity in the folded state implies the existence of parallel pathways that accelerate effective folding rates. Specifically in this case, does the existence of multiple GR isomers in the Pu22 WT folded ensemble lead to more rapid adoption of a folded state, starting from an unfolded chain? If the commitment to a particular GR isomer occurs after the transition state for G4 folding, then the answer is likely no. The folding rate would depend only on the height of a single dominant barrier, regardless of the number of possible GR isomers existing on the far side, which would be separated from each other by smaller energy barriers. In contrast, if the commitment to a given GR isomer occurs early in the folding process then there is a separate transition state for each GR isomer. Each one corresponds to a separate folding pathway, whose rates sum to produce a net acceleration. There are several lines of evidence suggesting that the second scenario applies to the G4s studied here. First, the exchange between different GR isomers occurs quite slowly. Rates are on the same timescale and enthalpic barriers are similar to those for complete unfolding of the G4 (23). If commitment to a given G-register occurred after the transition state, one would expect GR isomers to be separated by energy barriers smaller than the one separating the folded and unfolded states, which is not what is observed. Second, model-free ΔT_m values and effective two-state folding rates extracted from our TH data indicated that fully trapped G4s with a single GR isomer generally fold more slowly than half-trapped mutants with two GR isomers, which largely fold more slowly than the WT with four. This is consistent with the idea that increasing the number of possible GR isomers accelerates folding. Finally, the global analysis verifies that the folding rates of the Pu22 WT and half-trapped mutants can be quantitatively accounted for in terms of parallel folding pathways, where the rate of each pathway is given by the folding rate of the corresponding fully trapped mutant.

The existence of parallel folding pathways in protein energy landscapes has long been recognized, both theoretically and experimentally (70–75), and pathway multiplicity has been directly linked to the overall folding rate. For example, Aksel and Barrick studied consensus ankyrin repeat proteins (CARPs), where the number of distinct folding pathways is equal to the number of repeats (47). They characterized the folding kinetics of CARPs of different lengths and observed that the folding rate constant increased in proportion to the number repeats present, directly demonstrating acceleration due to multiple folding pathways. The folding mechanisms of nucleic acids have been less intensively studied than those of proteins; however, there are examples of molecules with multiple folding reaction pathways similar to those observed here. For example, in a study of the vertebrate telomeric i-motif sequence, Lieblein et al. observed formation of the thermodynamically more stable 5′E intercalation topology through a rapidly folding and slowly unfolding 3′E topology intermediate (76). Bessi et al. studied a telomeric G4 sequence, which initially formed two different topologies with similar rate constants (42). The initial folding reaction was followed by a period of several days over which the population ratio shifted from about 1:1 to 4:1 for the two isomers. Similarly to what was seen here, the effective overall folding rate for the telomere G4 is about twice as large as for either of the individual isomers, and the effective unfolding rate decreases by about a factor of two as the populations slowly equilibrate.

One unique aspect of systems undergoing GR exchange is that the existence of parallel folding pathways can be inferred directly from the nucleotide sequence, unlike other nucleic acids where multiple pathways are only revealed by detailed biophysical analyses. In principle, an estimate of the number of GR isomers is given by (19)

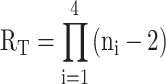(10)

where n_i is the number of dG residues in the i_th G-tract and a G4 core of three G-tetrads is assumed. When a G4 folds with only two G-tetrads (7), even more GR isomers become available to the sequence, since there would then be n - 1 possible alignments for a given G-tract with respect to the other G-tracts that form the core as opposed to n - 2 in Equation 10. We note that this equation does not account for additional conformational heterogeneity that may exist in addition to, or superposed on GR exchange. In principle, each GR isomer can have a different topology, or populate multiple alternate topologies, as we have previously shown for the PIM1 and hTERT promoter G4s (19,23). Some G4s form bulges where internal Gs are extruded from the core and the flanking Gs shift inward to fill these gaps (5). As well, some DNA sequences include a fifth, or ‘spare tire’ G-tract (77), with G4s forming from different subsets of four of the five G-tracts (78,79). Additional conformations present in the folded ensemble would likely lead to additional parallel folding pathways that could further accelerate folding. If we make the very rough approximation that the folding rate of each pathway is comparable, then the total acceleration factor due to the existence of parallel pathways is simply equal to the number of pathways (similar to Equation 8). Equation 10 gives a conservative estimate for the number of GR isomers that can be formed by a given DNA sequence and the associated acceleration factor for G4 folding. We previously analyzed a database of human gene promoter regions for potential G4-forming sequences that could undergo GR exchange, according to Equation 10. Of roughly 28 000 putative G4s, nearly 20% could adopt 12 or more GR isomers and 5% could form >20 (19). Assuming that folding rates to the individual GR isomers are relatively similar (as they are for Pu22) many of these G4s could fold more than an order of magnitude faster than they would if they only adopted a single GR isomer.

There is an important distinction to be made between parallel folding pathways and misfolding. In the Pu22 G4, as well as the telomeric G4 and i-motif mentioned above, some or most of the folding pathways lead to conformational isomers that are not highly populated at equilibrium. These rarer states are formed transiently after folding is initiated, but essentially disappear at long time-points. This begs the question of whether their formation represents folding acceleration or rather kinetic trapping by transiently misfolded species. The best answer to this question lies in the details of biological function. In many cases, it is believed that G4s exert their biological effects simply by virtue of being folded. For instance, folded G4s are proposed to act as physical obstacles that impede the procession of DNA and RNA polymerases (14). Alternatively, G4 folding in the nontemplate strand of DNA could reduce its ability to displace RNA:DNA hybrids formed after RNA synthesis, leading to stalling of the polymerase (15). Similarly, G4 folding in both open reading frames and untranslated regions of mRNAs can reduce translation and influence ribosomal frameshifting and co-translational protein folding (26). In all of these examples, it would be expected that folding to both thermodynamically favored and disfavored states would have similar biological consequences. Thus, reaction pathways to rare GR isomers can be considered to legitimately accelerate folding. In other cases, a greater degree of structural specificity might be expected. There are examples of transcription factors and other proteins that recognize the G4 fold (80). Nucleolin, which binds G4s in the c-myc and VEGF gene promoter regions (81), binds different c-myc GR isomers with different affinities (22). Similarly, it has been reported that different helicases are active on different G4 folds (82). Nevertheless, the ability of G4s to influence transcription, translation and replication simply by folding suggests that, for the most part, a reaction pathway leading to any member of the folded conformational ensemble contributes to the activity of a functional G4.

The relationships between G4 sequence, folding kinetics and biological function are still in the very early stages of being uncovered. Many of the relevant processes are highly complex and orchestrated through the coordinated activity of diverse molecular machines. Furthermore, G4 stability is highly sensitive to the concentrations of K⁺ and Na⁺ ions, molecular crowding, and mechanical stress (e.g. helical over- or under-winding) (83–85) and folding rates are likely to be similarly affected (86). This study was performed on short, homogeneous oligonucleotides, at a concentration of K⁺ lower than that found intracellularly (2 mM versus ∼140 mM), and in the absence of crowding agents, so the absolute rates of folding are different (and likely much slower) than those occurring in vivo. Nevertheless, the principle of folding acceleration by parallel reaction pathways applies universally, since the rates of all pathways likely scale similarly as solution conditions vary, as we have shown in Supplementary Figure S16. The combination of mutagenesis, TH, and global fitting that we have developed provides a rapid and inexpensive of way of mapping folding landscapes with parallel pathways, and requires only that folding occurs slowly enough to produce thermal hysteresis and that individual folded isomers can be trapped with nucleotide substitutions. Parallel G4 folding pathways associated with GR isomerization are likely common in nature, can be easily identified by sequence analysis, and lend themselves to being characterized by this approach. These techniques thus provide an avenue toward a better understanding of the complex dynamics underlying G4 function.

DATA AVAILABILITY

Experimental data and computer programs for performing all data analyses described herein are available from the corresponding author upon request.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Natural Sciences and Engineering Research Council of Canada (NSERC) [327028-09]. Funding for open access charge: Natural Sciences and Engineering Research Council of Canada (NSERC) [327028-09].

Conflict of interest statement. None declared.