SCHISTOX: An individual based model for the epidemiology and control of schistosomiasis

Abstract

A stochastic individual based model, SCHISTOX, has been developed for the study of schistosome transmission dynamics and the impact of control by mass drug administration. More novel aspects that can be investigated include individual level adherence and access to treatment, multiple communities, human sex population dynamics, and implementation of a potential vaccine. Many of the model parameters have been estimated within previous studies and have been shown to vary between communities, such as the age-specific contact rates governing the age profiles of infection. However, uncertainty remains as there are wide ranges for certain parameter values and a few remain relatively unknown. We analyse the model dynamics by parameterizing it with published parameter values. We also discuss the development of SCHISTOX in the form of a publicly available open-source GitHub repository. The next key development stage involves validating the model by calibrating to epidemiological data.

1. Introduction

Schistosomiasis is a parasitic disease caused by trematode blood flukes of the genus Schistosoma. It is currently endemic in 52 countries with over 290 million people requiring treatment in 2018 (WHO, 2020a). The target for schistosomiasis has been recently drafted as elimination as a public health problem in the 2030 roadmap for neglected tropical diseases (NTDs) by the World Health Organization (WHO) (WHO, 2020b). Although morbidity and mortality as a result of schistosomiasis has declined over the years, effective control of schistosomiasis remains a challenge for populations living in endemic areas of the tropical and subtropical regions of the world (Verjee, 2020). Two of the major species found in Africa are Schistosoma mansoni (intestinal) and S. haematobium (urogenital).

An important element of the transmission of schistosomiasis is human contact with cercariae-infested bodies of water. The life cycle requires freshwater in which the eggs excreted from infected humans will hatch into miracidia. The miracidia penetrate suitable snail hosts where they mature into cercariae. The cercariae are shed by their snail host and penetrate the human skin where they develop inside the body to adult worms. Adult worms live in couples, pairing with the opposite sex, copulating and ovipositing which starts the whole cycle again (Allen & Victory, 2003 ; LoVerde, 2019, pp. 45–70).

In addition to the contamination of water by human faeces or urine (depending on the species of schistosome), the production of cercariae requires the presence of suitable snail hosts. As such water from safe sources will likely be schistosome free and reduce the chances of exposure (Grimes et al., 2015). Additionally, good sanitation and hygiene have been shown to be associated with lower odds of infection with S. mansoni and S. haematobium (Freeman et al., 2017). However, more data are needed to determine the impact of improved water, sanitation and hygiene (WASH) measures on schistosomiasis control.

The main approach applied to control schistosomiasis is mass drug administration (MDA) with the anthelmintic drug, praziquantel. This aims to lessen the morbidity and mortality due to infection and to prevent new infection by limiting transmission through reduction of the overall prevalence in the population (Li, Gurarie, Lo, Zhu, & King, 2019). MDA generally leads to a reduction of schistosome worms in the human host, which in turn reduces the quantity of schistosome eggs excreted and ultimately reduces the level of contamination in the environment and infection of the snail population. School aged children (SAC; 5–14 years) typically have a higher likelihood of being infected with Schistosoma parasites than other age groups mainly as a result of age-related water contact activities. Therefore, treatment is usually focused on SAC to minimise morbidity in this important stage of development with delivery through school-based programmes. Treatment of at-risk adults is also important and recommended by WHO, particularly in higher prevalence settings (WHO, 2006). Infected individuals that are not covered by MDA may still spread the infection (King, 2009). Hence, in settings with high adult burdens of infection or low school enrolment levels, community-wide treatment can be more effective for achieving elimination as a public health problem (Toor et al., 2019).

Studies of the transmission dynamics of the Schistosoma infections date as far back as 1965 when the first mathematical model of schistosome epidemiology was developed by George Macdonald (Macdonald, 1965). His model, which was based on differential equations, describes the evolution of the mean worm burden in the human host whilst accounting for the dioecious nature of the schistosome worms. Many different models have been published since then, using more advanced mathematical approaches and accounting for more complexities known to be present in real life, as outlined in a recent extensive review (Anderson, Turner, Farrell, & Truscott, 2016). Individual based models (IBMs) of schistosomiasis transmission evolved from differential equation models, capturing several heterogeneous factors such as variations in local demographics and exposure patterns which contribute to the persistence of schistosomiasis (Wang & Spear, 2015). These models track every individual in the population and their interaction with the environment.

Schistosomiasis IBMs are important as they can be used to inform policymakers and programme managers on priority questions, such as recommendations for treatment guidelines and surveillance criteria for detecting elimination. Several IBMs of schistosome infection exist in the literature (Collyer et al., 2019, Hu et al., 2010, Kura, Truscott, Toor, & Anderson, 2019, Vlas et al., 1996, Wang and Spear, 2015), though they are not readily available for public use. As such, there is a need for an individual based framework for schistosomiasis that is publicly accessible.

In this paper, we describe the development of an open source individual based model, SCHISTOX, for the dynamics of infection, transmission and control of schistosomiasis. The model comprises the life history of the Schistosoma parasite, its transmission and the impact of control. The effects of MDA control strategies on the burden of infection can be evaluated, thereby allowing for model-based predictions on control strategies being implemented and recommendations for optimal treatment strategies. The model is designed such that it can be parameterised for either S. mansoni or S. haematobium.

2. Methods

2.1. Model structure and parameters

Models of schitosomiasis transmission typically include the different aspects of the life cycle of schistosomes to different degrees of detail depending on the questions the model seeks to explore (supplementary table S1). The factors included within SCHISTOX can be grouped into four parts: human population, parasite population (the two larval stages of the schistosome parasite: miracidia and cercariae), transmission and control. Briefly, humans uptake cercariae from the environment, which become worms within the host, leading to excretion of eggs which become miracidia larvae in the environment. The miracidia then transitions through the intermediate snail host resulting in cercariae (schematic of the model shown in Fig. 1). It is implemented in a synchronous stochastic simulation. Details on the simulation approach are given below, but first we describe the biological processes and provide an event table (Table 1).

Fig. 1.

Schematic representation of the structure of the model.

Table 1.

Events in SCHISTOX simulation.

Event	Probability	Description
Birth of individuals	$Bin(N,b)$	The birth rate is set per 1000 individuals, and at each time point, the number of births is randomly selected from a binomial distribution with population size $\left(N\right)$ and birth rate ($b)$.
Death of an individual	Time of death is pre-determined for each individual.	Time of death is set at birth and is dependent on death rates per 1000 in each age bracket.
Egg production	$E~NegBin(\lambda W_p\exp \left(-z{W}_F\right),r)$	Number of eggs in individuals $\left(E\right)$ follow a negative binomial distribution with mean. It depends on the maximum fecundity $\left(\lambda \right)$, worm pairs $\left(W_P\right)$, number of female worms $\left(W_F\right)$ , exponential decay constant $\left(z\right)$, and aggregation parameter for egg production (r).
Worm maturity	$\frac{t_S{W}_S}{L_W\ast 365}$	$W_S$ is the worm stage,$\left(t_S\right)$ is the time step and $\left(L_W\right)$ is the average lifespan of the worms.
Miracidia production	$\frac{{\beta }_{age}E}{\text{max}\left({\beta }_{age}\right)}$	Eggs from each individual ($E)$ will be released into the environment relative to the maximum age dependent contact rate $\text{max}\left({\beta }_{age}\right)$.
Cercarial maturity	$\mu$	Number of days for miracidia to mature into cercarcia (life expectancy in the intermediate snail host used as a proxy).
Uptake of cercariae	$C~Poisson\left(\frac{t_S\beta {\beta }_{age}Py}{N}\right)$	Depends on overall contact rate $\left(\beta \right)$, age dependent contact rate $\left({\beta }_{age}\right)$ , individual predisposition $\left(P\right)$ and the available number cercariae in the environment $\left(y\right)$. It is density dependent as otherwise if the population grows, then the relative rate of uptake increases proportional to population size.
Intervention implementation (MDA or vaccination)	Coverage levels, frequency and timing of intervention is pre-set.

There are published values for many of the SCHISTOX input parameters (Table 2). However, some of these have wide ranges and a few have limited information. Certain parameter values, such as the age dependent contact rates, will vary for different settings. Currently in the model, all these values can be explicitly specified. However, these would need to be calibrated to epidemiological data to provide more robust estimates.

Table 2.

Parameter values from some published studies have been outlined, some of these would vary from one population to another and a few would need to be estimated from epidemiological data as there is limited information about them.

Parameter	Values/ranges	Source
Maximum fecundity $\left(\lambda \right)$	S. mansoni:$\left(0.05-0.34\right)\text{eggs}/\text{worm pair}$ S. haematobium:$5.2\text{ eggs}/\text{worm}/10\text{ml specimen}$	(Anderson & May 1982; de Vlas, Nagelkerke, & Habbema, 1993; De Vlas, Van Oortmarssen, Habbema, Gryseels, & Polderman, 1992; Truscott et al., 2017)
Aggregation parameter $\left(\alpha \right)$	$0.04-0.24$	( Anderson & May 1982; Anderson, Turner, Farrell, & Truscott, 2016; Chan et al., 1995; Toor et al., 2019)
Density dependent fecundity $\left(z\right)$	S. mansoni$0.0007$/female worm S. haematobium$0.0006$/female worm	(Anderson & May 1982; Anderson, Turner, Farrell, & Truscott, 2016; Turner et al., 2017)
Mean adult worm life span $\left(L_W\right)$	S. mansoni:$(2.7-10.5)$years S. haematobium:$\left(3-5\right)$years	(Anderson & May 1985; Anderson & May, 1991; Sturrock & Butterworth, 1995)
Drug efficacy	S. mansoni:$(79-92.5)\%$ S. haematobium:$(63-100)\%$	(Kihara et al., 2007, Utzinger et al., 2000) (Ojurongbe et al., 2014; Tchuem Tchuenté et al., 2004, Utzinger et al., 2000)
Mean parasite life expectancy in snail host $(\mu )$	S. mansoni in Biomphalaria glabarata$\left(7-42\right)\text{days}$ S. haematobium in Bulinus globusus$(14-28)\text{days}$	(Anderson & May, 1991)
Egg production aggregation parameter (r)	0 - 0.1	(Gurarie, King, Yoon, & Li, 2016)
Contact rate $\left(\beta \right)$	Varies according to study population	–
Age dependent contact rates $\left({\beta }_{age}\right)$	Varies according to study population	–
Number of worms, miracidia and cercaria	Relatively unknown	–
Proportion of miracidia which become cercariae	Relatively unknown.	–
Proportion of cercariae that survive each time step	Relatively unknown.	–

2.1.1. Human population

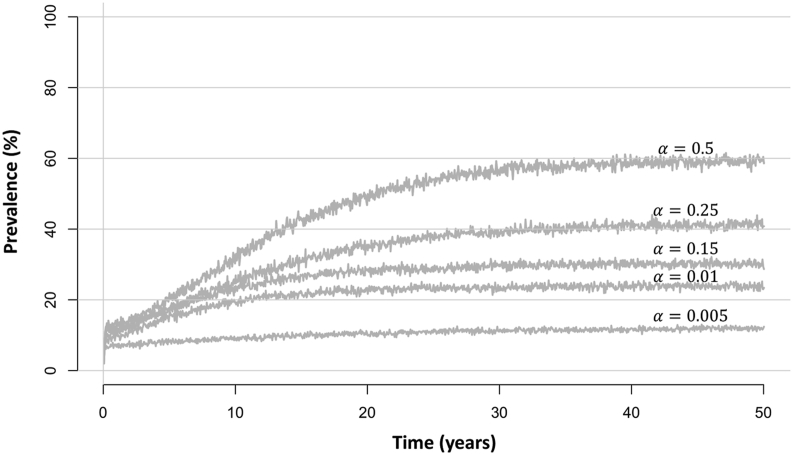
The dynamics of the human population are determined by its birth and death rates. We assume that some individuals are more predisposed to uptaking larvae, with individuals randomly assigned a level of predisposition, $P$ , from a gamma distribution with shape $\alpha$ and scale $1/\alpha$ at birth (where $\alpha$ is the aggregation parameter). The aggregation parameter varies inversely with the degree of parasite aggregation in the population. Therefore, a large $\alpha$ value will result in all people having the same predisposition hence picking up approximately the same number of larvae (dependent on their age). With a low value, the level of aggregation will be large, and hence a few individuals will pick up high numbers of larvae, whilst many individuals will pick up very few or no larvae. In scenarios with lower prevalence, $\alpha$ also tends to be smaller (corresponding to a higher level of aggregation) as a the infection is concentrated in a few individuals with a high number of worms (Fig. 2).

Fig. 2.

Plots of equilibrium levels of total population prevalence using different values for the aggregation parameter $\left(\alpha \right)$. The simulation was run using N = 1000, ${\beta }_{age}$= (0.032, 0.61, 1, 0.06) for 0–5 year olds, 5–10 year olds, 10–16 year olds and 16+ year olds, respectively (corresponding to a moderate adult burden of infection setting) (Turner et al., 2017), $\beta =0.065$, $\alpha =$0.24 and $L_W=5.7$years.

Exposure to infection depends on an individual’s risk and their age. The uptake of cercariae occurs at a rate which is age dependent, with the rate generally highest in SAC. Specific age profiles of infection (patterns of contact rates by age) can be considered by specifying the age parameter values, which describe the relationship between the level of contact in non-SAC age groups (i.e. infants, pre-SAC, SAC and adults) relative to SAC. As the age profile of infection is setting specific (Fig. 3), the ${\beta }_{age}$ values will vary for different settings.

Fig. 3.

Observed age intensity profiles of infection for S. mansoni and S. haematobium showing Kenyan data from Iietune village (Sturrock & Butterworth, 1995), Matithini village (Sturrock & Butterworth, 1995), Katheka village (King et al., 2003), and 12 villages in the Msambweni region of Coastal Kenya (Gurarie et al., 2016). Figure adapted from (Turner et al., 2020).

As individuals may have varying levels of adherence and access to intervention programmes (Adriko et al., 2018; Inobaya et al., 2018), these aspects can be considered within the model. Adherence refers to whether an individual who is given an intervention will actually adhere to the treatment. On the other hand, access to treatment describes whether an individual is covered by MDA, as individuals in hard-to-reach areas may be missed.

When an individual is “born”, their age of death (based on the probability of death within each age group of the population) and predisposition is chosen, along with their adherence and access to intervention, all of which are fixed for the remainder of their life in the population. At each time step any individuals older than their age of death are removed from the population.

2.1.2. Parasite population

To generate erlang distributed worm lifespans, the worms within a human host are split into a specified number of stages, $(W_S=\mathrm{1,2},\dots )$, and are aged through all these stages before they die. For example, if the number of stages is set to 1, then the first step of maturity would be death. The worms are assumed to age through each of the stages at the same rate with $L_W$ denoting the mean adult worm lifespan. Hence, the probability of aging out of each worm stage at each step forward in time is given by $\frac{t_S{W}_S}{L_W\ast 365}$ where $t_S$ is the time step. The number of worms aging out of each stage follows a binomial distribution, $B(n,p)$, with $n$ denoting the number of worms currently in that stage and $p=\frac{t_S{W}_S}{L_W\ast 365}$.

The worms are assumed to reproduce monogamously (Beltran & Boissier, 2008; Steinauer, 2009), hence the total number of potential worm pairs within an individual is simply the minimum of the number of female and male worm pairs, $W_P$. The expected number of eggs, $E$, is assumed to be density dependent, where an increase in the number of worms does not lead to a linear increase in the expected number of eggs, due to overcrowding (Medley & Anderson, 1985). The expected number of eggs is defined as

$$E~NegBin(\lambda W_p\exp \left(-z{W}_F\right),r)$$

where $\lambda$is the maximum fecundity of the female worms, $z$ is the exponential decay and $W_F$ is the number of female worms. The number of eggs produced in humans is assumed to follow a negative binomial distribution with this mean and aggregation assumed to be $r$.

We do not explicitly model the intermediate snail host but consider a single shared environmental reservoir of infection which includes the miracidial and cercarial stages. For miracidia production, we assume that each individual can contribute up to the number of eggs that their worms have produced, which is then scaled relative to the age dependent contact rate of each individual. For example, if an individual has 40 eggs, and belongs to the highest contact age group, then they will produce 40 miracidia. If they are in an age group with half the level of age dependent contact, then they will produce 20 miracidia. The number of infective cercariae in the environment, $y$, is updated based on the number of miracidia which are shed in the environment $\mu$days earlier. The parameter $\mu$ is used as a proxy for the lifespan of the parasite in the intermediate snail host.

As free-living miracidia and cercariae are relatively short-lived (ranging from 4 to 20 h ( Anderson, Turner, Farrell, & Truscott, 2016), these stages are not explicitly included within the model (i.e. we assume these are uptaken by their host immediately or do not survive). The initial number of worms, miracidia and cercariae can be specified in the model. Although it is unlikely to know what these initial numbers are, they do not affect the equilibrium level of infection. However, the smaller these initial numbers, the longer the model takes to reach equilibrium.

2.1.3. Transmission

Humans become infected when exposed to water bodies infested with cercariae. The number of cercariae uptaken by an individual each time step, $C$, is modelled as

$$C~Poisson\left(\frac{t_S\beta {\beta }_{age}Py}{N}\right)$$

where $\beta$ and ${\beta }_{age}$ are the scaling contact rate for every individual in the population and an age dependent contact rate, respectively, and $N$ is the population size. Dividing by $N$ ensures that as the population grows, the rate of uptake of cercariae for everyone does not increase at a proportional rate. When cercariae are uptaken, this is performed for every individual in the population in a random order and each uptaken cercariae is removed from the environmental pool.

2.1.4. Treatment and control

Control of infection is administered through MDA and/or vaccination. This is set to occur at given times in the simulation, hence at each time step we check whether we have reached the specified time for the MDA or vaccination to take place. When we perform MDA or vaccination, the process is very similar. A lower and upper age limit, the coverage level, the timing and frequency for the intervention are specified (Fig. 5). Additionally, as described earlier, everyone in the population has two characteristics: adherence and access, which determine whether they partake in any intervention. Adherence is only applicable for MDA and not vaccination as this is administered by a healthcare individual in a way that cannot be avoided.

Fig. 5.

The impact of annual mass drug administration (MDA) on SAC and adult prevalence for S. mansoni with a moderate adult burden of infection setting (${\beta }_{age}=(0.032,0.61,1,0.06)$for 0–5 year olds, 5–10 year olds, 10–16 year olds and 16+ year olds, respectively (Turner et al., 2017)) with coverage levels of A) 75% SAC and B) 75% SAC and 30% adults. The plot shows the mean prevalence for 100 realizations of the model assuming 100% adherence,$\alpha =0.055$, drug efficacy = 86% and $L_W=5.7$.

To select individuals for an intervention, we firstly identify all the individuals in the specified age bracket who have access to the intervention. Then we narrow this down to only cover the population at the coverage level selected, and then for each person who adheres to the intervention (all individuals in the case of vaccination), we administer the intervention. If there is full adherence and access, then individuals (falling within the specified age group) are selected at random at each round of treatment. Note that if there is an access constraint, the specified level of coverage is not actually achieved, for example, if 100% coverage rate is specified but only 50% of the population have access to the intervention, then only 50% of the population will receive the intervention.

Interventions are assumed to reduce the worm burden in individuals. For MDA, this is a one-time decrease in these burdens, whilst for vaccination, there is lasting protection (for a specified length of time) against rebuilding these burdens, enacted as a reduction in the rate of uptaking larvae.

2.2. Implementation and simulations

Running a simulation of the model starts by creating an initial human population with specified size, age and sex distribution. Human characteristics such as age at death, access and adherence to treatment are chosen at random by the appropriate distributions. The initial number of worms, miracidia and cercariae can also be specified. In a simulation, we step forward by a specified number of days at a time. To ensure that an epidemiological equilibrium is reached, the model is generally run for several decades (Fig. 4).

Fig. 4.

Distribution of worms in the population and prevalence when SCHISTOX is run to equilibrium over 100 years assuming a moderate adult burden of infection setting (${\beta }_{age}=(0.032,0.61,1,0.06)$for 0–5 year olds, 5–10 year olds, 10–16 year olds and 16+ year olds, respectively (Turner et al., 2017)). Here $N=1000,\beta =0.0423,$N = 1000, $\alpha =0.007$ for the moderate transmission setting and $\alpha =0.24$ for the high transmission setting. A) and C) show the probability of having a specified worm burden (with bins 0, 1–5, 6–10, 11–15, …, 96–100, 100+) for the simulation in moderate and high transmission settings, respectively. B) and D) show the prevalence in school-aged children (SAC; 5–14 years old) and adults (15+ years old) over time for moderate and high transmission settings, respectively.

The code is written in Julia programming language but we also provide an R-interface which is available from (https://github.com/mattg3004/SchistoIndividual). To provide a benchmark for performance, to run a single realization of the model with population size $N=1000$ to equilibrium and then implement 10 annual rounds of MDA in a high prevalence setting requires ~ 4.96 seconds to run on a laptop with 1.7 GHz intel core i5 processor and 8 Gb of memory (note: for lower prevalence settings a simulation would run relatively quicker).

The model can be adapted to different transmission settings by varying the input parameters. The aggregation parameter $\alpha$ and contact rates $\beta$ and ${\beta }_{age},$which both affect the uptake rate, can be adjusted to obtain different transmission settings. Computational simulations of SCHISTOX are shown in Fig. 4, Fig. 5. The model output can be presented with several degrees of detail depending on the purpose of the simulation. In its most detailed form, epidemiological information can be obtained for each individual or grouped by sex and/or age.

2.3. Computational specialties of using SCHISTOX

SCHISTOX is publicly available on GitHub with options of being run in julia (https://github.com/mattg3004/Schistoxpkg.jl) or by using the R user-interface (https://github.com/mattg3004/SchistoIndividual). Both Julia and R are free programming languages. Using Julia means the model is quick to run computationally (due to Julia’s combination of multiple-dispatch and just in time compilation) without relying on a lower level language such as C. The added option of the user-friendly R interface allows for the model to be accessible to R-users.

2.4. Model validation and fitting to data

Although there are published estimates for most of the SCHISTOX parameters, some of these parameters have a wide range and vary according to the Schistosoma spp and/or study population (Table 2 and Fig. 3). Important on-going next steps are model validation by fitting to epidemiological data. This requires good longitudinal data on the intensity of infection across all ages from a variety of transmission settings. Two of the parameters, the proportion of cercariae and miracidia uptaken from the environment, have limited information in published data. The impact of varying these parameters on the transmission dynamics can also be investigated to determine their importance.

2.5. Further model aspects for investigation

SCHISTOX has been designed to incorporate several features depending on the question being investigated. The model framework currently allows for implementation of multiple communities, with a shared environmental reservoir of infection. The number of communities is specified by the user alongside the contact rates for each community. Another aspect that can be investigated is gender. The simulations can be set up in such a way that one human sex has a lower or higher predisposition to infection or adherence to treatment. This provides the opportunity to study the effects of gender on schistosomiasis burden (Ayabina et al., 2020).

Aside from MDA programmes, other forms of schistosomiasis control can be implemented in the model. As discussed, the framework allows the implementation of vaccines, with vaccine coverage and effectiveness set up by the user at the start of the simulation. Although SCHISTOX does not explicitly model the snail population, snail control can be implemented via the parameters that govern miracidia and cercariae maturity and uptake in the environment.

3. Discussion

We have presented an individual based modelling framework for the study of schistosomiasis transmission and control. This is not the first individual based model designed for the study of schistosomiasis transmission and control. However, SCHISTOX offers the advantage of being publicly available on github with options of being run in Julia or through the R user-interface. We have analysed its dynamics using published parameter values and shown that SCHISTOX can produce expected disease dynamics and describe the impact of MDA.

Many of the parameters in SCHISTOX are used to describe the characteristics of a specific population and control programme. As such, it can be easily adapted to make predictions in a variety of transmission settings. In the hope that SCHISTOX will contribute to the planning and evaluation of control programmes, model validation and data fitting are currently underway.

To conclude, SCHISTOX is a flexible framework that can be used to investigate the impact of control strategies and to produce model-based recommendations for treatment programmes. Control strategies can be specified in a detailed way as level of adherence and access, coverage, treatment and vaccine effectiveness are specified by the user. Its flexible design and public availability make SCHISTOX a helpful tool to researchers and stakeholders in the control of schistosomiasis.

Funding statement

All authors gratefully acknowledge funding of the NTD Modelling Consortium by the Bill and Melinda Gates Foundation [OPP1184344].

Author contributions

Matthew Graham: Writing - original draft, Conceptualization, Methodology, Software, Investigation, Visualization; Diepreye Ayabina: Writing - review & editing, Conceptualization, Methodology, Visualization; Tim CD Lucas: Writing - review & editing, Conceptualization, Software; Benjamin S Collyer: Methodology and Software; Graham F Medley: Conceptualization; T. Deirdre Hollingsworth: Writing - review & editing, Funding acquisition, Supervision; Jaspreet Toor: Writing - review & editing, Conceptualization, Methodology, Software, Visualization, Supervision.

Declaration of competing interest

We have no conflicts of interest.

Handling Editor: Dr Y. Shao

Appendix A. Supplementary data

The following is the Supplementary data to this article: