The Relation of Lotic Fish and Benthic Macroinvertebrate Condition Indices to Environmental Factors Across the Conterminous USA

Abstract

National and regional ecological assessments are essential for making rational decisions concerning water body conservation and management at those spatial extents. We analyzed data from 4597 samples collected from 3420 different sites across the conterminous USA during the U.S. Environmental Protection Agency’s 2008–2009 and 2013–2014 National Rivers and Streams Assessment. We evaluated the relationship between both fish and macroinvertebrate multimetric index (MMI) condition scores and 38 environmental factors to assess the relative importance of natural versus anthropogenic predictors, contrast site-scale versus watershed-scale predictors, and examine ecoregional and assemblage differences. We found that most of the environmental factors we examined were related to either fish and/or macroinvertebrate MMI scores in some fashion and that the factors involved, and strength of the relationship, varied by ecoregion and between assemblages. Factors more associated with natural conditions were usually less important in explaining MMI scores than factors more directly associated with anthropogenic disturbances. Local site-scale factors explained more variation than watershed-scale factors. Random forest and multiple regression models performed similarly, and the fish MMI-environment relationships were stronger than macroinvertebrate MMI-environment relationships. Among ecoregions, the strongest environmental relationships were observed in the Northern Appalachians and the weakest in the Southern Plains. The fish and macroinvertebrate MMIs were only weakly correlated with each other, and they generally responded more strongly to different groups of variables. These results support the use of multiple assemblages and the sampling of multiple environmental indicators in ecological assessments across large spatial extents.

1. Introduction

Quantitative ecological assessment of all water bodies at continental-scales is an extremely difficult undertaking—despite their importance in making rational and effective environmental policies and management decisions that are relevant to those scales. Historically, nearly all quantitative water body assessments were conducted only at local or basin scales or through assessing aggregations of disparate data from multiple sources (Hughes et al. 2000). However, such limited numbers of local- and basin-scale assessments cannot be accurately extrapolated to entire continents, nations, or large river basins with known confidence intervals. The same is true of aggregating data derived from differing sources, because of substantial differences in sampling methodologies and data collection gaps (Hughes et al. 2000; Heinz 2008; Maas-Hebner et al. 2015). Although several states in the USA have implemented very thorough and quantitative statewide ecological assessments of their surface waters; this is not the rule (Yoder and Barbour 2009). To fill these gaps, federal agencies in the USA have implemented standardized ecological assessments of the condition of streams and rivers nation-wide (USEPA 2016b; Meador et al. 2008; Meador and Carlisle 2009). In Europe, continental-scale ecological assessments have been implemented by calibrating different national approaches (Hering et al. 2004) or by employing standard sampling methods and data analyses (Pont et al. 2006; Schinegger et al. 2016; Grizzetti et al. 2017), but those assessments are constrained in their capability to make robust inferences beyond the set of sampled sites.

Traditional ecological indicators such as total species richness and assemblage composition (e.g., assemblage patterns depicted in ordinations) are imperfect indicators of assemblage condition (Hughes 2019). Total species richness can be a problematic indicator of disturbance because of the tendency of non-native and tolerant fish species to increase because of low levels of anthropogenic disturbance (Hughes et al. 1998; McCormick et al. 2001; Mebane et al. 2003; Lomnicky et al. 2007). Similarly, both fish and macroinvertebrate assemblage richness are very sensitive to sampling effort (Cao et al. 2002; Kanno et al. 2009) and local environmental conditions (Hawkins et al. 2000; Leal et al. 2018; Leitão et al. 2018). Ordinations of assemblage composition, as well as species richness, tend to be driven by natural variation (Vannote et al. 1980; Fausch et al. 2002). Therefore, multimetric indices (MMIs), which are derivations of the original Index of Biotic Integrity (IBI) first developed by Karr (1981), are increasingly being used globally for evaluating assemblage condition (Ruaro and Gubiani 2013; Ruaro et al. 2019; Buss et al. 2015). MMIs have become popular because they incorporate multiple variables deemed important for understanding deterioration in assemblage composition and function into a single index. Many different MMIs have been developed over the years for assessing relatively small areas, but more recently continent-wide MMIs have been developed for assessing assemblage condition for lotic fish (e.g., Esselman et al. 2013), lotic macroinvertebrates (Stoddard et al. 2008), lotic and lentic diatoms (Stevenson et al. 2013; Tang et al. 2016), and wetland vegetation (Magee et al. 2019).

Fish and macroinvertebrate assemblages are most commonly used for assessing stream and river condition (Ruaro and Gubiani 2013; Ruaro et al. 2019), with diatoms a close third. Fish assemblages in streams and rivers offer several unique advantages to assess ecological condition, based on their mobility, longevity, trophic relationships, and socioeconomic importance (Barbour et al. 1999). There are numerous examples of MMIs developed for fish assemblages in smaller streams (e.g., McCormick et al. 2001, Hughes et al. 2004, Bramblett et al. 2005) as well as for larger rivers (e.g., Lyons et al. 2001, Mebane et al. 2003). The taxonomic composition and relative abundance of different taxa that make up the benthic macroinvertebrate assemblage present in a stream have also been used extensively to assess how human activities affect ecological condition (Barbour et al. 1999; Buss et al. 2015). Both fish and macroinvertebrate MMI scores have been related to a wide variety of site-level environmental factors in various parts of the world.

In addition to the effect of local site conditions on assemblage condition, there is a growing recognition of the importance of landscape conditions on surface waters (Allan 2004; Johnson and Host 2010; Hughes et al. 2006, 2019). For example, Wang et al. (2003) reported that watershed variables explained 4% and 11% of the variability in stream fish assemblage characteristics and presence-absence, respectively; but markedly less than that explained by site variables in the Northern Lakes and Forest Ecoregion of Minnesota, Wisconsin, and Michigan. For French rivers, Marzin et al. (2012b) determined that watershed land use explained 5% of fish assemblage composition and 11% of macroinvertebrate assemblage structure, but less than that explained by site characteristics. Macedo et al. (2014) found that watershed land use explained 10% and 28% of the variance in fish and macroinvertebrate assemblage richness, respectively, in two Brazilian Cerrado (savanna) hydrologic units, but less than that explained by local-scale site conditions. Terra et al. (2015) determined that watershed land use explained 2–5% of fish assemblage functional and taxonomic variability, respectively, in an Atlantic Forest basin, but less than that explained by local-scale site variables. Studying Brazilian Amazon streams, Leal et al. (2018) found that watershed land use explained 2–5% of fish species abundance and functional guild abundances across three different river basins, and less than that explained by instream or riparian predictors. In a study of fish assemblage richness in four Cerrado hydrologic units, Pompeu et al. (2019) determined that land use explained 0–14% of fish assemblage structure as measured by Bray-Curtis similarity. Through use of structural equation modeling, Leitão et al. (2018) found that watershed deforestation explained nearly 30% of fish taxonomic diversity and evenness and functional originality and identity in one Brazilian Amazon basin, but not in another. Unlike the other studies, watershed conditions had greater or comparable effects on fish assemblages than local-scale site conditions. Clearly, the relative importance of watershed land use on fish and macroinvertebrate assemblage responses varies regionally and with the response indicator, statistical analyses employed, and range of land use disturbance evaluated (Wang et al. 2006).

Because of the difficulties and expense of conducting large-scale surveys, there have been many more data-driven studies across small areas than continental extents. To address this shortcoming, the EPA’s National Aquatic Resource Surveys (NARS) began in 2004 and were designed to estimate the condition of surface waters throughout the USA. A large number (~1000) of randomly selected lakes, streams, rivers, wetlands or near coastal sites are visited each year during a defined index period (e.g., summer baseflow for streams/rivers). Each of the five water body types are visited once every 5 years. For logistical reasons, stream and river sampling were combined into one survey (the National Rivers and Streams Assessment or NRSA) and done over a 2-year period, every 5 years. At each site, fish and macroinvertebrate assemblages, water quality, and physical habitat data are collected during a 1-day sampling visit. National MMI scores have been developed for both macroinvertebrates (Stoddard et al. 2008) and fish (USEPA 2016a). MMI scores have also been converted to good/fair/poor condition classes for both fish and macroinvertebrates (USEPA 2016a). Thus, the NRSA data provide a unique opportunity to investigate the relationship between MMI scores and environmental factors at a continental scale through use of consistently collected data.

In this study, we had two objectives. First, we sought to compare and contrast the strength of major environmental predictors on lotic fish and macroinvertebrate MMI scores regionally and nationally. Second, we wanted to compare and contrast major site-scale stressors and watershed-scale stressors associated with lotic fish and macroinvertebrate MMI scores in terms of predicting poor versus good assemblage condition class at regional and national scales. Based on previous publications, we hypothesized that (1) natural predictors would be more important than anthropogenic predictors at the scales at which we were evaluating, (2) that site-scale predictors would explain more variation than watershed-scale predictors, and (3) that key stressors would vary by region and assemblage type.

2. Methods

2.1. Study Design

Field crews for the National Rivers and Streams Assessment (NRSA) made 2,309 sample visits during the summers of 2008 and 2009, and 2,288 sampling visits during the summers of 2013 and 2014 across the conterminous USA. (Figure 1). The NRSA used a probability-based design to select the sites (Stevens and Olsen 2004; Olsen and Peck 2008; USEPA 2016a) with a target population of all streams and rivers with flowing water during the June-September index period. Sites were selected from the National Hydrography Dataset (USGS 2013), which generally reflects the blue-line network at the 1:100,000 map scale. The NRSA is representative of a target population of 1,231,000 km of lotic systems ranging from the Mississippi River to headwater streams. The design was spatially balanced and stratified by state, ecoregion, and stream order to even out the sample site distribution across areas and stream sizes (Table 1; Figure 1). Within each year, approximately 10% of the sites were randomly selected for a second visit to assess within-year variability. In addition, nearly 40% of the sites sampled in 2008–2009 were resampled in 2013–2014 to assess between-year variability and estimate change in ecological condition. Lastly, in addition to the probability-selected sites, 497 sites that were hand-picked by regional experts using best professional judgment were sampled to increase the number of potentially least-disturbed reference sites (USEPA 2009). At each one-day site visit, field crews collected data on fish and benthic macroinvertebrate assemblages along with measurements of water chemistry and physical habitat.

Figure 1.

Locations of the sites sampled in 2008–1014 and the nine study ecoregions.

Table 1.

Number of unique sample sites in each ecoregion with fish and macroinvertebrate (Macr) MMI scores and the ecoregional Pearson correlation coefficient between the macroinvertebrate and fish MMI scores. The number of revisit sites used as validation sites are given in parentheses.

Ecoregion	Code	Fish Sites	Macr Sites	Correlation
Coastal Plain	CPL	433 (127)	484 (150)	0.383
Northern Appalachians	NAP	369 (141)	392 (148)	0.535
Southern Appalachians	SAP	449 (157)	494 (183)	0.385
Upper Midwest	UMW	261 (84)	284 (97)	0.317
Temperate Plains	TPL	397 (127)	421 (134)	0.321
Northern Plains	NPL	254 (69)	288 (96)	0.459
Southern Plains	SPL	225 (68)	266 (89)	0.263
Xeric West	XER	245 (67)	339 (111)	0.350
Western Mountains	WMT	299 (90)	434 (141)	0.256
Total NRSA 2008–2014	ALL	2932 (930)	3402 (1149)	0.328

2.2. Fish Data

Fish were collected as described in detail in USEPA (2009, 2013a, b). Briefly, a sample site was established around the randomly chosen sample point of sufficient extent to characterize the fish assemblage within the site (Reynolds et al. 2003; Hughes and Peck 2008). Nearly all the sites were sampled by backpack or boat electrofishing; 2% of the sites were sampled with seines because of very high conductivity water. In wadeable sites <13 m wide, a reach length equal to 40 channel widths, or a minimum of 150 m for headwater streams, was sampled. For wadeable sites >13 m wide, and boatable sites, the minimum reach length sampled was the longer of 500 m or 20 channel widths. In large wadeable and boatable sites, sampling continued beyond the minimum reach length until 500 individuals were collected or a reach length equal to 40 channel widths was sampled. Fish were tallied and identified at the site, then released alive unless used for fish tissue analyses or vouchers (USEPA 2012). Taxonomic names were based primarily on those accepted by the American Fisheries Society (Nelson et al. 2004, Page et al. 2013).

For developing fish assemblage metrics, fish species autecologies were based on published information (McCormick et al. 2001; Goldstein and Meador 2004; Whittier et al. 2007; Frimpong and Angermeier 2009). Traits included habitat guilds (lotic habitat and temperature regime), trophic guilds, reproductive guilds (lithophils), migration strategies, and relative tolerance to anthropogenic disturbance. The NRSA determined whether each species was native or non-native to the basin in which it was collected using distribution maps from NatureServe (http://www.natureserve.org), the USGS Nonindigenous Species Database (http://nas.er.usgs.gov), Page and Burr (2011) or relevant state fish books.

2.3. Macroinvertebrate data

Macroinvertebrates were collected as described in detail in USEPA (2009, 2013a, b) and Hughes and Peck (2008). As for fish, sites were 20 to 40 channel widths long, or a minimum of 150 m for headwater streams. Eleven subsamples were taken in a systematic zig-zag pattern at each of 11 equidistant transects through use of a D-frame kick net (500-um mesh, 0.09 m² area). For wadeable streams, samples were collected in a left, center, right alternating order. At boatable sites, samples were collected at alternating left and right bank locations from the wadeable margins of the river. The 11 subsamples were combined, preserved in ethanol, and shipped to the laboratory, where a fixed laboratory count of 500 individuals were identified to the lowest possible taxon through use of multiple local, regional, and national keys (USEPA 2012). The 500 individual count goal in the laboratory was not always achieved so the samples were rarified to a fixed 300 count for data analysis to ensure count consistency across all samples. Taxa autecological information for calculating assemblage metrics was based on Merritt and Cummins (1996), Barbour et al. (1999), Klemm et al. (2003), and Carlisle et al. (2007).

2.4. Environmental data

We analyzed 38 environmental variables for their relationship to both fish and macroinvertebrate MMI scores (Table 2). For water quality variables, one water grab sample was collected from the randomly selected point in the middle of the site for wadeable streams, and at the downstream end of the site for boatable rivers (USEPA 2009). Samples were shipped by overnight courier to a central analytical laboratory except for a few states that used their own state laboratories. The water quality variables (Table 2) were analyzed in the lab using meters to measure pH and conductivity. Sulfate and chloride concentrations were measured by ion chromatography, total phosphorus and total nitrogen were measured by acid persulfate digestion and colorimetry, dissolved organic carbon (DOC) was measured using a carbon analyzer, and turbidity was measured with a nephelometer. Lab methodologies are detailed in USEPA (2012).

Table 2.

Variables used to predict MMI scores and their code. Variables are ordered by class used for data interpretation.

Variable (units)	Code	Variable (units)	Code
Water Quality		Watershed Land Use
Total Nitrogen (ug/L)	TN*	Agriculture (%)	AGR_WS
Total Phosphorus (ug/L)	TP*	Developed Land (%)	DEVL_WS
Conductivity (μS)	COND*	Wetlands (%)	WETL_WS
Dissolved Organic Carbon (mg/L)	DOC*	Population Density (#/km2)	POPDEN*
Chloride (μeq/L)	CL*	Road Density	ROADDEN*
Sulfate (μeq/L)	SO4*	Dam Disturbance Index	DAM*
Turbidity (NTU)	TURB*
pH	PH	Climate
		Mean Precipitation (cm/yr)	PRECIP*
Physical Habitat Condition		Mean Runoff (cm/yr)	RUNOFF*
Riparian Cover Index	RIPCOV*	Maximum Temperature (°C)	TEMPMAX
Natural Fish Cover (% area)	FISHCOV*	Minimum Temperature (°C)	TEMPMIN
Fast Water Habitat (% length)	FASTPCT
Pool Habitat (% length)	POOLPCT	Geophysical
Riparian Disturbance Index	RIP_DIST	Latitude (degrees)	LAT
Agricultural Riparian Disturb.	RIP_AGR	Longitude (degrees)	LON
Non-Agricultural Riparian Disturb.	RIP_NOAG	Site Elevation (m)	ELEV*
		Watershed Area (km2)	WSAREA*
Substrate		Mean Thalweg Depth (cm)	DEPTH*
Fine Substrate (% area)	FINES	Mean Wetted Width (m)	WIDTH*
Sand+Fine Substrate (% area)	SANDFINE	Channel Slope (%)	SLOPE*
Geometric Mean Diameter (mm)	SUBSIZE	Soil Erodibility Factor	ERODE
Relative Bed Stability Index	RBS	Boatable or Wadeable	LOTIC

^*Log₁₀(x+1) transformed for data analysis, except for SLOPE (Log₁₀(x+0.001), and DAM, RIPCOV, and FISHCOV (Log₁₀(x+0.1).

Physical habitat condition and substrate variables were collected as described in Hughes and Peck (2008), USEPA (2009, 2013a, b), and Kaufmann et al. (1999). Multiple measurements were made at the 11 evenly-spaced transects where macroinvertebrates were sampled. Woody riparian vegetation cover, anthropogenic disturbances, fish cover, substrate composition, and wetted width and depth data were collected at each transect through use of standardized field forms based on consistent disturbance and cover checklists. Anthropogenic disturbances on the checklist included stresses from agriculture, residences, recreation, industry, logging, mining, roads and other human activities. Between transects, crews determined slope and collected depth, width, substrate and habitat unit data at systematic intervals. Field data were converted into physical habitat metrics (Table 2) following the methodology described in Kaufmann et al. (1999). In brief, fish cover is calculated from transect summaries as percent of wetted surface area. Pool habitat and fast water habitat are percents of site length. Riparian cover and disturbance variables are indices summarized from standardized measurements at both banks at each transect. Substrate data are based on pebble counts. Percent substrate variables are a percent of wetted surface area and substrate size is the geometric mean diameter of the pebble counts. Relative bed stability is calculated as the difference between observed and expected geometric mean substrate size where expected size is calculated from site stream power and shear stress (Kaufmann et al. 2008).

Geophysical, climate, and land use variables (Table 2) were based on either the sample point or the entire watershed. Latitude, longitude, and elevation data are for the sample point. Mean wetted width, thalweg depth, and channel slope were averages of multiple site measurements in the field as described in Kaufmann et al. (1999). The remaining variables were watershed averages. Watershed climate, soils, and anthropogenic stressor data (2011 era coverages) were taken from StreamCat (Hill et al. 2016). StreamCat contains metrics for over 250 environmental attributes, the chosen ones listed in Table 2 are those that we thought most relevant to stream condition. NRSA uses nine aggregate ecoregions for data assessment and analysis (see Figure 1). The nine NRSA ecoregions are aggregations of Omernik and Griffith (2014) level-III ecoregions, aggregated as described in Herlihy et al. (2008).

2.5. Data Analyses

2.5.1. Fish & macroinvertebrate MMI development

In NRSA, fish and benthic macroinvertebrate condition are assessed through use of MMIs derived from summing the scores of multiple assemblage metrics. Separate MMIs were developed for each of the nine aggregated ecoregions (Figure 1) for both macroinvertebrate and fish assemblages. The metrics and scoring involved with the MMIs were based on screening hundreds of candidate metrics by evaluating their ranges, determining their repeatability, calibrating for natural variation, assessing their sensitivity to anthropogenic disturbance, and determining their redundancy (Hughes et al. 1998; McCormick et al. 2001; Klemm et al. 2003; Stoddard et al. 2008).

The metrics and their scoring for the NRSA macroinvertebrate and fish MMIs are described in detail in USEPA (2016a). Each macroinvertebrate MMI consists of six metrics each chosen as the optimal one to assess one of the six metric classes: richness, taxonomic composition, tolerance, feeding group, habit, and diversity. Candidate fish MMI metrics were selected as the optimal one to represent each of eight metric classes: non-native, taxonomic composition, habitat guild, reproductive guild, migratory strategy, richness, tolerance to disturbance, and trophic guild. Because fish richness is strongly related to stream size, metrics were adjusted for watershed area if the R² value of the metric-area relationship at least-disturbed reference sites was > 0.10.

For both macroinvertebrate and fish assemblages, the selected metrics were each scored from 0 to 10 by linear interpolation between floor and ceiling values set for each metric (USEPA 2016a). The eight fish metrics or six macroinvertebrate metric 0–10 scores were summed and multiplied by (10/number of metrics) to yield an MMI score of 0–100. Note that the metrics in the MMIs and their scoring differ among ecoregions. Thus, specific numeric scores do not mean the same thing across ecoregions.

2.5.2. Statistical analyses

We assessed fish and macroinvertebrate MMI scores in each of the 9 ecoregions versus the 38 environmental predictor variables (Table 2) through use of multiple linear regression and random forests. To explore the variables, we made graphical displays (boxplots, histograms), and calculated descriptive statistics and correlations. We purposely did not select any environmental variables that were highly correlated (r ≥ |0.9|) with each other. Percentage variables and MMI scores that ranged from 0–100 were not transformed, nor were the environmental variables that had ranges less than 0–10. The other predictor variables had very skewed distributions and were log transformed as described in Table 2. Note that pH, substrate size, and relative bed stability are inherently logarithmic and were not transformed. To not overweight sites with multiple visits, we only modeled the data from the first visit to each site. The data from site revisits was reserved as a validation dataset. Sites that lacked fish or macroinvertebrates received respective MMI scores of zero with the exception of small watersheds (area < 2 km²) which could be naturally fishless. These sites received no fish MMI scores (missing values). Zero MMI scores were very strong outliers in the MMI distribution so we dropped all MMI=0 sites from the analysis (112 fish and 45 macroinvertebrate samples).

For the multiple regression, we ran a full 38 variable model and then selected a final most parsimonious model by doing an exhaustive search and variable selection based on the lowest Bayesian Information Criteria (BIC) value using the LEAPS package (Lumley and Miller 2009) in R version 3.2.2. We checked model fit with residual plots and graphed the relationship between the observed and fitted data. The amount of variability accounted for in the models was assessed using adjusted R² to account for the varying number of variables included in the different models. The BIC regression model for each ecoregion was also run on the validation data for that ecoregion as a test of model fit.

Random forests are a machine learning method that uses ensembling algorithms to construct multiple decision trees and then average the trees into one model. Each tree is created using a different sample from the original dataset using 2/3 of the cases. The left-out cases are used to get an estimate of the error as the trees are added to the forest. The method does not overfit and there is no need for cross-validation as it is done internally in the process of constructing the final model. We used the library randomForest (R version 3.2.2), which implements Breiman’s random forest algorithm (Liaw and Wiener 2002). We tabulated the percent of variability explained from the random forest models predicting MMI scores for each of the ecoregions and compared them with regression adjusted R² values. Variable importance for each model was calculated by taking the total increase in node purity from splitting on the variable, averaged over all trees measured by the residual sum of squares. To explore model fit and the possibility of bias in both the regression and random forest models we calculated the slopes and correlations of the modeled MMI versus the observed MMI values for all ecoregions in both modeled (first visit) and validation (repeat visit) datasets. The degree of correlation is an indicator of the tightness of fit or variance in model predictions and the deviation of the slope from 1 is an indication of bias.

Lastly, we predicted MMI condition class using logistic regression (Vølstad et al. 2003). As part of NRSA, MMI scores are classified into good, fair, or poor classes based on ecoregion-specific thresholds determined from the percentiles of the MMI scores at the least-disturbed reference sites in each ecoregion (Herlihy et al., 2008; USEPA 2016a). The good-fair threshold was set at the 25^th percentile and the fair-poor threshold at the 5^th percentile. We used stepwise logistic regression to predict poor MMI sites from good MMI sites (fair sites were removed) by using a subset of the environmental variables in Table 2. We used a criterion of p<0.005 for variable entry into the model and a p<0.01 for staying in the model.

Logistic regression coefficients may also be described as an odds ratio (how many times more likely is poor condition given a one unit increase in the predictor variable). To better interpret the results, we selected environmental variables that were more conceptually linked to disturbance (AGR_WS, DEVL_WS, POPDEN, ROADDEN, DAM, FISHCOV, RIPCOV, RIP_DIST, FINES, RBS, ERODE, TN, TP, SO4, CL, and TURB from Table 2). It is also easier to interpret odds ratios if the variables are all roughly on the same scale and have a positive monotonic relationship with disturbance. Therefore, for the logistic regression analysis, we transformed the percentage variables by dividing by 10 so they ranged from 0–10. Road density, damming index, and soil erodibility factor were multiplied by 10 to put them in the 0–10 range. Other log transformed variables were already in the approximate range. Riparian cover and fish cover are negatively related to disturbance, so they were converted to negative numbers to make them positively related. Lastly, an absolute value of relative bed stability was analyzed because deviation from zero is indicative of a departure from expected condition.

3. Results

3.1. Data Distribution

There were 4597 samples from 3420 unique sites in the 2008–09 and 2013–14 NRSA sampling that had either fish or macroinvertebrate data (Table 1). Of this data, 61% were sampled as wadeable streams and the other 39% as boatable rivers. The wadeable versus boatable variable was a categorical variable and only applied to random forest modeling where it was never above 5% importance in any of the models we examined. The distributions of the MMI scores from the first visit to each unique site, what we call the model data, varied widely (Figure 2). The fish MMI scores ranged from 0–96 with a spread between first and third quartiles (Q1-Q3) of 38–63. The macroinvertebrate MMI ranged from 0–100 with a Q1-Q3 of 23–54. Nationally, the fish and macroinvertebrate MMIs were not highly correlated with each other (r=0.33). By ecoregion, the highest correlation of the MMIs was in the Northern Appalachians (r=0.54) and the lowest was in the Western Mountains (r=0.26, Table 1).

Figure 2.

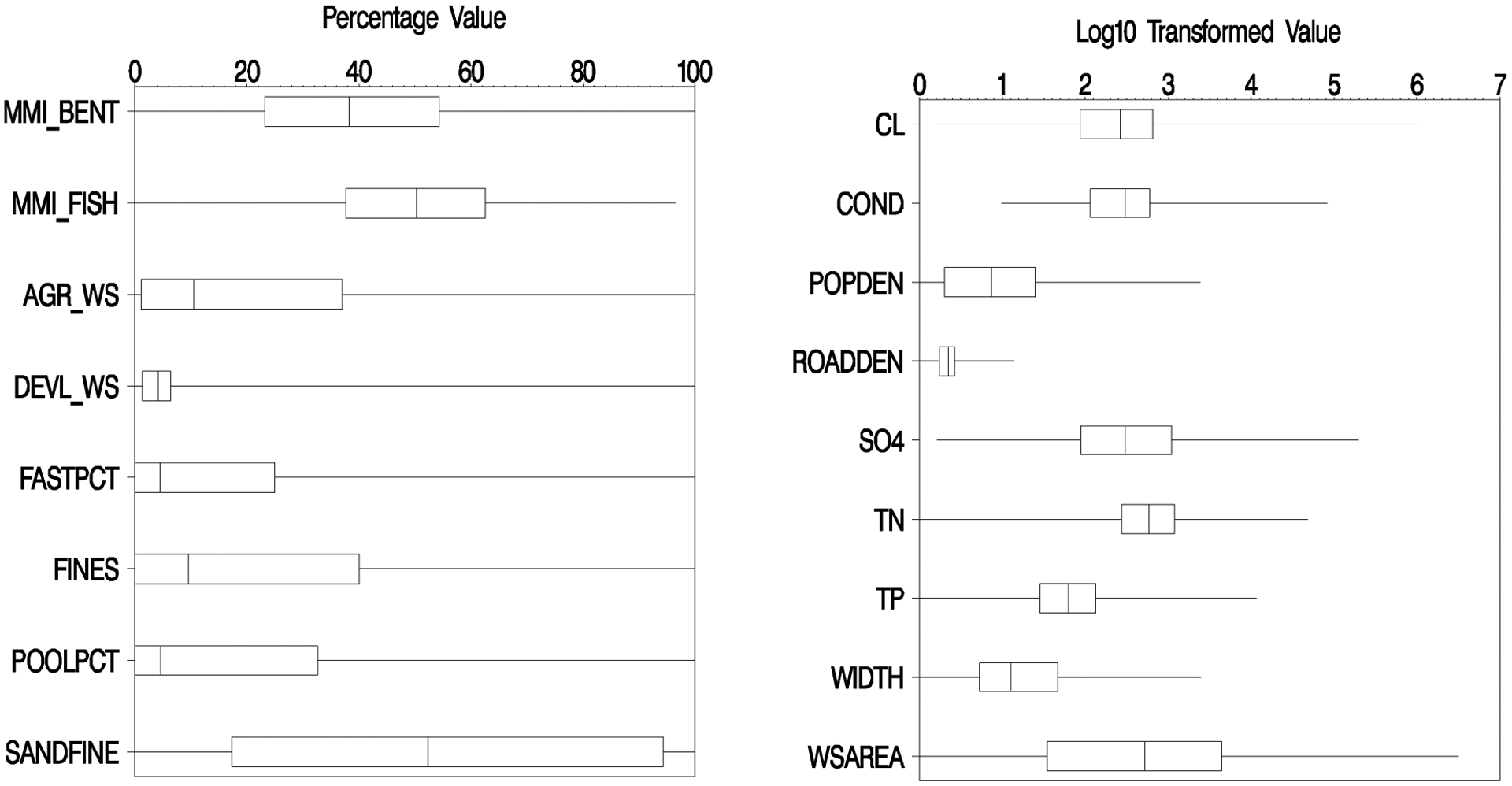
Distribution of selected variables in the first-visit model data for fish and macroinvertebrate MMI scores and percentage-based variables; and log₁₀-transformed variables. Boxes show the interquartile range, the line in the box is the median, and the whiskers show the minimum/maximum values. Full variable names, transforms, and units are given in Table 2.

As one might expect with a continental-scale survey, the range in the environmental data (Table 2) was quite large (Figure 2). Percentage-based data covered the whole 0–100% range. The Q1-Q3 in sand+fine substrate (17–94%) almost covered the entire range of the data. For log₁₀ transformed variables, the range in the data was often 3–6 orders of magnitude. Of the water quality variables, chloride had the largest range, from 1 to 1,000,000 μeq/L (Figure 2). Watershed area had a Q1-Q3 spread of 33–4300 km² with a total range from tiny headwater streams (<1 km² area) to the Mississippi River >3,000,000 km² area). Similarly, wetted width ranged from 0.03–2480 m with a Q1-Q3=4.3–46 m, and thalweg depth (not shown) ranged from 2.5–3910 cm (Q1-Q3=17–82 cm).

We constructed a 37×37 correlation matrix of all the continuous environmental variables listed in Table 2 through use of Pearson correlation coefficients. In general, the variables were not or only weakly correlated with each other (absolute r<0.5). The vast majority of pairs had absolute r<0.3. Only 5 pairs had absolute value of r>0.7, chloride-conductivity, sulfate-conductivity, fine substrate-substrate size, relative bed stability-substrate size, and sand+fine substrate-substrate size, and another 4 pairs had absolute r values between 0.5–0.7 (population density-elevation, population density-longitude, sulfate-pH, sand+fine substrate-fast water habitat).

3.2. Fish MMI-environmental relationships

After removing sites with fish MMI=0 as outliers and sites with incomplete environmental data, there were 2459 sites in the model data that we used to run regression and random forest models to examine the relationship between fish MMI and environmental data (Table 3). Random forest and BIC selection regression models had very similar performance in terms of variance explained (Table 3). Among the 9 ecoregions, 5 had slightly higher variance explained with regression models versus 3 ecoregions with random forest (the Temperate Plains was a virtual tie). The strongest models were seen in the Northern Appalachians (random forest variance explained = 0.72) and the weakest in the Western Mountains (random forest variance explained = 0.34. The root mean square error (RMSE) of the predicted MMI from BIC regression ranged from 7.88 to 11.8 among the ecoregions (Table 3).

Table 3.

Full 38 variable multiple regression model adjusted R², BIC variable selected multiple regression model adjusted R², and random forest (RF) proportion variance explained (Var) for fish and macroinvertebrate (Macr) MMI models by ecoregion. The BIC regression model root mean square errors (RMSE) are also shown.

Eco	Sample Size Fish/Macr	Fish				Macroinvertebrate
		Full	BIC	RF	BIC	Full	BIC	RF	BIC
		R2	R2	Var	RMSE	R2	R2	Var	RMSE
CPL	288/331	0.598	0.563	0.545	8.25	0.396	0.348	0.391	14.8
NAP	352/369	0.704	0.699	0.718	10.5	0.598	0.572	0.558	15.0
SAP	398/436	0.535	0.543	0.566	9.36	0.473	0.457	0.425	13.8
UMW	231/251	0.353	0.320	0.406	11.8	0.392	0.356	0.325	12.7
TPL	315/338	0.614	0.589	0.591	9.93	0.433	0.422	0.403	15.3
NPL	237/273	0.531	0.515	0.490	9.64	0.547	0.543	0.515	14.7
SPL	198/239	0.430	0.441	0.361	7.88	0.262	0.216	0.185	15.3
XER	193/303	0.647	0.615	0.578	11.3	0.429	0.406	0.458	15.0
WMT	247/400	0.427	0.425	0.340	9.94	0.497	0.448	0.500	15.1

Regression and random forest models often identified the same variables or types of variables as being significant or important in the fish MMI model (Table 4). For example, in the Coastal Plain, DOC, fine substrate, watershed agriculture, and watershed area were BIC selected for the regression model and had variable importance > 5% in the random forest model. Total nitrogen was very important in the random forest model but not the regression model whereas total phosphorus was important in the regression model but not the random forest model. There tended to be more variables selected for inclusion into the BIC regression models than the number of variables with >5% importance in the random forest models (Table 4). A variable importance of 5% is somewhat arbitrary, but it was where there was often a major break point in the random forest variable importance plots.

Table 4.

Variables predicting fish MMI scores by ecoregion that were either BIC selected for inclusion in the regression model or had random forest model percent importance >5% (†) or >10% (††). Numeric values are the regression coefficients, variable units and transforms are listed in Table 2, and -- indicates the variable was not selected in the regression.

Variable	CPL	NAP	SAP	UMW	TPL	NPL	SPL	XER	WMT
Water Quality
TN	--††	--	--	--	--	--†	--†	--	--
TP	−5.6	--	--	--	−8.1	--	−5.8†	−6.0	--
COND	--	−6.7	5.6	--	--	--	--	--†	--
DOC	−8.4	−12	−12†	--	−7.7	−13	−9.0†	--	--
CL	--	--†	--	--	8.4	−4.5	--	−5.4††	--
SO4	--	--	−5.4	--	−6.8	--	--	--	--
TURB	--	--	−4.2	--	--	--	--	--	--
Physical Habitat Condition
FISHCOV	--	--	--	--	3.8	--	--	--	5.8
FASTPCT	--	0.23††	0.08†	--	--†	--	--	--	--
POOLPCT	−0.05	--	--	--	--	--	--	--	--
Substrate
FINES	−0.06†	--	−0.08	--	--	--	--	--	--
SANDFINE	--	--	--	--††	−0.16††	--	--	--	−0.16†
SUBSIZE	--	--	--	5.1†	--	--	--	2.9	--†
Watershed Land Use
AGR_WS	−0.12†	--	−0.09	--	--	0.15	--	--	--
DEVL_WS	−0.14	--	--	--	−0.17	--	--	--	--
WETL_WS	--	--	--	--	--	--	1.6	--	--
POPDEN	--	--†	−3.1	--	--	--	−2.3	--	−4.6
DAM	−7.4	--	--†	--	--	--	--	--	--
Climate
PRECIP	41	--	−34	--	--††	--	--	--	--†
RUNOFF	--	--	--	33†	--	--††	--	--	--
TEMPMAX	--	--†	--	--	--	−2.5††	--	--†	--
TEMPMIN	--	−1.4	--	--	--	--	--	--	--
Geophysical
LAT	--	--	--	--	--	--	--	1.9†	--
LON	--	−1.2	0.30	--	--	--†	--	--	0.53†
ELEV	5.3	6.2	8.3†	35	--	--	--	4.1	−6.1†
WSAREA	4.0†	−4.8	−3.2††	--†	−4.6††	5.1	−2.4	−4.5††	--
DEPTH	--	3.6	--	4.3	4.3	--	--	--	--
SLOPE	--	--††	--†	--	--	--	4.9†	--	3.3
Model Intercept	−77.2	125	134	−131	93.0	118	77.5	10.5	35.9

Among the 9 ecoregions, there was a wide variation as to which specific variables were significant in their fish MMI models (Table 4). By variable classes, water quality variables were significant in all ecoregions except the Western Mountains and Upper Midwest. Physical habitat condition had no significant variables in the Northern Plains, Southern Plains, Upper Midwest and Xeric West whereas substrate had no significant variables in the Northern Appalachians, Northern Plains and Southern Plains. Significant geophysical variables were present in all ecoregions (Table 4). It’s hard to compare magnitude of effects with regression coefficients because they are related to variable values; however, random forest variable importance is a good way to compare important variables across ecoregions. Table 4 shows all variables with >5% variable importance, most of the variables were in the 5–10% importance range. Variables with over 10% importance were total nitrogen in the Coastal Plain; chloride in the Xeric West; fast water habitat and stream slope in the Northern Appalachians; watershed area in the Southern Appalachians, Temperate Plains and Xeric West; sand+fine substrate in the Upper Midwest and Temperate Plains; precipitation in the Temperate Plains; and maximum temperature and runoff in the Northern Plains.

3.3. Macroinvertebrate MMI-environmental relationships

As was seen for fish, BIC regression models and random forest models for macroinvertebrate MMI scores gave similar results in terms of model performance (Table 3). The proportion of variance explained was slightly higher for 3 ecoregions for random forest models versus 6 ecoregions for BIC regression models. Variance explained ranged from 0.185 in the Southern Plains for the random forest model to 0.572 for the BIC regression model in the Northern Appalachians. The RMSE of the BIC regression models for the macroinvertebrate MMI ranged from 12.7 to 15.3 among the ecoregions, somewhat higher than observed for predicting the fish MMI (Table 3).

Again, as was seen for fish, the regression and random forest models often identified the same variables or classes of variables as being significant or important in the benthic macroinvertebrate MMI models (Table 5). For example, in the Northern Plains, both random forest and the BIC selection identified DOC, chloride, sand+fine substrate, and maximum temperature as being important. There was also a wide variation among ecoregions as to which specific variables were significant in their respective benthic MMI models. By variable classes, water quality, substrate, and geophysical variables were significant in every region for both model types. No land use variables were significant in the regression models in the Coastal Plain, Northern Appalachians, Southern Plains, and Xeric West ecoregions and no land use variable had a random forest variable importance > 5%. Variables that had over 10% importance in the random forest models included substrate size in the Coastal Plain, Northern Appalachians, Northern Plains and Western Mountains; sand+fine substrate and fast water habitat in the Northern Appalachians; and watershed area in the Temperate Plains (Table 4).

Table 5.

Variables predicting macroinvertebrate MMI scores by ecoregion that were either BIC selected for inclusion in the regression model or had random forest model percent importance >5% (†) or >10% (††). Numeric values are the regression coefficients, variable units and transforms are listed in Table 2, and -- indicates the variable was not selected in the regression.

Variable	CPL	NAP	SAP	UMW	TPL	NPL	SPL	XER	WMT
Water Quality
TN	−7.9†	--	--	--	--	--	--	−12†	−8.4†
TP	−7.3	--	--	--	--	--	--	--	--
COND	--	−27	−8.5	--	--	--	--	--	--
DOC	--	--	--†	--	--	−15†	−15	--	--
CL	--	--	−7.5	--	--	−7.2†	−5.1	--	--
SO4	--	--	--	--	--	--	--	−3.6	--
TURB	--	--	−8.6	−6.8†	−8.7	--	--	5.7	--
PH	--	19	8.2	--	7.7	--	--	--	--
Physical Habitat Condition
RIPCOV	--	--	--	--	9.0†	4.0	--	--	--
FASTPCT	--	0.11††	0.19†	--	--	--	--	--†	--†
POOLPCT	−0.08	--	--	−0.12	--	−0.10	--	--	--
RIPDIST	--	−2.5	−3.0	--	--	--	--	--	--
Substrate
FINES	−0.12†	--	--	--	--	--	--	−0.23	--
SANDFINE	--	--††	−0.12†	--	−0.18	−0.19†	−0.16†	--†	−0.33†
SUBSIZE	--††	7.4††	--†	--†	--†	--††	--†	--†	--††
RBS	--	--	--	3.2	--	--	--	--	--
Watershed Land Use
AGR_WS	--	--	--	−0.15	--	--	--	--	--
DEVL_WS	--	--	--	--	−0.26	--	--	--	--
ROADDEN	--	--	--	--	--	28	--	--	--
DAM	--	--	−20	--	--	−12	--	--	−21
Climate
PRECIP	--	--	--	--	64	--	--	27	--
RUNOFF	--	--	--	--	--	--†	--	--	--
TEMPMAX	--	--	−1.2	--	−1.8	−1.9†	--	--	--
TEMPMIN	--	1.8	--	--	--	--	--	--	1.4
Geophysical
LAT	--	--	--	--	--	--	--	--	1.2
LON	−0.45	−2.2	--	--	--	--	--	--	--
ELEV	9.3	8.0	--	--	28	--	--	11	12
WSAREA	--	--	4.5	4.3†	5.6††	5.2	--	--	--
DEPTH	--	--	--	--	8.3†	--	--	--	--
WIDTH	--	--	--	--	--	--	7.9	−4.1	--
SLOPE	--†	--	--	9.3†	--	--	--	--	--
ERODE	--	--	--†	--	--	--	--	--	--
Model Intercept	107	117	27.2	52.9	−224	119	63.2	−16.5	−24.3

3.4. Composite variable models

We compared the relationship between MMI scores, and the 6 variable classes shown in Table 2 by constructing multiple regression models using all the variables in that class (and only that class) and calculating the model R². For example, the water quality model R² is based on the regression of MMI versus TN, TP, COND, DOC, CL, SO4, TURB, and PH (Table 2).

For the fish MMIs, the Northern Appalachians had high R² models for all classes with a high of 0.56 for the geophysical model (Figure 3). On the other hand, none of the classes had R² over 0.12 in the Western Mountains. Note that the full model (all 37 variables) R² in each ecoregion for fish ranged from 0.35 in the Upper Midwest to 0.70 in the Northern Appalachians (Table 3). All the variable classes had a model R² > 0.25 in at least one ecoregion. Water quality and geophysical class models tended to have higher R² than the other classes (Figure 3).

Figure 3.

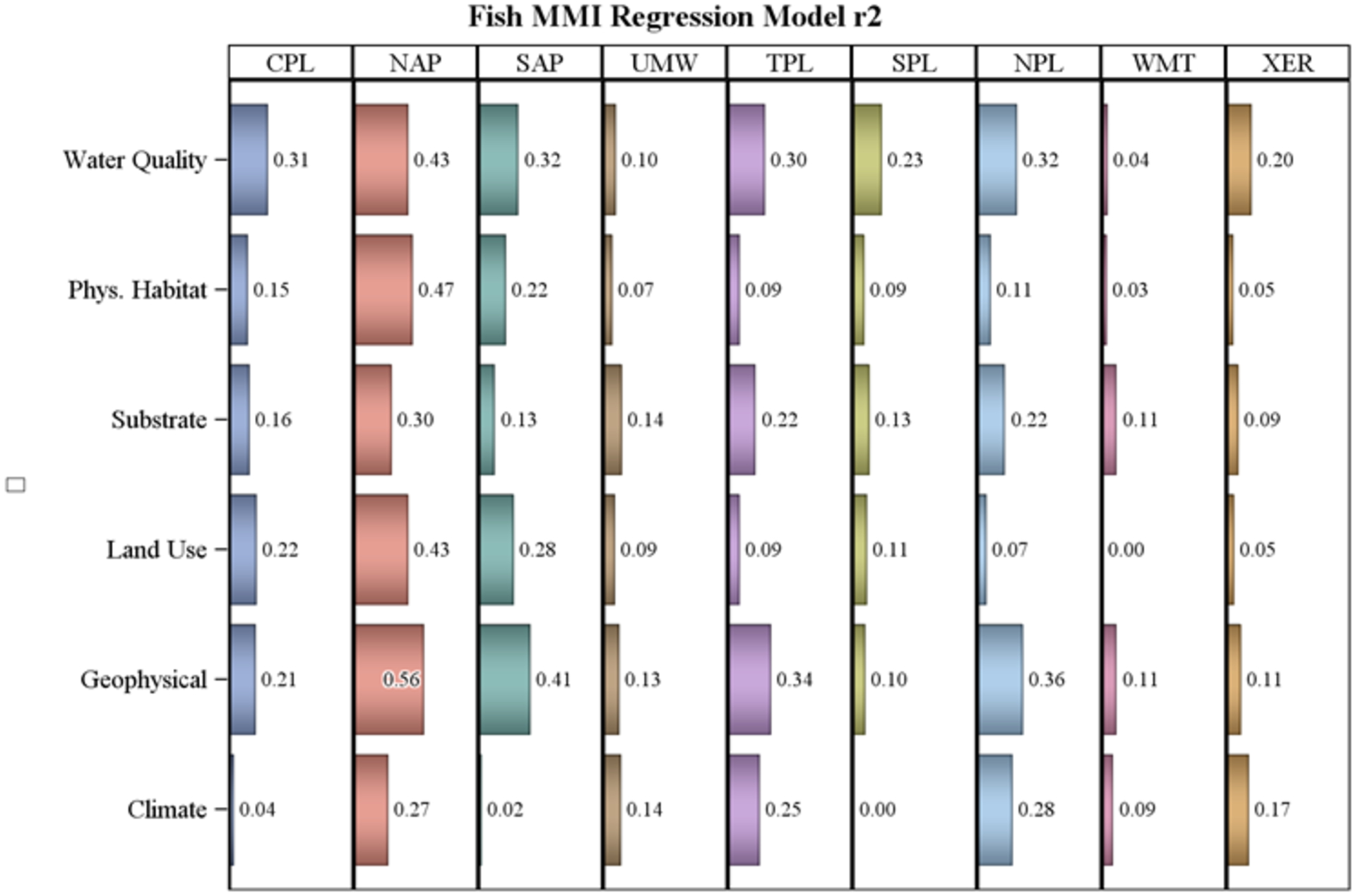
Fish MMI multiple regression R² for models based only on the variables within each predictor class by ecoregion. Ecoregion codes are given in Table 1, predictor classes are listed in Table 2.

The composite regression models for the macroinvertebrate MMIs had the highest R² models in the Northern Appalachians, Northern Plains, and Western Mountains with a high of 0.41 for the substrate model in the Northern Appalachians (Figure 4). The Southern Plains and Temperate Plains had the lowest R² class models (all < 0.18). For comparison, the full (all 38 variables) model R² for macroinvertebrates in each ecoregion ranged from 0.26 in the Southern Plains to 0.60 in the Northern Appalachians (Table 3). All the variable classes had a model R² > 0.2 in at least one ecoregion. There was no pattern of one class having consistently higher R² than any other class across all ecoregions (Figure 4).

Figure 4.

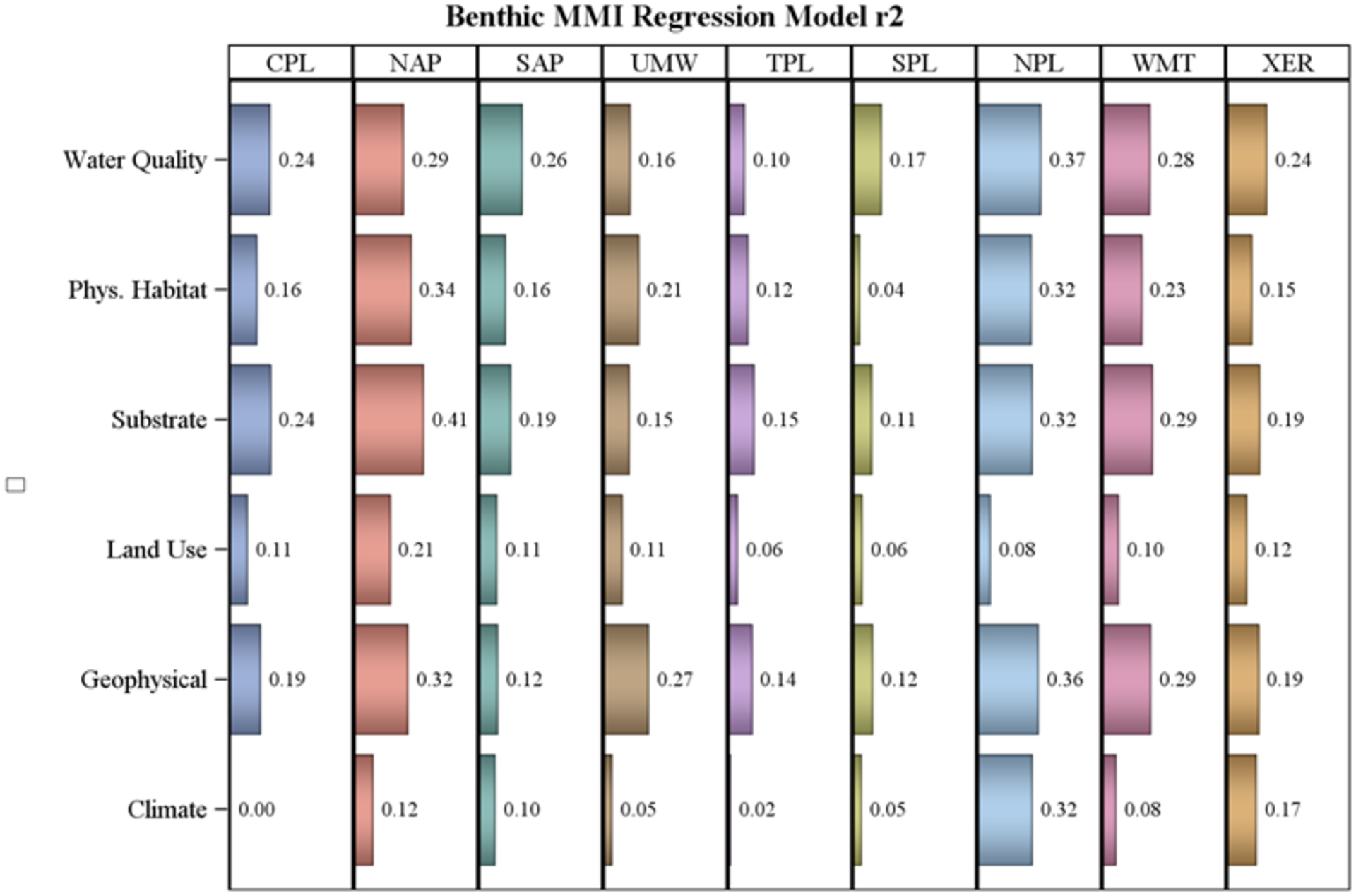
Macroinvertebrate MMI multiple regression adjusted R² for models based only on the variables within each predictor class by ecoregion. Ecoregion codes are given in Table 1, predictor classes are listed in Table 2.

3.5. Model Performance

We evaluated both regression and random forest model performance by examining the relationship between model predicted MMIs and observed MMIs for both fish and macroinvertebrates. Plots of the relationship for an ecoregion with high model R², the Northern Appalachians (Figure 5) and low R², the Southern Plains (Figure 6) show a strong relationship between predicted and observed MMIs with the Northern Appalachians having higher correlation between predicted and observed (r=0.75–0.85) than the Southern Plains (0.43–0.68). Correlations for the ecoregions not shown in figures 5 and 6 are tabulated in Table 6 and correlation coefficients ranged from 0.46 to 0.84 for BIC regression models and from 0.43 to 0.90 for random forest models. Predicted versus observed MMI correlations were not noticeably different between the two model types.

Figure 5.

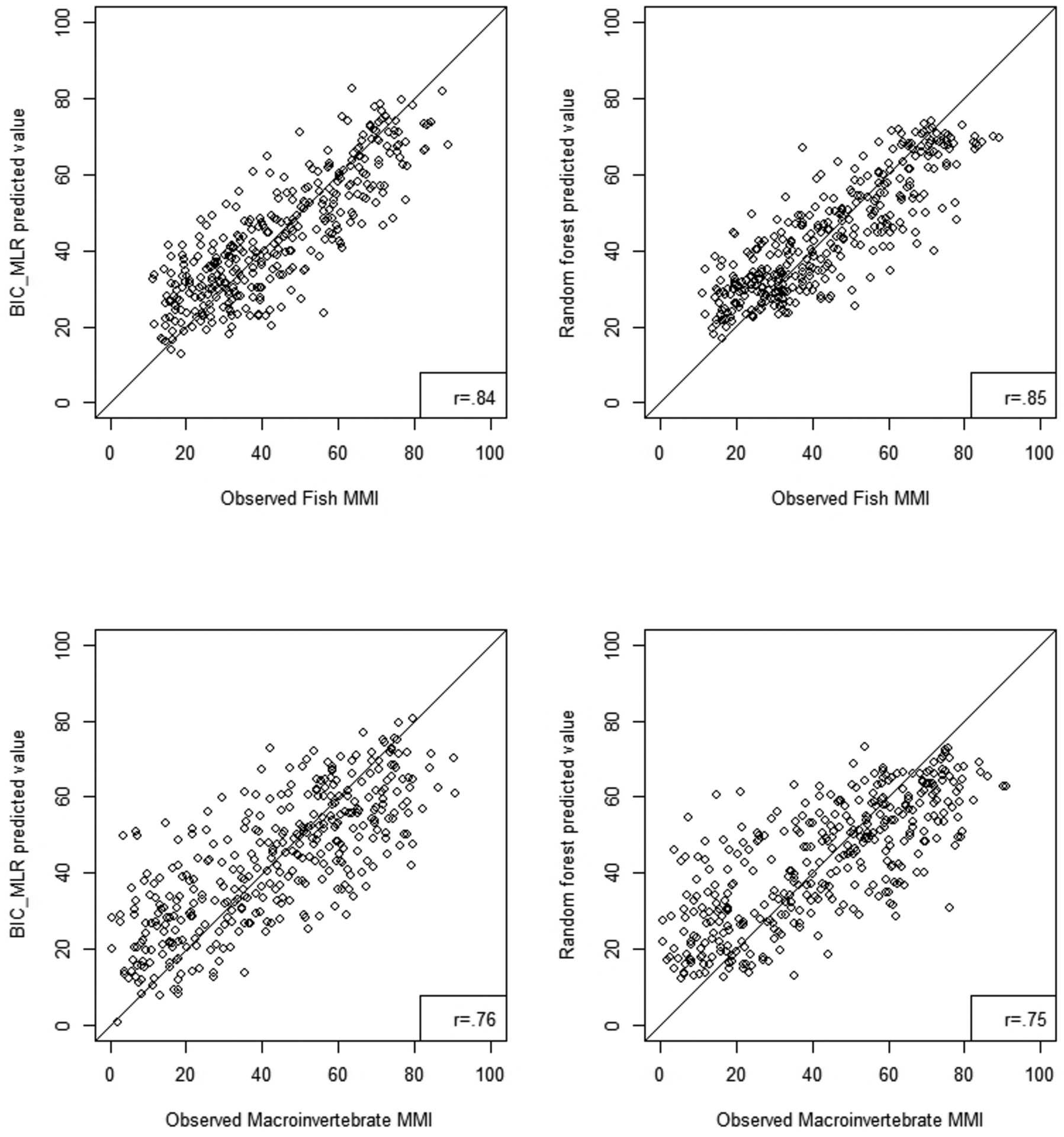
Scatterplot comparison of Random Forest and BIC-MLR predicted fish and macroinvertebrate MMI scores to observed MMI scores in the Northern Appalachians ecoregion. The solid line is a 1:1 line and the r-value is the Pearson correlation coefficient of the scatterplot.

Figure 6.

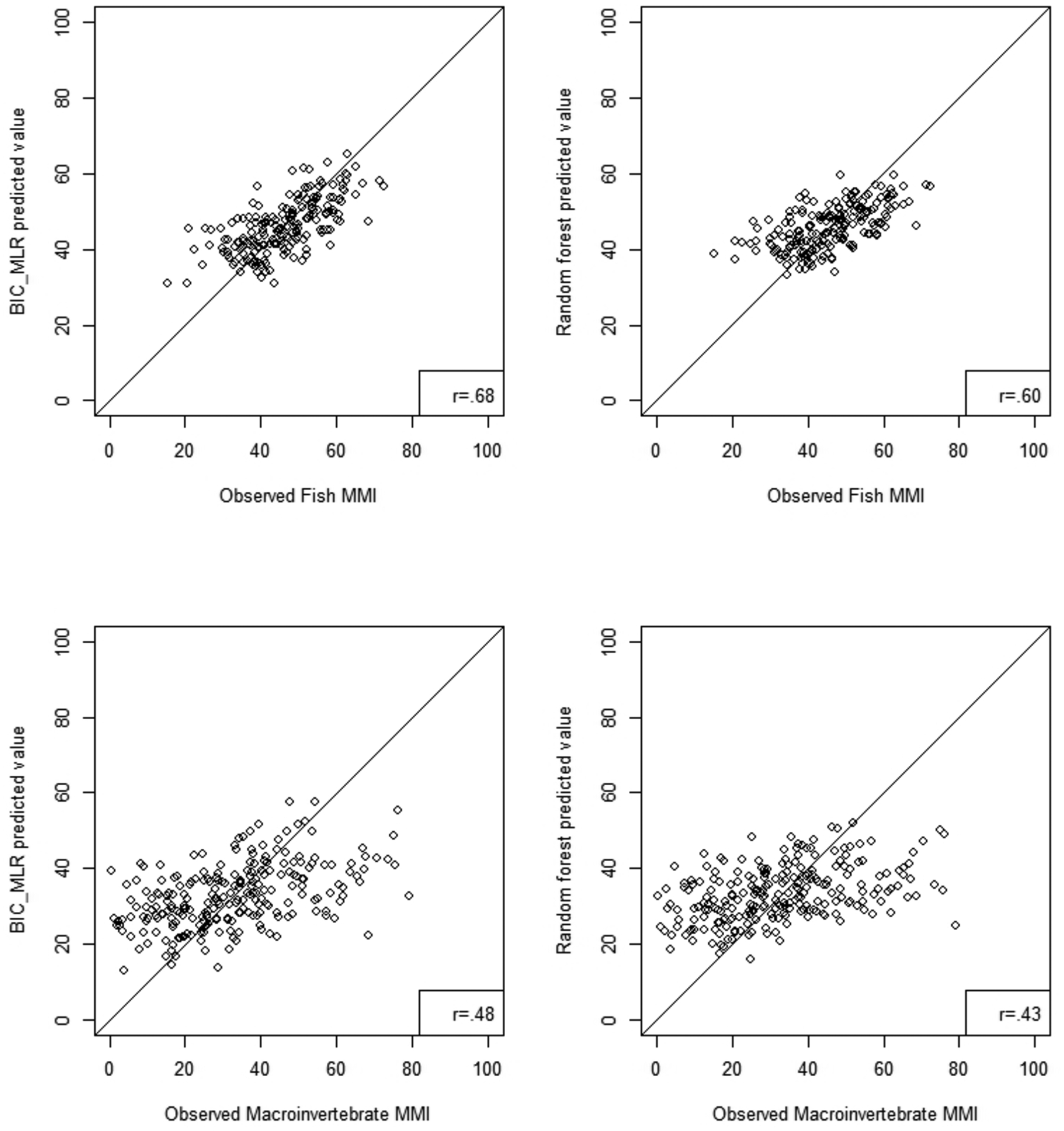
Scatterplot comparison of Random Forest and BIC-MLR predicted fish and macroinvertebrate MMI scores to observed MMI scores in the Southern Plains ecoregion. The solid line is a 1:1 line and the r-value is the Pearson correlation coefficient of the scatterplot.

Table 6.

Statistics for the model predicted versus observed fish and macroinvertebrate (Macr) MMI score relationship by ecoregion (Eco). Results include the Pearson correlation coefficient (r) and slope for both the BIC variable selection multiple regression model (BIC) and random forest model (RF) predictions for both the first visit data (First) and repeat visit validation data (Valid).

Eco	MMI	BIC First r	BIC Valid r	RF First r	RF Valid r	BIC First Slope	BIC Valid Slope	RF First Slope	RF Valid Slope
CPL	Fish	0.76	0.71	0.75	0.72	0.58	0.50	0.47	0.45
CPL	Macr	0.60	0.50	0.63	0.66	0.36	0.31	0.36	0.40
NAP	Fish	0.84	0.80	0.85	0.90	0.71	0.70	0.66	0.74
NAP	Macr	0.76	0.72	0.75	0.82	0.58	0.52	0.53	0.59
SAP	Fish	0.75	0.71	0.76	0.76	0.56	0.56	0.50	0.57
SAP	Macr	0.69	0.66	0.66	0.72	0.47	0.45	0.37	0.43
UMW	Fish	0.58	0.57	0.65	0.71	0.33	0.34	0.35	0.46
UMW	Macr	0.61	0.47	0.58	0.64	0.37	0.25	0.28	0.31
TPL	Fish	0.78	0.80	0.77	0.87	0.60	0.69	0.55	0.66
TPL	Macr	0.66	0.46	0.65	0.64	0.44	0.28	0.34	0.35
NPL	Fish	0.72	0.79	0.70	0.89	0.53	0.68	0.45	0.73
NPL	Macr	0.75	0.70	0.72	0.74	0.56	0.57	0.47	0.54
SPL	Fish	0.68	0.64	0.60	0.70	0.46	0.44	0.34	0.42
SPL	Macr	0.48	0.55	0.43	0.71	0.23	0.25	0.18	0.30
XER	Fish	0.79	0.78	0.77	0.83	0.63	0.66	0.51	0.61
XER	Macr	0.65	0.58	0.68	0.74	0.42	0.48	0.42	0.52
WMT	Fish	0.66	0.71	0.58	0.74	0.44	0.45	0.33	0.43
WMT	Macr	0.68	0.69	0.71	0.79	0.46	0.48	0.46	0.55

The slopes of the predicted versus observed MMI relationships were always less than 1 for both model types for both fish and macroinvertebrate MMIs (Table 6). Slopes below 1 indicate that the model is overpredicting the observed MMI at low MMI values and underpredicting the observed MMI at high MMI values (see Figures 5 and 6). For BIC regression model predicted versus observed MMIs, slopes ranged from 0.23 in the Southern Plains macroinvertebrate data (Figure 6) to 0.71 in the Northern Appalachians fish data (Figure 5). For the random forest model, slopes ranged from 0.18 to 0.66 in those same ecoregions (Figures 5 and 6). Random forest model predicted versus observed slopes were almost always lower than BIC regression slopes.

We used the repeat visit sites as a validation dataset to test model performance. Models constructed from the first visit model data were applied to this validation dataset. Correlation coefficients and slopes for the model predicted versus observed MMI values for validation sites (Table 6) show the same ecoregional pattern as that seen in the first visit data. Values of the correlation coefficients in the validation data were usually similar or slightly smaller than first visit data for the regression model; slopes were more similar. For the random forest model validation, correlation coefficients and slopes were almost always higher in the validation data than in the first visit data. Correlation coefficients for the random forest validation data were always higher than those in the regression validation data.

3.6. Predicting Poor MMI Condition Class

Our best logistic regression model for predicting good versus poor MMI condition class in each of the study ecoregions had 1 to 5 predictor variables (Tables 7 and 8). McFadden’s R² varied between 0.151 for fish in the Upper Midwest and 0.511 for fish in the Northern Appalachians. According to McFadden (1978), R² values between about 0.2 and 0.4 suggest a very good fit. The only models with R²<0.2 were for fish in both the Upper Midwest and Western Mountains.

Table 7.

Logistic regression model results for predicting poor versus good fish MMI condition. The numbers in the table are the regression coefficients (odds ratios) for the significant predictor variables identified from the stepwise model selection process. Ecoregion codes are given in Table 1, variable codes are given in Table 2. Model R² is McFaddens R² for logistic regression.

Variable	CPL	NAP	SAP	UMW	TPL	NPL	SPL	XER	WMT
TN	22.8	9.19	--	--	--	19.9	--	--	--
TP	--	--	--	--	59.7	--	11.4	--	--
CL	--	--	9.70	--	--	--	3.46	10.6	--
SO4	--	--	--	--	6.51	--	--	--	2.06
TURB	--	8.38	4.13	3.76	--	--	--	--	--
FINEPCT	1.33	--	1.40	1.22	2.61	--	--	--	1.49
RBS	--	2.23	--	--	--	--	--	--	--
DEVL_WS	--	--	--	--	--	--	--	--	0.05
POPDEN	--	7.68	--	--	--	--	--	--	--
DAM	--	1.92	1.54	1.23	--	--	--	--	--
ERODE	--	--	--	--	0.16	5.73	--	--	--
Model R2	0.295	0.511	0.350	0.151	0.391	0.289	0.303	0.315	0.156

Table 8.

Logistic regression model results for predicting poor versus good macroinvertebrate MMI condition. The numbers in the table are the regression coefficients (odds ratios) for the significant predictor variables identified from the stepwise model selection process. Ecoregion codes are given in Table 1, variable codes are given in Table 2. Model R² is McFaddens R² for logistic regression.

Variable	CPL	NAP	SAP	UMW	TPL	NPL	SPL	XER	WMT
TN	15.9	6.63	--	5.47	--	--	--	5.68	7.23
TP	--	--	--	--	--	--	3.54	--	--
CL	--	--	2.94	--	--	--	--	2.57	--
SO4	--	--	--	--	--	--	2.96	--	--
TURB	--	9.77	5.02	5.03	2.39	--	--	--	3.17
RIPCOV	--	--	--	9.46	4.58	--	--	--	--
FINEPCT	1.4	--	--	--	--	1.33	--	1.52	2.21
RBS	--	4.97	2.55	--	2.44	--	--	--	--
POPDEN	--	2.23	--	--	0.22	--	--	--
ROADDEN	--	--	--	--	2.80	--	--	--	--
DAM	--	--	1.15	--	--	--	0.76	1.33	1.27
ERODE	--	--	3.29	--	--	6.69	--	--	--
Model R2	0.273	0.371	0.253	0.232	0.256	0.304	0.185	0.318	0.358

The logistic regression coefficients in Tables 7 and 8 can be interpreted as odds ratios. For every one-unit increase in the value of the disturbance variable, the odds of having poor MMI condition as opposed to good condition is X times more likely (where X is the odds ratio). Recall that we transformed the disturbance variables for this logistic regression analysis so that a unit change in the percentage variables is 10 percentage points (original percent divided by 10) and a unit change in chemistry and the other log transformed variables is a factor of 10 (they were log₁₀ transformed). These transformations were done for the logistic regression because they make the odds ratios more comparable among disturbance variables.

For fish logistic regression models, the highest odds ratios were seen for water quality variables (Table 7). For a 10-fold increase in total phosphorus, it is 60 times more likely in the Temperate Plains and 11 times more likely in the Southern Plains that a site will have poor fish condition based on the MMI score. Similarly, high odds ratios for total nitrogen were observed in the Coastal Plain (22.8), Northern Appalachians (9.2), and Northern Plains (19.9). Other significant variables for predicting fish MMI condition class were relative bed stability, population density, damming index, and soil erodibility factor.

A wide variety of predictor variables were significant across the nine ecoregions for predicting poor macroinvertebrate condition class based on MMI scores. Macroinvertebrate logistic regression models were also strongly driven by water quality variables with either total nitrogen, turbidity or both being significant in seven ecoregions (Table 8). The highest odds ratio for the macroinvertebrate logistic regression was for total nitrogen in the Coastal Plain, where a ten-fold increase in total nitrogen is 16 times more likely to lead to poor condition. Predictor variables related to sedimentation (fine substrate, relative bed stability, soil erodibility factor), were also significant in seven ecoregions with the highest odds ratios being 5.0 for relative bed stability in the Northern Appalachians and 6.7 for soil erodibility factor in the Northern Plains. Riparian cover was also a significant predictor in two ecoregions and population density and road density were important in one ecoregion each (Table 8).

4. Discussion

4.1. MMI-Environmental Relationships

Almost all of the numeric environmental variables we assessed in this analysis (34 of 37) were significant in at least one of the statistical models for predicting fish or macroinvertebrate MMI score. Although some variables appeared in more models than others, there was no clear “master variable” that was driving either fish or macroinvertebrate MMI scores in every ecoregion across the continent. This is likely because the ecoregions are very different both in terms of what environmental variables control aquatic condition, and the scale or range of these variables within individual ecoregions. Environmental variables with narrow ranges within an ecoregion will not be good predictors of biotic condition (Wang et al. 2006).

The fish and macroinvertebrate MMIs were only weakly correlated with each other when examined at the ecoregion scale (Table 1) and they generally responded more strongly to different groups of variables. For example, the fish MMI models responded most strongly to differences in the water quality and geophysical variables whereas the macroinvertebrate MMI models responded strongly to all the variable groups except the climatic and land use variables (Figures 3 and 4). In addition, the prediction of poor fish condition class was much more sensitive to elevated nutrient levels than was poor macroinvertebrate condition class. Furthermore, a wide range of local and watershed predictor variables were important in both fish and macroinvertebrate MMI models and for predicting poor MMI scores. These results support using both assemblages and collecting a broad suite of environmental variables in rigorous water body monitoring and assessment programs (Hughes et al. 2000; Hughes and Peck 2008; Yoder and Barbour 2009).

In terms of the error in predicting MMI scores, fish regression models had lower RMSE than macroinvertebrate models in all ecoregions. Fish statistical models also tended to have higher percent variance explained than macroinvertebrate models. Brazner et al. (2007) and (Marzin et al. (2012a) also reported that fish assemblage indicators were more responsive to anthropogenic perturbation than macroinvertebrate indicators across the Laurentian Great Lakes Region and France, respectively. The ecoregion pattern in model strength (e.g., highest in Northern Appalachians, lowest in the Southern Plains) was similar between the fish and macroinvertebrate models.

The logistic regression analysis indicated that increased total nitrogen, total phosphorus and chloride had significant effects on predicting poor fish condition class in six of the nine ecoregions; for macroinvertebrates, total nitrogen and/or turbidity had highly significant effects on predicting poor condition in seven of the nine ecoregions (Tables 5 & 6). For both assemblages, these site-scale disturbance variables more strongly and more often predicted poor condition than watershed-scale variables such as damming index, soil erodibility factor, road density, or population density. These site- versus watershed-scale results agree with those from other comparable studies in the USA (Hughes et al. 2006; USEPA 2016b; Wang et al. 2003), Europe (Marzin et al. 2012b; Sály et al. 2011), and Brazil (Leal et al. 2018; Macedo et al. 2014; Silva et al. 2018; Terra et al. 2015). However, separating direct site-scale predictors from indirect watershed-scale anthropogenic pressures and natural gradients may over-simplify critical drivers and variable interactions (Grace 2008; Leitão et al. 2018; Mora et al. 2018). Our observation of stronger site-scale predictors may be due to the large-scale nature of our study or that we made detailed quantitative site-scale measures of disturbance based on field observations at the time of sampling whereas our watershed-scale measures of disturbance were based on more general GIS based interpretations of disturbance like agriculture or population density. Percent watershed disturbance is not very specific as to the location, type, or intensity of disturbance and as a metric doesn’t appear to be as strongly related to poor biotic condition as actual crew observations and rating of disturbance in the riparian zone.

Few examples exist for making rigorous regional or national assessments of the relationship between biological condition indices and environmental factors based on statistical survey designs and analyses of quantitative ecological data. Examples of such assessments conducted at river basin scales include those of Mulvey et al. (2009), Jimenez-Valencia et al. (2014), Silva et al. (2018) and Larson et al. (2019). Mulvey et al. (2009) reported that the top four stressors for fish assemblages in Oregon’s Willamette River Basin were excess water temperature, insufficient riparian canopy cover, insufficient riparian vegetation, and low water quality index scores. For macroinvertebrate assemblages, the key stressors were insufficient riparian canopy cover, insufficient riparian vegetation, low water quality index scores, and excess total phosphorus. In the Guapiaçu-Macacu River Basin (Brazil), Jimenez-Valencia (2014) found that poor physical habitat structure was strongly associated with poor macroinvertebrate assemblage condition. Silva et al. (2018) concluded that excess turbidity, excess fines, and percent agriculture were the major stressors associated with poor macroinvertebrate assemblage condition in two hydrologic units (Tres Marias, Nova Ponte). However, total nitrogen, excess turbidity, excess fines, and percent agriculture limited macroinvertebrates in Volta Grande, whereas total nitrogen, excess turbidity, and riparian disturbance were limiting in Sao Simao. Regionally, total nitrogen, excess turbidity, excess fines, and percent agriculture were most strongly associated with poor macroinvertebrate assemblage condition, further indicating the differing effects of landscape scale and location on key stressors. Larson et al. (2019) concluded that stressors related to substrate condition were most strongly associated with poor macroinvertebrate assemblage condition in perennial streams in Washington, USA. Thornbrugh et al. (2018) developed a GIS-based index of watershed integrity for all stream segments in the conterminous USA and related them to the 2008–2009 NRSA fish and macroinvertebrate MMIs. They found significant relationships nationally, but the amount of variation explained by the index of watershed integrity was low (adjusted R² <0.12). As in our findings, they found the strongest relationships in the Northern Appalachians ecoregion.

4.2. Model Performance

Both random forest and regression models had biased predictions in that they overpredicted both fish and macroinvertebrate MMI scores at the low end of the range and underpredicted MMI scores at the high end of the range (Figures 5 and 6). A likely explanation of this result is that the very good sites and the very bad sites are driven by environmental variables that were not measured in NRSA and are not in our statistical models. For example, toxic chemicals, livestock grazing, agricultural type, watershed mining activities, and hydrologic flow alterations all have significant effects on stream biota, are not included in the models, and could be responsible for very low MMI scores (Poff et al. 1997; Mebane et al. 2003; Beschta et al. 2013; Daniel et al. 2015; Cooper et al. 2017). Similarly, there are unmodeled environmental factors that can cause biological “hot spots”, such as proximity to channel confluences, natural lakes, or preserved (refuge) areas (Hughes et al. 2004; Hitt and Angermeier 2008) that would result in very high MMI scores.

In our analyses, regression and random forest models had very similar performance in terms of amount of variation explained and which types of variables were related to MMI scores. Regression model predictions of MMI scores are much more easily transferable than random forest predictions in that one can provide a simple equation predicting an MMI score. Transferring random forest prediction requires the same R software, model data, and random number seed, which can be quite cumbersome and requires some statistical sophistication by the end user. The variable importance plots from random forest, however, are an excellent way to evaluate the importance of each variable put into the model. Just because a variable is not in a particular regression model doesn’t necessarily mean that it is unimportant. Also, it should be noted that the proportion of variance explained by these models ranged from 0.34 to 0.72 for fish and from 0.19 to 0.60 for macroinvertebrates (Table 3). Thus, they are only explaining about half of the variability in observed MMI scores.

The models predicting MMI scores were much stronger by proportion variance explained in some ecoregions than others. For example, both the fish and macroinvertebrate models for both random forest and regression were much stronger in the Northern Appalachians than in the Southern Plains (compare Figures 5 and 6). This is likely a result of the varying strength of the environmental gradients in each ecoregion. The Northern Appalachians has a very large gradient of condition ranging from areas with very high-quality streams (Adirondacks, White and Green Mountains) to the most urbanized corridor of the USA (the Boston-New York megalopolis). The Southern Plains, in contrast, has a more uniform gradient of conditions with no high-quality areas, resulting in weaker statistical models of MMI scores. It is also possible that MMI quality is a factor as well. The relative accuracy and precision of the MMIs developed for each ecoregion vary in quality. High-gradient mountainous ecoregions tended to have MMIs that better discriminated least- from most-disturbed sites than low-gradient Plains ecoregions (Stoddard et al. 2008; USEPA 2016a).

We used our revisit data as a way to test the validity of the statistical models. Although these samples are not truly independent samples because they are revisits to the same sites either within the same year or 4–6 years apart, they still provide useful information on the robustness of the models (Table 6). As measured by correlation of modeled to observed MMI scores, the regression models, in most cases, performed almost as well in the validation data as they did with the first visit data. The random forest models performed better in the validation data than they did in the first visit data. This may result from the extensive cross-validation done during the random forest modeling (Breiman 2001; Liaw and Weiner 2002). The validation results do indicate that the statistical models are a robust representation of the MMI-environmental data relationships we report from the NRSA data.

4.3. Predicting Risk of Poor Condition

The logistic regression analysis presents odds ratios that relate the risk of poor biotic condition with respect to changes in continuous numeric stressor variables. It is analogous to the relative risk analysis routinely carried out in NARS assessments (Van Sickle and Paulsen 2008, USEPA 2016b, Herlihy et al. 2019) except that relative risk is based on categorizing the continuous stressor data into two classes (e.g. high versus low) and thus evaluates the risk of having poor condition when the stressor class is high versus low. Relative risk results are therefore dependent on the thresholds used to define stressor classes, a problem that is avoided in the logistic regression analysis which uses continuous numerical stressor data. Our logistic regression analysis also looked at all the variables together as candidates and is more reflective of any synergisms that may occur among variables whereas relative risk analysis is univariate and looks at each stressor variable independently.

We found that water quality and substrate variables were most often associated with poor fish and macroinvertebrate MMI scores. In its assessment of the 2008–2009 NRSA data, USEPA (2016b) evaluated risks of poor MMI scores for both fish and macroinvertebrates. It reported that high levels of total phosphorus, acidity, and fine sediments were most strongly associated with poor macroinvertebrate assemblage condition in upland areas of the eastern USA. High nitrogen, fine sediments, and salinity were most strongly associated with poor macroinvertebrate condition in the western USA. Nationally, excess fine sediments, total nitrogen, and total phosphorus were most strongly associated with poor macroinvertebrate assemblage condition. For fish assemblages, USEPA (2016b) reported that poor condition in the upland areas of the eastern USA was most strongly associated with excess levels of total nitrogen, total phosphorus, and salinity. In the western USA, poor riparian vegetation condition and excess salinity were most strongly associated with poor fish assemblage condition. Nationally, excess salinity, excess total nitrogen, and poor riparian vegetation condition were most strongly associated with poor fish assemblage condition.

4.4. Conclusions

In summary, we found that most of the environmental factors we examined were related to either fish and/or macroinvertebrate MMI scores in some fashion and that the factors involved, and strength of the relationship, varied by ecoregion and assemblage. Factors more associated with natural conditions were usually less important in explaining MMI scores than factors more directly associated with anthropogenic disturbances. Local site-scale factors explained more variation than watershed-scale factors. Random forest and multiple regression models performed similarly, and the fish MMI-environment relationships were stronger than macroinvertebrate MMI-environment relationships. Among ecoregions, the strongest environmental relationships were observed in the Northern Appalachians and the weakest in the Southern Plains. The fish and macroinvertebrate MMIs were only weakly correlated with each other, and they generally responded more strongly to different groups of variables. These results support the use of multiple assemblages and the sampling of multiple environmental indicators in large-scale ecological assessments.

Highlights.

• A wide variety of environmental factors were related to condition.

• Local site-scale factors explained more variation than watershed-scale factors.

• Fish had stronger environmental relationships than macroinvertebrates.

• The strongest relationships were observed in the Northern Appalachians.

• Fish and macroinvertebrate conditions were only weakly correlated.