Alkali Dispersion in (Ag,Cu)(In,Ga)Se₂ Thin Film Solar Cells—Insight from Theory and Experiment

Abstract

Silver alloying of Cu(In,Ga)Se₂ absorbers for thin film photovoltaics offers improvements in open-circuit voltage, especially when combined with optimal alkali-treatments and certain Ga concentrations. The relationship between alkali distribution in the absorber and Ag alloying is investigated here, combining experimental and theoretical studies. Atom probe tomography analysis is implemented to quantify the local composition in grain interiors and at grain boundaries. The Na concentration in the bulk increases up to ∼60 ppm for [Ag]/([Ag] + [Cu]) = 0.2 compared to ∼20 ppm for films without Ag and up to ∼200 ppm for [Ag]/([Ag] + [Cu]) = 1.0. First-principles calculations were employed to evaluate the formation energies of alkali-on-group-I defects (where group-I refers to Ag and Cu) in (Ag,Cu)(In,Ga)Se₂ as a function of the Ag and Ga contents. The computational results demonstrate strong agreement with the nanoscale analysis results, revealing a clear trend of increased alkali bulk solubility with the Ag concentration. The present study, therefore, provides a more nuanced understanding of the role of Ag in the enhanced performance of the respective photovoltaic devices.

1. Introduction

Cu(In,Ga)Se₂ (CIGSe) photovoltaics is a promising technology combining high power conversion efficiency (PCE), relatively low production cost, excellent outdoor stability, and high radiation hardness.^1,2 One effective way of enhancing the device performance is by tuning the bandgap energy (E_g) at different parts of the absorber via adjusting the absorber composition profiles, which in effect also improves band alignment and suppresses recombination at interfaces. CIGSe is thermodynamically stable within a wide range of chemical compositions at usual deposition temperatures, allowing bandgap engineering by alloying,³ which motivates the efforts to further boost the PCEs. Tailoring of E_g by alloying can be achieved during processing through varying the composition of the quaternary alloy, typically the [Ga]/([Ga] + [In]) ratio (referred to as GGI), incorporation of an additional alloying element (such as Al, Ag, S, or Te), or combinations thereof.⁴ For CIGSe, the band gap varies from ∼1.0 eV for CuInSe₂ to ∼1.7 eV for CuGaSe₂,⁵ making the alloy suitable not only for single-junction solar cells but also for tandem applications. Alloying with Ag to form (Ag,Cu)(In,Ga)Se₂ (ACIGSe) allows lowering the deposition temperature because of a reduction of the melting point,⁶ an improvement of the crystal quality,^7,8 an increase in the carrier collection length,⁹ and an enhancement of the open-circuit voltage (V_OC).¹⁰⁻¹³ Ag substitutes Cu in the lattice structure, which decreases the p–d hybridization, inducing a downward shift of both band edges and a slight band gap widening.⁸ It has been established that an [Ag]/([Ag] + [Cu]) value (referred to as AAC) of approximately 0.2 (at a GGI value of ∼0.45) is optimal for improving the PCE of single-junction solar cells.⁹ Hence, ACIGSe is a highly interesting chalcogenide alloy that may eventually outcompete CIGSe if the merits of the Ag addition for PCE offset the higher cost of raw materials.

Addition of alkali elements into the CIGSe absorber bulk or at its surface is another common practice because of the positive effect on device performance.^14,15 Increased V_OC and fill factor (FF) are frequently reported for alkali-treated devices, stemming from the increased hole carrier density (improved conductivity) and presumably grain boundary (GB) passivation optimizing local band bending.^16,17 Alkali elements have limited solubility in CIGSe grain interiors (GIs),¹⁸ with preferential segregation to lattice defects and phase boundaries in the polycrystalline film.¹⁹ This is especially apparent for heavy alkali elements (referring to K, Rb, or Cs) because of the higher defect formation energies and increased diffusion barriers in bulk CIGSe.²⁰ Nonetheless, because the volume fraction of GBs is small compared with that of the GIs, the integral Na amounts can be comparable.²¹ An ambiguity with bulk incorporation, however, is that the most stable alkali-on-Cu defects (Alk_Cu) are charge neutral, and thus electrically inactive.²⁰ In an attempt to reconcile these results with the observed changes in the hole concentration,²² a kinetic model of alkali out-diffusion from GIs to GBs upon cooling was developed.²³ The situation became even more complicated when a combination of Na with heavy alkali treatments demonstrated even higher PCEs in CIGSe compared to single-alkali postdeposition treatment (PDT).²⁴ Studies on the diffusion mechanism of alkali elements in CIGSe have shown that an interplay occurs between light (referring to Li and Na) and heavy alkalis regarding their distribution in the GIs and at GBs, which is influenced by the substrate temperature as well as the alkali supply dose.²² There is still an ongoing debate whether the positive effects of alkali incorporation are related to their dispersion in the GIs or GBs, as well as their modification of the absorber surface.^23,25 Furthermore, it is reasonable to suppose that the incorporation and influences of alkali elements could vary when the CIGSe absorber is modified by Ag alloying, as described above.

Alkali elements can be introduced via predeposition treatment (alkali-containing precursor layer), coevaporation, or PDT, where the light and/or heavy alkali elements can be chosen.⁴ For heavy alkali elements, PDT is the most common supply technique, whereas light alkali elements can be supplied with all three techniques. Substantial incorporation of alkali elements is also caused by in-diffusion from glass substrates during processing if no diffusion barrier is used. Irrespective of the selected alkali element or doping technique, it has been shown that there is an optimum alkali amount, which if exceeded leads to degradation of V_OC and lower PCE values, observed in both CIGSe and ACIGSe.²⁶⁻²⁹ The effect seems to be more severe in the case of ACIGSe, where the PCE can drop significantly.³⁰ It has also been reported for Ag-alloyed CuInSe₂ (ACISe).³¹ This could be anticipated because the optimum amount of KF PDT for ACIGSe was found to be lower compared to CIGSe synthesized under similar conditions.^10,26 Understanding the underlying cause of this distinction is critical to further development of successful PDT strategies. Although the reason for this variance is currently unknown, it could be because of the differences in (1) solubility limits for alkalis (i.e., a thermodynamic effect) or (2) rate of in-diffusion from the alkali-rich source (i.e., a kinetic effect). There are some studies supporting both hypotheses. Kim et al.¹¹ showed using secondary ion mass spectrometry (SIMS) that the Na concentration in the absorber increases upon addition of Ag in CIGSe grown on soda-lime glass (SLG) substrates, with the authors arguing in favor of faster in-diffusion of alkalis in ACIGSe. However, in a more recent study of ACIGSe/CIGSe tandem devices,¹² the same authors presented SIMS profiles with nearly an order of magnitude stronger Na signal within the ACIGSe top layer compared to the CIGSe bottom cell. Considering that the only source of alkalis was the SLG substrate, all Na in the top cells must have diffused through the bottom CIGSe cell first. As such, the preference for Na accumulation in the top ACIGSe cell points to higher alkali solubility in ACIGSe.

It, therefore, remains unclear how alkali elements are distributed in ACIGSe and what role they play in enhancing the performance of CIGSe devices upon Ag alloying. Among the few experimental techniques capable of investigating local compositions of GBs and GIs, atom probe tomography (APT) has been proven exceptionally useful for quantitative elemental mapping in three dimensions.^{19,21,32−45} To utilize this unique capability, we perform in this work a comparative APT characterization of alkali distributions in polycrystalline ACIGSe and CIGSe films. Additionally, we employ first-principles calculations within the density functional theory (DFT) to verify and explain the experimental trends in solubility. With the synergy of these methods, we can draw a clearer picture of the complex phenomena behind the improved efficiency of ACIGSe and CIGSe absorbers with alkali incorporation.

2. Experimental and Computational Methods

2.1. Solar Cell Processing

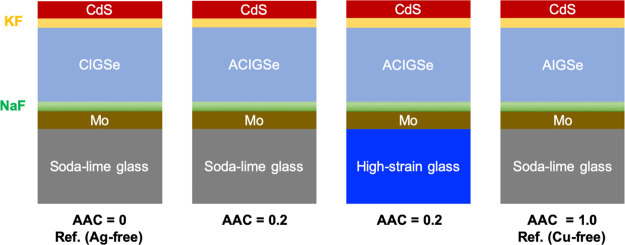
Two different glass substrates were used, namely SLG, which is Na-rich and high-strain glass (HSG), which is K-rich. Mo back contacts were DC-sputtered (target purity 99.97%) on the cleaned glass substrates, followed by evaporation of ∼15 nm thick NaF alkali precursor layers. CIGSe, ACIGSe, and Ag(In,Ga)Se₂ (AIGSe) absorbers were coevaporated in a three-stage process using metal targets (99.999% purity) and 4N Se target (99.99% purity). The three-stage process follows an evaporation profile consisting of I-poor, I-rich, and finally I-poor stages, with all stages having the same [Ag]/[Cu] ratio for ACIGSe. The CIGSe (Ag-free, AAC = 0) and AIGSe (Cu-free, AAC = 1) devices grown on SLG were produced here to be used for comparison (reference samples). The substrate temperature was about 400 °C in the first stage and ramped up to about 550 °C in the following two stages. The deposition time for the absorber layers was about 30 min, resulting in film thicknesses of around 2 μm. High-Ga and low-In deposition rates were used at the initial stage of the absorber deposition to induce a Ga grading at the back contact. The elemental AAC, GGI, and ([Ag] + [Cu])/([Ga] + [In]) ([I]/[III]) ratios in the absorbers were determined using X-ray fluorescence (XRF) spectroscopy. KF PDT was performed on all samples for 10 min after ramping down the substrate temperature to 350 °C at a rate of approximately 5 °C/min. A 40 nm CdS buffer layer was deposited using chemical bath deposition (CBD). A 125 ml solution with 4.5 mM Cd acetate and 1.7 M ammonium hydroxide was preheated in a 60 °C water bath, after which 50 mL of thiourea (0.35 M) was added and the samples were immersed. The CdS growth was terminated after 6 min, after which the samples were rinsed and dried. Schematic of the four samples investigated is shown in Figure 1. Devices used for electronic measurements were completed by depositing a front stack of 100 nm of undoped ZnO, followed by 200 nm of ZnO/Al using RF magnetron sputtering (both targets of 99.99% purity). A metal stack of Ni–Al–Ni was deposited by electron beam evaporation through a shadow mask (target purity: 99.9% Ni and 99.999% Al). Finally, cells with an area of 0.5 cm² were defined by mechanical scribing. JV data are extracted from standard test conditions. All measurements were done sweeping from low to high voltage, with no significant hysteresis effects observed. The temperature during measurements was controlled to 25 °C by a metal plate cooled with a Peltier element (no preconditioning used). Illumination was made using a halogen light calibrated to a photon flux corresponding to 1000 W/m² with a calibration Si solar cell. External quantum efficiency (EQE) measurements were carried out and the EQE intensity was used to calculate the current density under short circuit conditions using the data for AM1.5 spectral distribution.

Figure 1.

Schematic illustration of the samples studied.

2.2. Materials Characterization

Glow discharge optical emission spectroscopy (GDOES) elemental profile measurements were performed on the devices in a Spectruma Analytik GDA 750 HR system. A dual-beam focused ion-beam/scanning electron microscope (FIB/SEM) instrument (Thermo-Fisher Versa 3D) was used to carry out site-specific specimen preparations for APT analysis via a standard lift-out technique.⁴⁶ Absorbers without front contacts (incomplete devices) were used for GDOES and APT characterization. A 100 nm thick Pt layer was deposited on top of the CdS layer using the electron beam in the FIB/SEM to minimize Ga-implantation. An acceleration voltage of 2 kV was used in the final steps of tip shaping to reduce Ga-implantation and surface amorphization effects. Laser-pulsed APT measurements were carried out using a LEAP 3000X HR CAMECA system using a green laser (λ = 532 nm) with a laser power set to 0.05 nJ, a repetition rate of 100 kHz, and base temperature of ∼50 K. 3D reconstructions and data analysis were performed using CAMECA IVAS 3.6.14 software.

2.3. Computational Details

The first-principles calculations were carried out within DFT using the Vienna Ab initio Simulation Package (VASP).⁴⁷⁻⁴⁹ The projector augmented wave pseudopotentials^50,51 with valence electron configurations of 4d¹⁰5s¹ for Ag, 3d¹⁰4s¹ for Cu, 4d¹⁰5s²5p¹ for In, 3d¹⁰4s²4p¹ for Ga, 4s²4p⁴ for Se, 3s¹ for Na, 3p⁶4s¹ for K, 4p⁶5s¹ for Rb, and 5s²5p⁶6s¹ for Cs were employed. The calculations were performed with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.⁵² All ACIGSe supercells contained 216 atoms with random occupation of the cationic sites (placing Ag/Cu on group-I and In/Ga on group-III positions) and were generated using the special quasirandom structure (SQS) algorithm,⁵³ as implemented in the Alloy-Theoretic Automated Toolkit (ATAT) package.⁵⁴ The Brillouin-zone integrations were performed using a 2 × 2 × 2 Γ-centered Monkhorst–Pack grid⁵⁵ and a cut-off energy of 350 eV. The ionic and lattice relaxations were continued until reaching a threshold of 0.01 eV/Å on atomic forces. For the defect calculations, NaInSe₂ was simulated with the delafossite (R3̅m [#166]) structure, whereas KInSe₂, RbInSe₂, and CsInSe₂ were modeled with a monoclinic (C2/c [#15]) cell. In contrast, the supercells of alkali alloys were initialized with a chalcopyrite structure but allowed to change symmetry during relaxation. The analysis was automatized using the Pymatgen library.⁵⁶

3. Results and Discussion

3.1. Absorber Composition and Device Performance

The absorber compositions were initially determined by XRF. The elemental AAC, GGI, and [I]/[III] of each sample are presented in Table 1. Device characteristics of the respective samples are presented in Table 2. For ACIGSe, the absorber deposited on HSG showed slightly higher J_SC and PCE values compared to the films grown on SLG.

Table 1. Integral Absorber Compositions Measured with XRF.

sample	AAC	GGI	[I]/[III]
CIGSe-SLG	0	0.38	0.89
ACIGSe-SLG	0.22	0.40	0.89
ACIGSe-HSG	0.19	0.43	0.87
AIGS-SLG	1	0.40	0.85

Table 2. Solar Cell Parameters for Selected Devices with the Standard Grid and without Antireflective Coating^a.

sample	VOC [mV]	JSC [mA/cm2]	FF [%]	PCE [%]
CIGSe-SLG	704 (706 ± 3)	31.8 (30.7 ± 0.3)	75.3 (75.0 ± 1.2)	16.8 (16.3 ± 0.4)
ACIGSe-SLG	769 (761 ± 6)	30.2 (30.1 ± 0.2)	77.9 (74.8 ± 2.6)	18.1 (17.4 ± 0.7)
ACIGSe-HSG	770 (759 ± 10)	31.0 (30.7 ± 0.2)	77.7 (76.8 ± 0.6)	18.6 (17.9 ± 0.5)
AIGSe-SLG	682 (667 ± 5)	25.1 (24.4 ± 0.9)	68.2 (66.4 ± 1.7)	11.6 (10.7 ± 0.4)

^aAverage values with their standard deviations are given in parentheses.

3.2. Alkali Distribution Profiles along the ACIGSe Absorber Thickness

Figure 2 shows GDOES profiles of alkalis in ACIGSe absorbers grown on the different substrates. The profiles start at the CdS/ACIGSe interface and end in the Mo layer. The absorber film grown on HSG was slightly thinner compared to the one grown on SLG, with the measured thicknesses of ∼1.7 and ∼2.1 μm, respectively (determined by XRF and verified with cross-sectional SEM images). Both films displayed an increase in Na and K concentrations at the CdS/ACIGSe and ACIGSe/Mo interfaces. As expected, the K increase at the back contact is more pronounced for the HSG substrate. Similar alkali profiles were reported in our previous work for CIGSe and ACIGSe,^10,57 as well as in multiple other studies reviewed in ref (22).

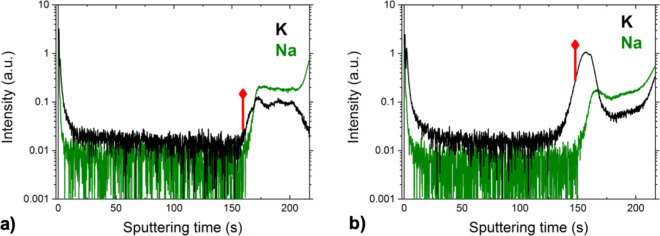
Figure 2.

GDOES depth profiles for ACIGSe samples on (a) SLG and (b) HSG, showing K and Na signals from the CdS/ACIGSe interface to the Mo back contact. The onset of the Mo signal is marked in red color.

The main optoelectronic effects of alkali segregation at the interfaces are suggested to be similar to those of alkalis dispersed in GBs, such as defect passivation and local band bending.⁵⁸ However, in addition, alkali enrichment at the heterojunction can promote alkali-rich compound formation (such as AlkInSe₂),⁵⁹ interactions with ordered defect compound (ODC) phases,^44,57 as well as altering the growth behavior of the buffer layer.^58,60 Surface chemical analysis was performed here using energy-dispersive X-ray spectroscopy (EDS) in SEM and revealed no alkali-rich compounds, despite the clear alkali enrichment identified at the absorber surface using GDOES. Thus, the quantities of these compounds were below the sensitivity limit of EDS or they were not stable under the electron beam. In our previous study on alkali treatment of ACIGSe,²⁶ we demonstrated that the alkali-rich surface compound, (Ag,K)InSe₂, only begins to form in samples treated with an excessive dose of KF. It is necessary to mention, however, that GDOES provides only qualitative analysis of the alkali distribution. Furthermore, it delivers in-depth compositional information averaged over a spot with a diameter of ∼2 mm. Hence, interpretation of the GDOES scans should be made with caution. Local compositional analysis was performed here on the CdS/ACIGSe interface using APT, where alkali segregation was found to be inhomogeneous at the nanometer scale (see Figure S1 in Supporting Information), that is, partial segregation occurs across the entire interface. This indicates that at a fine scale, the alkali is most likely to be distributed as islands at the CdS/ACIGSe interface. The alkali concentrations at the interface are well below 1 at. %, which is unfortunately not possible to map using SEM–EDS, for instance.

It seems likely that the alkali segregation detected using GDOES near the surface is not connected with nucleation of ODCs because no clear group-I depletion is observed (not presented here). The formation of ODCs is governed by the absorber composition, specifically the [I]/[III] ratio, as we have recently shown for wide-gap ACIGSe.⁵⁷

3.3. Nanoscale Analysis of Alkali Dispersion by Atom Probe Tomography

In addition to GDOES depth profiling, spatial distributions of the matrix and alkali elements in three dimensions were examined at the nanoscale using APT. The primary objective is analyzing the composition at GBs and in GIs, separately. Because of the limited volume analyzed using this technique and the compositional variations between grains, a minimum of five successful APT measurements was carried out from each sample with datasets of at least 10 million atoms, in order to attain reasonable statistics.

3.3.1. Grain Boundaries

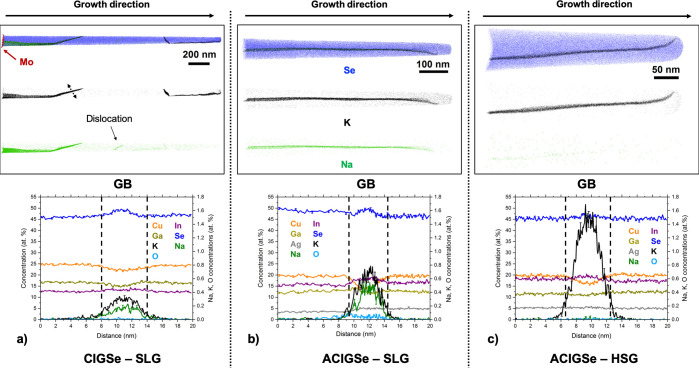
The effect of Ag alloying on the GB composition and alkali dispersion is investigated here by analyzing the two ACIGSe samples and comparing them to the CIGSe absorber grown on SLG (Ag-free reference sample). Figure 3 shows APT analyses of the three samples. Each presented 3D reconstruction includes at least one GB. In all cases, the concentrations of matrix elements in the GBs differ from those in the adjacent grains, which is a common observation in CIGSe.^{32−35,38−40,42,45} The GBs here display slight Cu-depletion and In-enrichment, which is especially evident for the ACIGSe samples. Interestingly, the measured Ag profiles are almost flat, translating into an increasing AAC ratio in the GBs. According to two earlier extensive APT studies,^42,61 it is now understood that the majority of GBs in CIGSe exhibit this kind of Cu-depletion. This tendency has also been reported using high-resolution XRF for CIGSe after RbF PDT.⁶² The compositional fluctuations of matrix elements at GBs are claimed to influence the electrical characteristics of solar cells because of the local band bending,⁶³ which can have beneficial, detrimental, or neutral impact on the device performance.³² For instance, Cu-depleted GBs are argued to reduce carrier recombination because they act as hole barriers because of a downshift of the valence band maximum.⁶⁴ Although structural information on planar defects is usually not accessible by APT, the observed features resemble random high-angle GBs and not stacking faults or twin boundaries. Such a distinction can be made from an irregular curvature of interfaces, which stems from an arbitrary connectivity of faceted grains in the absorber.

Figure 3.

APT analysis of GBs in the CIGSe (SLG) and both ACIGSe samples. 1D concentration profiles are shown below the respective reconstructions. The uppermost reconstructions show overlaid Se (blue), K (black), and Na (green) atoms, with individual reconstructions for alkalis shown separately below. (a) CIGSe grown on SLG (reference) showing four GBs in the absorber and a Na-decorated dislocation. Some GBs appear thicker because the GB planes are not parallel to the viewing direction. The 1D profile is measured across the GB highlighted by dotted arrows. (b) ACIGSe grown on SLG and (c) ACIGSe grown on HSG, both showing one GB per reconstruction.

Segregation of alkali elements at the GBs is observed for all samples. Both Na and K are found in dissimilar quantities at different GBs, which agrees with previous studies on CIGSe.^40,42,61 The effective thickness of the GBs, measured by the compositional change at the interfaces, was in the range of 4–6 nm (see Figure 3). The extent of alkali segregation can be additionally quantified by calculating the Gibbs interfacial excess (Γ) values.⁶⁵ The values were extracted for all GBs shown in Figure 3. In the CIGSe sample, the Γ_Na and Γ_K values varied among the four GBs recognized in Figure 3a from 0.03 to 2.74 at./nm² and from 0.97 to 3.14 at./nm², respectively. In the ACIGSe sample grown on SLG, the Γ_Na and Γ_K values in the single GB seen in Figure 3b were 0.83 and 1.87 at./nm², respectively. For comparison, in the ACIGSe sample grown on HSG, the Γ_Na and Γ_K values in the GB shown in Figure 3c were 0.04 and 3.66 at./nm², respectively. Traces of O were detected at some GBs for each of the samples investigated, which is a common finding in CIGSe and CZTS absorbers.^66,67 Oxygen contamination is argued to arise primarily through diffusion from the substrate and/or surface oxidation before deposition of a buffer layer. Preferential O segregation is reported for GBs with a specific misorientation angle,⁴⁰ but no such correlation has been established for alkali elements.⁶¹ Herein, we observe no significant difference in the behavior of alkalis at GBs of ACIGSe and CIGSe. However, three important observations can be made: (1) concentrations of alkalis are dissimilar in different GBs within the same sample, which is in agreement with earlier APT studies on CIGSe.^40,42,61 (2) K segregation is more consistently observed compared to Na, with some GBs being nearly devoid of Na, even in the absorber grown on SLG, as seen in Figure 3a. (3) GBs in the ACIGSe sample grown on the HSG substrate show greater K segregation and only small traces of Na. Hence, this indicates that the HSG substrate is clearly the leading source of K in the GBs. According to the model/hypothesis of interplay between light and heavy alkali elements in GBs and GIs of chalcopyrite thin films (ion exchange mechanism),^22,68 it is understood that heavier alkalis replace Na at the GBs if supplied in a higher dosage or if the films are deposited at higher temperatures. This mechanism is expected to be driven by thermodynamic as well as kinetic factors. An increased concentration of K in the GBs because of a higher dosage is usually accompanied by segregations at the heterojunction, as observed here. It may lead to secondary phase formation (such as KInSe₂) on the absorber surface, which emphasizes that interpretation of changes in device performance cannot solely be based on alkali effects at the GBs. It is important to mention that alkali-decorated GBs may have either detrimental or benign effects on the cell efficiency depending on the composition of the GBs, as reported in ref (61). This highlights the complexity of alkali effects in polycrystalline CIGSe (and ACIGSe) and encourages investigating the alkali dispersion in the bulk, at the heterojunction and at the rear-interface simultaneously.

3.3.2. Grain Interiors

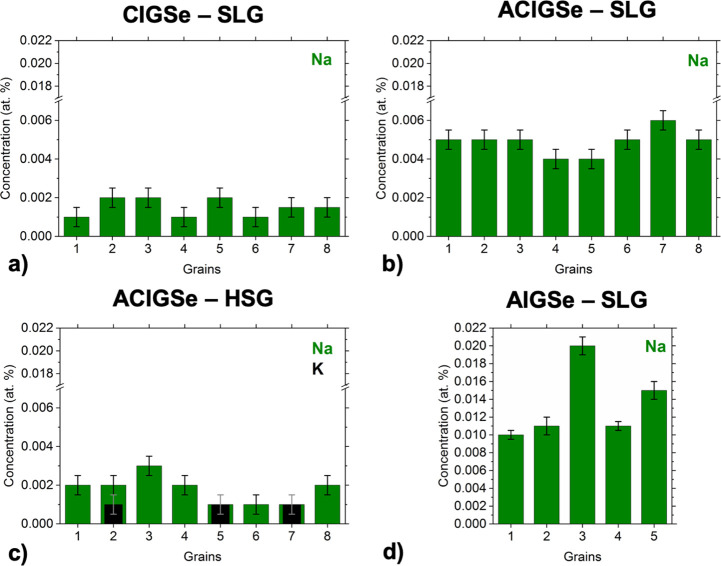
Figure 4 shows a plot for the alkali concentrations measured with APT in eight different grains of the CIGSe and ACIGSe samples, and in five different grains of the AIGSe sample. Na is found to be widely distributed in the GIs, contrary to K, which is more localized at the GBs, especially when a higher dosage of K is introduced by using HSG, as shown above. These results are consistent with the ion exchange mechanism for alkali elements.^22,68 The concentration of Na in the CIGSe reference sample varies from 10 to 20 ppm in the GIs, where the detection limit here in the measurements is ∼5 ppm. The Na concentrations in the GIs for CIGSe fit well into the range of values reported from APT measurements in the literature for CIGSe and CuInSe₂ (CISe) absorbers.^34,36−38 Such a consistency implies that Na reaches a solubility limit in the CIGSe bulk. Exceptional cases can be found in the literature though, such as 148 ppm of Na in the GIs of CIGSe reported by Choi et al.³⁵ using APT. In that case, a fine-structured CIGSe absorber (high defect density) with Na-containing defect clusters in the GIs was examined, which likely contributed to such a high level of Na. It is important to also point out that high alkali content values are sometimes reported for CIGSe using SIMS analysis.^21,69 This quantification, however, should be treated with caution because SIMS cannot resolve alkali-enriched dislocations, stacking faults, and clustering, even if GBs and GIs are duly separated. These limitations render APT concentrations of alkalis more reliable when resolution of different areas in a microstructure is concerned. It is important to note that significantly fewer decorated defects (such as dislocations) were detected using APT in the GIs of ACIGSe samples compared to the CIGSe sample. The specimen volume analyzed with APT is limited to evaluate defect densities and only decorated defects can be identified, however, these observations may support the arguments of suppressed formation of intragrain defects in ACIGSe.^7,70

Figure 4.

Alkali concentrations measured with APT in different grains of (a) CIGSe grown on SLG, (b) ACIGSe grown on SLG, (c) ACIGSe grown on HSG, and (d) AIGSe grown on SLG.

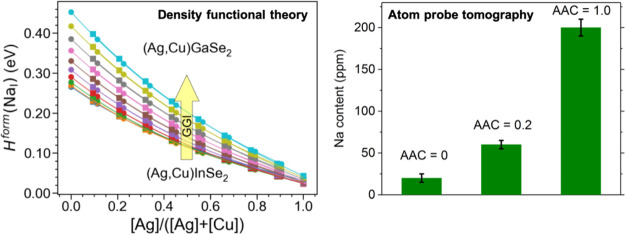
The ACIGSe sample grown on SLG shows a clear increase in the Na content in the GIs. The Na concentration in this sample varies between 40 and 60 ppm, whereas the K concentration is below the detection limit. It is important to note here that in the reconstruction shown in Figure 3b, it may appear as if some K is detected in the GIs of this sample. This issue, however, is an artifact, which arises because of a small peak overlap of ⁷⁸Se²⁺ and ³⁹K¹⁺ at 39 Da in the mass spectrum. Considering the natural isotope abundances, this peak overlap is deconvoluted in calculations of GI compositions and 1D concentration profiles. For the ACIGSe grown on HSG, Na concentration varies from 10 to 30 ppm and some GIs show a K concentration of ∼10 ppm. APT analysis of the AIGSe (Cu-free) sample grown on SLG revealed even higher Na concentrations in GIs reaching up to ∼200 ppm. Fewer grains were possible to examine for the AIGSe sample because of the mechanical instability of the APT specimens during measurements. This is likely stemming from different mechanical properties of the AIGSe absorber (details regarding specimen yield in APT analysis are discussed in ref (71)). Hence, all results here point to an increase in the Na solubility in GIs upon the addition of Ag in the chalcopyrite absorber. One can expect similar tendencies to exist for heavier alkalis because of similarities in their chemical properties to Na. However, concentrations of heavier alkalis are anticipated to be lower imposed by higher formation energies of alkali-related point defects in GIs.²⁰ The maximum concentration of Na detected in samples grown on SLG is plotted in Figure 5 to highlight the trend. As discussed in Section 1, the increase in the alkali content is more likely to be of a thermodynamic origin (higher solubility), which is investigated using first-principles calculations in the next section.

Figure 5.

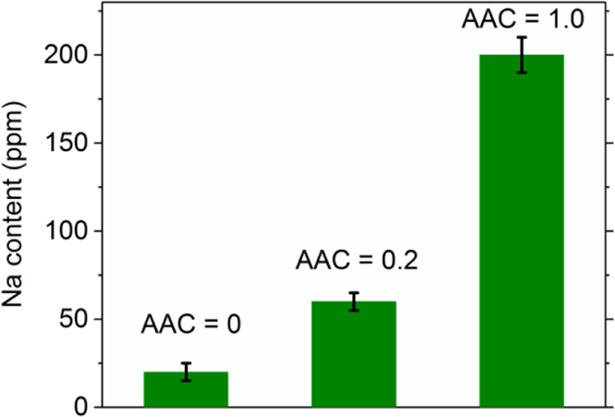
Plot of the highest Na content measured by APT in each of the three samples grown on SLG with different AAC ratios.

3.4. Density Functional Theory Calculations

In order to compare the solubilities of alkali elements in ACIGSe and CIGSe, we utilized DFT for computing formation energies of alkali elements on Cu or Ag site defects (Alk_Cu and Alk_Ag) as a function of the alloy composition (i.e., GGI and AAC). We only considered the substitutional defects because Alk_Cu is the most stable alkali-related defect in CIGSe,²⁰ and is most likely to remain dominant with addition of Ag. The defect formation energies were computed according to the following equation

1

where E_tot(Alk_I) and E_tot(bulk) are the total energies of ACIGSe with Alk_Cu and of the pristine supercell; E_tot(I^el) and E_tot(Alk^el) are the total energies (per atom) of group-I and Alk elemental ground states; Δμ_I and Δμ_Alk are the chemical potentials of group-I and Alk species with respect to those in the elemental ground states, respectively. The dependence on the Fermi level and all corrections in eq 1 are omitted because of the charge-neutral nature of Alk_Cu.

To reproduce the stochastic nature of ACIGSe while avoiding large deviations in energies because of the multiplicity of possible cationic arrangements, the total energies of the supercells computed with DFT were processed with the cluster expansion (CE) formalism using the correlation functions of truly random systems. The CE for an alkali-free alloy was constructed from energies of 100 supercells generated using the SQS algorithm, with compositions spanning the 0 ≤ GGI ≤ 1 and 0 ≤ AAC ≤ 1 range and a uniform 10 × 10 grid. In a similar manner, CEs for supercells containing defects were constructed for each alkali separately by replacing one randomly selected group-I cation (either Cu or Ag, whenever applicable) in the alloy supercell (yielding 180 nonequivalent systems). The results obtained without CE processing are given in Supporting Information (see Figure S2) for comparison.

To estimate the chemical potentials of elements in ACIGSe, we utilize the following relation

2

where x ≡ GGI and y ≡ AAC in the equations. Obviously, in contrast with the conventional methodology for defect calculations,⁷² all chemical potentials and ACIGSe formation energy (ΔH^f(ACIGSe)) are functions of (x, y) composition. Therefore, nontrivial thermodynamic considerations should be introduced. Herein, we extract an analytical expression for ΔH^f(ACIGSe) from our earlier study by setting T = 0 K in the equation for free energy derived within the regular solution approximation.⁷³ This knowledge allows relating chemical potentials as

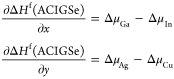3

Combining eqs 2 and 3, one can obtain a system of three equations with five unknowns. The other two free variables can be estimated from the stability diagrams according to the well-established formalism for point defect calculations.⁷² Herein, we present the results obtained for equilibrium between the ACIGSe and AlkInSe₂ phases. An alternative scenario of equilibrium between ACIGSe and ODC was also explored and discussed in the Supporting Information. Both approximations provide qualitatively similar results, with only one exception specified below.

The choice of equilibrium with AlkInSe₂ phases is stipulated by the established experimental knowledge. Specifically, formation of AlkInSe₂ crystals at CIGSe surfaces after alkali treatments was reported for all four considered alkali elements (Alk = Na, K, Rb, and Cs).⁷⁴⁻⁷⁷ Such crystals are assumed to be nearly Cu-free because AlkInSe₂ exhibits limited miscibility with CuInSe₂,⁷⁴ even though Muzzillo et al.⁷⁸ claimed successful synthesis of (Cu,K)InSe₂ alloys. These factors constitute AlkInSe₂ as a good system for extracting chemical potentials for Ga-poor CIGSe.^15,20 In ACIGSe, the appearance of (Ag,K)InSe₂ has been detected after KF PDT in our recent work,²⁶ suggesting that a similar approximation can be applied to Ag-alloyed CIGSe. With this in mind, an expression for the formation energy of AlkInSe₂ can be written as

4

which can then be combined with eqs 2 and 3 to yield

5

and eq 5 can then be substituted in eq 1 for the defect formation energy calculations in the case of Alk_Cu. Following the same approach, a similar expression can be deduced for Δμ_Ag – Δμ_Alk and substituted in eq 1 to calculate formation energies of Alk_Ag.

Figure 6 illustrates computed formation energies of Alk_Cu and Alk_Ag when ACIGSe is in equilibrium with AlkInSe₂. The first thing to note there is that formation energies of Alk_Cu and Alk_Ag follow the same trends. This could be expected because both defects represent the same imperfection in the crystal lattice, Alk_I. In other words, concentration of Alk_I in the dilute limit is defined by the formation energy, which must be independent of the type of the substituted cation. In fact, the same total energies computed with DFT could be (but were not) used for calculating formation energies of both Alk_Cu and Alk_Ag by selecting an appropriate chemical potential (Δμ_I) for the formally substituted ion and the corresponding energy of the elemental state (E_tot(I^el)) in eq 1. The matching of the formation energies is, therefore, not a material property but a validation of the employed methodology for defect calculations in random alloys.

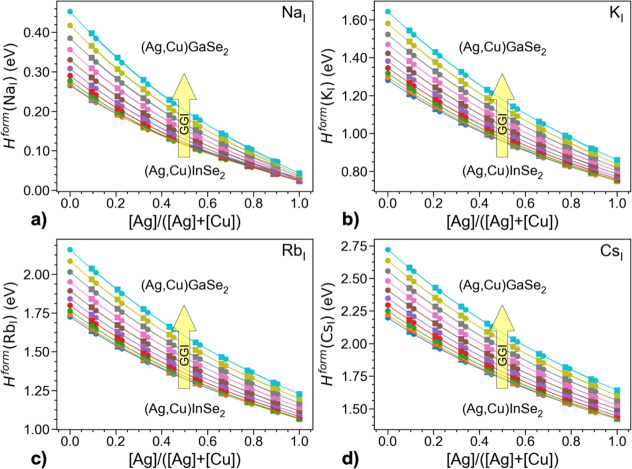
Figure 6.

Computed formation energies of Alk_Cu (circle markers) and Alk_Ag (square markers) in ACIGSe in equilibrium with the AlkInSe₂ phase for (a) Alk = Na, (b) Alk = K, (c) Alk = Rb, and (d) Alk = Cs. The abscissa gives AAC values for supercells after substitution of the group-I element with the corresponding alkali. The series of curves represent ACIGSe alloys with different GGI values spanning the full range of compositions with equal intervals.

More importantly, formation energies of all four considered alkalis decrease monotonically with AAC irrespective of GGI, meaning that their solubilities increase with Ag content. These results are in good agreement with our APT findings here and previous studies reporting a higher Na content in ACIGSe.^11,12 The formation energy demonstrates a stronger dependence on AAC for heavier alkalis. For instance, the computed difference in energy of Na_I in CuInSe₂ and AgInSe₂ is only 0.23 eV, whereas the corresponding values for K_I, Rb_I, and Cs_I are 0.53, 0.66, and 0.78 eV, respectively. As for the absolute values, heavier alkalis have much higher formation energies (lower solubilities), which is explained by the larger ions inflicting more stress on the lattice.²⁰ This is probably also the reason why we did not detect any considerable K content in GIs with APT, as it had probably diffused into the GBs during cooling. At the same time, despite the decrease in formation energies upon Ag alloying, the solubility for Rb and Cs in GIs would possibly remain below the detection limit of APT if the absorbers were treated with Rb or Cs PDT. As such, charge-neutral Rb_I and Cs_I are expected to play practically no role in properties of bulk ACIGSe.

The formation energies increase slightly (but consistently) with GGI. This dependence is weaker compared to that on AAC and thus should be treated with more caution. This trend might even be invisible against random variations under the growth conditions, and hence, we did not attempt to verify it experimentally. The sensitivity of this result is evident, for instance, as the formation energy of Na_Ag increases slightly with GGI when Ag(Ga,In)Se₂ is in equilibrium with AlkInSe₂ but decreases when an alternative approach assuming equilibrium with ODC is considered (see Supporting Information). Such a behavior is not surprising because the equilibrium with AlkInSe₂ compounds is, strictly speaking, inapplicable to Ga-rich systems because other Alk containing Ga-rich phases would segregate in those systems instead. Despite this limitation, the computed dependences on AAC are not strongly affected by the assumed equilibrium, suggesting that both approximations are able to reasonably reproduce the actual chemistry of the alloy.

The computed energies can be used to estimate the ratio of equilibrium Na_I concentrations in ACIGSe and CIGSe as

6

Assuming equilibration during PDT at 350 °C, the estimated Na concentrations in ACIGSe with GGI = 0.3 and AAC of 0.2, 0.5, and 1.0 are roughly 4, 17, and 120 times higher than in CIGSe, respectively. Importantly, the predicted four-fold increase in the Na content for AAC = 0.2 is not far from our chemical quantifications of GIs using APT. The value for AAC = 0.5 is also in reasonable agreement with one order-of-magnitude higher Na content measured with SIMS in the top ACIGSe cell of the tandem device fabricated by Kim et al.,¹² but is lower than that reported in their earlier work,¹¹ possibly because of the presence of impurity phases and/or variations under the growth conditions. In contrast, the predicted increase in the Na concentration for AAC = 1.0 does not match the ∼10 times higher Na content from our APT measurements on the Cu-free reference sample (see Figure 5), although the trend is correct on a qualitative level. A likely explanation for the discrepancy is that the maximum solubility is not reached during processing for this sample because much greater amount of Na from the substrate is required to saturate the absorber. Further analysis of this hypothesis from the perspective of alloy formation rather than the dilute limit approximation is provided below.

The observed trends in solubility versus AAC can be explained by a mismatch of ionic sizes of the group-I cations and alkali impurities. According to Shannon,⁷⁹ crystal ionic radii of four-coordinated ions are 1.13 Å for Na¹⁺, 1.51 Å for K¹⁺, 0.74 Å for Cu¹⁺, and 1.14 Å for Ag¹⁺. As one can see, the Na¹⁺ ion is considerably larger than Cu¹⁺ but of the same size as Ag¹⁺, suggesting that Alk_I induces less stress on the lattice and thus has lower formation energy (on average) in Ag-rich ACIGSe. The size mismatch increases for heavier alkalis, but it always remains smaller in Ag-based systems, resulting in a general tendency of increasing solubility with AAC.

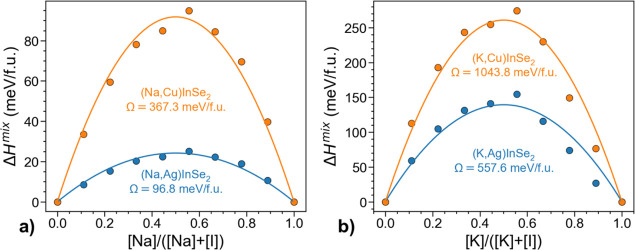
To further explore the role of lattice stress and consider the alkali incorporation beyond the dilute limit, we also computed mixing enthalpies of (Na,Ag)InSe₂, (Na,Cu)InSe₂, (K,Ag)InSe₂, and (K,Cu)InSe₂ alloys as

7

where E_tot represents computed total energies for supercells of different compositions. The Ga-based alloys were not considered because of the lack of structural information on NaGaSe₂ in the literature, which might be a sign of its instability. The alloy interaction (bowing) parameters for mixing enthalpies were extracted from parabolic fits to the computed energy values, as shown in Figure 7. Furthermore, the consolute temperatures (the points at which the alloys become fully miscible) were estimated from a regular solution approximation as T_c = Ω/2k_B. The obtained interaction parameters Ω for the respective systems are 96.8, 367.3, 557.6, and 1043.8 meV/f.u. (per formula unit), which yield consolute temperatures of 288, 1858, 2962, and 5783 °C, in agreement with the earlier results for Cu-based chalcopyrites.¹⁵ As expected, the mixing enthalpies are lower in Ag-based systems because of the aforementioned smaller ionic size mismatch. This tendency was also observed for Rb and Cs, but the corresponding mixing parameters are not extracted because of severe relaxation experienced by the alkali-rich supercells. These consolute temperatures for all except (Na,Ag)InSe₂ alloys are beyond the reach of synthesis as the chalcopyrite systems melt at lower temperatures.⁸⁰ As such, the wide miscibility gap during processing clearly limits alkali solubility for most systems. However, the exception of (Na,Ag)InSe₂ means that this alloy can form during absorber deposition (550 °C) as well as during the PDT (350 °C). Practically, it means that the solubility of Na in AgInSe₂ absorbers is not thermodynamically limited but instead governed by the processing parameters (primarily time and temperature because of the thermally activated nature of Na in-diffusion from the substrate), as we hypothesized above. Considering that the dependence of Na_I formation energy on GGI (see Figure 6a) is weak, this conclusion can also be generalized to all AIGSe alloys, thereby explaining why the increase in the Na concentration in the Cu-free reference AIGSe sample deduced from the APT analysis was below the predicted equilibrium value.

Figure 7.

Computed mixing enthalpies for (Alk,Cu)InSe₂ and (Alk,Ag)InSe₂ alloys in the case of (a) Alk = Na and (b) Alk = K. The markers and lines represent the computed values and parabolic fits, respectively.

4. Conclusions

In this work, we studied the relationship of Ag alloying in CIGSe on the alkali dispersion in bulk and at interfaces to better understand the enhancements in device performance related to the addition of Ag. Experimental analysis is performed for ACIGSe absorbers deposited on two different (K- and Na-rich) glass substrate types. The ion exchange mechanism commonly discussed in the literature for light and heavy alkali elements in CIGSe is observed for Na and K distributions in GBs and GIs. Alkali segregations at the CdS/ACIGSe and rear interfaces, as well as in the GBs, were detected. K segregation appears to dominate over Na at the GBs in CIGSe and ACIGSe. While this behavior can be expected with the HSG substrate, simply because more K is supplied, stronger Na segregations would be expected when using the SLG substrate if not for the ion exchange mechanism. At the same time, GIs contain greater concentrations of Na than K, even for the absorber grown on the HSG substrate. This indicates higher solubility of Na in GIs compared to K. Furthermore, it is found that the Na concentration in the GIs increases with Ag-alloying. The nanoscale experimental analysis was combined with first-principles calculations, providing strong indications of increased solubility of alkali elements in GIs of ACIGSe compared to CIGSe. Such a behavior stems from a mismatch of ionic sizes of group-I cations and alkali impurities, with Na¹⁺ ions, for instance, being similar in size to Ag¹⁺ but considerably larger than Cu¹⁺, and hence, inflicting less stress upon formation of Na_I in Ag-alloyed CIGSe. The same rationale applied to heavier alkali elements as well. Hence, an increase in V_OC of CIGSe devices with the addition of Ag can be related to higher acceptance of alkali elements in the matrix, as well as improved band alignments and/or other factors discussed earlier. The fundamental difference in alkali dispersion demonstrated here for Ag-alloyed CIGSe absorbers should be taken into consideration when designing optimized alkali treatments in single- or multiple-junction solar cells using these types of absorbers.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.0c20539.

• Local chemical analysis of the CdS/ACIGSe interface; as-computed formation energies of Alk_I in ACIGSe supercells without additional processing with the CE formalism; defect formation energies assuming equilibrium between (Ag,Cu)(In,Ga)₃Se₅ and ACIGSe with the same AAC and GGI ratios; and primitive cell used for simulation of (Ag,Cu)(In,Ga)₃Se₅ (in CIF format) (PDF)

Swedish Foundation for Strategic Research, grant/award number: RMA15-0030.

The authors declare no competing financial interest.