Probing Local Electrostatics of Glycine in Aqueous Solution by THz Spectroscopy

Abstract

Based upon precise terahertz (THz) measurements of the solvated amino acid glycine and accompanying ab‐initio molecular‐dynamics simulations, we show that the N‐C‐C‐O open/close mode at 315 cm⁻¹ serves as a sensitive, label‐free probe for the local protonation of the amide group. Experimentally, we can show that this holds not only for glycine but also for diglycine and valine. The approach is more general, since the changes due to protonation result in intensity changes which can be probed by THz time domain (0–50 cm⁻¹) as well as by precise THz‐FT spectroscopy (50–400 cm⁻¹). A detailed analysis allows us to directly correlate the titration spectra with pK _a values. This demonstrates the potential of THz spectroscopy to probe the charge state of a natural amino acid in water in a label‐free manner.

Based upon precise terahertz (THz) measurements of the solvated amino acid glycine and accompanying ab‐initio molecular‐dynamics simulations, it is shown that the N‐C‐C‐O open/close mode at 315 cm⁻¹ serves as a sensitive, label‐free probe for the local protonation of the amide group.

Introduction

Fundamental solvent properties such as pH and polarity are well defined for homogeneous bulk liquids. However, evidence is accumulating that rather the local than the global properties determine the reaction rate or control the biological function. Downsizing the concepts of electrostatics and pH to a local property is an experimental as well as a theoretical challenge.[ ¹ , ² ] The most prominent sensor molecule to probe the local polarity of a solvent is Reichardt's dye. ^[3] Due to its solvatochromic properties the dye changes its color depending on the polarity of the solvent. Following this approach, a variety of fluorescent based sensor molecules has been developed. ^[4] Boxer, Jan and co‐workers introduced a fluorescent amino acid, Aladan, which can probe the electrostatic character of a protein at multiple sites. ^[5] The Stark shift of vibrational probes which are introduced on inhibitors, by modification of amino acids and by incorporation of unnatural amino acids, has been used to map electric fields of proteins. ^[6]

Based on these local probes, local electric fields in the active site of ketosteroid isomerase could be mapped demonstrating their relevance for catalysis.[ ⁷ , ⁸ ] Site specific incorporation of vibrational probes allowed to study the crucial role of protein electrostatics for enzymatic catalysis. ^[9] The local electrostatic interaction or the local pH can be probed by Stark shift of a specific IR absorption band ^[10] and also by a frequency shift of the EPR and NMR signals via a spin probe. ^[11] In all these cases, the incorporation of a synthetic molecular label is mandatory. However, inserting a probe might affect function. We want to explore here whether it is possible to probe in a label‐free manner the changes of the local electric field via THz spectroscopy.

In a theoretical study, Fedotova et al. simulated ion binding between chloride salts and charged groups of the zwitterion glycine and found strong electrostatic interactions between both. ^[12] A water‐mediated interaction of cations with glycine, in agreement with the Hofmeister series, has also been indirectly proposed by the application of Raman and dielectric spectroscopies. ^[13] So far, the lack of a general experimental technique for measuring electrostatic interaction of unlabeled probes has made it impossible to address experimentally even the most basic questions: How localized is Na⁺ or Cl⁻ at the anionic or cationic group of a zwitterion? How does this affect the electrostatic interaction and how does it affect the hydration water?

In the present study, we want to observe the changes in the THz spectrum of solvated glycine upon protonation. Glycine is the simplest of the 20 proteinogenic standard amino acids and has served as a prototype for many hydration studies of zwitterions.[ ¹² , ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ ] Under physiological conditions glycine is a zwitterion with a negatively charged carboxyl group and a positively charged amino group. Under acidic/basic conditions glycine is present in a protonated/deprotonated state,[ ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ , ²¹ ] whereas it is neutral in the gas phase. ^[22] Recently we reported the THz absorption spectra of solvated glycine. ^[23] In conjunction with ab initio molecular dynamics (AIMD) simulations ^[24] we were able to decipher the low frequency spectrum of the zwitterion. The spectrum could be decomposed into contributions due to intramolecular modes of the supermolecular solvation complex and intermolecular modes of the solute with the solvent such as cage libration and cage rattling modes. ^[23] The so‐called N‐C‐C‐O open/close mode of glycine at 315 cm⁻¹ has been identified as the most pronounced mode in the THz absorption spectrum.

Here, we report precise measurements of glycine in water in the THz region as a function of pH, which show that the low frequency spectrum including the N‐C‐C‐O open/close mode is very sensitive to protonation. Beyond the specific case, we demonstrate that the intensity of the THz spectrum of the solvated amino acid serves as a non‐invasive probe of the local pH value.

Results and Discussion

We present the results of a titration study of glycine aqueous solutions. In general, effective THz absorption coefficients, ${\alpha }_{\mathrm{s}}^{\mathrm{eff}}$ , are obtained by subtracting the concentration‐weighted bulk water absorption from that of each sample solution. In order to depict the changes upon titration, here, we subtract the THz absorption of 1 m glycine solution from the 1 m glycine HCl/NaOH solution and define the difference [Eq. 1]:

$${\displaystyle {\alpha }_{\mathrm{Gly}+\mathrm{HCl}/\mathrm{NaOH}}^{\mathrm{eff}}-{\alpha }_{\mathrm{Gly}}^{\mathrm{eff}}.}$$ (1)

In Figure 1 we plot the result as a function of HCl/NaOH concentration, see SI for details. Below 67 cm⁻¹, we recorded the spectrum using our THz time domain spectrometer (THz‐TDS). A Bruker Vertex 80v Fourier‐Transform spectrometer was used to obtain spectra in the frequency range between 50 and 400 cm⁻¹. For all the details of the experiment, see SI and Ref. [23] We want to point out that the spectra recorded with the two different spectrometers fit together nearly seamlessly without any adjustment, thus demonstrating the precision of absolute THz intensities independent of the set‐up, see Figure 1.

Figure 1.

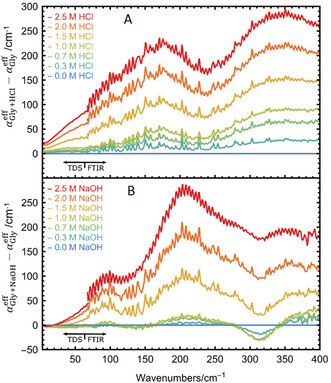
Effective absorption difference ${\alpha }_{\mathrm{Gly}+\mathrm{HCl}/\mathrm{NaOH}}^{\mathrm{eff}}-{\alpha }_{\mathrm{Gly}}^{\mathrm{eff}}$ as a function of HCl (A) and NaOH (B) concentrations in the frequency range between 0 and 400 cm⁻¹. Signals below 67 cm⁻¹ were recorded with a THz‐TDS and signals above 67 cm⁻¹ were recorded with a FTIR spectrometer (see text). All measurements were carried out at 20 °C and low humidity.

The effective absorption spectrum of solvated glycine in pure water is known to be dominated by the cage librations and rattling modes of the solute within its hydration cage below 100 cm⁻¹, the glycine‐water hydrogen bond stretching modes at about 200 cm⁻¹ and at the N‐C‐C‐O open/close mode at 315 cm⁻¹.[ ²⁵ , ²⁶ ] Upon increasing HCl concentration, we observe an increase in absorption with increasing concentration. These spectra show pronounced broad absorption bands at 170 and 340 cm⁻¹ and a shoulder at 100 cm⁻¹. In contrast, upon titration with NaOH (up to 1 m) the intensity at 315 cm⁻¹ decreases with increasing concentration, whereas narrow bands appear at 95 cm⁻¹ and 210 cm⁻¹.

For co‐solvent concentrations ≥1 m, glycine is fully titrated. Thus, the observed spectrum contains not only contributions from glycine but from solvated HCl or NaOH (see SI for details). To separate the spectral contributions of the different protonation states of Gly, as well as those due to the co‐solvents HCl and NaOH, we employed a principal component analysis (PCA) approach. PCA allows us to dissect the spectra into their individual components with respect to one variable, here the co‐solvent concentration.[ ²⁷ , ²⁸ , ²⁹ ] A more detailed description of the titration studies of glycine as a function of NaOH and HCl concentrations is presented in the SI.

In Figure 1 a, we plot ${\alpha }_{\mathrm{Gly}+\mathrm{HCl}}^{\mathrm{eff}}-{\alpha }_{\mathrm{Gly}}^{\mathrm{eff}}$ , which is defined for acidic solutions as the difference of the effective absorption of the glycine + HCl sample (compared to bulk water) and the effective absorption of solvated glycine (compared to bulk water). This can be dissected into [Eq. 2]:

$${\displaystyle {\alpha }_{\mathrm{Gly}+\mathrm{HCl}}^{\mathrm{eff}}-{\alpha }_{\mathrm{Gly}}^{\mathrm{eff}}=c_{H_3{O}^{+}}·{ϵ}_{H_3{O}^{+}}^{\mathrm{eff}}+c_{\mathrm{C}{\mathrm{l}}^{-}}·{ϵ}_{\mathrm{C}{\mathrm{l}}^{-}}^{\mathrm{eff}}+c_{\mathrm{Gl}{\mathrm{y}}^{\pm }}·{ϵ}_{\mathrm{Gl}{\mathrm{y}}^{\pm }}^{\mathrm{eff}}+c_{{\mathrm{Gly}}^{+}}·{ϵ}_{{\mathrm{Gly}}^{+}}^{\mathrm{eff}}-c_{\mathrm{Gly}}·{ϵ}_{{\mathrm{Gly}}^{\pm }}^{\mathrm{eff}},}$$ (2)

where c _Gly is the glycine concentration obtained from the (weighted) amount of glycine added to the solution and the solution density. An analogous equation is used for NaOH titration, whereas c _Gly is 1 m for all samples. For the concentrations of H₃O⁺, Cl⁻, Gly^± and Gly⁺ we used the following equations, with β being the dissociation degree calculated by the Henderson‐Hasselbalch equation (assuming full dissociation of HCl, see the SI for details) [Eqs. 3–6]:

$${\displaystyle c_{{\mathrm{H}}_3{\mathrm{O}}^{+}}=c_{\mathrm{HCl}}-c_{\mathrm{Gly}}·\beta }$$ (3)

$${\displaystyle c_{{\mathrm{Cl}}^{-}}=c_{\mathrm{HCl}}}$$ (4)

$${\displaystyle c_{{\mathrm{Gly}}^{\pm }}=c_{\mathrm{Gly}}·\left(1-\beta \right)}$$ (5)

$${\displaystyle c_{{\mathrm{Gly}}^{+}}=c_{\mathrm{Gly}}·\beta .}$$ (6)

By insertion into Equation (2) we obtain [Eq. 7]:

$${\displaystyle {\alpha }_{\mathrm{Gly}+\mathrm{HCl}}^{\mathrm{eff}}-{\alpha }_{\mathrm{Gly}}^{\mathrm{eff}}=c_{\mathrm{HCl}}·\left({ϵ}_{H_3{O}^{+}}^{\mathrm{eff}}+{ϵ}_{\mathrm{C}{\mathrm{l}}^{-}}^{\mathrm{eff}}\right)+c_{\mathrm{Gly}}·\beta ·\left({ϵ}_{\mathrm{Gl}{\mathrm{y}}^{+}}^{\mathrm{eff}}-{ϵ}_{\mathrm{Gl}{\mathrm{y}}^{\pm }}^{\mathrm{eff}}-{ϵ}_{H_3{O}^{+}}^{\mathrm{eff}}\right).}$$ (7)

Based on Equation (7) and the results of our analysis of the titration study, we are able to dissect the spectra into $\left({ϵ}_{{\mathrm{H}}_3{\mathrm{O}}^{+}}^{\mathrm{eff}}+{ϵ}_{{\mathrm{Cl}}^{-}}^{\mathrm{eff}}\right)$ and $\left({ϵ}_{{\mathrm{Gly}}^{+}}^{\mathrm{eff}}-{ϵ}_{Gl{y}^{\pm }}^{\mathrm{eff}}-{ϵ}_{{\mathrm{H}}_3{\mathrm{O}}^{+}}^{\mathrm{eff}}\right)$ . In a similar way, the titration induced changes upon addition of NaOH allow us to deduce $\left({ϵ}_{{\mathrm{Gly}}^{-}}^{\mathrm{eff}}-{ϵ}_{Gl{y}^{\pm }}^{\mathrm{eff}}-{ϵ}_{{\mathrm{OH}}^{-}}^{\mathrm{eff}}\right)$ .

In a second step, we measured separately the absorption coefficients of 1 m aqueous solutions of glycine, HCl and NaOH, respectively. In brief, solvated HCl displays the typical Cl⁻ rattling mode at 180 cm⁻¹ and two peaks at 120 and 340 cm⁻¹, assigned to a low‐frequency hydration water mode and to the rattling motion of H₃O⁺ in its solvation cage, respectively. ^[27] The NaOH spectrum has two pronounced bands at about 100 and 200 cm⁻¹ and a broad band at 310 cm⁻¹. Based on our previous studies on salts, the modes at 100 cm⁻¹ is assigned to the Na⁺ rattling modes.[ ²⁸ , ³⁰ ] We propose that the modes at 200 and 310 cm⁻¹ can be attributed to a mode of the solvated OH⁻. Using the recorded spectra of ${ϵ}_{\mathrm{HCl}}\approx {\alpha }_{{\mathrm{H}}_3{\mathrm{O}}^{+}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Cl}}^{-}}^{\mathrm{eff}}$ and ${ϵ}_{\mathrm{NaOH}}\approx {\alpha }_{{\mathrm{OH}}^{-}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Na}}^{+}}^{\mathrm{eff}}$ of 1 m HCl and 1 m NaOH solutions, respectively, and by adding the spectrum of the zwitterion $\left({\alpha }_{{\mathrm{Gly}}^{+}}^{\mathrm{eff}}-{\alpha }_{Gl{y}^{\pm }}^{\mathrm{eff}}-{\alpha }_{{\mathrm{H}}_3{\mathrm{O}}^{+}}^{\mathrm{eff}}\right)$ at 1 m, we obtain [Eqs. 8–9]:

$${\displaystyle {\alpha }_{\mathrm{Gly}+\mathrm{HCl}}^{\mathrm{eff}}=[{\alpha }_{{\mathrm{Gly}}^{+}}^{\mathrm{eff}}-{\alpha }_{{\mathrm{Gly}}^{\pm }}^{\mathrm{eff}}-{\alpha }_{{\mathrm{H}}_3{\mathrm{O}}^{+}}^{\mathrm{eff}}]+\left[{\alpha }_{{\mathrm{Gly}}^{\pm }}^{\mathrm{eff}}\right]+[{\alpha }_{{\mathrm{H}}_3{\mathrm{O}}^{+}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Cl}}^{-}}^{\mathrm{eff}}]={\alpha }_{{\mathrm{Gly}}^{+}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Cl}}^{-}}^{\mathrm{eff}}}$$ (8)

$${\displaystyle {\alpha }_{\mathrm{Gly}+\mathrm{NaOH}}^{\mathrm{eff}}=[{\alpha }_{{\mathrm{Gly}}^{-}}^{\mathrm{eff}}-{\alpha }_{{\mathrm{Gly}}^{\pm }}^{\mathrm{eff}}-{\alpha }_{{\mathrm{OH}}^{-}}^{\mathrm{eff}}]+\left[{\alpha }_{{\mathrm{Gly}}^{\pm }}^{\mathrm{eff}}\right]+[{\alpha }_{{\mathrm{OH}}^{-}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Na}}^{+}}^{\mathrm{eff}}]={\alpha }_{{\mathrm{Gly}}^{-}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Na}}^{+}}^{\mathrm{eff}}}$$ (9)

The resulting spectra, namely ${\alpha }_{{\mathrm{Gly}}^{+}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Cl}}^{-}}^{\mathrm{eff}}$ and ${\alpha }_{{\mathrm{Gly}}^{-}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Na}}^{+}}^{\mathrm{eff}}$ , are displayed in Figure 2 A. Moreover, the extracted zwitterionic glycine spectrum (grey) is in excellent agreement with the previously published THz absorption spectrum of a pure aqueous glycine solution. ^[23]

Figure 2.

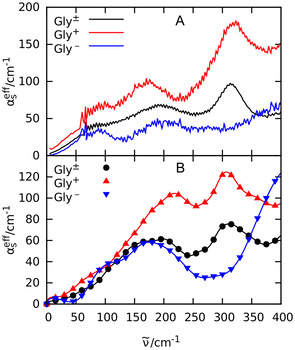
(A) Experimental effective absorption spectrum of 1 m aqueous solution of glycine (black) and the reconstructed absorption spectra of ${\alpha }_{{\mathrm{Gly}}^{+}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Cl}}^{-}}^{\mathrm{eff}}$ (red) and ${\alpha }_{{\mathrm{Gly}}^{-}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Na}}^{+}}^{\mathrm{eff}}$ (blue); see text. (B) Computed effective absorption spectrum of zwitterionic glycine Gly^± (black circles), Gly⁺ + Cl⁻ (red triangles pointing up), and Gly⁻+ Na⁺ (blue triangles pointing down); see Simulation Details for methodology and setup.

Interestingly, the ${\alpha }_{{\mathrm{Gly}}^{+}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Cl}}^{-}}^{\mathrm{eff}}$ spectrum shows increased THz intensities compared to the glycine spectrum in the entire spectral range. However, the intensity increase of the prominent N‐C‐C‐O band at 315 cm⁻¹ is most pronounced, see peak height difference in Figure 2 A.

In contrast, for ${\alpha }_{{\mathrm{Gly}}^{-}}^{\mathrm{eff}}+{\alpha }_{{\mathrm{Na}}^{+}}^{\mathrm{eff}}$ , the intensity is decreased over the entire spectral range—compared to the solvated glycine spectrum with the exception of the high frequency regime (above 350 cm⁻¹). We want to point out that in this case the prominent N‐C‐C‐O band at 315 cm⁻¹ is missing completely.

In summary, we find a prominent spectral change upon protonation and deprotonation of glycine in the THz spectral range, particular for the band at 315 cm⁻¹. Previously, we assigned this band to an intramolecular N‐C‐C‐O open/close mode of the zwitterionic glycine. ^[23] While in case of protonation of the carboxyl group (Gly⁺ + Cl⁻ spectrum) the N‐C‐C‐O open/close mode is still clearly visible, this spectral signature is essentially absent in case of a deprotonation of the amino group (Gly⁻ + Na⁺ spectrum). Thus, the charges localized at the amino group—and not those at the carboxyl group—seem to be crucial for the high intensity in that THz spectral window.

For comparison, we investigated glycine aqueous solutions upon addition of NaCl, NaNO₃ and CsBr. The corresponding THz spectra are shown in Figure S8. The results show that upon addition of these salts, intensity in the low frequency range is nearly not affected. In particular, no changes within experimental uncertainty were observed in the frequency range below 200 cm⁻¹. This is in agreement with previous mid‐infrared studies. ^[21]

In order to unravel the underlying molecular mechanism of the observed changes upon titration, we carried out complementary AIMD simulations for all three charge states of glycine in water as described in the SI. The computed effective THz spectra as displayed in Figure 2 B include the counterion contributions in case of Gly⁺ and Gly⁻, being absent for the zwitterion Gly^±, to enable a one‐to‐one comparison to the corresponding experimental spectra in Figure 2 A. As shown in Figure 3 A, the experimentally observed changes of the prominent band at 315 cm⁻¹ depending on pH can be convincingly reproduced from the corresponding mode selective spectra of the N‐C‐C‐O open/close mode depending on the proper protonation state of glycine (obtained from SSC analysis, see Simulation Details in SI). We note in passing that the slight blue‐shift of the peak at roughly 220 cm⁻¹ in the computed Gly⁺ spectrum compared to experiment is unrelated to solvated glycine itself but can rather be traced back to a corresponding computational blue‐shift of the counter ion, Cl⁻, as demonstrated in supporting Figure S13.

Figure 3.

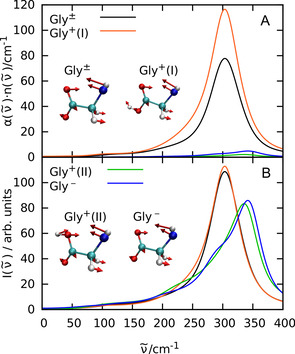
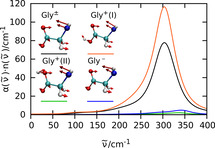
Mode selective THz spectra (A) and mode selective vibrational density of states (B) of the intramolecular N‐C‐C‐O open/close mode of zwitterionic glycine (black), protonated glycine in trans (I: red) and cis (II: green) conformation, and deprotonated glycine (blue) in water. The insets visualize this mode for all four cases as indicated; note that the hydrogen atoms at the N terminus have been replaced by a single (average) pseudo site for the sake of simplification. The relative transition dipoles and thus the corresponding THz intensities in panel A from these modes are 100 % (Gly^±), 144 % (Gly⁺ (I)), 4 % (Gly⁺ (II)), and 8 % (Gly⁻) implying that the N‐C‐C‐O open/close mode of both, Gly⁺ (II) and Gly⁻ is essentially THz silent as discussed in the text.

More detailed analyses reveal that the protonated species features two different protonation states, one with the proton at the oxygen closer to the NH₃ ⁺ group (cis conformation or II) and one with the proton at the other oxygen (trans or I). The THz active N‐C‐C‐O open/close mode of the zwitterionic and the trans‐protonated glycine are both located at about 304 cm⁻¹ and contribute prominently to the respective total THz absorption spectra in Figure 2 B, whereas the essentially THz inactive N‐C‐C‐O open/close mode of both, deprotonated and cis‐protonated glycine are blue‐shifted to 342 and 336 cm⁻¹, respectively, as nicely revealed by their vibrational density of states in Figure 3 B.

Interestingly, the changes of THz intensities are not due to a suppressed particle dynamics as a result of deprotonation, as can be seen from the mode analysis of the vibrational density of states in Figure 3 B. Instead, the distinct THz responses can be attributed solely to the changes in the transition dipoles: While the trans‐protonated glycine has a 44 % larger transition dipole for this mode compared to the zwitterionic case, the deprotonated and cis‐protonated glycine have only a transition dipole of 8 % and 4 % compared to the zwitterionic transition dipole of this mode (insets of Figure 3). These vastly different transition dipole moments can be easily explained by noting that in the N‐C‐C‐O open/close mode the heavy COO⁻ group does not move much and most motion stems from the N terminus. In the deprotonated case, the NH₂ group is formally charge neutral, and, hence, does not contribute much to a transition dipole. In contrast, the positively charged NH₃ ⁺ group in the other three cases contributes significantly to the transition dipole. But why then is the N‐C‐C‐O open/close mode of the protonated cis conformer THz silent as seen for deprotonated glycine? In this cis‐protonated case, the contribution of the NH₃ ⁺ group is nearly canceled by the additional proton which moves counter to the NH₃ ⁺ group in that backbone opening and closing mode. In contrast, the additional proton in the trans‐protonated glycine moves in phase with the NH₃ ⁺ group. This additional positive correlation even enhances the transition dipole moment over the zwitterionic case.

Overall, the THz spectra at 315 cm⁻¹ of both, zwitterionic and (trans‐) protonated glycine in water, experimentally corresponding to neutral and acidic pH conditions, respectively, are dominated by the prominent N‐C‐C‐O open/close mode, whereas this very mode is THz silent in case of deprotonated glycine as measured at basic pH.

In order to test whether our approach to use the N‐C‐C‐O open/close mode as a label‐free probe for local pH around proteins can be generalized beyond glycine, we recorded the THz spectra of valine and diglycine. Interestingly, we observe here the same phenomenon: While the N‐C‐C‐O open/close mode is slightly shifted to about 350 and 340 cm⁻¹, respectively (see Refs. [26] and [31]), we measure for this mode a similar increase in intensity upon protonation, see SI for details.

In a more general approach, we combined the results from PCA analysis and Henderson‐Hasselbalch equation to deduce the pK _a and pK _b values of solvated glycine, valine and diglycine solely based on their THz spectra. As is well known, pK _a is equal to pH when the acid and the conjugate base are present in equal amounts. Thus, we first determine the turning point of the scores of the PCA of the titration THz spectra. At this concentration we assume full protonation. This concentration was then divided by a factor of two to determine the concentration at which pH=pK _a. The results are listed in Table 1. Remarkably, these are in good agreement with the respective literature values. Thus, we conclude that precise intensity measurements in the THz range are a general method to deduce the local pK _a of amino acids and peptides, even in more complex systems.

Table 1.

Comparison of the pK _a and pK _b values for glycine, valine and diglycine aqueous solutions as deduced from the observed intensity changes of the low frequency spectrum with literature values.

	pK a	pK b	Reference
glycine	2.34	9.58	[32]
	2.20±0.15	9.76±0.56	This work
valine	2.27	9.52	[32]
	2.93±0.94	8.98±0.72	This work
diglycine	3.13	8.10	[32]
	3.30±0.25	8.10±0.81	This work

Due to a coupling of low frequency modes, intensity changes can be probed in the entire frequency range up to 400 cm⁻¹. By combining THz‐TDS and FTIR measurements on glycine we are able to deduce even more precise pK _a value than by considering only the frequency range >200 cm⁻¹.

Conclusion

In summary, we find that the low‐frequency (<400 cm⁻¹) spectrum of glycine in aqueous environments can serve as a sensitive, label‐free probe for the protonation state of an amino group. This study paves the way for more comprehensive investigations in the THz spectral regime to determine in situ local pK _a values and to map local electrostatic interactions at the surface of biomolecules.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

F. Sebastiani, C. Y. Ma, S. Funke, A. Bäumer, D. Decka, C. Hoberg, A. Esser, H. Forbert, G. Schwaab, D. Marx, M. Havenith, Angew. Chem. Int. Ed. 2021, 60, 3768.