Combining T₂ measurements and crusher gradients into a single ASL sequence for comparison of the measurement of water transport across the blood–brain barrier

Abstract

Purpose

Arterial spin labeling can be used to assess the transition time of water molecules across the blood–brain barrier when combined with sequence modules, which allow a separation of intravascular from tissue signal. The bipolar gradient technique measures the intravascular fraction by removing flowing spins. The T₂‐relaxation‐under‐spin‐tagging (TRUST) technique modulates the TE to differentiate between intravascular and extravascular spins based on T₂. These modules were combined into a single time‐encoded pseudo‐continuous arterial spin labeling sequence to compare their mechanisms of action as well as their assessment of water transition across the blood–brain barrier.

Methods

This protocol was acquired on a scanner with 9 healthy volunteers who provided written, informed consent. The sequence consisted of a Hadamard‐encoded pseudo‐continuous arterial spin labeling module, followed by the TRUST module (effective TEs of 0, 40, and 80 ms) and bipolar flow‐crushing gradients (2, 4, and ∞ cm/s). An additional experiment was performed with TRUST and a 3D gradient and spin‐echo readout.

Results

Gradients imperfectly canceled the intravascular signal, as evidenced by the presence of residual signal in the arteries at early postlabeling delays as well as the underestimation of the intravascular fraction as compared with the TRUST method. The TRUST module allowed us to detect the transport of water deeper into the vascular tree through changes in T₂ than the used crusher gradients could, with their limited b‐value.

Conclusion

Of the implemented techniques, TRUST allowed us to follow intravascular signal deeper into the vascular tree than the approach with (relatively weak) crusher gradients when quantifying the transport time of water across the blood–brain barrier.

1. INTRODUCTION

The blood–brain barrier (BBB) is a boundary between the intravascular and extravascular spaces in the brain. Its role is to regulate the exchange of molecules such as nutrients between these spaces and prevent pathogens from entering. ¹ , ² , ³ Although many organs possess a similar membrane, the BBB distinguishes itself by the presence of very tight junctions that prohibit bulk flow of water. Water transport across the BBB is mediated in large part through aquaporin‐4 channels ⁴ and is on the order of magnitude of diffusion. ¹ In contrast, gadolinium‐based contrast‐agent molecules cannot cross the healthy BBB because of their size. In pathology, the BBB progressively disintegrates and allows easier exchange of molecules, including contrast agents. This BBB break down has been observed in neurodegenerative diseases such as Alzheimer’s disease ⁵ , ⁶ as well as in epilepsy, stroke, brain tumors, and more generally in aging brains. ² , ⁷ It remains unclear whether BBB disruptions are a cause or consequence of these neurological disorders. ⁷ Effective, noninvasive BBB characterization could shed light on this issue, by longitudinal monitoring of these disruptions.

There are several methods of assessing BBB integrity in vivo, each associated with their own limitations. Nuclear medicine uses radio‐labeled isotopes, which require injection and exposure to ionizing radiation. The CSF/serum albumin ratio can show protein leakage into the CSF, but requires a lumbar puncture and gives no localized information. Contrast‐enhanced CT has similar issues as nuclear imaging. ⁸ In MRI, gadolinium‐based contrast agents are used in dynamic susceptibility contrast imaging MRI as well as DCE‐MRI, with the latter considered the gold standard in MRI‐based BBB assessment. The need for contrast injection is a limiting factor for repeated measurements, and it suffers from high variability between sites and protocols. ⁸ Moreover, in normally functioning BBB, there is minimal transport of the gadolinium‐based molecules to measure, limiting detection of early BBB disruption. Water, moreover, is a much smaller molecule that is transported across the BBB at varying rates in health and disease; hence, using it as a tracer could allow for the measurement of more subtle changes in BBB integrity.

Arterial spin labeling (ASL) is a method that measures tissue perfusion, using water as an endogenous tracer. Therefore, ASL contrast could be leveraged to measure the transport of water across the BBB in a noninvasive manner, provided that the intravascular and extravascular water signal can be differentiated. ⁹ Two such methods are investigated in this study. The first is T₂ relaxation under spin‐tagging (TRUST), which allows the localization of the label in the intravascular and extravascular compartments ¹⁰ , ¹¹ by exploiting significant differences between blood and tissue T₂. ¹² , ¹³ The second method applies bipolar crusher gradients (in literature, both relatively weak crusher gradients that target fast flowing spins [b‐values below 20 s/mm²] as well as stronger, higher b‐value gradients that target diffusing spins have been used), which remove signal from the vasculature based on the velocity of blood along the gradient direction, making it possible to calculate the proportion of signal in the vascular and tissue compartments. ¹⁴ , ¹⁵ , ¹⁶ Both methods have been used to investigate the distribution of the ASL signal in these compartments and its position along the vascular tree. Combining them with a dynamic method such as Hadamard encoding ¹⁷ , ¹⁸ offers a time‐resolved portrait of the transition across the BBB. ¹⁰ , ¹⁹ , ²⁰ , ²¹ There has been no study directly comparing the results of TRUST and motion‐sensitizing gradient techniques. This paper aims to accomplish this by combining both contrast mechanisms into a single time‐encoded ASL sequence, as a means to gather more insight into their different mechanisms of action on the ASL signal and their comparative strengths and weaknesses in imaging the water transition across the BBB. In addition, after one of the methods appeared to be sensitive to the transition of the ASL signal deeper into the vasculature, it was combined on its own with a more efficient readout to reduce scan length to a more clinically relevant time frame, while improving signal quality.

2. METHODS

2.1. Arterial spin labeling sequence

The main sequence in our protocol, shown schematically in Figure 1, combined a Hadamard‐8 pseudo‐continuous ASL preparation, followed by TRUST pulses before a 2D‐EPI readout with bipolar gradients. The Hadamard‐matrix block timings were chosen to encompass the full passage of the labeled water from large arteries to tissue perfusion. The first blocks are longer, to compensate for the reduction in signal due to T₁ relaxation, and the later blocks are shorter, to provide a higher temporal resolution during the vascular phase. Foci background‐suppression pulses were applied between blocks 2 and 3 and 6 and 7, a timing that was optimized to minimize signal from gray and white matter simultaneously. Within the dynamic imaging cycle (ie, repeats of one complete Hadamard‐encoding matrix), the different gradient and TRUST schemes were interleaved. Bipolar gradients were applied as crushers into the gradient‐echo readout, with three different velocity encodings (V_enc) of 2, 4, and ∞ (no gradient) cm/s, later referred to as the 100%, 50%, and 0% strength gradients, respectively. When interpreting these as diffusion‐weighting gradients, b‐values were 3.42, 0.85, and 0 s/mm², respectively. These gradients were applied in three perpendicular directions at once, resulting in a combined effective gradient of a factor $\sqrt{3}$ higher strength and effective b‐values of 10.3, 2.57, and 0 s/mm² in the composite direction. The TRUST method consisted of a T₂‐preparation (T₂‐prep) module whose effect was to modify the effective TE (eTE) of the sequence. The pulse train first incorporates a 90° pulse, tipping magnetization into the transverse plane, then followed by n equidistant 180° refocusing pulses to avoid ${\mathrm{T}}_2^{\ast }$ effects, and a final −90° pulse to tip it back along the longitudinal axis. Three schemes were used: no module (eTE = 0 ms), n = 4 module (eTE = 40 ms), and n = 8 module (eTE = 80 ms). More dynamics were acquired with longer eTEs to account for the lower SNR of these images. This resulted in an 18‐dynamic scheme, illustrated in Figure 1B, which was repeated four times. Eleven slices of 7‐mm thickness, without gaps, were acquired with an in‐plane acquisition resolution of 3.2 × 3.2 mm² and reconstructed at 2.75 × 2.75 mm² (FOV = 220 × 220 mm², SENSE factor = 2.5, single‐shot EPI readout, TE = 19 ms, TR = 4950 ms, and total scan time = 50 minutes).

FIGURE 1.

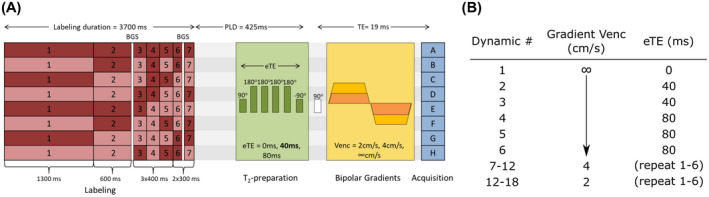
Magnetic resonance imaging sequence design. A, One of the lines of the Hadamard encoding matrix is applied (dark red, label; light red, control), followed by the T₂‐relaxation‐under‐spin‐tagging (TRUST) T₂‐preparation (T₂‐prep) module, then the bipolar gradient, and finally the image acquisition scheme. A‐H, The eight Hadamard images acquired following the corresponding line in the labeling scheme. B, The sequence interleaves the acquisition of different effective TEs (eTEs) and gradient strengths within the dynamic cycle. Abbreviations: BGS, background suppression pulse; PLD, postlabeling delay; V_enc, encoding velocity

In total, 9 volunteers were examined with this protocol (6 male and 3 female, ages 21‐36 years) and provided written, informed consent in compliance with our institutional review board guidelines. All examinations were carried out on a 3T Ingenia‐CX scanner (Philips, Best, the Netherlands) with a 32‐channel head coil.

2.2. Three‐dimensional gradient and spin‐echo protocol

An additional scan was performed in 1 other subject (female, 43 years old), which focused on the use of a 3D readout in combination with the TRUST measurements. This approach adheres to the consensus recommendation of using a 3D readout with ASL, ²² while showing the potential of the method for higher SNR in a shorter scan time when it is performed on its own without the combination with motion‐sensitizing gradients. In this protocol, the same Hadamard preparation and background suppression pulses were performed, followed by a T₂‐prep module with eTE = 0, 40, 80 or 160 ms, and finally a 3D gradient and spin‐echo readout (three shots, two averages per eTE, 3.75 × 3.80 × 7 mm³, SENSE = 2.3 [right–left], 11 slices while oversampling with a factor 1.8, reconstructed at 3 × 3 mm², TR/TE = 5100/10 ms, and scan time = 18 minutes 20 seconds).

2.3. Data analysis

All postprocessing and analysis were performed in MATLAB (The MathWorks, Natick, MA). A schematic representation of the analysis pipeline is shown in Figure 2A. Hadamard decoding was performed to extract the ASL signal at the seven postlabeling delays (PLDs). An arterial mask was created individually for each subject by thresholding the averaged ASL image over the first three time points, and similarly in the gray matter using the average of images from the last two time points. The threshold was selected manually so that anatomical features were preserved (such as the circle of Willis in the arterial mask and the gyri of the gray matter), and a similar number of voxels was included for all subjects (1043 ± 165 for the arteries, 4488 ± 385 for the gray matter). Voxels contained in the arterial mask were excluded from the gray‐matter mask. An example of this procedure is shown in Figure 2B. All images were smoothed using a 2 × 2‐voxel Gaussian kernel (σ = 1 voxel). The ASL signal was averaged over the arterial and gray‐matter masks separately and in combination. This resulted in signal curves through time for each combination of gradient strength and eTE. These values were normalized to the maximum of the noncrushed, eTE = 0 ms curve for each subject.

FIGURE 2.

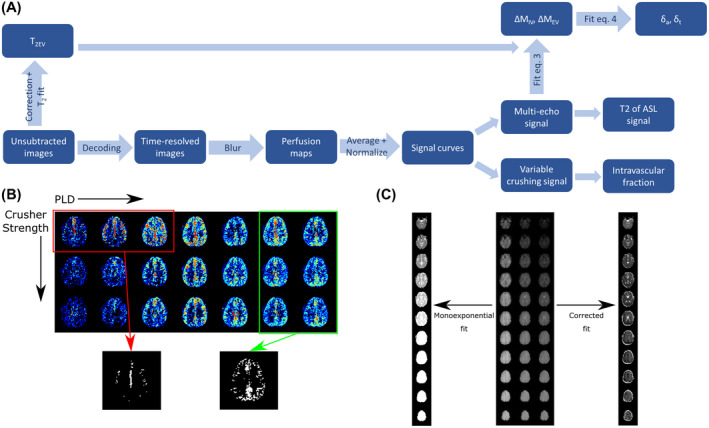
A, Data analysis pipeline. B, The masking step. The three earliest time points of the uncrushed perfusion maps are averaged and thresholded to obtain the vascular mask. The two last time points of images from all crusher settings are averaged and thresholded for the gray‐matter mask, and any voxels from the arterial mask are removed. C, The T_2EV maps without (left) and with (right) correction for the sequential slice acquisition

The TRUST sequence allows the measurement of T₂ by fitting the mono‐exponential decay of the signal as a function of eTE. This calculation was conducted on the average signal of the whole sampled population in the gray matter and arteries, using the nlinfit MATLAB function. In the 3D sequence, the T₂ was calculated on a voxel‐by‐voxel basis after smoothing using a Gaussian kernel (3 × 3 voxels, σ = 2). The intravascular fraction of the signal was calculated using the crushed and noncrushed signal, assuming that the bipolar gradients would crush all signal inside the vasculature. The intravascular fraction (IVF) was estimated as the percentage of the noncrushed signal, which is removed by the application of gradients: IVF = 100*(noncrushed − crushed)/noncrushed.

2.4. Two‐compartment dynamic analysis

To quantitatively assess water transport across the BBB, a compartmental analysis was performed. ⁴ This is used to separate and fit the vascular and extravascular components of the signal, extracting timing parameters corresponding to the label arrival time in the vasculature (arterial transit time, δ_a) and in the tissue (tissue transit time, δ_t). The difference between these gives an estimate of the transport time across the BBB, or exchange time, T_ex.

First, the T₂ value of tissue (T_2EV) is calculated by fitting the multi‐echo unsubtracted data to a mono‐exponential decay, which had to be modified to account for multislice acquisition (higher slices experience T₁ relaxation in the time between the T₂‐prep module and the excitation pulse, leading to an apparent decrease in measured T₂):

$$S_c=S_0\exp \left(‐eTE/T_{2EV}\right)$$ (1)

where T_2EV is the tissue T₂, and S_c is the corrected unsubtracted signal:

$$S_c=\frac{\left(S_m‐M_0\left(1‐q\right)\right)}{q}$$ (2)

$$q=\exp \left(\frac{‐\left(\left(n‐1\right)t_s+t_{2ex}\right)}{T_{1GM}}\right)$$

where S_m is the measured signal; M ₀ is the equilibrium magnetization (measured in a separate scan); n is the slice number, from the inferior to the superior; t_s is the acquisition time per slice; and t _{2 ex} is the time between the application of the TRUST module and the first slice acquisition. The T _{2 EV} maps obtained without and with this correction are shown in Figure 2C, where the increase in T₂ from the bottom slice (top of the image) to the top in the uncorrected images is clearly apparent. This step was omitted in the 3D data set, as the time between T₂‐prep and readout does not vary across slices in that case.

The T _{2 EV} calculated from the unsubtracted images was then included in the compartmental analysis:

$$\mathrm{\Delta }M=\mathrm{\Delta }{M}_{\mathit{EV}}\exp \left(‐eTE/T_{2EV}\right)+\mathrm{\Delta }{M}_{\mathit{IV}}\exp \left(‐eTE/T_{2IV}\right)$$ (3)

where ΔM is the ASL signal; ΔM_EV and ΔM_IV are the parts of it that arise from the tissue and vascular compartments, respectively; and T _{2 EV} and T _{2 IV} are the relaxation times for the corresponding compartments. All time points are fitted simultaneously, with T _{2 EV} taken from the unsubtracted signal and ΔM_EV, ΔM_IV, and T _{2 IV} fitted. Although the first two could vary, T _{2 IV} was held constant over the PLDs.

The dynamic model that was adapted from Ohene et al ⁴ for pseudo‐continuous ASL instead of flow‐sensitive alternating inversion recovery (FAIR) ²³ is as follows:

$$\mathrm{\Delta }{M}_{\mathit{IV}}\left(\omega ,\tau \right)=\left\{\begin{array}{c}0,\omega <{\delta }_a‐\tau \\ 0,\omega \ge {\delta }_t\\ 2M_0\frac{f}{\lambda }\alpha T_{1b}\left(\exp \left(\frac{\left(\text{min}\left({\delta }_a‐\omega ,0\right)‐{\delta }_a\right)}{T_{1b}}\right)‐\exp \left(\frac{‐\text{min}\left(\omega +\tau ,{\delta }_t\right)}{T_{1b}}\right)\right),\text{otherwise}\end{array}\right)$$ (4)

$$\mathrm{\Delta }{M}_{\mathit{EV}}\left(\omega ,\tau \right)=\left\{\begin{array}{c}0,\omega +\tau <{\delta }_t\\ 2M_0\frac{f}{\lambda }\alpha T_1^{\prime }{e}^{\frac{‐{\delta }_t}{T_{1b}}}\left(\exp \left(\frac{\text{min}\left({\delta }_a‐\omega ,0\right)}{T_1^{\prime }}\right)‐\exp \left(\frac{\left({\delta }_t‐\omega ‐\tau \right)}{T_1^{\prime }}\right)\right),\text{otherwise}\end{array}\right)$$

$$T_1^{\prime }=\frac{1}{T_{1GM}}+\frac{f}{\lambda }$$

where ω is the PLD; τ is the length of the labeling block; f is the cerebral blood flow; λ is the blood–brain partition coefficient (λ = 0.9); α is the labeling efficiency (α = 0.85); and T_{1 b} and T _{1 GM} are the relaxation times of blood (T _{1 b} = 1665 ms) and tissue (T_{1 GM} = 1250 ms). This analysis was conducted separately on the data from the three crusher settings, to compare the effect of crusher strength on the calculated transit times. The 95% confidence intervals on the fitted timing parameters were also reported. In the 3D data set, this fit was performed on a voxel‐by‐voxel basis, resulting in parameter maps for T₂ at all time points, as well as δ_a, δ_t and T_ex in the gray matter.

3. RESULTS

3.1. Arterial spin‐labeling signal maps

Figure 3 shows the effect of variable gradient strengths on ASL signal maps for three slices in one subject. Early time points (PLD < 1025 ms) are characterized by the presence of high signal in the arteries, which is removed by bipolar gradients. Although the effect for the weaker gradient is already large, there is a noticeable additional decrease in signal at full strength. In contrast, later time points (PLD > 1825 ms) show almost no difference in signal when gradients are applied.

FIGURE 3.

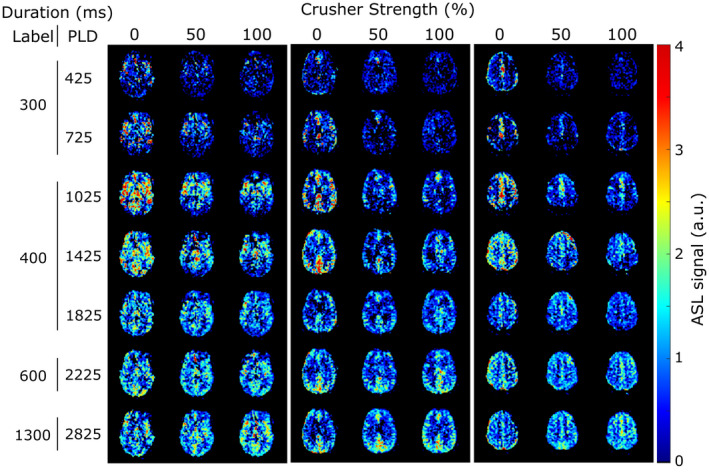
Arterial spin labeling(ASL) signal maps with variable crushing at all time points in three slices of 1 subject. All images were acquired with an eTE of 0 ms

3.2. Time‐dependent behavior of signal

Figure 4 shows the behavior of the average normalized signal through time for the whole studied population. The first column corresponds to the arterial signal, and the second column the gray matter. The top row compares the signal with different crusher gradient strengths (eTE = 0 ms), and the bottom row shows variable TEs (without crushers). The shape of these curves differs from the typical “Buxton curve” ²⁴ because of the variable lengths of the labeling blocks of the Hadamard encoding. The extent of crushing of the arterial signal can be appreciated in Figure 4A, where the high signals for PLDs shorter than 1 second are almost completely removed by the application of even the lowest crusher strength. Doubling the gradient strength provides an additional reduction in signal. At later time points, there is almost no effect from the gradients. The graph in Figure 4B reveals that the effect of gradients on the gray‐matter (perfusion) signal is lower than in arteries, but also most apparent for early PLDs. Figure 4C,D shows that with longer eTEs, the signal is smaller (as expected), both for the vascular and tissue regions of interest. This serves as a representation of the different mechanisms of the two methods: While the T₂‐prep module affects the signal in all compartments (the signal is reduced at all time points, no matter where it is situated along the vascular tree or in the tissue), the gradients, by their nature, only remove the signal from flowing spins above a certain cutoff velocity, and the amount of label that is crushed and how deep into the vasculature depends on their b‐value. This can be seen in the difference between the shapes of the gradient curves in Figure 4A,B, which shows that different gradient parameters lead to different timings for the arterial peak as well as shapes of the transition along PLDs.

FIGURE 4.

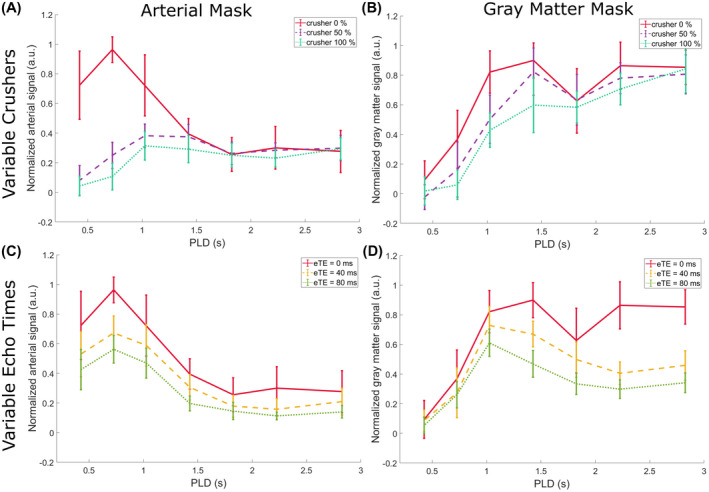
Average normalized gray matter and arterial signal through time, showing effects of crushers and TEs. Error bars indicate the SEM of the subjects

3.3. Two‐compartment dynamic modeling

Figure 5A‐C shows the first step of the compartmental model fitting: the separation of the ASL signal into intravascular and extravascular components. The T2_EV values from the fit of the unsubtracted images were 48 ± 9 ms, 47 ± 8 ms, and 46 ± 9 ms, for the weakest to strongest gradient. The T2_IV was estimated to be 240 ms, 300 ms, and 300 ms (highest permitted value) in the same order (the error on the fit of these values exceeds the values themselves). It can be observed that the intravascular signal (red dotted line) follows the expected time course: a high early peak followed by a subsequent decrease and an almost complete elimination of the signal. The extravascular component, moreover, displays more erratic behavior, although it tends to increase for longer PLDs.

FIGURE 5.

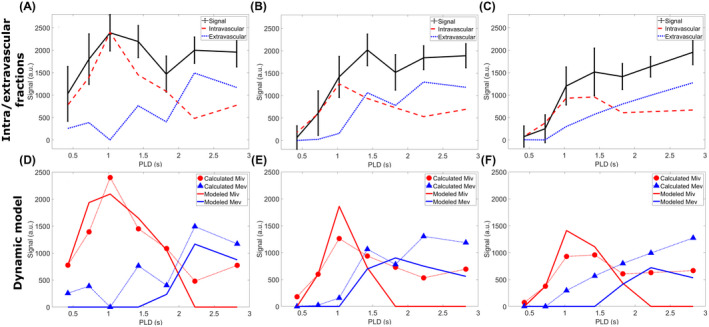
Results of the dynamic model fitting. In the top row, the ASL signal is broken down into intravascular and extravascular components (∆M_IV and ∆M_EV, respectively), using T₂ differences (Equation 3). On the bottom row, these same components (dotted lines with markers) are fitted to Equation 4, and the resulting dynamic fit is given by the solid lines (red for intravascular, blue for extravascular). This analysis was performed on the population average data, and repeated for all three applied gradient strengths (no gradient in left column to highest gradient strength on the right). Confidence intervals were calculated for each point in the fit but were too large to be shown here

The dynamic fit to the modified Buxton model (Equation 4) can be found in the bottom row (Figure 5D‐F). The arterial transit time, δ_a, extracted from this fit was 620 ms (95% confidence interval: 480‐750), 910 ms (720‐1110), and 930 ms (690‐1180) for gradients strengths of 0%, 50%, and 100%, respectively, and the tissue transit time, δ_t, was 2140 ms (1900‐2390), 1610 ms (1390‐1830), and 2010 ms (1670‐2350), for a resulting BBB transition time T_ex of 1520 ms, 700 ms, and 1080 ms. These values are consistent with literature, ¹⁴ , ²³ , ²⁵ , ²⁶ , ²⁷ considering that they combine effects from all gray‐matter regions), and the uncrushed signal is associated with lower δ_a and narrower confidence intervals than the crushed. In contrast, the δ_t, exhibits a less clear relationship to the amount of crushing.

3.4. Comparison of intravascular fractions

In Figure 6, the IVFs as calculated with both techniques are compared. This refers to the IVF as described by the difference in signal between the crushed and uncrushed data, and ∆M_IV / (∆M_IV + ∆M_EV), which results from the fitting of Equation 3 to the TRUST data. The ∆M calculation is performed on the total signal with contributions from both the vasculature and the tissue; therefore, in this figure, the IVF is also calculated by combining the signal from the arterial and gray‐matter masks. Figure 6A shows the time course of these fractions. With both methods, the IVF observes a negative trend as the labeled water travels from the arteries into the tissue. However, the TRUST‐based IVF is almost systematically higher than the crusher‐based IVF. This is made clear in Figure 6B, where a scatterplot of the values for both methods is shown, highlighting the relative underestimation of the IVF in the gradients method. Furthermore, a paired Student’s t‐test (using the different PLDs as samples) was performed, which showed a statistically significant difference between the TRUST‐based IVF and the 50% gradient IVF (P = .037) and a nonsignificant difference between the TRUST‐based IVF and the 100% gradient (P = .090), demonstrating that both gradient strengths underestimate the amount of intravascular signal, and substantially stronger gradients would be needed to close the gap and lead to a measurement of IVF that is consistent with values estimated by the TRUST method.

FIGURE 6.

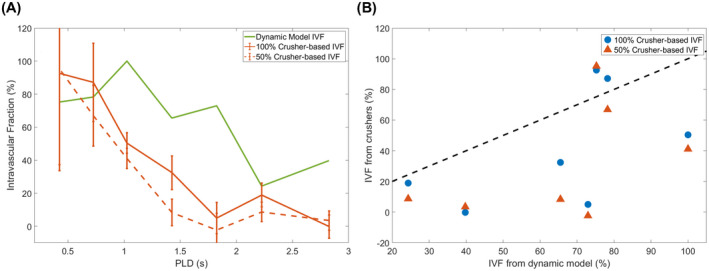
Comparison of the intravascular fractions (IVFs) as calculated with both methods. A, The IVFs are shown through time, for the crusher‐gradient technique (orange) and the compartmental model applied to the variable eTE data (green). B, Scatterplot showing the direct comparison of IVF values from both techniques (the black dotted line represents a perfect match)

3.5. Analysis of 3D data set

Figure 7 shows the T₂ maps in gray matter as a function of PLD. The transition from high T₂ values, concentrated in the arteries for early PLDs, to lower T₂ values distributed across the gray matter for later PLDs is readily apparent. Differences between brain regions are also seen, particularly at PLD = 1825 ms, where a higher T₂ is present in the posterior brain region. Figure 8 shows the results of the dynamic analysis performed on a voxel‐by‐voxel basis, represented by maps of the arterial transit time δ_a (top row), the tissue transit time δ_t (middle row), and transit time across the BBB T_ex (or δ_t‐δ_a, bottom row).

FIGURE 7.

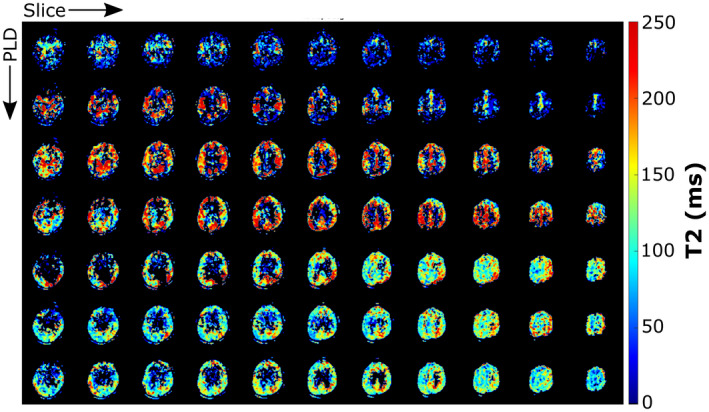
Map of the T₂ calculated on the 3D‐acquired data set with the TRUST technique, for all time points. Voxels with an uncertainty on the fit higher than 200 ms or lower than 0.5 ms were removed from this image (ill‐fitting points)

FIGURE 8.

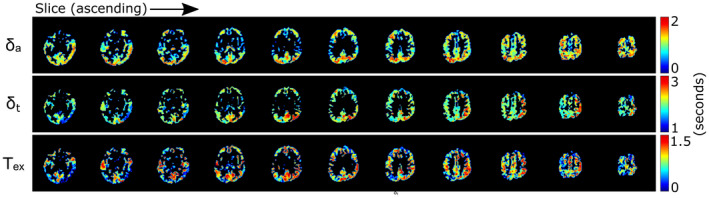
Results of the dynamic compartmental analysis on the 3D data set performed on a voxel‐by‐voxel basis. Only the gray matter is shown, as the arteries are not suitable for this type of fit, and the white‐matter signal is too low for fitting

4. DISCUSSION

In this study, the TRUST and crusher gradient methods were combined into a single ASL sequence to compare their properties when measuring water transport across the BBB. Measuring the two different approaches in a single sequence is important, as cerebral physiology is notoriously variable, such as depending on end‐tidal CO₂ and alertness. ³⁰ While both methods allow the separation of intravascular from extravascular signal to a certain extent, their mechanisms differ in key manners. The main findings of this study were threefold.

First, the used crusher gradients did not affect the entirety of the arterial signal. This is qualitatively apparent in the perfusion maps of Figure 3. At the two shortest PLDs (425 and 725 ms), where arterial signal is prominent on the uncrushed images, there is still some signal left when crusher gradients are applied. This conclusion is also supported by Figure 4A, where a qualitative look at the shape of the curves shows that the arterial peak is strongly attenuated by the application of gradients, but the initial increase and subsequent decrease in early time points for crushed signal curves indicates the presence of residual label in the arteries. The results shown in Figure 5 also point to this conclusion. When the same fit, separating the intravascular from the extravascular signal based on their T₂ values, is performed on the crushed data, an arterial peak indicating the presence of intravascular signal is seen, even when using the strongest gradient. The longer δ_a values calculated with these data reflect the fact that the fastest flowing spins (those that arrive the earliest in the imaging plane) are removed by the gradients, resulting in a longer arrival time for the arterial spins that do make it to the imaging area. Moreover, the comparison between the intravascular fractions obtained with the two methods (Figure 6B) shows a systematic underestimation of the fraction by gradients (statistically significant in the case of the weaker gradient), revealing their limited reach into the microvasculature and the difficulty in isolating the entirety of the blood pool signal. These IVF values are comparable to those obtained by St‐Lawrence et al, ¹⁵ who also looked at the fraction of signal located in the microvasculature at different PLDs with ASL. Their results for the intravascular fraction are on the same order of magnitude, but lower than both our TRUST and gradients methods results, likely because their technique, with its stronger gradients, allows the separation of the signal more specifically in the capillaries and not the whole of the vasculature.

The imperfect arterial signal cancelation resulting from the application of gradients can be explained by various factors. First, gradients only work perfectly for flow which has a sufficient velocity component parallel to their orientation. Additionally, the crusher gradient method relies on a parabolic flow profile in the vessels, ³¹ which may not be true in all vessels. At the capillary level, pseudo‐random orientation of the capillaries can lead to signal saturation, as is exploited in intravoxel incoherent motion. ³² Because of the relatively low b‐value (even when looking at our highest b‐value) used in the current study, this will only lead to an approximately 18% decrease in signal when assuming a D* of 0.02 mm²/s. ³² Stronger gradients would allow crushing further into the vascular tree, but in our gradient‐echo sequence the concomitant increase in TE resulting from the need to create space for even stronger gradients would result in too low SNR. Moreover, we note the inherent variability of the effect of gradients, which changes, among other things, with the blood‐flow velocity (see, for example, the difference in IVFs between the two gradient strengths in Figure 6), meaning that variations in blood velocity between subjects, or at different times, or caused by other factors, will result in differences in the fraction of the vasculature that is targeted.

Second, TRUST is a better tool to differentiate between the capillary and tissue compartments compared with the (relatively weak) gradients used in this study. In Figures 3 and 4, we demonstrate that the T₂‐prep module affects the signal at all PLDs, and therefore reaches the entirety of the vascular tree and the tissue, as opposed to crushers, whose reach into the vascular tree is dependent on the gradient strength. Figure 6 shows that crushers systematically underestimate the intravascular component of the signal when compared with the TRUST method, which can more comprehensively target the vasculature, no matter what eTEs are used.

This discrepancy is explained by the different mechanism of TRUST. Because this approach is based on the T₂ of water, which changes as it travels across the BBB, it discriminates between intravascular and extravascular signal due to the differences in T₂ (ie, the biexponential decay). Therefore, there is no limit as to how deep into the vascular tree the T₂‐prep module will probe, whereas the b‐value of the gradient, chosen to separate the vascular from the tissue compartment, dictates the extent to which gradients affect vascular signal. Although differences in parameters for the TRUST technique can also affect results (eg, the accuracy and precision of measured T₂ values are influenced by the TEs used ¹³ ), the choice of b‐value will determine how close to the exchange site the label is crushed. Using smaller b‐values, as in this study, this will be weighted more toward the arterial side than for higher b‐values, which will be closer to the exchange site (ie, capillary signal).

Our third conclusion is that combining these techniques does not add value in BBB assessment, although it was essential in comparing the two approaches. This is especially made clear by the quantitative dynamic compartmental analysis that we performed. This analysis requires only the multiple eTE (TRUST) data to measure δ_a and δ_t, and by extension T_ex. Performing it on the data with different crusher strength (Figure 5) provided shorter δ_a values for the uncrushed data, which is expected, as the gradients remove signal from the fastest‐flowing (shortest δ_a) spins. This does not reveal supplementary information about the nature of the BBB transition, but only on vascular transport. Moreover, the confidence intervals on the fit of the crushed data were significantly larger, because this model expects intravascular signal. Therefore, using only the TRUST technique is sufficient to provide all of the relevant information, and allows a shorter readout TE, boosting the overall SNR. This was demonstrated in an additional experiment that could now be done with a 3D readout. The 3D experiment did show that the TRUST technique can provide the desired results within a shorter sequence duration (18 minutes as compared with 50 minutes for the combined sequence), while also resulting in image quality high enough to allow whole‐brain voxel‐wise T₂ mapping (Figure 7) and arrival‐time mapping (Figure 8). The δ_a map shows a pattern that is consistent with literature, ²⁸ , ²⁹ with the central part of the middle cerebral artery flow territories showing shorter arrival times, just as in lower slices, whereas the posterior region exhibits longer arrival times. The δ_t map shows a less clear spatial dependence, although higher values appear to be present for areas with higher δ_a. Finally, the T_ex map, which is in fact the subtraction of the first two, by its nature highlights variations and noise that are present in the other maps. It is still possible to see that the pattern does not appear to depend strongly on vascular territories, as, for example, high values are present in all parts of the brain. It appears that deeper cortical regions may be associated with longer T_ex; however, a study including a larger sample of participants would be necessary to confirm this.

The main limitations affecting this study were the low SNR of our data as well as the limited strength of the gradients used. Arterial spin labeling is famously associated with low SNR, as it is a subtractive technique, representing a few percent at most of the total signal in the brain. In this protocol, additional sequence modules reduced signal further, resulting in noisier data. As a consequence, a considerable amount of averaging was required. Not only was the signal averaged over the whole gray matter or arterial mask, but it also necessitated averaging over the studied population. This averaging was beneficial to counter the low SNR; however it led to the inclusion of different flow territories, associated with variable arrival times, ²⁸ which in turn may have influenced the results of fitting. The main sequence also took a long time to perform (~50 minutes), and an additional data set with only one of these techniques showed that better SNR can be achieved in a shorter time frame when focusing on a single approach. Moreover, without the crusher gradients, a shorter TE of the readout sequence could be used, also resulting in a higher SNR. Additionally, our protocol focused on lower b‐values and lacked a higher b‐value, which would allow a two‐stage approach such as suggested by St. Lawrence et al ¹⁵ for a more quantitative measurement of water transport parameters. In its current form, our protocol cannot properly assess the actual transition across the BBB with the gradients method, as the gradient V_enc is not low enough to target blood flow in capillaries. Our choice for these strengths was made because the combination of T₂‐prep and motion‐sensitizing gradients was done more easily with a gradient‐echo readout as compared with spin echo. Longer gradients would have led, however, to too much signal loss due to ${\mathrm{T}}_2^{\ast }$ and thus to further lowering the SNR, which was already an issue with our protocol. Moreover, a limitation of the TRUST method as applied in this study should be mentioned. To stabilize the dynamic model fit, we applied in Equation 3 the assumption that the intravascular T_2iv is constant for all PLDs. This assumption is based on the rapid exchange of water with tissue when the capillary bed is reached. Although changes in oxygenation occur along the whole length of the microvasculature, which takes 2 seconds or more on average, ³³ extravasation of water is more rapid (0.2‐1 seconds), ¹⁵ , ¹⁹ , ³⁴ which means that most of the water moves to the tissue before significant changes in oxygenation occur. Because the T₂ of blood is strongly dependent on oxygenation, ³⁵ further into the capillary bed our assumptions will fail. The uncertainty on the calculated T_2iv was high, which may be a result of the high variability of arterial signal for the early PLDs, combined with the notorious instability of bi‐exponential fitting. Finally, although it is possible to add the gradients into the T₂‐prep module, we decided against it for two reasons: First, with the varying duration and number of pulses of the T₂‐prep, it is challenging to keep the crushing effects of the gradients similar (ie, also for higher‐order moments). Second, as the crushing effects could not be guaranteed to be the same for all eTEs, an interdependency between the TRUST and gradient approach would be introduced, which would make it difficult if not impossible to separate these effects convincingly.

A limitation of our analysis protocol was the use of thresholding of perfusion images for gray matter and arterial masking. The resulting masks have been prone to some contamination; in particular, some of the arterial signal could still be included in the gray matter. Using a T₁‐weighted image would have allowed a standard delineation of brain regions; however, at the low resolution used for ASL, there will always be partial‐voluming issues, and it is not possible to remove all contamination from arteries and white matter. Thresholding was therefore deemed sufficient for this analysis.

5. CONCLUSIONS

Our comparison of the use of crusher gradients and TRUST to measure the transport of water across the BBB showed that TRUST provides a more accurate and complete picture of this process than crusher gradients, because TRUST can separate the signal from spins in the vasculature and those in tissue, whereas with gradients, only part of the intravascular signal is effectively excluded. Moreover, it has been shown that a full TRUST protocol can be performed in a reasonable scan time and with high enough SNR to provide voxel‐wise and regional BBB assessments. It remains to be studied whether the use of much stronger crusher gradients might alleviate some of these issues.

CONFLICT OF INTEREST

The group of Matthias van Osch receives research support from Philips. Matthias van Osch is member of the advisory board of Biogen, Boston, USA.

Petitclerc L, Schmid S, Hirschler L, van Osch MJP. Combining T₂ measurements and crusher gradients into a single ASL sequence for comparison of the measurement of water transport across the blood–brain barrier. Magn Reson Med. 2021;85:2649–2660. 10.1002/mrm.28613