Abstract
Based on the breakthrough technology of water muting on photoacoustic spectroscopy, a single wavelength photoacoustic system in the short-wavelength-infrared (SWIR) region was developed to sense the endogenous molecules (e.g. glucose, lactate, triglyceride, and serum albumin found in blood and interstitial fluid) in aqueous media. The system implemented a robust photoacoustic resonant cell that can significantly enhance the signal-to-noise ratio of the acoustic waves. The sensitivity of the system was explored, and the experimental results exhibit a precision detection of physiological concentrations of biomolecules by combining the techniques of water muting and photoacoustic resonant amplification in a portable and low-cost single wavelength laser system.
1. Introduction
Diabetes mellitus is a very common disease in the twenty-first century which cannot be cured but only be controlled by regulating the blood sugar intake level becomes one of the biggest worldwide epidemics with a rapid increase in prevalence from 4.9% in 2011 to 9.3% in 2019 [1,2]. Till date, all clinically accurate methods for monitoring blood sugar levels are invasive in nature where extracting blood by pricking of human body site is necessary [3]. To relief diabetic patients from this painful and inconvenient process, many efforts have been devoted for developing a non-invasive blood-glucose-monitoring technique especially those based on optical spectroscopy techniques. However, most of these techniques lack adequate accuracy to go for clinical trial due to the complex nature of the optical scattering of skin layer and the strong absorption of water in human body [4–9]. Among all non-invasive optical spectroscopic techniques, the photoacoustic spectroscopy attracts much attentions nowadays which measures acoustic pressure wave generated from rapid heating of glucose molecules by absorbing near- or mid- infrared light [10–14]. Unlike the conventional optical spectroscopy, the photoacoustic technique converts optical absorptions to acoustic waves and overcome the existing limitation of high scattering loss and low-collection-efficiency of optical signal from opaque samples such as skin [15,16]. Furthermore, the problem of low sensitivity caused by strong absorption of water is minimized by implementing the so-called water muting technique into the conventional photoacoustic spectroscopy in SWIR region [17]. Water muting technique takes the advantage of zero thermal expansion coefficient of water at 4 °C to supress the strong interference signal from optical absorption of water in aqueous solution and drastically improves the sensitivity of glucose detection. However, the photoacoustic spectroscopy arrangement in [17] was based on an expensive, complex, and bulky optical parametric oscillator (OPO) nanosecond laser system to provide high optical pumping power for generating a strong acoustic response from glucose. Inspired by the preliminary result, this work explored the possibility of achieving similar performance in detecting glucose along with other endogenous molecules based on a much simpler and lower cost system, which is believed to pave the way for advances in medical applications.
In this work, a temperature dependent photoacoustic system was developed by using a short-wavelength-infrared (SWIR) diode laser working at a glucose sensitive wavelength of 1630 nm. To overcome the drawback of low acoustic signal generated by the diode laser, a strategy was taken for amplifying the acoustic signal by using a novel technique similar to photoacoustic resonant cavity. By implementing a temperature stabilization and feedback loop control module, the system achieved an accurate and stable temperature in the solution near water muting temperature of 4 °C. The experimental results demonstrated that, instead of using a complicated broadband spectroscopy system, accurate detection of glucose solute concentration can be achieved based on a low-cost single wavelength laser with the help of water muting technique. It is further showcased that the system can be used to determine the solute concentrations of biological analytes in blood, such as lactate, triglyceride, and serum albumin, in aqueous medium.
2. System design and experiment setup
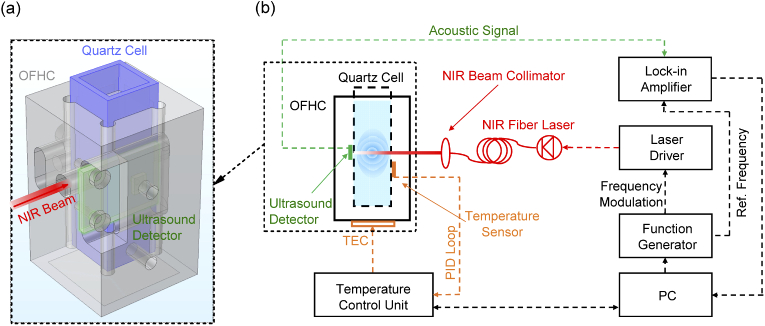
The schematic of the experimental setup of a single wavelength water muted photoacoustic system is shown in Fig. 1(b). The optical pumping source was employed by a commercial SWIR fiber laser (FPL1054p from Thorlabs Inc.) working at the wavelength of 1630 nm with a maximum output power of 80 mW. The laser driver that provided the electrical control to the SWIR laser was frequency-modulated at around 23 kHz with square waves of a duty cycle of 5% by a function generator (Agilent 55321A). The output light of the laser was collimated by a near-infrared beam collimator. The collimated beam with a diameter of around 2 mm was incident to the temperature-controlled quartz photoacoustic cell unit to achieve optical pumping for generating acoustic waves. Figure 1(a) shows a three-dimensional view of the geometric structure of the quartz photoacoustic cell unit. In experiment, a SWIR-wavelength-transparent quartz cell (from Hellma Inc.) containing the aqueous solution of interest was plugged into the metal structure made of oxygen-free-high thermal conductivity (OFHC) copper to provide a stable temperature with a variance of below 0.02 °C (as shown in Fig. S2.). The surface of this structure was further electroplated with gold to prevent any degradation of thermal conductivity due to oxidation during the temperature dependent measurement. On one sidewall of the copper unit, a through-hole was drilled to let the SWIR beam incident into the aqueous solution inside a quartz cell. The generated acoustic signal inside the aqueous solution was collected by an ultrasound detector with center frequency of around 23 kHz (SPU0410LR5H-QB) attached to the sidewall of the quartz cell and recorded by a lock-in amplifier (SR830). A thermoelectrical cooler (TEC) module with a maximum cooling power of 17 W was used to cool the temperature of the quartz photoacoustic cell unit down to below 4 °C (water muting temperature). A custom-made proportional-integral-derivative (PID) feedback loop circuit was used to provide a real-time adjustment on cooling power of TEC based on the temperature reading from the aqueous solution.
Fig. 1.
(a). Three-dimensional view of the geometric structure of quartz photoacoustic cell unit which shows OFHC, oxygen-free-high thermal conductivity-copper in grey color, plugged quartz cell in blue color, and ultrasound detector in green color. The SWIR laser beam (in red) is incident into the hole on the side wall of the OFHC unit. (b). Schematic representation of a single wavelength SWIR photoacoustic system. The modules of SWIR diode laser, acoustic detection, and temperature control are marked in red, green, and orange color, respectively.
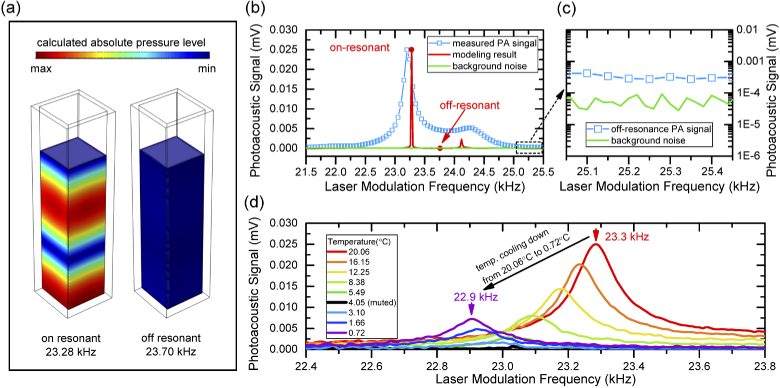
Based on the general theory of photoacoustic wave generation in an inviscid medium such as aqueous solutions studied in this work, the generated pressure wave is approximately proportional to the time-variant heating energy from the laser source [18]. In earlier works of photoacoustic spectroscopy experimental setups, OPO laser with ultrashort pulse width of several nanoseconds and peak power less than one millijoule were generally used as pumping sources [10,17] with an energy-conversion (from light to heat) changing rate of around 104 J/s. However, the pulse widths of commercially available diode lasers are in the range of several hundreds of nanoseconds to microseconds due to the limitation of electrical modulation of driven current. In this case, even considering all the optical power (less than 80 mW in our system) is converted to the heating energy by the aqueous solutions, an energy-conversion changing rate of around 0.1 J/s is obtainable by commercial diode lasers. Therefore, the detection of such weak a photoacoustic signal from a diode laser remains challenging even with the help of signal amplification from lock-in amplifier. To overcome this problem, the resonant behavior similar to the photoacoustic resonant cavity was taken for further amplifying the weak acoustic waves in this system [19,20]. The geometry of the quartz cell used in the measurements as a SWIR wavelength transparent container for aqueous solutions can work as a natural resonant cavity at some specific frequencies of modulations (eigenfrequencies). One eigenfrequency of the quartz cell was found to be at around 23 kHz when filled with aqueous solutions. This resonant behavior was confirmed by both simulations and experiments, as shown in Fig. 2(a). The simulation work was based on three-dimensional acoustic-structure interaction module in COMSOL Multiphysics. In this simulation, a monopole point source was used to imitate the generation of photoacoustic waves inside medium of DI water. All material parameters such as sound velocities and densities were directly taken from [21,22]. Figure 2(a) shows 3D contour maps of simulated distribution of pressure levels inside a quartz cell at on-resonant and off-resonant frequencies. The rainbow color inside the on-resonance cavity shows the formation of amplified pressure waves in a resonant condition, while the uniform blue color of the off-resonance cavity indicates that the pressure level is too low to be observed in the same intensity scale.
Fig. 2.
(a). Three-dimensional contour maps of acoustic pressure levels in quartz cell units simulated by COMSOL. The rainbow color shows the acoustic pressure levels at on-resonant frequency of 23.28 kHz (left) and at off-resonant frequency of 23.70 kHz (right). (b). Comparison of simulation (red line)/experiment (blue square-line) of photoacoustic spectrum and background noise (green line) within the laser modulation frequency range from 21.5 to 25.5 kHz. (c). Enlarged area of measured photoacoustic spectrum and background noise at the frequency range far away from the resonance peak. (d) Measured temperature dependent photoacoustic spectrums of DI water within temperature range from 20.06 to 0.72 °C. The arrows show the peak frequency measured at 20.06 °C (red) and at 0.72 °C (purple).
Figure 2(b) depicts the simulated and measured photoacoustic spectrums at the frequency range of resonance at a temperature of 20 °C. For comparison, the simulated resonant peak intensity is normalized to that of the experimental result. The background noise measured by removing the DI water from the quartz cell is plotted as well. Although no fitting parameters were used, a good agreement was obtained between the simulated resonant frequency of 23.28 kHz and the experimental value of 23.23 kHz. The presence of a small shoulder at the right side of the main resonant peak in the experimental spectrum can be explained by a small side resonant mode of the cavity from the simulated resonant peak at ∼24.3 kHz. The signal amplification by the effect of resonance was estimated by comparing the intensity of the detected photoacoustic signal at resonance peak and far way from it in the collected spectrum. Without taking the effect of resonance, the photoacoustic signal from off-resonance position of the spectrum is only 4 times stronger than that of the background noise level (∼3×10−4 mV vs of 7×10−5 mV) as shown in Fig. 2(c). This is indeed a very weak signal to be detected even at the lower temperature where acoustic signal from water is muted. Apparently, by taking into the account of resonant effect of the quartz cell, the detected photoacoustic signal level is significantly increased by around 90 times 0.026 mV vs 0.0003 mV) along with signal-to-noise ratio. Figure 2(d) shows the measured temperature dependent photoacoustic spectrum of DI water, where the water muting effect of photoacoustic signal is observed from the change in peak intensities of the temperature dependent photoacoustic spectrums. The peak intensity of the photoacoustic spectrum declines with decreasing temperature from 20.06 °C until the signal becomes undetectable (muted) at 4.05 °C. Further decreasing in temperature leads to the re-appearance of the photoacoustic spectrums. Another behavior of the photoacoustic resonance observed from the system is the shift of resonant frequency in the temperature dependent measurements. Figure 2(d) shows the resonant frequency of photoacoustic signal (peak frequency) moves from 23.4 kHz to 22.9 kHz from temperature at 20.06 °C to 0.72 °C. The resonant frequency of a quartz cell is mainly associated with the sound velocity, density, and volume (cavity height) of the filled aqueous solution. The change of sound velocity due to the change of solute concentration can be negligible because most aqueous solutions are low in concentrations (e.g. less than g/dL). Also, the volume (height) of the aqueous solution in the quartz cell can shift the resonant peak, however, this variation can be kept within 20 Hz by precisely controlling the amount of the filled solution. On the contrary, the temperature dependent change of sound velocity of the aqueous solution is identified as a major contribution to the shift of resonant frequency (as shown in the simulation result in Fig. S.3.). However, the normalization to the frequency dependent response of the ultrasound detector is not needed in these measurements as this temperature induced frequency shift of the resonant peak is relatively narrow (∼500 Hz range).
3. Result and discussion
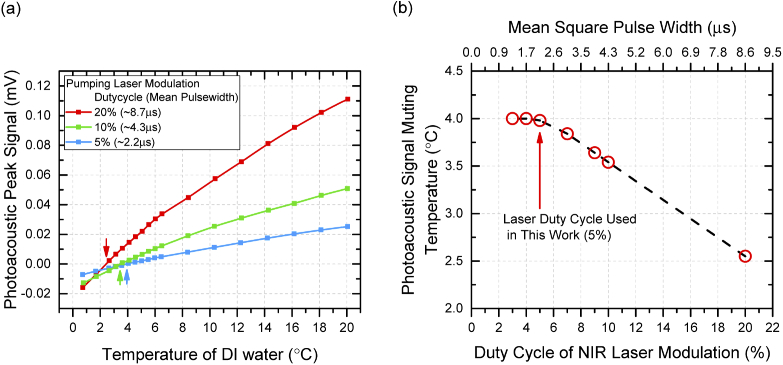
To examine the muting property of aqueous solution in our system, experiments were conducted to investigate the photoacoustic signal as a function of temperature on DI water. In earlier work of investigating muting effect in aqueous solutions, the OPO laser system provided a very strong laser excitation pulse of around 104 W which eventually transmitted only 10−3 W of time averaged heating power to the aqueous solution due to the ultrashort pulse width (∼10 ns) and ultralow duty cycle (∼10−5%) and increased the instantaneous temperature of the aqueous medium only in the order of ten millikelvins [17,18]. However, the system developed in this work used an electrically modulated diode laser with longer excitation pulse which increased the temperature of the aqueous medium in the order of several hundreds of millikelvins at the beam-solution interaction region where the photoacoustic signal is generated. Figure 3(a) illustrates the heating effect of excitation laser with three different modulated pulse widths of 20%, 10%, and 5%. In the experiments, the intensity at the resonant frequency of the photoacoustic spectrum (photoacoustic peak intensity) was used to track the muting effect of the photoacoustic signals. For all three curves, the photoacoustic peak intensities decreased monotonously with temperatures from 20 °C to the different muting points of 2.43, 3.46, and 3.98 °C, respectively, and then resumed at temperatures below muting points (plotted with negative intensities in this paper). The water muting curves are supposed to follow the change of thermal expansion coefficient in water with a zero value at 4°C, however, the localized overheating in solution caused by long pumping pulse widths (e.g. 10% and 20%) shifted the observed muting point of photoacoustic waves. Although a longer duty cycle laser pulse can provide strong energy to generate acoustic waves, however, the resulting shift of muting points interferes when solutes are involved. Thus, investigation was carried out on the influence of duty cycle (pulse width) of pumping laser on water muting points to obtain a trade-off value between the duty cycle and the photoacoustic signal strength, as shown in Fig. 3(b). The measured muting points increased quickly with the decrease of the duty cycle from 20% to 7% which corresponded to a fast cooling of the overheated laser excitation area before it started to stabilize from 5% duty cycle. This stable temperature near muting point at around 5% of duty cycle indicated that the heating effect from the laser could be neglected. Based on this result, the 5% duty cycle of the modulation of pumping laser is considered as an optimized value for the system and used in the rest of the experiments.
Fig. 3.
(a). Measured peak intensities of photoacoustic spectrums of DI water as a function of temperature at different laser modulation duty cycles of 20% (red), 10% (green), and 5% (blue). The arrows show the muting temperature of each curve. (b). Photoacoustic signal muting temperatures as a function of laser modulation duty cycles. The muting temperatures were extracted from the intercepts of temperature dependent photoacoustic peak signal curves (e.g. curves in (a)) on zero intensity axis.
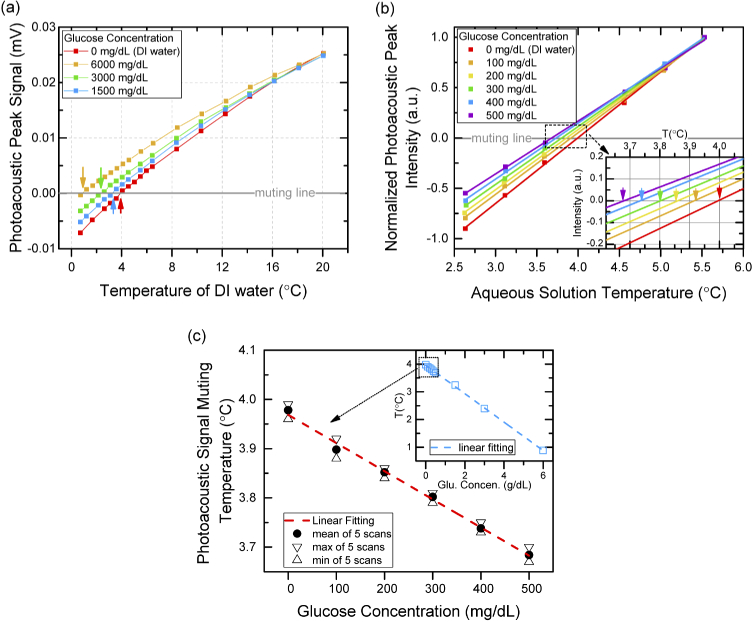
Following the experimental setup on DI water, measurements were performed to examine the single wavelength SWIR photoacoustic system on measuring the glucose aqueous solutions. Initially, the aqueous solution was prepared to a high solute concentration of 6000 mg/dL with D(+) glucose (Sigma-Aldrich) be dissolved in DI water and then diluted to the lower solute concentrations of 3000, 1500, 500, 400, 300, 200, 100 mg/dL. The existence of glucose solutes in DI water alters the muting temperature of the photoacoustic signal compared to DI water (∼4 °C) by changing the total thermal expansion coefficient of the aqueous solution. The amount of such changes in muting temperature (ΔT) as a function of glucose solute concentration (C) is expressed by the Despretz law (i.e. ΔT = KdC) [23,24], where Kd is the Despretz constant that depends on the thermodynamic property of solutes. Figure 4(a) presents the measured temperature dependent photoacoustic resonant signals for DI water and the aqueous solutions of glucose with high solute concentrations of 6000, 3000, and 1500 mg/dL. Due to the strong contribution of thermal expansion coefficient from water, the intensities of photoacoustic signal for four different aqueous solutions are very similar at 20 °C which indicates that, even for aqueous solution with glucose concentration as high as 6000 mg/dL, the detection of glucose induced photoacoustic signal is still extremely challenging. However, the photoacoustic signals of four aqueous solutions become distinguishable when the temperature gradually decreases to 4 °C. Eventually, the shift of muting temperatures (ΔT) by glucose solutes are observed to be 3.10, 1.61, and 0.74 °C for glucose concentrations of 6000, 3000, and 1500 mg/dL, respectively. To further explore the capability of this system, measurements were conducted on low glucose concentrations of glucose solutions of 500, 400, 300, 200, and 100 mg/dL, which corresponds to hyperglycemic to normal glucose levels in human blood [25,26]. The experiments focused on temperature range closed to 4 °C while charactering the low concentration of glucose to capture any minor changes in muting temperatures. Figure 4(b) shows the typical measured values of photoacoustic peak signal vs. temperature for aqueous solution of glucose concentration from 100-500 mg/dL and DI water. The measured photoacoustic peak intensities for each solute concentration were normalized to the value at highest measurement temperature of 5.5 °C to provide a clear view for comparison purpose which does not change the muting temperature because they are determined by the intercepts of photoacoustic signal curve on temperature axis equals to 0 °C. Considering the linear approximation of thermal expansion coefficient of DI water at around 4 °C [17], linear fitting was used to figure out the muting temperature of each curve. As shown in the inset of Fig. 4(b), the muting temperatures of aqueous solutions with glucose concentrations of 0, 100, 200, 300, 400, and 500 mg/dL were found to be 3,99, 3.91, 3.85, 3.74, and 3.68 °C, respectively. To further explore the accuracy of detecting glucose in water, a series of measurement with 5 independent scans for each solution were conducted (the temperature dependent photoacoustic peak signal for all measurement results were plotted in Fig. S4.). As shown in Fig. 4(c), the mean value of 5 independent reading of muting temperatures for each glucose concentration are plotted by solid circles. A linear relationship between muting temperatures and glucose solute concentrations with a slope of 0.057 °C per 100 mg/dL (which is also representing the Despretz coefficient) is observed. The average uncertainty of of 0.026 °C is estimated by the difference between maximum (triangles) and minimum (inverted triangles) temperature readings for glucose solute concentrations in the range of 0-500 mg/dL. The sensitivity of the glucose detection for this system (the minimum difference in concentration of glucose can be detected by the system without considering the accuracy) is estimated to be 17.5 mg/dL by using the equation: sensitivity = minimum shifted muting temperature reading (0.01°C) × slope of the linear regression data (1750mg/dL per °C). Also, the limit of detection (LoD) on glucose concentration of 21.8 mg/dL was calculated based on the linear regression of the data in Fig. 4(c) by using the equation LoD = 3×standard deviation of intercept/slope. Analyzing the measured muting temperatures from both the high and the low glucose solute concentration, a reasonable agreement with the prediction of Despretz law (as is shown in the inset of Fig. 4(C)) is found which confirmed the accuracy on detecting the glucose concentration by our system.
Fig. 4.
(a). Measured peak intensities of photoacoustic spectrums of glucose aqueous solutions (with high glucose concentration of 6000 (orange), 3000 (green), and 1500 (blue) mg/dL) and DI water (red) as a function of temperature. The arrows show the muting temperature of each curve. (b). Measured peak intensities of photoacoustic spectrums of glucose aqueous solutions (with low glucose concentration of 500 (purple), 400 (blue), 300 (green), 200 (yellow), and 100 (orange) mg/dL) and DI water (red) as a function of temperature. Linear fitting is used on each curve for reading muting temperature (intercept with muting line). Inset: enlarged area of muting temperature reading for each solution. (c). Measured photoacoustic signal muting temperatures of glucose aqueous solutions as a function of glucose concentrations. For each solution, 5 independent measurements were deployed. The solid circles, triangles, and inversed triangles represent mean value, maximum value, and minimum value of 5 readings, respectively. Inset: muting temperature vs. glucose concentrations for all solutions (both low and high glucose concentrations)
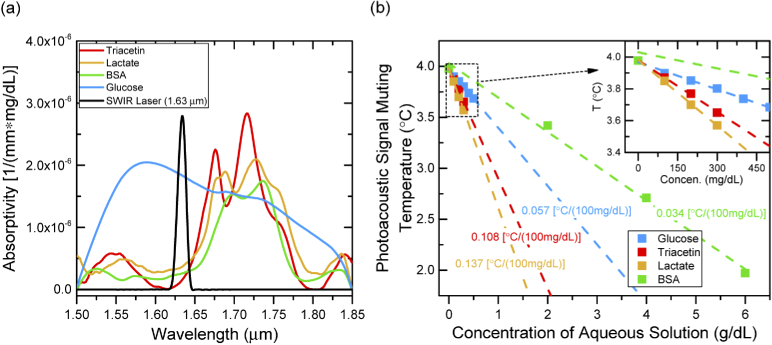
The subsequent experiments studied the muting effect of photoacoustic signal on several other analytes found in human blood such as lactate, triacetin (triglyceride), and BSA (serum albumin). These analytes (from Sigma-Aldrich) were prepared in aqueous solution with high concentrations of 1000 mg/dL (lactate and triacetin), and 6000 mg/dL (BSA), and then dissolved to lower concentrations for photoacoustic measurements. The optical absorptivity of all analytes was firstly investigated through aqueous solutions of high solute concentration by Fourier transform infrared spectroscopy (FTIR) at the wavelength from 1.5-1.85 µm, as shown in Fig. 5(a) along with the measured emission spectrum of SWIR laser. The operating wavelength of the SWIR laser (∼1.63 µm) lies in the strong absorption region of the glucose where the intensity of other analytes such as lactate, triacetin, and BSA have minimal absorption strength. Although the low optical absorption of lactate, triacetin, or BSA at the wavelength of ∼1.63 µm provides limited contribution to the generation of photoacoustic signal, the unique thermodynamic properties of the analyte is expected to shift the overall muting temperature as a function of solute concentration (Despretz coefficients). In a complex solution like human blood plasma, the existence of multiple biochemical analytes brings a mixed contribution of thermal expansion mechanism. Hence, investigating the muting effect of individual analytes helps us understand both the potential and the limitation of this technique when a complicated real blood sample is of a concern. By following the same technique on glucose solution, experiments were conducted for detecting the shift of muting temperatures on lactate, triacetin with solute concentrations of 100, 200, and 300 mg/dL, and BSA with the solute concentration of 2, 4, and 6 g/dL (because BSA is found with high concentration in blood plasma). Figure 5(b) shows the muting temperatures with good linear relationship with solute concentrations for individual analyte. The Despretz coefficients of the analytes were calculated through linear regression fitting of experimental data. Although higher Despretz coefficients of 0.108 and 0.137 °C per 100 mg/dL on triacetin and lactate are observed, the relatively low day-to-day variation in physiological concentration of these two analytes (i.e. ∼20% variation in less than 150 mg/dL triglyceride [27], and ∼15% variation in less than 20 mg/dL lactate [28] in human blood for general condition) is expected to contribute a moderate interference on shift of muting temperature (<0.03 °C). On the contrary, the high concentration of serum albumin (BSA) in blood (i.e. 3.5 to 5.0 g/dL [29]) can significantly shift the muting temperature of the tested solution. Therefore, for physiological samples, even a small day-to-day variation of serum albumin will cause significant interference on sensing the concentration of other analytes such as glucose. In future, a second laser diode operating at the strong absorption region of the BSA can be incorporated to our system. Thus, the differential photoacoustic signal from these two excitation sources at muting temperature is expected to distinguish glucose from BSA.
Fig. 5.
(a). Absorptivity of triacetin (red), lactate (orange), BSA (green), and glucose (blue) analytes and the emission spectrum (normalized) of SWIR laser (black) in this work. All spectroscopies are calculated based on transmission measurements of aqueous solution of these analytes by a Fourier transform infrared spectroscopy system. (b). Measured photoacoustic signal muting temperatures of triacetin, lactate, BSA, and glucose aqueous solution as a function of solute concentration of each. Inset: enlarged area of low solute concentration. Linear regression (dash lines) was used to calculate the Despretz coefficient of each analyte.
4. Conclusion
A water muted photoacoustic system was developed based on a low-cost single wavelength SWIR diode laser for detecting physiological level of endogenous analytes found in human blood or intestinal fluid such as glucose, lactate, triacetin, and BSA in aqueous solutions from the shift of muting temperatures. By theoretically and experimentally studying the resonant behavior of the photoacoustic waves, the photoacoustic cavity was used in the system to amplify the generated acoustic signal by around two orders of magnitude. In addition, a temperature control module with a feedback-loop circuit was designed and implanted to obtain accurate and stable system temperature. A suitable duty-cycle for modulating the diode laser was used by studying the heating effect of the long pulse duration of the diode laser caused anomalies in obtaining muting temperature of the solutes. The solute-sensing performance of this system was explored, and the results showcased an accurate solute concentration detection with LoD of 21.8 mg/dL in glucose aqueous solutions. The further experiments demonstrated the potentiality of the system in sensing an accurate concentration of individual bio analytes by investigating the muting effect on other endogenous analytes of lactate, triacetin, and BSA in aqueous solutions. It is identified that BSA is a strong source of interference in detecting blood glucose level and the use of more than one wavelength is expected to help distinguish BSA from glucose. Besides, when deploying this water muting technique into an in-vivo system, the mechanism of light penetration and scattering in skin will surely cause more interference on the detection accuracy, and worth further investigation in the following work. In conclusion, this work achieves a water muted photoacoustic spectroscopy comprised of a portable and low-cost diode laser system with a possibility of bringing this technique from laboratory to clinic applications.
Acknowledgement
This work has been supported by the Natural Science and Engineering Research Council (NSERC), Ontario Center of Excellence (OCE), Mitacs and University of Waterloo, AIH Technologies Inc.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
See Supplement 1 (1.5MB, pdf) for supporting content.
References
- 1.Scully T., “Diabetes in numbers,” Nature 485(7398), S2–S3 (2012). 10.1038/485S2a [DOI] [PubMed] [Google Scholar]
- 2.Saeedi P., Petersohn I., Salpea P., Malanda B., Karuranga S., Unwin N., Williams R., “Global and regional diabetes prevalence estimates for 2019 and projections for 2030 and 2045: Results from the International Diabetes Federation Diabetes Atlas,” Diabetes Res. Clin. Pract. 157, 107843 (2019), 9th edition. 10.1016/j.diabres.2019.107843 [DOI] [PubMed] [Google Scholar]
- 3.Shokrekhodaei M., Quinones S., “Review of non-invasive glucose sensing techniques: optical, electrical and breath acetone,” Sensors 20(5), 1251 (2020). 10.3390/s20051251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jernelv I. L., Milenko K., Fuglerud S. S., Hjelme D. R., Ellingsen R., Aksnes A., “A review of optical methods for continuous glucose monitoring,” Appl. Spectrosc. Rev. 54(7), 543–572 (2019). 10.1080/05704928.2018.1486324 [DOI] [Google Scholar]
- 5.Zhang W., Liu R., Zhang W., Jia H., Xu K., “Discussion on the validity of NIR spectral data in non-invasive blood glucose sensing,” Biomed. Opt. Express 4(6), 789–802 (2013). 10.1364/BOE.4.000789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Delbeck S., Michael Heise H., “Evaluation of opportunities and limitations of mid-infrared skin spectroscopy for noninvasive blood glucose monitoring,” J. Diabetes Sci. Technol., 1–9 (2020). 10.1177/1932296820936224 [DOI] [PMC free article] [PubMed]
- 7.Siesler H. W., Ozaki Y., Kawata S., Heise H. M., Near-infrared Spectroscopy: Principles, Instruments, Applications (Wiley-VCH, 2002).
- 8.Jacques S. L., “optical properties of biological tissues: A review,” Phys. Med. Biol. 58(11), R37–R61 (2013). 10.1088/0031-9155/58/11/R37 [DOI] [PubMed] [Google Scholar]
- 9.Rassel S., Xu C., Zhang S., Ban D., “Noninvasive blood glucose detection using a quantum cascade laser,” Analyst 145(7), 2441–2456 (2020). 10.1039/C9AN02354B [DOI] [PubMed] [Google Scholar]
- 10.Ghazaryan A., Ovsepian S. V., Ntziachristos V., “Extended near-infrared optoacoustic spectrometry for sensing physiological concentrations of glucose,” Front. Endocrinol. 9, 112 (2018). 10.3389/fendo.2018.00112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pleitez M. A., Lieblein T., Bauer A., Hertzberg O., Lilienfeld-Toal H. V., Mantele W., “In vivo noninvasive monitoring of glucose concentration in human epidermis by mid-infrared pulsed photoacoustic spectroscopy,” Anal. Chem. 85(2), 1013–1020 (2013). 10.1021/ac302841f [DOI] [PubMed] [Google Scholar]
- 12.Pleitez M. A., Hertzberg O., Bauer A., Seeger M., Lieblein T., Lilienfeld-Toal H. V., Mantele W., “Photothermal deflectometry enhanced by total internal reflection enables non-invasive glucose monitoring in human epidermis,” Analyst 140(2), 483–488 (2015). 10.1039/C4AN01185F [DOI] [PubMed] [Google Scholar]
- 13.Sim J. Y., Ahn C., Jeong E., Kim B. K., “In vivo microscopic photoacoustic spectroscopy for non-invasive glucose monitoring invulnerable to skin secretion products,” Sci. Rep. 8(1), 1059 (2018). 10.1038/s41598-018-19340-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kottmann J., Rey J. M., Sigrist M. W., “Mid-infrared photoacoustic detection of glucose in human skin: towards non-invasive diagnostics,” Sensors 16(10), 1663 (2016). 10.3390/s16101663 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ghazaryan A., Omar M., Tserevelaskis G., Ntziachristos V., “Optoacoustic detection of tissue glycation,” Biomed. Opt. Express 6(9), 3149–3156 (2015). 10.1364/BOE.6.003149 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Filimonova T. A., Volkov D. S., Proskurnin M. A., Pelivanov I. M., “Optoacoustic spectroscopy for real-time monitoring of strongly light-absorbing solutions in applications to analytical chemistry,” Photoacoustics 1(3-4), 54–61 (2013). 10.1016/j.pacs.2013.08.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Prakash J., Seyedebrahimi M. M., Ghazaryan A., Malekzadeh-Najafabadi J., Gujrati V., Ntziachristos V., “Short-wavelength optoacoustic spectroscopy based on water muting,” PNAS 117(8), 4007–4014 (2020). 10.1073/pnas.1910597117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang L. V., Wu H. I., Biomedical Optics: Principles and Imaging (Wiley-Interscience, 2012), ed. 1.
- 19.Pleitez M. A., Lieblein T., Bauer A., Hertzberg O., Lilienfeld-Toal H. V., Mantele W., “Windowless ultrasound photoacoustic cell for in vivo mid-IR spectroscopy of human epidermis: Low interference by changes of air pressure, temperature, and humidity caused by skin contact opens the possibility for a non-invasive monitoring of glucose in the interstitial fluid,” Rev. Sci. Instrum. 84(8), 084901 (2013). 10.1063/1.4816723 [DOI] [PubMed] [Google Scholar]
- 20.El-Busaidy S., Baumann B., Wolff M., Duggen L., Bruhns H., “Experimental and numerical investigation of a photoacoustic resonator for solid samples: towards a non-invasive glucose sensor,” Sensors 19(13), 2889 (2019). 10.3390/s19132889 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Smith A. H., Lawson A. W., “The velocity of sound in water as a function of temperature and pressure,” J. Chem. Apys. 22(3), 351–359 (1954). 10.1063/1.1740074 [DOI] [Google Scholar]
- 22.Blinick J. S., Maris H. J., ““Velocities of first and zero sound in quartz,” Phys,” Rev. B 2(6), 2139–2146 (1970). 10.1103/PhysRevB.2.2139 [DOI] [Google Scholar]
- 23.Petrova E., Liopo A., Oraevsky A. A., Ermilov S. A., “Temperature-dependent optoacoustic response and transient through zero Gruneisen parameter in optically contrasted media,” Photoacoustics 7, 36–46 (2017). 10.1016/j.pacs.2017.06.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kaulgud M. V., Pokale W. K., “Measurement of the temperature of maximum density of aqueous aolutions of some salts and acids,” J. Chem. Soc. Faraday Trans. 91(6), 999–1004 (1995). 10.1039/ft9959100999 [DOI] [Google Scholar]
- 25.Freckmann G., Hagenlocher S., Baumstark A., Jendrike N., Gillen R. C., Rossner K., Haug C., “Continuous glucose profiles in healthy subjects under everyday life conditions and after different meals,” J. Diabetes Sci. Technol. 1(5), 695–703 (2007). 10.1177/193229680700100513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rose A. J., Richter E. A., “Skeletal muscle glucose uptake during exercise: How is it regulated?” Physiol. 20(4), 260–270 (2005). 10.1152/physiol.00012.2005 [DOI] [PubMed] [Google Scholar]
- 27.Bookstein L., Gidding S. S., Donovan M., Smith F. A., “Day-to-day variability of serum cholesterol, triglyceride, and high-density lipoprotein cholesterol levels,” Arch Intern Med. 150(8), 1653–1657 (1990). 10.1001/archinte.1990.00040031653012 [DOI] [PubMed] [Google Scholar]
- 28.Francaux M. A., Jacqmin P. A., Sturbois X. G., “Variations in lactate apparent clearance during rest and exercise in normal man,” Arch. Int. Physiol. Biochim. Biophys. 101(5), 303–309 (1993). 10.3109/13813459309003929 [DOI] [PubMed] [Google Scholar]
- 29.Merlot A. M., Kalinowski D. S., Richardson D. R., “Unraveling the mysteries of serum albumin-more than just a serum protein,” Front. Endocrinol. 5, 299 (2014). 10.3389/fphys.2014.00299 [DOI] [PMC free article] [PubMed] [Google Scholar]