Detection and grading of prostate cancer using temporal enhanced ultrasound: combining deep neural networks and tissue mimicking simulations

Abstract

Purpose

Temporal Enhanced Ultrasound (TeUS) has been proposed as a new paradigm for tissue characterization based on a sequence of ultrasound radio frequency (RF) data. We previously used TeUS to successfully address the problem of prostate cancer detection in the fusion biopsies.

Methods

In this paper, we use TeUS to address the problem of grading prostate cancer in a clinical study of 197 biopsy cores from 132 patients. Our method involves capturing high-level latent features of TeUS with a deep learning approach followed by distribution learning to cluster aggressive cancer in a biopsy core. In this hypothesis-generating study, we utilize deep learning based feature visualization as a means to obtain insight into the physical phenomenon governing the interaction of temporal ultrasound with tissue.

Results

Based on the evidence derived from our feature visualization, and the structure of tissue from digital pathology, we build a simulation framework for studying the physical phenomenon underlying TeUS-based tissue characterization.

Conclusion

Results from simulation and feature visualization corroborated with the hypothesis that micro-vibrations of tissue microstructure, captured by low-frequency spectral features of TeUS, can be used for detection of prostate cancer.

Introduction and background

Prostate cancer (PCa) is the third leading cause of cancer related death in American men, and the second most common cancer in men worldwide. American Cancer Society predicts that approximately 12.9% of men will be diagnosed with PCa at some point during their lifetime. In 2017, it is estimated that 161,360 American men will be diagnosed and 26,730 will die from PCa. Early diagnosis, and accurate grading and staging of PCa plays a significant role in the choice and the success of treatments [25]. Diagnosis involves measuring the level of Prostate Specific Antigen (PSA) in the blood serum and Digital Rectal Examination (DRE). If either test is abnormal, core needle biopsy is performed under Transrectal Ultrasound (TRUS) guidance. Grading of PCa is established by histopathological analysis of the obtained cores and staging determines the extent of the disease beyond the prostate itself.

Therapeutic aspects of PCa have progressed significantly, over the recent years, for patients with advanced disease [30]. However, men with indolent PCa, who constitute the vast majority of diagnosed cases, are overtreated with the traditional options of surgery or radiation therapy, leading to a decline in their quality of life. For this group of patients, active surveillance has has been shown to be an effective choice for disease management [9,29,30]. The utility of active surveillance is dependent on accurate assessment of the disease grade and extent. Using a sensitive imaging modality for tissue-characterization and for biopsy guidance can substantially contribute to appropriate and adequate treatment of PCa. Since TRUS is blind to intraprostatic pathology, TRUS-guided biopsies lead to a over- and under-estimation of the PCa. An additional factor that contributes to inaccuracies in PCa diagnosis is the heterogeneity in morphology and pathology of prostate. In recent years, the fusion of multi-parametric Magnetic Resonance Imaging (mp-MRI) and TRUS has emerged as a promising technology to target potential prostate lesions identified in mp-MRI [29]. While mp-MRI has negative predictive values as high as 94% [28], it has a high false positive rate, and can miss smaller foci of high-grade disease [20]. Additionally, registration of preoperative MRI to TRUS images is an unresolved challenge leading to inaccurate biopsies. Augmentation of ultrasound (US), a low cost, readily accessible and real-time technology, can substantially help with more accurate detection and grading of PCa and potentially alleviate the need for multi-modality registration. There have been a large number of efforts to adopt US-based tissue characterization for PCa detection during the biopsy procedure. Most contributions focus on the analysis of texture [22] and spectral features [11] within a single US frame. Elastography [6] and Doppler imaging [27] also aim to distinguish different tissue types based on their measured tissue stiffness and blood circulation, respectively. Accurate characterization of aggressive from indolent PCa is still an open problem [19].

Over the last decade, our group has investigated another US-based approach by acquiring and analyzing time series of US Radio-Frequency (RF) data, referred to as Temporal Enhanced Ultrasound (TeUS) (Fig. 1). Features extracted from TeUS data have been used in a machine learning framework to predict labels provided by histopathology as the ground-truth. TeUS has been used successfully for characterization of cancerous and non-cancerous prostate tissue in ex vivo [24,25] and in vivo [1,3,15,16,26] studies. In these studies, area under receiver operating characteristic curve (AUC) of 0.76–0.93 have been reported. TeUS has also been used to distinguish between various cancer grades in preliminary whole-mount studies [19]. Recently [2], we proposed a cancer grading approach for TRUS-guided prostate biopsy based on the analysis of in vivo TeUS data. In that work, we use histopathological grading of PCa that report the statistics of cancer distribution in a biopsy core. Our coarse-to-fine classification approach, similar to histopathology reporting, uses statistical analysis and deep learning to determine the distribution of aggressive cancer in US image areas surrounding a biopsy target. In a preliminary study [2], we showed that by using the learned high-level features, we could successfully differentiate among aggressive PCa, clinically less significant PCa, and non-cancerous prostate tissues. The underlying physical phenomena governing TeUS is still under investigation. It has been hypothesized that the acoustic radiation force of the transmit ultrasound signal increases the tissue temperature, and changes the speed of sound [8]. An alternative hypothesis is that micro-vibrations of acoustic scatterers contribute to tissue typing.

Fig. 1.

Temporal enhanced ultrasound (TeUS). a TeUS data generation, b preprocessing and ROI selection

In this manuscript, we extend our previous work [2] to further explore the underlying physical phenomena governing TeUS. The main contributions of this work are as follows: (1) We present a method for visualization and interpretation of the learned features from TeUS data. (2) We simulate the effect of micro-vibration as a potential source of TeUS tissue typing properties, using nuclei locations extracted from 14 whole-mount histopathology slides. (3) We also provide additional details on implementation and results of our previously proposed prostate cancer grading method [2], along with a parameter sensitivity analysis. We demonstrate that by analyzing high-level features learned by deep learning, we are able to provide insight into TeUS.

Temporal enhanced ultrasound data

Temporal Enhanced Ultrasound or TeUS is defined as the time series of US RF frames captured from insonification of tissue over time, without intentionally moving the tissue or the US probe. As it in shown in Fig. 1a, the tissue response to this prolonged insonification consists of reflected US echo-intensity values.

Data acquisition

Data was obtained from fusion prostate biopsy procedures where the biopsy target locations were identified using mp-MRI information, and the biopsy was guided by TRUS. The study was approved by the ethics review board of the National Cancer Institute, National Institutes of Health (NIH) in Bethesda, Maryland. One hundred and thirty-two (132) enrolled subjects provided informed consent to participate. Every subject underwent preoperative mp-MRI examination with three pulse sequences: T2-weighted, Diffusion Weighted Imaging (DWI), and Dynamic Contrast Enhanced (DCE) imaging. Before the biopsy procedure, suspicious lesions were identified using mp-MRI and scored by two independent radiologists, according to a previously published protocol [31]. Each radiologist assigned an overall score in the range from 1 (no cancer) to 5 (aggressive cancer) to a suspicious area. The consensus scores were grouped into three descriptors of “low” (score of ≤2), “moderate” (score of 3) and “high” (score of ≥4), and referred to as the MR suspicious level assigned to the area. These scores are based on findings on each mp-MRI sequence using previously described criteria [29], which indicate both the presence of prostate cancer and tumor grade. The standardized PI-RADS criteria were not in use for this study. The identified mp-MRI lesions were delineated on the T2-weighted MR image as the biopsy targets. At the beginning of the procedure, a 3D US volume of the prostate was reconstructed by obtaining a series of electromagnetically (EM) tracked 2D TRUS images. Then, using UroNav MR/US fusion system (Invivo Inc., a subsidiary of Philips Healthcare), T2-weighted MR images were fused with the 3D TRUS volume of the prostate [23,33]. Following the registration of TRUS and MR volumes, the target locations for biopsy were transformed to the EM coordinate frame. A clinician then navigated in the prostate volume towards the MR-identified target. TRUS transducer was held steady for about 5 seconds to acquire 100 frames of temporal US data from the target, followed by firing the biopsy gun to acquire a tissue sample. Two cores from axial and sagittal imaging planes were obtained per target location, respectively. Hereafter, we refer to these cores as “axial sample” and “sagittal sample”, respectively. TeUS data was only recorded from the primary lesion in the axial imaging plane to minimize disruption to the clinical workflow. In this paper, we use histopathology labeling of the cores as the ground-truth (described in more detail in [3,29]).

Histopathology labeling

Histopathology reports include the Gleason Score (GS) and the % distribution of PCa in the axial and sagittal samples from each target. The GS is the most common system to describe the level of abnormality in the prostate tissue. Gleason grades range from 1 (resembling normal tissue) to 5 (aggressive cancerous tissue). Gleason score is reported as a sum of the grades of the two most common patterns in a tissue specimen [9]. We only include cores in our study where the pathology of the axial and sagittal samples of that target match. The mismatch between the histology of two samples from the same target can be due to either the tumor being small or inaccurate MR/US registration. One hundred and ninety seven cores met our criteria, 57 of which are cancerous with the following histopathology labels: 12 GS of 3 + 3, 19 GS of 3 + 4, four GS of 4 + 3, 20 GS of 4 + 4, and two GS of 4 + 5. The remaining 140 cores had non-cancerous histology including benign or fibromuscular tissue, chronic inflammation, atrophy and Prostatic Intraepithelial Neoplasia (PIN). We divide the data from 197 cores into training and test sets as explained in Table 1. For building the classification model, we need to use homogeneous tissue regions with known gold standard. Given the potential misregistration between MR and TRUS images [1], we use biopsy cores with at least 7 mm of cancer for a typical core length of 18 mm to build our model. Training data is made up of 32 biopsy cores from 27 patients with the following histopathology labels: 19 benign, 0 GS of 3+3, 5 GS of 3 + 4, 2 GS of 4 + 3, 4 GS of 4 + 4 and, 2 GS of 4 + 5. The test data consists of 165 cores from 114 patients, with the following distribution: 121 benign, 12 GS of 3 + 3, 14 GS of 3 + 4, 2 GS of 4 + 3, and 16 GS of 4 + 4.

Table 1.

Gleason score distribution in different data divisions

Dataset	Benign	GS 3 + 3	GS 3 + 4	GS 4 + 3	GS 4 + 4	GS 4 + 5
Train	19	0	5	2	4	2
Test	121	12	14	2	16	0

Preprocessing and region of interest

For each biopsy target, we analyze an area of 2 × 10 mm² around the target location in the lateral and axial directions, respectively. This area is along the projected needle path in the US image and centered on the target location. We divide this region to 20 equally-sized Regions of Interest (ROI) of size 1 × 1 mm × mm (see Fig. 1b). We then compute the spectrum of TeUS data obtained from each biopsy target and in each region of interest. For this purpose, we take the Discrete Fourier Transforms (DFT) of all zero-mean US time series corresponding to the RF samples in each ROI, normalized to the frame rate. Then, we calculate the mean absolute values of the Fourier transforms of the RF time series in each ROI. Finally, each ROI is represented by 50 positive frequency components.

Prostate cancer grading

PCa grading can be viewed as a multi-class classification problem where the objective is to detect the PCa aggressiveness level (benign or Gleason grades 3, 4 or 5) for a given area in the tissue. Training a multi-class classifier given the histopathology reports of prostate biopsy as the ground-truth is non-trivial. Challenges associated with PCa grading are: (1) the ground-truth reports a measure of the statistical distribution of cancer in a biopsy core (e.g., % of cancer in core); (2) the exact location of the cancerous tissue in the core is not provided; and (3) as a result of partial information in (1) and (2), the exact label of each ROI in a core is not known. The statistics of ROIs with various labels in a core are the only known information. In this paper, similar to pathology reporting, we propose a coarse-to-fine classification approach to finding a statistical representation of the distribution of ROIs in various classes (benign and Gleason grades 3, or 4). Figure 2 shows an illustration of the proposed grading method. There are two major steps: (1) feature learning to extract latent features that maximally separate benign from cancerous tissues; and (2) distribution learning to model the statistical distribution of PCa grades in the space of learned features.

Fig. 2.

An illustration of the proposed cancer grading approach

Feature learning

We use a Deep Belief Network (DBN) [3,5] to automatically learn a high-level latent feature representation of the TeUS data that can separate benign and cancerous lesions. The network structure includes 100, 50 and 6 hidden units in three consecutive layers, where the last hidden layer represents the latent features. In the pre-training step, the learning rate is fixed at 0.001, mini-batch size is 5, and the epoch is 100. Momentum and weight cost are set to defaults of 0.9, and 2 × 10⁻⁴, respectively. In the discriminative fine-tuning step, we add a node to represent the labels of observations, and back-propagation with a learning rate of 0.01 for 70 epochs and mini-batch size of 10 is used. Due to a limited number of cancerous cores, we have not used any validation set in this work. In order to test the generalization of the trained DBN, we make certain that the test data is never used to pre-train or fine-tune the network parameters. The trained network maps the set of 50 spectral components for each ROI to six high-level latent features. Then, we perform dimensionality reduction in the space of the 50 latent features. We use Zero-phase Component Analysis [4] to whiten the features and to determine the top two eigen vectors, f₁ and f₂. We call this space the eigen feature space.

Distribution learning

To learn the distribution of different Gleason grades in the eigen feature space, we use a Gaussian Mixture Model (GMM) [32]. The K-component GMM is denoted by Θ = {(ω_k, μ_k, Σ_k)|k = 1,…, K}, where ω_k is the mixing weight $({\sum }_{k=1}^K{\omega }_k=1)$, μ_k is the mean and Σ_k is the covariance matrix of the k-th mixture component. Starting with an initial mixture model, the parameters of Θ are estimated with Expectation-Maximization (EM) [32]. Since the EM algorithm is a local optimization method, it is particularly sensitive to the initialization of the model. Instead of random initialization, we use the prior knowledge from pathology to devise a simple but efficient method for this purpose.

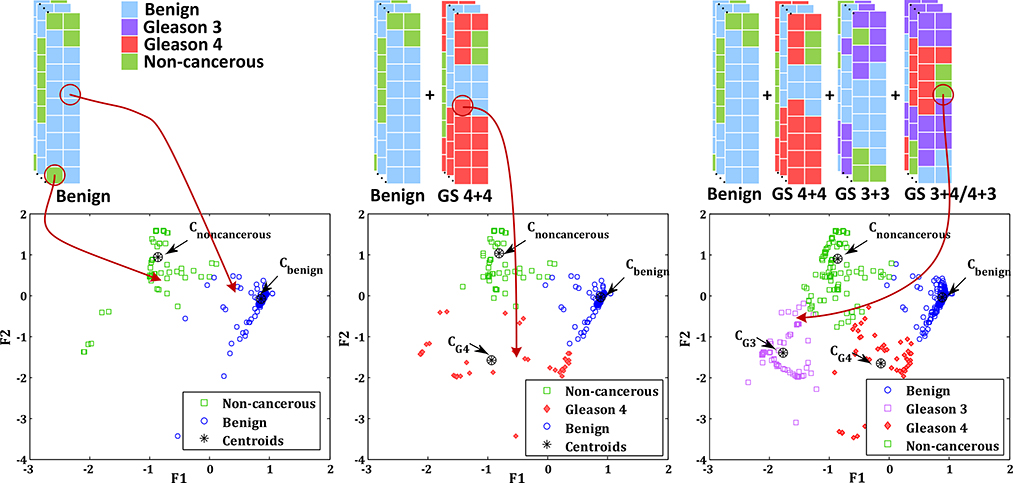
Figure 3 shows an overview of the proposed GMM initialization technique. Let X_H be the set of all ROIs of the cores in training data with histopathology labels H ∈ {benign, GS 3 + 4, GS 4 + 3, GS 4 + 4}. First, we map the distribution of the ROIs from benign cores, X_benign, in the eigen feature space; we observe two distinct clusters that span histopathology labels of normal and fibromuscular tissue, chronic inflammation, atrophy, and PIN. We use k-means clustering to separate the two clusters and consider the cluster with the maximum number of “normal tissue” ROIs as the dominant benign cluster, and the second cluster as a representative for other non-cancerous tissue. Next, we map ROIs in the training dataset that corresponds to the cores with GS 4+4, X_GS4+4 in the eigen feature space, to identify the dominant cluster that represents Gleason 4 pattern. Finally, we use all other ROIs from cancerous cores that correspond to GS 3 + 4 and GS 4 + 3 to determine the cluster for Gleason 3 pattern in the eigen feature space. We denote the centroid of all clusters by C = {C_benign, C_G4, C_G3,C_noncancerous}. To initialize the K-component GMM, we set K = 4 to model the four tissue patterns with mean, μ_k, for each Gaussian component equal to the centroid of each cluster. We use the equal covariance matrices for all components and set Σ_k to the covariance of X_H. Each ω_k, k = 1,…, K is randomly drawn from a uniform distribution between [0, 1] and normalized by ${\sum }_{k=1}^K{\omega }_k$.

Fig. 3.

An illustration of the proposed GMM initialization method

Prediction of Gleason score

To predict the Gleason score of each core, we map the data from 20 ROIs in that core to the eigen feature space (see Fig. 2). Subsequently, we assign a label from {benign, G3, G4, non-cancerous} to each ROI based on its proximity to the corresponding cluster centre in the eigen feature space. To determine a GS for a test core, Y, we follow the histopathology guidelines where we use the ratio of the number of ROIs labeled as benign, G3 (N_G3) and G4 (N_G4) (e.g., a core with a large number of G4 and a small number of G3 ROIs has GS 4 + 3):

$$Y=\{\begin{array}{ll}\text{GS}4+3\text{or}\text{higher,}& N_{G4}\ne 0\&N_{G4}\ge N_{G3}\\ \text{GS}3+4\text{or}\text{lower,}& N_{G3}\ne 0\&N_{G4}<N_{G3}\\ \text{benign,}& \text{otherwise}\end{array}$$

Since none of the cores labeled by histopathology as GS 3+3 did not make our selection criteria for training samples, we use cores with GS 3 + 4 and 4 + 3 to derive the features that describe Gleason grade 3.

Feature visualization

To determine the characteristics of the non-cancerous and cancerous tissue samples in the TeUS data and their correlation with the learned features, we propose a feature visualization approach. We use this approach to identify the most discriminative frequency components of the TeUS RF data as learned in the feature learning step (see “Preprocessing and region of interest” and “Feature learning”). Figure 4 shows an overview of the proposed method. First, TeUS test data is propagated through the trained DBN, and the activations of the last hidden layer (i.e., the learned latent features) are computed. We then use the GMM along with the learned features, as explained in “Distribution learning” section to assign a PCa grades to each ROIs of the test dataset. To examine the significance of the ith (i = 1,…,6) individual learned latent feature in the detection of different grades, the activations of all other five hidden units in the third layer are set to zero. The activation of the non-zero learned feature is back-propagated to the input layer. The resulting reconstructed signal, displayed in the input layer as a series of frequency components, highlights those components that contribute to the activation of the non-zero learned feature. By comparing the components activated for ROIs labeled as GS pattern of 3, 4 as well as non-cancerous tissue in “Prediction of Gleason score” section, we can identify those frequency ranges that are different between two tissue types. This process is performed for all the six latent features.

Fig. 4.

An illustration of the proposed feature visualization method

The results of feature visualization (Fig. 11a) suggest that frequencies between 0 and 2 Hz provide the most discriminative features for distinguishing between Gleason pattern 3 and 4 as well as non-cancerous tissue samples (see “Feature visualization and simulation results” section). Moreover, the identified frequency range is also consistent with the ranges that we have observed in our previous independent studies [1,16,17]. Our results to-date suggest that tissue micro-vibration, possibly due to pulsation from the heart beat (∼1.2 Hz), is a key contributor to the tissue typing capability of TeUS. To further examine this hypothesis, we continue our study with a histopathology mimicking simulation as explained in the next section.

Fig. 11.

a Differences of distributions between cancerous tissues with GS 3 and 4 as well as benign tissues back projected in the input neurons corresponds to the first neuron in the third hidden layer; b spectral difference of the simulated TeUS in benign and different cancer tissues

Histopathology mimicking simulation

A primary source of the observed backscattered US signal from the tissue has been associated with the scattering from the cell nuclei [13]. PCa primarily presents as changes in tissue microstructure where different density, size and spatial arrangement of nuclei are observed [7,14]. Subtle differences in scattering distribution results in significant changes in the back-scattered signal [12]. We hypothesize that the induced tissue micro-motion due to blood pulsation can cause different US scattering patterns in various microstructures of the prostate, which in turn can be captured by TeUS for PCa grading. We use a digital pathology dataset [14] to investigate this hypothesis in a histopathology-based simulation framework. Figure 5 shows an overview of our simulation design to explore this effect.

Fig. 5.

Pathology mimicking simulations framework

Numerical simulation design

For the simulation of mechanical micro-vibrations, we design tissue-mimicking phantoms which are generated using 14 digital histology slides of PCa patients [14]. We extract the locations of nuclei in the whole-mount digital slides. We divide each slide to blocks of 2 × 2 mm². We then generate a 2D model of nuclei positions based on their coordinates in the blocks. A total number of 42 blocks including 14 with GS ≥ 4, 14 with GS = 3 and 14 from non-cancerous tissue types is selected. We place each block at the center of a homogeneous linear viscoelastic phantom as shown in Fig. 5. The size of the phantom is 5 × 5 × 5 cm³, and the elasticity and viscosity are set to 25 kPa and 2.15 Pa.s, respectively [21].

To capture micro-motion due to an external excitation source, we use a finite element model (FEM) simulation in COMSOL Multiphysics 5.2 (Burlington, MA, USA). The external vibration source is defined as a sinusoidal wave with the frequency of 1 Hz and amplitude of 100 μm. We pulsate the inferior surface of the defined tissue-mimicking phantom with this low-frequency signal. The cells’ nuclei, which are embedded in tissue phantom, are displaced in our FEM as a result of the applied mechanical vibration.

TeUS simulation

For each block, we simulate TeUS data using Field II [18] from the displacement data generated by the FEM. In US simulation, the speed of the sound, the sampling frequency, and the probe frequency are set to 1540 m/s, 80 MHz and 6.6 MHz, respectively. We use 40 active elements in transmit and receive aperture while the imaging focal point is set at 2 cm. The first RF frame is created based on the initial positions of scatterers; this is followed by sequential US simulations given FEM displacement information over 2.5 s to generate TeUS data. We subdivide each block to four 1 × 1 mm² ROIs along the lateral and axial directions. It results in 168 ROIs with 56 ROIs of GS ≥4, GS = 3 and non-cancerous tissue, each. Finally, we generate the spectral features for each ROI as explained in “Preprocessing and region of interest” section.

Results and discussion

To assess the performance of our method, we use sensitivity, specificity, and accuracy of the approach in detecting cancerous tissue samples. We consider all cancerous cores as the positive class, and other non-cancerous cores as the negative class. Sensitivity or recall is the percentage of cancerous cores that are correctly identified while specificity is the proportion of non-cancerous cores that are correctly classified. Accuracy is the ratio of the true results (both true positives and true negatives) over the total number of cores. We also report the overall performance of our approach using the area under the receiver operating characteristic curve (AUC). Receiver operating characteristic curves (ROC) are two-dimensional graphs of sensitivity versus (1-specificity), depicting the relative trade-offs between sensitivity and specificity. Accuracy can be reported at any particular threshold on this curve. The maximum AUC is 1, where larger AUC values indicate better classification performance [10].

PCa detection and grading

Tables 2 and 3 show the classification and grading performance based on the inter-class AUC, accuracy, sensitivity, and specificity. To investigate the effect of the size of the tumor on our detection performance, we also show the AUC versus the largest length of the tumor in MRI. This length ranges from 0.3 cm to 3.8 cm in our data. As seen in Table 2, in cores with MR-tumor-size ≥2.0 cm, we obtain AUC of 0.80 in classifying cores with GS ≥ 4 + 3 from non-cancerous cores. Moreover, we achieve AUC, accuracy, sensitivity and specificity of 0.70, 70, 70, and 71%, respectively, in detection of cancerous from non-cancerous cores with MR-tumor-size ≥2.0 cm.

Table 2.

Model performance for PCa grading in the test dataset using TeUS only and by integration of TeUS and mp-MRI

Method	TeUS		TeUS + mp-MRI
	All cores	L ≥ 2.0 cm	All cores	L ≥ 2.0 cm
Non-cancerous vs. GS ≥ 4 + 3	0.69	0.80	0.82	0.89
Non-cancerous vs. GS ≤ 3 + 4	0.62	0.63	0.67	0.81
GS ≤ 3 + 4 vs. GS ≥ 4 + 3	0.61	0.67	0.71	0.71

L is the largest length of the tumor visible in mp-MRI

Table 3.

Model performance for classification of cancerous vs. non-cancerous cores in the test dataset using TeUS only and Integration of TeUS and mp-MRI

Evaluation	TeUS		TeUS + mp-MRI
	All cores	L ≥ 2.0 cm	All cores	L ≥ 2.0 cm
Accuracy	65%	70%	68%	70%
Sensitivity	62%	70%	63%	70%
Specificity	67%	71%	67%	72%
AUC	0.65	0.70	0.72	0.76

L is the greatest length of the tumor visible in mp-MRI

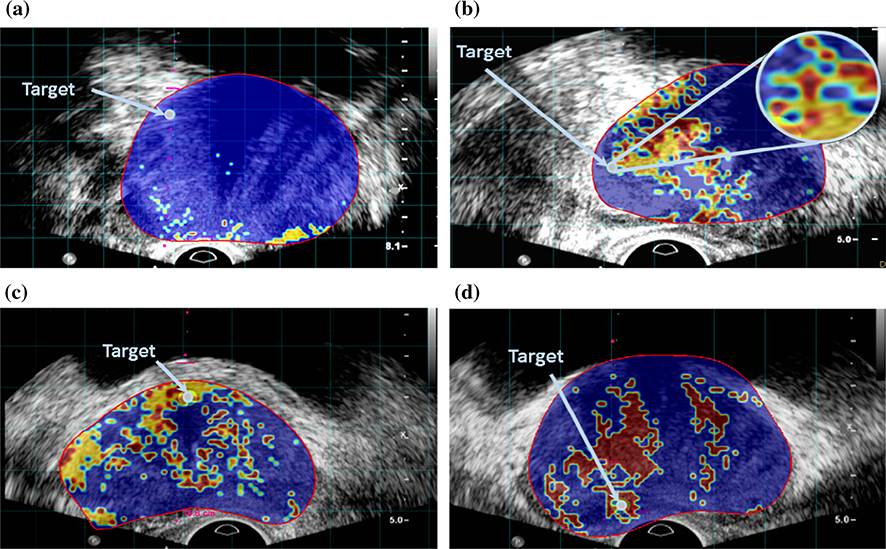
Figure 6 shows examples of the cancer likelihood maps from test dataset, derived from the output of the proposed clustering algorithm. Cancer colormaps overlaid on B-mode US image, along the projected needle path in the TeUS data and centered on the target. The red boundary shows the segmented prostate in MRI projected in TRUS coordinates. In the colormaps, red and yellow regions show 1 × 1 mm² ROIs which we detect as Gleason grades 4 and 3, respectively. The blue areas belong to non-cancerous ROIs.

Fig. 6.

Cancer likelihood maps overlaid on B-mode USi mage, along the projected needle path in the TeUS data and centered on the target. The ROIs for which we detect as Gleason grade of 4 and 3 are colored in red and yellow, respectively. The non-cancerous ROIs are colored as blue. The red boundary shows the segmented prostate in MRI projected in TRUS coordinates and the arrow pointer shows the target. a MRI lesion length = 27 mm, benign target, b MRI lesion length = 36 mm, GS ≤ 3 + 4, c MRI lesion length = 24 mm, GS ≤ 3 + 4 and d MRI lesion length = 17 mm, GS ≥ 4 + 3

Figure 6(b) shows a case where the axial and sagittal histopathology results do not agree (see “Data acquisition” section). The axial pathology indicates GS 3 + 4 whereas the sagittal pathology report the core as GS 4+4. The colormap demonstrates using our approach, the clinician could have reoriented the needle to biopsy a more aggressive region.

Integration of TeUS and mp-MRI

To take advantage of mp-MRI information, we combine the TeUS cancer detection results with readings from mp-MRI suspicious levels. If mp-MRI declares cancer suspicious level as low or high for a core, we use that prediction alone and report the core as benign or aggressive cancer, respectively. However, when mp-MRI declares the suspicious level as intermediate (70% of all cores in our data), we use predictions based on TeUS. For tumors with L ≥ 2.0 cm, the integrated approach leads to an AUC of 0.76 for predicting cancer grades compared that of 0.65 using mp-MRI alone, and 0.70 using TeUS data alone. Moreover, for classification of cores with GS ≥ 4 + 3 from non-cancerous cores, the combined AUC is 0.82. The results indicate both TeUS and integration of TeUS with mp-MRI have higher performance for larger tumors.

Sensitivity analysis

Performance in anatomical zones

Figure 7 (top) summarizes the biopsy target locations, distribution, and histopathology outcomes for the test data. The prostate region is divided into anterior/posterior, and central/peripheral zones for the base, midgland, and apex regions. In our test data, 34% (19 out of 56 biopsies) of all cancerous cores were in the central region where 24% (25 out of 109 biopsies) were in the peripheral region. Figure 7 (middle) shows the predictions of PCa grades using TeUS in different anatomical zones. Although more biopsies were performed in the peripheral zone, a higher portion of positive biopsies was observed in the central zone. In the central zone, we can differentiate between non-cancerous targets and clinically significant cancer (GS ≥ 4 + 3) with an AUC of 0.80. The bottom row depicts PCa grading performance integrating TeUS and MRI information.

Fig. 7.

Target location and distribution of biopsies in the test data. Light and dark gray indicate central and peripheral zones, respectively. The pie charts show the number of cores and their histopathology. The size of the chart is proportional to the number of biopsies (in the range from 1 to 25), and the colors dark red, light red and blue refer to cores with GS ≥ 4 + 3,GS ≤ 3 + 4 and benign pathology, respectively. The top, middle and bottom rows depict histopathology results, TeUS prediction, and integration of TeUS and MRI, respectively

Choice of the training data

We also analyzed the sensitivity of our approach to the choice of training data. To create new training and test sets we permute our original data where in each permutation, we exchange a randomly selected cancerous or benign core in the primary training and test data. This results in 32 different data divisions. As Fig. 8 shows, the average AUC of the sensitivity analysis follows our previous performance results, which supports the generalization of the proposed model.

Fig. 8.

Model performance for PCa grading in the test dataset and permutation set

Size of the training data

We also investigate the effect of training data size on on the grading performance by gradually increasing the size of the dataset from 16 to 56 cores. When choosing new training samples to add, we use biopsy cores with at least 4.0 mm of cancer for a typical core length of 18 mm (given the potential misregistration between MR and TRUS images [1] it is a prudent step). Otherwise, we randomly select an equal number of benign and cancerous cores. Figure 9 shows the AUC, of differentiation between PCa and non-cancerous tissue, versus the size of the dataset. In general, there is an increasing trend for the AUC and our approach has a higher performance using more training samples.

Fig. 9.

Model performance for different sizes of training dataset

Number of features

It has been shown that two features (f₁ and f₂) are very effective in classification. We further analyze the effect of including any of the six features in the model over the final results. Figure 10 shows the AUC of differentiation between cancerous and non-cancerous tissues, versus the number of features that we used to generate the final GMM model. To investigate the effect of the size of the tumor on our detection performance, we also show the AUC versus the largest length of the tumor in MRI. In general, decreasing the number of features used for model generation increases the model performance. In particular, as seen in Fig. 10b in cores with MR-tumor-size ≥ 2.0 cm, this trend is more clear. One possible explanation is that increasing the number of features leads to more complexity, which could not be learnt using a small number of samples in each category.

Fig. 10.

Model performance versus the number of features that we used to generate the final model: a For all of the cores; b for cores with MR-tumor-size ≥2.0 cm. Decreasing the number of features improves the model performance

Feature visualization and simulation results

For the feature visualization experiment, by subtracting the distributions of GS pattern 3, 4 and benign samples in the input layer (“Feature visualization” section), we found that feature one, corresponding to hidden activity of the first neuron of the third layer, along with features four and five, are those that maximally differentiate between different PCa grades, especially in lower frequency range. Figure 11(a) shows the visualization of distribution differences for GS patterns 3, 4 and benign tissue related to the first learned features of the third hidden layer, back propagated to the input layer. Figure 11(b) also depicts the similar spectral difference of the simulated TeUS for benign and cancer tissues. The simulation results also show a noticeable amplitude differences between benign and cancerous tissue regions in lower frequency range.

Figure 12 depicts the distribution of the power spectrum of TeUS at 1 Hz excitation frequency (Fig. 12a) and its first harmonic (Fig. 12b) across benign, GS3 and GS4 ROIs. The distributions in both frequencies are statistically significantly different between benign and cancerous ROIs (all p < 0.001 using a paired t-test).

Fig. 12.

a Distribution of the power spectrum in the frequency spectrum of simulated TeUS data at the excitation frequency, b distribution of the power spectrum in the frequency spectrum of simulated TeUS data at the first harmonic of the excitation frequency

Conclusion and future directions

In this paper we proposed: 1) a deep learning approach for grading PCa using TeUS during MRI-TRUS guided biopsy; and, 2) a simulation framework, derived from the deep learning approach, that can help explain the interaction of TeUS with tissue for identifying PCa.

For grading PCa, we learned high-level latent features from TeUS data using a DBN. This was followed by modeling the distribution of different Gleason patterns present in the data with a GMM. In data from 197 biopsy cores, we showed that our approach could successfully differentiate among aggressive PCa (GS ≥ 4 + 3), clinically less significant PCa (GS ≤ 3 + 4), and non-cancerous prostate tissue. We also showed that the simple integration of TeUS and mp-MRI has the potential to outperform either modality alone in detection of PCa. An AUC of 0.8 was achieved for separation of aggressive PCa from non-cancerous tissue for tumors that were larger than 2 cm in their greatest dimension in MRI. Additionally, suspicious levels from MRI, when added to TeUS information, led to an AUC of 0.89 for classification of aggressive PCa from non-cancerous tissue for tumors larger than 2 cm in MRI.

Evidence derived from our deep learning-based feature visualization pointed to low-frequency components of TeUS as the most informative features for tissue classification. These components potentially represent the effect of pulsation on prostate tissue microstructure. As a result, we next simulated mechanical micro-vibrations of scatterers in phantoms with various scatterer distributions, reflecting benign and cancerous tissue, derived from digital histopathology data. We demonstrated that the micro-vibrations of scatterers could be captured by low-frequency spectral features of TeUS, similar to our in vivo results. These observations together with our previous results suggest that the distribution and micro-vibration of scatterers could lead to tissue typing information in TeUS. One of the limitations of the current study is that all of the cores come from prostate regions where presence of cancer is suspected in mp-MRI. Future work will be focused on further evaluation of the method for the cases that mp-MRI does not show any suspicious cancer region. Currently, we are exploring further simulations for examination of the physical phenomena governing TeUS, and an inter-institution patient study to determine the accuracy of our PCa grading approach across a wide range of patient subpopulations. Furthermore, analyzing the TeUS data without spectral preprocessing is the focus of our current research.