A multiscale framework for disentangling the roles of evenness, density, and aggregation on diversity gradients

Abstract

Disentangling the drivers of diversity gradients can be challenging. The Measurement of Biodiversity (MoB) framework decomposes scale‐dependent changes in species diversity into three components of community structure: species abundance distribution (SAD), total community abundance, and within‐species spatial aggregation. Here we extend MoB from categorical treatment comparisons to quantify variation along continuous geographic or environmental gradients. Our approach requires sites along a gradient, each consisting of georeferenced plots of abundance‐based species composition data. We demonstrate our method using a case study of ants sampled along an elevational gradient of 28 sites in a mixed deciduous forest of the Great Smoky Mountains National Park, USA. MoB analysis revealed that decreases in ant species richness along the elevational gradient were associated with decreasing evenness and total number of species, which counteracted the modest increase in richness associated with decreasing spatial aggregation along the gradient. Total community abundance had a negligible effect on richness at all but the finest spatial grains, SAD effects increased in importance with sampling effort, and the aggregation effect had the strongest effect at coarser spatial grains. These results do not support the more‐individuals hypothesis, but they are consistent with a hypothesis of stronger environmental filtering at coarser spatial grains. Our extension of MoB has the potential to elucidate how components of community structure contribute to changes in diversity along environmental gradients and should be useful for a variety of assemblage‐level data collected along gradients.

Introduction

A critical limitation of most studies examining patterns of biodiversity along ecological or biogeographic gradients is that the most common measure of biodiversity—species richness—is limited in its utility for differentiating between several competing hypotheses that contribute to spatial variation in biodiversity. This limitation arises for two related reasons: (1) estimates of species richness are sensitive to the relative abundances of different species, the absolute numbers of individuals in a community, as well as their spatial distribution; (2) species richness depends on spatial scale in a nonlinear way (Rahbek 2005, Chase et al. 2018, McGlinn et al. 2019).

Examining variation in the total and relative abundance, as well as the spatial distribution of species along environmental gradients, provides information that allows for distinguishing among drivers of biodiversity. For example, species richness is typically a positive function of the amount of energy that enters an ecosystem. One prominent hypothesis for this relationship is that the energy input into an ecosystem leads to increases in the numbers of individuals, which in turn supports higher species richness (Wright 1983, Evans et al. 2008). Under this “more‐individuals hypothesis” (Srivastava and Lawton 1998) changes in species richness would be expected to be closely linked to changes in total numbers of individuals but not changes in species relative abundances or their spatial distributions if only sampling effects are operating (Storch et al. 2018). In contrast, if higher energy decreased competitive exclusion, then changes in richness could be linked to changes in the relative abundance of species rather than the total number of all individuals (Evans et al. 2005, Hurlbert and Jetz 2010). Additionally, if energy changes the spatial pattern or relevance of environmental heterogeneity, then species spatial structure would be expected to change. As a result, data and analyses that explicitly incorporate abundances of species and their spatial distribution across scales, rather than just a single scale‐agnostic measure, can provide deeper insights into the potential underlying causes of variation in biodiversity.

The Measurement of Biodiversity (MoB) framework (Chase et al. 2018, McGlinn et al. 2019) was developed to dissect the abundance and distribution patterns that underlie changes in species richness explicitly. Specifically, MoB decomposes variation in richness into the contributions from three components of community structure:

1. Species abundance distribution (SAD; including evenness and the size of the species pool). Communities that are sampled from species pools with higher evenness and/or more total species will have higher richness all else being equal.

2. The community‐level density of individuals (N); simply by sampling more individuals from a species pool, more species will be found.

3. Within‐species spatial aggregation (aggregation). When individuals of particular species are clustered (clumped) in the community, local species richness will typically be lower compared to a community in which individuals are randomly or overdispersed on the landscape.

These three components are largely sufficient for predicting many macroecological patterns of species richness (McGill 2010) and thus provide an important starting point for deciphering biodiversity patterns (see also He and Legendre 2002, Chase and Knight 2013). If species richness differs from one site to another, it does so because the SAD, N, and/or aggregation of species changes between those sites. It is important to note that directionality of causality between richness and these community components cannot necessarily be assumed a priori, however (Storch et al. 2018).

As it was originally developed (Chase et al. 2018, McGlinn et al. 2019), MoB consists of two complementary analyses for examining if a discrete explanatory variable (e.g., an experimental treatment like the presence or absence of a top predator) influences biodiversity: the two‐scale, multimetric analysis and the multiscale, richness analysis. However, discrete variables are not the only variables that influence variation in species richness. Species richness often varies along continuous gradients as well, such as gradients in temperature, latitude, or elevation. It is straightforward to extend the two‐scale, multimetric MoB, which uses a collection of traditional diversity metrics to gradients using regression analyses (Blowes et al. 2017). However, these discrete‐scale, multimetric MoB analyses ignore potentially complex patterns of scale dependence, and they do not provide a direct quantitative decomposition of component contributions to changes in species richness. Moreover, interpreting a collection of metrics is challenging even when those metrics are carefully chosen to reflect different components of community structure (Chase et al. 2018). In contrast, multiscale MoB provides a framework for uncovering complex patterns of scale dependence in species richness by using a range of scales rather than just two. These scale‐dependent changes can be related to specific components of community structure by considering what information about the community is used in the definition of a specific rarefaction curve. Lastly, the interpretation of multiscale MoB analysis is more straightforward because the relative magnitude of the relationships between the different components of richness can be compared since they have the same units (number of species).

Here, we outline an extension of multiscale MoB for decomposing species richness along continuous geographical or environmental gradients. We provide a conceptual overview and exposition within the mobr v2.0.0 R package (McGlinn et al. 2020) to dissect the influence of the components of species richness (N, SAD, and aggregation) across ecological gradients. We apply the approach to a case study on spatial variation in ant diversity along an elevational gradient in the southern Appalachian mountains (USA; from Sanders et al. 2007). We demonstrate that the application of multiscale MoB quantifies how changes in the SAD, N, and aggregation contribute to the multiscale pattern of richness change along gradients.

Methods

To illustrate the motivation and the method of extending the multiscale MoB framework, it is helpful to consider three simple scenarios (Fig. 1) where a single component of community structure is responsible for variation in species richness along a gradient. For example, richness may decline along a gradient because of a decrease in evenness (Fig. 1A, referred to as the SAD effect), a decrease in the number of individuals (Fig. 1B; N effect), or increased aggregation (Fig. 1C; aggregation effect). In reality, changes in species richness along a gradient are likely caused by changes in more than one of these components of community structure. Nevertheless, this simple example illustrates three key points: (1) species richness can change at one scale (plot scale) but not another (site scale), (2) species richness can change in apparently similar ways due to very different changes in the underlying components, and (3) a more direct focus on changes in these components across scales can elucidate their underlying contributions to changes in species richness.

Fig 1.

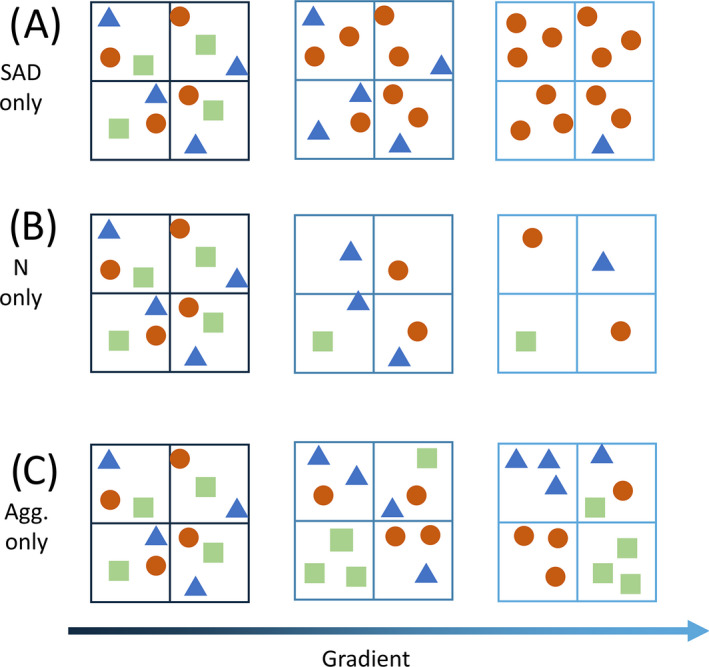
Cartoon communities from three sites arranged along a gradient (color gradient from dark blue to light blue) in three simple scenarios in which only the (A) SAD, (B) N, or (C) aggregation shifts along the gradient. The large boxes represent sites, the small boxes represent plots, and the different symbols represent individuals of different species.

Each of our simple scenarios show a decrease in plot‐scale species richness along the gradient, and next we show how our extension of the multiscale MoB framework can quantify how each component of community structure contributes to changes in S across scales (Fig. 2). We define scale as the number of samples (i.e., “plots”) or the number of individuals accumulated (McGill 2011). Multiscale MoB takes advantage of the unique information captured by three different types of rarefaction curves (Fig. 2):

Fig 2.

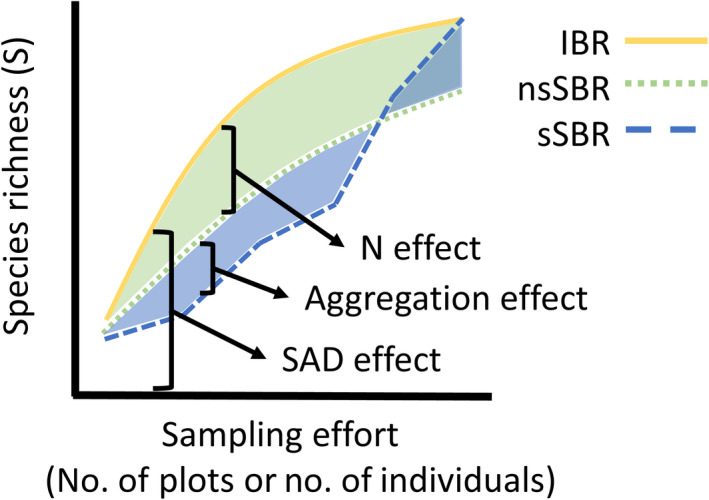
The three rarefaction curves compared at one site along a gradient in which this particular site has lower individual density than an average site on the gradient (i.e., a negative N effect is illustrated here). The individual‐based rarefaction (IBR) is a direct expression of the SAD (yellow line). The nonspatial, sample‐based rarefaction (nsSBR) reflects both the SAD and variation in N; thus the difference between the nsSBR and the IBR provides an estimate of the N effect (light green area). The spatial, sample‐based rarefaction (sSBR) also takes spatial position into consideration; thus the effect of spatial aggregation is the difference between the sSBR and the nsSBR (light blue area). Note that the nsSBR must eventually intersect the IBR and sSBR at this site (i.e., all curves converge to the same total S once enough effort is considered).

1. Spatial, sample‐based rarefaction (sSBR) is the accumulation of species by collecting the closest plots first. All possible focal samples are considered and the resulting curves are averaged over (Fig. 2). The sSBR reflects information on aggregation, N, and the SAD, and it can be thought of as a nested species–area relationship over a contiguous or noncontiguous area.

2. Nonspatial, sample‐based rarefaction (nsSBR) is the number of species given k plots in which all N individuals are randomly reassigned to plots while maintaining observed individual density (Fig. 2). The nsSBR reflects variation in both N and the SAD.

3. Individual‐based rarefaction (IBR) is the number of species given a random sample of n individuals out of N total individuals (Fig. 2). The IBR only reflects variation in the SAD.

Combining these curves allows us to dissect out the contribution of each component to changes in S across a range of scales less than the maximum spatial grain considered (Fig. 2). The difference between the sSBR and the nsSBR quantifies how changes in aggregation contribute to changes in S (i.e., the aggregation effect); the difference between the nsSBR and the IBR reflects how changes in N contribute to changes in S (i.e., the N effect); and by eliminating N and aggregation effects, the IBR shows how changes to the SAD covary with S (Fig. 2).

In the simple scenario in which only the SAD changes along the gradient (Fig. 1A), the IBRs diverge as sampling effort increases (Fig. 3A, gradient location represented by dark blue to light blue line colors, as in Fig. 1). Because the IBRs diverge, the strength of the detected SAD effect increases with effort (Fig. 3B). We can estimate the relationship between the gradient and the SAD effect on S using linear models (or nonlinear if more appropriate; Fig. 3B, only three scales shown for clarity) that allow us to quantify whether the strength of this relationship shows scale dependence (Fig. 3C). The scale dependence of the SAD effect may be particularly strong if the IBR curves from different points along the gradient intersect. In such cases the SAD effect may shift from positive at small scales to negative at large scales, for example, which would indicate changes in both evenness and species pool size. Alternatively, the SAD may not change along the gradient. In this case, the IBR curves for different points along the gradient would lie on top of each other: the SAD effect would be zero everywhere, have no relationship to the gradient and make no contribution to any changes to richness observed along the gradient.

Fig 3.

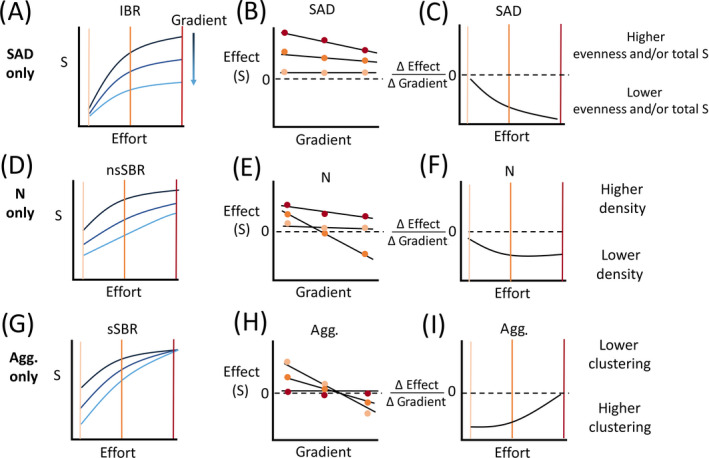
The three sets of hypothetical results illustrating the measurement of biodiversity (MoB) multiscale approach using the cartoon communities considered in Fig. 1. (A), (D), and (G) display three types of rarefaction curves that detect different components of community structure (for clarity only the relevant rarefaction curves are shown to detect the component of community structure known to have shifted). IBR = individual‐based rarefaction; nsSBR = nonspatial, sample‐based rarefaction; and sSBR = spatial, sample‐based rarefaction. For each type of rarefaction curve three curves are computed at each site along the gradient (colored dark blue to light blue as in Fig. 1). Three sampling efforts (orange vertical lines in (A), (C), (D), (F), (G), and (I) and points in (B), (E), and (H)) are highlighted to emphasize that the variation in the curves (i.e., effect sizes) change with scale. (B), (E), and (H) display the strength of the SAD, N, and aggregation effects ([Agg.] in units of species), respectively, on S plotted against the gradient. Regression lines are fit to the relationship between effect size and the gradient, and the strength (the estimated regression slope) of those fits are plotted in panels (C), (F), and (I) as a function of sampling effort. The dashed line denotes zero effect ((B), (E), and (H)) or slope ((C), (F), (I), the null expectation).

If only N changes across the gradient (e.g., decreasing N in the illustrated scenario, Fig. 1B), the nsSBRs vary along the gradient (Fig. 3D), but not the IBR and the sSBR curves (not shown). As with the SAD effects, we can model the relationship between the N effect (i.e., the difference between the nsSBR and IBR, Fig. 2) and the gradient across spatial grains (Fig. 3E). The net result on S is shown in Fig. 3F, where the decrease in N along the gradient is captured as a negative slope.

Finally, if only species aggregation changes along the gradient, the sSBRs will vary along the gradient (Fig. 3G), but not the other two rarefaction curves (IBR and nsSBR not shown). In the simple scenario we considered plot scale S decreases along the gradient as spatial clustering increases (Fig. 1C). Spatial clustering causes fewer species to be accumulated than expected under a random spatial distribution (i.e., a negative aggregation effect; Fig. 3H). In this scenario, the strength of aggregation is most negative at fine spatial scales indicating that species clustering primarily influences local scale richness (Fig. 3I). Note that regardless of the specific scenario considered in a balanced experimental design (i.e., same number of subplots at each site along the gradient), the effect of aggregation must converge on zero at the maximum sampling effort (i.e., all plots collected) because at this scale the sSBR must be identical to the nsSBR (McGlinn et al. 2019).

In summary, we have extended the multiscale MoB comparisons between categorical treatments to continuous gradients. This can be thought of as extending MoB from a t‐test to a regression analysis. We have released a new version of the mobr R package (McGlinn et al. 2020) to carry out the following steps of the gradient analysis illustrated in Fig. 3.

1. Compute three rarefaction curves that capture different information on the influence of N, the SAD, and aggregation for each set of samples (i.e., a site) along the gradient of interest: IBR, nsSBR, and sSBR (Fig. 3A, D, G, respectively).

2. Compute the differences between rarefaction curves at each site along the gradient. N effect = nsSBR − IBR (Fig. 3E); aggregation effect = sSBR − nsSBR (Fig. 3H). Note that the SAD effect is calculated directly from the IBR; that is, it is equal to S for a given sampling effort at a given point along the gradient (Fig. 3A, and B).

3. Model the relationship between the gradient and the estimates of the SAD, N, and aggregation effects (Fig. 3B, E,H).

4. Examine how the rate of change in the gradient and the effect (i.e., slope of model) vary with sampling effort. (Fig.  3C,F, I).

5. Compare the observed results to randomization‐based null models (described in McGlinn et al. 2019) for each component of community structure (i.e., SAD, N, and aggregation; Fig. 3C, F, I) to examine if the effects and their relationship to the gradient are different than expected from a null expectation.

In our simple example, S decreases monotonically along the gradient, as it often does along environmental gradients. And using the MoB approach, we estimate how each component of community structure—N, SAD, and aggregation—is associated with the richness gradient. Although our simple examples only showed richness gradients corresponding to changes in a single component of community structure, it is likely that more than one component will change along richness gradients in real communities. A sensitivity analysis suggested that the multiscale MoB approach can reliably detect the signature of simultaneous changes in multiple components of community structure on S (McGlinn et al. 2019).

Data requirements

The cartoon in Fig. 1 illustrates the basic data requirements to use MoB to explore variation in S along gradients. Obviously, sampling sites must be distributed along an environmental gradient. At each sampling site, there must be a collection of several (≥5) georeferenced samples that contain data on the abundances and identities of each species in a sample. It is not necessary for the sampling design to have the same number of samples at each site along the gradient, but the sSBR should be truncated to the smallest common number of samples per site across the gradient (to minimize any influence of spatial extent). Similarly, the IBR and the nsSBR should be truncated to the smallest number of individuals observed and therefore sites (not necessarily samples) should have enough individuals so that rarefaction results are meaningful—differences in rarefaction curves are constrained to be small at low sample sizes. It is also important that the spatial grain and spatial arrangement of plots is consistent along the gradient. Otherwise the investigator runs the risk that the variation in sampling design is responsible for changes in the components of community structure. If a given sampling design is not consistent among sites along a gradient, then it may be necessary to subset the samples so that sites along the gradient have comparable spatial extents. It is more important to ensure a constant extent across sites than a balanced design when using rarefaction curves to compare biodiversity. Although there may be slight differences in their numbers and spatial arrangement, it is more important that samples are standardised across all sites so they relate to a constant unit of effort (e.g., area).

Case study

To demonstrate our new methods we use data from Sanders et al. (2007), who examined spatial variation in richness along an elevational gradient (379–1,742 m) in the Great Smoky Mountains National Park, USA. Sanders et al. (2007) collected ant samples from each site along the elevational gradient by visiting each site once between June and August in 2004–2006 when ants in the national park are typically most active (Dunn et al. 2007). All sites were located in mixed hardwood forests and away from any area of recent human disturbance. We removed one site (site code = “NODI”) which only contained six individuals across the 16 samples, resulting in a data set of 28 sites.

At each site, data come from a randomly placed 50 × 50 m plot, from which 16 1–m² quadrats were arranged in a nested design: 10 × 10 m subplots were placed in the corners of each 50 × 50 m plot, and 1‐m² quadrats were placed in the corners of each 10 × 10 m subplot, for a total of 16 1‐m² quadrats per site. Ants were sampled by collecting all leaf litter within each quadrat and sifting through it with a coarse mesh screen (1‐cm grid) to remove the largest fragments and concentrate the fine litter. Concentrated litter from each quadrat was then put in its own mini‐Winkler sack for 2 d in the lab. Winkler samplers are common and efficient for quantifying ant abundance and diversity (Fisher 2005). After 2 d, all worker ants were extracted and enumerated. The data for this reanalysis were published to Dryad (Sanders et al. 2020). The code to reproduce the analysis is also available as an online supplement (DataS1.zip, as described in MetadataS1.pdf).

Here we will primarily focus on the insights gained from the multiscale MoB analysis. However, to clarify the added insights gained with our new method, we first discuss the results of a multimetric MoB analysis, which uses a collection of traditional diversity metrics (Appendix S1). Multimetric MoB reveals that at the site scale species richness and total number of individuals decrease with elevation (these effects were not as strong at the quadrat scale, Appendix S1: Fig. S1, S2A). However, rarefied richness, which controls for site‐specific differences in number of individuals, also decreases with elevation (Appendix S1: Fig. S2B), which indicates that although density effects cannot be ruled out, they do not provide a complete explanation for why richness is lower at higher elevations. A metric of evenness decreases with elevation (Appendix S1: Fig. S2C), whereas a metric of beta diversity thought to reflect spatial aggregation did not change along the elevational gradient (Appendix S1: Fig. S2F). The multimetric analysis suggests that at higher elevations richness is lower, and that it may be related to the lower density of individuals (N effects) and lower evenness (SAD effects), but it is not due to increased spatial clustering (aggregation effects). This analysis also suggests that diversity displays scale‐dependent responses to elevation because several of the trends with elevation were weaker at the quadrat scale than at the site scale. Next we demonstrate that the multiscale MoB analysis provides a more direct, quantitative multiscale decomposition of changes in richness with elevation that implicates different components of community structure.

We deployed the full multiscale MoB analysis using mobr (Fig. 4). The sSBRs show a general trend of higher S at lower elevations (Fig. 4A, darker curves), but the shape of these curves varied with spatial scale (x‐axis). Note that many of the sSBRs cross at intermediate scales, indicating that the ranking of site diversity across elevations depends on scale. The nsSBR curves, from which spatial aggregation has been removed, also tend to show that the lower‐elevation sites have higher S (Fig. 4B). Again, many of these nsSBR curves cross at intermediate scales (Fig. 4B) indicating scale dependence. Finally, the IBRs showed qualitatively similar patterns to the nsSBRs.

Fig 4.

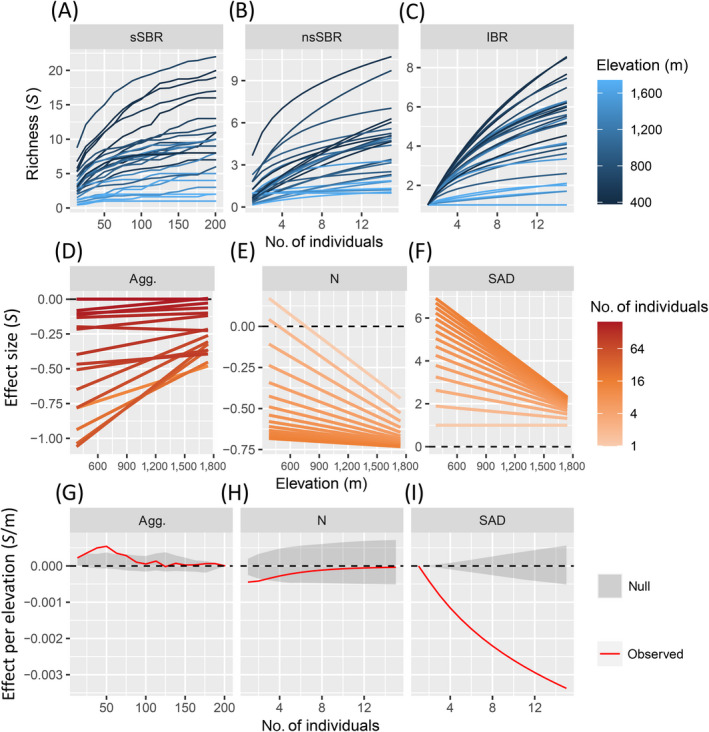
Multiscale analysis for the ant communities. (A) The spatial, sample‐based rarefaction (sSBR), (B) the nonspatial, sample‐based rarefaction (nsSBR), and (C) the individual‐based rarefaction (IBR) all expressed against number of individuals where each curve was constructed from a different site along the elevational gradient (black to blue lines). Panels (D)–(F) show the regression lines of the linear model of ΔS ~ elevation (m) at each sampling scale (light orange to dark orange lines) because of (D) aggregation (Agg.), (E) density (N), and (F) species abundance distribution (SAD) effects. Note that the sampling effort color gradient is log transformed. Panels (G)–(I) show how the linear regression slope for each component of community structure changes across sampling efforts (range varies across panels) relative to null model expectations (gray polygon is the 95% quantile of the null model).

The aggregation effects were predominantly negative because species richness was lower than expected due to spatial clustering across the gradient (Fig. 4D). Additionally, aggregation effects display a positive relationship with elevation (Fig. 4D), which indicates that spatial clustering was weaker at higher elevations. The relationship between the aggregation effect on richness and elevation was strongest at coarser spatial grains but indistinguishable from the null model at the largest spatial grains (Fig. 4G). Although the effect of aggregation on richness was statistically significant it was relatively modest. The magnitude of the largest aggregation slope was 0.0007 species/m, which equates to a gain of half a species associated with decreased spatial clustering across the approximately 1,000 m of elevation covered by the gradient.

The N effects were also predominantly negative. This indicates that richness was lower at most sites than would be expected if the total number of individuals was uniform across the gradient (Fig. 4E). This effect was negatively correlated with elevation, indicating that higher‐elevation sites had lower richness because they have fewer individuals (Fig. 4E; Appendix S1: Fig. S1), but this was only true at the finest spatial scale (Fig. 4H). This means that when we consider the multiscale nature of the N effect, it is clear that low‐elevation sites were not more species rich simply because they have more individuals. Lastly, richness values from random subsampling of the observed SADs (i.e., the SAD effects) were lower at high elevations because these sites had lower evenness and/or fewer total number of species (Fig. 4F). The strength of this negative relationship increased as coarser sampling scales were considered (Fig. 4I), where for a 1,000‐m change in elevation, an average of three fewer species occurred in quadrats at high elevation sites.

Using the multiscale MoB analysis we found that the Smokies ant elevational diversity gradient is largely associated with changes in the SAD and aggregation effects across elevation. Interestingly, these two components of community structure change in counteracting ways along the gradient. However, there are more species lost with elevation as a result of the change in evenness and species pool size than gained through the change in spatial structure, especially at larger scales. Consequently, we find a scale‐dependent net decline of species richness with elevation (see Appendix S1).

Discussion

Diversity gradients are rich testing grounds for ecological theory. However, the most common metric of diversity, species richness, may respond similarly to different processes and thus cannot provide unambiguous tests. Our extension of the MoB analysis to continuous explanatory variables allows us to decompose diversity gradients into the effects of the different components—evenness, density, or spatial aggregation—changing along the gradient. By quantifying the contribution of changes in these components to changes in richness, we can provide more powerful tests of ecological hypotheses.

An example is the data set on ants that we described above. One major feature that varies along elevational gradients is the amount of energy available to species. In species–energy theory, the more‐individuals hypothesis (Wright 1983, Srivastava and Lawton 1998, Storch et al. 2018) proposes that richness should be linked to N effects. In the ant data set we examined, however, we found little support for this hypothesis. Although there was a decrease at the site scale in total ant abundance with increasing elevation (Appendix S1: Fig. S1), this reduction in N was not associated with decreases in species richness across at all but the finest spatial scale (Fig. 4H). Instead, we found that declines in richness at higher elevations were primarily associated with decreases in evenness and total number of species, and to a lesser degree with decreases in spatial clustering. Many hypotheses can be linked to shifts in the SAD and spatial aggregation we observed (e.g., changes in competitive dominance, dispersal limitation, and/or environmental filtering) and information beyond what our analysis considers would be necessary to differentiate these hypotheses more fully. For the same data set, Machac et al. (2011) found that ant species in higher elevations were more closely related than expected by chance, which they interpreted as a signal of stronger environmental filtering because of low temperatures at high elevations. Our analysis using multiscale MoB is consistent with this hypothesis. If only a few cold‐tolerant species exist in high elevations, then this could explain why the SADs of the high‐elevation sites had fewer total species and lower evenness. It also seems reasonable that this mechanism could be responsible for the decrease in spatial clustering at high elevations (species may be less spatially clustered in environments in which they are competitively superior). However, without data on microhabitat features and species traits we are unable to rule out the possibility that higher elevations simply have less subsite environmental heterogeneity or that the cold‐tolerant species have evolved different foraging or social behaviors that result in less clumped spatial distributions.

More generally, decomposing richness into its components along ecological gradients may help provide resolution to apparently discordant empirical patterns of richness. For example, little consistency has emerged from some of the most well‐studied ecological gradients of species richness, such as those along disturbance gradients (Mackey and Currie 2001, Svensson et al. 2012) and productivity gradients (e.g., Mittelbach et al. 2001, Adler et al. 2011). Some of the variation observed along these gradients is most certainly because of differences in the scales in which observations are taken (e.g., Rahbek 2005, Chase et al. 2018), but much of the variation could be because of the differential influence of these gradients on the components of species richness, such as on the density of individuals, the SAD, or aggregation. By examining how these components change along gradients in a more consistent way, we can begin to achieve greater synthesis than is currently possible with information only on species richness.

The multiscale version of MoB that we have extended here has important advantages over traditional analyses of collections of diversity metrics along gradients (e.g., multimetric MoB). For example, the results of the multimetric MoB (Appendix S1) largely reflected a complementary subset of the multiscale MoB findings with some important exceptions: (1) multimetric MoB found no evidence of aggregation effects, whereas multiscale MoB did; (2) multimetric MoB could not rule out N effects completely, whereas multiscale MoB demonstrated this depended on scale; and (3) multimetric MoB provided a collection of trends in different metrics, whereas multiscale MoB related all trends back to change in species richness, arguably the most intuitive and popular metric of biodiversity.

Although the gradient version of multiscale MoB provides an important advance over the previous version that was only able to compare among categorical variables, there are many more directions in which the framework could be extended further. For example, both MoB analyses examine spatial scaling of subplots but cannot, in their current form, address scaling patterns between sites (i.e., sets of subplots). MoB also relies on species abundance data so that rarefactions can be performed. Often such data are unavailable, though presence–absence data are available. For such cases, it should be straightforward to apply MoB to presence–absence data with a goal to partition changes in richness due to occupancy and spatial aggregation (see e.g., Tjørve et al. 2008 for a similar approach using presence–absence data). Additionally, for some taxa, separation into individuals is difficult if not impossible, and relative abundance data are instead available as estimates of visual cover or biomass. It is less clear how to interpret MoB metrics when using cover or biomass, which in many communities may not be correlated with numbers of individuals. Finally, although we applied our approach using linear models of diversity change along a single explanatory variable (e.g., elevation), a logical next step would be to consider a multiple regression framework in which the partial effects of several variables are considered simultaneously, as well as to include the potential for nonlinear effects.

Supporting information

Appendix S1

Data S1

Metadata S1

McGlinn, D. J. , Engel T., Blowes S. A., Gotelli N. J., Knight T. M., McGill B. J., Sanders N. J., and J. M., Chase . 2021. A multiscale framework for disentangling the roles of evenness, density, and aggregation on diversity gradients. Ecology 102(2):e03233 10.1002/ecy.3233

Data Availability

Code and data are available from the Dryad Digital Repository² (Sanders et al. 2020).