Abstract
A new method is presented for full-field optical coherence tomography imaging, which permits capturing single shot phase sensitive imaging through simultaneous acquisition of four phase-shifted images with a single camera using unpolarized light for object illumination. Our method retains the full dynamic range of the camera by using different areas of a single camera sensor to capture each image. We demonstrate the performance of our method by imaging phantoms and live cultures of fibroblast, cancer, and macrophage cells to achieve 59 dB sensitivity with isotropic resolution down to 1 μm, and displacement sensitivity down to 0.1 nm. Our method can serve as a platform for developing high resolution imaging systems because when used in conjunction with broadband spatially incoherent light sources, the resolution is not affected by optical aberrations or speckle noise.
1. Introduction
Label-free microscopy is re-emerging as the preferred approach for observing cells and living organisms in their natural state [1,2]. Optical coherence microscopy (OCM) [3,4] is a label-free imaging technique based on low coherence interferometry. OCM is particularly well suited for label-free biomedical imaging [5–9] as it can provide phase and amplitude information while using incoherent illumination with low average and low peak power at the sample plane.
Full-field OCM (FF-OCM) imaging [10] employs a camera for detection of intensity maps of interferograms, formed by interference of the light backscattered from an object and reference arms of an interferometric imaging system. Coherence gating permits decoupling of axial and lateral resolution, and allows the rejection of light originating from outside of the coherence gate, which is defined by the optical spectrum of illumination source that is used for imaging. Time domain (TD-)FF-OCM is one of the fastest implementations of FF-OCM, permitting observation of a single en-face imaging plane at rates limited by the camera frame rate. Typically, to reconstruct a TD-FF-OCM image containing phase and intensity information, at least three interferograms with different phase shifts between the object and reference arms are required [11,12]. For rapid and robust implementation of TD-FF-OCM, interferograms required for image reconstruction should be captured in quick succession, or preferably, simultaneously.
Phase sensitive coherence gated imaging can provide multiple additional benefits beyond optical sectioning [13]. A key advantage of phase sensitive optical coherence interferometry is that it permits observation of sample displacements on the scale several orders of magnitude lower than the axial resolution, down to the sub-nanometer scale [14–17]. If sufficient phase stability can be achieved, phase sensitive coherence gated imaging unlocks new applications in angiography [18], neuro-imaging [19], and other fields [20]. Additionally, complex images captured with stable phase sensitive imaging systems can benefit from correction with computational adaptive optics [21].
Single shot phase sensitive OCM has been implemented either by using holographic coherence (off-axis) imaging [22], or by spatially separated phase stepped imaging [23,24]. While being simple to implement, off-axis configurations [22] rely on spatially coherent illumination and require a compromise between resolution and dynamic range. Alternatively, FF-OCM implementations relying on geometrical phase shifts can provide achromatic phase shifts across a broad spectrum, and can work with spatially incoherent illumination. However, the configurations presented to date allow for only a single orientation of linearly polarized light returning from the object arm to be detected, with other polarization states discarded by the use of a polarizing beamsplitter between the object and reference arms [23,24].
Here, we present a new method for phase-sensitive single-shot time-domain OCM. Our approach, with its inherent resistance to speckle noise and optical aberrations, permits high spatial and temporal resolution, and provides a foundation for developing the next generation of fast, high-resolution FF-OCM imaging modalities.
2. Results
2.1. Phase shifting
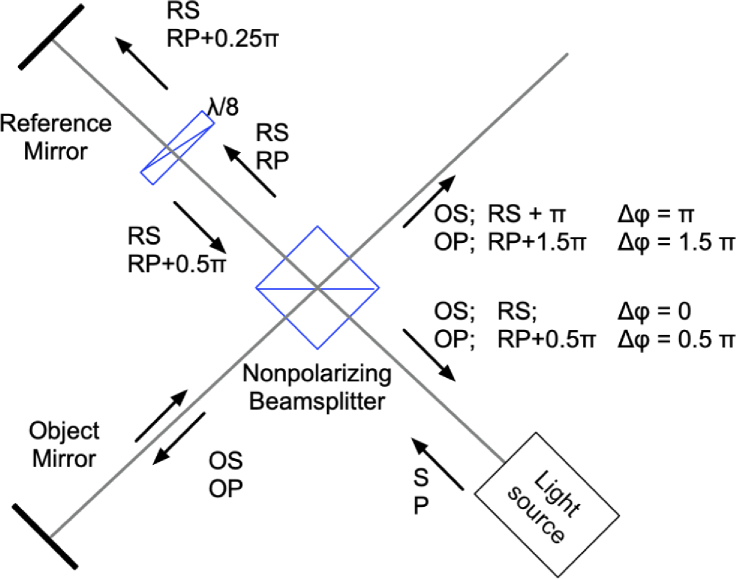
Our method employs a phase shifting strategy visualized in Fig. 1. To our knowledge, this approach has never been employed in OCM. While somewhat similar phase-shifting logic was explored in interferometry [25,26] and in 4-pi microscopy [27], these modalities require the use of very different imaging technology and methodologies. We use an unpolarized light source with similar intensity in S-polarized and P-polarized modes. The light from the source is propagated through a 50:50 cube beamsplitter and divided into an object beam (OS and OP modes) and a reference beam (RS and RP modes). At the beamsplitter the light phase is shifted by only during the reflection on the way back from the reference arm [28,29]. It is important to note that the phase shifts at the beamsplitter may vary depending on the beamsplitter design [30]. Here, we used an off-the-shelf cube beamsplitter (BS13, Thorlabs). The dielectric beamsplitter coating was applied to the hypotenuse of one of the two prisms that make up the cube. The cement was used to bind the two prism halves together. An additional shift between S and P polarization modes is induced through the dual pass through the waveplate.
Fig. 1.
Phase shifting strategy. Unpolarized light emitted from a light source can be treated as a sum of two orthogonally polarized components S and P. The light is divided into object (OS and OP) and reference (RS and RP) arms. In the reference arm, the component RP is delayed by by a waveplate. After reflection from the beamsplitter, the reflected components RS and RP undergo a further phase shift in relation with transmitted light. This results in four distinct phase shifts between the light returned from object and the reference arm.
Once the object and reference beams are recombined, we obtain four distinct phase shifts, stepped by between the object and reference beams in S and P polarization modes. These phase-shifted channels can then be spatially separated using a polarizing beamsplitter and recorded using a single camera as shown in Figs. 1 and 4. Our phase shifting approach is compatible with the use of broadband light sources in OCM. The beamsplitter-induced phase shift is geometric and is constant across all wavelengths, while the shift induced by the waveplate can be also achromatized through the use of achromatic waveplates or other achromatic phase shifting methods as described in the Discussion. The achieved phase shifts are stable due to the absence of moving parts, permitting extremely high sub-nanometer sensitivity and accurate OCM reconstructions.
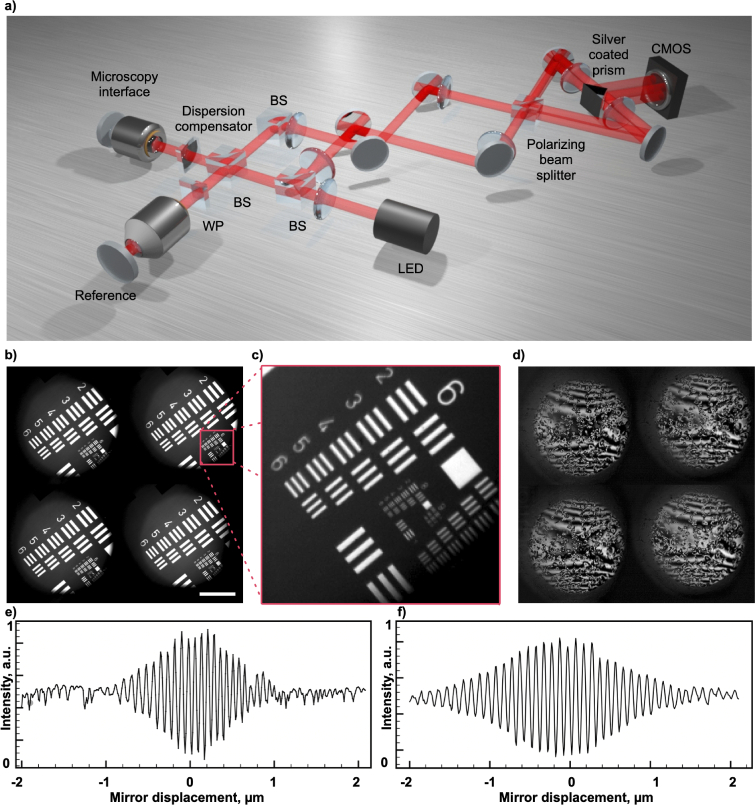
Fig. 4.
4-phase OCM imaging setup. a) Simplified schematic of the imaging setup. Light from an LED-based light source is split into object and reference arms using a 50:50 non-polarizing beamsplitter. After being recombined, the light from both sides of the beamsplitter (channel groups 1 and 2) is displaced vertically using a pair of steering mirrors, and a polarizing beamsplitter further separates the polarization channels S and P. All four phase-shifted channels are imaged onto a single camera, so that they are captured simultaneously. b) A single area from a calibration target is imaged on the four quadrants of a camera sensor. Here the reference arm is blocked and a circular field aperture limits the illuminated area, c) Zoomed-in area from b). d) Four phase - shifted interferograms of B16-F10 mouse melanoma cells, after background subtraction. Plot e) shows the interferometric autocorrelation fuction, measured by imaging a tilted mirror using a 565 nm LED as a light source, while f) shows the autocorrelation function measured using a 660 nm LED. The scale bar represents 100
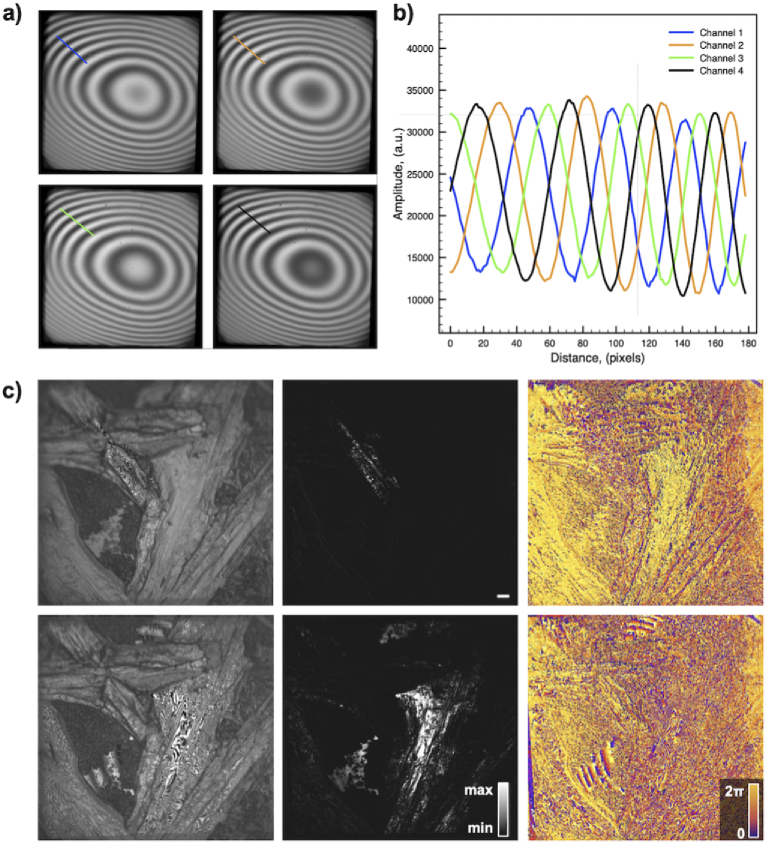
Figure 2(a,b) shows four phase-shifted patterns and their corresponding intensity profiles (for locations indicated in the image) that were obtained with our set-up using a flat mirror as an object. All images shown were captured at the camera frame rate of 500 Hz. Figure 2(c) depicts images of urea crystals grown on a glass slide and acquired from two different axial positions separated by approximately 10 . Figure 5(c) (first column) shows one of four interferograms used to reconstruct the amplitude (center column) and the phase maps (last column).
Fig. 2.
4-phase OCM imaging. a) Four simultaneously captured interferograms from a flat mirror used as a sample. b) The intensity profiles from the interferograms depicted in a), showing that the phase in each channel is shifted by the expected step of radians. c) Urea crystals grown on a glass coverslip. Images show one of the raw channels used for reconstruction (left), as well as the intensity (center) and phase (right) of the OCM reconstructions for two axial locations.
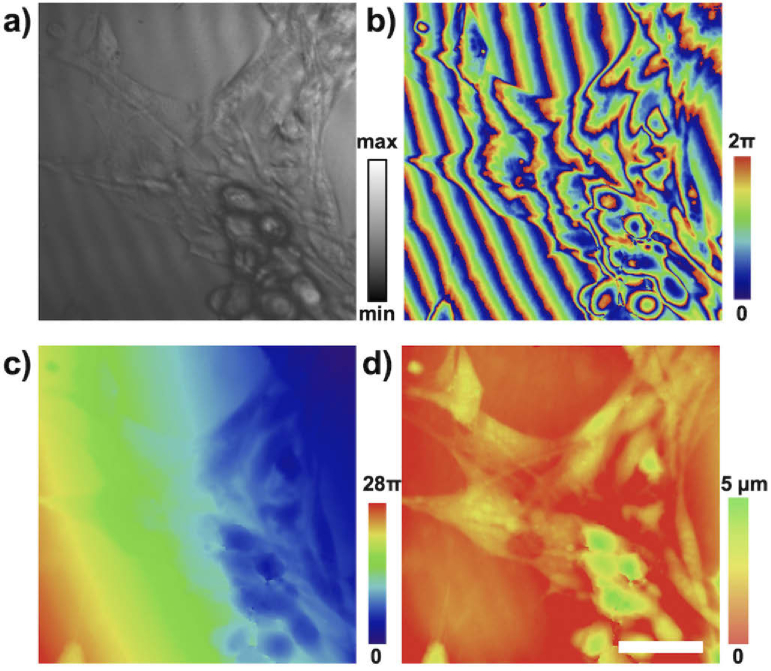
Fig. 5.
Phase sensitive OCM imaging of live fibroblast cell cultures. Imaging the surface of a collagen substrate to which the cells are attached permits sensing cumulative optical path differences induced by the cells. (a) The intensity component and (b) phase components are shown. Phase image is unwrapped (c) and flattened to produce quantitative images indicating the optical path delay induced by the cell (d). Representative images are shown with no averaging, captured at a 500 Hz framerate. Scale bar represents 20 .
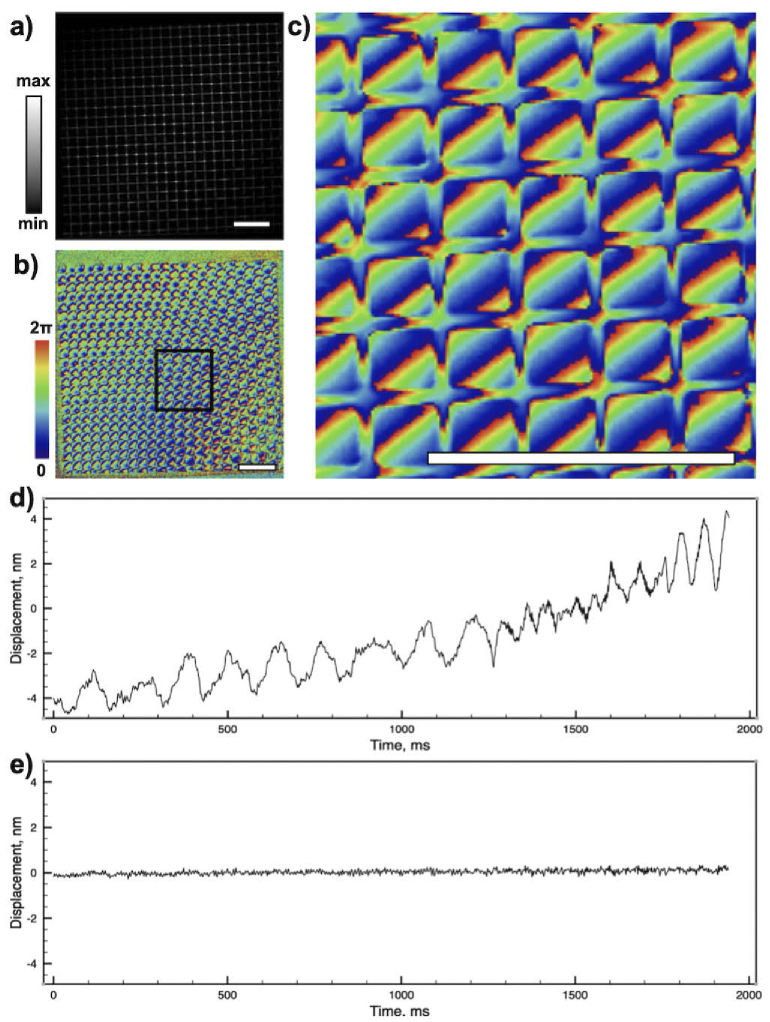
Additionally, we have imaged a reflective grid to measure the phase stability, as shown in Fig. 3. The sequence of 1000 frames was captured over 2 seconds and the phase drift at a single pixel was measured. Figure 3(d) shows the phase drift over time. In many situations, global phase drift caused by mechanical instabilities of the system can be compensated, as it affects the phase of the whole image frame in the same way. After computational correction of system drift, we have achieved a phase stability of 0.014 nm rms over two seconds of measurement (Fig. 3(e)).
Fig. 3.
Phase sensitive imaging. Complex images of a calibration target demonstrate high dynamic range and stability of the set-up. Images a), b), and c) depict amplitude and phase components of the image. The scale bars represent 50 . d) and e) Phase stability measurements over time before and after, respectively, computational correction of global drift.
2.2. Set-up
A simplified schematic of the set-up, which unites optical design elements from Linnik and Mach-Zehnder interferometers, is depicted in Fig. 4. Here we use a Light Emitting Diode (LED) as a light source (Thorlabs M565L3) with a central wavelength of 565 nm and a spectral full width at half maximum of 104 nm. Sufficient uniformity of the source emission permits critical, or Nelsonian, illumination, where the source is imaged on the sample, preserving the spatial incoherence of the source. This was implemented by magnifying and imaging the active area of the LED onto the field aperture of the system. The illumination module was designed to overfill the pupil of the imaging objective. The light was injected into the imaging system through a 70:30 (R:T) non-polarizing beamsplitter (Thorlabs BS022). The illumination light was then split into the object and reference arms with matched optical components using a 50:50 non-polarizing beamsplitter cube (Thorlabs BS013). In the reference arm, a Soleil-Babinet compensator (SBC) (Thorlabs SBC-VIS) was used to achieve the required retardation. In the object arm, a custom dispersion compensator assembled to match the dispersion introduced by the SBC was inserted. For the microscopy interface, the objective lenses were mounted in the upright configuration and pairs of either 0.25 NA dry (Leica 439) or 0.8 NA water immersion objectives (Olympus LUMPLFLN40XW) were used for imaging.
After backreflecting from the reference arm mirror (Thorlabs PF10-03-P01) and from the object, the light from the reference and object arms was recombined at the non-polarizing beamsplitter cube. After that, two steering mirrors were used to ensure that the images formed on the camera sensor were laterally displaced and did not overlap along the vertical axis (direction perpendicular to the drawing plane in Fig. 4). The S and P polarization modes were separated by the polarizing beamsplitter cube (Thorlabs PBS251). Throughout the setup, telescopes were assembled from achromatic doublets with focal lengths f = 150 mm (Thorlabs AC508-150-A) in 4-f configurations. The same lenses were also used to form the images of the four phase-shifted channels on the camera. A knife-edge right angle silver coated prism (Thorlabs MRAK25-P01) was used to ensure that the images would be positioned close enough but separated on the camera sensor. For image detection, a CMOS camera (Adimec Q-2HFW-Hm/CXP-6-0.4) was coupled with a frame grabber (Euresys Coaxlink Quad G3).
2.3. Requirements for the light source
The operation of FF-OCM relies on parallel detection of light waves that are reflected or scattered back from the sample. The object light interferes with the reference if the optical path length is matched to within the coherence length of the source, producing the signal which is later used to re-construct the image of the sample. In FF-OCM, optical aberrations or multiple scattering events can lead to incorrect mapping of the light and unintended interference signal. Therefore, spatially incoherent light sources are particularly suitable for this 4-phase OCM imaging approach. If the sample is illuminated with a light source with low spatial and temporal coherence, the scattered or aberrated light returned from the sample becomes spatially and temporally misaligned with the reference and does not interfere. As a result, the resolution is not compromised and only SNR is affected. Paired with broadband spatially incoherent light sources, 4-phase OCM should not be susceptible to speckle noise. Our imaging is compatible with all major types of light sources commonly used in FF-OCM, such as superluminescent diodes (SLD), supercontinuum [31] or other broadband light sources. However, it is ideally positioned to benefit from the use of spatially incoherent source such as Light Emitting Diodes (LEDs) or sources with random phase [32]. Additionally, our implementation requires having similar intensities in S and P polarized channels, making non-polarized illumination desirable.
Another important consideration when imaging with high numerical aperture objective lenses and non-collimated light is that the longitudinal spatial coherence of the source starts to affect the dimensions of the coherence gate. For example, for 0.8 NA objective, LSC becomes close to 1 micrometer [33–35], and this effect becomes even more pronounced as the numerical aperture is increased. This phenomenon can be exploited in future work for designing the 4-phase implementations of high NA FF-OCM systems [36] that harness the spatial gating produced by longitudinal spatial coherence effects while using narrow-band illumination sources.
2.4. Imaging
We have demonstrated the performance of the set-up by imaging two types of cell cultures. In the first example we have imaged the surface of a collagen matrix, on which murine fibroblast cells were cultured. This imaging configuration allowed for observing the cumulative phase change of light as it travelled through the cells, permitting quantitative imaging of phase changes at a 500 Hz framerate. Figure 5(a,b) shows representative intensity and phase reconstructions. A relatively smooth phase profile of the sample permits phase unwrapping and flattening (Fig. 5(c,d)).
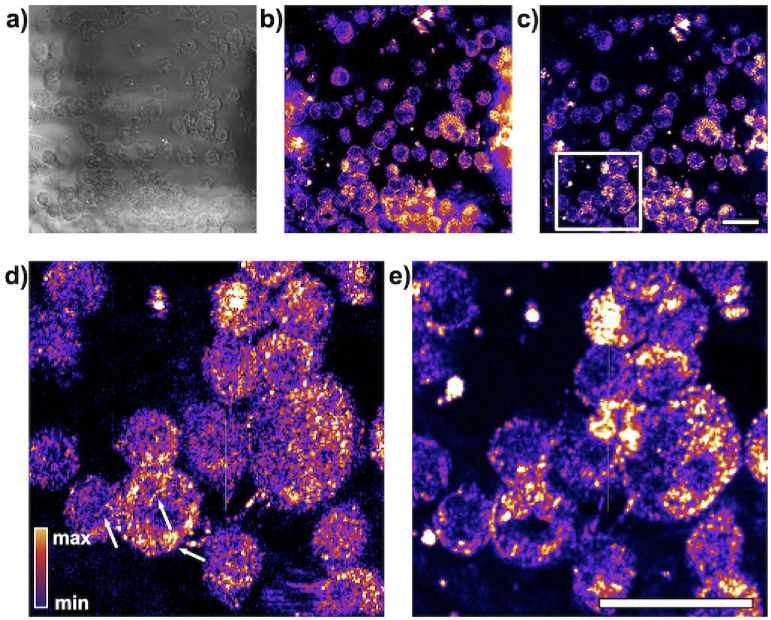
Inherently stable phase detection permits dynamic FF-OCM imaging of intracellular structures in murine macrophages (Fig. 6). Typically, long sequences of OCM images are preferred for dynamic imaging because imaging contrast depends on the magnitude of the displacement of imaged structures, and longer integration times typically lead to excellent contrast between the nuclei and cytoplasm of cells [37,38]. However, during longer acquisitions, subcellular features are commonly washed out and cannot be resolved. Here we have used our set-up to demonstrate dynamic OCM imaging. Shorter image sequences (500 frames captured at 500 Hz framerate) permit resolving of individual parts of the cytoskeleton (Fig. 6(d)), while longer image sequences (500 frames captured at 1 Hz framerate) allow for better contrast between the nucleus and cytoplasm (Fig. 6(e)).
Fig. 6.
Dynamic imaging of live macrophage cells reveal metabolic activity at the subcellular level. a) Average of intensity of OCM reconstructions. b) Average temporal frequency content (average of pixel-wise FFT with DC component excluded). c) Variance of the frequency content. Frequency analysis produces higher contrast between the cell nuclei and cytoplasm if longer image sequences are analyzed - 500 s in e). However, for shorter sequences captured at a 500 Hz rate over 1 s as shown in d), individual organelles become more pronounced (white arrows). d) and e) are cropped image subregions as indicated by the white box in c). Scale bar represents 20 .
3. Discussion
While we use a four phase shifting strategy to retrieve amplitude and phase information, in principle, only three phase-shifted images are necessary for the same operation. In our case, four phase shifts lead to a better SNR. However, in future work, we intend to exploit the redundant channel to harness different types of information, such as spectroscopic measurements, for dual color ratiometric imaging or additional polarization information. We expect future work will fully exploit this, as well as implement other modalities such as dual-wavelength interferometry for unambiguous phase extraction [39], or for simultaneous two color imaging [27,40].
Another benefit, which is inherent to single shot phase retrieval, is the resilience of the phase measurements to the fluctuations in the illumination intensity. If the interferograms are captured sequentially, the temporal illumination variance has a similar effect as small random phase shifts during the pixel-wise phase fitting step. This noise is particularly detrimental for dynamic OCM measurements. In our single-shot implementation, all channels are exposed at the same time, and changes of intensity affect all four points used for phase fitting, resulting in stable reconstructions even if the intensity fluctuates over time. This feature is particularly beneficial when using low-cost light sources, for example, with relatively noisy power supplies.
The current implementation of the 4-phase OCM phase shifting set-up, presented in this paper, is somewhat limited by the use of the Soleil-Babinet compensator for achieving the phase shift between S and P polarization channels. This element acts as a tunable zero-order waveplate. However, the real phase shifts achieved vary slightly for different wavelengths. In the future implementations, this element can be replaced with a fully achromatic phase shifting strategy, where the internal reflection from a prism hypotenuse surface is used to achieve wavelength independent shifts. Another limitation is that due to the need for mechanical scanning for capturing 3D information about the object, 3D imaging can be rather slow. Therefore our current implementation of 4-phase OCM is best suited for 2D observations.
We envisage that our method will enable new applications in biomedical research, as it can provide a new form of label-free contrast that contains information about the unperturbed dynamics of cell organelles at the subcellular level. Coherence gating permits dynamic contrast from unlabeled cells located in their native environment, in cell cultures and in tissues. We expect that the method will be applied for measuring and comparing tissue responses at the sub-cellular level during different pharmaceutical treatments. Also, the dynamic contrast alone can be useful for functionally phenotyping cells, such as describing the metabolic activity of different cell phenotypes for bioreactor research. Another research field that will benefit from the high speed and high sensitivity of our approach is label-free neuroimaging. Sub-nanometer level sensitivity to optical phase change can be achieved by imaging either neurons directly, or the substrates on which the cultures of neural cells are established. Cumulative phase of the light modulated by neuronal activation will contain information of both the morphology of the cells and the cell network activation patterns.
In conclusion, we have demonstrated the concept and practical implementation of a novel FF-OCM imaging approach which permits capturing four phase-shifted imaging channels on the same camera. The 4-phase shifting approach provides a robust platform for phase sensitive coherence gated imaging. It permits imaging at speeds only limited by the camera framerate with a phase stability that is not affected by the intensity or spectral fluctuations of the light source. With this robust design and high light-efficiency, we expect that this approach will function as a preferred platform for dynamic high-resolution FF-OCM imaging.
4. Methods
4.1. Image reconstruction
Intensity and phase images were reconstructed using a standard algorithm commonly used in 4-phase stepped interferometry [41]. Here, we only briefly outline the key reconstruction steps. We assume the image is formed through the interference of light returned from the Object and Reference on the camera as outlined in Eq. (1):
| (1) |
where is the recorded intensity of the signal at each pixel, indicates the phase stepped image number, and are the transmission coefficients for the object and reference light, respectively, is the envelope of the interference signal as a function of optical path mismatch, and is the optical phase step between the phase stepped images. The coherence-gated images of the amplitude and phase components can be reconstructed using Eq. (2) and Eq. (3):
| (2) |
| (3) |
Four simultaneously captured phase-shifted interferograms are shown in Fig. 2(a). Here, the surface of a flat silver mirror positioned at the focus of the imaging objective was used as an object. The interference bands are visible when the coherence gate is not matched with the focal plane and can be eliminated through further alignment or computational correction [42].
The detection sensitivity for our system at shot noise-limited conditions can be defined as where is he minimum detectable reflectivity (at SNR = 1). can be found using Eq. (4); for full derivation of Eq. (4) please refer to [41].
| (4) |
Here is determined by the full well capacity of the camera. With no binning it is specified as 2,000,000 e-. The is the total electrical noise which is equal to the read noise of 945 e- in our case. is the gain, is the number of accumulations, and and represent the relative intensities of the light returned from the object and the reference arms, respectively. Using Eq. (4) we can find that the sensitivity is -59 dB when imaging in conditions where the object and the reference reflectivity are matched.
The round trip coherence gate length in the set-up was determined by the central wavelength and the bandwidth of the light source was measured to be . The interferometric autocorrelation function measurements presented in Fig. 4(e) corresponds well to the theoretically calculated coherence gate length in water. The phase sensitivity, determined from the standard deviation of the signal from a single pixel in 50 frames, measured using a mirror as a sample, was 1.2 mrad, corresponding to displacement sensitivity of 0.1 nm.
4.2. Data pre-processing
The phase shifted images are propagating through different optical paths, and therefore the images formed on the camera are affected by different geometrical distortions. To correct for this, after each system re-alignment, an image of a reflective structure with sufficient spatial structure (flat surface of a sand-blasted steel sample) was captured with the reference arm blocked. This frame was used to extract four imaging channels . Image from the first imaging channel was used as a reference to calculate the displacement maps for the other three channels, using a non-parametric diffeomorphic image registration algorithm [43] implemented in Matlab (Mathworks Inc, Massachusetts, USA). The calculated displacement maps were saved and stored for computational correction of imaging data in further experiments.
Immediately before each imaging session, a background frame was captured and saved as an average of at least 100 frames, captured with the object light blocked with a shutter located just before the imaging objective in the sample arm. The intensity values were subtracted from the image to reduce the effects of fixed pattern noise, otherwise clearly visible in the raw images.
4.3. Sample preparation
Collagen gel was prepared by using rat collagen type 1 (3447-020-01, Millipore Sigma, St. Louis, MO, USA). A volume of 2 mL of the collagen solution in 20 mM of acetic acid with an initial concentration of 3 mg/mL was mixed with 0.3 mL of phosphate buffered saline, 25 mL of 7.5% NaHCO3, and 0.675 mL of water for a final collagen concentration of 2 mg/mL and a pH of 7.3. All mixed solutions were kept on ice, and 0.5 mL of the solution was added to a 35 mm Petri dish with a cell adherent coating and incubated at 37 °C for 1 hour to promote gelation. Secondary cultures of NIH 3T3 mouse fibroblasts (CRL-1658, American Type Culture Collection, Manassas, VA, USA) were grown in Iscove’s Modified Dulbecco’s Medium with no phenol red (21056023, Thermo Fisher Scientific, Waltham, MA, USA) and supplemented with 10% v/v fetal bovine serum (16140071, Thermo Fisher Scientific, Waltham, MA, USA) and Penicillin-Streptomycin-Glutamine (10378016, Thermo Fisher Scientific, Waltham, MA, USA). Cultures were maintained in an incubator at 37 °C in an environment with 95% air and 5% , were seeded in the collagen gel, and grown overnight. The cells were imaged at room temperature within 30 minutes of being removed from the incubator.
B16-F10 murine melanoma cells (ATCC CRL-6475) and murine macrophage cells J774A.1 (ATCC TIB-67) were cultured in an environment with 95% air and 5% in Iscove’s Modified Dulbecco’s Medium with no phenol red (21056023, Thermo Fisher Scientific, Waltham, MA, USA) and supplemented with 10% v/v fetal bovine serum (16140071, Thermo Fisher Scientific, Waltham, MA, USA) and Penicillin-Streptomycin-Glutamine (10378016, Thermo Fisher Scientific, Waltham, MA, USA). The cells were imaged at room temperature within 30 minutes of being removed from the incubator.
Acknowledgments
The authors would like to thank Edita Aksamitiene and Eric Chaney for providing cell culture samples, and Darold Spillman Jr. for administrative support.
Funding
National Institutes of Health10.13039/100000002 (R01EB023232); Air Force Office of Scientific Research10.13039/100000181 (FA9550-17-1-0387).
Disclosures
The authors declare no conflicts of interest.
References
- 1.Marx V., “It’s free imaging - label-free, that is,” Nat. Methods 16(12), 1209–1212 (2019). 10.1038/s41592-019-0664-8 [DOI] [PubMed] [Google Scholar]
- 2.Hammer D. X., Agrawal A., Villanueva R., Saeedi O., Liu Z., “Label-free adaptive optics imaging of human retinal macrophage distribution and dynamics,” Proc. Natl. Acad. Sci. 117(48), 30661–30669 (2020). 10.1073/pnas.2010943117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Izatt J. A., Hee M. R., Owen G. M., Swanson E. A., Fujimoto J. G., “Optical coherence microscopy in scattering media,” Opt. Lett. 19(8), 590–592 (1994). 10.1364/OL.19.000590 [DOI] [PubMed] [Google Scholar]
- 4.Vinegoni C., Ralston T., Tan W., Luo W., Marks D. L., Boppart S. A., “Integrated structural and functional optical imaging combining spectral-domain optical coherence and multiphoton microscopy,” Appl. Phys. Lett. 88(5), 053901 (2006). 10.1063/1.2171477 [DOI] [Google Scholar]
- 5.Pande P., Shelton R. L., Monroy G. L., Nolan R. M., Boppart S. A., “Low-cost hand-held probe for depth-resolved low-coherence interferometry,” Biomed. Opt. Express 8(1), 338–348 (2017). 10.1364/BOE.8.000338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Graf B. W., Boppart S. A., “Multimodal in vivo skin imaging with integrated optical coherence and multiphoton microscopy,” IEEE J. Sel. Top. Quantum Electron. 18(4), 1280–1286 (2012). 10.1109/JSTQE.2011.2166377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bower A. J., Mahmassani Z., Zhao Y., Chaney E. J., Marjanovic M., Lee M. K., Graf B. W., De Lisio M., Kong H., Boppart M. D., Boppart S. A., “In vivo assessment of engineered skin cell delivery with multimodal optical microscopy,” Tissue Eng., Part C 23(7), 434–442 (2017). 10.1089/ten.tec.2017.0185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zurauskas M., Podoleanu A. G., “Multiplexing-based polarization sensitive en-face optical coherence tomography,” J. Biomed. Opt. 18(10), 106010 (2013). 10.1117/1.JBO.18.10.106010 [DOI] [PubMed] [Google Scholar]
- 9.Iyer R. R., Žurauskas M., Cui Q., Gao L., Smith R. T., Boppart S. A., “Full-field spectral-domain optical interferometry for snapshot three-dimensional microscopy,” Biomed. Opt. Express 11(10), 5903–5919 (2020). 10.1364/BOE.402796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thouvenin O., Grieve K., Xiao P., Apelian C., Boccara A. C., “En-face coherence microscopy,” Biomed. Opt. Express 8(2), 622–639 (2017). 10.1364/BOE.8.000622 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Safrani A., Abdulhalim I., “Real-time phase shift interference microscopy,” Opt. Lett. 39(17), 5220–5223 (2014). 10.1364/OL.39.005220 [DOI] [PubMed] [Google Scholar]
- 12.Safrani A., Abdulhalim I., “Full-field parallel interferometry coherence probe microscope for high-speed optical metrology,” Appl. Opt. 54(16), 5083–5087 (2015). 10.1364/AO.54.005083 [DOI] [PubMed] [Google Scholar]
- 13.Leitgeb R., “En-face optical coherence tomography: a technology review,” Biomed. Opt. Express 10(5), 2177–2201 (2019). 10.1364/BOE.10.002177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ney M., Safrani A., Abdulhlaim I., “Instantaneous high-resolution focus tracking and a vibrometery system using parallel phase shift interferometry,” J. Opt. 18(9), 09LT02 (2016). 10.1088/2040-8978/18/9/09LT02 [DOI] [Google Scholar]
- 15.Ney M., Safrani A., Abdulhalim I., “Three wavelengths parallel phase-shift interferometry for real-time focus tracking and vibration measurement,” Opt. Lett. 42(4), 719–722 (2017). 10.1364/OL.42.000719 [DOI] [PubMed] [Google Scholar]
- 16.Aizen A., Ney M., Safrani A., Abdulhalim I., “A compact real-time high-speed high-resolution vibrometer, surface profiler and dynamic focus tracker using three wavelengths parallel phase-shift interferometry,” Opt. Lasers Eng. 107, 304–314 (2018). 10.1016/j.optlaseng.2018.04.007 [DOI] [Google Scholar]
- 17.Nazarov A., Ney M., Abdulhalim I., “Compact and fast sub-nm scale displacement probe using a phase mask and parallel phase-shift interferometry,” J. Phys. D: Appl. Phys. 51(33), 335102 (2018). 10.1088/1361-6463/aad265 [DOI] [Google Scholar]
- 18.Sirotkina M. A., Gubarkova E. V., Plekhanov A. A., Sovetsky A. A., Elagin V. V., Matveyev A. L., Matveev L. A., Kuznetsov S. S., Zagaynova E. V., Gladkova N. D., Zaitsev V. Y., “In vivo assessment of functional and morphological alterations in tumors under treatment using OCT-angiography combined with OCT-elastography,” Biomed. Opt. Express 11(3), 1365–1382 (2020). 10.1364/BOE.386419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Spahr H., Pfäffle C., Burhan S., Kutzner L., Hilge F., Hüttmann G., Hillmann D., “Phase-sensitive interferometry of decorrelated speckle patterns,” Sci. Rep. 9(1), 11748–15 (2019). 10.1038/s41598-019-47979-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Won J., Huang P.-C., Boppart S. A., “Phase-based Eulerian motion magnification reveals eardrum mobility from pneumatic otoscopy without sealing the ear canal,” J. Phys Photonics 2(3), 034004 (2020). 10.1088/2515-7647/ab8a59 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhu D., Wang R., Žurauskas M., Pande P., Bi J., Yuan Q., Wang L., Gao Z., Boppart S. A., “Automated fast computational adaptive optics for optical coherence tomography based on a stochastic parallel gradient descent algorithm,” Opt. Express 28(16), 23306–23319 (2020). 10.1364/OE.395523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sudkamp H., Koch P., Spahr H., Hillmann D., Franke G., Münst M., Reinholz F., Birngruber R., Hüttmann G., “In-vivo retinal imaging with off-axis full-field time-domain optical coherence tomography,” Opt. Lett. 41(21), 4987–4990 (2016). 10.1364/OL.41.004987 [DOI] [PubMed] [Google Scholar]
- 23.Dunsby C., Gu Y., French P., “Single-shot phase-stepped wide-field coherence-gated imaging,” Opt. Express 11(2), 105–115 (2003). 10.1364/OE.11.000105 [DOI] [PubMed] [Google Scholar]
- 24.Hrebesh M. S., Dabu R., Sato M., “In vivo imaging of dynamic biological specimen by real-time single-shot full-field optical coherence tomography,” Opt. Commun. 282(4), 674–683 (2009). 10.1016/j.optcom.2008.10.070 [DOI] [Google Scholar]
- 25.Brock N., Hayes J., Kimbrough B., Millerd J., North-Morris M., Novak M., Wyant J. C., “Dynamic interferometry,” in Novel Optical Systems Design and Optimization VIII, vol. 5875 Sasian J. M., Koshel R. J., Juergens R. C., eds., International Society for Optics and Photonics (SPIE, 2005), pp. 101–110. [Google Scholar]
- 26.Millerd J., “Vibration Insensitive Interferometry,” in ESA Special Publication, vol. 621 (2006), p. 68. [Google Scholar]
- 27.Aquino D., Schönle A., Geisler C., Middendorff C. V., Wurm C. A., Okamura Y., Lang T., Hell S. W., Egner A., “Two-color nanoscopy of three-dimensional volumes by 4Pi detection of stochastically switched fluorophores,” Nat. Methods 8(4), 353–359 (2011). 10.1038/nmeth.1583 [DOI] [PubMed] [Google Scholar]
- 28.León-Rodríguez M., Rayas J. A., Cordero R. R., Martínez-García A., Martínez-Gonzalez A., nones A. T.-Q., nez Contreras P. Y., Medina-Cázares O., “Dual-plane slightly off-axis digital holography based on a single cube beam splitter,” Appl. Opt. 57(10), 2727–2735 (2018). 10.1364/AO.57.002727 [DOI] [PubMed] [Google Scholar]
- 29.Zetie K. P., Adams S. F., Tocknell R. M., “How does a Mach-Zehnder interferometer work?” Phys. Educ. 35(1), 46–48 (2000). 10.1088/0031-9120/35/1/308 [DOI] [Google Scholar]
- 30.Hamilton M., “Phase shifts in multilayer dielectric beam splitters,” Am. J. Phys. 68(2), 186–191 (2000). 10.1119/1.19393 [DOI] [Google Scholar]
- 31.Tu H., Zhao Y., Liu Y., Liu Y.-Z., Boppart S. A., “Noise characterization of broadband fiber Cherenkov radiation as a visible-wavelength source for optical coherence tomography and two-photon fluorescence microscopy,” Opt. Express 22(17), 20138–20143 (2014). 10.1364/OE.22.020138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stremplewski P., Auksorius E., Wnuk P., Kozon L., Garstecki P., Wojtkowski M., “In vivo volumetric imaging by crosstalk-free full-field OCT,” Optica 6(5), 608–617 (2019). 10.1364/OPTICA.6.000608 [DOI] [Google Scholar]
- 33.Abdulhalim I., “Competence between spatial and temporal coherence in full field optical coherence tomography and interference microscopy,” J. Opt. A: Pure Appl. Opt. 8(11), 952–958 (2006). 10.1088/1464-4258/8/11/004 [DOI] [Google Scholar]
- 34.Safrani A., Abdulhalim I., “Spatial coherence effect on layer thickness determination in narrowband full-field optical coherence tomography,” Appl. Opt. 50(18), 3021–3027 (2011). 10.1364/AO.50.003021 [DOI] [PubMed] [Google Scholar]
- 35.Abdulhalim I., “Spatial and temporal coherence effects in interference microscopy and full-field optical coherence tomography,” Ann. Phys. 524(12), 787–804 (2012). 10.1002/andp.201200106 [DOI] [Google Scholar]
- 36.Safrani A., Abdulhalim I., “Ultrahigh-resolution full-field optical coherence tomography using spatial coherence gating and quasi-monochromatic illumination,” Opt. Lett. 37(4), 458–460 (2012). 10.1364/OL.37.000458 [DOI] [PubMed] [Google Scholar]
- 37.Münter M., vom Endt M., Pieper M., Casper M., Ahrens M., Kohlfaerber T., Rahmanzadeh R., König P., Hüttmann G., Schulz-Hildebrandt H., “Dynamic contrast in scanning microscopic OCT,” Opt. Lett. 45(17), 4766–4769 (2020). 10.1364/OL.396134 [DOI] [PubMed] [Google Scholar]
- 38.Scholler J., Groux K., Goureau O., Sahel J.-A., Fink M., Reichman S., Boccara C., Grieve K., “Dynamic full-field optical coherence tomography: 3D live-imaging of retinal organoids,” Light: Sci. Appl. 9(1), 140–149 (2020). 10.1038/s41377-020-00375-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Houairi K., Cassaing F., “Two-wavelength interferometry: extended range and accurate optical path difference analytical estimator,” J. Opt. Soc. Am. A 26(12), 2503–2511 (2009). 10.1364/JOSAA.26.002503 [DOI] [PubMed] [Google Scholar]
- 40.Bossi M., Fölling J., Belov V. N., Boyarskiy V. P., Medda R., Egner A., Eggeling C., Schönle A., Hell S. W., “Multicolor far-field fluorescence nanoscopy through isolated detection of distinct molecular species,” Nano Lett. 8(8), 2463–2468 (2008). 10.1021/nl801471d [DOI] [PubMed] [Google Scholar]
- 41.Dubois A., Handbook of Full-field Optical Coherence Microscopy: Technology and Applications (CRC Press, 2016). [Google Scholar]
- 42.Graf B. W., Adie S. G., Boppart S. A., “Correction of coherence gate curvature in high numerical aperture optical coherence imaging,” Opt. Lett. 35(18), 3120–3122 (2010). 10.1364/OL.35.003120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Vercauteren T., Pennec X., Perchant A., Ayache N., “Diffeomorphic demons: Efficient non-parametric image registration,” NeuroImage 45(1), S61–S72 (2009). 10.1016/j.neuroimage.2008.10.040 [DOI] [PubMed] [Google Scholar]