Structural templates for imaging EEG cortical sources in infants

Abstract

Electroencephalographic (EEG) source reconstruction is a powerful approach that allows anatomical localization of electrophysiological brain activity. Algorithms used to estimate cortical sources require an anatomical model of the head and the brain, generally reconstructed using magnetic resonance imaging (MRI). When such scans are unavailable, a population average can be used for adults, but no average surface template is available for cortical source imaging in infants. To address this issue, we introduce a new series of 13 anatomical models for subjects between zero and 24 months of age. These templates are built from MRI averages and boundary element method (BEM) segmentation of head tissues available as part of the Neurodevelopmental MRI Database. Surfaces separating the pia mater, the gray matter, and the white matter were estimated using the Infant FreeSurfer pipeline. The surface of the skin as well as the outer and inner skull surfaces were extracted using a cube marching algorithm followed by Laplacian smoothing and mesh decimation. We post-processed these meshes to correct topological errors and ensure watertight meshes. Source reconstruction with these templates is demonstrated and validated using 100 high-density EEG recordings from 7-month-old infants. Hopefully, these templates will support future studies on EEG-based neuroimaging and functional connectivity in healthy infants as well as in clinical pediatric populations.

1. Introduction

Our ability to study the functional connectivity of the brain during its early years is crucial in understanding neurotypical development as well as abnormal developmental trajectories associated with conditions like attention deficit hyperactivity disorder (Konrad and Eickhoff, 2010) and autism (O’Reilly et al., 2017). However, most EEG studies in infants are performed at the scalp level, and therefore cannot localize the cortical or subcortical origin of the activity (Nunez and Srinivasan, 2006; Van de Steen et al., 2019) and are easily confounded by the effect of the recording reference (Bringas Vega et al., 2019; Guevara et al., 2005) and volume conduction (Nunez et al., 1997; O’Reilly and Elsabbagh, 2020; Van de Steen et al., 2019).

Different approaches have been developed to address these limitations, including algorithms to estimate the neuronal sources that give rise to EEG scalp activity. Such algorithms can estimate sources within volumes or over surfaces, depending on how dipolar sources are placed in the model of the head. For example, all dipolar contributions can be postulated to sum linearly and be represented with equivalent current dipoles (ECD) whose position and orientation are estimated from scalp EEG activity. Such an approach presents some analytic advantages (e.g., mathematical tractability when used with spherical head models) and can be motivated when one or a few specific sources of activity clearly dominates like in the context of epileptic activity (Ebersole, 1994) or for localized independent components (Acar et al., 2016). By generalizing the ECD approach to a large number of dipoles and using sophisticated finite element models (FEM) of the head, we can also perform current density reconstruction (CDR). In general, these volumetric approaches (i.e., CDR, ECD) localize dipoles using fewer a priori constraints than source localization methods based on cortical surfaces. For example, dipoles obtained from volumetric approaches may be positioned outside of gray matter regions and their orientation may not consider known structural information such as cytoarchitectural properties.

Alternatively, sources can be estimated over surfaces in order to constrain the position and the orientation of dipolar sources based on our understanding of EEG generative mechanisms. Scalp EEG is generally modeled as being a volume-conducted open field generated when a large number of postsynaptic currents impinges simultaneously on the apical dendrites of many pyramidal cells comprised within a small cortical patch (Baillet et al., 2001). This assumption is motivated by 1) the proximity of the cortex to the scalp, 2) the creation of a dipolar source between the apical tree and the soma of pyramidal cells following postsynaptic depolarization of apical dendrites, and 3) the creation of an open field due to the parallel alignment of the apical dendrites. Given this understanding of EEG generative mechanisms, it is a common practice to estimate EEG cortical sources by fitting the amplitude of dipoles positioned and orientated following the cortical surface. Further, aside from this physiological motivation, there are good reasons for wanting to use surface-based source estimation. For example, from a structural point of view, using surfaces has been shown to result in more precise co-registration (Ghosh et al., 2010). Also, it is worth noting that functionally relevant cortical parcellations follow the topology of the cortical sheet and that the distances along this surface are consequently generally more functionally relevant than 3D Euclidean distances. For example, the properties of inter-hemispheric connectivity have been shown to be impacted by whether two neuronal populations are in homotopic regions (i.e., depending on the cortical topology) rather than by whether they are separated by short homotopic distances (i.e., depending on 3D Euclidean distances) (O’Reilly and Elsabbagh, 2020). Due to the folding of the cortical sheet, regions that are very close in space (e.g., on the opposite sides of a sulcus or a fissure) may be relatively far apart with respect to the cortical sheet and, hence, may be functionally very different. A small localization error on volumes can therefore result in attributing sources to substantially different functional regions.

Surface and volume source estimation can eventually be combined, for example by aligning dipoles according to the cortical mesh or to the estimated orientation of the cortical columns (Bonaiuto et al., 2020) while placing volumetric grids of dipoles with free orientation in subcortical nuclei (Attal and Schwartz, 2013). Additional information from other modalities (e.g., tractography or functional MRI) can also be used to further constrain the source models (Lei et al., 2015), although such functionalities are generally not readily available in the main source estimation toolboxes and therefore require custom implementation.

Source estimation has not been frequently reported in the infant EEG literature, with the notable exception of a few research groups that used volumetric approaches such as CDR with realistic head models built from MRIs of head-size-matched individuals (Xie and Richards, 2017) or from age-matched MRI averages (Lunghi et al., 2019), or using ECD with a four-shell ellipsoidal head model (Ortiz-Mantilla et al., 2019). Source imaging is more frequently used in magnetoencephalography (MEG) (Kao and Zhang, 2019), but it generally relies on over simplistic spherical models to overcome the absence of realistic head models (Imada et al., 2006; Kuhl et al., 2014) or it uses custom-built subject-specific head models that are not reusable by the research community (Ramírez et al., 2017; Travis et al., 2011).

The Neurodevelopmental MRI Database (NMD; Richards et al., 2016) contains average volume segmentations of head tissues based on BEM and FEM. These segmentations can be used directly by some toolboxes, such as FieldTrip (Oostenveld et al., 2011), to build head models for volume-based source estimation. This functionality is, however, by no means available in all popular toolboxes. FieldTrip also supports surface-based source estimation directly from volumetric data by interfacing with external surface extraction software such as iso2mesh (Fang and Boas, 2009), Brain2Mesh (Tran and Fang, 2017), or FreeSurfer (Fischl, 2012). However, these procedures have been developed for adult subjects and are unlikely to perform well on infant MRIs due to various issues such as poor white matter/gray matter contrast (Phan et al., 2018; Schumann et al., 2010). Furthermore, other popular software packages such as Brainstorm (Tadel et al., 2011) and MNE-Python (Gramfort et al., 2013) require the user to provide pre-computed cortical surfaces and provide only a limited support for volumetric BEM or FEM segmentations.

In addition to EEG sensor recordings, estimating neuronal sources requires 1) a structural model of the head (conductor model); 2) a model of source distributions (source space); 3) the position of the EEG sensors on the subjects’ head (electrode placement, coregistered with the source and head model); 4) a method for estimating scalp activity generated by neuronal sources (forward modeling); and 5) an inversion scheme for estimating the probable neuronal sources corresponding to the observed scalp activity (inverse modeling). The first component, the structural head model, is generally built by post-processing the participants MRI using specialized software designed for that purpose, such as FreeSurfer (Fischl, 2012), CIVET (MacDonald et al., 2000), the Computational Anatomy Toolbox (Gaser and Dahnke, 2016), BrainVISA (Rivière et al., 2009), SPM (Mattout et al., 2007), FSL (Jenkinson et al., 2012), or BrainSuite (Shattuck and Leahy, 2002). However, the time and expense associated with MRI scanning may be prohibitive or not possible with certain groups of participants because of health issues or ethical concerns. To address the lack of structural information in EEG analysis, population averages of head and brain structures have been proposed and can be used for computing approximate forward models (Fuchs et al., 2002; Valdés-Hernández et al., 2009). The objective of the current study is to extend these methods to infants by leveraging the recently published infant version of the FreeSurfer pipeline that supports surface extraction from MRI in participants from zero to 24 months of age (Zöllei et al., 2020). As an outcome of this work, we are releasing 13 new surface templates that can be used for standardized surface-based source reconstruction in infants within this age range.

2. Method

2.1. Volumetric dataset

To build age-specific head models that can be used for surface-based EEG source reconstruction, we used the infant and preschool segments of the NMD version 2 (Richards et al., 2016), which contains brain and head MRI averages, boundary element method (BEM) and finite element method (FEM) volume segmentation of head tissues, as well as corresponding electrode placements. The NMD provides distinct MRI averages for the brain and head, obtained from the same sample, but optimizing the alignment of brain structures and outer head tissues, respectively. See (Sanchez et al., 2012a) for more details on volume averaging. We will refer to the coordinate space for these two kinds of volumes as brain space and head space, respectively.

To extract outer head surfaces, we used NMD’s four-compartment BEM segmentation “BEM4 ”, which labels every non-null voxel in head space as belonging either to the skin, the skull, the cerebrospinal fluid (CSF), or the brain. The identification of the brain, the skull, and the scalp on individual MRI was based on FSL Brain Extraction Tool (Bartlett and Smith, 1999; Smith, 2002). See (Richards, 2013) for more details about the individual MRI segmentation approach adopted for building the NMD.

Table 1 lists the sample size per gender as well as the age range of the children included in every average. All averages are based on 3T scans using a T1 magnetization-prepared rapid gradient-echo (MPRAGE) sequence.

Table 1.

Sample size and age range for the different MRI averages.

Template	Female	Male	N/A	Age (months)
2 week	26	17	0	<= 0.5
1 month	42	60	0	0.5–1.5
2 month	40	29	0	2–2.5
3 month	21	17	0	2.5–4
4.5 month	29	25	0	4–5.5
6 month	55	56	0	5.5–7
7.5 month	33	62	0	7–8.5
9 month	36	25	0	8.5–10
10.5 month	21	21	0	10–11.5
12 month	68	101	0	11.5–13
15 month	41	37	0	14.5–17
18 month	31	45	0	17.5–20
2 year	57	76	2	23–26

2.2. Software

The brain averages were co-registered with the head averages using FLIRT (Jenkinson et al., 2002) and brain surfaces were extracted using the Infant FreeSurfer pipeline (Zöllei et al., 2020). Most of the data processing and analyses have been performed using custom code relying on various Python packages, the principal ones being connected-components-3d 1.5.0 (Kemnitz and Silversmith, 2020), Matplotlib 3.1.2 (Hunter, 2007), MNE-Python 0.20.0 (Gramfort et al., 2014, 2013), NiBabel 3.0.0 (Brett et al., 2019), Numpy 1.18.2 (Oliphant, 2006; Walt et al., 2011), Pandas 1.0.3 (McKinney, 2010; The pandas development team, 2020), Pillow 7.0.0 (Clark et al., 2020), PyCortex 1.2.0 (Gao et al., 2015), PyMeshFix 0.13.3 (Attene, 2010), Scikit-Image 0.16.2 (Walt et al., 2014), Scipy 1.4.1 (Virtanen et al., 2020), trimesh 3.5.12 (Dawson-Haggerty et al., 2020), and XArray 0.15.1 (Hoyer and Hamman, 2017). Further, FieldTrip and the SimBio toolbox (Vorwerk et al., 2018) were also used for our comparative analysis between surface and volume source estimation.

2.3. Head-brain co-registration

Because the brain and head surfaces are computed from different MRI averages, we used FLIRT to find optimal affine transforms for transforming the average brains to head space. For this procedure, we used the skull-stripped MRI and weighted the contribution of the voxels in the brain average using a binary mask that excluded from the objective function the contribution of voxels outside of the brain volume. Such a weighting was used for the brain averages but not the head averages in order to ensure that the brains snugly fit within the skull cavity in head space.

2.4. Surface extraction

To extract the brain surfaces, we normalized the intensity of the MRI of brain averages (FreeSurfer mri_nu_correct command) and converted them to a standard 256 × 256 × 256 1-mm isotropic space (FreeSurfer mri_convert -conform command). Then, we used the Infant FreeSurfer reconstruction pipeline (infant_recon_all; de Macedo Rodrigues et al., 2015; Zöllei et al., 2020) to extract the surfaces separating the pia mater, the gray matter, and the white matter. During this process, the Desikan et al. (2006) and the Destrieux et al. (2010) cortical parcellations were automatically computed. We skipped the skull stripping step included in the Infant FreeSurfer pipeline since the brain averages from the NMD are already skull stripped.

For the head surfaces, we used the “BEM4 ” segmentation and ran a cube marching algorithm (scikit-image marching_cubes_lewiner function) followed by a Laplacian smoothing (trimesh filter_laplacian function) and a mesh decimation (MNE-Python decimate_surface function). Surface topological defects such as holes, inverted vertex normals, or vertices with fewer than three neighbors were corrected using custom Python code relying on external functions (MeshFix.repair from PyMeshFix; repair.fix_normals and Trimesh.remove_degenerate_faces from trimesh) and on code snippets adapted from various MNE-Python functions. Final meshes were checked for water tightness using trimesh. Further, one BEM volume had artifacts appearing as small line segments over the background. We corrected these by zeroing any small separated cluster of non-null voxels using the connected_components function from connected-components-3d.

Surface intersections were verified using a ray tracing algorithm from trimesh and outer meshes were pushed back along their vertex normal direction where intersections were detected. Out of 39 surfaces (i.e., the scalp, outer skull, and inner skull surfaces for the 13 templates), 17 needed 2.86% (± 3.37%) of their vertices to be corrected by 1.27 mm (+/−1.82 mm) on average. Examples of the initial volumes and extracted surfaces using these two parallel pipelines are illustrated in Fig. 1.

Fig. 1.

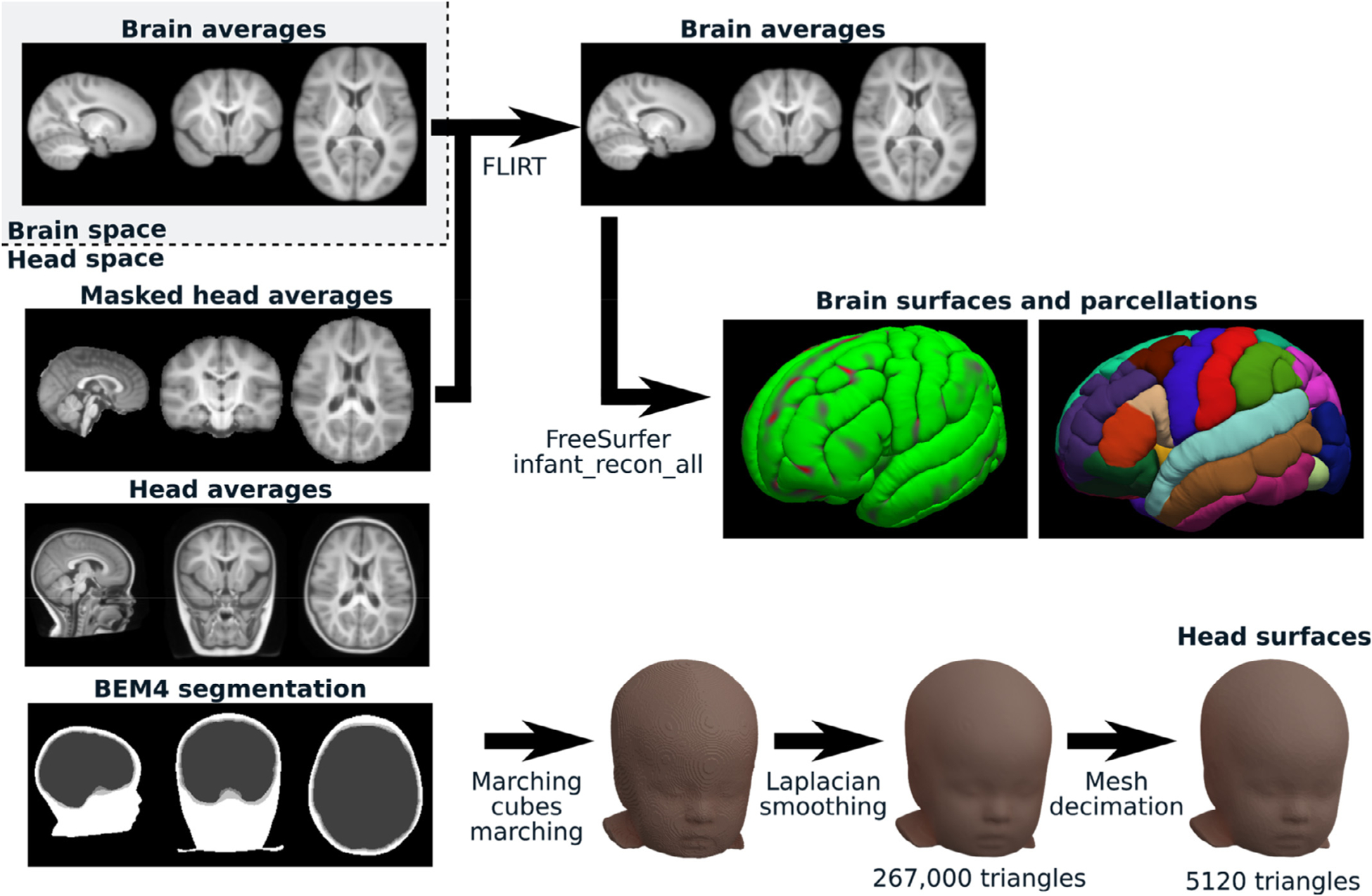
Surface extraction. An example of the types of volumes we used from NMD is shown on the left side. From this volumetric dataset, two parallel processes were run to extract the brain surfaces and cortical parcellations (top right; using FLIRT and Infant FreeSurfer) as well as the head surfaces (bottom right; using custom Python code).

2.5. Sensor co-registration

To map the scalp activity to neuronal sources, the EEG sensors must be placed over the scalp of the head model. Average electrode placement for the 3-, 4.5-, 6-, 7.5-, 9-, 12-, and 24-month time points were previously computed from recorded placements for the HydroCel GSN 128 channel sensor net and the 10–5, 10–10, and 10–20 systems (Richards et al., 2015). These average placements are available in the NMD. Since no empirical data were available, the electrode placement for the 2-week, 1- and 2-month templates were obtained from the 3-month average electrode placement. This was done by registering the 10–10 positions from the 3-month average template to every participant of those age in the NMD, using the coherent point drift method (Myronenko et al., 2006; Myronenko and Song, 2010), and translating the 3-month electrode placement into the participant space. Then the participant MRIs were registered to their age-appropriate average template and their electrode positions were appropriately translated into the average template space and averaged across participants. The averaged electrode positions were further scaled to fit the head in the head MRI average. The same procedure was used to fit the 12-month electrode placement to the 10.5-, 15-, and 18-month time points. Further, the electrode placements were compared to the scalp surface of the head models and the electrodes were automatically moved to the closest point on this surface. These fitted electrode placement are included with the templates presented here to facilitate re-use.

2.6. Validation dataset

For source reconstruction, we used the same set of EEG recordings to validate the different templates in order not to confound the effect the recordings with the effect of the templates. The exact properties of the scalp signals are not of any particular relevance for these tests and, accordingly, simulated signals could have been used. However, to ensure a higher ecological validity, we used real recordings from 7-month-old infants (female = 62; male = 36; unknown = 2) from the London segment of the International Infant EEG Data Integration Platform (EEG-IP; van Noordt et al., 2020). These EEGs were recorded at 500 Hz with HydroCel GSN 128 channel sensor nets during an event-related paradigm with a 200 ms baseline period followed by the presentation of a visual stimulus and a 800 ms response period. Images of faces looking directly at or away from the participant were used as target stimuli and randomized noise images were used as a control condition. For our analyses, we used the version of the EEG-IP that has been preprocessed using the EEG-IP-L pipeline (Desjardins et al., 2021), which includes an automatic artifact rejection step and a thorough manual quality control.

2.7. Comparison of modeling approaches

We used FieldTrip to compare the sources estimated with our new surface templates and the volume templates from the NMD. We distinguished the impact of the source model (surface versus volume distributions) and the head model (FEM versus BEM) by using a 2 × 2 factorial approach. We performed these comparisons for the seven ages for which FEM segmentations were publicly available in NMD at the time of the analysis (3-, 4.5-, 6-, 7.5-, 9-, 12-, 24-month).

The BEM head models were computed from our surface templates using FieldTrip’s dipoli method (Oostendorp and Oosterom, 1989) and the following standard conductivities: gray matter: 0.3300 S/m; skull: 0.0041 S/m; scalp: 0.3300 S/m. The FEM head models were built using the SimBio toolbox and the MND 10-compartment FEM segmentation with the following conductivities (Gabriel, 1996; IT’IS Foundation): white matter: 0.14 S/m; gray matter: 0.33 S/m; CSF: 1.79 S/m; dura mater: 0.368 S/m; skull: 0.01 S/m; skin: 0.43 S/m; muscle: 0.355 S/m; eyes: 1.55 S/m (conductivity for the vitreous humor); nasal cavity: 3e-15 S/m (conductivity for air at 20 °C); non myelinated axons: 0.33 S/m (conductivity for gray matter).

Around 8000 (±4 due to discretization errors) dipoles were placed within the cortical gray matter for each source model. For the surface source models, we used FieldTrip’s meshresample function to down-sample the cortical meshes from our surface templates and placed the sources at the position of the remaining vertices. For the volume source models, the dipoles were placed at the center of voxels randomly sampled so that their volumetric density was constant across the cortical regions. The voxel classification used for this process was taken from the FreeSurfer standard aseg+aparc.mgz file (i.e., subcortical segmentation plus cortical parcellation according to the Desikan-Killiany scheme) available with the surface templates.

The dipole orientation in the leadfield was unconstrained. However, for the source estimation from the surface model, the leadfield dipoles were projected along the normals of their corresponding cortical mesh vertex. This alignment allows factoring into the surface model the biophysical a priori that EEG source dipoles are aligned with the pyramidal apical projections, orthogonal to the cortical surface. Sources were estimated using minimum norm estimation (MNE) with the regularization parameter λ² = 1.

Since the dipoles are not placed at the same positions in the different source models, we need to average sources within brain regions to make them comparable across models. For statistical analyses, we used a k-d tree (Bentley, 1975) and a nearest neighbor rule to attribute source dipoles to brain regions by comparing dipole positions with aseg+aparc.mgz voxel positions.

2.8. Source estimation for the functional analysis

For this analysis, EEG event-related source potentials (ERSP) were estimated using MNE-Python and compared between our 13 infant templates and FreeSurfer’s “fsaverage” adult template. This latter template was built using spherical surface averaging (Fischl et al., 1999) of the Buckner40 cohort which comprises 40 non-demented subjects (21 women) ranging in age from 18 to 30 and 65 to 93 years of age (FreeSurfer team, 2020a). The same parameters were used for source estimation across templates. We used the dynamical statistical parameter mapping (dSPM; Dale et al., 2000) minimum-norm inverse operator with regularization parameter λ² = 1. The other parameters were left to their default value, as set by MNE-Python, including the conductivities (gray matter: 0.3 S/m; skull: 0.006 S/m; scalp: 0.3 S/m). The covariance matrix was estimated using method = “auto” in the mne.compute_covariance function, which uses four different estimators (the Ledoit-Wolf estimator (Ledoit and Wolf, 2004) with cross-validation for optimizing alpha, diagonal regularization, sample covariance, and factor analysis with low-rank (Barber, 2012)) and chooses the optimal solution based on log-likelihood estimation and cross-validation (Engemann and Gramfort, 2015).

3. Results

3.1. Templates and source reconstruction

We built surface-based structural templates at 13 time points between 2 weeks and 2 years of age (Fig. 2). These templates have been verified to be compatible for source reconstruction with Brainstorm, FieldTrip, and MNE-Python.

Fig. 2.

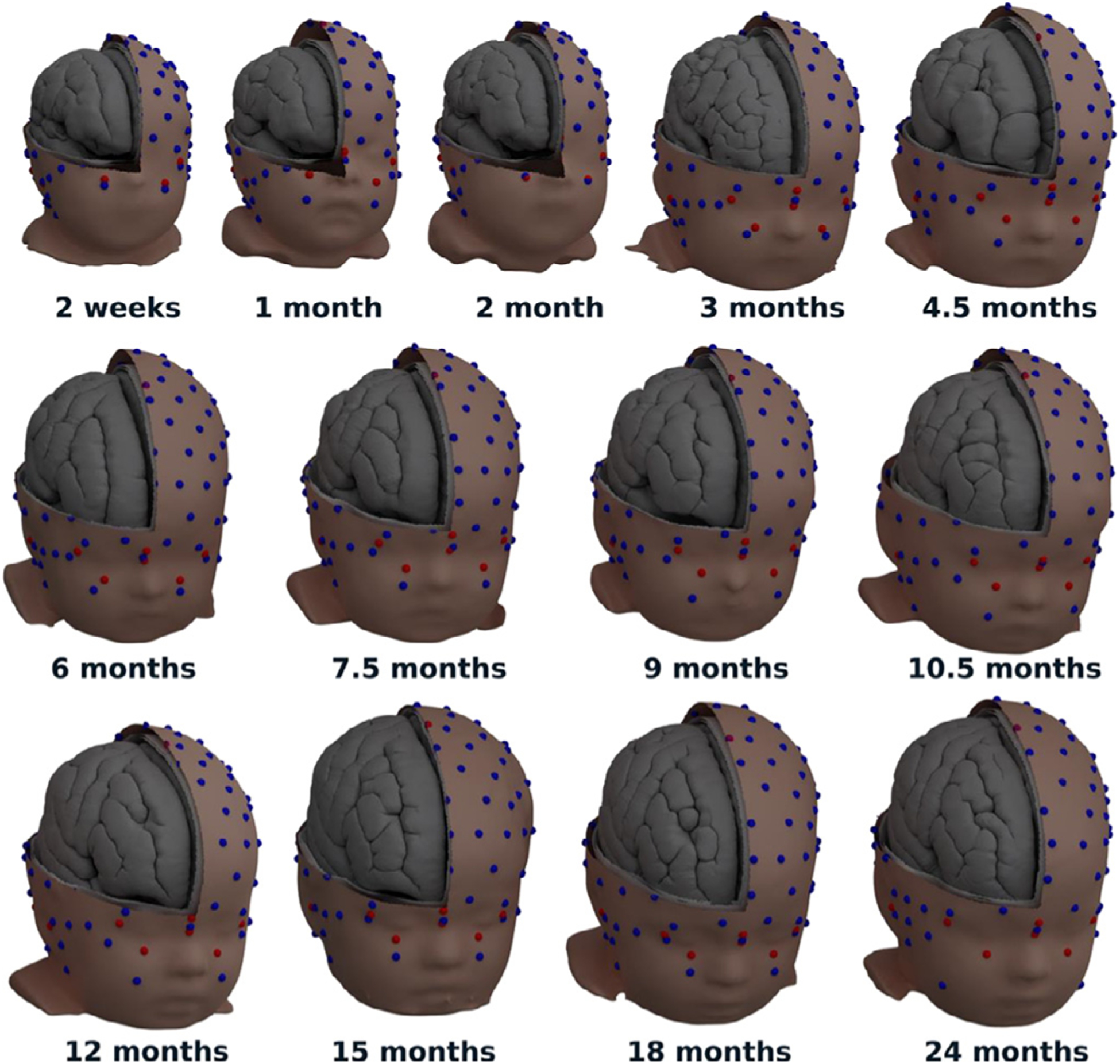
Thirteen templates from 2 weeks to 2 years of age including head surfaces for the scalp and the outer and inner faces of the skull, as well as cortical surfaces separating the meninges, the gray matter, and the white matter. Showing non-decimated meshes rendered with Blender. Spheres with a 5 mm diameter show the placement of electrodes for the HydroCel GSN 128 channel sensor net (blue) and standard fiducial points (red).

3.2. Comparison with volume source models and FEM head models

The event-related potentials (ERP) for the “noise” (control) and the “face” conditions for an occipital channel (E75/Oz) across the recordings of the validation dataset are shown in Fig. 3.a. These are consistent with the ERP previously reported for this database (Desjardins et al., 2021). The noise condition in this experiment produced consistently much larger ERP, potentially because these events were presented less frequently than the face stimuli, causing a surprise effect similar to what is found in an oddball paradigm. Given the higher amplitude of its response, the analysis in this section is performed for the noise condition only.

Fig. 3.

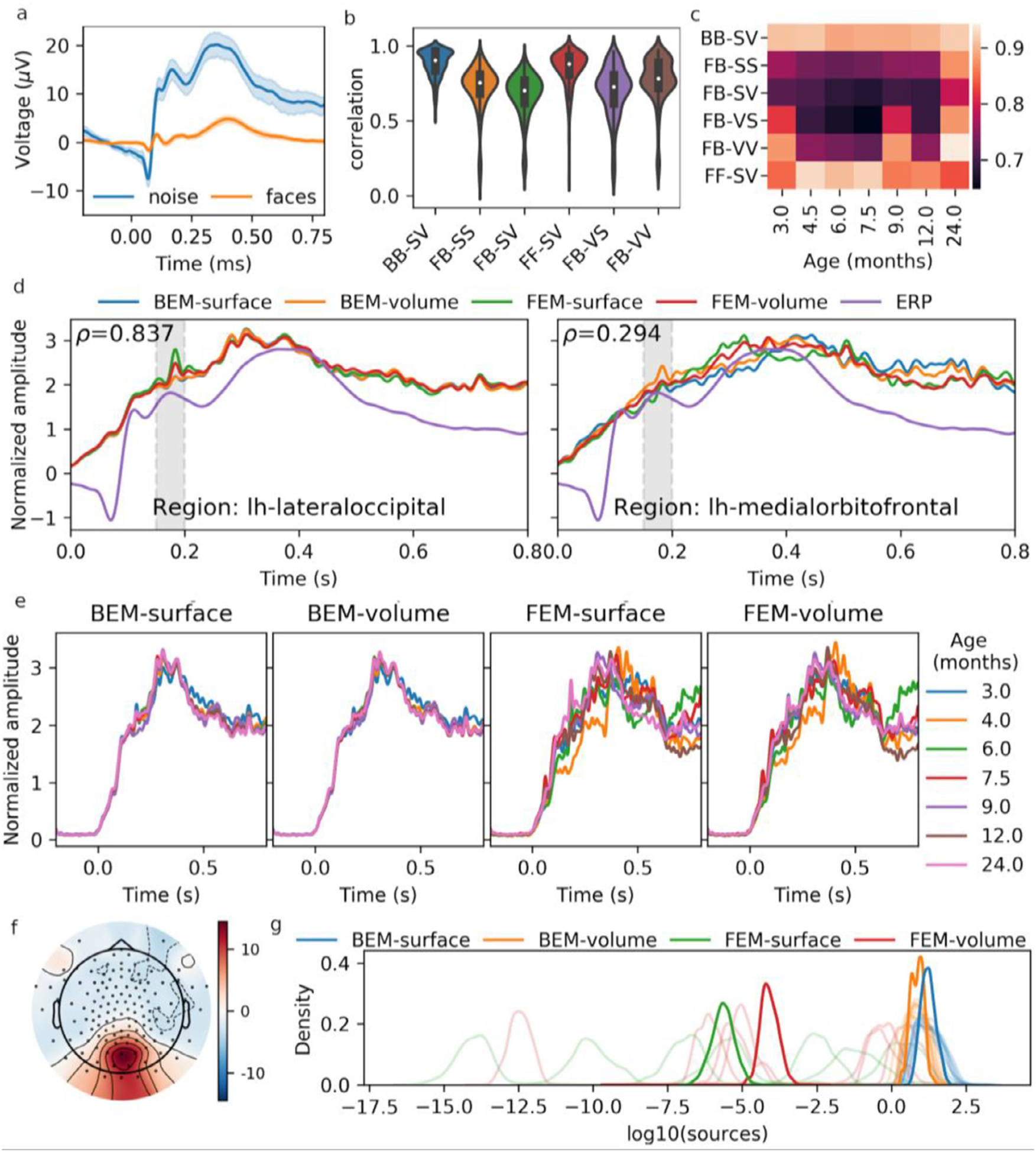
a) ERP for the “noise” and the “face” conditions, averaged across epochs and subjects, for the E75/Oz channel. b) Distribution of the correlation of brain region ERSP between pairs of models. Model comparisons are labeled as H₁ H₂ -S₁ S₂, where H₁ and H₂ represent the two head models and S₁ and S₂ represent the two source models, with the models being identified with the following shorthand notations: F: FEM, B: BEM, S: surface, V: volume. c) Median (across brain regions) correlation between pairs of models, for each template separately. d) ERSP for the regions which show the highest and the lowest correlation for the FB-SV model comparison. The ERP (channel E75/Oz) is also overlaid on this plot. The average of the activity within the grayed window (150–200 ms) is used for the subsequent panels and for source distributions in Fig. 4. e) Similar to the right part of panel d, this panel shows ERSP for the regions with the highest correlation for the FB-SV model comparison, but illustrate the ERSP separately for the different templates. g) Topomap of the scalp ERP. h) Distribution of time-averaged ERSP for the four models. Light-colored lines show the distribution for the different templates, whereas the darker colors show the distribution after averaging across templates.

We averaged the ERSP¹ within brain regions and compared them across combinations of head and source models using Pearson’s coefficient of correlation (Fig. 3.b). The median values of these distributions are shown separately for each different template in Fig. 3.c. ERSP for the regions with the highest (ρ=0.837; left hemisphere lateraloccipital region) and the lowest (ρ=0.294; left hemisphere medialorbitofrontal region) correlations between the FEM-surface and the BEM-volume models are shown in Fig. 3.d. Similarly, Fig. 3.e shows the ERSP for the left hemisphere lateraloccipital region, but overlays the ERSP estimated for all the seven different templates in order to visualize how much these sources vary across templates. We averaged the activity within a window covering the 150–200 ms peak of activity (shown as a grayed region in Fig. 3.d) and plotted the topomap for the ERP (Fig. 3.f) and the source distribution over the cortex for the ERSP (Fig. 4). The scale of the FEM source estimates we obtained from the FieldTrip-SimBio software were found to depend on the template (Fig. 3.g). To make source profiles more comparable, we normalized the ERSP and ERP by dividing them by their standard deviation in Fig. 3.a,d,e. Also, to make it easier to compare source distributions across models and templates, the source amplitudes shown in Fig. 4 have been mapped to their corresponding percentile, and values from the 75th percentile upward were linearly mapped to a color gradient ranging from transparent (< 75th percentile) to dark red (100th percentile). With this mapping, every reconstruction shown in Fig. 4 has the same proportion of red coloration, only the spatial distribution varies across models and templates.

Fig. 4.

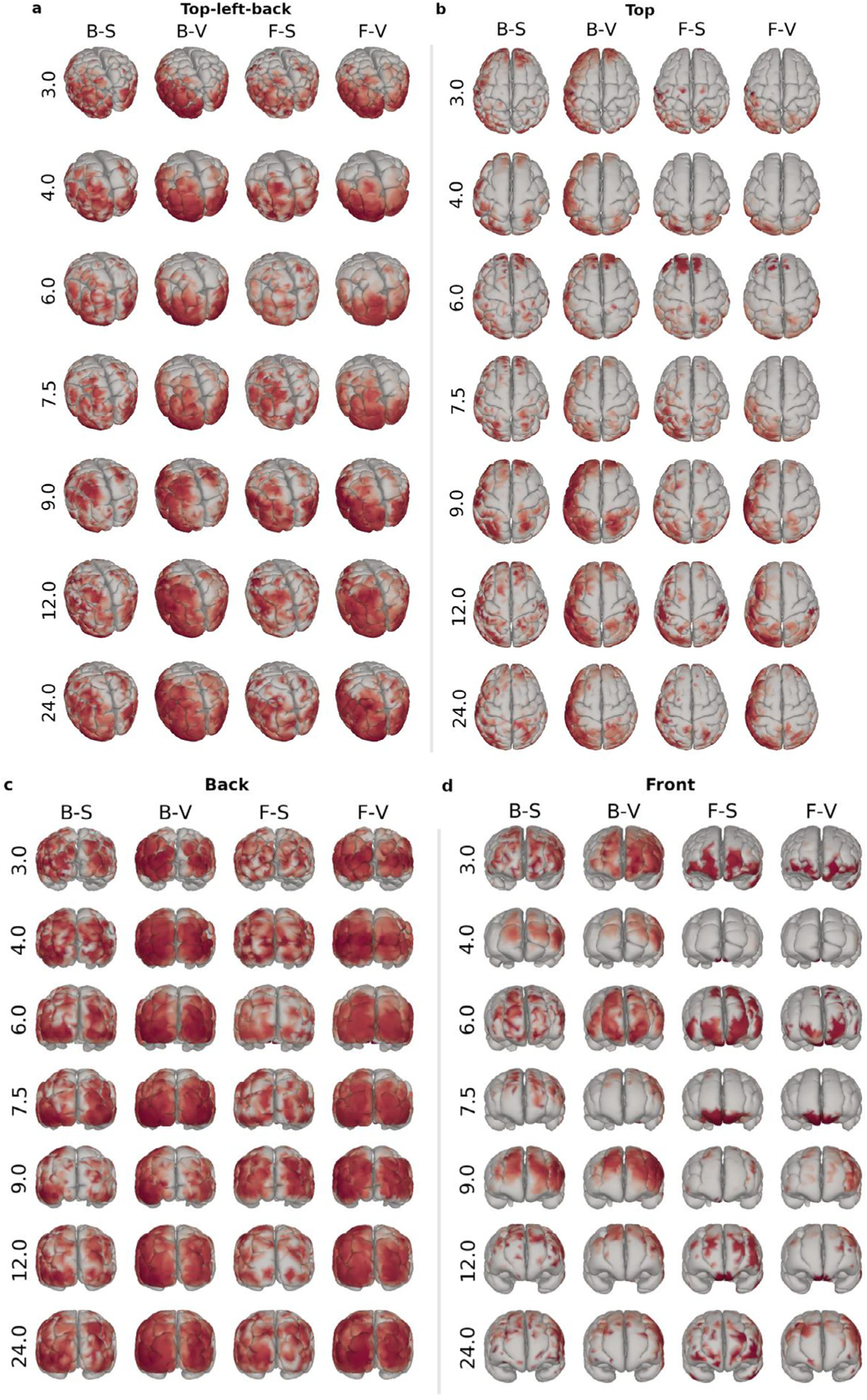
Spatial source distributions for the different models (columns) and templates (rows) shown from different views (panels a-d). The models are coded as H-S, where H represents the head model and S represents the source model, with models identified with the following shorthand notations: F: FEM, B: BEM, S: surface, and V: volume. The values at the right of each row indicate the template age, in months. Identical data are shown in different views from top-left-back (a), top (b), back (c), and front (d). Sources with larger amplitude than the 75th percentile are color-coded linearly according to the percentile, from transparent (75th percentile) to dark red (100th percentile).

In order to compare the impact of the age templates, the head models, and the source models, we linearly regressed the values of the median ERSP correlations between pairs of head-source models (as computed for Fig. 3.c) against a linear model including as factors the template, the head model pair (FF: FEM-FEM; BB: BEM-BEM; FB: FEM-BEM), and the source model pair (SS: surface-surface, VV: volume-volume; SV: surface-volume). The regression results are summarized in Table 2. As can be seen from p-values and regression coefficients, with our specific modeling choice, the head model is the factor that has the largest effect, followed by the source model. The difference between age templates is either marginally (0.5 < p -value < 0.1) or not statistically significant in these comparisons. Since Fig. 3.e suggest that the effect of the age template may be different for BEM and FEM head models, we computed one-way ANOVAs of the median correlation (across brain regions) separately for the BEM and the FEM, treating the template as a factor. As could be expected from Fig. 3.e, there was a significant effect of template for the FEM ANOVA (F_{6, 480} = 7.35, p = 1.5e-7) but not for the BEM ANOVA (F_{6, 480} = 1.04, p = 0.40).

Table 2.

Linear regression using the model “correlation ~ template + source_model + head_model”. Only model comparisons where only one factor (head model or source model) has been modified (i.e., FF-SV, BB-SV, FB-SS, and FB-VV) were used. Median correlations are used (i.e., no repeated measures).

	coefficient	standard error	t-value	P-value
Intercept	0.7142	0.022	32.499	<0.001
Template: 3 vs 24 month	−0.0419	0.039	−1.08	0.295
Template: 4.5 vs 24 month	−0.06	0.039	−1.545	0.140
Template: 6 vs 24 month	−0.078	0.039	−2.008	0.060
Template: 7.5 vs 24 month	−0.0751	0.039	−1.932	0.069
Template: 9 vs 24 month	−0.0467	0.039	−1.202	0.245
Template: 12 vs 24 month	−0.0741	0.039	−1.907	0.073
Source model: SS vs SV	0.1021	0.019	5.429	<0.001
Source model: VV vs SV	0.1485	0.019	7.899	<0.001
Head model: BB vs FB	0.2426	0.019	12.903	<0.001
Head model: FF vs FB	0.221	0.019	11.75	<0.001

3.3. Structural validation

The structural validity of the proposed templates is directly dependent on the validity of MND’s MRI averages used as input data and the infant freesurfer pipeline used to extract the surfaces, which have both been validated in previous studies (de Macedo Rodrigues et al., 2015; Fillmore et al., 2015b, 2015a; Sanchez et al., 2012a, 2012b; Xie et al., 2015; Zöllei et al., 2020). Nevertheless, to validate the final result, we calculated the relative volume of brain regions (v_r) as the number of voxels per subcortical and cortical brain region, as defined in the FreeSurfer aseg + aparc.mgz files, divided by the total number of voxels in all segmented brain regions. These relative volumes appear to be very consistent across the templates, as demonstrated by very high correlations across models from the different ages (Fig. 5.a,b). We also computed how much the relative size of each region is different from the average relative size across the templates (i.e., (ν_r − ν_r)/ν_r) (Fig. 5.c,d).

Fig. 5.

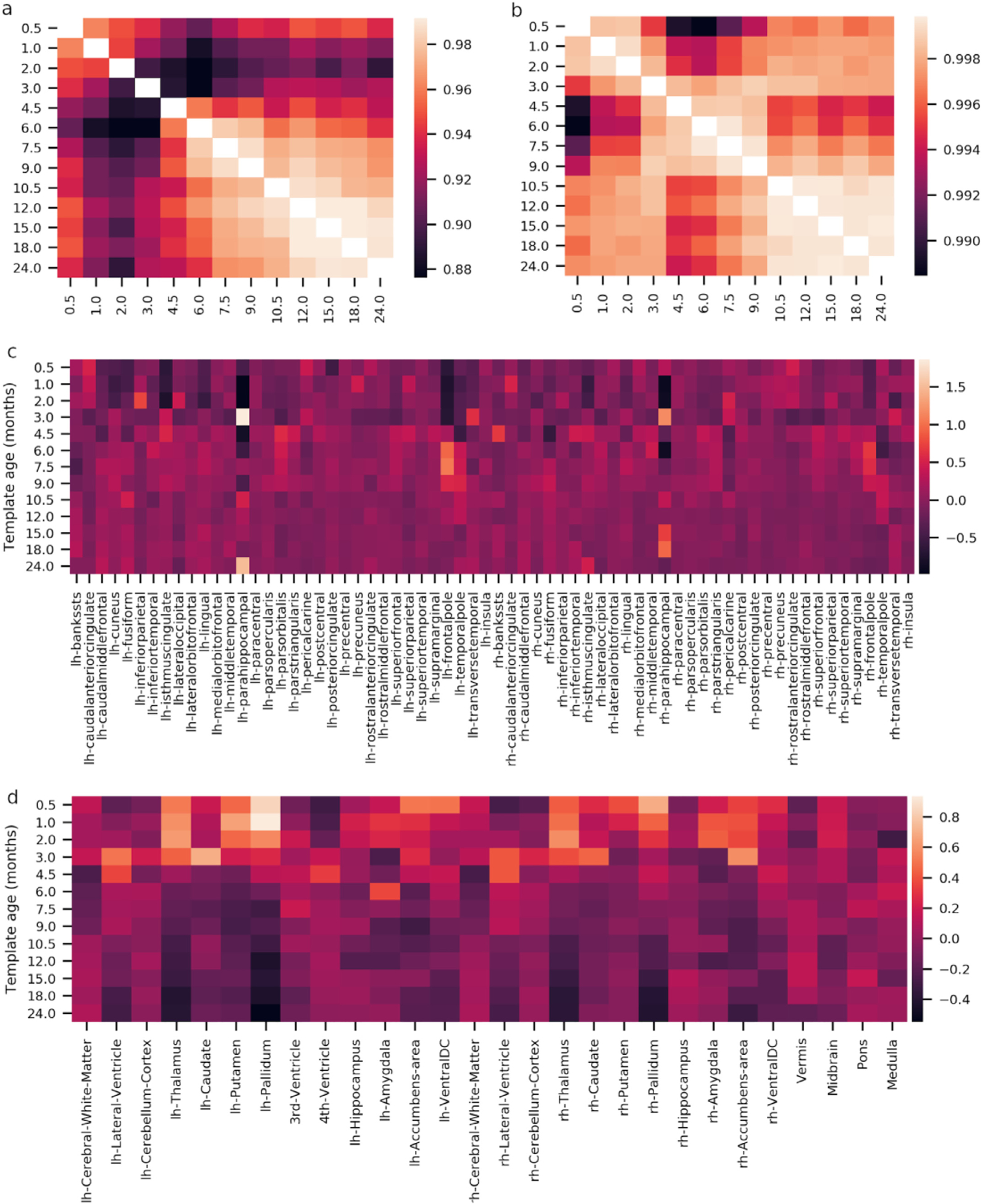
Structural validation of the surface templates. a,b) Correlation of the relative volume ν_r of cortical (a) and subcortical (b) regions between templates. Note that the lower end of the correlation colorbar is greater than 0.998. c,d) Relative differences between a template ν_r and the across-template averages (ν_r) for cortical (c) and subcortical (d) regions.

We do not observe large inconsistencies across the templates, except for the parahippocampal and the frontalpole regions which average volume is less consistent than the other regions. We should note that some variations are expected due to the development of the brain. Although we do not have normative data for a systematic comparison, the pattern of variations can distinguish potential modeling issues from normal developmental effects. For example, the smooth and constant patterns of decreasing relative volume of the thalamus across the ages and its similarity across hemispheres (Fig. 5.d) suggest that this effect is probably associated with normal development, which is compatible with what is reported in the literature (Sussman et al., 2016). This contrasts for example with the comparatively erratic pattern of variation for the parahippocampal region (Fig. 5.c), which is more likely due to difficulties in accurately parcellating this region during the first years of life. We can also see that the correlations of the relative volume of brain regions across the templates are larger for subcortical segmentations than for cortical parcellations. This observation may be partly due to the fact that the Desikan-Killiany parcellation scheme is based on the topology of sulci and gyri which are not fully formed in infants.

3.4. Functional validation

We further validated the templates by testing the hypothesis that EEG sources should be more correlated when estimated from templates of similar age than from templates with greater age differences. Thus, we computed correlations between the ERSP for pairs of templates and averaged these correlation coefficients across stimulus conditions, subjects, and Desikan-Killiany brain regions. Heat maps in Fig. 6.a,b show high average correlations between infant templates within the 0–2 year age range. However, there is a general tendency for correlations close to the diagonal to be larger than those far from the diagonal, confirming that differences in estimated sources increase with template age differences. Further, the correlation with the sources computed using fsaverage is substantially lower than any correlation infant templates, confirming inaccurate source estimation when using an adult template for analyzing infant EEG.

Fig. 6.

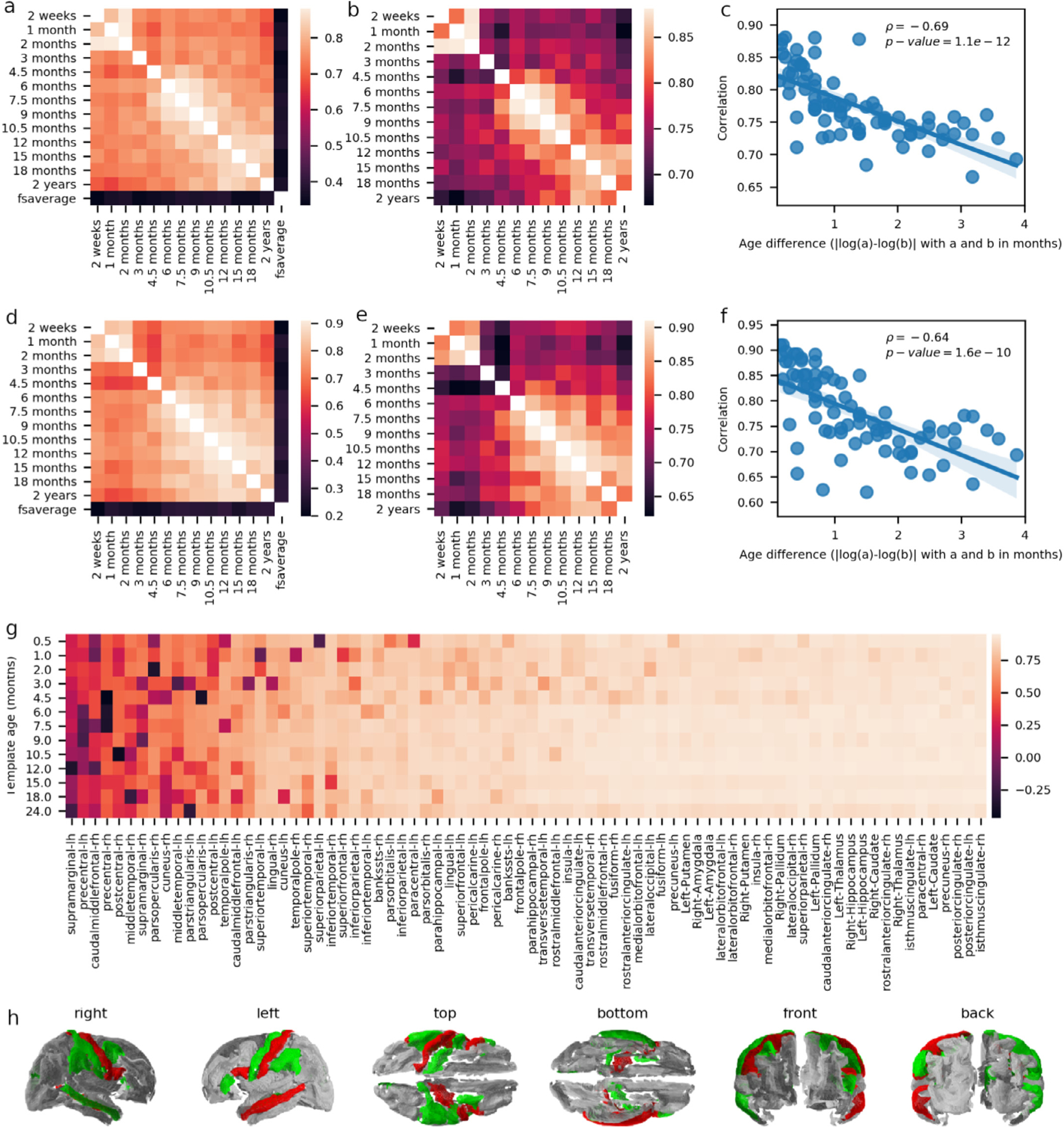
a) Average correlations between the ERSP time-series computed from different templates. b) As in a, but excluding the fsaverage template and adjusting the scale to emphasize the pattern of variation between the infant templates. c) Average correlations (as computed for panels a and b) as a function of the log-transformed age difference between templates. d-f) Similar as for panels a-c, but reporting Pearson correlation coefficients across brain regions instead of time. g) Average ERSP time-series correlation computed separately for every region and averaged for each template separately. h) Cortical representation showing average time-series correlation (mean values per column of panel g) lower than 0.6 colored in red or green, depending on whether they show (red) or not (green) the typical decrease in correlations with increasing age differences.

The anti-correlation between the similarity of estimated sources and differences in template age (i.e., the smaller the difference in template age, the larger the similarity between estimated sources) is clearly demonstrated by linearly regressing the correlations plotted in Fig. 6.a,b by the absolute differences between the logarithm of the template ages (ρ= −0.67; R²=0.479, p-value =1.1e-12, N = 78; Fig. 6.c). Similar observations can be made by correlating ERSP across brain regions rather than across time (ρ= −0.64; R²= 0.408, p-value = 1.6e-10, N = 78; Fig. 6, d–f). We further computed the average correlations between any given templates and all other templates, for each region separately, and observed that the correlation of the ERSP between templates is very high for most regions but is lower and more variable in some cases (Fig. 6.g), particularly around the motor and somatosensory areas (Fig. 6.h).

4. Discussion

A reliable estimation of EEG cortical sources requires the use of individualized or, when not available, population-averaged structural model of the head. Standard automated approaches developed for building such head models from adult MRI scans do not provide satisfactory results in the pediatric population due to a lower contrast between white and gray matter (Phan et al., 2018; Schumann et al., 2010). Further, most automated pipelines rely on co-registering individual MRI against a population average, which may cause significant errors when using an adult average for co-registering younger populations. With some manual intervention to guide or correct white matter and gray matter classification, FreeSurfer can provide satisfactory results in children who are at least five years old (Schumann et al., 2010) but not younger (FreeSurfer team, 2020b). For that reason, an infant version of the FreeSurfer pipeline has recently been developed that covers the 0–2 year age range (Zöllei et al., 2020). To our knowledge, no similar approach currently exists that covers the 2–5 year range, which is a topic that should definitely be addressed by future studies. To further support the use of source reconstruction in EEG and MEG neurodevelopmental studies in infants, we used this pipeline to develop 13 new surface templates for infants in this age range. These templates can be used with any software relying on surfaces of the brain and the head for their forward models.

For approaches relying on volume source models (e.g., CDR) instead of surface source models, BEM and FEM segmentations are available in the NMD. We demonstrated how sources estimated with models built using these different volumes and surfaces can be compared using a factorial design distinguishing the impact of the head model (FEM or BEM) and the source model (surface or volume). In doing so, we observed that the FEM models seem more sensitive (or the BEM models are more stable) across templates, but the data currently available do not allow establishing with certainty if the FEM approach is more sensitive to signal or noise (i.e., whether increased between-template differences for FEM in Fig. 3.e indicate a finer capacity to capture age-specific differences, or if it reflects some unreliability or instability of this modeling approach).

BEM head models are designed as successive layers of tissues with different conductivities, and algorithms using these models generally rely on the fact that the inner compartments fit within the outer compartments. Some of these algorithms, for example, cannot work correctly with meshes that are not watertight. Therefore, as opposed to FEM, this modeling approach cannot accommodate local layer discontinuities such as ventricular CSF or fontanels. This can be considered a limitation of the BEM approach for infant studies since these local features have been shown to have a significant effect on source reconstruction in FEM studies (Azizollahi et al., 2016; Lew et al., 2013; Pursiainen et al., 2016). When available, infant-compatible MEG systems can also be used to complement EEG in order to obtain source estimates that are more robust to the effects of fontanels (Lew et al., 2013). As MEG and EEG systems are recording related but complementary signals, EEG should not be simply supplanted by MEG. Source accuracy should rather be improved by combining both modality whenever possible (Sharon et al., 2007).

The use of head models for different ages within the 0–2 year range resulted in relatively mild differences in estimated EEG sources as opposed to the use of an adult template, which resulted in much more dissimilar sources. These results suggest that our templates are fairly consistent across age. They might nevertheless be improvable in some regions that showed lower and more variable correlations between templates (Fig. 6.g). In the absence of quantitative resources reporting maturity indices per age and brain regions, it is difficult to establish whether these lower correlations are due to larger maturational changes in these regions during the developmental period covered by our analyses. We nevertheless note that most of these regions are around the motor and somatosensory areas, which are known to develop at a fast rate in the first few months following birth (Ganzetti et al., 2014), whereas the correlations are reliably high in frontal associative regions (Fig. 6.h), which are known to develop later in life (Sowell et al., 1999).

We validated the structure of the templates by comparing the relative volume of their cortical and subcortical regions. We further validated these templates functionally by assessing how the age impacts the source estimation. We also verified that this modeling approach was producing sensible results by comparing the estimated sources from these surface models against sources obtained using alternative FEM head models and volume source models. A more complete validation could be performed in the future by comparing these measures against a “gold standard”. For example, with respect to structural validation, the differences in the relative size of brain regions between the templates could be compared against normative curves extracted from a sample of individual infant MRIs. Further functional validation could rely on source reconstruction using individual subject head models or using experimental paradigms for which the activated brain regions are well known (e.g., medial nerve stimulation).

In the future, increased surface template accuracy may be achievable by using a surface-based registration directly rather than extracting surfaces from a volume-based average (Ghosh et al., 2010). It is unclear, however, if such improvements would translate into a significant improvement regarding EEG source estimation since the gain obtained by increasing the template accuracy may be insignificant compared to the difference between the population average template and the brain of each individual participant. It would also be interesting to investigate the extent to which the use of different templates would affect source imaging in studies using MEG instead of EEG, given that these two modalities measure fundamentally related but complementary components of the electromagnetic fields produced by cerebral activity (Hämäläinen et al., 1993; Sharon et al., 2007).

Up to recently, no open-access population average surface models were available to estimate cortical sources in infants. By releasing these 13 new templates, we are making source reconstruction based on cortical surfaces accessible for situations where individual MRI are not available and population averages are required, addressing a clear need in the EEG and MEG community. Although these templates can be used by any software package performing source reconstruction using surface templates, to allow researchers to easily benefit from them, we are currently working on integrating these templates directly within MNE-Python and Brainstorm. This resource will undoubtedly come particularly handy for cross-sectional and longitudinal studies of typical and atypical neurodevelopment.

Abbreviations:

BEM

boundary element method

CDR

current density reconstruction

CSF

cerebrospinal fluid

EEG

electroencephalography

EEG-IP

International Infant EEG Data Integration Platform

ERP

Event-related potential

ERSP

Event-related source potential

FEM

finite element method

MEG

magnetoencephalography

MPRAGE

magnetization-prepared rapid gradient-echo

NMD

Neurodevelopmental MRI Database

MRI

magnetic resonance imaging