Formidable females redux: male social integration into female networks and the value of dynamic multilayer networks

Abstract

The development of multilayer network techniques is a boon for researchers who wish to understand how different interaction layers might influence each other, and how these in turn might influence group dynamics. Here, we investigate how integration between male and female grooming and aggression interaction networks influences male power trajectories in vervet monkeys Chlorocebus pygerythrus. Our previous analyses of this phenomenon used a monolayer approach, and our aim here is to extend these analyses using a dynamic multilayer approach. To do so, we constructed a temporal series of male and female interaction layers. We then used a multivariate multilevel autoregression model to compare cross-lagged associations between a male’s centrality in the female grooming layer and changes in male Elo ratings. Our results confirmed our original findings: changes in male centrality within the female grooming network were weakly but positively tied to changes in their Elo ratings. However, the multilayer network approach offered additional insights into this social process, identifying how changes in a male’s centrality cascade through the other network layers. This dynamic view indicates that the changes in Elo ratings are likely to be short-lived, but that male centrality within the female network had a much stronger impact throughout the multilayer network as a whole, especially on reducing intermale aggression (i.e., aggression directed by males toward other males). We suggest that multilayer social network approaches can take advantage of increased amounts of social data that are more commonly collected these days, using a variety of methods. Such data are inherently multilevel and multilayered, and thus offer the ability to quantify more precisely the dynamics of animal social behaviors.

Social structure in animal groups is often generated through multiple kinds of behavioral interactions and is therefore intrinsically multidimensional. In other words, interactions of different kinds can influence and feedback on each other, in ways that depend on aspects of individual identities, such as age, sex, and dominance rank. Until recently, it has been difficult to capture this complexity in our analyses of animal social structure. Instead, the tendency has been to create composite indices of behavior to produce a single monolayer network—in effect, collapsing or flattening the different behavioral interaction networks, with an attendant loss of information about the social structuring within a group. Pulling the different layers apart, and understanding how network structure within layers influences structure across layers is a central goal of multilayer network analysis (MLNA) (Finn et al. 2019).

Among highly social species, such as the anthropoid primates, the promise of MLNA is that the more nuanced analysis of social structure, made possible by these new techniques, will give rise to a deeper understanding of within-group social dynamics. This, in turn, will provide a means of identifying how particular network structures are formed, maintained, and exert their known effects on fitness. For example, a multilayer network allows us to model the dependence between different interaction layers, as well as potentially look at these layers across time (Pinter-Wollman et al. 2014). Using this approach, it becomes possible to generate a meta-network that describes the dependencies between the layers of interest within the multilayer network. By these means, we can investigate how changes in one behavioral layer influence subsequent patterns of behavior in another, facilitating the identification of the mechanisms by which social life influences reproductive and life history parameters (Ostner and Schülke 2018). The assumption here, then, is that a multilayer network approach will provide much greater insight into social processes than monolayer networks and that this will compensate for the greater investment of time and effort entailed by the construction and interpretation of multilayer networks.

Here, we use a dynamic multilayer network approach to help test this assumption. In previous work on our long-term study population of vervet monkeys Chlorocebus pygerythrus, we used a monolayer network approach to investigate how male–female social dynamics influenced a male’s social standing in the group. Female vervets are codominant with males and are frequently top-ranking (Young et al. 2017). This being so, we asked whether associating with particular females allowed males to dominate other males, thereby improving their rank and, potentially, their mating opportunities. We found that males with high degree in the female spatial proximity network and those with high eigenvector centrality in the female grooming network were more likely to show an upward rank trajectory across time (Young et al. 2017). Here, we revisit this outcome by considering whether the effect persists across a later period of the study and whether a dynamic multilayer approach provides additional insights that the previous monolayer approach cannot match. That is, we use a temporal multilayer network to ask whether male integration into the female grooming network leads to a rise in male Elo rating (i.e., we now address the direction of the effect), and extend our previous analyses by investigating whether changes in one network exert an influence on other layers in the network across time.

To do so, we 1) define our measures of interest, 2) construct a multilayer network for our vervet study groups, 3) slide the multilayer network through time using a moving window approach (Bonnell and Vilette 2020) to generate a time series of network and individual state measures, and 4) estimate the dependencies between these measures. The estimated dependencies then inform us how changes in one individual’s measure in a particular layer influence that individual’s measures in other layers.

On the one hand, our approach could be seen as a more complex variant of traditional monolayer approaches. That is, we use conventional monolayer centrality measures for each interaction network in our analysis, and investigate the dependencies between them (i.e., how changes in one layer influences another), whereas most multilayer network analyses to date have used network metrics over the entire network. On the other hand, we would argue that, if an analysis involves the construction of a multilayer network then, by definition, it is a multilayer network analysis, and the specific metrics used are not definitional in this same sense (after all, one can calculate multilayer metrics only if one has constructed a multilayer network, which suggests it is the latter that is absolutely necessary and not the former). In short, we have used the metrics and analyses we feel most appropriate to address our question, which, as already noted, is to estimate the dependencies between network measures taken from different layers of the multilevel network. This allows us to investigate whether and how changes in one layer precede changes in another (i.e., multilayer dependence), and potentially identify feedback loops within the multilayer network structure.

Materials and Methods

Species and study site

Vervets are a moderately sexually dimorphic, female philopatric, Old World monkey species. Males leave their natal groups at sexual maturity, after which they may sequentially migrate into one or more other groups during the course of their lives (Young et al. 2019). Data for these analyses were collected between January 2015 and November 2018 from 3 troops (RBM, RST, and PT) of habituated and individually recognizable vervet monkeys occupying riverine woodland at the Samara Game Reserve in the semiarid Karoo Biome of South Africa (RBM males: 4–10, RBM females: 2–11; RST males: 5–17, RST females: 7–16; PT males: 2–10, PT females: 8–10; Pasternak et al. 2013). Data were collected 5 days per week on each of the troops. In our previous work, we considered the period between March 2012 and September 2015. Scan samples of individual animals’ identity and activity were collected every 30 min, including grooming interactions. In each case, the identity of the individuals involved and the direction of grooming (i.e., which animal was groomed and which performed the grooming) were noted. Each scanning period lasted a maximum of 10 min to ensure that as many animals as possible were sampled within each group. For agonistic interactions, data were collected ad libitum, with the identity of the individuals involved recorded, along with the direction of the aggression, and the outcome of the encounter (i.e., methods follow Young et al. 2017). Analyses are based on 14,779 grooming interactions and 18,982 agonistic interactions among adult troop members.

Network construction

We constructed a dynamic multilayer network using the frequency of grooming and agonistic interactions. We further subdivided these data into construct separate network layers for males and females. From this multilayered construction, we then adopted a moving window approach in order to generate a time series of network layers (Figure 1; Bonnell and Vilette 2020). This method consists of 1) subsampling the data within a time window (e.g., 1 January 2015–1 April 2015), 2) generating networks from this subset of data, 3) extracting network measures from these networks, and finally, 4) returning to 1 and shifting the time window through time (e.g., 1 February 2015—1 May 2015). In this way, our network consisted of layers for each sex, each behavior, and each time period.

Network measurement extraction

From the time series of networks, we extracted network measures at the individual level to describe the integration of males in the female network (Table 1). To measure the extent of a male’s integration into the female network, we identified the number of females that a male groomed (i.e., grooming out-degree), and the number of females that groomed the male (i.e., grooming in-degree). To assess whether the particular females that a male groomed had any influence on his rank, we extracted a male’s centrality in the female grooming network. To do so, we considered each male in turn and calculated his eigenvector centrality within the female grooming layer, that is, a network was created using all female–female edges along with the selected male’s edges to/from females in turn. This network was then used to estimate eigenvector centrality for the male node. This was repeated for each male (Figure 1). Hence, if the male groomed, or was groomed by, more central females then his position within the female grooming layer would also be more central.

Table 1.

Social network measures used to describe male integration within social groups

Social network measure	Network layer
A male’s out-degree to females	Male → female grooming layer
A male’s in-degree from females	Male ← female grooming layer
Centrality of a male within male grooming network	Male–male grooming layer
Centrality of a male within female grooming network	Male–female grooming layer
A male’s aggression from other males	Male aggression layer
Change in a male’s Elo rating	Male aggression layer

Figure 1.

Illustrative diagram of the construction of the dynamic multilayer network. The network is composed of 2 behavioral layers, aggression, and grooming, broken into sex-specific layers, male (blue) and female (orange). This construction is then shifted through time (using a 30-day window) to generate a time series of networks.

We also entered the agonistic data into the “EloRating” package in R (Albers and Vries 2001; Neumann et al. 2011; Vilette et al. 2019) in order to estimate changes in Elo ratings for each male. We used the Elo rating method as it allows for the dynamic updating of individual rank status within the group, and included agonistic interactions between all individuals (males, females, and juveniles). We used a 4-month burn-in period (1 September 2014–1 January 2015) and calculated continually updated Elo ratings for each male over the entire study period. These individual Elo ratings were then combined with network measures extracted using the moving window approach. To determine whether increased male integration resulted in increased aggression/isolation from other males, we also estimated the number of males that showed aggression toward a male (i.e., aggression in-degree), and the eigenvector centrality of the male within the male grooming network. We followed our earlier work in using eigenvector centrality to measure the network position of males in the male and female grooming layers (Young et al. 2017).

To generate time-aggregated layers of the multilayer network, we adopted a moving window approach using the “netTS” package in R (R Core Team 2018; Bonnell and Vilette 2020). We calculated sample entropy on time series generated from multiple window sizes. That is, we performed a multiscale entropy analysis, within the time scales relevant to the biological question, to determine whether there were time scales that gave rise to more predictable time series. Our analyses suggested no strong evidence for any natural scale (Supplementary Figures S1 and S2). We, therefore, chose a window size of 120 days (4 months) as bootstrap tests suggested that, at this temporal scale, grooming in-/out-degree, and aggression in-degree were robust, although eigenvector centrality measures showed a relatively larger amount of noise, particularly male eigenvector within the male grooming layer (Supplementary Figure S3). Window sizes smaller than 4 months resulted in greater measurement noise in all centrality measures, whereas window sizes larger than 4 months start to aggregate the data beyond time scales thought to be important for social integration. In particular, within our study population, the mating season (April–June) and birth seasons (October–December) are thought to roughly encompass 3-month time periods (Young et al. 2019). Given the results of the bootstrap test, we opted for 4 months as a compromise between desired temporal aggregation and noise in our estimated network measures. We additionally ran models with 5- and 6-month windows to estimate the sensitivity of our main results to the choice of window size (Supplementary Figure S4). To create a time series of these 4-month networks over the study period, we shifted the window forward by 30 days each time.

Statistical analysis

We used a multilevel multivariate autoregressive model (MMAR) to estimate the dependence between changes in an individual’s social network measures (Table 1). We then used this model to test whether male Elo ratings are influenced by male centrality within the female grooming layer. This model approach allows for the estimation of both lagged and cross-lagged effects. Lagged effects can be thought of as the momentum of a particular measure, for example, how autocorrelated an individual social network measure is over time, whereas cross-lagged associations estimate how changes in an individual’s social network measure at 1 time period influences another measure in the next time period (Schuurman et al. 2016). We estimated the mean effect across individuals and allowed for individual differences in these effects (i.e., random effects), using a multilevel model. As our data consists of multiple males measured over time, and a number of males within our study period attempt to integrate into multiple groups (i.e., RBM, RST, or PT), we specified each male integration attempt, that is, male ID by troop, as a random effect. This multilevel approach takes into account data that are grouped within individuals, pools this information to help estimate lagged and cross-lagged parameters in the model, and quantifies the interdependence between individual differences in these parameters. We fitted this model using a Bayesian framework in R (R Core Team 2018) with rStan (Stan Development Team 2018). Main effects were given weakly informative priors centered on zero (i.e., normal [0,1]), starting the model off with the highest probability mass for each parameter at zero. Variables were also scaled and centered within individuals. Model code is presented in the supplementary Material (Supplementary 1). With this particular prior setup, we assume to begin with that there is no dependence between or within network layers through time.

Model predictions of network dynamics

MMAR models identify nonlinear feedbacks, capturing cascading influence across network layers. Given that there are many parameters in the model, and that they interact with each other through time, interpretation from the individual estimates alone is difficult. We, therefore, used the model to make predictions about how an individual would respond to a given change in one of its social network measures (Figure 3). For example, if a male’s aggression in-degree were to be increased at time t, how would this then cascade through the multiple layers over time? To make predictions for each time point, we started all measures at mean values (i.e., 0), drew from the posterior distributions to parameterize the MMAR model, and then used the parameterized model to make predictions about social network measures at the next time point. All predictions used mean estimated parameters, so essentially we made predictions for the average vervet male. At time t, we adjusted one network measure by +2 and recorded subsequent impacts on all the network measures. As all network measures were scaled and centered, changes are shown as deviations from 0.

Figure 3.

Model predicted mean change to all network-level measures following an introduced change in 1 measure: (A) rank increase, (B) increase in aggression, (C) increase in centrality within the female network, (D) increase in centrality in the male network, (E) increase in out-grooming partners, and (F) increase in in-grooming partners. Shaded regions indicate the 95% credible interval from 100 simulated predictions. Time on the x-axis is in months. In each panel, there is an induced change in 1 measure at t = 0, and the cascade of impacts on all measures can then be seen to the right of the induced change, in terms of both their amplitude (height on the y-axis) and duration of their effects (how long the measure takes to return to 0 on the x-axis). As all measures have been scaled the induced change of 2 scaled units would be considered as a large positive change.

Given that the MMAR model also estimates uncertainty and the dependence in uncertainty between social network measures, we assessed the influence of this noise on predictions. Here, we again started all network measures at 0 (i.e., the mean), and made predictions using a parameterized MMAR model using draws from the posterior distribution of our fitted model. In this case, however, we did not introduce a change to any of the network measures, rather we included the estimated error and dependencies in the error when making our predictions, and simulated changes across the network layers due to this noise alone. This allowed us to estimate the role of uncertainty in determining the dynamics of the multilayer network.

Results

Dependence between an individual’s social network measures

Male grooming in- and out-degree, aggression in-degree, and eigenvector centrality within the male and female grooming network layers all showed high positive autocorrelation (i.e., previous measures are related to current measures) (Figure 2a: vertical lines). Changes in male Elo ratings showed negative autocorrelation, although the value was lower than for other measures, suggesting a degree of volatility in Elo ratings (i.e., changes in a particular direction at 1 time point were likely to be reversed in the next).

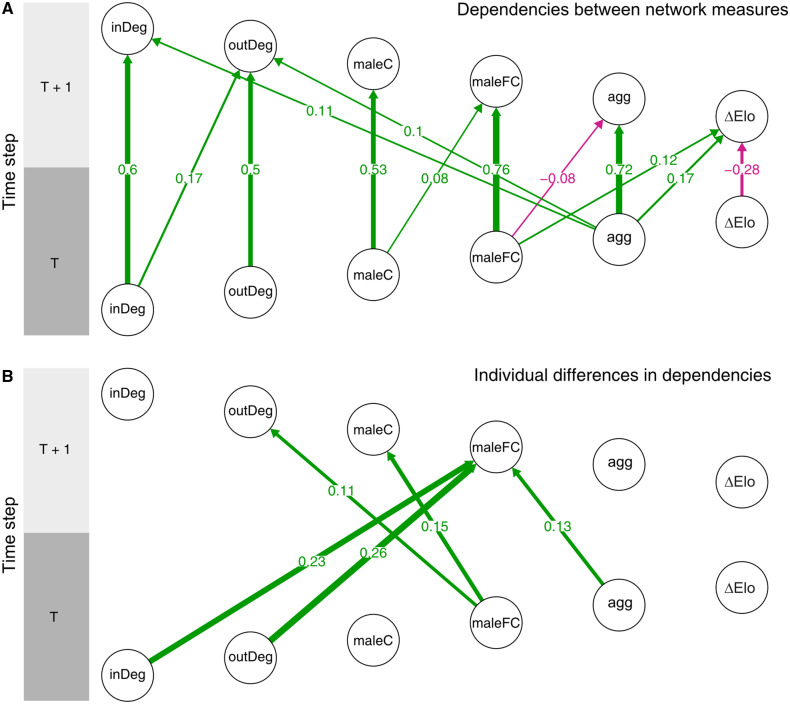
Figure 2.

Estimated lagged and cross-lagged associations for (A) main effects and (B) individual-level differences. Edges between nodes represent associations, red for negative, green for positive, where the width of the edge corresponds to the magnitude of the association. In (a), edges for associations where 95% CI contained 0 were removed for visual clarity. Similarly, in (b), as edges represent estimates of standard deviation, we chose to remove edges when the 95% CI estimates contained 0.01, highlighting those estimates likely to contain individual differences. Node labels: grooming in-degree (inDeg), grooming out-degree (outDeg), male centrality in the male grooming layer (maleC), male centrality in the female grooming layer (maleFC), aggression in-degree (agg), and change in Elo rating (ΔElo). The top nodes represent measures at time T + 1, whereas those below represent those measures at the previous time point (T).

We also found crossed-lagged associations, where changes in 1 layer were associated with subsequent changes in another layer (Figure 2b diagonal lines). The association of most interest—the main effect of a male’s eigenvector centrality within the female grooming layer—was found to be positively associated with changes in a male’s change in Elo rating at the next time step. Additionally, a male’s eigenvector centrality within the female grooming layer was negatively related to in-coming aggression from other males in the next time step. Reduced aggression in-degree from males, in turn, showed a positive relationship with both grooming in- and out-degree with females. Furthermore, grooming in-degree from female partners had a positive relationship with grooming out-degree with female partners in the next time step.

The model also suggested heterogeneity in cross-lagged associations between males. For example, the estimates of individual differences (i.e., random effects) suggested there was moderate variability across individuals in the extent to which grooming in- and out-degree altered a male’s centrality in the female network at the next time step. We also found individual differences in the extent to which aggression in-degree (i.e., the number of males aggressing a given male) altered a male’s eigenvector centrality in the female grooming network. The model also suggested that males differ in how eigenvector centrality in the female grooming network influenced both out-degree and male’s eigenvector centrality in the male grooming layer (Figure 2b). However, all these influences were found to have estimates that centered on zero, that is, the positive and negative relationships shown by individual males tended to cancel each other out, so there was little evidence of a mean effect (Supplementary Figure S5).

Our model also suggested few dependencies between these individual-level effects. The only dependence found was a weak negative relationship between the effect of a male’s in- and out-grooming on eigenvector centrality in the female network (r = −0.25, 95% CI: –0.55, 0.03) (Supplementary Figure S6a). That is, if the effect of grooming in-degree on eigenvector centrality was lower than average for a particular male, the effect of that male’s grooming out-degree on eigenvector centrality in the female network was likely to be higher than average. We did, however, find strong dependence on the errors associated with these social network measures, particularly between grooming in-degree, grooming out-degree, and to a lesser extent, a male’s eigenvector centrality in the female network (Supplementary Figure S6b). This suggests that there remains covariance between these network measures, and can often point to common drivers, for example, changes in the physical environmental might impact both grooming in- and out-degree.

Model predictions of network dynamics

Inducing a positive change in a male’s Elo rating produced little effect on other layers (Figure 3a), whereas increasing aggression from other males led to a reduction in male centrality in his grooming layer, and an increase in Elo rating and grooming in-/out-degree with females (Figure 3b). Inducing an increase in a male’s eigenvector centrality in the female grooming network layer generated the longest lasting impacts (t + 20 months), largely via decreasing aggression in-degree from other males (Figure 3c). An increase in male eigenvector centrality in the male grooming layer principally resulted in an increase in the male’s eigenvector centrality in the female grooming layer (Figure 3d). Finally, grooming in- and out-degree with females showed reciprocal effects, with in-degree showing more of an influence than out-degree (Figure 3e and f). Note that all induced changes to a male’s social network measures showed high resilience, reverting back to the male’s mean values (i.e., 0) within 15–20 months after the introduced disturbances at t = 0 (Figure 3).

The results of the simulations with noise alone indicate that noise is likely to play a large role in a male’s social network measures, and this uncertainty drives large changes beyond those described by the main effects in our model (Figure 4). This suggests that there are likely to be important factors that are absent from our model, and/or that stochastic factors—injury, for example—can also result in changes to a male’s social network position.

Figure 4.

Model predictions including the influence of uncertainty on the development of a male’s social network measures. Initial conditions are set to the mean level of each social network measure, with no induced changes, that is, all changes observed in the plot are due to the effects of noise (and the interdependence in noise between social network measures) for (A) 100 simulated model predictions summarized into a mean line and 95% credible interval ribbons and (B) 1 simulated model prediction.

Discussion

The results of our MMAR analyses showed that there was high positive autocorrelation within several of our network measures for both males and females, indicating that individual social measures were persistent and stable across time. It should also be noted, however, that some moderate autocorrelation was expected due to the overlap in our moving windows. Nevertheless, as all network measures were calculated with the same amount of window overlap, we can compare their relative magnitudes to gain insight into which measures have higher/lower autocorrelation patterns: for example, the relatively higher autocorrelation of male eigenvector centrality within the female network and aggression in-degree from males compared with, for example, the lower autocorrelation in male grooming toward females. This suggests much of the autocorrelation reflects social processes and is not simply an artifact of the moving window approach. That is, it points to resilience in the network, as we discuss in more detail below. We also found that changes in male Elo rating were negatively autocorrelated (although the value was lower than for other measures) suggesting a degree of volatility in male rank trajectories. That is, changes in a male’s Elo rating at 1 time point were likely to be reversed at the next. This corroborates patterns observed in related analyses (e.g., Vilette et al., submitted for publication).

We also found meaningful cross-lagged associations, and this allowed us to confirm the central finding of our original analyses: namely, a positive relationship between male eigenvector centrality in the female network and male Elo rating in the next time step. Crucially, our ability to calculate cross-lagged associations allowed us to establish the direction of these effects, which our original analyses did not permit, and demonstrate that it was changed to male centrality in the female network that preceded any change in Elo rating and not vice versa; although it was also clear that this effect was short-lived. We also found that changes to a male’s grooming centrality within the female network had implications for other social layers beyond effects on Elo rating, with changes in one layer causing a cascade of impacts across all layers. Specifically, we were able to show that male eigenvector centrality within the female grooming network reduced the level of aggression received from males in the next time step and that this, in turn, led to increased amount of grooming both received from and given to females. In addition, the more grooming a male received from females in 1 time step led to increased grooming of females by males in the subsequent time step. This pattern of results fits with our earlier suggestion that female codominance with males would increase females’ ability to choose the males with which they associated, in contrast to other species, like baboons, where a female’s choice of male partners is highly constrained (Young et al. 2017).

Having said all this, it is also the case that changes in Elo ratings had little influence on other layers in the network and, as already noted, showed negative temporal autocorrelation. This suggests that the changes to Elo ratings were short-lived and returned quickly to mean levels. In addition, there was a moderate level of heterogeneity in cross-lagged associations (i.e., meaningful differences in the random effects), which suggests that male centrality in the female grooming was influenced by different factors across males (i.e., grooming more females did not always lead to higher network centrality, but appeared to depend on the identity of the males in question). This lack of any lasting effect on Elo ratings, combined with variability in how a male integrates into the female network, thus calls into question our original conclusion that rank-based changes could exert a long-term influence on male social status, and thus have a positive impact on mating success and hence individual fitness. Recent paternity analyses support this new conclusion, in that reproductive skew in our population is low, with mating access unrelated to male rank, and only weak associations between rank and paternity (and only in some years; Minkner et al. 2018). Combined with our analyses here, this suggests that further investigation of male-female social dynamics, independently of any effect on rank, will be informative with respect to the determinants of male mating and paternity success.

It is also apparent, however, that we may have failed to include some relevant ecological or social measures that predict male integration or, equally, that chance plays a large role in male social network position. Specifically, our analyses showed that the estimated dependencies between social network measures contributed little to the changes observed in individual male social position (Figure 4). The potential for noise to influence male social integration has particularly interesting implications for variability in male social behavior. If chance influences which males will become integrated, selection would be predicted to be weaker for specific behaviors. Essentially, there may be “lucky” males that become integrated due to processes beyond their direct control, and who then experience certain social benefits that influence their behavior. This may lead to increased variation between males, with potential downstream consequences for mating opportunities and other fitness-related benefits. The ability to quantify individual responses to changes in other behavioral layers and to compare these estimates to the magnitude of error/chance could be a promising avenue of research with a multilayer network approach. By the same token, a comparison between predictable responses across layers versus noise could prove useful in understanding the role of chance in social group formation.

This last point links to our social perturbation simulations, where we investigated how changes in network layers affected the temporal properties of the global network. Our results here suggested that the social system was resilient, with perturbations to individual positions returning to their mean levels over time (Figure 4). That is, we found no evidence that changes in 1 layer resulted in any kind of positive feedback loop, where changes compounded over time through layers. Rather, it appears that the system has homeostatic qualities, and returns to its former state. The mechanisms by which this resilience to perturbation comes about, and its consequences, are the focus of ongoing work, but one potential mechanism is compensation. For example, in our previous work on baboons, we found that perturbation of the network, due to the loss of a high ranking female, resulted in changes to the troop’s proximity network layer (specifically, there was an increase in clustering, signaling that interactions became more conservative and predictable) and this restored stability to the network as a whole (Barrett et al. 2012).

Turning now to the limitations of our approach, we found that the great flexibility offered in the construction of multilayer networks poses a problem of choosing exactly how to construct the layers. In our case here, we have had a precedent, in the form of specific question and a known previous outcome (Young et al. 2017), to help guide our choice of which layers to include, how to include them, and what measures to use. Nevertheless, there remained many decisions for which there were no definitive choices, such as whether to create sex-specific layers for grooming, which measure to use to calculate male centrality, which behavioral layers to include or not, and whether environmental measures should be included. Although the accumulation of various ambiguities in the decision-making process is present in all analyses, the use of multiple layers amplifies the number of possible choices. Navigating such choices will be one of the major challenges going forward. Given that this challenge is shared with many other statistical analyses, potential solutions, or mitigation strategies from the wider field of statistics may be helpful. For example, better theory will help us to make better choices, as will relying on the precedents set by previous studies, sensitivity analyses, and transparency regarding the choices made (and not made), for example, by sharing code and data. All of these strategies have been suggested and used to reduce ambiguity in statistical analyses in this more general sense (Gelman et al. 2013; Weisberg 2014; McElreath 2016).

Another potential limitation of the multilayer approach adopted in this article is that the MMAR setup asks how 1 particular network measure influences other measures across multiple layers. As such, it focuses only on quantifying patterns of change in social networks, rather than identifying the specific processes by which these changes occur. The MMAR approach could productively be combined with more process-based techniques that model the behavior of individuals (i.e., nodes) directly within the network (Butts 2008; Snijders et al. 2010). With a combined approach, process models can be compared with the patterns extracted from real systems. For example, could a process model reproduce the directional effects, level of noise, and individual differences identified in the real system using the MMAR approach? Similarly, process models can provide insight into how the patterns extracted from a system using MMAR emerge. We suggest that the combination of process and pattern-based approaches with dynamic multilayer networks will be a promising avenue of research.

To conclude, we would note that the advent of multilayer network approaches means it is now possible to envision highly detailed descriptions of relationships between individuals and how they change over time. Tied to this more detailed level of social description is the ability to extract individual behavioral and physiological states through a growing number of on-animal sensors (Handcock et al. 2009; Krause et al. 2013), for example, weight, rank, stress, temperature, and location. A challenge then presents itself: what do these data-driven, data-rich descriptions of social systems offer that were not possible before? What kinds of questions can we now address? We suggest that we need big theory to be able to take best advantage of these big data (Coveney et al. 2016). Life history theory is one framework that is likely to be of considerable value here (Alberts 2019), especially where individual life-lines can be described in detail from birth until death. A longitudinal multilevel analysis of the social group could be constructed alongside such lifelines, giving us a better understanding of how individual lifelines shape, and are shaped by, social structure. From this point of view, our dynamic multilayer approach would thus benefit from a closer integration with life history theory and collective behavior. Similarly, with the ability of multilayer network approaches to address longitudinal questions at multiple social scales, it also seems possible to test some important social evolutionary mechanisms. There have been a plethora of correlational and simulation studies suggesting that some social structures influence fitness-related traits, via social learning, or by promoting/inhibiting disease transmission (Altizer et al. 2003; Griffin and Nunn 2012; Allen et al. 2013; Duboscq et al. 2016). How these structures emerge, are maintained, and respond to environmental pressures, could provide important insight into how selection operates in social systems and can be profitably analyzed with careful multilayer, dynamic network analyses.