Bayesian Scalar on Image Regression With Nonignorable Nonresponse

Abstract

Medical imaging has become an increasingly important tool in screening, diagnosis, prognosis, and treatment of various diseases given its information visualization and quantitative assessment. The aim of this article is to develop a Bayesian scalar-on-image regression model to integrate high-dimensional imaging data and clinical data to predict cognitive, behavioral, or emotional outcomes, while allowing for nonignorable missing outcomes. Such a nonignorable nonresponse consideration is motivated by examining the association between baseline characteristics and cognitive abilities for 802 Alzheimer patients enrolled in the Alzheimer’s Disease Neuroimaging Initiative 1 (ADNI1), for which data are partially missing. Ignoring such missing data may distort the accuracy of statistical inference and provoke misleading results. To address this issue, we propose an imaging exponential tilting model to delineate the data missing mechanism and incorporate an instrumental variable to facilitate model identifiability followed by a Bayesian framework with Markov chain Monte Carlo algorithms to conduct statistical inference. This approach is validated in simulation studies where both the finite sample performance and asymptotic properties are evaluated and compared with the model with fully observed data and that with a misspecified ignorable missing mechanism. Our proposed methods are finally carried out on the ADNI1 dataset, which turns out to capture both of those clinical risk factors and imaging regions consistent with the existing literature that exhibits clinical significance. Supplementary materials for this article, including a standardized description of the materials available for reproducing the work, are available as an online supplement.

1. Introduction

The present study is motivated by a dataset extracted from the Alzheimer’s Disease Neuroimaging Initiative (ADNI). Since its launch in 2004, ADNI collected imaging, clinical, and laboratory data at multiple time points from cognitively normal controls (CN) and subjects with mild cognitive impairment (MCI) or Alzheimer’s disease (AD). ADNI initially recruited approximately 800 subjects (ADNI-1) according to its initial aims and was extended by three follow-up studies, namely, ADNI-GO, ADNI-2, and ADNI-3. The overall goal of ADNI is to discover, optimize, standardize, and validate clinical trial measures and biomarkers used in AD research by determining the relationships between the clinical, cognitive, imaging, genetic, and biochemical biomarker characteristics for the entire spectrum of AD. More information on ADNI can be obtained at the official website (www.adni-info.org).

The primary objective of this study is to examine whether patients’ numerous baseline biomarkers (e.g., structural imaging) can accurately predict their cognitive decline. The ability to accurately predict the rate of cognitive decline is critical for effective trial design for developing therapies for AD prevention and treatment, but the utility of these baseline biomarkers for such accurate prediction is not well established (Allen et al. 2016; Weiner et al. 2017a, 2017b). We consider the learning score of the Rey auditory verbal learning test (RAVLT), which is a widely used neuropsychological evaluation method that tests episodic declarative memory. The RAVLT learning scores of each subject were obtained at baseline and every 6 months thereafter across multiple study phases. We consider the RAVLT scores measured at the 36th month as the primary clinical outcome and the demographic, imaging, and clinical variables measured at baseline as predictors. To build an accurate predictive model for the RAVLT score, we have to appropriately deal with at least two challenging issues, including (I) missing RAVLT scores, particularly when the missing mechanism is nonignorable, and (II) high-dimensional imaging data.

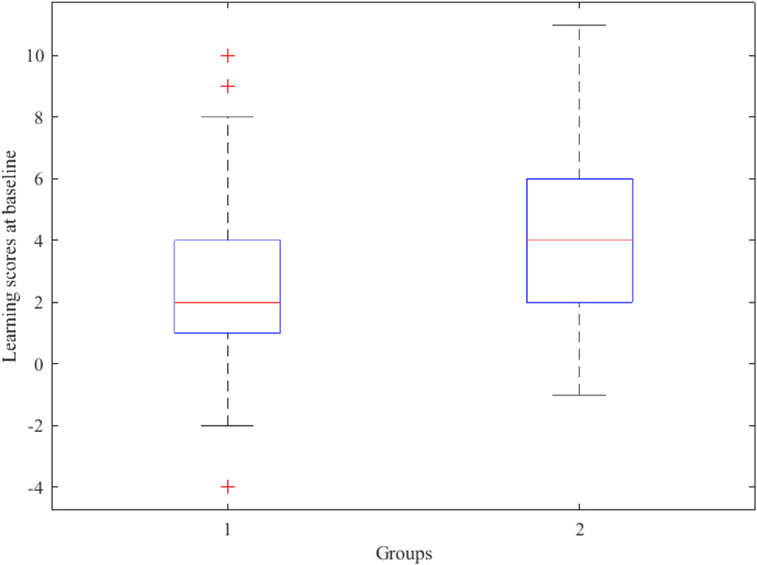
The first challenge is that the nonresponse rate of the RAVLT score increases over time and attains a level of 45.6% at the 36th month, while the missing mechanism is nonignorable. To justify the missingness assumption, we divide the samples into two groups according to whether they are nonrespondents (Group 1) or respondents (Group 2) at the 36th month. Figure 1 summarizes the learning scores of both groups at baseline. Apparently, the subjects in Group 1 have considerably lower learning ability than those in Group 2. This finding implies that low learning ability at baseline is negatively associated with nonresponse probability at the 36th month. That is, elderly adults with weak cognitive ability tend to drop out early from the follow-up study. Thus, the missing data mechanism is likely to be nonignorable and a missing data model should be considered to identify possible effects of learning ability together with other imaging and scalar covariates on the probability of data missingness.

Figure 1.

Learning scores at the baseline of the subjects from two groups in the ADNI dataset, where Group 1 includes the patients who exhibit missing learning scores at the 36th month and Group 2 contains the patients with observed learning scores at the same month.

In large-scale longitudinal neuroimaging studies, follow-up clinical outcomes are frequently missing from the dataset. Thus, appropriately managing nonresponse is of great importance. A nonresponse is regarded as ignorable when its probability is independent of the missing values (Little and Rubin 2002). However, the probability of nonresponse often depends on the observed and missing observations, and disregarding such a missing mechanism may destroy the representativeness of the remaining samples and subsequently lead to biased estimation results (Baker and Laird 1988; Diggle and Kenward 1994; Ibrahim, Lipsitz, and Chen 1999; Ibrahim, Chen, and Lipsitz 2001; Molenberghs and Kenward 2007). Modeling nonignorable missingness is challenging because the missing mechanism is generally unknown and may elicit additional model identifiability issues (Chen 2001; Qin, Leung, and Shao 2002; Tang, Little, and Raghunathan 2003; Ibrahim et al. 2005). Recently, two advanced methods have been proposed to facilitate model identification when dealing with nonignorable missingness under the exponential tilting model proposed by Kim and Yu (2011). The first method, which was developed by Kim and Yu (2011), relies on a set of external data obtained from an independent study, where further responses can be obtained in a subset of nonrespondents (see also Zhao, Zhao, and Tang 2013; Tang, Zhao, and Zhu 2014). Through the use of external data, the tilting parameter can be estimated, and the exponential tilting model for the formulation of nonresponse is well identified. However, such an external dataset is often unavailable in practice, making the procedure infeasible. The second method can address such a problem by introducing an instrumental variable, such as a covariate associated with the response but conditionally independent of the probability of data missingness. The advantage of this method has been demonstrated in recent works (Wang, Shao, and Kim 2014; Yang et al. 2014; Zhao and Shao 2015; Shao and Wang 2016). However, these methods are limited to modeling scalar responses and predictors.

The second challenge is the use of high-dimensional medical images (or functional data) observed at a set of grid points to accurately predict clinical outcomes. Many imaging studies have collected high-dimensional imaging data, such as magnetic resonance imaging (MRI) data and computed tomography, to extract useful information associated with the pathophysiology of various diseases, such as lung cancer and AD. Such information can further facilitate clinical decision-making (Gillies, Kinahan, and Hricak 2015). For instance, data obtained from MRI-based investigations may greatly contribute to the discovery and validation of prognostic biomarkers used to identify subjects at great risk of cognitive decline, thereby aiding researchers and clinicians in monitoring the progression of MCI and early AD, as well as developing new treatments and reducing the time and cost of clinical trials.

A functional linear model (FLM) and its variations have received extensive attention in the last two decades as popular predictive models based on functional predictors (Ramsay and Silverman 2005; Ferraty and Vieu 2006; Horváth and Kokoszka 2012; Morris 2015; Fraiman, Gimenez, and Svarc 2016; Wang, Chiou, and Mueller 2016). Many estimation methods have been developed to estimate the coefficient function of the FLM and its variations, but they differ in terms of the choice of basis or some combination thereof, and the approach to regularization (Morris 2015; Wang, Chiou, and Mueller 2016; Wang and Zhu 2017). The most common choices for basis include functional principal components, splines, and wavelets, among many others (Ramsay and Silverman 2005; Ferraty and Vieu 2006; Hall and Horowitz 2007; Yuan and Cai 2010). Functional principal component analysis (FPCA) is an important tool that reduces the dimensionality of functional data (Müller and Stadtmüller 2005; Yao, Müller, and Wang 2005; Reiss and Ogden 2007, 2010; Goldsmith et al. 2011, among many others). Furthermore, FLM analysis is feasible given the connection between FPCA and ordinary linear mixed models (James 2002).

Although missing data problems have been extensively investigated, minimal work has focused on the analysis of functional data with missing scalar clinical outcomes. Preda, Saporta, and Mbarek (2010) considered a nonlinear iterative partial least squares method to accommodate functional predictors subject to data missingness. Gertheiss et al. (2013) conducted longitudinal scalar-on-function regression, which allows for ignorable missingness in functional regressors. Ferraty, Sued, and Vieu (2013) studied the mean estimation problems for scalar-on-function regression with ignorable nonresponse. Their study was extended by Ling, Liang, and Vieu (2015), who considered stationary ergodic functional processes as predictors with ignorable nonresponse. Chiou et al. (2014) modeled traffic monitoring data as functional processes and imputed missing values in the functional data by using a conditional expectation approach. However, the aforementioned developments focused only on functional data with ignorable missingness, and none of them considered ultrahigh-dimensional imaging data in the presence of nonignorable missingness. To the best of our knowledge, the study by Li et al. (2018) is the only article that developed a functional linear model for the joint modeling of functional predictors and nonignorable missing clinical outcomes. The methodology they proposed is a frequentist method that depends on an external dataset, which is rarely available in real applications.

The aim of this article is to develop a Bayesian scalar-on-image (BSOI) regression model that uses high-dimensional imaging data and other scalar variables as explanatory covariates to predict clinical outcomes that are not fully observed. The proposed approach comprises two stages. The first stage uses FPCA to extract the principal directions of variation in large-scale neuroimaging data, and the extraction is performed through the singular value decomposition (SVD) technique (Zipunnikov et al. 2011a; Zhu, Fan, and Kong 2014; Wang, Chiou, and Mueller 2016). For simplicity, we use FPCA in the development of BSOI although it is easy to use some fixed basis functions, such as a B-spline and wavelet. The second stage incorporates the extracted major principal scores into the regression. Regarding the modeling of nonignorable missingness, we propose an imaging exponential tilting model that is analyzed jointly with the BSOI regression. The imaging predictors involved in the exponential tilting model can be similarly assessed through FPCA. An instrumental variable is introduced to facilitate the identification of the proposed model. We conduct a full Bayesian analysis, not only given its power and efficiency in managing complex models and data structures but also because it incorporates useful prior information. Appropriate prior distributions can add valuable information for the inference of the missing mechanism and thus assist model identification and estimation (Ibrahim, Chen, and Lipsitz 2002). For instance, if a set of external data is available for preliminary analysis on the missing data model, the estimation results can be incorporated as prior inputs into the Bayesian analysis to improve the estimation accuracy.

The remainder of this article is organized as follows: Section 2 introduces the FPCA technique, a BSOI regression model, and an exponential tilting model with imaging predictors. Section 3 discusses how an instrumental variable improves model identification and estimation and develops a Bayesian approach with Markov chain Monte Carlo (MCMC) algorithms for statistical inference. Section 4 conducts simulations to examine the finite sample performance of the proposed method. Section 5 presents a comprehensive data analysis of the ADNI dataset presented above. Section 6 concludes the article with some discussions.

2. Model Description

2.1. FPCA for High-Dimensional Imaging Data

Suppose we have samples of imaging data W_i(v) observed at V grid points v in a compact space $\mathcal{V}$ for i = 1, …, n. The observed images are formulated through a functional model as follows:

$$W_i(v)=\mu (v)+X_i(v),v\in \mathcal{V},$$ (1)

where μ(v) is the mean image, and X_i(v) is a centered second-order stochastic process with covariance operator K_X(v₁, v₂) = E{X_i(v₁)X_i(v₂)}. Similar to those of Zipunnikov et al. (2011a), the measurement errors of the imaging observations are not included in the model. This assumption is reasonable because the images are usually presmoothed. The Karhunen–Loeve expansion of the random process is based on the eigen-decomposition of the covariance operator, which yields

$$X_i(v)=\sum _{k=1}^{\infty }{\xi }_{ik}{\psi }_k(v),$$ (2)

where ψ_k(v) represents the eigenimages of K_X(v₁, v₂) for the multidimensional imaging data, ξ_ik denotes the uncorrelated eigenscores of the ith subject with nonincreasing variances λ_k, and λ_k is the eigenvalues of K_X(v₁, v₂). FPCA commonly retains the first K eigenimages that account for most of the functional variability for the expansion (2) (Di et al. 2009; Zipunnikov et al. 2011a; Zhu, Fan, and Kong 2014; Wang, Chiou, and Mueller 2016). In practical applications, retaining a large number of eigenimages may lead to overfitting. Thus, we use the Bayesian information criterion (BIC) to select K for the analysis of the ADNI dataset in Section 5. The mean image μ(v) can be regarded as a zero vector by centralizing W_i(v). Thus, the functional model (1) can be rewritten as follows:

$$W_i(v)=X_i(v)=\sum _{k=1}^K{\xi }_{ik}{\psi }_k(v).$$ (3)

Owing to the ultrahigh-dimensionality, eigen-decomposing the covariance operator of the functional process X_i(v) is challenging. For example, we consider a two-dimensional image {X_i(v)} with 300 grids on each dimension, that is, V = 90,000. This results in a covariance operator K_X = {K_X(v₁, v₂)} of dimension 90,000 × 90,000. Consequently, a brutal-force eigenanalysis on K_X requires O(V³) operations, which are essentially impossible. To address such a problem, Zipunnikov et al. (2011a) developed an FPCA procedure based on SVD for high-dimensional data. The method exploits the relationship between the SVD on X_i(v) and the eigen-decomposition on K_X. It also exploits the advantage that the number of subjects, n, is usually small to modest. Specifically, we consider a V × n matrix X = (X₁, …, X_n), whose rank is at most min(n, V), X_i = (X_i(v) : all grid points $v\in \mathcal{V}$) is a V × 1 vector for each i. The SVD of X can then be represented as

$$\mathbf{X}=\mathbf{U}\mathbf{S}{\mathbf{V}}^T,$$ (4)

where U and V are V × n and n × n unitary orthogonal matrices, respectively, and S is an n × n diagonal matrix with nonnegative singular values of X as its diagonal elements. The computational cost to obtain the SVD is O(Vn² + n³) (Golub and Loan 1996), which is much smaller than that required for the direct eigen-decomposition of the covariance operator. The eigenimage (eigenfunction) ψ_k(v), eigenvalue λ_k of K_X and the eigenscores ξ_ik of the subjects can be calculated as follows. The eigenimage Ψ_k = ψ_k(v) is given by the kth column of U. The eigenvalue λ_k equals $s_k^2$, where s_k is the kth diagonal element of S. The eigenscores ξ_ik are given by the columns of SV^T truncated to the first K coordinates. To implement the SVD, we first express the spectral decomposition of X^TX as X^TX = VS²V^T. Then, U can be calculated as U = XVS⁻¹.

Notably, for an ultrahigh-dimensional V, the centered imaging data matrix X may be extremely large and thus cannot be loaded into the computer memory. In such an instance, X can be partitioned into several blocks as ${\mathbf{X}}^T=[{({\mathbf{X}}^{(1)})}^T|{({\mathbf{X}}^{(2)})}^T|\dots \mid {({\mathbf{X}}^{(M)})}^T]$, where the number of blocks, M, can be selected to make each block adapt to the available computer memory so that it is feasible to calculate X^TX and U as follows: ${\mathbf{X}}^T\mathbf{X}={\sum }_{m=1}^M{({\mathbf{X}}^{(m)})}^T{\mathbf{X}}^{(m)},{\mathbf{U}}^{(m)}={\mathbf{X}}^{(m)}\mathbf{V}{\mathbf{S}}^{-1}$, and ${\text{U}}^T=[{({\text{U}}^{(1)})}^T|{({\text{U}}^{(2)})}^T|\dots \mid {({\text{U}}^{(M)})}^T]$. Alternatively, we may employ the efficient algorithm of multidimensional FPCA from Chen and Jiang (2017).

2.2. BSOI Regression

We consider observations $\left\{y_i,{\mathbf{z}}_i,\left(X_i(v):v\in \mathcal{V}\right)\right\}$ for i = 1, …, n from n independent subjects, where y_i is the clinical variable of interest subject to missingness, z_i is a Q × 1 vector of observed scalar covariates, and X_i(v) represents the imaging data described above. The BSOI regression model is thus defined as follows:

$$y_i=\alpha +{\int }_{\mathcal{V}}{X}_i(v)\beta (v)dv+{\mathit{\gamma }}^T{\mathbf{z}}_i+{\delta }_i,$$ (5)

where α is the intercept, β(·) is a coefficient image, γ is a Q × 1 vector of the coefficients for the covariates, and δ_i is normal random noise with the variance parameter σ². The β(v) is the coefficient corresponding to the vth voxel of the image. Thus, a natural interpretation of β(·) is that the regions of imaging data with large |β(v)| have strong effects on the clinical outcome of interest.

With the eigenimages derived in the previous section, both X_i(·) and β(·) can be approximated by truncated Karhumen–Loeve expansions as $X_i(v)\approx {\sum }_{k=1}^K{\xi }_{ik}{\psi }_k(v)$ and $\beta (v)\approx {\sum }_{k=1}^K{\beta }_k{\psi }_k(v)$, where the β_ks’ are the eigenbasis coefficients of β(·). Subsequently, model (5) can be rewritten as

$$y_i=\alpha +\sum _{k=1}^K{\beta }_k{\xi }_{ik}+{\mathit{\gamma }}^T{\mathbf{z}}_i+{\delta }_i.$$ (6)

Therefore, the BSOI regression becomes a high-dimensional linear regression model, which can be readily analyzed.

2.3. Exponential Tilting Model for Nonignorable Missingness

We introduce an indicator variable r_i to model the missingness of y_i such that r_i = 1 if y_i is missing and r_i = 0 otherwise. Naturally, we assume a Bernoulli distribution of r_i as follows:

$$r_i\mid \left(y_i,X_i(\cdot ),{\mathbf{z}}_i\right)~\mathrm{Bernoulli}\left({\pi }_i\right),$$ (7)

where π_i = π(y_i, X_i(·), z_i) is the probability of missingness for y_i, and r_i and r_j are assumed to be independent for i ≠ j. Furthermore, an exponential tilting model with imaging predictors is proposed for π_i as follows:

$$\begin{gathered} {\pi }_i\equiv \mathrm{Pr}\left(r_i=1\mid y_i,X_i(\cdot ),{\mathbf{z}}_i\right) \\ =\frac{\exp \left({\int }_{\mathcal{V}}{X}_i(v){\beta }_r(v)dv+{\mathit{\gamma }}_r^T{\mathbf{z}}_i+\varphi y_i\right)}{1+\exp \left({\int }_{\mathcal{V}}{X}_i(v){\beta }_r(v)dv+{\mathit{\gamma }}_r^T{\mathbf{z}}_i+\varphi y_i\right)}, \end{gathered}$$ (8)

where ϕ is the tilting parameter that determines the amount of departure from the ignorability of the missing mechanism. Model (8) can be regarded as an extension of the linear missing data model proposed by Ibrahim, Chen, and Lipsitz (2001). Furthermore, by using ${\sum }_{k=1}^K{\beta }_{rk}{\psi }_k(v)$ to approximate β_r(v), model (8) reduces to

$$\begin{gathered} {\pi }_i\equiv \mathrm{Pr}(r_i=1\mid y_i,X_i(v),{\mathbf{z}}_i) \\ =\frac{\exp ({\alpha }_r+{\sum }_{k=1}^K{\beta }_{rk}{\xi }_{ik}+{\mathit{\gamma }}_r^T{\mathbf{z}}_i+\varphi y_i)}{1+\exp ({\alpha }_r+{\sum }_{k=1}^K{\beta }_{rk}{\xi }_{ik}+{\mathit{\gamma }}_r^T{\mathbf{z}}_i+\varphi y_i)}. \end{gathered}$$ (9)

Finally, our BSOI model consists of Equations (6), (7), and (9).

3. Estimation

3.1. Identifiability

The identifiability of a nonignorable missing mechanism is often a challenging issue and thus requires careful investigation. As remarked by Lindley (1972), it is always possible to conduct a Bayesian analysis by assigning proper priors on model parameters regardless of the model identifiability. However, a practical consequence of a nonidentifiable model is that it may trap Bayesian implementations into the possibility of drifting to extreme values even with proper priors (Gelfand and Smith 1990). Therefore, achieving model identification is crucial for Bayesian analyses. The formal notion of Bayesian identifiability from Dawid (1979) has established that Bayesian nonidentifiability is equivalent to a lack of identifiability in the likelihood (Gelfand and Sahu 1999). This equivalence implies that the Bayesian model is identifiable as long as two different populations do not exhibit the same observed data likelihood. We thus investigate the identifiability of the model likelihood below.

The observed data likelihood function of our BSOI model is

$$\begin{gathered} \prod _i{[\mathrm{Pr}(r_i=0\mid y_i,X_i(\cdot ),{\mathbf{z}}_i)p(y_i\mid X_i(\cdot ),{\mathbf{z}}_i)]}^{1-r_i} \\ {[\int \mathrm{Pr}(r_i=1\mid y,X_i(\cdot ),{\mathbf{z}}_i)p(y\mid X_i(\cdot ),{\mathbf{z}}_i)dy]}^{r_i}, \end{gathered}$$ (10)

where $\int \mathrm{Pr}\left(r_i=1\mid y,X_i(\cdot ),{\mathbf{z}}_i\right)p\left(y\mid X_i(\cdot ),{\mathbf{z}}_i\right)dy$ is given by

$$\begin{gathered} \int \left\{1-\mathrm{Pr}\left(r_i=0\mid y,X_i(\cdot ),{\mathbf{z}}_i\right)\right\}p\left(y\mid X_i(\cdot ),{\mathbf{z}}_i\right)dy \\ =1-\int \mathrm{Pr}\left(r_i=0\mid y,X_i(\cdot ),{\mathbf{z}}_i\right)p\left(y\mid X_i(\cdot ),{\mathbf{z}}_i\right)dy. \end{gathered}$$

Thus, the joint model is identifiable when two different populations do not provide the same Pr(r = 0|y, X(·), z)p(y|X(·), z) for all possible (y, X(·), z). Although the proposed model assumes a parametric framework, identifiability remains nontrivial, as demonstrated by the following example.

Example 1.

Suppose that models (5) and (9) exclude the functional covariate, while model (9) satisfies ϕ ≠ 0. Then, we have

$$\mathrm{Pr}(r=0\mid y,z)p(y\mid z)=\frac{\exp \{-{(y-\alpha -\gamma z)}^2/2{\sigma }^2\}}{\sqrt{2\pi {\sigma }^2}\{1+\exp \left({\alpha }_r+{\gamma }_{r}z+\varphi y\right)\}}.$$

Letting {α, γ, σ, α_r, γr, ϕ} and $\left\{{\alpha }^{\prime },{\gamma }^{\prime },{\sigma }^{\prime },{\alpha }_r^{\prime },{\gamma }_r^{\prime },{\varphi }^{\prime }\right\}$ denote two sets of parameters, and

$$\begin{gathered} \frac{\exp \{-{(y-\alpha -\gamma z)}^2/2{\sigma }^2\}}{\sqrt{2\pi {\sigma }^2}\{1+\exp \left({\alpha }_r+{\gamma }_{r}z+\varphi y\right)\}} \\ =\frac{\exp \{-{\left(y-{\alpha }^{\prime }-{\gamma }^{\prime }z\right)}^2/2{\sigma }^{\prime 2}\}}{\sqrt{2\pi {\sigma }^{\prime 2}}\{1+\exp \left({\alpha }_r^{\prime }+{\gamma }_r^{\prime }z+{\varphi }^{\prime }y\right)\}},\forall (y,z), \end{gathered}$$ (11)

it can be shown that model (11) holds if σ′ = σ, ${\alpha }_r^{\prime }=-{\alpha }_r$, ${\gamma }_r^{\prime }=-{\gamma }_r$, ϕ′ = −ϕ, ${\alpha }_r={\varphi }^2{\sigma }^2/2-\varphi \alpha ,{\alpha }^{\prime }=\alpha -\varphi {\sigma }^2$, γ′ = γ, ϕ = −γ_r/γ, implying that the model is unidentifiable.

This simple example sheds new insights on the construction of identifiability conditions. Specifically, two possible solutions of (11) are given by

$$\begin{array}{l}\text{Scenario}\text{(}\mathit{\text{i}}\text{)}\{\begin{array}{l}\exp \{-{(y-\alpha -\gamma z)}^2/2{\sigma }^2\}{\sigma }^{\prime }\hfill \\ =\exp \{-{\left(y-{\alpha }^{\prime }-{\gamma }^{\prime }z\right)}^2/2{\sigma }^{\prime 2}\}\sigma ,\hfill \\ \exp \{-{(y-\alpha -\gamma z)}^2/2{\sigma }^2\}{\sigma }^{\prime }\hfill \\ \exp \left({\alpha }_r^{\prime }+{\gamma }_r^{\prime }z+{\varphi }^{\prime }y\right)\hfill \\ =\exp \{-{\left(y-{\alpha }^{\prime }-{\gamma }^{\prime }z\right)}^2/2{\sigma }^{\prime 2}\}\sigma \hfill \\ \exp \left({\alpha }_r+{\gamma }_{r}z+\varphi y\right),\hfill \end{array}\\ \text{Scenario}\text{(}\mathit{\text{ii}}\text{)}\{\begin{array}{l}\exp \{{(y-\alpha -\gamma z)}^2/2{\sigma }^2\}{\sigma }^{\prime }\hfill \\ =\exp \{-{\left(y-{\alpha }^{\prime }-{\gamma }^{\prime }z\right)}^2/2{\sigma }^{\prime 2}\}\sigma \hfill \\ \exp \left({\alpha }_r+{\gamma }_{r}z+\varphi y\right),\hfill \\ \exp \{-{\left(y-{\alpha }^{\prime }-{\gamma }^{\prime }z\right)}^2/2{\sigma }^{\prime 2}\}\sigma \hfill \\ =\exp \{-{(y-\alpha -\gamma z)}^2/2{\sigma }^2\}{\sigma }^{\prime }\hfill \\ \exp \left({\alpha }_r^{\prime }+{\gamma }_r^{\prime }z+{\varphi }^{\prime }y\right).\hfill \end{array}\end{array}$$

If Scenario (i) holds for all (y, z) in their domain, then $\left(\alpha ,\gamma ,\sigma ,{\alpha }_r,{\gamma }_r,\varphi \right)=\left({\alpha }^{\prime },{\gamma }^{\prime },{\sigma }^{\prime },{\alpha }_r^{\prime },{\gamma }_r^{\prime },{\varphi }^{\prime }\right)$ holds naturally. Then, the model is identifiable if one can exclude Scenario (ii). This can be achieved by introducing some additional assumptions. One such assumption is that a covariate u exists in z = (z^*T, u)^T such that Pr(y|z) depends on u, whereas Pr(r = 0|y, z) does not. The covariate u is called a nonresponse instrument, which has been demonstrated to be essential for the identification and estimation of a nonignorable missing mechanism in regression without functional covariates (Wang, Shao, and Kim 2014; Shao and Wang 2016). As an illustration, we set z* to be a nonzero constant and u = z as the instrumental variable. In this case, the use of the instrumental variable u = z implies γ_r = 0, yielding that exp(α_r + γ_rz + ϕy) becomes exp(α_r + ϕy) and is independent of z. However, given that $\exp \{-{(y-\alpha -\gamma z)}^2/2{\sigma }^2\}{\sigma }^{\prime }/\exp \{-{\left(y-{\alpha }^{\prime }-{\gamma }^{\prime }z\right)}^2/2{\sigma }^{\prime 2}\}/\sigma$ depends on z for any (α, γ, σ) ≠ (α′, γ′, σ′), Scenario (ii) can be excluded and the model is identifiable.

In many real applications, it is not difficult to identify the instrumental variable. For example, we are interested in predicting monthly income, which is often only partially observed to protect privacy. It may be reasonable to assume that the probability of data missingness is independent of gender, age group, and educational level conditional on monthly income (Wang, Shao, and Kim 2014; Shao and Wang 2016). Since monthly income is usually associated with gender, age group, and educational level, we may choose any of the three covariates as the instrumental variable. Based on the existing literature (Wang, Shao, and Kim 2014; Zhao and Shao 2015; Shao and Wang 2016) and our experience, we have the following recommendations for choosing the instrumental variable. (i) The instrumental variable u has to be related to the response y and conditionally independent of the nonresponse probability. That is, Pr(y|X(·), z*, u) should depend on u, whereas Pr(r = 0|y, X(·), z*, u) should not. Experimental analyses that include all covariates in both the scalar on image regression and the exponential tilting model could provide clues on the covariates that have potential to serve as the instrumental variable. (ii) A sensitivity analysis with different choices of the instrumental variable may be considered.

We give a theoretical justification below in a more general setting and provide the proof in Appendix A. Specifically, we assume $\mathrm{Pr}(y\mid X(\cdot ),\mathbf{z})=\mathrm{Pr}\left(y\mid X(\cdot ),\mathbf{z};{\mathit{\theta }}_y\right)$ and $\mathrm{Pr}(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*})=\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_r\right)$, where θ_y and θ_r contain unknown parameters in the imaging regression y|(X(·), z) and the missing data model r|(y, X(·), z*), respectively. Let $\mathcal{D}\left({\mathbf{\theta }}_y\right)\otimes \mathcal{D}\left({\mathbf{\theta }}_r\right)$ be the domains of (θ_y, θ_r), where ⨂ is the tensor product of two spaces and $\mathcal{D}\left({\mathbf{\theta }}_y\right)$ and $\mathcal{D}\left({\mathbf{\theta }}_r\right)$ are the domain of θ_y and that of θ_r, respectively. We will show that the instrumental variable is useful for model identification and estimation in the presence of functional covariates. Moreover, we provide further evidence by including instrumental variables in the simulation study and real data analysis.

Theorem 1.

Suppose that there is a nonresponse instrumental covariate u in z = (z^*T, u)^T such that Pr(y|X(·), z) depends on u, whereas $\mathrm{Pr}(r=0\mid y,X(\cdot ),\mathbf{z})=\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*}\right)$ does not depend on u. The model is identifiable under conditions (C1)–(C3) stated below:

(C1) there exists a set S ⊆ the support of (y, X(·), z*), such that $\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathbf{\theta }}_r\right)\ne 0$ for all (y, X(·), z*) ∈ S and ${\mathit{\theta }}_r\in \mathcal{D}\left({\mathit{\theta }}_r\right)$;

(C2) $\mathrm{Pr}\left(r=0|y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r1}\right)=\mathrm{Pr}\left(r=0|y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r2}\right)$ for all $\left(y,X(\cdot ),{\mathbf{z}}^{*}\right)\in S\iff {\mathit{\theta }}_{r1}={\mathit{\theta }}_{r2}$;

(C3) $p\left(y|X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y1}\right)p\left(y|X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathit{\theta }}_{y2}\right)=p(y|X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y2})p\left(y|X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathit{\theta }}_{y1}\right)$ holds for all (u₁, u₂) and $\left(y,X(\cdot ),{\mathbf{z}}^{*}\right)\in S\iff {\mathit{\theta }}_{y1}={\mathit{\theta }}_{y2}$.

Theorem 1 extends the theoretical results of Wang, Shao, and Kim (2014) from generalized linear models to the BSOI model. Specifically, these identifiability conditions (C1)–(C3) can be divided into two parts, including the identifiability of Pr(r = 0|y, X(·), z^*; θ_r) and the identifiability of the likelihood ratio $p(y\mid X(\cdot ),{({\mathbf{z}}^{*T},u_1)}^T;{\mathbf{\theta }}_y)/p(y\mid X(\cdot ),{({\mathbf{z}}^{*T},u_2)}^T;{\mathbf{\theta }}_y)$ without missingness. These identification conditions do not need to specify the explicit form of a regression model and are applicable to a large class of model settings, such as semiparametric BSOI regression and the semiparametric imaging exponential tilting model.

As a special case, conditions (C1)–(C3) for the BSOI regression and exponential tilting model can be further clarified to facilitate verification. We need to introduce some notations. Denote the topological support of the random process X(·) by $\mathcal{X}$, which is assumed to be a subset of the quadratically integrable function space $L_2(\mathcal{V})$. Denote the support of z^∗ and u by ${\mathcal{Z}}^{*}$ and $\mathcal{U}$, which are subsets of ${ℝ}^{Q-1}$ and $ℝ$, respectively. It is assumed that the sup\port of (X(·), z^∗, u) is $\mathcal{X}\otimes {\mathcal{Z}}^{*}\otimes \mathcal{U}$. Given aHilbert space H(⟨·, ·⟩) and subsets S₁, S₂ ⊆ H, we define

$$\begin{gathered} \mathcal{L}\left(S_1\right) \\ =\left\{\sum _{j=1}^J{a}_j\left(s_j-{\tilde{s}}_j\right)\mid s_j,{\tilde{s}}_j\in S_1,a_j\in ℝ\text{for}j=1,\dots ,J,J\in {\mathbb{Z}}_{+}\right\} \end{gathered}$$

and $\overline{\mathcal{L}}\left(S_1\right)$ as the closure of $\mathcal{L}\left(S_1\right)$. Moreover, we define

$$\mathcal{L}{\left(S_1,S_2;H\right)}^{\perp }=\left\{h\in S_2\mid \langle h,s\rangle =0\text{for}\text{all}s\in \overline{\mathcal{L}}\left(S_1\right)\right\}.$$

Note that $\overline{\mathcal{L}}\left(S_1\right)$ is the closed linear span of S₁ if 0 ∈ S₁, and $\mathcal{L}{\left(S_1,S_2;H\right)}^{\perp }$ is the perpendicular complement of $\overline{\mathcal{L}}\left(S_1\right)$ if S₂ = H.

The following proposition holds, and the proof can be found in Appendix B.

Proposition 1.

Consider the model specified by (5), (7), and (8) with an instrumental variable as follows:

$$\begin{gathered} y_i=\alpha +{\int }_{\mathcal{V}}{X}_i(v)\beta (v)dv+{\mathit{\gamma }}_{*}^T{\mathbf{z}}_i^{*}+{\gamma }_u{u}_i+{\delta }_i,{\delta }_i~N\left(0,{\sigma }^2\right), \\ \mathrm{Pr}\left(r_i=1\mid y_i,X_i(v),{\mathbf{z}}_i\right) \\ =\frac{\exp \left({\alpha }_r+{\int }_{\mathcal{V}}{X}_i(v){\beta }_r(v)dv+{\mathit{\gamma }}_r^T{\mathbf{z}}_i^{*}+\varphi y_i\right)}{1+\exp \left({\alpha }_r+{\int }_{\mathcal{V}}{X}_i(v){\beta }_r(v)dv+{\mathit{\gamma }}_r^T{\mathbf{z}}_i^{*}+\varphi y_i\right)}. \end{gathered}$$

The following conditions are sufficient conditions of (C1)–(C3):

1. there exists an ϵ > 0 such that |γ_u| ≥ ϵ;

2. $\min \left(\Vert \mathcal{X}{\Vert }_0,{\Vert {\mathcal{Z}}^{*}\Vert }_0,\Vert \mathcal{U}{\Vert }_0\right)\ge 2$, where || ·||₀ is the number of elements.

3. $\mathcal{L}(\mathcal{X},\mathcal{D}(\beta (\cdot ))$; ${L_2(\mathcal{V}))}^{\perp }$, $\mathcal{L}(\mathcal{X},\mathcal{D}\left({\beta }_r(\cdot )\right)$; ${L_2(\mathcal{V}))}^{\perp }$, $\mathcal{L}({\mathcal{Z}}^{*},{\mathcal{D}\left({\mathit{\gamma }}_{*}\right);{ℝ}^{Q-1})}^{\perp }$, and $\mathcal{L}{\left({\mathcal{Z}}^{*},\mathcal{D}\left({\mathit{\gamma }}_r\right);{ℝ}^{Q-1}\right)}^{\perp }$ are zero, where $\mathcal{D}(\beta (\cdot ))$, $\mathcal{D}\left({\beta }_r(\cdot )\right)$, $\mathcal{D}\left({\mathit{\gamma }}_{*}\right)$ and $\mathcal{D}\left({\mathit{\gamma }}_r\right)$ are the domains of β(·), β_r(·), γ_*, and γ_r, respectively.

Conditions (i), (ii), and (iii) in Proposition 1 can be easily satisfied, as demonstrated in the following example.

Example 2.

Let $\mathcal{V}=[0,T]$ for some T > 0. X(·) is a continuous stochastic process on $\mathcal{V}$ with topological support $\mathcal{X}=\{X(\cdot )\in C[0,T]\mid X(0)=0\}$, for example, the one-dimensional Wiener process with nonsingular covariance matrix. The β(·) and β_r(·) ∈ C[0, T] are continuous functions on [0, T], indicating $\mathcal{D}\left({\beta }_r(\cdot )\right)=\mathcal{D}(\beta (\cdot ))=C[0,T]$. It follows from the fact that $\mathcal{X}$ is dense in $\tilde{\mathcal{X}}=\left\{X(\cdot )\in L_2[0,T]\mid X(0)=0\right\}$ that we have

$$\begin{gathered} \mathcal{L}{\left(\mathcal{X},\mathcal{D}(\beta (\cdot ));L_2(\mathcal{V})\right)}^{\perp }=\mathcal{L}{\left(\mathcal{X},\mathcal{D}\left({\beta }_r(\cdot )\right);L_2(\mathcal{V})\right)}^{\perp } \\ =\mathcal{L}{\left(\tilde{\mathcal{X}},C[0,T];L_2([0,T])\right)}^{\perp }=0. \end{gathered}$$

Suppose ${\mathcal{Z}}^{*}={ℝ}^{Q-1},\mathcal{D}\left({\mathit{\gamma }}_{*}\right)={ℝ}^{Q-1}$, and $\mathcal{D}\left({\mathit{\gamma }}_r\right)={ℝ}^{Q-1}$. Then, we have

$$\begin{gathered} \mathcal{L}{\left({\mathcal{Z}}^{*},\mathcal{D}\left({\mathit{\gamma }}_{*}\right);{ℝ}^{Q-1}\right)}^{\perp }=\mathcal{L}{\left({\mathcal{Z}}^{*},\mathcal{D}\left({\mathit{\gamma }}_r\right);{ℝ}^{Q-1}\right)}^{\perp } \\ =\mathcal{L}{\left({ℝ}^{Q-1},{ℝ}^{Q-1};{ℝ}^{Q-1}\right)}^{\perp }=0. \end{gathered}$$

The key condition |γ_u| ≥ ϵ guarantees that the dependency of the response y on the instrumental variable u exists.

3.2. Bayesian Inference

Let y_obs and y_mis be the vectors of observed and missing responses, respectively; y = (y_obs, y_mis); Z = (z₁, …, z_n) be the matrix of observed covariates; and r = (r₁, …, r_n)^T be a vector of missingness indicators. We also denote ${\mathit{\theta }}_y={(\alpha ,{\beta }_1,\dots ,{\beta }_K,{\gamma }_1,\dots ,{\gamma }_Q,{\sigma }^2)}^T$ as a vector that includes all the unknown parameters involved in the BSOI regression model (6), ${\mathit{\theta }}_r={({\alpha }_r,{\beta }_{r1},\dots ,{\beta }_{rK},{\gamma }_{r1},\dots ,{\gamma }_{r,Q-1})}^T$ as a vector that includes all the unknown parameters involved in missing data model (9), and θ = (θ_y, θ_r). Recall that X is the matrix of imaging observations.

After performing FPCA on the imaging observations X_i(v), we can consider the eigenscores ξ_ik as known covariates in the regression model. Consequently, the BSOI regression model is reduced to a conventional linear model and is readily analyzed under the Bayesian framework. We then assign conjugate priors for the parameters in θ_y as follows:

$$\begin{gathered} p(\alpha )\stackrel{D}{=}\text{N}({\alpha }_0,{\sigma }_{\alpha 0}^2);p({\beta }_k)\stackrel{D}{=}\text{N}({\beta }_{k0},{\sigma }_{{\beta }_{k}0}^2),k=1,\dots ,K; \\ p({\gamma }_q)\stackrel{D}{=}\text{N}({\gamma }_{q0},{\sigma }_{{\gamma }_{q}0}^2),q=1,\dots ,Q;\text{and} \\ p({\sigma }^{-2})\stackrel{D}{=}\mathrm{Gamma}(a_{\sigma 0},b_{\sigma 0}), \end{gathered}$$ (12)

where α₀, ${\alpha }_0,{\sigma }_{\alpha 0}^2,{\beta }_{k0},{\sigma }_{{\beta }_{k}0}^2,{\gamma }_{q0},{\sigma }_{{\gamma }_{q}0}^2,a_{\sigma 0}$, and b_σ0 are the hyperparameters, and their values are prespecified according to the information from historical analyses or prior knowledge. For the parameter vector θ_r involved in (9), we assign the prior distribution as follows:

$$p\left({\mathbf{\theta }}_r\right)\stackrel{D}{=}\text{N}\left({\mathbf{\theta }}_{r0},{\mathbf{\Sigma }}_{r0}\right),$$ (13)

where θ_r0 and ${\mathrm{\Sigma }}_{r0}$ are prespecified hyperparameters.

The Bayesian estimate of θ can be obtained through sampling from p(θ|y_obs, Z, X). Owing to the existence of nonresponses, this posterior distribution involves a high-dimensional integral and is therefore intractable. With the use of a data augmentation technique (Tanner and Wong 1987), we work on the joint posterior distribution p(θ, y_mis|y_obs, r, Z, X). MCMC methods, such as the Gibbs sampler and the Metropolis–Hastings algorithm, are used iteratively to sample (I) y_mis from p(y_mis|θ, y_obs, r, Z, X), (II) θ_y from p(θ_y|y_mis, y_obs, Z, X), and (III) θ_r from p(θ_r|y_mis, y_obs, r, Z, X). The conditional distributions and technical details are provided in Appendix C. The computer program is written in the R language with the aid of RcppArmadillo package (Eddelbuettel and Sanderson 2014) for speeding up loops in the code, and the main functions are summarized in the R package “BSOINN.”

4. Simulation Study

In this section, two simulations are conducted to evaluate the empirical performance of the proposed method. In Simulation 1, we assess the Bayesian estimation of the BSOI regression with nonignorable, ignorable, and fully observable data. In Simulation 2, we further consider several numerical studies that evaluate effectiveness of the instrumental variable in improving the model identification and estimation of our proposed method.

4.1. Simulation 1

We consider 2D V₁ × V₂ imaging data with V₁ = V₂ = 300, resulting in a X_i with a length of V = 90,000. The data are simulated from the following model:

$$y_i={\int }_{\mathcal{V}}{X}_i(v)\beta (v)dv+{\gamma }_1{z}_{i1}+{\gamma }_2{z}_{i2}+{\gamma }_3{u}_i+{\delta }_i$$ (14)

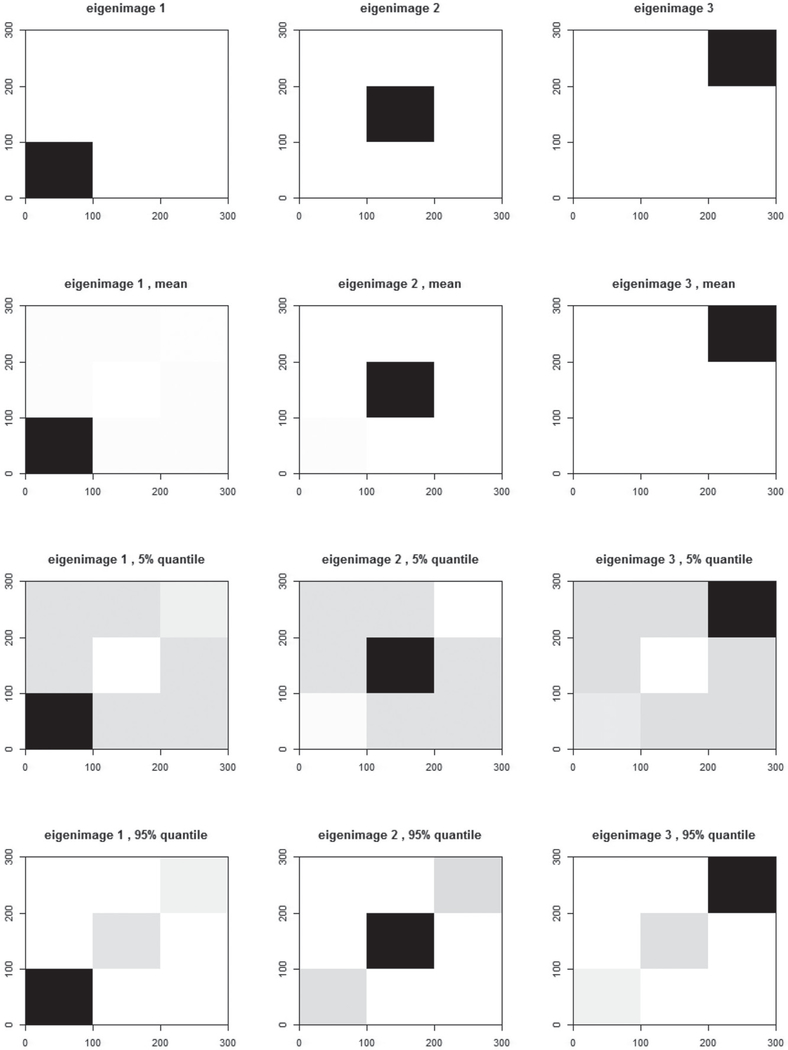
with $X_i(v)={\sum }_{k=1}^3{\xi }_{ik}{\psi }_k(v)$ and $\beta (v)={\sum }_{k=1}^3{\beta }_k{\psi }_k(v)$, where ξ_ik ~ N(0, 0.5^k−1), β₁ = 0.5, β₂ = 1, β₃ = −1, γ₁ = 1.5, γ₂ = −1, γ₃ = 0.5, and δ_i ~ N(0, 1). The covariates z_i1 and z_i2 are independently generated from U(0, 1) and N(0, 1), respectively. Moreover, U(0, 1) denotes the uniform distribution in [0, 1], and u_i denotes a binary instrumental variable with equal probabilities taking the values of 1 and −1. The eigenimages ψ_k are presented in the first row of Figure 2. They can be regarded as two-dimensional grayscale images with pixel intensities on a [0,1] scale, where the black pixels are set as 1 and white pixels are set as 0. Such a method of generating imaging data from eigenimages can also be found in studies conducted by Zipunnikov et al. (2011a, 2011b).

Figure 2.

True (top row), estimated mean (2nd row), 5th pointwise percentile (3rd row), and 95th pointwise percentile (bottom row) grayscale eigenimages in Simulation 1 with the sample size n = 500.

The two missing mechanisms are considered as follows.

• Mechanism 1 (Nonignorable): The missing data are generated on the basis of an exponential tilting model with imaging predictors as follows:

  $$\mathrm{logit}\left({\pi }_i\right)={\int }_{\mathcal{V}}{X}_i(v){\beta }_r(v)dv+{\gamma }_{r1}{z}_{i1}+{\gamma }_{r2}{z}_{i2}+\varphi y_i,$$ (15)

  where ${\beta }_r(v)={\sum }_{k=1}^3{\beta }_{rk}{\psi }_k(v)$, β_r1 = −1, β_r2 = 0.5, β_r3 = 0.5, γ_r1 = −0.7, γ_r2 = −0.7, and ϕ = −1.2. The overall missing proportion is approximately 40%.
• Mechanism 2 (Ignorable): The missing data are generated on the basis of a logistic regression model with imaging predictors as follows:

  $$\mathrm{logit}\left({\pi }_i\right)={\int }_{\mathcal{V}}{X}_i(v){\beta }_r(v)dv+{\gamma }_{r1}{z}_{i1}+{\gamma }_{r2}{z}_{i2},$$ (16)

  where β_r1 = −1, β_r2 = 0.5, β_r3 = 0.5, γ_r1 = −1, and γ_r2 = 0.7. Mechanism 2 is in fact a special case of Mechanism 1, the tilting parameter ϕ of which is set to zero. The overall missing proportion is also approximately 40%.

In the above designs, Mechanism 1 is used to evaluate whether the proposed method can accurately retrieve the information of nonignorable missingness, whereas Mechanism 2 is employed to investigate the implication of overspecification of a missing data model. Thus, we consider the following models in the data analysis:

• BSOI-NN: BSOI regression (14) and a nonignorable missing model (8) specified as model (15).

• BSOI-IN: BSOI regression (14) and an ignorable missing model (8) specified as model (16).

• BSOI-Full: BSOI regression (14) with fully observed data.

Notably, the BSOI-Full model assumes that the values of the missing observations are known. Thus, it can be considered as an oracle model, and its corresponding estimation results can be considered as a benchmark for comparison.

Regarding the prior distributions in (12) and (13), we set vague prior inputs as follows: α₀ = 0, ${\sigma }_{\alpha 0}^2=10$, β_k0 = 0 ${\sigma }_{{\beta }_{k}0}^2=10$, γ_q0 = 0, ${\sigma }_{{\gamma }_{q}0}^2=10$, and a_σ0 = 9, b_σ0 = 3, θ_r0 = 0, and ${\mathrm{\Sigma }}_{r0}=\text{I}$, where 0 and I denote the zero vector and identity matrices with appropriate dimensions, respectively. We assess the convergence of the MCMC algorithm using three parallel sequences with well-separated starting values. The MCMC algorithm converges within 4000 iterations. Thus, we collect 6000 observations after 4000 burn-in iterations to conduct Bayesian inference.

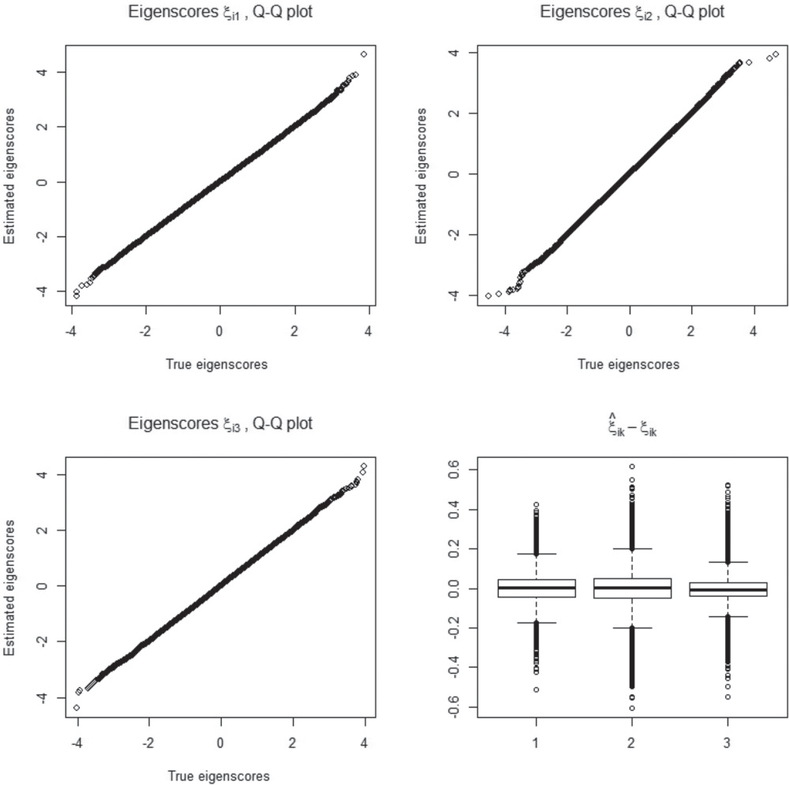
In this simulation, three sample sizes, n = 100, n = 500, and n = 1000, are considered. A total of 100 replicated datasets are generated under each sample size and missing mechanism. We first look at the performance of FPCA on the imaging data. The estimated eigenimages and eigenscores with the moderate sample size n = 500 are depicted in Figures 2 and 3. In Figure 2, the first and second rows from left to right provide the true eigenimages and the means of their estimates, respectively, whereas the last row displays the means and the 5th and 95th percentiles of the estimated eigenimages. The estimated eigenimages are normalized through $({\widehat{\psi }}_k(v)-{\min }_v{\widehat{\psi }}_k(v))/({\max }_v{\widehat{\psi }}_k(v)-{\min }_v{\widehat{\psi }}_k(v))$ to obtain grayscale images with pixel values in the [0,1] interval. As shown in Figure 2, the means of the estimated eigenimages perfectly recover the spatial configuration. The small distortions from the true eigenimages to their 5th and 95th percentiles reflect the good performance of the estimated eigenimages. Figure 3 reports the estimation result of the eigenscores. Both the Q-Q plot and the boxplots show that the estimated eigenscores are very close to their true values.

Figure 3.

Q-Q plots between the true and estimated eigenscores and the boxplots of ${\widehat{\xi }}_{ik}-{\xi }_{ik}$ in Simulation 1 with the sample size n = 500.

To evaluate the finite sample performance of the parameter estimates, we compute the bias (BIAS) and root mean squared error (RMS) between the Bayesian estimates of the unknown parameters and their true population values. Table 1 (upper panel) presents the estimation results obtained from the 100 replicated datasets generated under Mechanism 1. As expected, the estimates under BSOI-Full (oracle case) have excellent performance with small BIAS and RMS values. The estimates under BSOI-NN (true mechanism) are not as good as those of BSOI-Full but are still satisfactory. The estimates under both cases improve when the sample size increases. Meanwhile, the estimates under BSOI-IN (oversimplified mechanism) perform unsatisfactorily with large BIAS and RMS values, indicating that ignoring an nonignorable missing mechanism can lead to seriously biased estimation results.

Table 1.

Bayesian parameter estimates in Simulation 1.

Para	n = 100						n= 500						n= 1000
	BSOI-Full		BSOI-IN		BSOI-NN		BSOI-Full		BSOI-IN		BSOI-NN		BSOI-Full		BSOI-IN		BSOI-NN
	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS
Mechanism 1
α = 0	−0.011	0.183	0.526	0.598	0.041	0.306	−0.007	0.083	−0.509	0.522	−0.012	0.157	−0.009	0.060	0.502	0.508	−0.018	0.117
β1 = 0.5	−0.011	0.213	−0.182	0.297	−0.002	0.226	0.008	0.076	−0.170	0.191	0.009	0.095	0.003	0.055	−0.170	0.180	0.010	0.071
β2 = 1	0.001	0.220	−0.072	0.255	−0.021	0.245	−0.019	0.094	−0.095	0.130	−0.021	0.104	−0.002	0.066	−0.072	0.099	0.004	0.077
β3 = −1	0.046	0.l81	0.254	0.393	0.025	0.322	0.005	0.109	−0.202	0.237	0.013	0.136	−0.001	0.071	0.173	0.191	−0.016	0.092
γ1 = 1.5	0.041	0.324	−0.299	0.557	−0.001	0.468	0.027	0.149	−0.269	0.317	−0.022	0.193	0.007	0.098	−0.283	0.307	0.005	0.135
γ2 = −1	−0.00l	0.099	0.053	0.131	0.001	0.125	0.000	0.045	0.064	0.080	0.009	0.052	−0.002	0.035	0.051	0.064	−0.005	0.039
γ3 = 0.5	− 0.0l4	0.095	−0.095	0.153	−0.026	0.125	0.003	0.038	−0.063	0.084	0.008	0.052	0.001	0.030	−0.068	0.079	0.003	0.038
${\sigma }_{\delta }^2$ = 1	−0.093	0.148	−0.252	0.284	−0.114	0.199	−0.024	0.067	−0.162	0.175	−0.020	0.099	−0.016	0.041	−0.150	0.156	−0.008	0.077
αr = 0.5					−0.128	0.468					−0.057	0.279					−0.030	0.195
βr1 = −1					−0.092	0.413					−0.029	0.163					−0.014	0.125
βr2 = 0.5					−0.058	0.550					0.071	0.314					0.062	0.243
βr3 = 0.5					0.037	0.552					−0.016	0.353					−0.070	0.253
γr1 = −0.7					0.118	0.603					0.094	0.501					0.039	0.350
γr2 = −0.7					0.020	0.423					−0.070	0.293					−0.061	0.235
φ = −1.2					−0.141	0.405					−0.134	0.323					−0.086	0.243
Mechanism 2
α = 0	−0.00l	0.192	0.013	0.287	−0.074	0.349	−0.006	0.087	−0.029	0.120	−0.007	0.168	−0.010	0.059	−0.001	0.087	−0.021	0.104
β1 = 0.5	−0.008	0.164	−0.005	0.212	0.024	0.209	−0.006	0.086	−0.001	0.101	0.015	0.111	0.004	0.055	0.002	0.065	0.009	0.065
β2 = 1	−0.006	0.205	−0.005	0.276	−0.020	0.226	0.000	0.088	−0.011	0.101	−0.017	0.102	−0.002	0.066	−0.001	0.081	−0.004	0.079
β3 = −1	0.018	0.270	0.039	0.306	0.025	0.308	−0.002	0.109	−0.007	0.133	−0.014	0.134	−0.001	0.070	−0.001	0.093	−0.004	0.093
γ1 = 1.5	−0.013	0.327	− 0.040	0.462	−0.019	0.470	0.004	0.144	0.023	0.195	0.039	0.195	0.008	0.097	−0.008	0.127	−0.001	0.129
γ2 = −1	0.034	0.101	0.026	0.154	0.003	0.163	0.002	0.047	0.003	0.060	−0.007	0.062	−0.002	0.035	−0.006	0.044	−0.010	0.045
γ3 = 0.5	0.001	0.105	−0.002	0.157	−0.000	0.157	0.001	0.045	−0.007	0.057	−0.006	0.056	0.001	0.030	−0.001	0.037	−0.001	0.037
${\sigma }_{\delta }^2$ = 1	−0.114	0.170	−0.187	0.241	−0.149	0.222	−0.023	0.063	−0.027	0.084	−0.012	0.083	−0.016	0.041	−0.025	0.055	−0.018	0.053
αr = 0					−0.295	0.448					−0.035	0.222					−0.042	0.155
βr1 = −1					−0.008	0.364					−0.001	0.162					0.005	0.114
βr2 = 0.5					0.241	0.539					0.103	0.261					0.052	0.187
βr3 = 0.5					−0.143	0.556					−0.091	0.271					−0.015	0.198
γr1 = −1.7					0.585	0.841					0.111	0.496					0.086	0.330
γr2 = 0.7					−0.101	0.407					−0.063	0.256					−0.030	0.159
φ = 0					−0.209	0.408					−0.090	0.232					−0.042	0.136

For comparison, the estimation results obtained on the basis of the 100 replicated datasets generated under Mechanism 2 are presented in Table 1 (lower panel). The performance of the estimates under BSOI-Full (oracle case) is excellent, whereas the performances of the estimates under BSOI-IN (true mechanism) and BSOI-NN (overspecified mechanism) are satisfactory and comparable. Thus, the BSOI-NN procedure does not distort the parameter estimates of BSOI regression even when the true missing mechanism is ignorable.

The sensitivity of Bayesian estimates to prior inputs is investigated by introducing certain disturbances to the hyperparameters. For example, we reanalyze the previous analysis by setting ${\sigma }_{\alpha 0}^2=100,{\sigma }_{{\beta }_{k}0}^2=100,{\sigma }_{{\gamma }_{q}0}^2=100$, and some ad hoc disturbances to other hyperparameters. The obtained results are similar and are not reported here.

4.2. Simulation 2

4.2.1. Part 1

In this part, we evaluate the effectiveness of the instrumental variable in improving model identification and estimation. Specifically, we generate datasets using the same setting of model (14) in Simulation 1 except that the instrumental variable u_i is removed. We generate 100 replicated datasets of different sample sizes under Mechanisms 1 and 2 that are specified by (15) and (16). The proposed BSOI-NN model, which consists of a BSOI regression (14)) without u_i and a nonignorable missing model (8) specified as the model of (15), is then applied to analyze the newly generated datasets. The estimation results are compared with those obtained in Simulation 1, which implements the BOSI-NN method on datasets with an instrumental variable (see Table 2). Notably, for the sake of fairness, the mean value of the instrumental variable u_i is intentionally set to 0 in Simulation 1 to ensure that the instrumental variable does not affect the overall missing rate of the responses.

Table 2.

Bayesian parameter estimates in Part 1 of Simulation 2.

	n = 100				n = 500				n = 1000
	Without		With		Without		With		Without		With
Para	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS
Mechanism 1
α = 0	0.124	0.356	0.041	0.306	−0.036	0.180	−0.012	0.157	0.026	0.173	−0.018	0.117
β1 = 0.5	−0.092	0.248	−0.002	0.226	−0.012	0.116	0.009	0.095	−0.018	0.092	0.010	0.071
β2 = 1	0.034	0.259	−0.021	0.245	0.001	0.109	−0.021	0.104	−0.002	0.075	0.004	0.077
β3 = −1	0.039	0.347	0.025	0.322	0.044	0.163	0.013	0.136	0.008	0.104	−0.016	0.092
γ1 = 1.5	−0.094	0.531	−0.001	0.468	−0.013	0.196	−0.022	0.193	−0.003	0.163	0.005	0.135
γ2 = −1			0.001	0.125			0.009	0.052			−0.005	0.039
γ3 = 0.5	0.033	0.141	−0.026	0.125	0.004	0.063	0.008	0.052	0.001	0.043	0.003	0.038
${\sigma }_{\delta }^2$ = 1	−0.149	0.231	−0.114	0.199	−0.019	0.108	−0.020	0.099	−0.012	0.104	−0.008	0.077
αr = 0.5	−0.296	0.527	−0.128	0.468	−0.097	0.288	−0.057	0.279	−0.031	0.207	−0.030	0.195
βr1 = −1	−0.165	0.487	−0.092	0.413	−0.061	0.207	−0.029	0.163	− 0.040	0.137	−0.014	0.125
βr2 = 0.5	−0.261	0.593	−0.058	0.550	−0.056	0.354	0.071	0.314	−0.019	0.363	0.062	0.243
βr3 = 0.5	0.146	0.650	0.037	0.552	0.096	0.375	−0.016	0.353	0.027	0.319	−0.070	0.253
γr1 = −0.7	0.121	0.612	0.118	0.603	−0.054	0.521	0.094	0.501	−0.091	0.521	0.039	0.350
γr2 = −0.7	0.212	0.445	0.020	0.423	0.063	0.357	−0.070	0.293	0.019	0.379	−0.061	0.235
φ = -1.2	0.064	0.410	−0.141	0.405	0.030	0.378	−0.134	0.323	0.020	0.413	−0.086	0.243
Mechanism 2
α = 0	−0.212	0.407	−0.074	0.349	−0.169	0.242	−0.007	0.168	−0.132	0.231	−0.021	0.104
β1 = 0.5	0.088	0.229	0.024	0.209	0.047	0.111	0.015	0.111	0.035	0.099	0.009	0.065
β2 = 1	−0.036	0.245	−0.020	0.226	−0.012	0.102	−0.017	0.102	−0.018	0.091	−0.004	0.079
β3 = −1	−0.027	0.347	0.025	0.308	−0.019	0.143	−0.014	0.134	−0.026	0.110	−0.004	0.093
γ1 = 1.5	0.065	0.496	−0.019	0.470	0.093	0.217	0.039	0.195	0.063	0.177	−0.001	0.129
γ2 = −1	−0.052	0.180	0.003	0.163			−0.007	0.062			−0.010	0.045
γ3 = 0.5			−0.000	0.157	−0.032	0.075	−0.006	0.056	−0.030	0.075	−0.001	0.037
${\sigma }_{\delta }^2$ = 1	−0.092	0.235	−0.149	0.222	0.025	0.104	−0.012	0.083	0.044	0.088	−0.018	0.053
αr = 0	− 0.240	0.459	−0.295	0.448	−0.174	0.276	−0.035	0.222	−0.159	0.231	− 0.042	0.155
βr1 = −1	0.145	0.353	−0.008	0.364	0.140	0.250	−0.001	0.162	0.108	0.245	0.005	0.114
βr2 = 0.5	0.413	0.576	0.241	0.539	0.361	0.475	0.103	0.261	0.258	0.474	0.052	0.187
βr3 = 0.5	−0.423	0.694	−0.143	0.556	− 0.340	0.490	−0.091	0.271	−0.269	0.473	−0.015	0.198
γr1 = −1.7	0.655	0.859	0.585	0.841	0.484	0.708	0.111	0.496	0.378	0.653	0.086	0.330
γr2 = 0.7	− 0.407	0.554	−0.101	0.407	−0.317	0.438	−0.063	0.256	−0.253	0.460	−0.030	0.159
φ = 0	− 0.462	0.525	−0.209	0.408	−0.351	0.448	−0.090	0.232	−0.264	0.450	− 0.042	0.136

As shown in Table 2, the estimation with an instrumental variable outperforms that without the instrumental variable. In particular, for the unknown parameters involved in the exponential tilting model, their estimates with an instrumental variable uniformly improve as the sample size increases. However, such improvement is not achieved when the instrumental variable is excluded, and the estimates of several parameters, such as β_r2, γ_r1, γ_r2, and ϕ, have undesirable results as the sample size increases from 500 to 1000. Thus, the instrumental variable facilitates model identification and estimation.

4.2.2. Part 2

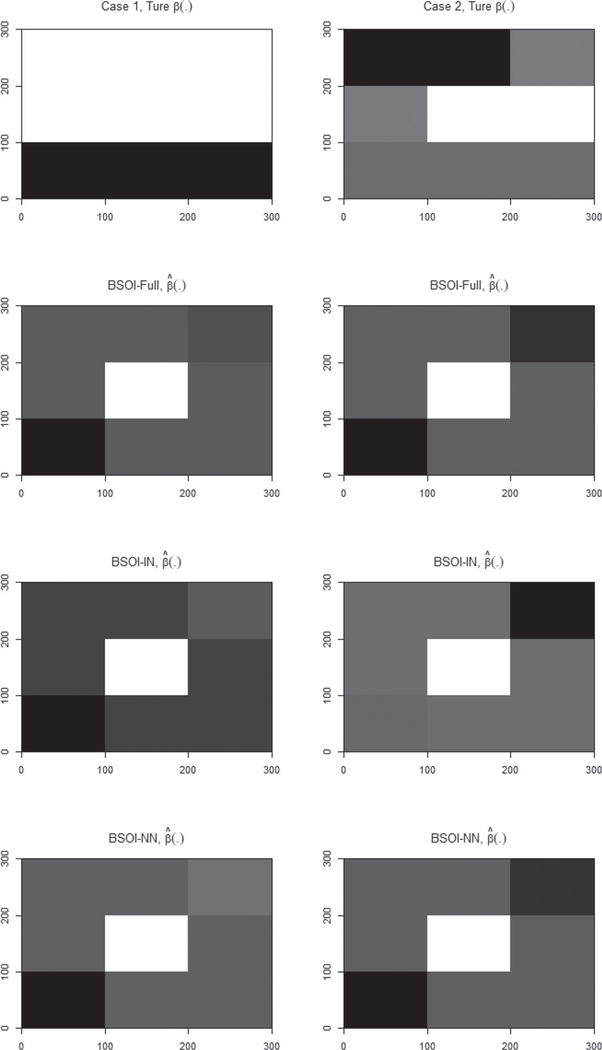
In Simulation 1, we assume that the coefficient image β(·) can be well represented by the eigenimages of X(·). This part aims to evaluate the performance of the proposed method when β(·) is not directly generated from the eigenimages. By fixing all the other settings exactly the same as Mechanism 1 of Simulation 1, we consider two cases of true β(·) as shown in Figure 4, which cannot be directly generated by the eigenimages (see Figure 2) of X(·). We consider a moderate sample size n = 500 in this simulation and generate 100 replicated datasets for each case. The three methods, BSOI-NN, BSOI-IN, and BSOI-Full, are utilized for data analysis. The estimation results are shown in Figure 4 and Table 3, with the estimation accuracy of β(·) being assessed through the following RMS measurement:

$$\text{RMS}=\sqrt{\frac{1}{100}\sum _{l=1}^{100}\left[\frac{1}{V}\sum _{v=1}^V{\{{\widehat{\beta }}_l(v)-\beta (v)\}}^2\right]},$$

where ${\widehat{\beta }}_l(v)$ is the estimate of β(v) at the vth voxel in the lth replication.

Figure 4.

Coefficient image β(·) in Part 2 of Simulation 2, where the first (second) column is for case 1 (case 2).

Table 3.

Bayesian parameter estimates in Part 2 of Simulation 2 with n = 500.

Para	Case 1						Case 2
	BSOI-Full		BSOI-IN		BSOI-NN		BSOI-Full		BSOI-IN		BSOI-NN
	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS	BIAS	RMS
α = 0	−0.012	0.092	0.486	0.503	− 0.040	0.152	−0.006	0.092	0.506	0.521	−0.028	0.168
β(·)		0.275		0.286		0.276		0.264		0.275		0.266
γ1 = 1.5	0.026	0.161	−0.254	0.333	0.048	0.218	0.002	0.165	−0.282	0.344	0.039	0.227
γ2 = −1	0.004	0.044	0.057	0.076	−0.003	0.052	0.004	0.043	0.065	0.080	0.002	0.051
γ3 = 0.5	−0.002	0.045	−0.066	0.085	0.006	0.058	0.003	0.044	−0.071	0.090	0.007	0.062
${\sigma }_{\delta }^2$ = 1	−0.025	0.072	−0.163	0.177	−0.013	0.118	−0.020	0.077	−0.175	0.190	−0.012	0.114
βr1 = −1					−0.081	0.257					−0.119	0.272
βr2 = 0.5					−0.005	0.188					−0.027	0.159
βr3 = 0.5					0.031	0.217					0.009	0.219
γr1 = −1.7					0.011	0.292					0.008	0.263
γr2 = 0.7					0.090	0.485					0.183	0.494
φ = 0					−0.069	0.281					−0.084	0.259
βr1 = −1					−0.121	0.321					−0.129	0.297

As depicted in Figure 4 and Table 3, we find that the BSOI-Full method with full observations still performs the best in both cases on reproducing β(·) and other parameters, and the proposed BSOI-NN method exhibits a comparable performance. In contrast, BSOI-IN method performs unsatisfactorily in both cases. Nonetheless, if β(·) cannot be well represented by the eigenimages, none of the three methods is able to recover β(·) accurately.

The considered scalar-on-image regression inherently requires certain structural assumptions on the coefficient image β(·) because the dimension of imaging covariates is much larger than the sample size (Happ, Greven, and Schmid 2018; Kang, Reich, and Staicu 2018; Wang and Zhu 2017, among others). A common assumption is that β(·) is a linear combination of the leading eigenimages of X(·), which we considered in the proposed BSOI model. This assumption seems plausible because areas with high variation in the imaging observations are likely to be relevant to the response values (Happ, Greven, and Schmid 2018). Recent advancements on scalar-on-image regression assume spatial sparsity and smoothness on voxels of β(·) to identify β(·) (Wang and Zhu 2017; Kang, Reich, and Staicu 2018). However, such voxelwise methods are extremely time consuming, especially for managing the current ultrahigh dimensional brain images. Nevertheless, none of the aforementioned assumptions fits every real situation. The existing literature (Happ, Greven, and Schmid 2018; Kang, Reich, and Staicu 2018) shows that the estimated β(·)s based on different assumptions may vary but should have some common features in the detected regions. Specifically, regions of β(·) estimated to be positive (negative) effects under one assumption tend to be positive (negative) under other assumptions. This suggests a remedy to check the estimation results using a different assumption in the real data analysis. It is worth noting that recovering β(·) accurately under different situations for imaging regression is still an active research area, and we can adopt advanced techniques of estimating β(·) to improve the proposed BSOI-NN method. We acknowledge this limitation in the final discussion and will investigate it further in our future research.

4.2.3. Part 3

This part evaluates the out-of-sample prediction performance of the proposed BSOI-NN method and compares its performance with those of several other models. In addition to BSOI-Full, BSOI-IN, and BSOI-NN, we also consider two scalaron-image regression models that were recently developed for fully observed imaging datasets, namely, the scalar-on-image regression model via the soft-thresholded Gaussian process (STGP, Kang, Reich, and Staicu 2018) and the scalar-on-image regression model via total variation (TV, Wang and Zhu 2017). The STGP method models the coefficient image β(·) through soft-thresholding of a latent Gaussian process, which not only ensures a gradual transition between the zero and nonzero effects of neighboring locations but also provides large support over the class of spatially varying regression coefficient images. In contrast, the TV method assumes that β(·) belongs to the space of bounded total variation, which explicitly accounts for the common piecewise smooth nature of imaging data. The STGP approach has been implemented in the R package “STGP,” and the default settings therein are used in this study. The TV approach has been implemented through MATLAB with suggested settings being applied. The target of considering these two alternatives is to assess how much improvement the proposed method can achieve by considering nonignorable missing responses compared with existing scalar-on-image regression methods that disregard missingness.

We reuse the 100 replicated datasets generated in Simulation 1 for Mechanism 1 with a moderate sample size n = 500. For each replicated dataset, we evenly distribute it into a training subset and a testing subset, ensuring that both subsets exhibit the same missing rate. The training subsets are utilized to fit the imaging regression model, and the testing subsets are used to evaluate the out-of-sample prediction accuracy. For BSOI-Full method, we again substitute the missing responses with their true values for the training subsets and use the full data to fit the model. The prediction performance of BSOI-Full serves as a benchmark in the comparison. For BSOI-IN and BSOI-NN methods, we use the training subsets with nonresponses to fit models. For STGP and TV methods, we discard the samples with missing responses and use the remaining observations to fit models. The parameter estimates obtained from different methods are used to obtain predicted responses. Following Li et al. (2018), we calculate the Pearson correlation between the predicted responses and their true values in testing subsets as the measurement of prediction accuracy. The obtained results for the five models are presented in the first panel of Table 4. As expected, BSOI-Full method with fully observed data exhibits the best prediction accuracy among all methods. The proposed BSOI-NN method also shows a satisfactory performance, whereas the other three methods do not perform very well due to the ignorance of nonignorable nonresponse.

Table 4.

Out-of-sample prediction accuracy in Part 3 of Simulation 2 with n=500.

	BSOI-Full	BSOI-IN	BSOI-NN	STGP	TV
Mechanism 1 of Simulation 1
Mean	0.843	0.833	0.839	0.822	0.832
Median	0.844	0.832	0.840	0.823	0.834
SD	0.018	0.022	0.019	0.025	0.021
Remove imaging covariate, X(·)
Mean	0.626	0.619	0.624
Median	0.624	0.620	0.624
SD	0.042	0.044	0.042
Remove one covariate,Z1
Mean	0.811	0.799	0.809	0.794	0.798
Median	0.812	0.800	0.808	0.797	0.796
SD	0.021	0.026	0.021	0.028	0.023

We further examine whether the use of imaging and scalar covariates lead to better prediction accuracy. We first remove the imaging covariate from the datasets and re-evaluate the prediction accuracy of all proposed methods. Without the imaging covariate, both STGP and TV models reduce to a conventional linear regression model and are not considered in this comparison. The obtained results are reported in the second panel of Table 4, showing that the prediction accuracy of all methods drops significantly without the imaging covariate. We then remove one covariate, z₁, from the datasets and re-evaluate the prediction performance of all methods. The obtained results are shown in the third panel of Table 4, depicting a lower prediction accuracy of all methods when ignoring a scalar covariate. The above analyses confirm the power of using imaging and scalar covariates in terms of prediction.

5. The Alzheimer’s Disease Neuroimaging Initiative Data

The proposed BSOI-NN method was applied to the ADNI dataset as described in the introduction section. The goal of this analysis is to investigate whether the baseline imaging and scalar covariates can accurately predict the RAVLT learning scores at the 36th month. The learning scores are subject to 45.6% nonresponses. The dataset consists of 802 subjects with 223 NC, 391 MCI patients, and 188 AD patients. Among them, 467 are males (mean age, 75.52 ± 6.78), and 335 are females (mean age, 74.78 ± 6.81).

MRI data were collected from each subject. These MRI images include the standard T1-weighted images obtained through volumetric three-dimensional sagittal magnetization prepared rapid gradient-echo or equivalent protocols with varying resolutions. The MRI images were generated across a variety of 1.5 Tesla MRI scanners with individualized protocols. The following parameters form a typical MRI protocol: repetition time = 2400 ms, inversion time = 1000 ms, flip angle = 8°, field of view = 24 cm with a 256×256×170 acquisition matrix in the x-, y- and z-dimensions, which yields a voxel size of 1.25×1.26×1.2 mm³ (Jack et al. 2008). The MRI data were preprocessed with standard steps as follows: Anterior commissure and posterior commissure corrections were performed on original images (McAuliffe et al. 2001). The images were then resampled to the dimension of 256 × 256 × 256. N2 bias field correction was implemented on the reconstructed images to reduce intensity inhomogeneity (Sled, Zijdenbos, and Evans 1998). A hybrid of the brain surface extractor (Shattuck et al. 2001) and brain extraction tool (Smith 2002) was used to address the problems in each method and ensure skull-stripping accuracy. Another intensity inhomogeneity correction was performed following the skull-stripping procedure. Afterward, the cerebellum was removed from the images according to registration by using a manually labeled cerebellum as a standard template. The deformation field obtained during registration was used to generate the 256 × 256 × 256 regional analysis of the volume in normalized space (RAVENS) images. The RAVENS images for different subjects had a unified shape and size in normalized space, and these intensity-based RAVENS maps preserve the local tissue volumes in original MRIs. The brain regions that were expanded during the normalization step will appear darker than their original counterparts because the same amount of tissue was spread over a larger area, and the regions that were decreased in size will appear proportionally brighter (Goldszal et al. 1998). The intensities of different voxels of a RAVENS map represent the local volume density at different locations relative to the density at the same locations of the template (Davatzikos et al. 2001). Finally, the RAVENS images were downsampled to 128 × 128 × 128 resolution for final statistical analysis.

Four domains of covariates that were motivated from the factors identified as important in the existing literature were considered in this analysis. The imaging covariates are the generated RAVENS images. The other covariates of interest include demographic variables, that is, gender (z₁: male = 1, female = 0), age (z₂), educational level (z₃), race (z₄: white = 1, other = 0), and whether the subject was ever married (z₅: never married = 1, ever married = 0); a biomarker variable that indicates the risk caused by variations in the APOE gene, such as APOE4 (z₆); and a diagnostic variable, such as whether the individual is diagnosed as having MCI or AD (z₇: MCI or AD = 1, NC = 0). We selected educational level as the instrumental variable. Specifically, the learning ability of an elderly adult is usually strongly correlated with their educational level, while the missingness of the learning abilities may be conditionally uncorrelated with the educational level conditional on the learning ability. To assess whether the educational level is a good candidate for the instrumental variable, we performed an experiment by including the educational level into the exponential tilting model in implementing the BSOI-NN method. The results suggest that educational level is highly correlated with the learning ability and conditionally independent of the missing probability. Moreover, we tried several other variables, including marital status and APOE4, as the instrumental variable. The experiments suggest that the results are not very sensitive to different choices of instrumental variable, and the experiments based on educational level show stable performance. The BSOI regression with n = 802 subjects and Q = 7 covariates was proposed to conduct the analysis.

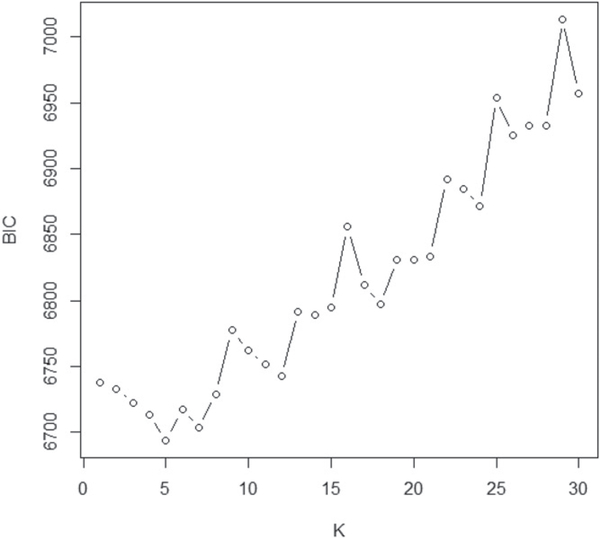
For statistical inference, we first applied FPCA on the imaging observations to obtain the corresponding eigenvalues, eigenimages, and eigenscores. Then, we considered the eigenscores as known covariates in the BSOI regression. The prior inputs were specified in the same manner as those in the simulation studies. Several pilot runs from well-separated starting values were then performed, and the results showed that the MCMC algorithm converged within 10,000 iterations. After the burn-in phase of 10,000 iterations, another 10,000 iterations were generated to conduct the posterior inference. For the determination of K, the number of eigenimages retained, we rotated K from 1 to 100 and applied BIC for selection. Figure 5 displays the first 30 BIC values, and those with K over 30 are large and thus are not reported. The BSOI-NN model with K = 5 eigenimages exhibits the best fit to the ADNI dataset.

Figure 5.

First 30 BIC scores of the BSOI-NN method with different number K of eigenimages in the ADNI data analysis.

Table 5 presents the estimation results obtained from the BSOI-NN and BSOI-IN models. Several predictors, such as educational level and APOE4, were apparently significant for BSOI-NN but nonsignificant for BSOI-IN. However, these variables were previously recognized as important influential factors for the cognitive ability of elderly people, especially educational level (Lee et al. 2003; Lièvre, Alley, and Crimmins 2008), marital status (Helmer et al. 1999; Petersen et al. 2010), and APOE4 status (Bekris et al. 2010; Petersen et al. 2010). Moreover, ϕ is highly significant in the BSOI-NN model, indicating the strong nonignorability of the missing mechanism. These observations confirm that the missing mechanism in this application is nonignorable, and the analysis can be misleading if the nonignorable missing mechanism is disregarded.

Table 5.

Bayesian parameter estimâtes for the BSOI-NN and BSOI-IN models in the analysis of the ADNI dataset.

Covariates	Para	BSOI-NN		BSOI-IN
		Est	SD	Est	SD
Scalar on image regression
eigenimage 1	β1	0.720*	0.158	0.530*	0.137
eigenimage 2	β2	0.668*	0.152	0.330*	0.132
eigenimage 3	β3	0.665*	0.140	0.267*	0.122
eigenimage 4	β4	0.502*	0.151	0.091	0.135
eigenimage 5	β5	0.870*	0.149	0.434*	0.131
gender	γ1	−0.190	0.332	−0.173	0.289
age	γ2	0.066*	0.023	0.031	0.023
educational level	γ3	0.152*	0.044	0.071	0.043
race	γ4	−0.035	0.534	−0.127	0.454
whether ever married	γ5	−2.605*	0.879	−1.168	0.816
APOE4	γ6	−0.482*	0.202	−0.327	0.182
whether have MCI or AD	γ7	−3.332*	0.295	−2.291*	0.245
Exponential tilting model
eigenimage 1	Βr1	0.147	0.204
eigenimage 2	βr2	−0.054	0.176
eigenimage 3	βr3	−0.207	0.162
eigenimage 4	βr4	−0.256	0.150
eigenimage 5	βr5	0.062	0.182
gender	γr1	−0.043	0.431
age	γr2	0.025	0.017
race	γr3	−0.610	0.586
whether ever married	γr4	−0.055	0.822
APOE4	γr5	−0.051	0.241
whether have MCI or AD	γr6	−1.105*	0.510
learning score	φ	−1.287*	0.215

^*Zero is not contained in the 95% credibility interval.

We tested the importance of the instrumental variable by excluding it (i.e., educational level) in the BSOI-NN analysis. Computationally, several MCMC chains did not converge because the instrumental variable was not included, while almost all of the Bayesian parameters estimated became insignificant. Such behavior did not occur for the BSOI-NN model with educational level as the instrumental variable. Moreover, even for converged MCMC chains, the posterior standard deviation of the tilting parameter ϕ was estimated to be 0.429 under the absence of the instrumental variable. See Table 6 for details. Such a standard deviation value is much larger than that of BSOI-NN with the instrumental variable, indicating that ϕ may be unidentifiable. This result is consistent with the findings in Shao and Wang (2016), revealing the importance of the instrumental variable.

Table 6.

Bayesian parameter estimates for the BSOI-NN and BSOI-IN models in the analysis of the ADNI datasetwithoutthe instrumental variable, educational level.

Covariates	Para	BSOI-NN		BSOI-IN
		Est	SD	Est	SD
Scalar on image regression
eigenimage 1	β1	0.653*	0.155	0.497*	0.129
eigenimage 2	β2	0.600*	0.171	0.326*	0.124
eigenimage 3	β3	0.547*	0.160	0.236*	0.115
eigenimage 4	β4	0.408*	0.180	0.071	0.131
eigenimage 5	β5	0.767*	0.182	0.407*	0.130
gender	γ1	−0.050	0.325	−0.132	0.277
age	γ2	0.047*	0.019	0.023	0.020
educational level	γ3
race	γ4	0.050	0.500	−0.121	0.456
whether ever married	γ5	−2.556*	0.897	−1.327	0.802
APOE4	γ6	−0.523	0.198	−0.357	0.174
whether have MCI or AD	γ7	−3.314*	0.379	−2.357*	0.236
Exponential tilting model
eigenimage 1	βr1	0.108	0.168
eigenimage 2	βr2	−0.112	0.179
eigenimage 3	βr3	− 0.245	0.156
eigenimage 4	βr4	−0.282	0.152
eigenimage 5	βr5	−0.060	0.208
gender	γ r1	−0.003	0.373
age	γ r2	0.012	0.019
race	γr3	− 0.483	0.581
whether ever married	γr4	0.118	0.795
APOE4	γr5	−0.051	0.222
whether have MCI or AD	γr6	− 0.648	0.777
learning score	φ	−1.046*	0.429

^*Zero is not contained in the 95% credibility interval

Based on the estimation results, we obtained the following findings. In the exponential tilting model, ϕ is significantly negative, implying that subjects with weak cognitive ability are likely to have future nonresponses. In addition, several elements of scalar covariates and imaging predictors significantly affect the probability of nonresponse. In BSOI regression, the scalar covariates exhibit diverse effects. Education has a positive effect on the learning ability of the elderly people, whereas the status of never married, APOE4, and the clinical outcome of MCI or AD exhibit negative effects. These findings agree with those in the current medical literature (e.g., Helmer et al. 1999; Lee et al. 2003; Bekris et al. 2010). Surprisingly, age has a slightly positive effect on learning ability. One possible explanation is that the ADNI study focused on the population of elderly people, and healthy elderly people tend to possess better cognitive ability and to live longer than unhealthy ones. Nonetheless, further investigation is required to understand this unexpected result.

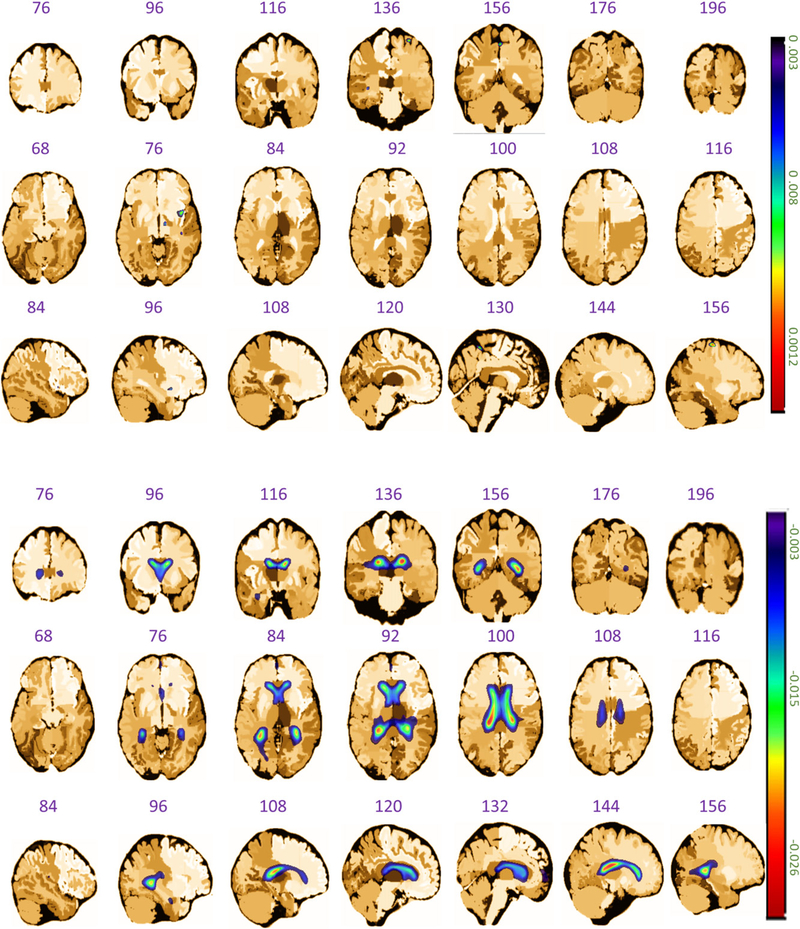
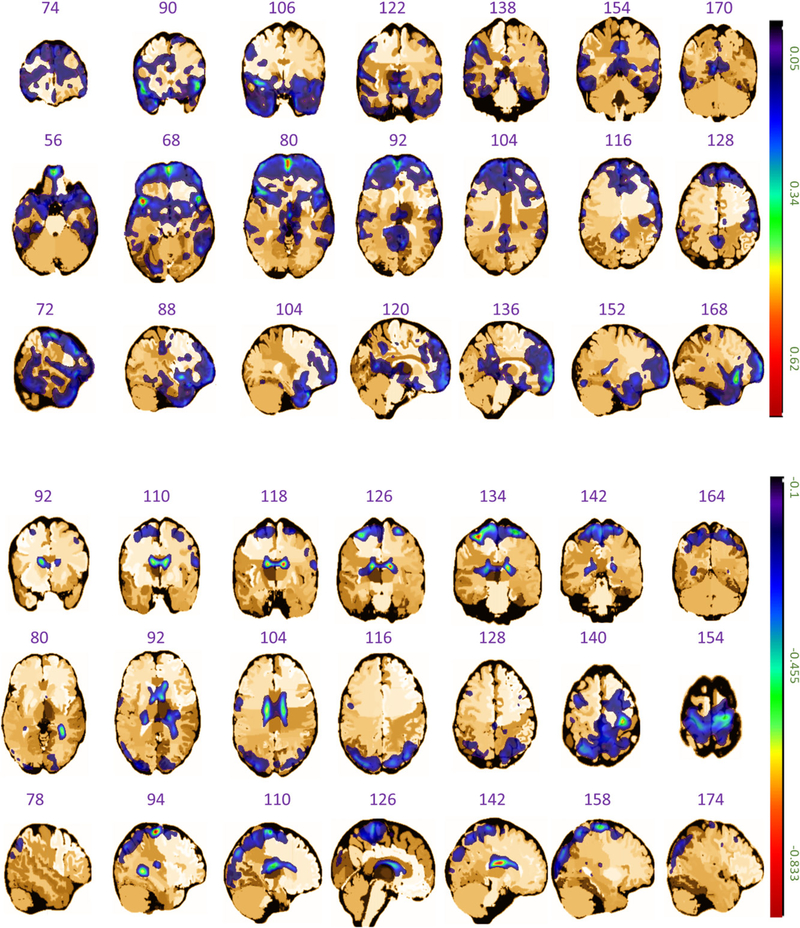
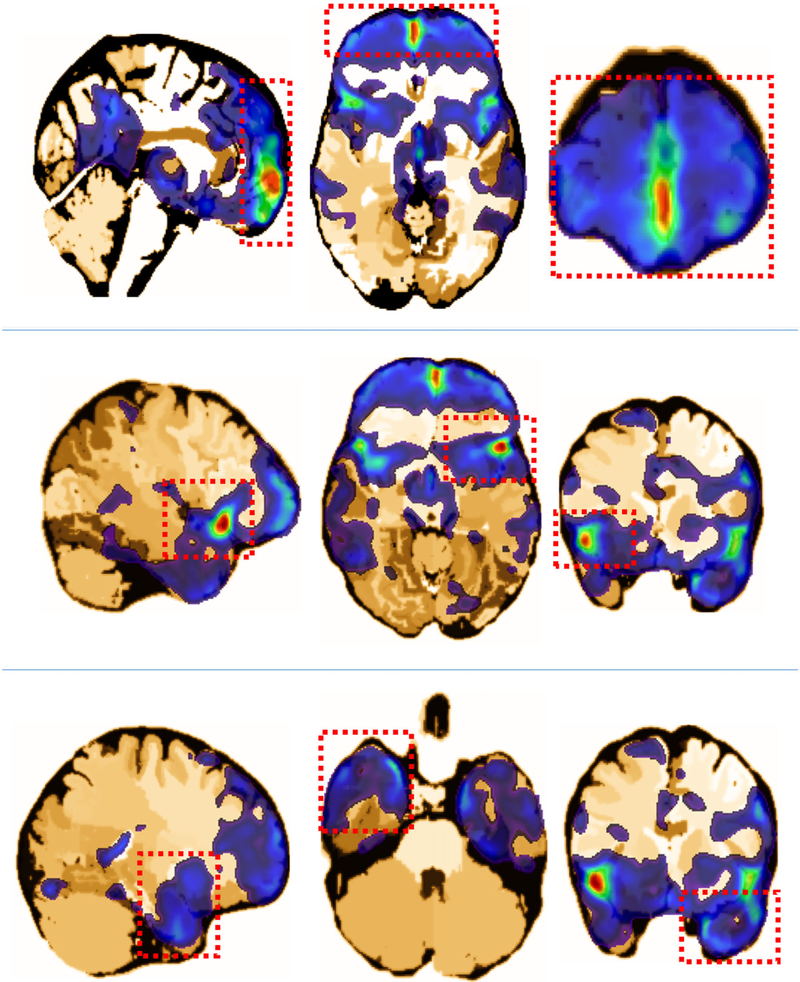
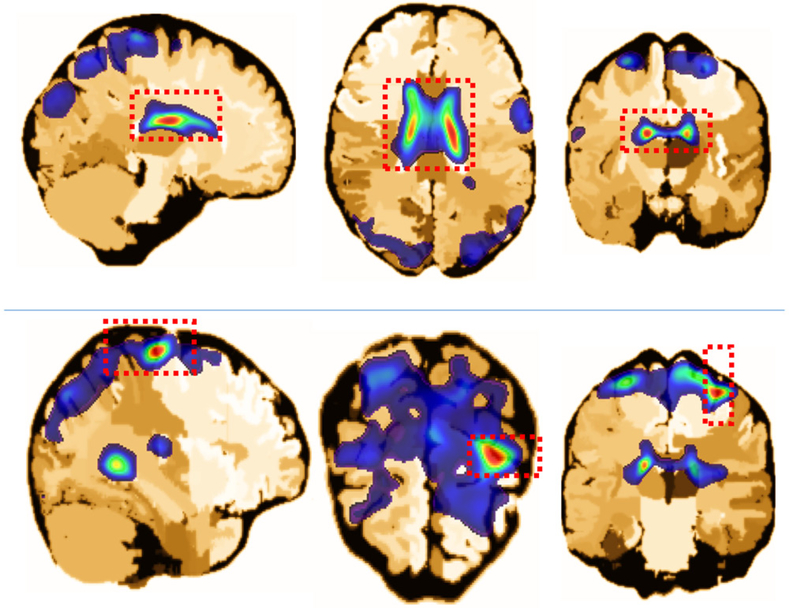
Regarding the imaging predictors, all five of the retained eigenimages exhibit highly significant effects on the learning scores, indicating that the imaging covariate is indeed an important risk factor for the learning ability of elderly people. β(·) was calculated via the Karhumen–Loeve expansion with estimated coefficients β_k and eigenimages (see Figure 6 for the first eigenimage as an example) from FPCA. For clarity, β(·) is depicted in Figure 7 such that its positive part is separated from its negative part, which denotes the positive and negative effects of the corresponding brain regions involved in learning ability, respectively. The results are in good agreement with related results reported in the existing literature. For instance, the positive effects of “frontal gyrus” (Figure 8, the top row), “superior temporal gyrus and insula” (Figure 8, the middle row), and “medial temporal lobe, perirhinal and entorhinal cortex” (Figure 8, the bottom row) are relatively large. This finding is consistent with the results in neuroscience studies, which revealed that MCI and AD are negatively associated with the volume or cortical thickness of the frontal brain regions (Hämäläinen et al. 2007; Whitwell et al. 2007; Im et al. 2008b), superior temporal regions (Harasty et al. 1999), insula regions (Foundas et al. 1997), medial temporal lobe (Visser et al. 2002), and perirhinal and entorhinal cortex (Yilmazer-Hanke and Joachim 1999). In brain regions that exhibit negative effects, the “lateral ventricle and caudate nucleus” (Figure 9, the top row), and “central sulcus” (Figure 9, the bottom row) are the most evident. These results are also supported by previous findings, which indicated that the sulcal span (Im et al. 2008a; Liu et al. 2012) and enlargement of the lateral ventricle (McKhann et al. 1984; Feng et al. 2004; Nestor et al. 2008; Ertekin et al. 2016) are associated with the decline in cognitive functions in AD and MCI patients. Notably, the proposed method reveals a significant negative effect of the volume of caudate nucleus on the learning ability of older people, which agrees with the very recent results in cognitive neurology (Persson et al. 2017, 2018).

Figure 6.

The coronal, axial, and sagittal planes of the estimated first eigenimage in the analysis of ADNI dataset, where the upper three rows represent the positive values and the lower three rows denote the negative values. Note that the sign of an eigenimage is not identifiable in FPCA, and the +/− signs are used here only for separating the regions of eigenimages that exhibit opposite signs.

Figure 7.

The coronal, axial, and sagittal planes of the estimated coefficient image β(·) in the analysis of ADNI dataset, where the upper three rows represent the positive values and the lower three rows denote the negative values.

Figure 8.

The coronal, axial, and sagittal planes of several positive parts of the estimated coefficient image β(·), which are located in the brain regions of the “frontal gyrus” (top row), “superior temporal gyrus and insula”(middle row), and “medial temporal lobe, perirhinal and entorhinal cortex”(bottom row), respectively.

Figure 9.

The coronal, axial, and sagittal planes of several negative parts of the estimated coefficient image β(·), which are located in the brain regions of “lateral ventricle and caudate nucleus”(top row) and “central sulcus”(bottom row), respectively.

In addition to the association analysis on the ADNI data, we also evaluated the out-of-sample prediction performance of the proposed method. We randomly partitioned the ADNI dataset into a training subset with n₁ = 401 and a testing subset with n₂ = 401, ensuring that both subsets exhibit the same nonresponse rate. For BSOI-NN and BSOI-IN methods, we used the training subset with nonresponse to fit model parameters. For STGP and TV methods, we discarded the samples with missing responses in the training subset and applied the remaining observations to fit model parameters. Unlike the simulation study, we did not have the true values of missing responses in the testing subset for validation. As a remedy, for a subject with no learning score at the 36th month, we obtained his/her most recently observed learning score as the true value at the 36th month, such as that from the 30th month, 24th month, or earlier. We repeated the above random partition and analysis for 100 times and computed the mean prediction accuracy (standard deviation) for BSOI-NN, BSOI-IN, STGP, and TV as 0.540 (0.028), 0.533 (0.029), 0.526 (0.030), and 0.527 (0.032), respectively. The results suggest that it is crucial to consider the nonignorable nonresponse in analyzing the ADNI dataset. We also examined whether the medical images are powerful in terms of prediction. We discarded the imaging covariates from the ADNI dataset and repeated the partition procedures and analyses. The prediction accuracy for BSOI-NN and BSOI-IN were computed as 0.508 (0.033) and 0.498 (0.033), respectively, confirming that the medical images are crucial predictors for the learning scores.

When predicting future learning scores, the baseline learning scores are often useful due to within-subject correlation. We therefore further considered the baseline learning scores (z₈) as a covariate in the BSOI model. This setting essentially tests the influence of baseline covariates on the change in the RAVLT learning scores at the 36th month relative to the baseline learning scores. Table 7 presents the estimation results, which are consistent with those of the previous analysis. As expected, elderly people with higher baseline learning scores tend to exhibit better learning ability in the follow-up phase. Notably, although the baseline learning scores exhibit a positive effect on the nonresponse probability, their strong negative mediation effect through the current learning scores on the nonresponse probability implies a negative total effect on the nonresponse probability. To verify this mediation effect, we separately analyzed the exponential tilting model by excluding the current learning scores y but retaining the rest. The effect of the baseline learning scores on the nonresponse probability became negative (−0.145*), which confirms the mediation effect and agrees with the results presented in Figure 1. In terms of out-of-sample prediction, we again repeated the random partition procedures for 100 times and computed the prediction accuracy for BSOI-NN, BSOI-IN, STGP, and TV as 0.615 (0.026), 0.610 (0.025), 0.606 (0.028), and 0.608 (0.031), respectively. These results indicate that baseline learning scores are predictive of future learning scores. It is reasonable to further infer that in addition to the baseline learning scores, the learning scores at other months previous to the 36th month should also be predictive of the learning scores at the 36th month. However, there are considerable missing values for the learning scores at these months, for example, the nonresponse rate at the 24th month is 23.4%. The proposed method can be further improved by allowing for nonignorable missing covariates so that the learning scores before the 36th month can be adjusted in the prediction model. We have acknowledged this limitation in the discussion section and included it in our research agenda.

Table 7.

Bayesian parameter estimates for the BSOI-NN and BSOI-IN models with the considération of the baseline learning scores.

Covariates	Para	BSOI-NN		BSOI-IN
		Est	SD	Est	SD
Scalar on image regression
eigenimage 1	β 1	0.691 *	0.145	0.525*	0.130
eigenimage 2	β 2	0.598*	0.140	0.304*	0.125
eigenimage 3	β 3	0.590*	0.132	0.248*	0.116
eigenimage 4	β 4	0.500*	0.149	0.116	0.125
eigenimage 5	β 5	0.759*	0.145	0.381 *	0.124
gender	γ1	0.026	0.311	0.031	0.270
age	γ2	0.055*	0.018	0.028	0.021
educational level	γ3	0.105*	0.036	0.044	0.038
race	γ4	−0.063	0.466	−0.116	0.423
whether ever married	γ5	−2.153*	0.826	− 0.947	0.785
APOE4	γ6	−0.267	0.193	−0.155	0.172
whether have MCI or AD	γ7	−2.294*	0.318	−1.570*	0.253
baseline learning score	γ8	0.407*	0.050	0.317*	0.045
Exponentialtilting model
eigenimage 1	βr1	0.184	0.205
eigenimage 2	βr2	−0.084	0.195
eigenimage 3	βr3	−0.238	0.166
eigenimage 4	βr4	−0.226	0.188
eigenimage 5	βr5	0.018	0.192
gender	γ r1	0.112	0.404
age	γ r2	0.013	0.017
race	γr3	−0.553	0.608
whether ever married	γr4	0.180	0.845
APOE4	γr5	0.029	0.254
whether have MCI or AD	γr6	−0.873	0.591
baseline learning score	γr7	0.164*	0.082
learning score	φ	−1.257*	0.225

^*Zero is not contained in the 95% credibility interval

Finally, we evaluated the validity of the conducted analyses through two robustness checks. The first one aims at assessing the impact of the model assumption that β(·) can be well represented by the leading eigenimages of X(·). As mentioned in Part 2 of Simulation 2, we may re-estimate β(·) under a different assumption. To this end, we used the Bayesian STGP method proposed by Kang, Reich, and Staicu (2018) to estimate β(·) in the scalar-on-image regression. The STGP method assumes β(·) to be piecewise-smooth, sparse and continuous, and estimates β(·) on the voxel level. However, as mentioned above, this voxelwise method is extremely computationally demanding. Therefore, we applied the STGP procedure to estimate β(·) only in the scalar-on-image regression and utilized the default settings of the STGP procedure in the R package “STGP.” The results based on the STGP method are provided in Appendix D. Two findings are obtained. First, the estimates of the parameters other than β(·) are largely consistent with those in Table 6 under the proposed BSOI-NN method. Second, the regions of β(·) detected by the STGP method largely overlap with those estimated by the proposed BSOI-NN method. Specifically, 81.3% (2375 among 2922 voxels) of the regions in β(·) detected to be positive by the STGP method were also estimated to be positive by the proposed BSOI-NN method, and 69.5% (332 among 478 voxels) of the negative regions detected by the STGP method were also estimated to be negative by the proposed BSOI-NN method. Notably, the estimated β(·) using STGP is highly sparse. Therefore, many regions, such as lateral ventricle, caudate nucleus, and central sulcus, which have been detected by our method and well validated by the existing literature (McKhann et al. 1984; Feng et al. 2004; Im et al. 2008a; Nestor et al. 2008; Liu et al. 2012; Ertekin et al. 2016), were not detected by STGP. These results indicate that the model assumption on β(·) may be plausible and the proposed BSOI model framework is potentially useful for substantive studies in the presence of ultrahigh dimensional imaging data and nonignorable missingness.

The second robustness check excluded the diagnostic status (z₇) from both the main analysis and the analysis with the baseline learning scores. The baseline diagnostic status is partially determined by the baseline RAVLT scores, so it is strongly correlated with the baseline and future RAVLT scores. Thus, the diagnostic status could be a substantial confounding factor in the analysis and may significantly affect the results. The estimation results are consistent with those of the above analyses, and thus are not reported to save space. This may provide further evidence of the validity of the previous analyses.

6. Discussion

We develop a Bayesian method for analyzing BSOI regression with nonignorable nonresponses. Ultrahigh-dimensional imaging data are considered in the regression model to explain clinical outcomes of interest. We propose an exponential tilting model with scalar and imaging predictors to examine their effects on the probability of nonresponse. An instrumental variable is introduced to the missing data model to aid model identifiability and estimation. FPCA for high-dimensional imaging observations is employed to lower the dimensionality of the imaging regression and missing data model to simplify the model representation. An efficient Bayesian method is developed and used with MCMC techniques to conduct statistical inference. The effectiveness of the proposed method is demonstrated through simulation studies. We believe that its application to the ADNI dataset provides new insights into AD risk factors.

The present study has limitations. First, the FPCA method used to reduce model dimensionality relies on the presmoothing of the covariance operator, while the spatial structures of the brain images are disregarded. The combination of Ising and Markov random field priors developed by Goldsmith, Huang, and Crainiceanu (2014) may be applied to accommodate the spatial correlations. However, such priors introduce high computational challenges under ultrahigh-dimensional settings. The feasibility of such development requires further investigation. Second, we assume β(·) to be well presented by the eigenimages of X(·). This may not be the case in certain circumstances. In fact, β(·) may have unknown jumps and edges. We can consider a generalization of the current approach by applying functional penalization methods to directly estimate β(·) (e.g., Crambes, Kneip, and Sarda 2009; Wang and Zhu 2017; Kang, Reich, and Staicu 2018). Third, to better explain the current learning scores, the proposed methodology can be further improved by allowing for nonignorable missing covariates so that the historical learning scores that are subjected to nonignorable missingness can be considered in the regression model. Fourth, longitudinal nonignorable nonresponse has been recognized as an important research problem in the literature (see, e.g., Diggle and Kenward 1994). We may extend the proposed BSOI-NN framework to handle longitudinal nonignorable nonresponse so that the entire trajectory of the learning scores that are subjected to nonignorable missingness can be linked with imaging covariates. Finally, we consider a parametric setting in the BSOI regression and missing mechanism. We may extend the proposed framework to a more sophisticated semiparametric context. Substantial efforts are required for these developments.

Appendix A: Proof for Theorem 1

Suppose that the following two equations hold for all (y, X(v), z*) ∈ S and (u1, u2) : u1 ≠ u2.

$$\begin{gathered} \mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r1}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y1}\right) \\ =\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r2}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y2}\right), \\ \mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r2}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathit{\theta }}_{y2}\right) \\ =\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r1}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathit{\theta }}_{y1}\right). \end{gathered}$$ (A1)

Multiplying the two equations gives

$$\begin{gathered} \mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r1}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y1}\right) \\ \mathrm{Pr}\left(r=0\mid y,X(v),{\mathbf{z}}^{*};{\mathbf{\theta }}_{r2}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathbf{\theta }}_{y2}\right) \\ =\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r2}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y2}\right) \\ \mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r1}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathit{\theta }}_{y1}\right). \end{gathered}$$ (A2)

Together with condition (C1) of Theorem 1, it follows that

$$\begin{gathered} p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y1}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathit{\theta }}_{y2}\right) \\ =p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y2}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathit{\theta }}_{y1}\right) \end{gathered}$$ (A3)

holds for all (y, X(·), z*). Together with condition (C2), we have θ_y1 = θ_y2. Then, we obtain from (A.1) that

$$\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r1}\right)=\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r2}\right)$$

for all (y, X(·), z*). Together with condition (C3), we have θ_r1 = θ_r2, and the identifiability is obtained.

Appendix B: Proof for Proposition 1

(I) Condition (C1) holds, because for all (θr, X(·), z^∗, y) we have

$$\begin{gathered} \mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_r\right) \\ =\frac{1}{1+\exp \left({\alpha }_r+{\int }_{\mathcal{V}}X(v){\beta }_r(v)dv+{\mathit{\gamma }}_r^T{\mathbf{z}}^{*}+{\varphi }_{1}y\right)}>0. \end{gathered}$$

(II) The fact that

$$\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r1}\right)=\mathrm{Pr}\left(r=0\mid y,X(\cdot ),{\mathbf{z}}^{*};{\mathit{\theta }}_{r2}\right),$$

for all(y, X(·), z*) is equivalent to

$$\begin{gathered} {\alpha }_{r1}+{\int }_{\mathcal{V}}X(v){\beta }_{r1}(v)dv+{\mathit{\gamma }}_{r1}^T{\mathbf{z}}^{*}+{\varphi }_{1}y \\ ={\alpha }_{r2}+{\int }_{\mathcal{V}}X(v){\beta }_{r2}(v)dv+{\mathit{\gamma }}_{r2}^T{\mathbf{z}}^{*}+{\varphi }_{2}y, \end{gathered}$$

for all (y, X(·), z*) ⟹

$$\begin{gathered} \left({\alpha }_{r1}-{\alpha }_{r2}\right)+{\int }_{\mathcal{V}}{X}_1(v)\left({\beta }_{r1}(v)-{\beta }_{r2}(v)\right)dv \\ +{\left({\mathit{\gamma }}_{r1}-{\mathit{\gamma }}_{r2}\right)}^T{\mathbf{z}}_1^{*}+\left({\varphi }_1-{\varphi }_2\right)y_1=0, \end{gathered}$$

$$\begin{gathered} \left({\alpha }_{r1}-{\alpha }_{r2}\right)+{\int }_{\mathcal{V}}{X}_1(v)\left({\beta }_{r1}(v)-{\beta }_{r2}(v)\right)dv \\ +{\left({\mathit{\gamma }}_{r1}-{\mathit{\gamma }}_{r2}\right)}^T{\mathbf{z}}_1^{*}+\left({\varphi }_1-{\varphi }_2\right)y_2=0, \end{gathered}$$

$$\begin{gathered} \left({\alpha }_{r1}-{\alpha }_{r2}\right)+{\int }_{\mathcal{V}}{X}_2(v)\left({\beta }_{r1}(v)-{\beta }_{r2}(v)\right)dv \\ +{\left({\mathit{\gamma }}_{r1}-{\mathit{\gamma }}_{r2}\right)}^T{\mathbf{z}}_1^{*}+\left({\varphi }_1-{\varphi }_2\right)y_1=0, \end{gathered}$$

$$\begin{gathered} \left({\alpha }_{r1}-{\alpha }_{r2}\right)+{\int }_{\mathcal{V}}{X}_1(v)\left({\beta }_{r1}(v)-{\beta }_{r2}(v)\right)dv \\ +{\left({\mathit{\gamma }}_{r1}-{\mathit{\gamma }}_{r2}\right)}^T{\mathbf{z}}_2^{*}+\left({\varphi }_1-{\varphi }_2\right)y_1=0, \end{gathered}$$

for all $\left(y_1,y_2,X_1(\cdot ),X_2(\cdot ),{\mathbf{z}}_1^{*},{\mathbf{z}}_2^{*}\right)\Rightarrow$

$$\left({\varphi }_1-{\varphi }_2\right)\left(y_1-y_2\right)=0,$$

$${\left({\mathit{\gamma }}_{r1}-{\mathit{\gamma }}_{r2}\right)}^T\left({\mathbf{z}}_1^{*}-{\mathbf{z}}_2^{*}\right)=0,$$

$${\int }_{\mathcal{V}}\left(X_1(v)-X_2(v)\right)\left({\beta }_{r1}(v)-{\beta }_{r2}(v)\right)dv=0,$$

for all $\left(y_1,y_2,X_1(\cdot ),X_2(\cdot ),{\mathbf{z}}_1^{*},{\mathbf{z}}_2^{*}\right)$. It follows that ϕ₁ − ϕ₂ = 0 because y1 ≠ y2, and

$$\begin{gathered} {\mathit{\gamma }}_{r1}-{\mathit{\gamma }}_{r2}\in \mathcal{L}{\left({\mathcal{Z}}^{*},\mathcal{D}\left({\mathit{\gamma }}_r\right);{ℝ}^{Q-1}\right)}^{\perp }, \\ {\beta }_{r1}(\cdot )-{\beta }_{r2}(\cdot )\in \mathcal{L}{\left(\mathcal{X},\mathcal{D}\left({\beta }_r(\cdot )\right);L_2(\mathcal{V})\right)}^{\perp }. \end{gathered}$$

Given $\mathcal{L}{\left(\mathcal{X},\mathcal{D}\left({\beta }_r(\cdot )\right);L_2(\mathcal{V})\right)}^{\perp }$ and $\mathcal{L}{\left({\mathcal{Z}}^{*},\mathcal{D}\left({\mathit{\gamma }}_r\right);{ℝ}^{Q-1}\right)}^{\perp }$ are both zero, we have ϕ1 = ϕ2, γ _r1 = γ _r2, and β_r1(·) = β_r2(·). Finally, we have α_r1 − α_r2 = 0.

(III) From the normal distribution assumption of random noise δi, the fact that

$$\begin{gathered} p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y1}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathit{\theta }}_{y2}\right) \\ \equiv p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_1;{\mathit{\theta }}_{y2}\right)p\left(y\mid X(\cdot ),{\mathbf{z}}^{*},u_2;{\mathit{\theta }}_{y1}\right), \end{gathered}$$

for all $\left(y,X(\cdot ),{\mathbf{z}}^{*},u_1,u_2\right)$ is equivalent to

$$\frac{\begin{array}{l}{\left(y-{\alpha }_1-{\int }_{\mathcal{V}}X(v){\beta }_1(v)dv-{\gamma }_{\ast 1}^T{\mathbf{z}}^{*}-{\gamma }_{u1}^T{u}_1\right)}^2\\ -{\left(y-{\alpha }_1-{\int }_{\mathcal{V}}X(v){\beta }_1(v)dv-{\gamma }_{\ast 1}^T{\mathbf{z}}^{\ast }-{\gamma }_{u1}^T{u}_2\right)}^2\end{array}}{2{\sigma }_1}$$

$$=\frac{\begin{array}{l}{\left(y-{\alpha }_2-{\int }_{\mathcal{V}}X(v){\beta }_2(v)dv-{\gamma }_{\ast 2}^T{\mathbf{z}}^{\ast }-{\gamma }_{u2}^T{u}_1\right)}^2\\ -{\left(y-{\alpha }_2-{\int }_{\mathcal{V}}X(v){\beta }_2(v)dv-{\gamma }_{\ast 2}^T{\mathbf{z}}^{\ast }-{\gamma }_{u2}^T{u}_2\right)}^2\end{array}}{2{\sigma }_2},$$

for all $\left(y,X(\cdot ),{\mathbf{z}}^{\ast },u_1,u_2\right)\Rightarrow$

$$\begin{gathered} \frac{1}{{\sigma }_1}[{\mathit{\gamma }}_{u1}({\mathit{\gamma }}_{u1}{u}_1+{\mathit{\gamma }}_{u1}{u}_2-2y \\ +2{\alpha }_1+2{\int }_{\mathcal{V}}X(v){\beta }_1(v)dv+2{\mathit{\gamma }}_{\ast 1}{\mathbf{z}}^{*})] \\ =\frac{1}{{\sigma }_2}[{\mathit{\gamma }}_{u2}({\mathit{\gamma }}_{u2}{u}_1+{\mathit{\gamma }}_{u2}{u}_2-2y+2{\alpha }_2 \\ +2{\int }_{\mathcal{V}}X(v){\beta }_2(v)dv+2{\mathit{\gamma }}_{*}2{\mathbf{z}}^{*})], \end{gathered}$$

for all (y, X(·), z*, u1, u2). Similar to the proof of (II), we have γ_u1/σ₁ = γ_u2/σ₂, β₁(·) = β₂(·), γ_*1 = γ_*2, γ_u1 = γ_u2, α₁ = α₂ using the fact that |γ_u1|/σ₁ ≥ ϵ/σ₁ > 0, which completes the proof.

Note that in this proposition the scalar u can be generalized to multidimensional in the model setting. Proof will be similar if we choose u₁ = u₁e_j, u₂ = u₂e_j to replace u₁, u₂ in the above proof, where e_j, j = 1, 2, …, d_u, are the basis of the space $\mathcal{U}$.

Appendix C: Full Conditional Distributions

Let β = (β₁, …, β_K)^T, ξi = (ξ_i1, …, ξ_iK)^T, and a vector a_(−k) denote _{a sub-vector of} a excluding the kth element.

(I) The conditional distributions of unknown parameters in θy are given as follows:

$$p(\alpha \mid \cdot )\stackrel{D}{=}\text{N}\left({\mathrm{\Sigma }}_{\alpha }[{\alpha }_0/{\sigma }_{\alpha 0}^2+\sum _{i=1}^n\left(y_i-{\mathit{\gamma }}^T{\mathbf{z}}_i-{\mathit{\beta }}^T{\mathit{\xi }}_i\right)/{\sigma }^2],{\mathrm{\Sigma }}_{\alpha }\right),$$

$$\begin{gathered} p({\beta }_k\mid \cdot )\stackrel{D}{=}\text{N}({\mathrm{\Sigma }}_{{\beta }_k}[{\beta }_{k0}/{\sigma }_{{\beta }_{k}0}^2+\sum _{i=1}^n(y_i-\alpha -{\mathit{\gamma }}^T{\mathbf{z}}_i-{\mathit{\beta }}_{(-k)}^T{\mathit{\xi }}_{i(-k)}) \\ {\xi }_{ik}/{\sigma }^2],{\mathrm{\Sigma }}_{\beta k}),k=1,\dots ,K, \end{gathered}$$

$$\begin{gathered} p\left({\mathit{\gamma }}_q\mid \cdot \right)\stackrel{D}{=}\text{N}({\mathrm{\Sigma }}_{{\mathit{\gamma }}_q}[{\mathit{\gamma }}_{q0}/{\sigma }_{{\mathit{\gamma }}_{q}0}^2+\sum _{i=1}^n(y_i-\alpha -{\mathit{\gamma }}_{(-q)}^T{\mathbf{z}}_{i(-q)}-{\mathit{\beta }}^T{\mathit{\xi }}_i) \\ {z}_{iq}/{\sigma }^2],{\mathrm{\Sigma }}_{{\mathit{\gamma }}_q}),q=1,\dots ,Q, \end{gathered}$$

$$p\left({\sigma }^{-2}\mid \cdot \right)\stackrel{D}{=}\mathrm{Gamma}\left(a_{\sigma 0}+n/2,b_{\sigma }\right),$$

where ${\mathrm{\Sigma }}_{\alpha }={(n/{\sigma }^2+1/{\sigma }_{\alpha 0}^2)}^{-1}$, ${\mathrm{\Sigma }}_{{\beta }_k}={({\sum }_{i=1}^n{\xi }_{ik}^2/{\sigma }^2+1/{\sigma }_{{\beta }_{k}0}^2)}^{-1}$, ${\mathrm{\Sigma }}_{{\gamma }_q}={({\sum }_{i=1}^n{z}_{iq}^2/{\sigma }^2+1/{\sigma }_{{\gamma }_{q}0}^2)}^{-1}$ and $b_{\sigma }=b_{\sigma 0}+\sum _{i=1}^n(y_i-\alpha -{{\mathit{\gamma }}^T{\mathbf{z}}_i-{\mathit{\beta }}^T{\mathit{\xi }}_i)}^2/2$.

(II) The conditional distribution of y_mis,i is

$$p(y_{\text{mis},i}\mid \cdot )\propto \frac{\begin{array}{l}\exp \{-{(y_{\mathrm{mis}}-\alpha -{\mathit{\gamma }}^T{\mathbf{z}}_{\text{mis},i}-{\mathit{\beta }}^T{\xi }_{\text{mis},i})}^2/2{\sigma }_{\delta }^2\\ +r_i({\alpha }_r+{\mathit{\gamma }}_r^T{\mathbf{z}}_{\text{mis},i}^{*}+{\mathit{\beta }}_r^T{\xi }_{\text{mis},i}+\varphi y_{\text{mis},i})\}\end{array}}{1+\exp ({\alpha }_r+{\mathit{\gamma }}_r^T{\mathbf{z}}_{\text{mis},i}^{*}+{\mathit{\beta }}_r^T{\xi }_{\text{mis},i}+\varphi y_{\text{mis},i})/},$$

where ${\mathbf{z}}_{\text{mis},i}^{*}$ is the covariate vector excluding the instrumental variable and corresponding to the subject with the missing response.

The above conditional distribution is not in a closed form. We propose the use of the Metropolis–Hastings algorithm to sample from it. At the jth iteration with a current value $y_{\text{mis},i}^{(j)}$, a new candidate value y_mis,i is generated from the proposed distribution $\text{N}(y_{\text{mis},i}^{(j)},{\sigma }_{y_{\text{mis}}}^2{\mathrm{\Sigma }}_{y_{\text{mis}},i})$, where

$${\mathrm{\Sigma }}_{y_{\text{mis}},i}^{-1}={\sigma }^{-2}+\frac{\exp ({\alpha }_r+{\mathit{\gamma }}_r^T{\mathbf{z}}_i^{*}+{\mathit{\beta }}_r^T{\xi }_i)}{{(1+\exp ({\alpha }_r+{\mathit{\gamma }}_r^T{\mathbf{z}}_i^{*}+{\mathit{\beta }}_r^T{\xi }_i))}^2}{\varphi }^2.$$

The new candidate value is accepted according to the following probability:

$$\min \left[1,\frac{p(y_{\text{mis},i}\mid \cdot )}{p(y_{\text{mis},i}^{(j)}\mid \cdot )}\right].$$

The variance of ${\sigma }_{y_{\mathrm{mis}}}^2$ is chosen such that the average acceptance rate is approximately 0.25 (Gelman, Roberts, and Gilks 1996).

(III) The conditional distribution of the unknown parameter vector θr is given as follows:

$$p({\mathit{\theta }}_r)\propto \frac{\begin{array}{l}\exp \{{\sum }_{i=1}^n{r}_i({\alpha }_r+{\mathit{\gamma }}_r^T{\mathbf{z}}_{\text{mis},i}^{*}+{\beta }_r^T{\xi }_{\text{mis},i}+\varphi y_{\text{mis},i})\\ -\frac{1}{2}{({\mathit{\theta }}_r-{\mathit{\theta }}_{r0})}^T{\mathrm{\Sigma }}_{r0}^{-1}(\phi -{\phi }_0)\}\end{array}}{{\prod }_{i=1}^n\{1+\exp ({\alpha }_r+{\mathit{\gamma }}_r^T{\mathbf{z}}_{\text{mis},i}^{*}+{\beta }_r^T{\xi }_{\text{mis},i}+\varphi y_{\text{mis},i})\}}.$$

This distribution is also not in a closed form. We again use the Metropolis–Hastings algorithm to sample from it. The proposed distribution is chosen as $\text{N}(0,{\sigma }_r^2{\mathrm{\Sigma }}_r)$, where

$${\mathrm{\Sigma }}_r^{-1}={\mathrm{\Sigma }}_{r0}^{-1}+\frac{1}{4}\sum _{i=1}^n{\text{e}}_i{\text{e}}_i^T,$$

in which ${\mathbf{e}}_i={(1,{\mathbf{z}}_{\text{mis},i}^{*\top },{\xi }_{\text{mis},i}^T)}^T$, and ${\sigma }_r^2$ is chosen to appropriately control the acceptance rate.

Appendix D: Results of Robustness Check 1

Table D1.

Bayesian parameter estimates of the BSOI-NN model with the STGP technique for estimating β(·) in the analysis of the ADNI dataset.

		BSOI-NN-STGP
Covariates	Para	Est	SD
Scalar on image regression
Imaging covariate	β(·)	Sparse
Gender	γ1	−0.253	0.266
Age	γ2	0.017	0.019
Educational level	γ3	0.109*	0.044
Race	γ4	0.024	0.479
Whether ever married	γ5	−1.554*	0.728
APOE4	γ6	−0.663*	0.207
Whether have MCI or AD	γ7	−3.490*	0.461
Exponential tilting model
Eigenimage 1	βr1	−0.039	.318
Eigenimage 2	βr2	−0.002	0.018
Eigenimage 3	βr3	−0.374	0.494
Eigenimage 4	βr4	0.547	0.805
Eigenimage 5	βr5	−0.060	0.214
Gender	γr1	−0.278	0.685
Age	γr2	−0.105	0.152
Race	γr3	−0.273	0.173
Whether ever married	γr4	−0.402*	0.126
APOE4	γr5	−0.475*	0.135
Whether have MCI or AD	γr6	−0.357*	0.137
Learning score	φ	−0.891*	0.306

^*Zero is not contained in the 95% credibility interval