Modeling airborne pathogen transport and transmission risks of SARS-CoV-2

Abstract

An integrated modeling approach has been developed to better understand the relative impacts of different expiratory and environmental factors on airborne pathogen transport and transmission, motivated by the recent COVID-19 pandemic. Computational fluid dynamics (CFD) modeling was used to simulate spatial-temporal aerosol concentrations and quantified risks of exposure as a function of separation distance, exposure duration, environmental conditions (e.g., airflow/ventilation), and face coverings. The CFD results were combined with infectivity models to determine probability of infection, which is a function of the spatial-temporal aerosol concentrations, viral load, infectivity rate, viral viability, lung-deposition probability, and inhalation rate. Uncertainty distributions were determined for these parameters from the literature. Probabilistic analyses were performed to determine cumulative distributions of infection probabilities and to determine the most important parameters impacting transmission. This modeling approach has relevance to both pathogen and pollutant dispersion from expelled aerosol plumes.

1. Introduction

In ~March 2020, social distancing was introduced throughout the United States to mitigate transmission of the SARS-CoV-2 virus, which causes COVID-19. Six feet (~2 m) was proposed as a safe separation distance to prevent the spread of COVID-19. The basis for six feet of separation stems from early studies [1], which determined that larger respiratory droplets (> ~100µm) that may carry infectious pathogens are likely to “fall out” due to gravity within ~1 – 2 m. However, more recent studies of COVID-19 suggest that smaller respiratory droplets (~ 5µm or less) can remain airborne for long periods, and SARS-CoV-2 can remain viable in these smaller aerosolized droplets for up to several hours [2,3]. In addition, these smaller droplets have been identified as a significant contributor to infectious aerosols [4,5]. Fig. 1 illustrates the potential airborne transmission pathways from expelled respiratory droplets.

Fig. 1.

Potential airborne transmission from respiratory droplets and aerosols.

Several COVID-19 outbreaks including a restaurant in Guangzhou, China [6], a call center in South Korea [7], and a choir practice in the state of Washington [8,9] also indicate a strong potential for airborne transmission of COVID-19. Fomite transmission can also occur through contact of contaminated surfaces, but this work focuses on transmission via inhalation of expelled aerosols during coughing/sneezing and breathing/talking and the impact of environmental factors.

1.1. Physics of expiratory events and aerosol generation

1.1.1. Coughs and sneezes

Expiratory events such as coughing and sneezing can yield thousands of small respiratory droplets ranging in size from ~1 – 1000µm that are expelled from the nose and mouth at high velocities [10], [11], [12]. During a sneeze, respiratory droplets are expelled at velocities over 20 m/s for brief periods typically lasting up to 0.25 s [12]. During this time, ~40,000 droplets (~3000 for a cough) are propelled forward together with the bulk motion of the exhaled air (~0.5 – 1.5 L). The peak velocity for coughs is ~10 – 20 m/s [11], and even higher for sneezing [14]. Assuming a mouth opening of ~4 cm², the peak Reynolds number is ~10,000 for coughing and ~40,000 for sneezing.

Previous studies have shown that expelled respiratory droplets can travel as far as 7 – 8 m (23 – 26 ft) [15]. Xie et al. [16] show that particles larger than ~100µm tend to fall out within 1 – 2 m, consistent with the early findings of Wells and Stone (1934) [1], and that relative humidity and temperature also play a role. Higher temperatures increase the vapor pressure and volatilization of respiratory droplets, while higher relative humidities reduce the amount of volatilization. Their model was compared to experiments and showed good correlation. Smaller particles less than ~10µm were able to stay airborne for significantly longer distances, indicating that coughs and sneezes can expel respiratory droplets that remain aloft for long periods and distances. Feng et al. [17] performed computational fluid dynamics (CFD) simulations of the impact of wind and relative humidity on the transport and dynamics of respiratory droplets and confirmed that microdroplets “follow the airflow streamlines well” and can travel further than 6 feet (1.8 m).

1.1.2. Breathing and talking

Breathing and talking yield fewer and smaller droplets per exhalation than coughing or sneezing [2,4,[18], [19], [20], [21]. Typical droplet sizes exhaled during breathing and talking are on the order of severalµm to several tens ofµm, and several hundred to several thousand droplets per second can be emitted [2,4,19,22]. Talking can yield several times more droplets than breathing, and singing can yield several times more droplets than talking [23]. The exhaled velocity during breathing or talking is on the order of 1 m/s assuming a mouth opening of ~4 cm², an exhaled volume of 0.5 – 1 L, and a breathing rate of 16 breaths/s (3.75 s/breath). This yields a Reynolds number on the order of 1000, which is 30 – 40 times less than the Reynolds number for coughing or sneezing. Thus, the exhaled aerosols during breathing and talking have much lower momentum than coughing or sneezing and do not propagate as far.

However, because the size of the droplets that are emitted during tidal breathing are small, the exhaled aerosol plume can remain suspended for long periods. Thus, despite the lower viral load per exhalation event relative to coughs or sneezes, the persistence of the small aerosolized droplets and continuous nature of breathing and/or talking can increase the potential for transmission, especially in enclosed spaces with low fresh-air exchange.

1.2. Objectives

Aerosol transport during various expiratory events has been simulated in previous studies using computational models to determine pathogen concentrations in various settings [24], [25], [26], [27], [28], [29], [30], [31], [32]. The models range from simple well-mixed compartment models to high-fidelity computational fluid dynamics (CFD) models. Previous CFD models were used to interrogate transient concentration distributions in environments ranging from offices to airplane cabins, and a few have quantified the probability of infection risks. You et al. [33] and Yan et al. [34] used the Wells-Riley equation to determine the probability of infection, which required an assumed quanta generation rate. In this work, we use published values to determine uncertainty distributions of infectivity, lung-deposition fraction, viral load, aerosol viability, and other infection-model parameters for viruses and SARS-CoV-2, when available. The objective of this work was to develop an integrated model that couples CFD-simulated pathogen concentrations in expelled aerosol/vapor plumes with infectivity models to determine the impact of face coverings and different airflow/ventilation conditions on quantified risks of exposure and infection. Probabilistic modeling using the uncertainty distributions was performed to identify most important input parameters that impacted the magnitude and uncertainty in the infection risk. This approach has relevance to both pathogen and pollutant transport of expelled aerosol plumes.

2. Methods

2.1. CFD modelling approach

The general modeling approach in this study is to use CFD models to simulate expelled aerosol plume dispersion and perform comparative studies of exposure risks of expiratory events under various scenarios. Spatial and temporal simulations of the relative concentrations of the expelled pathogen (assumed to be uniformly distributed in the vapor plume) are compared and used to determine risks of exposure and probability of infection. High-fidelity turbulence models are available to simulate time-varying turbulent processes initiated by violent expiratory events (e.g., Large Eddy Simulation (LES) [35]). However, in the current studies, a time-averaged turbulence model was implemented to reduce the computational expense and evaluate a large number of scenarios.

Relative trends in time-integrated concentrations and exposure risks as a function of time and location are assumed to be adequately captured by the time-averaged turbulence models; the objective is to perform comparative risk analyses of different configurations and scenarios rather than to make absolute predictions. In addition, we assume that the relative distribution and concentration of pathogens (droplet nuclei) can be represented by the transient dispersion of the expelled vapor plume. We neglect potential transmission from large droplets, which we assume will fall out due to gravity. Thus, the analyses in this work focuses on small droplets (aerosols) that remain aloft in the air for long periods and have been identified as a significant contributor to airborne transmission [4].

Several modeling and experimental studies have shown that these small particles (a fewµm or smaller) follow the bulk airflow and can be accurately represented by a tracer gas [17,30,31,36]. In the experimental study of Bivolarova et al. [36], particles of three sizes (0.07, 0.7, and 3.5µm) and nitrous oxide tracer gas were generated in a room simultaneously at the same location with various ventilation rates and configurations. Sampling at different locations within the room showed that “tracer gas can be used to evaluate the distribution of aerosol particles in ventilated rooms.” Gupta et al. [30] and Zhang et al. [31] also concluded that small particles behaved like a tracer gas and followed the bulk airflow during testing and modeling of particle transport in an airplane cabin, and Gupta et al. [30] simulated various expiratory events including coughing, talking, and breathing.

Solidworks Flow Simulation is a commercial software package [37] that was used to perform the CFD simulations in this study. Flow Simulation solves the conservation of mass, momentum, energy, and species equations using a discrete numerical finite-volume approach. For turbulent flows, Flow Simulation solves the Favre-Averaged Navier-Stokes (FANS) equations. FANS uses a mass-weighted time-averaging scheme, which can avoid complications associated with the Reynolds Averaged Navier Stokes (RANS) solutions for compressible flows (for incompressible low-Mach flow conditions such as those in the current study, FANS and RANS solutions are similar). Previous studies have demonstrated the use of FANS turbulence models for incompressible flows at various Mach numbers [38], [39], [40]. A k-ε turbulence model is employed using a laminar/turbulent near-wall model with modified wall functions [37]. Meshing is performed using a combination of hexahedral and polyhedral elements, which accommodate curved boundaries between phases or materials. Spatial derivatives are approximated with implicit difference operators of second-order accuracy, and time derivatives are approximated with an implicit Euler scheme of first-order accuracy. The time-step size at each iteration is determined using the Courant–Friedrichs–Lewy convergence criterion, where the smallest cell size and a characteristic velocity of the flow field are used. Additional details of the numerical formulations, conservation equations, constitutive relations, meshing, and solution techniques can be found in the technical reference manual [37]. Flow Simulation is integrated within the 3D CAD package Solidworks, which makes geometry and mesh creation seamless and efficient for various scenarios and configurations.

2.1.1. Boundary conditions

The simulated mouth was 2 cm x 2 cm with a 24° curvature in the vertical direction to account for vertical spread. The thermodynamic boundary conditions that were used for the exhaled vapor and ambient conditions are summarized in Table 1 along with the relevant literature sources for the assumed geometry and parameter values. The simulated cough was assumed to have a triangular exhaled velocity profile, which conforms to typical values reported in the literature for velocity, duration, and total volume of air expelled. The exhaled air is assumed to have a relative humidity of 100% at 37°C (98.6°F). The ambient temperature is assumed to be 20°C with a relative humidity of 50%. The corresponding water vapor mass fractions in the exhaled and ambient air are 0.0390 and 0.00722, respectively. The total pressure of the ambient air is assumed to be 101 kPa. It should be noted that the simulated mass of expelled water vapor per cough assuming 1 L of expelled air at 37°C and 100% relative humidity is about 40 mg while the mass of expelled respiratory droplets assuming 3000 droplets per cough and a droplet size distribution measured by Duguid [18] is about 7 mg. Thus, simulations of exhaled water vapor as a proxy for discrete pathogen-laden respiratory droplets during coughing is likely to yield conservatively high estimates of expelled pathogen concentrations.

Table 1.

Simulated boundary conditions for a cough/sneeze.

Feature	Value	Notes
Mouth
Mouth opening (cm2)	4	Bourouiba et al. [12]
Mouth emittance angle (°)	24	Bourouiba et al. [12]
Exhaled volume (m3)	0.001	McCool [41]; Gupta et al. [42], Park et al. [43]
Duration (s)	0.2	Bourouiba et al. [12], Scharfman et al. [13]
Time of peak velocity (s)	0.05	Gupta et al. [42]; peak observed to occur at ~20 – 25% of total cough duration
Peak velocity (m/s)	25	Velocity assumed to increase linearly to peak and then decrease to zero over remaining duration. Integrated velocity profile yields prescribed exhaled volume of 0.001 m3. Average velocity is consistent with measurements by Kwon et al. [11].
Temperature (°C)	37	Corresponds to 98.6°F; Fevers may elevate temperature, but exhaled temperatures can be lower than core body temperature (Morawska et al. [44]
Relative humidity of expired air (Pv/Psat(T)) (%)	100	Morawska et al. [44]; reported range of 85 – 100%
CO2 content of expired air (% by volume)	4	Dodig et al. [45]
Ambient
Temperature (°C)	20	Assumed
Pressure (kPa)	101.3	Assumed
Relative humidity (%)	50	Assumed

A representative computational domain used to simulate a cough is shown in Fig. 2 . Lateral symmetry is assumed in the z-direction under quiescent conditions or when airflow is in the x-direction such that a vertical symmetry plane is applied at z=0 to reduce the size of the computational domain. When airflow is in the z-direction (crossflow), symmetry is not applied, and the lateral boundary is extended in the z-direction. Vertical symmetry is not assumed due to buoyancy effects. Pressure-opening boundary conditions are applied at all external boundaries to allow for flow into and out of the domain. Air flowing into the domain due to local pressure gradients is assumed to be at ambient conditions with properties shown in Table 1.

Fig. 2.

Illustration of representative mesh used in CFD simulations.

A sensitivity study was performed to evaluate the impact of the size of the computational domain on the simulated parameters. A doubling of the width and height of the domain in the y and z directions with the same mesh resolution yielded nearly identical results in the simulated pressures, temperatures, and vapor concentrations as a smaller domain. The smaller domain with x, y, and z dimensions of 3 m, 0.6 m, and 0.4 m (z=2 m under crossflow conditions), respectively, was therefore used in the comparative simulations for computational expediency. A grid convergence study was also performed and is described in Section 2.1.3.

The number of elements that were generated ranged from ~10⁵ – 10⁶ hexahedral cells (polyhedral cells near the mouth and other facial features or coverings were also generated to represent the curved interface between solid and fluid cells). Element sizes as small as 0.4 mm were generated near the mouth and increased in size further away from the mouth up to a distance 3 m away. The element aspect ratios were ~1 near the mouth, up to ~5 at distances of approximately one meter away from the mouth, and up to ~10 three meters away from the mouth. Point monitors were located along the x-axis at distances of 1 mm, 0.30 (1 ft), 0.91 m (3 ft), 1.8 m (6 ft), and 2.7 m (9 ft) away from the mouth to evaluate cumulative exposure as a function of time, distance, and different environmental conditions. The transient cumulative exposure was calculated as the ratio of the time-integrated concentration at various locations (1, 3, 6, and 9 ft away) to the time-integrated concentration at the mouth (1 mm away). Physical receptors were not simulated to avoid additional uncertainties associated with buoyant thermal plumes, inhalation rates, facial features, motion, etc. The addition of a physical receptor, assuming all features of the receptor (e.g., temperature, geometry, inhalation rate) are kept constant among the simulations, is not expected to change the relative exposure risks in the different ventilation scenarios that were simulated. Nevertheless, future studies should consider the impact of these uncertainties and physical receptors on simulated exposure risks.

2.1.2. Sensitivity studies

Fig. 3 shows a sensitivity study comparing the simulated results of different mouth shapes (square arc vs. circular) and exhaled velocity profiles (step function vs. triangular) following a cough. The circular mouth has a diameter of 0.0226 m, which is slightly larger than the sides of the square-arc mouth (0.02 m) to yield the same total area. All velocity profiles yield the same mass and total volume of exhaled air and water vapor. Results show that slight changes in the shape of the mouth and exhaled velocity profile can yield differences in the overall profile of the transient exhaled water vapor concentrations. The square-shaped velocity profile, while shorter in duration than the triangular velocity profile, yields higher initial sustained velocities resulting in plumes that propagate further. The square-arc shape of the mouth and triangular velocity profile appear to produce a more bimodal plume shape relative to the circular mouth that eventually results in separation and a “pinch-off” of the leading edge (see Section 2.1 for more details). For consistency, the square-arc mouth shape and triangular velocity profile were used as a baseline to simulate coughs under varying environmental and face-covering scenarios.

Fig. 3.

Simulated impact of different mouth shapes and exhaled velocity profiles on expelled water vapor concentration (expressed as relative humidity) after a cough at 1.8 s: (a) square mouth, triangular velocity; (b) circular mouth, triangular velocity; (c) circular mouth, square velocity.

An additional sensitivity study was performed to evaluate the impact of the inclusion of a human head on the simulated water-vapor concentrations. Initial simulations to determine the relative exposure risks under different external wind conditions used only the simulated mouth described above as the boundary condition. Later, interest in the impact of face coverings led to the inclusion of a simulated human head together with the simulated mouth. The inclusion of the head yielded slight differences in the simulated entrainment of air around the mouth, but the overall trend in the results remained similar. Simulations using the head were used only for illustrative purposes to examine transient water-vapor concentrations from expelled plumes during a cough with and without face coverings under quiescent conditions.

Sensitivity studies were also performed to evaluate the relative impact of the relative humidity and temperatures used in the simulations. Results showed that the source temperature of exhaled air (assumed to be 37°C), together with the presence of lower-density exhaled water vapor, was the predominant factor in yielding observed buoyancy effects on the transient plume, which exhibited upward motion following the initial pulse of expelled air and water vapor from the mouth. The relative humidity of the exhaled and ambient air did not have a significant impact on buoyancy due to the relatively low concentration of water vapor in the exhaled air. Previous studies have shown that increased relative humidity can also reduce evaporation of respiratory droplets, leading to larger droplet sizes and increased deposition [17].

2.1.3. CFD model solution verification

A grid convergence study was performed on simulations of a cough under quiescent conditions with different numbers of elements. Fig. 4 shows simulated relative humidities as a function of distance from the source for different times (t = 0.05 s, 0.2 s, and 1 s) following the initiation of a cough for different numbers of elements. Results show that for coarse meshes with a total number of elements less than ~50,000, the results display evidence of numerical dispersion. At 0.05 s, which is the time of peak velocity during the cough, the meshes with greater than ~50,000 elements yielded a sharp profile of the relative humidity, indicating a propagating wave-like pulse while the expelled velocity remained high. The coarser meshes exhibited a more diffuse profile, indicative of numerical dispersion. At 0.2 s, the cough had ended and the simulated relative humidity decreased from 100% near the source to values near 50% (ambient) further away. The simulated relative humidities in the finer meshes decreased to 50% at ~0.7 m, indicating that the expelled plume had not yet reached that location. The simulated relative humidities in the coarser meshes were above 50% at these longer distances, another indication of numerical dispersion. Finally, at a time of 1.0 s, the simulated relative humidities decreased to values just above 50% as the water vapor plume dispersed throughout the domain. All simulations showed a similar trend at 1 s, although beyond ~0.8 m, the coarser meshes yielded slightly higher relative humidity values than the finer meshes. The grid convergence index (GCI) was calculated by selecting the distance the expelled vapor plume propagated along an isopleth of RH=0.5 at 0.05 s for fine (~480K cells), medium (~98K cells), and coarse (~12K cells) meshes. The GCI for the fine and coarse meshes were 0.078 and 0.13, respectively, and the ratio of the GCI accounting for the grid refinement ratio and convergence order was 1.04, indicating that the results were in the asymptotic range [46]. The simulated pressures, temperatures, and velocities were also evaluated as part of the grid convergence study, and results converged to an asymptotic solution at ~100K – 200K cells.

Fig. 4.

Plots of simulated relative humidity as a function of distance at 0.05, 0.2, and 1.0 s following the initiation of a cough for different mesh resolutions.

As a result of these grid convergence studies, the simulations used for the comparative cough scenarios used meshes with at least ~10⁵ elements, which corresponded to element sizes of ~1 mm near the mouth, ~1 cm within ~0.5 m of the mouth, and element sizes of several centimeters or more further away from the mouth, depending on the size of the simulated domain.

CFD simulations were also qualitatively compared to high-speed images of a sneeze (Fig. 5 ). The experimental visualizations revealed that the expelled plume of droplets exhibited a counter-rotating flow pattern near the leading edge as the plume propagated forward (smoke-ring effect), entraining air along the flow path of the plume. The effects of buoyancy were also observed at later times as the plume propagated upward following the initial jet-like pulse from the sneeze.

Fig. 5.

High-speed camera images of a sneeze illustrating salient processes of counter-rotating flow at the leading edge and bifurcation of the droplet plume (Bourouiba et al. [12]).

Simulations of the physical sneeze using the CFD tools and models described in this study were performed. Boundary conditions described in Bourouiba et al. [12] were used (Table 1). Results showed that the simulation matched salient physical features and processes of the physical tests, including air entrainment along the boundary of the propagating vapor plume, counter-rotating flow at the leading edge of the plume, and a subsequent upward rise due to buoyancy. At a time of ~0.3 s, both the simulated and observed propagation of the expelled plume reached a distance of 0.7 – 0.8 m (Fig. 6 ). Finally, the simulations showed a bifurcation of the plume, likely caused by the non-uniform (triangular) velocity profile imposed as a boundary condition, the angular shape of the simulated mouth, and the resulting shear in the velocity profile caused by the counter-rotating flow and entrainment at the leading edge of the plume. The high-speed images in the experiments also show a bifurcation of the droplet plume, which could be due to the difference in particles sizes, with larger particles moving forward at a faster rate, in addition to bulk fluid dynamics. Uncertainties in the position of the tongue, teeth, lips, etc. along with head motion and nasal contributions will likely cause a large vertical spread of ejected droplets during a cough or sneeze, which are not captured in the model.

Fig. 6.

Simulated vapor plume and velocity vectors at 0.3 s during a sneeze under quiescent conditions using the boundary conditions provided in Table 1.

For further validation, the velocity distribution measured by Kwon et al. [11] during a cough was simulated. Data from Kwon et al. [11] was chosen because they used a non-invasive laser-imaging method to measure the velocities induced by a cough from human subjects. The velocities of atomized oil droplets were recorded using particle image velocimetry within a field of view of ~0.25 m (horizontal x-direction) by ~0.18 m (vertical direction) immediately in front of the mouth. Simulations used the same methods and boundary conditions described in Sections 2.1.1 and 2.1.2 except that the mouth angle was increased to 38° to correspond to the values measured by Kwon et al. [11]. Fig. 7 shows the measured and simulated velocity distributions during the peak cough velocity within the measured field of view. Results show that the simulated velocity distribution overpredicts the velocities greater than 6 m/s and underpredicts the velocities in the range of 1 – 6 m/s. However, the general trend in the measured velocity distribution is captured by the simulations and provides further verification of the simulation method.

Fig. 7.

Measured (Kwon et al. [11]) vs. simulated peak velocity distribution during cough.

2.2. Exposure modeling

The risk of exposure to expelled aerosolized pathogens during various expiratory events is modeled by using the simulated spatial and temporal expelled vapor concentrations (recall that airborne pathogens are assumed in this study to be uniformly distributed in the aerosol plume, which is represented by the bulk motion of the expelled vapor plume). The normalized cumulative exposure (exposure risk) at a particular location is defined in this study as the time-integrated concentration at that location divided by the time-integrated concentration at the source (mouth) as a function of time following an expiratory event. The cumulative exposure was determined at several distances from the source as shown in Fig. 8 .

Fig. 8.

Locations used to determine cumulative exposure risks in this study at 1 ft (0.30 m), 3 ft (0.91 m), 6 ft (1.8 m), and 9 ft (2.7 m) away from the source.

For violent expiratory events such as coughing and sneezing, the normalized cumulative exposure is expected to increase rapidly for distances close to the source. At further distances, the exposure risk is expected to decrease due to dilution and dispersion of the expelled aerosol plume. In addition, the exposure risk increases more slowly at further distances since it takes time for the aerosol plume to propagate to longer distances. For talking or breathing, the impacts of time and distance are expected to be even more pronounced since the velocity and number of expelled pathogens are less. Section 3.1.2 provides simulated results of the normalized cumulative exposures following a cough for different external wind conditions.

2.3. Modeling probability of infection

The modeling methods and tools described in the previous sections were used to simulate spatial and temporal vapor concentrations following an expiratory event under varying environmental conditions. This enabled a calculation of the normalized cumulative exposure risks by taking the ratio of time-integrated concentrations at various locations to the time-integrated concentration at the source and plotting those values as a function of time and distance (Section 3.1.2). This section presents a model of infection probability that uses the CFD results together with viral transmission parameters (e.g., viral load, lung deposition fraction, aerosol viability, infectivity).

The infection model in this study assumes an exponential probability density function for infection as a function of dose. Watanabe et al. [47] found that an exponential model fit the dose-response relationship for infection of both mice to the SARS coronavirus (SARS-CoV) and humans to the HCoV-229E coronavirus. The probability of infection, P(x,t), can be expressed as follows for an exponential distribution:

$$P_I(x,t)=1-{\mathrm{e}}^{-rd}$$ (1)

where

• r = infectivity rate or probability that a single pathogen will cause an infection (infection probability/deposited pathogen)

• d = dose (TCID₅₀ or PFU)

• TCID₅₀ = median tissue culture infectious dose

• PFU = plaque forming unit (infectious pathogen)

In this study, the dose, d, is calculated as the amount of pathogen that is deposited into the lungs and can be expressed as follows (adapted from Sze-To et al. [48]):

$$d=\beta \frac{c}{{\rho }_{mucus}}p{\int }_0^t{\rho }_{vapor}(x,t)f\left(t\right)dt$$ (2)

where

• β = pathogen deposition fraction in lungs (pathogen deposited/pathogen inhaled)

• c = viral load (TCID₅₀/mL respiratory fluid)

• ρ_mucus = density of respiratory fluid (kg/m³ or g/mL)

• p = inhalation rate (L/min)

• ρ_vapor = density of exhaled water vapor (kg/m³ or g/L)

• x = distance (m)

• t = time (s or min)

• f(t) = viability function or decay rate of pathogen in aerosol (-)

Eqs. (1) and (2) yield the following expression for the probability of infection:

$$P_I(x,t)=1-\exp \left(-r\beta \frac{c}{{\rho }_{mucus}}p{\int }_0^t{\rho }_{vapor}(x,t)f\left(t\right)dt\right)$$ (3)

The infectivity rate, r, can be expressed in terms of the median infectious dose, d = ID₅₀, required to infect 50% of a population by setting Eq. (1) to 0.5 and solving for r:

$$r=\frac{-\ln \left(0.5\right)}{I{D}_{50}}=\frac{\ln \left(2\right)}{I{D}_{50}}$$ (4)

Although the median infectious dose , ID₅₀, has not been reported for SARS-CoV-2 as of the writing of this report, a range of ID₅₀ (0.6 – 3 TCID₅₀) has been reported in the literature for influenza A aerosols (≤ 3 μm) [49,50] and is used in this study to determine the infectivity rate, which ranges from 0.23 to 1 (infections per TCID₅₀).

The lung deposition fraction, β, is a function of particle size and has been reported in the literature for particle sizes range from 0.015 – 5µm using 67 human subjects ranging in age from 7 – 70 years [51]. The deposition fraction ranged from ~0.3 – 0.9 and exhibited a non-monotonic behavior with the lowest deposition occurring ~0.2 – 0.5µm and increasing deposition for smaller and larger particle sizes.

The viral load, c, for SARS-CoV-2 has been reported in the literature and can vary by orders of magnitude depending the patient, stage of illness, and sample location (e.g., throat, nose). Pan et al. [52] report median values of SARS-CoV-2 viral load from throat and sputum samples of 7.99×10⁴ and 7.52×10⁵ RNA copies/mL, respectively, with individual sample loads ranging from 641 to 1.34×10¹¹ copies/mL. Zou et al. [53] report SARS-CoV-2 viral loads ranging from ~1.5×10⁴ to 1.5×10⁷ in nasal and throat swabs, and Wolfel et al. [54] reported average and maximum SARS-CoV-2 viral loads in sputum of 7×10⁶ copies/mL and 2.35×10⁹ copies/mL, respectively.

It should be noted that viral load can be expressed as viral copies per mL, PFU/mL, or TCID₅₀/mL, where PFU and TCID₅₀ are based on culturable (infectious) viruses. Pantelic et al. [50] and Murphy et al. [55] report the median viral loads for influenza A from seven patients as 5×10⁵ TCID₅₀/mL. The correlation between SARS-CoV-2 viral load and culturable virus is currently unknown [53], but some studies have shown that ~1 TCID₅₀/mL or ~1 PFU/mL correspond to ~1000 viral copies/mL since not all viral copies are culturable [19,56]. Based on these studies, despite the enormous reported range of viral loads, we assume a modest range of infectious viral loads for SARS-CoV-2 between ~10⁵ and 10⁶ TCID₅₀/mL in this study. Assuming ~1000 viral copies/TCID₅₀ [19,56], this corresponds to ~10⁸ – 10⁹ copies/mL, which falls well within the reported ranges for SARS-CoV-2 [52], [53], [54].

The density of respiratory fluid , ρ_mucus, is assumed to be similar to that of liquid water with variations due to dissolved solids (e.g., salts) and oils [13].

The inhalation rate is calculated from reported average values of inhalation volume per breath and breaths per minute during tidal breathing.

The density (or concentration) of exhaled water vapor , ρ_vapor, is obtained from CFD simulations described in earlier sections. The concentrations can vary in space and time depending on the expiratory event and environmental conditions.

The fraction of pathogens that remain viable in aerosol form as a function of time has been measured for SARS-CoV-2 by van Doremalen et al. [3]. We normalized the viability data to the maximum TCID₅₀ per liter of air and assumed that the maximum viability once aerosolized was 10% for comparison to past data reported in Pantelic et al. [50] for influenza A. Fig. 9 shows that the decay of SARS-CoV-2 matches the decay of influenza A. Assuming an initial viability of 10% once aerosolized, the viability of SARS-CoV-2 drops to ~2% after ~2 – 3 h. The expression for the viability of aerosolized SARS-CoV-2 as a function of time, t (hours), that is used in this study is given as follows:

$$f\left(t\right)=0.0897e^{-0.599t}$$ (5)

Fig. 9.

Viability of SARS-CoV-2 from van Doremalen et al. compared to previous data reported in Pantelic et al. [50] for influenza A. Dotted line shows the curve fit of the normalized data from van Doremalen [3] used in this study.

Table 2 provides a summary of the parameters and uncertainty distributions used in the infection model. References for each of the parameter values are also provided.

Table 2.

Summary of parameters and uncertainty distributions used in infection model.

Parameter	Distribution	Min or -St. Dev.	Max or +St. Dev.	Nominal or Mean	Notes
Infectivity rate, r (infection rate/TCID50)	Uniform	0.231	1	0.385	Pantelic et al. [50], Alford et al. [49]; for influenza A calculated as r=-ln(0.5)/ID50. ID50 was assumed to be a uniform distribution from 0.6 – 3 TCID50 (Alford et al. [49]).
Deposition fraction in lungs, β (deposited pathogen/inhaled pathogen)	Uniform	0.26	0.86	0.56	From Rissler et al. [51] for particle sizes between ~0.2 – 5µm from 67 subjects from 7 – 70 years.
Viral load, c (TCID50/mL respiratory fluid)	Uniform	105	106	5×105	Assumed range falls within the range of viral loads reported for SARS-CoV-2 of 103 – 1011 copies/mL [52–54] (see discussion regarding conversion to TCID50/mL). Nominal value is equal to reported viral load by Pantelic et al. [50] and Murphy et al. [55] for influenza A.
Density of respiratory fluid, ρmucus (g/mL)	Uniform	0.9	1.1	1	Density from Scharfman et al. [13]; assumed 10% variation.
Inhalation volume per breath (mL/breath)	Uniform	300	500	400	https://www.physio-pedia.com/Lung_volumes
Breaths per minute	Uniform	12	20	16	https://my.clevelandclinic.org/health/articles/10881-vital-signs
Inhalation rate, p (L-air/min)	Uniform	3.6	10	6.4	Calculated from two rows above
Vapor density from CFD, ρvapor (g/L)	Normal	0.2* (centerline value from CFD)	0.2* (centerline value from CFD)	From CFD	Centerline values of vapor density obtained from CFD as a function of distance and time; relative deviation of 0.2 estimated from average variations at four locations and six times within a diameter of 1 ft about the centerline
Viability function, f(t) (viable inhaled pathogen/inhaled pathogen)	Normal	0.41*(value from Eq. (5))	0.41*(value from Eq. (5))	Eq. (5)	From van Doremalen et al. [3]. The relative deviation of 0.41 was calculated from the +/- standard deviations reported in van Doremalen et al. [3].
Integral of product of ρvapor(x,t) and f(t)	Normal	0.46* (integrated product at time, t)	0.46* (integrated product at time, t)	Integral of ρvapor(x,t)*f(t)	The value of 0.46 is calculated as the propagated relative errors from ρvapor(x,t) and f(t) (i.e., root sum square)

3. Results

3.1. CFD modeling results

3.1.1. Flow visualizations under quiescent conditions

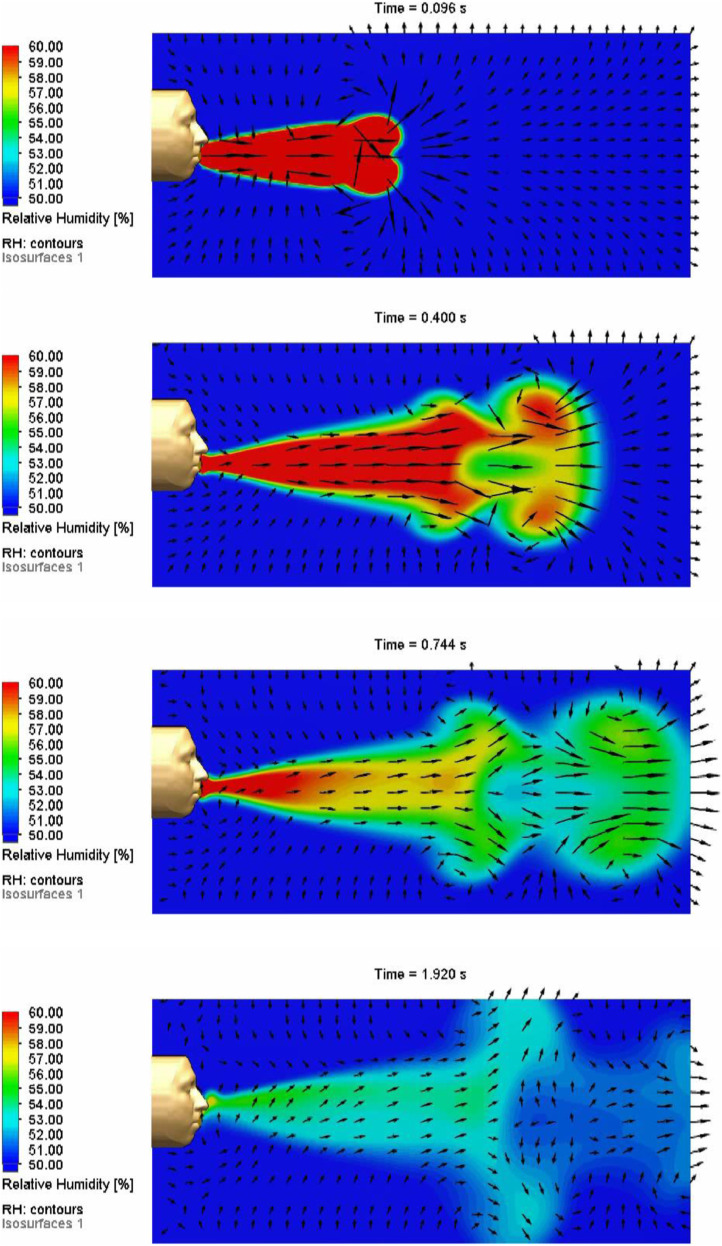
Fig. 10 shows time-lapse images of the simulated relative-humidity and velocity profiles of a simulated cough using the boundary conditions provided in Table 1. The simulated mouth described in Section 2.1.1 is embedded in the simulated face and head shown in Fig. 10. At early times during the cough, a jet-like pulse is propagated forward from the mouth, producing an expanding vortical flow structure at the leading edge with air entrainment along the lateral edges of the plume. After the cough ends at 0.2 s, the vapor plume continues to move forward, entraining air from the surroundings and expanding in size. Starting at 0.4 s, Fig. 10 shows that a bifurcation occurs as the head of the plume separates from the trailing portions of the plume. We hypothesize that the shear from the counter-rotating flow behind the propagating vortical structure at the leading edge of the plume together with the angular and transient velocity profile of the cough contribute to the plume bifurcation.

Fig. 10.

Simulated relative humidities and velocity profiles of a cough at 0.096, 0.4, 0.744, and 1.92 s. Boundary conditions are reported in Table 1. The length of the simulated domain is 1 m.

3.1.2. Exposure assessments under varying wind conditions

Section 2.2 described the method developed to assess exposure risks from simulated expiratory events. The CFD-simulated time-integrated vapor concentration at several locations downstream of the source (mouth) was divided by the simulated time-integrated vapor concentration at the source to yield the normalized cumulative exposure as a function of time and distance. Figs. 11 –14 show the simulated normalized cumulative exposures for four different ambient wind scenarios: (1) quiescent, (2) receptors located downwind of source, (3) receptors located upwind of source, and (4) receptors located crosswind of source. In each of the three scenarios with wind, a velocity of 0.25 m/s was chosen because the American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE) has recommended that value as a maximum air velocity for indoor thermal comfort [57]. In each figure, a snapshot of the expelled vapor plume and the receptor locations are shown together with the exposure plot for reference. It is important to note that the absolute values of the exposure values are less important than the relative differences and trends impacted by time, distance, and wind direction.

Fig. 11.

Simulated normalized cumulative exposures as a function of time and distance for a cough under quiescent conditions.

Fig. 14.

Simulated normalized cumulative exposures as a function of time and distance for a cough with receptors located crosswind of the source.

In Fig. 11, under quiescent conditions, the normalized cumulative exposure increases with time and decreases with distance from the source (this general behavior occurs in all the scenarios). At 1 ft (0.3 m), the exposure increases rapidly and reaches a maximum value within a fraction of a second. At separation distances of 3 ft (0.9 m), the relative magnitude of exposure is decreased by over an order of magnitude relative to the exposure resulting from a separation distance of 1 ft. At distances of 6 ft (1.8 m) and greater, the relative magnitude of exposure is decreased by two orders of magnitude, and the time to exposure increases to several seconds or more. This indicates that “social distancing” provides additional time and distance for dispersion and dilution of the aerosol plume (as well as time to walk away).

Fig. 12 shows the simulated normalized cumulative exposures as a function of time and distance for receptors located downwind of the cough. In this case, there is increased dispersion of the expelled vapor plume along the direction of air flow, but there is less lateral dispersion. This “confinement” of the plume by the wind leads to an increase in the cumulative exposures relative to the quiescent scenario. In addition, although the movement of the plume is initially propelled by the high velocity of the cough (up to 25 m/s) relative to the speed of the wind (0.25 m/s), the plume is aided by the wind and reaches longer receptor distances (e.g., 6 ft (1.8 m) and beyond) faster than under quiescent conditions. At 9 ft (2.7 m), the simulated plume reaches the receptor at ~3 s under wind-aided conditions but takes over 10 s to reach the same distance under quiescent conditions.

Fig. 12.

Simulated normalized cumulative exposures as a function of time and distance for a cough with receptors located downwind of the source.

Fig. 13 shows the simulated normalized cumulative exposures as a function of time and distance for receptors located upwind of the cough. In this scenario, receptors located 6 ft (1.8 m) or greater from the source do not experience any exposure from the expelled plume, which is blown back toward the source by the wind. Recall that only the expelled air and vapor are being simulated and not discrete droplets, which could be propelled to potentially greater distances if the droplets have sufficient momentum, even against the wind.

Fig. 13.

Simulated normalized cumulative exposures as a function of time and distance for a cough with receptors located upwind of the source.

Fig. 14 shows the simulated normalized cumulative exposures as a function of time and distance for receptors located crosswind of the cough. In this scenario, receptors located 3 ft (0.9 m) or greater from the source do not experience any exposure from the expelled plume, which is blown sideways relative to the source and receptors. Recall that only the expelled air and vapor are being simulated and not discrete droplets, which could be propelled to greater distances if the droplets are sufficiently large (> ~100µ), even in the presence of a crosswind.

Fig. 15 shows the impact of wind speed (0.1, 0.25, and 1 m/s) on the normalized cumulative exposure as a function of time and separation distance for cases when the receptor is located downwind, upwind, and crosswind of the cough source. For the downwind-receptor scenario, higher wind speeds result in greater exposure risks at all times for a prescribed distance. When the cough is aligned with the direction of the wind, the plume is confined with less lateral dispersion. Higher wind speeds also result in the plume reaching the receptor within a shorter period of time. For the upwind-receptor scenario, a wind speed of 1 m/s was sufficient to prevent exposure at upwind distances of 3 ft (0.91 m) and beyond. At wind speeds of 0.1 m/s and 0.25 m/s, the relative exposure was limited to upwind distances of 3 ft (0.91 m) or less. At an upwind distance of 3 ft (0.91 m), a wind speed of 0.25 m/s delayed the plume from reaching the receptor a bit more than a wind speed of 0.1 m/s, but the bulk of the plume hovered at 3 ft (0.91 m) for a longer period before being pushed back toward the receptor, which increased the normalized cumulative exposure relative to a wind speed of 0.1 m/s after ~0.5 s. For the crosswind-receptor scenario, wind speeds of 0.25 m/s or greater prevented exposure at crosswind distances of 3 ft (0.91 m) and beyond. At 0.1 m/s, the plume was able to reach a crosswind distance of 3 ft (0.91 m) before being blown sideways. At 1 m/s, the expelled plume exhibited a bifurcation that reached 1 ft (0.3 m) and caused a non-steady rise in the normalized cumulative exposure at ~0.8 – 0.9 s.

Fig. 15.

Simulated normalized cumulative exposures as a function of time and distance for a cough with receptors located (a) downwind, (b) upwind, and (c) crosswind with wind speeds of 1 m/s (solid line), 0.25 m/s (dashed line), and 0.1 m/s (dotted line).

The results of these simulations indicate that social distancing of 6 ft (1.8 m) or more can increase the dispersion and dilution of expelled aerosol plumes under both quiescent and ventilated conditions, reducing the normalized cumulative exposure by two orders of magnitude or more relative to normalized exposures resulting from a separation distance of 1 ft (0.3 m) or less. Being physically distanced at 6 ft (1.8 m) or greater also increases the time it takes for the plume to reach the receptor by several seconds or more.

In general, scenarios with airflow helped to disperse, dilute, and/or move the simulated plume away from the receptors. However, if the receptors are located directly downwind of the source, the normalized cumulative exposures could be increased. Therefore, people should avoid being downwind of potential sources of airborne pathogens. These findings are consistent with those of Feng et al. [17], which found that downwind exposure to expelled respiratory droplets could occur beyond 6 ft (1.8 m).

3.1.3. Impact of face coverings

The impact of face coverings (face masks and face shields) on the expelled vapor plume and resulting exposure risks during a cough were evaluated using the CFD tools described in Section 2.1. The hydrodynamic and thermodynamic boundary conditions for the cough were based on measured values in the literature as summarized in Section 2.1.1.

Face masks. The mask was simulated with assumed hydraulic properties of a MERV 11 (1-inch) filter1 (Minimum Efficiency Reporting Value; MERV 11 rating indicates most particles >1 micron will be filtered). Although particle and pathogen filtration resulting from electrostatics and other deposition processes (e.g., turbophoresis, thermophoresis, inertial effects, Brownian motion) were neglected in these simulations, the pressure drop as a function of flow rate (e.g., permeability) for a MERV 11 material was used to analyze the impact of face masks on bulk flow and transport of small aerosols. In addition, Leung et al. [58] measured the efficacy of surgical masks as a function of respiratory droplet size and showed that during 30 min of breathing, masks were effective at blocking larger droplets (>5µm) for both seasonal coronavirus and influenza virus. However, results were mixed for smaller aerosol droplets (<5µm). Leung et al. [58] observed a reduction in detected small aerosols of coronavirus for those who wore a mask (from 4 of 10 to 0 of 11), but mask wearing did not yield a significant reduction in detected small aerosols (<5µm) of influenza virus. Thus, while masks may be effective at blocking larger droplets, smaller aerosolized droplets may pass through.

Fig. 16 shows the simulated velocities near the mask at 0.05 s, which is at the time of the peak velocity (25 m/s). Results show that the velocity exiting the mouth is ~25 m/s but reduces to ~13 m/s near the interior side of the mask and to less than ~4 m/s at the exterior side of the mask. The reduced velocities and flow rate across the mask are due to the reduced permeability and prescribed pressure drop across the simulated porous mask as a function of velocity as shown in Fig. 16. Konda et al. [59] and Davies et al. [60] provide measurements of pressure drop and particle filtration efficiency for masks made of different materials. (Fig. 15)

Fig. 16.

Left: Simulated velocities around the mask at 0.05 s of the cough (peak velocity = 25 m/s). Right: Prescribed pressure drop vs. velocity of the mask material (MERV 11 1-inch).

Fig. 17 shows the simulated mass fractions of the expelled water vapor plume at 0.5 s after the initiation of a cough that lasted 0.2 s with and without a mask under quiescent conditions. The inset figure in the top image of Fig. 17 shows simulated flow trajectories inside the mask during the cough at 0.05 s, indicating a reduction in the forward momentum of the cough where flow is diverted toward the sides and throughout the entire area of the mask. Fig. 18 shows a series of time-lapse images of the simulated mass fractions of expelled water vapor during the cough with a mask. The results show that the mask disrupts the forward propagation and breaks the expelled plume into multiple vortical structures that move forward with reduced momentum relative to the cough without a mask. After ~3 s, buoyancy effects cause the vapor plume to rise.

Fig. 17.

Simulated mass fractions of expelled water vapor and velocity vectors from a cough with a face mask (top) and without a face mask (bottom) after 0.5 s.

Fig. 18.

Time-lapse images of simulated mass fractions of expelled water vapor plume following a cough with a mask.

Fig. 19 shows the normalized cumulative exposure as a function of time for the simulated cough with and without a mask. The simulated plume only reached a distance of ~1 ft (0.3 m) downstream of the mouth before dissipating upward. At 1 ft, the cumulative normalized exposure is about an order of magnitude lower than the cumulative normalized exposure without a mask. In addition, the mask slowed the breakthrough of the plume at 1 ft by about 0.2 s and the time to peak cumulative normalized exposure by several seconds. Thus, although Leung et al. [58] showed that masks may not be as effective at filtering small aerosols (< 5µm), the current study shows that masks are effective at reducing the forward propagation and momentum of the expelled breath and vapor. These effects, together with an increased time to exposure, are potential benefits that the mask provides to reducing probability of transmission by allowing additional dilution of the expelled plume. A caveat is that these simulations reveal that the mask may yield temporarily increased aerosol concentrations in the vicinity of the source for several seconds before the plume has time to disperse. If a receptor were to move into that region immediately after the expiratory event, the receptor may be exposed to higher concentrations relative to a plume that was dispersed by a cough without a mask. These results complement the CFD simulations performed by Feng et al. [17] and Khosronejad et al. [35], which showed that masks can significantly reduce expelled droplets in the air.

Fig. 19.

Simulated normalized cumulative exposures as a function of time and distance for a cough under quiescent conditions with and without a mask.

Face Shield.Fig. 20 shows the results of a simulated cough with a face shield (top) and with a face shield and mask (bottom under quiescent conditions). Because the face shield is impermeable, the expelled vapor concentrations do not propagate forward, and there were no measured concentrations or cumulative exposures at distances of 1 ft (0.3 m) or beyond for either case. The simulation with both a face shield and a face mask resulted in expelled vapor concentrations that persisted in the face shield. In the simulations without a mask, the explosive flow and momentum from the unimpeded cough were sufficient to clear the face shield of much of the expelled water vapor. In the simulation with the mask, the reduced momentum of the cough allowed a greater accumulation of water vapor within the shield.

Fig. 20.

Simulated vapor plume at 1 s of a cough with a face shield (top) and with a face shield and mask (bottom). The mask was simulated with hydraulic properties of a MERV 11 (1-inch) filter.

As discussed in the case of a face mask, these simulations reveal that a face shield may yield temporarily increased aerosol concentrations in the vicinity of the source for several seconds before the plume has time to disperse. If a receptor were to move into that region immediately after the expiratory event, the receptor may be exposed to higher concentrations relative to a plume that was dispersed by a cough without a face shield or a mask.

3.2. Probability of infection results

Fig. 21 shows the simulated probability of infection (Eq. (3)) as a function of distance and time for a cough under quiescent conditions using the nominal parameters shown in Table 2. The expelled vapor concentrations were taken from the CFD simulations described in Section 2.1. The resulting plots are similar in shape and trend to the normalized cumulative exposure plots shown in Fig. 11, which is expected since the only transient parameters are the CFD-simulated vapor concentrations and the viability term, f(t), which does not change significantly in the short time frame of interest (~100 s).

Fig. 21.

Simulated probability of infection as a function of time and distance for a cough under quiescent conditions using nominal infection parameters in Table 2 assuming the receptor is stationary and directly exposed to and inhaling the pathogen over the entire duration.

The probability of infection at a particular location increases with time as the expelled vapor plume reaches that location. At 1 ft (0.3 m) away from the source, the probability of infection increases rapidly as the plume moves past quickly (within ~1 s). The time for a 50% probability of infection occurs at ~0.1 s. At a distance of 6 ft (1.8 m), the probability of infection is lower at any given time and takes ~7 s to reach 50%. In general, the probability of infection decreases with increasing distance as a result of dilution and dispersion of the vapor plume. The results presented in Fig. 21 are intended to illustrate general trends in the probability of infection. Uncertainties in the infection parameters can vary widely as seen in Table 2. To include and determine the impact of these uncertainties, probabilistic models are developed in the next section.

3.3. Probabilistic modeling

Significant uncertainties exist in the input parameters used in the infection model. Viral load can vary by orders of magnitude, and the deposition fraction and infectivity can vary by several factors. The dose-response curve for SARS-CoV-2 is currently unpublished and uncertain. The simulated vapor concentrations can also include uncertainties due to time-varying turbulent fluctuations, physical movement, and non-uniform airflow in actual environments. Probabilistic modeling was used to honor these inherent uncertainties and achieve the following objectives: (1) quantify the resulting uncertainty in the simulated probability of infection and (2) determine the parameters that most impact the magnitude and uncertainty of the probability of infection.

The probabilistic modeling approach consists of three primary steps: (1) creating uncertainty distributions of stochastic parameters and sampling the distributions n times, (2) running the infection model n times using the sampled variables, and (3) evaluating the distribution of n results to quantify uncertainty and sensitivity. The uncertainty distributions (e.g., uniform, normal) can be based on experimental data, modeling, or professional judgment. Monte Carlo or Latin Hypercube sampling methods are then implemented in the model to generate many different (but equally probable) realizations of the system performance [61]. Latin Hypercube sampling implements a stratified sampling method and requires fewer realizations than Monte Carlo sampling, which is prone to clustering, and allows prescribed correlations among parameters. The ensemble of realizations generates a cumulative probability distribution that can be used to quantify the uncertainty in the probability of infection. A stepwise rank regression analysis is then performed to determine the input parameters that are most correlated to the simulated metric, indicating those parameters or processes that are most important to the probability of infection. These types of analyses provide additional useful information not available in deterministic analyses (or even parametric analyses where only a few prescribed values are varied in a “one-off” fashion).

In this study 300 realizations were found to be sufficient to adequately represent the cumulative distribution function of the probability of infection for the uncertainty distributions provided in Table 2. Latin Hypercube Sampling was used to sample 300 values from each of the input parameters in Table 2. Eq. (3) was then solved for each of the 300 realizations. Figs. 22 –24 shows the resulting cumulative distribution functions for the probability of infection of a cough under quiescent conditions as a function of different distances (1, 3, 6, and 9 ft) and times (1, 10, and 100 s).

Fig. 22.

Cumulative distribution function of simulated probability of infection for a cough under quiescent conditions at 1 s using uncertainty distributions in Table 2 assuming the receptor is stationary and directly exposed to and inhaling the pathogen over the entire duration.

Fig. 24.

Cumulative distribution function of simulated probability of infection for a cough under quiescent conditions at 100s using uncertainty distributions in Table 2 assuming the receptor is stationary and directly exposed to and inhaling the pathogen over the entire duration.

At 1 s (Fig. 22), only distances of 1 and 3 ft yielded any probability of infection; the expelled plume had not yet reached 6 ft or beyond at 1 s. At 1 ft, the probabilistic model shows that the median (50th percentile) probability of infection is ~98%. At a distance of 3 ft, the median probability of infection is 69%. The 90th percentile for the probability of infection is ~100% and 95% at distances of 1 ft and 3 ft, respectively. These simulations assume that the receptor is directly and continuously exposed to the expelled pathogen plume over the entire duration and that the receptor is inhaling continuously at an average rate for tidal breathing (Table 2).

At 10 s (Fig. 23 ), the expelled plume had not yet reached 9 ft, but distances of 6 ft or less yielded probabilities of infection. The median probability of infection at 10 s is ~100%, 98%, and 65% at 1 ft, 3 ft, and 6 ft, respectively. The 90^th percentile for the probability of infection is nearly ~100% for distances of 1 ft and 3 ft, and ~97% for a distance of 6 ft.

Fig. 23.

Cumulative distribution function of simulated probability of infection for a cough under quiescent conditions at 10s using uncertainty distributions in Table 2 assuming the receptor is stationary and directly exposed to and inhaling the pathogen over the entire duration.

At 100 s (Fig. 24 ), the median probability of infection is ~100%, 99%, 95%, and 80% at distances of 1 ft, 3 ft, 6 ft, and 9 ft, respectively. The 90^th percentile for the probability of infection approaches ~100% for all distances. It should be emphasized that these simulations assume direct and continuous exposure by the receptor with continuous inhalation and no external airflow. Nevertheless, such high likelihoods and probabilities of infection at long distances may indicate that the range of assumed infectiousness or viral load in Table 2 may be too high. In particular, the range of median viral load was taken from measurements of SARS-CoV-2 in units of RNA copies/mL, but as referenced in Table 2, there may be only ~1 infectious virus out of every ~1000 measured RNA copies.

The cumulative probabilities span a large range due to the large uncertainties in the input parameters. A stepwise linear (rank) regression is performed to quantify the relative impact of each input parameter on the magnitude and spread of the simulated probability of infection. The stepwise regression generates a sequence of regression models that successively adds the most important input parameters to the regression to improve the overall correlation. In the end, the regression identifies those parameters that are significantly correlated to the performance metric and omits those parameters that are not. Results can help guide and prioritize future research to better characterize the most important parameters and processes.

The sensitivity of the independent variables can be represented by ΔR², the change in the coefficient of determination when a new independent variable is added to the model. The value of ΔR² describes the percentage of the uncertainty or variability in the simulated metric that is caused by the uncertainty in each input variable. In addition to ΔR², the standardized regression coefficient, B, is another statistical measure that evaluates the relative contributions of each input parameter to the magnitude of the dependent variable (as opposed to the variability of the dependent variable). The sign of B also gives the direction of correlation. The importance ranking of the independent variables using either ΔR² or B are typically the same.

As an example, Figs. 25 and 26 show plots of the ΔR² and the standardized regression coefficients for the probabilistic simulation of a cough under quiescent conditions at a distance of 6 ft and at a time of 10 s. Results show that the viral load, which can vary by orders of magnitude, had the most impact on the variability and magnitude of the simulated probability of infection. The other important input parameters included the product of the vapor density (from CFD simulations) and the viability function, the infectivity rate, lung deposition fraction, inhalation rate, and mucus density. All of the parameters were positively correlated to the probability of infection except for the mucus density, which showed a negative correlation according to the standardized regression coefficient in Fig. 26. The positive or negative correlations among the input variables and the probability of infection can be seen in Eq. (3). A larger mucus density, ρ_mucus (g/mL), means that for a given viral load, c (pathogens/mL), fewer pathogens will exist per mass of respiratory fluid (c/ρ_mucus). So, for a simulated mass of expelled respiratory fluid (simulated as pathogen-laded water vapor in this study), the simulation with a larger assumed mucus density will yield a smaller number of pathogens and a lower probability of infection.

Fig. 25.

Plot of the incremental coefficient of determination, ΔR², indicating the parameters most important to the variation of the simulated probability of infection.

Fig. 26.

Plot of standardized regression coefficients indicating the parameters most important to the magnitude of the simulated probability of infection.

4. Conclusions

This study developed a modeling approach that coupled CFD models with exposure and infection models to quantify impacts of ventilation and face coverings on airborne transmission risks. CFD models were developed to evaluate aerosol plume dynamics and the impacts of face coverings and ventilation. The simulations were used to quantify relative exposure risks as a function of time and location for a cough under various airflow conditions. Infection models were also developed using the results of the spatial and temporal pathogen concentrations derived from the CFD simulations assuming a passive scalar representation of the aerosol plume. Probabilistic analyses were performed to quantify uncertainties and determine important parameters associated with the large uncertainties in the infection-model parameters. Key findings are summarized as follows:

• •Results showed that CFD simulations were useful in performing comparative analyses of different transmission scenarios. The simulations used in the current study provided a good balance of physics-based modeling and expedient run times to evaluate many scenarios and configurations.
• •The normalized cumulative exposure at prescribed location was defined as the time-integrated concentration divided by the time-integrated concentration at the source. The cumulative exposure was plotted as a function of time for different separation distances and airflow conditions. Results showed that social distancing significantly reduced the normalized cumulative exposure (by two orders of magnitude) and allowed time for dilution and dispersion of the expelled plume. Being upwind or crosswind of the source of the cough also significantly reduced risk (no simulated exposures from the exhaled plume at distances of 6 ft (1.8 m) or beyond for wind speeds of 0.1 m/s or greater). Being directly downwind of the cough increased exposure risks relative to quiescent conditions since lateral dispersion was confined.
• •Wearing a face mask or face shield significantly reduced the forward plume propagation and normalized cumulative exposure by an order of magnitude. However, the vapor concentrations near the face were more persistent than without face coverings due to the reduced forward momentum.
• •Uncertainty distributions were assigned to each model parameter, and Latin Hypercube Sampling was used to perform probabilistic simulations. A stepwise rank regression analysis was performed to identify key parameters that impacted the probability of infection. Viral load, pathogen concentration in the air, and infectivity were among the most important parameters impacting the variability and magnitude of the probability of infection.

Limitations of the current study and recommended future work include the following:

• •
  We assumed that the expelled pathogens consisted of aerosols (< 5µm), which could be represented by a passive scalar (e.g., water vapor) [17,30,31,36]. Droplet dynamics and evaporation were neglected.

  • ∘
    Additional studies comparing the use of a passive scalar vs. evaporating droplets should be performed to elucidate discrepancies in relative exposure risks for simulated scenarios.
• •
  Time-averaged turbulence models were used in the CFD simulations

  • ∘
    Additional studies comparing LES vs. RANS-based CFD simulations should be performed to elucidate differences in relative exposure risks for simulated scenarios.
• •Although transient simulations of the cough and subsequent flow patterns were performed, the imposed wind (when simulated) was assumed to be steady.
• •Physical receptors were not simulated, and physical processes of receptor inhalation and exhalation were not modeled. Feng et al. [17] simulated a physical receptor and reported complex fluid interactions with the source and receptor bodies in the presence of wind. Motion of the source and receptor, thermal plume emanating from the receptor, and inhalation/exhalation by the receptor may also impact fluid and pathogen transport.
• •Simulations of coughs with a mask neglected filtering effects of particles; only permeability effects on the pressure drop and fluid hydraulics were investigated.