Abstract
The current universally challenging SARS-COV-2 pandemic has transcended all the social, logical, economic, and mortal boundaries regarding global operations. Although myriad global societies tried to address this issue, most of the employed efforts seem superficial and failed to deal with the problem, especially in the healthcare sector. On the other hand, the Internet of Things (IoT) has enabled healthcare system for both better understanding of the patient’s condition and appropriate monitoring in a remote fashion. However, there has always been a gap for utilizing this approach on the healthcare system especially in agitated condition of the pandemics. Therefore, in this study, we develop two innovative approaches to design a relief supply chain network is by using IoT to address multiple suspected cases during a pandemic like the SARS-COV-2 outbreak. The first approach (prioritizing approach) minimizes the maximum ambulances response time, while the second approach (allocating approach) minimizes the total critical response time. Each approach is validated and investigated utilizing several test problems and a real case in Iran as well. A set of efficient meta-heuristics and hybrid ones is developed to optimize the proposed models. The proposed approaches have shown their versatility in various harsh SARS-COV-2 pandemic situations being dealt with by managers. Finally, we compare the two proposed approaches in terms of response time and route optimization using a real case study in Iran. Implementing the proposed IoT-based methodology in three consecutive weeks, the results showed 35.54% decrease in the number of confirmed cases.
Keywords: Supply chain design, Epidemic outbreaks, Industry 4.0, COVID-19, SARS-COV-2
1. Introduction
Nowadays, relief supply chains have been given overwhelming support due to the recent natural disasters, major incidents, and pandemic. Since governments are usually unable to predict the impending nature of these happenings, a meticulous plan is needed to face them. Having an efficient scheme to confront these rough conditions enables immediate actions and most of all saves human lives. In this sense, the relief supply chain is a sort of humanitarian supply chain that has emerged to execute plans for pre- and post-disaster response, especially at the time of major outbreaks. This area has become increasingly conspicuous in the context of humanitarian and relief logistics and their correlation with supply chain networks.
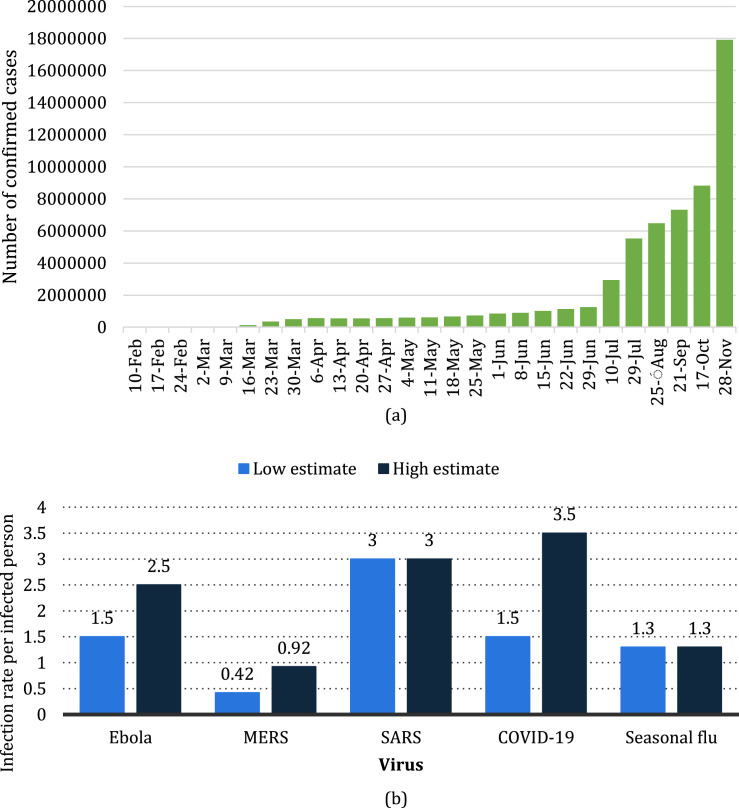
The recent SARS-COV-2 outbreak arose from Wuhan, China and rapidly spread to all other nations and affected their economies and also human lives rapidly. Besides, it drastically undermined the settings of current supply chain networks globally. In addition, due to its high infection rate and increasing number of positive cases astounded international society as immediate action is needed to react to this special condition ([1]). Meanwhile, the issue of this pandemic has received considerable critical attention as its infection rate is severe and even most developed countries have failed to address the numerous patients ([2]). According to the recent published report by the World Health Organization (www.who.int), the total number of confirmed cases is increasing daily and the attempts to control the condition has not been successful (See Fig. 1). Therefore, due to both the increasing total number of death and its high infection rate, the WHO encourages governments to employ social distancing at work and isolation ([3], [4]). However, this proposed plan only works for healthy people and is not applicable to the confirmed and hospitalized or suspicious cases for both managing required inventories and transportation ([5]). Therefore, an efficient plan is needed to both visit suspicious cases and carry them to the medical centers in a relatively short time. Such a plan could not be met unless an efficient supply chain management (SCM) is implemented.
Fig. 1.
(a) Total number of confirmed cases worldwide and (b) Infectious rate of SARS-COV-2 among all known viruses (www.who.int).
Recently, a considerable literature has grown up around the theme of supply chain and SCM. SCM as a form of location, allocation, scheduling, etc. can be utilized not only to address the patients, but also to procure the needed medical items and all the associated goods in the time of pandemics, especially the SARS-COV-2 outbreak.
In this regard, in the early weeks of 2020, several studies have published in this area of SARS-COV-2. In addition, pandemics such as SARS or SARS-COV-2 could happen again in the near future. Therefore, this issue have motivated many researchers to consider different aspects of the pandemic from various perspectives. Some studies consider the aspects of SARS-COV-2 virology such as ([6]) and ([7]), while others investigate the SARS-COV-2 pandemic from different perspectives such as its social and economic effects ([8], [9]), preventing disease ([10]), optimization methodologies ([11], [12]), future anticipation ([13], [2]) and its learning behavior ([14], [15]).
Regarding the recent SARS-COV-2 outbreak, some authors have tried to address this issue by designing a supply chain network in order to better service the infected people. In this regard, Ivanov [2] investigated the effect of the SARS-COV-2 outbreak on the global supply chain utilizing simulation analysis. It also considers the prediction of the epidemic in short- and long-term periods. Fernandes [16] considered the economic impacts of the SARS-COV-2 pandemic on industries. Lockdown duration, the capability of different countries to respond to the pandemic, and economic risks are taken into account. Similarly, Yu and Aviso [9] address the economic impacts on SARS-COV-2 on various industries and Currie et al. [17] emphasized the impact on effective molding to address this issue.
Ivanov and Dolgui [18] design an intertwined supply chain network to reduce the mortality rate during the SARS-COV-2 outbreak. The dynamic, game-theoretic model of the proposed network consists of suppliers, focal firms, and markets that contribute to better decision-making in this situation. In another study, Choi [19] emphasizes that utilizing the supply chain logistics with mobile service operations could lead to both better response to SARS-COV-2 cases and reduced total logistics cost. Similarly, Rowan and Laffey [20] suggested that using smart communication channels could be highly efficient for providing protective healthcare items in the supply chain network. Yu et al. [21] design a reverse supply chain network in order to convey hospital waste to other locations during the SARS-COV-2 outbreak. Their multi-objective model aims to locate temporary locations to transfer waste in a short time. From the supply chain perspective and planning, these considerations could be discussed in the field of relief supply chain focusing on humanitarian logistics to address the affected people at the time of major incidents and natural disasters, including pandemics.
When designing a relief supply chain network, different conditions were considered in previous studies. It was first introduced by Toregas et al. [22] when they conducted research on covering the total demand using relief facilities. The objective function of crisis response is defined in the model. A good relief supply chain network is presented in Özdamar et al. [23]. In their distribution network, they represent a time-based model to collect goods into affected sites. Hence, an objective function of minimizing the unmet demand is used based on the type of products. Using shelters as a base camp, as suggested by Alçada-Almeida et al. [24], they utilize a multi-objective model for planning the evacuation along with shelters location best routes for backup. The model seeks to find optimal travel times and distances. Horner and Widener [25] considered a model to maximize facility access during tornados. The proposed transportation network model aims to optimize facility locations and the cost of accessing relief goods.
Considering the inherent uncertainty of natural disasters and pandemics, some previous studies conducted their researches in this context in order to better address real-life problems. In order to distribute relief commodities, Rottkemper et al. [26] designed a model to cover the uncertain demands of affected people. The aim of the study was to minimize contributed costs and unmet demands. The dynamic problem of delivering multiple relief goods using various vehicles is considered in Lin et al. [27]. The proposed model is solved using deterministic (weighted sum approach) and meta-heuristic methods.
To locate distribution centers in disaster-stricken areas, Bozorgi-Amiri et al. [28] develop a cost-saving model. The Particle Swarm Optimization (PSO) method is used to find the optimal solution. A fuzzy multi-objective programming model to address the issue of relief commodities and their supply in crisis condition with different transportation modes is proposed by Zheng and Ling [29]. Two meta-heuristics including Genetic Algorithm (GA) and Tabu Search (TS) are applied to solve the model.
For a case of crisis management, Bozorgi-Amiri et al. [30] develop a multi-objective model to minimize the total associated cost while maximizing the fulfilled demand. In addition, the aspect of uncertainty is considered for response time and stochastic programming was used to address this issue. A bi-objective mixed-integer mathematical model for humanitarian relief logistics is developed by Rezaei-Malek and Tavakkoli-Moghaddam [31] to reduce costs and response time. The model used to verify the location of different centers including inventory, warehouses, and good distribution when earthquakes strike. Hu et al. [32] verify a risk-based model for flood disasters. In various scenarios, the authors assess two objectives of shortage and cost to reduce them. A bi-level programming is designed by Gutjahr and Dzubur [33] to address the problem of distribution centers and their locations. The first level aims to minimize distribution costs and maximize the total coverage while the second level seeks to select the best facilities. The problem is solved using Pareto solutions. A relief supply chain network is proposed by Zokaee et al. [34]. Scenario-based uncertainty is utilized to optimize the total cost along with the human response. The model is applied to a real case problem for a high-risk earthquake zone. Some previous studies include meta-heuristic approaches to solve their proposed relief supply chain network. To assign relief centers in an earthquake crisis, Saeidian et al. [35] studied a model and verified the optimal answers using GA and Bees Algorithm.
Recently, a large and growing body of literature has studied the humanitarian aid and relief supply chain network. Fahimnia et al. [36] designed a bi-objective model to reduce costs and delivery time in an uncertain condition for blood distribution in disasters. Similarly, Salehi et al. [37] developed a blood distribution model in a possible case of earthquake which considered various blood types. The model utilized stochastic programming in order to cover the uncertain demand. A humanitarian supply chain to enable the proper flow of relief items is introduced by Tavana et al. [38]. The proposed MILP model considered pre and post-disaster conditions with the aim to locate central warehouses to manage perishable products and is solved using the NSGA-II algorithm. Dubey and Gunasekaran [39] discuss contributive factors to design a sustainable humanitarian supply chain to fulfill its requirement and to identify its major advantages and limitations. Zhang et al. [40] design a distribution model for relief goods for natural disaster. The three-level proposed model is formulated to locate a distribution center for the post-disaster situation.
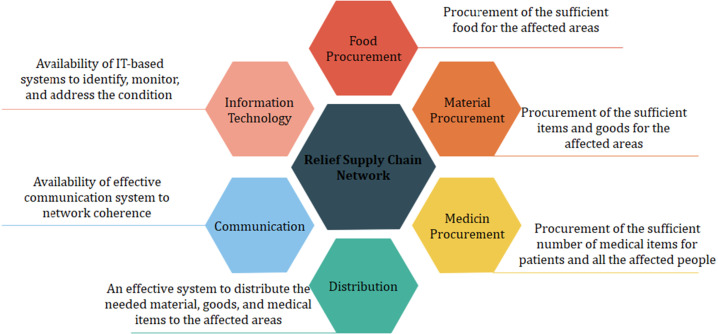
The ever-growing number of natural disasters and also recent pandemics require more efficient planning and implementation of relief supply chain networks. Since logistics costs are a large part of aid spending by governments, it makes it not only a major lever for cost reduction, but also an important aspect of delivery time. Although the investment in supply chain infrastructure as a means of relief supply chain is mandatory, considering time to address patients and positive cases is critical. An efficient relief supply chain network should have the following capabilities (See Fig. 2).
Fig. 2.
Relief supply chain network capabilities.
Although there are multiple methods to address disruptions, risks, and natural disasters, the current situation needs the emergence of new and innovative approaches to fulfill the myriad needs of pandemics including identification of suspicious cases, procurement of medical items, transportation of positive cases to medical centers, and to monitor the system in real-time.
In such an agitated environment, the application of IoT could be of great benefit. IoT-based technology can provide ways to monitor the whole system during the SARS-COV-2 outbreak. Therefore, it can be utilized to tackle the challenges in this turbulent situation by automating the required processes including transportation of ambulances to visit suspicious cases.
According to Singh et al. [41], an effective IoT system in the healthcare section would both impact by reducing healthcare cost and by improving treatment outcomes for the infected patients. In addition, new innovative approaches try to combine the application of supply chain management with IoT to control, monitor, and decide the determinative parameters of their proposed network. In this regard, utilizing IoT could be a true game changer. Singh et al. [42] utilized IoT to track the fleeing positive cases. Ting et al. [43] emphasized the new innovative technologies such as IoT and blockchain to control and address the outbreaks, especially SARS-COV-2 in real time conditions. Vaishya et al. [44] reviewed number of developed studies using artificial intelligence and IoT in the SARS-COV-2 pandemic and concluded that technology plays an important role to detect the cluster of cases in the healthcare sector. To predict, prevent, and control the emerging infectious diseases such as SARS-COV-2, Rahman et al. [45] introduced the application of IoT system to analyze the data gathered from patients and to forecast the future. Bai et al. [46] introduced an IoT cloud-based system to diagnose SARS-COV-2 cases by a simple device-based application and questionnaire which categorizes patients into three clusters and addresses them based on the severity of their condition. The application of Industry 4.0 and specifically IoT is detailed in Javaid et al. [47] . The benefits of implementing IoT, such as isolation of the infected patients, digital diagnosis, and reducing physical crowding of patients in medical centers are discussed in their study.
Additionally, some recent studies devoted their resources to address different aspects of SARS-COV-2 in the concept of supply chain network. Grida et al. [48] applied uncertainty to evaluate the impact on Covid-19 on supply chain policies on various industries including food industry, electronics industry, pharmaceutical industry, and textile industry. The proposed policy claimed to enhance the supply chain features when dealing uncertain condition. Toward sustainability in the disrupting condition of Covid-19 pandemic, Karmaker et al. [49] provided a structural modeling. The provided protocols aimed to long-term sustainability in the current pandemic situation. Nagurney [50] applied game theory to address a supply chain modeling for Covid-19 pandemic for laboring of fresh products. The results of the study showed beneficial outcomes both economically and operationally. Using a real case data, Govindan et al. [51] introduced new practical approach to address Covid-19 pandemic based on the risk level. Providing multiple regulations within a proposed supply chain, the results showed effectiveness and accuracy in its output. Habib et al. [52] considered the impact of Covid-19 on the metal industry and compared the results in pandemic condition and in a safe condition. The study concluded that there is better need in supplying metal products within disruptive condition of the current pandemic.
Hence, in this study, a relief supply chain network to address SARS-COV-2 suspected cases is firstly taken into account. In this supply chain network, there is a fleet of ambulances with interconnected IoT-based system. This system consists of the complex of hardware, software, computers, and all other network elements. The system dynamically organizes and prioritize ambulances to visit suspected cases as determined by a mobile application and in the next step seeks the best route according to distance, traffic, and case severity of patients with the aim to minimizing total time.
Two novel approaches (prioritizing approach and allocating approach) are utilized in this regard. The first approach (prioritizing approach) tries to minimizes the maximum ambulances response time, while the second approach (allocating approach) minimizes the total critical response time. In addition, the use of IoT based system is novel in this regard. The developed approaches are then applied on a real cases data to investigate their efficiency. In a nutshell, the novelties of our work are:
-
•
Proposing two distinct approaches to visit suspected cases,
-
•
Utilizing Internet of Things (IoT) optimized the developed approaches,
-
•
Investigating a real-world case of SARS-COV-2,
-
•
Analyzing the sensitivity of the response time and selected routes.
Furthermore, due to the NP-hardness of the problem, set of efficient meta-heuristics and hybrid ones are proposed to verify the model’s answers and to monitor its behavior.
The difference among the recent related literature and the proposed study is described in Table 1.
Table 1.
Recent related studies concerning relief supply chain network (Y: YES, N: NO).
| Author(s) | Utilized approach |
Applying heuristics (Y/N) | Including IoT (Y/N) | ||
|---|---|---|---|---|---|
| Deterministic | Stochastic | Fuzzy | |||
| Wang et al. [53 ] | * | N | N | ||
| Nagurney and Nagurney [54 ] | * | N | N | ||
| Mohammadi et al. [55 ] | * | Y | N | ||
| Sung and Lee [56 ] | * | N | N | ||
| Zhou et al. [57 ] | * | Y | N | ||
| Jha et al. [58 ] | * | Y | N | ||
| Al Theeb and Murray [59 ] | * | Y | N | ||
| Manopiniwes and Irohara [60 ] | * | N | N | ||
| Li et al. [61 ] | * | N | N | ||
| Samani et al. [62 ] | * | * | N | N | |
| Cao et al. [63 ] | * | Y | N | ||
| Safaei et al. [64 ] | * | N | N | ||
| Hong and Jeong [65 ] | * | N | N | ||
| John et al. [66 ] | * | N | N | ||
| Ghaffari et al. [67 ] | * | Y | N | ||
| Akbarpour et al. [68 ] | * | N | N | ||
| Aghajani et al. [69 ] | * | N | N | ||
| This study | * | Y | Y | ||
The rest of the paper is organized as follows. In Section 2, the problem statement and the proposed mathematical modeling along with two effective approaches are presented. Section 3 discusses the solution approach to solve the proposed network. The computational results, comprehensive analysis on a real case study, and the main findings of the proposed research are provided in Section 4. Finally, Section 5 contains conclusions and managerial insights.
2. Problem statement and mathematical models
As aforementioned in the previous section, the behaviors of the Sars-Cov-2 virus are unpredictable. The instant changes in the attributes of suspected and confirmed cases and also the available capacity of responsiveness, including identifying cases, transporting them, and their treatment, force the involved managers to assign resources and schedule them in an efficient and effective fashion. Different methodologies to tackle such problems have been presented and reported in the literature. Nevertheless, considering the instant changes of SARS-COV-2, this literature is quite limited. In addition, there are no previously published works on utilizing IoT in this area. As a consequence, in this paper, the IoT-based methodology is developed to receive real-time information, analyze the data, and respond to the suspected cases based on optimal scheduling.
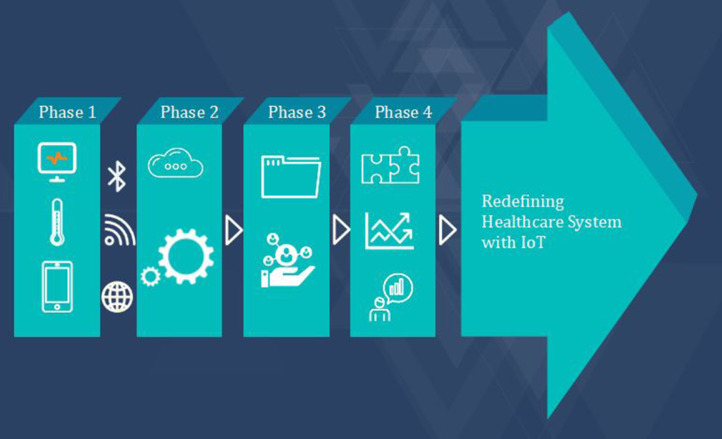
Fig. 3 shows the scale of the proposed IoT-system. In addition, steps toward redefining the proposed healthcare approach are presented with the utilized hardware and software in four phases:
Fig. 3.
Scale and phases of the proposed IoT system.
Phase 1: This phase includes the interconnected devices such as sensors, actuators, wireless systems, monitors, detectors, Bluetooth system, camera systems etc. These devices are responsible to collect and transmit the data.
Phase 2: The second phase required to covert the received analog date into digital form for further data processing.
Phase 3: The digitized date then moved to the data center.
Phase 4: The received data then analyzed in various required levels. Advance data analysis is needed in this phase in order to both bring business insight and also decision-making tool for managers.
This would lead to an increased performance for the healthcare system, especially in the harsh condition of epidemic outbreaks and patients can experience better services with utilizing such system ([70], [71]).
In this section, a methodology is proposed to serve the suspected cases of SARS-COV-2 in the most appropriate way and also adapt to the instant changes. In fact, a methodology is presented not only to identify the suspected cases of SARS-COV-2 in the shortest time, but also to minimize the response time. Thus, the proposed methodology includes two main steps:
Step (1): Identifying the suspected cases in the shortest possible time (See Fig. 4).
Fig. 4.
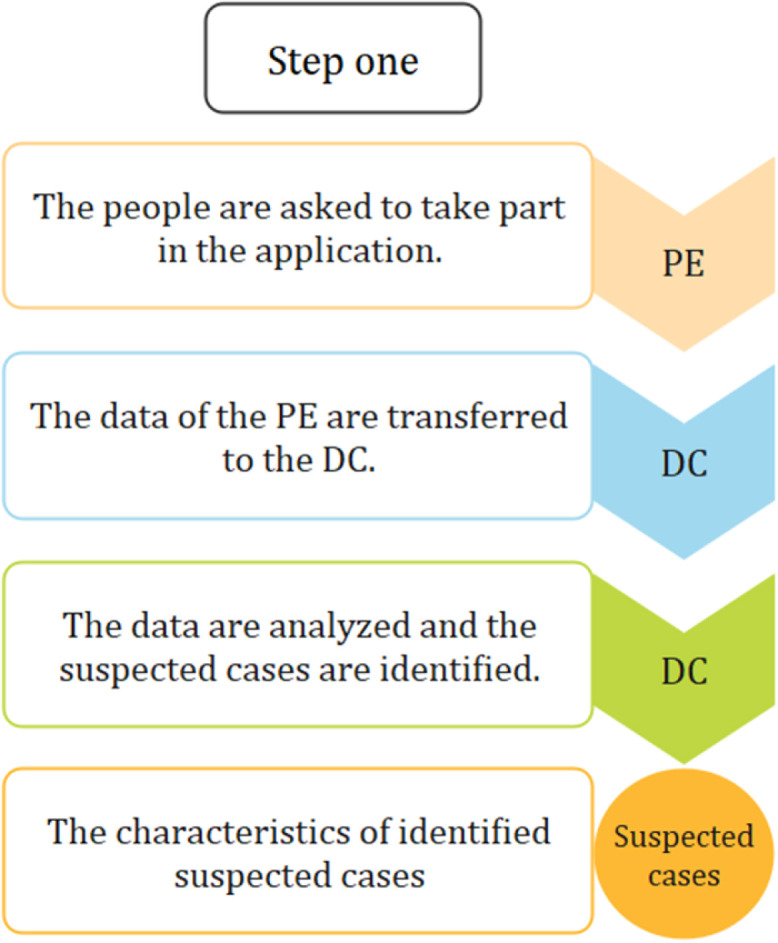
Step one of the proposed methodology.
Step (2): Scheduling the response plan dynamically by prioritizing suspected cases based on their severity, allocating ambulances and CMCs (Central Medical Center) to the suspected cases, visiting the suspected cases, and transferring the suspected cases to the CMC if they need additional care (See Fig. 5).
Fig. 5.
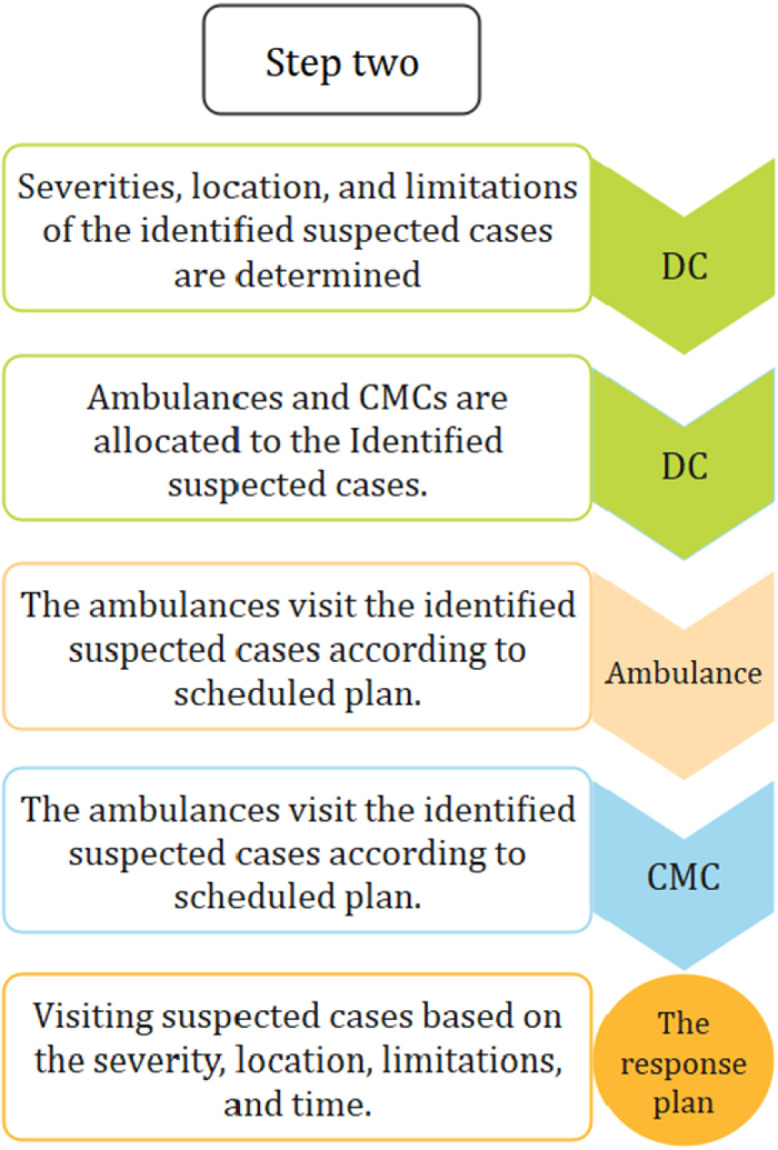
Step two of the proposed methodology.
As a result, the main objectives of this paper are described as follows:
-
1.
Identifying the suspected cases of SARS-COV-2 in the shortest time.
-
2.
Separating healthy and unaffected people from suspected cases.
-
3.
Keeping people away from dangerous areas including CMCs, SARS-COV-2 pharmacies, and SARS-COV-2 testing laboratories.
-
4.
Allocating available resources optimally.
-
5.
Considering instant changes of the SARS-COV-2’s behaviors in dynamical fashion (considering real-time changes on the methodology outputs).
2.1. Methodology suppositions
The suppositions of the proposed methodology are stated below:
-
•
There are multiple ambulances and CMCs that have limited capacity.
-
•
Each suspected case is visited by a single ambulance and also hospitalized in a single CMC.
-
•
The location of each suspected case is known and pre-determined.
2.2. How to identify suspected cases by proposed methodology?
It is important to identify confirmed cases in the shortest possible time before other people are infected by these patients. SARS-COV-2 usually has three periods including latent, mild, and severe symptoms on a confirmed case ([72], [1]). Generally, the initial symptoms appear after 2–14 days ([73], [74], [75], [76], [77]). Therefore, identification of patients after the initial symptoms can significantly control the spread of virus.
According to the WHO,1 the symptoms are usually mild and emerge gradually. Therefore, identifying the patient after manifestation of the early SARS-COV-2’s symptoms can significantly prevent its spread. As a consequence, at first, an internet-based application is employed. The application contains a platform to identify common and known symptoms of SARS-COV-2 with a user-friendly interface (step by step and with simple and short questions and answers). People are asked to use the application. This process is named Primary Evaluation (PE). The data of the PE are transferred to Data Center (DC) over the network. Afterwards, the data are analyzed by the DC to identify suspected cases of SARS-COV-2. This information is then analyzed by the DC. Then, by analyzing the gathered data, the outputs of the PE identify the suspected cases of SARS-COV-2, the severity of each suspected case, and their locations.
2.3. How to serve identified suspected cases by each ambulance and CMC?
Serving the suspected cases is as important as identifying them. Hence, the medical system should visit and treat the suspected cases in the shortest possible time in order to separate healthy and unaffected people from patients, keep people away from the dangerous areas, and also help to stop the spread chain of SARS-COV-2. On the other hand, in every region (province, city, town, and etc.), there are at least one ambulance and one CMC. In this paper, a region is considered as a territory like a town with multi-ambulance, multi-CMC, and limited capacity (medical resources). An ambulance may not travel more than a specific time in a day and a CMC cannot hospitalize more than a given number of patients in a period.
An ambulance travels and visits the suspected cases identified by the IoT system. Visiting the suspected cases by the ambulances results in identification of two types of people including healthy and unaffected people and also the suspected cases with high severity who require the SARS-COV-2 tests ([78]) and probably additional care in a CMC. Afterwards, the ambulance transfers the high severity suspected cases to a CMC, and then it either continues its current plan or reschedules if any changes occur. The change can be with respect to the number of identified suspected cases, the locations of the suspected cases, their severity, the travel time, the visit time, the sanitizing time, and the capacity of ambulances and CMCs.
2.4. How does an ambulance decide on the severity of each suspected case after visiting them?
In the proposed methodology, the ambulances are responsible for visiting suspected cases at their locations and also for transferring the high severity suspected cases to CMCs. According to the WHO, the most common symptoms of SARS-COV-2 are fever, dry cough, and tiredness. Other symptoms that are less common and may affect some patients include aches and pains, nasal congestion, headache, conjunctivitis, sore throat, diarrhea, loss of taste or smell, or a rash on skin or discoloration of fingers or toes ([79], [80], [74], [81], [75], [76], [77]). On the other hand, the real-time rapid test for SARS-COV-2 takes about 2–3 h ([78]). So, in case of severity, the ambulance should stay at the suspected case’s place at least 2-3 h. This affects the scheduling to visit the next cases. In addition, at each visitation, an ambulance examines the blood oxygen level, checks the suspected case’s obvious symptoms and medical history, and decides whether the person needs additional care or must be transported to a CMC.
Although suspected cases are identified by the IoT system, several decisions remain to be made, including priority of visiting suspected cases, the route of each ambulance, and the responsible ambulance and CMC that should serve each suspected case. Determination of the best possible route for each ambulance along with prioritizing each suspected case greatly affect the total response time. In this paper, two approaches are considered to optimize the total response time.
2.5. Prioritizing approach
As mentioned earlier in Section 2.2, each identified suspected case has its own severity and distinct location. In this approach, the route direction of each ambulance and prioritization of suspected case are determined jointly in order to minimize the maximum response time of each ambulance. In other words, this approach prioritizes the visitation sequence of the suspected cases and simultaneously assigns the ambulances to them. Meanwhile, routes are determined for the ambulances (See Fig. 6).
Fig. 6.
Description of proposed prioritizing approach.
2.5.1. The mathematical model for prioritizing approach
Although the proposed methodology to identify the suspected cases of SARS-COV-2 is presented in Section 2.3, the ambulances’ directions and visiting priorities are not determined. As a consequence, the proposed mathematical model of prioritizing approach allocates the ambulances to the suspected cases and CMCs simultaneously based on their severity, travel time, visiting time, and sanitizing time. In this part, the objective is to both minimize the maximum response time of the ambulances (by decreasing the response time of a suspected case with last priority) and meet the capacities of each ambulance and CMC in the planning horizon. The notations, parameters, and variables of the mathematical model for prioritizing approach are shown in Table 2.
Table 2.
The notations, parameters, and variables of the proposed mathematical model for prioritizing approach.
| Notations | Definition | |
|---|---|---|
| : | Set of suspected cases | |
| : | Set of CMCs | |
| : | Set of ambulances | |
| : | Set of priority | |
| : | Set of all locations | |
| Parameters | ||
| : | Travel time between location i and j | |
| : | Visitation time of suspected case i | |
| : | Sanitizing time of each ambulance in CMC j | |
| : | The penalty time | |
| : | The capacity of CMC m | |
| : | The capacity of ambulance k | |
| : | The decision parameter concerning the severity condition of suspected case i after visitation | |
| : | The severity of suspected case i after PE | |
| : | A large number | |
| Variables | ||
| : | 1, if the ambulance k travels between location i and j; otherwise 0 | |
| : | 1, if the ambulance k visits suspected case i with priority u; otherwise 0 | |
| : | Starting time of visitation suspected case with priority u by ambulance k | |
| : | Penalty time of visitation suspected case with priority u by ambulance k |
The proposed mathematical model is formulated as a Mixed Integer Non-linear Programming (MINLP) considering multi-ambulance, multi-CMC, and one objective function. The objective function for prioritizing approach (Eq. (1)) minimizes the maximum response time. In fact, the objective function minimizes the starting time of visiting the suspected case with lowest priority by each ambulance and penalty time of visitation. The penalty time function ensures that the suspected cases with higher severity are visited with higher priorities.
| (1) |
The corresponding constraints for prioritizing approach are given by Eqs. (2)–(19):
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
Constraints (2)–(4) ensure that only one ambulance can travel between two locations and that this travel happen only one time. These constraints utilize the model to avoid sub-tours. In addition, they allocate the ambulances to the routes. Constraints (5)–(7) assign each ambulance to each suspected case considering its priority. Eq. (8) guarantees that the total visitations must not exceed the total number of suspected cases. Constraints (9)–(11) represent the outgoing routes from a location. In fact, these equations ensure that each ambulance, after visiting a suspected case, travels to either another suspected case or a CMC. Constraint (12) states that the ambulance can travel between two suspected cases, if they have consecutive priorities. Eq. (13) states that the number of hospitalized suspected cases in each CMC must not exceed their capacity.
Constraint (14) shows that the total travel time of each ambulance must not surpass the available time. Constraint (15) indicates the route of each ambulance after visiting each suspected case based on its priority and constraint (16) shows the outgoing route of each ambulance from a CMC based on the priorities of the suspected cases. Eq. (17) calculates the starting visitation time of a suspected case with highest priority for each ambulance. In addition, the starting visitation time of other suspected cases are calculated by Eq. (18). Constraint (19) expresses that a suspected case with higher severity should be visited before another suspected case with lower severity. Moreover, it calculates the penalty time if this condition is not met.
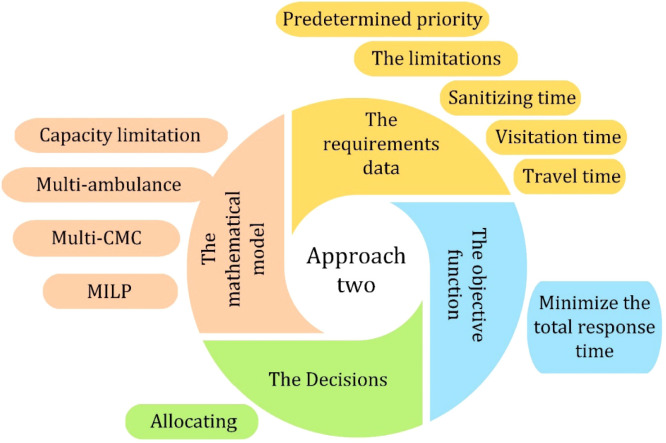
2.6. Allocating approach
In the allocating approach, the ambulances and CMCs are assigned to the suspected cases. Unlike prioritizing approach, visiting priorities are predetermined by the DC. It means that, the higher the severity of suspected cases, the higher priority of visitation. Therefore, each ambulance has to visit each suspected case with higher severity before any suspected case with lower priority. The aim of this approach is to minimize the total response time. In fact, allocating approach minimizes the critical total response time. The word “critical” here defines the condition in which suspected cases are in a severe condition and the ambulance must visit each suspected patient and carry them back to CMCs (See Fig. 7).
Fig. 7.
The descriptions of the proposed allocating approach.
2.6.1. The mathematical model for allocating approach
As mentioned in Section 2.2, the people are asked to take part in PE. The data of the PE are transferred to the DC. Then, the DC analyzes the collected data and the results of these analyses determine the suspected cases, their severity level, and their locations. In the allocating approach, the DC prioritizes the visitation of suspected cases based on their severity condition before the ambulances and the CMCs are assigned to the suspected cases. Therefore, the proposed mathematical modeling for allocating approach allocates the ambulances and CMCs to the suspected cases in order to minimize the total response time, and also meet the capacity of the ambulances and CMCs. To formulate, the notations, parameters, and variables are shown in Table 3.
Table 3.
The notations, parameters, and variables of the proposed mathematical model for allocating approach.
| Notations | Definition | |
|---|---|---|
| : | Set of suspected cases | |
| : | Set of medical centers | |
| : | Set of ambulances | |
| : | Set of all locations | |
| Parameters | ||
| : | Travel time between location i and j | |
| : | Visitation time of suspected case i | |
| : | Sanitizing time of each ambulance in CMC j | |
| : | The capacity of CMC m | |
| : | The capacity of ambulance k | |
| Variables | ||
| : | 1, if the suspected case i transfers to CMC m by ambulance k; otherwise 0 |
The proposed mathematical model is an Integer Linear Programming (ILP) which minimizes the critical response time (See Eq. (20)). The critical response time means all suspected cases have high severity and each ambulance has to transfer each suspected case to CMC after visiting them.
| (20) |
The constraints for allocating approach are formulated as Eqs. (21)–(26):
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
Constraints (21)–(23) guarantee that only one ambulance can travel between two locations and that this travel happen only once. In fact, these equations allocate an ambulance and a CMC to each suspected case. Eq. (24) ensures that the total number of allocated ambulances and CMCs must not exceed the total number of suspected cases. Constraint (25) indicates that the number of hospitalized suspected cases in each CMC must not surpass their capacity. Eq. (26) states that the critical traveling time of each ambulance must not exceed its capacity.
2.7. How to consider instant changes dynamically?
The most important question to be addressed through this study is how to confront the instant changes of external (SARS-COV-2 symptoms, infection map, suspected cases, and confirmed cases) and Internal (capacities of testing, identifying, transportation, and treatment) factors. In the proposed methodology, first, the people are evaluated via the PE. As a result, the suspected cases of SARS-COV-2 are identified. Due to the characteristics of SARS-COV-2, the external and internal factors of the medical system change instantly. For example, it is possible that one or number of new suspected cases are identified or the severity of identified some suspected cases change before or after visitation or during the time of visitation. These changes could happen in various settings including traveling time, sanitizing time, and the capacities of some ambulances or CMCs during the planned schedule. Therefore, in the proposed methodology, we consider the real-time changes by monitoring, analyzing, and rescheduling, provided new changes occur. In addition, the response plan depends on whether prioritizing approach or allocating approach is chosen by managers.
As aforementioned, prioritizing approach prioritizes the suspected cases and also allocates the suspected case to the ambulances and CMCs simultaneously in order to minimize the maximum response time, whereas allocating approach allocates the ambulances and CMCs according to predetermined priorities of suspected cases to minimize the critical response time. The DC monitors all the received information. Depending on which approach is selected, the DC transfers the evaluated external and internal information. Then, the results of these evaluation are transmitted to each ambulance and CMC. The recommended methodology for prioritizing approach and allocating approach to meet the real-time changes are illustrated in Fig. 8, Fig. 9, respectively. All in all, the utilization of IoT in the medical system not only coordinates the medical system with changes in real-time, but also provides the data to monitor the behavior and symptoms of SARS-COV-2 and also identify the spread map of this disease. Furthermore, the healthy and unaffected people are separated from suspected and confirmed cases and take away from dangerous areas. As a consequence, it is imperative to describe a methodology to confront the unpredictability of a SARS-COV-2 outbreak. Otherwise, it not only can endanger the health and safety of the society, but also can increase the response time and its associated costs significantly (see Fig. 9).
Fig. 8.
Pseudo-code of rescheduling in a real-time situation in prioritizing approach.
Fig. 9.
Pseudo-code of rescheduling in a real-time situation in the allocating approach.
3. Solution approach
In this section, the solution approaches for the proposed problem along with the encoding and decoding schemes are represented. When it comes to solving large-size problems, it could be difficult to obtain the best solutions by exact approaches as they usually consume both time and cost ([82]). Therefore, although the proposed models are validated with an exact solver (GAMS), for the larger size problems, multiple meta-heuristic algorithms and hybridized ones are utilized.
Behind the use of efficient meta-heuristic algorithms and hybridized ones, lies the special privilege of intensification and diversification phases of these approaches, since these phases bring the algorithms to their optimal solutions more quickly. Hence, some efficient algorithms, both capable old and recently developed algorithms, including Simulated Annealing (SA) and Social Engineering Optimization (SEO), as two strong old and recent single point algorithms, and Particle Swarm Optimization (PSO), as one of the efficient population-based algorithm in the literature ([83], [84]), and hybrid SA and PSO (SAPSO), hybrid SA and SEO (SASEO), and hybrid PSO and SEO (PSOSEO). The proposed encoding and decoding schemes are presented in the following subsection.
3.1. Encoding and decoding scheme
While there are multiple methods to implement encoding and decoding schemes, one effective plan must be used for each specific problem in order to achieve the best output results. Hence, in the proposed problem, the application of a “random key” approach is taken into account. The schematic representation of the utilized approach is depicted in Fig. 10. According to this figure and the methodology of a “random key” approach, a random number in the interval is generated. In order to obtain the priority for each patient, the priorities are sorted based on their number from smaller to larger numbers ([85], [86]). Then the priority is set according to the position of each number ([87]).
Fig. 10.
The proposed encoding and decoding scheme.
3.2. Simulated Annealing (SA)
Because the addressed problem is NP-hard, we propose several meta-heuristics to solve the problem. Simulated Annealing (SA) is a meta-heuristic algorithm that searches for solutions locally. It was first presented by Kirkpatrick et al. [88]. Based on the predefined model, we utilize a form of SA to deal with the proposed problem. First of all, SA initiates and finds a best solution among generated random solutions. Then, using a specified approach, neighbor solutions are generated near its position ([89]). Three different neighborhood approaches are employed in this study, which include Swap, Reversion, and Insertion. For further explanation we refer the readers to see Grobelny and Michalski [90]. The pseudocode of the proposed SA algorithm is shown in Fig. 11.
Fig. 11.
The pseudocode of the SA algorithm.
3.3. Social Engineering Optimization (SEO)
Here, a single-solution meta-heuristic is suggested for this problem that is known as the SEO meta-heuristic algorithm. Fathollahi-Fard et al. [91] initially introduced this algorithm and generalized social engineering in real-world studies. The solution to this algorithm represents each person as well as their features. For instance, the math capability, working, etc. are all the variables of the solution searching area. The algorithm initiates by defining attacker and defender. The algorithm benefits from the fact that on one hand, the attacker recognizes a social engineering attack and on the other hand controls the defender. The attacker itself is a good solution.
By conducting multiple tests, the traits of the defenders are obtained and the attacker tries to probe the defender by these traits. Consequently, in the search space, the algorithm duplicates a trait from the attacker to the same trait from the defender. More details are accessible in ([92], [93], [91], [94]). Fig. 12, represents the proposed pseudo-code of the SEO algorithm.
Fig. 12.
The pseudocode of the SEO algorithm.
3.4. Particle Swarm Optimization (PSO)
Particle Swarm Optimization is a type of evolutionary algorithm which was first established by Kennedy and Eberhart [95]. The basics of the algorithm involve evolving the particles to come near optimal solutions by determining the velocity. To achieve this, three types of elements are needed which are best particle status (), the best particle so far (), and the velocity ([96]). Considering this, the following equations are evaluated to set the new particle position and its velocity.
| (27) |
| (28) |
In Eqs. (27)–(28), and are the positive values that should be determined by parameter tuning. and are the interval random number within . In the steps of the PSO algorithm, each particle is a possible solution in the feasible solution space. These particles achieve new locations by defining velocity in each iteration of the algorithm ([97]). In each iteration, these particles approach near the best feasible solutions until the stopping condition of the algorithm is met. The pseudocode of the PSO algorithm is illustrated in Fig. 13.
Fig. 13.
The pseudocode of the PSO algorithm.
3.5. Hybrid meta-heuristics
Beside exploiting the SA, SEO and PSO algorithms, we propose three hybrid meta-heuristics including hybrid SA and PSO (SAPSO), hybrid SA and SEO (SASEO), and hybrid PSO and SEO (PSOSEO) algorithms to solve the proposed relief supply chain problem. The obvious advantage of SA is that it allows searching many points in search space by setting the temperature. On the other hand, utilizing the PSO algorithm as a sub-loop iteration enables the SA algorithm to takes advantage of the notable benefits of the PSO algorithm simultaneously. In addition, in the PSO algorithm iterations, a large number of new particles are searched locally and globally. Therefore, the convergence rate is generally slow because of the natural random oscillation of the local optimal solutions ([98]). But the SA algorithm cab enable the PSO particles to restrict position change and accelerate the convergence rate of the algorithm. The pseudocode of the proposed SAPSO is presented in Fig. 14.
Fig. 14.
The pseudocode of the proposed SAPSO algorithm.
In addition to the SAPSO algorithm, the characteristic of the SA algorithm is combined with newly introduced SEO algorithm to investigate the results. The properties of SA enable the algorithm to work and use the characteristics of other algorithms. This time, after obtaining and updating the algorithm’s best temperature in the SA’s steps, the SEO algorithm is applied to the achieved local best results of SA in order to find the global best among SA’s generated solutions. The proposed pseudocode of SASEO is defined in Fig. 15.
Fig. 15.
The pseudocode of the proposed SASEO algorithm.
The last utilized hybrid meta-heuristic involves combining the characteristics of PSO and SEO algorithms. In this hybrid approach, the steps of the PSO algorithm is combined with SEO for each generated particle. Each PSO particle is compared with the generated SEO solution and replaced with the best solution. This would result to even better answers in each iteration of the algorithm. Fig. 16, shows the proposed pseudocode of PSOSEO algorithm.
Fig. 16.
The pseudocode of the proposed PSOSEO algorithm.
4. Computational results
This section presents the computational testing and the achieved results of the proposed meta-heuristics and hybrid ones. These computations are conducted in various steps. In the first step, a random data set is generated and, in the second, the application of a Taguchi experiment is taken into account. The Taguchi approach helps to set the algorithm parameters for each meta-heuristics and hybrid ones. In order to set these parameters, Response Surface Methodology (RSM) is implemented to not only compare each algorithm with each other, but also to obtain the best solution for the proposed models ([99]). The results from various defined algorithms then are obtained for diverse problem sizes to investigate the efficiency of these algorithms in a wide variety of settings.
4.1. Generating data sets
In this subsection, various problem sizes (small, medium, and large), including three types of problems, are examined to verify the effectiveness of the proposed meta-heuristics and hybrid ones. The complexity of the problems increases as its associated number increases. Therefore, by solving a considerable number of problems in diverse sizes, the efficiency and performance of each meta-heuristic and hybrid heuristic is observed and the obtained results are compared. The dimensions of the considered problems and their sizes are documented in Table 4.
Table 4.
Problem classification.
| Classification | Instance | Problem size (prioritizing approach) | Problem size (allocating approach) |
|---|---|---|---|
| Small | SP1 | (3, 1, 1, 3) | (3, 1, 1,) |
| SP2 | (6, 1, 2, 6) | (6, 1, 2,) | |
| SP3 | (10, 2, 3, 10) | (10, 2, 3) | |
| Medium | MP4 | (20, 3, 4, 20) | (20, 3, 4) |
| MP5 | (30, 3, 5, 30) | (30, 3, 5) | |
| MP6 (case study) | (45, 4, 8, 45) | (45, 4, 8) | |
| MP7 | (75, 6, 11, 75) | (75, 6, 11) | |
| Large | LP8 | (100, 8, 16, 100) | (100, 8, 16) |
| LP9 | (150, 12, 20, 150) | (150, 12, 20) | |
| LP10 | (200, 15, 25, 200) | (200, 15, 25) | |
The values of the implemented parameters are presented in Table 5.
Table 5.
Values of parameters.
| Prioritizing approach |
Allocating approach |
|||
|---|---|---|---|---|
| Parameters | Value | Parameters | Value | |
4.2. Setting the parameters
To evaluate the efficiency of the proposed meta-heuristic algorithms and hybrid ones, a specific approach must be employed. One approach to get the best out of these algorithms is to set and tune the algorithm’s parameters. Tuning the algorithm parameters both increases the efficiency of the algorithm and the quality of the solutions. Hence, there must be some levels to tune these parameters for each algorithm. To achieve this, Taguchi experiments were employed ([100]). The Taguchi approach proposes a set of experiments in order to determine the appropriate level for each algorithm parameter. Taguchi experimental design allows a limited number of experiments to estimate the best value for each parameter ([101], [102]). The considered parameters along with their relevant levels are shown in Table 6.
Table 6.
The proposed meta-heuristic algorithm’s factors and their levels.
| Algorithm | Factor | Levels |
Best Level |
||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | Prioritizing approach | Allocating approach | |||
| SA | A: Sub-iteration (Sub-it) | 25 | 35 | 45 | 35 | 25 | |
| B: Initial temperature () | 1100 | 1200 | 1300 | 1200 | 1200 | ||
| C: Rate of reduction (R) | 0.93 | 0.95 | 0.97 | 0.97 | 0.95 | ||
| D: Used methodology of local search (Tm) | Reversion | Swap | Insertion | Insertion | Swap | ||
| SEO | A: Rate of collecting data () | 0.21 | 0.29 | 0.32 | 0.29 | 0.21 | |
| B: Rate of connecting attacker () | 0.044 | 0.051 | 0.056 | 0.051 | 0.056 | ||
| C: Number of connections (N) | 45 | 55 | 65 | 55 | 45 | ||
| PSO | A: Population size (n-pop) | 35 | 45 | 55 | 45 | 45 | |
| B: Weight of particles (W) | 0.55 | 0.65 | 0.85 | 0.55 | 0.65 | ||
| C: C1 | 1.2 | 1.3 | 1.4 | 1.4 | 1.3 | ||
| D: C2 | 1.3 | 1.4 | 1.5 | 1.4 | 1.4 | ||
| E: Maximum iteration (MaxIt) | 150 | 250 | 350 | 150 | 250 | ||
| SAPSO | A: Sub-iteration (Sub-it) | 25 | 35 | 45 | 35 | 25 | |
| B: Initial temperature () | 1100 | 1200 | 1300 | 1200 | 1100 | ||
| C: Rate of reduction (R) | 0.93 | 0.95 | 0.97 | 0.97 | 0.93 | ||
| D: Used methodology of local search (Tm) | Reversion | Swap | Insertion | Insertion | Reversion | ||
| E: Weight of particles (W) | 0.55 | 0.65 | 0.85 | 0.55 | 0.85 | ||
| F: C1 | 1.2 | 1.3 | 1.4 | 1.4 | 1.4 | ||
| G: C2 | 1.3 | 1.4 | 1.5 | 1.3 | 1.3 | ||
| H: Maximum iteration (MaxIt) | 150 | 250 | 350 | 250 | 250 | ||
| SASEO | A: Sub-iteration (Sub-it) | 25 | 35 | 45 | 25 | 35 | |
| B: Initial temperature () | 1100 | 1200 | 1300 | 1100 | 1200 | ||
| C: Rate of reduction (R) | 0.93 | 0.95 | 0.97 | 0.95 | 0.95 | ||
| D: Used methodology of local search (Tm) | Reversion | Swap | Insertion | Reversion | Reversion | ||
| E: Rate of collecting data () | 0.21 | 0.29 | 0.32 | 0.29 | 0.21 | ||
| F: Rate of connecting attacker () | 0.044 | 0.051 | 0.056 | 0.044 | 0.051 | ||
| G: Number of connections (N) | 45 | 55 | 65 | 65 | 55 | ||
| PSOSEO | A: Population size (n-pop) | 35 | 45 | 55 | 55 | 45 | |
| B: Weight of particles | 0.55 | 0.65 | 0.85 | 0.65 | 0.85 | ||
| C: C1 | 1.2 | 1.3 | 1.4 | 1.3 | 1.4 | ||
| D: C2 | 1.3 | 1.4 | 1.5 | 1.5 | 1.4 | ||
| E: Maximum iteration (MaxIt) | 150 | 250 | 350 | 150 | 150 | ||
| F: Rate of collecting data () | 0.21 | 0.29 | 0.32 | 0.21 | 0.21 | ||
| G: Rate of connecting attacker () | 0.044 | 0.051 | 0.056 | 0.051 | 0.044 | ||
| H: Number of connections (N) | 45 | 55 | 65 | 45 | 45 | ||
According to the objective function of minimization, the response of “smaller-is-better” is employed for the experimental tests of the Taguchi approach. The Taguchi method provides a unique design of orthogonal arrays to study the entire parameter space with a small number of experiments. By computing the objective function value for each array, the signal-to-noise (S/N) ratio is computed for parameters. This ratio is used to measure the deviation of quality characteristics from the desired values. The larger the S/N ratio, the better the performance characteristic ([103]). Eq. (29) shows the signal-to-noise ratio and its calculation.
| (29) |
In Eq. (29), n is the number of experiments and Y is the observed data. Following this trend, the algorithm’s parameters and their levels could be determined. To choose the best level for each algorithm’s parameters, the signal-to-noise plot is calculated for two proposed approaches.
As aforementioned, three problem classifications in ten test problems are replicated 40 times in order to determine the best levels for each algorithm parameter. Since the problem could not be solved to optimality, the Relative Percentage Deviation (RPD) is employed. The reason is that each problem dimension is different from others. The settings of RPD is defined by Eq. (30) ([104], [105]).
| (30) |
In Eq. (30), and are values of the objective function in individual trials and the best solution among those trials, respectively. After determining the objective function value using different test problems, in the next step, these values are converted to RPD value and their mean value is also calculated. Afterwards, the Taguchi approach calls for converting these values to a signal-to-noise ratio and averaging all of them for each considered level. Generally, Taguchi recommends a set of orthogonal arrays ([106], [107]). These arrays reduce the number of total trials for each algorithm. In this regard, L9 design is selected for SEO, whereas L16 design is selected for SA and PSO, and L27 for SAPSO, SASEO, and PSOSEO to decrease the number of total experiments. The tuned parameters for each algorithm are reported in the last two columns of Table 5.
4.3. Experimental results
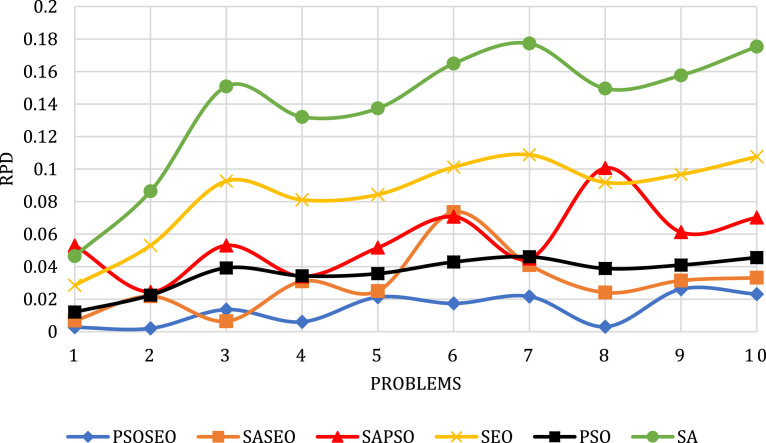
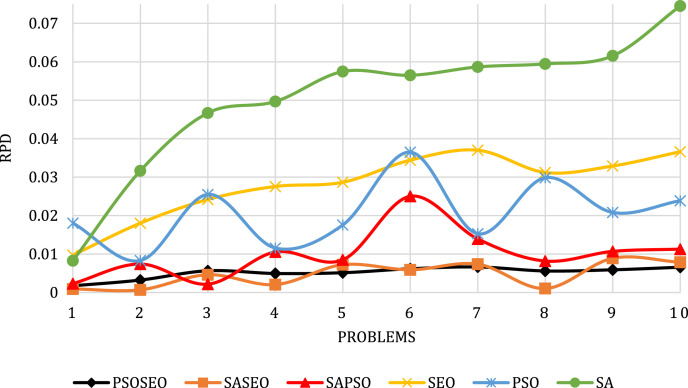
After obtaining the best levels for each algorithm parameter, the performance of the various solution methods can be compared in diverse test problems by means of RPD. In this subsection, three metrics, including RPD, objective function, and processing time are considered to evaluate the efficiency of the proposed algorithms. The mean RPD for the considered meta-heuristics and hybrid ones is depicted in Fig. 17, Fig. 18.
Fig. 17.
The mean RPD of each algorithm for prioritizing approach.
Fig. 18.
The mean RPD of each algorithm for allocating approach.
In addition, Table 7, Table 8 compare the meta-heuristic and hybrid algorithms by the means of RPD, objective function, and processing time.
Table 7.
The obtained results for prioritizing approach (TP Test Problem, PT Processing Time).
| Algorithm | TP | SP | SP | SP | MP | MP | MP | MP | LP | LP | LP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SA | Obj. | 133 | 248 | 373 | 747 | 971 | 1397 | 2433 | 3058 | 4546 | 6190 |
| PT | 0.17 | 1.26 | 5.02 | 7.18 | 10.6 | 31.29 | 76.6 | 149.88 | 212.8 | 259.67 | |
| RPD | 0.046523 | 0.086401 | 0.150869 | 0.13206 | 0.137355 | 0.164881 | 0.177232 | 0.14954 | 0.157626 | 0.175349 | |
| PSO | Obj. | 131 | 242 | 366 | 624 | 921 | 974 | 2157 | 2787 | 3914 | 5180 |
| PT | 0.35 | 2.03 | 6.44 | 7.5 | 19.19 | 41.27 | 118.28 | 214.89 | 385.49 | 551.81 | |
| RPD | 0.012096 | 0.022464 | 0.039226 | 0.034335 | 0.035712 | 0.042869 | 0.04608 | 0.03888 | 0.040982 | 0.04559 | |
| SEO | Obj. | 133 | 247 | 368 | 708 | 972 | 1227 | 2332 | 3049 | 4442 | 5485 |
| PT | 0.29 | 1.38 | 5.2 | 8.08 | 13.06 | 31.77 | 82.6 | 163.5 | 238.8 | 291.3 | |
| RPD | 0.02856 | 0.05304 | 0.092616 | 0.08107 | 0.08432 | 0.101218 | 0.1088 | 0.0918 | 0.096764 | 0.107644 | |
| SAPSO | Obj. | 137 | 242 | 355 | 624 | 943 | 1012 | 2157 | 3058 | 4138 | 5219 |
| PT | 0.71 | 3.18 | 8.99 | 9.59 | 24.38 | 41.38 | 181.3 | 315.09 | 480.23 | 685.26 | |
| RPD | 0.05304 | 0.02448 | 0.05304 | 0.034 | 0.05168 | 0.07072 | 0.044948 | 0.10064 | 0.0612 | 0.070176 | |
| SASEO | Obj. | 125 | 242 | 348 | 624 | 899 | 1070 | 2157 | 2799 | 3914 | 5179 |
| PT | 0.52 | 3.5 | 10.78 | 10.16 | 28.02 | 55.04 | 248.16 | 469.04 | 619.07 | 741.38 | |
| RPD | 0.0068 | 0.02176 | 0.006392 | 0.031008 | 0.025024 | 0.073576 | 0.040936 | 0.024072 | 0.031457 | 0.033184 | |
| PSOSEO | Obj. | 128 | 239 | 353 | 608 | 899 | 953 | 2107 | 2718 | 3908 | 5169 |
| PT | 0.55 | 3.76 | 13.12 | 16.23 | 28.31 | 70.06 | 262.93 | 447.64 | 647.41 | 876.04 | |
| RPD | 0.00272 | 0.00204 | 0.0136 | 0.006059 | 0.02125 | 0.017374 | 0.021658 | 0.00306 | 0.02618 | 0.02312 |
Table 8.
The obtained results for allocating approach (TP Test Problem, PT Processing Time).
| Algorithm | TP | SP | SP | SP | MP | MP | MP | MP | LP | LP | LP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SA | Obj. | 155 | 331 | 511 | 882 | 1147 | 1648 | 2659 | 3827 | 5189 | 6882 |
| PT | 0.31 | 0.46 | 0.465 | 0.577 | 0.615 | 0.864 | 0.925 | 1.576 | 3.013 | 6.18 | |
| RPD | 0.00826 | 0.031651 | 0.04668 | 0.049662 | 0.05746 | 0.056484 | 0.058655 | 0.059451 | 0.061551 | 0.074511 | |
| PSO | Obj. | 165 | 318 | 504 | 827 | 1071 | 1590 | 2647 | 3460 | 4973 | 6335 |
| PT | 0.904 | 1.01 | 2.7 | 2.82 | 3.73 | 5.48 | 7.64 | 11.7 | 28.2 | 57.07 | |
| RPD | 0.018034 | 0.008323 | 0.025484 | 0.01156 | 0.017571 | 0.036485 | 0.015282 | 0.029846 | 0.020808 | 0.02386 | |
| SEO | Obj. | 155 | 326 | 502 | 858 | 1072 | 1577 | 2652 | 3644 | 5071 | 6660 |
| PT | 0.75 | 0.96 | 1.27 | 1.52 | 1.81 | 3.74 | 4.37 | 7.66 | 16.41 | 32.18 | |
| RPD | 0.00971 | 0.018034 | 0.024187 | 0.027564 | 0.028669 | 0.034414 | 0.036992 | 0.031212 | 0.0329 | 0.036599 | |
| SAPSO | Obj. | 153 | 318 | 487 | 827 | 1040 | 1571 | 2638 | 3460 | 4873 | 6258 |
| PT | 1.45 | 1.53 | 3.49 | 4.41 | 5.22 | 9.68 | 13.9 | 32.9 | 59.07 | 107.02 | |
| RPD | 0.002312 | 0.007398 | 0.002173 | 0.010543 | 0.008508 | 0.025016 | 0.013918 | 0.008184 | 0.010695 | 0.011283 | |
| SASEO | Obj. | 151 | 310 | 490 | 815 | 1040 | 1483 | 2628 | 3425 | 4861 | 6234 |
| PT | 1.5 | 2.129 | 3.61 | 7.11 | 8.04 | 13.66 | 26.153 | 41.74 | 93.2 | 146.46 | |
| RPD | 0.000925 | 0.000694 | 0.004624 | 0.00206 | 0.007225 | 0.005907 | 0.007364 | 0.00104 | 0.008901 | 0.007861 | |
| PSOSEO | Obj. | 153 | 313 | 490 | 817 | 1040 | 1483 | 2605 | 3443 | 4816 | 6234 |
| PT | 1.5 | 3.84 | 4.73 | 8.85 | 10.477 | 19.98 | 26.5 | 54.26 | 97.49 | 162.3 | |
| RPD | 0.001742 | 0.003235 | 0.005648 | 0.004944 | 0.005143 | 0.006173 | 0.006636 | 0.005599 | 0.005901 | 0.006565 |
According to Table 7, Table 8 and Fig. 16, Fig. 17, SASEO proved it superiority among all the proposed approaches by showing the lowest values for RPD. This means not only that SASEO yields the best results, but also that its final results are more convergent with the lowest variance among all tested algorithms. In this regard, PSOSEO, combined with the two-population based and single-point based algorithms, yields good results. In fact, in some problem sizes it showed better results than other meta-heuristics and hybrid methods. In addition, SAPSO showed superiority for smaller problem sizes. It also worth mentioning that although the SASEO and PSOSEO algorithms obtained the best results among all algorithms, they take more time to reach their optimal results.
4.4. A case study
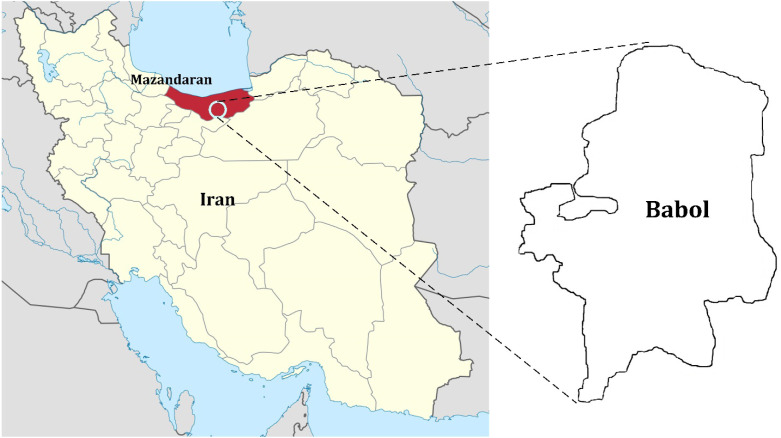
In the present study, the proposed methodology has been implemented in Iran. According to the www.who.int, Iran is the 14th country with the most confirmed cases of SARS-COV-2 and also the 8th country in terms of SARS-COV-2 deaths. Among the different cities in Iran, Babol, one of the biggest cities in the Mazandaran Province and also in northern Iran, with more than 800,000 in population, has one of the highest numbers of confirmed cases of SARS-COV-2. Hence, in this section, we present a real case study of Babol, Mazandaran, Iran, and apply the proposed methodology in this city. In this research, we collected the contributed data from daily observations and Iranian governmental organizations.2 The location of Babol in Iran is illustrated in Fig. 19.
Fig. 19.
The location of Babol in Mazandaran province, Iran.
According to the proposed methodology, the IoT system was utilized to identify suspected SARS-COV-2 cases in the shortest time in order to confront the outbreak chain. There is no time limit for individuals to participate in the PE. The number of people who were taken account in the PE were 3187 in this zone. The age range of the participants is between 10 and 63 years old. Regarding the gender of the participants, 41.8% were male (1333 persons) and 58.2% female (1854 persons). After the PE, the data were transferred to the DC and analyzed. The identified suspected cases were 45 (N=45) persons, and the genders of suspected cases were 64.4% male (29 persons) and 35.6% female (16 persons). The characteristics of the identified suspected cases are shown in Table 9.
Table 9.
Characteristics of identified suspected case by PE.
| Number | Gender | Identification date | Symptoms of suspected cases | Severity by PE: b(n) |
|---|---|---|---|---|
| 1 | Male | 1:12 | Fever, cough, muscle pains, nasal congestion | 60 |
| 2 | Female | 1:35 | Fever, dry cough, tiredness, rash on skin | 85 |
| 3 | Male | 6:47 | Fever, cough | 40 |
| 4 | Male | 7:00 | Dry cough, muscle pains | 35 |
| 5 | Female | 7:02 | Fever, fatigue, shortness of breath, headache | 75 |
| 6 | Male | 7:02 | Fever, rash on skin | 55 |
| 7 | Female | 7:03 | Muscle pains, headache, tiredness, diarrhea | 40 |
| 8 | Male | 7:12 | Fatigue, diarrhea, cough | 35 |
| 9 | Female | 7:12 | Fever, cough, shortness of breath, nasal congestion | 70 |
| 10 | Male | 7:15 | Nausea, conjunctivitis | 30 |
| 11 | Male | 7:46 | Fever, muscle pains | 40 |
| 12 | Male | 8:13 | Dry cough, fatigue, headache | 50 |
| 13 | Female | 8:16 | Shortness of breath, discoloration of fingers or toes | 80 |
| 14 | Female | 8:18 | Fever, cough | 50 |
| 15 | Male | 8:20 | Muscle pains, conjunctivitis | 40 |
| 16 | Female | 8:38 | Fever, headache, nausea | 50 |
| 17 | Female | 9:37 | Fatigue, headache, loss of taste or smell | 50 |
| 18 | Female | 9:53 | Fever, dry cough | 80 |
| 19 | Male | 10:08 | Dry cough, muscle pains | 55 |
| 20 | Female | 10:10 | Muscle pains, headache, cough | 45 |
| 21 | Male | 10:16 | Fever, dry cough, shortness of breath | 100 |
| 22 | Male | 10:49 | Shortness of breath, cough | 60 |
| 23 | Male | 11:02 | Fever, fatigue | 35 |
| 24 | Male | 11:19 | Muscle pains, nausea, tiredness, loss of taste or smell | 55 |
| 25 | Female | 11:49 | Fever, dry cough, headache | 75 |
| 26 | Male | 12:32 | Loss of taste or smell, headache, fever | 60 |
| 27 | Female | 13:14 | Dry cough, muscle pains, shortness of breath, headache | 80 |
| 28 | Female | 13:46 | Muscle pains, conjunctivitis, diarrhea | 60 |
| 29 | Male | 15:28 | Fever, headache | 35 |
| 30 | Male | 15:51 | Fever, muscle pains, tiredness | 60 |
| 31 | Male | 16:44 | Cough, nausea | 30 |
| 32 | Female | 18:01 | Dry cough, conjunctivitis | 35 |
| 33 | Female | 18:37 | Cough, loss of taste or smell | 45 |
| 34 | Female | 19:09 | Fever, fatigue, headache | 45 |
| 35 | Male | 19:09 | Fever, dry cough | 70 |
| 36 | Male | 19:23 | Fever, headache, rash on skin | 90 |
| 37 | Female | 19:27 | Muscle pains, discoloration of fingers or toes | 35 |
| 38 | Female | 19:44 | Fatigue, headache, cough | 60 |
| 39 | Male | 20:21 | Fever, cough, nasal congestion, nausea | 70 |
| 40 | Male | 20:39 | Tiredness, loss of taste or smell | 65 |
| 41 | Male | 21:07 | Dry cough, pains, tiredness | 70 |
| 42 | Male | 21:58 | Nasal congestion, tiredness | 35 |
| 43 | Male | 22:02 | Dry cough, shortness of breath | 75 |
| 44 | Female | 22:09 | Fever, muscle pains, shortness of breath | 100 |
| 45 | Male | 22:18 | Dry cough, shortness of breath | 90 |
According to Table 9, the suspected cases have been identified by time of day and also have different severities. The approximate location of each suspected case and CMC in the study area (Babol) are shown in Fig. 20. In addition, the approximate travel time between locations was obtained from Google Maps.
Fig. 20.
The map of identified suspected cases.
In this city exist four CMCs, which all hospitalize and treat SARS-COV-2 patients. Eight ambulances are responsible for serving and visiting suspected cases of SARS-COV-2 in the planning horizon. Therefore, the scheduled response plan is sent to each ambulance and CMC in real-time based on the identified suspected cases, their severities, their locations, and the capacities of the ambulances and CMCs. As aforementioned, there are two approaches to schedule the response plan of each ambulance. Here to consider the two proposed approaches, two attitudes has taken into account. In attitude one, suspected cases are identified during the planning horizon while in attitude two, all suspected cases are identified at the beginning of the planning horizon. We verified and analyzed these two approaches according to these attitudes.
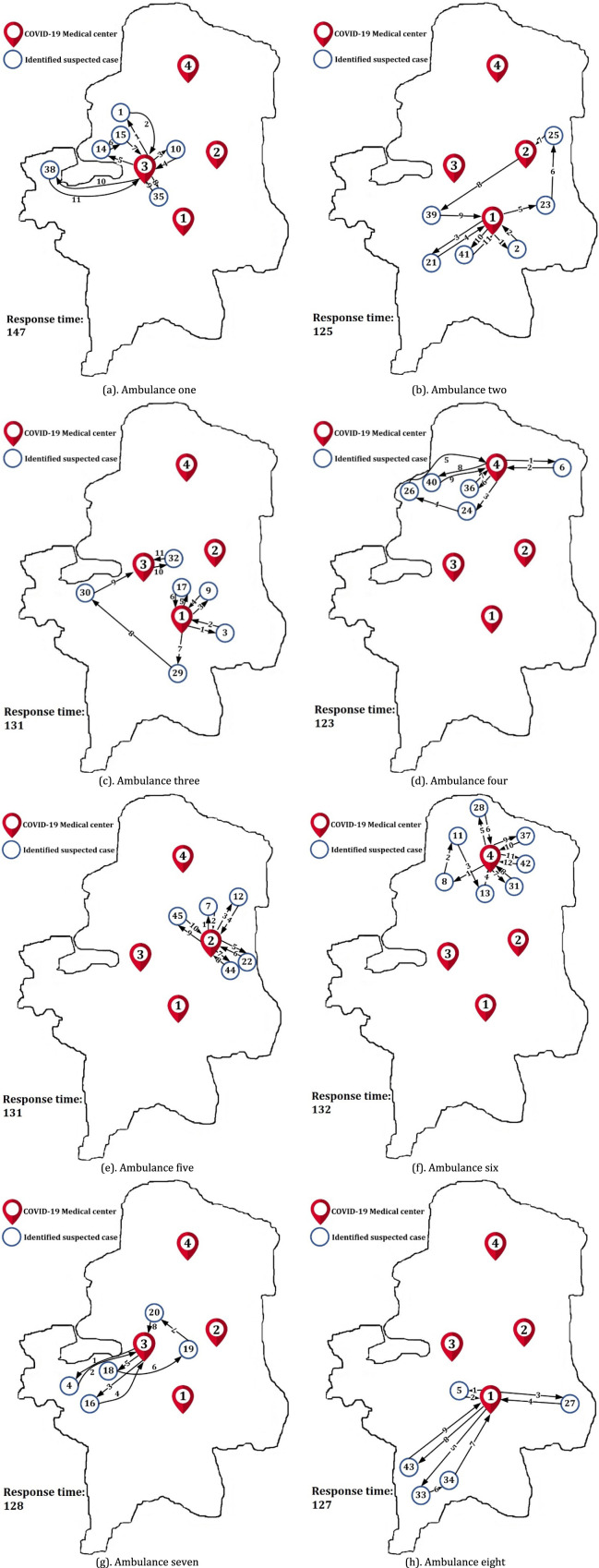
Prioritizing approach allocates the ambulances and the CMCs to the suspected cases in order to minimize the maximum response time. Based on prioritizing approach, the routes of the eight ambulances are shown in Fig. 21(a)–(h).
Fig. 21.
The directions of eight ambulances, based on prioritizing approach.
As shown in Fig. 21, the longest response time of the ambulances is 147 min and the shortest one is 125 min, and the total response time is 1044 min. In addition, the longest waiting time among the suspected cases is 18 min and the shortest one is 4 min. Although the number of each ambulance’s trips and also the number of suspected cases allocated to ambulances are different, the response times of the ambulances are similar.
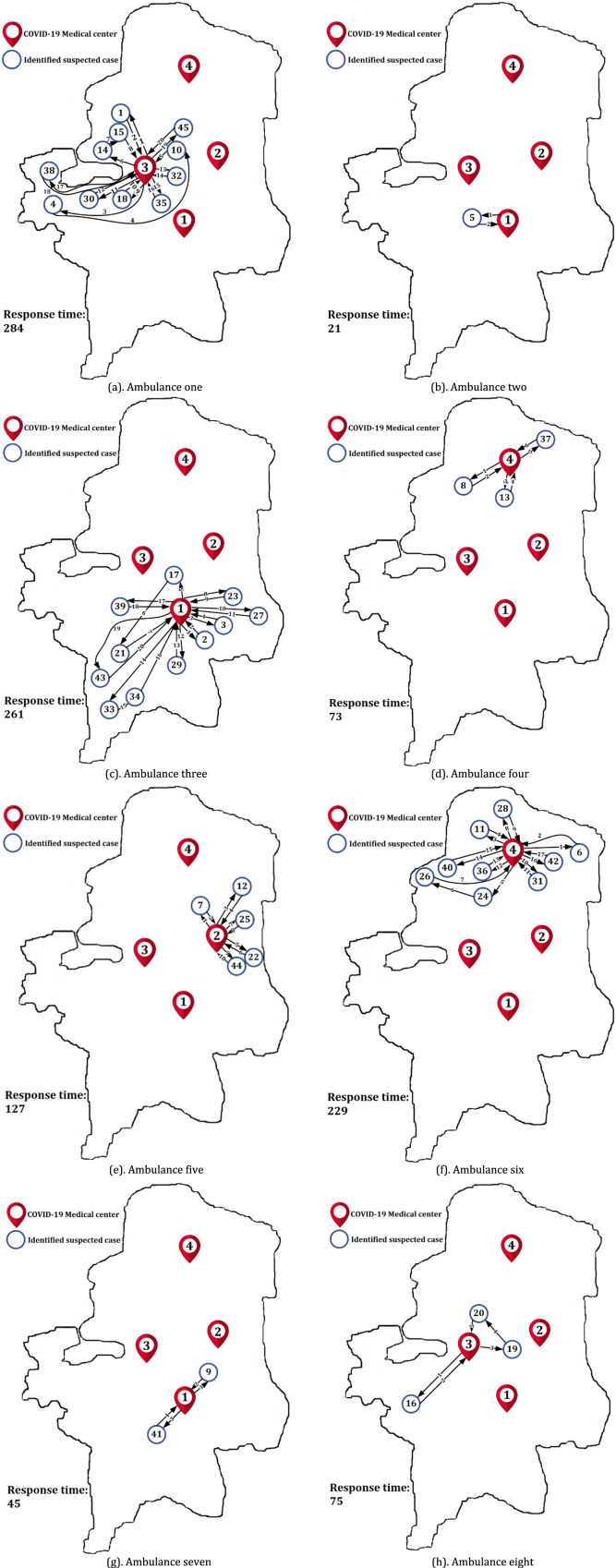
Allocating approach assigns the suspected cases to the ambulances and CMCs based on predetermined priorities in order to minimize the total response time. For allocating approach, the routes of the eight ambulances are illustrated in Fig. 22(a)–(h).
Fig. 22.
The directions of eight ambulances, based on allocating approach.
The longest response time of the ambulances is 284 min and the shortest one is 21 min, and the total response time is 1115 min. In addition, the longest waiting time among the suspected cases is 23 min and the shortest one is 5 min. Moreover, the number of each ambulance’s trips, the number of the allocated suspected cases, and the response time of the ambulances are much different from each other. In this modality, the suspected cases are identified over the planning horizon (day). As a result, the number of suspected cases is different at various time during a day. Therefore, in addition to the capacities of ambulances and CMCs, severities of suspected cases, travel time, visit time, sanitizing time, and the identification time of suspected cases is also among the criteria for responsiveness planning. For example, according to Fig. 20, Fig. 21, the suspected case with less severity (60%) is visited earlier than the suspected case with more severity (75%). As a consequence, there is a need to schedule in a real-time manner.
In this attitude (attitude one), suspected cases are identified in real-time (along the planning horizon). Although the total response time and waiting time of patients in the prioritizing approach is less than the allocating approach, but there is not much difference between them. In addition, the response time differences ambulances using the prioritizing approach is much closer to each other than the allocating approach since they have various routing networks.
4.5. If all suspected cases are identified at the beginning of the planned horizon?
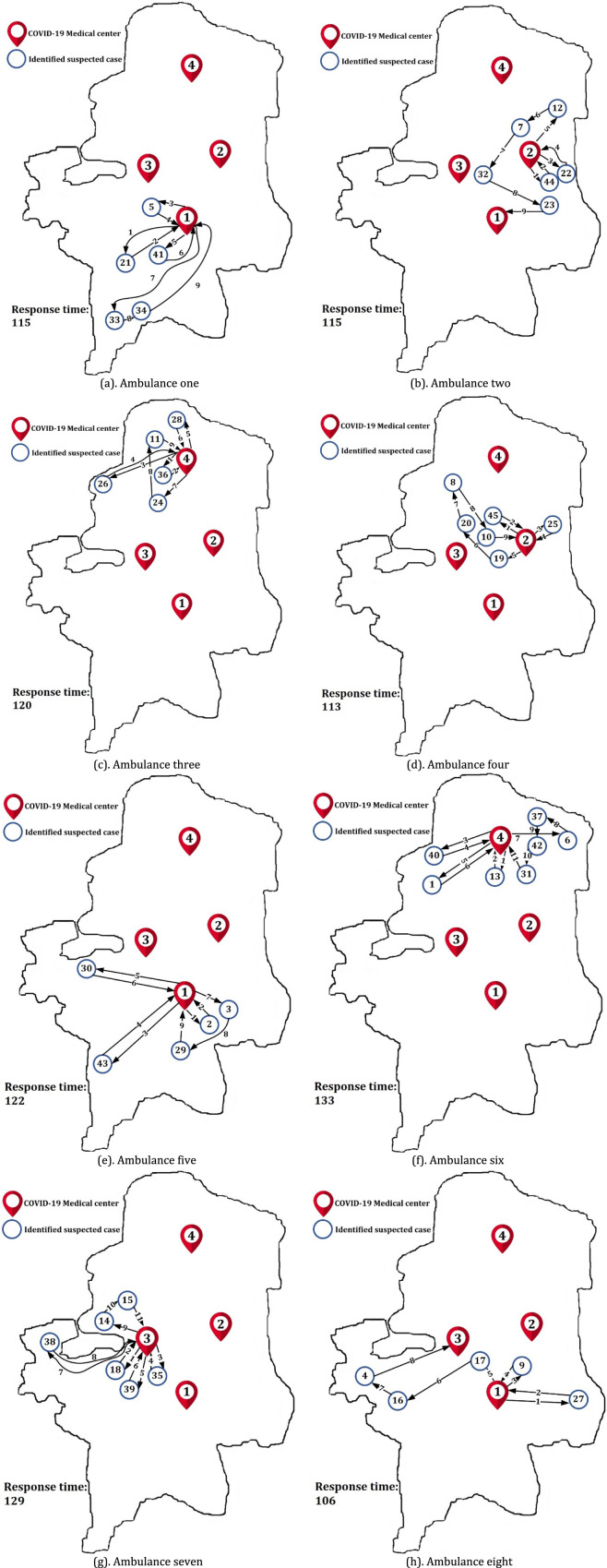
If all suspected cases are identified at the beginning of the planned horizon, identification time of suspected cases is not a criterion of planning anymore. Hence, as in the prioritizing approach, all suspected cases are prioritized and then are allocated to the ambulances and CMCs in order to minimize the maximum response time based on the capacities of ambulances and CMCs, severity of suspected cases, travel time, visit time, and sanitizing time. The routes of the eight ambulances are indicated in Fig. 23(a)–(h).
Fig. 23.
The direction of eight ambulances, based on prioritizing approach.
As shown in Fig. 22, the longest response time of the ambulances is 133 min and the shortest one is 106 min and also the total response time is 953 min. In addition, the greatest waiting time of the suspected cases is 129 min and the least is 3 min.
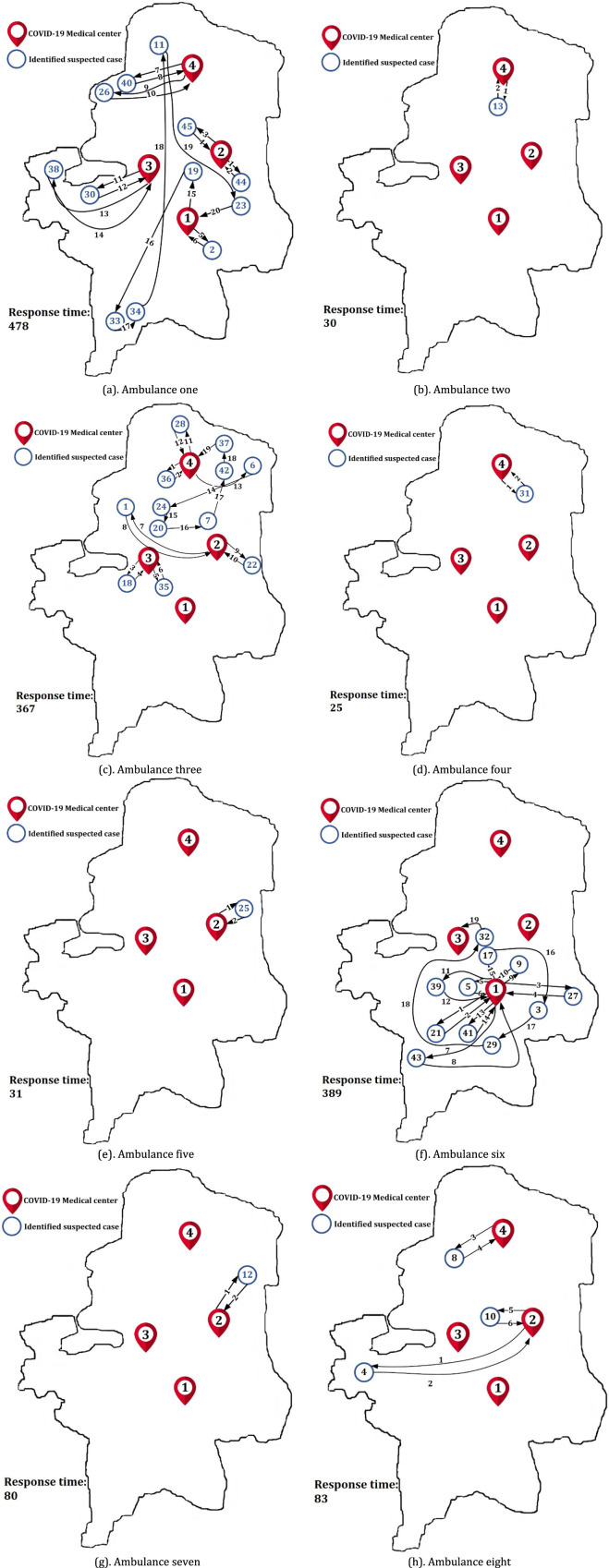
In the allocating approach, all suspected cases are allocated to the ambulances and CMCs in order to minimize the total response time based on the capacities of ambulances and CMCs, severities of suspected cases, travel time, visit time, sanitizing time, and the predetermined priorities. The routes of the eight ambulances are shown in Fig. 24(a)–(h).
Fig. 24.
The directions of eight ambulances, based on allocating approach.
As indicated in Fig. 23, the longest response time among the ambulances is 478 min and the shortest one is 30 min, and the total response time is 1483 min. In addition, the most waiting time of the suspected cases is 459 min and the less one is 3 min.
In attitude two, the suspected cases are identified at the beginning of the planned horizon. In this attitude, the total response time and the suspected cases waiting of prioritizing approach are also less than allocating approach. In addition, the response time of ambulances of prioritizing approach is much closer than allocating approach.
4.6. Prioritizing approach or allocating approach?
The results of the case study (attitude one and attitude two) and test problems are illustrated in Figs. 20–23 and Table 6, Table 7, respectively. There are big differences between prioritizing approach and allocating approach. The main observations about the first attitude in Fig. 20, Fig. 21, the second attitude in Fig. 22, Fig. 23, and test problems in Table 6, Table 7 are:
-
•
Both approaches respect the capacity limitations of the ambulances and the CMCs.
-
•
In both approaches, the suspected cases are visited based on their severities. In fact, the suspected cases with higher severities are visited earlier than the suspected cases with lower severities. In prioritizing approach, considering the penalty time, the suspected cases with higher severities are visited earlier. On the other hand, in allocating approach, the suspected cases are prioritized after PE and then they are assigned to the ambulances and the CMCs.
-
•
In prioritizing approach, the response time of the ambulances is more balanced than in allocating approach. Therefore, the number of available ambulances in prioritizing approach are more than in allocating approach at any moment.
-
•
During the scheduling, if the number of identified suspected cases at any moment is less than the number of ambulances, the total response time and waiting time in both approaches are similar and there is no significant difference between them. But the responsiveness structure (allocation of suspected cases to the ambulances and CMCs and also visit network) is different in both approaches.
-
•
If the number of identified suspected cases at any moment of the planned horizon is greater than the number of the available ambulances, the total response time and waiting time with prioritizing approach is much less than with allocating approach. In fact, in prioritizing approach, in addition to the travel time of ambulances from CMCs to the suspected cases and vice versa, the visiting time, the sanitizing time, the severity, and the capacities of CMCs and the ambulances, the travel time between two suspected cases is also considered to decrease the total response time by visiting a suspected case after visiting another one if it is possible. Therefore, this criterion prevents unnecessary return travel as well as extra travels. But allocating approach minimizes the critical response time. It does not consider the relevance travel time between the suspected cases. As a result, the ambulances travel longer (longer distances) from one suspected case to another.
-
•
The proposed mathematical model for prioritizing approach is a nonlinear mixed integer program and the mathematical model for the allocating approach is a mixed integer linear program. The results, as shown Table 6, Table 7, obviously indicate that the greater the number of identified suspected cases, the greater the processing time (solution time). Although the processing time for prioritizing approach is longer than for allocating approach, this difference in processing time is not obvious for the less complex test problems (TP 1-6).
All in all, managers should choose the most suitable approach based on instant changes in the SARS-COV-2 pandemic. As a result, the number of suspected cases at any moment, available resources, the ratio of the number of identified suspected cases to ambulances and CMCs change instantly, and also the parameters of visit time, disease severity, and disinfection time are not known exactly because of the behavior of the SARS-COV-2 pandemic. According to the observations, the total response time, the response time of each ambulance, and the waiting time of the suspected cases with prioritizing approach is much better than with allocating approach. When the number of suspected cases increases the processing time to solve the mathematical model, it is also very important to be able to instantly determine the routes and responsiveness structure for ambulances. According to Table 6, to solve and obtain the right answer for test problem six (45 suspected cases at any moment) takes about a minute. Therefore, the solution time performance of prioritizing approach can be considered to be better and more acceptable than of allocating approach.
4.7. Why IoT?
The proposed methodology has two steps. The first is to identify suspected cases of SARS-COV-2 and the second is response scheduling. As mentioned in section two, in step one, the people participate in the PE. The data received by the DC are analyzed. Then, the suspected cases are identified. There is still a question that is: why should managers utilize the IoT-system to identify suspected cases? To answer this question, we peruse the impacts of utilizing the IoT-system on the numbers of received calls, face-to-face visitations, participants in PE, confirmed cases of SARS-COV-2, the identified confirmed cases of SARS-COV-2 by PE, the identified confirmed cases of SARS-COV-2by other means (calls and face-to-face visitations), and the ambulances trips for three weeks as shown in Fig. 25, Fig. 26, Fig. 27, Fig. 28, Fig. 29.
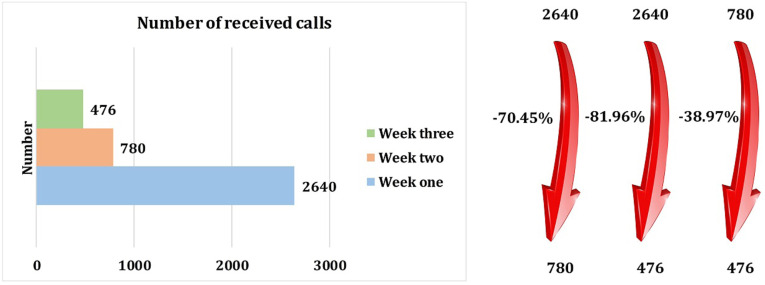
Fig. 25.
The number of received calls in three weeks.
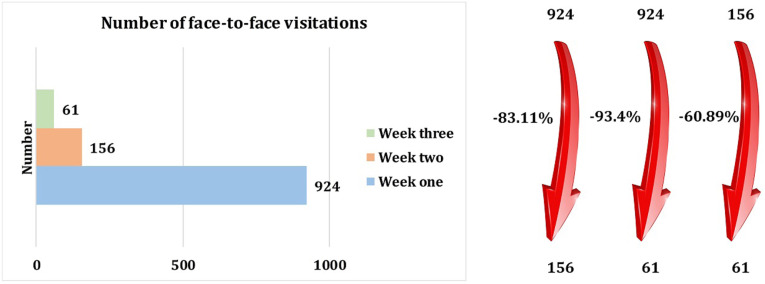
Fig. 26.
The number of face-to-face visitations in three weeks.
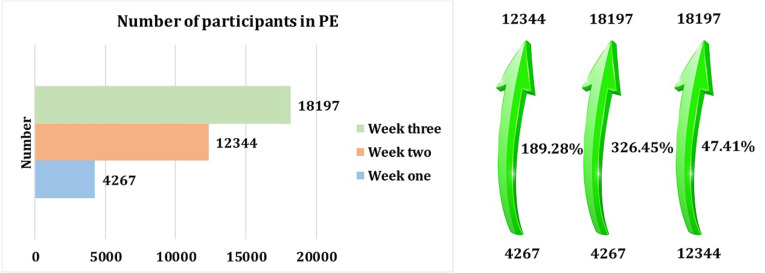
Fig. 27.
The number of participants in the PE in three weeks.
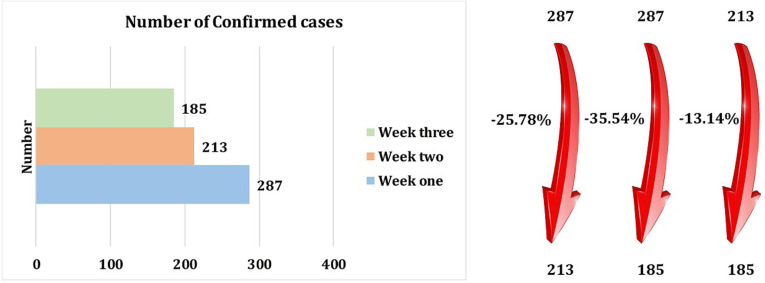
Fig. 28.
The number of confirmed cases in three weeks.
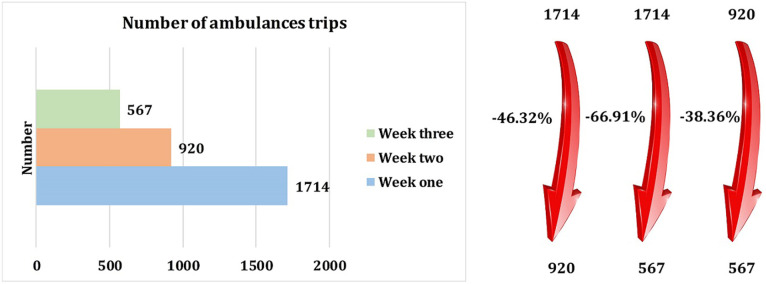
Fig. 29.
The number of ambulances trips in three weeks.
During three weeks, the number of participants in PE increased as shown in Fig. 27. The differences between weeks two and one and also between weeks three and one are 189.28 percent and 326.45 percent increases, respectively. Thus, with the increase in the number of participants in PE:
-
•
The number of received calls decreases 70.45 percent and 81.96 percent after one week (week two vs week one) and after two weeks (week three vs week one), respectively (See Fig. 25).
-
•
The number of face-to-face visitations decreases 83.12 percent and 93.4 percent after one week and two weeks, respectively (See Fig. 26).
-
•
The number of identified confirmed cases decreases 13.14 percent and 25.78 percent after one week and two weeks, respectively (See Fig. 28).
-
•
The number of ambulances trips decreases 46.35 percent and 66.91 percent after one week and two weeks, respectively (See Fig. 29).
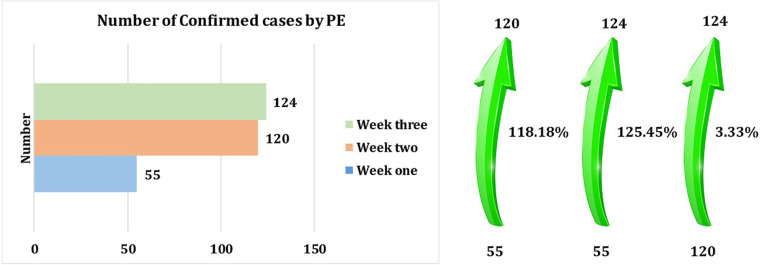
The most interesting aspect of this graph is regarding the number of identified confirmed cases. Although the number of identified confirmed cases during these three weeks does not decrease significantly (See Fig. 28), the number identified by the PE (proposed methodology) increases notably (See Fig. 30, Fig. 32).
Fig. 30.
The number of identified confirmed cases by the PE in three weeks.
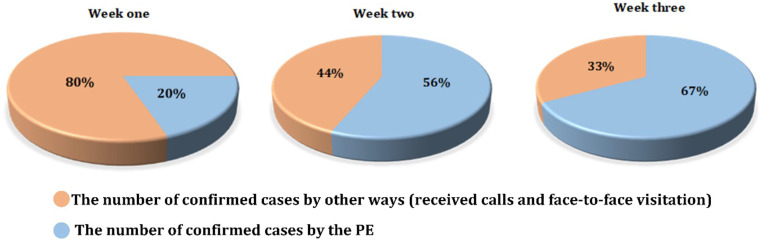
Fig. 32.
The comparison of identified confirmed cases in the PE and other ways in three weeks.
What is interesting about the data in these figures is that the proposed methodology has the following significant impacts:
-
•
Fewer operators are needed to answer the calls, and managers can assign human resources elsewhere.
-
•
By reducing the number of face-to-face visitations, healthy and unaffected people are kept away from the dangerous environments along with treatment resources and diagnostic kits to be used for the groups that require them. This would result in a reduction in the consumption of medical resources, especially when dealing with limited resources in some zones (see Fig. 31).
-
•
Reducing the number of ambulance trips means reducing the number of unnecessary trips and increasing access to resources.
-
•
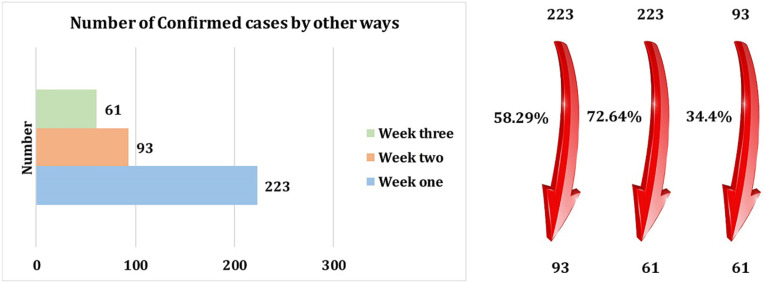
Increased participation in the PE reflects people’s trust in IoT-systems. As a result, managers can efficiently meet the needs of the people by launching the IoT-system in each department.
Fig. 31.
The number of identified confirmed cases by other ways in three weeks.
5. Conclusions
In this study, an IoT system was applied to a relief supply chain network. IoT provides an integrated system of interconnected devices and utilities in the healthcare sector that is highly vital to fight the SARS-COV-2 outbreak. Suspected cases and all medical devices including the control center, ambulances, and patients are connected to the internet network and, at the time of a serious condition, it can automatically inform the medical staff. Accordingly, the ambulances traverse certain routes in accordance with the case severity of each patient, their priority, available routes, available time, and the medical center capacity. The application of this smart platform makes it suitable for the decision-making process among managers. In addition, it can avoid superfluous trips to each location by the means of online monitoring of patients situated in various far districts. Another benefit of such a plan is a real-time process of ambulance assignment to visit each patient within a time horizon. IoT gathers information from suspected cases using a simple mobile application and, based on their priorities, instantly schedules the ambulance to visit them.
In this regard, and to address the aforementioned issues, two approaches are proposed to address the SARS-COV-2 cases in various locations. The results from prioritizing approach indicates that the model tries to optimize the capacity to visit patients in a balanced manner for each ambulance. In comparison to allocating approach, prioritizing approach makes it more possible for each patient to receive care in a given time by taking into account the patient’s severity, selecting the best possible route, and the plan scheduling. While prioritizing approach provides more benefits, allocating approach is superior when dealing with multiple patients. In other words, if the number of patients gets far beyond the ambulances’ capacity within a given time horizon, allocating approach is much more suitable to address these suspected cases. This a vital tool for managers during severe outbreaks when immediate actions and plans are needed to fight against pandemics such a SARS-COV-2 outbreak. Various considered scenarios enable the managers to decide in a real-time manner.
In addition to the above-mentioned contributions, solving the problem with newly combined meta-heuristic algorithms is another advancement in this field of study. Various meta-heuristics and hybrid ones allow efficient solutions of the proposed models in the two approaches, especially for larger problem sizes. Furthermore, conducting a sensitivity analysis on a case study showed diverse situations that mangers could face during the pandemic. The proposed model, along with the utilized approaches, have the capability to be implemented in different cities and countries because its requirements are easily met in diverse environments and the IoT-based scheme can easily solve for the optimal solution based on various conditions. Mangers in the healthcare sector, governments, and all the concerned stakeholders in this field of study could invest in such a system to benefit people in the agitated condition of outbreaks. Moreover, further studies could be done in this field by the means of considering new assumptions like adding time window constraints, considering number of nurses, categorizing cases based on ages and also new approaches to solve the problem such as exact ones like epsilon constraint and Benders decomposition method and also applying heuristics and new hybrid meta-heuristics by utilizing recent algorithms like GAKA and GASEO.
CRediT authorship contribution statement
Ali Zahedi: Design and implementation of the research, Analysis of the results, Writing of the manuscript. Amirhossein Salehi-Amiri: Design and implementation of the research, Analysis of the results, Writing of the manuscript. Neale R. Smith: Design and implementation of the research, Analysis of the results, Writing of the manuscript. Mostafa Hajiaghaei-Keshteli: Design and implementation of the research, Analysis of the results, Writing of the manuscript.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
World Health Organization: https://www.who.int.
Link: https://behdasht.gov.ir.
References
- 1.Mardani M., Nadji S.A., Sarhangipor K.A., Sharifi-Razavi A., Baziboroun M. COVID-19 infection recurrence presenting with meningoencephalitis. New microbes and new infections. 2020;37 doi: 10.1016/j.nmni.2020.100732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. E. 2020;136 doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shaban W.M., Rabie A.H., Saleh A.I., Abo-Elsoud M. A new COVID-19 patients detection strategy (CPDS) based on hybrid feature selection and enhanced KNN classifier. Knowl.-Based Syst. 2020;205 doi: 10.1016/j.knosys.2020.106270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sohrabi C., Alsafi Z., O’Neill N., Khan M., Kerwan A., Al-Jabir A., et al. World health organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19) Int. J. Surgery. 2020 doi: 10.1016/j.ijsu.2020.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hajiaghaei-Keshteli M., Sajadifar S.M., Haji R. Determination of the economical policy of a three-echelon inventory system with (R,Q) ordering policy and information sharing. Int. J. Adv. Manuf. Technol. 2011;55(5–8):831–841. [Google Scholar]
- 6.Shereen M.A., Khan S., Kazmi A., Bashir N., Siddique R. COVID-19 infection: Origin, transmission, and characteristics of human coronaviruses. J. Adv. Res. 2020 doi: 10.1016/j.jare.2020.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Atri D., Siddiqi H.K., Lang J., Nauffal V., Morrow D.A., Bohula E.A. COVID-19 for the cardiologist: a current review of the virology, clinical epidemiology, cardiac and other clinical manifestations and potential therapeutic strategies. JACC: Basic Transl. Sci. 2020 doi: 10.1016/j.jacbts.2020.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nicola M., Alsafi Z., Sohrabi C., Kerwan A., Al-Jabir A., Iosifidis C., et al. The socio-economic implications of the coronavirus and COVID-19 pandemic: a review. Int. J. Surgery. 2020 doi: 10.1016/j.ijsu.2020.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yu K.D.S., Aviso K.B. Modelling the economic impact and ripple effects of disease outbreaks. Process Integr. Optimiz. Sustain. 2020:1–4. [Google Scholar]
- 10.Wu Z., McGoogan J.M. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: summary of a report of 72 314 cases from the chinese center for disease control and prevention. JAMA. 2020;323(13):1239–1242. doi: 10.1001/jama.2020.2648. [DOI] [PubMed] [Google Scholar]
- 11.Ivanov D. Viable supply chain model: integrating agility, resilience and sustainability perspectives—lessons from and thinking beyond the COVID-19 pandemic. Ann. Oper. Res. 2020;1 doi: 10.1007/s10479-020-03640-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ivanov D., Dolgui A. Viability of intertwined supply networks: extending the supply chain resilience angles towards survivability, a position paper motivated by COVID-19 outbreak. Int. J. Prod. Res. 2020;58(10):2904–2915. [Google Scholar]
- 13.Al-Qaness M.A., Ewees A.A., Fan H., Abd El Aziz M. Optimization method for forecasting confirmed cases of COVID-19 in China. J. Clin. Med. 2020;9(3):674. doi: 10.3390/jcm9030674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Abdel-Basset M., Chang V., Hawash H., Chakrabortty R.K., Ryan M. FSS-2019-nCov: A deep learning architecture for semi-supervised few-shot segmentation of COVID-19 infection. Knowl.-Based Syst. 2020 doi: 10.1016/j.knosys.2020.106647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Too J., Mirjalili S. A hyper learning binary dragonfly algorithm for feature selection: A COVID-19 case study. Knowl.-Based Syst. 2020 [Google Scholar]
- 16.Fernandes N. 2020. Economic effects of coronavirus outbreak (COVID-19) on the world economy. Available at SSRN 3557504. [Google Scholar]
- 17.Currie C.S., Fowler J.W., Kotiadis K., Monks T., Onggo B.S., Robertson D.A., Tako A.A. How simulation modelling can help reduce the impact of COVID-19. J. Simul. 2020:1–15. [Google Scholar]
- 18.Ivanov D., Dolgui A. Viability of intertwined supply networks: extending the supply chain resilience angles towards survivability. a position paper motivated by COVID-19 outbreak. Int. J. Prod. Res. 2020:1–12. [Google Scholar]
- 19.Choi T.-M. Innovative bring-service-near-your-home operations under corona-virus (COVID-19/SARS-CoV-2) outbreak: Can logistics become the messiah? Transp. Res. E. 2020 doi: 10.1016/j.tre.2020.101961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rowan N.J., Laffey J.G. Challenges and solutions for addressing critical shortage of supply chain for personal and protective equipment (PPE) arising from coronavirus disease (COVID19) pandemic–case study from the Republic of Ireland. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.138532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yu H., Sun X., Solvang W.D., Zhao X. Reverse logistics network design for effective management of medical waste in epidemic outbreaks: Insights from the coronavirus disease 2019 (COVID-19) outbreak in wuhan (China) Int. J. Environ. Res. Public Health. 2020;17(5):1770. doi: 10.3390/ijerph17051770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Toregas C., Swain R., ReVelle C., Bergman L. The location of emergency service facilities. Oper. Res. 1971;19(6):1363–1373. [Google Scholar]
- 23.Özdamar L., Ekinci E., Küçükyazici B. Emergency logistics planning in natural disasters. Ann. Oper. Res. 2004;129(1–4):217–245. [Google Scholar]
- 24.Alçada-Almeida L., Tralhao L., Santos L., Coutinho-Rodrigues J. A multiobjective approach to locate emergency shelters and identify evacuation routes in urban areas. Geograph. Anal. 2009;41(1):9–29. [Google Scholar]
- 25.Horner M.W., Widener M.J. The effects of transportation network failure on people’s accessibility to hurricane disaster relief goods: a modeling approach and application to a florida case study. Natural Hazards. 2011;59(3):1619–1634. [Google Scholar]
- 26.Rottkemper B., Fischer K., Blecken A., Danne C. Inventory relocation for overlapping disaster settings in humanitarian operations. OR Spectrum. 2011;33(3):721–749. [Google Scholar]
- 27.Lin Y.-H., Batta R., Rogerson P.A., Blatt A., Flanigan M. A logistics model for emergency supply of critical items in the aftermath of a disaster. Soc.-Econom. Plann. Sci. 2011;45(4):132–145. [Google Scholar]
- 28.Bozorgi-Amiri A., Jabalameli M.S., Alinaghian M., Heydari M. A modified particle swarm optimization for disaster relief logistics under uncertain environment. Int. J. Adv. Manuf. Technol. 2012;60(1–4):357–371. [Google Scholar]
- 29.Zheng Y.-J., Ling H.-F. Emergency transportation planning in disaster relief supply chain management: a cooperative fuzzy optimization approach. Soft Comput. 2013;17(7):1301–1314. [Google Scholar]
- 30.Bozorgi-Amiri A., Jabalameli M.S., Al-e Hashem S.M. A multi-objective robust stochastic programming model for disaster relief logistics under uncertainty. OR spectrum. 2013;35(4):905–933. [Google Scholar]
- 31.Rezaei-Malek M., Tavakkoli-Moghaddam R. Robust humanitarian relief logistics network planning. Uncertain Supply Chain Manage. 2014;2(2):73–96. [Google Scholar]
- 32.Hu S.-L., Han C.-F., Meng L.-P. A scenario planning approach for propositioning rescue centers for urban waterlog disasters. Comput. Ind. Eng. 2015;87:425–435. [Google Scholar]
- 33.Gutjahr W.J., Dzubur N. Bi-objective bilevel optimization of distribution center locations considering user equilibria. Transp. Res. E. 2016;85:1–22. [Google Scholar]
- 34.Zokaee S., Bozorgi-Amiri A., Sadjadi S.J. A robust optimization model for humanitarian relief chain design under uncertainty. Appl. Math. Model. 2016;40(17–18):7996–8016. [Google Scholar]
- 35.Saeidian B., Mesgari M.S., Ghodousi M. Evaluation and comparison of genetic algorithm and bees algorithm for location–allocation of earthquake relief centers. Int. J. Disaster Risk Reduct. 2016;15:94–107. [Google Scholar]
- 36.Fahimnia B., Jabbarzadeh A., Ghavamifar A., Bell M. Supply chain design for efficient and effective blood supply in disasters. Int. J. Prod. Econ. 2017;183:700–709. [Google Scholar]
- 37.Salehi F., Mahootchi M., Husseini S.M.M. Developing a robust stochastic model for designing a blood supply chain network in a crisis: A possible earthquake in tehran. Ann. Oper. Res. 2019;283(1–2):679–703. [Google Scholar]
- 38.Tavana M., Abtahi A.-R., Di Caprio D., Hashemi R., Yousefi-Zenouz R. An integrated location-inventory-routing humanitarian supply chain network with pre-and post-disaster management considerations. Soc.-Econom. Plann. Sci. 2018;64:21–37. [Google Scholar]
- 39.Dubey R., Gunasekaran A. The sustainable humanitarian supply chain design: agility, adaptability and alignment. Int. J. Logist. Res. Appl. 2016;19(1):62–82. [Google Scholar]
- 40.Zhang P., Liu Y., Yang G., Zhang G. A distributionally robust optimization model for designing humanitarian relief network with resource reallocation. Soft Comput. 2020;24(4):2749–2767. [Google Scholar]
- 41.Singh R.P., Javaid M., Haleem A., Suman R. Internet of things (IoT) applications to fight against COVID-19 pandemic. Diab. Metabol. Syndrome: Clin. Res. Rev. 2020 doi: 10.1016/j.dsx.2020.04.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Singh V.K., Chandna H., Kumar A., Kumar S., Upadhyay N., Utkarsh K. 2020. IoT-Q-Band: A low cost internet of things based wearable band to detect and track absconding COVID-19 quarantine subjects. [Google Scholar]
- 43.Ting D.S. W., Carin L., Dzau V., Wong T.Y. Digital technology and COVID-19. Nature Med. 2020;26(4):459–461. doi: 10.1038/s41591-020-0824-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Vaishya R., Javaid M., Khan I.H., Haleem A. Artificial intelligence (AI) applications for COVID-19 pandemic. Diab. Metabol. Syndrome: Clin. Res. Rev. 2020 doi: 10.1016/j.dsx.2020.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rahman M.S., Peeri N.C., Shrestha N., Zaki R., Haque U., Ab Hamid S.H. Defending against the novel coronavirus (COVID-19) outbreak: How can the internet of things (IoT) help to save the world? Health Policy Technol. 2020 doi: 10.1016/j.hlpt.2020.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bai L., Yang D., Wang X., Tong L., Zhu X., Bai C., Powell C.A. Chinese experts’ consensus on the internet of things-aided diagnosis and treatment of coronavirus disease 2019. Clin. eHealth. 2020 [Google Scholar]
- 47.Javaid M., Haleem A., Vaishya R., Bahl S., Suman R., Vaish A. Industry 4.0 technologies and their applications in fighting COVID-19 pandemic. Diab. Metabol. Syndrome: Clin. Res. Rev. 2020 doi: 10.1016/j.dsx.2020.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Grida M., Mohamed R., Zaied A.N.H. Evaluate the impact of COVID-19 prevention policies on supply chain aspects under uncertainty. Transp. Res. Interdiscip. Perspect. 2020 doi: 10.1016/j.trip.2020.100240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Karmaker C.L., Ahmed T., Ahmed S., Ali S.M., Moktadir M.A., Kabir G. Improving supply chain sustainability in the context of COVID-19 pandemic in an emerging economy: Exploring drivers using an integrated model. Sustain. Product. Consump. 2020;26:411–427. doi: 10.1016/j.spc.2020.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Nagurney A. Supply chain game theory network modeling under labor constraints: Applications to the Covid-19 pandemic. European J. Oper. Res. 2020 doi: 10.1016/j.ejor.2020.12.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Govindan K., Mina H., Alavi B. A decision support system for demand management in healthcare supply chains considering the epidemic outbreaks: A case study of coronavirus disease 2019 (COVID-19) Transp. Res. E. 2020;138 doi: 10.1016/j.tre.2020.101967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Habib K., Sprecher B., Young S.B. COVID-19 impacts on metal supply: How does 2020 differ from previous supply chain disruptions? Resour. Conserv. Recy. 2021;165 [Google Scholar]
- 53.Wang X., Wu Y., Liang L., Huang Z. Service outsourcing and disaster response methods in a relief supply chain. Ann. Oper. Res. 2016;240(2):471–487. [Google Scholar]
- 54.A. Nagurney, L.S. Nagurney, A mean–variance disaster relief supply chain network model for risk reduction with stochastic link costs, time targets, and demand uncertainty, in: Paper presented at the International Conference on Dynamics of Disasters, 2016.
- 55.Mohammadi R., Ghomi S.F., Jolai F. Prepositioning emergency earthquake response supplies: A new multi-objective particle swarm optimization algorithm. Appl. Math. Model. 2016;40(9–10):5183–5199. [Google Scholar]
- 56.Sung I., Lee T. Optimal allocation of emergency medical resources in a mass casualty incident: Patient prioritization by column generation. European J. Oper. Res. 2016;252(2):623–634. [Google Scholar]
- 57.Zhou Y., Liu J., Zhang Y., Gan X. A multi-objective evolutionary algorithm for multi-period dynamic emergency resource scheduling problems. Transp. Res. E. 2017;99:77–95. [Google Scholar]
- 58.Jha A., Acharya D., Tiwari M. Humanitarian relief supply chain: a multi-objective model and solution. Sādhanā. 2017;42(7):1167–1174. [Google Scholar]
- 59.Al Theeb N., Murray C. Vehicle routing and resource distribution in postdisaster humanitarian relief operations. Int. Trans. Oper. Res. 2017;24(6):1253–1284. [Google Scholar]
- 60.Manopiniwes W., Irohara T. Stochastic optimisation model for integrated decisions on relief supply chains: preparedness for disaster response. Int. J. Prod. Res. 2017;55(4):979–996. [Google Scholar]
- 61.Li X., Batta R., Kwon C. Effective and equitable supply of gasoline to impacted areas in the aftermath of a natural disaster. Soc.-Econom. Plann. Sci. 2017;57:25–34. [Google Scholar]
- 62.Samani M.R. G., Torabi S.A., Hosseini-Motlagh S.-M. Integrated blood supply chain planning for disaster relief. Int. J. Disaster Risk Reduct. 2018;27:168–188. [Google Scholar]
- 63.Cao C., Li C., Yang Q., Liu Y., Qu T. A novel multi-objective programming model of relief distribution for sustainable disaster supply chain in large-scale natural disasters. J. Cleaner Prod. 2018;174:1422–1435. [Google Scholar]
- 64.Safaei A.S., Farsad S., Paydar M.M. Emergency logistics planning under supply risk and demand uncertainty. Oper. Res. 2018:1–24. [Google Scholar]
- 65.Hong J.-D., Jeong K.-Y. Goal programming and data envelopment analysis approach to disaster relief supply chain design. Int. J. Logist. Syst. Manage. 2019;33(3):291–321. [Google Scholar]
- 66.John L., Gurumurthy A., Soni G., Jain V. Modelling the inter-relationship between factors affecting coordination in a humanitarian supply chain: a case of chennai flood relief. Ann. Oper. Res. 2019;283(1):1227–1258. [Google Scholar]
- 67.Ghaffari Z., Nasiri M.M., Bozorgi-Amiri A., Rahbari A. Emergency supply chain scheduling problem with multiple resources in disaster relief operations. Transport. A. 2020;16(3):930–956. [Google Scholar]
- 68.Akbarpour M., Torabi S.A., Ghavamifar A. Designing an integrated pharmaceutical relief chain network under demand uncertainty. Transp. Res. E. 2020;136 [Google Scholar]
- 69.Aghajani M., Torabi S.A., Heydari J. A novel option contract integrated with supplier selection and inventory prepositioning for humanitarian relief supply chains. Socio-Econom. Plann. Sci. 2020 [Google Scholar]
- 70.Hamza R., Yan Z., Muhammad K., Bellavista P., Titouna F. A privacy-preserving cryptosystem for IoT E-healthcare. Inform. Sci. 2020;527:493–510. [Google Scholar]
- 71.Selvaraj S., Sundaravaradhan S. Challenges and opportunities in IoT healthcare systems: a systematic review. SN Appl. Sci. 2020;2(1):1–8. [Google Scholar]
- 72.Davide P., Andrea P., Martina O., Andrea E., Davide D., Mario A. The impact of the COVID-19 pandemic on patients with OCD: effects of contamination symptoms and remission state before the quarantine in a preliminary naturalistic study. Psych. Res. 2020 doi: 10.1016/j.psychres.2020.113213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Jutzeler C.R., Bourguignon L., Weis C.V., Tong B., Wong C., Rieck B., et al. 2020. Comorbidities, clinical signs and symptoms, laboratory findings, imaging features, treatment strategies, and outcomes in adult and pediatric patients with COVID-19: A systematic review and meta-analysis. medRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Lechien J.R., Chiesa-Estomba C.M., Cabaraux P., Mat Q., Huet K., Harmegnies B., et al. Features of mild-to-moderate COVID-19 patients with dysphonia. J. Voice. 2020 doi: 10.1016/j.jvoice.2020.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Mirza F.N., Malik A.A., Couzens C., Omer S.B. Influenza-negative influenza-like illness (fnILI) Z-score as a proxy for incidence and mortality of COVID-19. J. Infect. 2020 doi: 10.1016/j.jinf.2020.08.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Weenink R.P., Preckel B., Hulst A.H., Hermanides J., de Jong M.D., Schlack W.S., et al. Second update for anaesthetists on clinical features of COVID-19 patients and relevant management. J. Clin. Med. 2020;9(8):2542. doi: 10.3390/jcm9082542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Zheng H., Hébert H.L., Chatziperi A., Meng W., Smith B.H., Yan J., et al. Perioperative management of patients with suspected or confirmed COVID-19: review and recommendations for perioperative management from a retrospective cohort study. Br. J. Anaesthesia. 2020 doi: 10.1016/j.bja.2020.08.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Contreras S., Biron-Lattes J.P., Villavicencio H.A., Medina-Ortiz D., Llanovarced-Kawles N., Olivera-Nappa A.´. 2020. Statistically-based methodology for revealing real contagion trends and correcting delay-induced errors in the assessment of COVID-19 pandemic. arXiv preprint arXiv:2005.12376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Gupta R., Gant V.A., Williams B., Enver T. Increased complement receptor-3 levels in monocytes and granulocytes distinguish COVID-19 patients with pneumonia from those with mild symptoms. Int. J. Infect. Dis. 2020;99:381–385. doi: 10.1016/j.ijid.2020.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Klopfenstein T., Zahra H., Lepiller Q., Royer P.-Y., Toko L., Gendrin V., Zayet S. New loss of smell and taste: Uncommon symptoms in COVID-19 patients on nord franche-comte cluster, France. Int. J. Infect. Dis. 2020 doi: 10.1016/j.ijid.2020.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Miaskowski C., Paul S.M., Snowberg K., Abbott M., Borno H., Chang S., et al. Stress and symptom burden in oncology patients during the COVID-19 pandemic. J. Pain Symptom Manage. 2020 doi: 10.1016/j.jpainsymman.2020.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Herrán A., Colmenar J.M., Duarte A. An efficient metaheuristic for the K-page crossing number minimization problem. Knowl.-Based Syst. 2020;207 [Google Scholar]
- 83.Golshahi-Roudbaneh A., Hajiaghaei-Keshteli M., Paydar M.M. Developing a lower bound and strong heuristics for a truck scheduling problem in a cross-docking center. Knowl.-Based Syst. 2017;129:17–38. [Google Scholar]
- 84.Sadeghi-Moghaddam S., Hajiaghaei-Keshteli M., Mahmoodjanloo M. New approaches in metaheuristics to solve the fixed charge transportation problem in a fuzzy environment. Neural Comput. Appl. 2017:1–21. [Google Scholar]
- 85.Fard A.F., Gholian-Jouybari F., Paydar M.M., Hajiaghaei-Keshteli M. A bi-objective stochastic closed-loop supply chain network design problem considering downside risk. Indust. Eng. Manage. Syst. 2017;16(3):342–362. [Google Scholar]
- 86.M. Hajiaghaei-Keshteli, M. Aminnayeri, Keshtel Algorithm (KA); a new optimization algorithm inspired by Keshtels’ feeding, in: Paper presented at the Proceeding in IEEE conference on industrial engineering and management systems, 2013.
- 87.Liao Y., Kaviyani-Charati M., Hajiaghaei-Keshteli M., Diabat A. Designing a closed-loop supply chain network for citrus fruits crates considering environmental and economic issues. J. Manuf. Syst. 2020;55:199–220. [Google Scholar]
- 88.Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by simulated annealing. Science. 1983;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 89.Golmohamadi S., Tavakkoli-Moghaddam R., Hajiaghaei-Keshteli M. Solving a fuzzy fixed charge solid transportation problem using batch transferring by new approaches in meta-heuristic. Electron. Notes Discrete Math. 2017;58:143–150. [Google Scholar]
- 90.Grobelny J., Michalski R. A novel version of simulated annealing based on linguistic patterns for solving facility layout problems. Knowl.-Based Syst. 2017;124:55–69. [Google Scholar]
- 91.Fathollahi-Fard A.M., Hajiaghaei-Keshteli M., Mirjalili S. Multi-objective stochastic closed-loop supply chain network design with social considerations. Appl. Soft Comput. 2018;71:505–525. [Google Scholar]
- 92.Fard A.M. F., Hajiaghaei-Keshteli M. A bi-objective partial interdiction problem considering different defensive systems with capacity expansion of facilities under imminent attacks. Appl. Soft Comput. 2018;68:343–359. [Google Scholar]
- 93.Fathollahi-Fard A.M., Hajiaghaei-Keshteli M., Mirjalili S. Hybrid optimizers to solve a tri-level programming model for a tire closed-loop supply chain network design problem. Appl. Soft Comput. 2018;70:701–722. [Google Scholar]
- 94.Fathollahi-Fard A.M., Hajiaghaei-Keshteli M., Tavakkoli-Moghaddam R. A bi-objective green home health care routing problem. J. Cleaner Prod. 2018;200:423–443. [Google Scholar]
- 95.J. Kennedy, R. Eberhart, Particle swarm optimization, in: Paper presented at the Proceedings of ICNN’95-International Conference on Neural Networks, 1995.
- 96.Zhang Y., Liu X., Bao F., Chi J., Zhang C., Liu P. Particle swarm optimization with adaptive learning strategy. Knowl.-Based Syst. 2020 [Google Scholar]
- 97.Amiri S.A. H.S., Zahedi A., Kazemi M., Soroor J., Hajiaghaei-Keshteli M. Determination of the optimal sales level of perishable goods in a two-echelon supply chain network. Comput. Ind. Eng. 2020;139 [Google Scholar]
- 98.Tao M., Huang S., Li Y., Yan M., Zhou Y. SA-PSO based optimizing reader deployment in large-scale RFID Systems. J. Netw. Comput. Appl. 2015;52:90–100. [Google Scholar]
- 99.Sahebjamnia N., Goodarzian F., Hajiaghaei-Keshteli M. Optimization of multi-period three-echelon citrus supply chain problem. J. Optim. Indust. Eng. 2020;13(1):39–53. [Google Scholar]
- 100.Hajiaghaei-Keshteli M., Fard A.M.F. Sustainable closed-loop supply chain network design with discount supposition. Neural Comput. Appl. 2019;31(9):5343–5377. [Google Scholar]
- 101.Abdi A., Abdi A., Akbarpour N., Amiri A.S., Hajiaghaei-Keshteli M. Innovative approaches to design and address green supply chain network with simultaneous pick-up and split delivery. J. Cleaner Prod. 2020;250 [Google Scholar]
- 102.Zahedi A., Salehi-Amiri A., Hajiaghaei-Keshteli M., Diabat A. Designing a closed-loop supply chain network considering multitask sales agencies and multimode transportation. Soft Comput. 2021 doi: 10.1007/s00500-021-05607-6. [DOI] [Google Scholar]
- 103.Nalbant M., Gökkaya H., Sur G. Application of taguchi method in the optimization of cutting parameters for surface roughness in turning. Mater. Design. 2007;28(4):1379–1385. [Google Scholar]
- 104.Cheraghalipour A., Paydar M.M., Hajiaghaei-Keshteli M. A bi-objective optimization for citrus closed-loop supply chain using Pareto-based algorithms. Appl. Soft Comput. 2018;69:33–59. [Google Scholar]
- 105.Cheraghalipour A., Paydar M.M., Hajiaghaei-Keshteli M. Designing and solving a bi-level model for rice supply chain using the evolutionary algorithms. Comput. Electron. Agric. 2019;162:651–668. [Google Scholar]
- 106.Gholian-Jouybari F., Afshari A.J., Paydar M.M. Utilizing new approaches to address the fuzzy fixed charge transportation problem. J. Indust. Produc. Eng. 2018;35(3):148–159. [Google Scholar]
- 107.Gholian Jouybari F., Afshari A., Paydar M. Electromagnetism-like algorithms for the fuzzy fixed charge transportation problem. J. Indust. Eng. Manage. Stud. 2016;3(1):39–60. [Google Scholar]