F-Seq2: improving the feature density based peak caller with dynamic statistics

Abstract

Genomic and epigenomic features are captured at a genome-wide level by using high-throughput sequencing (HTS) technologies. Peak calling delineates features identified in HTS experiments, such as open chromatin regions and transcription factor binding sites, by comparing the observed read distributions to a random expectation. Since its introduction, F-Seq has been widely used and shown to be the most sensitive and accurate peak caller for DNase I hypersensitive site (DNase-seq) data. However, the first release (F-Seq1) has two key limitations: lack of support for user-input control datasets, and poor test statistic reporting. These constrain its ability to capture systematic and experimental biases inherent to the background distributions in peak prediction, and to subsequently rank predicted peaks by confidence. To address these limitations, we present F-Seq2, which combines kernel density estimation and a dynamic ‘continuous’ Poisson test to account for local biases and accurately rank candidate peaks. The output of F-Seq2 is suitable for irreproducible discovery rate analysis as test statistics are calculated for individual candidate summits, allowing direct comparison of predictions across replicates. These improvements significantly boost the performance of F-Seq2 for ATAC-seq and ChIP-seq datasets, outperforming competing peak callers used by the ENCODE Consortium in terms of precision and recall.

INTRODUCTION

High-throughput sequencing (HTS) is a central technology in deciphering genomic and epigenomic landscapes. Assays for detecting genome-wide chromatin accessibility (1–3), transcription factor (TF) binding (4) and histone modifications (5) are among the most commonly used methods. The short read sequences produced by these assays are usually filtered and mapped back to a reference genome, then accumulated and piled up in genomic regions. The enrichment (e.g. counts) of mapped reads can be abstractly viewed as a digital signal of relevant biological events varying along the genome. The genome-wide enrichment signal can be further processed with a peak-calling program, or peak caller, to find the arguments of local maxima (argmax), representing discrete loci with statistically significant enrichment over background for the relevant biological event. For example, individual TF-binding sites in a ChIP-seq experiment.

We introduced F-Seq as a general peak caller for DNase-seq and ChIP-seq in 2008 (6). Unlike other recent methods (7,8), F-seq calls peaks in HTS signals that are the probabilistic estimates of the genome-wide short read density at single-nucleotide resolution reconstructed by a kernel density estimator (KDE) (9,10). KDE-based reconstructed signal is smoother and more accurate than histogram-based methods (e.g. sliding window), but still interpretable and useful for visualization as the estimate is proportional to the probability of finding a read at a given base pair (11). A Gaussian kernel with a chosen bandwidth is centered at each read and kernels are summed up to obtain the density estimate. Peak regions are then called if the signal is higher than the threshold calculated from a simulated background model. F-Seq has been widely used in the ENCODE project (12) and beyond, which is shown to be more accurate and sensitive than competing peak callers for DNase-seq data (13). However, F-Seq lacks native support for a separate control dataset. Consequently, F-Seq cannot capture or eliminate local biases affecting read distribution along the genome, such as copy number variation, read mappability and local chromatin structure (7). This limits the performance of F-Seq especially on ChIP-seq data since the majority of ChIP-seq experiments have corresponding control data that contain unique information for accurate peak calling (14). In addition, F-Seq does not report test statistics (e.g. P-value or q-value) apart from the signal value at each position.

To address these shortcomings, we have developed F-Seq version 2 (F-Seq2), a complete rewrite of the original F-Seq in Python. F-Seq2 implements a dynamic parameter to conduct local statistical analysis with an underlying ‘continuous’ Poisson distribution that is approximated by logarithmic interpolation of P-values. This allows a Poisson test for continuous signal values (i.e. amplitude) at each genomic position to the local background distribution. By combining the power of the local test and the KDE, which model the read probability distribution with statistical rigor, we robustly account for local biases and solve ties that occur when ranking candidate summits, making results suitable for irreproducible discovery rate (IDR) analysis (15). We compared F-Seq2 with four peak callers used by the ENCODE Consortium (12) on simulated and real ChIP-seq and ATAC-seq datasets, demonstrating performance gains arising from the joint effect of KDE and the local test, especially in the absence of control data.

MATERIALS AND METHODS

Density profiles and peak calling

Density profiles for HTS reads at any base pair position 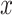of the genome are defined as

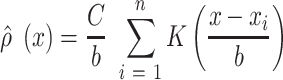where 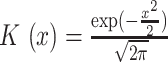is a Gaussian kernel density function, and 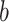is the bandwidth parameter controlling the smoothness of the estimation. In contrast to the original KDE, F-Seq2 density profiles represent unnormalized estimates (i.e. not normalized to the total read count) for computational convenience of following statistical analysis. 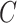is a scaling constant so that the sum at any given position is limited to the number of proximal sample points. For experiments including a control dataset, scaling between control and treatment datasets was necessary to account for different sequencing depths. The total control read count was linearly scaled to be equal to the total treatment read count at the individual chromosome level as the ratios of total reads fluctuated between different chromosomes. The reconstructed signal by KDE was treated as a digital signal emitted on a chromosome. Argmax of the signal, which are the positions of local maxima in the estimated density function, were established by comparing neighboring values. Only a subset of argmax were retained as the candidate summits for statistical testing to reduce potential false positives. Candidates were selected by their local maxima properties; we specified the minimum height and prominence of the local maxima for candidates as the simulated background threshold and the minimum distances between adjacent local maxima as the estimated fragment size. Estimation of the fragment size for ChIP-seq data and the simulated background threshold for defining and selecting candidate summits and delineating final peak regions were implemented the same between F-Seq2 in Python and the original F-Seq in Java.

We adopted and modified the dynamic testing idea introduced by MACS2 (7) to assign each candidate summit a statistical enrichment value related to a background distribution. Rather than using a constant background estimation for all candidates, a local background distribution was estimated for each candidate, providing a more accurate method to calculate enrichment P-values due to the local fluctuations of read enrichment distributions. The Poisson distribution (characterized by 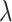) was used to model the number of reads (or signal value) from a genomic region as this has been proven to be more mathematically powerful compared to Binomial distribution in peak calling (16). Specifically, 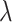for a summit is defined as 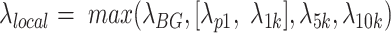, where 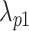is the maximum signal value for one pseudo-read, 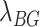is the estimate of the individual chromosome background, and 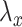is the estimate of a 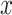bp window centered at the summit. All estimates are calculated in the control dataset where available; otherwise, estimates were only calculated in the treatment dataset, and regions in the square brackets of formula were excluded to alleviate the background estimation boost by the summit signal value.

Since the underlying Poisson distribution of the statistical test is a discrete distribution while the test sample (i.e. the signal value) is continuous, many ties in test statistics P-value calculated by survival function were observed. Supposing 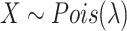, the Poisson survival function is then defined as 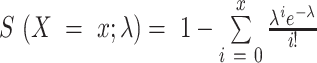. Ties often occurred when the sequencing data had a low signal-to-noise ratio and KDE estimated signal values were close to each other (i.e. between two integers), such as 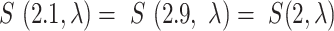. We interpolated the P-value in the logarithmic space of the survival function to allow for continuous input, and break any ties that occurred. The interpolated P-value in logarithmic space is calculated as

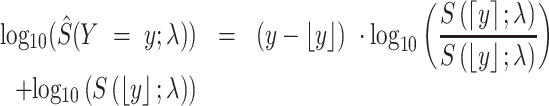where 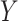is a continuous random variable, 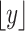is the floor function and 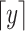is the ceiling function. The precision gained by this interpolation improved the rankings of summits compared to the rankings calculated using discrete values. The interpolation bridges KDE and the dynamic Poisson testing to combine their power. Multi-test correction was conducted with the Benjamini–Hochberg approach (17) to calculate q-values (more precisely, false discovery rate adjusted P-values) from the interpolated P-values.

Benchmarking with selected peak callers

Four peak callers and F-Seq2 were selected to benchmark our improved method on 100 simulated HTS datasets, 3 real ChIP-seq datasets and 1 ATAC-seq dataset. The comparison methods, which are routinely utilized by the ENCODE Consortium (12), included Model-based Analysis for ChIP-Seq version 2 (MACS2) (7), SPP (18), MUltiScale enrIchment Calling for ChIP-Seq (MUSIC) (8) and Genome wide Event finding and Motif discovery (GEM) (19). Hundred treatment datasets and their paired control samples were simulated to closely approximate real ChIP-seq datasets (16), allowing for the evaluation of the peak callers under different scenarios where the ground truth is known. Real ChIP-seq datasets for three different TFs tested in three different cell lines were obtained from ENCODE (12). As the ground truth is unknown in real datasets, one common approach is to use the presence of a matched TF-binding motif to indicate true positive peak predictions. Motifs were obtained from the JASPAR database (20) irrespective of cell line specificity, and used for the three real ChIP-seq datasets. Similarly, the union set of conservative IDR peaks from 117 independent ENCODE TF ChIP-seq experiments were used as the ‘ground truth’ for ATAC-seq benchmarking (12). Raw ATAC-seq bam files were downloaded from Buenrostro et al. (2) (see availability for data accession numbers).

Performance for all peak callers was evaluated across a range of significance thresholds representing a different number of top ranked peaks. The main evaluation metric was the F-score defined as

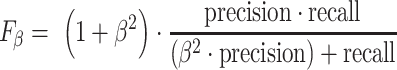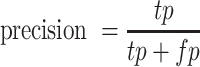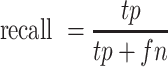When 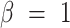, we refer to it as F-score, or more specifically, F1-score; when 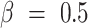, we refer to it as F0.5-score. 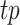is the number of true positives, 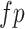is the number of false positives, and 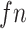is the number of false negatives. A higher F-score indicates a more balanced performance in terms of precision and recall. All peak callers were run with recommended settings and the least stringent thresholds (i.e. set P-value or q-value threshold to 1 or fold enrichment threshold to 0; see Availability for parameters settings).

Evaluation for simulated data

Peak calling results are typically not directly comparable as they possess different peak widths and estimated P-values or q-values that are generated from different statistical tests. To address this issue, all tools were first run with the least stringent threshold to obtain an extensive list of peaks on each simulated dataset for each tool. All peaks were limited to a 200 bp window centered at the peak summit or peak centers, depending on available dataset information. Operating characteristics can be evaluated by varying the threshold to obtain the same top number of peaks from each tool, where peaks are ranked by individual significance measurements. F-score was used as the evaluation metric, which is the harmonic mean of precision and recall. Specifically in the simulation evaluation, 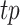was defined as the number of predicted peaks that overlap with ground truth peaks. 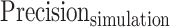was defined as the fraction of 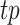in all predictions, and 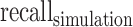as the fraction of 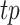in all ground truth peaks. The mean and 95% confidence intervals across 100 peak calling results were estimated by generalized additive models (GAMs) (21) for each peak caller. A linear GAM was fit to the results for regression analysis. Using the fitted model to predict on the varying threshold generated the mean curve and 95% prediction intervals, which was defined as 95% confidence intervals for each peak caller. Since the lengths of the operating characteristics curves varied due to the different maximum number of peaks called by each peak caller, and different P-values or q-values sensitivities responding to the varying threshold, the area under the curve statistics used to summarize the curve were not directly comparable. We then used the highest F-score and the overall trend of the curve for peak caller evaluation. The higher the overall curve, the larger the area under the curve, the more balanced and optimal the performance of a peak caller is in terms of precision and recall.

Evaluation for ATAC-seq data

Evaluation of F-Seq2 and MACS2 used the union set of conservative IDR peaks from 117 TF ChIP-seq datasets as the ‘ground truth’. All IDR peaks were in the GM12878 cell line to be comparable to the ATAC-seq dataset. Each tool was run with the least stringent threshold and two main modes: single-end (SE) and paired-end (PE) mode. Paired-end mode has the advantage of knowing the exact fragment length, which is useful when filtering out fragments whose length falls within a certain range to avoid peak calls on nucleosome centers (2). Operating characteristic curves were plotted similarly as described in the evaluation for simulation data by varying the respective thresholds. The main difference was the evaluation metric was changed to F0.5-score along with new definitions for true positives, precision and recall. We used F0.5-score to put more emphasis on precision versus recall due to the incompleteness of the ‘ground truth’. 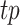was redefined as the number of base pairs (bp) of the predicted peaks that overlap with ground truth peaks, 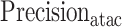as the fraction of correctly predicted base pairs in all predictions, and 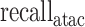as the fraction of correctly predicted base pairs in all ground truth peaks. New definitions were required as ATAC-seq peak lengths are usually larger than TF ChIP-seq peak lengths. We shifted focus from evaluating summits around a window size to the narrow peak regions for a more comprehensive evaluation.

Evaluation for real TF ChIP-seq data

Evaluations of real TF ChIP-seq peak calling results required JASPAR motif Position Weight Matrices (PWM) of each TF. K-mers matching to each TF PWM were identified by the TFM P-value program (22) with the threshold of 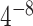. Motif positions were detected in the hg19 human genome by mapping the K-mers using the Bowtie program suite (23). For each ChIP-seq dataset, the selected tool called a list of significant peaks with their default thresholds. The shortest distances between the significant peaks and the corresponding TF motifs were obtained and used as the main evaluation metric. Specifically, we evaluated the fraction of top 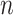up to 1000 peaks, ranked by significance within a 100 bp window of a motif. We also examined the empirical cumulative distribution of the shortest distance of those top 1000 peaks for each tool.

F-Seq2 auto filter design for paired-end ATAC-seq data peak calling

We designed the PE auto filter based on the fragment size distribution partitions modeled by Buenrostro et al. (2), where fragment lengths under 100 bp, between 180 and 247 bp, between 315 and 473 bp, and between 558 and 615 bp were considered to originate from nucleosome free, mono-, di-, and tri-nucleosomes, respectively. Our auto filter included more fragments compared to that of Buenrostro’s analysis (2), in which they only used fragments under 100 bp for open chromatin analysis (Supplementary Figure S1). By excluding fragment ranges between the non-overlapping cutoffs, a large percentage (∼15%) were discarded, leading to a reduction in recall. These fragments (e.g. between 100 and 180 bp) may contain useful information for identifying open chromatin regions (24). F-Seq2 takes advantage of more available reads to accurately estimate background distribution, and only fragments within mono-, di- and tri-nucleosomes ranges were excluded. Fragments >558 bp (i.e. multinucleosome-sized fragments) were also rejected as these fragments are associated with condensed heterochromatin (2).

RESULTS

Performance on simulated datasets

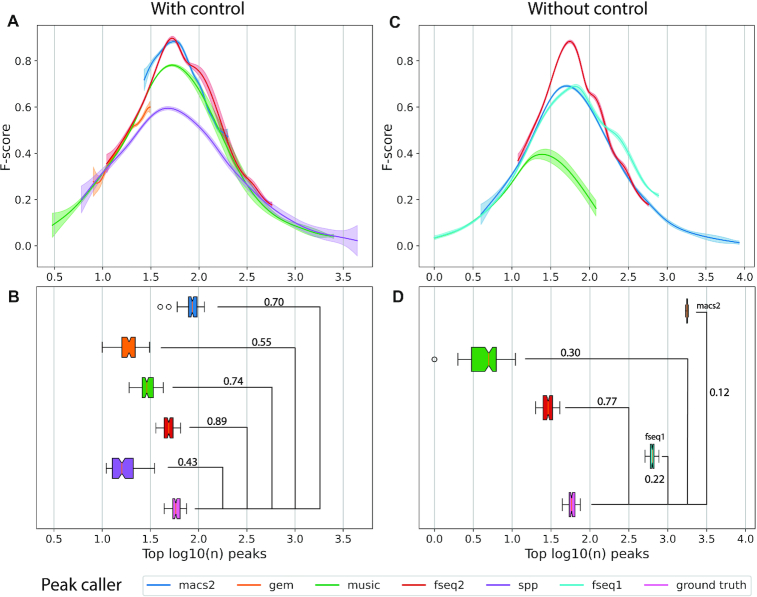
To accurately evaluate the peak callers under a variety of scenarios, each method was benchmarked on 100 sets of paired simulated treatment and control data. F-Seq2 and MACS2 were found to be the top two performers with the highest overall F-score operating characteristic curves (Figure 1A). The highest F-scores estimated by generalized additive models across 100 pairs were 0.897, and 0.884 for F-Seq2 and MACS2, respectively. Both methods outperformed MUSIC, the third-best method, by a margin of ∼0.1 (MUSIC 0.781). Despite differences in implementing a dynamic parameter 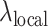between F-Seq2 and MACS2, the performance gap suggests using a dynamic parameter 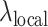in ranking peaks is a huge advantage, effectively removing false positives, consistent with the conclusion from Thomas et al. (16). The number of peaks called by the default threshold of each peak caller was compared to the number of peaks in the ground truth (Figure 1B). F-Seq2 best correlated with the ground truth ( 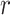= 0.88) while MUSIC ( 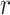= 0.74) had a slightly better correlation compared to MACS2 ( 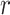= 0.70). The high correlation observed for F-Seq2 indicates the default threshold of our program is reliable when estimating the number of significant peaks under a simulation setting.

Figure 1.

Comparison of peak callers on 100 pairs of simulated transcription factor ChIP-seq datasets. (A) The F-score operating characteristic curve where F-score is plotted as a function of the log₁₀ top number of peaks called with control data. Generalized additive models are used to estimate the mean and 95% confidence intervals (shaded areas) of 100 peak calling results for each peak caller. (B) Boxplot of the number of peaks called by each peak caller with default threshold with control data, and the number of significant peaks in ground truth. Numbers are shown in log₁₀ scale. Pearson’s correlation coefficient 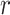is shown above the bridge linking peak caller and ground truth. (C) The F-score plot without control data. SPP was not able to run without control. GEM resulted in few peaks which is not shown in the plot. (D) Boxplot without control data.

Although control data are often essential for modeling background distributions for candidate summits, F-Seq2 demonstrated a highly balanced performance between precision and recall on simulated ChIP-seq data without controls (Figure 1C and D). F-Seq2 had the highest overall curve, which stood out among the other peak callers, including MACS2 and the original F-Seq, and achieved comparable performance (0.883) to those with control datasets (0.897). These results suggest that a significant amount of control information is contained within treatment dataset at a large scale. This is also evident in the real FoxA1 ChIP-seq dataset (7) where control read counts correlated well with treatment read counts in 10 kb windows across the genome. The observed high correlation and performance of F-seq2 implies that control information can be robustly extracted from treatment data and can be used to estimate background distribution for peak calling, given it does not greatly contradict with the treatment data and given a statistically rigorous modeling method for treatment data (e.g. F-Seq2 KDE). For real ChIP-seq datasets, especially where the correlation is low between control and treatment data, calling peaks without control data is less accurate due to the loss of unique information and cannot be recovered from treatment data (14).

Performance on real datasets

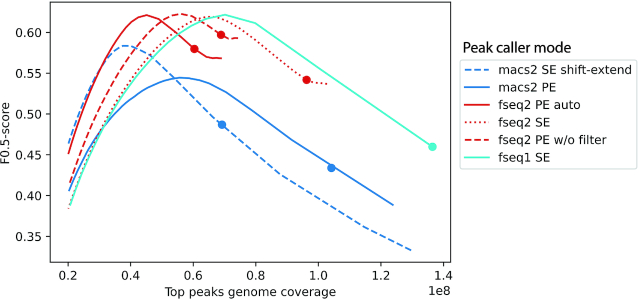
The absence of control data is more often seen in DNase-seq and ATAC-seq experiments compared to ChIP-seq. Therefore, F-seq2 was directly compared to MACS2 on ATAC-seq data to further evaluate performance in the absence of control data (Figure 2). Both F-Seq2 with paired-end (PE) auto mode and MACS2 with single-end (SE) shift-extend mode, which are two different strategies to avoid calling peaks on nucleosome centers, precisely identified open chromatin regions with their top ranked peaks (see ‘Materials and Methods’ section for auto filter design details). The higher overall characteristic curve of F-Seq2 (highest F-0.5 score = 0.62) indicates the filter-based method is more effective in avoiding peaks called on nucleosomes compared to the shift-based method. MACS2 SE shift-extend mode outperformed its PE mode (highest F-0.5 scores: 0.58 versus 0.54) at low genome coverage (1% of human genome). This precision gained by the shift-extend strategy is likely why single-end data is used as part of the official ENCODE ATAC-seq data analysis pipeline (12). At larger genome coverage (2%), F-Seq2 PE without filter mode, and SE mode showed superior performance versus all other modes (both had the highest value for F-0.5 score = 0.62 at different coverages). This observation suggests that the additional data improved precision for medium ranked peaks in F-Seq2 in its non-filter-based mode, which takes advantage of the greater genomic information available for more robust and accurate background estimations at the cost of precision at low genome coverage.

Figure 2.

Comparison of F-Seq2 and MACS2 on the ATAC-seq paired-end data in GM12878. The F0.5-score operating characteristic curve where F0.5-score is plotted as a function of the genome coverage in base pairs by the top ranked peaks. F0.5-score put more emphasis on precision than recall due to the incompleteness of our ‘ground truth’. MACS2 was run with two modes: SE shift-extend mode and PE mode. SE shift-extend mode first shifted both 5′ and 3′ ends 75 bp toward outside (5′ end in 3′ to 5′ direction, 3′ end in 5′ to 3′ direction), then extended 150 bp toward inside. This approach smoothed the counts of cutting events by the extension size, which is used by the ENCODE ATAC-seq data analysis pipeline (12). F-Seq2 was run with three modes: PE auto mode, PE without filter mode and SE mode. PE auto mode used the F-Seq2 auto filter that is designed based on nucleosome-related fragment length information (see ‘Materials and Methods’ section for design details). Dots on curves indicate the genome coverage of significant peaks by the default threshold of each peak caller.

Interestingly, the original F-Seq1 with SE mode had a similar characteristic curve to F-Seq2 with SE mode, and even better performance at larger genome coverage. The similar performance observed for both versions validates the assumption F-Seq1 made that the peaks with higher signals are more likely to be true positives (versus false positives) in open chromatin datasets compared to those in ChIP-seq datasets. This alleviates the need to further conduct the dynamic Poisson tests in DNase-seq and ATAC-seq datasets while maintaining high F-0.5 scores. Despite the effectiveness of the dynamic Poisson test at filtering out false positives in ChIP-seq datasets, it potentially filters out more true positives in ATAC-seq datasets, shown by the superior performance of the original F-Seq with SE mode at larger genome coverage. F-Seq peak ranks can be reproduced in F-Seq2 by ranking peaks with signal values.

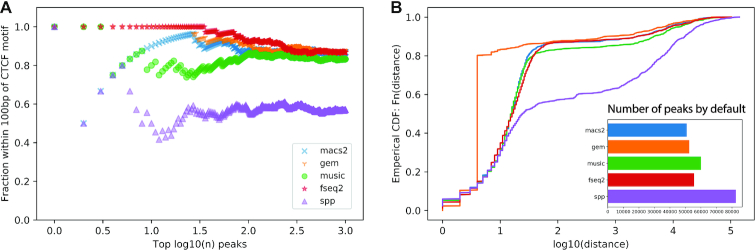
F-Seq2 was benchmarked on three real ChIP-seq datasets to confirm that the observed high performance under the simulated situations can be recapitulated using real data. F-Seq2 had the largest fraction of top 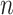peaks (up to 1000 peaks) within 100 bp of a CTCF motif (Figure 3). GEM was the second largest with slightly better performance than MACS2. The empirical distribution of the distance of called peaks to the nearest CTCF motif showed a clear performance advantage for GEM in detecting peaks centered around motifs: 80% of the 1000 most significant peaks were within 4 bp of a CTCF motif. This performance differential is due to GEM’s utilization of motifs, where the tool intends to improve peak calling accuracy at the expense of increased run time, and potentially introducing bias by ranking peaks without motifs lower than those containing a TF motif. MACS2 and F-Seq2 had the shortest execution time for the CTCF datasets while maintaining favorable performance relative to GEM (Supplementary Figure S2). Similar trends were observed in the MAFK ChIP-seq dataset benchmarking results, with SPP being an exception as it had the most variable number of peaks called by a default threshold between the two TFs (Supplementary Figure S3). However, all peak callers had a much lower and barely distinguishable performance between each other on STAT1 (Supplementary Figure S4). Karimzadeh and Hoffman (25) showed that 76 out of 220 chromatin factor ChIP-seq peaks lacked relevant sequence motifs, and STAT1 peaks were low in motif occupancy (below 50%), suggesting that evaluating peak callers using motifs may not reflect actual performance. As the motif-centered evaluation is likely problematic, it is necessary to use the more accurate and precise simulated ground truth data when assessing tool performance.

Figure 3.

Comparison of peak callers on the CTCF ChIP-seq in ascending aorta female adult (51 years). (A) The fraction of top 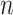peaks within 100 bp of a CTCF motif. (B) The empirical distribution of the shortest distance of the called peaks to a CTCF motif. The subplot shows the number of significant peaks called by each method using the default threshold.

DISCUSSION

The highly balanced performance of F-Seq2 between precision and recall across different assays is noteworthy. Kernel density estimation (KDE), which is a nonparametric method to model the read probability distribution, has an advantage over explicit modeling methods. Confounding experimental and biological factors, such as antibody specificity, DNA susceptibility to enzymes and sequencing read mappability make it difficult to form explicit assumptions (26), especially across different assays. The advantage of KDE has been demonstrated by the original peak caller F-Seq, which is the top-performing peak caller on DNase-seq datasets (1), and frequently used for FAIRE-seq data peak calling (3). We designed a new statistical framework and introduced new features to F-Seq to further improve the performance in this second version. Adding support for user-input control data allows for F-Seq2 to more accurately model background reads distribution together with the treatment reads distribution. With the help of a dynamic parameter 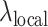, read distributions around candidate summits can be summarized into significance values accounting for local biases, leading to statistically robust peak ranks and peak calls. The joint effect of KDE and the dynamic parameter demonstrated superior performance in our benchmarking results, especially without control data. This suggests control information can be extracted from treatment data, given control and treatment data are well correlated. The support of control data allows for a more biologically meaningful signal to be reconstructed by weighting the treatment with control data, which leads to a better sanity-check when comparing and combining signals from different datasets (11).

Whether control data is a dispensable dataset for ChIP-seq peak calling requires further investigation. Recent papers (14,27) that predict the linear weights for control datasets from treatment datasets provide evidence that control information can be extracted from treatment data. In our simulation results, a comparable performance was observed when using or omitting control data. F-Seq2 runs using experiments with real ChIP-seq data showed only a slightly decrease in performance without control data (data not shown). We suspect that the high correlations between control and treatment data explain the observation that control data are not required in a simulation setting. However, conclusions cannot be made based on the small performance difference on the real ChIP-seq datasets due to evaluation biases with motifs. We are unable to determine if a large observable discrepancy (low correlation) between control and treatment data is due to either the low quality of the datasets or the indispensable information contained within control dataset.

F-Seq2 is compatible and suitable for IDR analysis that we recommend as a more reliable approach to determine a significance threshold when working with replicates. The IDR algorithm requires peak callers to run at a relaxed threshold to include both signal and noise peaks within the output to detect the consistency transition point between the two groups (15). During benchmarking, the MACS2 peak width detection was observed to be tied to peak detection. When the q-value threshold was lowered, by default MACS2 called not only more peaks, but larger width peaks, and may cause irreproducibility as a side-effect (i.e. changing the significance scores and ranks of called peaks). We developed F-Seq2 with summit-focused statistical testing and used separate parameters for peak width detection and summit detection. F-Seq2 reliably reproduces the same exact summits and peaks when lowering the P-value or q-value threshold, and an individual significance score for each summit is calculated. Having separate scores for each summit and less rank ties by P-value interpolation are essential for IDR to precisely identify the transition point, representing the desired threshold. We have built a peak calling pipeline for a pair of replicates with F-Seq2 followed by an integrated IDR analysis with our recommended settings, which is directly accessible through the command line interface.

F-Seq2 further pushes the potential in the mature field of peak calling. The accuracy of peak calling is essential for downstream analysis, such as differential and motif analysis, to discover new biological insights and mechanisms with HTS data.

DATA AVAILABILITY

Data accessibility and peak caller parameter settings. Simulated data were reproduced from Thomas et al. (16). The adapted scripts to simulate ChIP-seq data, and the scripts to run all peak callers are available at https://github.com/Boyle-Lab/F-Seq2-Paper-Supplementary. The accession numbers of all ENCODE data, and the IDs of all JASPAR motifs used in this study are also available at this website.

Software availability. The F-Seq2 software and documentation are available at https://github.com/Boyle-Lab/F-Seq2. F-Seq2 can be installed through the Python Package Index (PyPI) and the Conda package manager.

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

NIH [U24 HG009293 to N.Z., A.P.B.].

Conflict of interest statement. None declared.