COMPREHENSIVE RECONSTRUCTION OF MULTI-SHOT MULTI-CHANNEL DIFFUSION DATA USING MUSSELS

Abstract

Echo planar imaging (EPI)- based magnetic resonance imaging (MRI) data are often corrupted by Nyquist ghost artifacts resulting from odd-even shifts of the EPI read-outs. Algorithms that corrects for the Nyquist ghost artifacts rely on calibration scans that are collected prior to the data acquisition. However, a more complex pattern of ghosting artifacts arises when diffusion-weighted data are acquired using segmented k-space EPI read-outs. The additional under-sampling present in the segmented acquisitions and the inter-shot motion during diffusion weighted acquistion cause ghosting artifacts in addition to the EPI ghosting arising from odd-even shifts. We propose a comprehensive method that can remove the Nyquist-ghosting artifacts as well as the inter-shot motion-induced ghosting artifacts in diffusion weighted images in a single step from partial Fourier data without the need for a calibration scan. We show very high quality diffusion data recovery using the proposed method.

1. INTRODUCTION

Diffusion weighted magnetic resonance imaging (DWI) is a widely used neuroimaging technique to study white matter connectivity in vivo. The MR pulse sequence is designed to make it sensitive to the microscopic motion of water molecules. The large gradients applied to sensitize the sequence to the Brownian motion of water also makes the sequence sensitive to bulk subject motion as well the inherent physiological motion. Subject motion in the presence of diffusion gradients introduce phase terms in the diffusion data [1]. To avoid the phase terms in the reconstructed diffusion weighted images, typically a single-shot echo-planar imaging (EPI) sequence is used which samples the entire k-space data after a single RF excitation and application of one diffusion gradient direction. This process is repeated for each gradient direction until all of the specified gradient directions is acquired.

A disadvantage of the single-shot EPI-based diffusion acquisition is the long echo-time (TE) required, which limits its utility for high resolution imaging especially at higher magnetic field strengths (eg. 7 Tesla). Multi-shot in combination with partial Fourier acquisitions are often used to achieve lower TE times. In multi-shot acquisitions, the k-space data corresponding to a diffusion direction is acquired across multiple RF excitations. Subject motion during the multiple RF excitations leads to different phase terms for each shot, which will result in ghosting artifacts in the reconstructed images if the k-space data is combined without first correcting for the different phases. Moreover, in EPI-based multi-shot diffusion imaging, the situation is made worse due to eddy currents, field inhomogeneities and other hardware imperfections. For example, the k-space trajectories corresponding to the odd and even read-outs are often mis-aligned, resulting in phase shifts in the images. These phase shifts are also manifested as ghosting artifacts in the images. Therefore, multi-shot DWI acquisition is corrupted with multiple sources of error that all contribute to ghosting artifacts in the reconstructed images. Hence, multi-shot diffusion data needs to be corrected for ghosting artifacts arising from the above sources of error before it can be used for further estimation of the diffusion process.

Typically during image reconstruction of multi-shot DWI data, the shifts between the odd and even lines of k-space are first corrected, followed by estimation and correction of phase errors of the inter-shot subject motion. Correction of phase shifts between the odd and even lines of k-space EPI-related ghosting artifacts typically relies on a calibration scan that is collected before the data acquisition and usually only corrects for 1D phase errors [2]. The odd-even shift can be measured with a non-phase encoded reference scan and can be applied to correct phase errors. The above method only corrects for bulk shifts along the frequency-encoding directions and do not correct for shifts along the phase encoding direction. The disadvantage of the calibration-based methods is that it has to be modified each time to match the number of shots used in the data acquisition. Moreover, the arbitrary k-space shifts induced by the local field inhomogeneities are often uncorrected. Once the ghosting artifacts from the odd-even shifts are corrected, the motion-induced phase errors are estimated using a SENSE-based reconstruction of each of the k-space segments. These phase terms are then removed from the k-space data before combing the k-space data to obtain the magnitude diffusion weighted images.

Recently, we proposed a “calibration-free” reconstruction method for multi-shot DWI data known as MUSSELS [3]. This method is able to achieve implicit phase correction of the diffusion data collected from multiple shots and thus provide ghost-free multi-shot diffusion image reconstruction.

In this work, we show that the correction of ghosting artifacts arising from shifts between the odd and even lines of EPI k-space data can be handled within the same framework leading to a comprehensive “calibration-free” method for ghosting artifact removal for EPI multi-shot diffusion data. The advantage of the above method is that it can correct for k-space shifts in any direction and not just in the frequency-encoding direction. The method does not need a reference scan and hence no pulse sequence modification is necessary. It can also reconstruct the full k-space data from a partial Fourier acquisition without using any specialized reconstructions such as homodyne-based reconstructions. We demonstrate the performance of the method on a 4-shot diffusion weighted data collected with partial Fourier acquisition.

2. PROPOSED ALGORITHM

The underlying idea of the proposed algorithm is that phase inconsistencies arising from the different mechanisms can be represented using a single phase term in the image domain.

2.1. Signal model in the absence of EPI artifacts

Let the DWI of a given diffusion direction be denoted as ρ(x, y), where x, y represents spatial coordinates. Then, the k-space signal equation for the n^th echo (denoted by s(k_x, n · Δk_y)) of an EPI acquisition can be written as

$$\begin{gathered} s(k_x,n\cdot \Delta k_y)\approx \int \int \rho (x,y)\cdot e^{-i(k_x\cdot x+n\Delta k_y\cdot y)} \\ \underset{\text{motion}}{\underbrace{\cdot e^{-i\varphi (x,y)}dxdy}}, \end{gathered}$$ (1)

where ϕ(x, y) is the phase term introduced due to inter-shot subject motion during the DW acquisition [1]. This can be written in the image domain as

$$m_l(x,y)=\rho (x,y){\varphi }_l(x,y),$$ (2)

where m_l(x, y) is the DWI measured from the l^th shot of the acquisition for a given diffusion gradient. The phase terms ϕ_l which vary from shot-to-shot needs to be removed before ρ(x, y) can be recovered from the measurements corresponding to the different shots l = 1 : N_s, N_s being the total number of k-space shots in the segmented k-space acquisition. We recently proposed an annihilating filter-based method known as MUSSELS [3] to recover the DWI using a structured low-rank matrix completion formulation using the idea that we can find a shift invariant filter in the frequency domain that can achieve the k-space shifting necessary to demodulate the phase variations. If such an annihilating filter exists, then we can construct a block-Hankel structured low-rank matrix

$${\mathbf{H}}_1(\widehat{\mathbf{m}})=[\mathbf{H}(\widehat{m_1})\mathbf{H}(\widehat{m_2})\dots \mathbf{H}(\widehat{m_{N_s}})]$$

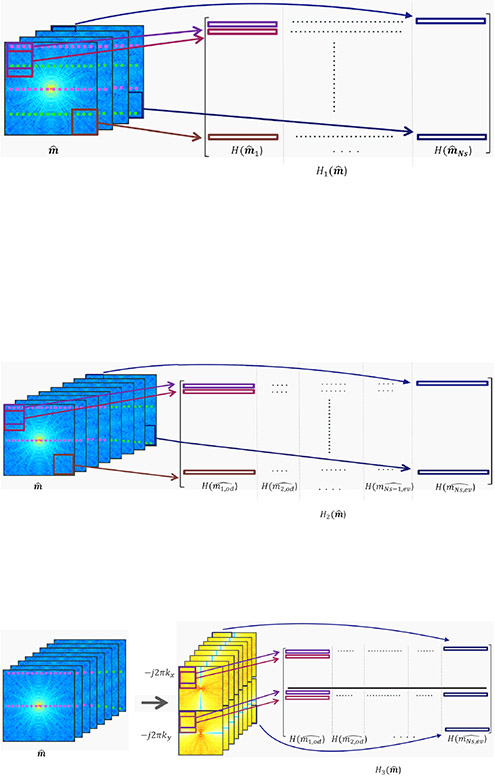
by lifting of the k-space data corresponding to the different shots. Here, $\widehat{m_l}$ denote the discrete Fourier coefficients of m_l(x, y) and $\mathbf{H}(\widehat{m_l}))$ is a block Hankel matrix of size (N₁ – r + 1)(N₂ – r + 1) × r² generated from the N₁ × N₂ Fourier samples of $\widehat{m_l}$ for a filter of size r × r. Figure 1 shows a pictorial representation of the matrix lifting for constructing ${\mathbf{H}}_1(\widehat{\mathbf{m}})$. Using a structured low-rank matrix completion scheme, we can recover any missing entries of the k-space data and thereby recover ρ(x, y) without explicitly computing the phase terms ϕ_l.

Fig. 1:

Construction of the block-Hankel structured low-rank matrices for various reconstructions

(a) The k-space data of each shot is stacked into a 3-D matrix. Using a moving filter of size r × r (marked by the rectanguar boxes), the k-space data is transformed (“lifted”) to form a structured matrix. The data from the different shots are stacked column-wise. The pink dotted lines etched over the k-space data denote the odd lines of the k-space acquisition while the green dotted lines denote the even lines of the k-space acquisition. Structured low-rank matrix completion using H₁($\widehat{\mathbf{m}}$) can recover the missing k-space data for each shot.

(b) In the presence of odd-even shifts, the k-space data of each shot is separated into data coming from odd and even lines and stacked as a 3D matrix. The structured matrix H₂($\widehat{\mathbf{m}}$) is constructed as explained above and is used for matrix completion.

(c) Construction of the structured low-rank matrix H₃($\widehat{\mathbf{m}}$) to incorporate smoothness regularization. The k-space data is multiplied by −j2πk_x and −j2πk_y respectively. H₃($\widehat{\mathbf{m}}$) is constructed by the lifting of the resulting k-space data as shown.

2.2. Signal model in the presence of inter-shot motion and EPI artifacts

To accommodate the odd-even shifts of the EPI acquisition, the equation for the n^th echo of an EPI sequence can be modified as [4]

$$\begin{gathered} s(k_x,n\cdot \Delta k_y)\approx \int \int \rho (x,y)\cdot e^{-i(k_x\cdot x+n\Delta k_y\cdot y)} \\ \underset{\text{motion}}{\underbrace{\cdot e^{-i\varphi (x,y)}}}\underset{\text{odd}-\text{even shift}}{\underbrace{\cdot e^{-i\gamma \cdot \Delta B_0(x,y)\cdot (T_n+(-1{)}^n(\frac{k_x}{\gamma G_x}))}}}dxdy \end{gathered}$$ (3)

where a second phase term now arises from local field inhomogeneity(ΔB₀(x, y))-induced shifts of odd and even echoes and has opposing sign depending upon the echo due to the (−1)ⁿ term. Here, T_n is the time for the n^th echo, γ is the gyromagnetic ratio and G_x is the readout gradient. Note that this phase is dependent on spatially varying field inhomogeneity. Calibration based correction can only model this as a phase ramp and hence only 1D correction is achieved wheres in the current formulation, 2D shifts can be modeled. The image-domain relation corresponding to Eq (3) can be written as

$$\begin{gathered} m_{l,od}(x,y)=\rho (x,y){\phi }_{l,od}(x,y) \\ \text{and} \\ {m}_{l,ev}(x,y)=\rho (x,y){\phi }_{l,ev}(x,y);\forall x,y, \end{gathered}$$ (4)

where φ(x, y) now accommodates both the phase terms in Eq (3) and m_l,od(x, y) and m_l,ev(x, y) are the DWI corresponding to the odd and even echoes of the l^th shot respectively. φ(x, y) is assumed to be a complex quantity such that ∣φ(x, y)∣ = 1; ∀x, y. The corresponding annihilation relations in frequency domain

$$\begin{gathered} {\widehat{m}}_{l,od}(k_x,k_y)\ast {\widehat{\phi }}_{l,ev}(k_x,k_y)- \\ {\widehat{m}}_{l,ev}(k_x,k_y)\ast {\widehat{\phi }}_{l,od}(k_x,k_y)=0 \end{gathered}$$ (5)

can be implemented as multiplication using Hankel matrices

$$\mathbf{H}(\widehat{m_{l,od}})\cdot {\widehat{\phi }}_{l,ev}-\mathbf{H}(\widehat{m_{l,ev}})\cdot {\widehat{\phi }}_{l,od}=0,$$ (6)

similar to the MUSSELS framework. Since this is true for all l = 1 : N_s, we can derive a new structured low-rank matrix

$$\begin{gathered} {\mathbf{H}}_2(\widehat{\mathbf{m}})= \\ [\mathbf{H}(\widehat{m_{1,od}})\dots \mathbf{H}(\widehat{m_{N_s,od}})\mathbf{H}(\widehat{m_{1,ev}})\dots \mathbf{H}(\widehat{m_{N_s,ev}})] \end{gathered}$$ (7)

which can be obtained by the lifting of the k-space samples of the different shots split into odd and even echoes as shown in Fig. 1b. Methods employing structured low-rank matrix completion can be used to recover the missing k-space samples in each of the k-space segments [5, 3].

2.3. Smoothness regularized reconstruction of DWI data with ghost correction

Since we split the k-space data corresponding to multiple segments both along the number of shots and the odd/even echoes, each individual k-space data is highly under-sampled in a structured manner. Hence, we employ a regularized reconstruction that impose smoothness constraints on the DWI to recover the image. It has been shown that such smoothness constraints can be easily incorporated into the structured low-rank matrix completion formulation [6] by performing an additional matrix lifting as shown in Fig 1c. Here, the derivatives of the DWI along the x- and y-dimension are computed in the frequency domain and the corresponding k-space data were subject to matrix lifting separately and stacked row-wise. The resulting structured matrix ${\mathbf{H}}_3(\widehat{\mathbf{m}})$ is also highly low-rank. We perform matrix completion on this structured matrix to recover the ghost-corrected DWI. We note here that recently another method was also proposed solely for EPI ghost correction using matrix completion that do not rely on coil sensitivity information [7].

2.4. Reconstruction of partial Fourier DWI data with ghost correction

Diffusion images are typically acquired using a partial Fourier acquisition in order to achieve lower TEs and thereby increase the SNR. In our work, we demonstrate that we can recover the full k-space data of the DWI by employing the smoothness regularized multi-channel reconstruction with prior estimates of the coil sensitivity maps. Thus, the full k-space reconstruction for the DWI with ghost correction can be formulated as

$$\widehat{\tilde{\mathbf{m}}}={\text{argmin}}_{\widehat{\mathbf{m}}}\Vert \mathcal{A}(\widehat{\mathbf{m}})-\widehat{\mathbf{y}}{\Vert }_{{\ell }_2}^2+\lambda \Vert {\mathbf{H}}_3(\widehat{\mathbf{m}}){\Vert }_{\ast },$$ (8)

where $\widehat{\mathbf{y}}$ is the measured k-space data. The first term imposes data consistency onto the measured k-space data using a regular SENSE formulation and ensures full k-space recovery. The operator $\mathcal{A}$ represents the concatenation of the following operations: $\mathcal{M}\circ \mathcal{F}\circ \mathcal{S}\circ {\mathcal{F}}^{-1}$ where $\mathcal{F}$ and ${\mathcal{F}}^{-1}$ represent the Fourier transform and the inverse Fourier transform operations respectively, $\mathcal{S}$ represents multiplication by coil sensitivities, and $\mathcal{M}$ represents multiplication by the k-space sampling mask corresponding to each shot-echo. The second term in Eq. (8) is the nuclear norm of the block-Hankel matrix of the shots, which is the convex relaxation for the rank penalty. λ is a regularization parameter.

3. RESULTS

We show the recovery of the DWI with ghost correction on a in-vivo data that was collected on a healthy adult volunteer on a GE 7T 950 MR scanner (GE Healthcare Waukesha, WI). A 32-channel Tx/Rx coil with transmit in quadrature mode was used for imaging. Stajeskal-Tanner diffusion sequence with 4-shot readout was used for data acquisition. DW imaging scan parameters included b-value=1000s/mm², FOV = 256mmx256mm, matrix size=128x128, slice thickness=2mm, partial Fourier= 5/8, TE=50ms, one non-diffusion weighted and 15 diffusion weighted acquisitions.

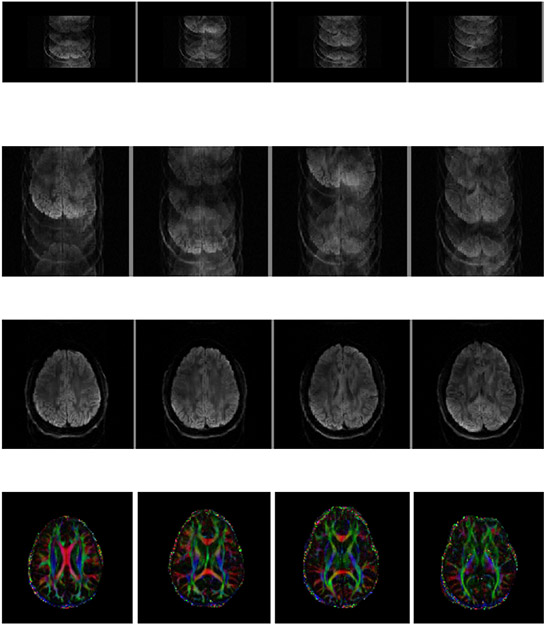
Figure 2(a) shows the direct Fourier reconstruction of partial-Fourier acquired DWI data which was not corrected for EPI ghost artifacts. Figure 2(c) shows the proposed reconstruction of the DWI which corrected for EPI ghost artifacts as well as inter-shot subject motion and figure 2(d) shows the color-coded fractional anisotropy maps recovered from a tensor fit using the 15 diffusion weighted images that were all corrected for ghosting artifacts using the proposed method. Figure 3 shows the full k-space data recovered from the partial Fourier acquisition using the proposed method.

Fig. 2:

Calibration-less ghosting correction of multi-shot DWI demonstrated on 4 different slices of the brain.

(a) DWI data collected from four slices with partial Fourier acquistion (128 × 80) corrupted by ghosting arising from inter-shot motion and EPI artifacts

(b) The partial Fourier data in (a) zero-filled to 128 × 128 matrix.

(c) DWI Images after ghost-correction using the proposed method

(d) Color-coded fractional anisotropy maps computed from all 15 DWIs corrected for ghosting artifacts

Fig. 3:

Acquired uncorrected partial Fourier data (a) and reconstructed full Fourier k-space data (b) recovered for a given channel. The full Fourier k-space data is recovered by smoothness regularization enabled k-space interpolation.

4. CONCLUSION

We introduced a comprehensive algorithm for the recovery of motion-corrected DWIs that also integrates correction for odd-even shifts of the EPI readout. The reconstruction algorithm does not require a calibration scan or the explicit estimates of motion-induced phase terms for the correction of motion-induced ghosting in multi-shot diffusion data. The coil-sensitivity enabled recovery combined with the smoothness regularized matrix completion scheme enable full recovery of the partially acquired k-space data from the available k-space data without resorting to any additional constraints. The method can enable routine high SNR, high resolution diffusion imaging using multi-shot acquisition in a single step directly from the k-space data.