An Interpretable Planning Bot for Pancreas Stereotactic Body Radiation Therapy

Abstract

Purpose:

Pancreas stereotactic body radiation therapy (SBRT) treatment planning requires planners to make sequential, time-consuming interactions with the treatment planning system to reach the optimal dose distribution. We sought to develop a reinforcement learning (RL)-based planning bot to systematically address complex tradeoffs and achieve high plan quality consistently and efficiently.

Methods and Materials:

The focus of pancreas SBRT planning is finding a balance between organ-at-risk sparing and planning target volume (PTV) coverage. Planners evaluate dose distributions and make planning adjustments to optimize PTV coverage while adhering to organ-at-risk dose constraints. We formulated such interactions between the planner and treatment planning system into a finite-horizon RL model. First, planning status features were evaluated based on human planners’ experience and defined as planning states. Second, planning actions were defined to represent steps that planners would commonly implement to address different planning needs. Finally, we derived a reward system based on an objective function guided by physician-assigned constraints. The planning bot trained itself with 48 plans augmented from 16 previously treated patients, and generated plans for 24 cases in a separate validation set.

Results:

All 24 bot-generated plans achieved similar PTV coverages compared with clinical plans while satisfying all clinical planning constraints. Moreover, the knowledge learned by the bot could be visualized and interpreted as consistent with human planning knowledge, and the knowledge maps learned in separate training sessions were consistent, indicating reproducibility of the learning process.

Conclusions:

We developed a planning bot that generates high-quality treatment plans for pancreas SBRT. We demonstrated that the training phase of the bot is tractable and reproducible, and the knowledge acquired is interpretable. As a result, the RL planning bot can potentially be incorporated into the clinical workflow and reduce planning inefficiencies.

Introduction

For patients with locally advanced pancreatic cancer, one standard of care is concurrent chemotherapy with conventionally fractionated radiation therapy. Owing to improvements in motion management, imaging technology, and treatment delivery accuracy, the use of stereotactic body radiation therapy (SBRT) is now possible for pancreatic cancer treatment with low risks of radiation-induced toxicity.¹ With SBRT, the radiation dose is delivered to patients over shorter periods of time and without significant delays in systemic therapy.² National database studies suggested that chemotherapy followed by SBRT results in better outcomes than chemotherapy alone or chemotherapy concurrent with conventionally fractionated intensity modulated radiation therapy (IMRT).^3,4 However, treatment planning of pancreas SBRT poses a challenge to planners given that pancreas SBRT treatments are inherently difficult to plan, considering patient-specific planning target volume (PTV) coverage, organ-at-risk (OAR) sparing tradeoff requirements, and high interpatient anatomy variability.

Treatment planning, especially pancreas SBRT planning, is inherently iterative and interactive. The planning process starts with a planner setting initial optimization constraints to the PTV and OARs, and executing the optimization algorithm embedded in the treatment planning system (TPS). The initial optimization constraint set will not generate the optimal plan owing to individual anatomy variations. Therefore, the planner is required to iteratively adjust the optimization objectives to make the plan clinically optimal. Due to the toxicity concerns of the gastrointestinal (GI) structures and their proximity to the PTVs, planners usually rely on a trial-and-error approach and repetitively interact with the TPS to achieve clinical optimality. This process is time-consuming, and the resultant plan quality is highly subjective to planner experience.

Reinforcement learning^5,6 presents a potential solution to this problem. A reinforcement learning agent (in our case, a planning bot) gains decision-making knowledge by repetitively interacting with the surrounding environment (TPS) and evaluating rewards (improvement of the plan dose distribution) associated with the action (changing of optimization objectives). State-action-reward-state-action (SARSA),⁷ also known as connectionist Q-learning, is a widely used reinforcement learning algorithm and has been proven to perform well in wide-ranging real-world applications, such as controlling power systems,⁸ advanced robotics,⁹ and playing video games.^10,11 This efficient, sampling-based algorithm sequentially changes the knowledge of the agent based on the interactive training process. We developed a SARSA-based treatment planning bot that assists planners to efficiently achieve consistent and high-quality plans for pancreas SBRT treatments. We hypothesize that, through repetitive interactions with the TPS, the autonomous planning bot can learn to make appropriate adjustments given anatomic information and intermediate planning results, and ultimately design clinical optimal plans.

Methods and Materials

Pancreas SBRT treatment planning is a highly interactive process. Although the TPS can optimize plans with respect to the objective function given by the planner, the setting of planning objectives is highly dependent on the shape, size, and location of the PTVs. The planner usually interacts with the TPS multiple times and performs various actions, including adjusting dose-volume constraints and creating necessary auxiliary structures to get desirable dose distributions. The action-making decisions are guided by the current planning status and the planner’s prior experience-based assessment. Herein, we adopt a SARSA reinforcement-learning framework to perform these tasks systematically. The formulation of SARSA is as follows:⁷

$$Q(s,a)\leftarrow Q(s,a)+\alpha ·\left[r\left(s,a,s^{\prime }\right)+\gamma ·Q\left(s^{\prime },a^{\prime }\right)-Q(s,a)\right],$$

where s and a denote the current state and action; s′ and a′ the next state and action; Q the value function; r the immediate reward; α the learning rate of the bot; and γ the discount factor of the system. In particular, the action value function Q predicts the expected long-term reward. The goal of the iteration during the training phase is to parameterize Q; which can be subsequently used to guide future decision making. With linear function approximation, we formulated the action value function of the treatment planning RL problem as:

$$Q_{\theta }(s,a)={\theta }^{\text{T}}\phi (s,a),$$

where Q_θ(s, a) represents the expected final score value at state s when action a is taken, θ^T denotes the feature vector that will be learned through the training process, and φ (s, a) is a set of features carefully engineered to reduce the complexity of the RL problem without losing out on generalization. In our implementation, the feature φ(s, a) is generated as an outer product of a state vector f(s) and an action vector g(a) : φ(s, a) = vec[f(s) ⊗ g(a). Here, ⊗ denotes the outer product operator, which multiplies each element of the row vector f(s) to each element of the column vector g(a). The state vector f(s) is formulated as f(s) = [ΔD₁, ΔD₂ …, ΔD_N], where $\Delta D_n={\overline{D}}_n-D_n$, n∈ [1, 2, 3, …, N] denotes the differences between the predicted/estimated dose constraints and the actual dose values at the current iteration. The complete state vector implemented for our pancreas SBRT planning module is listed in the supplementary materials.

The action vector g(a) = [1(a = A₁), 1(a = A₂), …, 1(a = A_M)^T is an array of M indicators that represent indices of M actions. The M action options are designed based on the actions commonly taken by our clinical planners during pancreas SBRT treatment planning. Since we are taking sequential steps, the vector only has one nonzero component at any step during the iterations. In total, 19 actions are designed to ensure the bot has an optimal choice in any given state that may lead to the optimal plan quality. The actions include adding constraints to the liver, kidney, cord, and auxiliary structures associated with the stomach, duodenum, bowel, and primary PTV in addition to the boost PTV. Full descriptions of the actions are listed in Table 1. Of note, the fixed priorities carried by the actions can be viewed as fixed step sizes. The bot takes 1 action per interaction and is allowed to take repeated actions.

Table 1.

Action options for the reinforcement learning planning program

Action index	Structure	Volume	Dose	Priority	Constraint type
A1, A2, A3	PTVpri minus overlapping region with GI OARs with 0, 4, and 6 mm expansion	96%	$\overline{{\text{D}}_{pri}}$	80	Lower
A4, A5, A6	PTVbst minus overlapping region with GI OARs with 0, 4, and 6 mm expansion	96%	$\overline{{\text{D}}_{bst}}$	80	Lower
A7, A8, A9	Bowel with 2, 4, and 6 mm expansion	0.5 cm3	D 1cc – 2 Gy	80	Upper
A10, A11, A12	Duodenum with 2, 4, and 6 mm expansion	0.5 cm3	D 1cc – 2 Gy	80	Upper
A13, A14, A15	Stomach with 2, 4, and 6 mm expansion	0.5 cm3	D 1cc – 2 Gy	80	Upper
A16	PTVpri minus PTVbst	20%	D20% – 2 Gy	50	Upper
A17	Liver	50%	12 Gy	50	Upper
A18	Kidneys	30%	12 Gy	50	Upper
A19	Cord	0	20 Gy	50	Upper

Abbreviations: GI = gastrointestinal; OAR = organ at risk; PTV = planning target volume. $\overline{{\text{D}}_{pri}}$ and $\overline{{\text{D}}_{bst}}$ denotes the prescription levels for the primary and boost PTV, respectively.

The reward r is assigned as the plan quality score improvement after each step: r = S′ − S, where S and S′ denote the plan quality score before and after taking the current action, respectively. The plan score metric S is set as a weighted combination of various clinical plan quality metrics:

$$S=-\sum _i{W}_{i}max\left(K_i-\overline{K_i},0\right)-\sum _j{W}_{j}max{\left(H_j-\overline{H_j},0\right)}^2,$$

where $\overline{K_i}$, $\overline{H_j}$ denote prescribed soft and hard constraints and K_i, H_j achieved soft and hard constraint values. In this study, hard constraints refer to the constraints assigned to the bowels, duodenum, stomach, and cord. Soft constraints are those for the liver and kidney. The plan quality score S was reevaluated each time the bot took 1 action. To keep the notation simple, we assigned positive values to the upper constraints (ie, OAR sparing, PTV hotspot, dose conformity) and negative values to the lower constraints (ie, PTV coverage). The weights were selected carefully to reflect clinical plan quality preferences, which were consulted and reviewed with physician coinvestigators during the experiment design. The current implementation focuses on getting as much of a target boost coverage as possible while satisfying GI structure D_1cc dose constraints. This strategy is consistent with our current clinical practice preference, because the boost PTV prescription dose is likely to be higher for therapeutic gains. Different weightings of the plan quality scores produce planning bots with different tradeoff preferences, as the bot’s perception of expected long term rewards are directly linked to plan quality scores.

The iteration scheme for the planning bot training process is provided in Algorithm 1. During each iteration in the training process (Fig. 1a), a random number generator produces a number between 0 and 1, and if the number is larger than the predetermined threshold ε, a random action is taken. Otherwise, optimal policy-based actions indicated by the current Q function are taken. The introduced randomness in the training process allows the bot possibility to explore different/unseen actions and evaluate the values of these actions associated with the current state. This learning approach is known as ε-greedy and allows for the planning bot to explore the action-value space and acquire planning knowledge without being fully confined to prior experience. In this study, ε is set to gradually decrease over time:

$$\epsilon =max\left(0.05,1-E/E_{max}\right),$$

where E and E_max denote current epoch number and maximum epoch number, respectively. In each epoch, the planning bot practices planning once on each training case. The value of ε decreases linearly as the number of epochs increases and stays ≥0.05. Of note, the randomness only exists in the training phase. In the validation phase, the planning bot only follows the guidance of the action-value function in every step.

Fig. 1.

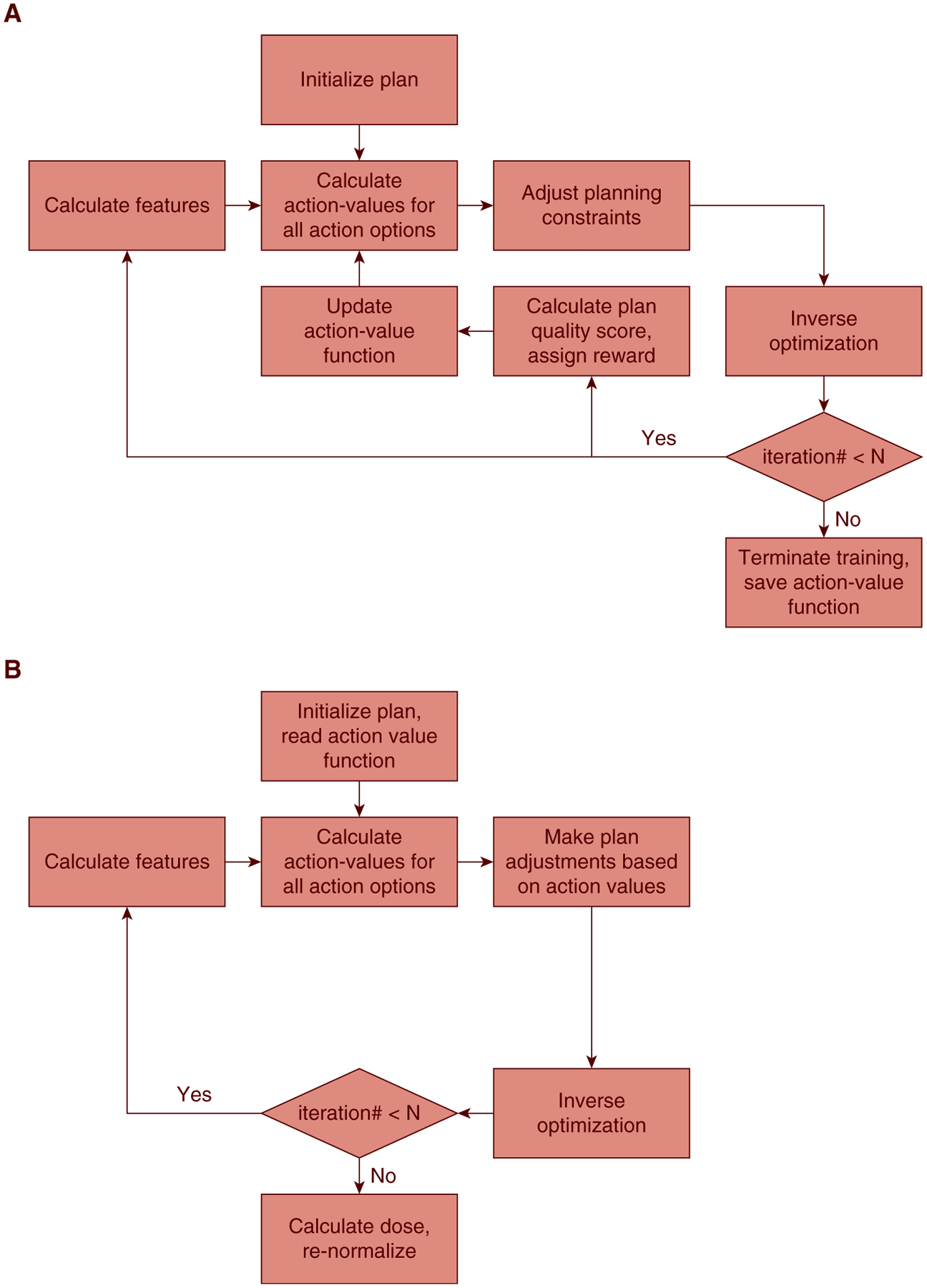
Workflow of the proposed reinforcement learning planning framework, including the (a) training phase, and (b) validation/application phase.

The RL training and validation workflow (Fig. 1) has been implemented in a research TPS environment (Eclipse Treatment Planning System, version 13.7, Varian Medical Systems, Palo Alto, CA). Actions are defined as a set of function calls inside the TPS during the planning phase, enabled by Eclipse Scripting Application Programing Interface. To evaluate the performance of the proposed planning bot framework, we anonymized and retrieved 40 patients with biopsy-proven pancreatic cancer who were previously treated at our institution. A triphasic imaging technique was used during the simulation for target delineation. The primary tumor and adjacent nodal disease were contoured on each imaging sequence. The union of these volumes was used as the internal target volume because this volume should provide a good estimation of the tumor motion range during treatments. The boost PTV prescribed to 33 Gy was defined as the gross tumor volume with a 2- to 3-mm margin and minus GI luminal structures. All 40 patients were treated with a simultaneous integrated boost technique to 25 Gy/33 Gy in 5 fractions. The OAR constraints of these patients were consistent with the multi-institutional phase 2 pancreas SBRT study by Herman et al,¹² in which the authors reported low rates of toxicity.

In this data set, 22 patients were planned on free-breathing computed tomography (CT), with 5 patients planned on average CT processed from free-breathing 4-dimensional CT sequences and the remaining 13 patients on breath-hold CT. The average sizes of the primary PTVs (PTV_25Gy) and boost PTVs (PTV_33Gy) were 200 ± 144 cm³ and 62 ± 32 cm³, respectively. The average volumes of the liver and kidneys were 1504 ± 307 cm³ and 320 ± 71 cm³, respectively. From the cohort, 16 patients were randomly selected to train the RL planning bot. We augmented the training set to 48 plans by expanding the PTV_33Gy by −2 mm, 0 mm, and 2 mm.

The training workflow for a patient, as illustrated in Fig. 1a, consisted of 15 sequential bot-TPS interactions. The RL system was trained with 20 epochs, meaning that the RL bot practiced planning by making 20 different plans for each of the 48 cases in the training set. For each plan, the planning bot initialized with a minimal set of optimization constraints, including PTV lower constraints, kidney, and liver upper constraints. The constraints are given to reduce the number of necessary bot-TPS interactions and accelerate the planning process. The only information carried over from an epoch to another was the weighting vector θ. After the RL bot was fully trained, after the workflow shown in Fig. 1b, we generated treatment plans for the remaining 24 patients and compared them with the clinical treatment plans.

Results

To determine the efficacy of using the proposed RL planning bot in the clinical environment, we validated the plan quality and examined the training process by analyzing the learning behavior of the planning bot, including state specificity of the bot during the training phase, knowledge interpretability, and knowledge reproducibility.

Plan quality and efficiency

Training an RL bot on a single Varian workstation took 5 days. For the validation set, the bot spent 7.3 ± 1.0 minutes on each case to create a deliverable plan from a set of contours. This is a significant improvement over manual planning, which typically takes 1 to 2 hours. Figure 2 shows the planning results for cases in the validation set. All 24 clinical plans and 24 RL bot plans met predefined GI constraints (V_33Gy < 1 cm³) and had sufficient PTV coverages. In particular, PTV_33Gy coverages were comparable between the bot and clinical plans (clinical: 94.6 ± 4.8%; bot: 94.7 ± 1.2%; P = .924). Although the bot plans had higher PTV_25Gy coverages than the clinical plans (clinical: 99.8 ± 0.2%; bot: 98.5 ± 1.4%; P < .001), the clinical plans showed lower bowel D_1cc (clinical: 23.7 ± 5.6 Gy; bot: 25.7 ± 4.2 Gy, P < .001), stomach D_1cc (clinical: 25.1 ± 7.0 Gy, bot: 26.3 ± 7.0 Gy, P = .007), and liver V_12Gy (clinical: 5.2 ± 6.0 Gy, bot: 6.1 ± 6.8 Gy, P = .007). No significant differences are observed for duodenum D_1cc (clinical: 27.2 ± 5.4 Gy, bot: 27.9 ± 4.8 Gy, P = .174), kidney V_12Gy (clinical: 4.2 ± 6.9 Gy, bot: 5.1 ± 5.2 Gy, P = .303), and cord D_max (clinical: 11.7 ± 3.6 Gy, bot: 12.1 ± 3.1 Gy, P = .425). The mean MU value of the bot plans is higher than that of clinical plans (clinical: 1742 ± 271 MU, bot: 1995 ± 351 MU; P = .002), indicating the complexity of the bot plans is slightly higher than that of the clinical plans.

Fig. 2.

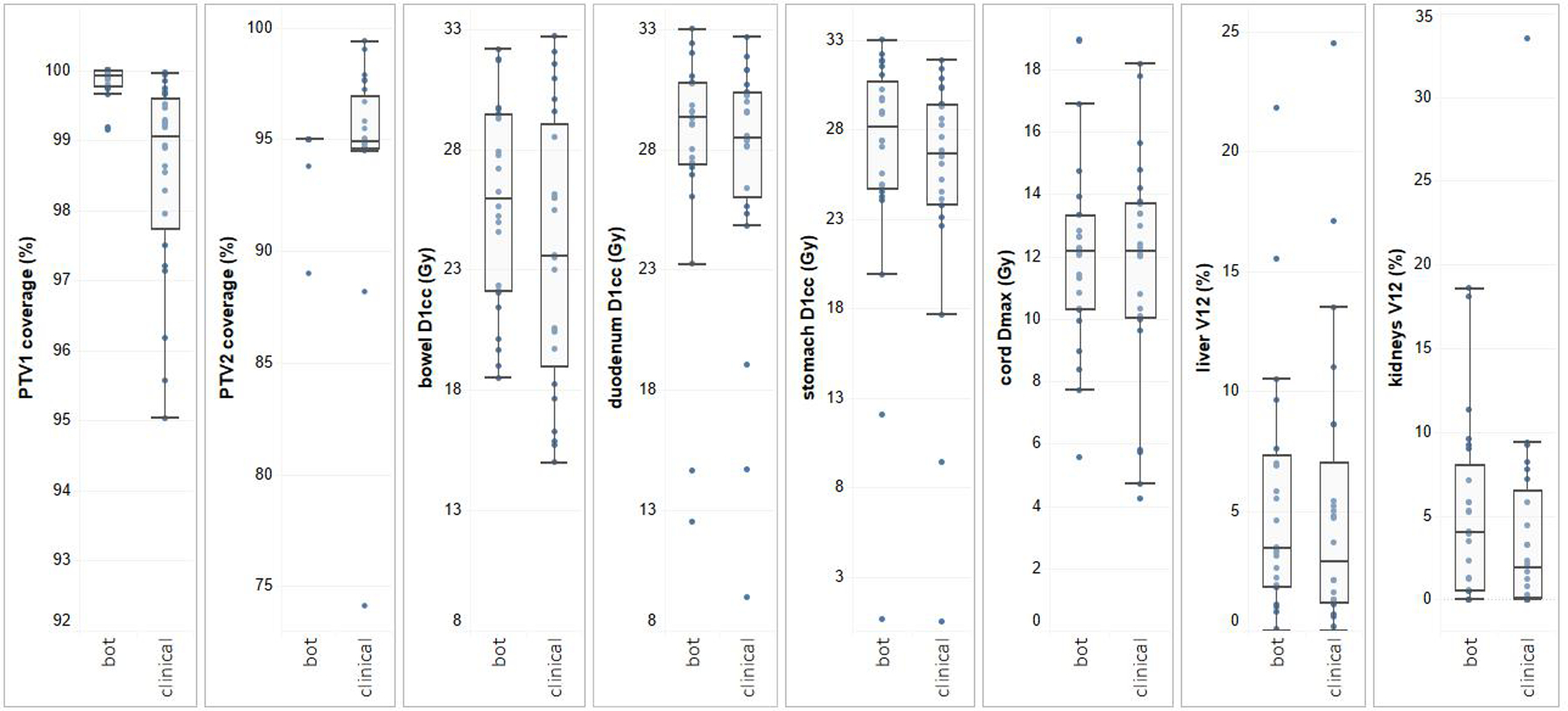
Dosimetric comparison between RL bot and clinical plans. The boxes represent quartiles, and the whiskers mark the datapoints within the 1.5 interquartile ranges from the median values. The clinical constraints for bowel D_1cc, duodenum D_1cc, and stomach D_1cc are 33 Gy. Cord D_max is limited to <20 Gy, and kidney V_12Gy is limited to <25% to 50%. All clinical and RL bot plans meet these clinical constraints.

Figure 3 shows the dose distributions of 2 randomly selected validation plans (Figs. 3d–f, j–l) and their corresponding clinical plans (Figs. 3a–c, g–i). The RL plans showed similar PTV coverages compared with the clinical plans. However, the RL plans tended to exhibit better conformity on 33 Gy isodose lines but overcover PTV_25Gy, which is likely due to the fact that the score function S does not explicitly penalize dose spill out of the primary PTV into non-OAR regions.

Fig. 3.

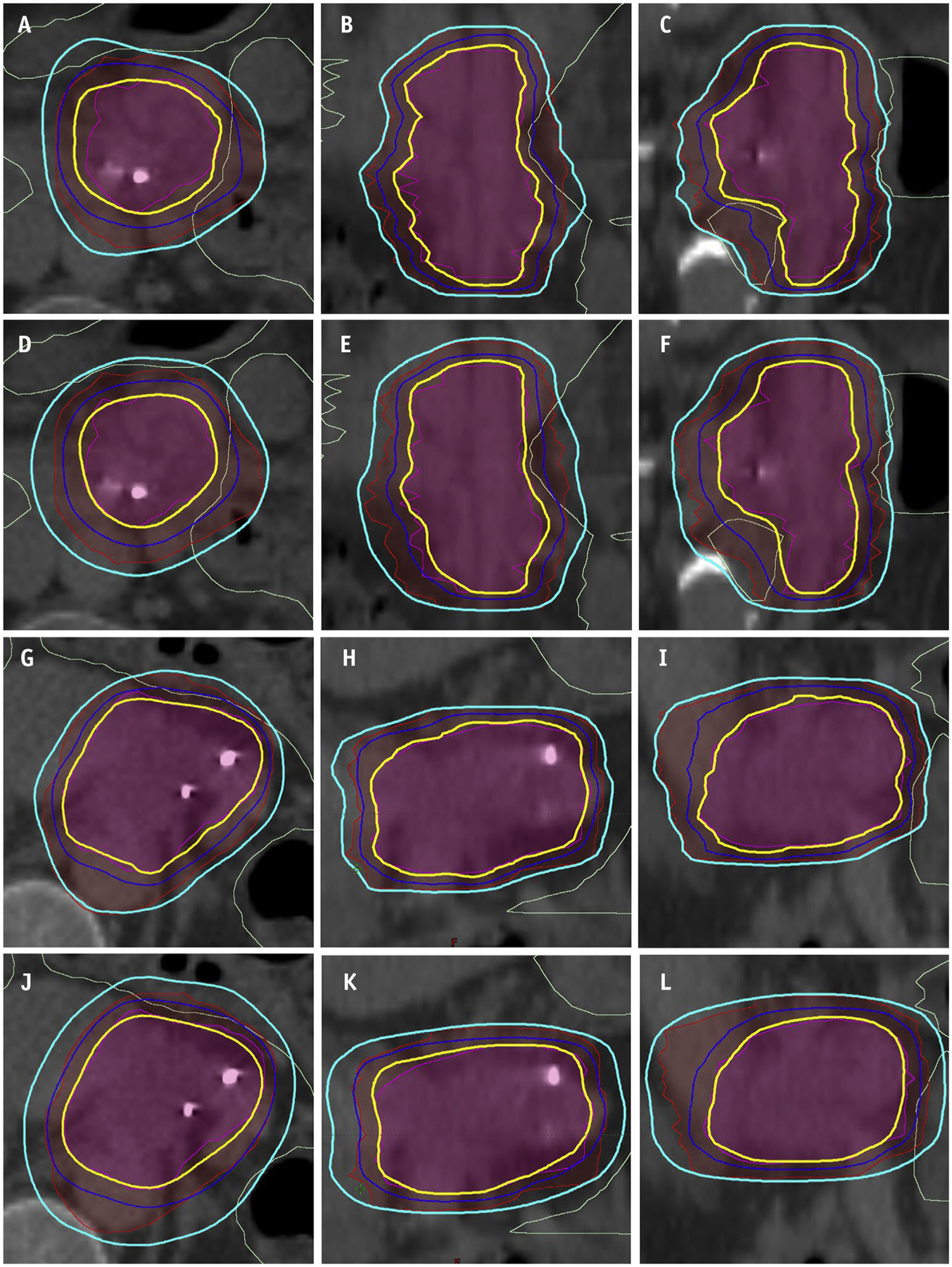
Cross-sections of (a-c; g-i) 2 randomly selected clinical plans and (d-f; j-l) the corresponding RL plans. The 3 rows, from top to bottom, are axial, coronal, and sagittal views. The prescription doses to the primary planning target volume (red segments) and boost planning target volume (magenta segments) are 25 Gy and 33 Gy, respectively. The 25 Gy and 33 Gy isodose lines are represented by cyan and yellow lines. The dose limit to gastrointestinal luminal structures (light green contours) is 33 Gy less than 1 cm³.

Knowledge interpretability

The feature weighting factors θ^T contains information regarding the expected plan quality change, measured by the plan quality score function S, after a certain action at a certain state. An action is usually considered optimal when the feature value vector is well aligned with the corresponding row on θ^T. This characteristic makes the model readily interpretable. Figure 4 shows 2 regions of the reshaped θ^T. The full feature map is shown in the supplementary material.

Fig. 4.

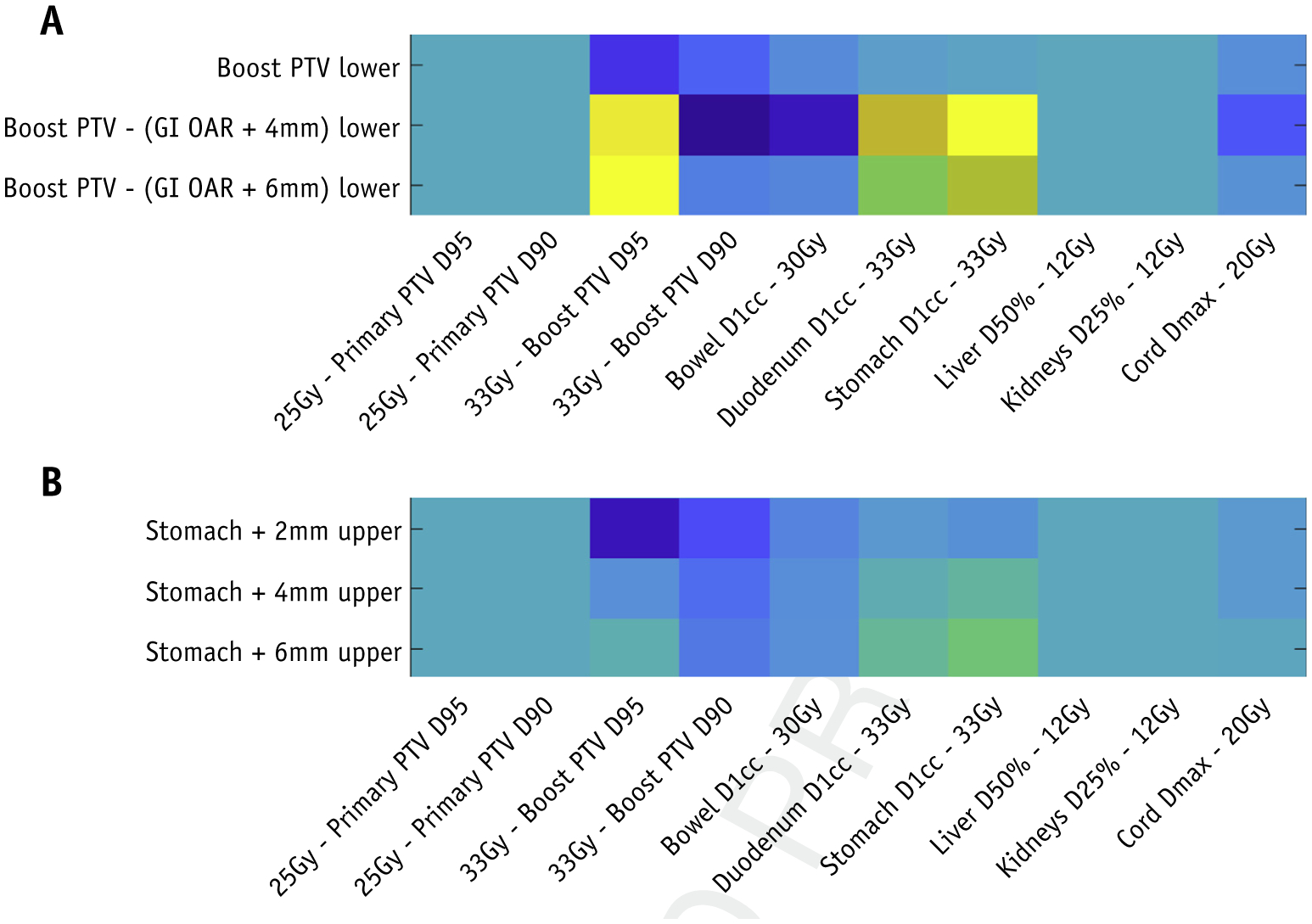
The weighting vector θ^Treshaped based on features and actions corresponding to (a) planning target volume coverage and (b) stomach constraints. The weightings are of arbitrary units. At each bot-treatment planning system interaction, we obtain action-value Q(s, a) by multiplying θ^T by the feature vector φ(s, a), which is evaluated in the treatment planning system at the step.

Figure 4A illustrates that the bot has learned that when both PTV_33Gy coverage and stomach D_1cc constraints are compromised, adding lower constraint to an auxiliary structure that avoids the overlapping region between the PTV and the stomach should be considered. In contrast, directly adding PTV lower constraints is often not effective. Similarly, Figure 4B shows that adding stomach +6 mm upper constraints is preferred when PTV_33Gy D_98% is slightly violated and the stomach D_1cc dose constraint is violated.

Such learned knowledge is consistent with our planning experience. Therefore, we conclude that the RL bot learns to make sensible choices given the state information, and our formulation of the action-value function offers meaningful insights into the learned planning strategies in the form of a knowledge map. RL provides a systematic and subjective methodology of learning planning knowledge.

Knowledge reproducibility

Our experiments also demonstrated that the training of the RL bot is highly reproducible. Figure 5 shows the average differences of feature weighting factors θ^T learned in 2 separate training sessions. The average absolute change is 2.5%. Considering that the training sessions involve substantial introduced stochasticity, the differences between the 2 knowledge maps are relatively small, which preliminarily shows that the model training procedure is reproducible.

Fig. 5.

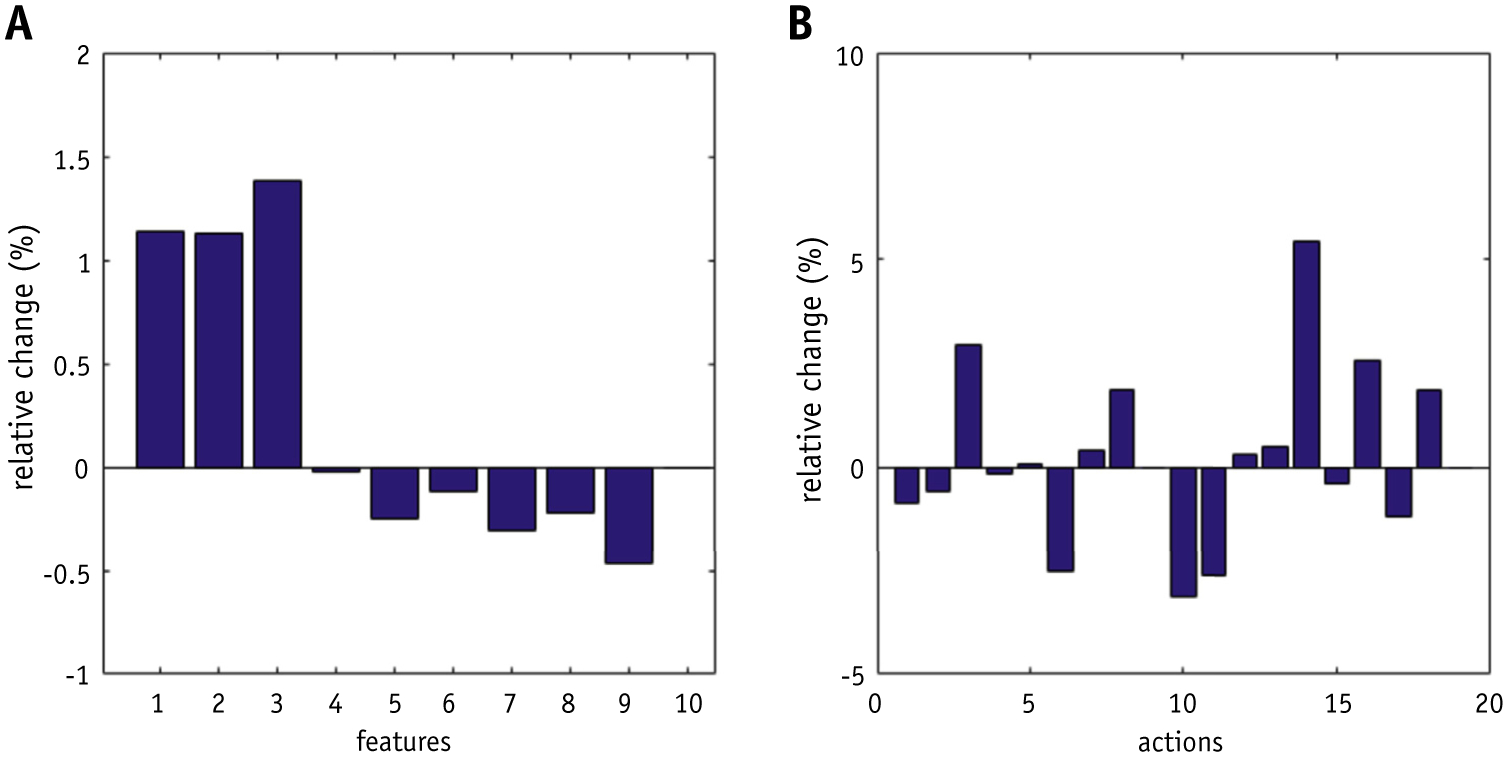
Average knowledge map differences across (a) different features and (b) different actions.

Discussion

In pancreas SBRT treatment planning, GI structures (small bowel including duodenum, large bowel, and stomach) are often the structures limiting full-boost PTV coverage owing to their proximity to the boost PTV. Planners iteratively evaluate the quality of boost PTV dose coverage with respect to GI constraints and make adjustments accordingly. Notably, several actions are often taken when a planner modifies a plan, including adjusting priority or placement of existing structures and adding auxiliary structures to guide the local/regional dose dispositions in both volume size and dose levels. We formulated this process into a finite-horizon RL framework, the crucial components of which include states, actions, and rewards. First, we discretized the states in a similar fashion to how planners evaluate plans (ie, constraint satisfaction). Second, we identified a set of common actions that planners would take to address different planning issues, such as insufficient coverage and dose spill. Third, we derived a reward system based on our physicians’ input. Finally, we managed to limit the complexity of the system and thereby created a planning bot that can be implemented in a clinical TPS.

The training stage of the planning bot essentially simulates the learning process of a human planner. The bot first takes many attempts in trying different actions at different states, and after each action the plan is reevaluated and a reward is assigned accordingly. As planning experience is gradually gained, the bot makes decisions with the guidance of retained prior knowledge, but also attempts to explore alternative methods for surprise gains. After completing the training process, the bot has acquired knowledge that can guide to the highest plan quality possible. The knowledge, summarized in an action-value function, contains the information of expected long-term rewards of taking certain actions at certain states. When planning a new patient case, the bot periodically evaluates the current state of the plan, infers the best option from the action-value function, and takes the corresponding action; thus, completing the navigation of the autonomous planning process.

To fully use the geometric information contained in the training data set, we augmented the training data set by expanding and shrinking the boost PTVs. This step effectively allows the bot to practice planning on sufficient anatomic variations without requiring more training cases. We introduced variations on the boost PTV because the primary focus of the planning bot is to effectively handle the contradicting boost PTV coverage requirements and GI OAR 1 cm³ constraints. Similar augmentation methods can potentially be applied to increase the variations on other OARs. During the development of the planning bot, we tuned the RL model by using the plan quality scores of a few holdout training cases to gauge the performance of the bot. Specifically, we determined the number of actions necessary and the number of cases required for model training in addition to the model parameters, such as ε and N. We estimated that >10 to 20 cases are necessary to train the bot, although the number of cases needed is dependent on the degree of anatomy variations for the treatment site and the requirements of the planning task.

The limitations of this model are 2-fold. First, the linear approximation used in this work, although interpretable, potentially limits the flexibility of the model when approximating the underlying action values (ie, ground truth of expected long-term reward) for more complicated planning tasks. In this study, we used a SARSA algorithm with linear action-value function approximation to determine optimal actions. Investigate the use of other types of value-function classes, such as deep neural networks, may be necessary.¹¹ However, a more complicated model is expected to have less interpretability and require more tuning, both of which are undesirable for clinical applications. Another potential limitation of the proposed method is that the actions have to be discretized to fit in the SARSA framework, which is reflected in the fact that we set the planning constraint priorities to be constant. The priorities were selected carefully such that placing a constraint introduces sufficient plan changes and yet does not overshoot. With policy gradient-based RL algorithms, learning the optimal policy directly in a continuous domain is possible. This class of algorithms is also worth investigating to perform treatment planning tasks. In this study, we applied the RL planning bot to solving a challenging planning task known to heavily rely on planner input. However, the RL bot is not limited to this specific treatment planning task. The model can be adopted for other treatment sites by using a different set of features and actions to match planning practices. In addition, the plan quality score should be redefined to reflect the clinical plan quality preferences.

Previously, automated planning based on supervised machine learning has gained widespread acceptance in the radiation therapy community,^13–16 and has been implemented in commercial TPS.¹⁷ This class of algorithms, collectively referred to as knowledge-based planning (KBP), train a model to represent the correlation between patient anatomy and dose distribution based on previously treated patients. For a new patient, KBP predicts the best achievable OAR dose-volume histograms and generates corresponding dose-volume constraints as input for plan optimization. Compared with KBP, the RL bot is different in 2 aspects. First, the bot does not rely on optimal plans in training data. The underlying assumption of KBP is that the plans used for model training are optimal under the current standard. In contrast, the RL bot acquires planning knowledge by trial and error, and thereby does not require previous plans. As a result, when a planning protocol gets updated, the planning bot can be simply retrained with an updated score function but KBP cannot be used until enough new plans have been collected and the model can be retrained. Second and more importantly, KBP places a set of estimated dose-volume constraints for optimization. This method, although performing well for many treatment sites, is not sufficient to address the complex local tradeoffs in pancreas SBRT. The lack of spatial information in dose-volume constraints results in inefficient cost-function assignment, and the planner often needs to create local optimization structures to encode the spatial information manually, which is time-consuming and defeats the purpose of auto-planning.

To our knowledge, there have been very few publications applying RL to external beam treatment planning tasks, and this is the first work on implementing RL planning in a clinical TPS. Shen el al. recently proposed a deep RL-based prostate IMRT virtual planner, which uses neural networks to adjust dose-volume constraints,¹⁸ and showed that the virtual planner improves plan quality upon the initialized plans and is a potentially promising planning method, acknowledging that the method can be a black box. In contrast, we made significant efforts to simplify the model to improve transparency and demonstrate the efficacy of an autonomous, yet interpretable planning bot powered by RL. We narrowed down features to a limited set of variables summarized from domain knowledge, namely those commonly used by our planners, to examine the treatment plans before implementing manual plan changes. Also, we used linear function approximation for the action-value determination, which presents a simple and interpretable model. In this study, we focused on the planning of pancreas SBRT treatments. However, the proposed framework should apply to other treatment sites with careful design of features and actions.

Conclusions

The planning bot generates clinically acceptable plans by taking consistent and predictable actions. Additionally, the knowledge maps learned in separate training sessions are consistent, and the knowledge learned by the RL bot is consistent with human planning knowledge. Therefore, the training phase of our planning bot is tractable and reproducible, and the knowledge obtained by the bot is interpretable. As a result, the trained planning bot can be validated by human planners and serve as a robust planning assistance routine in the clinics.