Acoustic cavitation at low gas pressures in PZT-based ultrasonic systems

Highlights

• •A relation between sonochemical activity and dissolved gas concentration is reported.
• •Acoustic cavitation is responsible for sonochemical activity in PZT based reactors.
• •A relatively higher dissolved gas concentration is needed for sonochemical activity at 2 MHz.
• •Sonochemiluminescence is a highly sensitive technique for the detection of sonochemical activity.

Abstract

The generation of cavitation-free radicals through evanescent electric field and bulk-streaming was reported when micro-volumes of a liquid were subjected to 10 MHz surface acoustic waves (SAW) on a piezoelectric substrate [Rezk et al., J. Phys. Chem. Lett. 2020, 11, 4655–4661; Rezk et al., Adv. Sci. 2021, 8, 2001983]. In the current study, we have tested a similar hypothesis with PZT-based ultrasonic units (760 kHz and 2 MHz) with varying dissolved gas concentrations, by sonochemiluminescence measurement and iodide dosimetry, to correlate radical generation with dissolved gas concentrations. The dissolved gas concentration was adjusted by controlling the over-head gas pressure. Our study reveals that there is a strong correlation between sonochemical activity and dissolved gas concentration, with negligible sonochemical activity at near-vacuum conditions. We therefore conclude that radical generation is dominated by acoustic cavitation in conventional PZT-based ultrasonic reactors, regardless of the excitation frequency.

1. Introduction

The generation of free radicals, e.g., H^•, OH^•, is the basis of several processes dealing with sonochemistry [1], electrochemistry [2] and photocatalysis [2]. There is a need to formulate more energy-efficient methods for such radical generation. Acoustic cavitation generated by ultrasound (frequency > 20 kHz) is considered a safe and convenient tool [1] to produce free radicals in bulk solutions without the use of external catalysts. Herein, ultrasound enables the growth of pre-existing gas nuclei to microbubbles and their collapse facilitate zones of very high temperature (~10,000 K) and pressure (~few tens of GPa) [3]. The non-condensable gas constituents are significantly compressed during the collapse stage of the bubble, and is accompanied by considerable heating. It is this heat energy that is converted to light, recorded as periodic nanosecond flashes known as sonoluminescence (SL) [4]. SL may thus be considered as an indirect measure of acoustic cavitation efficiency of ultrasonic reactors. However, a more informative test for sonochemical activity (i.e., the potential to generate radicals) is sonochemiluminescence (SCL), where the amount of OH radicals generated is quantified using luminol solution [5]. Additionally, wholesome estimates of radical concentration are provided by other dosimetry techniques, e.g. Weissler [6], Fricke [7], TPPS (5,10,25,20-Tetrakis (4-sulfotophenyl) porphyrin (H₂TPPS^4-)) [8] and other methods [9].

An important factor governing the overall cavitation efficiency of a sonochemical reactor is the number density of active cavitation bubbles. Active cavitation bubbles refer to those undergoing near-adiabatic collapse and are responsible for sonochemical activity generated in a reactor. In the absence of cavitation, no radicals are expected to be formed in conventional reactors. However, recently Vinatoru and Mason [10] have hypothesized the possibility of cavitation-free radical generation, most likely in solvents with piezoelectric/electrostriction properties (e.g., Rochelle salt, polymers, liquid crystals, etc.) through a certain “ordering effect” of molecules during the compression phase of an acoustic wave, such that electric charges could develop. These charges could foster electron movement between molecules and hence facilitate chemical reaction without any role of bubble-collapse. The authors suggested a similar pathway for breakdown of water molecules as well, but this is yet to be experimentally verified.

In support of the above hypothesis, Rezk et al. [11] have reported the formation of radicals within a few seconds of operation in degassed water by generating Rayleigh surface acoustic waves (SAW) on a piezoelectric substrate. The cause for this is suggested to be the evanescent electric field (~10⁸ V/m) associated with the SAW that drives the self-ionization of solvent molecules without any intervention of bubble generation and collapse, aided by the SAW-generated acoustic-streaming motion that prevents recombination of ionized solvent molecules. The authors conducted this test on small liquid droplets (10 μl) placed on the surface of a piezoelectric substrate (single crystal lithium niobate, i.e., LiNbO₃) that locally vibrates both in- and out-of-plane in a retrograde manner along the surface at a higher frequency (10 MHz) and at a lower input power (~0.4 W) to that of conventional ultrasonic transducers. Besides the nature of the vibration (i.e., surface vs bulk acoustic waves), these configurations are therefore quite unlike PZT (Lead Zirconate Titanate) based sonochemical reactors that operate on much larger volumes and over a conventional range of frequency (20 kHz – 3 MHz) and power (>1 W) [5]. Also, for the SAW in Rayleigh mode, the acoustic energy is transmitted both laterally (in-plane) and perpendicularly (out-of-plane) through nano-sized undulations of the surface having direct contact with the liquid, whereas for PZT, the energy is transmitted perpendicular to the transducer-metal plate arrangement (periodic longitudinal displacement) without any evolving spatial deformations.

Notwithstanding the above differences, there has been dearth of studies systematically exploring sonochemical activity under ‘controlled cavitation-free’ conditions. To address this, the current work examines whether sonochemistry occurs in conventional PZT-based reactors in the absence of cavitation using two independent methods. This is achieved by controlling the number of bubble-nuclei via dissolved gas concentration, which in turn is controlled by the overhead gas pressure to near vacuum conditions. In addition, this work also investigates how sonochemistry changes as a function of dissolved gas concentration/overhead gas pressure.

2. Experimental details

2.1. Materials

Milli-Q water (resistivity 18.2 MΩ-cm, Merck Millipore, Bayswater, VIC, Australia) was used in all experiments. Luminol (C₈H₇N₃O₂ – Sigma Aldrich Pty. Ltd., Castle Hill, NSW, Australia), NaOH (Chem-Supply Pty. Ltd., Gillman, SA, Australia), hydrogen peroxide (H₂O₂); potassium iodide (KI), ammonium molybdate tetrahydrate ((NH₄)₆Mo₇O₂₄·4H₂O) and potassium hydrogen phthalate (C₈H₅KO₄) were used as received without further purification.

2.2. Methodology

Generally, luminol solution was used under two experimental conditions: air-saturated, and air-depleted (liquid is introduced into a degassing setup shown in Fig. 1). A total of 4 variations of the solution were tested (shown by the arrows in Fig. 1). Briefly, a 2 mM luminol solution was prepared in 0.1 M NaOH solution in air-saturated milli-Q water, described in [12]. The solution was either placed in a glass-flask attached with a transducer (i.e., air-saturated condition), or subjected to further gas purging and degassing protocols.

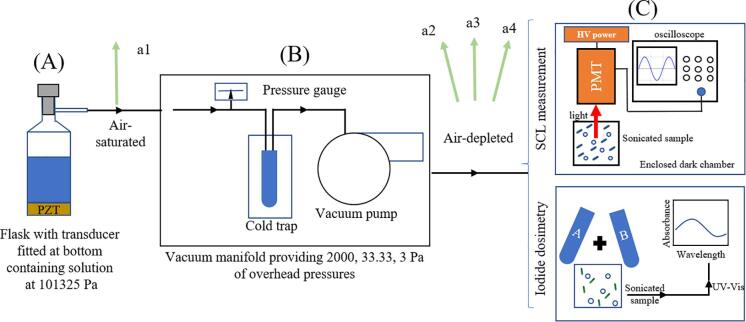
Fig. 1.

Schematic showing the experimental setup using A) a fabricated flask with stopper; B) degassing setup providing different overhead gas pressures; C) measurement of sonochemical activity by 2 methods. The arrows indicate where the 4 types of solution with different gas concentrations (a1: 101325 Pa, a2: 2000 Pa, a3: 33 Pa, a4: 3 Pa) were acquired.

Ultrasound was triggered by a piezoelectric ceramic (PZT) transducer, operating at either 760 kHz or 2 MHz, connected to the bottom of the fabricated glass-cell with a stopper on the top (Fig. 1A). These transducers were purchased from Honda Electrics, Japan and the cell/reactor was custom made in the workshop. The available opening on the flask was used to connect to a degassing setup (Fig. 1B), comprising a liquid nitrogen trap and vacuum pump (John Morris Scientific Pty. Ltd., Australia). The transducers were powered by a T&C Power Conversion, Inc. frequency generator/amplifier at 20 W. The cavitation activity was quantified by measuring the radical yield by the two methods described below.

Method 1: Determination by Sonochemiluminescence (SCL): This method is generally preferred due to its high sensitivity, rapid output and simplicity [12], [13], [14], without the need for ambient-interference. The chemiluminescence from sonicated luminol was recorded in a dark room to avoid intrusion of external light using a photomultiplier tube (PMT- Hamamatsu Photonics K.K., Hamamatsu City, Shizuoka Prefecture, Japan) connected to a high-voltage (HV) amplifier (Hamamatsu) and an oscilloscope (Wavejet 332/334; LeCroy, Chestnut Ridge, NY). A schematic is shown in Fig. 1C. Photons emitted from the sample were detected on an oscilloscope as a consistent shift (averaged over 32 sweeps) from the baseline signal. This method has previously been used for both SL and SCL quantification [5], [12], [15]. SCL measurements were used for monitoring the relative changes in cavitation activity under varying dissolved air concentrations.

Method 2: Determination by iodide dosimetry (Weissler method): The OH^• radicals generated (5 min for 760 kHz, 15 min for 2 MHz) in sonicated water was quantified by this method. OH^• radicals can react to form H₂O₂ which can then oxidize iodide ions to molecular iodine [6]. In the presence of excess iodide ions, molecular iodine is converted to a tri-iodide complex (I₃^-). Sonicated water was added to solutions A (0.4 M KI, 0.05 M NaOH, 0.00016 M (NH₄)₆Mo₇O₂₄·4H₂O) and B (0.1 M C₈H₅KO₄) to foster I₃^- formation—this helps to determine the OH^• radical concentration by measuring the absorbance at 351 nm using ε (extinction coefficient) = 26400 M⁻¹ cm⁻¹, as illustrated in Fig. 1C. Experiments were carried out in triplicate to check for reproducibility. The error bars provided in figures are based on at least three independent measurements.

3. Results & discussion

As mentioned in the introduction, the aim of this study was to ascertain if radicals can be generated in the absence of acoustic cavitation in conventional PZT-based sonochemical reactors. It is known that dissolved gas molecules are needed to form bubble nuclei that ultimately cavitate in an acoustic field. To avoid/limit the formation of cavitation bubbles, the sonication cell containing water was connected to a vacuum line for degassing. With our experimental set up, the minimum overhead pressure we could obtain was 3 Pa (near-vacuum condition). Radical formation was therefore tested in water with an overhead pressure of either 3 Pa or 101325 Pa. The experiment was carried out at 760 kHz at an acoustic power of 20 ± 2 W and the results are presented in Fig. 2.

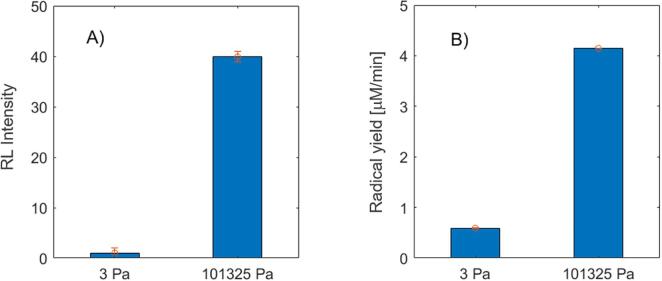
Fig. 2.

A) SCL signal and 2B) radical yield at near vacuum conditions (3 Pa) with volume of PZT cell ~50 mL at a frequency of 760 kHz. SCL signals are normalized; Error bars are shown on the top of each bar with a circle marker.

Fig. 2A shows the SCL results observed under 3 Pa and 101325 Pa. It can be seen that detectable radical production occurs even at 3 Pa overhead pressure at this frequency. However, the SCL signal at 101325 Pa is almost 40 times higher than that observed at the lower pressure. Fig. 2B shows the OH^• yield measured by iodide dosimetry (Weissler) method. The radical yields were found to be 0.6 and 4 μM/min at 3 Pa and 101325 Pa, respectively.

For the SCL test, the RL Intensity measurement reading was 81.62 and 2.046 at the two pressures in Fig. 2A, hence a relative scaling of (81.62/2.046) ~ 40 times. Similarly, dosimetry values measure 4 and 0.6 μM/min respectively hence a relative scaling of (4/0.6) ~ 6.66 times. Ideally this relative scaling between the two pressure conditions (40 times for SCL vs 6 times for dosimetry) for both these methods should be comparable. For SCL reaction, the OH^• generated within the collapsing bubble instantly reacts with luminol at the bubble/solution interface generating SCL. However, for iodide dosimetry, the OH^• produced within the bubble undergo further reactions to generate H₂O₂ which then reacts with I^– in bulk solution to produce I₃^-. The number of secondary steps for iodide dosimetry necessitates time during which some H₂O₂ might be lost due to thermal decomposition; this may account for the incomparable relative differences. As the current study is focused on the effect of dissolved gas on the cavitation efficiency (radical production), the trends observed by these methods rather than the absolute differences observed are important. It should be noted that both methods indicate that cavitation efficiency at 3 Pa is much lower than that at 101325 Pa.

In fact, 101325 Pa of overhead gas pressure would lead to a typical dissolved air concentration of 22.7 mg/L (calculated using Henry’s Law [16]) in water whereas 3 Pa gas pressure would reduce this dissolved air concentration to roughly around 0.00065 mg/L or 0.65 μg/L. This reduced gas-solubility would lower the chances of nucleation, contributing to considerably fewer active cavitation bubbles under similar experimental conditions. Since it was practically not possible to completely degas the liquid, there might still be some leftover gases in the vessel that would contribute to negligible signal/noise. However, the hypothesis of “ordering effect” being responsible for breakdown of water molecules as suggested by Vinatoru and Mason [10] is not strongly evidenced with the above results. It should not be influenced by gas concentration. Also, the phenomenon responsible for radical generation with the SAW [11] does not occur in the present PZT setup given the different experimental conditions (larger volume, different wave mode and different transducer operating at a relatively lower frequency) used.

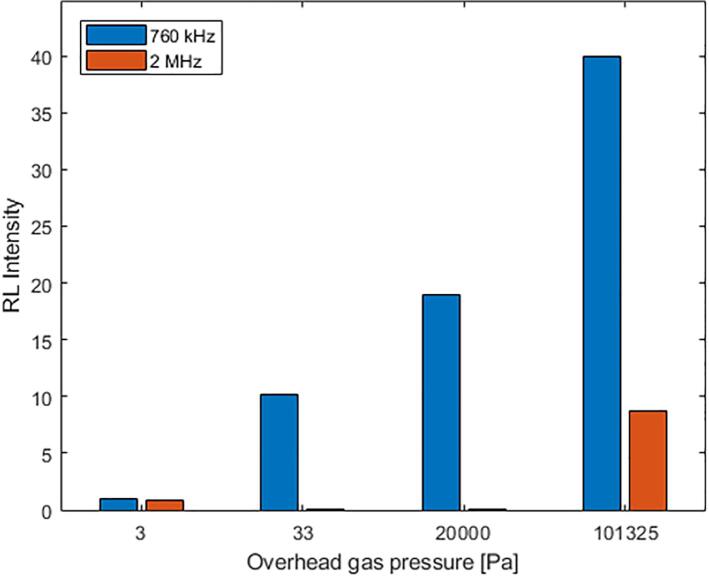
In order to understand how cavitation efficiency correlates with overhead gas pressures, further experiments were conducted at 3, 33, 20,000 and 101325 Pa overhead gas pressures. Experiments were also performed at an additional frequency of 2 MHz (closer to the 10 MHz SAW frequency at which Rezk et al. [11] found evidence that the evanescent electric field associated with the nanoscale SAW undulations was responsible for the radical formation within few seconds of operation). The relative SCL intensity for different gas pressures and frequencies are shown in Fig. 3. Firstly, the SCL intensities for 2 MHz are significantly lower compared to those observed for 760 kHz at the same gas pressures. Secondly, it can be observed that the SCL signal attenuates gradually with reducing overhead gas pressures to a certain limit below which there is little or no SCL intensity. This is irrespective of the frequency of sonication used in this study.

Fig. 3.

SCL intensity observed at different dissolved gas pressures (in Pa) in sonicating luminol solution.

Generally, the use of a higher frequency (2 MHz) generates larger bubble populations but smaller bubble resonance size, thereby decreasing the collapse-intensities. This lowers the resulting bubble temperatures, reducing the radical yield per bubble. In addition to this, higher frequencies invite shorter time for volatile molecules [17] to diffuse into the bubble during each expansion cycle, further lowering the chance of yielding radicals. These effects cumulatively cause the cavitation efficiency at 2 MHz to reduce relative to that at 760 kHz. This is reflected in the difference between the SCL intensity values for fixed gas pressures. A similar drop in radical activity was also noted by Mason et al. from 863 kHz to 1142 kHz that was attributed to an increase in cavitation threshold with an increase in frequency [18]. Another key observation is the almost negligible signal at the lowest pressure condition (3 Pa) and at 2 MHz. This suggests that the phenomenon responsible for radical generation under SAW does not occur for PZT-based transducers even at higher (MHz) frequencies, the latter being more reliant on bubble-collapse for its radical generation.

A decrease of SCL intensity with reducing overhead gas pressures (Fig. 3) is anticipated owing to the reduction in gas solubility, reducing the bubble-nuclei and hence the number of active bubbles, as discussed earlier.

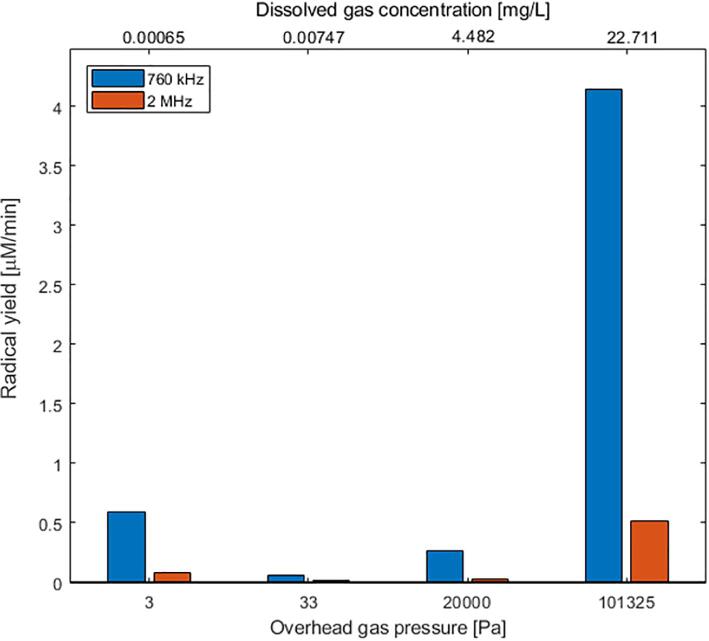
To further support our results, radical measurement was conducted using iodide dosimetry. Fig. 4 shows the OH^• radical-yield per minute for water as a function of the overhead gas pressure and dissolved gas concentration; the overhead gas pressures of 3, 33, 20000, 101325 Pa roughly corresponding to dissolved air concentrations of 0.00065, 0.00747, 4.482 and 22.711 mg/L in water, respectively.

Fig. 4.

Radical yield measurements (μM/min) for different dissolved gas pressures on sonicating water at different frequencies.

Firstly, the concentration of radical yield was largely found to reduce with reducing overhead gas pressure/ dissolved gas concentration. Also, the yield diminishes with increasing frequency for a fixed gas pressure. The trend between radical yield and frequency is quite similar to that obtained from the SCL study (Fig. 3). Previous studies have shown [18] that the radical yield peaks around 300 kHz and decreases gradually with an increase in frequency under similar experimental conditions.

Another key takeaway from Fig. 4 is that the high frequency (2 MHz) PZT-based reactor failed to exhibit significant sonochemical activity up to a critical overhead gas pressure/concentration. This critical or threshold value lingers between 20000 Pa and 101325 Pa for 2 MHz. Studies [19] indicate a particular Blake threshold pressure is necessary for a bubble to overcome its surface tension in order to grow and eventually collapse. Alternately, the Blake threshold demarcates the regimes between gently oscillating and violently collapsing bubbles, the latter being characteristic of active bubble-collapse that is largely instrumental in dictating the acoustic efficiency of a system [20]. However, the threshold pressure that our system points out deals with the number of available bubble nuclei, a function of the static pressure of the liquid and should not be correlated to the Blake threshold. Nevertheless from both Fig. 3, Fig. 4, a brisk similarity is found to exist in that both the critical overhead gas pressure and the Blake threshold pressure seem to increase with the frequency of irradiation, which could be responsible for the observed sudden spike in sonochemical activity above 20,000 Pa at 2 MHz.

4. Conclusions

We developed an experimental setup to examine radical generation in bulk liquids under 2 frequencies (760 kHz, 2 MHz) and dissolved gas concentrations without major regassification. In particular, we found that PZT-based ultrasonic systems exhibit almost negligible sonochemical activity due to limited acoustic cavitation (lower number of active bubbles) at very low overhead gas pressures (3 Pa) due to leftover dissolved gases (~0.65 μg/L of air in water). The sonochemical efficiency measured by the total radical yield (via SCL method and iodide dosimetry) undergoes a steep change with an increase in gas pressure beyond a certain critical value. This value may be related to the Blake threshold of the ultrasonic system due to its direct dependence on the frequency of the system. Our results indicate threshold values feature between 33 Pa and 20000 Pa for 760 kHz and between 20000 Pa and 101325 Pa for 2 MHz sonoreactors using water. The feasibility of cavitation-free radical generation in water therefore appears to be challenging in conventional sonoreactors via “ordering effects”. This is because acoustic cavitation is largely dependent on the number of active bubbles, even at sub-vacuum conditions. However, tests using solvents having piezoelectric/electrostriction properties can help better understand this domain. Overall, the SCL technique is well suited for dynamic radical detection under low partial pressure conditions without any intrusion of ambient gases, thereby helping estimate the threshold for sonochemical activity in ultrasonic systems. Such testing would facilitate an understanding about acoustic cavitation under stringent gas conditions and high frequencies, the likes of which is necessary for precision control during biomedical HIFU (high-intensity focused ultrasound) applications. Besides these, it can support research in potential avenues of sterilization, nanomaterials [21] and cancer therapy, etc. which are somewhat sensitive to dissolved gas concentrations.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.