Using Open Data to Rapidly Benchmark Biomolecular Simulations: Phospholipid Conformational Dynamics

Abstract

Molecular dynamics (MD) simulations are widely used to monitor time-resolved motions of biomacromolecules, although it often remains unknown how closely the conformational dynamics correspond to those occurring in real life. Here, we used a large set of open-access MD trajectories of phosphatidylcholine (PC) lipid bilayers to benchmark the conformational dynamics in several contemporary MD models (force fields) against nuclear magnetic resonance (NMR) data available in the literature: effective correlation times and spin–lattice relaxation rates. We found none of the tested MD models to fully reproduce the conformational dynamics. That said, the dynamics in CHARMM36 and Slipids are more realistic than in the Amber Lipid14, OPLS-based MacRog, and GROMOS-based Berger force fields, whose sampling of the glycerol backbone conformations is too slow. The performance of CHARMM36 persists when cholesterol is added to the bilayer, and when the hydration level is reduced. However, for conformational dynamics of the PC headgroup, both with and without cholesterol, Slipids provides the most realistic description because CHARMM36 overestimates the relative weight of ∼1 ns processes in the headgroup dynamics. We stress that not a single new simulation was run for the present work. This demonstrates the worth of open-access MD trajectory databanks for the indispensable step of any serious MD study: benchmarking the available force fields. We believe this proof of principle will inspire other novel applications of MD trajectory databanks and thus aid in developing biomolecular MD simulations into a true computational microscope—not only for lipid membranes but for all biomacromolecular systems.

Introduction

Ever since the conception of the Protein Data Bank (PDB)^1,2 and Genbank,^3,4 open access to standardized and searchable pools of experimental data has revolutionized scientific research. Constantly growing and improving in fidelity due to collaborative effort,⁵⁻⁸ the now hundreds of databanks⁹ fuel the data-driven development of biomolecular structure determination,¹⁰ refinement,¹¹ prediction,¹² and design¹³ approaches as well as the development of drugs,^14,15 materials,^16,17 and more.^18,19 It is clear that open data enables scientific progress that is far beyond the resources of a single research group or institute. Consequently, the call for public availability and conservation of data has extended to molecular dynamics (MD) simulation trajectories of biomolecules,²⁰⁻²² and the discussion on how and by whom such databanks for dynamic structures would be set up is currently active.²³⁻²⁶ While there are currently no general MD databanks in operation, individual databanks are accepting contributions on nucleic acid,²⁷ protein/DNA/RNA,²⁸ cyclodextrin,²⁹ G-protein-coupled receptor,³⁰ and lipid bilayer³¹ simulations.

Since 2013, the NMRlipids Project (nmrlipids.blogspot.fi) has promoted a fully open collaboration approach, where the whole scientific research process—from initial ideas and discussions to analysis methods, data, and publications—is all the time publicly available.³² While its main focus has been on conformational ensembles of different lipid headgroups and on ion binding to lipid membranes,³²⁻³⁴ the NMRlipids Project has also built a databank³¹ (zenodo.org/communities/nmrlipids) containing hundreds of atomistic MD trajectories of lipid bilayers and indexed at nmrlipids.fi.

MD databanks are expected to be particularly relevant for disordered biomolecules, such as biological lipids composing cellular membranes or intrinsically disordered proteins. These, in contrast to folded proteins or DNA strands, cannot be meaningfully described by the coordinates of a single structure alone. Realistic MD simulations, however, can provide the complete conformational ensemble and dynamics of such molecules as well as enable studies of their biological functions in complex biomolecular assemblies. Unfortunately, the current MD force fields largely fail to capture the conformational ensembles of lipid headgroups and disordered proteins.^32,34−37 Therefore, before they can be used to draw conclusions, the quality of MD simulations must always be carefully assessed against structurally sensitive experiments. For lipid bilayers, such evaluation is possible against NMR and scattering data.³⁸

Here, we demonstrate the use of a pre-existing, publicly available set of MD trajectories to rapidly evaluate the fidelity of phospholipid conformational dynamics in state-of-the-art force fields. The rate at which individual molecules sample their conformational ensemble is traditionally used to assess if a given MD simulation has converged. Going beyond such practicalities, realistic dynamics are particularly desired for the intuitive interpretation of NMR experiments sensitive to molecular motions³⁹ as well as to understand the dynamics of biological processes where molecular deformations play a rate-limiting role, such as membrane fusion.⁴⁰ The here presented comprehensive comparison of dynamics between experiments and different MD models at various biologically relevant compositions and conditions is thus likely to facilitate the development of increasingly realistic phospholipid force fields.

Above all, our results demonstrate the power of publicly available MD trajectories in creating new knowledge at a lowered computational cost and high potential for automation. We believe that this paves the way for novel applications of MD trajectory databanks as well as underlines their usefulness—not only for lipid membranes but for all biomolecular systems.

Methods

Lipid Conformational Dynamics in NMR Data

We analyzed the veracity of phosphatidylcholine (PC) lipid dynamics in MD based on two quantities that are readily available from published^39,41−4313C NMR experiments and directly quantifiable from atomistic MD simulations: the effective C–H bond correlation times τ_e and the spin–lattice relaxation rates R₁.

Effective C–H Bond Correlation Times τ_e

In a lipid bilayer in the liquid crystalline state, each individual lipid samples its internal conformational ensemble and rotates around the membrane normal. Lipid conformational dynamics are reflected in the second-order autocorrelation functions of its C–H bonds

1

where the angular brackets depict time average, μ⃗(t) is the unit vector in the direction of the C–H bond at time t, and P₂ is the second-order Legendre polynomial .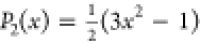

To analyze the internal dynamics of lipids, the C–H bond autocorrelation function is often written as a product

2

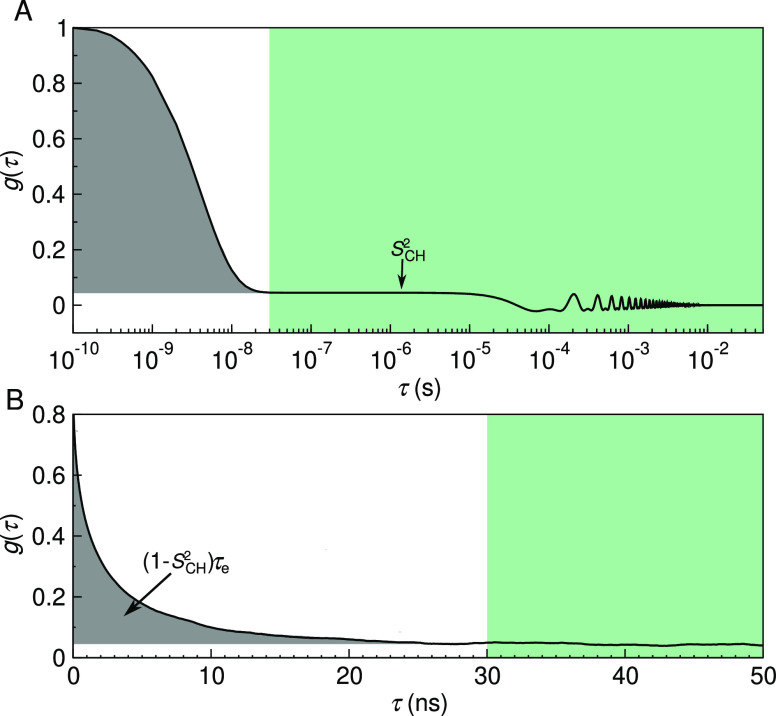
where g_f(τ) characterizes the fast decays owing to, e.g., the internal dynamics and rotation around membrane normal, and g_s(τ) the slow decays that originate from, e.g., lipid diffusion between lamellae with different orientations and periodic motions due to magic-angle spinning conditions (Figure 1). Ferreira et al.⁴¹ have experimentally demonstrated that, for all phospholipid carbons, the motional correlation times contributing to g_f are well below μs and to g_s well above 100 μs. This separation of timescales gives rise to the plateau g(1 μs ≲ τ ≲ 100 μs) = S_CH² illustrated in Figure 1. S_CH is the C–H bond order parameter

3

where θ(t) is the angle between the C–H bond and the bilayer normal. S_CH can be independently measured using dipolar coupling in ¹³C or quadrupolar coupling in ²H NMR experiments. Knowing the set of S_CH for all the C–H bonds in a lipid is highly useful in order to evaluate its conformational ensemble.³⁸

Figure 1.

C–H bond autocorrelation function g(τ). (A) Idealized illustration of the fast (white background) and the slow (green) mode of the correlation function in solid-state NMR experiments. The fast mode decays to a plateau on which g(τ) = S_CH², while the slow mode gives the final descent to zero. Oscillations at the slow mode region are due to magic-angle spinning. (B) Typical g(τ) obtained from an MD simulation, showing the decay toward S_CH². The gray area under the curve is equal to (1 – S_CH²)τ_e.

As S_CH describe the conformational ensemble of the lipid, the fast-decaying component g_f of the C–H bond autocorrelation function intuitively reflects the time needed to sample these conformations. The complex internal dynamics containing multiple timescales can be conveniently summarized using the effective correlation time

4

which is related to the gray shaded area below the correlation function in Figure 1. The τ_e detects essentially an average over all the timescales relevant for the lipid conformational dynamics. Their relation to process speeds is intuitive: an increase in long-lived correlations increases τ_e.

Spin–Lattice Relaxation Rates R₁

The C–H bond dynamics relate to R₁, the spin–lattice relaxation rate, through

5

where ω_H is the ¹H and ω_C the ¹³C NMR Larmor frequency and N_H is the number of hydrogens covalently bonded to the carbon. The rigid dipolar coupling constant d_CH ≈ – 2π × 22 kHz for the methylene bond. The spectral density j(ω) is given by the Fourier transformation

6

of the C–H bond autocorrelation function g(τ) (eq 1). Clearly, the connection between R₁ and molecular dynamics is not straightforward; the magnitude of R₁ does, however, reflect the relative significance of processes with timescales near the inverse of ω_H and ω_C. These two frequencies depend on the field strength used in the NMR experiments: Typically, R₁ is most sensitive to motions with timescales of ∼0.1–10 ns. (In our experimental data,^39,41−43 ω_C = 125 MHz and ω_H = 500 MHz, which gives (2π × 125 MHz)⁻¹ = 1.3 ns and (2π × 625 MHz)⁻¹ = 0.25 ns.) A change in given R₁, therefore, indicates a change in the relative amount of processes occurring in a window around the sensitive timescale; inferring also the direction to which the processes changed (speedup/slowdown) requires measuring R₁ at various field strengths.

Data Acquisition and Analysis

All the experimental quantities used in this work were collected from the literature sources^39,41−43 cited at the respective figures.

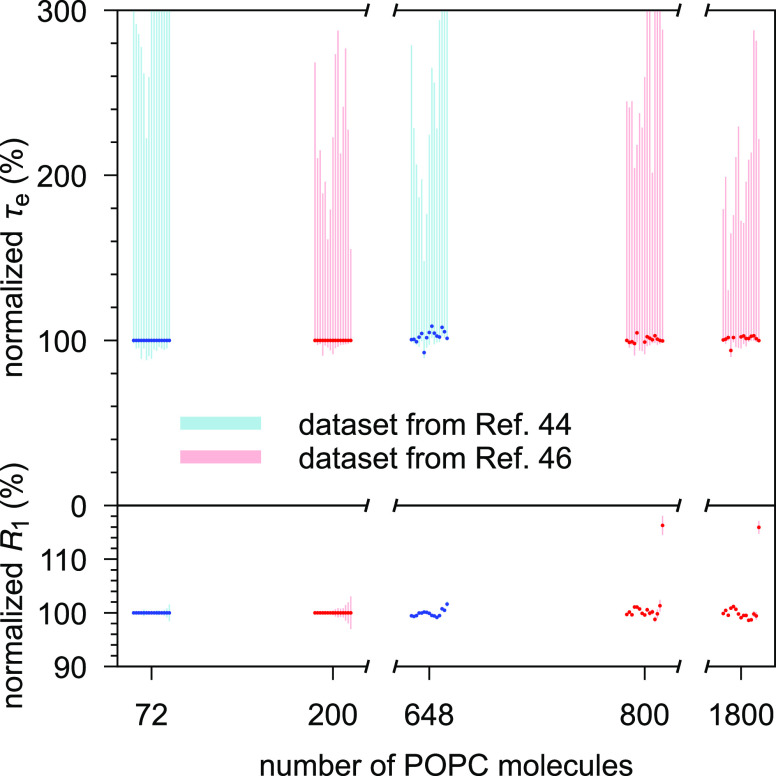
The simulation trajectories were collected from the general-purpose open-access repository Zenodo (zenodo.org), with the majority of the data originating from the NMRlipids Project^32,33 (nmrlipids.blogspot.fi). The trajectories were chosen by hand based on how well the simulation conditions matched the available experimental data (lipid type, temperature, cholesterol content, and hydration) and how precisely one could extract the quantities of interest from the trajectory (length of simulation and system size). Note that, apart from the sampling accuracy, simulation size does not affect τ_e and R₁ (Figure 2). Table 1 lists the chosen trajectories of pure POPC (1-palmitoyl-2-oleoyl-glycero-3-phosphocholine) bilayers at/near room temperature and at full hydration; Table 2 lists the trajectories with cholesterol; and Table 3 those with varying hydration. Full computational details for each simulation are available at the cited Zenodo entry.

Figure 2.

Effective correlation times (τ_e, upper panel) and R₁ rates (lower panel) do not markedly depend on the system size. Shown are two CHARMM36 POPC data sets that varied the size while keeping other simulation parameters fixed: ref (44) (blue, system sizes 72 and 648 lipids)⁴⁵ and ref (46) (red, system sizes 200, 800, and 1800 lipids). Both data sets are shown normalized against their smallest system. The 15 datapoints shown for each system correspond, from left to right, to the carbon segments γ, β, α, g₃, ..., C17/C15′, C18/C16′, cf. Figure 3.

Table 1. Analyzed Open-Access MD Trajectories of Pure POPC Lipid Bilayers at Full Hydration.

force-field lipid/water	Nla	Nwb	Tc (K)	tanald (ns)	filese
Berger-POPC-0747/SPC48	256	10,240	300	300	[49]
CHARMM3650/TIP3P51	256	8704	300	300	[52]
MacRog53/TIP3P54	128	5120	300	500	[55]
Lipid1456/TIP3P54	72	2234	303	50	[57]
Slipids58/TIP3P54	200	9000	310	500	[59]
ECC60/SPC-E61	128	6400	300	300	[62]

^aNumber of POPC molecules.

^bNumber of water molecules.

^cSimulation temperature. Note that the temperature varied across these openly available simulation data, but in no case was T lower than in the experiment. Thus, as dynamics slows down when the temperature drops, any overestimation of τ_e by MD (as typically seen in Figure 3) would get worse if the simulations were done at the experimental 298 K.

^dTrajectory length used for analysis.

^eReference for the openly available simulation files.

Table 2. Analyzed Open-Access MD Trajectories of Cholesterol-Containing POPC Bilayers at Full Hydration.

force-field POPC/water+cholesterol	cchola	Ncholb	Nlc	Nwd	Te (K)	tanalf (ns)	filesg
Berger-POPC-0747/SPC48	0%	0	128	7290	298	50	[63]
+Höltje-CHOL-1364,65	50%	64	64	10,314	298	50	[66]
CHARMM3650/TIP3P51	0%	0	200	9000	310	500	[67]
+CHARMM3668	50%	200	200	18,000	310	500	[69]
MacRog53/TIP3P54	0%	0	128	6400	310	500	[70]
+MacRog53	50%	64	64	6400	310	500	[70]
Slipids58/TIP3P54	0%	0	200	9000	310	500	[59]
+Slipids71	50%	200	200	18,000	310	500	[59]

^aBilayer cholesterol content (mol %).

^bNumber of cholesterol molecules.

^cNumber of POPC molecules.

^dNumber of water molecules.

^eSimulation temperature.

^fTrajectory length used for analysis.

^gReference for the openly available simulation files.

Table 3. Analyzed Open-Access MD Trajectories of PC Lipid Bilayers under Varying Hydration Level.

force field lipid/water	lipid	nw/la	Nlb	Nwc	Td (K)	tanale (ns)	filesf
Berger-POPC-0747/SPC48	POPC	40	256	10,240	300	300	[49]
	POPC	7	128	896	298	60	[72]
Berger-DLPC-1373/SPC-E61	DLPCg	24	72	1728	300	80	[74]
	DLPCg	16	72	1152	300	80	[75]
	DLPCg	12	72	864	300	80	[76]
	DLPCg	4	72	288	300	80	[77]
CHARMM3650/TIP3P51	POPC	40	128	5120	303	140	[78]
	POPC	34	256	8704	300	500	[55]
	POPC	31	72	2232	303	20	[79]
	POPC	15	72	1080	303	20	[80]
	POPC	7	72	504	303	20	[81]
MacRog53/TIP3P54	POPC	50	288	14,400	310	40	[82]
	POPC	25	288	7200	310	50	[82]
	POPC	15	288	4320	310	50	[82]
	POPC	10	288	2880	310	50	[82]
	POPC	5	288	1440	310	50	[82]

^aWater/lipid molar ratio.

^bNumber of lipid molecules.

^cNumber of water molecules.

^dSimulation temperature.

^eTrajectory length used for analysis.

^fReference for the openly available simulation files.

^g1,2-Dilauroyl-sn-glycero-3-phosphocholine.

The trajectories were analyzed using in-house scripts. These are available in ref (83), along with a Jupyter notebook outlining an example analysis run. To enable automated analysis of several force fields with differing atom naming conventions, we used the mapping scheme developed within the NMRlipids Project to automatically recognize the atoms and bonds of interest for each trajectory.

After downloading the necessary files from Zenodo, we processed the trajectory with Gromacs gmx trjconv to make the molecules whole; that is, we made sure that, for each covalent bond, the partaking atoms are from the same periodic image of the molecule. For the united atom Berger model, hydrogens were added using the Gromacs 4.0.2 tool g_protonate. We then calculated the S_CH (eq 3) with the OrderParameter.py script that uses the MDanalysis^84,85 Python library. The C–H bond correlation functions g(τ) (eq 1) were calculated with Gromacs 5.1.4⁸⁶ gmx rotacf (note that on MD timescales g_s = 1 so that g = g_f) after which the S_CH were used to normalize the g_f to obtain the reduced and normalized correlation function

7

that is, the integrand in eq 4.

The effective correlation times τ_e were then calculated by integrating g_f^′(τ) from τ = 0 until τ = t₀. Here, t₀ is the first time point at which g_f reached zero: t₀ = min{t | g_f^′(t) = 0}. If g_f did not reach zero within t_anal/2, the τ_e was not determined, and we report only its upper and lower estimates.

To quantify the error on τ_e, we first estimate the error on g_f^′(τ), where we account for two sources of uncertainty: g_f(τ) and S_CH². Performing linear error propagation on eq 7 gives

8

Here, the ΔS_CH was determined as the standard error of the mean of the S_CH over the N_l individual lipids in the system.³² Similarly, we quantified the error on g_f(τ) by first determining the correlation function g_f^m(τ) for each individual lipid m over the whole trajectory and then obtaining the error estimate Δg_f(τ) as the standard error of the mean over the N_l lipids. Importantly, this gives an uncertainty estimate for g_f(τ) at each time point τ.

To obtain the lower bound on τ_e, we integrate the function g_f^′(τ) – Δg_f(τ) over time from τ = 0 until τ = t_l. Here

9

That is, t_l equals the first time point at which the lower error estimate of g_f^′ reached zero, or t_l = t_anal/2, if zero was not reached before that point.

To obtain the upper error estimate on τ_e, we first integrate the function g_f^′(τ) + Δg_f(τ) over time from τ = 0 until t_u = min{t₀, t_anal/2}. Note, however, that this is not yet sufficient, because there could be slow processes that the simulation was not able to see. Although these would contribute to τ_e with a low weight, their contribution over long times could still add up to a sizable effect on τ_e. That said, it is feasible to assume (see Figure 1A) that there are no longer-time contributions to g_f than something that decays with a time constant of 10^–6 s. We use this as our worst case estimate to assess the upper bound for τ_e, that is, we assume that all the decay of g_f from the time point t_u onward comes solely from this hypothetical slowest process that decays with a time constant of 10^–6 s. The additional contribution to the upper bound for τ_e then reads

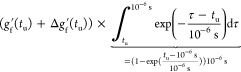10

The R₁ rates were calculated using eq 5. The spectral density j(ω) was obtained from the normalized correlation function g_f^′ by fitting it with a sum of 61 exponentials

11

with logarithmically spaced timescales τ_i ranging from 1 ps to 1 μs and then calculating the spectral density of this fit based on the Fourier transformation⁴¹

12

The R₁ rate of a given C–H pair was first calculated separately for each lipid m (using eq 5 with N_H = 1, and j^m(ω) obtained for the normalized correlation function g_f^′m). The resulting N_l measurements per C–H pair were then assumed independent: their mean gave the R₁ rate of the C–H pair, and the standard error of the mean its uncertainty. The total R₁ rate of a given carbon was obtained as a sum of the R₁ rates of its C–H pairs. When several carbons contribute to a single experimental R₁ rate due to the overlapping peaks (for example, in C2 carbon in the acyl chains and the γ carbons), the R₁ from simulations was obtained as an average over carbons with overlapping peaks. The segment-wise error estimates were obtained by standard error propagation, starting from the uncertainties of the R₁ rates of the C–H pairs.

To gain some qualitative insight on the timescales at which the main contributions to the R₁ rates arise, we also calculated “cumulative” R₁ rates, R₁(τ), which contained those terms of the sum in eq 12 for which τ_i < τ. Note that here the g_f^′ averaged over lipids was used; therefore, the “cumulative” R₁(τ→∞) does not necessarily have exactly the same numerical value as the actual R₁.

Finally, we note that the fit of eq 11 provides an alternative to estimating τ_e because

13

When the simulation trajectory is not long enough for the correlation function to reach the plateau, integrating g_f^′ gives a lower bound estimate for τ_e, while the sum of eq 13 includes also (some) contribution from the longer-time components via the fitting process. However, in practice, the fit is often highly unreliable in depicting the long tails of the correlation function, and thus we chose to quantify τ_e using the area under g_f and estimate its uncertainty as detailed above.

Results and Discussion

Using open-access MD simulation trajectories, we benchmark phospholipid conformational dynamics in six MD force fields. We start with pure POPC bilayers in their liquid crystalline fully hydrated state (see Table 1 for simulation details and Figures 3 and 4 for the data) and then proceed to check the changes in dynamics when cholesterol is added to the bilayer (Table 2 and Figure 5) and when the hydration level is reduced (Table 3 and Figure 6). Our yardsticks are the effective correlations times τ_e (eq 4) and the R₁ rates (eq 5) measured at 125 MHz ¹³C (500 MHz ¹H) Larmor frequency; an MD model with correct rotational dynamics in a window around ∼1 ns will match the experimental R₁ rates, whereas the τ_e reflect all the sub-μs timescales (Figure 1).

Figure 3.

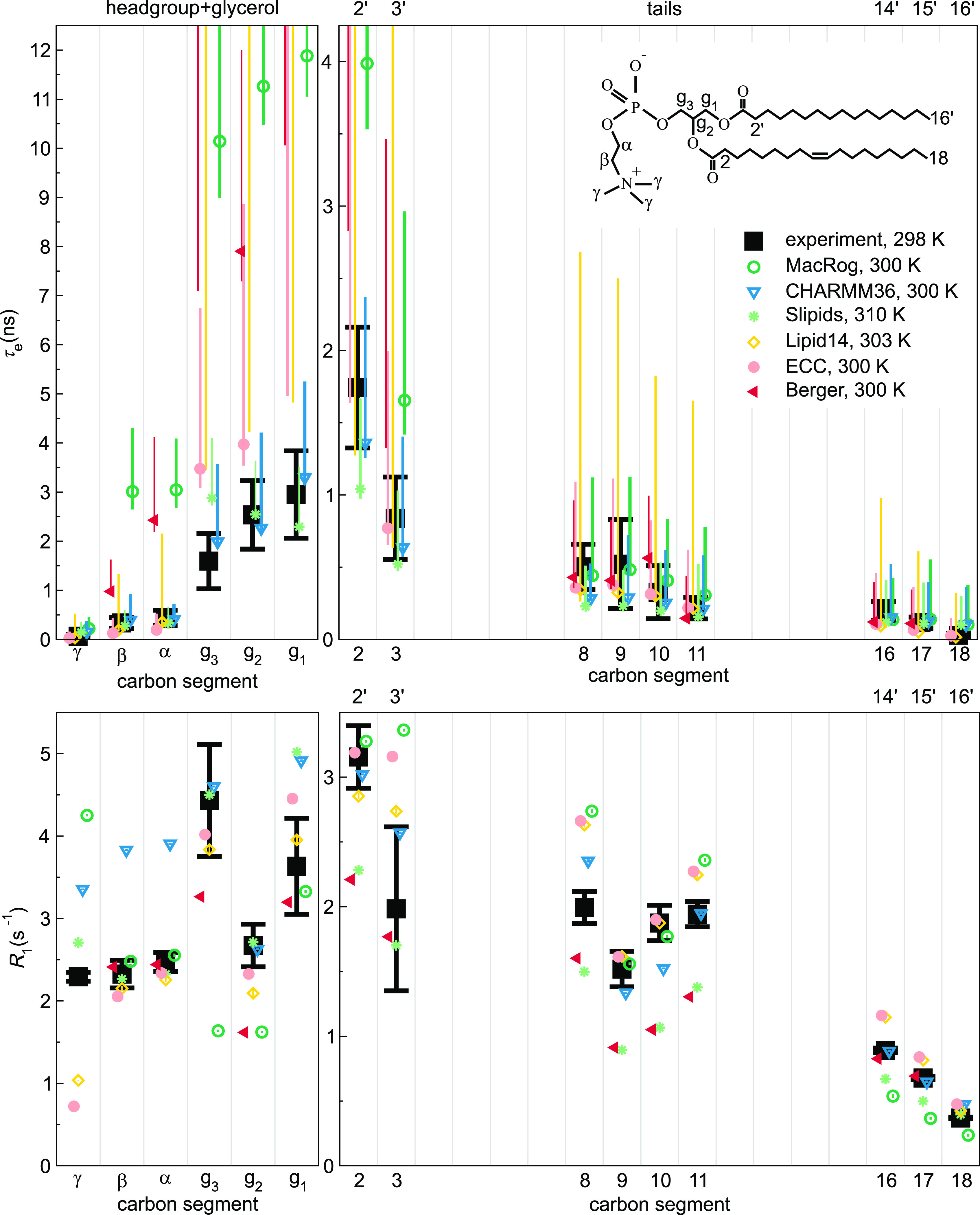
Effective correlation times (τ_e, top) and R₁ rates (bottom) in experiments³⁹ (black) and MD simulations (colored) of POPC bilayers in the L_α phase under full hydration. Inset shows the POPC chemical structure and carbon segment labeling. Each plotted value contains contributions from all the hydrogens within its carbon segment; the data for segments 8–11 are only from the sn-2 (oleoyl) chain, whereas the (experimentally non-resolved) contributions of both tails are included for segments 2–3 (2′–3′ in the sn-1 chain) and 16–18 (14′–16′). Simulation results are only shown for the segments for which experimental data were available. For τ_e, a simulation data point indicates the average over C–H bonds; however, if τ_e could not be determined for all bonds, only the error bar (extending from the mean of the lower to the mean of the upper error estimates) is shown. The Berger data for segments γ, C18, and C16′ are left out as the protonation algorithm used to construct the hydrogens post-simulation in united atom models does not preserve the methyl C–H bond dynamics. Table 1 provides further simulation details, while information on the experiments is available at ref (39).

Figure 4.

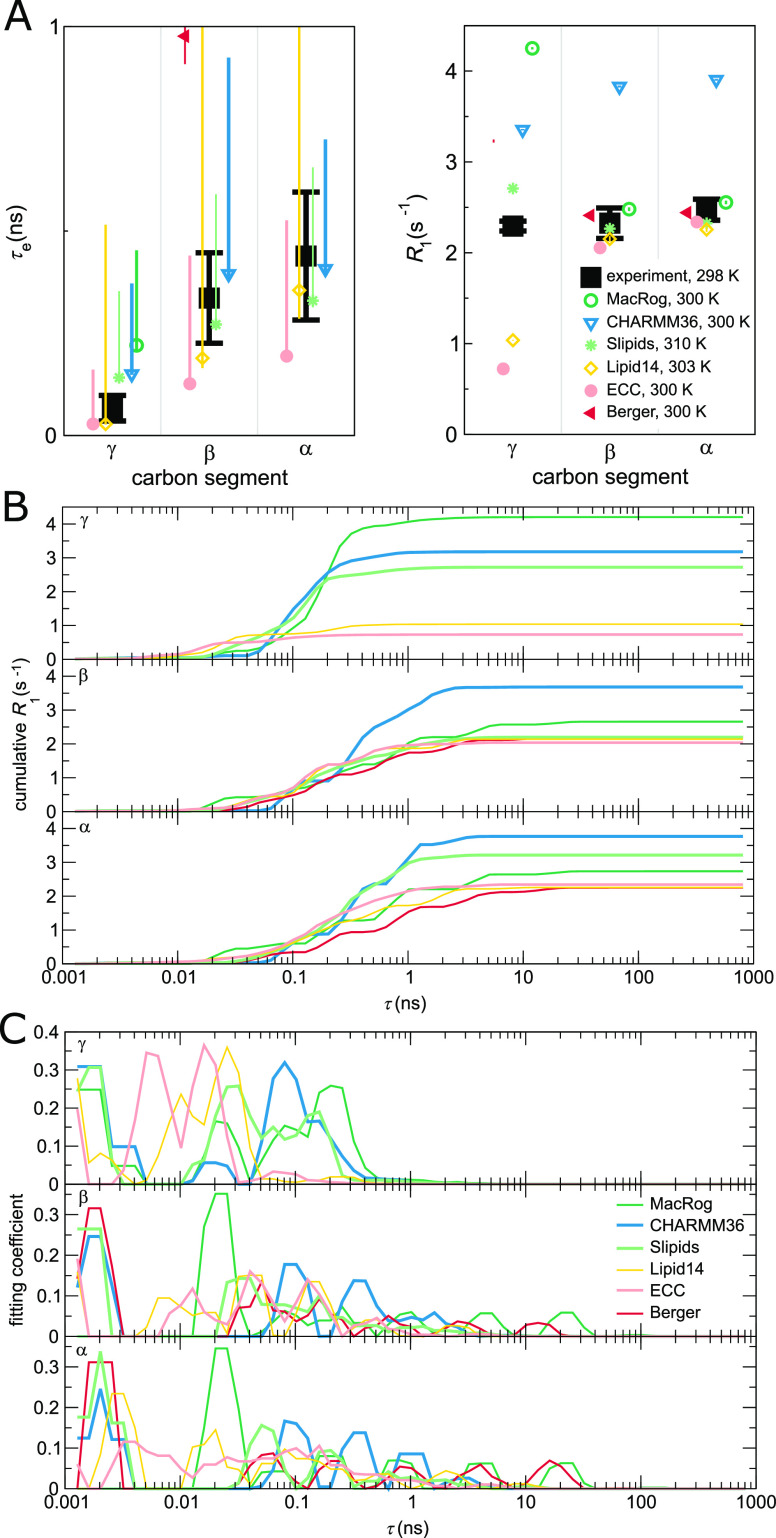
Contributions to the dynamics of the headgroup segments. (A) Zoom on the headgroup τ_e (left panel) and R₁ (right). (B) “Cumulative” R₁(τ) of the γ (top panel), β (middle), and α (bottom) segments. R₁(τ) is obtained, as detailed in Methods, by including in the sum of eq 12 only terms with τ_i < τ. Consequently, at τ → ∞, the R₁(τ) approaches the actual R₁. (C) Prefactor weights α_i from eq 11 of γ (top), β (middle), and α (bottom). Note that panels (B) and (C) show a sliding average over three neighboring data points.

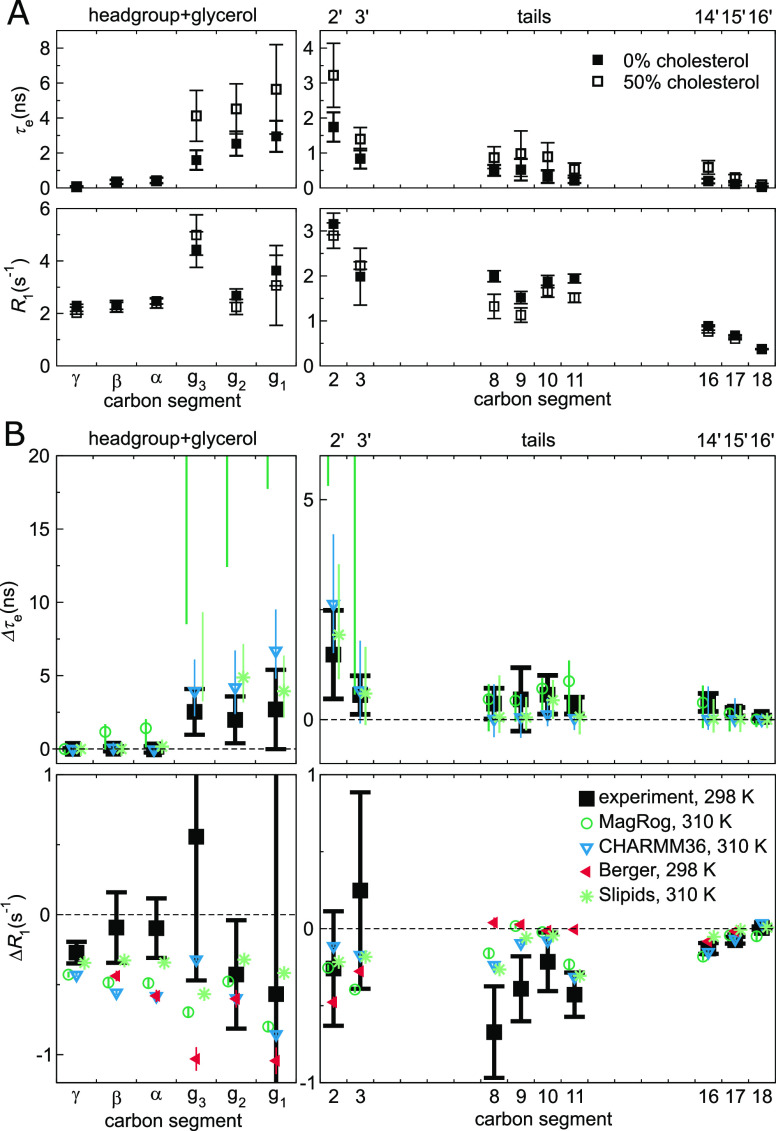
Figure 5.

Effect of cholesterol on POPC conformational dynamics. (A) Experimental effective correlation times τ_e (top panels) and R₁ rates (bottom) in 100/0 and 50/50 POPC/cholesterol bilayers at full hydration, see ref (39) for further details. (B) Change in τ_e (Δτ_e, top panels) and R₁ (ΔR₁, bottom), in NMR (black) and MD (color), when the bilayer composition changes from pure POPC to 50% cholesterol. Error estimates for the simulated Δτ_e are the maximal possible based on the errors at 0% and 50% cholesterol; for other data, regular error propagation is used. The Berger Δτ_e is not shown because the available open-access trajectories were too short to determine meaningful error estimates. Table 2 provides further simulation details; for segment labeling, see Figure 3.

Figure 6.

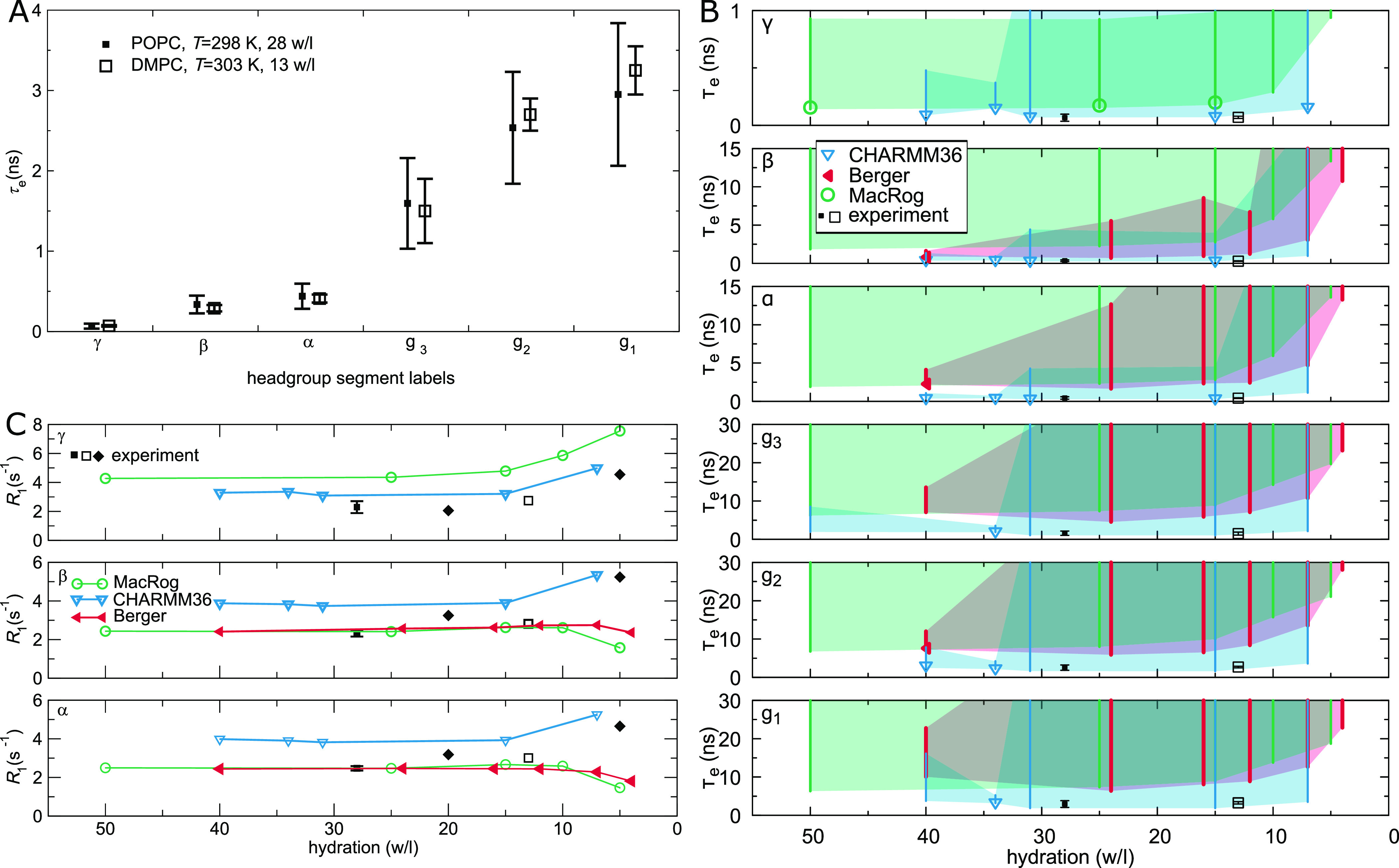
Effect of drying on PC headgroup and glycerol backbone conformational dynamics. (A) Experimental effective correlation times τ_e for DMPC at low hydration (from ref (42)) do not significantly differ from the τ_e for POPC at full hydration (from ref (39)). (B) Calculated τ_e for POPC at decreasing hydration in three MD models. Symbols indicate the mean of segment hydrogens if τ_e could be determined for all of them; otherwise, only the error bar (extending from the mean of the lower to the mean of the upper uncertainty estimates) is drawn. The area limited by the error bars shaded for visualization. Note that four Berger data points (24, 16, 12, and 4 w/l) are from DLPC. (C) ¹³C NMR R₁ rates (at ω_C = 125 MHz) of the PC headgroup segments in experiments and simulations: experiments indicate an increasing trend upon dehydration. Experimental POPC (T = 298 K) data at 28 w/l is from ref (39) (solid boxes), POPC (298 K) at 20 and 5 w/l from ref (43) (solid diamonds), and DMPC (303 K) at 13 w/l from ref (42) (open boxes). See Table 3 for simulation details.

Pure POPC at Full Hydration: Slipids and CHARMM36 Reproduce τ_e Excellently

The top panels of Figure 3 compare the effective correlation times τ_e obtained for fully hydrated POPC bilayers in experiments (black) and in six different MD force fields (color). We see that—as implied by the discussion leading to eq 10—sub-μs MD simulations typically lead to asymmetric error bars on τ_e; if these open-access trajectories were extended, the τ_e values would more likely increase than decrease. Qualitatively, every force field captures the general shape of the τ_e profile: dynamics slows down toward the glycerol backbone in both the headgroup and the tails.

Quantitatively, most MD simulations tend to produce too slow dynamics in the glycerol region (Figure 3). This is consistent with previous results for the Berger model⁴¹ and with the insufficient conformational sampling of glycerol backbone torsions observed in 500-ns-long CHARMMc32b2^87,88 simulations of a PC lipid.⁸⁹

The best overall τ_e performance is seen in Slipids and in particular CHARMM36 (Figure 3). This is in line with CHARMM36 reproducing the most realistic conformational ensembles for the headgroup and glycerol backbone among the MD simulation force fields benchmarked here.^32,34 Indeed, it is important to keep in mind that the conformational ensembles greatly differ between force fields and are not exactly correct in any of them.^32,34 Consequently, the calculated τ_e times and R₁ rates depict the dynamics of sampling a somewhat different and incorrect phase space for each model. To this end, we try to avoid overly detailed discussion on the models and rather concentrate on common and qualitative trends. That said, there are a few carbon segments in the data for which the experimental order parameters, R₁, and τ_e are all (almost) reproduced by simulations, suggesting that both the conformational ensemble and the dynamics are correctly captured by MD in these cases. For example, Slipids performs well at the β and α and CHARMM36 at the g₃, g₂, and C2 segments. These are, however, exceptions.

An Excellent τ_e May Be Accompanied by a Poor R₁, or Vice Versa

The lower panels of Figure 3 compare the experimental and simulated R₁ rates under the same conditions that were used for the τ_e above. Notably, there are several instances where the R₁ comparison distinctly differs from what was seen for τ_e.

There are cases where a matching R₁ is accompanied by a larger-than-experimental τ_e. MacRog for the β, α, and g₁ segments provides a prominent example of this. Such a combination suggests that MD has the correct relative weight of 1 ns-scale dynamics but has too slow long-time dynamics.

There are also cases where τ_e matches experiments but R₁ does not, such as the β and α segments in CHARMM36. Therein, a cancellation of errors occurs in τ_e: the overestimation of the relative weight of 1 ns-scale dynamics is compensated by wrong dynamics at the other timescales. As CHARMM36 overall performs rather well for C–H bond order parameters, R₁, and τ_e, we proceed to study this shortcoming on the headgroup R₁ rates in some more detail.

Conformational Dynamics of PC Headgroup Segments in MD

Figure 4A zooms in on the headgroup (γ, β, and α) segments, whose τ_e were not clearly visible on the scale of Figure 3. We see that, for γ, no force field provides both τ_e and R₁, but Slipids comes closest. For β and α, Slipids captures both measurables near perfectly. In other words, among the benchmarked force fields, Slipids gives the most realistic description of the conformational dynamics in the headgroup region. CHARMM36, e.g., overestimates (R₁) the relative weight of timescales around ∼1 ns.

To investigate closer how the differences between force fields arise, Figure 4B shows the “cumulative” R₁(τ), where the ranges of steepest increase indicate timescales that most strongly contribute to R₁ rates.

For the γ segment, Figure 4B shows that, for models that overestimate the R₁ rate (MacRog, CHARMM36, and Slipids, see Figure 4A), the major contribution to R₁ arises at τ > 50 ps, whereas for models that underestimate R₁ (Lipid14 and ECC), the major contribution comes from τ < 50 ps. This also manifests in the distribution of fitting weights (α_i in eq 11) in Figure 4C: the later non-zero weights occur, the larger is the resulting R₁ of γ.

For the β and α segments, Figure 4B shows that the main contribution to R₁ rates arises from processes between 100 ps and 1 ns. CHARMM36 has the largest relative weights of all models in this window (Figure 4C), which explains its overestimation of R₁ of β and α. All the other models have R₁ rates close to experiments, but only Slipids simultaneously gives also the τ_e correctly. Notably, Slipids has its largest weights at τ < 100 ps. Indeed, the considerable weights at short (<10 ps) timescales in all models except MacRog and at long (>10 ns) timescales in MacRog and Berger hardly manifest in R₁. However, the latter contribute heavily to τ_e, which is thus considerably overestimated by MacRog and Berger (Figure 3).

It would be highly interesting to identify the origins of the observed artificial timescales, particularly for the 0.1–1 ns window overpresented in CHARMM36, and propose how to correct those in the simulation models. After all, it is known that the R₁ rates of mono- and disaccharides⁹⁰ and proteins⁹¹ in solution agree satisfactorily with experiments when the artificially low viscosity of TIP3P water is accounted for by a simple scaling. Viscosity at the bilayer–water interface, however, remains an open question—although one which a careful comparison between spin relaxation rates of lipid headgroups in simulations and experiments might be able to answer. Nevertheless, we refrain from further analysis here as the connection between the fitted correlation times and the correlation times of distinct motional processes, such as dihedral rotations and lipid wobbling, turns out to be highly non-trivial.

Effect of Cholesterol

An essential component in cell membranes, cholesterol has various biological functions. It is well known to order the acyl chains in lipid bilayers, but its effect on the headgroup is more controversial.^65,92 For example, it has been proposed that lipid headgroups reorganize to shield cholesterol from water.⁹² However, while acyl chains do substantially order, NMR experiments show no significant conformational changes in the headgroup upon addition of even 50% of cholesterol, which suggests that the tail and head regions behave essentially independently.^32,65 In principle, the headgroups could shield cholesterol from water even without changing their conformational ensemble: by reorienting only laterally on top of the cholesterol. In this case, one would expect the rotational dynamics of headgroup segments to change when cholesterol is added.

Top panels of Figure 5A depict the experimental effective correlation times τ_e in pure POPC bilayers and in bilayers containing 50% cholesterol. The τ_e at the glycerol backbone slow down markedly when cholesterol is added. Tail segment dynamics slows down too, most notably close to the glycerol backbone. In stark contrast, the τ_e of the headgroup segments (γ, β, and α) remain unaffected. Furthermore, cholesterol induces no measurable change in the headgroup β and α segment dynamics at short (∼1 ns) timescales, as demonstrated by the experimental R₁ rates (Figure 5A, bottom panels). That said, there is a small but measurable impact on R₁ at γ. In summary, these experimental findings support the idea³⁹ that the acyl chains and the headgroup can respond—in agreement with the relative uncoupling of the PC head and tails reported in simulations⁹³—almost independently to changes in conditions and composition.

All four benchmarked force fields (Figure 5B) qualitatively reproduce the experimental increase in τ_e: Slipids and CHARMM36 give rather decent magnitude estimates, while MacRog grossly overestimates the slowdown of glycerol, C2, and C3 segments. Notably, MacRog appears to predict slowdown also for the headgroup (β and α), for which experiments detect no change. Note that, while CHARMM36 correctly shows no change in τ_e of the γ, β, and α segments, it does predict an erroneous ΔR₁ for all three, indicating some inaccuracies in the headgroup rotational dynamics. Such inaccuracies might be reflected in the recent findings⁹⁴ (obtained using CHARMM36) that the headgroups of PC-lipids neighboring (within 6.6 Å) a lone cholesterol spend more time on top of the said cholesterol than elsewhere. Interestingly, the tail ΔR₁ seem to be qualitatively reproduced by all three all-atom force fields, whereas Berger fails to capture the trend at the oleoyl double bond. All these findings are in line with the general picture obtained from C–H bond order parameters:³⁸ MD simulations capture the changes in the acyl chain region rather well but changes in and near the glycerol backbone region can be overestimated. Of the benchmarked force fields, CHARMM36 appears most realistic in reproducing the effects of cholesterol on the glycerol backbone—and Slipids on the PC headgroup—conformational dynamics.

Effect of Drying

Understanding the impact of dehydration on the structure and dynamics of lipid bilayers is of considerable biological interest. Dehydrated states are found, e.g., in skin tissue. Most prominently, the process of membrane fusion is always preceded by removal of water between the approaching surfaces, and thus the dehydration-imposed changes can considerably affect fusion characteristics, such as its rate.

Figure 6A shows how a mild dehydration affects C–H bond dynamics in the PC headgroup and glycerol backbone; the plot compares the experimental effective correlation times τ_e measured for POPC at full hydration and for DMPC (1,2-dimyristoyl-sn-glycero-3-phosphocholine) at 13 waters per lipid. The τ_e are the same within experimental accuracy, which suggests two conclusions. First, the headgroup (γ, β, and α) τ_e are rather insensitive to the chemical identities of the tails. This is analogous to what was seen experimentally when adding cholesterol (Figure 5A): structural changes in the tail and glycerol regions do not (need to) affect the headgroup dynamics. Second, a mild dehydration does not alter the τ_e in the headgroup and glycerol regions.

Figure 6B shows the effects of dehydration in three MD models. Combination of the unrealistically slow dynamics, especially in the glycerol backbone (Figure 3), and the relatively short lengths of the available open-access trajectories (Table 3) led to large uncertainty estimates; thus, we only point out qualitative trends here. For all headgroup and glycerol segments, the simulated τ_e indicate slowdown upon dehydration. This is manifested in the increase in the magnitude of the error estimate (cf. the Berger data for β and α) as well as in the increase in the lower limit of the error. For CHARMM36 the lower error estimates stay almost constant all the way until 7 w/l, whereas for Berger and MacRog, they hint that a retardation of dynamics starts already between 15 and 10 w/l.

These simulational findings suggest that experiments reducing hydration levels below 10 w/l would also show an increase in τ_e. This prediction is in line with the exponential slowdown of the headgroup conformational dynamics upon dehydration that was indicated by ²H NMR R₁ measurements of DOPC bilayers: R₁ ≈ exp( – n_w/l/4).⁹⁵ The slowdown was attributed to the reduced effective volume available for the headgroup⁹⁵ as it tilts toward the membrane upon dehydration; such tilt is observed via changes of the lipid headgroup order parameters⁹⁶ and is qualitatively reproduced by all the simulation models.³²

Figure 6C shows a collection of experimental ¹³C NMR R₁ rates for the headgroup segments at different water contents; in addition to the full hydration POPC data from Figure 3, DMPC at 13 w/l⁴² and POPC at 20 and 5 w/l⁴³ are shown. Experimentally, an increasing trend with decreasing hydration is observed for all three segments, indicating changes of headgroup dynamics at short (∼1 ns) timescales. Interestingly, only CHARMM36 captures this, whereas Berger and MacRog give decreasing R₁ rates for β and α.

The slowdown characteristics discussed here are of significance not only for computational studies of intermembrane interactions, such as fusion, but also when simulating a bilayer (stack) under low hydration: slower dynamics require longer simulation times for equilibration, for reliably quantifying the properties of the bilayers, and for observing rare events.

Conclusions

We have here demonstrated that open-access databanks of MD trajectories enable the creation of new scientific information without running a single new simulation. More specifically, we have benchmarked (against published NMR data^39,41−43) the conformational dynamics of a wide range of phosphatidylcholine MD models using existing open-access trajectories from the Zenodo repository, in particular those belonging to the NMRlipids Databank (zenodo.org/communities/nmrlipids).

We found that every MD model captures the ¹³C NMR effective correlation time (τ_e) profile of POPC qualitatively, but that most are prone to too slow dynamics of the glycerol backbone C–H bonds (Figure 3). While no force field perfectly reproduces all the experimental data, CHARMM36 and Slipids have overall impressive τ_e. This is a particularly exciting finding concerning CHARMM36 as it is also known to reproduce quite well the experimental conformational ensemble.³² That said, we do find that CHARMM36 struggles with the balance of dynamics in the headgroup region: The R₁ rates, sensitive for ∼1 ns processes, are too high for the γ, β, and α segments (Figure 4). In fact Slipids, which also reproduces the experimental headgroup order parameters,³² appears to outperform CHARMM36 when it comes to headgroup conformational dynamics (Figure 4).

Further, we found that when cholesterol is mixed into a POPC bilayer, MD qualitatively captures the slowdown of conformational dynamics in the tail and glycerol regions (Figure 5). However, the benchmarked force fields overestimate the changes in the ∼1 ns dynamics of the headgroup—except Slipids, which captures well the effects of cholesterol on PC headgroup conformational dynamics.

Finally, we found that, upon reducing the water content below 10 waters per lipid, MD exhibits slowdown of headgroup and backbone dynamics in qualitative agreement with experimental data. That said, only CHARMM36 (but not Berger or MacRog) qualitatively captures the experimentally detected increase in R₁ rates upon dehydration (Figure 6).

While work is still needed in capturing even the correct phospholipid conformations,³² realistic dynamics will be an essential part of developing MD into a true computational microscope. Here, we gathered a set of published experimental ¹³C NMR data on phosphatidylcholine conformational dynamics and charted the typical features of the existing MD models against it, thus laying the foundation for further improvement of MD force fields. Importantly, our work demonstrates the potential of open-access MD trajectories in achieving such benchmarks at a reduced computational and labor cost—but it also highlights the challenges inherent in using such data: not all system permutations might readily exist (here the dehydration data for Lipid14 and Slipids were lacking, see Figure 6); the available sampling (simulation length and size) might vary, requiring extreme care with error estimation; and one has to remain aware of the subtle differences in the many simulation parameters (barostats, temperatures, characteristics of the MD engines, etc.). That said, it has not escaped our notice that a pool of well indexed and documented open-access data provides an ideal platform for automation, which in turn will facilitate faster progress in pinpointing the typical failures of the existing force fields, in identifying key differences in models describing chemical variations of the same molecule type (such as different lipid headgroups), and in developing better models through data-driven approaches.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.0c01299.

• SMILES database (ZIP)

The authors declare no competing financial interest.