Abstract
NMR spectroscopy is a powerful tool for studying protein dynamics. Conventionally, NMR studies on protein dynamics have probed motions of protein backbone NH, side-chain aromatic, and CH3 groups. Recently, there has been remarkable progress in NMR methodologies that can characterize motions of cationic groups in protein side chains. These NMR methods allow investigations of the dynamics of positively charged lysine (Lys) and arginine (Arg) side chains and their hydrogen bonds as well as their electrostatic interactions important for protein function. Here, describing various practical aspects, we provide an overview of the NMR methods for dynamics studies of Lys and Arg side chains. Some example data on protein–DNA complexes are shown. We will also explain how molecular dynamics (MD) simulations can facilitate the interpretation of the NMR data on these basic side chains. Studies combining NMR and MD have revealed the highly dynamic nature of short-range electrostatic interactions via ion pairs, especially those involving Lys side chains.
1. INTRODUCTION
To elucidate mechanisms underlying protein functions, it is essential to understand the atomic-level behavior of individual side chains at functionally important sites on proteins. Charged side chains and their electrostatic interactions are of fundamental importance for molecular recognition, association, and catalysis by proteins (Honig & Nicholls, 1995; Sheinerman, Norel, & Honig, 2000). The mobility of these side chains should affect electrostatic interactions and hydrogen bonds crucial for the functional activities of proteins. However, the dynamic aspects of these fundamental interactions involving the charged moieties of protein side chains are not well understood from experimentally obtained data.
Solution NMR spectroscopy is a powerful tool in experimental research on protein dynamics and has provided insight into dynamics–function relationship of proteins (Boehr, Dyson, & Wright, 2006; Clore & Iwahara, 2009; Loria, Berlow, & Watt, 2008; Mittermaier & Kay, 2009; Palmer, 2014). However, when protein dynamics are studied, the vast majority of NMR studies focus on the motions of either protein backbone or side-chain CH3 groups. NMR investigations of polar or charged side chains remain rare. More investigations into the dynamic behavior of these side chains would deepen our knowledge about the functional roles of protein dynamics.
Our goal in this chapter is to provide other researchers with a practical overview of the NMR methods for dynamics investigations of lysine (Lys) and arginine (Arg) side chains. Hydrogen bonds and electrostatic interactions involving Lys side-chain NH3+ groups and Arg NεH groups are of particular interest. Over the past decade, we have conducted NMR studies of basic side chains, primarily to obtain a better understanding of protein–DNA interactions. Lys and Arg side chains are crucial for electrostatic interactions with DNA phosphates and for recognition of DNA bases (Luscombe, Laskowski, & Thornton, 2001; Privalov, Dragan, & Crane-Robinson, 2011; Rohs et al., 2010). Due to our research background, the majority of the examples shown here are for protein–DNA complexes. However, the NMR methodology for Lys and Arg side chains introduced in this chapter is applicable to other protein systems as well. Furthermore, we explain how molecular dynamics (MD) simulations can facilitate interpretation of NMR data regarding the behavior of basic side chains.
2. NMR OF Lys AND Arg SIDE CHAINS
2.1. 1H, 13C, and 15N Resonances of Lys/Arg Side Chains
2.1.1. Chemical Shifts and Protonation States
Typical 1H, 13C, and 15N chemical shifts of Lys and Arg side chains of proteins are shown in Table 1. Side-chain methylene 1H and 13C resonances can be assigned using standard three-dimensional (3D) NMR spectra, such as HCCH-TOCSY, HCCH-COSY, H(CCO)NH, and C(CO)NH spectra (Clore & Gronenborn, 1998). 1H and 15N resonances from the NH/NH2/NH3+ groups of Lys and Arg side chains are located in unique regions in 1H–15N heteronuclear spectra (e.g., see Fig. 1A), and additional experiments are required to assign these 1H and 5N resonances, as explained in Section 2.4. The NMR-based determination of the pKa of protein side chains has been reviewed recently (Hass & Mulder, 2015; Platzer, Okon, & McIntosh, 2014). Because the typical pKa of Lys side chains is 10.5, Lys side-chain amino groups are usually protonated in the form of NH3+ in neutral and acidic pH conditions. Lys side-chain 15Nζ chemical shifts are typically 31–35 ppm in the protonated state (i.e., NH3+) (Andre, Linse, & Mulder, 2007; Iwahara et al., 2007; Poon et al., 2006). NH3+ groups that form a hydrogen bond with other moieties tend to exhibit a relatively large 15N chemical shift (Blaum et al., 2010; Esadze, Li, Wang, Brüschweiler, & Iwahara, 2011; Sepuru, Iwahara, & Rajarathnam, 2018). The deprotonated state (i.e., NH2) of a Lys side-chain amino group exhibits 15N chemical shift of 22–26 ppm in the deprotonated state (Andre et al., 2007; Kougentakis et al., 2018; Poon et al., 2006; Takayama et al., 2008). The typical pKa of Arg side chains has recently been updated to 13.8 (Fitch, Platzer, Okon, Garcia-Moreno, & McIntosh, 2015). Due to their typical pKa values, the deprotonated states of Lys and Arg side chains are rare at physiological pH, especially for Arg. In this chapter, we focus on the positively charged, protonated states of Lys and Arg side chains.
Table 1.
Typical 1H, 13C, and 15N Chemical Shifts (in ppm) of Lys and Arg Residuesa
| Lys | Arg | |||
|---|---|---|---|---|
| 1H | HN | 7.5–8.8 | HN | 7.3–9.2 |
| Hα | 3.8–4.7 | Hα | 3.8–4.8 | |
| Hβ2/β3 | 1.5–2.0 | Hβ2/β3 | 1.4–2.1 | |
| Hγ2/γ3 | 1.1–1.6 | Hγ2/γ3 | 1.2–1.8 | |
| Hδ2/δ3 | 1.0–2.3 | Hδ2/δ3 | 2.8–3.4 | |
| Hε2/ε3 | 2.7–3.1 | Hεb | 7.2-9.2 | |
| Hζ1/ζ2/ζ3 (NH3+)c | 7.2–8.2 | Hη11/η12/ η21/η22d | 6.7–8.7 | |
| Hζ1/ζ2 (NH2)e | 0.8–1.2 | |||
| 13C | C═O | 171–183 | C═O | 173–180 |
| Cα | 54–60 | Cα | 53–60 | |
| Cβ | 30–36 | Cα | 28–33 | |
| Cγ | 22–28 | Cγ | 24–30 | |
| Cδ | 26–32 | Cδ | 40–46 | |
| Cε | 39–45 | Cζ | 154–167 | |
| 15N | N (backbone) | 116–126 | N (backbone) | 116–126 |
| Nζ (NH3+)c | 30–35 | Nεb | 78–90 | |
| Nζ (NH2)f | 22–26 | Nη1/η2d | 68–74 |
Unless indicated otherwise, data are from the Biological Magnetic Resonance Bank (BMRB). Each range corresponds to average ± standard deviation in the BMRB chemical shift statistics table.
From data in the literature (e.g., Esadze et al., 2016; Nguyen, Hoffpauir, & Iwahara, 2017; Yamazaki, Pascal, Singer, Formankay, & Kay, 1995).
From data in the literature (e.g., Iwahara, Jung, & Clore, 2007; Poon et al., 2006).
From data in the literature (e.g., Nieto et al., 1997; Yamazaki et al., 1995).
Observed only for those buried in a hydrophobic core (Kougentakis et al., 2018; Takayama, Castaneda, Chimenti, Garcia-Moreno, & Iwahara, 2008).
From data in the literature (Andre et al., 2007; Kougentakis et al., 2018; Poon et al., 2006; Takayama et al., 2008).
Fig. 1.
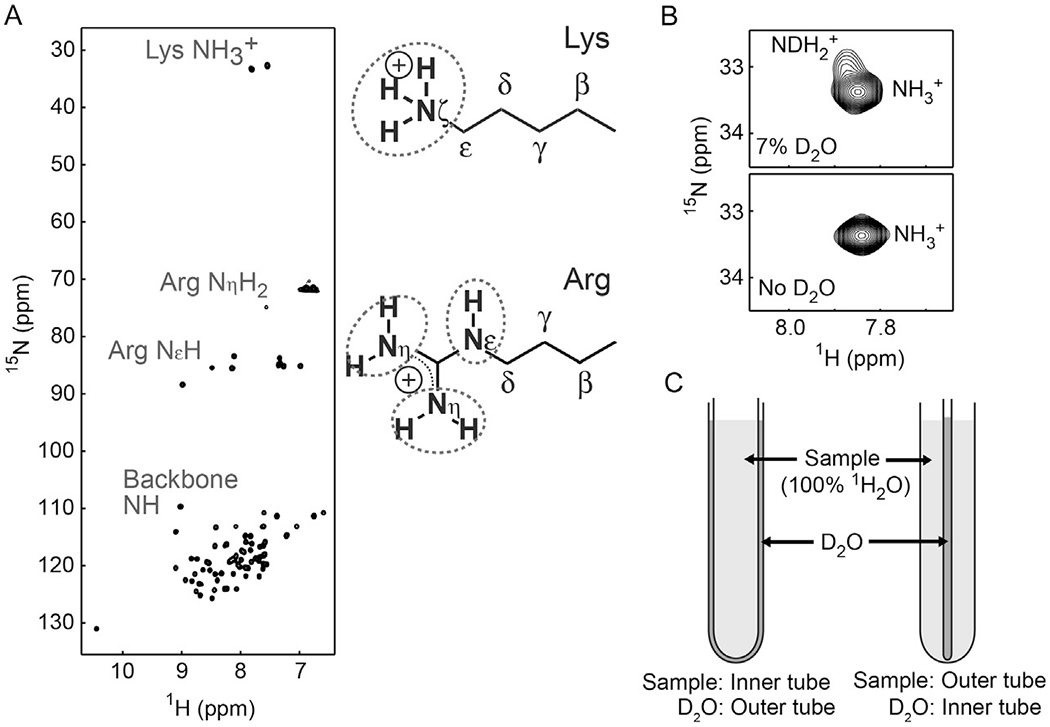
(A) 1H and 15N resonances of the Lys and Arg side chains of the HoxD9 homeodomain bound to 24-bp specific DNA at 35°C. (B) Effect of D2O in the sample buffer. D2O for NMR lock should separately be sealed to avoid exchange between isotopically different species (i.e., NH3+, NDH2+, ND2H+). (C) Two types of coaxial NMR tubes for separating the sample and D2O.
2.1.2. Degenerate 1H Resonances of Lys NH3+
The resonances of the three 1H nuclei within a Lys NH3+ group are degenerate due to rapid rotations around the Cε–Nζ bond. This degeneracy occurs even in the presence of hydrogen bonds with other moieties. For example, in ubiquitin, the Lys27 NH3+ group forms three hydrogen bonds with other moieties, but the bond rotations of this NH3+ occur on a nanosecond timescale, making the 1H resonances of its three 1H nuclei completely degenerate (Esadze et al., 2011). As described in Section 5, the hydrogen bonding of Lys side chains is dynamic, allowing rapid Cε–Hζ bond rotations. The intrinsic 15N transverse relaxation of Lys NH3+ is very slow owing to the rapid Cε–Nζ bond rotations. Although rapid hydrogen exchange with water causes some adverse effects on NMR experiments (see Section 2.3), heteronuclear 1H–15N NMR of Lys NH3+ groups is useful for investigating the conformational dynamics, hydrogen-bond dynamics, and ion-pair dynamics of proteins.
2.1.3. Hindered 180° Rotations of Arg Guanidinium Cζ–N Bonds
Arg side-chain guanidinium moieties involve five hydrogen (Hε, Hη11, Hη12, Hη21, and Hη22) and three nitrogen (Nε, Nη1, and Nη2) atoms. In general, it is relatively easy to analyze the 1H and 15N resonances of NεH groups but not those of NηH2 groups. The so-called hindered 180° rotations along the Nε–Cζ, Cζ–Nη1, and Cζ–Nη2 bonds within each planar guanidinium moiety cause interconversions between the two NηH2 groups and between the two hydrogen atoms of each NηH2 group. These interconversions tend to occur in the intermediate exchange regime on the 1H and 15N chemical shift timescale at physiological temperature (Yamazaki et al., 1995). Because these interconversions cause severe broadening of 1Hη resonances, the four 1Hη resonances of Arg NηH2 groups are rarely isolated. This broadening effect makes the NMR investigations of Arg NηH2 groups challenging, though quantitative kinetic analysis of the Cζ–N bond rotationsis possible in favorable cases (Gerecht, Figueiredo, & Hansen, 2017; Nieto et al., 1997). In contrast, the 1H and 15N resonances of Arg NεH groups are unaffected by the hindered 180° bond rotations and exhibit relatively sharp NMR signals when the hydrogen exchange is slow enough. Thus, NεH groups are most convenient for 1H–15N NMR investigations of Arg side-chain guanidinium moieties.
2.2. Impact of Hydrogen Exchange on Lys/Arg Side-Chain NMR
2.2.1. Direct Influence of Hydrogen Exchange on 1H Line Shapes
Hydrogen exchange with water broadens the 1H line shapes of signals from the NH/NH2/NH3+ groups of Arg and Lys side chains. When direct 1H observation of a particular NH, NH2, or NH3+ group is possible, its hydrogen exchange rate, kex,w, is typically <200 s−1. This corresponds to a slow exchange regime on the NMR chemical shift timescale because the 1H chemical shift difference (Δδ) between NH/NH2/NH3+ and water resonances is typically >1000 Hz (i.e., kex,w ≪ 2πΔδ). This slow exchange increases the apparent 1H transverse relaxation rate by the first-order rate constant for the transition from NH/NH2/NH3+ to water. Note that this rate constant is virtually identical to the hydrogen exchange rate kex,w (sum of the rate constants for the forward and backward transitions), since the population of water is far larger in this exchange. Therefore, the line width of the 1H signal from NH/NH2/NH3+ is broadened by kex,w/πHz due to hydrogen exchange.
2.2.2. Indirect Influence of Hydrogen Exchange on 15N Line Shapes
Hydrogen exchange impacts the 15N dimension unless in-phase single-quantum coherence is maintained throughout the 15N evolution period. This broadening effect on the 15N dimension is easier to understand for HMQC because multiple-quantum terms such as 2NxHy should be impacted by hydrogen exchange in the manner explained above. Actually, hydrogen exchange broadens 15N line shapes not only in HMQC spectra but also in HSQC spectra. The impact of hydrogen exchange on 15N line shape in HSQC spectra occurs through scalar relaxation of antiphase single-quantum terms (Iwahara et al., 2007). In the first half of the 15N evolution period (t1/2) before a 1H 180° pulse, the 2NyHz term generated through the first INEPT scheme produces 2NxHz, Nx, and Ny terms for NH; 2NxHz, Nx, Ny, 4NxHzHz, and 4NyHzHz for NH2; and 2NxHz, Nx, Ny, 4NxHzHz, 4NyHzHz, 8NxHzHzHz, and 8NxHzHzHz for NH3+ groups. For antiphase single-quantum 15N transverse terms with respect to 1H, scalar relaxation arises from autorelaxation of the coupled 1H nuclei (Abragam, 1961; Bax, Ikura, Kay, Torchia, & Tschudin, 1990) and substantially increases the relaxation rates of the 2Nx(y)Hz, 4Nx(y)HzHz, and 8Nx(y)HzHzHz terms, compared to the relaxation rates of the in-phase single-quantum terms Nx(y). The scalar relaxation rate Rsc for each 1H nucleus is given by Rsc = ρHH + kex,w, where ρHH is the rate of autorelaxation arising from dipole–dipole (DD) interactions with external 1H nuclei (Iwahara et al., 2007). Scalar relaxation rates for the N+, 2N+Hz, 4N+HzHz, and 8N+HzHzHz terms are 0, Rsc, 2Rsc, and 3Rsc, respectively (Esadze et al., 2011). The hydrogen exchange rate kex,w is typically faster than ρHH rates and intrinsic 15N relaxation rates, and therefore governs 15N line shapes in HSQC spectra for NH3+ groups (Anderson et al., 2013; Esadze et al., 2011; Iwahara et al., 2007; Zandarashvili, Esadze, & Iwahara, 2013). In HSQC, hydrogen exchange broadens 15N line width by 1.5kex,w/π Hz for Lys NH3+ groups and by 0.5kex,w/πHz for Arg NεH groups. The impacts of scalar relaxation and hydrogen exchange on the 15N dimension of heteronuclear 1H–15N correlation experiments are summarized in Fig. 2A and B.
Fig. 2.
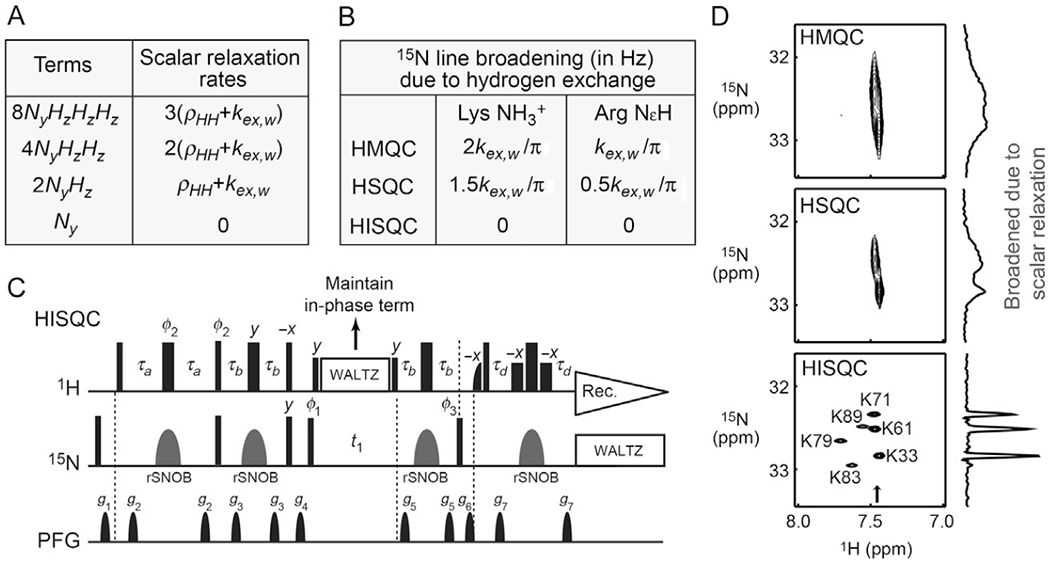
The importance of maintaining the in-phase single-quantum term during the 15N evolution period in 1H–15N NMR experiments for Lys and Arg side chains. (A) Impact of scalar relaxation on different single-quantum terms of 15N coherence. (B) Broadening of 15N line shapes due to hydrogen exchange in the 15N dimensions of HSQC, HMQC, and HISQC spectra for Lys NH3+ and Arg NεH groups. The increases in 15N half-height widths are given in Hz units. (C) The pulse sequence of the water-flip-back HISQC experiment for Lys NH3+ or Arg NεH groups. Thin and bold bars in black represent hard rectangular 90° and 180° pulses, respectively. Water-selective half-Gaussian (2.1 ms) and soft-rectangular (1.2 ms) 90° pulses are represented by half-bell and short-bold shapes, respectively. Unless indicated otherwise, pulse phases are along x, and the carrier position for 1H was set to the position of the water resonance. The 15N carrier position is set to ~33 ppm for Lys NH3+ groups and to ~85 ppm for Arg NεH groups. A gray bell-shape for 15N represents a 1.0-ms rSNOB 180° pulse (Kupče, Boyd, & Campbell, 1995) selective to Lys 15Nζ or Arg 15Nε nuclei. The delays τa and τb are set as follows: τa = 2.7 ms and τb = 1.3 ms for Lys NH3+ groups; τa = 2.3 ms and τb = 2.7 ms for Arg NεH groups. This setting for Arg side chains suppresses signals from NηH2 groups; τb = 1.3 ms can be used to avoid this suppression of NηH2 signals. Phase cycles: φ1 = (y, −y); φ2 = (2(y), 2(−y)); φ3 = (4x, 4(−x));receiver = (x, 2(−x), x, −x, 2x, −x). Quadrature detection in the t1 domain was achieved using States-TPPI, incrementing the phase φ1. The third 1H 90° pulse along −x (before the gradient g4) serves two purposes: it purges unnecessary 15N antiphase magnetization by generating multiple quantum coherence and it flips the water magnetization back to +z. In the HISQC experiment, 1H WALTZ-16 decoupling pulses maintain 15N in-phase single-quantum coherence during the 15N evolution period t1 and thereby suppress the broadening of 15N line shapes due to rapid scalar relaxation arising from hydrogen exchange. (D) HISQC drastically improves 1H–15N correlation spectra for Lys NH3+ groups through suppression of scalar relaxation during the 15N evolution period. This panel compares the HMQC, HSQC, and HISQC spectra recorded for the Lys NH3+ groups of the 15N-labeled Egr-1 zinc-finger–DNA complex at pH 5.8 and 10°C. For each spectrum, the data were acquired using the same number of scans and the same digital resolutions and were processed identically. F1-slices at the position indicated by an arrow are shown to indicate 15N line shapes.
2.2.3. Self-decoupling Due to Hydrogen Exchange
Due to the self-decoupling effect (Cavanagh, Fairbrother, Palmer, Rance, & Skelton, 2007; Harbison, 1993), the apparent magnitude of J-coupling between the 15N and 1H nuclei of NH/NH2/NH3+ becomes smaller than the intrinsic value when the hydrogen exchange rate is comparable to or faster than π1JNH s−1. Theoretical consideration of the self-decoupling effect through hydrogen exchange is presented in the supporting information of Takayama et al. (2008). Because the hydrogen exchange rates for Lys NH3+ groups at pH > 7 are typically far greater than π1JNH (Segawa, Kateb, Duma, Bodenhausen, & Pelupessy, 2008), self-decoupling of 1JNH can easily occur for Lys side chains. Under such conditions, H2(C)N spectra recorded without 1H decoupling in the 15N dimension exhibit singlet (rather than quartet) 15N resonances of Lys NH3+ groups due to the self-decoupling effect.
2.3. Importance of Maintaining In-Phase Single-Quantum 15N Coherence
2.3.1. HISQC Drastically Improves Lys NH3+ 15N Line Shapes
To avoid the severe broadening of 15N line shapes due to rapid scalar relaxation arising from hydrogen exchange, Iwahara et al. developed NH3+-selective heteronuclear in-phase single-quantum coherence (HISQC) and its derivatives (Iwahara et al., 2007). The pulse sequence of the HISQC experiment is shown in Fig. 2C. In this 1H–15N heteronuclear correlation experiment, the in-phase single-quantum term Nx or Ny is created at the beginning of the 15N evolution period, and the in-phase single-quantum coherence N+ (=Nx + iNy) is maintained via the 1H WALTZ decoupling scheme throughout the evolution period. By maintaining the in-phase single-quantum terms Nx and Ny and thereby removing the scalar relaxation from the t1 time domain for the 15N dimension, the HISQC experiment drastically improved the sensitivity and resolution in detection of signals from NH3+ groups, compared to the corresponding HMQC and HSQC experiments (Fig. 2D). Although the typical range of the 15N chemical shifts of Lys NH3+ groups is relatively narrow, the signal dispersion in HISQC spectra is typically excellent owing to the intrinsically slow 15N transverse relaxation of NH3+ groups. Many NMR pulse sequences for NH3+ groups have implemented the principle of HISQC and minimized the adverse impacts of scalar relaxation of antiphase terms with respect to 1H nuclei (Anderson et al., 2013; Esadze et al., 2011; Esadze, Zandarashvili, & Iwahara, 2014; Iwahara et al., 2007; Zandarashvili et al., 2013; Zandarashvili, Li, Wang, Brüschweiler, & Iwahara, 2011).
2.3.2. HISQC Can Also Improve Arg 15Nε Line Shapes
The hydrogen exchange rates kex,w of Arg NεH groups are generally slower than those of Lys NH3+ group. Furthermore, while hydrogen exchange of Lys NH3+ groups broadens the Lys 15N line width by 1.5kex,w/π in HSQC, hydrogen exchange of Arg NεH groups broadens the Arg 15N line width only by 0.5kex,w/π (see Fig. 2B). Because of the smaller impact of scalar relaxation arising from hydrogen exchange, the advantage of 1H–15N HISQC for Arg NεH groups is not as great as that for Lys NH3+groups. However, when hydrogen exchange is rapid (e.g., due to a relatively high pH), the HISQC spectra of Arg NεH groups can be significantly better than the HSQC spectra (Yuwen & Skrynnikov, 2014a). To maximize the sensitivity for Arg NεH groups, the delay ωb in the HISQC pulse sequence in Fig. 2D should be set to 2.7 ms. This setting also suppresses signals from Arg NηH2 groups and simplifies the spectrum, allowing the use of a narrower spectral width for the 15N dimension. TROSY for Arg NεH groups is not as advantageous as that for backbone NH groups because the 15N chemical shift anisotropy (CSA) of Arg Nε (−114 ppm) (Trbovic et al., 2009) is significantly smaller than that of backbone N (−162 to −173 ppm) (Yao, Grishaev, Cornilescu, & Bax, 2010). The 15N dimension of TROSY also suffers from scalar relaxation arising from hydrogen exchange.
2.4. Resonance Assignment for Lys/Arg Side Chains
2.4.1. Resonance Assignment for Lys Side-Chain NH3+ Groups
Several 1H, 3C, 5N triple-resonance experiments for resonance assignment of Lys side-chain amino groups have been developed (Andre et al., 2007; Esadze et al., 2014; Iwahara et al., 2007). Resonance assignment for Lys side-chain NH3+ groups requires long-range correlation spectra. Short-range correlations between NH3+ and 1Hε/13Cε resonances are usually insufficient for unambiguous assignment due to poor dispersion of their chemical shifts. Due to high mobility, few 1H–1H NOE cross-peaks are observed for Lys NH3+ groups, rendering NOE-based resonance assignment difficult. We found that the combined use of (H2C)N(CC) H-TOCSY, H3NCECD, H3NCG, H2(C)N, and HISQC spectra can greatly facilitate assignment of 1H and 15N resonances for Lys side-chain NH3+ groups (Esadze et al., 2014). Fig. 3 shows an example of this approach. H2(C)N (Andre et al., 2007) and (H2C)N(CC)H-TOCSY (Esadze et al., 2014) experiments allow observation of the 15N resonances of Lys NH3+ groups even if direct 1H detection of the NH3+ groups is impossible due to their rapid hydrogen exchange. Because multiple side-chain 1H resonances are observed at high resolution along the 1H direct-detection dimension with excellent separation by sharp 15Nζ resonances, the (H2C)N(CC)H-TOCSY spectrum greatly facilitates 15Nζ resonance assignment for Lys NH3+ groups. The temperature dependence of the H2(C)N spectra allows us to track the change in 15Nζ resonances as a function of temperature. These data together with the 3D H3NCG and H3NCECD spectra allowed us to unambiguously assign 1H–15N HISQC signals from the Lys NH3+ groups of some protein–DNA complexes at relatively low temperature.
Fig. 3.
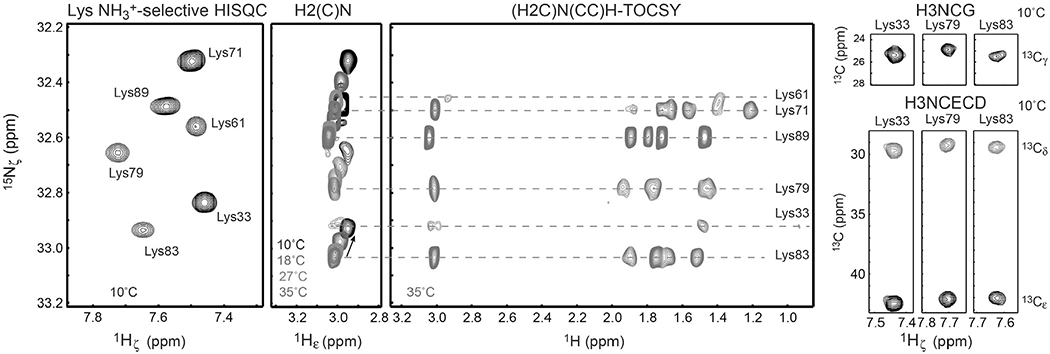
Assignment of the 1H and 15N resonances of Lys NH3+ groups using 2D 13C-decoupled HISQC, 2D H2(C)N (Andre et al., 2007), 2D (H2C)N (CC)H-TOCSY (Esadze et al., 2014), 3D H3NCG (Esadze et al., 2014), and 3D H3NCECD (Esadze et al., 2014) spectra. The spectra were recorded for the 13C/15N-labeled Egr-1 zinc-finger–DNA complex at indicated temperatures and pH 5.8.
2.4.2. Resonance Assignment for Arg Guanidinium Moieties
Some 1H, 3C, 5N triple-resonance experiments on Arg side chains have been proposed (Andre et al., 2007; Iwahara & Clore, 2006; Yamazaki et al., 1995). Compared to the guanidinium NηH2 moieties, Arg 15Nε and 1Hε resonances are relatively easy to assign. When broadband 15N 180° pulses are used, 3D HNCACB for backbone amide groups also gives signals from Arg side chains, which correlate Arg side-chain 1Hε, 15Nε, and 13Cγ/13Cδ resonances (Iwahara & Clore, 2006). Alternatively, the same correlation signals can be observed selectively for Arg side chains by using 15Nε-selective pulses (see Section 2.4.3) in 3D HNCACB. NOE cross-peaks of 1Hε nuclei in 3D 15N-edited NOESY also facilitate resonance assignment for Arg NεH groups. Fig. 4 shows an example of Arg 15Nε and 1Hε resonance assignment based on 13Cγ/13Cδ resonances and NOE data. Some double- or triple-resonance experiments were developed for resonance assignment of Arg side-chain NηH2 groups (Gerecht et al., 2017; Löhr & Rüterjans, 1998; Yamazaki et al., 1995), though this is more challenging due to the above-mentioned hindered 180° rotations that tend to occur in the intermediate exchange regime at physiological temperature.
Fig. 4.

(A) 1H–15N HISQC spectra recorded for the Arg NεH groups of the Antp homeodomain–DNA complex at pH 5.8 and 25°C (Nguyen, Hoffpauir, et al., 2017). (B) Strips of 3D 15N-edited NOESY and broadband HNCACB (Iwahara & Clore, 2006) spectra for some Arg side chains of the Antp homeodomain–DNA complex. The broadband HNCACA spectrum shows correlation of Arg side-chain 1Hε, 13Cγ, 13Cδ, and 15Nε resonances.
2.4.3. Selective 15N Pulses for Lys and Arg Side Chains
The 15N resonances of Lys (~25–35 ppm) and Arg (~65–90 ppm) side chains are significantly different from those of protein backbone (~105–135 ppm). Largely because the practically available RF strength for the 15N channel is relatively weak (up to ~7 kHz), standard 1H–15N NMR experiments optimized for the backbone give significantly compromised signals from Lys and Arg side chains (Iwahara & Clore, 2006; Iwahara et al., 2007). The pulse imperfection for off-resonance 15N nuclei adversely impacts quantitative 1H–15N heteronuclear NMR experiments, particularly measurements of 15N transverse relaxation rates. The simultaneous observation with a reasonably high digital resolution for 15N requires aliasing in the 15N dimension, which can cause accidental overlaps of nonaliased and aliased signals. For these reasons, we typically conduct 1H–15N NMR experiments for the backbone, Arg side chains, and Lys NH3+ groups separately. For selective observation of Lys or Arg side-chain signals, we use 1-ms rSNOB pulses (Kupče et al., 1995) as 15N 180° pulses selective for Lys NH3+ or Arg NεH 15N nuclei. The rSNOB pulse works as an inversion pulse for Nz and as a refocusing pulse for Nx and Ny magnetizations. The bandwidth of a 1-ms rSNOB pulse is approximately ±1.1 kHz and is well suited to selectively observe either Arg 15Nε (75–90 ppm) nuclei or Lys 15Nζ (30–35 ppm; NH3+) nuclei. We incorporate 15N rSNOB pulses into many Lys- or Arg-selective NMR experiments.
2.4.4. Chemical Approach
A chemical approach can be used for resonance assignment of basic side chains that form intermolecular ion pairs with DNA or RNA (Anderson et al., 2015). In this approach, 1H–15N correlation spectra for the basic side chains of the protein–DNA (or RNA) complexes are compared with and without oxygen-to-sulfur substitution in a backbone phosphate group. This chemical modification is relatively mild because it retains the tetrahedral geometry and overall charge of the phosphate group. Thiophosphoramidites, which are commercially available from Glen Research Co., allow synthesis of DNA containing phosphorodithioate using standard DNA synthesizers. Site-specific oxygen-to-sulfur substitution in a backbone phosphate significantly perturbs the NMR chemical shifts of the interfacial cationic group at the modification site and allows one to identify the NMR signal from the interfacial Lys or Arg groups. This approach was demonstrated initially with dithioate derivatives of phosphate (Anderson et al., 2015) and later with monothioate derivatives of phosphate (Nguyen, Zandarashvili, White, & Iwahara, 2016). Although synthesis of DNA/RNA containing a monothioate derivative produces a mixture of RP and SP diastereomers, chromatographic separation of these two forms is possible (Frederiksen & Piccirilli, 2009; Nguyen et al., 2016).
2.5. Sample Conditions for NMR Studies of Lys/Arg Cations
2.5.1. Two Critical Factors: pH and Temperature
A major challenge for NMR studies of Lys NH3+ and Arg NεH groups is their rapid hydrogen exchange with water. For example, the hydrogen exchange rates for Lys NH3+ groups can exceed 1000s−1 at pH 7.5 and 27°C (Segawa et al., 2008). Under such conditions, direct observation of the 1H signals from Lys NH3+ groups is virtually impossible. However, direct 1H detection can become possible if hydrogen exchange is substantially slowed down due to (1) lower pH, (2) lower temperature, or (3) structural effects such as hydrogen bonding and steric hindrance (Esadze et al., 2011; Iwahara et al., 2007; Poon et al., 2006; Takayama et al., 2008; Tomlinson, Ullah, Hansen, & Williamson, 2009). For the feasibility of heteronuclear 1H–15N NMR experiments for Lys and Arg side chains, temperature and pH are two critical factors that should be set carefully.
The dependence of hydrogen exchange rates on pH is particularly strong. In general, a decrease in pH by 1 unit reduces the hydrogen exchange rate by a factor of 10 (Englander, Downer, & Teitelbaum, 1972; Liepinsh & Otting, 1996). For example, if the pH is decreased from 7.5 to 5.8, the hydrogen exchange rates become 50-fold slower. It should be noted that hydrogen exchange rates depend on the buffer used (e.g., slower in a succinate buffer than in a phosphate buffer at the same pH). The temperature dependence of hydrogen exchange rates is also strong. Upon a decrease in temperature by 10°C, hydrogen exchange rates become ~two- to fourfold slower for Lys NH3+ and Arg NεH groups, depending on the activation energy. The temperature dependence of hydrogen exchange seems to be stronger for Arg NεH groups than for Lys NH3+ groups (Segawa et al., 2008). We typically conduct NMR experiments on Lys and Arg side chains at pH 5–6 and 2–35°C.
2.5.2. Coaxial NMR Tubes to Avoid Partial Deuteration by D2O
For quantitative NMR experiments on Lys NH3+ and Arg NεH groups, a D2O for NMR lock should not be included in the sample buffer. In general, the 15N chemical shifts of NH/NH2/NH3+ moieties are significantly different when they are partially deuterated in the form of NHD, NH2D, or NHD2 by D2O. The partial deuteration causes not only additional signals (see Fig. 1B) (Iwahara et al., 2007) but also additional broadening effects on the 15N dimension due to the exchange between 1H-attached and 2H-attached states for which 15N resonances differ (Yuwen & Skrynnikov, 2014a). We use coaxial NMR tubes to resolve the problems arising from deuterated NH/NH2/NH3+ moieties by separating D2O from the sample solution. The sample solution (typically, 0.4–1.0 mM protein) does not contain D2O, and therefore, deuteration of NH/NH2/NH3+ moieties does not occur. Depending on the applications, we use two different configurations of NMR coaxial tubes (Fig. 1C). In one type of NMR coaxial tube (e.g., Shigemi cat. # SC-002), the protein solution is in the inner tube, and D2O is in the outer tube. For this type, we use a sample solution in the inner tube (270 μL) and D2O in the outer tube (~100 μL). In the other type of NMR coaxial tube (e.g., Norell cat. # NI5CCI-B), we use a sample solution in the outer tube (370 μL) and D2O in the inner stem (~ 100 μL). In general, this type of configuration with a thin inner stem gives a higher sensitivity for the same solution, mainly because the sample molarity in the detected region of the tube is higher due to a larger volume. However, a practical problem about this coaxial tube is that shimming is more difficult. Shimming for coaxial tube samples should not rely on deuterium signals because D2O and the sample solution are located in different compartments. In our experience, the gradient shimming method based on H2O imaging (van Zijl, Sukumar, Johnson, Webb, & Hurd, 1994) works fine in the one-dimensional mode but not in the three-dimensional mode to achieve magnetic-field homogeneity of solution samples in coaxial NMR tubes. When a high-salt concentration is required, the configuration with the sample in the inner tube is more suitable for the reason described in some papers on NMR studies of high ionic-strength samples (Takeda et al., 2011; Voehler, Collier, Young, Stone, & Germann, 2006).
2.5.3. Dealkalization of NMR Tubes
Due to the intrinsically rapid hydrogen exchange, the 1H signals from Lys side-chain NH3+ groups are sensitive to an increase in pH. Previously, we often found that a gradual increase in pH occurred over a few weeks in NMR tubes even in the presence of buffer. This increase was noticeable in NMR experiments because the signals from Lys NH3+ groups became significantly weaker or even disappeared due to the more rapid hydrogen exchange. In fact, the original spectra of such samples were restored through buffer exchange. We speculate that the increase in pH might be due to gradual contamination of sodium ions leached from the glass surface through the Na+–H+ exchange mechanism (Bunker, 1994). We found that dealkalization treatment of NMR tubes can prevent the gradual increase in pH. In this treatment, we put 0.5 M nitric acid into coaxial NMR tubes, incubate the tubes in a hot water bath (60–80°C) for 2–3 h, extensively wash the tubes with pure water, and dry them in a heat dryer. We routinely perform this dealkalization for new coaxial tubes before their use for NMR experiments on Lys NH3+ and Arg NεH groups.
3. CONFORMATIONAL DYNAMICS OF Lys/Arg SIDE CHAINS
The 15N NMR relaxation and scalar coupling data of Lys NH3+ and Arg NεH groups can provide information on the mobility of the cationic moieties of these basic side chains. Here, we describe practical aspects of the analysis of the conformational dynamics of Lys and Arg side chains.
3.1. 15N Relaxation Analysis for Lys NH3+ Groups
The theoretical details of the 15N relaxation of Lys side-chain NH3+ groups are somewhat complicated due to cross-correlation within the AX3 spin system and are beyond the scope of this chapter. Readers interested in the theoretical issues regarding the 15N relaxation of Lys NH3+ groups should refer to our previous publication (Esadze et al., 2011). General descriptions of the cross-correlation effects on the NMR relaxation of AX3 spin systems can be found in other articles (Kay & Torchia, 1991; Kumar, Grace, & Madhu, 2000; Ollerenshaw, Tugarinov, & Kay, 2003).
3.1.1. Removal of Adverse Effects of Multispin Terms
Fig. 5 shows the pulse sequences used to measure 15N relaxation for Lys side-chain NH3+ groups. The first step for measuring 15N longitudinal (R1) and transverse (R2) relaxation rates is to create the 15N in-phase single-quantum term via coherence transfer from 1H to 15N nuclei through a refocused INEPT scheme (Ernst, Bodenhausen, & Wokaun, 1987). The product operator terms Nx, 2NyHz, 4NxHzHz, and 8NyHzHzHz are generated in the period of 2τb in the first refocused INEPT scheme of our pulse sequence for 15N R1 and R2 measurements. The 2NyHz and 8NyHzHzHz terms are eliminated by the pulsed field gradient (PFG) g4 after the 1H 90°(−x) and 15N 90°(γ) pulses at the end of the refocused INEPT scheme, but the 4NxHzHz term is not eliminated because a PFG alone cannot destroy the homonuclear zero-quantum coherence 4NzHyHy (van de Ven, 1995). The coefficients of the transfers from 2NyHz to Nx and to 4NxHzHz are given by cos2θsinθ and (3cos2θ − 1)sinθ, respectively, in which θ = 2π 1JNH τb and 1JNH represents the one-bond 1H–15N scalar coupling constant (Ernst et al., 1987). The use of the time τb satisfying 3cos2θ − 1 = 0 thus eliminates the 4NxHzHz term but retains the Nx term, and this condition is achieved by ρb = 2.1 ms in the original pulse sequences (Esadze et al., 2011). This approach was also used for 13C R1 and R2 relaxation measurements for protein CH3 groups (Kay et al., 1992; Palmer, Wright, & Rance, 1991). A practical problem of this approach is that it reduces the efficiency of the transfer from 2NyHz to Nx (i.e., cos2θsinθ) and weakens the signals from NH3+ groups. Recently, we resolved this problem by implementing schemes that eliminate any contributions arising from 4NxHzHz (Nguyen, Lokesh, et al., 2017). The pulse sequences shown in Fig. 5 implement such schemes and allow the use of τb = 1.3 ms to maximize cos2θsinθ, improving the sensitivity by a factor of 1.8 without compromising the accuracy in 15N relaxation measurements (Nguyen, Lokesh, et al., 2017).
Fig. 5.
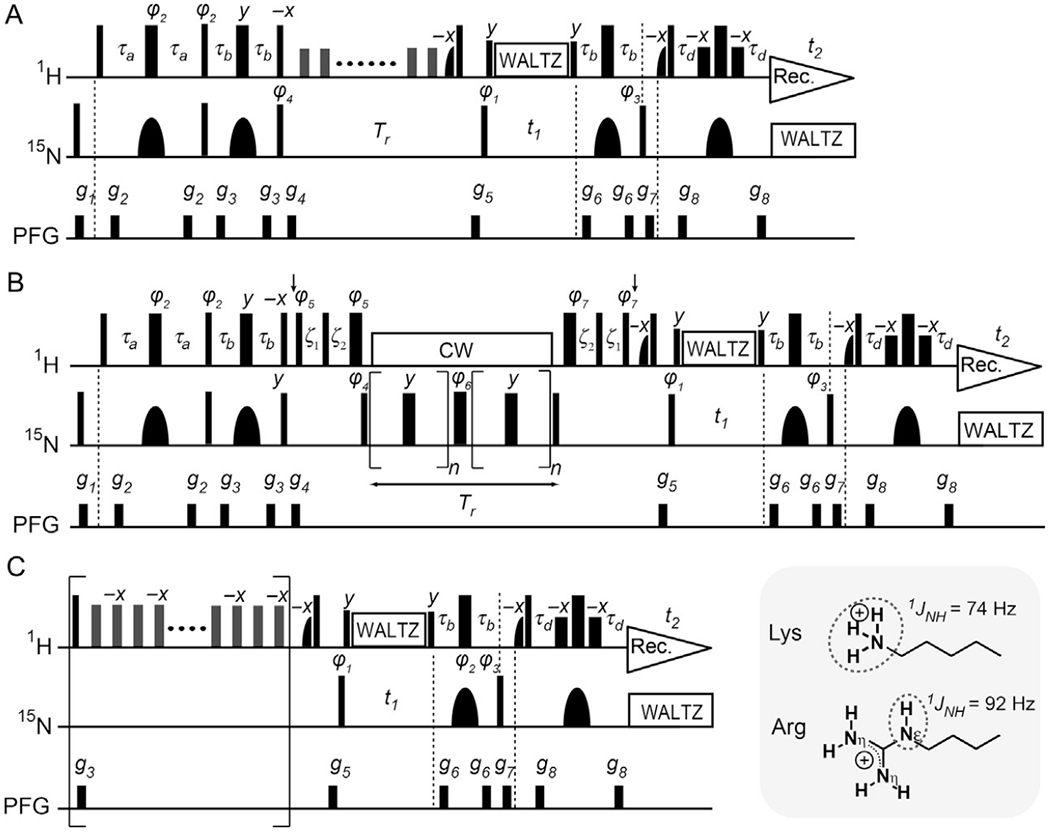
15N relaxation measurements for Lys NH3+ and Arg NεH groups (Esadze et al., 2016, 2011; Nguyen, Lokesh, Volk, & Iwahara, 2017). Symbols representing pulses are the same as those used in Fig. 2C. The delays τa = 2.7 ms and τb = 1.3 ms are used for Lys NH3+ groups, whereas τa = 2.3 ms and τb = 2.7 ms are used for Arg NεH groups. The 15N carrier position is set to ~33 pm for Lys NH3+ groups and to ~85 ppm for Arg NεH groups. The 1H carrier position is set to the H2O resonance. Quadrature detection in the t1 domain was achieved using States-TPPI, incrementing the phase φ1. Although the use of τb = 1.3 ms for Lys NH3+ groups retains 4NxHzHz terms, the impact of these terms is eliminated in other parts of these pulse sequences (Nguyen, Lokesh, et al., 2017). To maintain the in-phase single-quantum 15N coherence, the 1H WALTZ composite pulses are used during the t1 period. (A) 15N longitudinal relaxation measurement. A 1H 180° pulse that does not affect H2O resonance is applied every 10 ms during the delay Tr for longitudinal relaxation. A recycle delay between scans is set to 2 s in this experiment. Phase cycles: φ1 = (2y, 2(−y)), φ2 = (y, −y), φ3 = (4x, 4(−x)), φ4 = (8y, 8(−y)), and receiver = (x, −x, −x, x, 2(−x, x, x, −x), x, −x, −x, x). (B) 15N transverse relaxation measurement. The 1H carrier position is shifted to 7.8 ppm at the position of the first vertical arrow (after the PFG g4) and set back to the position of water resonance at the position of the second arrow. Typically we use the CPMG frequency νCPMG of 417 Hz. For this, the RF strength ωCW/2π of 1H CW during the CPMG is set to 5 kHz, satisfying ωCW/2π = 2kνCPMG (k, integer) (Hansen, Vallurupalli, & Kay, 2008). However, when a lower CPMG frequency is used, a stronger RF strength is required for 1H CW to maintain the in-phase single-quantum 15N coherence during the CPMG scheme. For Arg NεH groups, the CPMG frequency, the RF strength, and 15N carrier position should be set to avoid the recoupling conditions for modulation by 2JNN couplings (Nguyen & Iwahara, 2018). The delays ξ1 and ξ2 are for alignment of 1H magnetization and given by ξ1 = 1/ωCW = (4/π)τ90H and ξ2 = τ90N − (2/π)τ90H (Hansen et al., 2008; Hansen & Kay, 2007), in which τ90 represents the relevant 90° pulse length. A recycle delay of 2.9 s is used. Phase cycles: φ1 = (4y, 4(−y)), φ2 = (8y, 8(−y)), φ3 = x, φ4 = (x, −x), φ5 = (2y, 2 (−y)), φ6 = (2x, 2(−x)), φ7 = (2(−y), 2y), and receiver = (x, −x, x, −x, 2(−x, x, −x, x), x, −x, x, −x). (C) Heteronuclear 1H–15N NOE measurement. Measurement with 1H saturation (5 s) is performed with a train of 180°x and 180°(−x) pulses (RF strength, 11 kHz) at an interval of 10 ms. The reference spectrum is measured without the scheme in the bracket. For measurements of heteronuclear NOE, we set a recycle delay (including the saturation period) to 12s for a 600-MHz spectrometer and to 18s for 750 or 800 MHz spectrometer. Phase cycles: φ1 = (y, −y), φ2 = (4x, 4y, 4(−x), 4(−y)), φ3 = (2x, 2(−x)), and receiver = (x, −x, −x, x, −x, x, x, −x).
3.1.2. 15N R1 Relaxation Measurements for Lys NH3+ Groups
The 15N R1 relaxation rates of Lys side-chain NH3+ groups are typically 0.2–1.5 s−1 at the 1H frequencies of 600–800 MHz. To measure the Lys 15N R1 rates with the pulse sequence shown in Fig. 5A, we typically record eight spectra in an interleaved manner with different lengths for the relaxation period Tr (=0.1, 0.2, 0.4, 0.6, 0.9, 1.2, 1.6, and 2.1 s). The minimum delay, Tr = 0.1 s, is long enough to let the 4NzHyHy term completely decay through its rapid relaxation (Nguyen, Lokesh, et al., 2017). We record the eight datasets in an interleaved manner, typically with 16 scans per free induction decay (FID) using a cryogenic probe. The total time for recording is ~20–30 h. The 15N R1 rates are determined through nonlinear least-squares fitting with a single exponential function.
3.1.3. 15N R2 Relaxation Measurements for Lys NH3+ Groups
Owing to rapid Cε–Nζ bond rotations, the Lys side-chain NH3+ groups exhibit very slow 15N transverse relaxation. For the protein–DNA complexes we studied (17–30 kDa), while 15N T2 relaxation times for the protein backbone NH groups were 50–80 ms, those for the Lys NH3+ groups were typically >300 ms even for the Lys side chains that form ion pairs with DNA. Fig. 5B shows the pulse sequence for the 15N transverse relaxation measurement, in which the CW-CPMG scheme (Hansen et al., 2008) is implemented to maintain the in-phase single-quantum coherence N+. This scheme contains two CPMG blocks (Carr & Purcell, 1954; Meiboom & Gill, 1958) that sandwich a refocusing pulse, and the 1H continuous wave (CW) is applied to eliminate scalar relaxation during each CPMG blocks. As is known for 13C transverse relaxation for CH3 groups, the 15N transverse relaxation for NH3+ groups should intrinsically be biexponential due to the strong effects of DD–DD cross-correlation between three 15N–1H DD interactions (Esadze et al., 2011). However, the biexponential decay and single-exponential decay according to exp(−R2,iniT) are virtually indistinguishable for the first 30% of decay, for which the use of single-exponential fitting for determination of the initial transverse relaxation rate R2,ini is valid (Esadze et al., 2011). The theoretical expression of the R2,ini rate is formulated in Esadze et al. (2011), and its practical use is described below (Section 3.3). Due to the use of only <30% decay, measurements of R2,ini rates for Lys NH3+ groups are typically not as precise as those of R1 rates in terms of error percentage. To compensate for this problem, we measure the 15N R2,ini rates using a larger number of scans (32 scans per FID) than that for 15N R1 measurements. We typically record nine spectra in an interleaved manner with different lengths for the transverse relaxation period (up to 120 ms). The total time for recording 15N transverse relaxation data for Lys NH3+ groups is ~35–50 h.
The pulse sequence shown in Fig. 5B can also be used to detect microsecond to millisecond timescale motions of NH3+ groups (Esadze et al., 2011) because the CW-CPMG scheme is well suited for relaxation dispersion experiments (Baldwin, Hansen, Vallurupalli, & Kay, 2009; Hansen et al., 2008). In fact, the relaxation dispersion data recorded with various CPMG frequencies in this pulse sequence were used to study the slow dynamics of Lys NH3+ groups (Esadze et al., 2016, 2011).
3.1.4. Heteronuclear 15N NOE for Lys NH3+ Groups
Due to rapid Cε–Nζ bond rotations, heteronuclear NOEs for Lys side-chain NH3+ groups are negative and typically ranges from −1.8 to −3.3. The pulse sequence to record heteronuclear 15N NOE data for Lys NH3+ groups is shown in Fig. 5C (Esadze et al., 2011; Nguyen, Lokesh, et al., 2017). The effects of DD/DD cross-correlation, which causes transitions between Nz and 4NzHzHz terms and between Hz and 4NzHzHz terms, are simplified by using 180° pulses instead of 120° pulses in the 1H saturation period (Esadze et al., 2011). Incomplete recovery of water 1H magnetization can introduce substantial errors in the heteronuclear NOEs and this problem is particularly serious when hydrogen exchange is rapid (Grzesiek & Bax, 1993; Idiyatullin, Daragan, & Mayo, 2001; Li & Montelione, 1994; Skelton et al., 1993). In the pulse sequence shown in Fig. 5C, this problem is avoided by implementation of the water-flip-back scheme (Grzesiek & Bax, 1993) and the use of a very long recycle delay (Renner, Schleicher, Moroder, & Holak, 2002). Our recycle delays in the heteronuclear NOE experiments for Lys NH3+ groups are 12 and 18 s at the 1H frequencies of 600 and 800 MHz, respectively. If a shorter time is used, the magnitude of heteronuclear NOE may appear to be larger due to weaker signal intensity in the reference spectrum. With 48 scans per FID and 100 complex points for each subspectrum, the total recording time is typically ~55–80h.
3.2. 15N Relaxation Analysis for Arg NεH Groups
3.2.1. NMR Relaxation Measurements for Arg 15Nε Nuclei
The pulse sequences shown in Fig. 5 can be used to measure 15N R1, R2, and heteronuclear NOE for Arg side-chain NεHε groups as well, though changes in some parameters are required due to the differences between Lys NH3+ and Arg NεH groups. The caption of Fig. 5 shows the required changes, many of which are related to the different spin systems (AX3 vs AX) and 1JNH coupling constants (74 vs 92 Hz) of Lys NH3+ and Arg NεH groups. In the 15N relaxation measurements for Arg NεH groups, we typically use a 15N carrier position at ~84ppm and a 15N spectral width of ~6–12ppm. These settings together with the use of 15N rSNOB 180° pulses in the INEPT schemes allow 15N relaxation measurements for Arg side-chain 15Nε nuclei only. Although simultaneous detection of Arg side-chain 15Nε and backbone 15N nuclei is possible, separate measurements have the following advantages. First, selective observation of Arg 15Nε allows the use of a narrower 15N spectral width for a high resolution without any concerns about undesired overlaps with folded signals from backbone NH or Lys NH3+ groups. Second, R2 measurements with the 15N carrier position set to the Arg Nε resonance allow application of on-resonance 180° pulses in the CPMG scheme. Simultaneous R2 measurements of backbone and Arg side-chain 15N nuclei require the use of a 15N carrier position that introduces significant off-resonance effects to the CPMG scheme (Korzhnev, Tischenko, & Arseniev, 2000) and decrease the data quality for either type of 15N nuclei. Furthermore, selective observation of Arg NεH groups allows higher sensitivity because the conditions optimized for backbone NH groups considerably weaken the signals from Arg NεH groups unless broadband 15N 180° pulses are used (Iwahara & Clore, 2006). For these reasons, we conduct the 15N relaxation experiments for backbone NH groups, Lys NH3+ groups, and Arg NεH group separately.
3.2.2. Impact of 15N–15N Couplings on Arg 15Nε R2 Measurements
The presence of two geminal couplings to 15Nη1 and 15Nη2 nuclei can in principle affect measurements of transverse relaxation of Arg 15Nε nuclei. However, our recent study shows that the impact of the 2JNN couplings on CPMG-based transverse relaxation measurements for Arg 15Nε nuclei is typically negligible (Nguyen & Iwahara, 2018). This result is due to the relatively small magnitudes of the 2JNN couplings (1.1–1.3 Hz) and also due to the so-called SITCOM mechanism (Dittmer & Bodenhausen, 2006) that efficiently quenches homonuclear J modulation. The use of selective refocusing pulses (e.g., REBURP) in the CPMG scheme was previously proposed to avoid modulation through the homonuclear 15N–15N scalar couplings (Yuwen & Skrynnikov, 2014b). However, the use of long shaped pulses during the CPMG scheme allows only low νCPMG frequencies, which may not completely cancel the exchange contribution to the measured R2 relaxation rates. Such use of 15Nε-selective shaped pulses during the CPMG scheme is unnecessary because the SITCOM effect effectively quenches the evolution of 2JNN couplings of Arg side chains during the CPMG scheme with typical rectangular 15N 180° pulses. However, the 15Nε R2 rates may be overestimated for very mobile Arg side chains, if the following condition (recoupling condition) (Aeby & Bodenhausen, 2008) is accidentally met:
| (1) |
where n is an integer; ΩS/(2π), the offset in Hz for off-resonance spin S; ν1, the RF strength in Hz for refocusing pulses; νCPMG, the CPMG field frequency in Hz. When ν1 ≫ νCPMG, Eq. (1) becomes ΩS/(2π) ≈ 2nνCPMG. When the difference between ΩS/(2π) and the nearest recoupling condition is less than 10% of νCPMG, significant amplitude modulation occurs and the apparent R2 rate becomes larger than the actual R2 relaxation rate. Not surprisingly, this adverse effect is weaker for a smaller magnitude of the homonuclear J coupling. When ΩS/(2π) is more significantly different from the recoupling conditions, effectively complete quenching of J-modulation occurs, allowing accurate measurements of the R2 rates. Recoupling conditions can be readily avoided through appropriate settings of the CPMG frequency νCPMG, the RF strength ν1, and the 15N carrier position.
3.2.3. 15Nε Relaxation Analysis Using Direct 13Cζ Detection
Hansen and coworkers analyzed Arg side-chain 15Nε relaxation through direct detection of 13Cζ nuclei (Werbeck, Kirkpatrick, & Hansen, 2013). A remarkable advantage of this approach is that it can be used at any pH because rapid hydrogen exchange does not impact 13Cζ detection. In fact, this method was successfully applied to a 42-kDa protein at pH 8.2. 1H detection of Arg side-chain NεH groups at this pH is virtually impossible due to the rapid hydrogen exchange with water. Because the 13Cζ resonances are unaffected by hydrogen exchange, 15Nε relaxation analysis through direct 13Cζ detection is possible. A drawback of this method is that it provides relaxation rates for 2CzNx and 2CzNz terms but not those for Nx and Nz terms. Werbeck et al. demonstrated that the order parameters determined using this method agree well with those determined using the standard 15N relaxation method.
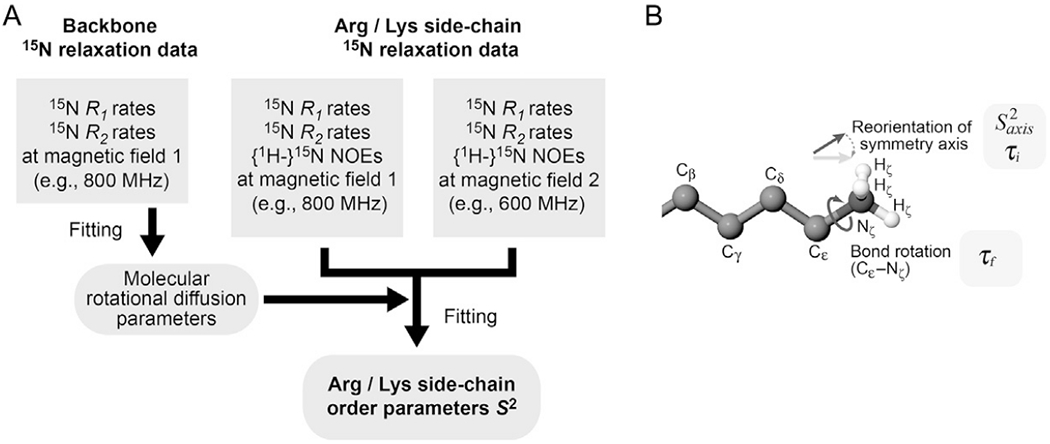
3.3. Determination of Lys/Arg Side-Chain Order Parameters
3.3.1. Overall Procedures
The 15N relaxation data for Lys and Arg side chains at multiple magnetic fields are used to calculate order parameters for relevant bonds. The overall procedures for this calculation are shown in Fig. 6A. To determine the order parameter and the correlation times for internal motions, the following function is minimized for each side chain:
| (2) |
where Yobs and Ycal stand for the observed and calculated quantities. The squared difference terms are summed for different types of relaxation parameters (i.e., R1, R2, and NOE) and for different magnetic fields. The use of multiple magnetic fields is important because up to three parameters for internal motions are optimized. Based on availability of our NMR spectrometers, we typically combine 15N relaxation data at 600 and 800 MHz for Lys NH3+ groups, and combine those at 600 and 750 MHz for Arg NεH groups. In Eq. (2), 1/w2 corresponds to the weight of each squared difference (Yobs − Ycal)2. For this kind of fitting calculation, two different weights have been used: w = Yobs (e.g., Dellwo & Wand, 1989; Nicholson et al., 1992) or w = σ, where σ represents the uncertainty in Yobs (e.g., Mandel, Akke, & Palmer, 1995; Palmer, Rance, & Wright, 1991). Although the latter approach may seem to be more reasonable, it is not necessarily the case when there is bias causing a large systematic error in Yobs that deviates from the true value. An example of such bias is on NOE data impacted by the saturation transfer effect (Grzesiek & Bax, 1993; Li & Montelione, 1994). The approach using w = Yobs is safer if some systematic errors may exist in the experimental data. Calculation of Ycal requires the use of an appropriate spectral density function relevant to the 15N relaxation parameters. The parameters involved in the spectral density function are optimized through minimization of the sum of the squared differences represented by Eq. (2).
Fig. 6.
(A) Procedures for determination of the order parameters S2 for Lys and Arg side chains. (B) Motion model for Lys side-chain NH3+ groups.
3.3.2. Determination of Molecular Rotational Correlation Time
Calculation of Ycal in Eq. (2) requires the molecular rotational correlation time. However, the 15N relaxation data of Lys and Arg side chains are not suitable for determination of the molecular rotational correlation time because many Lys and Arg side chains are highly flexible and internal motions govern the 15N relaxation parameters. Therefore, the molecular rotational correlation time is determined using backbone 15N R1 and R2 relaxation data for rigid regions of the same protein under the identical conditions. For calculations of rotational diffusion anisotropy, the atomic coordinates of the 3D structure are also required. In many cases, the axially symmetric diffusion model (Woessner, 1962) is suitable for the rotational diffusion calculation. Through nonlinear least-squares fitting, rotational diffusion parameters (D∥, D⊥, and two polar angles for the main principal axis) for the axially symmetric diffusion model are determined from the R1/R2 ratio data for backbone 15N nuclei (Tjandra, Feller, Pastor, & Bax, 1995). For this calculation, we use a C program (Iwahara, Peterson, & Clubb, 2005). The effective rotational correlation time τr,eff and the anisotropy of the rotational diffusion r are given by (2D∥ + 4D⊥)−1 and D∥/D⊥, respectively (Woessner, 1962). The effective rotational correlation time τr,eff is used as a fixed-value parameter to calculate Ycal when Lys/Arg side-chain order parameters are determined through minimization of Eq. (2).
3.3.3. Determination of Lys NH3+ Order Parameters
The spectral density function for dipole–dipole (DD) autorelaxation of the 15N nucleus in an NH3+ group is given by (Esadze et al., 2011):
| (3) |
where ; μ0, the vacuum permeability; h, Planck’s constant; γ, the nuclear gyromagnetic ratio; rij, the N–H distance; , the generalized order parameter for the symmetry axis of the NH3+ group; τm, the overall molecular rotational correlation time; ; ; ; τi, the correlation time for reorientation of the symmetry axis; and τf, the correlation time for bond rotation around the symmetry axis. Fig. 8B depicts the physical meanings of the parameters , τf, and τi. The spectral density function of Eq. (3) is a modification of Eq. (15) of Kay and Torchia (1991) for CH3 groups, and is derived from the product of correlation functions for overall motions, internal motions of symmetry axis, and bond rotation (Esadze et al., 2011). The total number of parameters involved is identical for these equations and if τi ≫ τf, the equations become the same. Eq. (3) is more general because it is applicable even when the inequality τi ≫ τf does not hold. This aspect of Eq. (3) is important because hydrogen bonds may slow down the bond rotation and make τi < τf. The 15N relaxation through CSA is negligible because |σ∥ – σ⊥| is as small as 15 ppm for Lys NH3+ groups (Sarkar et al., 1987). With the spectral density function jDD(ω), the 15N relaxation parameters of the NH3+ group are given by:
| (4) |
| (5) |
| (6) |
Fig. 8.
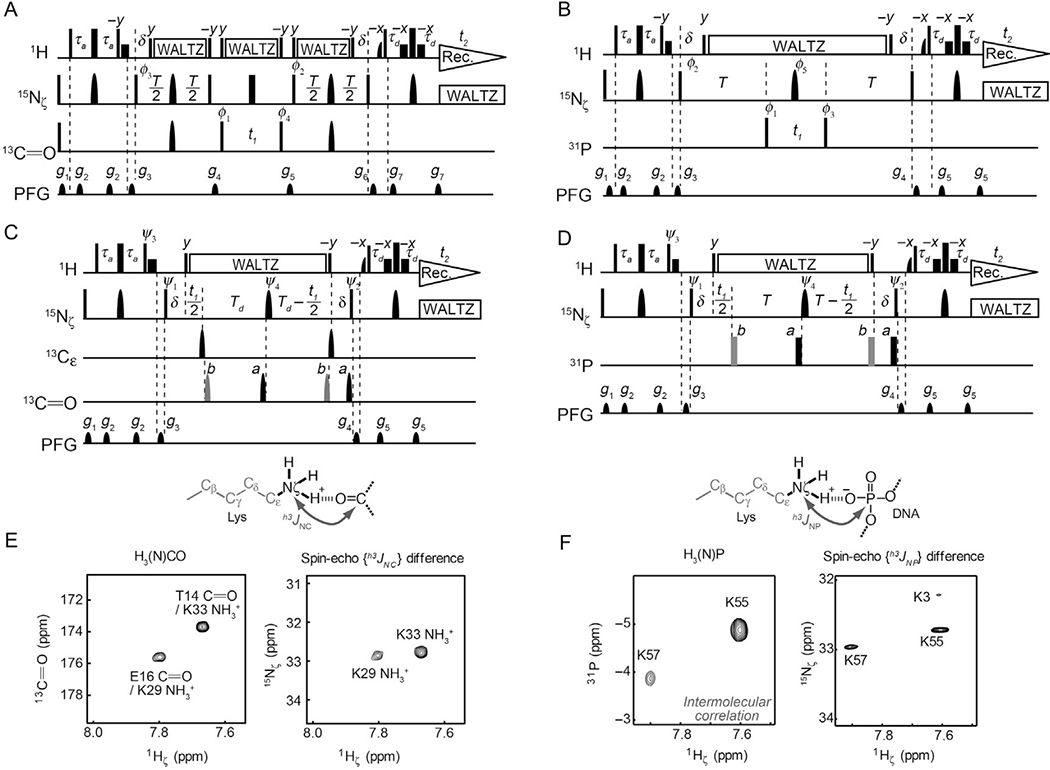
NMR experiments for observing hydrogen-bond scalar couplings of Lys NH3+ groups (Anderson et al., 2013; Zandarashvili et al., 2011). (A, B) 2D heteronuclear correlation experiments to observe signals arising from hydrogen-bond scalar couplings. Resonances of the coupling partner nuclei (13C═O for (A) and 31P for (B)) are directly observed in these experiments. Symbols representing pulses are the same as those used in Fig. 2C. Shaped 13C pulses represent IBURP-2 180° pulses (1.1 ms). Delays: τa = 2.7 ms; δ = 2.6 ms, T = 212 ms; and Td = 206 ms. Carrier positions: 1H, the position of the water resonance; 15N, 33 ppm; 13Cε, 45 ppm; 13C═O, 177 ppm; and 31P, −3ppm (31P referencing to trimethyl phosphate). Phase cycles: φ1 = (2x, 2(−x)), φ2 = (4x, 4(−x)), φ3 = (x, −x), φ4 = (8x, 8(−x)), φ5 = (8x, 8y, 8(−x), 8(−y)), and receiver = (x, −x,− x, x, 2(−x, x, x, −x), x, −x, −x, x). Quadrature detection in the t1 domain was achieved using States-TPPI for φ1. (C, D) 2D spin-echo J-modulation constant-time HISQC experiments to measure the magnitude of h3JNC (C) or h3JNP (D) couplings. Phase cycles: ψ1 = (2x, 2 (−x)), ψ2 = (4x, 4(−x)), ψ3 = (y, −y), ψ4 = (8x, 8y, 8(−x), 8(−y)), and receiver = (x, −x, −x, x, 2(−x, x, x, −x), x, −x, −x, x). Quadrature detection in the t1 domain was achieved using States-TPPI for ψ1. (E) Observation of h3JNC couplings for the Lys NH3+ groups of ubiquitin (Zandarashvili et al., 2011). (F) Observation of intermolecular h3JNP couplings between Lys side-chain 15N and DNA 31P nuclei (Anderson et al., 2013). For the spin-echo J-modulation data, the difference spectra (i.e., subspectrum b minus subspectrum a) are shown to demonstrate the presence of the hydrogen-bond scalar couplings, although the magnitudes of these couplings are determined using the signal intensities in the individual subspectra, as described in Section 4.1.
For calculations of the order parameters and the internal motion correlation times for Lys NH3+ groups, the complete source code of the Mathematica® script is available in the supporting information of Esadze et al. (2011). This script does not take the anisotropy of molecular rotational diffusion into consideration because the rotational anisotropy exerts only very minor effects on 15NH3+ relaxation, as is evident from Eq. (6) of Tjandra et al. (1995) and the small overall order parameters (i.e., ) for NH3+ groups.
3.3.4. Determination of Arg NεH Order Parameters
Since each Arg side-chain group can be regarded as an AX spin system, the relaxation parameters of Arg 15Nε nuclei can be analyzed using the same equations as those for backbone 15N nuclei. Therefore, computer programs to calculate the order parameters and the correlation times for the internal motions of backbone NH groups [e.g., the ModelFree program by Palmer (Mandel et al., 1995); the Mathematica® script by Spyracopoulos (Spyracopoulos, 2006)] can be used to compute the corresponding model-free parameters for Arg NεH groups. However, it should be noted that different settings are required for the 15N CSA values and the 15N–1H distance rNH of Arg side-chain NεH groups: |σ∥ − σ⊥| = 114 ppm and rNH = 1.04 Å should be used for Arg side-chain 15Nε nuclei (Trbovic et al., 2009), whereas |σ∥ − σ⊥| = 170 ppm and rNH = 1.02 Å are typically used for backbone 15N nuclei (Tjandra, Szabo, & Bax, 1996).
3.3.5. Different Dynamic Properties of Lys and Arg Side Chains
To show typical ranges of Lys/Arg side-chain order parameters, the data for the Lys and Arg side chains of the Antp homeodomain and the Egr-1 zinc-finger protein in the free and DNA-bound states are shown in Fig. 7. Note that the order parameters of Lys NH3+ groups are defined for the C3 symmetry axis, which corresponds to the Cε–Nζ bond. Although the same number of rotatable bonds (i.e., four covalent bonds) is involved between Lys Cα and Cε atoms and between Arg Cα and Nε atoms, the ranges of the measured order parameters were remarkably different for Lys Cε–Nε and Arg Nε–Hε bonds. Compared to Lys Cε–Nε bonds, Arg Nε–Hε bonds exhibited a wider range of order parameters as well as larger changes in order parameters upon binding to DNA. The mobility of Arg side chains seems to be more sensitive to the surrounding environment, compared to Lys side chains.
Fig. 7.
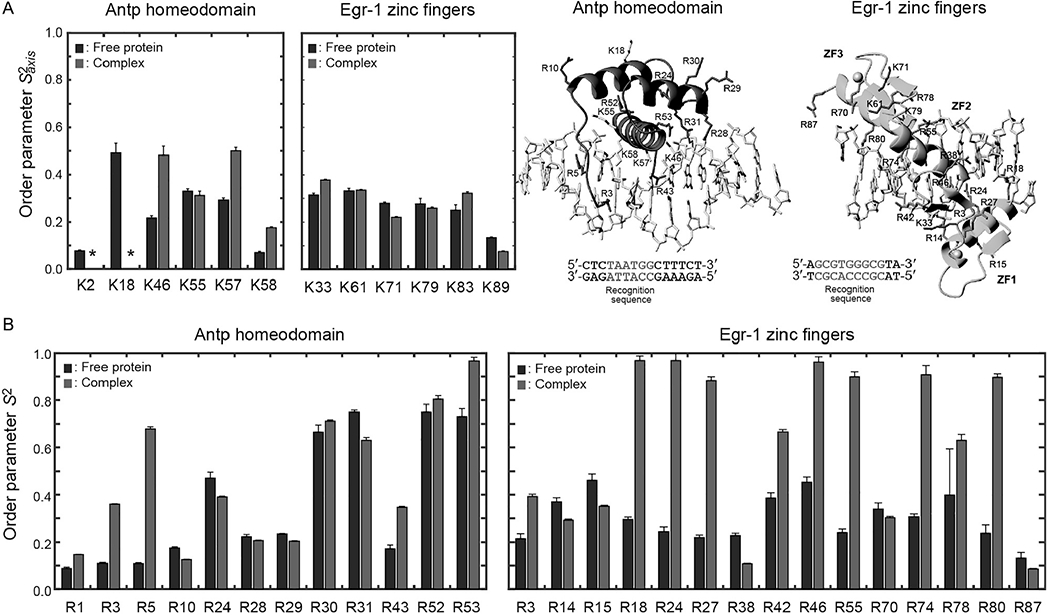
Lys and Arg side-chain order parameters determined for the Egr-1 zinc-finger protein and the Antp homeodomain in the free form and in the complexes with specific DNA (Esadze et al., 2016; Nguyen, Hoffpauir, et al., 2017).
3.4. 3JCN Measurements to Analyze Side-Chain Dynamics
Three-bond J-coupling data reflect the dynamics of torsion angles (Chou, Case, & Bax, 2003; Perez, Löhr, Rüterjans, & Schmidt, 2001; Zandarashvili et al., 2011). Those between 15N and 13C nuclei are relatively easy to measure using quantitative J-modulation experiments. The spin-echo J-modulation constant-time HSQC or HNCG experiments (Hu & Bax, 1997) can be used to measure the 3JNC couplings between backbone 15N and side-chain 13Cγ nuclei relevant to χ1 angles of Lys and Arg side chains and other side chains. For 3JCN couplings between Lys 13Cγ and 15Nζ nuclei relevant to χ4 angles can be measured through the spin-echo 3JCN-modulation constant-time HISQC experiment selective for NH3+ groups (Zandarashvili et al., 2011). The 3JCN coupling constants are typically less than 0.5–3 Hz. The precision of the measured coupling constants 3JCN relevant to χ4 angles is high owing to the very slow 15N relaxation of the Lys NH3+ groups allowing the use of a long period for J-modulation. 3JCN data can be interpreted by means of the Karplus equation (Karplus, 1959) together with empirical parameters (see Section 5.1). Due to the conformational fluctuation, the experimental 3JNC data agree better with those predicted from MD trajectories than with those calculated from crystal structures (see Section 5.1).
4. ION PAIRS AND HYDROGEN BONDS INVOLVING Lys/Arg SIDE CHAINS
NMR studies of Lys and Arg side chains provide unique information on electrostatic interactions, hydrogen bonds, and their dynamics. Recent NMR studies illuminated the dynamic nature of short-range electrostatic interactions via ion pairs (also known as salt bridges).
4.1. Hydrogen-Bond Scalar Couplings
4.1.1. Heteronuclear Correlation via Hydrogen-Bond Scalar Couplings
Hydrogen-bond scalar couplings reflect the orbital overlaps in hydrogen bonds and provide unique information about hydrogen bonding (Grzesiek, Cordier, Jaravine, & Barfield, 2004). Hydrogen-bond scalar couplings provide direct evidence of hydrogen bonds and, in fact, are included in IUPAC’s recently updated criteria for hydrogen bonds (Arunan et al., 2011). Hydrogen-bond scalar couplings can also provide information about dynamics because these couplings are influenced by the transient distortion or breakage of the hydrogen bonds as well (Jaravine, Alexandrescu, & Grzesiek, 2001; Markwick, Sprangers, & Sattler, 2003; Zandarashvili et al., 2016, 2011).
Owing to the very slow 15N transverse relaxation of NH3+ groups, which permits the use of a long period for J-modulation, hydrogen-bond scalar coupling constants in the range of 0.1–1.0 Hz can readily be measured for Lys side chains of midsize (~30kDa) systems studied by NMR. This allows direct detection and characterizations of hydrogen bonds involving Lys NH3+ by NMR. Fig. 8A and B shows the NMR pulse sequences for observing 15N–13C or 15N–31P scalar couplings across hydrogen bonds involving Lys NH3+ groups (Anderson et al., 2013; Zandarashvili et al., 2011). The F2 dimension corresponds to 1Hζ resonances of the NH3+ groups, and the F1 dimension corresponds to 13C or 31P resonances of nuclei coupled to Lys 15Nζ. Some examples are shown in Fig. 8E and F. The h3JNP couplings with DNA phosphate 31P nuclei were observed for the interfacial Lys side chains of several protein–DNA complexes (Anderson et al., 2013, 2015; Chen et al., 2015; Esadze et al., 2016; Zandarashvili, Esadze, et al., 2015; Zandarashvili, Nguyen, et al., 2015).
4.1.2. Determination of Hydrogen-Bond Scalar Coupling Constants
Although the abovementioned heteronuclear correlation spectra via hydrogen-bond scalar couplings are useful to identify the acceptor groups for the hydrogen bonds of Lys NH3+ groups, these spectra do not provide quantitative information on the hydrogen-bond scalar couplings. The values of |h3JNC| or |h3JNP| can be determined using the spin-echo h3J-modulation constant-time HISQC experiments selective for NH3+ groups (Fig. 8C and D) (Anderson et al., 2013; Zandarashvili et al., 2011). In these experiments, two subspectra are recorded in an interleaved manner: one with the 13C or 31P 180° pulses at position a (subspectrum a) and the other at position b (subspectrum b). The values of |h3J| can be calculated from Ia/Ib = cos2πJ(Td + δ), in which Ia and Ib represent signal intensities in subspectra a and b, respectively. For h3JNP coupling, we use a cryogenic 1H/13C/15N/31P QCI probe (Bruker) operated at the 1H frequency of600 MHz. This probe is well suited to study hydrogen-bond scalar couplings involving DNA/RNA 31P nuclei. Using this probe, we were also able to observe h3JNP and h2JHP couplings between zinc-coordinating His side-chain 1H/15N and DNA phosphate 31P nuclei in the Egr-1 zinc-finger–DNA complex as well (Chattopadhyay, Esadze, Roy, & Iwahara, 2016).
4.2. Dynamic Ion Pairs and Hydrogen Bonds
4.2.1. Dynamic Hydrogen Bonding and Ion Pairing
Although one may expect that side chains forming hydrogen bonds and/or ion pairs could be immobilized, recent NMR data show that this situation is not always the case for basic side chains (Anderson et al., 2013; Chen et al., 2015; Esadze et al., 2016; Nguyen, Hoffpauir, et al., 2017; Trbovic et al., 2009; Zandarashvili et al., 2011). Hydrogen bonds involving basic side chains can rapidly break and form, depending on the energy barriers involved. If the breakage and formation of hydrogen bonds occur on a picosecond–nanosecond timescale, the NMR order parameters and internal motion correlation times reflect the hydrogen-bond dynamics. A recent NMR study on the temperature dependence of the Lys side-chain 15N relaxation suggested that the free energy of activation (ΔG‡) is as small as 2–5 kcal/mol for breaking hydrogen bonds of Lys NH3+ groups, though the enthalpy of activation (ΔH‡) is as large as 5–14kcal/mol (Zandarashvili & Iwahara, 2015). Recent NMR studies showed that the Lys NH3+ groups interacting with DNA phosphate groups exhibit small order parameters and sizable h3JNP couplings, indicating the coexistence of high mobility and hydrogen bonding (Anderson et al., 2013; Chen et al., 2015; Esadze et al., 2016; Nguyen, Hoflpauir, et al., 2017). This somewhat puzzling behavior can be understood in terms of the dynamic equilibrium between the contact ion-pair (CIP) and solvent-separated ion-pair (SIP) states (Iwahara, Esadze, & Zandarashvili, 2015), as described in Section 5.2. It should be noted that the CIP–SIP transitions do not decouple (but do attenuate) the h3JNP couplings between the Lys 15N and DNA 31P nuclei as long as the |α〉 or |β〉 spin states of the coupled 31P nuclei are largely maintained during the h3JNP evolution period for the 15N coherence. Small order parameters of the interfacial Lys NH3+ groups can also be explained by the CIP–SIP transitions occurring on a pico-to-nanosecond timescale, as suggested by MD simulations (Chen et al., 2015; Esadze et al., 2016).
4.2.2. Self-decoupling Due to Molecular Dissociation
Hydrogen-bond scalar couplings are very useful data that represent direct evidence of hydrogen bonds. However, it should be noted that the intermolecular hydrogen-bond scalar couplings between two molecules can be observed only when the residence time of the complex is sufficiently long. When the residence time is shorter than or comparable to 1/(πhJ), the self-decoupling effect makes the apparent coupling constant smaller than hJ. We recently studied the self-decoupling effect theoretically and experimentally (Zandarashvili et al., 2016). Self-decoupling is easy to qualitatively understand. Consider a protein side-chain 15N nuclei coupled to DNA phosphate 31P nuclei for example. In solution, the protein can dissociate from a DNA molecule and associate with another DNA molecule of the same kind. When this happens, the spin state of the interacting 31P nuclei can change from |α〉 to |β〉 or vice versa. Therefore, rapid translocation of the protein effectively mixes the |α〉 to |β〉 spin states of the coupled 31P nuclei and causes decoupling of h3JNP for protein 15N nuclei. A Liouville equation description allows the self-decoupling effect of intermolecular hydrogen-bond scalar coupling to be quantitatively analyzed and gain information about the residence time of macromolecular complexes. This approach was demonstrated for intermolecular hydrogen-bond scalar couplings between Lys side-chain 15N and DNA 31P nuclei measured for protein–DNA complexes at various ionic strengths (Zandarashvili et al., 2016). The self-decoupling-based method is unique in that it does not require different chemical shifts for the interconverting states, while such conditions are crucial for other NMR methods for kinetic investigations of protein–DNA interactions (Iwahara, Zandarashvili, Kemme, & Esadze, 2018). Although self-decoupling is typically regarded as a nuisance in NMR scalar coupling measurements (Cavanagh et al., 2007; Harbison, 1993; Kuboniwa, Grzesiek, Delaglio, & Bax, 1994), the quantitative analysis of self-decoupling presents a useful tool for kinetic investigations of processes that accompany breakage of intermolecular hydrogen bonds.
5. DATA INTERPRETATION FACILITATED BY MOLECULAR DYNAMICS SIMULATIONS
NMR spectroscopy can provide atomic-level information about the structures and dynamics of proteins and their complexes, but experimental data are available only for particular analyzable atoms of proteins. In contrast, MD simulations can give information on all atoms of the system including solvent molecules and free ions, but the computational studies are based on empirical models that need experimental validation, especially for electrostatic interactions. NMR and MD are complementary in this sense. MD simulations have greatly facilitated the interpretation of NMR data on basic side chains and their electrostatic interactions (Chen et al., 2015; Esadze et al., 2016, 2011; Trbovic et al., 2009; Zandarashvili et al., 2011). In what follows, we describe how MD simulations can facilitate the interpretation of NMR data on basic side chains.
5.1. NMR vs MD for Dynamics of Basic Side Chains
5.1.1. Lys/Arg Side-Chain Order Parameters From MD Trajectories
The calculation of order parameters from MD trajectories and comparison of experimental and computational order parameters have been conducted since 1980s (Chatfield, Szabo, & Brooks, 1998; Levy et al., 1985; Lipari, Szabo, & Levy, 1982). However, it is only recently that NMR- and MD-derived order parameters were compared for cationic moieties of basic side chains (Chen et al., 2015; Esadze et al., 2016, 2011; Trbovic et al., 2009). For such comparison, the behavior of Lys Cε–Nζ and Arg Nε–Hε bonds in the MD trajectories should be analyzed. Lys Cε–Nζ bonds are used because the NMR order parameter for each Lys side-chain NH3+ is defined for its symmetry axis.
The dynamic behavior of a bond vector from MD trajectories can be studied by calculating the autocorrelation function for internal motions CI(t). This function is given by (Case, 2002; Lipari & Szabo, 1982):
| (7) |
where μ(t0)μ(t0+t) is the projection of a unit vector pointing along a bond vector at time t0 onto itself at time t0 + t; P2(x) = (3x2 − 1)/2 is the second Legendre polynomial; and the brackets denote a time average over the trajectory. The trajectory frames are superimposed onto an optimal (in the least squares sense) common reference frame to remove the effects of overall tumbling and translation. Then, the time dependence of the autocorrelation for the reorientational motion is better described in Clore’s extended model-free formulism (Clore et al., 1990):
| (8) |
where and τf correspond to the amplitude and correlation time due to fast librational motion; and S2 and τi are the order parameter and correlation time of the reorientational motion of a bond vector. Using a single exponential in the case of methyl group dynamics is often satisfactory (Frederick, Sharp, Warischalk, & Wand, 2008), while for the more chemically complex basic side chains, we found that method of analysis gave poor results. The implication is that these side chains have a rich dynamical range of motion and are strongly coupled to their surroundings with varied time scales. Some CI(t) functions calculated for the Lys Cε–Nζ and Arg Nε–Hε bonds of the Egr-1 zinc-finger protein bound to its target DNA are shown in Fig. 9A. Use of sufficiently long (on μs order) MD trajectories is important for accurate computation of the order parameters (Bowman, 2016). This seems to be particularly important for the analysis of Arg side chains because we noticed that the CI(t) functions for Arg Nε–Hε bonds tend to exhibit slow convergence or decay.
Fig. 9.
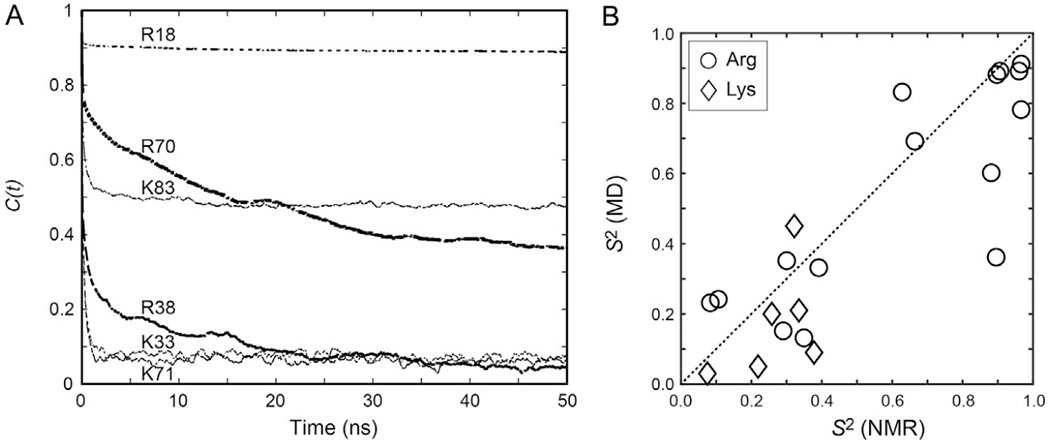
Comparison of NMR-derived vs MD-derived order parameters for the Lys and Arg side chains of the Egr-1 zinc-finger protein bound to its target DNA. (A) Examples of autocorrelation functions calculated for Lys Cε–Nζ and Arg NεH bonds from 0.6-μs MD trajectories. (B) Correlation between the NMR-derived and MD-derived order parameters for the Lys NH3+ and Arg NεH groups of the Egr-1–DNA complex.
The correlation between the NMR and MD order parameters for the Lys and Arg side chains of the Egr-1 zinc-finger protein bound to its target DNA is shown in Fig. 9B. In general, the order parameters calculated from MD trajectories tend to be smaller than the NMR-derived order parameters, as pointed out by Brüschweiler and coworkers (Gu, Li, & Brüschweiler, 2014). This is because the impact of CI(t) on the overall correlation function relevant to NMR relaxation is scaled by exp(−t/τr) (Lipari & Szabo, 1982), thereby making NMR data insensitive to motions on a 10−8–10−6s timescale. Since τr is typically 5–50ns for most proteins analyzed by NMR, an order parameter as a plateau of CI(i) beyond 50 ns has only little impact on NMR relaxation. In addition, depending on the details of the system, some find consistent estimates of S2 from different force fields (Bowman, 2016), while the details of methyl dynamics can display more variations (O’Brien et al., 2016). Nevertheless, significant correlations have been found between the NMR and MD order parameters for Arg/Lys side chains (Chen et al., 2015; Esadze et al., 2016, 2011; Trbovic et al., 2009). These correlations with the experimental data validate MD-based investigations into the properties of basic side chains that are difficult to assess by NMR (see Sections 5.2 and 5.3).
5.1.2. Three-Bond Scalar Couplings From MD Trajectories
The dihedral angles χ of long side chains can dynamically change through conformational fluctuations. Three-bond 3JNC coupling constants relevant to Lys and Arg side-chain χ angles can be measured through spin-echo 3JNC modulation experiments, as described in Section 3.4. The three-bond coupling constants can directly be compared with those predicted from MD trajectories. This analysis utilizes the Karplus equation (Karplus, 1959) for the relationship between the 3JNC coupling constant and the dihedral angle χ between the coupled 15N and 13C nuclei:
| (9) |
The parameters A, B, and C are empirically determined, for example, A = 1.29, B = −0.49, and C = 0.37 for χ1 angles (Perez et al., 2001) and A = 1.29, B = −0.49, and C = 0.63 for Lys χ4 angles (Huang & MacKerell, 2013). Ensemble averages, 〈3JNC〉, are calculated from χ angles in numerous snapshots sampled from MD trajectories. Interestingly, experimental 3JNC data tend to exhibit far better correlation with the 〈3JNC〉 data predicted from the MD ensemble than with those predicted from the crystal structure (Chen et al., 2015; Zandarashvili et al., 2011), as shown in Fig. 10. These results suggest that the χ torsion angles of these side chains are actually as dynamic as seen in the MD simulation. Thus, 3JNC data can also illuminate the dynamic nature of basic side chains.
Fig. 10.
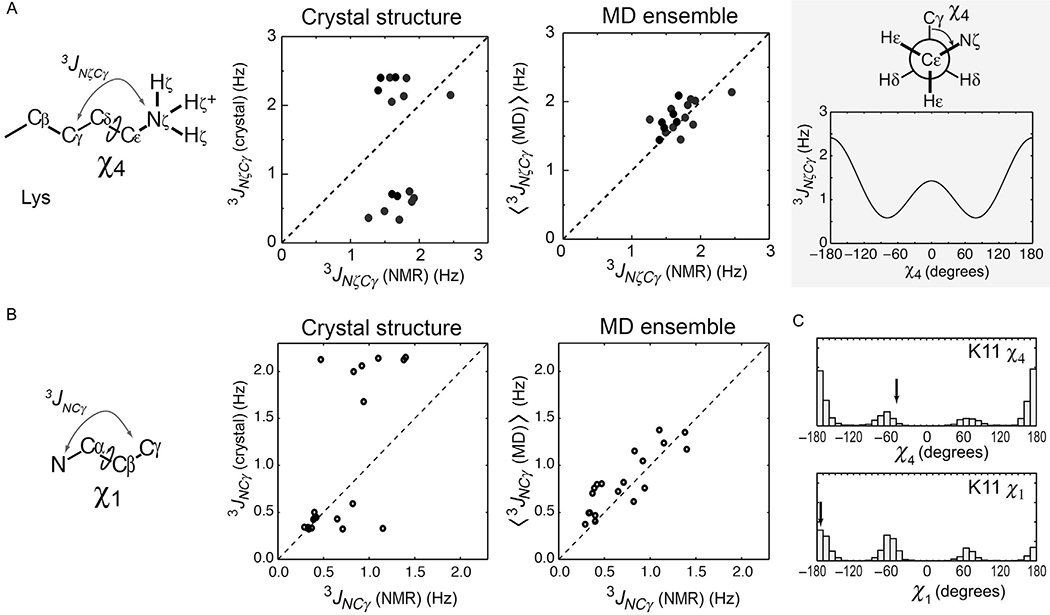
3JNC coupling data indicating dynamic alterations of side-chain torsion angles. (A) Correlations between the observed and predicted χ4-relevant 3JNζCγ couplings for the Lys side chains of ubiquitin (Zandarashvili et al., 2011), the Antp homeodomain–DNA complex, and the Egr-1–DNA complex (Chen et al., 2015). The 3JNζCγ couplings were predicted from crystal structures (PDB 1UBQ, 9ANT, and 1AAY) or MD ensembles. (B) Corresponding data for the 3JNCγ couplings between backbone 15N and side-chain 13Cγ nuclei related to the χ1 angles of ubiquitin side chains. (C) Distribution of the χ1 and χ4 angles of the K11 side chain of ubiquitin in the MD trajectory (Zandarashvili et al., 2011). Arrows indicate the angles in the crystal structure.
5.2. Ion-Pair Dynamics in MD Simulations
Ion pairs with charged side chains can involve both strong short-range electrostatic interactions and hydrogen bonds. Although the NMR data of hydrogen-bond scalar couplings (h3JNP) between protein 15N and DNA 31P nuclei indicate the presence of hydrogen bonds in the intermolecular ion pairs, the NMR S2 and 3JNC data clearly indicate that the Lys side chains interacting with DNA phosphates are highly mobile (Anderson et al., 2013; Chen et al., 2015). How can the Lys side-chain NH3+ groups exhibit high mobility despite the simultaneous presence of hydrogen bonds and strong short-range attractive electrostatic interactions? While the answer to this question was not immediately obvious from the NMR investigations alone, MD simulations provided useful insight into this question and facilitated interpretation of the NMR data.
5.2.1. Analysis of CIP–SIP Transitions
The dynamic behavior of biomolecular ion pairs becomes evident through analysis of the distances between cationic and anionic moieties in MD trajectories. Fig. 11A shows the N…O distances from the interfacial Lys side-chain NH3+ group to the closest DNA phosphate in the 0.6-μs MD trajectories for the Antp homeodomain–DNA complex and the Egr-1 zinc-finger–DNA complex (Chen et al., 2015). These N…O distances dynamically fluctuated between two ranges: one between 2.5 and 3.2 Å, corresponding to the CIP states, and the other between 3.8 and 6.0 Å, corresponding to the SIP states. The transitions between the CIP and SIP states occurred on a pico-to-nanosecond timescale. This dynamic behavior of biomolecular ion pairs is reasonable in light of the fundamental concepts that were established for small ions over the last several decades (Fennell, Bizjak, Vlachy, & Dill, 2009; Marcus & Hefter, 2006; Masnovi & Kochi, 1985; Masunov & Lazaridis, 2003; Peters & Li, 1994; Pettitt & Rossky, 1986; Szwarc, 1972). The order parameters and 3JNζCγ coupling constants predicted from the MD trajectories were consistent with experimental data from NMR experiments. The CIP–SIP transitions make the interfacial Lys side chains highly dynamic, making the order parameters small, whereas the major presence of CIP causes sizable hydrogen-bond scalar couplings h3JNP.
Fig. 11.
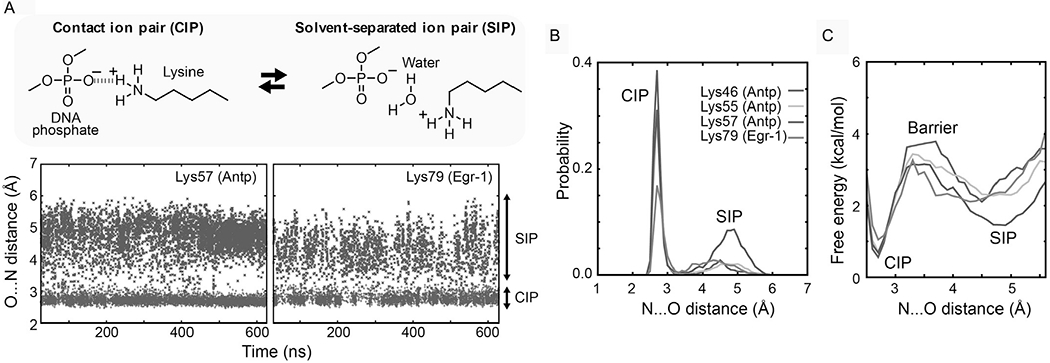
Dynamic transitions between the CIP and SIP states of the intermolecular ion pairs of Lys side-chain NH3+ and DNA phosphate groups observed in the 0.6-μs MD simulations for the Antp–DNA and Egr-1–DNA complexes. (A) The trajectories of the distances from the Lys Nζ atoms to the closest DNA phosphate oxygen atoms are shown for the intermolecular ion pairs for which the presence of CIP was experimentally confirmed. (B) Probability distribution of the CIP and SIP states as a function of the distance from the Lys Nζ atom to the closest DNA phosphate oxygen atom. (C) PMFs for the intermolecular ion pairs of the protein side-chain NH3+ and DNA phosphate groups in the Antp homeodomain–DNA complex and the Egr-1 zinc-finger–DNA complex.
5.2.2. Free-Energy Analysis of the CIP–SIP Equilibria
MD trajectories enable calculations of the potentials of mean force (PMFs) for these ion pairs. PMFs represent the effective potential or free-energy landscapes given as a function of the interionic distance. Fig. 11C shows the PMFs as a function the N…O distance (rNO) for the ion pairs of the Lys side-chain NH3+ and DNA phosphate groups (Chen et al., 2015). These PMFs were obtained though analysis of the probability distribution p(rNO) (Fig. 11B), which is based on a histogram of the rNO values in the MD trajectory. The free energy is calculated as G = −RT ln p(rNO), where R is the gas constant; T is the standard temperature (i.e., T = 298.15 K). The two minima in PMFs correspond to the CIP and SIP states. The peak between these states corresponds to the effective free energy barrier for the CIP–SIP transition, provided that the PMFs represent the reaction coordinates. With a higher energy barrier, the CIP–SIP transitions should be slower. For the protein–DNA ion pairs whose CIP states were experimentally detected, the free energy differences between CIP and SIP states were determined to be 0.8–1.6 kcal/mol. The energy barriers for CIP → SIP transitions were determined to be 2.2–3.2kcal/mol, which are qualitatively consistent with the mean lifetimes of the CIP states. The relatively small free energy difference between CIP and SIP as well as the low-energy barrier between these states can explain the highly dynamic nature of the interfacial ion pairs involving Lys side chains.
5.3. Conformational Entropy of Basic Side Chains
Changes in the conformational entropies of protein side chains can make significant contribution to the overall change in free energy upon molecular association (Wand, 2013; Wand & Sharp, 2018). Because basic side chains are important constituents of electrostatic interactions in molecular recognition by proteins, the conformational entropies of these side chains are of particular interest. For CH3-containing side chains, the order parameters for CH3 groups are used as “meters” of side-chain conformational entropy (Kasinath, Sharp, & Wand, 2013; Li & Brüschweiler, 2009). For Lys and Arg side chains, however, the order parameters of their cationic groups do not necessarily serve as good meters of the conformational entropy of the entire side chain because CH2 moieties could remain flexible even if the cationic moieties are restricted by hydrogen bonds (Li & Brüschweiler, 2009; Trbovic et al., 2009). Lys and Arg side-chain conformational entropies can be calculated from the distributions of the dihedral angles sampled during an MD simulation (Karplus & Kushick, 1981; Trbovic et al., 2009):
| (10) |
where R is the gas constant and is the probability density as a function of the dihedral angles χ1, χ2, χ3, and χ4 of each Arg or Lys side chain. We tested the dependence of the entropies on the bin size of the integral mesh and chose 5° (Esadze et al., 2016). The bin size of the integral mesh affects the absolute entropy but, given reasonable resolution, does not affect the change in conformational entropy. Fig. 12A displays the change in conformational entropy of each Arg/Lys side chain of the Egr-1 zinc-finger protein upon binding to its target DNA, which was calculated from the MD trajectories using Eq. (10) (Esadze et al., 2016). Fig. 12B shows the correlation between the changes in the NMR-derived order parameters of the Lys NH3+ and Arg NεH groups and the changes in the MD-derived conformational entropy of the same side chains upon complex formation.
Fig. 12.
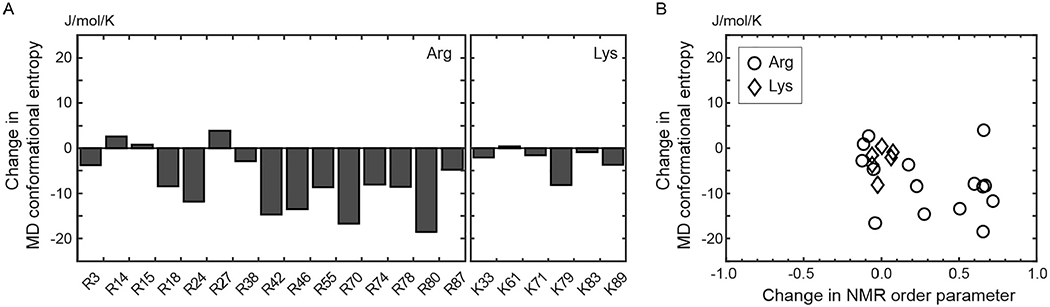
Changes in side-chain conformational entropy for the Lys and Arg side chains of the Egr-1 zinc-finger protein upon binding to the target DNA. (A) Changes in the side-chain conformational entropy of Lys and Arg side chains calculated from 0.6-μs MD trajectories for the free protein and the complex. (B) Correlation between changes in the NMR order parameters and changes in the MD conformational entropy upon complex formation.
6. CONCLUDING REMARKS
NMR experiments on Lys and Arg side chains can provide unique insights into their conformational dynamics, hydrogen bonds, and electrostatic interactions. Functionally important Lys and Arg side chains tend to show relatively slow hydrogen exchange due to hydrogen bonding, which facilitates NMR-based characterizations of these side chains. For the NMR experiments to work, optimization of pH and temperature can be necessary so that hydrogen exchange becomes slow enough to detect 1H signals from the cationic groups. The intrinsic 15N transverse relaxation of Lys NH3+ groups is very slow, which makes it possible to precisely measure small scalar couplings, including those across hydrogen bonds. The pulse programs and parameter sets for the pulse sequences introduced in this chapter are available upon request at our laboratory website (https://scsb.utmb.edu/labgroups/iwahara/software/).
ACKNOWLEDGMENTS
This work was supported by Grant CHE-1608866 from the National Science Foundation (to J.I.) and partly by Grants R01-GM066813 (to B.M.P.) and R01-GM037657 (to B.M.P.). D.N. is a recipient of the Houston Area Molecular Biophysics Program fellowship (supported by NIH Grant T32-GM008280).
REFERENCES
- Abragam A (1961). Thermal relaxation in liquids and gases In The principle of nuclear magnetism (pp. 264–353). Oxford: Carendon Press. [Google Scholar]
- Aeby N, & Bodenhausen G (2008). Determination of transverse relaxation rates of individual spins while quenching echo modulations due to homonuclear scalar couplings. Chemical Physics Letters, 463(4–6), 418–421. [Google Scholar]
- Anderson KM, Esadze A, Manoharan M, Brüschweiler R, Gorenstein DG, & Iwahara J (2013). Direct observation of the ion-pair dynamics at a protein-DNA interface by NMR spectroscopy. Journal of the American Chemical Society, 135(9), 3613–3619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson KM, Nguyen D, Esadze A, Zandrashvili L, Gorenstein DG, & Iwahara J (2015). A chemical approach for site-specific identification of NMR signals from protein side-chain NH3+ groups forming intermolecular ion pairs in protein-nucleic acid complexes. Journal of Biomolecular NMR, 62(1), 1–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andre I, Linse S, & Mulder FA (2007). Residue-specific pKa determination of lysine and arginine side chains by indirect 15N and 13C NMR spectroscopy: Application to apo calmodulin. Journal of the American Chemical Society, 129(51), 15805–15813. [DOI] [PubMed] [Google Scholar]
- Arunan E, Desiraju GR, Klein RA, Sadlej J, Scheiner S, Alkorta I, et al. Nesbitt DJ, (2011). Definition of the hydrogen bond (IUPAC Recommendations 2011). Pure and Applied Chemistry, 83(8), 1637–1641. [Google Scholar]
- Baldwin AJ, Hansen DF, Vallurupalli P, & Kay LE (2009). Measurement of methyl axis orientations in invisible, excited states of proteins by relaxation dispersion NMR spectroscopy. Journal of the American Chemical Society, 131(33), 11939–11948. [DOI] [PubMed] [Google Scholar]
- Bax A, Ikura M, Kay LE, Torchia DA, & Tschudin R (1990). Comparison of different modes of two-dimensional reverse-correlation NMR for the study of proteins. Journal of Magnetic Resonance, 86, 304–318. [Google Scholar]
- Blaum BS, Deakin JA,Johansson CM, Herbert AP, Barlow PN, Lyon M,et al. (2010). Lysine and arginine side chains in glycosaminoglycan-protein complexes investigated by NMR, cross-linking, and mass spectrometry: A case study of the factor H-heparin interaction. Journal of the American Chemical Society, 132(18), 6374–6381. [DOI] [PubMed] [Google Scholar]
- Boehr DD, Dyson HJ, & Wright PE (2006). An NMR perspective on enzyme dynamics. Chemical Reviews, 106(8), 3055–3079. [DOI] [PubMed] [Google Scholar]
- Bowman GR (2016). Accurately modeling nanosecond protein dynamics requires at least microseconds of simulation. Journal of Computational Chemistry, 37(6), 558–566. [DOI] [PubMed] [Google Scholar]
- Bunker BC (1994). Molecular mechanisms for corrosion of silica and silicate-glasses. Journal of Non-Crystalline Solids, 179, 300–308. [Google Scholar]
- Carr HY, & Purcell EM (1954). Effects of diffusion on free precession in nuclear magnetic resonance experiments. Physics Review, 94, 630–638. [Google Scholar]
- Case DA (2002). Molecular dynamics and NMR spin relaxation in proteins. Accounts of Chemical Research, 35(6), 325–331. [DOI] [PubMed] [Google Scholar]
- Cavanagh J, Fairbrother WJ, Palmer AG III, Rance M, & Skelton NJ (2007). Chemical exchange effects in NMR spectroscopy protein NMR spectroscopy: Principles and practice (2nd ed., pp. 391–402).Burlignton: Elsevier, Academic Press. [Google Scholar]
- Chatfield DC, Szabo A, & Brooks BR (1998). Molecular dynamics of staphylococcal nuclease: Comparison of simulation with 15N and 13C NMR relaxation data. Journal of the American Chemical Society, 120(21), 5301–5311. [Google Scholar]
- Chattopadhyay A, Esadze A, Roy S, & Iwahara J (2016). NMR scalar couplings across intermolecular hydrogen bonds between zinc-finger histidine side chains and DNA phosphate groups. The Journal of Physical Chemistry. B, 120, 10679–10685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CY, Esadze A, Zandarashvili L, Nguyen D, Pettitt BM, & Iwahara J (2015). Dynamic equilibria of short-range electrostatic interactions at molecular interfaces of protein-DNA complexes. Journal of Physical Chemistry Letters, 6(14), 2733–2737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou JJ, Case DA, & Bax A (2003). Insights into the mobility of methyl-bearing side chains in proteins from 3JCC and 3JCN couplings. Journal of the American Chemical Society, 125(29), 8959–8966. [DOI] [PubMed] [Google Scholar]
- Clore GM, & Gronenborn AM (1998). Determining the structures of large proteins and protein complexes by NMR. Trends in Biotechnology, 16(1), 22–34. [DOI] [PubMed] [Google Scholar]
- Clore GM, & Iwahara J (2009). Theory, practice, and applications of paramagnetic relaxation enhancement for the characterization of transient low-population states of biological macromolecules and their complexes. Chemical Reviews, 109(9), 4108–4139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clore GM, Szabo A, Bax A, Kay LE, Driscoll PC, & Gronenborn AM (1990). Deviations from the simple 2-parameter model-free approach to the interpretation of 15N nuclear magnetic-relaxation of proteins. Journal of the American Chemical Society, 112(12), 4989–4991. [Google Scholar]
- Dellwo MJ, & Wand AJ (1989). Model-independent and model-dependent analysis of the global and internal dynamics of cyclosporine-A. Journal of the American Chemical Society, 111(13), 4571–4578. [Google Scholar]
- Dittmer J, & Bodenhausen G (2006). Quenching echo modulations in NMR spectroscopy. Chemphyschem, 7(4), 831–836. [DOI] [PubMed] [Google Scholar]
- Englander SW, Downer NW, & Teitelbaum H (1972). Hydrogen exchange. Annual Review of Biochemistry, 41, 903–924. [DOI] [PubMed] [Google Scholar]
- Ernst RR, Bodenhausen G, & Wokaun A (1987). Heteronuclear polarization transfer In Principles of nuclear magnetic resonance in one and two dimensions. New York: Oxford University Press. [Google Scholar]
- Esadze A, Chen C, Zandarashvili L, Roy S, Pettitt BM, & Iwahara J (2016). Changes in conformational dynamics of basic side chains upon protein-DNA association. Nucleic Acids Research, 44(14), 6961–6970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esadze A, Li DW, Wang T, Brüschweiler R, & Iwahara J (2011). Dynamics of lysine side-chain amino groups in a protein studied by heteronuclear 1H-15N NMR spectroscopy. Journal of the American Chemical Society, 133, 909–919. [DOI] [PubMed] [Google Scholar]
- Esadze A, Zandarashvili L, & Iwahara J (2014). Effective strategy to assign 1H-15N heteronuclear correlation NMR signals from lysine side-chain NH3+ groups of proteins at low temperature. Journal of Biomolecular NMR, 60(1), 23–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fennell CJ, Bizjak A, Vlachy V, & Dill KA (2009). Ion pairing in molecular simulations of aqueous alkali halide solutions. The Journal of Physical Chemistry. B, 113(19), 6782–6791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitch CA, Platzer G, Okon M, Garcia-Moreno BE, & McIntosh LP (2015). Arginine: Its pKa value revisited. Protein Science, 24(5), 752–761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frederick KK, Sharp KA, Warischalk N, & Wand AJ (2008). Re-evaluation of the model-free analysis of fast internal motion in proteins using NMR relaxation. The Journal of Physical Chemistry. B, 112(38), 12095–12103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frederiksen JK, & Piccirilli JA (2009). Separation of RNA phosphorothioate oligonucleotides by HPLC. Methods in Enzymology, 468, 289–309. [DOI] [PubMed] [Google Scholar]
- Gerecht K, Figueiredo AM, & Hansen DF (2017). Determining rotational dynamics of the guanidino group of arginine side chains in proteins by carbon-detected NMR. Chemical Communications (Cambridge), 53(72), 10062–10065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grzesiek S, & Bax A (1993). The importance of not saturating H2O in protein NMR. Application to sensitivity enhancement and NOE measurements. Journal of the American Chemical Society, 115, 12593–12594. [Google Scholar]
- Grzesiek S, Cordier F, Jaravine V, & Barfield M (2004). Insights into biomolecular hydrogen bonds from hydrogen bond scalar couplings. Progress in NMR Spectroscopy, 45(3–4), 275–300. [Google Scholar]
- Gu Y, Li DW, & Brüschweiler R (2014). NMR order parameter determination from long molecular dynamics trajectories for objective comparison with experiment. Journal of Chemical Theory and Computation, 10(6), 2599–2607. [DOI] [PubMed] [Google Scholar]
- Hansen DF, & Kay LE (2007). Improved magnetization alignment schemes for spin-lock relaxation experiments. Journal of Biomolecular NMR, 37(4), 245–255. [DOI] [PubMed] [Google Scholar]
- Hansen DF, Vallurupalli P, & Kay LE (2008). An improved 15N relaxation dispersion experiment for the measurement of millisecond time-scale dynamics in proteins. The Journal of Physical Chemistry. B, 112(19), 5898–5904. [DOI] [PubMed] [Google Scholar]
- Harbison GS (1993). Interference between J-couplings and cross-relaxation in solution NMR-spectroscopy—Consequences for macromolecular structure determination. Journal of the American Chemical Society, 115(7), 3026–3027. [Google Scholar]
- Hass MA, & Mulder FA (2015). Contemporary NMR studies of protein electrostatics. Annual Review of Biophysics, 44, 53–75. [DOI] [PubMed] [Google Scholar]
- Honig B, & Nicholls A (1995). Classical electrostatics in biology and chemistry. Science, 268(5214), 1144–1149. [DOI] [PubMed] [Google Scholar]
- Hu JS, & Bax A (1997). χ1 angle information from a simple two-dimensional NMR experiment that identifies trans 3JNCγ couplings in isotopically enriched proteins. Journal of Biomolecular NMR, 9(3), 323–328. [DOI] [PubMed] [Google Scholar]
- Huang J, & MacKerell AD Jr. (2013). CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. Journal of Computational Chemistry, 34(25), 2135–2145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Idiyatullin D, Daragan VA, & Mayo KH (2001). Improved measurement of 15N-{1H} NOEs in the presence of H(N)-water proton chemical exchange. Journal of Magnetic Resonance, 153(1), 138–143. [DOI] [PubMed] [Google Scholar]
- Iwahara J, & Clore GM (2006). Sensitivity improvement for correlations involving arginine side-chain Nε/Hε resonances in multi-dimensional NMR experiments using broadband 15N 180° pulses. Journal of Biomolecular NMR, 36(4), 251–257. [DOI] [PubMed] [Google Scholar]
- Iwahara J, Esadze A, & Zandarashvili L (2015). Physicochemical properties of ion pairs of biological macromolecules. Biomolecules, 5(4), 2435–2463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwahara J,Jung YS, & Clore GM (2007). Heteronuclear NMR spectroscopy for lysine NH3 groups in proteins: Unique effect of water exchange on 15N transverse relaxation. Journal of the American Chemical Society, 129(10), 2971–2980. [DOI] [PubMed] [Google Scholar]
- Iwahara J, Peterson RD, & Clubb RT (2005). Compensating increases in protein backbone flexibility occur when the Dead ringer AT-rich interaction domain (ARID) binds DNA: A nitrogen-15 relaxation study. Protein Science, 14(5), 1140–1150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwahara J, Zandarashvili L, Kemme CA, & Esadze A (2018). NMR-based investigations into target DNA search processes of proteins. Methods. 10.1016/j.ymeth.2018.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaravine VA, Alexandrescu AT, & Grzesiek S (2001). Observation of the closing of individual hydrogen bonds during TFE-induced helix formation in a peptide. Protein Science, 10(5), 943–950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karplus M (1959). Contact electron-spin coupling of nuclear magnetic moments. The Journal of Chemical Physics, 30(1), 11–15. [Google Scholar]
- Karplus M, & Kushick JN (1981). Method for estimating the configurational entropy of macromolecules. Macromolecules, 14(2), 325–332. [Google Scholar]
- Kasinath V, Sharp KA, & Wand AJ (2013). Microscopic insights into the NMR relaxation-based protein conformational entropy meter. Journal of the American Chemical Society, 135(40), 15092–15100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay LE, Bull TE, Nicholson LK, Griesinger C, Schwalbe H, Bax A, et al. (1992). The measurement of heteronuclear transverse relaxation-times in AX3 spin systems via polarization-transfer techniques. Journal of Magnetic Resonance, 100(3), 538–558. [Google Scholar]
- Kay LE, & Torchia DA (1991). The effects of dipolar cross-correlation on 13C methylcarbon T1, T2, and NOE measurements in macromolecules. Journal of Magnetic Resonance, 95(3), 536–547. [Google Scholar]
- Korzhnev DM, Tischenko EV, & Arseniev AS (2000). Off-resonance effects in 15N T2 CPMG measurements. Journal of Biomolecular NMR, 17(3), 231–237. [DOI] [PubMed] [Google Scholar]
- Kougentakis CM, Grasso EM, Robinson AC, Caro JA, Schlessman JL, Majumdar A, et al. (2018). Anomalous properties of Lys residues buried in the hydrophobic interior of a protein revealed with 15N-detect NMR spectroscopy. Journal of Physical Chemistry Letters, 9(2), 383–387. [DOI] [PubMed] [Google Scholar]
- Kuboniwa H, Grzesiek S, Delaglio F, & Bax A (1994). Measurement of H-N-H-alpha J-couplings in calcium-free calmodulin using new 2D and 3D water-flip-back methods. Journal of Biomolecular NMR, 4(6), 871–878. [DOI] [PubMed] [Google Scholar]
- Kumar A, Grace RCR, & Madhu PK (2000). Cross-correlations in NMR. Progress in NMR Spectroscopy, 37(3), 191–319. [Google Scholar]
- Kupče E, Boyd J, & Campbell ID (1995). Short selective pulses for biochemical applications. Journal of Magnetic Resonance. Series B, 106(3), 300–303. [DOI] [PubMed] [Google Scholar]
- Levy RM, Sheridan RP, Keepers JW, Dubey GS, Swaminathan S, & Karplus M (1985). Molecular dynamics of myoglobin at 298 K. Results from a 300-ps computer simulation. Biophysical Journal, 48(3), 509–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li DW, & Brüschweiler R (2009). A dictionary for protein side-chain entropies from NMR order parameters. Journal of the American Chemical Society, 131(21), 7226–7227. [DOI] [PubMed] [Google Scholar]
- Li YC, & Montelione GT (1994). Overcoming solvent saturation-transfer artifacts in protein NMR at neutral pH—Application of pulsed-field gradients in measurements of 15N Overhauser effects. Journal of Magnetic Resonance. Series B, 105(1), 45–51. [DOI] [PubMed] [Google Scholar]
- Liepinsh E, & Otting G (1996). Proton exchange rates from amino acid side chains—Implications for image contrast. Magnetic Resonance in Medicine, 35(1), 30–42. [DOI] [PubMed] [Google Scholar]
- Lipari G, & Szabo A (1982). Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1. Theory and range of validity. Journal of the American Chemical Society, 104(17), 4546–4559. [Google Scholar]
- Lipari G, Szabo A, & Levy RM (1982). Protein dynamics and NMR relaxation—Comparison of simulations with experiment. Nature, 300(5888), 197–198. [Google Scholar]
- Löhr F, & Rüterjans H (1998). Detection of nitrogen-nitrogen J-couplings in proteins. Journal of Magnetic Resonance, 132(1), 130–137. [Google Scholar]
- Loria JP, Berlow RB, & Watt ED (2008). Characterization of enzyme motions by solution NMR relaxation dispersion. Accounts of Chemical Research, 41(2), 214–221. [DOI] [PubMed] [Google Scholar]
- Luscombe NM, Laskowski RA, & Thornton JM (2001). Amino acid-base interactions: A three-dimensional analysis of protein-DNA interactions at an atomic level. Nucleic Acids Research, 29(13), 2860–2874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandel AM, Akke M, & Palmer AG 3rd. (1995). Backbone dynamics of Escherichia coli ribonuclease HI: Correlations with structure and function in an active enzyme. Journal of Molecular Biology, 246(1), 144–163. [DOI] [PubMed] [Google Scholar]
- Marcus Y, & Hefter G (2006). Ion pairing. Chemical Reviews, 106(11), 4585–4621. [DOI] [PubMed] [Google Scholar]
- Markwick PR, Sprangers R, & Sattler M (2003). Dynamic effects on J-couplings across hydrogen bonds in proteins. Journal of the American Chemical Society, 125(3), 644–645. [DOI] [PubMed] [Google Scholar]
- Masnovi JM, & Kochi JK (1985). Direct observation of ion-pair dynamics. Journal of the American Chemical Society, 107(26), 7880–7893. [Google Scholar]
- Masunov A, & Lazaridis T (2003). Potentials of mean force between ionizable amino acid side chains in water. Journal of the American Chemical Society, 125(7), 1722–1730. [DOI] [PubMed] [Google Scholar]
- Meiboom S, & Gill D (1958). Modified spin-echo method for measuring nuclear relaxation times. The Review of Scientific Instruments, 29, 688–691. [Google Scholar]
- Mittermaier AK, & Kay LE (2009). Observing biological dynamics at atomic resolution using NMR. Trends in Biochemical Sciences, 34(12), 601–611. [DOI] [PubMed] [Google Scholar]
- Nguyen D, Hoffpauir ZA, & Iwahara J (2017). Internal motions of basic side chains of the Antennapedia homeodomain in the free and DNA-bound states. Biochemistry, 56(44), 5866–5869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen D, & Iwahara J (2018). Impact of 15N-15N scalar couplings on 15N transverse relaxation measurements for arginine side chains of proteins. Journal of Biomolecular NMR, 71(1), 45–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen D, Lokesh GLR, Volk DE, & Iwahara J (2017). A unique and simple approach to improve sensitivity in 15N-NMR relaxation measurements for NH3+ groups: Application to a protein-DNA complex. Molecules, 22(8), 1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen D, Zandarashvili L, White MA, & Iwahara J (2016). Stereospecific effects of oxygen-to-sulfur substitution in DNA phosphate on ion pair dynamics and protein-DNA affinity. Chembiochem, 17(17), 1636–1642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholson LK, Kay LE, Baldisseri DM, Arango J, Young PE, Bax A, et al. (1992). Dynamics of methyl groups in proteins as studied by proton-detected 13C NMR spectroscopy. Application to the leucine residues of staphylococcal nuclease. Biochemistry, 31(23), 5253–5263. [DOI] [PubMed] [Google Scholar]
- Nieto PM, Birdsall B, Morgan WD, Frenkiel TA, Gargaro AR, & Feeney J (1997). Correlated bond rotations in interactions of arginine residues with ligand carboxylate groups in protein ligand complexes. FEBS Letters, 405(1), 16–20. [DOI] [PubMed] [Google Scholar]
- O’Brien ES, Wand AJ, & Sharp KA (2016). On the ability of molecular dynamics force fields to recapitulate NMR derived protein side chain order parameters. Protein Science, 25(6), 1156–1160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ollerenshaw JE, Tugarinov V, & Kay LE (2003). Methyl TROSY: Explanation and experimental verification. Magnetic Resonance in Chemistry, 41(10), 843–852. [Google Scholar]
- Palmer AG 3rd. (2014). Chemical exchange in biomacromolecules: Past, present, and future. Journal of Magnetic Resonance, 241, 3–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer AG, Rance M, & Wright PE (1991). Intramolecular motions of a zinc finger DNA-binding domain from Xfin characterized by proton-detected natural abundance 13C heteronuclear NMR-spectroscopy. Journal of the American Chemical Society, 113(12), 4371–4380. [Google Scholar]
- Palmer AG, Wright PE, & Rance M (1991). Measurement of relaxation-time constants for methyl-groups by proton-detected heteronuclear NMR-spectroscopy. Chemical Physics Letters, 185(1–2), 41–46. [Google Scholar]
- Perez C, Löhr F, Rüterjans H, & Schmidt JM (2001). Self-consistent Karplus parametrization of 3J couplings depending on the polypeptide side-chain torsion χ1. Journal of the American Chemical Society, 123(29), 7081–7093. [DOI] [PubMed] [Google Scholar]
- Peters KS, & Li BL (1994). Picosecond dynamics of contact ion-pairs and solvent-separated ion-pairs in the photosolvolysis of diphenylmethyl chloride. The Journal of Physical Chemistry, 98(2), 401–403. [Google Scholar]
- Pettitt BM, & Rossky PJ (1986). Alkali-halides in water—Ion solvent correlations and ion ion potentials of mean force at infinite dilution. The Journal of Chemical Physics, 84(10), 5836–5844. [Google Scholar]
- Platzer G, Okon M, & McIntosh LP (2014). pH-dependent random coil 1H, 13C, and 15N chemical shifts of the ionizable amino acids: A guide for protein pKa measurements. Journal of Biomolecular NMR, 60(2–3), 109–129. [DOI] [PubMed] [Google Scholar]
- Poon DK, Schubert M, Au J, Okon M, Withers SG, & McIntosh LP (2006). Unambiguous determination of the ionization state of a glycoside hydrolase active site lysine by 1H-15N heteronuclear correlation spectroscopy. Journal of the American Chemical Society, 128(48), 15388–15389. [DOI] [PubMed] [Google Scholar]
- Privalov PL, Dragan AI, & Crane-Robinson C (2011). Interpreting protein/DNA interactions: Distinguishing specific from non-specific and electrostatic from non-electrostatic components. Nucleic Acids Research, 39(7), 2483–2491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renner C, Schleicher M, Moroder L, & Holak TA (2002). Practical aspects of the 2D 15N-{1H}-NOE experiment. Journal of Biomolecular NMR, 23(1), 23–33. [DOI] [PubMed] [Google Scholar]
- Rohs R, Jin X, West SM,Joshi R, Honig B, & Mann RS (2010). Origins of specificity in protein-DNA recognition. Annual Review of Biochemistry, 79, 233–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarkar SK, Hiyama Y, Niu CH, Young PE, Gerig JT, & Torchia DA (1987). Molecular dynamics of collagen side chains in hard and soft tissues. A multinuclear magnetic resonance study. Biochemistry, 26(21), 6793–6800. [DOI] [PubMed] [Google Scholar]
- Segawa T, Kateb F, Duma L, Bodenhausen G, & Pelupessy P (2008). Exchange rate constants of invisible protons in proteins determined by NMR spectroscopy. Chembiochem, 9(4), 537–542. [DOI] [PubMed] [Google Scholar]
- Sepuru KM, Iwahara J, & Rajarathnam K (2018). Direct detection of lysine side chain NH3+ in protein-heparin complexes using NMR spectroscopy. Analyst, 143(3), 635–638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheinerman FB, Norel R, & Honig B (2000). Electrostatic aspects of protein-protein interactions. Current Opinion in Structural Biology, 10(2), 153–159. [DOI] [PubMed] [Google Scholar]
- Skelton NJ, Palmer AG, Akke M, Kordel J, Rance M, & Chazin WJ (1993). Practical aspects of 2-dimensional proton-detected 15N spin relaxation measurements. Journal of Magnetic Resonance. Series B, 102(3), 253–264. [Google Scholar]
- Spyracopoulos L (2006). A suite of Mathematica notebooks for the analysis of protein main chain 15N NMR relaxation data. Journal of Biomolecular NMR, 36(4), 215–224. [DOI] [PubMed] [Google Scholar]
- Szwarc M (1972). Ions and ion pairs in organic reactions. Vol. 1 New York: Wiley-Interscience. [Google Scholar]
- Takayama Y, Castaneda CA, Chimenti M, Garcia-Moreno B, & Iwahara J (2008). Direct evidence for deprotonation of a lysine side chain buried in the hydrophobic core of a protein. Journal of the American Chemical Society, 130(21), 6714–6715. [DOI] [PubMed] [Google Scholar]
- Takeda M, Hallenga K, Shigezane M, Waelchli M, Lohr F, Markley JL, et al. (2011). Construction and performance of an NMR tube with a sample cavity formed within magnetic susceptibility-matched glass. Journal of Magnetic Resonance, 209(2), 167–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjandra N, Feller SE, Pastor RW, & Bax A (1995). Rotational diffusion anisotropy of human ubiquitin from 15N NMR relaxation. Journal of the American Chemical Society, 117(50), 12562–12566. [Google Scholar]
- Tjandra N, Szabo A, & Bax A (1996). Protein backbone dynamics and 15N chemical shift anisotropy from quantitative measurement of relaxation interference effects. Journal of the American Chemical Society, 118(29), 6986–6991. [Google Scholar]
- Tomlinson JH, Ullah S, Hansen PE, & Williamson MP (2009). Characterization of salt bridges to lysines in the protein G B1 domain. Journal of the American Chemical Society, 131(13), 4674–4684. [DOI] [PubMed] [Google Scholar]
- Trbovic N, Cho JH, Abel R, Friesner RA, Rance M, & Palmer AG 3rd., (2009). Protein side-chain dynamics and residual conformational entropy. Journal of the American Chemical Society, 131(2), 615–622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Ven FJM (1995). Dephasing coherences In Multidimensional NMR in liquids: Basic principles and experimental methods (pp. 211–224). New York: VCH Publishers. [Google Scholar]
- van Zijl PCM, Sukumar S, Johnson MO, Webb P, & Hurd RE (1994). Optimized shimming for high-resolution NMR using 3-dimensional image-based field mapping. Journal of Magnetic Resonance. Series A, 111(2), 203–207. [Google Scholar]
- Voehler MW, Collier G, Young JK, Stone MP, & Germann MW (2006). Performance of cryogenic probes as a function of ionic strength and sample tube geometry. Journal of Magnetic Resonance, 183(1), 102–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wand AJ (2013). The dark energy of proteins comes to light: Conformational entropy and its role in protein function revealed by NMR relaxation. Current Opinion in Structural Biology, 23(1), 75–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wand AJ, & Sharp KA (2018). Measuring entropy in molecular recognition by proteins. Annual Review of Biophysics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werbeck ND, Kirkpatrick J, & Hansen DF (2013). Probing arginine side-chains and their dynamics with carbon-detected NMR spectroscopy: Application to the 42 kDa human histone deacetylase 8 at high pH. Angewandte Chemie (International Ed. in English), 52(11), 3145–3147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woessner DE (1962). Nuclear spin relaxation in ellipsoids undergoing rotational Brownian motion. The Journal of Chemical Physics, 37, 647–654. [Google Scholar]
- Yamazaki T, Pascal SM, Singer AU, Formankay JD,& Kay LE (1995). Nmr pulse schemes for the sequence-specific assignment of arginine guanidino 15N and 1H chemical-shifts in proteins. Journal of the American Chemical Society, 117(12), 3556–3564. [Google Scholar]
- Yao L, Grishaev A, Cornilescu G, & Bax A (2010). Site-specific backbone amide 15N chemical shift anisotropy tensors in a small protein from liquid crystal and cross-correlated relaxation measurements. Journal of the American Chemical Society, 132(12), 4295–4309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuwen T, & Skrynnikov NR (2014a). CP-HISQC: A better version of HSQC experiment for intrinsically disordered proteins under physiological conditions. Journal of Biomolecular NMR, 58(3), 175–192. [DOI] [PubMed] [Google Scholar]
- Yuwen T, & Skrynnikov NR (2014b). Proton-decoupled CPMG: A better experiment for measuring 15N R2 relaxation in disordered proteins. Journal of Magnetic Resonance, 241, 155–169. [DOI] [PubMed] [Google Scholar]
- Zandarashvili L, Esadze A, & Iwahara J (2013). NMR studies on the dynamics of hydrogen bonds and ion pairs involving lysine side chains of proteins. Advances in Protein Chemistry and Structural Biology, 93, 37–80. [DOI] [PubMed] [Google Scholar]
- Zandarashvili L, Esadze A, Kemme CA, Chattopadhyay A, Nguyen D, & Iwahara J (2016). Residence times of molecular complexes in solution from NMR data of intermolecular hydrogen-bond scalar coupling. Journal of Physical Chemistry Letters, 7(5), 820–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandarashvili L, Esadze A, Vuzman D, Kemme CA, Levy Y, & Iwahara J (2015). Balancing between affinity and speed in target DNA search by zinc-finger proteins via modulation of dynamic conformational ensemble. Proceedings of the National Academy of Sciences of the United States of America, 112(37), E5142–E5149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandarashvili L, & Iwahara J (2015). Temperature dependence of internal motions of protein side-chain NH3+ groups: Insight into energy barriers for transient breakage of hydrogen bonds. Biochemistry, 54(2), 538–545. [DOI] [PubMed] [Google Scholar]
- Zandarashvili L, Li DW, Wang T, Brüschweiler R, & Iwahara J (2011). Signature of mobile hydrogen bonding of lysine side chains from long-range 15N-13C scalar J-couplings and computation. Journal of the American Chemical Society, 133(24), 9192–9195. [DOI] [PubMed] [Google Scholar]
- Zandarashvili L, Nguyen D, Anderson KM, White MA, Gorenstein DG, & Iwahara J (2015). Entropic enhancement of protein-DNA affinity by oxygen-to-sulfur substitution in DNA phosphate. Biophysical Journal, 109(5), 1026–1037. [DOI] [PMC free article] [PubMed] [Google Scholar]


