Lung mass density prediction using machine learning based on ultrasound surface wave elastography and pulmonary function testing

Abstract

Objective: The objective of this study is to predict in vivo lung mass density for patients with interstitial lung disease using different gradient boosting decision tree (GBDT) algorithms based on measurements from lung ultrasound surface wave elastography (LUSWE) and pulmonary function testing (PFT). Methods: Age and weight of study subjects (57 patients with interstitial lung disease and 20 healthy subjects), surface wave speeds at three vibration frequencies (100, 150, and 200 Hz) from LUSWE, and predicted forced expiratory volume (FEV1% pre) and ratio of forced expiratory volume to forced vital capacity (FEV1%/FVC%) from PFT were used as inputs while lung mass densities based on the Hounsfield Unit from high resolution computed tomography (HRCT) were used as labels to train the regressor in three GBDT algorithms, XGBoost, CatBoost, and LightGBM. 80% (20%) of the dataset was used for training (testing). Results: The results showed that predictions using XGBoost regressor obtained an accuracy of 0.98 in the test dataset. Conclusion: The obtained results suggest that XGBoost regressor based on the measurements from LUSWE and PFT may be able to noninvasively assess lung mass density in vivo for patients with pulmonary disease.

I. INTRODUCTION

Lung disease, the third-leading cause of mortality in the United States, is responsible for 4 00 000 deaths each year (Xu, 2010). While death rates from other major diseases such as cancer and cardiovascular disease are declining, mortality rate due to lung disease is increasing (American Lung Association, 2008). Many lung diseases, including interstitial lung disease (ILD), are associated with changes in the lung's biomechanical properties. ILD comprises of serious diseases in which the lung tissue is stiffened by fibrosis. Computed tomography (CT) is the clinical standard for diagnosing lung fibrosis (Mathieson et al., 1989; Verschakelen, 2010), but it substantially increases radiation exposure for patients, even when using various techniques to reduce the dose (Mayo, 2009).

Lung ultrasound imaging has recently attract attention for assessing lung disease (Demi et al., 2017; Mohanty et al., 2017; Demi et al., 2020; Soldati et al., 2019a; Soldati et al., 2019b; Mento et al., 2020). Given the COVID-19 epidemic, lung ultrasound has increasingly been used for disease diagnosis and early screening (Soldati et al., 2020). Safety issues related to using ultrasound imaging for assessing lung disease have been discussed (Miller et al., 2018). A deep learning framework has been proposed for classification and localization of COVID-19 markers in lung ultrasound (Roy et al., 2020). We have developed a lung ultrasound surface wave elastography (LUSWE) technique for noninvasively measuring surface wave speeds of superficial lung tissue for patients with ILD and found there is a statistical difference in the surface wave speed between patients and healthy controls (Zhang et al., 2011; Zhang et al., 2017a; Zhang et al., 2018a; Zhang et al., 2018b; Zhou et al., 2019). ILD is difficult to classify because>200 disorders have similar clinical, radiographic, physiologic, or pathologic manifestations, with limited consensus regarding the best management practices(Loscalzo, 2010). Because ILD has multiple causes, our work focuses on systemic sclerosis–associated ILD (SSc-ILD). This strategy has several advantages. First, patients with SSc have a high incidence of lung fibrosis (Steen and Medsger, 2000; Hudson et al., 2010). Second, lung involvement in patients with SSc may be predicted at early stages by evaluation of skin fibrosis because skin manifestation is an early and easily detectable marker of SSc disease activity. In this research, we do not study the analysis of lung mass density for different types of ILD.

This paper aims to develop LUSWE based artificial intelligence (AI) techniques to noninvasively analyze lung mass density. Lung mass density is an important biomarker that reflects lung health. However, there are currently no validated clinical imaging techniques to analyze lung mass density. A few studies have shown that the extent of emphysema measured by pathology scores in resected lung tissue is well correlated with lung density values obtained from preoperative computed tomography (CT) of the lung (Gould et al., 1988; Bankier et al., 1999). We first developed a method to relate the lung mass density with the Hounsfield unit (HU) of CT (Zhou et al., 2020a) These estimated lung mass densities were labeled for training the deep neural network (DNN) model. In a previous study (Zhou et al., 2020a), a DNN model was developed using the data of 57 ILD patients and 20 healthy controls. The accuracy was 0.84 and 0.89, respectively, for the rectified linear activation unit (ReLU) and exponential linear unit (ELU). The lung mass density of the ILD patients (317.68 ± 59.69 kg/m³) was statistically higher than that of the healthy subjects (218.75 ± 23.05 kg/m³).

Machine learning (ML) has increasingly been recognized in the field of medical imaging. Among ML algorithms, the gradient boosting decision tree (GBDT) algorithm is regarded as best-in-class for small-to-medium structured/tabular data. Gradient boosting is an ensemble technique where new models which predict the residuals of prior models via a gradient descent algorithm to minimize the loss are constructed and then combined together sequentially to make the final prediction until no further improvements can be achieved (Friedman, 2001, 2002). GBDT is a widely used ML algorithm due to its efficiency, accuracy and interpretability. XGBoost (short for extreme gradient boosting) is a decision-tree-based ensemble ML implementation that uses a gradient boosting framework (Chen et al., 2015; Chen and Guestrin, 2016). It has widely been used by data scientists to achieve state-of-the-art results on many ML challenges (Mangal and Kumar, 2016). CatBoost is a GBDT implementation that efficiently handles both categorical and numerical features (Prokhorenkova et al., 2018). LightGBM is also a GBDT implementation which uses gradient-base one-side sampling and exclusive feature bundling techniques to reduce the number of data instances and the number of features for the situations where the feature dimension is high and data size is large (Ke et al., 2017).

This study is a continuation of our previous investigation on the prediction of lung mass density based on LUSWE (Zhou and Zhang, 2018). The objective of this study is to predict in vivo lung mass density for patients with ILD using different GBDT algorithms based on measurements from LUSWE and pulmonary function testing (PFT). The forced volume capacity (FVC) level in PFT has traditionally been regarded as the measure of disease severity, and a decrease in FVC has been associated with increased mortality in ILD.

II. MATERIALS AND METHODS

A. Datasets

This was a retrospective study. From February 2016 to May 2017, there was a cumulative total of 91 patients (M/F: 51/40, mean age: 62.4 ±_12.9 years) and 30 healthy controls (M/F: 16/14, mean age: 45.4 ± _14.6 years) who underwent LUSWE; however, among them, HRCT and PFT data were available for 57 patients (M/F: 30/29, mean age: 60.9 ± 14.3 years) and 20 healthy subjects (M/F: 10/10, mean age: 44 ± 15.4 years). For LUSWE, a Verasonics ultrasound system with an L11-4 ultrasound probe with a central frequency of 6.4 MHz is used. The mechanical index of 0.15 was used in this study. In this study, the surface wave speed on the lung is measured at three frequencies of 100, 150, and 200 Hz (Clay et al., 2019; Wiley et al., 2019). The frequency ranges chosen in this study consider the wave motion amplitude, spatial resolution and wave attenuation (Zhou et al., 2020b; Zhou et al., 2020c). The lung is tested at total lung capacity when the subject takes a deep breath and holds for a few seconds. Both lungs of the subject are tested. Surface wave speeds at three frequencies, predicted forced expiratory volume (FEV1%pre), ratio of forced expiratory volume to forced vital capacity (FEV1% = FVC%), age, and weight of patients and healthy subjects were used as features for training ML models. A fivefold cross-validation was conducted by dividing the dataset into training (80%) and testing (20%) and repeated five times to calculate mean values and standard deviations so as to assess the performance of different algorithms.

B. GBDT algorithms

XGBoost, CatBoost, and LightGBM libraries all use decision trees as the base weak learner and gradient boosting to iteratively fit a sequence of such trees. LightGBM uses gradient-based one-side sampling to filter out the data instances for finding a split value while XGBoost uses pre-sorted algorithm or computing the best split. CatBoost has the flexibility of giving indices of categorical column using one-hot encoding. These algorithms were implemented in Python using the libraries XGBoost, CatBoost, and LightGBM in this study.

C. Feature importance assessment

In order to evaluate the importance of features used in training the models, a framework called SHAP (Shapley additive explanations) was used (Lundberg and Lee, 2017). SHAP is a unified approach to explain the result of any deep learning model, which connects the theory of games with local explanations joining several methods and representing the additive feature attribution method. SHAP assigns each feature an importance value for a particular prediction. These explain the model output as a sum of real values attributed to each input feature. Given the various GBDT algorithms used in this study, an implementation of Tree SHAP called TreeExplainer, which is a fast and exact algorithm to compute SHAP values for trees and ensembles of trees, was used (Lundberg et al., 2019).

III. RESULTS

Mean-square error (MSE) and correlation coefficients (R2) of the test dataset of three algorithms were shown in Table I. XGBoost obtained the best results. Predefined and predicted lung mass densities of three algorithms for the test dataset were shown in Table II. It showed that the prediction of XGBoost was in agreement with the predefined lung mass densities more than CatBoost or LightGBM.

TABLE I.

Comparison in metrics of the regressor in different GBDT libraries.

	R2	MSE Loss
XGBoost	0.932 ± 0.112	3109.38 ± 104.5
CatBoost	0.817 ± 0.235	4166.54 ± 365.47
LightGBM	0.558 ± 0.247	3643.38 ± 433.56

TABLE II.

Predefined and predicted lung mass densities from XGBoost, CatBoost, and LightGBM in the test dataset.

Predefined	XGBoost	CatBoost	LightGBM
353	343	351	324
379	379	365	321
292	300	313	321
325	329	331	328
312	313	309	305
279	288	303	302
305	304	326	308
337	342	364	321
271	272	280	295
238	245	283	278
327	330	332	304
278	277	300	289
235	231	223	270
189	195	204	260

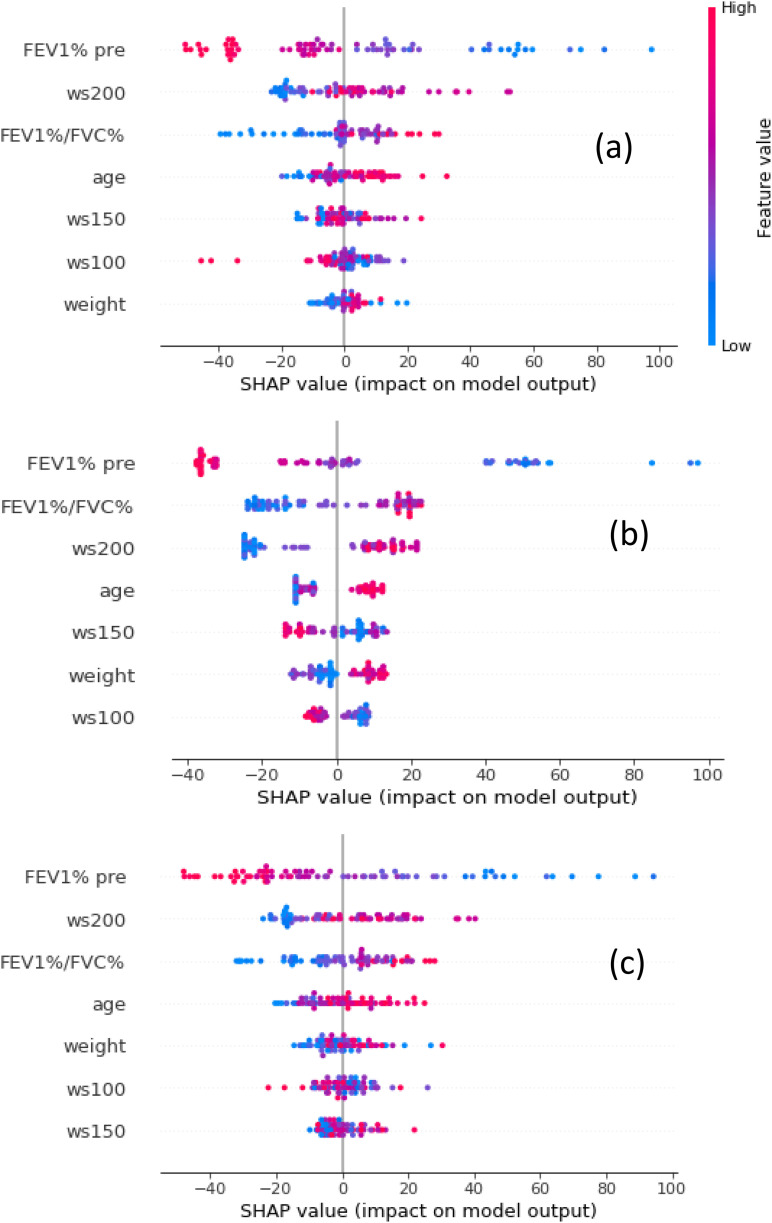
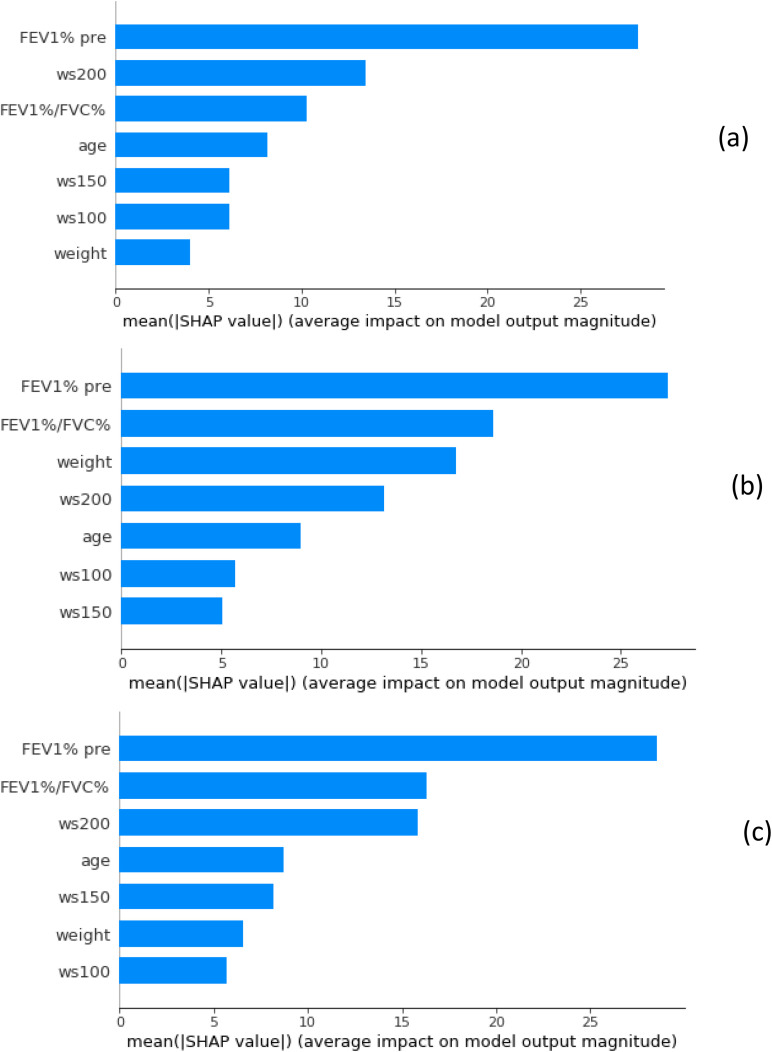
The importance of the seven features used in this study was shown in Figs. 1 and 2. In Fig. 1, features are sorted by the sum of the magnitudes of the SHAP values in all the samples, i.e., by their global impact. SHAP values are used to show the distribution of the impacts that each feature has on the model output. SHAP values are drawn horizontally. Each point represents a row of the dataset (FEV1% pre, FEV1%/FVC%, age, weight, ws100, ws150, ws200). The gradient color indicates the original value of that feature (high red, low blue). The average absolute value of the SHAP values for each feature was calculated to get a standard bar graph, Fig. 2. The SHAP values are represented along the horizontal axis and they quantify the change in log-odds.

FIG. 1.

(Color online) SHAP summary plots of the XGBoost (a), CatBoost (b), and LightGBM (c) models.

FIG. 2.

(Color online) The relative importance for each feature obtained by taking the average absolute value of the SHAP values from the XGBoost (a), CatBoost (b), and LightGBM (c) models.

IV. DISCUSSIONS

The aim of this study was to compare the performances of regressors from XGBoost, CatBoost, and LightGBM implementations to predict in vivo lung mass density based on age and weight of study subjects, as well as measurements obtained from LUSWE and PFT. The GBDT regressors were trained with surface wave speeds at three vibration frequencies, FEV1% pre and FEV1%/FVC% from PFT, age, weight, and predefined lung mass densities from HRCT. The obtained results show that XGBoost can be used to predict lung mass density with high accuracy.

It showed that the order of importance of the seven features changed with different algorithms, indicating that relative weights of features considering in XGBoost, CatBoost, and LightGBM. Moreover, FEV1% pre and FEV1%/FVC% are the top two features in all algorithms, suggesting good correlation between measurements from PFT to lung mass density predictions. This should be helpful for this technique combined with PFT to be translated in clinic. XGBoost is fast in execution and memory efficient compared with other GBDT algorithms and bagged decision trees. XGBoost is also dominant for structured or tabular datasets on classification and regression predictive modeling problems. In order to be used in gradient boosting algorithms, categorical features are preprocessed to convert categories to their target statistics which causes target leakage and prediction shift. Catboost uses an ordered boosting technique to avoid prediction shift caused by target leakage usually present in implementations of gradient boosting algorithms. CatBoost performs well only for categorical variables in the data. Since there are no categorical variables in our dataset, the CatBoost model cannot reach its maximum performance. LightGBM uses a novel technique of gradient-based one-side sampling to filter out the data instances for finding a split value while XGBoost uses pre-sorted algorithm and histogram-based algorithm for computing the best split. LightGBM can also handle categorical features by taking the input of feature names. It does not convert to one-hot coding and is much faster than one-hot coding. LGBM uses a special algorithm to find the split value of categorical features.

We used the seven features in this research. These features were obtained by clinical data and LUSWE measurements. It is interesting to know the contribution of each feature for predicting the lung mass density. We analyzed how SHAP values are attributed to the features globally in Figs. 1 and 2. In this case, all features are continuous and they are vertically sorted by their average impact on the predictions. We can see how FEV1% pre has the maximum impact of the prediction with high values of FEV1% pre associated with negative impacts on lung mass density predictions. High values of age are also significant and proportionally related to lung mass density predictions. FEV1%/FVC%, weight, age, and wave speeds at three frequencies, on the other hand, show a mixed pattern with high values associated both to high and low impacts on the predictions.

In this research, we use the CT data to label the lung mass density for training the DNN model. After the DNN models are developed, only the surface wave speeds and PFTs will be used to analyze lung mass density for patients. With known lung mass density, we can calculate two important biomarkers, lung elasticity, and viscosity, using LUSWE measurements. Thus, lung mass density, elasticity, and viscosity will be noninvasively analyzed for the first time. These novel biomarkers could prove useful for determining the clinical trajectory and prognosis of patients with ILD. CT is the clinical standard for lung assessment, but is costly, uses radiation, and typically is not performed often. In contrast, LUSWE can be used frequently to noninvasively evaluate the changes in lung mass and viscoelasticity. While conventional CT will remain the work-horse for initial lung disease diagnosis owing to its widespread availability and routine clinical adoption, we envision using LUSWE for follow up patient care so as to reduce potential radiation risk, mitigate the high costs associated with repeated CT.

Numerous deep learning techniques have been used in lung ultrasound imaging. This technique may be used to assess multiple lung disorders such as pulmonary edema when the alveoli are partly filled with blood or fluid. For congestive heart failure and inflammatory conditions, pulmonary edema is a basic characteristic. Extravascular lung water suggests worse development in critically ill patients and a higher risk of heart failure readmission or death (Gargani, 2015). In these “wet” lungs, ultrasound may penetrate deeper in the diseased tissue than healthy lung tissue, allowing imaging of deeper tissue (Zhou and Zhang, 2019). The development of a robust, quantitative method for lung mass density analysis has the potential to expand LUSWE in an almost exponential manner across a multitude of clinical applications. For example, quantitative LUSWE could be incorporated into the care of heart failure patients both in hospital practice and in outpatient clinics. In hospital practice, practitioners could perform daily LUSWE on patients undergoing diuresis for congestive heart failure and individually tailor medical therapy based on quantitative changes in LUSWE findings (Zhang et al., 2017b). Since each patient serves as their own reference standard, improvement in lung density through diuresis could be clearly documented and monitored. Outpatient providers could use quantitative LUSWE to monitor for increases in extravascular lung water and implement more timely changes in therapy.

Several limitations in this study should be taken into consideration when interpreting the results. First, this was a retrospective study on a dataset that was available at the time of the study. Further prospective investigation on the use of the GBDT in predicting in vivo lung mass density would be valuable. Second, the sample size used in this study is limited. The number of ILD patients and healthy subjects are not equal. Moreover, the age of ILD patients is statistically higher than that of healthy subjects. In the future, we plan to recruit more patients and older healthy subjects to enlarge the pool and further validate this technique. Third, lung density is dependent on pulmonary pressure. The measurements from LUSWE and PFT were obtained when the subject was taking a deep breath and holding. It could be difficult for critically patients with pulmonary fibrosis to hold their breath for more than one second. In this case, improvements need to be developed for LUSWE. In the future, we will investigate the relationship between lung mass density and pulmonary pressure using LUSWE, PFT, and GBDT.

V. CONCLUSIONS

In this study, we use different GBDT algorithms for in vivo lung mass density prediction based on measurements obtained from LUSWE and PFT, as well as subject age and weight information. The obtained results showed that given the tested algorithms and data, XGBoost outperforms the other two algorithms to predict in vivo lung mass density with high accuracy.