Abstract
The prediction of acid dissociation constants (pKa) is a prerequisite for predicting many other properties of a small molecule, such as its protein-ligand binding affinity, distribution coefficient (log D), membrane permeability, and solubility. The prediction of each of these properties requires knowledge of the relevant protonation states and solution free energy penalties of each state. The SAMPL6 pKa Challenge was the first time that a separate challenge was conducted for evaluating pKa predictions as part of the Statistical Assessment of Modeling of Proteins and Ligands (SAMPL) exercises. This challenge was motivated by significant inaccuracies observed in prior physical property prediction challenges, such as the SAMPL5 log D Challenge, caused by protonation state and pKa prediction issues. The goal of the pKa challenge was to assess the performance of contemporary pKa prediction methods for drug-like molecules. The challenge set was composed of 24 small molecules that resembled fragments of kinase inhibitors, a number of which were multiprotic. Eleven research groups contributed blind predictions for a total of 37 pKa distinct prediction methods. In addition to blinded submissions, four widely used pKa prediction methods were included in the analysis as reference methods. Collecting both microscopic and macroscopic pKa predictions allowed in-depth evaluation of pKa prediction performance. This article highlights deficiencies of typical pKa prediction evaluation approaches when the distinction between microscopic and macroscopic pKas is ignored; in particular, we suggest more stringent evaluation criteria for microscopic and macroscopic pKa predictions guided by the available experimental data. Top-performing submissions for macroscopic pKa predictions achieved RMSE of 0.7–1.0 pKa units and included both quantum chemical and empirical approaches, where the total number of extra or missing macroscopic pKas predicted by these submissions were fewer than 8 for 24 molecules. A large number of submissions had RMSE spanning 1–3 pKa units. Molecules with sulfur-containing heterocycles or iodo and bromo groups were less accurately predicted on average considering all methods evaluated. For a subset of molecules, we utilized experimentally-determined microstates based on NMR to evaluate the dominant tautomer predictions for each macroscopic state. Prediction of dominant tautomers was a major source of error for microscopic pKa predictions, especially errors in charged tautomers. The degree of inaccuracy in pKa predictions observed in this challenge is detrimental to the protein-ligand binding affinity predictions due to errors in dominant protonation state predictions and the calculation of free energy corrections for multiple protonation states. Underestimation of ligand pKa by 1 unit can lead to errors in binding free energy errors up to 1.2 kcal/mol. The SAMPL6 pKa Challenge demonstrated the need for improving pKa prediction methods for drug-like molecules, especially for challenging moieties and multiprotic molecules.
Keywords: SAMPL, blind prediction challenge, acid dissociation constant, pKa, small molecule, macroscopic pKa, microscopic pKa, macroscopic protonation state, microscopic protonation state
1. Introduction
The acid dissociation constant (Ka) describes the protonation state equilibrium of a molecule given pH. More commonly, we refer to pKa = − log10 Ka, its negative logarithmic form. Predicting pKa is a prerequisite for predicting many other properties of small molecules such as their protein binding affinity, distribution coefficient (log D), membrane permeability, and solubility. As a major aim of computer-aided drug design (CADD) is to aid in the assessment of pharmaceutical and physicochemical properties of virtual molecules prior to synthesis to guide decision-making, accurate computational pKa predictions are required in order to accurately model numerous properties of interest to drug discovery programs.
Ionizable sites are found often in drug molecules and influence their pharmaceutical properties including target affinity, ADME/Tox, and formulation properties [1]. It has been reported that most drugs are ionized in the range of 60-90% at physiological pH [2]. Drug molecules with titratable groups can exist in many different charge and protonation states based on the pH of the environment. Given that experimental data of protonation states and pKa are often not available, we rely on predicted pKa values to determine which charge and protonation states the molecules populate and the relative populations of these states, so that we can assign the appropriate dominant protonation state(s) in fixed-state calculations or the appropriate solvent state weights/protonation penalty to calculations considering multiple states.
The pH of the human gut ranges between 1–8, and 74% of approved drugs can change ionization state within this physiological pH range [3]. Because of this, pKa values of drug molecules provide essential information about their physicochemical and pharmaceutical properties. A wide distribution of acidic and basic pKa values, ranging from 0 to 12, have been observed in approved drugs [1, 3].
Drug-like molecules present difficulties for pKa prediction compared with simple monoprotic molecules. Drug-like molecules are frequently multiprotic, have large conjugated systems, often contain heterocycles, and can tautomerize. In addition, drug-like molecules with significant conformational flexibility can form intramolecular hydrogen bonding, which can significantly shift their pKa values compared to molecules that cannot form intramolecular hydrogen bonds. This presents further challenges for modeling methods, where deficiencies in solvation models may mispredict the propensity for intramolecular hydrogen bond formation.
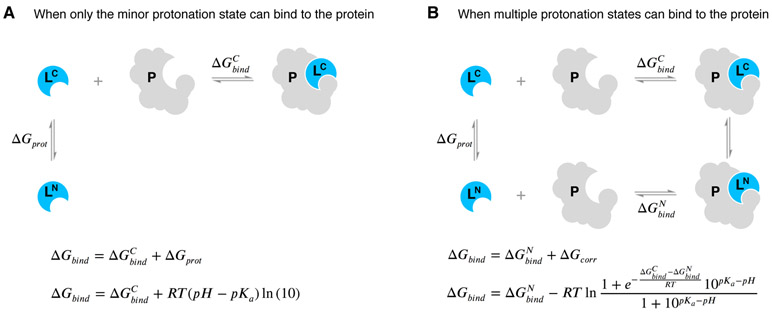
Accurately predicting pKas of drug-like molecules accurately is a prerequisite for computational drug discovery and design. Small molecule pKa predictions can influence computational protein-ligand binding affinities in multiple ways. Errors in pKa predictions can cause modeling the wrong charge and tautomerization states which affect hydrogen bonding opportunities and charge distribution within the ligand. The dominant protonation state and relative populations of minor states in aqueous medium is dictated by the molecule’s pKa values. The relative free energy of different protonation states in the aqueous state is a function of pH, and contributes to the overall protein-ligand affinity in the form of a free energy penalty for populating higher energy protonation states [4]. Any error in predicting the free energy of a minor aqueous protonation state of a ligand that dominates the complex binding free energy will directly add to the error in the predicted binding free energy, and selecting the incorrect dominant protonation state altogether can lead to even larger modeling errors. Similarly for log D predictions, an inaccurate prediction of protonation states and their relative free energies will be detrimental to the accuracy of transfer free energy predictions.
For a monoprotic weak acid (HA) or base (B)—whose dissociation equilibria are shown in Equation 1—the acid dissociation constant is expressed as in Equation 2, or, commonly, in its negative base-10 logarithmic form as in Equation 3. The ratio of ionization states can be calculated with Henderson-Hasselbalch equations shown in Equation 4.
| (1) |
| (2) |
| (3) |
| (4) |
For multiprotic molecules, the definition of pKa diverges into macroscopic pKa and microscopic pKa [5-7]. Macroscopic pKa describes the equilibrium dissociation constant between different charged states of the molecule. Each charge state can be composed of multiple tautomers. Macroscopic pKa is about the deprotonation of the molecule, rather than the location of the titratable group. A microscopic pKa describes the acid dissociation equilibrium between individual tautomeric states of different charges. (There is no pKa defined between tautomers of the same charge as they have the same number of protons and their relative populations are independent of pH.) The microscopic pKa determines the identity and distribution of tautomers within each charge state. Thus, each macroscopic charge state of a molecule can be composed of multiple microscopic tautomeric states. The microscopic pKa value defined between two microstates captures the deprotonation of a single titratable group with other titratable groups held in a fixed background protonation state. In molecules with multiple titratable groups, the protonation state of one group can affect the proton dissociation propensity of another functional group, therefore the same titratable group may have different proton affinities (microscopic pKa values) based on the protonation state of the rest of the molecule.
Different experimental methods are sensitive to changes in the total charge or the location of individual protons, so they measure different definitions of pKas, as explained in more detail in prior work [8]. Most common pKa measurement techniques such as potentiometric and spectrophotometric methods measure macroscopic pKas, while NMR measurements can determine microscopic pKas by measuring microstate populations with respect to pH. Therefore, it is important to pay attention to the source and definition of pKa values in order to correctly interpret their meaning.
Many computational methods can predict both microscopic and macroscopic pKas. While experimental measurements more often provide only macroscopic pKas, microscopic pKa predictions are more informative for determining relevant microstates (tautomers) of a molecule and their relative free energies. Predicted microstate populations can be converted to predicted macroscopic pKas for direct comparison with experimentally obtained macroscopic pKas. In this paper, we explore approaches to assess the performance of both macroscopic and microscopic pKa predictions, taking advantage of available experimental data.
Microscopic pKa predictions can be converted to macroscopic pKa predictions either directly with Equation 5 [9],
| (5) |
or through computing the macroscopic free energy of deprotonation between ionization states with charges N and N − 1 via Boltzmann-weighted sum of the relative free energy of microstates (Gi) as in Equations 6 and 7 [10].
| (6) |
| (7) |
In Equation 6 ΔGN−1,N is the effective macroscopic protonation free energy. δNi,N−1 is equal to unity when the microstate i has a total charge of N − 1 and zero otherwise. RT is the ideal gas constant times the absolute temperature.
1.1. Motivation for a blind pKa challenge
SAMPL (Statistical Assessment of the Modeling of Proteins and Ligands) is a series of annual computational prediction challenges for the computational chemistry community. The goal of the SAMPL community is to evaluate the current performance of computational models and to bring the attention of the quantitative biomolecular modeling field on problems that limit the accuracy of protein-ligand binding models. SAMPL Challenges aim to enable computer-aided drug discovery to make sustained progress toward higher accuracy by focusing the community on critical challenges that isolate one accuracy-limiting problem at a time. By conducting a series of blind challenges—which often feature the computation of specific physical properties critical for protein-ligand modeling—and encouraging rapid sharing of lessons learned, SAMPL aims to accelerate progress toward quantitative accuracy in modeling.
SAMPL Challenges that focus on physical properties have assessed intermolecular binding models of various protein-ligand and host-guest systems, as well as the prediction of hydration free energies and distribution coefficients to date. These blind challenges motivate improvements in computational methods by revealing unexpected sources of error, identifying features of methods that perform well or poorly, and enabling the participants to share information after each successive challenge. Previous SAMPL Challenges have focused on the limitations of force field accuracy, finite sampling, solvation modeling defects, and tautomer/protonation state predictions on protein-ligand binding predictions.
During the SAMPL5 log D Challenge, the performance of models in predicting cyclohexane-water log D was worse than expected—accuracy suffered when protonation states and tautomers were not taken into account [11, 12]. Many participants simply submitted log P predictions as if they were equivalent to log D, and many were not prepared to account for the contributions of different ionization states to the distribution coefficient in their models. Challenge results highlighted that log P predictions were not an accurate approximation of log D without capturing protonation state effects. The calculations were improved by including free energy penalty of the neutral state which relies on obtaining an accurate pKa prediction [11]. With the goal of deconvoluting the different sources of error contributing to the large errors observed in the SAMPL5 log D Challenge, we organized separate pKa and log P challenges in SAMPL6 [8, 13, 14]. For this iteration of the SAMPL challenge, we isolated the problem of predicting aqueous protonation states and associated pKa values.
This is the first time a blind pKa prediction challenge has been fielded as part of SAMPL. In this challenge, we aimed to assess the performance of current pKa prediction methods for drug-like molecules, investigate potential causes of inaccurate pKa estimates, and determine how the current level of accuracy of these models might impact the ability to make quantitative predictions of protein-ligand binding affinities.
1.2. Approaches to predict small molecule pKas
There are a large variety of pKa prediction methods developed for the prediction of aqueous pKas of small molecules. Broadly, we can divide pKa predictions as knowledge-based empirical methods and physical methods. Empirical methods include the following categories: Database Lookup (DL) [15], Linear Free Energy Relationship (LFER) [16-18], Quantitative Structure-Property Relationship (QSPR) [19-22], and Machine Learning (ML) approaches [23, 24]. DL methods rely on the principle that structurally similar compounds have similar pKa values and utilize an experimental database of complete structures or fragments. The pKa value of the most similar database entry is reported as the predicted pKa of the query molecule. In the QSPR approach, the pKa values are predicted as a function of various quantitative molecular descriptors, and the parameters of the function are trained on experimental datasets. A function in the form of multiple linear regression is common, although more complex forms can also be used such as the artificial neural networks in ML methods. The LFER approach is the oldest pKa prediction strategy. They use Hammett-Taft type equations to predict pKa based on classification of the molecule to a parent class (associated with a base pKa value) and two parameters that describe how the base pKa value must be modified given its substituents. Physical modeling of pKa predictions requires Quantum Mechanics (QM) models. QM methods are often utilized together with linear empirical corrections (LEC) that are designed to rescale and unbias QM predictions for better accuracy. Classical molecular mechanics-based pKa prediction methods are not feasible as deprotonation is a covalent bond breaking event that can only be captured by QM. Constant-pH molecular dynamics methods can calculate pKa shifts in large biomolecular systems where there is low degree of coupling between protonation sites and linear summation of protonation energies can be assumed [25]. However, this approach can not generally be applied to small organic molecule due to the high degree of coupling between protonation sites [26-28].
2. Methods
2.1. Design and logistics of the SAMPL6 pKa Challenge
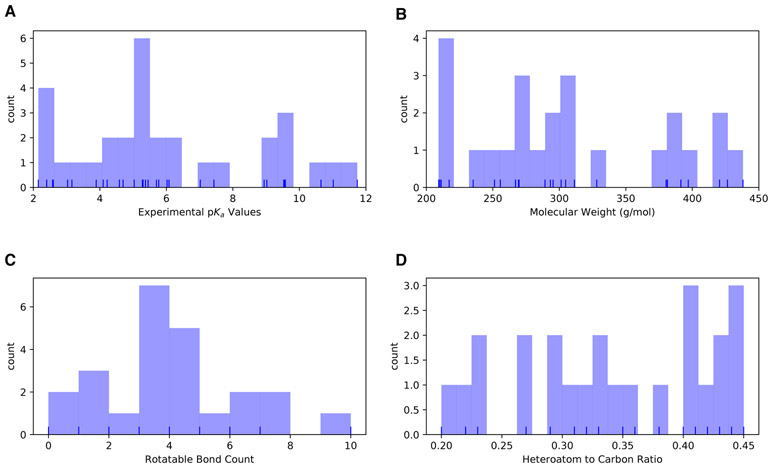
The SAMPL6 pKa Challenge was conducted as a blind prediction challenge and focused on predicting aqueous pKa values of 24 small molecules not previously reported in the literature. The challenge set was composed of molecules that resemble fragments of kinase inhibitors. Heterocycles that are frequently found in FDA-approved kinase inhibitors were represented in this set. The compound selection process was described in depth in the prior publication reporting SAMPL6 pKa Challenge experimental data collection [8]. The distribution of molecular weights, experimental pKa values, number of rotatable bonds, and heteroatom to carbon ratio are depicted in Fig. 1. The challenge molecule set was composed of 17 small molecules with limited flexibility (less than 5 non-terminal rotatable bonds) and 7 molecules with 5–10 non-terminal rotatable bonds. The distribution of experimental pKa values was roughly uniform between 2–12. 2D representations of all compounds are provided in Fig. 5. Drug-like molecules are often larger and more complex than the ones used in this study. We limited the size and the number of rotatable bonds of compounds to create molecule set of intermediate difficulty.
Figure 1. Distribution of molecular properties of the 24 compounds from the SAMPL6 pKa Challenge.
A Histogram of spectrophotometric pKa measurements collected with Sirius T3 [8]. The overlaid rug plot indicates the actual values. Five compounds have multiple measured pKas in the range of 2–12. B Histogram of molecular weights calculated for the neutral state of the compounds in SAMPL6 set. Molecular weights were calculated by neglecting counterions. C Histogram of the number of non-terminal rotatable bonds in each molecule. D The histogram of the ratio of heteroatom (non-carbon heavy atoms including, O, N, F, S, Cl, Br, I) count to the number of carbon atoms.
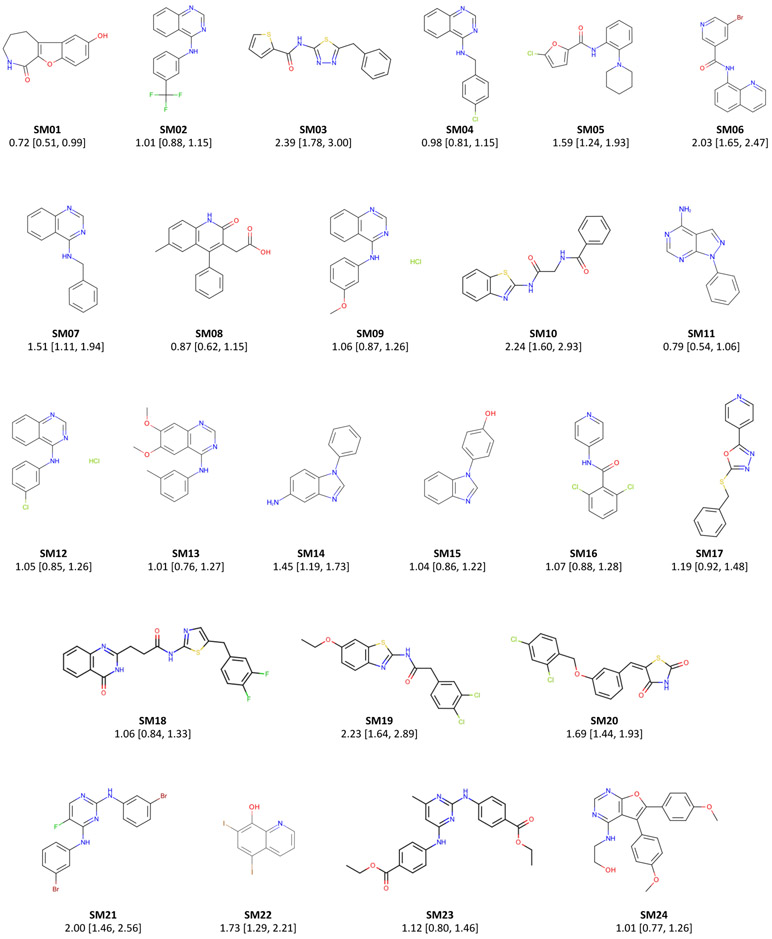
Figure 5. Molecules from the SAMPL6 Challenge with MAE calculated for all macroscopic pKa predictions.
The MAE calculated over all prediction methods indicates which molecules had the lowest prediction accuracy in the SAMPL6 Challenge. MAE values calculated for each molecule include all the matched pKa values. SM06, SM14, SM15, SM16, SM18, and SM22 were multiprotic. Hungarian matching algorithm was employed for pairing experimental and predicted pKa values. MAE values are reported with 95% confidence intervals.
The dataset composition and experimental details—without the identity of the small molecules—were announced approximately one month before the challenge start date. Experimental macroscopic pKa measurements were collected using a spectrophotometric method with the Sirius T3 (Sirius Analytical), at room temperature, in ionic strength-adjusted water with 0.15 M KCl [8]. The instructions for participation and the identity of the challenge molecules were released on the challenge start date (October 25, 2017). A table of molecule IDs (in the form of SM##) and their canonical isomeric SMILES was provided as input. Blind prediction submissions were accepted until January 22, 2018.
Following the conclusion of the blind challenge, the experimental data was made public on January 23, 2018. The SAMPL organizers and participants gathered at the Second Joint D3R/SAMPL Workshop at UC San Diego, La Jolla, CA on February 22–23, 2018 to share results. The workshop aimed to create an opportunity for participants to discuss the results, evaluate methodological choices by comparing the performance of different methods, and share lessons learned from the challenge. Participants reported their results and their own evaluations in a special issue of the Journal of Computer-Aided Molecular Design [29].
While designing this first pKa prediction challenge, we did not know the optimal format to capture pKa predictions of participants. We wanted to capture all necessary information that will aid the evaluation of pKa predictions at the submission stage. Our strategy was to directly evaluate macroscopic pKa predictions comparing them to experimental macroscopic pKa values and to use collected microscopic pKa prediction data for more in-depth diagnostics of method performance. Therefore, we asked participants to submit their predictions in three different submission types:
Type I: microscopic pKa values and related microstate pairs
Type II: fractional microstate populations as a function of pH in 0.1 pH increments
Type III: macroscopic pKa values
For each submission type, a machine-readable submission file template was specified. For type I submissions, participants were asked to report the microstate ID of the protonated state, the microstate ID of deprotonated state, the microscopic pKa, and the predicted microscopic pKa standard error of the mean (SEM). The method of microstate enumeration and why it was needed are discussed further in Section 2.2 "Enumeration of Microstates". The SEM aims to capture the statistical uncertainty of the prediction method. Microstate IDs were preassigned identifiers for each microstate in the form of SM##_micro###. For type II submissions, the submission format included a table that started with a microstate ID column and a set of columns reporting the natural logarithm of fractional microstate population values of each predicted microstate for 0.1 pH increments between pH 2 and 12. For type III submissions participants were asked to report molecule ID, macroscopic pKa, and macroscopic pKa SEM.
We required participants to submit predictions for all fields for each prediction, but it was not mandatory to submit predictions for all the molecules or all three submission types. Although we accepted submissions with partial sets of molecules, it would have been a better choice to require predictions for all the molecules for a better comparison of overall method performance. The submission files also included fields for naming the method, listing the software utilized, and a free text section to describe the methodology used in detail.
Participants were allowed to submit predictions for multiple methods as long as they created separate submission files. While anonymous participation was allowed, all participants opted to make their submissions public. Blind submissions were assigned a unique 5-digit alphanumeric submission ID, which will be used throughout this paper. Unique IDs were also assigned when multiple submissions exist for different submissions types of the same method such as microscopic pKa (type I) and macroscopic pKa (type III). These submission IDs were also reported in the evaluation papers of participants to allow cross-referencing. Submission IDs, participant-provided method names, and method categories are presented in Table 1. In many cases, multiple types of submissions (type I, II, and III) of the same method were provided by participants as challenge instructions requested. Although each prediction set was assigned a separate submission ID, we matched the submissions that originated from the same method according to the reports of the participants for cases where multiple sets of predictions came from a given method. Submission IDs for both macroscopic (type III) and microscopic (type I) pKa predictions for each method are shown in Table 1.
Table 1. Submission IDs, names, category, and type for all the pKa prediction sets.
Reference calculations are labeled as nb###. The method name column lists the names provided by each participant in the submission file. The “type” column indicates if a submission was or a post-deadline reference calculation, denoted by “Blind” or “Reference” respectively. The methods in the table are grouped by method category and not ordered by performance.
| Method Category |
Method | Microscopic pKa (Type I) Submission ID |
Macroscopic pKa (Type III) Submission ID |
Submission Type |
Ref. |
|---|---|---|---|---|---|
| DL | Substructure matches to experimental data in pKa OpenEye pKa Prospector Database v1.0 | 5nm4j | Null | [36] | |
| DL | OpenEye pKa-Prospector 1.0.0.3 with Analog Search ion identification algorithm | pwn3m | Null | [36] | |
| LFER | ACD/pKa GALAS (ACD/Percepta Kernel v1.6) | v8qph | 37xm8 | Blind | [37] |
| LFER | ACD/pKa Classic (ACD/Percepta Kernel, v1.6) | xmyhm | Blind | [38] | |
| LFER | Epik Scan (Schrödinger v2017-4) | nb007 | Reference | [30] | |
| LFER | Epik Microscopic (Schrödinger v2017-4) | nb008 | nb010 | Reference | [30] |
| QSPR/ML | OpenEye Gaussian Process | 6tvf8 | hytjn | Blind | [12] |
| QSPR/ML | OpenEye Gaussian Process Resampled | q3pfp | Blind | [12] | |
| QSPR/ML | S+pKa (ADMET Predictor v8.5, Simulations Plus) | hdiyq | gyuhx | Blind | [24] |
| QSPR/ML | Chemicalize v18.23 (ChemAxon MarvinSketch v18.23) | nb015 | Reference | [39] | |
| QSPR/ML | MoKa v3.1.3 | nb016 | nb017 | Reference | [22, 40] |
| QM | Adiabatic scheme with single point correction: SMD/M06-2X//6-311++G(d,p)//M06-2X/6-31+G(d) for bases and SMD/M06-2X//6-311++G(d,p)//M06-2X/6-31G(d) for acids + thermal corrections | ko8yx | ryzue | Blind | [41] |
| QM | Direct scheme with single point correction: SMD/M06-2X//6-311++G(d,p)//M06-2X/6-31+G(d) for bases and SMD/M06-2X//6-311++G(d,p)//M06-2X/6-31G(d) for acids + thermal corrections | w4z0e | xikp8 | Blind | [41] |
| QM | Adiabatic scheme: thermodynamic cycle that uses gas phase optimized structures for gas phase free energy and solution phase geometries for solvent phase free energy. SMD/M06-2X/6-31+G(d) for bases and SMD/M06-2X/6-31G(d) for acids + thermal corrections | wcvnu | 5byn6 | Blind | [41] |
| QM | Vertical scheme: thermodynamic cycle that uses only gas phase optimized structures to compute gas hase and solvation free energy. SMD/M06-2X/6-31+G(d) for bases and SMD/M06-2X/6-31G(d) for acids + Thermal corrections | arcko | w4iyd | Blind | [41] |
| QM | Direct scheme: solution phase free energy is determined by solution phase geometries without thermodynamic cycle SMD/M06-2X/6-31+G(d) for bases and SMD/M06-2X/6-31G(d) for acids + thermal corrections | wexjs | y75vj | Blind | [41] |
| QM + LEC | Jaguar (Schrödinger v2017-4) | nb011 | nb013 | Reference | [42] |
| QM + LEC | CPCM/B3LYP/6-311+G(d,p) and global fitting | y4wws | 35bdm | Blind | [10] |
| QM + LEC | CPCM/B3LYP/6-311+G(d,p) and separate fitting for neutral to negative and for positive to neutral transformations | qsicn | p0jba | Blind | [10] |
| QM + LEC | EC-RISM/MP2/6-311+G(d,p)-P3NI-q-noThiols-2par | kxztt | ds62k | Blind | [43] |
| QM + LEC | EC-RISM/MP2/cc-pVTZ-P2-q-noThiols-2par | ftc8w | 2ii2g | Blind | [43] |
| QM + LEC | EC-RISM/MP2/6-311+G(d,p)-P2-phi-all-2par | ktpj5 | nb001 | Blind* | [43] |
| QM + LEC | EC-RISM/MP2/6-311+G(d,p)-P2-phi-noThiols-2par | wuuvc | nb002 | Blind* | [43] |
| QM + LEC | EC-RISM/MP2/6-311+G(d,p)-P3NI-phi-all-2par | 2umai | nb003 | Blind* | [43] |
| QM + LEC | EC-RISM/MP2/6-311+G(d,p)-P3NI-phi-noThiols-2par | cm2yq | nb004 | Blind* | [43] |
| QM + LEC | EC-RISM/MP2/6-311+G(d,p)-P2-phi-all-1par | z7fhp | nb005 | Blind* | [43] |
| QM + LEC | EC-RISM/MP2/6-311+G(d,p)-P3NI-phi-all-1par | 8toyp | nb006 | Blind* | [43] |
| QM + LEC | EC-RISM/MP2/cc-pVTZ-P2-phi-noThiols-2par | epvmk | ttjd0 | Blind | [43] |
| QM + LEC | EC-RISM/MP2/cc-pVTZ-P2-phi-all-2par | xnoe0 | mkhqa | Blind | [43] |
| QM + LEC | EC-RISM/MP2/cc-pVTZ-P3NI-phi-noThiols-2par | 4o0ia | mpwiy | Blind | [43] |
| QM + LEC | EC-RISM/B3LYP/6-311+G(d,p)-P3NI-q-noThiols-2par | nxaaw | ad5pu | Blind | [43] |
| QM + LEC | EC-RISM/B3LYP/6-311+G(d,p)-P3NI-phi-noThiols-2par | 0xi4b | f0gew | Blind | [43] |
| QM + LEC | EC-RISM/B3LYP/6-311+G(d,p)-P2-phi-noThiols-2par | cywyk | np6b4 | Blind | [43] |
| QM + LEC | PCM/B3LYP/6-311+G(d,p) | gdqeg | yc70m | Blind | [43] |
| QM + LEC | COSMOtherm_FINE17 (COSMOtherm C30_1701, BP/TZVPD/FINE//BP/TZVP/COSMO) | t8ewk | 0hxtm | Blind | [44, 45] |
| QM + LEC | DSD-BLYP-D3(BJ)/def2-TZVPD//PBEh-3c[DCOSMO-RS] + RRHO(GFN-xTB[GBSA]) + Gsolv(COSMO-RS[TZVPD]) and linear fit | xvxzd | Blind | [46] | |
| QM + LEC | ReSCoSS conformations // DSD-BLYP-D3 reranking// COSMOtherm pKa: DSD-BLYP-D3(BJ)/def2-TZVPD// PBE-D3(BJ)/def2-TZVP/COSMO + RRHO[GFN-xTB + GBSA-water] + Gsolv[COSMO-RS(FINE17/TZVPD)] level and COSMOtherm pKa applied at the single conformer pair level (COSMOthermX17.0.5 release and BP-TZVPD-FINE-C30-1701 parameterization) ReSCoSS conformations // COSMOtherm pKa: DSD-BLYP-D3(BJ)/def2-TZVPD// PBE-D3(BJ)/def2-TZVP/COSMO + RRHO[GFN-xTB + GBSA-water] + Gsolv[COSMO-RS(FINE17/TZVPD)] | eyetm | 8xt50 | Blind | [46] |
| QM + LEC | ReSCoSS conformations // COSMOtherm pKa: DSD-BLYP-D3(BJ)/def2-TZVPD// PBE-D3(BJ)/def2-TZVP/COSMO + RRHO[GFN-xTB + GBSA-water] + Gsolv[COSMO-RS(FINE17/TZVPD)] level and COSMOtherm pKa was applied directly on the resulting conformer sets with at least 5% Boltzmann weights for each microspecies (COSMOthermX17.0.5 release and BP-TZVPD-FINE-C30-1701 parameterization) | ccpmw | yqkga | Blind | [46] |
| QM + MM | M06-2X/6-31G*(for bases) or 6-31+G*(for acids) for gas phase, solvation free energy using TI with explicit solvent and GAFF, solvation free energy of proton −265.6 kcal/mol | 0wfzo | Blind | [47] | |
| QM + MM | M06-2X/6-31G*(for bases) or 6-31+G*(for acids) for gas phase, solvation free energy using TI with explicit solvent and GAFF, solvation free energy of proton −271.88 kcal/mol | z3btx | Blind | ||
| QM + MM | M06-2X/6-31G*(for bases) or 6-31+G*(for acids) + thermal state correction for gas phase, solvation free energy using TI with explicit solvent and GAFF, solvation free energy of proton −265.6 kcal/mol | 758j8 | Blind | ||
| QM + MM | M06-2X/6-31G*(for bases) or 6-31+G*(for acids) + thermal state correction for gas phase, solvation free energy using TI with explicit solvent and GAFF, solvation free energy of proton −271.88 kcal/mol | hgn83 | Blind |
Microscopic pKa submissions were blind, however, participant requested a correction after blind submission deadline for macroscopic pKa submissions. Therefore, these were assigned submission IDs in the form of nb###.
2.2. Enumeration of microstates
To capture both the pKa value and titrating proton position for microscopic pKa predictions, we needed microscopic pKa values to be reported together with a pair of microstates which describe the protonated and deprotonated states corresponding to each microscopic transition. String representations of molecules such as canonical SMILES with explicit hydrogens can be written, however, there can be inconsistencies between the interpretation of canonical SMILES written by different software and algorithms. To avoid complications while reading microstate structure files from different sources, we decided that the safest route was pre-enumerating all possible microstates of challenge compounds, assigning microstate IDs to each in the form of SM##_micro###, and requiring participants to report microscopic pKa values along with microstate pairs specified by the provided microstates IDs.
We created initial sets of microstates with Schrödinger Epik [30] and OpenEye QUACPAC [31] and took the union of results. Microstates with Epik were generated using Schrödinger Suite v2016-4, running Epik to enumerate all tautomers within 20 pKa units of pH 7. For enumerating microstates with OpenEye QUACPAC, we had to first enumerate formal charges and for each charge enumerate all possible tautomers using the settings of maximum tautomer count 200, level 5, with carbonyl hybridization set to False. Then we created a union of all enumerated states written as canonical isomeric SMILES generated by OpenEye OEChem [32]. Even though resonance structures correspond to different canonical isomeric SMILES, they are not different microstates, therefore it was necessary to remove resonance structures that were replicates of the same tautomer. To detect equivalent resonance structures, we converted canonical isomeric SMILES to InChI hashes with explicit and fixed hydrogen layer. Structures that describe the same tautomer but different resonance states lead to explicit hydrogen InChI hashes that are identical, allowing replicates to be removed. The Jupyter Notebook used for the enumeration of microstates is provided in Supplementary Information.
We provided microstate ID tables with canonical SMILES and 2D depictions to aid participants in matching predicted structures to microstate IDs. A canonical SMILES representation was selected over canonical isomeric SMILES, because resonance and geometric isomerism do not lead to different microstates according to our working microstate definition. The only exception was for molecule SM20, which should be consistently modeled as the E-isomer.
During the course of the SAMPL6 Challenge, participants identified new microstates that were not present in the initial list that we provided. Despite combining enumerated charge states and tautomers generated by both Epik and OpenEye QUACPAC, to our surprise, the microstate lists were still incomplete. Based on participant requests for new microstates, we iteratively had to update the list of microstates and assign new microstate IDs. Every time we received a request, we shared the updated microstate ID lists with all challenge participants. Some participants updated their pKa prediction by including the newly added microstates in their calculations. In the future, developing a better algorithm that can enumerate all possible microstates (not just the ones with significant populations) would be very beneficial for anticipating microstates that may be predicted by pKa prediction methods.
A microscopic pKa definition was provided in challenge instructions for clarity as follows: Physically meaningful microscopic pKas are defined between microstate pairs that can interconvert by single protonation/deprotonation event of only one titrable group. So, microstate pairs should have total charge (absolute) difference of 1 and only one heavy atom that differs in the number of associated hydrogens, regardless of resonance state or geometric isomerism. All geometric isomer and resonance structure pairs that have the same number of hydrogens bound to equivalent heavy atoms are grouped into the same microstate. Pairs of resonance structures and geometric isomers (cis/trans, stereo) are not considered as different microstates, as long as there is no change in the number of hydrogens bound to each heavy atom. Transitions where there are shifts in the position of protons coupled to changes in the number of protons were also not considered as microscopic pKa values [26]. Since we wanted participants to report only microscopic pKas that describe single deprotonation events (in contrast to transitions between microstates that are different in terms of two or more titratable protons), we have also provided a pre-enumerated list of allowed microstate pairs.
Provided microstate ID and microstate pair lists were intended to be used for reporting microstate IDs and to aid parsing of submissions. The enumerated lists of microstates were not created with the intent to guide computational predictions. This was clearly stated in the challenge instructions. However, we noticed that some participants still used the microstate lists as an input for their pKa predictions as we received complaints from participants that due to our updates to microstate lists they needed to repeat their calculations. This would not have been an issue if participants used pKa prediction protocols that did not rely on an external pre-enumerated list of microstates as an input. None of the participants reported this dependency in their method descriptions explicitly, so it was also not obvious how participants were using the provided states in their predictions. We could not identify which submissions used these enumerated microstate lists as input for predictions and which have followed the challenge instructions and relied only on their prediction method to generate microstates.
2.3. Evaluation approaches
Since the experimental data for the challenge was mainly composed of macroscopic pKa values of both monoprotic and multiprotic compounds, evaluation of macroscopic and microscopic pKa predictions was not straightforward. For a subset of 8 molecules, the dominant microstate sequence could be inferred from NMR experiments. For the rest of the molecules, the only experimental information available was the macroscopic pKa value. The experimental data—in the form of macroscopic pKa values—did not provide any information on which group(s) are being titrated, the microscopic pKa values, the identity of the associated macrostates (which total charge), or microstates (which tautomers). Also, experimental data did not provide any information about the charge state of protonated and deprotonated species associated with each macroscopic pKa. Typically charges of states associated with experimental pKa values are assigned based on pKa predictions, not experimental evidence, but we did not utilize such computational charge assignment. For a fair performance comparison between methods, we avoided relying on any particular pKa prediction to assist the interpretation of the experimental reference data. This choice complicated the pKa prediction analysis, especially regarding how to pair experimental and predicted pKa values for error analysis. We adopted various evaluation strategies guided by the experimental data. To compare macroscopic pKa predictions to experimental values, we had to utilize numerical matching algorithms before we could calculate performance statistics. For the subset of molecules with experimental data about microstates, we used microstate-based matching. These matching methods are described in more detail in the next section.
Three types of submissions were collected during the SAMPL6 pKa Challenge. We have only utilized the type I (microscopic pKa value and microstate IDs) and the type III (macroscopic pKa value) predictions in this article. Type I submissions contained the same prediction information as the type II submissions which reported the fractional population of microstates with respect to pH. We collected type II submissions in order to capture relative populations of microstates, not realizing they were redundant. The microscopic pKa predictions collected in type I submissions capture all the information necessary to calculate type II submissions. Therefore, we did not use type II submissions for challenge evaluation. In theory, type III (macroscopic pKa) predictions can also be calculated from type I submissions, but collecting type III submissions allowed the participation of pKa prediction methods that directly predict macroscopic pKa values without considering microspeciation and methods that apply special empirical corrections for macroscopic pKa predictions.
2.3.1. Matching algorithms for pairing predicted and experimental pKa values
Macroscopic pKa predictions can be calculated from microscopic pKa values for direct comparison to experimental macroscopic pKa values. One major question must be answered to allow this comparison: How should we match predicted macroscopic pKa values to experimental macroscopic pKa values when there could multiple pKa values reported for a given molecule? For example, experiments on SM18 showed three macroscopic pKas, but prediction of xvxzd method reported two macroscopic pKa values. There were also examples of the opposite situation with more predicted pKa values than experimentally determined macroscopic pKas: One experimental pKa was measured for SM02, but two macroscopic pKa values were predicted by xvxzd method. The experimental and predicted values must be paired before any prediction error can be calculated, even though there was not any experimental information regarding underlying tautomer and charge states.
Knowing the charges of macrostates would have guided the pairing between experimental and predicted macroscopic pKa values, however, not all experimental pKa measurements can determine determine the charge of protonation states. The potentiometric pKa measurements just captures the relative charge change between macrostates, but not the absolute value of the charge. Thus, our experimental data did not provide any information that would indicate the titration site, the overall charge, or the tautomer composition of macrostate pairs that are associated with each measured macroscopic pKa that can guide the matching between predicted and experimental pKa values.
For evaluating macroscopic pKa predictions taking the experimental data as reference, Fraczkiewicz [23] delineated recommendations for fair comparative analysis of computational pKa predictions. They recommended that, in the absence of any experimental information that would aid in matching, experimental and computational pKa values should be matched preserving the order of pKa values and minimizing the sum of absolute errors.
We picked the Hungarian matching algorithm [33, 34] to match experimental and predicted macroscopic pKa values with a squared error cost function as suggested by Kiril Lanevskij via personal communication. The algorithm is available in the SciPy package (scipy.optimize.linear_sum_assignment) [35]. This matching algorithm provides optimum global assignment that minimizes the linear sum of squared errors of all pairwise matches. We selected the squared error cost function instead of the absolute error cost function to avoid misordered matches, For instance, for a molecule with experimental pKa values of 4 and 6, and predicted pKa values of 7 and 8, Hungarian matching with absolute error cost function would match 6 to 7 and 4 to 9. Hungarian matching with squared error cost would match 4 to 7 and 6 to 9, preserving the increasing pKa value order between experimental and predicted values. A weakness of this approach would be failing to match the experimental value of 6 to predicted value of 7 if that was the correct match based on underlying macrostates. But the underlying pair of states were unknown to us both because the experimental data did not determine which charge states the transitions were happening between and also because we did not collect the pair of macrostates associated with each pKa predictions in submissions. Requiring this information for macroscopic pKa predictions in future SAMPL challenges would allow for better comparison between predictions, even if experimental assignment of charges is not possible. There is no perfect solution to the numerical pKa assignment problem, but we tried to determine the fairest way to penalize predictions based on their numerical deviation from the experimental values.
For the analysis of microscopic pKa predictions we adopted a different matching approach. For the eight molecules for which we had the requisite data for this analysis, we utilized the dominant microstate sequence inferred from NMR experiments to match computational predictions and experimental pKa values. We will refer to this assignment method as microstate matching, where the experimental pKa value is matched to the computational microscopic pKa value which was reported for the dominant microstate pair observed for each transition. We have compared the results of Hungarian matching and microstate matching.
Inevitably, the choice of matching algorithms to assign experimental and predicted values has an impact on the computed performance statistics. We believe the Hungarian algorithm for numerical matching of unassigned pKa values and microstate-based matching when experimental microstates are known were the best choices, providing the most unbiased matching without introducing assumptions outside of the experimental data.
2.3.2. Statistical metrics for submission performance
A variety of accuracy and correlation statistics were considered for analyzing and comparing the performance of prediction methods submitted to the SAMPL6 pKa Challenge. Calculated performance statistics of predictions were provided to participants before the workshop. Details of the analysis and scripts are maintained on the SAMPL6 GitHub Repository (described in Section 5).
Error metrics
There are six error metrics reported for the numerical error of the pKa values: the root-mean-squared error (RMSE), mean absolute error (MAE), mean error (ME), coefficient of determination (R2), linear regression slope (m), and Kendall’s Rank Correlation Coefficient (τ). Uncertainty in each performance statistic was calculated as 95% confidence intervals estimated by non-parametric bootstrapping (sampling with replacement) over predictions with 10 000 bootstrap samples. Calculated errors statistics of all methods can be found in Table S2 for macroscopic pKa predictions and Tables S4 and S4 for microscopic pKa predictions.
Assessing macrostate predictions
In addition to assessing the numerical error in predicted pKa values, we also evaluated predictions in terms of their ability to capture the correct macrostates (ionization states) and microstates (tautomers of each ionization state) to the extent possible from the available experimental data. For macroscopic pKas, the spectrophotometric experiments do not directly report on the identity of the ionization states. However, the number of ionization states indicates the number of macroscopic pKas that exists between the experimental range of 2.0–12.0. For instance, SM14 has two experimental pKas and therefore three different charge states observed between pH 2.0 and 12.0. If a prediction reported 4 macroscopic pKas, it is clear that this method predicted an extra ionization state. With this perspective, we reported the number of unmatched experimental pKas (the number of missing pKa predictions, i.e., missing ionization states) and the number of unmatched predicted pKas (the number of extra pKa predictions, i.e., extra ionization states) after Hungarian matching. The latter count was restricted to only predictions with pKa values between 2 and 12 because that was the range of the experimental method. Errors in extra or missing pKa prediction errors highlight failure to predict the correct number of ionization states within a pH range.
Assessing microstate predictions
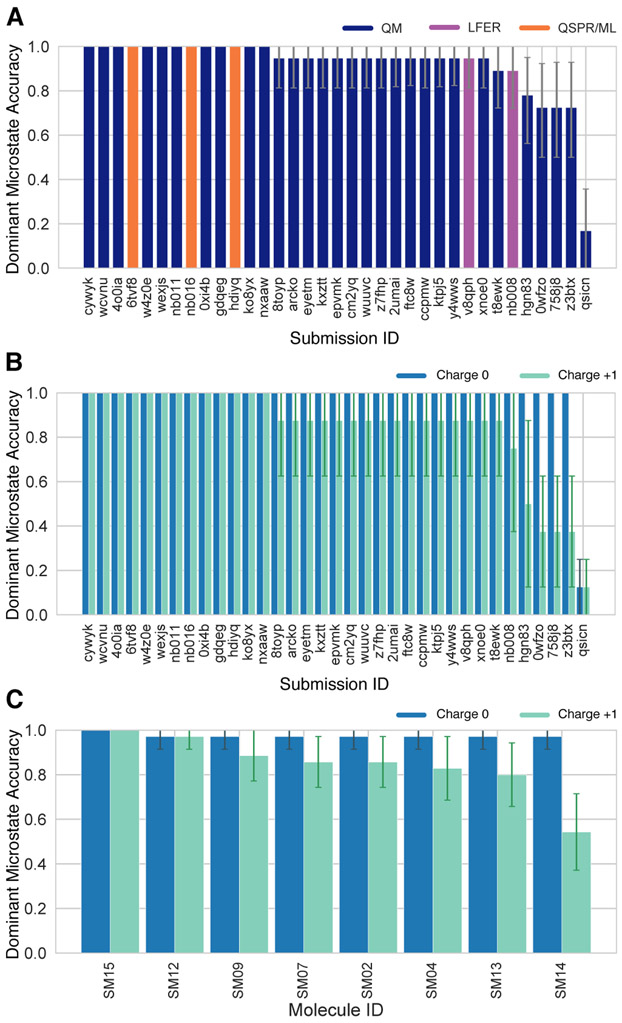
For the evaluation of microscopic pKa predictions, taking advantage of the available dominant microstate sequence data for a subset of 8 compounds, we calculated the dominant microstate prediction accuracy which is the ratio of correct dominant tautomer predictions for each charge state divided by the total number of dominant tautomer predictions. Dominant microstate prediction accuracy was calculated over all experimentally detected ionization states of each molecule which were part of this analysis. In order to extract the sequence of dominant microstates from the microscopic pKa predictions sets, we calculated the relative free energy of microstates selecting a neutral tautomer and pH 0 as reference following Equation 8. Calculation of relative microstate free energies was explained in more detail in a previous publication [26].
The relative free energy of a state with respect to reference state B at pH 0.0 (arbitrary pH value selected as reference) can be calculated as follows:
| (8) |
ΔmAB is equal to the number protons in state A minus that in state B. R and T indicate the molar gas constant and temperature, respectively. By calculating relative free energies of all predicted microstates with respect to the same reference state and pH, we were able to determine the sequence of predicted dominant microstates. The dominant tautomer of each charge state was determined as the microstate with the lowest free energy in the subset of predicted microstates of each ionization state. This approach is feasible because the relative free energy of tautomers of the same ionization state is independent of pH and therefore the choice of reference pH is arbitrary.
Identifying consistently top-performing methods
We created a shortlist of top-performing methods for macroscopic and microscopic pKa predictions. The top macroscopic pKa predictions were selected if they ranked in the top 10 consistently according to two error metrics (RMSE, MAE) and two correlation metrics (R-Squared, and Kendall’s Tau), while also having fewer than eight missing or extra macroscopic pKas for the entire molecule set (eight macrostate errors correspond to macrostate prediction mistake in roughly one third of the 24 compounds). These methods are presented in Table 2. A separate list of top-performing methods was constructed for microscopic pKa with the following criteria: ranking in the top 10 methods when ranked by accuracy statistics (RMSE and MAE) and perfect dominant microstate prediction accuracy. These methods are presented in Table 3.
Table 2. Four consistently well-performing prediction methods for macroscopic pKa prediction based on consistent ranking within the Top 10 according to various statistical metrics.
Submissions were ranked according to RMSE, MAE, R2, and τ. Consistently well-performing methods were selected as the ones that rank in the Top 10 in each of these statistical metrics. These methods also have less than 2 unmatched experimental pKas and less than 7 unmatched predicted pKas according to Hungarian matching. Performance statistics are provided as mean and 95% confidence intervals.
| Submission ID | Method Name | RMSE | MAE | R2 | Kendall’s Tau (τ) |
Unmatched Exp. pKa Count |
Unmatched Pred. pKa Count [2, 12] |
|---|---|---|---|---|---|---|---|
| xvxzd | Full quantum chemical calculation of free energies and fit to experimental pKa | 0.68 [0.54, 0.81] | 0.58 [0.45, 0.71] | 0.94 [0.88, 0.97] | 0.82 [0.68, 0.92] | 2 | 4 |
| gyuhx | S+pKa | 0.73 [0.55, 0.91] | 0.59 [0.44, 0.74] | 0.93 [0.88, 0.96] | 0.88 [0.8, 0.94] | 0 | 7 |
| xmyhm | ACD/pKa Classic | 0.79 [0.52, 1.03] | 0.56 [0.38, 0.77] | 0.92 [0.85, 0.97] | 0.81 [0.68, 0.9] | 0 | 3 |
| 8xt50 | ReSCoSS conformations // DSD-BLYP-D3 reranking // COSMOtherm pKa | 1.07 [0.78, 1.36] | 0.81 [0.58, 1.07] | 0.91 [0.84, 0.95] | 0.80 [0.68, 0.89] | 0 | 0 |
Table 3. Top-performing methods for microscopic pKa predictions based on consistent ranking within the Top 10 according to various statistical metrics calculated for 8 molecule dataset.
Performance statistics are provided as mean and 95% confidence intervals. Submissions that rank in the Top 10 according to RMSE and MAE and have perfect dominant microstate prediction accuracy were selected as consistently well-performing methods. Correlation-based statistics (R2, and Kendall’s Tau), although reported in the table, were excluded from the statistics used for determining top-performing methods. This was because correlation-based statistics were not very discriminating due to the narrow dynamic range and the small number of data points in the 8 molecule dataset with NMR-determined dominant microstates.
| Submission ID |
Method Name | Dominant Microstate Accuracy |
RMSE | MAE | R2 | Kendall’s Tau | Unmatched Exp. pKa Count |
Unmatched Pred. pKa Count [2,12] |
|---|---|---|---|---|---|---|---|---|
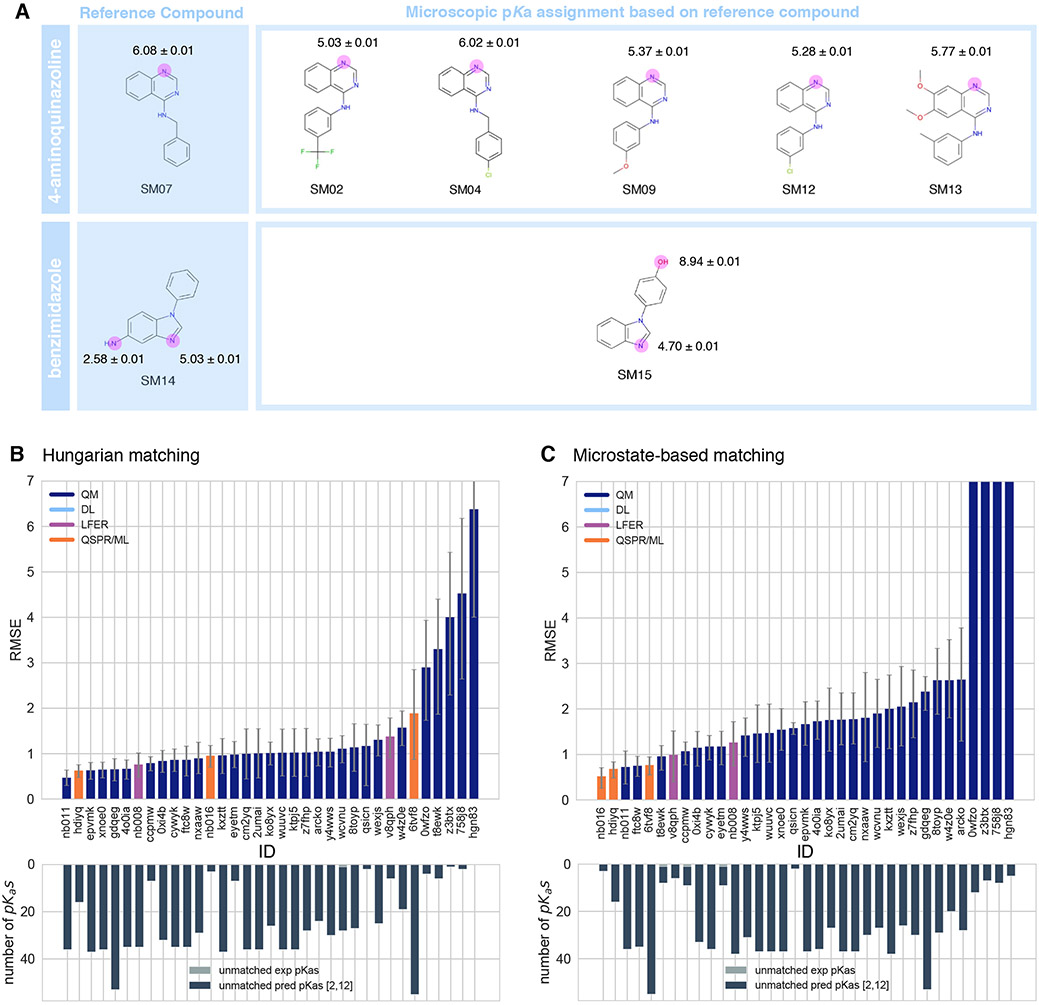
| nb016 | MoKa | 1.0 [1.0, 1.0] | 0.52 [0.25, 0.71] | 0.43 [0.23, 0.65] | 0.92 [0.05, 0.99] | 0.62 [−0.14, 1.00] | 0 | 3 |
| hdiyq | S+pKa | 1.0 [1.0, 1.0] | 0.68 [0.49, 0.83] | 0.60 [0.39, 0.80] | 0.86 [0.47, 0.98] | 0.78 [0.40, 1.00] | 0 | 16 |
| nb011 | Jaguar | 1.0 [1.0, 1.0] | 0.72 [0.35, 1.07] | 0.54 [0.28, 0.86] | 0.86 [0.18, 0.98] | 0.64 [0.26, 0.95] | 0 | 36 |
| 6tvf8 | OE Gaussian Process | 1.0 [1.0, 1.0] | 0.76 [0.55, 0.95] | 0.68 [0.46, 0.90] | 0.92 [0.78, 0.99] | 0.87 [0.6, 1.00] | 0 | 55 |
| 0xi4b | EC-RISM/B3LYP/6-311+G(d,p)-P3NI-phi-noThiols-2par | 1.0 [1.0, 1.0] | 1.15 [0.75, 1.50] | 0.98 [0.63, 1.36] | 0.77 [0.02, 0.98] | 0.51 [−0.14, 1.00] | 0 | 33 |
| cywyk | EC-RISM/B3LYP/6-311+G(d,p)-P2-phi-noThiols-2par | 1.0 [1.0, 1.0] | 1.17 [0.88, 1.41] | 1.06 [0.74, 1.35] | 0.73 [0.02, 0.98] | 0.56 [−0.08, 1.00] | 0 | 36 |
Determining challenging molecules
In addition to comparing the performance of methods, we also wanted to compare pKa prediction performance for each molecule to determine which molecules were the most challenging for pKa predictions considering all the methods in the challenge. For this purpose, we plotted prediction error distributions of each molecule calculated over all prediction methods. We also calculated MAE for each molecule over all prediction sets as well as for predictions from each method category separately.
2.4. Reference calculations
Including a null model is helpful in comparative performance analysis of predictive methods to establish what the performance statistics look like for a baseline method for the specific dataset. Null models or null predictions employ a simple prediction model which is not expected to be particularly successful, but it provides a simple point of comparison for more sophisticated methods. The expectation or goal is for more sophisticated or costly prediction methods to outperform the predictions from a null model, otherwise the simpler null model would be preferable. In SAMPL6 pKa Challenge there were two blind submissions using database lookup methods that were submitted to serve as null predictions. These methods, with submission IDs 5nm4j and 5nm4j both used OpenEye pKa-Prospector database to find the most similar molecule to query molecule and simply reported its pKa as the predicted value. Database lookup methods with a rich experimental database do present a challenging null model to beat, however, due to the accuracy level needed from pKa predictions for computer-aided drug design we believe such methods provide an appropriate performance baseline that physical and empirical pKa prediction methods should strive to outperform.
We also included additional reference calculations in the comparative analysis to provide more perspective. Some widely used methods by academia and industry were missing from the blind challenge submission. Therefore, we included those methods as reference calculations: Schrödinger/Epik (nb007, nb008, nb010), Schrödinger/Jaguar (nb011, nb013), Chemaxon/Chemicalize (nb015), and Molecular Discovery/MoKa (nb016, nb017). Epik and Jaguar pKa predictions were collected by Bas Rustenburg, Chemicalize predictions by Mehtap Isik, and MoKa predictions by Thomas Fox. All were done after the challenge deadline avoiding any alterations to their respective standard procedures and any guidance from experimental data. Experimental data was publicly available before these calculations were complete, therefore reference calculations were not formally considered as blind submissions.
All figures and statistics tables in this manuscript include reference calculations. As the reference calculations were not formal submissions, these were omitted from formal ranking in the challenge, but we present plots in this article which show them for easy comparison. These are labeled with submission IDs of the form nb### to clearly indicate non-blind reference calculations.
3. Results and Discussion
Participation in the SAMPL6 pKa Challenge was high with 11 research groups contributing pKa prediction sets for 37 methods. A large variety of pKa prediction methods were represented in the SAMPL6 Challenge. We categorized these submissions into four method classes: database lookup (DL), linear free energy relationship (LFER), quantitative structure-property relationship or machine learning (QSPR/ML), and quantum mechanics (QM). Quantum mechanics models were subcategorized into QM methods with and without linear empirical correction (LEC), and combined quantum mechanics and molecular mechanics (QM + MM). Table 1 presents method names, submission IDs, method categories, and also references for each approach. Integral equation-based approaches (e.g.EC-RISM) were also evaluated under the Physical (QM) category. There were 2 DL, 4 LFER, and 5 QSPR/ML methods represented in the challenge, including the reference calculations. The majority of QM calculations include linear empirical corrections (22 methods in QM + LEC category), and only 5 QM methods were submitted without any empirical corrections. There were 4 methods that used a mixed physical modeling approach of QM + MM.
The following sections present a detailed performance evaluation of blind submissions and reference prediction methods for macroscopic and microscopic pKa predictions. Performance statistics of all the methods can be found in Tables S2 and S4. Methods are referred to by their submission ID’s which are provided in Table 1.
3.1. Analysis of macroscopic pKa predictions
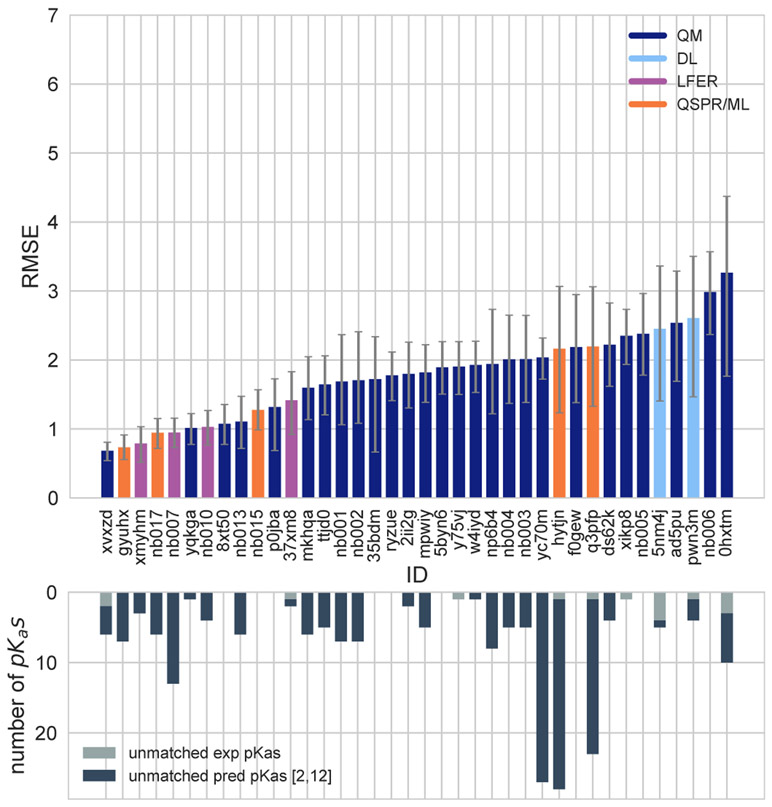
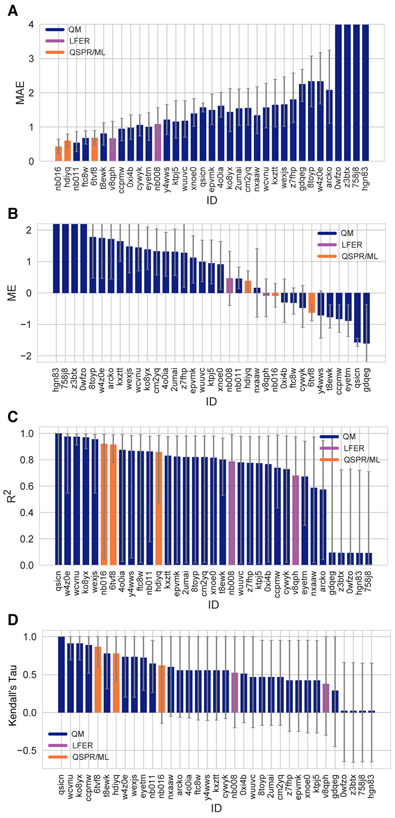
The performance of macroscopic pKa predictions was analyzed by comparison to experimental pKa values collected by the spectrophotometric method via numerical matching following the Hungarian method. Overall pKa prediction performance was worse than we hoped. Fig. 2 shows RMSE calculated for each prediction method represented by their submission IDs. Other performance statistics are depicted in Fig. 3. In both figures, method categories are indicated by the color of the error bars. The statistics depicted in these figures can be found in Table S2. Prediction error ranged between 0.7 to 3.2 pKa units in terms of RMSE, while an RMSE between 2-3 log units was observed for the majority of methods (20 out of 38 methods). Only five methods achieved RMSE less than 1 pKa unit. One is QM method with COSMO-RS approach for solvation and linear empirical correction (xvxzd (DSD-BLYP-D3(BJ)/def2-TZVPD//PBEh-3c[DCOSMO-RS] + RRHO(GFN-xTB[GBSA]) + Gsolv(COSMO-RS[TZVPD]) and linear fit)), and the remaining four are empirical prediction methods of LFER (xmyhm (ACD/pKa Classic), nb007 (Schrödinger/Epik Scan)) and QSPR/ML categories (gyuhx (Simulations Plus), nb017 (MoKa)). These five methods with RMSE less than 1 pKa unit are also the methods that have the lowest MAE. xmyhm and xvxzd were the only two methods for which the upper 95% confidence interval of RMSE was lower than 1 pKa unit.
Figure 2. RMSE and unmatched pKa counts vs. submission ID plots for macroscopic pKa predictions based on Hungarian matching.
Methods are indicated by submission IDs. RMSE is shown with error bars denoting 95% confidence intervals obtained by bootstrapping over challenge molecules. Submissions are colored by their method categories. Light blue colored database lookup methods are utilized as the null prediction method. QM methods category (navy) includes pure QM, QM+LEC, and QM+MM approaches. Lower bar plots show the number of unmatched experimental pKa values (light grey, missing predictions) and the number of unmatched pKa predictions (dark grey, extra predictions) for each method between pH 2 and 12. Submission IDs are summarized in Table 1. Submission IDs of the form nb### refer to non-blinded reference methods computed after the blind challenge submission deadline. All others refer to blind, prospective predictions.
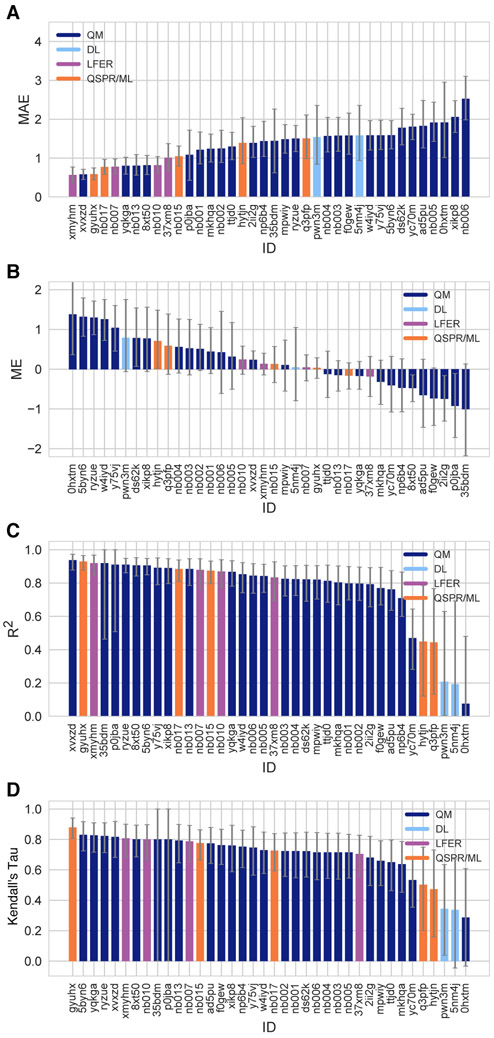
Figure 3. Additional performance statistics for macroscopic pKa predictions based on Hungarian matching.
Methods are indicated by submission IDs. Mean absolute error (MAE), mean error (ME), Pearson’s R2, and Kendall’s Rank Correlation Coefficient Tau (τ) are shown, with error bars denoting 95% confidence intervals were obtained by bootstrapping over challenge molecules. Refer to Table 1 for the submission IDs and method names. Submissions are colored by their method categories. Light blue colored database lookup methods are utilized as the null prediction method.
In terms of correlation statistics, many methods have good performance, although the ranking of methods changes according to R2 and Kendall’s Tau. Therefore, many methods are indistinguishable from one another, considering the uncertainty of the correlation statistics. 32 out of 38 methods have R and Kendall’s Tau higher than 0.7 and 0.6, respectively. 8 methods have R2 higher than 0.9 and 6 methods have Kendall’s Tau higher than 0.8. The overlap of these two sets are the following: gyuhx (Simulations Plus), xvxzd (DSD-BLYP-D3(BJ)/def2-TZVPD//PBEh-3c[DCOSMO-RS] + RRHO(GFN-xTB[GBSA]) + Gsolv(COSMO-RS[TZVPD]) and linear fit), xmyhm (ACD/pKa Classic), ryzue (Adiabatic scheme with single point correction: MD/M06-2X//6-311++G(d,p)//M06-2X/6-31+G(d) for bases and SMD/M06-2X//6-311++G(d,p)//M06-2X/6-31G(d) for acids + thermal corrections), and 5byn6 (Adiabatic scheme: thermodynamic cycle that uses gas phase optimized structures for gas phase free energy and solution phase geometries for solvent phase free energy. SMD/M06-2X/6-31+G(d) for bases and SMD/M06-2X/6-31G(d) for acids + thermal corrections). It is worth noting that ryzue and 5byn6 are QM predictions without any empirical correction. Their high correlation and rank correlation coefficient scores signal that with an empirical correction their accuracy based performance could improve. Indeed, the participants have shown that this is the case in their own challenge analysis paper and achieved RMSE of 0.73 pKa units after the challenge [41].
Null prediction methods based on database lookup (5nm4j and pwn3m) had similar performance, with an RMSE of roughly 2.5 pKa units, an MAE of 1.5 pKa units, R2 of 0.2, and Kendall’s Tau of 0.3. Many methods were observed to have a prediction performance advantage over the null predictions shown in light blue in Fig. 2 and Fig. 3 considering all the performance metrics as a whole. In terms of correlation statistics, the null methods are the worst performers, except for 0hxtm. From the perspective of accuracy-based statistics (RMSE and MAE), only the top 10 methods were observed to have significantly lower errors than the null methods considering the uncertainty of error metrics expressed as 95% confidence intervals.
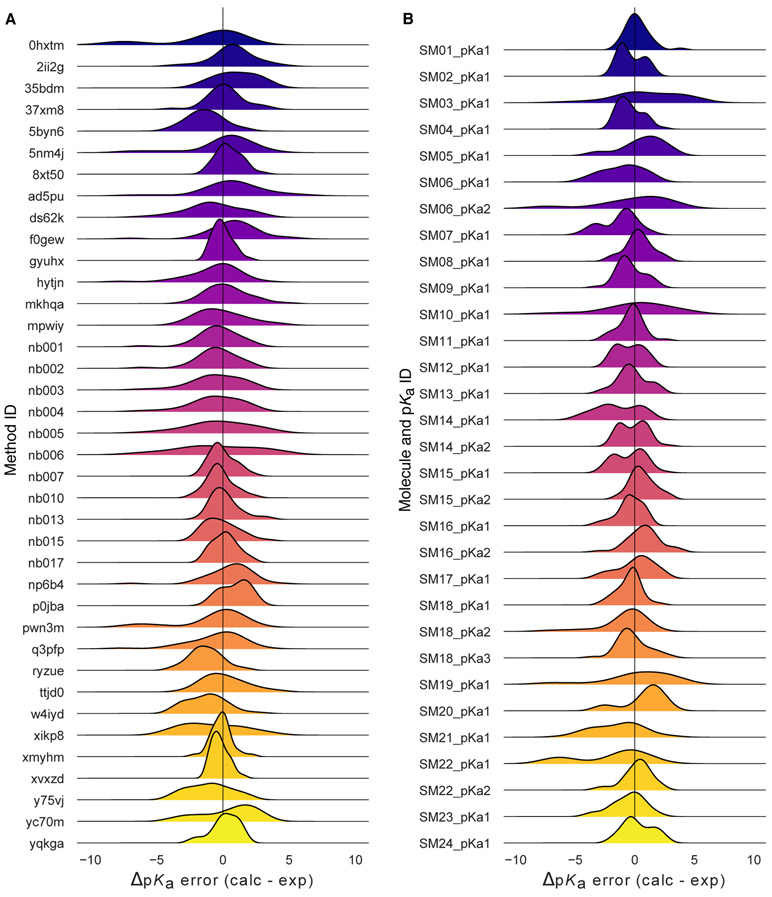
The distribution of macroscopic pKa prediction signed errors observed in each submission was plotted in Fig. 7A as ridge plots using the Hungarian matching scheme. 2ii2g, f0gew, np64b, p0jba, and yc70m tended to overestimate, while 5byn6, ryzue, and w4iyd tended to underestimate macroscopic pKa values.
Figure 7. Macroscopic pKa prediction error distribution plots show how prediction accuracy varies across methods and individual molecules.
(A) pKa prediction error distribution for each submission for all molecules according to Hungarian matching. (B) Error distribution for each SAMPL6 molecule for all prediction methods according to Hungarian matching. For multiprotic molecules, pKa ID numbers (pKa1, pKa2, and pKa3) were assigned in the direction of increasing experimental pKa value.
Four submissions in the QM+LEC category used the COSMO-RS implicit solvation model. While three of these achieved the lowest RMSE among QM-based methods (xvxzd, yqkga, and 8xt50) [46], one of them showed the highest RMSE (0hxtm (COSMOtherm_FINE17)) among all SAMPL6 Challenge macroscopic pKa predictions. All four methods used COSMO-RS/FINE17 to compute solvation free energies. The major difference between the three low-RMSE methods and 0hxtm seems to be the protocol for determining relevant conformations for each microstate. xvxzd, yqkga, and 8xt50 used a semi-empirical tight binding (GFN-xTB) method and GBSA continuum solvation model for geometry optimization, followed by high level single-point energy calculations with a solvation free energy correction (COSMO-RS(FINE17/TZVPD)) and rigid rotor harmonic oscillator (RRHO[GFN-xTB(GBSA]) correction. yqkga, and 8xt50 selected conformations for each microstate with the Relevant Solution Conformer Sampling and Selection (ReSCoSS) workflow [46]. The conformations were clustered according to shape, and the lowest energy conformations from each cluster (according to BP86/TZVP/COSMO single point energies in any of the 10 different COSMO-RS solvents) were considered as relevant conformers. The yqkga method further filtered out conformers that have less than 5% Boltzmann weights at the DSD-BLYP-D3/def2-TZVPD + RRHO(GFNxTB) + COSMO-RS(fine) level. The xvxzd method used an MF–MD–GC//GFN-xTB workflow and energy thresholds of 6 kcal/mol and 10 kcal/mol, for conformer and microstate selection. On the other hand, the conformational ensemble captured for each microstate seems to be more limited for the 0hxtm method, judging by the method description provided in the submission file (this participant did not publish an analysis of the results that they obtained for SAMPL6). The 0hxtm method reported that relevant conformations were computed with the COSMOconf 4.2 workflow which produced multiple relevant conformers for only the neutral states of SM18 and SM22. In contrast to xvxzd, yqkga, and 8xt50, the 0hxtm method also did not include a RRHO correction. Participants who submitted the three low-RMSE methods report that capturing the chemical ensemble for each molecule including conformers and tautomers and high-level QM calculations led to more successful macroscopic pKa prediction results and RRHO correction provided a minor improvement [46]. Comparing these results to other QM approaches in the SAMPL Challenge also points to the advantage of the COSMO-RS solvation approach compared to other implicit solvent models.
In addition to the statistics related to the pKa value, we also analyzed missing or extra pKa predictions. Analysis of the pKa values with accuracy- and correlation-based error metrics was only possible after the matching of predicted macroscopic pKa values to experimental pKa values through Hungarian matching, although this approach masks pKa prediction issues in the form of extra or missing macroscopic pKa predictions. To capture this class of prediction errors, we reported the number of unmatched experimental pKas (missing pKa predictions) and the number of unmatched predicted pKas (extra pKa predictions) after Hungarian matching for each method. Both missing and extra pKa prediction counts were only considered for the pH range of 2–12, which corresponds to the limits of the experimental assay. The lower subplot of Fig. 2 shows the total count of unmatched experimental or predicted pKa values for all the molecules in each prediction set. The order of submission IDs in the x-axis follows the RMSD based ranking so that the performance of each method from both pKa value accuracy and the number of pKas can be viewed together. The omission or inclusion of extra macroscopic pKa predictions is a critical error because inaccuracy in predicting the correct number of macroscopic transitions shows that methods are failing to predict the correct set of charge states, i.e., failing to predict the correct number of ionization states that can be observed between the specified pH range.
In the analysis of these challenge results, extra macroscopic pKa predictions were found to be more common than missing pKa predictions. In pKa prediction evaluations, the accuracy of predicted ionization states within a pH range is usually neglected. When predictions are only evaluated for the accuracy of the pKa value with numerical matching algorithms, a larger number of predicted pKas lead to greater underestimation of prediction errors. Therefore, it is not surprising that methods are biased to predict extra pKa values. The SAMPL6 pKa Challenge experimental data consists of 31 macroscopic pKas in total, measured for 24 molecules (6 molecules in the set have multiple pKas). Within the 10 methods with the lowest RMSE, only the xvxzd method predicts too few pKa values (2 unmatched out of 31 experimental pKas). All other methods that rank in the top 10 by RMSE have extra predicted pKas ranging from 1 to 13. Two prediction sets without any extra pKa predictions and low RMSE are 8xt50 (ReSCoSS conformations // DSD-BLYP-D3 reranking // COSMOtherm pKa) and nb015 (ChemAxon/Chemicalize).
3.1.1. Consistently well-performing methods for macroscopic pKa prediction
Methods ranked differently when ordered by different error metrics, although there were a couple of methods that consistently ranked in the top fraction. By using combinatorial criteria that take multiple statistical metrics and unmatched pKa counts into account, we identified a shortlist of consistently well-performing methods for macroscopic pKa predictions, shown in Table 2. The criteria for selection were the overall ranking in Top 10 according to RMSE, MAE, R2, and Kendall’s Tau and also having a combined unmatched pKa (extra and missing pKas) count less than 8 (a third of the number of compounds). We ranked methods in ascending order for RMSE and MAE and in descending order for R2, and Kendall’s Tau to determine methods. Then, we took the intersection set of Top 10 methods according to each statistic to determine the consistently-well performing methods. This resulted in a list of four methods that are consistently well-performing across all criteria.
Consistently well-performing methods for macroscopic pKa prediction included methods from all categories. Two methods in the QM+LEC category were xvxzd (DSD-BLYP-D3(BJ)/def2-TZVPD//PBEh-3c[DCOSMO-RS] + RRHO(GFN-xTB[GBSA]) + Gsolv(COSMO-RS[TZVPD]) and linear fit) and (8xt50) (ReSCoSS conformations // DSD-BLYP-D3 reranking // COSMOtherm pKa) and both used COSMO-RS. Empirical pKa predictions with top performance were both proprietary software. From QSPR and LFER categories, gyuhx (Simulations Plus) and xmymhm (ACD/pKa Classic) were consistently well-performing methods. The Simulation Plus pKa prediction method consisted of 10 artificial neural network ensembles trained on 16,000 compounds for 10 classes of ionizable atoms, with the ionization class of each atom determined using an assigned atom type and local molecular environment [48]. The ACD/pKa Classic method was trained on 17,000 compounds, uses Hammett-type equations, and captures effects related to tautomeric equilibria, covalent hydration, resonance effects, and α, β-unsaturated systems [38].
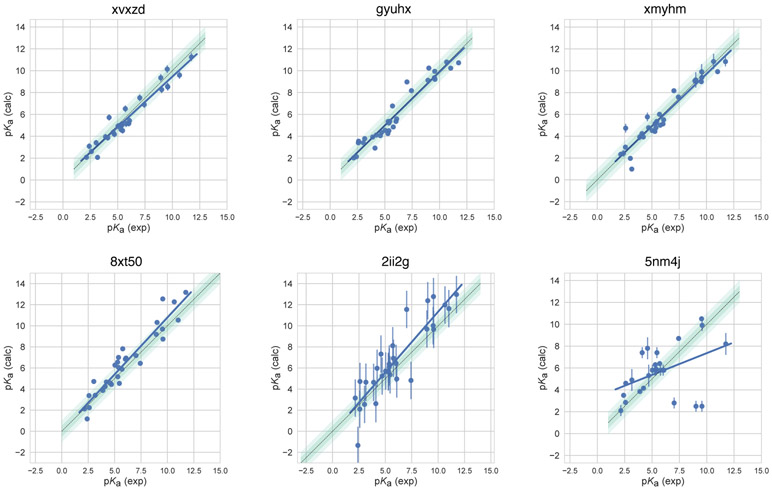
Figure 4 plots predicted vs. experimental macroscopic pKa predictions of four consistently well-performing methods, a representative average method, and the null method(5nm4j). We selected the method with the highest RMSE below the median of all methods as the representative method with average performance: 2ii2g (EC-RISM/MP2/cc-pVTZ-P2-q-noThiols-2par).
Figure 4. Predicted vs. experimental macroscopic pKa prediction for four consistently well-performing methods, a representative method with average performance (2ii2g), and the null method (5nm4j).
When submissions were ranked according to RMSE, MAE, R2, and τ, four methods ranked in the Top 10 consistently in each of these metrics. Dark and light green shaded areas indicate 0.5 and 1.0 units of error. Error bars indicate standard error of the mean of predicted and experimental values. Experimental pKa SEM values are too small to be seen under the data points. EC-RISM/MP2/cc-pVTZ-P2-q-noThiols-2par method (2ii2g) was selected as the representative method with average performance because it is the method with the highest RMSE below the median.
3.1.2. Which chemical properties are driving macroscopic pKa prediction failures?
In addition to comparing the performance of methods that participated in the SAMPL6 Challenge, we also wanted to analyze macroscopic pKa predictions from the perspective of challenge molecules and determine whether particular compounds suffer from larger inaccuracy in pKa predictions. The goal of this analysis is to provide insight on which molecular properties or moieties might be causing larger pKa prediction errors. In Fig. 5, 2D depictions of the challenge molecules are presented with MAE calculated for their macroscopic pKa predictions over all methods, based on Hungarian match. For multiprotic molecules, the MAE was averaged over all the pKa values. For the analysis of pKa prediction accuracy observed for each molecule, MAE is a more appropriate statistical value than RMSE for following global trends, as it is less sensitive to outliers than the RMSE.
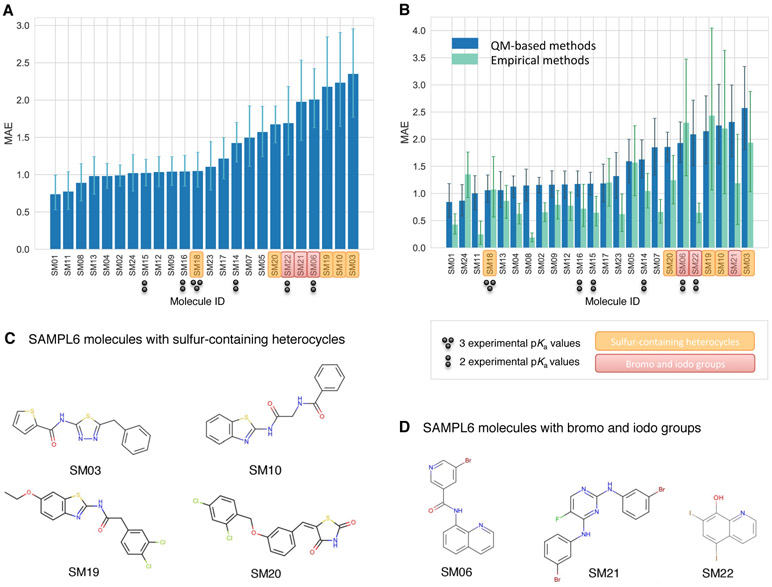
A comparison of the prediction accuracy of individual molecules is shown in Fig. 6. In Fig. 6A, the MAE for each molecule is shown considering all blind predictions and reference calculations. A cluster of molecules marked orange and red have higher than average MAE. Molecules marked red (SM06, SM21, and SM22) are the only compounds in the SAMPL6 dataset with bromo or iodo groups and they suffered a macroscopic pKa prediction error in the range of 1.7–2.0 pKa units in terms of MAE. Molecules marked orange (SM03, SM10, SM18, SM19, and SM20) have sulfur-containing heterocycles, and all these molecules except SM18 have MAE larger than 1.6 pKa units. Despite containing a thiazole group, SM18 has a low prediction MAE. SM18 is the only compound with three experimental pKa values, and we suspect the presence of multiple experimental pKa values could have a masking effect on the errors captured by the MAE when the Hungarian matching scheme is used due to more potential pairing choices that may artificially lower the error.
Figure 6. Average prediction accuracy calculated over all prediction methods was poorer for molecules with sulfur-containing heterocycles, bromo, and iodo groups.
(A) MAE calculated for each molecule as an average of all methods. (B) MAE of each molecule broken out by method category. QM-based methods (blue) include QM predictions with or without linear empirical correction. Empirical methods (green) include QSAR, ML, DL, and LFER approaches. (C) Depiction of SAMPL6 molecules with sulfur-containing heterocycles. (D) Depiction of SAMPL6 molecules with iodo and bromo groups.
We separately analyzed the MAE of each molecule for empirical (LFER and QSPR/ML) and QM-based physical methods (QM, QM+LEC, and QM+MM) to gain additional insight into prediction errors. Fig. 6B shows that the difficulty of predicting pKa values of the same subset of molecules was a trend conserved in the performance of physical methods. For QM-based methods, sulfur-containing heterocycles, amides proximal to aromatic heterocycles, and compounds with iodo and bromo substitutions have lower pKa prediction accuracy.
The SAMPL6 pKa set consists of only 24 small molecules and lacks multiple examples of many moieties, limiting our ability to determine with statistical significance which chemical substructures cause greater errors in pKa predictions. Still, the trends observed in this challenge point to molecules with iodo-, bromo-, and sulfur-containing heterocycles as having systematically larger prediction errors in macroscopic pKa value. We hope that reporting this observation will lead to the improvement of methods for similar compounds with such moieties.
We have also looked for correlation with molecular descriptors for finding other potential explanations as to why macroscopic pKa prediction errors were larger for certain molecules. While testing the correlation between errors and many molecular descriptors, it is important to account for the possibility of spurious correlations. We haven’t observed any statistically significant correlation between numerical pKa predictions and the descriptors we have tested. First, having more experimental pKa values (Fig. 6A) did not seem to be associated with poorer pKa prediction performance. Still, we need to keep in mind that multiprotic compounds were sparsely represented in the SAMPL6 set (5 molecules with 2 macroscopic pKa values and one with 3 macroscopic pKa). Second, we checked the following other descriptors: presence of an amide group, molecular weight, heavy atom count, rotatable bond count, heteroatom count, heteroatom-to-carbon ratio, ring system count, maximum ring size, and the number of microstates (as enumerated for the challenge). Correlation plots and R2 values can be seen in Fig. S2.
We had suspected that pKa prediction methods may perform better for moderate values (4–10) than extreme values as molecules with extreme pKa values are less likely to change ionization states close to physiological pH. To test this we look at the distribution of absolute errors calculated for all molecules and challenge predictions binned by experimental pKa value 2 pKa unit increments. As can be seen in Fig. S3B, the value of true macroscopic pKa values was not a factor affecting the prediction error seen in SAMPL6 Challenge.
Fig. 7B is helpful to answer the question "Are there molecules with consistently overestimated or underestimated pKa values?". This ridge plots show the error distribution of each experimental pKa. SM02_pKa1, SM04_pKa1, SM14_pKa1, and SM21_pKa1 were underestimated, predicting lower protein affinity by more than 1 pKa unit by majority of the prediction methods. SM03_pKa1, SM06_pKa2, SM19_pKa1, and SM20_pKa1 were overestimated by the majority of the prediction methods by more than 1 pKa unit. SM03_pKa1, SM06_pKa2, SM10_pKa1, SM19_pKa1, and SM22_pKa1 have the highest spread of errors and were less accurately predicted overall.
3.2. Analysis of microscopic pKa predictions using microstates determined by NMR for 8 molecules
The most common approach for analyzing microscopic pKa prediction accuracy has been to compare it to experimental macroscopic pKa data, assuming experimental pKa values describe titrations of distinguishable sites and, therefore, correspond to microscopic pKas. But this typical approach fails to evaluate methods at the microscopic level.
Analysis of microscopic pKa predictions for the SAMPL6 Challenge was not straightforward due to the lack of experimental data with microscopic resolution of the titratable sites and their associated microscopic pKas. For 24 molecules, macroscopic pKa values were determined with the spectrophotometric method. For 18 molecules, a single macroscopic titration was observed, and for 6 molecules multiple experimental pKa values were observed and characterized. For 18 molecules with a single experimental pKa, it is probable that the molecules are monoprotic and, therefore, macroscopic pKa value is equal to the microscopic pKa. There is, however, no direct experimental evidence supporting this hypothesis aside from the support from computational predictions, such as the predictions by ACD/pKa Classic. There is always the possibility that the macroscopic pKa observed is the result of two different titrations overlapping closely with respect to pH if any charge state has more than one tautomer. We did not want to bias the blind challenge analysis with any prediction method. Therefore, we believe analyzing the microscopic pKa predictions via Hungarian matching to experimental values with the assumption that the 18 molecules have a single titratable site is not the best approach. Instead, an analysis at the level of macroscopic pKa values is much more appropriate when a numerical matching scheme is the only option to evaluate predictions using macroscopic experimental data.
For a subset of eight molecules, dominant microstates were inferred from NMR experiments. Six of these molecules were monoprotic and two were multiprotic. This dataset was extremely useful for guiding the assignment between experimental and predicted pKa values based on microstates. In this section, we present the performance evaluations of microscopic pKa predictions for only the 8 compounds with experimentally-determined dominant microstates.
3.2.1. Microstate-based matching revealed errors masked by pKa value-based matching between experimental and predicted pKas
Comparing microscopic pKa predictions directly to macroscopic experimental pKa values with numerical matching can lead to underestimation of errors. To demonstrate how numerical matching often masks pKa prediction errors, we compared the performance analysis done by Hungarian matching to that from microstate-based matching for 8 molecules presented in Fig. 8A. RMSE calculated for microscopic pKa predictions matched to experimental values via Hungarian matching is shown in Fig. 8B, while Fig. 8C shows RMSE calculated via microstate-based matching. The Hungarian matching incorrectly leads to significantly (and artificially) lower RMSE compared to microstate-based matching. The reason is that the Hungarian matching assigns experimental pKa values to predicted pKa values only based on the closeness of the numerical values, without consideration of the relative population of microstates and microstate identities. Because of this, a microscopic pKa value that describes a transition between very low population microstates (high energy tautomers) can be assigned to the experimental pKa if it has the closest pKa value. This is not helpful because, in reality, the microscopic pKa values that influence the observable macroscopic pKa the most are the ones with higher microstate populations (transitions between low energy tautomers).
Figure 8. NMR determination of dominant microstates allowed in-depth evaluation of microscopic pKa predictions for 8 compounds.
A Dominant microstate sequence of two compounds (SM07 and SM14) were determined by NMR [8]. Based on these reference compounds, the dominant microstates of 6 related compounds were inferred and experimental pKa values were assigned to titratable groups with the assumption that only the dominant microstates have significant contributions to the experimentally observed pKa. B RMSE vs. submission ID and unmatched pKa vs. submission ID plots for the evaluation of microscopic pKa predictions of 8 molecules by Hungarian matching to experimental macroscopic pKa values. C RMSE vs. submission ID and unmatched pKa vs. submission ID plots showing the evaluation of microscopic pKa predictions of 8 molecules by microstate-based matching between predicted microscopic pKas and experimental macroscopic pKa values. Submissions 0wfzo, z3btx, 758j8, and hgn83 have RMSE values bigger than 10 pKa units which are beyond the y-axis limits of subplot C and B. RMSE is shown with error bars denoting 95% confidence intervals obtained by bootstrapping over the challenge molecules. Lower bar plots show the number of unmatched experimental pKas (light grey, missing predictions) and the number of unmatched pKa predictions (dark grey, extra predictions) for each method between pH 2 and 12. Submission IDs are summarized in Table 1.
The number of unmatched predicted microscopic pKas is shown in the lower bar plots of Fig. 8B and C, to emphasize the large number of microscopic pKa predictions submitted by many methods. In the case of microscopic pKa, the number of unmatched predictions does not indicate an error in the form of an extra predicted pKa, because the spectrophotometric experiments do not capture all microscopic pKas theoretically possible (transitions between all pairs of microstates that differ by one proton). pKas of transitions to and from very high energy tautomers are very hard to measure by experimental methods, including the most sensitive methods like NMR. Prediction of extra microscopic pKa values can cause underestimation of prediction errors when numerical matching algorithms such as Hungarian matching are used. We also checked how often Hungarian matching led to the correct matches between predicted and experimental pKa in terms of the microstate pairs, i.e., how often the microstate pair of the Hungarian match recapitulates the dominant microstate pair of the experiment. The overall accuracy of microstate pair matching was found to be low for the SAMPL6 Challenge submission. Fig. S4 shows that for most methods the predicted microstate pair selected by the Hungarian match did not correspond to the experimentally-determined microstate pair. This means lower RMSE (better accuracy) performance statistics obtained from Hungarian matching are artificially low. This problem could be avoided by matching experimental and predicted values on the basis of microstate IDs, if experimental microscopic assignments are available.
Unfortunately, we were only able to perform this more reliable microstate-based analysis for a subset of compounds. The conclusions in this section reflect only eight compounds with limited structural diversity: Six molecules with 4-aminoquinazoline and two with benzimidazole scaffolds, with a total of 10 pKa values. The sequences of dominant microstates for SM07 and SM14 were determined by NMR experiments directly [8], while dominant microstates of their derivatives were inferred by taking them as a reference (Fig. 8). Although we believe that microstate-based evaluation is more informative, the lack of a large experimental dataset limits the conclusions to a very narrow chemical diversity. Still, microstate-based matching revealed errors masked by pKa value-based matching between experimental and predicted pKas.
3.2.2. Accuracy of pKa predictions evaluated by microstate-based matching
Both accuracy- and correlation-based statistics were calculated for the predicted microscopic pKa values after microstate-based matching. RMSE, MAE, ME, R2, and Kendall’s Tau results of each method are shown in Fig. 8C and Fig. 9. A table of the calculated statistics can be found in Table S4. Due to the small number of data points in this set, correlation-based statistics have large uncertainties and thus have less utility for distinguishing better-performing methods. Therefore, we focused more on accuracy-based metrics for the analysis of microscopic pKas than correlation-based metrics. In terms of accuracy of predicted microscopic pKa values, all three QSPR/ML based methods (nb016 (MoKa), hdiyq (Simulations Plus), 6tvf8 (OE Gaussian Process)), three QM-based methods (nb011 (Jaguar), ftc8w (EC-RISM/MP2/cc-pVTZ-P2-q-noThiols-2par), t8ewk (COSMOlogic_FINE17)), and one LFER method (v8qph (ACD/pKa GALAS)) achieved RMSE lower than 1 pKa unit. The same six methods also have the lowest MAE.
Figure 9. Additional performance statistics for microscopic pKa predictions for 8 molecules with experimentally determined dominant microstates.
Microstate-based matching was performed between experimental pKa values and predicted microscopic pKa values. Mean absolute error (MAE), mean error (ME), Pearson’s R2, and Kendall’s Rank Correlation Coefficient Tau (τ) are shown, with error bars denoting 95% confidence intervals obtained by bootstrapping over challenge molecules. Methods are indicated by their submission IDs. Submissions are colored by their method categories. Refer to Table 1 for submission IDs and method names. Submissions 0wfzo, z3btx, 758j8, and hgn83 have MAE and ME values bigger than 10 pKa units which are beyond the y-axis limits of subplots A and B. A large number and wide variety of methods have statistically indistinguishable performance based on correlation statistics (C and D), in part because of the relatively small dynamic range and small size of the set of 8 molecules.
3.2.3. Evaluation of dominant microstate prediction accuracy
For many computational chemistry approaches, including structure-based modeling of protein-ligand interactions, predicting the ionization state and the exact position of protons is necessary to establish what to include in the modeled system. In addition to being able to predict pKa values accurately, we require pKa prediction methods to be able to capture microscopic protonation states accurately. Even when the predicted pKa value is accurate, the predicted protonation sites can be incorrect, leading to potentially large modeling errors in quantities such as the computed free energy of binding. Therefore, we assessed whether methods participating in the SAMPL6 pKa Challenge were correctly predicting the sequence of dominant microstates, i.e., dominant tautomers of each charge state observed between pH 2 and 12.
Fig. 10 shows how well methods perform for predicting the dominant microstate, as analyzed for eight compounds with available experimental microstate assignments. The dominant microstate sequence is essentially the sequence of states that are most visible experimentally due to their higher fractional population and relative free energy within the tautomers at each charge. To extract the dominant tautomers predicted for the sequence of ionization states of each method, the relative free energy of microstates were first calculated at reference pH 0 [26]. To subsequently determine the dominant microstate at each formal charge, we selected the lowest energy tautomer for each ionization state based on the relative microstate free energies calculated at pH 0. The choice of reference pH is arbitrary, as relative free energy difference between tautomers of the same charge is always constant with respect to pH. This analysis was performed only for the charges −1, 0, 1, and 2—the charge range captured by NMR experiments. Predicted and experimental dominant microstates were then compared for each charge state to calculate the fraction of correctly predicted dominant tautomers. This value is reported as the dominant microstate accuracy for all charge states (Fig. 10A).
Figure 10. Some methods predicted the sequence of dominant tautomers inaccurately.
Prediction accuracy of the dominant microstate of each charged state was calculated using the dominant microstate sequence determined by NMR for 8 molecules as reference. (A) Dominant microstate accuracy vs. submission ID plot was calculated considering all the dominant microstates seen in the experimental microstate dataset of 8 molecules. (B) Dominant microstate accuracy vs. submission ID plot was generating considering only the dominant microstates of charge 0 and +1 seen in the 8 molecule dataset. The accuracy of each molecule is broken out by the total charge of the microstate. (C) Dominant microstate prediction accuracy calculated for each molecule averaged over all methods. In (B) and (C), the accuracy of predicting the dominant neutral tautomer is shown in blue and the accuracy of predicting the dominant +1 charged tautomer is shown in green. Error bars denoting 95% confidence intervals obtained by bootstrapping.
Many of the methods which participated in the challenge made errors in predicting the dominant microstate. 10 QM and 3 QSPR/ML methods did not make any mistakes in dominant microstate predictions, although, they are expected to make mistakes in the relative population of tautomers (free energy difference between microstates) as reflected by the pKa value errors. While all participating QSPR/ML methods showed good performance in dominant microstate prediction, LFER and some QM methods made mistakes. The accuracy of the predicted dominant neutral tautomers was perfect for all methods, except qsicn (Fig. 10B), but errors in predicting the major tautomer of charge +1 were much more frequent. 22 out of 35 prediction sets made at least one error in predicting the lowest energy tautomer with +1 charge. We didn’t include ionization states with charges −1 and +2 in this assessment because we had only one compound with these charges in the dataset. Nevertheless, errors in predicting the dominant tautomers seem to be a bigger problem for charged tautomers than the neutral tautomer.
Only eight compounds had data on the sequence of dominant microstates. Therefore conclusions on the performance of methods in terms of dominant tautomer prediction are limited to this limited chemical diversity (benzimidazole and 4-aminoquinazoline derivatives). We present this analysis as a prototype of how microscopic pKa predictions should be evaluated. Hopefully, future evaluations can be performed with larger experimental datasets following the strategy we demonstrated here in order to reach broad conclusions about which methods are better for capturing dominant microstates and ratios of tautomers. Even if experimental microscopic pKa measurement data is not available, experimental dominant tautomer determinations are still informative for assessing computational predictions.
The most frequent misprediction was the major tautomer of the SM14 cationic form, as shown in Fig. 10. This figure shows the accuracy of the predicted dominant microstate calculated for individual molecules and for charge states 0 and +1, averaged over all prediction methods. SM14, the molecule that exhibits the most frequent error in the predicted dominant microstate, has two experimental pKa values that were 2.4 pKa units apart, and we suspect that could be a contributor to the difficulty of predicting microstates accurately. Other molecules are monoprotic (4-aminoquinazolines) or their experimental pKa values are very well separated (SM14, 4.2 pKa units). It would be very interesting to expand this assessment to a larger variety of drug-like molecules to discover for which structures tautomer predictions are more accurate and for which structures computational predictions are not as reliable.
3.2.4. Consistently well-performing methods for microscopic pKa predictions
We have identified different criteria for determining consistently top-performing predictions of microscopic pKa than macroscopic pKa: having perfect dominant microstate prediction accuracy, unmatched pKa count of 0, and ranking in the top 10 according to RMSE and MAE. Correlation statistics were not found to have utility for discriminating performance due to large uncertainties in these statistics for a small dataset of 10 pKa values. Unmatched predicted pKa count was also not considered since experimental data was only informative for the pKa between dominant microstates and did not capture all the possible theoretical transitions between microstate pairs. Table 3 reports six methods that have consistent good performance according to many metrics, although evaluated only for the 8 molecule set due to limitations of the experimental dataset. Six methods were divided evenly between methods of QSPR/ML category and QM category. nb016 (MoKa), hdiyq (Simulations Plus), and 6tvf8 (OE Gaussian Process) were QSPR and ML methods that performed well. nb011 (Jaguar), 0xi4b(EC-RISM/B3LYP/6-311+G(d,p)-P2-phi-noThiols-2par), and cywyk (EC-RISM/B3LYP/6-311+G(d,p)-P2-phi-noThiols-2par) were QM predictions with linear empirical corrections with good performance with microscopic pKa predictions.
The Simulations Plus pKa prediction method is the only method that appeared to be consistently well-performing in both the assessment for macroscopic and microscopic pKa prediction (gyuhx and hdiyq). However, it is worth noting that two methods that were in the list of consistently top-performing methods for macroscopic pKa predictions lacked equivalent submissions of their underlying microscopic pKa predictions, and therefore could not be evaluated at the microstate level. These methods were xmyhm (ACD/pKa Classic) and xvxzd(DSD-BLYP-D3(BJ)/def2-TZVPD//PBEh-3c[DCOSMO-RS] + RRHO(GFN-xTB[GBSA]) + Gsolv(COSMO-RS[TZVPD]) and linear fit).
3.3. How do pKa prediction errors impact protein-ligand binding affinity predictions?
pKa predictions provide a key input for computational modeling of protein-ligand binding with physical methods. The SAMPL6 pKa Challenge focused only on small molecule pKa prediction and showed how pKa prediction accuracy observed can impact the modeling of ligands. Many affinity prediction methods such as docking, MM/PBSA, MM/GBSA, absolute or alchemical relative free energy calculation methods predict the affinity of the ligand to a receptor using a fixed protonation state for both ligand and receptor. These models can sensitively depend upon pKa and dominant tautomer predictions for determining possible protonation states of the ligand in the aqueous environment and in a protein complex, as well as the free energy penalty to access those states [4]. The accuracy of pKa predictions can become a limitation for the performance of physical models that try to quantitatively describe molecular association.
In terms of ligand protonation states, there are two ways in which pKa prediction errors can influence the prediction accuracy for protein-ligand binding free energies as depicted in Fig. 11. The first scenario is when a ligand is present in aqueous solution in multiple protonation states (Fig. 11A). When only the minor aqueous protonation state contributes to protein-ligand complex formation, the overall binding free energy (ΔGbind) needs to be calculated as the sum of binding free energy of the minor state and the protonation penalty of that state (ΔGprot). ΔGprot is a function of both pH and pKa. A 1 unit of error in predicted pKa would lead to 1.36 kcal/mol error in overall binding free energy if the protonation state with the minor population binds the protein and this minor protonation state is correctly selected to model the free energy of binding; if the incorrect dominant protonation state for the complex is selected, the dominant contribution to the free energy of binding may be missed entirely, leading to much larger modeling errors in the binding free energy. Other scenarios—in which multiple protonation states can be significantly populated in complex—can lead to more complex scenarios in which the errors in predicted pKa propagate in more complex ways. The equations in Fig. 11A show the overall free energy for a simple thermodynamic cycle involving multiple protonation states.
Figure 11. Aqueous ligand pKa can influence overall protein-ligand binding affinity.
A When only the minor aqueous protonation state contributes to protein-ligand complex formation, the overall binding free energy (ΔGbind) needs to be calculated as the sum of binding affinity of the minor state and the protonation penalty of that state. B When multiple charge states contribute to complex formation, the overall free energy of binding includes a multiple protonation states correction (MPSC) term (ΔGcorr). MPSC is a function of pH, aqueous pKa of the ligand, and the difference between the binding free energy of charged and neutral species .
In addition to the presence of multiple protonation states in the aqueous environment, multiple charge states can contribute to complex formation (Fig. 11B). Then, the overall free energy of binding needs to include a Multiple Protonation States Correction (MPSC) term (ΔGcorr) [4]. MPSC is a function of pH, aqueous pKa of the ligand, and the difference between the binding free energy of charged and neutral species as shown in Fig. 11B.
Using the equations in Fig. 11B, we can model the true MPSC (ΔGcorr) with respect to the difference between pH and the pKa of the ligand to see when this value has a significant impact on the overall binding free energy. In Fig. 12, the true MPSC that must be added to is shown for ligands with varying binding affinity difference between protonation states . Fig. 12A shows the case of a monoprotic base in which the charged state has a lower affinity than the neutral state. Solid lines depict the accurate correction value. In cases where the pKa is lower than the pH, the correction factor disappears as the ligand fully populates the neutral state . As the pH dips below the pKa, the charged state is increasingly populated and ΔGcorr increases to approach ΔΔG.
Figure 12. Inaccuracy of pKa prediction (± 1 unit) affects the the accuracy of MPSC and overall protein-ligand binding free energy calculations to varying degrees based on aqueous pKa and relative binding affinity of individual protonation states .
All calculations are made for 25°C, and a ligand with a single basic titratable group. A, C, E, and G show MPSC (ΔGcorr) calculated with true vs. inaccurate pKa. B, D, F, and H show the comparison of the absolute error to ΔGbind caused by ignoring the MPSC completely (solid lines) vs. calculating MPSC based in inaccurate pKa value (dashed lines). These plots provide guidance on when it is beneficial to include MPSC correction based on pKa error, pH - pKa, and ΔΔG.
It is interesting to note the pH-pKa range over which ΔGcorr changes significantly. It is often assumed that, for a basic ligand, if the pKa of a ligand is more than 2 units higher than the pH, only 1% of the population is in the neutral state according to Henderson-Hasselbalch equation, and it is safe to approximate the overall binding affinity with . Based on the magnitude of the relative free energy difference between ligand protonation states, this assumption is not always correct. As seen in Fig. 12A, the responsive region of ΔGcorr can span 3 pH units for a system with ΔΔG = 1kcal/mol, or 5 pH units for a system with ΔΔG = 4kcal/mol. This highlights that the range of pKa values that impact binding affinity predictions is wider than 2 pH units. Molecules with pKa values several units away from the physiological pH can still impact the overall binding affinity significantly due to the MPSC.
Despite the need to capture the contributions of multiple protonation states by including the MPSC in binding affinity calculations, inaccurate pKa predictions can lead to errors in ΔGcorr and overall free energy of binding prediction. In Fig. 12A dashed lines show predicted ΔGcorr based on pKa error of −1 units. We have chosen a pKa error of 1 unit as this is the average inaccuracy expected from the pKa prediction methods based on the SAMPL6 Challenge. Underestimation of the pKa causes the ΔGcorr to be underestimated as well and will result in overestimated affinities (i.e., too negative binding free energy) for a varying range of pH - pKa values depending on the binding affinity difference between protonation states(ΔΔG). In Fig. 12B dashed lines show how the magnitude of the absolute error caused by calculating ΔGcorr with an inaccurate pKa varies with respect to pH. Different colored lines show simulated results with varying binding free energy differences between protonation states. For a system whose charged state has higher binding free energy than the neutral state (ΔΔG = 2 kcal/mol), the absolute error caused by underestimated pKa by 1 unit can be up to 0.9 kcal/mol. For a system whose charged state has an even lower affinity (more positive binding free energy) than the neutral state (ΔΔG = 4 kcal/mol), the absolute error caused by underestimated pKa by 1 unit can be up to 1.2 kcal/mol. The magnitude of errors contributing to overall binding affinity is too large to be neglected. Improving the accuracy of small molecule pKa prediction methods can help to minimize the error in predicted MPSC.
With the current level of pKa prediction accuracy as observed in SAMPL6 Challenge, is it advantageous to include the MPSC in affinity predictions that may include errors caused by pKa predictions? We provide a comparison of the two choices to answer this question: (1) Neglecting the MPSC completely and assuming overall binding affinity is captured by , (2) including MPSC with a potential error in overall affinity calculation. The magnitude of error caused by Choice 1 (ignoring MPSC) is depicted as a solid line in Fig. 12B and the magnitude of error caused by MPSC computed with inaccurate pKa is depicted as dashed lines. What is the best strategy? Error due to choice 1 is always larger than error due to choice 2 for all pH-pKa values. In this scenario, including the MPSC improves overall binding affinity prediction accuracy. The error caused by the inaccurate pKa is smaller than the error caused by neglecting the MPSC.
We can also ask whether or not an MPSC calculated based on an inaccurate pKa should be included in binding affinity predictions in different circumstances, such as underestimated or overestimated pKa values and charged states with higher or lower affinities than the neutral states. We tried to capture these circumstances in four quadrants of Fig. 12. In the case of overestimated pKa values (Fig. 12E-H), it can be seen that for most of the pH-pKa range, it is more advantageous to include the predicted MPSC in affinity calculations, except a smaller window where the opposite choice would be more advantageous. For instance, for the system with ΔΔG = 2 kcal/mol and overestimated pKa (Fig. 12E) for the pH-pKa region between −0.5 and 2, including the predicted ΔGcorr introduces more error than ignoring the MPSC.
In practice, we normally do not know the exact magnitude or the direction of the error of our predicted pKa. Therefore, using simulated MPSC error plots to decide when to include MPSC in binding affinity predictions is not possible. However, based on the analysis of a case with 1 unit of pKa error, including the MPSC correction would be more often than not helpful in improving binding affinity predictions. The detrimental effect of pKa inaccuracy is still significant. Hopefully, future improvements in pKa prediction methods will improve the accuracy of the MPSC and binding affinity predictions of ligands which have multiple protonation states that contribute to aqueous or complex populations. Being able to predict pKa values with 0.5 units accuracy, for example, would significantly aid binding affinity models in computing more accurate MPSC terms.
The whole analysis presented in this section assumes that at least the dominant protonation state of the ligand is correctly included in the modeling of the protein-ligand complex. We have not discussed the case of omitting this dominant state from the free energy calculations entirely when it is erroneously predicted to be a minor state in solution. Such a mistake could be the most problematic, and the errors in estimated binding free energy could be very large.
3.4. Take-away lessons from SAMPL6 pKa Challenge
The SAMPL6 pKa Challenge showed that, in general, pKa prediction accuracy of computational methods is lower than expected for drug-like molecules. Our expectation prior to the blind challenge was that well-developed methods would achieve prediction errors as low was 0.5 pKa units, and make reliable predictions of dominant charge and tautomer states in solution. There are many factors that complicate predicting pKa values of drug-like molecules: multiple titratable sites, including tautomerization, frequent presence of heterocycles, and extended conjugation patterns, as well as high numbers of rotatable bonds and the possibility of intramolecular hydrogen bonds. Macroscopic pKa predictions have not yet reached experimental accuracy (where the inter-method variability of macroscopic pKa measurements is around 0.5 pKa units [23]). There was not a single method in the SAMPL6 Challenge that achieved RMSE around 0.5 or lower for macroscopic pKa predictions for the 24 molecule set of kinase inhibitor fragment-like molecules. Smaller RMSEs were observed in the microscopic pKa evaluation section of this study for some methods; however, the 8 molecule set used for that analysis poses a very limited dataset to reach conclusions about general expectations for drug-like molecules.
As the majority of experimental data was in the form of macroscopic pKa values, we had to adopt a numerical matching algorithm (Hungarian matching) to pair predicted and experimental values to calculate performance statistics of macroscopic pKa predictions. Accuracy, correlation, and extra/missing pKa prediction counts were the main metrics for macroscopic pKa evaluations. An RMSE range of 0.7 to 3.2 pKa units was observed for all methods. Only five methods achieved RMSE between 0.7–1 pKa units, while an RMSE between 1.5–3 log units was observed for the majority of methods. All four methods of the LFER category and three out of 5 QSPR/ML methods achieved RMSE less than 1.5 pKa units. All the QM methods that achieved this level of performance included linear empirical corrections to rescale and unbias their pKa predictions.
Based on the consideration of multiple error metrics, we compiled a shortlist of consistently-well performing methods for macroscopic pKa evaluations. Two methods from QM+LEC methods, one QSPR/ML, two empirical methods achieved consistent performance according to many metrics. The common features of the two empirical methods were their large training sets (16000–17000 compounds) and commercial nature.
There were four submissions of QM-based methods that utilized the COSMO-RS implicit solvation model. While three of these achieved the lowest RMSE among QM-based methods (xvxzd, yqkga, and 8xt50) [46], one of them showed the highest RMSE (0hxtm (COSMOtherm_FINE17)). The comparison of these methods indicates that capturing the conformational ensemble of microstates, using high-level QM calculations, and including RRHO corrections contribute to better macroscopic pKa predictions. Linear empirical corrections applied QM calculations improved results, especially when the linear correction is calibrated for an experimental dataset using the same level of theory as the deprotonation free energy predictions (as in xvxzd). This challenge also points to the advantage of the COSMO-RS solvation approach compared to other implicit solvent models.
Molecules that posed greater difficulty for pKa predictions were determined by comparing the macroscopic pKa prediction accuracy of each molecule averaged over all methods submitted to the challenge. pKa prediction errors were higher for compounds with sulfur-containing heterocycles, iodo, and bromo groups. This trend was also conserved when only QM-based methods were analyzed. The SAMPL6 pKa dataset consisted of only 24 small molecules which limited our ability to statistically confirm this conclusion, however, we believe it is worth reporting molecular features that coincided with larger errors even if we can not evaluate the reason for these failures.
Utilizing a numerical matching algorithm to pair experimental and predicted macroscopic pKa values was a necessity, however, this approach did not capture all aspects of prediction errors. Computing the number of missing or extra pKa predictions remaining after Hungarian matching provided a window for observing macroscopic pKa prediction errors such as the number of macroscopic transitions or ionization states expected in a pH interval. In pKa evaluation studies, it is typical to just focus on pKa value errors evaluated after matching and to ignore pKa prediction errors that the matching protocol can not capture [49-53]. Frequently ignored prediction errors include predicting missing or extra pKas and failing to predict the correct charge states. The SAMPL6 pKa Challenge results showed sporadic presence of missing pKa predictions and very frequent tendency to make extra pKa predictions. Both indicate failures to capture the correct ionization states. The traditional way of evaluating pKas that only focuses on the pKa value error after some sort of numerical match between predictions and experimental values may have motivated these types of errors as there would be no penalty for missing a macroscopic deprotonation and predicting an extra one. This problem does not seem to be specific to any method category.
We used the eight molecule subset of SAMPL6 compounds with NMR-based dominant microstate sequence information to demonstrate the advantage of evaluating pKa prediction on the level of microstates. Comparison of statistics computed for the 8 molecule dataset by Hungarian matching and microstate-based matching showed how Hungarian matching, despite being the best choice when only numerical matching is possible, can still mask errors in pKa predictions. Errors computed by microstate-based matching were larger compared to numerical matching algorithms in terms of RMSE. Microscopic pKa analysis with numerical matching algorithms may mask errors due to the higher number of guesses made. Numerical matching based on pKa values also ignores information regarding the relative population of states. Therefore, it can lead to pKas defined between very low energy microstate pairs to be matched to the experimentally observable pKa between microstates of higher populations. Of course, the predicted pKa value could be correct however the predicted microstates would be wrong. Such mistakes caused by Hungarian matching were observed frequently in SAMPL6 results, and therefore we decided microstate-based matching of pKavalues provides a more realistic picture of method performance.
Some QM and LFER methods made mistakes in predicting the dominant tautomers of the ionization states. Dominant tautomer prediction seemed to be particularly difficult for charged tautomers compared with neutral tautomers. The easiest way to extract the dominant microstate sequence from predictions was to calculate the relative free energy of microstates at any reference pH, determining the lowest free energy state in each ionization state. Errors in dominant microstate predictions were very rare for neutral tautomers, but more frequent in cationic tautomers with +1 charge of the 8 molecule set. SM14 was the molecule with the lowest dominant microstate prediction accuracy, while dominant microstates predictions for SM15 were perfect for all molecules. SM14 and SM15 both possess two experimental pKas and a benzimidazole scaffold. The difference between them is the distance between the experimental pKa values, which is smaller for SM14. These results make sense from the perspective of relative free energies of microstates. Closer pKa values mean that the free energy difference between different microstates is smaller for SM14, and therefore any error in predicting the relative free energy of tautomers is more likely to cause reordering of relative populations of microstates and impact the accuracy of dominant microstate predictions. It would have been extremely informative to evaluate the tautomeric ratios and relative free energy predictions of microstates, however, the experimental data needed for this approach was not available. Tautomeric ratios could not be measured by the experimental methods available to us. Resolving tautomeric ratios would require extensive NMR measurements, but these measurements can suffer from lower accuracy especially when the free energy difference between tautomers is large.
The overall assessment of the SAMPL6 pKa Challenge captured non-stellar performance for microscopic and macroscopic pKa predictions which can be detrimental to the accuracy of protein-ligand affinity predictions and other pH-dependent physicochemical property predictions such as distribution coefficients, membrane permeability, and solubility. Protein-ligand binding affinity predictions utilize pKa predictions in two ways: determination of the relevant aqueous microstates and quantification of the free energy penalty to reach these states. More accurate microscopic pKa predictions are needed to be able to accurately incorporate multiple protonation state corrections (MPSC) into overall binding affinity calculations.
We simulated the effect of overestimating or underestimating pKa of a ligand by one unit on overall binding affinity prediction for a ligand where both cation and neutral states contribute to binding affinity. A pKa prediction error of this magnitude (assuming dominant tautomers were predicted correctly) could cause up to 0.9 and 1.2 kcal/mol error in overall binding affinity when the binding affinity of protonation states are 2 or 4 kcal/mol different, respectively. For the case of 4 kcal/mol binding affinity difference between protonation states, the pH-pKa range that the error would be larger than 0.5 kcal/mol surprisingly spans around 3.5 pH units. The worse case, of course, is where there is a significant difference in binding free energy between the two protonation states, but we include the wrong one in our free energy calcuation. We demonstrated that the range of pH-pKa value that the MPSC needs to be incorporated in binding affinity predictions can be wider than the widely assumed range of 2 pH units, based on the affinity difference between protonation states. At the level of 1 unit pKa error, incorporating the MPSC would improve binding affinity predictions more often than not. If the microscopic pKa could be predicted with 0.5 pKa units of accuracy, MPSC calculations would be much more reliable.
There are multiple factors to consider when deciding which pKa prediction method to utilize. These factors include the accuracy of microscopic and macroscopic pKa values, the accuracy of the number and the identity of ionization states predicted within the experimental pH interval, the accuracy of microstates predicted within the experimental pH interval, the accuracy of tautomeric ratio (i.e., relative free energy between microstates), how costly is the calculation in terms of time and resources, and whether one has access to software licenses that might be required.
All of the top-performing empirical methods were developed as commercial software that requires a license to run, and there were not any open-source alternatives for empirical pKa predictions. Since the completion of the blind challenge, two publications reported open-source machine learning-based pKa prediction methods, however, one can only predict the most acidic or most basic macroscopic pKa values of a molecule [54] and the second one is only trained for predicting pKa values of monoprotic molecules [55]. Recently, a pKa prediction methodology was published that describes a mixed approach of semi-empirical QM calculations and machine learning that can predict macroscopic pKas of both mono- and polyprotic species [56]. The authors reported RMSE of 0.85 for the retrospective analysis performed on the SAMPL6 dataset.
3.5. Suggestions for future blind challenge design and evaluation of pKa predictions
This analysis helped us understand the current state of the field and led to many lessons informing future SAMPL challenges. We believe the greatest benefit can be achieved if further iterations of small molecule pKa prediction challenges can be organized, creating motivation for improving protonation state prediction methods for drug-like molecules. In future challenges, it is desirable to increase chemical diversity to cover more common scaffolds [57] and functional groups [58] seen in drug-like molecules, gradually increasing the complexity of molecules.
Microscopic pKa measurements are needed for careful benchmarking of pKa predictions for multiprotic molecules.
Future challenges should promote stringent evaluation for pKa prediction methods from the perspective of microscopic pKa and microstate predictions. It is necessary to assess the capability of pKa prediction methods to capture the free energy profile of microstates of multiprotic molecules. This is critical because pKa predictions are often utilized to determine relevant protonation states and tautomers of small molecules that must be captured in other physical modeling approaches, such as protein-ligand binding affinity or distribution coefficient predictions. Different tautomers can have different binding affinities and partition coefficients.
In this paper, we demonstrated how experimental microstate information can guide the analysis further than the typical pKa evaluation approach that has been used so far. The traditional pKa evaluation approach focuses solely on the numerical error of the pKa values and neglects the difference between macroscopic and microscopic pKa definitions. This is mainly caused by the lack of pKa datasets with microscopic detail. To improve pKa and protonation state predictions for multiprotic molecules, it is necessary to embrace the difference between macroscopic and microscopic pKa definitions and select strategies for experimental data collection and prediction evaluation accordingly. In the SAMPL6 Challenge, the analysis was limited by the availability of experimental microscopic data as well. As is usually the case, macroscopic pKa values were abundant (24 molecules) and limited data on microscopic states was available (8 molecules), although the latter opened new avenues for evaluation. For future blind challenges for multiprotic compounds, striving to collect experimental datasets with microscopic pKas would be very beneficial, despite the high cost of these measurements. Benchmark datasets of microscopic pKa values with assigned microstates are currently missing because experimental determination of these are much more expensive and time-consuming than macroscopic pKa measurements. This limits the ability to improve pKa and tautomer prediction methods for multiprotic molecules. If the collection of experimental microscopic pKas is not possible due to time and resource costs of such NMR experiments, at least supplementing the more automated macroscopic pKa measurements with NMR-based determination of the dominant microstate sequence or tautomeric ratios of each ionization state can create very useful benchmark datasets. This supplementary information can allow microstate-based assignment of experimental to predicted pKa values and a more realistic assessment of method performance.
Evaluation strategy for pKa predictions must be determined based on the nature of experimental pKa measurements available.
If the only available experimental data is in the form of macroscopic pKa values, the best way to evaluate computational predictions is by calculating predicted macroscopic pKa from microscopic pKa predictions. With the conversion of microscopic pKa to macroscopic pKas, all structural information about the titration site is lost, and the only remaining information is the total charge of macroscopic ionization states. Unfortunately, most macroscopic pKa measurements—including potentiometric and spectrophotometric methods—do not capture the absolute charge of the macrostates. The spectrophotometric method does not measure charge at all. The potentiometric method can only capture the relative charge changes between macrostates. Only pH-dependent solubility-based pKa estimations can differentiate neutral and charged states from one another. It is, therefore, very common to have experimental datasets of macroscopic pKa without any charge or protonation position information regarding the macrostates. This causes an issue of assigning predicted and experimental pKa values before any error statistics can be calculated.
As delineated by Fraczkiewicz [23], the fairest and most reasonable solution for the pKa matching problem involves an assignment algorithm that preserves the order of predicted and experimental microstates and uses the principle of smallest differences to pair values. We recommend Hungarian matching with a squared-error penalty function. The algorithm is available in SciPy package (scipy.optimize.linear_sum_assignment) [35]. In addition to the analysis of numerical error statistics following Hungarian matching, at the very least, the number of missing and extra pKa predictions must be reported based on unmatched pKa values. Missing or extra pKa predictions point to a problem with capturing the right number of ionization states within the pH interval of the experimental measurements. We have demonstrated that for microscopic pKa predictions, performance analysis based on Hungarian matching results in overly optimistic and misleading results—instead the employed microstate-based matching provided a more realistic assessment when microstate data is available.
Lessons from the first pKa blind challenge will guide future decisions on challenge rules, prediction reporting formats, and challenge inputs.
We solicited three different submission types in SAMPL6 to capture all the necessary information related to pKa predictions. These were (1) macroscopic pKa values, (2) microscopic pKa values and microstate pair identities, and (3) fractional population of microstates with respect to pH. We realized later that collecting fractional populations of microstates was redundant since microscopic pKa values and microstate pairs capture all the necessary information to construct fractional population vs. pH curves [26]. Only microscopic and macroscopic pKa values were used for the challenge analysis presented in this paper.
While exploring ways to evaluate SAMPL6 pKa Challenge results, we developed a better way to capture microscopic pKa predictions, as presented in Gunner et al. [26]. This alternative reporting format consists of reporting the charge and relative free energy of microstates with respect to an arbitrary reference microstate and pH. This approach presents the most concise method of capturing all necessary information regarding microscopic pKa predictions and allows calculation of predicted microscopic pKas, microstate population with respect to pH, macroscopic pKa values, macroscopic population with respect to pH, and tautomer ratios. Still, there may be methods developed to predict macroscopic pKas directly instead of computing them from microstate predictions that justifies allowing a macroscopic pKa reporting format. In future challenges, we recommend collecting pKa predictions with two submission types: (1) macroscopic pKa values together with the charges of the macrostates and (2) microstates, their total charge, and relative free energies with respect to a specified reference microstate and pH. This approach is being used in SAMPL7.
In SAMPL6, we provided an enumerated list of microstates and their assigned microstate IDs because we were worried about parsing submitted microstates in SMILES from different sources correctly. There were two disadvantages to this approach. First, this list of enumerated microstates was used as input by some participants which was not our intention. (Challenge instructions requested that predictions should not rely on these microstate lists and only use them for matching microstate IDs.) Second, the first iteration of enumerated microstates was not complete. We had to add new microstates and assign them microstate IDs for a couple of rounds until reaching a complete list. In future challenges, a better way of handling the problem of capturing predicted microstates would be asking participants to specify the predicted protonation states themselves and assigning identifiers after the challenge deadline to aid comparative analysis. This would prevent the partial unblinding of protonation states and allow the assessment of whether methods can predict all the relevant states independently, without relying on a provided list of microstates. Predicted states can be submitted as mol2 files that represent the microstate with explicit hydrogens. The organizers must only provide the microstate that was selected as the reference state for the relative microstate free energy calculations.
In the SAMPL6 pKa Challenge, there was not a requirement that participants should report predictions for all compounds. Some participants reported predictions for only a subset of compounds, which may have led these methods to look more accurate than others due to missing predictions. In the future, it will be better to allow submissions of only complete sets for a better comparison of method performance.
A wide range of methods participated in the SAMPL6 pKa Challenge—from very fast QSPR methods to QM methods with a high-level of theory and extensive exploration of conformational ensembles. In the future, it would be interesting to capture computing costs in terms of average compute hours per molecule. This can provide guidance to future users of pKa prediction methods for selection of which method to use.
It is advantageous to field associated challenges with common set of molecules for different physicochemical properties.
Future blind challenges can maximize learning opportunities by evaluating predictions of different physicochemical properties for the same molecules in consecutive challenges. In SAMPL6, we organized both pKa and log P challenges. Unfortunately only a subset of compounds in the pKa datasets were suitable for the potentiometric log P measurements [8]. Still, comparing prediction performance of common compounds in both challenges can lead to beneficial insights especially for physical modeling techniques if there are common aspects that are beneficial or detrimental to prediction performance. For example, in SAMPL6 pKa and log P Challenges COSMO-RS and EC-RISM solvation models achieved good performance. Having access to a variety of physicochemical property measurements can also help the identification of error sources. For example, dominant microstates determined for pKa challenge can provide information to check if correct tautomers are modeling in a log P or log D challenge. pKa prediction is a requirement for log D prediction and experimental pKa values can help diagnosing the source of errors in log D predictions better. The physical challenges in SAMPL7, for which the blind portion of the challenges have just concluded on October 8th, 2020, follow this principle and include both pKa, log P, and membrane permeability properties for a set of monoprotic compounds. We hope that future pKa challenges can focus on multiprotic drug-like compounds with microscopic pKa measurements for an in-depth analysis.
4. Conclusion
The first SAMPL6 pKa Challenge focused on molecules resembling fragments of kinase inhibitors, and was intended to assess the performance of pKa predictions for drug-like molecules. With wide participation, we had an opportunity to prospectively evaluate pKa predictions spanning various empirical and QM based approaches. In addition to community participants, a small number of popular pKa prediction methods that were missing from blind submissions were added as reference calculations after the challenge deadline.
Practical experimental limitations restricted the overall size and microscopic information available for the blind challenge dataset [8]. The experimental dataset consisted of spectrophotometric measurements of 24 molecules, some of which were multiprotic. For a subset of molecules there was also NMR data to inform the dominant microstate sequence, though microscopic pKa measurements were not performed. We conducted a comparative analysis of methods represented in the blind challenge in terms of both macroscopic and microscopic pKa prediction performance avoiding any assumptions about the interpretation of experimental pKas.
Here, we used Hungarian matching to assign predicted and experimental values for the calculation of accuracy and correlation statistics, because the majority of experimental data was macroscopic pKa values. In addition to evaluating error in predicted pKa values, we also reported the macroscopic pKa errors that were not captured by the match between experimental and predicted pKa values. These were extra or missing pKa predictions which are important indicators that predictions are failing to capture the correct ionization states.
We evaluated microscopic pKa predictions utilizing the experimental dominant microstate sequence data of eight molecules. This experimental data allowed us to use microstate-based matching for evaluating the accuracy of microscopic pKa values in a more realistic way. We have determined that QM and LFER predictions had lower accuracy in determining the dominant tautomer of the charged microstates than the neutral states. For both macroscopic and microscopic pKa predictions we have determined methods that were consistently well-performing according to multiple statistical metrics. Focusing on the comparison of molecules instead of methods for macroscopic pKa prediction accuracy indicated molecules with sulfur-containing heterocycles, iodo, and bromo groups suffered from lower pKa prediction accuracy.
The overall performance of pKa predictions as captured in this challenge is concerning for the application of pKa prediction methods in computer-aided drug design. Many computational methods for predicting target affinities and physicochemical properties rely on pKa predictions for determining relevant protonation states and the free energy penalty of such states. 1 unit of pKa error is an optimistic estimate of current macroscopic pKa predictions for drug-like molecules based on SAMPL6 Challenge where errors in predicting the correct number of ionization states or determining the correct dominant microstate were also common to many methods. In the absence of other sources of errors, we showed that 1 unit over- or underestimation of the pKa of a ligand can cause significant errors in the overall binding affinity calculation due to errors in multiple protonation state correction factor.
The SAMPL6 GitHub Repository contains all information regarding the challenge structure, experimental data, blind prediction submission sets, and evaluation of methods. The repository will be useful for future follow up analysis and the experimental measurements can continue to serve as a benchmark dataset for testing methods.
In this article, we aimed to demonstrate not only the comparative analysis of the pKa prediction performance of contemporary methods for drug-like molecules, but also to propose a stringent pKa prediction evaluation strategy that takes into account differences in microscopic and macroscopic pKa definitions. We hope that this study will guide and motivate further improvement of pKa prediction methods.
5. Code and data availability
SAMPL6 pKa challenge instructions, submissions, experimental data and analysis is available at SAMPL6 GitHub Repository: https://github.com/samplchallenges/SAMPL6
Supplementary Material
TABLE S1: SMILES and InChI identifiers of SAMPL6 pKa Challenge molecules.
TABLE S2: Evaluation statistics calculated for all macroscopic pKa prediction submissions based on Hungarian match for 24 molecules.
TABLE S3: Evaluation statistics calculated for all microscopic pKa prediction submissions based on Hungarian match for 8 molecules with NMR data.
TABLE S4: Evaluation statistics calculated for all microscopic pKa prediction submissions based on microstate match for 8 molecules with NMR data.
FIGURE S1: Dominant microstates of 8 molecules were determined based on NMR measurements.
FIGURE S2: MAE of macroscopic pKa predictions of each molecule did not show any significant correlation with any molecular descriptor.
FIGURE S3: The value of macroscopic pKa was not a factor affecting prediction error seen in SAMPL6 Challenge according to the analysis with Hungarian matching.
FIGURE S4: There was low agreement between experimental dominant microstate pairs and the predicted microstate pairs selected by Hungarian algorithm for microscopic pKa predictions.
An archive copy of the pKa Challenge directory of SAMPL6 GitHub Repository (SAMPL6-repository-pKa-directory.zip)
Table S1 in CSV format (SAMPL6-pKa-chemical-identifiers-table.csv)
Table S2 in CSV format (macroscopic-pKa-statistics-24mol-hungarian-match.csv)
Table S3 in CSV format (microscopic-pKa-statistics-8mol-hungarian-match-table.csv)
Table S4 in CSV format (microscopic-pKa-statistics-8mol-microstate-match-table.csv)
Figure S1 in CSV format (experimental-microstates-of-8mol-based-on-NMR.csv)
The Jupyter Notebook used for the enumeration of microstates (enumerate-microstates-with-Epik-and-OpenEye-QUACPAC.ipynb)
A CSV table of SAMPL6 molecule IDs and OpenEye OEChem generated SMILES (molecule_ID_and_SMILES.csv)
8. Acknowledgments
We would like to acknowledge the infrastructure and website support of Mike Chiu that allowed a seamless collection of challenge submissions. Mike Chiu also provided assistance with constructing a submission validation script to ensure all submissions adhered to the machine-readable format. We are grateful to Kiril Lanevskij for suggesting the Hungarian algorithm for matching experimental and predicted pKa values. We would like to thank Thomas Fox for providing MoKa reference calculations. We acknowledge Caitlin Bannan for guidance on defining a working microstate definition for the challenge and guidance for designing the challenge. We thank Brad Sherborne for his valuable insights at the conception of the pKa challenge and connecting us with Timothy Rhodes and Dorothy Levorse who were able to provide resources and expertise for experimental measurements performed at MRL. We acknowledge Paul Czodrowski who provided feedback on multiple stages of this work: challenge construction, purchasable compound selection, and manuscript draft. MI, JDC, and DLM gratefully acknowledge support from NIH grant R01GM124270 supporting the SAMPL Blind Challenges. MI, ASR, AR, and JDC acknowledge support from the Sloan Kettering Institute. JDC acknowledges support from NIH grant P30CA008748 and NIH grant R01GM121505. DLM appreciates financial support from the National Institutes of Health (R01GM108889) and the National Science Foundation (CHE 1352608). MI acknowledges Doris J. Hutchinson Fellowship. MI, ASR, AR, and JDC are grateful to OpenEye Scientific for providing a free academic software license for use in this work. MI, ASR, AR, and JDC thank Janos Fejervari and ChemAxon team that gave us permission to include ChemAxon/Chemicalize pKa predictions as a reference prediction in challenge analysis.
Abbreviations
- SAMPL
Statistical Assessment of the Modeling of Proteins and Ligands
- pKa
−log10 of the acid dissociation equilibrium constant
- log P
log10 of the organic solvent-water partition coefficient (Kow) of neutral species
- log D
log10 of organic solvent-water distribution coefficient (Dow)
- SEM
Standard error of the mean
- RMSE
Root mean squared error
- MAE
Mean absolute error
- τ
Kendall’s rank correlation coefficient (Tau)
- R2
Coefficient of determination (R-Squared)
- MPSC
Multiple protonation states correction for binding free energy
- DL
Database Lookup
- LFER
Linear Free Energy Relationship
- QSPR
Quantitative Structure-Property Relationship
- ML
Machine Learning
- QM
Quantum Mechanics
- LEC
Linear Empirical Correction
Footnotes
Disclaimers
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Disclosures
JDC was a member of the Scientific Advisory Board for Schrödinger, LLC during part of this study, and is a current Scientific Advisory Board member for OpenEye Scientific and scientific advisor to Foresite Labs. DLM is a current member of the Scientific Advisory Board of OpenEye Scientific and an Open Science Fellow with Silicon Therapeutics.
The Chodera laboratory receives or has received funding from multiple sources, including the National Institutes of Health, the National Science Foundation, the Parker Institute for Cancer Immunotherapy, Relay Therapeutics, Entasis Therapeutics, Vir Biotechnology, Silicon Therapeutics, EMD Serono (Merck KGaA), AstraZeneca, Vir Biotechnology, XtalPi, the Molecular Sciences Software Institute, the Starr Cancer Consortium, the Open Force Field Consortium, Cycle for Survival, a Louis V. Gerstner Young Investigator Award, The Einstein Foundation, and the Sloan Kettering Institute. A complete list of funding can be found at http://choderalab.org/funding.
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
References
- [1].Manallack DT, Prankerd RJ, Yuriev E, Oprea TI, Chalmers DK. The Significance of Acid/Base Properties in Drug Discovery. Chem Soc Rev. 2013; 42(2):485–496. doi: 10.1039/C2CS35348B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Charifson PS, Walters WP. Acidic and Basic Drugs in Medicinal Chemistry: A Perspective. Journal of Medicinal Chemistry. 2014. December; 57(23):9701–9717. doi: 10.1021/jm501000a. [DOI] [PubMed] [Google Scholar]
- [3].Manallack DT, Prankerd RJ, Nassta GC, Ursu O, Oprea TI, Chalmers DK. A Chemogenomic Analysis of Ionization Constants-Implications for Drug Discovery. ChemMedChem. 2013. February; 8(2):242–255. doi: 10.1002/cmdc.201200507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].de Oliveira C, Yu HS, Chen W, Abel R, Wang L. Rigorous Free Energy Perturbation Approach to Estimating Relative Binding Affinities between Ligands with Multiple Protonation and Tautomeric States. Journal of Chemical Theory and Computation. 2019. January; 15(1):424–435. doi: 10.1021/acs.jctc.8b00826. [DOI] [PubMed] [Google Scholar]
- [5].Darvey IG. The Assignment of pKa Values to Functional Groups in Amino Acids. Biochemical Education. 1995. April; 23(2):80–82. doi: 10.1016/0307-4412(94)00150-N. [DOI] [Google Scholar]
- [6].Bodner GM. Assigning the pKa’s of Polyprotic Acids. Journal of Chemical Education. 1986. March; 63(3):246. doi: 10.1021/ed063p246. [DOI] [Google Scholar]
- [7].Murray R Microscopic Equilibria. Analytical Chemistry,. 1995. August; p. 1. [Google Scholar]
- [8].Işık M, Levorse D, Rustenburg AS, Ndukwe IE, Wang H, Wang X, Reibarkh M, Martin GE, Makarov AA, Mobley DL, Rhodes T, Chodera JD. pKa Measurements for the SAMPL6 Prediction Challenge for a Set of Kinase Inhibitor-like Fragments. Journal of Computer-Aided Molecular Design. 2018. October; 32(10):1117–1138. doi: 10.1007/s10822-018-0168-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Bochevarov AD, Watson MA, Greenwood JR, Philipp DM. Multiconformation, Density Functional Theory-Based p K a Prediction in Application to Large, Flexible Organic Molecules with Diverse Functional Groups. Journal of Chemical Theory and Computation. 2016. December; 12(12):6001–6019. doi: 10.1021/acs.jctc.6b00805. [DOI] [PubMed] [Google Scholar]
- [10].Selwa E, Kenney IM, Beckstein O, Iorga BI. SAMPL6: Calculation of Macroscopic pKa Values from Ab Initio Quantum Mechanical Free Energies. Journal of Computer-Aided Molecular Design. 2018. October; 32(10):1203–1216. doi: 10.1007/s10822-018-0138-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Pickard FC, König G, Tofoleanu F, Lee J, Simmonett AC, Shao Y, Ponder JW, Brooks BR. Blind Prediction of Distribution in the SAMPL5 Challenge with QM Based Protomer and pK a Corrections. Journal of Computer-Aided Molecular Design. 2016. November; 30(11):1087–1100. doi: 10.1007/s10822-016-9955-7. [DOI] [PubMed] [Google Scholar]
- [12].Bannan CC, Mobley DL, Skillman AG. SAMPL6 Challenge Results from $$pK_a$$ Predictions Based on a General Gaussian Process Model. Journal of Computer-Aided Molecular Design. 2018. October; 32(10):1165–1177. doi: 10.1007/s10822-018-0169-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Işık M, Levorse D, Mobley DL, Rhodes T, Chodera JD. Octanol–Water Partition Coefficient Measurements for the SAMPL6 Blind Prediction Challenge. Journal of Computer-Aided Molecular Design. 2020. April; 34(4):405–420. doi: 10.1007/s10822-019-00271-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].şık M, Bergazin TD, Fox T, Rizzi A, Chodera JD, Mobley DL. Assessing the Accuracy of Octanol–Water Partition Coefficient Predictions in the SAMPL6 Part II Log P Challenge. Journal of Computer-Aided Molecular Design. 2020. April; 34(4):335–370. doi: 10.1007/s10822-020-00295-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Kogej T, Muresan S. Database Mining for pKa Prediction. Current Drug Discovery Technologies. 2005; 2(4):221–229. doi: 10.2174/157016305775202964. [DOI] [PubMed] [Google Scholar]
- [16].Perrin DD, Dempsey B, Serjeant EP. pKa Prediction for Organic Acids and Bases. 1 ed. London and New York: Chapman and Hall; 1981. [Google Scholar]
- [17].Hammett LP. Physical Organic Chemistry. New York: McGraw-Hill; 1940. [Google Scholar]
- [18].Taft RW, Lewis IC. Evaluation of Resonance Effects on Reactivity by Application of the Linear Inductive Energy Relationship. V. Concerning a σR Scale of Resonance Effects1,2. Journal of the American Chemical Society. 1959; 81(20):5343–5352. doi: 10.1021/ja01529a025. [DOI] [Google Scholar]
- [19].Xing L, Glen RC, Clark RD. Predicting p K a by Molecular Tree Structured Fingerprints and PLS. Journal of Chemical Information and Computer Sciences. 2003. May; 43(3):870–879. doi: 10.1021/ci020386s. [DOI] [PubMed] [Google Scholar]
- [20].Zhang J, Kleinöder T, Gasteiger J. Prediction of p K a Values for Aliphatic Carboxylic Acids and Alcohols with Empirical Atomic Charge Descriptors. Journal of Chemical Information and Modeling. 2006. November; 46(6):2256–2266. doi: 10.1021/ci060129d. [DOI] [PubMed] [Google Scholar]
- [21].Cruciani G, Milletti F, Storchi L, Sforna G, Goracci L. In Silico p K a Prediction and ADME Profiling. Chemistry & Biodiversity. 2009. November; 6(11):1812–1821. doi: 10.1002/cbdv.200900153. [DOI] [PubMed] [Google Scholar]
- [22].Milletti F, Storchi L, Sforna G, Cruciani G. New and Original p K a Prediction Method Using Grid Molecular Interaction Fields. Journal of Chemical Information and Modeling. 2007. November; 47(6):2172–2181. doi: 10.1021/ci700018y. [DOI] [PubMed] [Google Scholar]
- [23].Fraczkiewicz R In Silico Prediction of Ionization In: Reference Module in Chemistry, Molecular Sciences and Chemical Engineering Elsevier; 2013.doi: 10.1016/B978-0-12-409547-2.02610-X. [DOI] [Google Scholar]
- [24].Simulations Plus ADMET Predictor v8.5;. Simulations Plus, Lancaster, CA, 2018. https://www.simulations-plus.com/software/admetpredictor/physicochemical-biopharmaceutical/. [Google Scholar]
- [25].Radak BK, Chipot C, Suh D, Jo S, Jiang W, Phillips JC, Schulten K, Roux B. Constant-pH Molecular Dynamics Simulations for Large Biomolecular Systems. Journal of Chemical Theory and Computation. 2017. December; 13(12):5933–5944. doi: 10.1021/acs.jctc.7b00875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Gunner MR, Murakami T, Rustenburg AS, Işık M, Chodera JD. Standard State Free Energies, Not pKas, Are Ideal for Describing Small Molecule Protonation and Tautomeric States. Journal of Computer-Aided Molecular Design. 2020. May; 34(5):561–573. doi: 10.1007/s10822-020-00280-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Ullmann GM. Relations between Protonation Constants and Titration Curves in Polyprotic Acids: A Critical View. The Journal of Physical Chemistry B. 2003. February; 107(5):1263–1271. doi: 10.1021/jp026454v. [DOI] [Google Scholar]
- [28].Yang AS, Gunner MR, Sampogna R, Sharp K, Honig B. On the Calculation of pKas in Proteins. Proteins: Struct, Funct, Genet. 1993; (15):252–265. [DOI] [PubMed] [Google Scholar]
- [29].Special Issue: SAMPL6 (Statistical Assessment of the Modeling of Proteins and Ligands); October 2018. Volume 32, Issue 10 Journal of Computer-Aided Molecular Design. [PubMed] [Google Scholar]
- [30].Shelley JC, Cholleti A, Frye LL, Greenwood JR, Timlin MR, Uchimaya M. Epik: A Software Program for pK a Prediction and Protonation State Generation for Drug-like Molecules. Journal of Computer-Aided Molecular Design. 2007. December; 21(12):681–691. doi: 10.1007/s10822-007-9133-z. [DOI] [PubMed] [Google Scholar]
- [31].QUACPAC Toolkit 2017February1;. OpenEye Scientific Software, Santa Fe, NM: http://www.eyesopen.com. [Google Scholar]
- [32].OEChem Toolkit 2017February1;. OpenEye Scientific Software, Santa Fe, NM: http://www.eyesopen.com. [Google Scholar]
- [33].Kuhn HW. The Hungarian Method for the Assignment Problem. Naval Research Logistics Quarterly. 1955. March; 2(1-2):83–97. doi: 10.1002/nav.3800020109. [DOI] [Google Scholar]
- [34].Munkres J. Algorithms for the Assignment and Transportation Problems. J SIAM. 1957. March; 5(1):32–28. [Google Scholar]
- [35].SciPy v1.3.1, Linear Sum Assignment Documentation; September 27, 2019. The SciPy community; https://docs.scipy.org/doc/scipy-1.3.1/reference/generated/scipy.optimize.linear_sum_assignment.html. [Google Scholar]
- [36].OpenEye pKa Prospector;. OpenEye Scientific Software, Santa Fe, NM: Accessed on Jan 23, 2018 https://www.eyesopen.com/pka-prospector. [Google Scholar]
- [37].ACD/pKa GALAS (ACD/Percepta Kernel v1.6);. Advanced Chemistry Development, Inc., Toronto, ON, Canada, 2018. https://www.acdlabs.com/products/percepta/predictors/pKa/. [Google Scholar]
- [38].ACD/pKa Classic (ACD/Percepta Kernel v1.6);. Advanced Chemistry Development, Inc., Toronto, ON, Canada, 2018. https://www.acdlabs.com/products/percepta/predictors/pKa/. [Google Scholar]
- [39].Chemicalize v18.23 (ChemAxon MarvinSketch v18.23);. ChemAxon, Budapest, Hungary, 2018. https://docs.chemaxon.com/display/docs/pKa+Plugin. [Google Scholar]
- [40].MoKa;. Molecular Discovery, Hertfordshire, UK, 2018. https://www.moldiscovery.com/software/moka/. [Google Scholar]
- [41].Zeng Q, Jones MR, Brooks BR. Absolute and Relative pKa Predictions via a DFT Approach Applied to the SAMPL6 Blind Challenge. Journal of Computer-Aided Molecular Design. 2018. October; 32(10):1179–1189. doi: 10.1007/s10822-018-0150-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Bochevarov AD, Harder E, Hughes TF, Greenwood JR, Braden DA, Philipp DM, Rinaldo D, Halls MD, Zhang J, Friesner RA. Jaguar: A High-Performance Quantum Chemistry Software Program with Strengths in Life and Materials Sciences. International Journal of Quantum Chemistry. 2013. September; 113(18):2110–2142. doi: 10.1002/qua.24481. [DOI] [Google Scholar]
- [43].Tielker N, Eberlein L, Guüssregen S, Kast SM. The SAMPL6 Challenge on Predicting Aqueous pKa Values from EC-RISM Theory. Journal of Computer-Aided Molecular Design. 2018. October; 32(10):1151–1163. doi: 10.1007/s10822-018-0140-z. [DOI] [PubMed] [Google Scholar]
- [44].Klamt A, Eckert F, Diedenhofen M, Beck ME. First Principles Calculations of Aqueous p K a Values for Organic and Inorganic Acids Using COSMO-RS Reveal an Inconsistency in the Slope of the p K a Scale. The Journal of Physical Chemistry A. 2003. November; 107(44):9380–9386. doi: 10.1021/jp034688o. [DOI] [PubMed] [Google Scholar]
- [45].Eckert F, Klamt A. Accurate Prediction of Basicity in Aqueous Solution with COSMO-RS. Journal of Computational Chemistry. 2006. January; 27(1):11–19. doi: 10.1002/jcc.20309. [DOI] [PubMed] [Google Scholar]
- [46].Pracht P, Wilcken R, Udvarhelyi A, Rodde S, Grimme S. High Accuracy Quantum-Chemistry-Based Calculation and Blind Prediction of Macroscopic pKa Values in the Context of the SAMPL6 Challenge. Journal of Computer-Aided Molecular Design. 2018. October; 32(10):1139–1149. doi: 10.1007/s10822-018-0145-7. [DOI] [PubMed] [Google Scholar]
- [47].Prasad S, Huang J, Zeng Q, Brooks BR. An Explicit-Solvent Hybrid QM and MM Approach for Predicting pKa of Small Molecules in SAMPL6 Challenge. Journal of Computer-Aided Molecular Design. 2018. October; 32(10):1191–1201. doi: 10.1007/s10822-018-0167-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Robert Fraczkiewicz MW, SAMPL6 pKa Challenge: Predictions of ionization constants performed by the S+pKa method implemented in ADMET Predictor software; February 22, 2018. The Joint D3R/SAMPL Workshop 2018. https://drugdesigndata.org/about/d3r-2018-workshop. [Google Scholar]
- [49].Balogh GT, Tarcsay Á, Keserű GM. Comparative Evaluation of pKa Prediction Tools on a Drug Discovery Dataset. Journal of Pharmaceutical and Biomedical Analysis. 2012. August; 67-68:63–70. doi: 10.1016/j.jpba.2012.04.021. [DOI] [PubMed] [Google Scholar]
- [50].Settimo L, Bellman K, Knegtel RMA. Comparison of the Accuracy of Experimental and Predicted pKa Values of Basic and Acidic Compounds. Pharmaceutical Research. 2014. April; 31(4):1082–1095. doi: 10.1007/s11095-013-1232-z. [DOI] [PubMed] [Google Scholar]
- [51].Meloun M, Bordovská S. Benchmarking and Validating Algorithms That Estimate pK a Values of Drugs Based on Their Molecular Structures. Analytical and Bioanalytical Chemistry. 2007. September; 389(4):1267–1281. doi: 10.1007/s00216-007-1502-x. [DOI] [PubMed] [Google Scholar]
- [52].Liao C, Nicklaus MC. Comparison of Nine Programs Predicting p K a Values of Pharmaceutical Substances. Journal of Chemical Information and Modeling. 2009. December; 49(12):2801–2812. doi: 10.1021/ci900289x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Manchester J, Walkup G, Rivin O, You Z. Evaluation of p K a Estimation Methods on 211 Druglike Compounds. Journal of Chemical Information and Modeling. 2010. April; 50(4):565–571. doi: 10.1021/ci100019p. [DOI] [PubMed] [Google Scholar]
- [54].Mansouri K, Cariello NF, Korotcov A, Tkachenko V, Grulke CM, Sprankle CS, Allen D, Casey WM, Kleinstreuer NC, Williams AJ. Open-Source QSAR Models for pKa Prediction Using Multiple Machine Learning Approaches. Journal of Cheminformatics. 2019. December; 11(1). doi: 10.1186/s13321-019-0384-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Baltruschat M, Czodrowski P. Machine Learning Meets pKa [Version 2; Peer Review: 2 Approved]. F1000Research. 2020; 9 (Chem Inf Sci)(113). doi: 10.12688/f1000research.22090.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Hunt P, Hosseini-Gerami L, Chrien T, Plante J, Ponting DJ, Segall M. Predicting p K a Using a Combination of Semi-Empirical Quantum Mechanics and Radial Basis Function Methods. Journal of Chemical Information and Modeling. 2020. June; 60(6):2989–2997. doi: 10.1021/acs.jcim.0c00105. [DOI] [PubMed] [Google Scholar]
- [57].Zdrazil B, Guha R. The Rise and Fall of a Scaffold: A Trend Analysis of Scaffolds in the Medicinal Chemistry Literature. Journal of Medicinal Chemistry. 2018. June; 61(11):4688–4703. doi: 10.1021/acs.jmedchem.7b00954. [DOI] [PubMed] [Google Scholar]
- [58].Ertl P, Altmann E, McKenna JM. The Most Common Functional Groups in Bioactive Molecules and How Their Popularity Has Evolved over Time. Journal of Medicinal Chemistry. 2020. August; 63(15):8408–8418. doi: 10.1021/acs.jmedchem.0c00754. [DOI] [PubMed] [Google Scholar]
- [59].OEMolProp Toolkit 2017February1;. OpenEye Scientific Software, Santa Fe, NM: http://www.eyesopen.com. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
TABLE S1: SMILES and InChI identifiers of SAMPL6 pKa Challenge molecules.
TABLE S2: Evaluation statistics calculated for all macroscopic pKa prediction submissions based on Hungarian match for 24 molecules.
TABLE S3: Evaluation statistics calculated for all microscopic pKa prediction submissions based on Hungarian match for 8 molecules with NMR data.
TABLE S4: Evaluation statistics calculated for all microscopic pKa prediction submissions based on microstate match for 8 molecules with NMR data.
FIGURE S1: Dominant microstates of 8 molecules were determined based on NMR measurements.
FIGURE S2: MAE of macroscopic pKa predictions of each molecule did not show any significant correlation with any molecular descriptor.
FIGURE S3: The value of macroscopic pKa was not a factor affecting prediction error seen in SAMPL6 Challenge according to the analysis with Hungarian matching.
FIGURE S4: There was low agreement between experimental dominant microstate pairs and the predicted microstate pairs selected by Hungarian algorithm for microscopic pKa predictions.
An archive copy of the pKa Challenge directory of SAMPL6 GitHub Repository (SAMPL6-repository-pKa-directory.zip)
Table S1 in CSV format (SAMPL6-pKa-chemical-identifiers-table.csv)
Table S2 in CSV format (macroscopic-pKa-statistics-24mol-hungarian-match.csv)
Table S3 in CSV format (microscopic-pKa-statistics-8mol-hungarian-match-table.csv)
Table S4 in CSV format (microscopic-pKa-statistics-8mol-microstate-match-table.csv)
Figure S1 in CSV format (experimental-microstates-of-8mol-based-on-NMR.csv)
The Jupyter Notebook used for the enumeration of microstates (enumerate-microstates-with-Epik-and-OpenEye-QUACPAC.ipynb)
A CSV table of SAMPL6 molecule IDs and OpenEye OEChem generated SMILES (molecule_ID_and_SMILES.csv)
Data Availability Statement
SAMPL6 pKa challenge instructions, submissions, experimental data and analysis is available at SAMPL6 GitHub Repository: https://github.com/samplchallenges/SAMPL6