Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jan 5;15(2):2240–2250. doi: 10.1021/acsnano.0c06902

Fast and Accurate Nanoparticle Characterization Using Deep-Learning-Enhanced Off-Axis Holography

Benjamin Midtvedt †,*, Erik Olsén ‡, Fredrik Eklund ‡, Fredrik Höök ‡, Caroline Beck Adiels †, Giovanni Volpe †, Daniel Midtvedt †,*
PMCID: PMC7905872  PMID: 33399450

Abstract

graphic file with name nn0c06902_0006.jpg

Characterization of suspended nanoparticles in their native environment plays a central role in a wide range of fields, from medical diagnostics and nanoparticle-enhanced drug delivery to nanosafety and environmental nanopollution assessment. Standard optical approaches for nanoparticle sizing assess the size via the diffusion constant and, as a consequence, require long trajectories and that the medium has a known and uniform viscosity. However, in most biological applications, only short trajectories are available, while simultaneously, the medium viscosity is unknown and tends to display spatiotemporal variations. In this work, we demonstrate a label-free method to quantify not only size but also refractive index of individual subwavelength particles using 2 orders of magnitude shorter trajectories than required by standard methods and without prior knowledge about the physicochemical properties of the medium. We achieved this by developing a weighted average convolutional neural network to analyze holographic images of single particles, which was successfully applied to distinguish and quantify both size and refractive index of subwavelength silica and polystyrene particles without prior knowledge of solute viscosity or refractive index. We further demonstrate how these features make it possible to temporally resolve aggregation dynamics of 31 nm polystyrene nanoparticles, revealing previously unobserved time-resolved dynamics of the monomer number and fractal dimension of individual subwavelength aggregates.

Keywords: particle characterization, optical microscopy, holography, deep learning, aggregation kinetics

Nanoparticles play a crucial role in many fields, including pharmaceutical sciences,1 food production,2,3 and environmental monitoring.4 As particle size and composition greatly influence particle function, fast and accurate characterization tools are essential and, ideally, should work in the native environment of the particles. For example, in pharmaceutical applications, the interaction between nanoparticles (e.g., protein aggregates, extracellular vesicles, and viruses) and biological cells depends crucially on particle size and composition,1,5−8 and studying this relation requires accurate characterization of nanoparticles in the complex extra- and intracellular environments. In food production, nanoparticles are used to stabilize emulsions, improving food texture and shelf life.2 In environmental monitoring, there is a need to identify and characterize nanoparticles that enter the air, water, and soil as a byproduct of industrial processes and waste disposal.4 In all of these applications, it is often necessary to determine and monitor particle properties and activity in an environment whose physicochemical properties are unknown.

Traditionally, individual submicron particles in dispersion have been indirectly sized by analyzing their diffusive Brownian motion in a solution of known viscosity (nanoparticle tracking analysis9,10). In this approach, the trajectory of a particle is tracked, its diffusion constant D is determined from the mean squared displacement of the measured trajectory, and finally, the particle radius r is estimated using Stokes–Einstein relation, i.e., 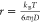Inline graphic, where kB is Boltzmann’s constant, T is the absolute temperature, and η is the viscosity of the medium. Even though this method is widely employed, it makes several assumptions and presents several limitations. First, as the Brownian motion is stochastic, the particle trajectory needs to be observed over many (>100) time steps to achieve a reliable estimate of the particle radius, which limits the applicability of diffusion-based methods in fast processes (e.g., high-flow sorting) or when the particle sizes change dynamically (e.g., dynamic aggregation processes). Second, the medium must be viscous with a known viscosity η, which prohibits the application of this method in biologically relevant media, which are often viscoelastic with unknown properties.

Third, this method can only be applied to particles close to thermodynamic equilibrium because it implicitly makes use of the fluctuation–dissipation relation, excluding several processes of interest that occur out of equilibrium, such as in living systems and in active matter.

In order to overcome these limitations, several methods have been proposed to determine the properties of the particle by measuring its scattering properties,11,12 instead of its motion. For example, novel microscopy techniques such as interferometric scattering microscopy (iSCAT13) have made it possible to quantify the optical scattering contrast of nanoparticles close to an interface. For particles larger than the wavelength of light, the angular distribution of the scattering intensity depends strongly on particle size, which has been exploited to characterize the size of particles14 and protein aggregates,15,16 both using classical image analysis17 as well as deep-learning methods.16 However, quantifying size and refractive index of particles smaller than the wavelength of light from optical scattering patterns in microscopy images remains challenging: The dependence of the angular distribution of the scattering on particle size is very weak, and in the limit of Rayleigh scatterers (r ≪ λ), the angular distribution is independent of size. The situation is further complicated by the fact that the microscope that collects the scattering pattern acts as a low-pass filter, collecting only the light scattered in a limited range of scattering angles determined by the numerical aperture of the objective. These problems make the use of traditional techniques for image analysis challenging; as a result, it has thus far not been possible to use the scattering properties alone to simultaneously characterize the size and refractive index of subwavelength particles.

Here, we demonstrate that holographic imaging combined with deep learning can simultaneously characterize the size and refractive index of subwavelength particles, while using 2 orders of magnitude shorter trajectories than required by standard methods and without assumptions about the physicochemical properties of the medium. In fact, because of its potential for better, more autonomous performance,18 deep learning has recently been employed to successfully solve several digital microscopy problems, such as particle tracking,19,20 anomalous diffusion characterization,21,22 image segmentation,23 and image super-resolution.24 In particular, deep-learning techniques have been shown to outperform traditional image analysis methods for signals with low signal-to-noise ratios in the range of 1–10,19 making them an attractive choice for the problem at hand. In this work, we develop a deep-learning-powered method to determine the radius and refractive index from a series of scattering patterns of subwavelength particles recorded by an off-axis holographic microscope.

We demonstrate that this method requires 2 orders of magnitude fewer observations than traditional methods to reach the same accuracy in size and refractive index. The reduction in the number of observations required for accurate characterization enables significantly faster characterization of subwavelength particles, which, for example, permits us to characterize individual subwavelength particles while they are flowing in a microfluidic device. We also demonstrate that this method correctly characterizes subwavelength particles without requiring knowledge of either particle shape or medium refractive index and viscosity, making it ideal for applications in native environments, whose physicochemical properties are often not known a priori. Finally, we demonstrate the ability of this method to enable applications beyond the state of the art, by continuously monitoring a nonstationary process, specifically the subsecond fluctuations in size and refractive index of aggregates of nanoparticles.

Results and Discussion

Experimental Setup and Acquisition of Experimental Data

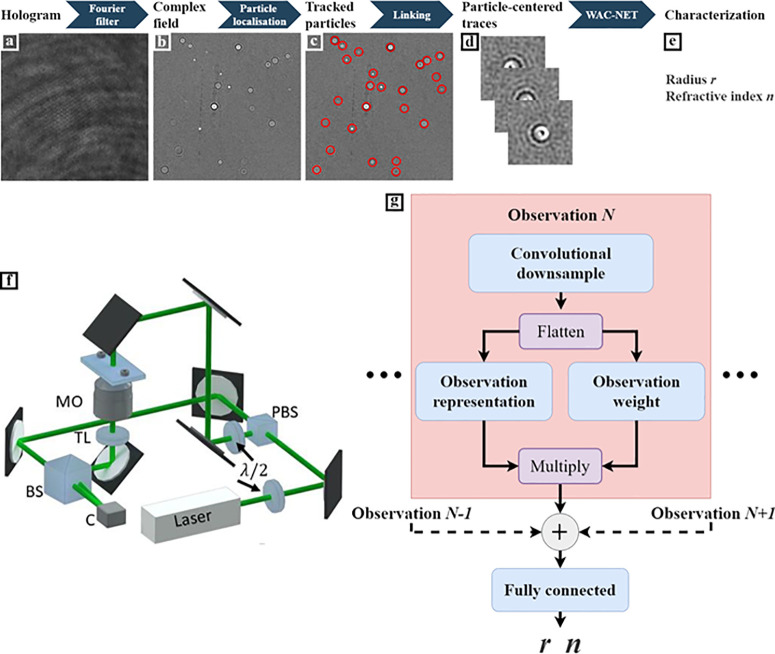
The scattering patterns of a volume of solution containing subwavelength particles are acquired using an off-axis holographic microscope with an illuminating wavelength of λ = 633 nm and an oil-immersion objective with a numerical aperture (NA) of 1.3 (see Figure 1f and Methods for a detailed description of the optical setup). The illuminating beam is split into two beams, one passing through the sample and one used as a reference. Then, these beams are recombined at the camera, which records their interference pattern. A representative example of such a pattern is shown in Figure 1a. This interference pattern contains sufficient information to reconstruct the optical field at the sample with diffraction-limited resolution (Figure 1b) by employing a Fourier transform and a low-pass filter (see Methods for a description of the reconstruction algorithm).

Figure 1.

Figure 1

Open in a new tab

Combining off-axis holography and deep learning to characterize subwavelength particles. (a) Interference pattern is acquired with an off-axis holographic microscope and (b) Fourier-transformed and low-pass-filtered to produce the reconstructed field at the camera plane (here, only the imaginary part of the complex field is shown). (c) These complex field images are used to track the three-dimensional particle position. (d) Region of interest is selected around each detected particle for each time step. (e) Finally, this sequence of observations is used to characterize the radius r and refractive index n using a specialized neural-network design, which we call weighted average convolutional neural network (WAC-NET). (f) Laser beam is split into two paths by a polarizing beam splitter (PBS). The relative intensities of the two paths are regulated by the initial λ/2-waveplate. One of the beams goes through the sample, and the light scattered from the sample is collected by a microscope objective (MO), after which a tube lens (TL) provides a focused image at the camera (C). The paths are recombined using a beam splitter (BS) at a slight offset angle, resulting in an interference pattern at the camera. The particles are suspended in liquid inside a straight microfluidic chip (ChipShop). Reprinted with permission from ref (25) under the Creative Commons license. (g) Schematic overview of WAC-NET. Each observation is downsampled and flattened using a convolutional network. From this flattened vector, a weight and a representation are calculated and multiplied. The weightings are normalized using a softmax transformation. The weighted representations are merged by summation, and the result is passed to a fully connected network that returns r and n.

The particles are imaged under constant flow in a microfluidic chip (see Methods for details on the chip). This enables us to gather scattering patterns from a large number of particles in a short amount of time (typically a few hundred particles per minute). In order to extract the scattering patterns from each particle, the particles are first localized in three dimensions using a previously published method12 (Figure 1c) and subsequently tracked using standard methods (see Methods for a detailed description). A region of 64 × 64 pixels centered around each particle detection is extracted. In this way, we record and store a collection of scattering patterns of each particle (Figure 1d), which is subsequently analyzed using a neural network (Figure 1e).

Structure of the Neural Network

Since the particles are smaller than the wavelength of the illuminating light, the features that are available for determining particle size are contained in the high frequencies of the image spectrum (corresponding to high scattering angles).26 At low signal-to-noise ratio, it is prohibitively difficult to analytically fit these features and determine the particle properties. Thus, to achieve a good signal-to-noise ratio, it is necessary to average over multiple observations of the same particle. However, direct averaging of observations requires perfect three-dimensional localization, which is in practice impossible to achieve because of the error intrinsic to any localization technique.

In order to overcome this problem, we employ machine learning. While in standard methods the user explicitly defines a set of rules to convert the input data to the desired output, in machine learning, the rules are inferred by providing the machine-learning model with a large collection of input–output pairs—this process is known as training of the machine-learning model.18 Neural networks are a very successful subset of machine-learning models27 and consist of interconnected layers which apply some, often simple, transformation to their input and pass the result to some other layer. The transformation each layer applies can be controlled by weights, which are optimized during the training.

The architecture of the neural network we employ is shown in Figure 1g. This architecture is designed to optimally combine the information contained in multiple scattering patterns of the same particle and provide a single prediction of its size and refractive index. As discussed above, the scattering patterns themselves cannot be averaged before being sent to the network, due to imperfect localization. We overcome this problem by averaging the scattering patterns not at the input but at an intermediate layer in the network. This allows the network to produce a representation of the scattering pattern that contains the information that it needs to characterize particle size and refractive index (including the scattering strength and angular spectrum), while disregarding other aspects that are of no importance to the characterization (such as the position of the particle within the image).

An additional complication in the task of characterizing a set of observations of a particle is that each individual observation may not be equally representative (due to, e.g., uncorrelated noise or interference of the scattering patterns of nearby particles). In order to overcome also this problem, the network additionally assigns a score to each observation. These scores are used as weights when averaging the representations of multiple scattering patterns, ensuring that scattering patterns that are corrupted by significant noise contributes less to the overall characterization. We call this neural network architecture weighted average convolutional neural network (WAC-NET).

Training of the Neural Network

In order to train the WAC-NET, we first must generate a training set that is representative of the data produced by the optical setup. Using experimental data for training the WAC-NET is challenging because they are limited in their number and have intrinsic experimental errors. We therefore generate synthetic training data by simulating the complex scattering patterns of subwavelength particles using Mie theory (see Methods for details on the scattering pattern simulation). The scattering patterns are convolved with the optical transfer function of the microscope, determined by analysis of reference particles of known size and refractive index (see Methods for details on this calibration procedure). We train the WAC-NET to infer particle sizes and refractive indices within a broad range of values by simulating 106 scattering patterns cropped to 64 pixel × 64 pixel images from particles having radii uniformly distributed in the range of 115 nm ≤ r ≤ 500 nm and refractive indices uniformly distributed in the range of 1.36 ≤ n ≤ 1.9, dispersed in a medium with refractive index 1.33. This choice captures a range of particle sizes where existing optical characterization techniques struggle to provide accurate sizing results. Specifically, for radii larger than 500 nm, particle sizing can be performed in off-axis holographic imaging by counting the number of pixels the particle occupies in the image.25 In the opposite limit, when entering the Rayleigh scattering regime, the angular distribution of the scattering pattern does not scale with particle size, prohibiting optical sizing. This consideration sets the lower limit to the sizes included in the training set. In order to make the training set representative of the experimental data, the observations of each particle are corrupted with inaccurate three-dimensional centering of the particle (with a standard deviation of the error of 0.1 μm, similar to the size of individual pixels) and synthetic noise in the form of spatially correlated background noise (with amplitude determined from empty slices of the image). A random number between 5 and 50 such observations are stacked to form the synthetic representation of a traced particle. An additional advantage of using synthetic data is that new data can be continuously generated during the training, eliminating the risk of overfitting due to a limited training set. Taking this approach, the training time of the network is about 12 h on a computer equipped with an NVIDIA GeForce GTX 1650 graphics card. The analysis of a single scattering pattern takes around 4 ms on the same computer.

Neural Network Performance on Simulated Data

We first test the trained WAC-NET on simulated data. We simulate the scattering patterns of a set of 2000 stacks of 0.20 μm (radius) polystyrene (PS) spheres (refractive index = 1.58, illumination wavelength λ = 633 nm, and objective NA = 1.3) dispersed in water, each stack consisting of 100 observations of a single particle. The orange symbols in Figure 2a,b represent the estimated values of the radius rest and refractive index nest as a function of the number of time steps during which a representative particle is observed. It can be seen that these estimates converge to the ground-truth values (solid black lines) within only a few observations. For comparison, the characterization based on conventional particle tracking (gray symbols) produces significantly worse results than those obtained by the WAC-NET and do not converge to the ground-truth value even when using 60 time steps.

Figure 2.

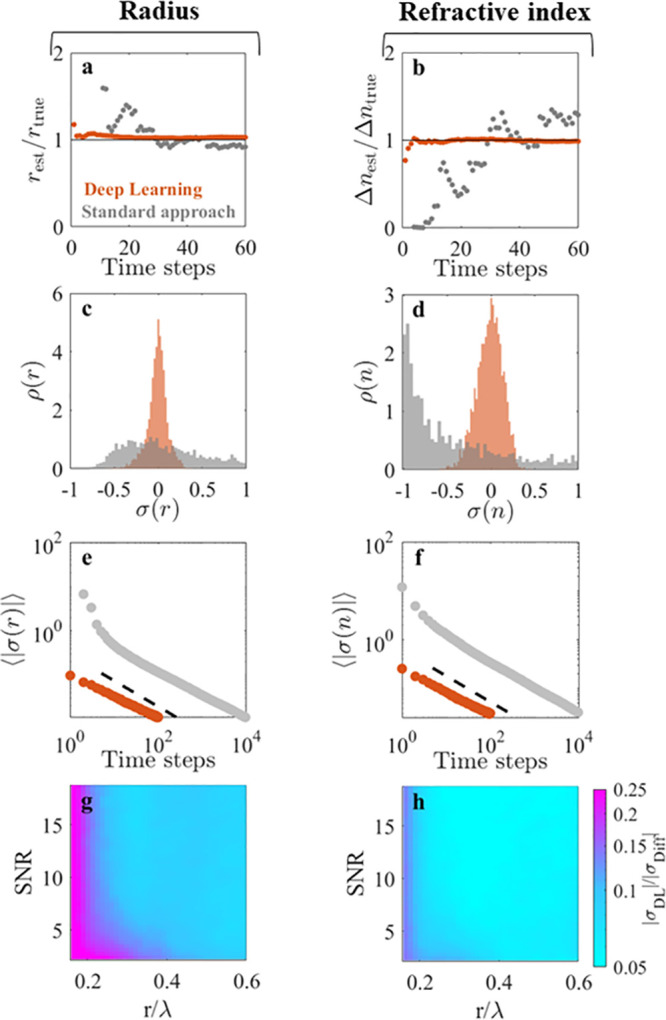
Figure 2

Open in a new tab

Deep learning enhances particle characterization on simulated data. (a,b) Radius rest normalized by the ground-truth radius rtrue = 0.20 μm and refractive index difference Δnest normalized by the ground-truth refractive index difference Δntrue = 0.25; rest and Δnest are estimated using deep learning (orange symbols) and a conventional diffusion-based approach (gray symbols) as a function of the number of observations of the particle. The deep-learning approach requires fewer observations to converge to the ground-truth values. (c,d) Distributions of the relative errors σr and σn for rest and nest, respectively, on the characterization of 2000 simulated particles using five observations. While the standard approach (gray histograms) fails to characterize the particles, the deep-learning approach (orange histograms) characterizes the radius to within 5% and refractive index to within 10% (mean absolute errors). (e,f) Scaling of the absolute relative errors ⟨|σr|⟩ and ⟨|σn|⟩ as a function of the number of observations used for the characterization. The dashed line represent the scaling 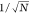Inline graphic, where N is the number of observations. (g,h) Ratio of the absolute relative error made by the deep-learning approach (σr,DL) and the diffusion-based approach (σDiff) using 20 observations shows that the deep-learning approach provides an order of magnitude more accurate characterization both for particle radius (g) and refractive index (h) in a wide range of particle radii r/λ (where λ is the wavelength of the illuminating light), even on noisy images (signal-to-noise ratio < 10).

To compare the network performance with regard to size determination to particle sizing using conventional particle tracking measurements, we simulate 2000 Brownian motions, each having N = 104 time steps with time step Δt. To estimate the diffusion constant corresponding to a Brownian motion, we use the standard approach based on the mean squared displacement in a time step, i.e., 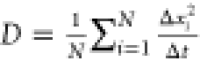Inline graphic, where Δxi is the length of the ith displacement. To determine the refractive index, there is no standard method for subwavelength particles. Nonetheless, it has previously been demonstrated that measuring either scattering intensity11 or phase contrast12 in combination with analysis of the Brownian motion allows simultaneous determination of size and refractive index.12 In order to compare the performance of WAC-NET with existing methods for the determination of refractive index, we assume that the phase contrast of the particles is known exactly at each time step and estimate the refractive index as described in ref (12).

Figure 2c,d shows the performance of WAC-NET (orange histograms) and diffusion-based characterization (gray histograms) on the ensemble of 2000 particles using five time steps for characterization. While the distributions of estimates produced by WAC-NET are well-defined and centered around the true value, the diffusion-based estimates are scattered in a wide range and are not centered around the true value, demonstrating that WAC-NET performs significantly better than diffusion-based methods when using few time steps. These results highlight the difference in the underlying principle of the two approaches. In contrast to the stochastic nature of the diffusional motion, the scattered field is deterministic, allowing our deep-learning approach to directly infer particle size from the optical scattering properties of the particle. Repeated observations of the same particle are used to refine this inference. Consequently, it is possible to reach high accuracy in particle sizing using only a few observations.

To determine whether the accuracy achieved by the WAC-NET is better than that of the diffusion-based method also when using many time steps for the characterization, we study the scaling of the estimated error of the two approaches (defined as σ(y) = ⟨(ypred/ytrue – 1)⟩), where y represents either size or refractive index, with the number of time steps in Figure 2e,f. 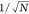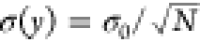We find that the error of both methods decreases as Inline graphic, where N is the number of time steps (dashed black lines), with the WAC-NET consistently producing results more than an order of magnitude better than those of the diffusion-based method. Consequently, the error of both methods can be parametrized as Inline graphic, where σ0 is a proportionality constant. In the case of diffusional motion, the determination of the diffusion constant in essence amounts to estimating the variance of the distribution of particle displacements. Assuming that N displacements are known exactly, the uncertainty in the estimated variance of the underlying distribution is given by σ2 = 2/N. This provides a lower bound on the proportionality constant for diffusional motion that cannot be improved upon by changes to the experimental parameters.28 In the case of the deep-learning approach, the prefactor is instead determined by the particle type and the quality of the image.

Figure 2g,h plots the prefactor σ0 as a function of the signal-to-noise ratio (SNR) of the image and the ratio of the particle radius to the illuminating wavelength (r/λ). This allows us to compare the performance of the network to that of the diffusion-based approach for a wide range of particle sizes and noise levels. We find that the deep-learning-based particle characterization method is more than 1 order of magnitude more accurate than diffusion-based methods for a fixed number of observations in a broad range of particle sizes, extending down to r ≈ λ/3. Owing to the scaling of the errors of the two methods with the number of observations, the diffusion-based method will need more than 2 orders of magnitude more observations to reach the same accuracy in this region of particle sizes. Furthermore, the network shows a considerable increase in accuracy compared to that with a diffusion-based approach even in poor illumination conditions (down to SNR = 2). Also, note that the positions of the simulated particles were known exactly, whereas in any experimental setting, error in the particle localization inevitably induces additional uncertainties in the determination of the diffusion constant; therefore, the stated improvement in accuracy is a lower bound.

The accuracy of the deep-learning method enables distinguishing particle populations that have similar properties. We find that populations differing by only 12 nm in radius or by 0.036 refractive index units can be distinguished using 20 observations for the characterization (supplementary Figure S1).

It is worth noting that, in principle, any physical characteristic of the particle that alters the optical scattering pattern, such as its morphology or internal refractive index distribution, can be characterized in this way by an appropriate choice of simulation method. As an example, we simulate the scattering patterns of stratified spheres and train the network to characterize the core radius, core refractive index, shell thickness, and shell refractive index based on the optical scattering patterns produced. The results in supplementary Figure S2 demonstrate the applicability of the proposed method also for this more complex scenario.

Neural Network Performance on Experimental Data

To verify that the increase in accuracy of the deep-learning characterization transfers to experimental data, we recorded holographic videos of 0.228 μm radius polystyrene spheres (NIST certified, standard deviation 6.8 nm) flowing through a microfluidic chip (see Methods for further details). In Figure 3a,b, the characterization of a representative particle is shown as a function of the number of time steps used for characterization. We find that the WAC-NET converges to estimates close to the expected values of size and refractive index using only a few time steps (orange symbols). In order to compare the accuracy of the network to conventional approaches, the particles were tracked and their hydrodynamic radii were estimated from their Brownian motion. The characterization based on conventional particle tracking shows considerably larger fluctuations (gray symbols). Similarly, WAC-NET produces predictions consistent with the expected values on the ensemble of particles using only five time steps (orange histograms in Figure 3c,d, expected values of size and refractive index are shown as solid black lines). On the other hand, the diffusion-based approach does not correctly characterize the sample using only five time steps (gray histograms).

Figure 3.

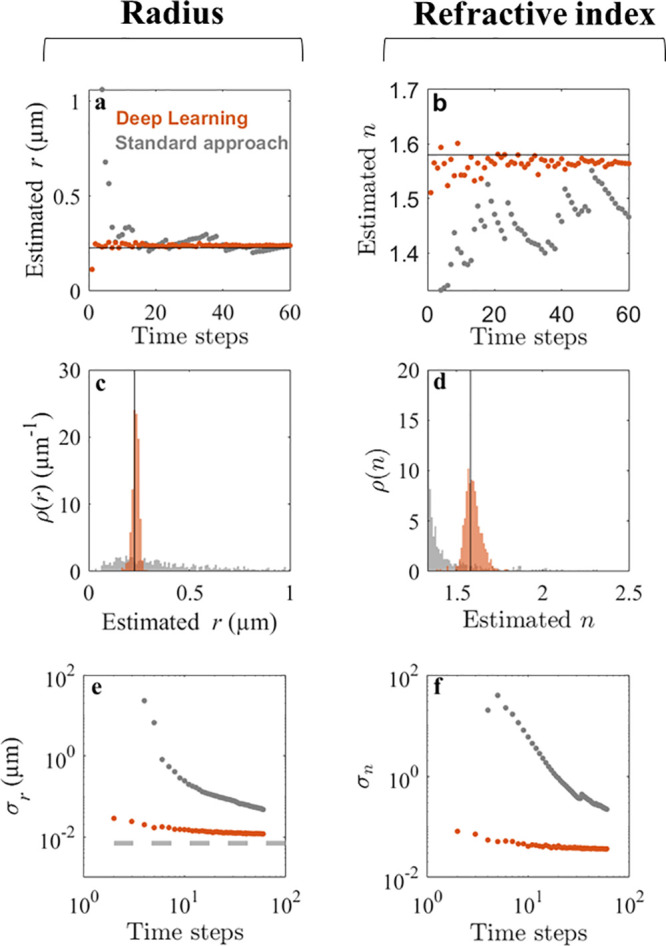
Figure 3

Open in a new tab

Deep learning enhances particle characterization on experimental data. (a,b) Estimated radius r and refractive index n of a polystyrene sphere as a function of the number of observations using deep learning (orange symbols) and a standard diffusion-based method (gray symbols). The manufacturer-provided NIST-certified radius is 0.228 ± 0.0068 μm, and the bulk value for the polystyrene refractive index is between 1.55 and 1.59. The accuracy of the deep-learning approach surpasses the diffusion-based approach with all numbers of observations. (c,d) Distribution of r and n on an experimental sample of 256 particles using five observations. While the diffusion-based approach (gray histograms) fails to characterize either property, the deep-learning approach (orange histograms) provides estimates of the radius with ±16 nm standard deviation and of the refractive index with ±0.05 standard deviation. (e,f) Scaling of the standard deviations σr and σn of the measured r and n of the population as a function of the number of observations. The standard deviation of the deep-learning approach (orange symbols) reaches ±11.9 nm in radius and ±0.03 in refractive index units using 60 observations. This performance is much better than that of the standard diffusion-based approach (gray symbols): σr is comparable to the size variation stated by the manufacturer (±6.8 nm NIST-certified standard deviation, gray dashed line in e), and σn is within the range of variability of the polystyrene refractive index.

When considering the scaling of the error of the predictions with the number of time steps, we find that the accuracy of the deep-learning approach, when applied to experimental data, appears to saturate around a standard deviation of 11.9 nm and 0.03 refractive index units for the size and refractive index, respectively (Figure 3e,f). This saturation partially reflects the distribution of sizes and refractive indices within the sample (the NIST-certified width of the size distribution of these particles is 6.8 nm, measured by disc centrifuge). The remaining variation might stem from spurious contaminants in the sample or false detections, increasing the tails of the size distribution. Indeed, fitting the central peak of the size distribution to a Gaussian function gives an estimated width of 8.2 nm, closely resembling the NIST-certified distribution width of 6.8 nm, also verified by transmission electron microscopy (see supplementary Figure S3). As the particles are imaged under flow, they could not be tracked for sufficiently long to determine a similar saturation point for the conventional particle tracking approach.

Characterization of a Multicomponent Sample

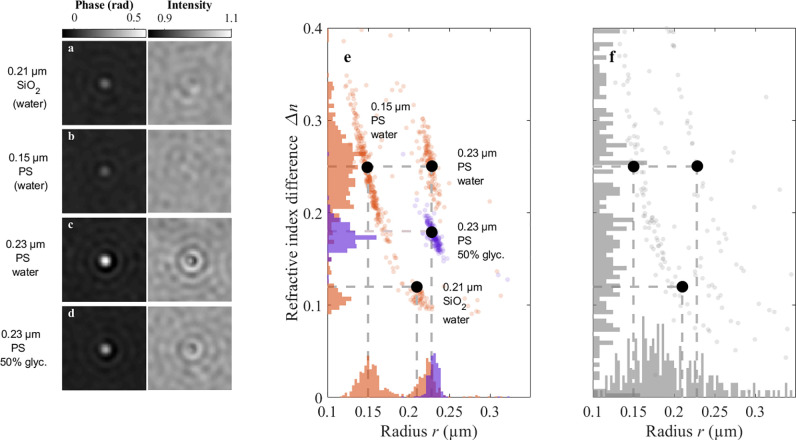
As a test of the performance of the network in a more complex and realistic scenario, we analyze a multicomponent sample consisting of PS particles of two different sizes (modal radii = 0.228 and 0.15 μm, refractive index = 1.58) and silica particles (modal radius = 0.21 μm, refractive index = 1.45). This sample is challenging to analyze using standard methods as 0.23 μm polystyrene and 0.21 μm silica are similar in size and are therefore hard to distinguish by diffusion alone, especially when only a few observations are available. In addition, 0.15 μm PS and 0.21 μm silica induce similar phase contrasts, and their scattering patterns are consequently visually similar. This is highlighted in Figure 4a–c, where the phase and amplitude contrasts of characteristic particles within the three subpopulations are shown.

Figure 4.

Figure 4

Open in a new tab

Deep-learning approach performance on particle mixtures and in different environments. (a–d) Phase and amplitude signals from a representative particle from each characterized population. (e) Deep-learning approach (using 60 observations) distinguishes and correctly characterizes subpopulations in a multicomponent mixture dispersed in water, consisting of 0.21 μm silica (SiO2), 0.15 μm PS, and 0.23 μm PS particles. Furthermore, the deep-learning approach accurately characterizes the radius r and the refractive index difference Δn of 0.23 μm PS particles dispersed in a 50% glycerol/water mixture, demonstrating that the measurements do not rely on detailed knowledge of the properties of the solution. The intersections of the dashed lines represent the expected positions of the populations. (f) When using a diffusion-based approach to characterize the multicomponent sample (dispersed in water), the size and refractive index distributions become very broad and the two smallest subpopulations cannot be distinguished when using 60 observations for the characterization.

Despite these similarities, the deep-learning approach successfully distinguishes the three subpopulations and accurately determines their modal characteristics (Figure 4e). Specifically, the sizes and refractive indices are estimated by WAC-NET to be r = 0.15 ± 0.01 μm (standard deviation), n = 1.58 ± 0.06 (0.15 μm PS); r = 0.22 ± 0.02 μm, n = 1.44 ± 0.02 (0.21 μm silica); and r = 0.22 ± 0.01 μm, n = 1.58 ± 0.03 (0.23 μm PS). The slightly larger variation observed in the smallest subpopulation is consistent with the discussion above in connection with Figure 2g,h: in our setup, a radius of 0.15 μm corresponds to a ratio r/λ ≈ 0.24, which is within the region where the precision of the WAC-NET starts to decay. In order to understand the correlation between estimated size and refractive index in this population, we note that the scattering amplitude for particles in this size regime scales approximately with 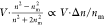Inline graphic to lowest order in Δn = n – nm, and where n and nm are the refractive index of the particle and the medium, respectively.12,26 For particles with r ≲ λ/4, the WAC-NET can still predict the scattering amplitude via the product V·Δn (see supplementary Figure S4a), but the precision by which the network can separate size and refractive index from this product deteriorates somewhat in this size regime. As a consequence, for particles with r ≲ λ/4, the estimated sizes and refractive indices are correlated in such a way as to keep the product V·Δn constant (supplementary Figure S4b).

For comparison, the results obtained from particle tracking and analysis of the Brownian motion of the sample are shown in Figure 4f. Particle tracking does not provide sufficient accuracy in size determination to distinguish 0.15 μm PS and 0.21 μm silica from each other. Thanks to the difference in phase contrast, the 0.23 μm PS population can be distinguished, but the distribution of estimated size and refractive index becomes very broad.

In the context of characterizing biological samples, it is important to characterize samples and separate particle populations having very low refractive index contrasts. As an example, extracellular vesicles, one important class of biological particles, have refractive indices estimated to be in the range of 1.35–1.38.29 In order to probe the accuracy of WAC-NET in the lower part of this range, we characterize silica particles having a refractive index of 1.42 dispersed in varying glycerol concentration, thereby tuning the refractive index contrast from 0.09 to 0.02, a range of refractive index contrasts relevant for biological particles. We find that WAC-NET accurately characterizes subwavelength particles down to a refractive index contrast of 0.03 refractive index units, demonstrating the applicability of WAC-NET for characterization of biological samples (supplementary Figure S5).

Characterization of Particles in an Unknown Environment

To test the performance of the network in situations where the properties of the solute are not known a priori, we also record holographic videos of 0.23 μm polystyrene particles dispersed in a 50% glycerol/water mixture. The presence of glycerol changes both the viscosity and the refractive index of the solution, and thus this solute is qualitatively different from the solute used for network calibration. In the case of holographic imaging, a change in the refractive index of the environment primarily changes the scattering amplitude but leaves the spatial structure of the scattering pattern approximately unchanged (Figure 4d, cf. Figure 4c). Thus, we expect the network to correctly recognize the particles having the same sizes in both environments but with a different relative refractive index. Indeed, we found that the particle populations measured in the two solutions overlap in size but are shifted in refractive index (Figure 4e). In order to relate the shift in estimated refractive index of PS particles to the difference between the refractive index of water (nw = 1.33) and that of the glycerol/water mixture (ng/w ≈ 1.40), we note that the shift in scattering amplitude is proportional to ng/w – nw, valid to lowest order in ng/w – nw. Thus, the shift in scattering amplitude is expected to produce a shift in the estimated refractive index of the particles that correspond to the difference in refractive index between the solutions. Indeed, we find that this is the case, demonstrating the capacity of the deep-learning-based method to characterize particles without prior knowledge of the physicochemical properties of their surrounding environment.

Monitoring Clusters of Nanoparticles

In the experiments presented until now, we have evaluated the network performance on spherical particles whose properties do not change over time. In order to test it in a more dynamic scenario beyond the state of the art of what can be done with standard techniques, we image a sample consisting of a solution of 31 nm radius polystyrene nanoparticles freely diffusing in a microfluidic chip and forming dynamic clusters (nanoparticle clustering is induced by adding a droplet (∼20 μL) of saturated NaCl solution to the inlet of the microfluidic chip, which alters the Debye screening length and destabilizes the suspension). These clusters are in general nonspherical, and their size and refractive index fluctuate over time. Since clustering of nanoparticles affects their reactivity, understanding how such clusters form, how they interact, and how their size and morphology evolve in time is important to understand and predict their behavior and performance.30 For instance, determining whether the formation of clusters is irreversible (aggregation) or reversible (agglomeration) is challenging, presently requiring combining a multitude of measurement techniques.31 In fact, with the exception of liquid-cell transmission electron microscopy, which suffers from complicated sample preparation and low throughput, existing methods for characterizing nanoparticle clusters only provide snapshots of the aggregation/agglomeration process and thus cannot be used to temporally monitor the clusters.32

Note that since the clusters are generally nonspherical and inhomogeneous, the radius and refractive index of the clusters are not well-defined concepts. Nonetheless, they will produce a scattered field that is similar to the field generated by a homogeneous sphere of radius reff and refractive index neff. In the following, the terms radius and refractive index of the clusters will refer to reff and neff.

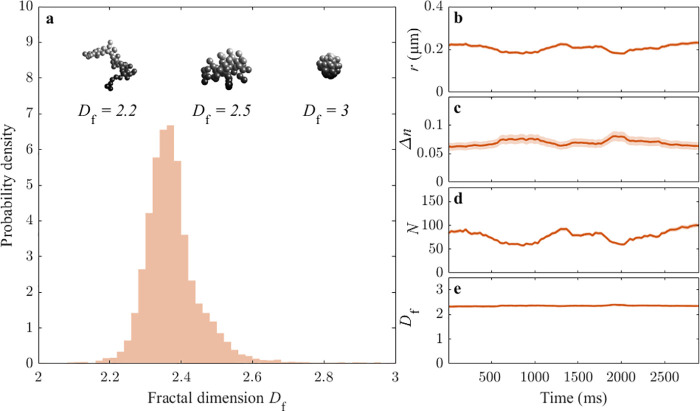
A signature of cluster formation is the fractal nature of the resulting structure. A fractal cluster can be characterized by its fractal dimension, Df, which dictates the scaling of the size with the number of monomers, N, in the cluster (see insets in Figure 5a): (r/r0) = k·Nf1/D, where r is the radius of the cluster, r0 is the radius of the monomers, and k is a proportionality constant (k ≈ 1 for clusters with fractal dimensions Df > 2,33 so in the following, we set k = 1). For close-packed spheres, the radius of the cluster scales as (r/r0) ∼ N1/3. The effective refractive index n of a cluster formed by identical spheres with radius r0 and refractive index n0 follows the Maxwell-Garnett relation, 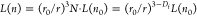Inline graphic, with Inline graphic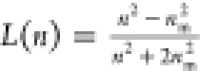, with nm being the refractive index of the surrounding medium.34 The latter expression can also be used to directly estimate the fractal dimension of a cluster, given that the radii and refractive indices of both the monomers and the cluster as a whole are known.

Figure 5.

Figure 5

Open in a new tab

Time-resolved dynamics of nanoparticle clusters. (a) Ensemble of particle clusters formed by 31 nm radius PS monomers features an average fractal dimension Df close to 2.35. The insets on the top show some pictorial depictions of possible clusters with various fractal dimensions. (b–e) Time-resolved behavior of a representative cluster, characterized in terms of its radius r (b), refractive index difference Δn (c), number of monomers N (d), and fractal dimension Df (e). While r, Δn, and N greatly vary over time, Df remains stable in time. The shaded regions represent the estimated standard deviation of the error. The cluster is characterized using a moving window of 20 observations, acquired at a frame rate of 30 frames per second. The fractal dimension of the cluster is estimated based on the scaling of its size and refractive index with the number of monomers, assuming a known monomer with a radius of 31 nm and a refractive index of 1.58.

For diffusion-limited clustering of monodisperse monomers, the fractal dimension is expected to be around Df = 2.5, whereas the value is lowered to Df = 1.75 if cluster–cluster clustering is taken into account.35 In line with this, previous measurements of the fractal dimension of colloidal clusters have yielded values in the range of Df ∼ 1.6–2.3, with the exact value depending on multiple factors, such as the concentration of salt in the solution and the concentration of monomers.35−39 Furthermore, the fractal dimension has been predicted to decrease with time, with early clusters having Df ∼ 2.5, decreasing to Df ∼ 1.8 as a function of time.40 Based on these results, we expect the fractal dimension in our experiment to be close to Df = 2.5. Consistent with this, we find that the fractal dimension of the structures are Df = 2.35 ± 0.1 (Figure 5a). This demonstrates that the deep-learning-based approach is sufficiently accurate even on nonspherical subwavelength particles to estimate their fractal dimension, and that the method does not require the shape of the particles to be known a priori.

The characterization of the clusters using the WAC-NET permits us also to investigate the temporal dynamics of the properties of individual nanoparticle clusters. To do so, we characterize the clusters using a sliding window of 20 time steps (at a frame rate of 30 fps), providing subsecond temporal resolution of size and refractive index of individual clusters. Fluctuations in these properties can, in general, be of two different physical origins: association/disassociation of monomers to the cluster will change the number of monomers in the cluster, without changing the fractal dimension, whereas internal rearrangements of monomers will cause a change to the fractal dimension, at a fixed monomer number. Thus, by monitoring the number of monomers N and fractal dimension Df, the physical origin of fluctuations in size and refractive index can be determined. Figure 5b,c shows the behavior of a representative cluster, displaying fluctuations of both size and refractive index. These fluctuations are attributed to a fluctuation in the number of monomers in the cluster (Figure 5d). Strikingly, the estimated fractal dimension of the structure remains constant in time despite the large temporal size fluctuations (Figure 5e), indicating that internal rearrangement of monomers does not occur at the time scale of the measurement. The large fluctuations of the number of monomers in the clusters can only be explained by continuous association/disassociation of monomers to the clusters, strongly suggesting that the clusters are in fact agglomerates (weakly/reversibly bound) rather than aggregates (strongly/irreversibly bound).

Conclusions

We have demonstrated the potential for deep-learning-enhanced optical characterization of subwavelength particles. Going beyond standard approaches, we have shown that the scattering patterns of individual particles recorded in off-axis holographic imaging contain sufficient information to extract size and refractive index of dielectric particles with a radius down to r = 0.15 μm.

With standard approaches, individual characterization of dispersed particles in the subwavelength regime requires the analysis of the Brownian motion of the particles through particle tracking. By instead using the optical scattering pattern to deduce size and refractive index, our approach offers several advantages compared to traditional approaches. Specifically, our method does not require prior knowledge of the physical properties of the surrounding medium, such as its viscosity or refractive index. This is particularly important in industrial and biological systems, where particles need to be characterized in complex environments. Furthermore, our method provides temporally resolved measurements of size and refractive index of the particles, potentially enabling direct monitoring of interaction kinetics of particles in their native environment.

Taking the approach presented in this article, we achieve an estimated error in particle sizing of <10% using as few as five time steps, orders of magnitude faster than diffusion-based methods. In addition to particle size, our method also estimates the particle refractive index with comparable accuracy, serving as a proxy for particle composition. The refractive index and particle size are estimated from the optical scattering profile, with no reference to particle motion, thus enabling accurate characterization in arbitrary environments.

It is also worth noting that the approach we propose requires only a few observations of each particle to accurately characterize both size and refractive index. Thus, deep-learning-based characterization enables temporally resolving dynamical changes in size and refractive index of individual particles on subsecond time scales. We demonstrate this capability by monitoring the aggregation kinetics of a sample consisting of polystyrene nanoparticles in a high-salt environment. Despite the unknown geometrical shape of the scatterers, our method can resolve changes in the number of monomers as well as the resulting changes in aggregate size and refractive index. This characterization is sufficiently accurate to provide a reliable time-resolved estimate of the fractal dimension of individual aggregates, which, to our knowledge, has not previously been reported.

Taken together, our results show that deep-learning-enhanced analysis of holographic scattering patterns allow improved accuracy in particle size and refractive index determination by more than an order of magnitude compared to traditional methods. The characterization is performed without assumptions on the physical properties of the environment and shape of the particle and can be performed with subsecond temporal resolution. In contrast to traditional techniques, this method can temporally resolve size and composition of individual subwavelength particles in their native environment. We anticipate that the drastic improvement in single-particle characterization offered by this technique will find widespread application in any area where subwavelength particles play an important role, ranging from industrial processes to drug discovery and pharmaceuticals.

Methods

Particles and Chemicals

The used monodisperse particles are 0.031 μm (modal radius) and 0.15 μm (modal radius) polystyrene (Invitrogen), 0.23 μm (modal radius, NIST-certified standard deviation ±6.8 nm) polystyrene (Polysciences), and 0.21 μm (modal radius) silica (Kisker) (sizes verified using nanoparticle tracking analysis (NanoSight)). Samples are imaged under flow in straight hydrophilized channels with a height of 20 μm and a width of 800 μm in chips made from Topas (COC, ChipShop).

Off-Axis Digital Holographic Microscope

A sketch of the setup employed in this study is shown in Figure 1f. A 633 nm HeNe laser (Thorlabs) beam is split into two light beams, one passing through the sample (collected by an Olympus 40× 1.3 NA oil objective) and one used as a reference. The two beams are recombined at a slight offset angle, and the resulting interference pattern is recorded by a CCD camera (AlliedVision, ProSilica GX1920). This interference pattern carries information about the optical field at the camera plane, as described below. Video files of particle samples are recorded at 30 frames per second with typical exposure times in the range of 2 to 4 ms.

Image Analysis

The interference patterns, or holograms, are analyzed using the homemade software written using MATLAB (Mathworks Inc.) to extract the amplitude and phase maps using standard methods.12 In brief, due to the off-axis configuration of our setup, the Fourier transform of the interference pattern contains two off-center peaks, which describe the object field multiplied by a plane wave (exp(±ik⃗p·x⃗), where k⃗p represents the projection of the wave-vector of the reference beam onto the imaging plane on the camera), in addition to the central peak which corresponds to the noninterferometric intensities. In order to isolate the object field, we numerically shift one of the off-center peaks to the center of the Fourier spectrum and apply a low-pass filter. The magnitude and phase of the resulting field correspond to the amplitude and phase of the optical field recorded by the camera. The obtained field is slightly distorted due to optical aberration in the beamline. This is corrected by fitting the phase of the field to a fourth-order polynomial, which is subsequently subtracted from the phase to obtain a close-to-aberration-free image of the real and imaginary part of the optical field.

Particle Localization and Tracking

In-plane subpixel localization of detected local extrema in the field amplitude is performed using the radial center method.41 Particles are subsequently distinguished from background noise by the degree of radial symmetry and the spatial extent of the local extremum. The z-position of the particle is defined as the plane where the standard deviation of the Fourier transform of the field is minimized.12 The scattering pattern of the particle is stored at this plane. Following a complete tracking of a frame, each observation is associated with a distance metric to particles in previous frames. Specifically, the observations are joined into traces by minimizing the sum of this metric using the Hungarian algorithm.42 In our setup, the track lengths are typically around 80–100 frames, and all tracks shorter than 20 frames are discarded in the analysis.

Particle Characterization Network Architecture and Training

The problem of characterizing subwavelength particles by their scattering is fundamentally that of noise reduction by averaging multiple observations of the particle and subsequently measuring properties of its scattering pattern, such as the induced phase shift and the radial profile. However, due to small differences in the particle’s subpixel position and spatially variable aberrations, observations typically cannot be directly averaged. This motivated the design of WAC-NET (Figure 1g), which consists of two main modules: a representation transforming network and a regression network. The representation transforming network is a convolutional neural network followed by a single fully connected layer. It transforms 64 × 64 × 2 images centered around a particle, where the two feature channels represent the real and the imaginary part of the complex field, into a one-dimensional vector representation with a length of 128. From this vector representation, the model also computes a single scalar that represents the confidence in the correctness of the vector representation using two fully connected layers. The regression network, in turn, receives a stack of vector representations and confidence values, representing all observations of a single particle. The confidence values are rescaled using the softmax function. The vector representation stack is averaged along the first axis using the rescaled confidence values as weights. This results in a single vector with a length of 128. Three fully connected layers then transform this vector into two scalars representing the radius and the refractive index of the particle. Both modules are trained simultaneously using synthetic data simulated with Mie theory; the point spread function is calibrated to match the microscope used to collect the data. Standard L1 error is used as loss function, and the Adam optimizer43 is used with a learning rate of 0.001.

Simulation of Training Data

The scattered field from dielectric particles is simulated using the MATLAB package MatScat.44 The fields are numerically propagated using the angular spectrum method through a lens with NA identical to that of the experimental system (NA = 1.3) and further propagated to the Fourier plane of the lens. The field at this plane corresponds to the Fourier transform of the field at the camera plane. Next, the optical system is modeled via the pupil function P(kx, ky), which relates the simulated fields Fsim(ky, kx) to the experimentally obtained fields F(kx, ky), as F(k⃗) = P(k⃗)Fsim(k⃗). This pupil function is estimated based on experimental images of particles of known size and refractive index (polystyrene spheres with radius 0.23 μm and refractive index of 1.58). The pupil function has support only inside a finite radius, i.e., P(k⃗) = 0 for kx2 + ky > kP2, where kP is set by the numerical aperture of the system as kP = π/λ·NA. In our system, kP = 6.45 μm–1. This finite support allows considerable dimensionality reduction, as only Fourier components within this radius contain relevant information. This leaves, in our case, 177 pixels in Fourier space.

Transmission Electron Microscopy Analysis

The transmission electron microscopy (TEM) measurements were performed using FEI Tecnai T20 operated at 200 kV. The particle solutions were drop-casted on copper TEM grids with carbon membranes (TED PELLA). A small droplet was placed on a TEM grid, and after approximately 15 min, the excess liquid was removed by slightly touching the droplet with a tissue paper. Thereafter, the grids were air-dried for 15–20 min, after which they were placed in a storage container until used. The TEM image analysis was performed in Matlab, where the image processing was based on the circular Hough transform combined with a global intensity threshold.

Acknowledgments

D.M. acknowledges support from the Swedish Research Council (Starting Grant No. 2019-05071). G.V., C.B.A., and D.M. acknowledge support from the Swedish Foundation of Strategic Research (SSF Works; Instrument, Technique, and Method Development Projects 2017 (ITM17-0384)). G.V. acknowledges support from the European Research Council (ERC) Starting Grant ComplexSwimmers (Grant No. 677511). The transmission electron microscopy measurements were performed at the Chalmers Material Analysis Laboratory (CMAL). The authors also wish to acknowledge Aykut Argun for assistance in preparation of the graphics.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.0c06902.

  • Quantification of WAC-NET resolution, core–shell particle simulation and characterization, TEM measurements, polarizability quantification, accuracy quantification at low refractive index contrasts (PDF)

The authors declare the following competing financial interest(s): D.M, E.O., B.M, and F.E. are cofounders of Holtra AB.

Supplementary Material

nn0c06902_si_001.pdf (1.2MB, pdf)

References

  1. Blanco E.; Shen H.; Ferrari M. Principles of Nanoparticle Design for Overcoming Biological Barriers to Drug Delivery. Nat. Biotechnol. 2015, 33, 941–951. 10.1038/nbt.3330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Singh T.; Shukla S.; Kumar P.; Wahla V.; Bajpai V. K.; Rather I. A. Application of Nanotechnology in Food Science: Perception and Overview. Front. Microbiol. 2017, 8, 1501. 10.3389/fmicb.2017.01501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Prasad R.; Bhattacharyya A.; Nguyen Q. D. Nanotechnology in Sustainable Agriculture: Recent Developments, Challenges, and Perspectives. Front. Microbiol. 2017, 8, 1014. 10.3389/fmicb.2017.01014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Kabir E.; Kumar V.; Kim K.-H.; Yip A. C.; Sohn J. Environmental Impacts of Nanomaterials. J. Environ. Manage. 2018, 225, 261–271. 10.1016/j.jenvman.2018.07.087. [DOI] [PubMed] [Google Scholar]
  5. Mailänder V.; Landfester K. Interaction of Nanoparticles with Cells. Biomacromolecules 2009, 10, 2379–2400. 10.1021/bm900266r. [DOI] [PubMed] [Google Scholar]
  6. Lu F.; Wu S.-H.; Hung Y.; Mou C.-Y. Size Effect on Cell Uptake in Well-Suspended, Uniform Mesoporous Silica Nanoparticles. Small 2009, 5, 1408–1413. 10.1002/smll.200900005. [DOI] [PubMed] [Google Scholar]
  7. Duan X.; Li Y. Physicochemical Characteristics of Nanoparticles Affect Circulation, Biodistribution, Cellular Internalization, and Trafficking. Small 2013, 9, 1521–1532. 10.1002/smll.201201390. [DOI] [PubMed] [Google Scholar]
  8. Zhao F.; Zhao Y.; Liu Y.; Chang X.; Chen C.; Zhao Y. Cellular Uptake, Intracellular Trafficking, and Cytotoxicity of Nanomaterials. Small 2011, 7, 1322–1337. 10.1002/smll.201100001. [DOI] [PubMed] [Google Scholar]
  9. Filipe V.; Hawe A.; Jiskoot W. Critical Evaluation of Nanoparticle Tracking Analysis (NTA) by NanoSight for the Measurement of Nanoparticles and Protein Aggregates. Pharm. Res. 2010, 27, 796–810. 10.1007/s11095-010-0073-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Manzo C.; Garcia-Parajo M. F. A Review of Progress in Single Particle Tracking: From Methods to Biophysical Insights. Rep. Prog. Phys. 2015, 78, 124601. 10.1088/0034-4885/78/12/124601. [DOI] [PubMed] [Google Scholar]
  11. van der Pol E.; Coumans F. A. W.; Sturk A.; Nieuwland R.; van Leeuwen T. G. Refractive Index Determination of Nanoparticles in Suspension Using Nanoparticle Tracking Analysis. Nano Lett. 2014, 14, 6195–6201. 10.1021/nl503371p. [DOI] [PubMed] [Google Scholar]
  12. Midtvedt D.; Eklund F.; Olsén E.; Midtvedt B.; Swenson J.; Höök F. Size and Refractive Index Determination of Subwavelength Particles and Air Bubbles by Holographic Nanoparticle Tracking Analysis. Anal. Chem. 2020, 92, 1908–1915. 10.1021/acs.analchem.9b04101. [DOI] [PubMed] [Google Scholar]
  13. Piliarik M.; Sandoghdar V. Direct Óptical Sensing of Single Unlabelled Proteins and Super-Resolution Imaging of their Binding Sites. Nat. Commun. 2014, 5, 4495. 10.1038/ncomms5495. [DOI] [PubMed] [Google Scholar]
  14. Yevick A.; Hannel M.; Grier D. G. Machine-Learning Approach to Holographic Particle Characterization. Opt. Express 2014, 22, 26884. 10.1364/OE.22.026884. [DOI] [PubMed] [Google Scholar]
  15. Wong N. A.; Uchida N. V.; Dissanayake T. U.; Patel M.; Iqbal M.; Woehl T. J. Detection and Sizing of Submicron Particles in Biologics with Interferometric Scattering Microscopy. J. Pharm. Sci. 2020, 109, 881. 10.1016/j.xphs.2019.05.003. [DOI] [PubMed] [Google Scholar]
  16. Altman L. E.; Grier D. G. CATCH: Characterizing and Tracking Colloids Holographically Using Deep Neural Networks. J. Phys. Chem. B 2020, 124, 1602–1610. 10.1021/acs.jpcb.9b10463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Lee S.-H.; Roichman Y.; Yi G.-R.; Kim S.-H.; Yang S.-M.; van Blaaderen A.; van Oostrum P.; Grier D. G. Characterizing and Tracking Single Colloidal Particles with Video Holographic Microscopy. Opt. Express 2007, 15, 18275–18282. 10.1364/OE.15.018275. [DOI] [PubMed] [Google Scholar]
  18. Cichos F.; Gustavsson K.; Mehlig B.; Volpe G. Machine Learning for Active Matter. Nature Machine Intelligence 2020, 2, 94–103. 10.1038/s42256-020-0146-9. [DOI] [Google Scholar]
  19. Helgadottir S.; Argun A.; Volpe G. Digital Video Microscopy Enhanced by Deep Learning. Optica 2019, 6, 506. 10.1364/OPTICA.6.000506. [DOI] [Google Scholar]
  20. Midtvedt B.; Helgadottir S.; Argun A.; Midtvedt D.; Volpe G. Quantitative Digital Microscopy with Deep Learning. arXiv 2010, 08260. 10.1117/12.2567479. [DOI] [Google Scholar]
  21. Bo S.; Schmidt F.; Eichhorn R.; Volpe G. Measurement of Anomalous Diffusion Using Recurrent Neural Networks. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2019, 100, 010102. 10.1103/PhysRevE.100.010102. [DOI] [PubMed] [Google Scholar]
  22. Granik N.; Weiss L. E.; Nehme E.; Levin M.; Chein M.; Perlson E.; Roichman Y.; Shechtman Y. Single-Particle Diffusion Characterization by Deep Learning. Biophys. J. 2019, 117, 185–192. 10.1016/j.bpj.2019.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ronneberger O.; Fischer P.; Brox T.. U-Net: Convolutional Networks for Biomedical Image Segmentation; ; Medical Image Computing and Computer-Assisted Intervention: Cham, 2015; pp 234–241. [Google Scholar]
  24. Liu T.; de Haan K.; Rivenson Y.; Wei Z.; Zeng X.; Zhang Y.; Ozcan A. Deep Learning-Based Super-Resolution in Coherent Imaging Systems. Sci. Rep. 2019, 9, 3926. 10.1038/s41598-019-40554-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Midtvedt D.; Olsén E.; Höök F.; Jeffries G. D. M. Label-Free Spatio-Temporal Monitoring of Cytosolic Mass, Osmolarity, and Volume in Living Cells. Nat. Commun. 2019, 10, 340. 10.1038/s41467-018-08207-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Novotny L.; Hecht B.. Principles of Nano-Optics; Cambridge University Press: Cambridge, 2006; pp 1–539. [Google Scholar]
  27. Chollet F.Deep Learning with Python, 1st ed.; Manning Publications Co.: Shelter Island, NY, 2017. [Google Scholar]
  28. Vestergaard C. L.; Blainey P. C.; Flyvbjerg H. Optimal Estimation of Diffusion Coefficients from Single-Particle Trajectories. Physical Review E - Statistical, Nonlinear, and Soft Matter Physics 2014, 89, 022726. 10.1103/PhysRevE.89.022726. [DOI] [PubMed] [Google Scholar]
  29. Rupert D. L.; Mapar M.; Shelke G. V.; Norling K.; Elmeskog M.; Lötvall J. O.; Block S.; Bally M.; Agnarsson B.; Höök F. Effective Refractive Index and Lipid Content of Extracellular Vesicles Revealed Using Optical Waveguide Scattering and Fluorescence Microscopy. Langmuir 2018, 34, 8522–8531. 10.1021/acs.langmuir.7b04214. [DOI] [PubMed] [Google Scholar]
  30. Hotze E. M.; Phenrat T.; Lowry G. V. Nanoparticle Aggregation: Challenges to Understanding Transport and Reactivity in the Environment. Journal of Environmental Quality 2010, 39, 1909–1924. 10.2134/jeq2009.0462. [DOI] [PubMed] [Google Scholar]
  31. Sokolov S. V.; Tschulik K.; Batchelor-McAuley C.; Jurkschat K.; Compton R. G. Reversible or Not? Distinguishing Agglomeration and Aggregation at the Nanoscale. Anal. Chem. 2015, 87, 10033–10039. 10.1021/acs.analchem.5b02639. [DOI] [PubMed] [Google Scholar]
  32. Liu J.; Wang Z.; Sheng A.; Liu F.; Qin F.; Wang Z. L. In Situ Observation of Hematite Nanoparticle Aggregates Using Liquid Cell Transmission Electron Microscopy. Environ. Sci. Technol. 2016, 50, 5606–5613. 10.1021/acs.est.5b06305. [DOI] [PubMed] [Google Scholar]
  33. Fung J.; Hoang S. Computational Assessment of an Effective-Sphere Model for Characterizing Colloidal Fractal Aggregates with Holographic Microscopy. J. Quant. Spectrosc. Radiat. Transfer 2019, 236, 106591. 10.1016/j.jqsrt.2019.106591. [DOI] [Google Scholar]
  34. Wang C.; Cheong F. C.; Ruffner D. B.; Zhong X.; Ward M. D.; Grier D. G. Holographic Characterization of Colloidal Fractal Aggregates. Soft Matter 2016, 12, 8774–8780. 10.1039/C6SM01790H. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Schaefer D. W.; Martin J. E.; Wiltzius P.; Cannell D. S. Fractal Geometry of Colloidal Aggregates. Phys. Rev. Lett. 1984, 52, 2371–2374. 10.1103/PhysRevLett.52.2371. [DOI] [Google Scholar]
  36. Zhou Z.; Chu B. Fractal Study of Polystyrene Latex and Silica Particle Aggregates. Phys. A 1991, 177, 93–100. 10.1016/0378-4371(91)90139-4. [DOI] [Google Scholar]
  37. Asnaghi D.; Carpineti M.; Giglio M.; Sozzi M.. Trends in Colloid and Interface Science VI; Steinkopff: Darmstadt, 1992; pp 60–61. [Google Scholar]
  38. Carpineti M.; Ferri F.; Giglio M.; Paganini E.; Perini U. Salt-Induced Fast Aggregation of Polystyrene Latex. Phys. Rev. A: At., Mol., Opt. Phys. 1990, 42, 7347–7354. 10.1103/PhysRevA.42.7347. [DOI] [PubMed] [Google Scholar]
  39. Amal R.; Coury J.; Raper J.; Walsh W.; Waite T. Structure and Kinetics of Aggregating Colloidal Haematite. Colloids Surf. 1990, 46, 1–19. 10.1016/0166-6622(90)80045-6. [DOI] [Google Scholar]
  40. Kostoglou M.; Konstandopoulos A. G. Evolution of Aggregate Size and Fractal Dimension During Brownian Coagulation. J. Aerosol Sci. 2001, 32, 1399–1420. 10.1016/S0021-8502(01)00056-8. [DOI] [Google Scholar]
  41. Parthasarathy R. Rapid, Accurate Particle Tracking by Calculation of Radial Symmetry Centers. Nat. Methods 2012, 9, 724–726. 10.1038/nmeth.2071. [DOI] [PubMed] [Google Scholar]
  42. Kuhn H. W. The Hungarian Method for the Assignment Problem. Naval Research Logistics Quarterly 1955, 2, 83–97. 10.1002/nav.3800020109. [DOI] [Google Scholar]
  43. Kingma D. P.; Ba J. L.. Adam: A Method for Stochastic Optimization. 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings, 2015.
  44. Schäfer J.-P.Implementierung und Anwendung analytischer und numerischer Verfahren zur Lösung der Maxwellgleichungen für die Untersuchung der Lichtausbreitung in biologischem Gewebe. Ph.D. thesis, Universität Ulm, 2011. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn0c06902_si_001.pdf (1.2MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES