Abstract
Strain engineering as a method to control functional properties has seen in the last decades a surge of interest. Heterostructures comprising 2D-materials and containing van der Waals(-like) gaps were considered unsuitable for strain engineering. However, recent work on heterostructures based on Bi2Te3, Sb2Te3, and GeTe showed the potential of a different type of strain engineering due to long-range mutual straining. Still, a comprehensive understanding of the strain relaxation mechanism in these telluride heterostructures is lacking due to limitations of the earlier analyses performed. Here, we present a detailed study of strain in two-dimensional (2D/2D) and mixed dimensional (2D/3D) systems derived from mica/Bi2Te3, Sb2Te3/Bi2Te3, and Bi2Te3/GeTe heterostructures, respectively. We first clearly show the fast relaxation process in the mica/Bi2Te3 system where the strain was generally transferred and confined up to the second or third van der Waals block and then abruptly relaxed. Then we show, using three independent techniques, that the long-range exponentially decaying strain in GeTe and Sb2Te3 grown on the relaxed Bi2Te3 and Bi2Te3 on relaxed Sb2Te3 as directly observed at the growth surface is still present within these three different top layers a long time after growth. The observed behavior points at immediate strain relaxation by plastic deformation without any later relaxation and rules out an elastic (energy minimization) model as was proposed recently. Our work advances the understanding of strain tuning in textured heterostructures or superlattices governed by anisotropic bonding.
Keywords: pulsed laser deposition, 2D/2D heterostructures, 2D/3D heterostructures, RHEED, strain engineering, van der Waals epitaxy
Tailoring the strain state in materials have attracted great interest, since it allows tuning of material properties by factors like energy gaps, carrier mobility, diffusivity in materials, and chemical reactivity.1−5 In fact, this strategy, referred to as strain engineering, significantly improved a plethora of thin film applications such as phase-change memory devices,6 solar cells,7 flexoelectricity,8 magnetocaloric effect,9 and thermoelectricity.10,11 With such a widespread application potential, it is important to understand how strain develops and relaxes during the thin film growth and how it behaves after the growth. In general, considering the bond hierarchy, films can be identified as traditional three-dimensionally (3D)-bonded, where strong bonds exist between adjacent atoms, or 2D bonded, where pronounced weak bonds, namely, van der Waals (vdWaals) bonds, link each repetitive block. To study the different scenarios of strain systems, as a matter of course, they can be subdivided into the 3D/3D system, 2D/2D system, and 2D/3D system.
The 3D/3D system films have been deeply studied. The most well-known case is Si/SiGe heterostructures, which have been applied in the transistors industry.12 The strain evolution has been extensively studied also for nitride heterostructures.13 Bourret et al. used AlN/GaN superlattices to prove that with the increase of the total thickness, the in-plane lattice parameter of top sublayers will finally oscillate toward the equilibrium lattice parameter because of the response to the elastic properties.14 In contrast, for 2D/2D systems, the surface layer seems to have no influence on the next layer in the system. Owing to the weak interlayer interaction in-between these 2D building blocks, a distinct epitaxial growth method (i.e., vdWaals epitaxy) was originally reported by Koma,15 where it was assumed that lattice parameter constraints are absent in vertically stacked heterostructures. This conjecture was subsequently verified for several cases, for example WSe2/MoS2 and MoS2/MoSe2, suggesting that mechanical strain is not involved here.16,17 However, Kumar et al. proved that there is strain transfer in such heterostructures.18 Moreover, recent experimental achievements show that many properties have been tuned by such strain in various 2D/2D systems by strain engineering including graphene/M (M is another 2D material),19−22 h-BN/M heterostructures,23 and transition metal dichalcogenide heterostructures.24−26 However, most of the research focused on bilayers and lacked in-depth reports on the internal strain evolution in these 2D materials. In our previous study, we discovered that the strain in stacked 2D layers of Bi2Te3 and Sb2Te3 is exponentially decaying as the thickness increases.27 The earliest hint of such odd behavior in 2D heterostructures was to the best of our knowledge shown by Wang et al. for the Bi2Se3/In2Se3 system.28 However, further discussion about this behavior was not found in the work. This was an unexpected result since, analogous to vdWaals epitaxy, it was widely accepted that layers should decouple quickly and completely in a 2D/2D system. It is, therefore, a question whether another relaxation mode exists upon direct growth of 2D heterostructures. Since the substrate (or first sublayer) influences the strain in the other 2D sublayers, we start here, compared to our previous work, with a different vdWaals substrate, mica, to grow Bi2Te3 films on. In this paper, a clear “step” relaxation process has been observed in a 2D/2D system; i.e., mica/Bi2Te3.
Recently, a number of papers reported on 2D/3D heterostructures, such as Sb2Te3/GeTe and MoS2/GaN, which also exhibit potential performance improvement in memory devices and photoluminescence devices.6,29−31 Furthermore, the combination of two kinds of bond hierarchy may provide a versatile platform for strain control. Hence, for further applications, it is crucial to understand the strain state in such heterostructures, especially because this topic has hardly received attention. In Bi2Se3/ZnSe multilayers, strain in the 3D sublayers (ZnSn) released abruptly, which suggests limited or no constraint at the interface.32 Wang et al. presented the results of strain evolution in Sb2Te3/GeTe superlattices onto Sb-buffered Si(111)-(√3 × √3)R30° substrate.33 They found that tuning and engineering of strain across the vdWaals gaps are possible and that strain relaxation shows an unconventional behavior, which is neither like coupled 3D/3D behavior nor like ideal 2D/2D behavior. At the same time, we also reported this intriguing behavior for multilayers based on all pairwise combinations of Sb2Te3, Bi2Te3, and GeTe grown on silicon wafers covered with a thin (native or thermal) layer of SiO2.27 Although the observed relaxation behavior in refs (27 and 33) was the same, the underlying models explaining the behavior showed principal differences. Wang et al. explained the behavior by an elastic energy minimization model, whereas Vermeulen et al. concluded that it is due to plastic deformation. Therefore, more experimental evidence is required to evaluate which mechanism is responsible for this different type of strain relaxation. In this work, the strain during growth of the various heterostructures is directly measured at the growth front using reflective high energy electron diffraction (RHEED). The strain inside the (top layer of the) heterostructure a long time after growth has been measured using three different techniques. X-ray diffraction was used for GeTe films with different thicknesses on a thin relaxed Bi2Te3 film (on mica). Atomic resolution scanning transmission electron microscopy (STEM) was used to probe the strain in (i) top layers of Bi2Te3 on relaxed Sb2Te3 in plane-view samples by depth profiling and (ii) an Sb2Te3 top layer on relaxed Bi2Te3 in a cross-section sample using geometric phase analysis (GPA).34 All these results consistently demonstrate that the surface strain measured during growth is unaltered by time and by overgrowth of additional material, proving that the relaxation is not controlled elastically but by immediate plastic deformation resulting in a long-range exponentially decaying strain.
Results and Discussion
The lattice parameters of all materials studied in the present work can be found in the Supporting Information, Table S1, and the in-plane mismatch can be calculated, i.e., mica/Bi2Te3 (16.8%), Bi2Te3/GeTe (4.7%), Bi2Te3/ Sb2Te3 (3.0%), and Sb2Te3/Bi2Te3 (−3.1%).
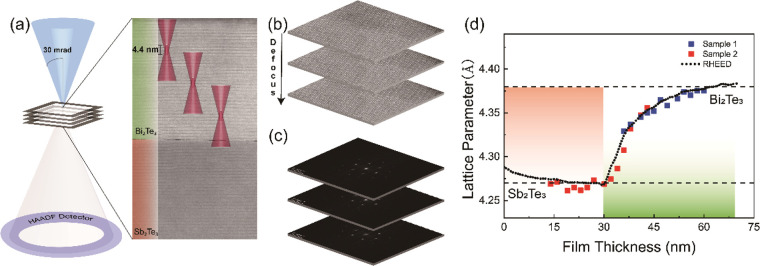
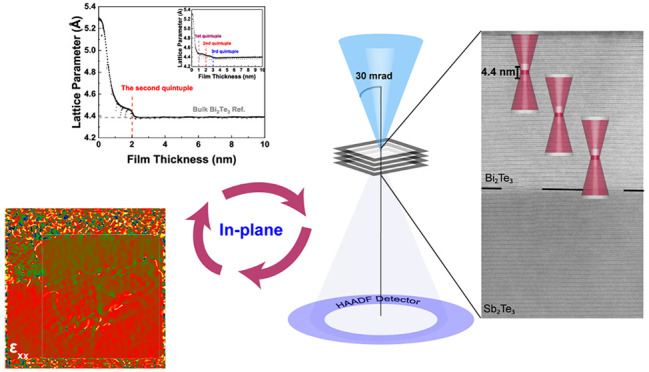
Exemplary results of RHEED analysis during the growth of the first ten nanometers of Bi2Te3 on mica are shown in Figure 1a. It plots the measured in-plane lattice parameter as a function of film thickness. Due to the very sharp texture in the Bi2Te3 films on mica with the c-axis of trigonal Bi2Te3 out-of-plane, the in-plane lattice parameter corresponds to the a lattice parameter of Bi2Te3 when described with hexagonal lattice parameters. Overall it can be observed readily that the film quickly relaxes to the bulk lattice parameter of Bi2Te3. However, interesting relaxation behavior can be observed. For a film thickness of 0 nm, of course the in-plane mica “a-lattice parameter” is observed, which is much larger than the one of Bi2Te3. When Bi2Te3 is grown on mica, the exponentially decaying penetration depth of the RHEED analysis, which is of the order of 1 nm,35 will for the first atomic layers of Bi2Te3 result in a weighted average of the lattice parameters of mica and Bi2Te3. The quickly decaying results indicate that Bi2Te3 does not form a lattice matched film on mica and quickly relaxes. Still, some tensile strain is present initially that relaxes abruptly for a Bi2Te3 thickness of 2 nm, which exactly corresponds to two quintuples. This abrupt relaxation proves two effects: (1) There is some in-plane tensile strain before the relaxation in the Bi2Te3 film with a thickness less than 2 nm. (2) Not only the surface of the Bi2Te3 relaxes, but at least the top quintuple relaxes to the bulk lattice parameter and maybe both quintuples. For most Bi2Te3 films grown, this abrupt relaxation for a thickness beyond two quintuples was observed. However, some deviating behavior was also observed (more rarely). An example is shown in the inset figure. There it can be observed that the relaxation after the second quintuple is only partial and full relaxation occurs only after the third one. Due to the high surface sensitivity of RHEED, it unfortunately cannot be proven if the whole Bi2Te3 film relaxes to its bulk lattice parameter or only the top quintuples and that lower quintuples still experience tensile strain. However, the stepwise partial relaxation suggests the latter scenario. In the present context it is interesting to note that self-aligned quintuple layers parallel to a planar surface are popular for acting as seed layers for subsequent epitaxial growth. Then it is frequently found that seed layers with a thickness of 3 or 4 nm (grown on flat surfaces) gives the best (epitaxy) results.36 On mica, this thus implies just fully relaxed films.
Figure 1.
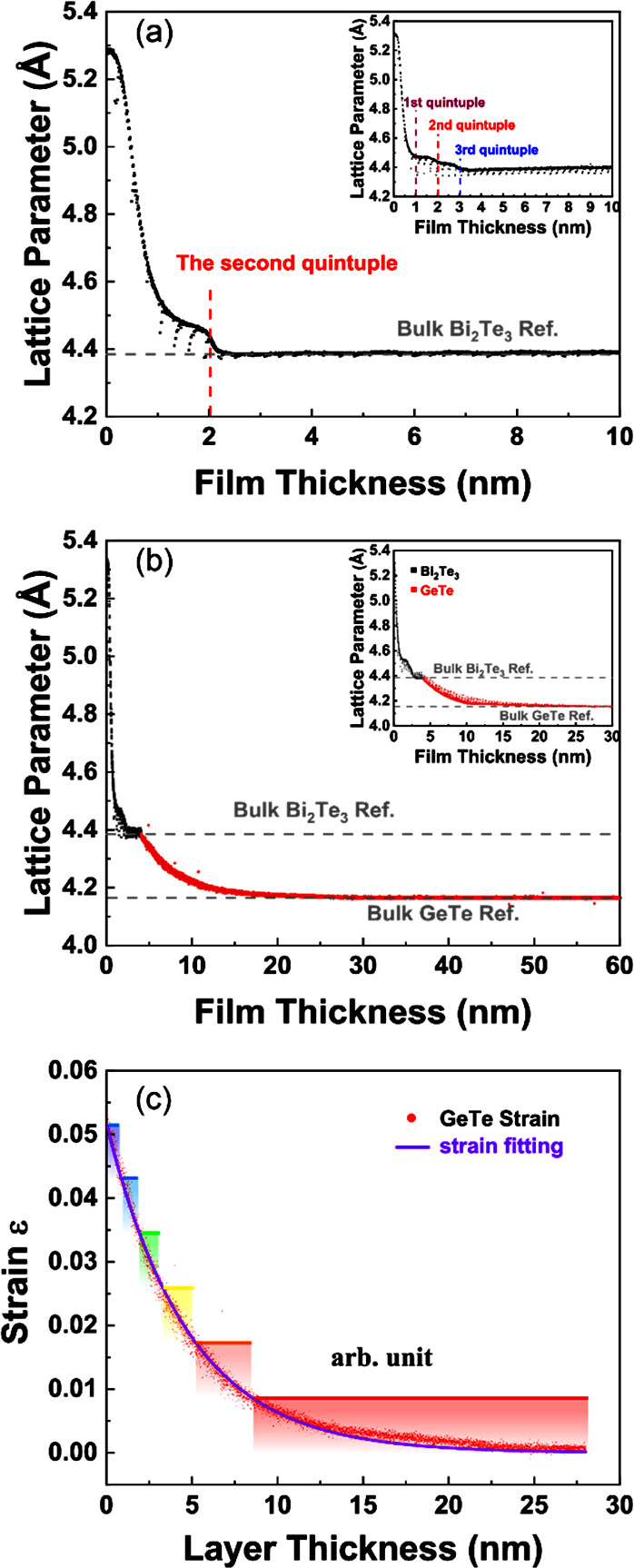
(a) Results of RHEED analysis showing the measured a lattice parameter as a function of film thickness during growth of the first 10 nm of Bi2Te3 (with c-axis out-of-plane) on mica. Abrupt relaxation of tensile strain in the Bi2Te3 film occurs for a 2 nm thick film corresponding to two quintuples. The inset shows a special case where partial relaxation occurs after the second quintuple and full relaxation after the third. (b) The measured lattice parameter evolution of the (4 nm/56 nm) Bi2Te3/GeTe heterostructure. The inset shows the evolution of the (4 nm/28 nm) Bi2Te3/GeTe heterostructure. In both cases, a long-range exponentially decaying strain is observed for the GeTe layer. (c) The absolute strain in a 28 nm GeTe layer as a function of layer thickness, where 0 nm is the Bi2Te3/GeTe interface. Equation ε(t) = A e–bt is fitted to the strain profile. The rainbow bars with the same width (strain interval) are displayed to show the distribution of GeTe in-plane lattice parameters that will be used as input to fit the GeTe(0006) XRD peak in Figure 2d.
Figure 1b shows the RHEED analysis during the growth on mica of first a Bi2Te3 seed layer of about 4 nm thickness followed by a GeTe layer with a thickness of about 56 nm. Starting from the relaxed Bi2Te3a-lattice parameter also the GeTe film relaxes toward its bulk a-lattice parameter, but the relaxation occurs very slowly. For reaching the bulk value at least a GeTe film thickness of 25 nm is required. Since this relaxation rate is so slow compared to the very shallow penetration depth of the RHEED analysis, the measured value for the a-lattice parameter as a function of thickness compared to the fully relaxed value can be directly translated into a tensile strain ε value as a function of thickness t, which is plotted in Figure 1c. The experimental data consisting of tiny red dots can be fitted very well with an exponentially decaying function of the form ε(t) = A e–bt, shown as a solid purple line in Figure 1c. This type of unusual relaxation behavior based on extensive RHEED analysis has been demonstrated, described and explained in detail before in two recent papers, published at the same time.27,33
However, more studies are needed to resolve some unknown issues and to arrive at a comprehensive understanding of this special type of strain relaxation. The most important unsolved issue is that RHEED only shows the evolution of the lattice parameter and thus strain at the surface of a growing film but cannot provide any information about how the strain develops subsurface. This issue is very relevant, because various scenarios can occur with the following two extremes. The first extreme case is that the strain state measured at the surface persists and will not change during additional annealing and/or when additional layers are grown on top of the surface. Then the exponentially decaying strain profile will remain present in a film when another film is grown on top of it. The other extreme case is that the whole sublayer relaxes and will get a uniform strain state, e.g., corresponding to the one measured for the surface.
The extremes can also be coupled to the different mechanisms by which strain can relax, namely, by elastic and/or plastic relaxation. In an elastic system, the strain exerted by a fresh sublayer grown on top of an existing sublayer will lead to a different balancing of the elastic forces and will thus lead to changes in the subsurface strain. However, when plastic relaxation already occurs during growth, then the driving force for additional relaxation reduces, which increases the probability that the strain state measured at the surface persists when additional layers are grown on top of the surface.
There is a relatively straightforward way to solve this issue. RHEED alone is insufficient. It has to be used together with another technique that can detect the subsurface strain state. In this respect, X-ray diffraction (XRD) is an obvious choice. For XRD, it is accurate to assume that just an averaging occurs over the total volume of the film without any depth dependence, because the penetration depth of the X-rays is much larger than the thickness of the thin films analyzed. So, if a whole sublayer relaxes to a single interplanar distance then relatively sharp XRD peaks are expected. If the strain gradients persist in sublayers then the XRD peaks must show the corresponding broadening. So, the concrete question now at hand is whether the exponentially decaying strain profile as observed at the surface of the growing GeTe film shown in Figure 1b is still present in the GeTe sublayer also with additional overgrowth a long time after growth or has relaxed to a more uniform value (which still might correspond to an overall strain value).
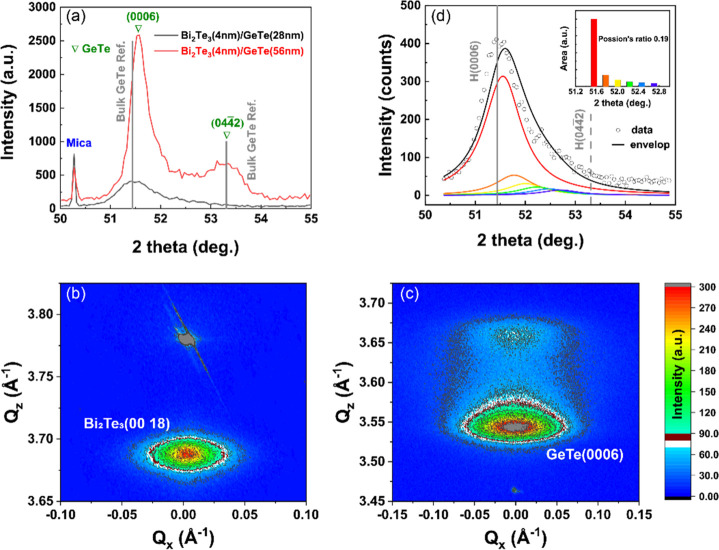
XRD patterns, measured using θ–2θ geometry, of Bi2Te3/GeTe heterostructures with different (28 and 56 nm) GeTe thicknesses are shown in Figure 2a. According to the RHEED analyses shown in Figure 1, it is known that the Bi2Te3 is fully relaxed and that strain is present in the GeTe layer during the deposition. However, the influence of subsurface relaxation due to overgrowth in combination with continuous heating during deposition and cooling after deposition on the strain in the films has not yet been clarified. To identify the strain in the as-deposited GeTe layers, short-range scans (50–55°) around the GeTe (0006) peak were recorded. The sharpest peak around 50.3° is a reflection from the mica (0011). For the two scans in Figure 2a, this peak occurs at identical 2θ positions, indicating the stability of the measurement and that the two scans can be directly compared. However, we also notice that the GeTe (0006) peak of the thicker film is slightly shifted to the right, which may be ascribed to a composition deviation (during prolonged PLD to grow the thicker film) and/or the mutual effect of domains with different orientations (which are effectively absent in the thinner film and clearly develop for the thicker film as demonstrated by the GeTe (044̅2) peak). It should be noted that apart from mica only the GeTe phase was detected in these two samples (see the Supporting Information, Figure S1, Bi2Te3 layers are too thin to be observable). Since only two (000L) peaks are present, as marked by the hollow triangles, for the thin (28 nm) GeTe layer, it can be concluded that the GeTe grew exclusively with a (000L) out-of-plane orientation on mica.
Figure 2.
(a) θ-2θ XRD scans of (4 nm/28 nm) Bi2Te3/GeTe (black line) and (4 nm/56 nm) Bi2Te3/GeTe (red line) heterostructure films focusing on the GeTe (0006) XRD peak close to the mica (001) specular rod. Reciprocal space maps of (b) 60 nm Bi2Te3 films and (c) (4 nm/56 nm) Bi2Te3/GeTe heterostructure films around the Bi2Te3 (00.18) and the GeTe (0006) peak, respectively. (d) Fitting of the GeTe (0006) XRD peak for the (4 nm/28 nm) Bi2Te3/GeTe heterostructure. The experimental data points are the open circles. For fitting, six peaks were used which positions and area ratios were obtained from the RHEED data in Figure 1c. The area ratios of the six XRD peaks are shown in the inset. For calculating the peak positions of the six peaks, the in-plane strain as shown in Figure 1c has first to be transformed into the out-of-plane strain using eq 2.
In the film with the thicker GeTe (56 nm) layer, however, a shoulder peak appears at around 53.3°, which can be assigned to the GeTe (044̅2) peak, consistent with the rhombohedral GeTe structure.37 This shoulder can be indexed as belonging to three of the four GeTe ⟨111⟩ reflections (using cubic coordinate system) that did not experience the Peierls-like rhombohedral distortion.38−40 The fourth GeTe ⟨111⟩ reflection, experiencing the Peierls-like rhombohedral elongation, has thus become the (0006) refection. For randomly oriented (nontextured) film the (044̅2) peak should be roughly three times as intense as the (0006) peak. This is not the case. On the contrary, the (0006) peak is about four times as intense as the (044̅2) peak. This indicates that the GeTe film is strongly textured with the c-axis out of plane, but not exclusively c-axis oriented as for instance is found for Bi2Te3 films of similar thickness. Interestingly, as the thickness decreases, the (044̅2) peak is invisible and only an asymmetric (0006) peak can be observed. This demonstrates that the texture with c-axis out of plane is more perfect for thinner GeTe and deteriorates with increasing GeTe film thickness, where also grains develop with the other, not rhombohedrally distorted, ⟨111⟩ directions perpendicular to the surface. The excellent quality of the texture of the Bi2Te3 seed-layer on mica and the deteriorating quality of the texture with increasing film thickness in the GeTe layer can also be directly inferred from the RHEED patterns recorded during growth (see the Supporting Information, Figure S2). It has also been observed that the surface roughness of GeTe films grown on Sb2Te3 or Bi2Te3 seed layers increase with increasing GeTe film thickness (see the Supporting Information, Figure S3), which is probably directly correlated with this deteriorating texture. Moreover, more importantly for the present work is that the asymmetry of the (0006) peak of the thin GeTe film around 51.5° cannot be reasonably ascribed to a very weak (044̅2) peak but must be mainly caused by (a gradient in out-of-plane) strain. It can be seen that asymmetry of the (0006) peak occurs at the higher angle side of the peak. This indicates a compressive out-of-plane strain with smaller (001)-spacing (d001) for the GeTe sublayers. Thus, this peak is broadened to the right. This is expected since it is grown on Bi2Te3, which has a larger in-plane lattice parameter than the initial GeTe layer. The in-plane strain in the GeTe is thus tensile. Due to lateral contraction (Poission’s ratio), the out-of-plane strain must then be compressive in agreement with the observed asymmetric broadening. The type of asymmetry observed in the (0006) GeTe peak in Figure 2a at first glance appears to correlate well with the exponentially decaying strain observed in the GeTe film according to Figure 1b. However, before proceeding to a more quantitative correlation, it is better to not only analyze the GeTe (0006) and (044̅2) peaks region in a θ–2θ scan but also in a reciprocal space map.
Reciprocal space maps of a 60 nm Bi2Te3 and the Bi2Te3/GeTe (4 nm/56 nm) heterostructure are compared in Figure 2b,c. Results of detailed TEM analyses for both layers, including atomic resolution images of the mica/Bi2Te3/GeTe cross-section, are shown in the Supporting Information, Figures S4 and S5, respectively. The 60 nm Bi2Te3 film exclusively shows its c-axis out of plane. The Bi2Te3/GeTe (4 nm/56 nm) heterostructure does not provide any observable Bi2Te3 reflections (as shown in Figure 2a) but clearly shows the GeTe (0006) and (044̅2) peaks. It can be seen in Figure 2b that the single Bi2Te3 layer peak exhibits a symmetric shape, which means the absence of strain, as expected based on Figure 1a,b. Due to the weak van der Waals bonding at the substrate–film interface, the mica surface has limited effect on the Bi2Te3 film. This is similar to the results described for Bi2Te2Se, MoO2 on mica.41,42 However, the GeTe (0006) peak in Figure 2c shows an asymmetric broadening in agreement with the θ–2θ scan. From Figure 2c, it can now be observed that this asymmetric broadening occurs solely in the Qz direction. The weak intensity of the (044̅2) peak with respect to the (0006) peak and their relatively clear separation along the Qz scale shows that the asymmetric broadening does not originate from their mutual interaction, but must be ascribed to a gradient in out-of-plane c-lattice parameter, correlating well with the exponentially decaying strain observed in the GeTe film according to Figure 1.
So both Figures 2a and 2c strongly suggest that the exponentially decaying strain profile in Figure 1 measured directly during GeTe growth still exists a long time (many months) after growth when the XRD measurements were performed. In order to show this convincingly, XRD curve fitting around the (0006) peak of the 28 nm GeTe sublayer is shown in Figure 2d. Unlike the 2D character of Bi2Te3 blocks, where relaxation is expected after each quintuple, we anticipate that in GeTe films (having the c-axis out-of-plane), the lattice constant develops gradually and continuously, changing after each GeTe bilayer. In order to do consistent curve fitting, the RHEED tensile strain profile, as shown in Figure 1c, is equally divided into six parts according to the shown “rainbow” bars. For the in-plane lattice parameter of each part, the central strain value of the bar was used. The length ratios of the bars from Figure 1c have been converted into the area ratios (based on area fraction, see inset in Figure 2d) of the corresponding six XRD curves in Figure 2d. However, one should notice that the RHEED tensile strain profile describes the distribution of the in-plane lattice parameter, whereas with XRD the distribution of out-of-plane lattice parameter are measured. In order to relate these two, Poisson’s ratio is used. Since there is no experimental data available on the rhombohedral GeTe Poisson’s ratio ν, a calculated average value of 0.19 was used.43 In fact, rhombohedral GeTe has 12 distinct elastic components. However, for the sake of simplicity, we assume that GeTe is isotropic with only two independent elastic constants: elastic modulus E and Poisson’s ratio ν.44 Starting from the general elastic isotropic case, where three normal strains εx, εy, εz are related to three normal stresses σx, σy, σz, it holds
| 1a |
| 1b |
| 1c |
In the case of an elastically isotropic thin film on a substrate, with x and y the in-plane direction and z the out-of-plane direction, it holds that εx = εy and σx = σy and, since no net stress can exist perpendicular to a free surface, it must hold that σz = 0. Then the relation between the out-of-plane strain εz and the in-plane strain εx as derived from eqs 1a–1c yields
| 2 |
So, when using a value of 0.19 for Poisson’s ratio, the measured out-of-plane strain with XRD is slightly less than half the in-plane strain measured with RHEED. Now the in-plane lattice parameter distribution measured by RHEED can be readily transformed into the out-of-plane lattice parameter distribution measured by XRD. For the six peaks used for fitting the overall GeTe(0006) XRD peak, a PsdVoigtII function was used, where the Gaussian fwhm, Lorentzian fwhm, and profile shape factor are kept the same for all six peaks. Note that the final results are not sensitive on the exact shape assumed for the six peaks. As can be observed from Figure 2d, the simulated envelope (black solid line) indeed obeys an asymmetric distribution fitting very well (quantitatively) the experimental data (black hollow circles). The quality of the fit is particularly good when taking the various simplifications into account: Only six discrete peaks are included in the fitting, a simple elastically isotropic model is used to relate the in-plane and out-of-plane strains and the Poisson ratio of 0.19 used is maybe a bit low. Therefore, the good fit demonstrates that the exponentially decaying strain measured using RHEED during growth of the GeTe films is still present many months after growth according to the present XRD analysis.
To provide additional proof that the strain measured with RHEED remains unaltered and that such persistent long-range exponentially decaying strains are not only observed in GeTe but also in Sb2Te3 and Bi2Te3 and thus a more general phenomenon, we also used atomic resolution STEM in two distinct ways. The results of these two methods are depicted in Figures 3 and 4, respectively.
Figure 3.
(a) Schematic illustration of plane-view STEM-HAADF imaging with depth-of-focus where the convergence semiangle is set to 30 mrad (left). Beam positions with different defocus (i.e., different depths) are shown on a typical Sb2Te3/Bi2Te3 heterostructure cross-section image, and the calculated depth resolution is 4.4 nm (right). (b) Typical atomic resolution images are captured at the various depths, and the corresponding FFT images are shown in part c. (d) Results of depth-of-focus analysis showing the evolution of the in-plane a lattice parameter during growth of the Sb2Te3/Bi2Te3 heterostructures with a top layer of 15 nm (red squares) and a top layer of 30 nm (blue squares). Black dotted curve shows the evolution of the a lattice parameter measured from the RHEED of the Sb2Te3/Bi2Te3 heterostructure with a top layer of 35 nm.
Figure 4.
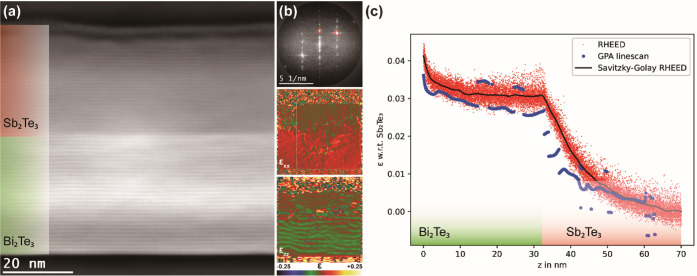
(a) Cross-sectional STEM-HAADF image of Bi2Te3/ Sb2Te3 heterostructure grown on a Si wafer covered with 300 nm SiO2. (b) The top shows the FFT image from the heterostructure, and the circled spots are used to derive strain in different directions. The in-plane component of the strain tensor (εxx) and out-of-plane component of the strain tensor (εzz) obtained from the STEM image by geometric phase analysis (GPA) are shown in the middle and bottom, respectively. (c) GPA linescan curve showing the evolution of in-plane strain in the out-of-plane direction is overlapped on the RHEED results from the same sample. Red dots are the original RHEED data, which are integrated into a smooth curve (black) by the Savitzky–Golay method.46 Despite the discontinuities present in the GPA linescan, it still shows a reasonable overall agreement with the strain measured during growth using RHEED analysis.
In the first method, we exploited the fact that the Angstrom-sized electron probe in aberration-corrected STEM can have a depth-of-focus of only several nanometers. Aberration correction is crucial, because only then the depth-of-focus can be reduced significantly (by increasing the convergence semiangle of the electron beam) while maintaining atomic resolution. For a plane-view TEM sample and a STEM image recorded with defocus zero (defined as the top surface of the specimen), this in principle implies that only an atomic resolution image of the atomic planes parallel to the top surface are recorded. With gradually increasing defocus, such that the probe moves down into the sample (actually defocus is made more negative), atomic resolution images of deeper atomic planes perpendicular to the electron beam can be recorded. Therefore, aberration-corrected STEM in principle allows depth profiling in plan-view samples as schematically depicted in Figure 3a. We applied this technique to measure the strain in a Bi2Te3 top layer grown on relaxed Sb2Te3, (grown on TEM grid with a 30 nm thick Si3N4 membrane). The atomic resolution in the images deteriorates for defocused values beyond −20 nm and therefore we could probe up to a maximum depth of about 20 nm. In order to probe the complete strain profile in the Bi2Te3 top layer, two different samples were analyzed. One with a top layer of 15 nm such that we could probe down across the Sb2Te3/Bi2Te3 interface and one with a top layer of 30 nm such that we can also probe the strain at larger distance from the Sb2Te3/Bi2Te3 interface. Figure 3b shows examples of atomic resolution images recorded at different defocusing in the 30 nm top layer sample, in principle, also implying corresponding depths with respect to the top surface. From all images recorded at the various depths, the Fourier transform was taken, see an example in Figure 3c where the FFTs were taken from the images in Figure 3b, and the a lattice parameter measured at each depth was quantified in an automatic manner (which is explained, together with some other details for the current depth profiling method, in the Supporting Information, Figure S6). The lattice parameter as a function of depth measured by STEM depth profiling is depicted as data points in Figure 3d and is overlaid on the RHEED profiles (continuous curves) measured for the heterostructure with the same structure. The results of the 15 nm top layer sample are depicted in red and for the 30 nm top layer sample in blue. The STEM results are consistent with the ones from RHEED. The depth resolution is 2λ/α,245 where λ is the wavelength of the electrons and α is the beam convergence semiangle. For a beam energy of 300 keV and a convergence semiangle of 30 mrad, the depth resolution of the images can be determined to be 4.4 nm. Therefore, some (more) deviation was expected since the depth resolution for RHEED of about 1 nm is clearly higher than for STEM.
In the second method, we used atomic resolution STEM to analyze a cross-section sample containing an Sb2Te3 top layer grown on relaxed Bi2Te3 (grown on Si wafer covered with 300 nm SiO2). In order to assess the strain present in the telluride layers, geometric phase analysis (GPA) was applied to the atomic resolution images.34 An example STEM-HAADF image is shown in Figure 4a. The excellent texture in the telluride heterostructure can be readily observed with only planes and vdW gaps parallel to the substrate surface and without any signature of the presence of even low-angle tilt boundaries. Based on this excellent texture, it would be expected that the strains in the out-of-plane direction εzz would be measured best by GPA. However, the GPA results on εzz are modulated by the overlapped (006) reflection (half of quintuple layer), making it difficult to extract out-of-plane strain. Still, GPA provides strain profiles for the in-plane strain that closely resemble the strain profiles measured with RHEED. An example is shown in Figure 4c. It can be observed that the strain in the Bi2Te3 bottom layer does not show any appreciable change when approaching the interface with the Sb2Te3 top layer. This is consistent with the RHEED results showing that the Bi2Te3 bottom layer is fully relaxed in this region. The Sb2Te3 top layer on the other hand shows a lattice matching with the Bi2Te3 at the interface, indicating maximum strain, which then decays when moving higher up in the Sb2Te3 top layer. When overlaying the GPA results on the RHEED results, which is relatively straightforward since both couple directly to the in-plane lattice spacing, a quite good match can be obtained in quantitative sense. Still, some varying results in the GPA analysis is observed. Few deviating parts in the GPA linescan exist as shown in Figure 4c. The result demonstrates that the relaxation in the Sb2Te3 at the interface with Bi2Te3 is relatively abrupt and does not show the gradual decay observed with RHEED. The reason that the GPA analysis does not completely match the strain profile as derived from the RHEED analysis probably has two main origins. The first one is that making a thin cross-section (using FIB) must cause additional relaxation of the biaxial strain imposed in the Sb2Te3 at its interface with Bi2Te3. This additional relaxation is completely avoided in the case of the depth profiling of plane-view samples as shown in Figure 3 and is probably the reason that better results were obtained. The second origin is that with GPA, the strain in rather small local nanoscale regions is obtained, containing local defects, whereas in RHEED an averaging over a large (millimeter sized) surface area of the film is performed. Then in combination with the plastic deformation, we show that is responsible for the strain relaxation, it is quite logical that the deformation can deviate from domain to domain in the film. The plastic deformation depends on how dislocations can be introduced into the film to relax the strain. Domain walls can be an important source from which dislocations can glide into the textured film. Then it is readily possible that the local structure of the domains and its walls vary and thus generate some variations in how each domain relaxes. In order to properly assess the average strain (relaxation) in the telluride heterostructures, global techniques like RHEED or XRD will be more accurate than local techniques with limited statistics. Nevertheless, the present atomic resolution STEM imaging combined with GPA again shows that persistent long-range decaying strains can be observed that are not compatible with strain relaxation based on elastic energy minimization.
Our work here demonstrates that in highly textured GeTe, Bi2Te3 or SbTe3 with the c-axis out of the plane, as grown on a c-axis oriented relaxed Bi2Te3 or Sb2Te3 seed layer, an exponentially decaying strain is present as observed directly during growth, but the same strain profile is still present many months after growth of the films as was demonstrated based on XRD and two types of STEM analyses. Apparently, the instantaneous strain measured by RHEED in these top-layers is not observably changed (further relaxed) by (1) overgrowth of a more top layer material, (2) prolonged annealing at the growth temperature (210 °C), (3) cooling back to room temperature, and (4) prolonged storage at room temperature. These results also directly show that the strain relaxation observed during RHEED cannot be coupled to an elastic model. It shows that there is relaxation by instantaneous plastic deformation. A first indication for this behavior was found when it was demonstrated that, when halfway during the exponentially decaying strain the film growth is stopped, the strain stays constant and does not show any further relaxation.27 However, the time interval the growth was interrupted and was relatively short of the order of seconds to a minute and could not exclude that still a further strain relaxation is possible on a much longer time scale (days to months). Therefore, the present results are important, showing that also many months later the exponentially decaying strain profile that directly develops during growth is still present without any further relaxation.
The likely explanation for this persistent strain profile is that after the immediate partial plastic relaxation insufficient driving force (stored strain energy per unit volume) remains present for achieving full strain relaxation. For the instantaneous relaxation it is required that dislocations glide parallel to the GeTe bilayers, Bi2Te3 or Sb2Te3 quintuple layers and are localized between these layers. For full strain relaxation, it is also required that dislocations glide across the bilayers or quintuples toward the interface with the Bi2Te3 or Sb2Te3 seed layer. For quintuple based materials like Bi2Te3 or Sb2Te3, which are typified as 2D materials, this is maybe not so surprising. However, for GeTe which is generally typified as a 3D material it is. Still, due to the bilayer structure of GeTe with alternating strong and weak bonds between the atomic layers, one might call it a pseudo-2D material. This type of anisotropic bonding is probably responsible for the fact that partial relaxation with an exponentially decaying strain occurs easily in these highly textured GeTe films (with the bilayers parallel to the surface) and that full relaxation is not observed. We also notice that such exponential behavior is not changed by the growth mode of GeTe that initially is 2D and then 3D (Stranski–Krastanov). The change from 2D to 3D growth is observable in RHEED data (Supporting Information, Figure S2) and also HAADF-STEM (see Figure S6), but there is not an observable change in the exponentially decaying strain as, e.g., measured using RHEED.
In a recent paper also, the exponentially decaying strain was observed based on RHEED pattern analysis during MBE growth of Sb2Te3/GeTe superlattices,33 where they write “Here, it is shown for the first time that superlattices of layered chalcogenides (Sb2Te3/GeTe) behave neither as fully decoupled two-dimensional (2D) materials nor as covalently bonded three-dimensional (3D) materials. Instead, they form a novel class of 3D solids with an unparalleled atomic arrangement, featuring a distribution of lattice constants, which is tunable.” In the paper, strain engineering of 2D/3D system is particularly emphasized and discussed, because it differs significantly from strain engineering in 2D/2D and 3D/3D systems. However, their explanation of this same phenomenon we observed at the same time27 is principally different from what we describe here. There an elastic spring model (elastic energy minimization) is assumed with certain limited coupling across vdWaals gaps and between the different sublayers of the heterostructures. For (ideal) 2D materials, no coupling occurs between the layers and the consequence is that in heterostructures the different sublayers just have their own fully relaxed lattice parameter. For the chalcogenide superlattices, the sublayers (e.g., Sb2Te3, and GeTe) are internally assumed elastic with in addition a limited elastic coupling between the different types of sublayers (across the Sb2Te3–GeTe interfaces). Such a model can explain well the instantaneous exponential variation in lattice parameters as observed using RHEED (and as well explain that there is no time dependence when the springs respond instantaneously), but it is in disagreement with the observations that the observed strain still persists unaltered (subsurface) with further overgrowth of the same or the other material.
Moreover, in this recent paper, it was assumed that GeTe acts as a 3D material with finally after growth of the heterostructure a uniform strain. The present work demonstrates that there is not a uniform strain but still an exponentially decaying strain in the GeTe. In the Sb2Te3, the final strain that persist in this sublayer shows, according to the elastic model, a gradient due to steps in strain values across the vdWaals gaps in the Sb2Te3 but much diminished compared to the gradient in strain instantaneously observed by RHEED. Grazing incidence XRD (GID) of an in-plane lattice spacing was used to experimentally measure the lattice spacing distributions present in the GeTe- Sb2Te3 superlattices,33 which were then fitted with the outcome of the elastic model obtained from fitting the initial RHEED curves. Comparing the experimental and modeled GID data shows rather dramatically that the modeled strains present in the superlattice show much less spread than the actual ones. Particularly on the GeTe side of the GID peak (at lower in-plane lattice spacings), the modeled peak is very sharp, whereas the experimental one is very broad. A similar but reduced mismatch occurs at the Sb2Te3 side of the GID peak. In light of the results presented here, these mismatches are obvious. A single strain and thus a single lattice spacing is assumed for GeTe, whereas in reality it keeps the large spread instantaneously measured by RHEED without any further relaxation. For Sb2Te3, the assumed additional elastic relaxation, diminishing the strain gradient, does also not occur but keeps the large spread instantaneously measured by RHEED. It is unfortunate that the authors of this article did not try to directly relate the in-plane lattice spacing measured with RHEED with the in-plane lattice spacing measured with GID without any intervention of the elastic model. It is very likely that a much better fit of the experimental GID peak would have been obtained.
Finally, some remarks have to be made on typifying materials as 2D or 3D. Obviously most materials are 3D bonded and there is no debate about that. However, for simplicity, we initially typified GeTe as a 3D bonded material and Bi2Te3 and Sb2Te3 as 2D bonded. In the end, these are gross simplifications that should not obscure a proper analysis of these material systems. GeTe in its stable low-temperature structure has a rhombohedral lattice that is formed out of its parent cubic structure by a Peierls-like distortion along one of the four ⟨111⟩ directions of the cubic phase. This distortion is thus accompanied by a dimerization of GeTe planes, such that each Ge or Te atom forms three short (strong) and three long (weak) bonds with each other. These bilayers provide a clear anisotropy to GeTe that in an exaggerated sense might be called pseudo-2D. This anisotropy is also the reason that GeTe films can be grown with their c-axis out-of-plane as has been exploited in the present work. This anisotropy is also the reason that the strain relaxation in GeTe behaves neither as holds for fully decoupled two-dimensional (2D) materials nor as holds for classically three-dimensional (3D) materials, as observed in the present work. Similarly, to call Bi2Te3 and Sb2Te3 2D materials is also too simple. Indeed, when looking at the structure of these materials, the 2D nature based on stacking of quintuple layers seems obvious. The relative large spacing between these quintuples, i.e., between Te–Te atomic layers, suggests them to be vdWaals gaps. However, an accurate analysis of these spacings for V2VI3 and many (IV–VI)x(V2VI3)1–x compounds shows that these VI–VI gaps, when compared with the average IV–VI and V–VI interplanar distances, are much smaller than expected for purely vdWaals gaps; see Figure 25 in ref (47). In contrast, the gaps in M–VI2 transition metal dichalcogenides demonstrate ideal spacings and thus pure vdWaals bonding. So, the stronger bonding across the vdWaals-like gaps in the V2VI3 and (IV–VI)x(V2VI3)1–x compounds shows that these are not true 2D materials. Strain relaxation in these compounds therefore also deviates from both the ones in fully decoupled two-dimensional (2D) materials and in classically three-dimensional (3D) materials. In the present work, for Bi2Te3 on mica strain relaxation occurs very fast, requiring only two or three quintuples, showing the weak coupling across the mica–Bi2Te3 interface, which comes close to truly 2D behavior. However, in both our earlier and this work, we show that the strain relaxation in Bi2Te3 on (relaxed) Sb2Te3 or Sb2Te3 on (relaxed) Bi2Te3 is of long-range exponentially decaying nature where the gradual reduction to 1/8 of the initial maximum strain level requires 20 quintuples. Therefore, this type of strain relaxation in these intriguing compounds depends sensitively on details of the substrate on which they are grown.
Conclusions
We reveal that the strain evolution of a “3D-bonded” material (GeTe) grown on “2D-bonded” material (Bi2Te3) exhibits an extraordinary long-range exponentially decaying relaxation mode, which is durable during and after growth. In contrast, the strain in Bi2Te3 grown on mica is found to be suddenly released after mostly two (sometimes three) quintuples, approaching the expected decoupled behavior of 2D materials. The long-range exponentially decaying strain in GeTe is also observed for Bi2Te3 on (relaxed) Sb2Te3 or vice versa. Moreover, these strains are measured directly at the surface during growth but turns out to be still present in a fairly unaltered way a long time after growth inside the film as shown by XRD and STEM analyses. This strain is therefore not dependent on time but importantly also not on additional film overgrowth. The observed behavior shows that the strain relaxation is not the result of an elastic (energy minimization) process but of plastic deformation. This long-range strain profile in these systems (and similar ones like Bi2Se3/In2Se3 multilayers) is attributed to pseudo-2D behavior with alternating stronger and weaker bonds (for bilayers of GeTe or quintuples for Bi2Te3 or Sb2Te3) in planes parallel to the growth surface. The weaker bonds allow a gradual strain release as film thickness progresses, but the stronger bonds then prevent misfit dislocations to glide to the heterostructure interface and thus full relaxation of a sublayer. Our work therefore suggests a proper pathway to simulate and engineer the mutual straining behavior in these pseudo-2D materials. Recent theoretical calculations show that the Seebeck coefficient of Sb2Te3 can be greatly improved because of the increased band extrema by changing the number of Sb2Te3 layers.48 It is well-known that the band structure in semiconductor materials can be influenced by strain, inducing rather dramatic changes of their electronic, quantum transport and photonic performances.24,49−51 We therefore anticipate that the exact observations and precise predictions of strain in these pseudo-2D materials hold great promise for tailoring their functionalities, e.g., in optoelectronic and thermoelectric applications.
Experimental Section
Samples Preparation and Growth
vdWaals epitaxial Bi2Te3 films and Bi2Te3/GeTe heterostructures have been grown on (001) freshly cleaved muscovite mica substrates by pulsed laser deposition (PLD), using a KrF excimer laser (λ = 248 nm) operating at 1 Hz repetition rate. The commercial stoichiometric compound targets were obtained from KTECH and have a purity of 99.999%. Once cleaved in air, the mica substrate was installed in the chamber and heated to the deposition temperature. In order to obtain Bi2Te3 and GeTe crystalline films, the deposition was carried out in argon gas at a pressure of 0.12 mbar with a 1 sccm flow, a laser fluence of 1 J cm–2 (spot size 1.3 mm2) with a substrate temperature of 210 °C. The background pressure was below 10–7 mbar and the target–substrate distance was 4 cm. In previous work, the growth rate was found to be approximately 1 nm per 50 pulses at such conditions.27 The thickness was also checked again in images based on FIB prepared cross sections (e.g., recorded at 30 kV in SEM or 300 kV in dedicated STEM, where typical examples can be found in the Supporting Information Figure S7 and Figure 4a). Similar PLD growth procedures were used for growing the Bi2Te3/Sb2Te3 and Sb2Te3/Bi2Te3 bilayers on the Si wafer covered with 300 nm thermal oxide.
RHEED Analysis
In situ RHEED was used to investigate the growth mode during the deposition. The RHEED images were obtained with an azimuth parallel to mica [11̅0] every 200 ms. This enables in situ analysis of the evolution of the in-plane lattice parameters of the film, which is calculated from the lateral spacing of the diffraction streaks (or spots). The method was described in detail by Vermeulen et al.(27) Since the Bi2Te3 film relaxes rapidly, the RHEED patterns of the last 20 pulses of the Bi2Te3 film were used as a reference for the calibration of the lattice spacings.
Characterizations of Films
The structure and strain of the films were characterized by X-ray diffraction (XRD), using a Panalytical X’pert Pro diffractometer operating in two ways: high-resolution θ–2θ specular scans and reciprocal space maps (RSMs) around the GeTe (0006) peak. Atomic force microscopy (AFM) images were obtained by a Bruker MultiMode 8 and analyzed by the Gwyddion software. Transmission electron microscopy (TEM) cross-section samples were prepared by focused ion beam (FIB, Helios G4 CX DualBeam), and TEM analysis was performed with a probe- and image-corrected Thermo Fisher Scientific Themis Z S/TEM operating at 300 kV. For the depth profiling experiments, the convergence semiangle was set to 30 mrad, yielding a depth-of-focus of about 4.4 nm. For plane-view samples, films were removed from the mica by floating them off at the water surface and transferred to TEM grids followed by analysis by TEM (JEOL 2010) operated at 200 kV.
Acknowledgments
This project has received funding from the European Union’s Horizon 2020 Research and Innovation Programme “BeforeHand” under Grant Agreement No. 824957. H. Zhang and B. J. Kooi gratefully acknowledge financial support from the China Scholarship Council (CSC, Grant No. 201706890019). All authors thank the support from the Zernike Institute for Advanced Materials. They kindly thank G. ten Brink and J. Baas for the technical support and M. Salverda for discussion on XRD data. H. Zhang wants to thank, in particular, moral support from Y. Li at this special Corona virus time in 2020.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.0c08842.
Table S1, lattice parameters and crystal structures of the materials used in our work; Figure S1, relatively large 2θ-range XRD curves; Figure S2, RHEED patterns of mica, Bi2Te3, and GeTe; Figure S3, AFM topography images of Bi2Te3 and Bi2Te3/GeTe heterostructures; Figures S4 and S5 show, TEM images of the local structure of Bi2Te3 and Bi2Te3/GeTe heterostructures, respectively; Figure S6, details for the aberration corrected STEM depth profiling method; and Figure S7, a typical STEM image (recorded at 30 kV in SEM) of an FIB prepared cross-sectional Bi2Te3/GeTe heterostructure (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Guinea F.; Katsnelson M. I.; Geim A. K. Energy Gaps and a Zero-Field Quantum Hall Effect in Graphene by Strain Engineering. Nat. Phys. 2010, 6, 30–33. 10.1038/nphys1420. [DOI] [Google Scholar]
- Niquet Y. M.; Delerue C.; Krzeminski C. Effects of Strain on the Carrier Mobility in Silicon Nanowires. Nano Lett. 2012, 12, 3545–3550. 10.1021/nl3010995. [DOI] [PubMed] [Google Scholar]
- Kushima A.; Yildiz B. Oxygen Ion Diffusivity in Strained Yttria Stabilized Zirconia: Where Is the Fastest Strain?. J. Mater. Chem. 2010, 20, 4809–4819. 10.1039/c000259c. [DOI] [Google Scholar]
- Kalikka J.; Zhou X.; Dilcher E.; Wall S.; Li J.; Simpson R. E. Strain-Engineered Diffusive Atomic Switching in Two-Dimensional Crystals. Nat. Commun. 2016, 7, 11983. 10.1038/ncomms11983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shea K. J.; Kim J. S. Influence of Strain on Chemical Reactivity. Relative Reactivity of Torsionally Distorted Double Bonds in Mcpba Epoxidations. J. Am. Chem. Soc. 1992, 114, 3044–3051. 10.1021/ja00034a042. [DOI] [Google Scholar]
- Zhou X.; Kalikka J.; Ji X.; Wu L.; Song Z.; Simpson R. E. Phase-Change Memory Materials by Design: A Strain Engineering Approach. Adv. Mater. 2016, 28, 3007–3016. 10.1002/adma.201505865. [DOI] [PubMed] [Google Scholar]
- Xue D. J.; Hou Y.; Liu S. C.; Wei M.; Chen B.; Huang Z.; Li Z.; Sun B.; Proppe A. H.; Dong Y.; Saidaminov M. I.; Kelley S. O.; Hu J. S.; Sargent E. H. Regulating Strain in Perovskite Thin Films through Charge-Transport Layers. Nat. Commun. 2020, 11, 1514. 10.1038/s41467-020-15338-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo R.; You L.; Lin W.; Abdelsamie A.; Shu X.; Zhou G.; Chen S.; Liu L.; Yan X.; Wang J.; Chen J. Continuously Controllable Photoconductance in Freestanding Bifeo3 by the Macroscopic Flexoelectric Effect. Nat. Commun. 2020, 11, 2571. 10.1038/s41467-020-16465-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosca D. H.; Vidal F.; Etgens V. H. Strain Engineering of the Magnetocaloric Effect in MnAs Epilayers. Phys. Rev. Lett. 2008, 101, 125503. 10.1103/PhysRevLett.101.125503. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Song L.; Madsen G. K.; Fischer K. F.; Zhang W.; Shi X.; Iversen B. B. Designing High-Performance Layered Thermoelectric Materials through Orbital Engineering. Nat. Commun. 2016, 7, 10892. 10.1038/ncomms10892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lv H. Y.; Lu W. J.; Shao D. F.; Sun Y. P. Enhanced Thermoelectric Performance of Phosphorene by Strain-Induced Band Convergence. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 085433. 10.1103/PhysRevB.90.085433. [DOI] [Google Scholar]
- Lee M. L.; Fitzgerald E. A.; Bulsara M. T.; Currie M. T.; Lochtefeld A. Strained Si, SiGe, and Ge Channels for High-Mobility Metal-Oxide-Semiconductor Field-Effect Transistors. J. Appl. Phys. 2005, 97, 011101. 10.1063/1.1819976. [DOI] [Google Scholar]
- Lee S. R.; Koleske D. D.; Cross K. C.; Floro J. A.; Waldrip K. E.; Wise A. T.; Mahajan S. In Situ Measurements of the Critical Thickness for Strain Relaxation in AlGaN/GaN Heterostructures. Appl. Phys. Lett. 2004, 85, 6164–6166. 10.1063/1.1840111. [DOI] [Google Scholar]
- Bourret A.; Adelmann C.; Daudin B.; Rouvière J.-L.; Feuillet G.; Mula G. Strain Relaxation in (0001) AlN/GaN Heterostructures. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 63, 245307. 10.1103/PhysRevB.63.245307. [DOI] [Google Scholar]
- Koma A. van der Waals Epitaxy-A New Epitaxial Growth Method for A Highly Lattice-Mismatched System. Thin Solid Films 1992, 216, 72–76. 10.1016/0040-6090(92)90872-9. [DOI] [Google Scholar]
- Fang H.; Battaglia C.; Carraro C.; Nemsak S.; Ozdol B.; Kang J. S.; Bechtel H. A.; Desai S. B.; Kronast F.; Unal A. A.; Conti G.; Conlon C.; Palsson G. K.; Martin M. C.; Minor A. M.; Fadley C. S.; Yablonovitch E.; Maboudian R.; Javey A. Strong Interlayer Coupling in van der Waals Heterostructures Built from Single-Layer Chalcogenides. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 6198–6202. 10.1073/pnas.1405435111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang J.; Li J.; Li S. S.; Xia J. B.; Wang L. W. Electronic Structural Moire Pattern Effects on Mos2/Mose2 2d Heterostructures. Nano Lett. 2013, 13, 5485–5490. 10.1021/nl4030648. [DOI] [PubMed] [Google Scholar]
- Kumar H.; Dong L.; Shenoy V. B. Limits of Coherency and Strain Transfer in Flexible 2D van der Waals Heterostructures: Formation of Strain Solitons and Interlayer Debonding. Sci. Rep. 2016, 6, 21516. 10.1038/srep21516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu C.; Song S.; Liu Z.; Chen L.; Wang L.; Fan D.; Kang N.; Ma X.; Cheng H. M.; Ren W. Strongly Coupled High-Quality Graphene/2D Superconducting Mo2C Vertical Heterostructures with Aligned Orientation. ACS Nano 2017, 11, 5906–5914. 10.1021/acsnano.7b01638. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Rodrigues J. N. B.; Luo Y. Z.; Li L.; Carvalho A.; Yang M.; Laksono E.; Lu J.; Bao Y.; Xu H.; Tan S. J. R.; Qiu Z.; Sow C. H.; Feng Y. P.; Neto A. H. C.; Adam S.; Lu J.; Loh K. P. Tailoring Sample-Wide Pseudo-Magnetic Fields on a Graphene-Black Phosphorus Heterostructure. Nat. Nanotechnol. 2018, 13, 828–834. 10.1038/s41565-018-0178-z. [DOI] [PubMed] [Google Scholar]
- Banerjee R.; Nguyen V. H.; Granzier-Nakajima T.; Pabbi L.; Lherbier A.; Binion A. R.; Charlier J. C.; Terrones M.; Hudson E. W. Strain Modulated Superlattices in Graphene. Nano Lett. 2020, 20, 3113–3121. 10.1021/acs.nanolett.9b05108. [DOI] [PubMed] [Google Scholar]
- Zhang H.; Huang J.-W.; Velasco J.; Myhro K.; Maldonado M.; Tran D. D.; Zhao Z.; Wang F.; Lee Y.; Liu G.; Bao W.; Lau C. N. Transport in Suspended Monolayer and Bilayer Graphene under Strain: A New Platform for Material Studies. Carbon 2014, 69, 336–341. 10.1016/j.carbon.2013.12.033. [DOI] [Google Scholar]
- Wang S.; Wang X.; Warner J. H. All Chemical Vapor Deposition Growth of MoS2:h-BN Vertical van der Waals Heterostructures. ACS Nano 2015, 9, 5246–5254. 10.1021/acsnano.5b00655. [DOI] [PubMed] [Google Scholar]
- Zhang X.; Meng F.; Christianson J. R.; Arroyo-Torres C.; Lukowski M. A.; Liang D.; Schmidt J. R.; Jin S. Vertical Heterostructures of Layered Metal Chalcogenides by van der Waals Epitaxy. Nano Lett. 2014, 14, 3047–3054. 10.1021/nl501000k. [DOI] [PubMed] [Google Scholar]
- He Y.; Yang Y.; Zhang Z.; Gong Y.; Zhou W.; Hu Z.; Ye G.; Zhang X.; Bianco E.; Lei S.; Jin Z.; Zou X.; Yang Y.; Zhang Y.; Xie E.; Lou J.; Yakobson B.; Vajtai R.; Li B.; Ajayan P. Strain-Induced Electronic Structure Changes in Stacked van der Waals Heterostructures. Nano Lett. 2016, 16, 3314–3320. 10.1021/acs.nanolett.6b00932. [DOI] [PubMed] [Google Scholar]
- Xie S.; Tu L.; Han Y.; Huang L.; Kang K.; Lao K. U.; Poddar P.; Park C.; Muller D. A.; DiStasio R. A.; Park J. Coherent, Atomically Thin Transition-Metal Dichalcogenide Superlattices with Engineered Strain. Science 2018, 359, 1131–1136. 10.1126/science.aao5360. [DOI] [PubMed] [Google Scholar]
- Vermeulen P. A.; Mulder J.; Momand J.; Kooi B. J. Strain Engineering of van der Waals Heterostructures. Nanoscale 2018, 10, 1474–1480. 10.1039/C7NR07607J. [DOI] [PubMed] [Google Scholar]
- Wang Z. Y.; Guo X.; Li H. D.; Wong T. L.; Wang N.; Xie M. H. Superlattices of Bi2Se3/In2Se3: Characteristics and Structural Properties. Appl. Phys. Lett. 2011, 99, 023112. 10.1063/1.3610971. [DOI] [Google Scholar]
- Zhou X.; Behera J. K.; Lv S.; Wu L.; Song Z.; Simpson R. E. Valanche Atomic Switching in Strain Engineered Sb2Te3-GeTe Interfacial Phase-Change Memory Cells. Nano Futures 2017, 1, 025003. 10.1088/2399-1984/aa8434. [DOI] [Google Scholar]
- Cecchi S.; Wang R.; Zallo E.; Calarco R. Unconventional Strain Relaxation of Sb2Te3 Grown on a GeTe/Sb2Te3/GeTe Heterostructure on Si (111). Nanosci. Nanotechnol. Lett. 2017, 9, 1114–1117. 10.1166/nnl.2017.2441. [DOI] [Google Scholar]
- Wan Y.; Xiao J.; Li J.; Fang X.; Zhang K.; Fu L.; Li P.; Song Z.; Zhang H.; Wang Y.; Zhao M.; Lu J.; Tang N.; Ran G.; Zhang X.; Ye Y.; Dai L. Epitaxial Single-Layer MoS2 on GaN with Enhanced Valley Helicity. Adv. Mater. 2018, 30, 1703888. 10.1002/adma.201703888. [DOI] [PubMed] [Google Scholar]
- Li H. D.; Wang Z. Y.; Guo X.; Wong T. L.; Wang N.; Xie M. H. Growth of Multilayers of Bi2se3/ZnSe: Heteroepitaxial Interface Formation and Strain. Appl. Phys. Lett. 2011, 98, 043104. 10.1063/1.3548865. [DOI] [Google Scholar]
- Wang R.; Lange F. R. L.; Cecchi S.; Hanke M.; Wuttig M.; Calarco R. 2D or Not 2D: Strain Tuning in Weakly Coupled Heterostructures. Adv. Funct. Mater. 2018, 28, 1705901. 10.1002/adfm.201705901. [DOI] [Google Scholar]
- Hÿtch M. J.; Snoeck E.; Kilaas R. Quantitative Measurement of Displacement and Strain Fields from HREM Micrographs. Ultramicroscopy 1998, 74, 131–146. 10.1016/S0304-3991(98)00035-7. [DOI] [Google Scholar]
- Brewer R.; Atwater H. A.; Groves J.; Arendt P. J. o. a. p. Reflection High-Energy Electron Diffraction Experimental Analysis of Polycrystalline Mgo Films with Grain Size and Orientation Distributions. J. Appl. Phys. 2003, 93, 205–210. 10.1063/1.1526156. [DOI] [Google Scholar]
- Saito Y.; Fons P.; Bolotov L.; Miyata N.; Kolobov A. V.; Tominaga J. A Two-Step Process for Growth of Highly Oriented Sb2Te3 Using Sputtering. AIP Adv. 2016, 6, 045220. 10.1063/1.4948536. [DOI] [Google Scholar]
- Chattopadhyay T; Boucherle J X; vonSchnering H G Neutron Diffraction Study on the Structural Phase Transition in GeTe. J. Phys. C: Solid State Phys. 1987, 20, 1431. 10.1088/0022-3719/20/10/012. [DOI] [Google Scholar]
- Vermeulen P. A.; Kumar A.; ten Brink G. H.; Blake G. R.; Kooi B. J. Unravelling the Domain Structures in GeTe and LaAlO3. Cryst. Growth Des. 2016, 16, 5915–5922. 10.1021/acs.cgd.6b00960. [DOI] [Google Scholar]
- Wang R.; Campi D.; Bernasconi M.; Momand J.; Kooi B. J.; Verheijen M. A.; Wuttig M.; Calarco R. Ordered Peierls Distortion Prevented at Growth Onset of GeTe Ultra-Thin Films. Sci. Rep. 2016, 6, 32895. 10.1038/srep32895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilmi I.; Lotnyk A.; Gerlach J. W.; Schumacher P.; Rauschenbach B. Influence of Substrate Dimensionality on the Growth Mode of Epitaxial 3D-Bonded GeTe Thin Films: From 3D to 2D Growth. Mater. Des. 2019, 168, 107657. 10.1016/j.matdes.2019.107657. [DOI] [Google Scholar]
- Liu Y.; Tang M.; Meng M.; Wang M.; Wu J.; Yin J.; Zhou Y.; Guo Y.; Tan C.; Dang W.; Huang S.; Xu H. Q.; Wang Y.; Peng H. Epitaxial Growth of Ternary Topological Insulator Bi2Te2Se 2D Crystals on Mica. Small 2017, 13, 1603572. 10.1002/smll.201603572. [DOI] [PubMed] [Google Scholar]
- Ma C.-H.; Lin J.-C.; Liu H.-J.; Do T. H.; Zhu Y.-M.; Ha T. D.; Zhan Q.; Juang J.-Y.; He Q.; Arenholz E.; Chiu P.-W.; Chu Y.-H. van der Waals Epitaxy of Functional MoO2 Film on Mica for Flexible Electronics. Appl. Phys. Lett. 2016, 108, 253104. 10.1063/1.4954172. [DOI] [Google Scholar]
- Gaillac R.; Pullumbi P.; Coudert F.-X. ELATE: An Open-Source Online Application for Analysis and Visualization of Elastic Tensors. J. Phys.: Condens. Matter 2016, 28, 275201. 10.1088/0953-8984/28/27/275201. [DOI] [PubMed] [Google Scholar]
- Sadd M. H.Elasticity: Theory, Applications, and Numerics; Academic Press: New York, 2009. [Google Scholar]
- Bosch E. G.; Lazić I. Analysis of Depth-Sectioning STEM for Thick Samples and 3D Imaging. Ultramicroscopy 2019, 207, 112831. 10.1016/j.ultramic.2019.112831. [DOI] [PubMed] [Google Scholar]
- Press W. H.; Teukolsky S. A. Savitzky-Golay Smoothing Filters. Comput. Phys. 1990, 4, 669–672. 10.1063/1.4822961. [DOI] [Google Scholar]
- Kooi B. J.; Wuttig M. Chalcogenides by Design: Functionality through Metavalent Bonding and Confinement. Adv. Mater. 2020, 32, 1908302. 10.1002/adma.201908302. [DOI] [PubMed] [Google Scholar]
- Li Z.; Miao N.; Zhou J.; Sun Z.; Liu Z.; Xu H. High Thermoelectric Performance of Few-Quintuple Sb2te3 Nanofilms. Nano Energy 2018, 43, 285–290. 10.1016/j.nanoen.2017.11.043. [DOI] [Google Scholar]
- Dai Z.; Liu L.; Zhang Z. Strain Engineering of 2D Materials: Issues and Opportunities at the Interface. Adv. Mater. 2019, 31, 1805417. 10.1002/adma.201805417. [DOI] [PubMed] [Google Scholar]
- Cahangirov S.; Sahin H.; Le Lay G.; Rubio A.. Introduction to the Physics of Silicene and Other 2D Materials; Springer International Publishing: Berlin, Germany, 2017. [Google Scholar]
- Kim S.; Gopalan V. Strain-Tunable Photonic Band Gap Crystals. Appl. Phys. Lett. 2001, 78, 3015–3017. 10.1063/1.1371786. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.