Abstract
A semianalytical coupled reservoir/wellbore model based on the volumetric source for horizontal wells of sulfur gas reservoirs is presented, which considers sulfur deposition and permeability heterogeneity. Compared to the results without considering the sulfur deposition effect, the results of this paper model is better fitted to field production data and average relative errors of two simulated results are 8.37% (considering sulfur deposition) and 23.38% (not considering sulfur deposition). Based on the model, we perform sensitivity in terms of various sulfur depositions, producing pressure drop, and permeability contrast. Results show that the production decreases with increased sulfur deposition, and the flow rate along the wellbore in the horizontal well decreases because of sulfur deposition. The production without and with sulfur deposition increases with increased producing pressure drop, while the production without sulfur deposition is higher. Also, higher producing pressure drop causes a higher nonuniform inflow profile along the horizontal well. Sulfur deposition can reduce a nonuniform biased inflow profile along the horizontal well in heterogeneous sulfur gas reservoirs, but the horizontal well production is reduced. Therefore, sulfur deposition is crucial for the production prediction and inflow profile along the horizontal well in heterogeneous sulfur gas reservoirs.
Introduction
Sulfur deposition has attracted increasing attention because it harms production in sulfur gas reservoirs. Sulfur deposition tends to occur when the temperature and pressure of high sulfur gas reservoirs change. The gas reservoir pressure drops, as the gas production increases; hence, sulfur saturation in the sulfur gas decreases.1−6 Based on sulfur saturation, some mathematical models were built to predict the influence of sulfur deposition on the gas inflow profile of horizontal wells,7−9 but these models are based on vertical wells. Furthermore, few researchers are concerned about the horizontal well inflow profile in heterogeneous sulfur gas reservoirs.
Over the past few decades, many researchers have focused on horizontal well oil/gas inflow along the horizontal wells,10−12 and this problem involves complex reservoir seepage, wellbore flow, and their relationship.13−20 Penmatcha and Aziz15 and Ozkan et al.16 developed reservoir/well models by the point source function to predict the flow rate and pressure distribution along the horizontal wellbore, and the point source function was also widely used for transient pressure analysis in other gas reservoirs such as the coalbed methane gas reservoir,17−19 but the solution of the point source function has the characteristic of singularity.20 Vicente et al.21 developed a three-dimensional implicit simulator to solve the coupling equation between the reservoir and wellbore. The numerical model can be used to analyze the flow rate and pressure distribution of horizontal wells accurately and deeply, and they need more data and more computation time than analytical solution and semi-analytical solution. Ouyang and Huang22 presented a coupled reservoir/wellbore model using experimental results, but did not consider porous media seepage in the reservoir. Karimifard and Durlofsky23 proposed a new method to consider the interaction between a wellbore model and a reservoir model. However, the boundary conditions in the wellbore model are constants, and this leads to erroneous results in applications.
Souza et al.24 proposed a numerical model to simulate the coupling of the wellbore and reservoir, which takes into account factors such as wellbore length, isotropy and anisotropy, completion scheme, and formation damage near the wellbore area. However, this method needs longer computational time than the analytical method and semianalytical method.25−28 The volumetric source method25 was proposed to evaluate the inflow profile for horizontal well completion with inflow control devices, and computational efficiency and high accuracy were obtained. The reservoir/well model of Furui was improved by Adesina et al.,29 who considered the pressure drop caused by acceleration. However, the influence of formation damage near the well area has not been effectively solved. Moreover, less attention was focused on the effects of sulfur deposition on the horizontal well inflow profile in the heterogeneous sulfur gas reservoir.
Sulfur Deposition Damage Model
For sulfur gas reservoir development, the main effects of sulfur deposition are the decrease of the porosity and the decrease of the permeability. It is assumed that the pressure change in time dt is dp and the change in sulfur solubility is dC. During the dt time, the volume of the precipitated solid sulfur in the saturated gas stream is given as follows
| 1 |
where Vs is the precipitated sulfur volume (m3); q is the flow rate (m3); Bg is the gas volume factor (m3/m3); C is the sulfur solubility in gas (g/m3); p is the reservoir pressure (MPa); t is the production time (d); T is the gas reservoir temperature (K); and ρs is the density of the solid sulfur (2.07 g/cm3).
The deposition amount of the sulfur element in the reservoir can be calculated by eq 1. The deposited solid sulfur clogs the rock pores, and so, the relationship between porosity changes and time can be expressed as30
| 2 |
where m = ((dC/dp)TμgBg2/k0).where ϕ is the porosity after sulfur deposition, which is dimensionless; ϕ0 is the initial porosity, which is also dimensionless; a is the laboratory coefficient, and its empirical value is −6.842; h is the net thickness (m); r is the sulfur deposition radius (m); μg is the gas viscosity (mPa·s); and k0 is the initial permeability (10–3 μm2).
The relationship between sulfur deposition saturation and porosity is given as
| 3 |
where Ss is sulfur deposition saturation.
By integrating eq 3, sulfur saturation can be expressed as
| 4 |
Sulfur deposition affects not only saturation but also the formation permeability. Based on the results reported by Robert,9 the formation permeability and the sulfur deposition saturation can be expressed as
| 5 |
where k is the permeability after sulfur deposition (10–3 μm2).
Therefore, the permeability after sulfur deposition can be expressed as
| 6 |
Semianalytical Model and Solution
Assumptions
As we can see in Figure 1, the sulfur gas reservoir is assumed to be a homogeneous reservoir. The gas reservoir (big box) and volumetric source (small box) are shaped as a cuboid box. There are five closed boundaries and one constant pressure boundary on the big box. The surface of the source (small box) is parallel to the gas reservoir. The horizontal well exists in the middle of the big box and fully penetrates the sulfur gas reservoir. It is assumed that the flow in the sulfur gas reservoir is a single steady flow, and the gas flow conforms to Darcy’s law. Sulfur is precipitated in the form of elementary substances during the production process.
Figure 1.

Schematic diagram of the box gas reservoir and horizontal well.
Reservoir Flow Model
As shown in Figure 1, the sulfur gas reservoir model is described by the following parameters: the sizes of the sulfur gas reservoir are xe, ye, and ze. In the heterogeneous sulfur gas reservoir, the gas production intensity of a volume source is q. The sizes of the volumetric source are 2wx, 2wy, and 2wz in three directions, and the center coordinate is (cx, cy, cz). Based on the abovementioned assumption, the diffusion equation of the gas flow in the sulfur gas reservoir can be expressed as
| 7 |
Boundary conditions
| 8 |
| 9 |
| 10 |
| 11 |
where
| 12 |
| 13 |
| 14 |
| 15 |
H(x – x0) is the Heaviside function
| 16 |
where ψi is the original pseudopressure of the gas reservoir, MPa; ψg is the pseudopressure at any point of the sulfur gas reservoir, MPa; qg is the volumetric source strength of the sulfur gas reservoir, m3/d; Vsource is the geometry size of the volumetric source, m3; k0 is the reservoir permeability, μm2; p is the reservoir pressure at any point of the sulfur gas reservoir, MPa; pini is the original gas reservoir pressure, MPa; μg is the gas viscosity, mPa·s; Z is the deviation factor of the sulfur gas reservoir; psc is the pressure under surface standard conditions, MPa; Tsc is the temperature under surface standard conditions, K; and T is the gas reservoir temperature, K.
The solution of the diffusion equation of the gas flow in the sulfur gas reservoir can be written by eq 16. A detailed derivation process of the solution for the diffusion equation based on the volumetric source model in this section can be found in the Appendix.19,20
 |
17 |
In this study, the cylindrical horizontal well is equivalent to a rectangle shape (Figure 1). The rectangle is divided into N parts (Figure 2), and each part is regarded as a volumetric sink, the length of part i is Li, the wellbore radius is rw, and the coordinates of i is (xi, yi, zi). Therefore, the coordinates of part i and dimensions of three directions are as follows
| 18 |
| 19 |
| 20 |
Figure 2.
Schematic of the horizontal well and gas reservoir division.
Corresponding to the division of horizontal wells, the gas reservoir is also divided into N parts, as shown in Figure 2. According to the superposition principle, the pressure drop at any point M(x,y,z) in the sulfur gas reservoir is obtained by the following equation
| 21 |
It is assumed that there is no cross flow between the two adjacent sulfur reservoir segments and that the point M(x,y,z) is located in the center of part i. According to eq 21, the pressure drop of point M can be expressed as
| 22 |
Eq 13 is substituted into eq 22 to obtain the pressure of part i
| 23 |
The s–k* approach31 was presented to model reservoir permeability heterogeneity near the wellbore region. s is a constant background permeability and k* is the effective skin along the horizontal well. The skin factor caused by the reservoir heterogeneity by Hawkins’ method32 can be expressed as
| 24 |
Substituting the eq 24 into the eq 23, the pressure of part i for the sulfur gas reservoir is
| 25 |
Substituting eq 16 into the eq 25, the eq 25 is converted as
| 26 |
Wellbore Flow Model
In this study, a single fluid is assumed to flow between two nodes, as shown in Figure 3. As shown in Figure 3, the mass conservation equation can be expressed as:
| 27 |
Figure 3.
Flow model in the horizontal wellbore.
According to eq 27, the following equation can be obtained as follows:
| 28 |
The conservation equation can be written as follows:
| 29 |
Let 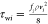 , and τwi and eq 28 are substituted
into eq 29 to obtain
the pressure drop
, and τwi and eq 28 are substituted
into eq 29 to obtain
the pressure drop
| 30 |
where the friction coefficient f can be written as33
 |
31 |
The ranges Re ≤ 2300, 2300 < Re < 4000, and Re ≥ 4000 correspond to laminar flow, transition flow, and turbulent flow, respectively.
The properties of the gas (pressure, density, and gas flow rate) by the ideal gas can be expressed as
| 32 |
| 33 |
Assuming that the fluid flow near the wellbore is uniform, the gas velocity of part i from the sulfur gas reservoir to the wellbore can be expressed as
| 34 |
From eqs 27–34, the pressure drop of the wellbore can be expressed as
| 35 |
where Zi is the deviation factor of part i.
It is to be noted that the frictional pressure drop is the first item, and the acceleration pressure drop is the second and third items.
Coupled Model and Solution
As shown in Figure 4, gas reservoir seepage and wellbore flow are coupled to study the influence of the horizontal well inflow profile in the heterogeneous sulfur gas reservoir.
Figure 4.
Coupling diagram of gas reservoir seepage and wellbore flow.
For production control
| 36 |
For bottom-hole pressure control
| 37 |
where Qmax is the maximum production, m3/d and pwf,min is the minimum bottom hole pressure, Mpa.
The coupled model is constituted by eqs 26–37. Because the model is nonlinear, this model can be solved by the Newton Raphson method. The detailed solution process is shown in Figure 5.
Figure 5.
Calculation flow chart for the model.
Results and Discussion
The effectiveness and application of the reservoir wellbore coupling model proposed in this paper are illustrated by a horizontal well of a sulfur gas reservoir. Basic parameters of the sulfur gas reservoir and horizontal well are shown in Table 1 and Figure 6. The comparison of the results is shown in Figure 7. The results of this paper model compared to the results of the model without considering the effect of sulfur deposition indicate that the new reservoir/wellbore model with sulfur deposition is better fitted to sulfur gas field data, and the average relative errors of the two simulation results are 8.37 and 23.38%, respectively. It shows that sulfur deposition in the sulfur gas reservoir is an important phenomenon that cannot be ignored.
Table 1. Basic Parameters of the Sulfur Gas Reservoir and Horizontal Well.
| parameters | value |
|---|---|
| sulfur gas reservoir length [m] | 980 |
| sulfur gas reservoir width [m] | 600 |
| top depth of the reservoir [m] | 6730.3 |
| porosity[fraction] | 0.16 |
| initial pressure [MPa] | 70 |
| gas density [kg/m3] | 0.69 |
| horizontal well length [m] | 980 |
| reservoir thickness [m] | 60 |
| horizontal well radius [mm] | 120 |
| gas viscosity [mPa·s] | 0.026 |
| wellbore roughness [m] | 0.04 |
Figure 6.
Permeability along the horizontal well.
Figure 7.
Comparison to field data.
Figures 8 and 9 illustrate production changes with sulfur deposition and the inflow profile of the horizontal well, respectively. For a horizontal well with a producing pressure drop of 3 Mpa, the production decreases with increased sulfur deposition. Also, the flow rate along the horizontal well decreases because the sulfur deposition is higher, which results in a lower flow rate along the horizontal well.
Figure 8.
Production changes with sulfur deposition.
Figure 9.
Influence of sulfur deposition.
Figure 10 illustrates the influence of producing pressure drop. The production both without and with sulfur deposition increases with increased producing pressure drop, while the production without sulfur deposition is higher. Figure 11 illustrates the flow rate without and with sulfur deposition along the horizontal well. The effect of sulfur deposition on the high part of the permeability is greater than that of the low part of the permeability with the increase in the production differential pressure. Also, higher producing pressure drop causes a higher nonuniform inflow profile along the horizontal well.
Figure 10.
Influence of producing pressure drop.
Figure 11.
Inflow profile of the horizontal well in the sulfur gas reservoir.
As shown in Table 2, the permeability of the three groups is set with different permeability contrasts (Jk). Figure 12 illustrates the bigger difference of the permeability contrast in production without and with sulfur deposition and the greater nonuniform inflow profile along the horizontal well in heterogeneous sulfur gas reservoirs. Also, sulfur deposition can reduce the nonuniform biased inflow profile along the horizontal well in heterogeneous sulfur gas reservoirs, but the production of horizontal wells is reduced.
Table 2. Distribution of Horizontal Permeability.
| permeability [10–3 μm2] |
|||
|---|---|---|---|
| distance from the heel [m] | Jk = 2.7 | Jk = 8.7 | Jk = 17.8 |
| 6760.3 | 2.601 | 3.179 | 3.05 |
| 6834.9 | 2.601 | 3.179 | 9.248 |
| 6894.9 | 2.601 | 3.179 | 1.0716 |
| 6940.9 | 3.468 | 3.757 | 4.046 |
| 6986.9 | 3.5102 | 3.6414 | 5.9245 |
| 7032.9 | 2.8033 | 3.179 | 0.8381 |
| 7078.9 | 1.9074 | 3.8148 | 1.6785 |
| 7124.9 | 3.757 | 0.8959 | 1.8785 |
| 7170.9 | 1.6005 | 1.6473 | 3.3235 |
| 7216.9 | 3.3235 | 3.8726 | 5.1 |
| 7262.9 | 2.9854 | 2.89 | 4.02 |
| 7308.9 | 3.5547 | 2.89 | 0.5202 |
| 7354.9 | 3.3524 | 1.6404 | 4.4217 |
| 7400.9 | 3.1501 | 1.1849 | 3.4391 |
| 7446.9 | 3.4969 | 4.9997 | 2.601 |
| 7492.9 | 2.1964 | 2.5744 | 1.445 |
| 7538.9 | 3.3501 | 0.578 | 2.023 |
| 7584.9 | 3.3056 | 2.312 | 0.8381 |
| 7630.9 | 3.2657 | 2.5432 | 2.89 |
| 7676.9 | 2.3987 | 4.3639 | 1.445 |
| 7728.3 | 1.3762 | 4.5373 | 0.6069 |
Figure 12.
Influence of the permeability contrast.
Conclusions
A new semianalytical model based on the volumetric source method for horizontal wells in sulfur gas reservoirs is developed. The production and the inflow performance of a horizontal well are simulated based on the new model. Compared with the results without considering the effect of sulfur deposition, the calculation results of the new reservoir/wellbore model with sulfur deposition are better fitted to sulfur gas field data, and the average relative errors of the two simulation results are 8.37% and 23.38%, respectively. Based on the model, we determine sensitivity in terms of various sulfur depositions, producing pressure drop, and permeability contrast. The results in detail are stated as follows:
-
(1)
The production decreases with increased sulfur deposition under a certain pressure. Also, the flow rate along the horizontal well decreases because sulfur deposition is higher, which results in a lower flow rate along the horizontal well.
-
(2)
The production without and with sulfur deposition increases with increased producing pressure drop, while the production without sulfur deposition is higher. With the increase of producing pressure drop, the effect of sulfur deposition on the high part of the permeability is greater than that of the low part of the permeability. Also, higher producing pressure drop results in a bigger nonuniform inflow profile along the horizontal well.
-
(3)
The bigger difference of the permeability contrast in production without and with sulfur deposition and the greater nonuniform inflow profile along the horizontal well in heterogeneous sulfur gas reservoirs are illustrated. Also, sulfur deposition can reduce the nonuniform biased inflow profile along the horizontal well in heterogeneous sulfur gas reservoirs, but the production of horizontal wells is reduced.
Acknowledgments
This work was financially supported by the Foundation of State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing (no. PRP/open-1901).
Appendix19,20
From eqs 6–9, the characteristic equation can be expressed as
 |
A.1 |
Let E = =X(x)Y(y)Z(z), according to separation variables, eq A.1 can be transformed as three one-dimensional eigenvalue problems
 |
A.2 |
where
| A.3 |
Based on eq 16, the characteristics values of three one-dimensional eigenvalue problems are
| A.4 |
| A.5 |
| A.6 |
According to eqs A.4–A.6, the characteristic value of three one-dimensional eigenvalue problems is
| A.7 |
The corresponding characteristic function system of three one-dimensional eigenvalue problems is
| A.8 |
The 2-norm of eigen function of the characteristic function is
| A.9 |
where
| A.10 |
Taking eqA.9 of the characteristic function system as transformation kernel, the model established in this paper is solved through orthogonal transformation. The corresponding orthogonal transformation can be described as follows
| A.11 |
Based on eqA.9, the inverse transformation of eq 27 is as follows
| A.12 |
Using orthogonal transformation in eqA.12, eqs 7–11 can be converted as
| A.13 |
Substituting eqA.13 into eqA.12, the solution of the model in this paper is
 |
A.14 |
where
 |
A.15 |
 |
A.16 |
| A.17 |
The authors declare no competing financial interest.
References
- Al-Majed M. A.New model to predict formation damage due to sulfur deposition in sour gas wells. SPE North Africa Technical Conference and Exhibition, Cairo, Egypt, 2012.
- Guo X.; Zhou X.; Zhou B. Prediction model of sulfur saturation considering the effects of non-Darcy flow and reservoir compaction. J. Nat. Gas Sci. Eng. 2015, 22, 371–376. 10.1016/j.jngse.2014.12.009. [DOI] [Google Scholar]
- Hu J.-H.; He S.-L.; Zhao J.-Z.; Li Y.-M.; Yang X.-F. Sulfur deposition experiment in the presence of non-movable water. J. Pet. Sci. Eng. 2012, 100, 37–40. 10.1016/j.petrol.2012.11.002. [DOI] [Google Scholar]
- Hu J.-H.; He S.-L.; Zhao J.-Z.; Li Y.-M.; Deng Y. Modeling of Sulfur Deposition Damage in the Presence of Irreducible Water. Pet. Sci. Technol. 2011, 29, 499–505. 10.1080/10916461003663008. [DOI] [Google Scholar]
- Kennedy H. T.; Wieland D. R. Equilibrium in the methane-carbon dioxide-hydrogen sulfide-sulfur system. Soc. Pet. Eng. J. 1960, 219, 166–169. 10.2118/1351-g. [DOI] [Google Scholar]
- Mahmoud M. A. A. Effect of elemental-sulfur deposition on the rock petrophysical properties in sour-gas reservoirs. SPE J. 2014, 19, 703–715. 10.2118/164440-pa. [DOI] [Google Scholar]
- Abou-Kassem J. H. Experimental and numerical modeling of sulfur plugging in carbonate reservoirs. J. Petrol. Sci. Eng. 2000, 26, 91–103. 10.1016/s0920-4105(00)00024-3. [DOI] [Google Scholar]
- Mei H.; Zhang M.; Yang X.. The effect of sulfur deposition on gas deliverability. SPE Gas Technology Symposium, Calgary, Alberta, Canada, 2006.
- Roberts B. E. The effect of sulfur deposition on gas well inflow performance. SPE Reservoir Eng. 1997, 12, 118–123. 10.2118/36707-pa. [DOI] [Google Scholar]
- Li T.; Tan Y.; Ahmad F. A.; Zhao J. Experimental study of sand distribution among perforation clusters in horizontal wellbore of shale gas reservoir. J. Chem. 2020, 2020, 1–7. 10.1155/2020/2704685. [DOI] [Google Scholar]
- Li T.; Tan Y.; Ahmad F. A.; Liu H. A new method to production prediction for the shale gas reservoir. Energy Sources, Part A 2020, 6, 615–622. 10.1080/15567036.2020.1779876. [DOI] [Google Scholar]
- Li T., Tan Y., Dai S., Zhou X., Yu J., Yang Q.. Semi-analytical model based on the volumetric source method to production simulation from nonplanar fracture geometry in tight oil reservoirs. ACS Omega 2020, 6DOI: 10.1021/acsomega.0c05119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kou Z.; Dejam M. Dispersion due to combined pressure-driven and electro-osmotic flows in a channel surrounded by a permeable porous medium. Phys. Fluids 2019, 31, 056603. 10.1063/1.5092199. [DOI] [Google Scholar]
- Kou Z.; Dejam M. Control of shear dispersion by the permeable porous wall of a capillary tube. Chem. Eng. Technol. 2020, 43, 2208–2214. 10.1002/ceat.201900687. [DOI] [Google Scholar]
- Penmatcha V. R.; Aziz K. A comprehensive reservoir/wellbore model for horizontal wells. SPE J. 1998, 4, 224–234. 10.2118/39521-MS. [DOI] [Google Scholar]
- Ozkan E.; Sarica C.; Haci M. Influence of pressure drop along the wellbore on horizontal-well productivity. SPE J. 1999, 4, 288–301. 10.2118/57687-pa. [DOI] [Google Scholar]
- Zhang L.; Kou Z.; Wang H.; Zhao Y.; Dejam M.; Guo J.; Du J. Performance analysis for a model of a multi-wing hydraulically fractured vertical well in a coalbed methane gas reservoir. J. Petrol. Sci. Eng. 2018, 166, 104–120. 10.1016/j.petrol.2018.03.038. [DOI] [Google Scholar]
- Kou Z.; Wang H. Transient pressure analysis of a multiple fractured well in a stress-sensitive coal seam gas reservoir. Energies 2020, 13, 3849. 10.3390/en13153849. [DOI] [Google Scholar]
- Wang H.; Kou Z.; Guo J.; Chen Z. A semi-analytical model for the transient pressure behaviors of a multiple fractured well in a coal seam gas reservoir. J. Petrol. Sci. Eng. 2021, 198, 108159. 10.1016/j.petrol.2020.108159. [DOI] [Google Scholar]
- Valkó P. P.; Amini S.. The method of distributed volumetric sources for calculating the transient and pseudosteady-state productivity of complex well-fracture configurations. SPE Hydraulic Fracturing Technology Conference, College Station, Texas, U.S.A., 2007.
- Vicente R.; Sarica C.; Ertekin T. A numerical model coupling reservoir and horizontal well flow dynamics: Transient behavior of single-phase liquid and gas flow. SPE J. 2002, 7, 70–77. 10.2118/77096-PA. [DOI] [Google Scholar]
- Ouyang L.; Huang W.. A comprehensive evaluation of well-completion impacts on the performance of horizontal and multilateral wells. SPE Annual Technical Conference and Exhibition, Dallas, Texas, 2005.
- Karimifard M.; Durlofsky L. J.. An expanded well model for accurate simulation of reservoir-well interactions. ECMOR XII-12th European Conference on the Mathematics of Oil Recovery, 2010.
- Souza G. D.; Pires A. P.; Abreu E.. Well-reservoir coupling on the numerical simulation of horizontal wells in gas reservoirs. SPE Latin America and Caribbean Petroleum Engineering Conference, Maracaibo, Venezuela, 2014.
- Luo W.; Li H.-T.; Wang Y.-Q.; Wang J.-C. A new semi-analytical model for predicting the performance of horizontal wells completed by inflow control devices in bottom-water reservoirs. J. Nat. Gas Sci. Eng. 2015, 27, 1328–1339. 10.1016/j.jngse.2015.03.001. [DOI] [Google Scholar]
- Tan Y.; Li Q.; Li H.; Zhou X.; Jiang B. A semi-analytical model based on the volumetric source method to predict acid injection profiles of horizontal wells in carbonate reservoirs. J. Energy Resour. Technol. 2020, 143, 053001. 10.1115/1.4048508. [DOI] [Google Scholar]
- Li H.; Tan Y.; Jiang B.; Wang Y.; Zhang N. A semi-analytical model for predicting inflow profile of horizontal wells in bottom-water gas reservoir. J. Pet. Sci. Eng. 2018, 160, 351–362. 10.1016/j.petrol.2017.10.067. [DOI] [Google Scholar]
- Tan Y.; Li H.; Zhou X.; Jiang B.; Wang Y.; Zhang N. A semi-analytical model for predicting horizontal well performances in fractured gas reservoirs with bottom-water and different fracture intensity. J. Energy Resour. Technol. 2018, 140, 102905. 10.1115/1.4040201. [DOI] [Google Scholar]
- Adesina A. P.; Orodu O.; Oladepo A.. An improved model for estimating productivity of horizontal drain hole. SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 2016.
- Ping Z.; Zhao J.; Zhou H. Formation damage from elemental sulfur deposition in sour gas reservoir. Pet. Explor. Dev. 2005, 32, 113–115. [Google Scholar]
- Wolfsteiner C.; Durlofsky L. J.; Khalid A. Approximate model for productivity of nonconventional wells in heterogeneous reservoirs. SPE J. 2000, 5, 218–226. 10.2118/62812-pa. [DOI] [Google Scholar]
- Hawkins M. F. A Note on the Skin Effect. J. Pet. Technol. 1956, 8, 65–66. 10.2118/732-g. [DOI] [Google Scholar]
- Sun E.; Li X. Study on horizontal wellbore pressure of low permeability reservoirs. Reservoir Eval. Dev. 2013, 3, 38–40. [Google Scholar]














