A new approach to analyzing regenerated bone quality in the mouse digit amputation model using semi-automatic processing of microCT data

Abstract

Bone regeneration is a critical area of research impacting treatment of diseases such as osteoporosis, age-related decline, and orthopaedic implants. A crucial question in bone regeneration is that of bone architectural quality, or how “good” is the regenerated bone tissue structurally? Current methods address typical long bone architecture, however there exists a need for improved ability to quantify structurally relevant parameters of bone in non-standard bone shapes. Here we present a new analysis approach based on open-source semi-automatic methods combining image processing, solid modeling, and numerical calculations to analyze bone tissue at a more granular level using μCT image data from a mouse digit model of bone regeneration. Examining interior architecture, growth patterning, spatial mineral content, and mineral density distribution, these methods are then applied to two types of 6-month old mouse digits – 1) those prior to amputation injury (unamputated) and 2) those 42 days after amputation when bone has regenerated. Results show regenerated digits exhibit increased inner void fraction, decreased patterning, different patterns of spatial mineral distribution, and increased mineral density values when compared to unamputated bone. Our approach demonstrates the utility of this new analysis technique in assessment of non-standard bone models, such as the regenerated bone of the digit, and aims to bring a deeper level of analysis with an open-source, integrative platform to the greater bone community.

1. Introduction

To further the treatment of age-, disease-, and trauma-related disorders in the skeletal system, precise and high-resolution structural analysis of healing of bone is crucial to accurately evaluating bone outcomes. Dual-energy x-ray absorptivity (DEXA), quantitative backscattered electron imaging (qBEI), and computed tomography (CT) are three of the most widely used approaches to evaluate mineral density and bone architecture in both clinic and animal research, however, difficulty remains in assessing structurally relevant parameters of bone, particularly in small bones and non-standard bone samples that are outside of the mainstream of bone research. New analysis methods would provide better ways of measuring bone quality, or the structural integrity of regenerated bone tissue. Bone architecture combined with the composition of extracellular matrix – collagenous proteins, non-collagenous proteins and hydroxyapatite [1] - together help define the structural quality of a bone. Here we address bone architecture and present a novel and adaptive open-source platform that can be used to better evaluate non-standard bone structure and aid in better visualizing differences in bone structure.

In the mouse model of digit amputation presented here, amputation of the distal 1/3 of the third phalangeal element (P3) results in regeneration of patterned bone via direct ossification. Following amputation, the digit undergoes inflammatory and histolytic stages, followed by cell dedifferentiation, patterning and new bone formation via direct ossification, whereas a more proximal amputation fails to produce a regenerative response. The mouse digit regeneration model has been a valuable model in studying mechanisms underlying bone regeneration and healing [2–10]. Regenerative bone architecture outcomes in this model have been largely quantified using μCT techniques coupled with FIJI, focusing on traditional bone parameters [11] such as length changes [12], trabecular spacing, trabecular thickness, and volumetric change [4,13–16], trabecular number, connectivity density, and structure model index (SMI) [16]. The regenerated distal bone is integrated with the original cortical stump which itself remains largely unchanged and can be analyzed using traditional cortical bone parameters, such as cortical thickness, porosity [16], and pore number [11]. Analysis of P3 architecture using μCT and traditional analysis methods has enabled valuable insight into understanding effects on bone formed under the regenerative process, however, a significant part of regeneration is pattern formation. In order to truly address the unique bone patterns, like that of the P3 digit, analysis techniques that quantify unconventional shapes, show pattern changes in density, and quantify void spaces are needed.

Bone mineral density (BMD) is one of the most powerful measurements for clinical diagnosis of diseases such as osteoporosis [17]. CT and DXA are both widely used for assessing bone mineral density in both clinic and animal research [18]. These approaches often provide an output of a conventional single measurement for averaged areal or volumetric BMD [19]. These measurements are reliable in producing a global overview of bone health, but do not address potential changes in distribution of mineralization. Correspondingly, use of more spatially-targeted bone mineral density values to measure and predict the response of bone to treatment has been limited [20].

As a result, the use of μCT in research to assess not just bone mineral density but also bone morphology has grown, coupled with image analysis and processing [21]. Methods of dual thresholding, 3D adaptive thresholding, genetic algorithms [22–24], and shape recognition using deep learning techniques [25,26] have been used for segmentation of regions of interest. However, these methods of automatic and semi-automatic bone analysis do not typically move beyond refining segmentation. Bone architecture analysis after image segmentation is also limited to parameters such as overall trabecular section thickness, volume measurements [21,27], and bone surface measurements [28].

Additional efforts to extract more information on bone tissue has investigated bone mineral density distribution (BMDD) of bone to provide additional information, such as examining bone mineral value distribution parameters in small animals [29,30], and evaluating Ca-content as measured through quantitative microradiaography, quantitative backscattered electron imaging (qBEI), and synchrotron radiation micro computed tomography [31,32]. Although not widely used, some analysis software is able to further refine BMDD output in the form of histograms and graphical representation. Recent image processing techniques available through use of well-known FIJI [33] software and associated plugins [34] have added great utility to bone analysis and created a detailed and accessible forum for researchers. In particular, this has allowed greater analysis control for researchers that focus on non-standard bone models of regeneration and healing, such as the mouse digit regeneration model. We have built upon these techniques to offer a flexible approach for analyzing BMDD, and new analysis techniques quantifying void spaces within bone.

Here we detail an integrative, open-source approach that builds on existing analysis techniques to analyze regenerated bone on a more granular level. We use methods of semi-automatic image processing, three-dimensional modeling and morphological analysis built on synthesis of modeling software, custom Python [35] scripting, and open-source Python packages, starting from raw μCT images as input to demonstrate both new analysis parameters such as inner void volume quantitation and graphical representation, and revisit BMD and BMDD outputs by offering an open-source approach for greater user-control of these parameters. This approach allows quantification of localized changes in interior digit architecture and interior growth morphology, as well as changes in mineral content and growth patterning, and spatial distribution of mineral content. Application to scans of 6-month old mouse digits highlights differences in bone architecture between unamputated and regenerated bone. This approach may offer analytical utility beyond the digit to non-standard bone structures such as cochlea [36], ectopic bone seen in heterotopic ossification [37], and the long, thin marrow cavities seen in the cranium [38] and long bones [39].

2. Material and methods

2.1. Ethics statement

All experiments were performed in accordance with the standard operating procedures approved by the Institutional Animal Care and Use Committee of Tulane University Health Sciences Center (Reference Number – 579).

2.2. Amputations and animal handling

Adult 6-month old male and female CD1 wild type mice were purchased from Charles River (Wilmington, MA). Mice were anesthetized with 1–5% isoflurane gas with continuous inhalation. The second and fourth digits of both hind limbs were amputated at the P3 distal level as described previously and regenerating digits were collected at day 42 (D42) for analysis. The third digit was used as an unamputated (UA) control [4,14,16]. The sample size of mice used was N = 14 for unamputated digits and N = 6 for day 42 regenerated digits.

2.3. Micro computed tomography

Ex vivo μCT images of mouse digits were acquired using a Bruker SkySkan 1172 scanner (Bruker, Kontich, Belgium) at 50 kV and 201 μA, with 2 K resolution and an isotropic voxel size of 3.9 μm. Images were captured at a rotation angle of 0.2 with frame averaging of 5. Raw images were processed with Nrecon and DataViewer (Bruker, Kontich, Belgium). Each scan was reconstructed with a beam hardening correction of 24%, no smoothing correction, and a dynamic range of 0.00–0.339. Reconstructed output files were in 8-bit BMP format.

Attenuated x-ray data values were calibrated to mineral density using standard 0.25 and 0.75 mg hydroxyapatite density phantoms and converted to greyscale output. These images served as the basis for the overall approach, seen in Fig. 1. (N = 6 D42 regenerated digits and N = 14 unamputated digits).

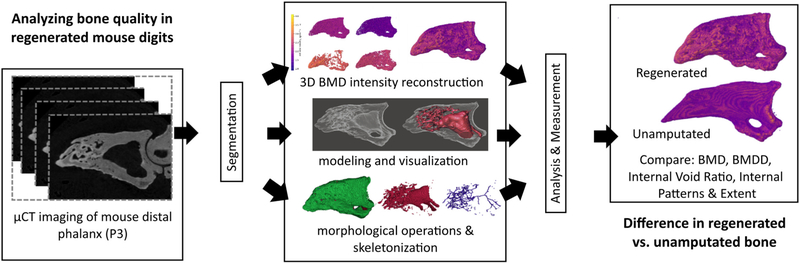
Fig. 1.

Image processing based approach. Raw μCT images are acquired and subjected to segmentation, followed by 3D BMD reconstruction, interior modeling and visualization, and morphological mathematical operations including skeletonization. Following this, analysis and measurement evaluate BMD, BMDD, internal void ratio, and cumulative skeleton length.

2.4. Spatial bone mineral density

Spatial bone mineral density analysis was performed on the entire P3 bone for unamputated digits (all cortical bone) and day 42 regenerated digits (both cortical and trabecular bone). Custom scripts were developed with Python [35] code to process the μCT image stacks of each mouse digit and create three dimensional models with color-differentiated mineral density values. Greyscale images with calibrated pixel intensity representing mineral density (g/cm³) were manually cropped and segmented using FIJI to remove the second phalangeal element and any material captured in the CT image proximal to the P3 digit as part of the imaging procedure. An automated process then imported the CT images and converted image data into matrix form, with thresholding applied using a value of 55 (out of 255 grey-scale, approximately 0.71 g/cm³) to remove out non-bone material and artifacts. Secondary thresholding was applied to create specific bone mineral density value groupings. Mineral density values were calculated through averaging greyscale pixel intensity using L³ sized voxels (L = 3 pixels) for each representative data point though iterative operation over the digit image stack, reducing computation time without avoiding loss of digit characteristics. Values were further sorted into 4 groups, as follows: Group 1 = [0.71–1.32 g/cm³], Group 2 = [1.32–1.72 g/cm³], Group 3 = [1.72–2.10 g/cm³], and Group 4 = [2.10–4.00 g/cm³], respectively, chosen for visual contrast. Using Python scripting, each group was then plotted in 3D space using Mayavi mlab [40] to better visualize the spatial distribution of higher and lower mineral values, using a color intensity scheme (viewable online in color print) to represent mineral value magnitude. A flowchart in the Appendix describes the process.

2.5. Distribution of bone mineral density values

Bone mineral density distribution analysis was performed on the entire P3 bone for unamputated digits (all cortical bone) and day 42 regenerated digits (both cortical and trabecular bone). Using data produced by the automatic process, the distribution of mineral density values was calculated. Mineral density value data were stripped of coordinate data and numerically evaluated for each digit, calculating the probability (frequency of mineral values over 30 bins) of values composing the whole distribution. A normal curve was fit (using a maximum-likelihood estimation) and mean and standard deviation were calculated. Mineral values as measured for each digit were processed into both histogram and violin plots, allowing visualization, analysis, and comparison. Single digit, digit-to-digit, and digit group comparisons are automated and presented here.

2.6. Internal void volume ratio

Inner void volume analysis was performed on the entire P3 bone for unamputated digits (the marrow space in the cortical bone) and day 42 regenerated digits (both the marrow space in the cortical bone and the trabecular spaces). Image stacks were converted into 3D models for the measurement of the surface area and volume of both external (bone) and internal (void) structures. For each digit μCT image sequences were imported into the FIJI image processing program, manually segmented to remove the second phalangeal element, and converted into a 3D surface (STL file format), before being imported into Autodesk® Mesh-mixer™ [41]. Once imported, a planar cut was made at the amputation site in order to isolate the regenerated volume of bone. Exterior surfaces were removed, and remaining surface normal reversed, leaving behind only the bone’s interior void space. Openings in the remaining structures formed during the removal of the exterior surface were manually identified and repaired in order to create a fully closed surface, leading to a full solid boundary model. Geometric properties were then computed by native geometric modeling kernel, which in Autodesk software is based off ACIS [42]. Measurements were corrected for native scaling through μCT voxel calibration data. To characterize the inner spaces of the regenerated bone, a digit void fraction was calculated from the following equations: T_v = V_v + S_v and V_f = V_V/T_v, where T_v = Total Volume of the digit, V_v = Void Volume, S_v = Solid Volume (volume of solid bone), and V_f is the digit void fraction.

2.7. Internal void Skeletonization

Skeletonization was performed on the entire P3 bone for unamputated digits (the marrow space in the cortical bone) and day 42 regenerated digits (both the marrow space in the cortical bone and the trabecular spaces). Building on skeletonization methods and techniques previously developed for image processing across a variety of applications [43,44], after processing to construct the internal void structure, automated Python scripting applied a three dimensional parallel thinning algorithm was applied to μCT image stack data, implemented through skimage-kit [43], returning the internal void skeleton data (N = 6 D42 regenerated digits and N = 14 unamputated digits). The inner void structure was reconstructed from a iterative sequence of mathematical morphology [45] convex hull [46], and Boolean logic operations on μCT image data of the mouse digit in order to return the structure of the negative inner void space in voxel form. The procedure steps are further described with a flowchart in the Appendix. Subsequently, skeleton patterning and morphological trends of both the bone tissue and the inner void were analyzed with Python scripting, using both skimage-kit and skan [47] Python libraries. Skeleton analysis returned skeleton segment types (junction-junction, junction-end, end-end, isolated cycle) and both branch and point to point distance measures. Quantifying a measure of inner void extant was found by summing all skeletonized segment distances in the digit into a single scalar value, a representative total skeleton distance (in micrometers).

2.8. Statistics analysis

Welch’s t-test (unequal variances t-test) was run on mineral value distribution data generated from the digit μCT stacks to check for statistical significance in differences shown. Basic statistics and t-test were calculated for digits and digit groups with scipy.stats package [48], and differences were considered significant when p < 0.05. For BMD group comparison a linear mixed model was fit to the BMD values using a fixed effect corresponding to regenerated or unamputated digits, and random effects for each individual digit. This approach allowed treatment of the individual BMD datapoints as independent given the digit-specific random effects. This was done in R statistical software [49] using the package lme4 [50]. Distribution of the standard deviations of the bone density data was evaluated using a Wilcoxon rank sum test. This was done by computing the standard deviation of the BMD values for each digit and then comparing the regenerated and unamputated digit standard deviations.

3. Results

3.1. Overall approach

As shown in Fig. 1, the overall approach proceeded as follows: μCT imaging of mouse P3 digits using Bruker SkyScan 1172 produced calibrated greyscale intensity image stacks. Image stacks were imported into FIJI for manual segmentation of the second phalangeal element. Segmentation was followed by three main paths:1) Automated Python scripting imported the image stacks, applied thresholding to remove non-bone artifacts and identify bone mineral ranges, reconstructed three-dimensional bone mineral density mapping through iterative processing of each image, and rendered three-dimensional models of the digit bone mineral density values. 2) Manual conversion into three-dimensional models using FIJI to convert image stacks into STL files, followed by import into Autodesk Meshmixer™ to isolate the regenerated tissue region through planar cuts and surface editing, manual pruning of exterior surfaces, reverse of remaining surface normals, local repair of surface gaps, and conversion of the subsequent closed surface to solid boundary model of the interior void space. Digit void fraction was calculated using the solid volume measurements. 3) Automated Python scripting imported segmented image stacks, reconstructed inner void volume from iterative sequence of mathematical morphology and computational geometry operations, skeletonized the three-dimensional void volume, and analyzed the resulting skeletonized structure, followed by three-dimensional rendering. Extensive prior research from the authors and others has confirmed no developmental or regenerative differences between the third control digit (unamputated) or the second and fourth digits [4,13–16,51,52].

3.2. Spatial bone mineral density

To quantify differences in structure and spatial density patterns of regenerated bone, we used Python scripting to generate three-dimensional bone mineral density plots, using color intensity to represent mineral density value.

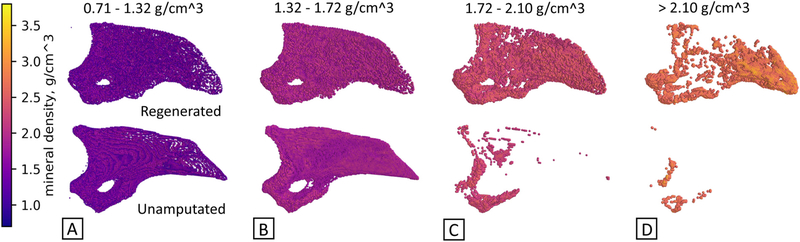
Results show distinct spatial trends in the mineral density for a 6- month old regenerated digit 42 days after amputation versus the unamputated digit (Fig. 2), with intensity representing BMD value. BMD values are categorized into separate groups or bands of mineralization. Four groups were defined and viewed as subplots together, representing the entire digit (Fig. 2a-d). Regenerated digits show a higher mineral content on the distal side of the P3 digit and appear to be concentrated near the surface. Areas of lower mineral content are located towards proximal third of P3. In contrast, unamputated digits show higher mineral content on the ventral/proximal side of the P3 digit, and in a more central area. Areas of lower mineral content are located towards the outer perimeter of P3. This method of analysis not only allows for viewing of spatial distribution and visual compartmentalization of values of mineral density, but also allows the user to focus on the location of a specified range of density values. Short videos of rotating, three-dimensional P3 renderings are available in Supplementary Material.

Fig. 2.

Spatial visualization of mineral density values can illustrate differences in structure. Mineral density groups compare unamputated and regenerated digits across four mineral value ranges, A-D, with intensity scale at left. Regenerated digits show a significantly increased incidence of high mineral content as compared to the unamputated digit, in particular at the distal end. N = 3 UA, N = 3 D42. Representative images shown.

3.3. Distribution of bone mineral density values

The mineralization of bone plays a significant role in determining its structural quality, due to its connection to mechanical properties [53,54]. Our approach incorporates traditional measures of bone mineral density distribution and enables visualization of single digits and comparative analysis of all groups. A quantitative display of mineral density in a single digit as a histogram (seen in Fig. 3a and b for one unamputated digit and one regenerated digit in comparison), where mineral density values are on the x-axis and probability of the value, or incidence rate on the y-axis, reveals new characteristics of the regenerative behavior. We developed a μCT-based approach to study the density value distribution similar to previous work that has analyzed bone mineral density distribution (BMDD) to provide information on mineralized bone tissue [29,30]. Automated processing using python scripting in our approach enables analysis of single digits, digit-to-digit (Fig. 3a). A normal distribution curve was fit to data and used to identify general trends. Single digit density value distribution parallels the spatial density distribution and shows that density values in a regenerated digit versus an unamputated digit have a distribution that is skewed into the higher density values.

Fig. 3.

Mineral density value distribution. A) Single digit histograms compare individual unamputated (UA) and regenerated (D42) digits, showing the probability (frequency) and spread (density value range) of density values. Best fit curve with normal distribution. N = 1 UA, N = 1 D42. B) Right lateral view of full mineral density spectrum for both digits, showing distinctly contrasting spatial distribution of mineral density. N = 3 UA, N = 3 D42. Representative images shown.

Overlapping comparative histogram analysis of the mineral density for a single regenerated digit 42 days after amputation as compared to a single unamputated (control) digit support this observation (Fig. 3a and b). The single regenerated digit has higher incidence of larger density values, with a mean value of 1.490 g/cm³, while the single unamputated digit is more tightly clustered around a mean value of 1.349 g/cm³. This digit-to-digit comparison capability can be expanded to address whole digit group-to-group comparisons (Fig. 4). Comparison of the two groups by fitting a linear mixed model to the BMD values using a fixed effect corresponding to regenerated/unamputated bone status and random effects for each digit showed that unamputated digits had an expected average BMD that was 0.074 g/cm³ (95% CI = 0.034–0.121) less than regenerated digits. This is reflected by the unadjusted BMD means of 1.424 g/cm³ for regenerated digits and 1.349 g/cm³ for unamputated digits.

Fig. 4.

Analysis of mineral density values for all unamputated and all regenerated digits shown as violin plots. Comparison of mineral content distribution between unamputated (UA) and regenerated (D42) digits. N = 1,559,938 values from N = 14 digits, UA. N = 858,333 values from N = 6 D42. Width of violin plot represents probability density.

Distribution of the standard deviations of the bone density data differed between the regenerated and unamputated groups using a Wilcoxon rank sum test (p-value <0.001), indicating that the spread of the BMD values differed significantly between the regenerated and unamputated groups. The mean and range of the density standard deviations for the regenerated group was 0.304 (Range = 0.255–0.341) compared to 0.208 (Range = 0.182–0.268) for the unamputated group. 10/11 unamputated digits had a density standard deviation smaller than all 6 regenerated digits. This indicates that the spread of the BMD values is higher, as visualized in the histogram of a representative digit (Fig. 3a) for regenerated digits than for unamputated digits. These results indicate that the average and standard deviation of the BMD values were significantly lower for unamputated digits than for regenerated digits 42 days after amputation.

3.4. Internal void volume ratios

Regenerated bone in the mouse digit has been previously measured using percent bone volume [4,13–16]. While useful, focus on bone volume ignores analysis of the void space volume where vascularization, soft tissue, and nutrient delivery occur. Additionally, visualization and quantitative analysis of spatial voids in bone using traditional grayscale or binary stacks is often prohibitively difficult, especially in three-dimensional space due to computational cost associated with data at fine resolutions. To overcome these obstacles, we used a combination of image processing and CAD modeling to create a “ghost” image through modification of contrast and transparency (Fig. 5). Inspection of digits shows vascular spaces that extend proximal to distal in a linear fashion are present as extensions of the marrow cavity. After regeneration, these distal vascular spaces take the form of a web-like network, losing some of the proximal to distal directionality (Fig. 5a and b) seen in the unamputated digit (Fig. 5c).

Fig. 5.

Internal visualization of digits. A) Regenerated digit. B) Regenerated digit with internal void structure superimposed for clarity. C) Unamputated digit with internal void structure superimposed for clarity. Internal void structure is darkened for contrast, and colorized (red). N = 3. Representative images shown. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

To quantify changes in bone morphometrics, traditional trabecular bone analysis utilizes “‘trabecular spacing” and “trabecular thickness” values to quantify the bone structure. In the case of native CT-scan analysis software this is often based on a sphere-fitting model and defined by the diameter of a sphere that encloses the point and is also bounded within the solid surfaces [55]. Distance transform methods that identify a medial axis of all structures allow spheres to be fitted for local thickness along this axis, creating thickness measurements for all voxels [56]. These voxel distances are then averaged. This produces a single averaged number for each bone and is optimally designed for spaces that are more akin to traditional trabecular bone patterns, such as that in the head of the femur. This type of analysis does not appropriately address the long, highly variable, vascular-like spaces that are seen in our samples (Fig. 5) and many other non-standard bone samples and produces a single space and thickness diameter (Supplemental Fig. 1A) which does not accurately reflect morphological changes in space volume. While bone volume is frequently utilized as in bone morphometrics (Supplemental Fig. 1B), space volume is not. To better analyze differences in the patterning of the spaces we evaluated the inner void space by calculating a void fraction. Analysis of inner void fraction as a percentage of total volume (void volume + bone volume) shows that regenerated digits have almost 5.5 times the inner void volume (9.1%) of unamputated digits (1.6%), a strong indication that they do not recapitulate the inner void space of the digit (Fig. 6a).

Fig. 6.

Internal void space. A) Inner void fraction. Inner volume as a fraction of void space volume plus bone volume in unamputated (UA) and regenerated (D42) digits for distal volumetric region past the amputation plane. Mean = 0.0167 UA and 0.0913 D42, respectively. N = 14 UA. N = 6 D42. B) Total void space length. Results from measurement of skeletonized inner void space geometry in unamputated (UA) and regenerated (D42) digits also show an increase in internal void length in regenerated mice digits. S.D. = 256.1, and 1378.3, respectively. N = 14 UA. N = 6 D42. Skeletonization of the entire internal void space of digits to evaluate patterning, shown in C-E) regenerated and F–H) unamputated representative digits. Whole bone is shown in green (C,F), inner void geometry shown in red (D,G), skeletonized void geometry shown in blue (E,H), for each representative sample shown (N = 3). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.5. Internal void morphology

In addition to volume we evaluated additional morphological characteristics and patterning to better speak to the web-like patterning of the void space that we see in the regenerated digit. In traditional bone morphometry analysis, Euler connectivity quantifies the number of connections between spaces [57] and is traditionally used to determine connectivity of trabecular spaces. Given that the inner void spaces in these P3 digits may have structures that are elongated with single branching points, which in turn have low connectivity close to 1 due to very few connective paths between parts, we sought to better graphically represent the patterning of the spaces and also employ total length of these spaces to better evaluate the inner void space. The cumulative length of the void space network for each digit was evaluated by applying a modified skeletonization procedure on the internal void volumes to measure and analyze interior patterning trends and providing a total length of skeletonization for each digit. Graphical results show the extent and shape of the entire inner void structure, with the reduction to a three-dimensional skeleton allowing for better visualization and quantification of pattern and length (N = 3, representative sample shown). The ability to quantify total skeleton length of each digit allows comparison of unamputated and regenerated digits that shows that the average total skeleton length of 6-month regenerated digits is almost 4 times larger than that of unamputated digits (approximately 5000 μm to 1300 μm) (Fig. 6b). Results for the regenerated digit at day 42 shows interconnected alignment of void spaces, predominantly in the distal region encompassing a large percentage of the regenerated region (Fig. 6c-e). In contrast, the unamputated digit shows a clear single marrow cavity and single segment extending into the distal tip, with relatively few major branches, and much lower total skeleton length (Fig. 6f-h). Analysis using skeletonization suggests that the regenerated digit is unable to successfully recapitulate the marrow cavity in a way that mimics the original unamputated digit.

4. Discussion

The quantification of bone architecture and mineral density is imperative for developing and confirming improved bone health treatments for both young and aged populations. Use of traditional bone morphometric methods have been integral in analyzing μCT data to describe, quantify, and visualize bone architecture, but these analytical approaches target traditional long-bone analysis such as the femur. These measures often are unable to fully capture the relevant patterns or trends of new bone growth in non-standard bone samples such as those utilized in digit regeneration. With the expanding use of novel and complex bone models in animal research, improved bone analysis methods that can be widely disseminated are needed to quantify and visualize bone architecture in order to more rigorously vet treatments and characterize disease states.

The mouse digit regeneration model highlights limitations in current bone morphology analysis. Traditional measures of bone density or architecture often fail to differentiate between the differences in patterning and structure of regenerated bone. With a new approach presented here, built on semi-automatic methods, we are able to better visualize and quantify variable bone regeneration patterns not previously seen in such detail, which in turn will allow us to better evaluate divergent bone quality outcomes as a result of bone disease and subsequent treatment. Using these methods, we show that 6-month regenerated digits have significantly higher mineral density than unamputated digits with differential spatial distribution of mineral density. This finding is surprising given that bone density is typically a function of time and regenerated bone is limited to 42 days. We also find that the regenerated bone has vastly different void space patterning after regeneration, which encompasses more of the overall regenerated space and does not perfectly mimic the patterning of the original unamputated digit, particularly with regard to the marrow cavity.

Our analysis approach provides both quantitative and visual outputs, both of which are critical in bone evaluation. The flexibility and customization available provides great utility in being able to visualize single sample comparisons and analyze group comparisons. And finally, this approach can be accessed using readily available scripting platforms and open source software. This type of analysis provides a more in-depth and tailored analysis of bone quality outcomes that can be readily disseminated throughout the research community for a more robust evaluation of non-standard bone architecture.

While we utilized the mouse digit regeneration model to showcase differences between regenerated and non-regenerated bone, these new semi-automatic methods may be used for analysis in other applications, both biologic and material-related. Results suggest that partnering engineering analysis and image processing approaches with traditional and non-traditional bone models to quantify new parameters can greatly improve assessments of bone quality and better guide development and outcome analysis of treatments. This work balances semi-automatic image processing with manual modeling techniques and highlights the continuing need for approaches to bulk processing and fully automatic analysis of bone quality using μCT image data.

5. Conclusion

This research shows the application of semi-automatic methods of analysis and visualization used in a novel approach provides key insights into the quality of regenerated mouse bone, and addresses select gaps in traditional methods by targeting quantification of volumetric void spaces, improved internal visualization and analysis of internal void morphology, spatial variation in bone mineralization, and analysis of mineral density value distributions, allowing for better quantification methods that speak directly to the digit regeneration model. The methods utilize Python-based image processing, numerical calculations, and conventional 3D modeling techniques in order to demonstrate new analysis of μCT bone images using an approach that is accessible to the broader bone research community, with Python script files made available on Github: (https://github.com/HLabProjects/RegenBoneAnalysis). Analysis of unamputated and regenerated digits from 6-month old mice and shows significant differences between regenerated and non-regenerated bone in mineral density values, location and statistical distribution, internal void volume ratio, and total internal void development. This approach may offer analytical utility beyond the digit to non-standard bone structures, to those such as the cochlea [36], ectopic bone seen in heterotopic ossification [37], and the long, thin marrow cavities seen in the cranium [38] and long bones [39].

Supplementary data to this article can be found online at https://doi.org/10.1016/j.bone.2020.115776.

Abbreviations:

P3

third/distal phalangeal element

BMD

bone mineral density

UA

unamputated

D42

42 days after amputation

Appendix A

Fig. A1.

Flowcharts of Spatial BMD and pre-skeletonization internal void processing methods. A) Creating 3D, spatial reconstructions of bone mineral density intensity and B) Process to reconstruct internal void volume prior to skeletonization.