Predicting the fMRI Signal Fluctuation with Recurrent Neural Networks Trained on Vascular Network Dynamics

Abstract

Resting-state functional MRI (rs-fMRI) studies have revealed specific low-frequency hemodynamic signal fluctuations (<0.1 Hz) in the brain, which could be related to neuronal oscillations through the neurovascular coupling mechanism. Given the vascular origin of the fMRI signal, it remains challenging to separate the neural correlates of global rs-fMRI signal fluctuations from other confounding sources. However, the slow-oscillation detected from individual vessels by single-vessel fMRI presents strong correlation to neural oscillations. Here, we use recurrent neural networks (RNNs) to predict the future temporal evolution of the rs-fMRI slow oscillation from both rodent and human brains. The RNNs trained with vessel-specific rs-fMRI signals encode the unique brain oscillatory dynamic feature, presenting more effective prediction than the conventional autoregressive model. This RNN-based predictive modeling of rs-fMRI datasets from the Human Connectome Project (HCP) reveals brain state-specific characteristics, demonstrating an inverse relationship between the global rs-fMRI signal fluctuation with the internal default-mode network (DMN) correlation. The RNN prediction method presents a unique data-driven encoding scheme to specify potential brain state differences based on the global fMRI signal fluctuation, but not solely dependent on the global variance.

Introduction

Neural oscillations have been extensively studied in both animal and human brains from cellular to systems levels (Steriade 2001; Buzsáki and Draguhn 2004; Masimore et al. 2004; Muller et al. 2018). Power profiles of EEG signals, as well as slow cortical potentials (SCP), exhibit a slow oscillation feature (<1 Hz), which is related to brain states mediating memory, cognition and task-specific behaviors (Birbaumer et al. 1990; Elbert 1993; He and Raichle 2009). Resting-state functional MRI (rs-fMRI) studies have revealed low-frequency hemodynamic signal fluctuations (<0.1 Hz) (Biswal et al. 1995; Biswal et al. 1997; Cordes et al. 2001; Fukunaga et al. 2006), which have been confirmed by intrinsic optical imaging (Kleinfeld et al. 1998), laser-doppler-flowmetry (Golanov et al. 1994), and near-infrared spectroscopy (Obrig et al. 2000). In particular, specific spatial correlation patterns can be observed in the slow oscillation of the rs-fMRI signal, e.g., the default-mode network (DMN) (Raichle et al. 2001; Greicius et al. 2003; Hampson et al. 2006). Concurrent fMRI and electrophysiology studies have shown a correlation of the fMRI signal fluctuation with the EEG signal power profile and SCP low-frequency oscillations, which are candidates for neural correlates of the rs-fMRI signal (Logothetis et al. 2001; Goldman et al. 2002; He et al. 2008; Shmuel and Leopold 2008; Scholvinck et al. 2010; Pan et al. 2013; Fultz et al. 2019). In addition, the slow oscillation of rs-fMRI and hemodynamic signals from vessels are highly correlated to simultaneously acquired intracellular Ca²⁺ signal fluctuations in rodents (Du et al. 2014; Ma et al. 2016; Schwalm et al. 2017; He et al. 2018; Chen et al. 2020).

Efforts have been made to interpret the functional indications of rs-fMRI spatial correlation patterns, including research revealing a rich repertoire of states and their transitions that constitute the rs-fMRI signal (Chang and Glover 2010; Handwerker et al. 2012; Hutchison et al. 2013; Liu et al. 2013; Liu and Duyn 2013; Hansen et al. 2015; Karahanoglu and Van De Ville 2015; Liang et al. 2015; Chen et al. 2016; Vidaurre et al. 2017; Yousefi et al. 2018), as well as arousal state-dependent global fMRI signal fluctuation studies (Chang et al. 2016; Turchi et al. 2018; Wang et al. 2018). Because of the high variability in different dynamic states, physiological and non-physiological confounding factors also contribute to the rs-fMRI low-frequency oscillation (Birn et al. 2006; Caballero-Gaudes and Reynolds 2017; Pais-Roldán et al. 2018; Tong et al. 2019). In particular, global fMRI signal fluctuations are one of the most controversial oscillatory features to be linked to dynamic brain signals (Fox et al. 2009; Murphy et al. 2009; Hahamy et al. 2014; Murphy and Fox 2017; Power et al. 2017; Billings and Keilholz 2018; Liu et al. 2018; Xu et al. 2018). Efforts have been made to disambiguate the global and vascular signals, to separate the physiological components of the global signal (Glasser et al. 2018) and to remove those components e.g., by using the signal from the white-matter tract as a nuisance regressor (Behzadi et al. 2007; Chang and Glover 2009). Interestingly, the global signal has been tied to behavioral traits (Li et al. 2019) and vigilance (Wong et al. 2013; Wong et al. 2016) of scanned subjects and the global signal fluctuation has been tied to the switching of whole brain spatial patterns (Gutierrez-Barragan et al. 2019). Moreover, simultaneous fMRI and EEG studies in the monkey brain demonstrate a strong linkage of brain state changes to the global rs-fMRI signal fluctuations (Scholvinck et al. 2010). This phenomenon has been observed at the level of single-vessel fMRI dynamic mapping with concurrent calcium recordings (Yu et al. 2016; He et al. 2018; Chen et al. 2019), showing stronger neural correlation from vessel voxels than parenchyma voxels given the highly deoxygen-hemoglobin-based T2^*-weighted contrast-to-noise ratio (CNR) changes (He et al. 2018). This highly coherent vessel-specific fMRI signal fluctuation is a direct signal source that is closely linked to global brain state changes. Here, we applied the artificial state-encoding recurrent neural network system in a prediction scheme to better model the brain state-specific coherent oscillatory features from the vessel voxels.

Recurrent neural networks (RNNs) provide a computational framework for temporally predicting dynamic brain signals. RNNs, through interactions of recurrently connected simple computational nodes (neurons), encode temporal patterns of input signals, i.e., the vessel specific rs-fMRI signals, into internal states. These states are then decoded to generate predictions e.g., using linear weighting. Two example RNN architectures both employing gating mechanisms and trained through backpropagating errors (Linnainmaa 1976; Rumelhart et al. 1988) are the gated recurrent unit (GRU) (Cho et al. 2014) and long short-term memory (LSTM) (Hochreiter and Schmidhuber 1997; Gers et al. 2003) networks. These RNNs have been applied to fMRI data to e.g., model hemodynamic response functions (Güçlü and van Gerven 2017), decode task properties (Li and Fan 2018), identify individuals (Chen and Hu 2018) and integrate behavioral and neuroimaging data in a decision task (Dezfouli et al. 2018). In particular, the artificial neural networks have been used to depict dynamic brain signals over a range of time scales and contexts (Plis et al. 2014; Yamins et al. 2014; Barrett et al. 2018; Hjelm et al. 2018; Wen et al. 2018).

In the present study, GRUs were trained to predict the slow oscillation dynamic changes of the rs-fMRI signal from both rat and human brains. Based on previous single-vessel fMRI studies (He et al. 2018), vessel-specific fMRI signals were used as training data to extract highly correlated neuronal oscillatory temporal features with varied noise profiles. Given the significantly reduced auto-regression features of the slow oscillation after a 10 s lag time, we trained the RNNs to predict the temporal evolution of slow oscillations with the 10 s interval into the future. The trained networks encoded unique temporal dynamic features of the rs-fMRI signal, enabling the differentiation of the global fMRI signal fluctuation from the DMN-specific temporal dynamic patterns in the Human Connectome Project (HCP) data (Van Essen et al. 2012). In particular, in contrast to the global variance analysis, the RNN-based prediction presents a linear association to the strength of DMN-specific network correlation indicating a unique data-driven encoding scheme to specify brain state differences.

Materials and Methods

GRU

Gated recurrent unit (GRU) (Cho et al. 2014) networks are an RNN architecture designed to tackle the vanishing and exploding gradient problems, which prevented effective learning in networks trained using backpropagation. They introduce gating mechanisms that control the flow of information into and out of the GRU units and allow the network to capture dependencies at different time scales in the processed data. The GRU encodes each element of the input single-vessel sequence 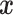into a hidden state vector 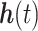by computing the following functions:

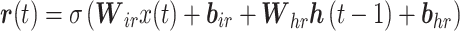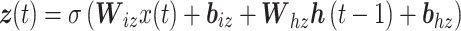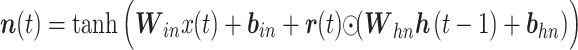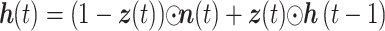where are the sigmoid and hyperbolic tangent functions, 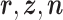are the reset, update and new gates, 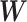are matrices connecting the gates, inputs and hidden states, 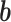are bias vectors and 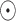is the elementwise product. A linear readout was used to generate the prediction based on the state vector:

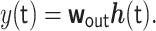The networks were trained in PyTorch (Paszke et al. 2019) and cross-validated across trials. The hyperparameters were found with Bayesian optimization using the tree of Parzen estimators algorithm (Hyperopt toolbox, n = 200) (Bergstra et al. 2011; Bergstra et al. 2013). The optimized hyperparameters have been described in Table 1.

Table 1.

Optimized GRU hyperparameters

Parameter name	Description	Range	Final value (rat | human)
Number of layers	Multiple layers of each of the recurrent units could be stacked on top of each other.	[1; 5]	2 | 1
Hidden size	Size of the hidden state vector.	[10; 500]	290 | 88
Loss function	As the Pearson correlation coefficient (CC) was the final evaluation metric of networks’ performance, it could be used as the cost function instead of the mean squared error (MSE) loss.	[MSE, CC, MSE and CC]	CC | CC
Learning rate	A parameter defining the rate at which network weights were updated during training.	[10−5; 1]	0.001 | 0.00121
L2	Strength of the L2 weight regularization.	[0; 10]	0.0003 | 0.0221
Gradient clipping	Gradient clipping (Pascanu et al. 2013) limits the magnitude of the gradient to a specified value.	[yes; no]	no | no
Dropout	In the case of using a multi-layer RNN, dropout (Srivastava et al. 2014) could be set.	[0; 0.2]	0.128 |—
Residual connection	Employing a residual connection i.e., feeding the input directly to the linear readout alongside the RNN’s hidden state.	[yes; no]	yes | no
Batch size	The number of single-vessel time courses processed by the network in the training stage before each weight update.	[3; 32]	22 | 10
Number of epochs	How many times the network processed the whole training dataset during training.	[1; 100]	87 | 69
Washout time	The number of input signals’ time points used to drive the network into a state that is specific to a given input. These time points are not used for readout training and prediction.	Fixed	250 | 250

ARMAX

The autoregressive-moving-average model with exogenous inputs (ARMAX) (Whittle 1951) was used as a comparative prediction method. ARMAX aims to model a time series using autoregressive, moving-average and exogenous input terms. This is depicted in the equation:

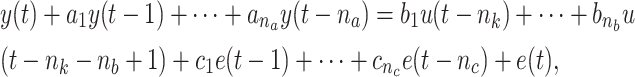where 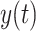is the model’s output at time 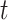; 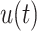is the exogenous input at time 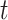; 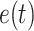is the noise term at time 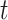; 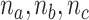are the numbers of model’s past outputs, inputs and error terms that influence the current output; 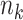is the delay after which the inputs influence the output; 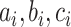are estimated model coefficients. To match the 10 s prediction scheme 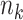was set to 10 and the raw inputs and slow oscillation outputs were not shifted. An extensive grid search was performed to find the 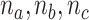values that led to the best predictions. All combinations of 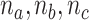values ranging from 1 to 50 with a step of 1 and from 1 to 150 with a step of 5 were evaluated to estimate the model’s coefficients 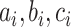. Exactly the same data as in GRU’s case were used for training and evaluation and the best set of 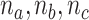values was also found through cross-validation. MATLAB armax and forecast functions were used to find the coefficient values and evaluate the models. The autoregressive model with exogenous input (ARX) and the autoregressive-integrated-moving-average model with exogenous inputs (ARIMAX) were also tested but yielded worse performances, hence are not reported.

Experimental Procedures

All experimental procedures were approved by the Animal Protection Committee of Tuebingen (Regierungsprasidium Tuebingen) and performed in accordance with the guidelines. All human subject experiments follow the guidelines of the regulation procedure in the Max Planck Institute, and the informed consents were obtained from all human volunteers. Single-vessel fMRI data acquired from 6 rats and 6 human subjects have been previously published (He et al. 2018). The rats were imaged under alpha-chloralose anesthesia. For details related to the experimental procedures refer to (Yu et al. 2010; He et al. 2018).

Rat MRI Data Acquisition

The measurements have been performed using a 14.1 T/26 cm horizontal bore magnet (Magnex) interfaced with an Avance III console (Bruker). To acquire the images a 6 mm (diameter) transceiver surface coil was used.

bSSFP rs-fMRI

The balanced steady-state free precession (bSSFP) sequence was used to acquire 2–5 trials of single-slice Blood-oxygen-level-dependent (BOLD) rs-fMRI for every rat. Each run had a length of 15 minutes with a one slice repetition time of 1 s. The bSSFP parameters were: echo time (TE) = 3.9 ms; repetition time (TR) = 7.8 ms; flip angle = 12°; matrix = 96 × 128; field of view (FOV) = 9.6 × 12.8 mm; slice thickness = 400 μm; in-plane resolution = 100 × 100 μm².

MGE A-V Map Acquisition in Rats

To detect individual blood vessels a 2D multi-gradient-echo (MGE) sequence was used. The sequence parameters were: TR = 50 ms; TE = 2.5, 5, 7.5, 10, 12.5 and 15 ms; flip angle = 40°; matrix = 192 × 192; in-plane resolution = 50 × 50 μm²; slice thickness = 500 μm. The second up to the fifth echoes of the MGE images were averaged to create arteriole-venule (A-V) maps (Yu et al. 2016). The A-V maps enable identifying venule voxels as dark dots due to the fast T2^* decay and arteriole voxels as bright dots because of the in-flow effect.

Human MRI Data Acquisition

Data from six healthy adult subjects (male, n = 3; female, n = 3; age: 20–35 years) were acquired using a 3-T Siemens Prisma with a 20-channel receive head coil. BOLD rs-fMRI measurements were performed using an echo-planar imaging (EPI) sequence with: TR = 1000 ms; TE = 29 ms; flip angle = 60°; matrix = 121 × 119; in-plane resolution = 840 μm × 840 μm; 9 slices with thicknesses of 1.5 mm. Image acquisition was accelerated with parallel imaging (GRAPPA factor: 3) and partial Fourier (6/8). Subjects had their eyes closed during each 15 minute trial. Respiration and pulse oximetry were simultaneously monitored using the Siemens physiologic Monitoring Unit.

Data Preprocessing

All data preprocessing was done using MATLAB and the Analysis of Functional Neuro Images (AFNI) software package (Cox 1996). The functional data were aligned with the A-V map using the mean bSSFP template and the 3dTagAlign AFNI function with 10 tags located in the venule voxels. Other details of the preprocessing procedure are reported in a previous study (Zhang et al. 2012). No spatial smoothing was done at any point.

Localization of Individual Veins

To localize venule voxels in A-V maps, local statistics analysis and thresholding were performed using AFNI. First, for each voxel, the minimum value in a 1 voxel-wide rectangular neighborhood was found. Then, the resulting image was filtered with a 10 voxel rectangular rank filter and divided by the size of the filter. Finally, the image was thresholded to create a mask with vein locations. For human data, the mean of EPI time series was used instead of the A-V map.

ICA Identification of Vascular Slow Oscillations

To extract signals only from vessels exhibiting strong slow oscillations an additional independent components analysis (ICA)-based mask was combined with the described above vessel localization method. The functional rs-fMRI data were processed using the Group ICA of fMRI Toolbox (GIFT, http://mialab.mrn.org/software/gift) in MATLAB. First, principal component analysis (PCA) was employed to reduce the dimensionality of the data. PCA output was used to find 10 independent components and their spatial maps using spatial Infomax ICA (Bell and Sejnowski 1995). If a component exhibiting slow oscillations predominantly in individual vessels had been found, it was thresholded and used together with the vascular mask to identify vessels of interest and extract their signals.

Frequency Normalization

To normalize the data, power density estimates of signals’ high-frequency components were used. Every time course had its mean removed and was divided by the mean power spectral density estimate (PSD) of its frequency components higher than 0.2 Hz. The 0.2 Hz point was chosen, as above this value spectra of extracted signals were centered on a horizontal, non-decaying line. Performing the division brought the mean PSD of high-frequency components to a common unit baseline for all signals.

This allowed to better compensate for different signal strengths across trials than when scaling the data using minimal and maximal values. Additionally, the relative strength of flatter signals and those exhibiting stronger low-frequency oscillations was better preserved when compared to variance normalization. Ultimately it also improved prediction performance.

Power Spectrum Analysis

The spectral analysis was performed in MATLAB. To compute the PSDs of utilized signals we employed Welch’s method (Welch 1967) with the following parameters: 1024 discrete Fourier transform points; Hann window of length 128; 50% overlap.

Filtering

To obtain target signals, single-vessel time courses were bandpass filtered in MATLAB using butter and filtfilt functions. The frequency bands (0.01–0.1 for human and 0.01–0.05 for rat data) were chosen based on the PSD curves of single-vessel and ICA time courses.

Surrogate Data Generation

Surrogate data methods are primarily used to measure the degree of nonlinearity of a time series (Theiler et al. 1992). They allow creating artificial time courses that preserve basic statistics of original data like the mean, variance and autocorrelation structure. In this study, Fourier based surrogate signals were generated for each single-vessel time course using the iterative amplitude adjusted Fourier transform (IAAFT) algorithm (Schreiber and Schmitz 1996).

To create a surrogate control, a list of a signal’s amplitude-sorted values and the complex magnitudes of its Fourier frequency decomposition need to be saved. First, the original signal is randomly reordered. The complex magnitudes of the shuffled signal are replaced by the stored values of the original signal with the new phases being kept. This changes the amplitude distribution. To compensate for this, the new signal’s sorted values are assigned values from the stored ordered amplitude distribution of the source signal (the new signal is only sorted for the assignment, its order is restored afterwards). In turn, matching the amplitudes modifies the spectrum, so the complex magnitude and amplitude matching steps are repeated and the modified phases of the resulting signal are kept through iterations.

The iteratively generated signals had the same amplitude distribution as the source data and extremely similar amplitudes of the power spectrum. However, the phases of their complex Fourier components were randomized.

Principal Component Analysis of GRU Hidden States

We used the MATLAB pca function to apply PCA to the network’s hidden states and generate PCA time courses.

Sliding Window Score Signals

For each time point we computed the correlation between the predicted and target single-vessel signal in 30 s windows. The first and last 15 values of each sliding window signal were based on shorter windows due to the window extending beyond available data.

HCP Data—Preprocessing

Data from 4012 15-minute sessions of rs-fMRI acquired by the Human Connectome Project (HCP) (Van Essen et al. 2012) were used to extract V1 signals and compute whole-brain correlation maps. The data set was preprocessed (Glasser et al. 2013; Smith et al. 2013), had artifacts removed via ICA + FIX (Griffanti et al. 2014; Salimi-Khorshidi et al. 2014) and was registered to a common space (Robinson et al. 2014; Glasser et al. 2016) by the HCP. The data were resampled from the original 0.72 s sampling rate to match the 1 s TR of our in-house datasets.

HCP Data—ROI Signal Extraction

The multi-modal cortical parcellations (Glasser et al. 2016) was used to extract 180 region of interest (ROI) signals per hemisphere. The DMN ROI was based on the DMN ROI specified in Yeo et al. (Yeo et al. 2011). Subcortical structures were extracted using the Connectome Workbench (Marcus et al. 2011). The global signal was computed by averaging signals of all cortical voxels.

HCP Data—ICA Parcellations

ICA spatial maps and their corresponding time courses for each rs-fMRI session were obtained from the S1200 Extensively Processed fMRI Data released by HCP. The spatial maps are based on group-PCA results generated using MIGP (MELODIC’s Incremental Group-PCA) (Smith et al. 2014). Spatial ICA was applied to the group-PCA output using FSL’s MELODIC tool (Hyvarinen 1999; Beckmann and Smith 2004). To derive component-specific time courses for each session, the spatial maps were regressed against the rs-fMRI data (Filippini et al. 2009). In this work, we used results from the 15-component decomposition. 4012 rs-fMRI sessions had the ICA results available.

Spatial Correlation Difference Maps Generation

To create a correlation map for one session, the time course of either the V1 ROI, DMN ROI, cortical global mean, DMN ICA or V1 ICA served as the seed which was correlated with all voxel time courses in that session. To generate the difference maps, individual maps of selected sessions were group averaged and subtracted.

Intrinsic DMN Correlation

Intrinsic DMN correlation in an individual trial was computed as the average correlation between the DMN ICA time course and all individual DMN ROI voxel signals.

Cross-Correlation

MATLAB xcorr and zscore functions were used to compute cross-correlation. Lag times were computed between predictions and desired outputs. Positive lags correspond to delayed predictions and negative lags to too early predictions.

Correlation Matrix Spectral Reordering

To change the order of matrix entries so that ROIs with similar whole-brain correlation patterns were clustered together, a Laplacian-based spectral reordering method was used (Barnard et al. 1995).

Statistical Tests

The statistical significance of the difference between real/surrogate and GRU/ARMAX prediction scores was verified using a paired t-test (MATLAB ttest function). To determine differences between seed-based correlation maps and PSDs two-sample t-tests were applied (MATLAB ttest2 function). Fisher’s z-transform has been applied to all correlation values before conducting statistical tests. The results have been controlled for false discovery rate with adjustment (Benjamini and Hochberg 1995; Yekutieli and Benjamini 1997). P values < 0.05 were considered statistically significant.

Results

Two datasets were used in our study, one from rats and another from humans. First, we trained a GRU to encode temporal dynamics of BOLD-fMRI signals from vessel voxels in anesthetized rat brains to estimate the prediction efficiency. Second, we trained another GRU to predict the slow oscillation of fMRI signals from occipital lobe sulcus veins of awake human subjects and applied the GRU trained on human data to classify the brain-state changes from rs-fMRI data acquired by the Human Connectome Project (HCP). We compared the GRU results with the predictions of autoregressive moving average with exogenous input modeling (ARMAX) (Whittle 1951; Box 1976). Lastly, we specified the RNN prediction-based DMN activity classification of the HCP datasets, showing a unique brain state encoding scheme, different from the global variance-based approach.

Extracting Slow Oscillatory Features of the Single-Vessel fMRI Signal from Rat Brains

We used recordings obtained from the balanced steady-state free precession (bSSFP) sequence (Scheffler and Lehnhardt 2003) on single-vessel fMRI data from anesthetized rats (He et al. 2018). Arteriole-venule (A-V) maps based on the multi-gradient-echo (MGE) sequence were acquired to localize individual venules penetrating the cortex, which were shown as dark dots due to the fast T2^* decay of the deoxygenated blood (Fig. 1A) (Yu et al. 2016). After registering functional data with the A-V map, fMRI time courses from individual venules were extracted and analyzed using independent component analysis (ICA) (Bell and Sejnowski 1995; Mckeown et al. 1998; Calhoun et al. 2009). Figure 1B shows the time series of the largest ICA component, which is dominated by the low frequency fluctuation (<0.1 Hz). The superposition of this ICA component with the single-vessel fMRI signal fluctuation on the A-V map overlapped with venule-dominated patterns (Fig. 1C). Figure 1D shows the raw bSSFP-fMRI signal fluctuation from three venules, as well as their power spectral density (PSD) plots. These data presented highly coherent oscillatory features of single-vessel fMRI signals, which can be used as a training set. It is important to note that this coherent oscillation of vessel-specific rs-fMRI signals is strongly correlated to the concurrent calcium transients, showing brain state-dependent dynamic fluctuation (He et al. 2018).

Figure 1.

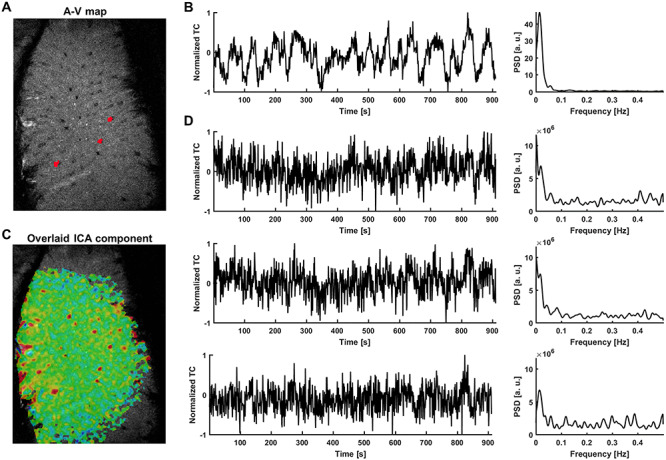
Extraction of signals from single venules exhibiting strong slow fluctuations—rat. (A) The A-V map enables localization of single venules (dark dots) in the rat somatosensory cortex (red—3 vessel masks; plotted in D. (B) Time course of the slowly changing ICA component shaping vascular dynamics and its PSD. (C) The corresponding ICA spatial map highlights the presence of slow fluctuations predominantly in veins. (D) Examples of extracted vascular time courses selected for further processing (marked as red dots on the A-V map in A along with their PSDs. The ICA component is present in the signals, but the noise level is much higher and individual differences are clearly visible.

Supervised Training of the GRU-Based Prediction of the fMRI Slow Oscillation

Figure 2A illustrates the data-driven training scheme for the RNN-based prediction of the rs-fMRI signal fluctuation. The single-vessel fMRI signals showing a strong slow oscillatory correlation (Fig. 1) were used as input time series for the supervised training. The targets of the output were bandpass-filtered fMRI signals from the voxels of the same vessel with a 10 s time shift. The 10 s time shift was selected as the autocorrelation of both rat and human signals is largely reduced at the 10 s lag (Supplementary Fig. 1). Pearson correlation analysis was performed to estimate the correlation coefficient (CC) between GRU’s output predictions and the filtered target signals, to measure the RNN’s performance. We used Bayesian optimization and cross validation to find the set of hyperparameter values that produced the best performing network, see details in the Methods section).

Figure 2.

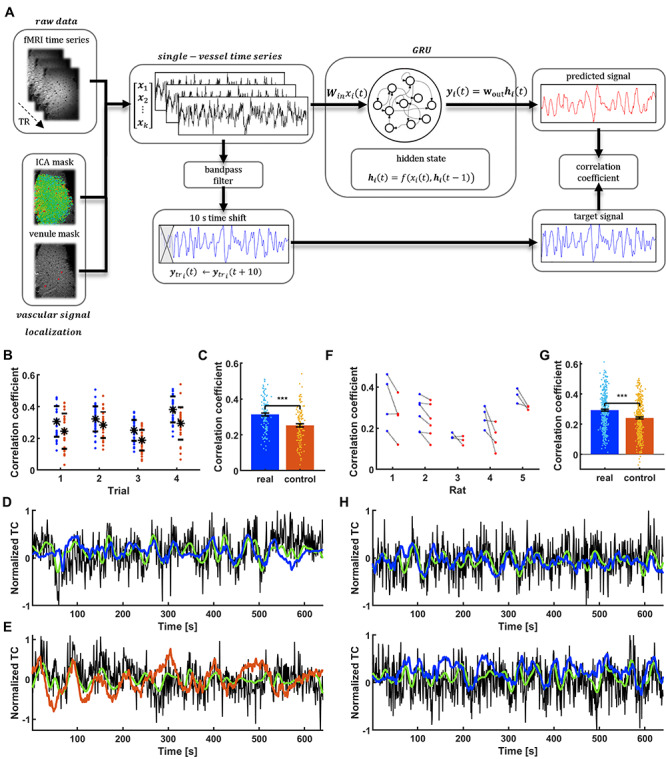
GRU prediction of the spontaneous slow fluctuation of rat vascular dynamics. (A) Prediction system operation pipeline. Raw vascular data are extracted from fMRI data using venule and ICA masks and are fed into the GRU. They are also bandpass filtered and shifted by 10 s to become target outputs of the network. The reservoir encodes the temporal dynamics of input signals into state vectors. The decoder interprets these states and generates a prediction of the slow fluctuation’s value 10 s ahead. After generating the full predicted time series, it is compared with the target output using Pearson’s correlation coefficient. (B) Prediction scores of all the signals extracted from a single rat (blue dots) ordered by trials. Real data are matched with controls (red dots) for every vessel. Black dots show mean scores across trials and bars are SD values. (C) Significantly higher mean of training rat real data prediction scores (CC = 0.31 ± 0.01 SEM) compared to controls (CC = 0.25 ± 0.01 SEM; paired-sample t-test, P = 3.7^*10^–10). (D) The signal from a single vessel with the best prediction score (CC = 0.51, t_lag = −1 s; black—raw data, green—target signal, blue—network prediction). (E) Surrogate signal created to match the real vascular signal shown in D (CC = 0.41, t_lag = −4 s; black—raw data, green—target, red—network prediction). (F) Mean prediction scores for trials extracted from five rats (blue) and their corresponding controls (red). (G) Significantly higher mean of different rats’ real data prediction scores (CC = 0.29 ± 0.01 SEM) than controls (CC = 0.24 ± 0.01 SEM; paired-sample t-test, P = 6.4^*10^–24). (H) Predictions of single-vessel signals from two different rats (v₁, CC = 0.51, t_lag = 0 s; v₂, CC = 0.52, t_lag = 0 s).

GRU-Based Single-Vessel fMRI Slow Oscillation Prediction in Anesthetized Rats

We first illustrate the predictive capacity of the trained GRU by analyzing correlation coefficients across all cross-validation tests. Figure 2B demonstrates the CC of the slow oscillation prediction of all vessels from a representative rat. For each vessel, we generated a surrogate control time course that mimicked the frequency power profile of the fMRI signal. To differentiate the control dataset from true brain dynamic signals, we randomized the phase distribution of its frequency components (Theiler et al. 1992; Schreiber and Schmitz 1996) (Supplementary Fig. 2, see Methods). The GRU prediction performance showed significantly higher mean CC for fMRI data (P = 3.7^*10⁻¹⁰; CC = 0.31 ± 0.01 SEM) than surrogate controls (CC = 0.25 ± 0.01 SEM) (Fig. 2C). Figure 2D shows the predicted time course from the vessel with the highest prediction score (CC = 0.51, t_lag = −1 s) in contrast to the surrogate control signal corresponding to the same vessel (CC = 0.41, t_lag = −4 s). This shows that the trained GRU was better at predicting the fMRI signal fluctuations.

In addition, the GRU trained on one rat was used to predict the fMRI fluctuation of five different rats. Figure 2F demonstrates trial-specific plots of mean CCs from all vessels in comparison to their surrogate controls (380 vessels from 5 rats), showing significantly higher CC of the fMRI signal (P = 6.4^*10⁻²⁴; CC = 0.29 ± 0.01 SEM) than that of surrogate controls (CC = 0.24 ± 0.01 SEM; Fig. 2G). Figure 2H shows predicted slow oscillatory time courses of two vessels from different rats based on the trained GRU (v₁, CC = 0.51, t_lag = 0 s; v₂, CC = 0.52, t_lag = 0 s). These results indicate that the fMRI signal fluctuation can be predicted by the trained RNN.

GRU-Based Single-Vessel fMRI Slow Oscillation Prediction in Awake Human Subjects

As previously reported (Barth and Norris 2007; He et al. 2018), the fMRI signal from sulcus veins of the occipital lobe demonstrated highly correlated slow-oscillatory features (Fig. 3). The vein-specific rs-fMRI signal fluctuations were recorded with high-resolution EPI-fMRI with 840 x 840 μm in-plane resolution and 1.5 mm thickness (Fig. 3A, veins are dark dots) and analyzed with ICA. The largest vascular ICA component exhibited slow oscillatory fluctuations in the 0.01–0.1 Hz frequency range (Fig. 3B) and its correlation map primarily highlighted the individual sulcus veins in the EPI image (Fig. 3C). Figure 3D shows raw fMRI time courses from two sulcus veins, demonstrating the vessel-specific time courses and PSDs with varied noise contributions to different veins. Differences between species are visible in the PSDs. A significantly wider range of frequencies contribute strongly to time courses extracted from human vessels compared to rat data (Supplementary Fig. 3, human_FWHM: 0.031 ± 0.01 Hz; rat_FWHM: 0.008 ± 0.001 Hz, P = 0.001). These results also enable the use of the GRU to encode the slow oscillation based on the vessel-specific fMRI signals from human brains.

Figure 3.

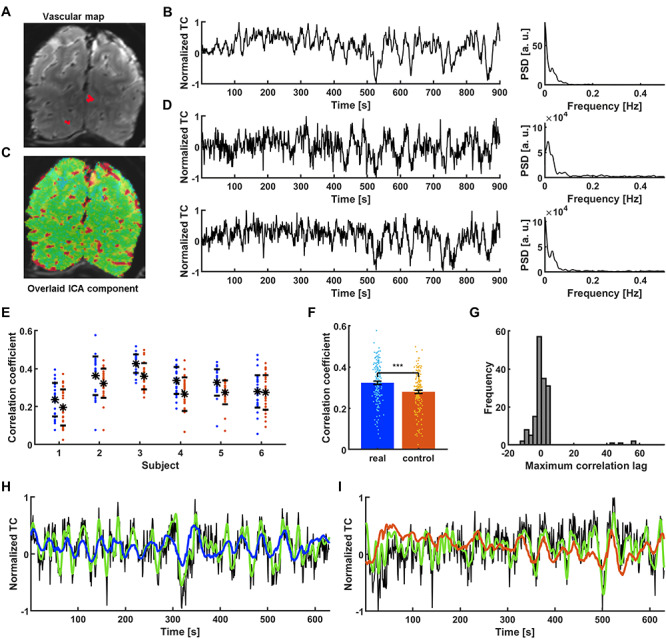
Extraction and prediction of the spontaneous slow fluctuation of human vascular dynamics. (A) The temporal mean of a human single-vessel EPI slice enables the localization of single veins (black dots) in the occipital cortex (red—3 vessel masks; plotted in D. (B) Time course of the slowly changing ICA component shaping vascular dynamics and its PSD. (C) An ICA spatial map highlights the presence of slow fluctuations predominantly in sulcus veins. (D) Two single vessel time courses selected for further processing (marked as red dots in A along with their PSDs. The ICA component is present in the signals, along with individual variations. (E) Prediction scores of all the signals extracted from 6 human subjects (blue dots). Real data are matched with controls for every subject (red dots). (F) Significantly higher mean prediction score of real data (CC = 0.32 ± 0.01 SEM) as compared to controls (CC = 0.28 ± 0.01 SEM; paired-sample t-test, P = 1.6^*10^–13). (G) Histogram of lags at which the correlation between target outputs and network predictions was the highest. Distribution centered around 0 s (median = 0 s) indicates that the prediction was not simply the filtered input. (H) Prediction plot of the signal that obtained the highest score among all training human vessels (CC = 0.58, t_lag = −1 s; black—raw data, green—target, blue—network prediction). (I) Prediction plot of the surrogate control signal created based on the real vascular signal shown in H (CC = 0.50, t_lag = 61 s; black—raw data, green—target prediction, red—network output).

In contrast to the multi-trial single-vessel rat fMRI studies, only one trial (15 min) was acquired from each human subject (159 veins from 6 subjects). To perform the supervised training, we designed the 5 + 1 cross-subject validation process (trials from 5 subjects were used for training, and the sixth trial was used for test validation). Specific surrogate control time courses were created based on PSD profiles of fMRI signals acquired from individual veins in the human brain. Using the trained RNN, higher CC values were obtained by predicting slow oscillatory fMRI signals of individual veins compared to their surrogate controls (P = 1.6^*10⁻¹³; Fig. 3E), demonstrating a significantly higher mean CC value for brain dynamic signals (CC = 0.32 ± 0.01 SEM) than for control datasets (CC = 0.28 ± 0.01 SEM) (Fig. 3F). Also, the histogram of cross-correlation lag times of the predicted and reference time courses showed a median of the lag time equal to 0, demonstrating the effective prediction (Fig. 3G). Figure 3H shows an example of a predicted slow oscillatory time course from a human subject based on the trained RNN (CC = 0.58, t_lag = −1 s). Figure 3I shows the less accurate performance of the matching surrogate control (CC = 0.50, t_lag = 61 s). These results demonstrate the GRU-based cross-subject prediction of slow oscillatory fMRI signals.

To inspect the trained network, we applied PCA to the hidden states of the human data-based GRU. Time courses associated with the first component were highly correlated with network inputs. The second component’s signals mostly resembled the generated prediction. Interestingly the third component correlated with the sliding-window score signal (Supplementary Fig. 4A). Trajectories of the hidden states in the space defined by the three components seem to be contained on a two dimensional manifold. Different regions of the manifold appear to correspond to the quality of generated predictions (Supplementary Fig. 4B). To investigate to which oscillatory features the trained networks were most sensitive, the trained RNNs predicted artificial time courses with a range of peak frequencies and spectral widths (Supplementary Fig. 5A and B). The predicted spread of the signal spectra preference for GRU_human was greater than for GRU_rat as shown in the two-dimensional graphs of peak vs. width of the CC distribution (Supplementary Fig. 5C and D). These species differences may reflect the difference in their rs-fMRI. Interestingly, the harmonic patterns had negative correlations for the preferred frequency, which could be a consequence of the trained RNNs favoring the dominating frequency ranges with the 10 s prediction interval.

GRU-Based Prediction of the fMRI Slow Oscillation in the Visual Cortex (V1) of HCP Data

Previously, we showed that smoothed single-vessel rs-fMRI correlation maps mimic conventional correlation maps in the human occipital area (He et al. 2018). As shown in the PSD plots (Fig. 3), the vessel-specific fMRI slow oscillation dominates the 0.01–0.1 Hz frequency range. To examine whether the GRU trained by the single-vessel fMRI scheme can be used to predict fMRI slow oscillations of a broader range of datasets, we applied the trained GRU to predict the rs-fMRI signals from the V1 of HCP data (a total of 4012 rs-fMRI sessions; V1 signal extracted from left and right hemispheres separately, yielding 8024 time courses resampled at 1 s TR, details in the Methods section). To examine the predictive capacity of the GRU on each trial of the HCP dataset, the CCs of all prediction trials were plotted in a histogram. The CC distribution resembled a normal distribution centered on 0.29 (median) (Fig. 4A).

Figure 4.

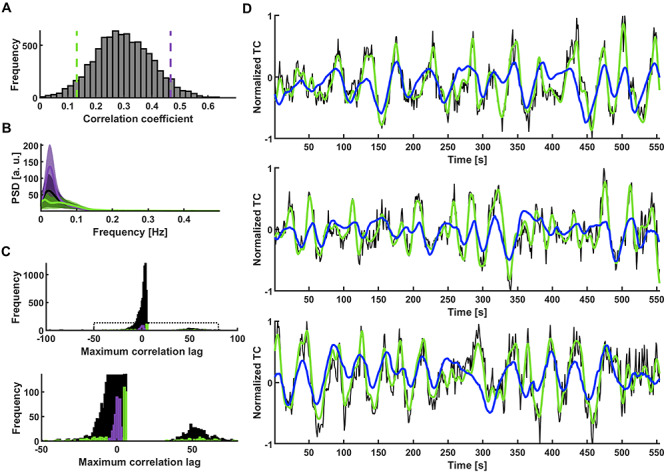
GRU categorization of V1 temporal patterns. (A) Histogram of prediction scores obtained by predicting slow fluctuations of 8024 single-hemisphere V1 ROI signals extracted from HCP data. The used GRU was trained on occipital cortex single-vessel signals of 6 in-house subjects. Green and violet dashed lines mark the bottom and top 5% of correlation coefficients. (B) Mean PSDs of time courses whose predictions obtained the bottom 5% (green) and top 5% (violet) scores. Shaded areas show SD. (C) Histogram of lags at which the correlation between targets and network outputs was the highest. The lags of top 5% of the predictions (violet) are concentrated around 0. The lags of bottom 5% (green) are spread across the highest and lowest lag values. Bottom: Enlarged region marked on the top plot. (D) Predictions of signals with three of the best correlations (CC₁ = 0.64, _tlag,1 = −1 s; CC₂ = 0.62, _{tlag, 2} = 1 s; CC₃ = 0.62, _{tlag, 3} = −1 s; black—raw data, green—target, blue—network prediction).

To specify the rs-fMRI signal temporal dynamics based on the prediction scores, we first selected two clusters of HCP sessions based on the top and bottom 5% CC scores of the overall histogram distribution (Fig 4A). The top 5% trials showed much higher power levels than the bottom 5% trials at the 0.01–0.1 Hz frequency range (Fig. 4B). The lag time distribution of the top 5% group is centered at zero, unlike the bottom 5% group covering the whole range of lag values (Fig. 4C). In particular, many lag values of the poorly predicted sessions show a delay of more than the full wavelength of GRU’s preferred frequency. Figure 4D shows three predicted slow oscillatory time courses from the HCP rs-fMRI sessions (top 5% group) (CC₁ = 0.64, t_lag,1 = −1 s; CC₂ = 0.62, t_lag,2 = 1 s; CC₃ = 0.62, t_{lag, 3} = −1 s). The predictions of the GRU were dominated by the low-frequency power in the rs-fMRI signals from individual trials.

Next, to verify the specific classification of the low-frequency rs-fMRI signal fluctuation by the RNN-based prediction, we compared the GRU predictions with those of ARMAX modeling. The best ARMAX models were found using an exhaustive grid search (see Methods). The RNN prediction scheme presented better performance than ARMAX modeling on our in-house datasets (Human: CC_GRU = 0.32 ± 0.01, CC_ARMAX = 0.30 ± 0.01; Rat: CC_GRU = 0.3 ± 0.01, CC_ARMAX = 0.26 ± 0.01; mean ± SEM) (Fig. 5A), as well as on the HCP datasets (Fig. 5B). In addition, different trials obtained the best and worst scores between the methods (Fig. 5C), as the sensitivity to low frequency oscillations was much less pronounced by the ARMAX modeling (Fig. 5D). These results confirmed the reliability of the RNN-based rs-fMRI signal predictions.

Figure 5.

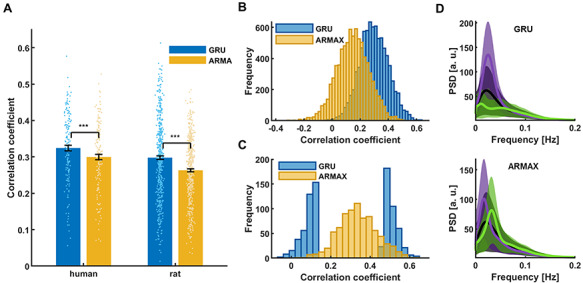
Comparison of different methods’ prediction results. (A) Mean prediction scores of all in-house human and rat vessel signals obtained using the best GRU and ARMAX models. Significantly higher scores (paired-sample t-test, phuman = 8.9^*10^–9, prat = 1.9^*10^–20) obtained by the RNN than ARMAX in both human (CC_GRU = 0.32 ± 0.01; CC_ARMAX = 0.30 ± 0.01; mean ± SEM) and rat cases (CC_GRU = 0.30 ± 0.01; CC_ARMAX = 0.26 ± 0.004; mean ± SEM). (B) GRU and ARMAX histograms of prediction scores of 8024 single-hemisphere V1 ROI signals extracted from HCP data. ARMAX predictions are much worse than those of the GRU. (C) GRU scores of sessions with the 5% best and worst predictions obtained by the both methods. The groups show little overlap. (D) Mean PSDs of time courses whose predictions obtained the bottom 5% (green) and top 5% (violet) scores (top—GRU; bottom—ARMAX). Shaded areas show SD. ARMAX shows less sensitivity to low-frequency power compared to the RNN.

RNN-Based Brain State Classification of HCP Data

Here, we investigated the DMN internal correlation, as a brain state marker of the HCP datasets based on the RNN prediction scores. First, we analyzed whole-brain correlation patterns of the HCP dataset, initially focusing on datasets with the top and bottom 5% GRU predictions. Figure 6 shows flattened cortical difference maps of seed-based correlations calculated for the two groups of HCP datasets. First, rs-fMRI time courses from the V1 ROI and the whole cortex (global mean) were used as seeds to calculate voxel-wise correlation maps. The V1 ROI and global mean-based differential maps of the two groups show similar patterns, demonstrating much more synchronized activity across the cortex in the group with top 5% predictions (Fig. 6A). Based on the global characteristic of the differences, we computed correlation matrices based on 360 ROIs predefined in the brain atlas (Glasser et al. 2016) as well as 19 subcortical ROIs defined using the Connectome Workbench (Marcus et al. 2011). The hippocampus and the brainstem were two subcortical regions which have shown the strongest increase in global correlation (Supplementary Fig. 6B). Importantly, we found that the DMN nodes formed a major cluster of regions that did not show the increase across the groups (Supplementary Fig. 6A). We followed this result and created the cortical correlation difference map using DMN ROI signals as seeds. Interestingly, although the DMN-ROI also shows higher correlation with the whole brain in the top 5% group, the internal correlations of the DMN-specific nodes do not show significant differences (Fig. 6A, the difference between correlations inside and outside of the DMN is significant, P = 1.52^*10⁻¹²⁷). Representative seed time courses of four subjects from each group are shown in Supplementary Figure 7.

Figure 6.

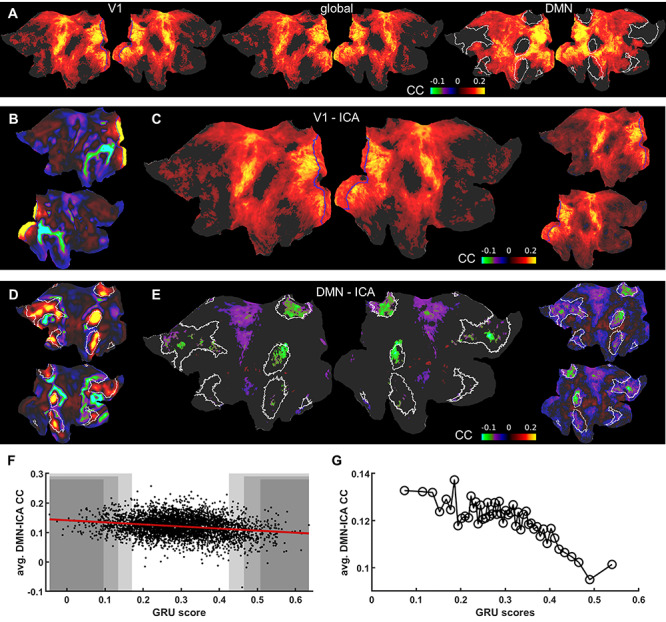
Difference maps for ICA seed-based correlation between well and poorly predicted fMRI sessions. (A) Flattened cortical maps showing the difference between the mean seed-based correlation maps of the 5% “top” and “bottom” groups. The seed signals were: the V1 ROI (left; V1 marked by blue borders), mean global cortical signal (center) and the DMN ROI (right; DMN marked by white borders). (B) V1 ICA component spatial map. V1 ROIs are marked by blue borders. (C) Flattened cortical map showing the difference between the mean seed-based correlation maps of the 5% “top” and “bottom” groups. The time course of the ICA component shown in B served as the seed. V1 ROIs are marked by blue borders. The result resembles the pattern in A obtained by using the V1 ROI as the seed. Nodes in which the difference was insignificant are masked. The same map is shown on the right without the threshold. (D) DMN ICA component spatial map. DMN ROIs are marked by white borders. (E) Flattened cortical map showing the difference between the mean seed-based correlation maps of the 5% “top” and “bottom” groups. The time course of the ICA component shown in D served as the seed. DMN ROIs are marked by white borders. Nodes in which the differences were insignificant are masked (threshold at P = 0.05). The intrinsic DMN signals show significantly reduced connectivity with DMN areas. The same map is shown on the right without the threshold. (F) GRU scores of all trials plotted against mean correlations of DMN voxels. Shaded areas cover the top and bottom 2% (dark), 5% and 10% (light) of all scores. (G) GRU scores of all 4012 trials averaged in 2% bins and plotted against mean correlations of DMN voxels.

To further investigate the relationship between the internal DMN correlations and the RNN prediction scores, we used ICA component time courses of the V1 area and of the DMN network to analyze the differential maps (Fig. 6B-E). Figure 6C shows that the visual ICA-based map resembled the V1 ROI seed-based differential map, demonstrating a higher correlation feature in the group with the top 5% CC scores. In contrast, as the DMN ICA time courses show a very small global signal content (mean global signal and DMN ICA signal correlation = −0.09+/−0.14 across all trials), significantly reduced internal DMN correlations were observed in the differential map when comparing the top vs. bottom 5% trials (Fig. 6D and E). To provide a holistic perspective of the RNN prediction scores and brain state relationship, we plotted the internal DMN connectivity as a function of the RNN prediction scores for all individual trials of the HCP datasets. The internal DMN correlations were decreasing as the prediction scores increased (Fig. 6F and G). This linear relationship of RNN prediction scores and internal DMN activity demonstrates a unique classification scheme to differentiate brain-state dependent rs-fMRI signal fluctuations in the HCP dataset.

Despite the strong linkage to the low frequency power of the rs-fMRI signal, the RNN-based prediction is not simply based on the variance of the rs-fMRI signal fluctuation. By applying a similar analysis scheme, we also classified the HCP datasets based on the variance of the global rs-fMRI signal. Interestingly, the identified groups of sessions with top vs. bottom 5% global signal variance do not show highly distinct GRU prediction CC scores and vice versa (Fig. 7A-C). In particular, the top and bottom 5% variance groups had much broader CC_GRU values and largely overlapped each other in the histogram plot (Fig. 7A). Trials with the bottom 5% of GRU predicted CC scores tend to have lower global signal variance, but they overlap with variances of trials with the top 5% scores which cover the whole range of variance values (Fig. 7C).

Figure 7.

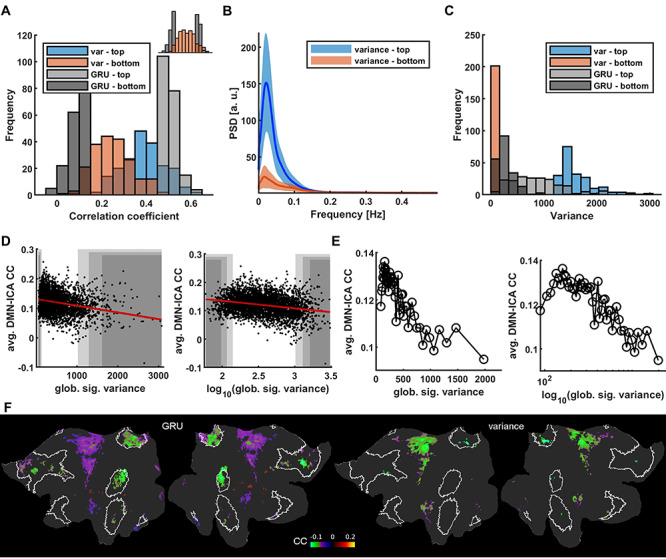
Differences of RNN scores and global signal variance as indicators of intrinsic DMN activity. (A) Prediction score histograms of the 5% best (light gray) and worst (dark gray) predicted sessions contrasted with prediction scores of signals with top 5% highest (blue) and lowest (red) variance. Variance levels are not conclusive of GRU’s performance. Top right: same data with top and bottom groups merged. (B) Mean PSDs of V1 signals from sessions with the top 5% highest (blue) and lowest (red) global signal variance. Shaded areas show standard deviations. The low power difference is more profound than in the RNN score based case (Fig. 4B). (C) Histogram of variance-based (red and blue) and GRU-based (gray) group variance values. Variances of signals having high or low prediction scores are distributed across the whole range of variance values. (D) Global signal variance and its logarithm of all trials plotted against mean correlations of DMN voxels. Shaded areas cover the top and bottom 2% (dark), 5% and 10% (light) of all scores. (E) Global signal variance and its logarithm of all 4012 trials averaged in 2% bins and plotted against mean correlations of DMN voxels. At low variance values the DMN correlations decrease breaking the trend. (F) Flattened cortical maps showing the difference between the mean DMN-ICA seed-based correlation maps of the 5% “top” and “bottom” groups based on GRU scores and global signal variance values. DMN ROIs are marked by white borders. Nodes in which the differences were insignificant are masked. The intrinsic DMN signals show significantly reduced connectivity with DMN areas.

To further understand the issues of the global variance relationship with the internal DMN correlation, we also plotted the DMN correlation values as a function of variance for all trials of the HCP datasets, showing a much more condensed distribution at the low variance ends in the linear scale plot (Fig. 7D and E). The negative correlation feature can be better depicted in the logarithmic scale plot, but, interestingly, this relationship breaks at low variance values, as for the lowest variance values the DMN correlations decrease (Fig. 7E). Thus, the variance-based differential maps of the top vs. bottom 5% trials also show much less DMN node-specific patterns than the RNN-based prediction (Fig. 7F). In particular, the RNN prediction-based differential maps highlighted the DMN nodes, e.g., the inferior parietal lobe and posterior cingulate and retrosplenial cortex. In contrast, the variance-based map is much less specific to the internal DMN nodes, but spread more to the somatomotor cortex as demonstrated in the flattened map (Fig. 7F). These results indicate that the RNNs trained with vessel-specific rs-fMRI signals encode specific brain state differences, which are not simply explainable by the variance of the rs-fMRI signal fluctuation.

Discussion

We used the time courses of single-vessel rs-fMRI signals as inputs to train RNN networks to predict the rs-fMRI signal 10 s ahead in both rodents and humans. We also showed that the single-vessel fMRI-based training leads to an RNN encoding specific to low-frequency rs-fMRI signal fluctuations. The trained network was used to analyze HCP datasets with diverse brain states. In particular, it allowed identifying trials, showing unique brain-wide synchrony and to decouple the global signal fluctuations from internal DMN correlations.

We selected the input fMRI time series from individual vessel voxels based on a previously established single-vessel fMRI mapping method (Yu et al. 2016; He et al. 2018; Chen et al. 2019). The BOLD fMRI signal has a direct vascular origin based on the oxy/deoxy-hemoglobin ratio changes (Bandettini et al. 1992; Kwong et al. 1992; Ogawa et al. 1992). The high-resolution single-vessel mapping method allows us to directly extract the venule-dominated BOLD signals with a much higher contrast-to-noise ratio (CNR) than the conventional EPI-fMRI integrating the BOLD signal from both tissue and vessels in large voxels (Menon et al. 1993; Zhang et al. 2012; Yu et al. 2016; He et al. 2018). Although different vessel voxels may present cardiorespiratory noises, e.g., the respiratory volume change (Birn et al. 2006; Birn et al. 2008) or the heartbeat variability (Shmueli et al. 2007; Napadow et al. 2008), a recent simultaneous fMRI and fiber-optic calcium recording study showed a strong correlation of the major ICA vascular component of the rs-fMRI signal fluctuation (Fig. 1) with the calcium signal oscillation (He et al. 2018). Also, these global hemodynamic signal changes are directly correlated with the calcium signal fluctuation through the whole cortex based on optical imaging (Du et al. 2014; Ma et al. 2016; Schwalm et al. 2017; Chen et al. 2020). Thus, the global fMRI signal fluctuation detected from individual vessels represents changing brain states, and not the non-physiological confounding artifacts uniformly distributed through the brain, e.g., the respiration-induced B0 offset (Van de Moortele et al. 2002; Pais-Roldán et al. 2018) or other sources (Murphy et al. 2013; Caballero-Gaudes and Reynolds 2017). In comparison to the voxel-wise or ROI-based time courses from low-resolution EPI images or signals extracted from the biggest major vessels (Tong et al. 2018; Colenbier et al. 2020), the single-vessel rs-fMRI signal provides highly selective datasets for the supervised RNN training to encode brain-state dependent global fMRI signal fluctuations.

The GRU prediction has been analyzed in a great detail from rodent to human rs-fMRI data. The predictions from the trained GRUs vary across vessels as well as across trials. To validate this measurement, we used surrogate controls designed using the IAAFT method (Schreiber and Schmitz 1996). For every vessel, we generated an artificial signal showing a similar frequency power profile (Supplementary Fig. 2) to its corresponding single-vessel rs-fMRI time course, but with randomized phases of complex Fourier components. It has been shown that high-frequency EEG power profiles are highly correlated to the low-frequency EEG signal fluctuation, i.e., phase-amplitude coupling (PAC), in both cortical and subcortical regions for a variety of brain states (Bragin et al. 1995; Steriade et al. 2001; Vanhatalo et al. 2004; Canolty et al. 2006; Fell and Axmacher 2011; Pais-Roldan et al. 2019). This feature has also been used for the correlation analysis of the concurrent EEG and rs-fMRI signal recordings from animals and humans (Goldman et al. 2002; Goense and Logothetis 2008; He et al. 2008; Shmuel and Leopold 2008; Scholvinck et al. 2010; Magri et al. 2012; Murta et al. 2017). Our analysis confirms that the phases of the slow oscillatory rs-fMRI signal carry critical dynamic brain state features (Muller et al. 2018). By randomizing the phases, the surrogate control excludes dynamic brain features but preserves a high similarity in terms of the signal amplitude/power spectral distribution and autocorrelation structure for the verification of the RNN encoding. Also, the spectral characteristics of the GRUs demonstrate different preference maps in terms of the center frequency and the bandwidth depending on the training data from either rat or human data (Supplementary Fig. 5). These training data showed differences in frequency power profiles given the inter-species diversity (de Zwart et al. 2005) and the presence of anesthetics (Du et al. 2014; Ma et al. 2016; Akeju and Brown 2017; Mateo et al. 2017; He et al. 2018; Wu et al. 2019).

The global rs-fMRI signal is a critical confound of correlation analysis with many contributing factors from both physiological and non-physiological sources. In particular, whether the global mean fMRI signal should be removed before the analysis, which can create spurious correlation features, has been debated (Fox et al. 2009; Murphy et al. 2009; Hahamy et al. 2014; Murphy and Fox 2017; Power et al. 2017; Billings and Keilholz 2018; Xu et al. 2018; Colenbier et al. 2019). Also, the global rs-fMRI signal can over-shadow specific intrinsic RSN features, e.g., the anti-correlation of the DMN and task-positive RSNs (Fox et al. 2005; Hampson et al. 2010; Chen et al. 2017). One intriguing observation based on the RNN predictions is that the internal DMN connectivity is negatively correlated to the prediction scores across trials (Fig. 6D and E), which is opposite to the positive global correlation observed through the whole brain (Fig. 6A-C). Both the global signal strength (Wong et al. 2013; Wong et al. 2016) and the intrinsic DMN correlations (De Havas et al. 2012; Ward et al. 2013) have been tied to arousal mediated brain states and the RNN scores reflect a gradient on this arousal axis (Fig. 6F-G). It is noteworthy that while the global signal variance is also tied to the brain state, its relationship with the internal DMN connectivity is not linear (Fig. 7D) and it stops being a good indicator for trials with low variance values. Consequently, the variance-based differential maps show less DMN specificity, but more widespread differences in the somatomotor cortex (Fig. 7D and E). Thus, the RNN-based approach reveals brain-state specific rs-fMRI signal fluctuations in the HCP datasets.

The contrast between internal DMN correlations and whole brain correlation patterns supports other sources of evidence that the global signals are dissociated from intrinsic brain network correlations (Turchi et al. 2018). Turchi et al. showed that the global rs-fMRI signal fluctuation can be directly modulated by inhibiting the activity of the basal forebrain nuclei, indicating that arousal leads to global rs-fMRI signals (Turchi et al. 2018). Global rs-fMRI signal fluctuations are also correlated with whether the eyes are open or closed (Yang et al. 2007; McAvoy et al. 2008; Bianciardi et al. 2009), pupil dilation (Yellin et al. 2015; Schneider et al. 2016; Pais-Roldán et al. 2020), subject vigilance (Wong et al. 2013; Wong et al. 2016) and dynamic brain state changes that occur during different sleep stages (Fukunaga et al. 2006; Schabus et al. 2007; Horovitz et al. 2008; Spoormaker et al. 2011; Tagliazucchi et al. 2012; Hjelm et al. 2018). Recent fMRI studies with concurrent astrocytic calcium recordings or optogenetics have shown that the rs-fMRI fluctuation can be regulated by the arousal ascending pathway through the central thalamic nuclei and midbrain reticular formation (Wang et al. 2018; Wang et al. 2019), implicating the subcortical regulation of the rs-fMRI signal fluctuation as previously reported from both non-human primate and human rs-fMRI studies (Chang et al. 2016; Liu et al. 2018; Turchi et al. 2018). Importantly, we also observed that the single-vessel rs-fMRI signal is specifically coupled to the global neuronal signal fluctuation (He et al. 2018), which supports our single-vessel RNN training scheme to encode the brain-state specific global rs-fMRI signal fluctuations.

Thus, the RNN-based approach provides a scheme to potentially differentiate brain states based on the global rs-fMRI fluctuation. Given the connection of global signal fluctuations with both neural activity (Scholvinck et al. 2010) and switching state dynamics (Gutierrez-Barragan et al. 2019) this method provides a rs-fMRI analysis approach complementary to previous work on the switching states. Combining the RNN-based fMRI signal prediction with EEG in both animal and human brains will provide direct evidence for the state-dependent features of this predictive approach in future exploration. Another promising direction for future work involves applying the proposed method to study the predictability of slow fluctuations in brain regions other than sensory cortices and to investigate which factors, besides arousal-related brain state changes, drive the predictions. Extending the platform to process whole-brain signals would provide a more synoptic view of regularities present in brain dynamics in different states. Finally, the method could be integrated into a real-time fMRI platform to provide feedback stimuli in a closed-loop control scheme.

Funding

This research was supported by NIH Brain Initiative funding (RF1NS113278–01, R01MH111438–01), German Research Foundation (DFG) YU215/2-1 and Yu215/3–1, BMBF 01GQ1702, internal funding from Max Planck Society.

Author Contributions

X.Y., F.S. designed the research; X.Y., Y.H., F.S. acquired the data; F. S., X.Y. developed the methods and performed data analysis; T.S. provided conceptual and methodological support, F.S., X.Y., T.S. wrote the paper.