Actin-Membrane Release Initiates Cell Protrusions

SUMMARY

Despite the well-established role of actin polymerization as a driving mechanism for cell protrusion, upregulated actin polymerization alone does not initiate protrusions. Using a combination of theoretical modeling and quantitative live-cell imaging experiments, we show that local depletion of actin-membrane links is needed for protrusion initiation. Specifically, we show that the actin-membrane linker ezrin is depleted prior to protrusion onset and that perturbation of ezrin’s affinity for actin modulates protrusion frequency and efficiency. We also show how actin-membrane release works in concert with actin polymerization, leading to a comprehensive model for actin-driven shape changes. Actin-membrane release plays a similar role in protrusions driven by intracellular pressure. Thus, our findings suggest that protrusion initiation might be governed by a universal regulatory mechanism, whereas the mechanism of force generation determines the shape and expansion properties of the protrusion.

In Brief

Using experiments and mathematical modeling, Welf et al. identify that plasma membrane detachment from actin is needed to initiate cell protrusion, regardless of whether actin polymerization or intracellular pressure create pushing forces. Their actin release model augments the tethered Brownian ratchet model, explaining why actin polymerization alone cannot initiate protrusion.

Graphical Abstract

INTRODUCTION

Cells change their shape via repeated cycles of protrusion and retraction (Lauffenburger and Horwitz, 1996). Despite the intense study of how cells generate the force for protrusion (Bodor et al., 2020; Maiuri et al., 2015; Mitchison and Cramer, 1996; Petrie et al., 2014; Ruprecht et al., 2015), we know surprisingly little about the mechanisms by which cells initiate a protrusion starting from a stationary or retracting edge. Experimental and theoretical findings do not support the common and implicit notion that increased actin polymerization initiates protrusion. On the experimental side, quantitative fluorescent speckle microscopy analyses showed that the rate of actin assembly peaks after the time point of the fastest protrusion (Ji et al., 2008) and the activity of actin polymerization regulators Rac1, PI3K, and Arp2/3 all increase after protrusion onset (Lee et al., 2015; Machacek et al., 2009; Welf et al., 2012). On the theoretical side, exquisitely accurate biophysical models have been proposed for how actin polymerization generates the force for protrusion propagation (Footer et al., 2007; Holz and Vavylonis, 2018; Marcy et al., 2004; Perilli et al., 2019; Prost and Bruinsma, 1996; Sadhu and Chatterjee, 2018; Schramm et al., 2019; Shao et al., 2012), but these models do not address the transition from a static to a protrusive state (Mogilner, 2006). Many coarse-grained models designed to study cell protrusion begin with the explicit assumption that increased actin polymerization causes protrusion initiation (Cao et al., 2019; Orly et al., 2014; Ryan et al., 2012; Welf et al., 2013). However, experimental evidence for this assumption is lacking.

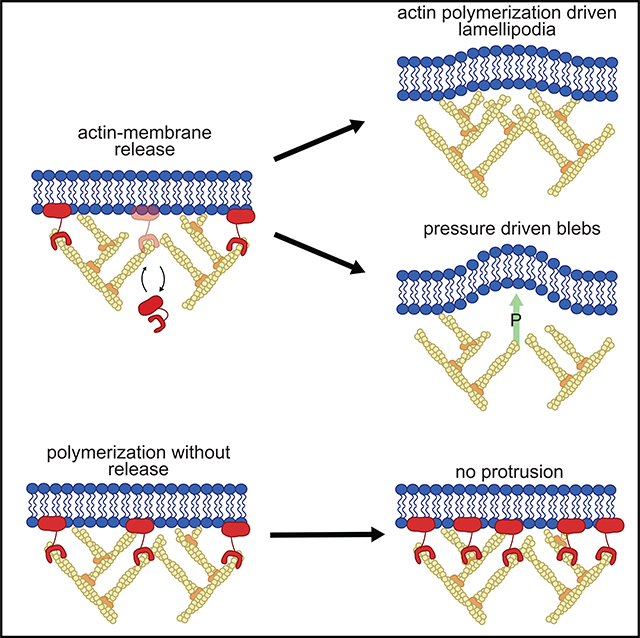
The notion that increased actin polymerization initiates protrusion arises from an implicit over-interpretation of the Brownian ratchet model for actin-based protrusion. First proposed in 1993, the Brownian polymerization ratchet model explains how the free energy of monomer addition to an actin filament tip is converted into mechanical force (Peskin et al., 1993). By incorporating the effects of the angular distribution of actin filaments (Mogilner and Oster, 1996) and the effect of membrane tethering on force generation (Mogilner and Oster, 2003), the model accurately explained the force-velocity relationship of cell protrusion at steady state. However, none of these works addressed protrusion initiation. In the most recent model of this family, the tethered Brownian ratchet model, the actin filament nucleator Arp2/3 must bind to membrane-bound WAVE in order to stimulate the addition of new actin filaments that create the branched actin structure most prominent in lamellipodial protrusions (Pollard, 2007; Sheetz, 2001). Tethered filaments must then unbind from WAVE to create working filaments that push the membrane outward. Thus, the Arp2/3-WAVE complex is both a polymerization factor and an actin-membrane tether, yielding a seemingly paradoxical relationship between actin filament addition and membrane tethering. Not considered in this treatment are the multitude of additional actin-membrane tethers, such as the prototypical actin-membrane linkers of the ERM (ezrin, radixin, and moesin) family. Here, we show that local depletion of actin-membrane links, such as those created by ezrin, is sufficient and necessary to initiate both actin-driven and pressure-driven protrusions. We place these observations into a theoretical context by showing how the actin-membrane linking function of ezrin works in concert with known actin-nucleation mechanisms to stimulate actin-driven protrusion.

RESULTS

Actin Fluctuations Alone Do Not Initiate Protrusion

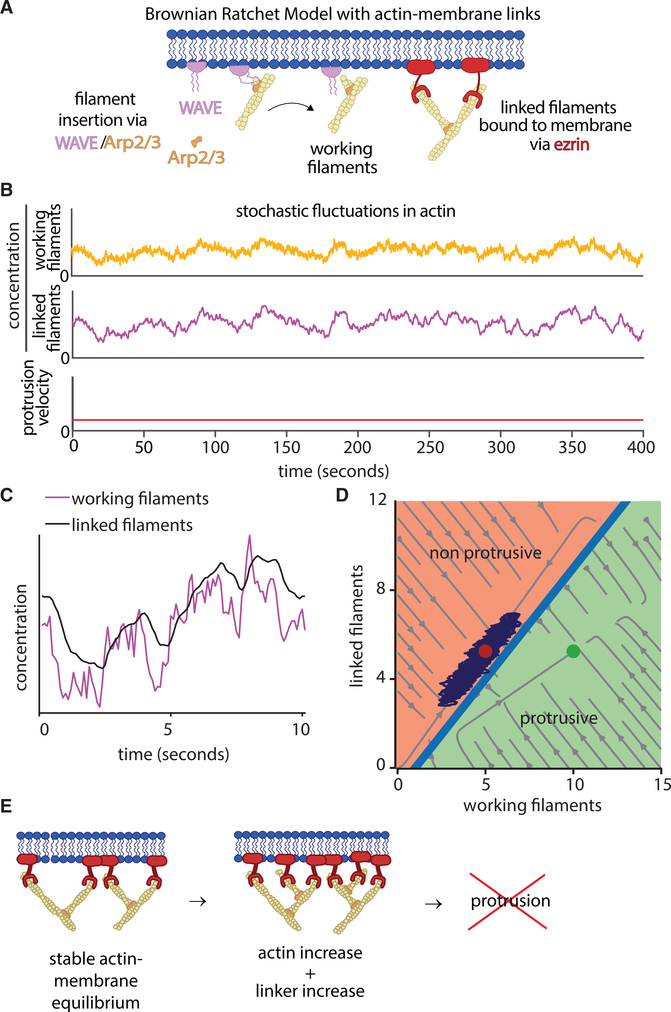
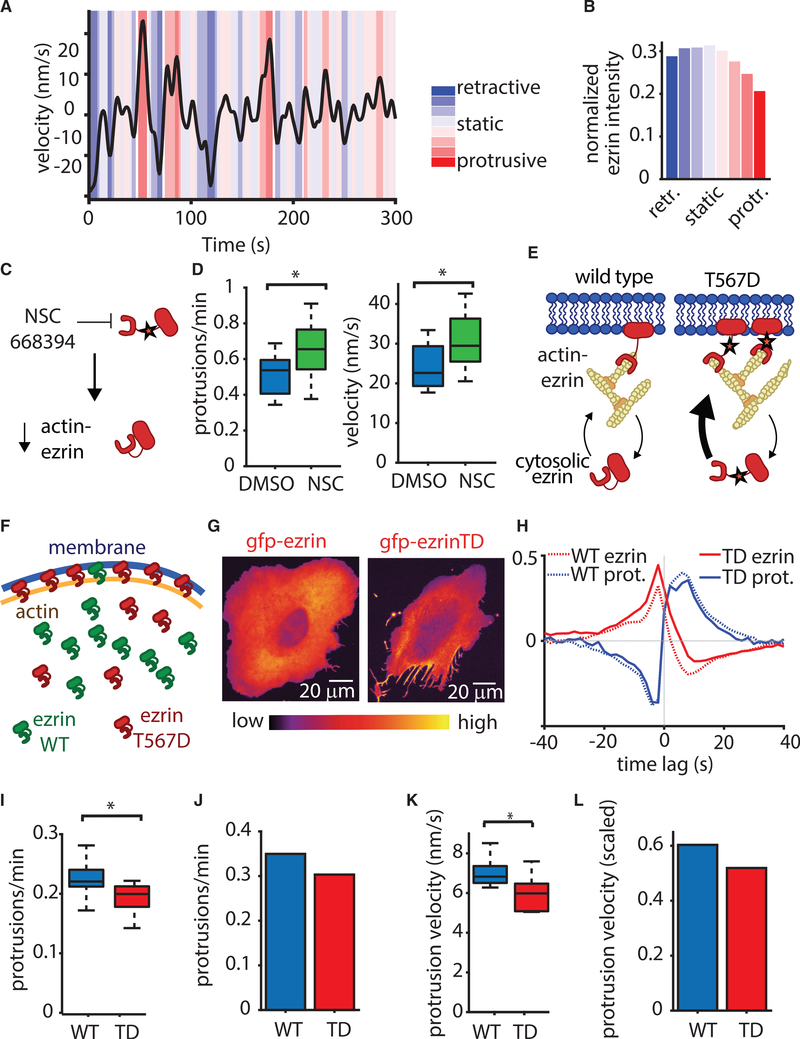
We incorporated the prototypical actin-membrane tethering factor ezrin into the tethered Brownian ratchet model (Figure 1A) by using detailed quantitative measurements of ezrin’s affinity for actin (Fritzsche et al., 2014). Synthesis of this new model leverages the same fundamental assumptions as the original tethered Brownian ratchet model, with the pivotal change of including actin-membrane tethering proteins that do not nucleate actin polymerization. Specifically, we assume that actin filaments bound to ezrin increase membrane rigidity and decrease membrane movement (Nöding et al., 2018). The model formalism is presented briefly in the STAR Methods section and in detail in Figure S1. We first tested the hypothesis that an increase in actin polymerization will cause protrusion under these assumptions. Simulation of the model with stochastic fluctuations in actin polymerization showed that increases in actin polymerization by themselves do not initiate protrusion (Figure 1B). This is because actin-membrane linkers rapidly reach a new equilibrium with newly added working filaments (Figure 1C). Analysis of stochastic simulation trajectories overlaid on the phase diagram of working filaments and linked filaments showed that fluctuations in working filaments do not create the ratio of working to linked actin filaments necessary to generate protrusion (Figure 1D). This theoretical result suggests that actin-membrane links prevent protrusion initiation by increased actin polymerization alone (Figure 1E).

Figure 1. Actin Fluctuations Alone Do Not Initiate Protrusion.

(A) Schematics of the tethered Brownian ratchet model for actin-driven protrusion, including the addition of ezrin as a canonical actin-membrane linker.

(B) Simulation of the model, including stochastic fluctuations in working actin filaments, resulting in no protrusion initiation events.

(C) Magnification of a portion of the data in (B) showing the relationship between working actin filaments and linked actin filaments.

(D) Phase diagram showing the computationally predicted relationship between working filaments and linked filaments. Circles indicate fixed points bifurcated by a separatrix, with red indicating the non-protrusive region and the green indicating the protrusive region. Light gray streamlines show deterministic model solutions, and the dark purple lines show an example simulation trajectory that never crosses over the separatrix.

(E) Schematic showing how actin-membrane links via ezrin equilibrate with newly polymerized actin filaments to prevent protrusion.

Ezrin Depletion Initiates Protrusion

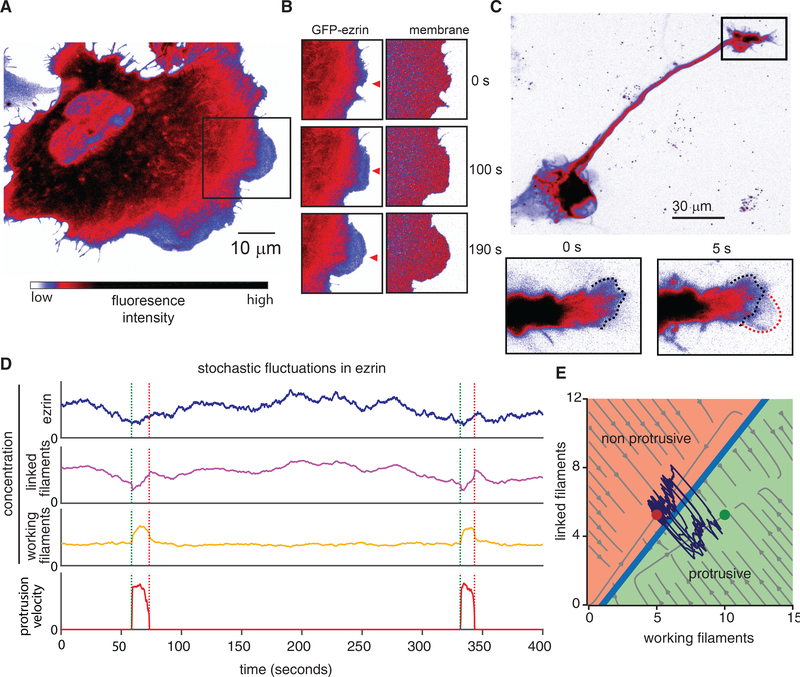
By extrapolation of the behaviors of the amended tethered Brownian ratchet model, we predicted a reduction in actin-membrane tethers as a necessary condition for protrusion initiation. To test this experimentally, we first imaged the localization of GFP-labeled ezrin in nascent protrusions in U2OS human osteosarcoma cells, which are a widely used model system for the study of actin-driven motility and cytoskeleton dynamics. The broad, flat lamellipodia were devoid of GFP-ezrin (Figure 2A; Video S1), whereas the intensity of a fluorescent membrane marker remained constant (Figure 2B). This indicates that the reduction in GFP-ezrin is not due to changes in membrane shape or illumination. Further analysis of 3D light-sheet microscopy of cells migrating on flat substrates confirmed that the reduction in GFP-ezrin was not due to protrusion thinning (Figure S1). We observed a similar relationship between protrusion and ezrin localization in a second canonical form of actin-driven protrusion, namely the dynamic growth cones in rat cortical neurons (Figure 2C). Thus, we conclude that ezrin depletion is a hallmark of the initiation phase of actin-driven protrusions.

Figure 2. Ezrin Depletion Initiates Protrusion.

(A) Spinning disk confocal microscope image showing GFP-ezrin in a U2OS cell exhibiting actin-driven protrusion in a lamellipodium in the boxed area. Image intensity scale applies to (A–D).

(B) Time-lapse image sequence of GFP-ezrin and tdTomato-membrane marker in the boxed area indicated in (A).

(C) Confocal microscope image showing GFP-ezrin during lamellipodial protrusion in the growth cone of a primary rat cortical neuron.

(D) Simulation of the model, including stochastic fluctuations in local ezrin concentration, resulting in repeated stochastic protrusion events.

(E) Phase diagram showing the relationship between working filaments and linked filaments in the computational model. Circles indicate fixed points bifurcated by a separatrix, with red indicating the non-protrusive region of the phase space and the green indicating the protrusive region. Light gray streamlines show deterministic model solutions, and the dark purple lines show an example simulation trajectory that crosses the separatrix multiple times, indicating repeated protrusions.

Phosphorylation of ezrin and other ERM family members is catalyzed by a multitude of kinases and phosphatases, resulting in conversion between states exhibiting either low-affinity or high-affinity for actin (Bretscher et al., 2002). This affinity switch ultimately modulates the local concentration of membrane-actin links (Bosk et al., 2011). To examine the effect of local fluctuations in ezrin occupancy, we simulated the extended tethered Brownian ratchet model with stochastic fluctuations in the local ezrin concentration. Unlike actin fluctuations, local ezrin fluctuations were sufficient to trigger protrusion initiation events (Figure 2D). Analysis of stochastic simulation trajectories overlaid on the phase diagram of working filaments and linked filaments showed that ezrin fluctuations are sufficient to create trajectories that cross the separatrix between non-protrusive and protrusive regions of the phase space (Figure 2E).

Decreases in Local Ezrin Concentration Precede Protrusion Onset

To determine if ezrin decreased as a result of protrusion or if it causes protrusion, we analyzed the density of working filaments and linked filaments in many simulated protrusion events and averaged the concentration of each species in relation to protrusion onset. These data predicted that the local concentration of ezrin linked to actin decreases before protrusion starts (Figure 3A). To test this prediction experimentally, we performed time-lapse imaging of two different models of actin-driven protrusion (U2OS osteosarcoma and MV3 melanoma). The concentration of GFP-ezrin is approximately equal to that of the endogenous ezrin (Figure S2). Ezrin activity is regulated by phosphorylation and different individual cells as well as different cell types can express drastically different amounts of ezrin (Thul et al., 2017; Wang et al., 2020) (www.proteinatlas.org). Accordingly, we do not find any significant change in protrusion as a result of GFP-ezrin expression (Figure S2). Leveraging a membrane marker to track local protrusion events and GFP-tagged ezrin to monitor local ezrin fluctuations, we used computational windowing (Ma et al., 2018) to sample thousands of protrusion/ezrin time courses that enabled us to quantify the temporal relations between ezrin fluctuations and protrusion initiation (Figure 3B). By aggregating ∼25,000 protrusion events from 1,700 time series in 12 different U2OS osteosarcoma cells, we could determine the kinetics of ezrin depletion during a stereotypical protrusion event. This analysis confirmed that GFP-ezrin systematically decreases ∼5s prior to protrusion initiation, in agreement with predictions from our model (Figure 3C). This behavior can be qualitatively discerned in many of the individual time courses (Figure 3D) and is quantitatively reproduced in protrusions of MV3 melanoma cells (Figures 3E and 3F). Altogether, these results support a model for actin-driven protrusion in which protrusion is normally constrained by actin-membrane links, but is enabled by the local detachment of these links to release the brakes for the existing idling “actin engine.” Accordingly, we refer to this model as the actin release model (Figure 3G).

Figure 3. Decreases in Local Ezrin Concentration Precede Protrusion Onset.

(A) Simulated time courses of total actin filaments, linked filaments, and protrusion velocities (2,324 simulated protrusion events averaged). Negative time lag indicates events before protrusion onset, positive lag indicates events after protrusion onset.

(B) Spinning disk confocal microscope image showing a protruding region in a U2OS cell analyzed by computational windowing to sample the local relation between edge motion via membrane marker and GFP-ezrin.

(C) Normalized edge velocity and GFP-ezrin intensity, aligned to protrusion onset in U2OS cells. Mean time courses extracted from 27,229 aligned protrusion events in 12 cells. Shaded areas represent 95% confidence intervals about the mean time course, calculated from the mean of each cell.

(D) Example time series of ezrin concentration and cell edge velocity sampled in a single window. Red arrows indicate onset of individual protrusion events (defined as switch from negative to positive edge velocity). Green arrows indicate decrease in ezrin intensity.

(E) Spinning disk confocal microscope image of an MV3 melanoma cell adhering to a glass coverslip and exhibiting actin-driven protrusion.

(F) Normalized edge velocity and GFP-ezrin localization aligned to protrusion in MV3 cells. Mean time courses extracted from 28,070 aligned protrusion events in 10 cells. Shaded areas represent 95% confidence intervals about the mean time course, calculated from the mean of each cell.

(G) Summary of the proposed actin release model.

Local Recruitment of an Ezrin Phosphatase Initiates Protrusion

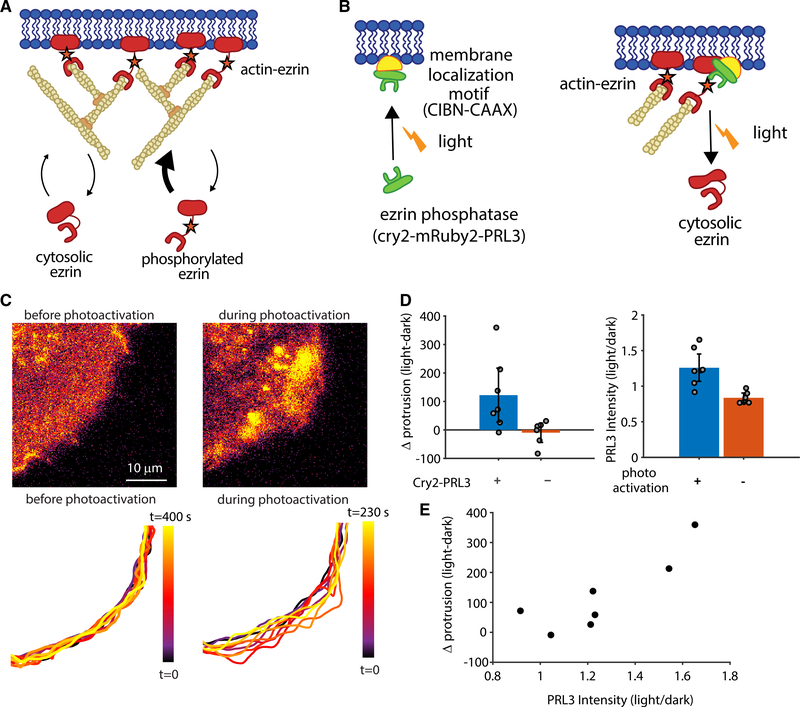
To test the actin release model more directly than observing GFP-ezrin fluctuations, we created an experimental system that would enable us to remove actin-membrane links in a controlled fashion. Protein knockdown or knockout of ezrin does not accomplish this goal because there are many other actin-membrane linkers ready to take ezrin’s place (Chugh and Paluch, 2018). Indeed, when we knocked out ezrin from U2OS cells, we noted an increase in the ERM family member radixin, which most likely compensates for ezrin knockout (Figure S3). To overcome this obstacle to ezrin perturbation, we developed the ability to locally and acutely reduce actin-membrane links by recruiting an ezrin phosphatase, PRL3, which dephosphorylates ezrin’s threonine 567 (Forte et al., 2008) (Figure 4A). We generated a form of PRL3 that could be recruited to the membrane and, thus, be brought in proximity of actin-bound ezrin by local light stimulation (Idevall-Hagren et al., 2012). Photoactivation increases PRL3 at the membrane, which dephosphorylates ezrin, thus reducing ezrin’s affinity for actin, and decreases the local concentration of actin-bound ezrin (Bosk et al., 2011) (Figure 4B).

Figure 4. Local Recruitment of an Ezrin Phosphatase by Photoactivation Initiates Protrusion.

(A) Schematic of the relationship between ezrin phosphorylation and actin-membrane linkage.

(B) Schematic of light-induced recruitment of PRL3 to the membrane, resulting in decreased ezrin phosphorylation and decreased actin-membrane links.

(C) Spinning disk confocal microscope images (top) and time-labeled cell outline (bottom) showing increased local protrusion upon stimulation of light-recruited cry2-mRuby2-PRL3.

(D) Change in the protrusive area because of photoactivation, calculated as mean positive area change during activation minus mean positive area change before activation (left; p = 0.043 two-sided t test, n = 7 cells expressing cry2-mRuby2-PRL3, blue, and n = 6 cells not expressing cry2-mRuby2-PRL3, orange) and cry2-mRuby2-PRL3 intensity expressed as a ratio of intensity during/before photoactivation (right; p = 0.0029 n = 7 areas with photoactivation, blue, and n = 7 areas without photoactivation, orange). Error bars represent 95% confidence intervals.

(E) Change in protrusion upon photoactivation as a function of the change in PRL3 intensity in the 7 cells/areas analyzed in (D).

To confirm that membrane recruitment of PRL3 to the membrane via the cry2-mRuby2-PRL3 construct results in dephosphorylation of ezrin, we used an LED array to stimulate a population of cells in culture and performed western blotting for phosphorylated ezrin. Despite the caveat that such global activation involves roughly six orders of magnitude lower watt density than focal activation (to reduce photodamage) and might have unintended compensation effects because of global stimulation, we nevertheless saw a reproducible decrease in ezrin phosphorylation of ∼15% upon photostimulation in three separate experiments (Figure S4). An mRuby2-tagged version of the photo-recruitable PRL3 (cry2-mRuby2-PRL3) showed that acute and local recruitment of the phosphatase resulted in an increase in local protrusion (Figures 4C and 4D; Video S2). Such a two-part photoactivation system does not always produce a robust response because it is sensitive to both the concentration of the membrane localization motif (CIBN-CAAX) as well as the recruited protein (cry2-mRuby2-PRL3). Indeed, we noted that in cells with a modest protrusion response, photoactivation yielded only mild elevation of cry2-mRuby2-PRL3 intensity, suggesting that the modest response was due to modest PRL3 recruitment. Overall, the extent of protrusion increase was correlated to the change in PRL3 intensity, suggesting that the effectiveness of local phosphatase recruitment regulates protrusion in this system (Figure 4E). Another possibility for a modest protrusion response to photoactivation in some regions is the lack of appropriate actin polymerization machinery for protrusion force generation. Thus, although the removal of ezrin releases the brakes, without a protrusion engine there is no edge motion.

Ezrin’s Actin-Membrane Linking Function Directly Regulates Protrusion Initiation

To further test the hypothesis that ezrin localization regulates protrusion, we first needed to develop a robust method for protrusion quantification, which filters insignificant directional switches in the saltatory cell edge movement. We employed a hidden Markov model (HMM) that divided the velocity time series of each sampling window at the cell edge into a series of distinct motion states while eliminating spurious velocity fluctuations, thus allowing a precise distinction of protrusion and retraction events (Figure 5A). Applied to edge velocity time series extracted from U2OS cells expressing GFP-ezrin, the HMM distinguished 4 protrusive and 4 retractive states. Although the ezrin concentration varied only slightly between retractive states, it sharply decreased between protrusion states of increasing mean velocity (Figure 5B). This directly confirmed our previous observation that ezrin decreases during protrusion.

Figure 5. Ezrin’s Actin-Membrane Linking Function Regulates Protrusion.

(A) Hidden Markov modeling is used to classify protrusion states in a time series.

(B) Normalized ezrin intensity during each of the eight HMM states defined in (A). Data include 1,710 velocity time series from n = 12 cells expressing WT GFP-ezrin.

(C) The ezrin inhibitor NSC668394 affects ezrin by inhibiting its phosphorylation, resulting in less actin-bound ezrin.

(D) Protrusion frequency and velocity during actin-driven protrusion in MV3 melanoma cells adhering to fibronectin-coated glass coverslips. p(frequency) = 0.0225, p(velocity) = 0.041 via two-sample t tests, n = 18 cells (NSC) and n = 10 cells (DMSO). Error bars represent 95% confidence intervals.

(E) Mutation of ezrin’s threonine 567 to aspartic acid (TD) increases the affinity of ezrin for actin, resulting in an enrichment of high-affinity ezrin linking actin to the membrane.

(F) Schematic depicting the functional effect of actin affinity of wild type and T567D ezrin on actin-membrane attachment.

(G) Spinning disk confocal microscope images showing morphological differences in typical U2OS cells resulting from overexpression of ezrin T567D.

(H) Normalized edge velocity and GFP-ezrin localization, aligned to protrusion onset imaged in 12 WT and 9-TD U2OS cells generating 27,229 and 25,329 protrusion events, respectively.

(I) Protrusion frequency in cells expressing either WT ezrin or TD ezrin, p = 0.039 via two-sample t test; n = 12 cells (WT) and n = 6 cells (TD). Error bars represent 95% confidence intervals.

(J) Simulations of the actin release model predicting the effect of TD expression on protrusion initiation frequency.

(K) Protrusion velocity in cells expressing either WT ezrin or TD ezrin, p = 0.027 via two-sample t test; n = 12 cells (WT) and n = 6 cells (TD). Error bars represent 95% confidence intervals.

(L) Simulations of the actin release model showing the effect of TD expression on protrusion velocity. In (I) and (K), box plots show the collective measurements for each cell; the central line is the median, the edges of the box are the 25th and 75th percentiles, and the whiskers extend to the most extreme data points.

Next, we applied the small molecule inhibitor NSC 668394 just prior to imaging to acutely decrease ezrin phosphorylation (Bulut et al., 2012) and, thus, reduce the number of ezrin molecules linking actin to the membrane (Figure 5C). This treatment increased the frequency of protrusion onsets and their velocity (Figure 5D), again in line with the predictions of the actin release model. At first sight, this outcome might appear paradoxical in light of reports of decreased migration under ezrin inhibition (Bulut et al., 2012; Ghaffari et al., 2019). However, our acute perturbation reflects the initial response of the cell to ezrin inhibition, devoid of long-term adaptations that exist during the chronic perturbations necessary for long-term cell-migration studies. We also note that protrusion is only part of the general cell-migration process. Thus, chronic ezrin inhibition might perturb cell polarity, which would decrease migration while increasing protrusion.

An advantage of studying ezrin as a prototypical actin-membrane linker is that we can experimentally leverage the affinity increase for actin caused by mutation of threonine residue 567 (T567D) (Figure 5E) (Bergert et al., 2021; Fritzsche et al., 2014) in order to test the effects of strengthened actin-membrane attachment on protrusion dynamics. This provides a complement to our methods of weakening ezrin-actin association via optogenetics and chemical perturbation. On the basis of published data (Fritzsche et al., 2014), we compiled a simple biochemical model, which predicts that the T567D mutant readily outcompetes endoegenous ezrin in forming membrane—actin links (see “Estimating the effect of ectopic expression of mutant T567D ezrin” in STAR Methods). Specifically, for a ratio WT:T567D of 1:1, which approximates the measured ratio in our experimental system (Figure S2), the model indicates ∼90% of the actin-bound ezrin will consist of high-affinity T567D mutant ezrin (Figures 5F and S5). The ability to increase the actin-membrane interaction by expression of an ezrin mutant in presence of WT ezrin is an essential experimental feature, as knockdown approaches for this protein are known to cause far-reaching side-effects, including changes of RhoA and Rac1 activity, myosin phosphorylation and cell contractility (Hatano et al., 2018; Jiao et al., 2018; Matsumoto et al., 2014), as well as the radixin overexpression documented in Figure S2.

Compared with cells expressing only WT ezrin, U2OS cells expressing the T567D mutant exhibit a notably less well-spread morphology (Figure 5G) but are still able to generate spontaneous protrusions, which exhibit reduced GFP-ezrin. This is expected because ezrin T567D’s increased affinity for actin does not prevent spontaneous unbinding from actin but merely increases the average time spent in the actin-bound state. Accordingly, in these remaining protrusions, GFP-labeled ezrin T567D followed the same dissociation/re-association pattern as WT GFP-ezrin in control cells (Figure 5H), although the frequency of protrusion events overall would be expected to be lower. To test this prediction, we used the HMM to classify protrusion and retraction states in cells expressing WT and T567D ezrin, and we identified individual protrusion events by finding switches from any retractive to any protrusive state. Indeed, the higher affinity of T567D ezrin decreased protrusion frequency (Figure 5I). To determine if the actin release model would quantitatively recapitulate this result, we simulated the experimental expression of mutant ezrin by adding a second ezrin species with higher affinity for actin, set at the same concentration as the WT ezrin to mimic our experimental measurement (Figure S3). In agreement with our experimental findings, this decreased protrusion frequency (Figure 5J). Likewise, the experimentally observed decrease in protrusion velocity upon expression of T567D ezrin (Figure 5K) was also reproduced by simulation of the actin release model (Figure 5L). In summary, multiple orthogonal experiments show that ezrin’s affinity for actin, and thus its actin-membrane linking function, directly regulate protrusion.

Actin-Membrane Release Works with Actin Polymerization to Regulate Protrusion

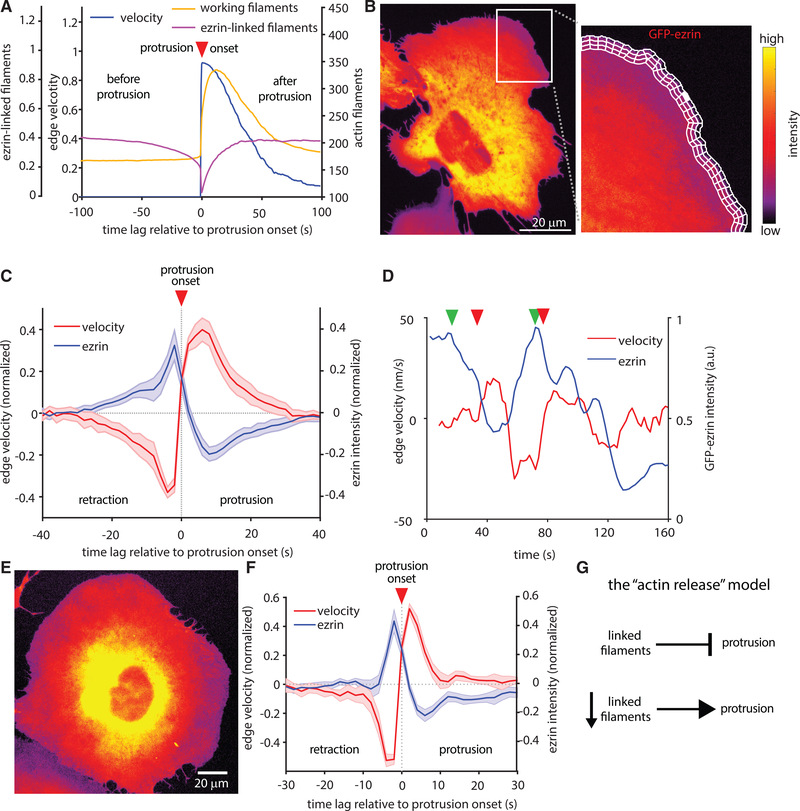
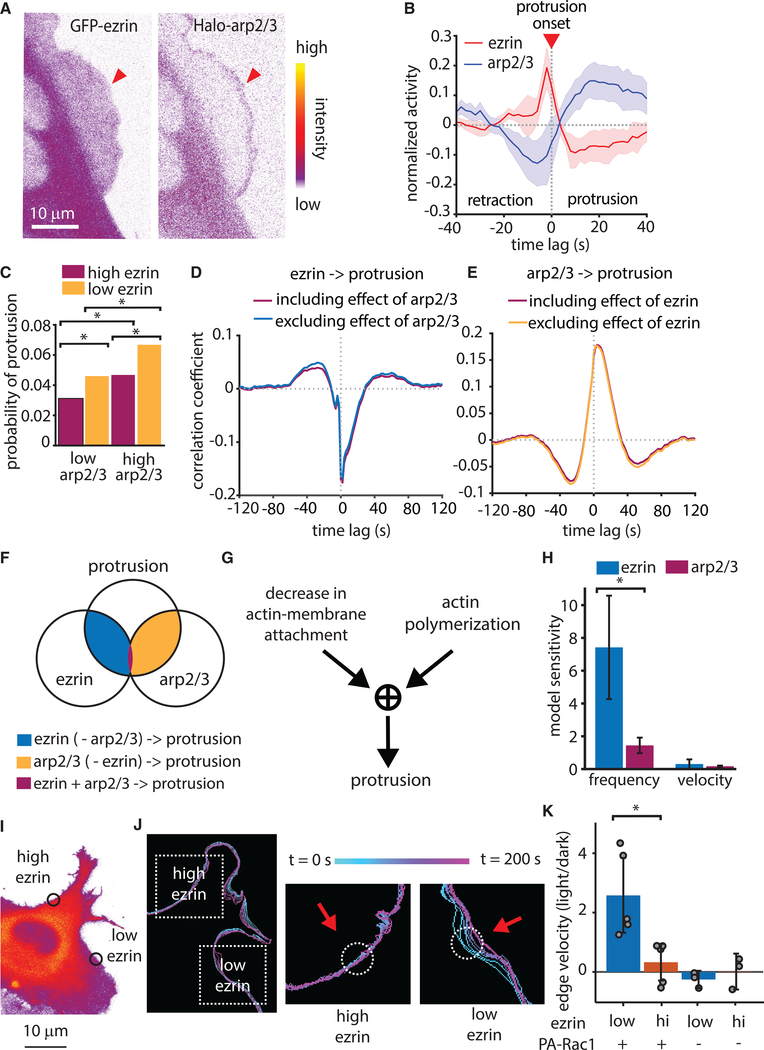
Our previous work on protrusion mechanics indicated that the growth of branched actin networks, promoted by Arp2/3 activation, primarily serves the reinforcement of actin assembly against mounting membrane tension (Lee et al., 2015; Mendoza et al., 2015). Therefore, we expected that Arp2/3 would be recruited after ezrin depletion and protrusion onset. Indeed, concurrent imaging of HaloTag-Arp2/3 and GFP-ezrin in the same cells (Figure 6A) showed that Arp2/3 recruitment increased after protrusion onset and reached a maximum well after ezrin reached minimal levels (Figure 6B). However, it remained to be determined if Arp2/3 only plays a role in protrusion reinforcement or if it also contributes to the promotion of protrusion onset. To address this question, we built a new HMM that identified intervals that were either enriched or depleted in ezrin or Arp2/3 in the intensity time series of HaloTag-Arp2/3 and GFP-ezrin and measured the frequency of protrusion events within those intervals. As expected, intervals of low ezrin were enriched for protrusion events compared with in intervals of high ezrin; but intervals of low ezrin and high Arp2/3 exhibited a further increase in the probability of protrusion events (Figure 6C), suggesting an additive effect of ezrin depletion and branched actin filament nucleation in protrusion initiation. Importantly, the finding that protrusions are sometimes initiated in a high ezrin state does not contradict the requirement of ezrin depletion prior to protrusion. The HMM analysis does not track local ezrin decreases, which are the critical factor in protrusion initiation.

Figure 6. Actin Polymerization and Ezrin Localization Cooperatively Drive Protrusion.

(A) Representative spinning disk confocal microscopy images of a U2OS cell expressing both GFP-ezrin and a HaloTag-Arp2/3.

(B) The normalized activity of GFP-Ezrin and HaloTag-Arp2/3, aligned to protrusion onset (t = 0). Data include 39,686 protrusion events form n = 5 U2OS cells. Shaded areas represent 95% confidence intervals.

(C) Probability of protrusion in sampling windows categorized by HMM of GFP-ezrin and HaloTag-Arp2/3 intensity. p < 0.01 for all comparisons via two-sample t test comparing probability per cell, n = 5 cells.

(D and E) Comparison of full cross-correlation and partial cross-correlation of GFP-ezrin intensity to protrusion (D) and HaloTag-Arp2/3 intensity to protrusion (E). Data include 39,686 multivariate time series from n = 5 cells.

(F) Schematic illustrating the overlap between the effects of ezrin and Arp2/3 on the protrusion.

(G) Diagram depicting a hypothetical AND gate whereby both actin polymerization and reduction in actin-membrane attachment are required for protrusion.

(H) Mean sensitivity of model simulation results for protrusion frequency and velocity calculated from simulations using 10 different parameter values. Error bars show 95% confidence intervals.

(I) Spinning disk confocal microscope image of a U2OS cell depicting regions of high and low ezrin concentration, within which photoactivation of Rac1 was performed.

(J) Outlines of the cell edge at different time points either before or during photoactivation. Dashed boxes indicate area of zoom for high and low ezrin regions, circles show areas of photoactivation, and the colorbar shows time information.

(K) Local edge velocity in either low or high ezrin regions, shown as the velocity in the light state divided by that in the dark state. p = 0.0136 via two-tailed t test n = 5 for each ezrin low and ezrin high conditions. Error bars represent 95% confidence intervals. Local ezrin concentration and presence of the PA-Rac1 construct are as indicated below the x axis.

To define the role of Arp2/3 within the context of ezrin dynamics, we performed partial correlation analysis between the protrusion and GFP-ezrin intensity, accounting for the effect of Arp2/3. Direct and partial correlation controlled for Arp2/3 were almost identical (Figure 6D), suggesting that the coupling of ezrin and protrusion modulation is independent of Arp2/3. Similar partial correlation analysis between protrusion and Arp2/3 controlled for ezrin indicated that the correlation between Arp2/3 and cell edge movement is independent of ezrin modulation (Figure 6E). Together these results showed that ezrin depletion and Arp2/3 recruitment play separate and complementary roles during protrusion, with very little functional overlap (Figure 6F). In combination with the HMM state analysis, these data led us to conclude that protrusion requires an AND gate between actin polymerization and actin-membrane detachment— both a force-generating engine and a brake-release mechanism are required to initiate protrusion (Figure 6G).

We further investigated whether the independence of membrane-actin interaction and branched actin assembly also emerges from the mathematical formalism of the actin release model. We performed simulations with progressively increasing values for the rate of branched actin polymerization and for the fraction of high-affinity ezrin. The resulting changes in protrusion properties were normalized by the incremental change to the parameter value (Arp2/3 activity or ezrin affinity). This analysis predicts that ezrin has a larger influence on protrusion onset frequency than Arp2/3, but that ezrin and Arp2/3 have roughly equal influence on protrusion velocity (Figure 5H). Altogether, these results firmly place actin-membrane detachment as a prerequisite for actin-mediated protrusion and define branched actin nucleation as a complementary, but an independent second factor for this process.

To definitively test the necessity of both ezrin reduction and actin polymerization for protrusion initiation, we employed the photoactivatable Rac1 construct, which can generate protrusion by local activation of Rac1 and ensuing Arp2/3-mediated actin polymerization (Wu et al., 2009). As predicted by our model, activation of Rac1 in regions of high ezrin failed to induce protrusion, whereas activation of Rac1 in regions with lower ezrin induced protrusion (Figures 6I and 6J). Quantifying the change in edge velocity due to photoactivation in high versus low ezrin regions showed that regions of low ezrin exhibit higher edge velocity than regions with high ezrin (Figure 6K). Illumination of cells without expression of the photoactivatable construct with the same laser intensity had no effect on the protrusion behavior. This result confirms that although upregulation of actin polymerization is capable of inducing protrusion, it can only do so if the local ezrin concentration is sufficiently low.

Actin-Membrane Links Are Also Depleted in Pressure-Driven Protrusions

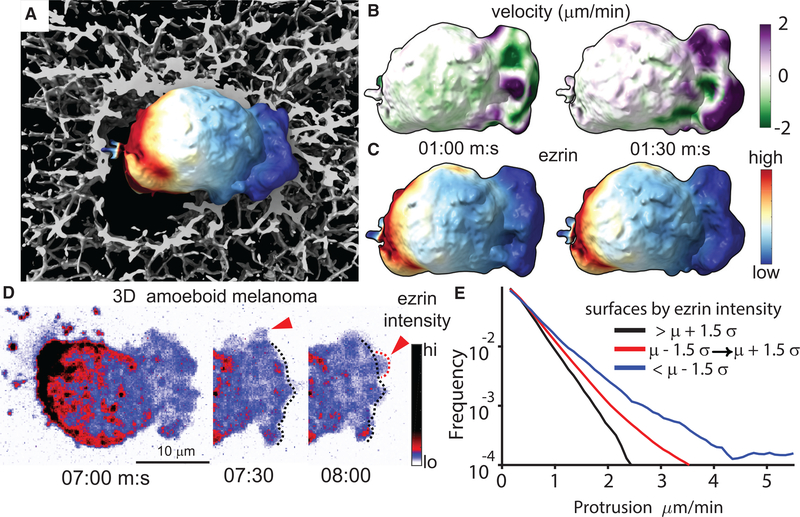
Ezrin is a well-known occupant of the actin cortex, but it has been primarily studied during cortex reformation following the formation of hemispherical, pressure-based protrusions called membrane blebs (Charras et al., 2006). Membrane blebs are a common feature of ameboid cells migrating through soft 3D microenvironments (Friedl and Wolf, 2010), and we have previously shown that melanoma cells exhibit persistent, non-apoptotic membrane blebs in 3D collagen (Welf et al., 2016). In order to determine if the actin release model applies to pressure-driven protrusion, we used light-sheet fluorescence imaging with isotropic resolution (Dean et al., 2015; Welf et al., 2016) to monitor ezrin localization in a melanoma cell, as it was digging through a 3D collagen matrix, whereby the tunneling behavior of the cell allowed us to identify a clear front and rear. Under these conditions, polarized melanoma cells exhibit persistent bleb formation at the front of the cell pointing into the collagen matrix (Figure 7A; Video S3). In agreement with previous reports (Lorentzen et al., 2011), ezrin was highly concentrated at the cell rear, where the cell was not in contact with collagen. Projections of local membrane motion (Figure 7B; Video S4) and ezrin concentration (Figure 7C; Video S5) from 3D cell image volumes onto the cell surface revealed that even outside the ezrin-enriched uropod, the protrusion is restricted to regions of only the lowest ezrin concentration. This observation stands in contrast to a more simplified model of 3D cell migration where a cell consists of a front with protrusion and a back with no protrusion. Instead, our observations support a model where 3D migrating cells also exhibit “sides” with intermediate ezrin concentration that nonetheless restrict protrusion. More detailed examination showed that ezrin was reduced just as an individual bleb appeared, suggesting that ezrin is specifically depleted in these pressure-based protrusions (Figure 7D; Video S5), just as it is depleted in actin-based protrusions. Using morphological motif classification via machine learning (Driscoll et al., 2019), we identified individual blebs on the cell surface and quantified the protrusive motion of these blebs as a function of ezrin intensity. This analysis showed that bleb surfaces with the lowest ezrin intensity exhibited most forward motion, whereas bleb surfaces with the highest ezrin advanced the least, supporting the model that ezrin depletion facilitates protrusion (Figure 7E).

Figure 7. Actin-Membrane Release Creates Pressure-Driven Protrusion.

(A) Surface rendering of melanoma cell in 3D collagen with the intensity of GFP-ezrin mapped to the cell surface, generated from light-sheet microscope images.

(B and C) Time-lapse data of the cell shown in (A) were used to quantify surface motion (B) and ezrin intensity (C) as a function of time.

(D) Maximum intensity projection (MIP) of light-sheet microscope images showing GFP-ezrin intensity during new bleb formation. Red arrows indicate newly formed blebs.

(E) Quantification of surface motion on blebs as a function of ezrin intensity measured in 21 cells. Data are displayed as the relative frequency in groups separated by ezrin intensity either above, below, or within ±1.5 times the standard deviation of all measurements.

DISCUSSION

Our extension of the tethered Brownian ratchet model in combination with diverse cell biological assays establish, in a remarkable qualitative and quantitative agreement between theory and experiment, the release of actin-membrane links as the necessary condition for protrusion initiation. This result defines the molecular mechanism regulating protrusion initiation and emphasizes the equal roles initiation and force generation play in driving productive protrusions. Our finding that actin-membrane detachment regulates actin-driven and pressure-driven protrusion raises the intriguing possibility that both types of protrusions are regulated by a common initiation mechanism regardless of the mode of force generation. This would explain how cells are able to maintain migration polarity when switching between protrusion modes (Bergert et al., 2012) and suggests that the mechanism of force generation determines the shape of the protrusion, but not where and when the protrusions will occur. This has major implications for the modes of integration between the regulatory signals that govern directed cell migration, polarity, and protrusion mechanics. Furthermore, the redundancy of actin-membrane linkers found in mammalian cells would render such a mechanism robust to genetic instability and enable control by different regulatory pathways (Chugh and Paluch, 2018).

Our actin release model is supported by parallel efforts, which report the lowest actin-membrane proximity at the protruding front of migrating endothelial cells (Bisaria et al., 2019). Although the cited work does not address the implications of this observation for a dynamic regulation of actin-membrane attachment, the results speak of the role of this process in migration. An additional report shows that differentiating cells exhibit reduced membrane tether force and increased cell spreading (Bergert et al., 2021). Given that membrane tether force is a measure of membrane-cortex attachment, this observation makes it tempting to speculate that a reduction in actin-membrane attachment is responsible for the increased cell spreading under these conditions. Finally, the recent finding that knockout of a phosphatase with activity for ezrin decreases protrusion in neurons in vivo provides further support to our data indicating ezrin dephosphorylation as a key event during protrusion (Urwyler et al., 2019).

Despite this independent evidence as well as our own experiments supporting the actin release model, we note that there is no way to directly monitor during a protrusion event the space between the membrane and actin network into which actin monomers are added. The dimensions of such a separation could be as small as a single actin monomer (5 nm), and standard light microscopy is unable to provide the resolution necessary for such an observation. Even localization-based microscopy, such as PALM or STORM, are unlikely to provide the resolution necessary to image such an event and the potentially short lifetime of such a separation before actin monomer addition coupled with the inherent temporal limitations of these approaches would make such an observation essentially impossible. STED microscopy is, in principle, capable of the temporal sampling necessary but in practice provides resolution in the range of 50–100 nm. Nonetheless, Clausen et al. measured the nanoscale spacing between the membrane and the actin cortex and found a bimodal distribution of this separation within a single cell, suggesting that some regions of the membrane are closer to the actin cytoskeleton than others (Clausen et al., 2017). Electron microscopy is, to our knowledge, the only imaging modality capable of resolving such small membrane-actin separations, but because of the static nature and sample preparation conditions inherent to electron microscopy, it is also not capable of capturing such a dynamic phenomenon. Likewise, there is no way to observe the localization of actin-membrane linkers without potentially perturbing their function. This is why we extended our study beyond descriptive observations to include multiple direct perturbations of ezrin function and a direct test of induced protrusion in regions that naturally exhibit different ezrin concentrations.

If not protrusion initiation, what is the role for polymerization of a branched actin network in this updated model? The previous finding that PI3K signaling is necessary to amplify small nascent protrusions into large protrusions suggests that PI3K-mediated actin polymerization through Rac1 could reinforce these nascent protrusions to generate lamellipodia (Welf et al., 2012). Other observations also suggested that polymerization of a branched actin network reinforces, rather than initiates, protrusion. Quantitative fluorescent speckle microscopy analyses showed that the rate of actin assembly peaks after the time point of the fastest protrusion (Ji et al., 2008), the activity of regulators of branched actin network polymerization, including Rac1, PI3K, and Arp2/3, all increase after protrusion onset (Lee et al., 2015; Machacek et al., 2009; Welf et al., 2012), and actin filament density increases when membrane tension increases (Mueller et al., 2017). The positive feedback between the protrusion and the ratio of working to linked filaments in the branched actin network defines an amplification motif, which provides a mechanism for the reinforcement function of the branched actin network. It should be noted that, by design, branched actin network polymerization is poised to only serve the purpose of reinforcement. As our analysis of the tethered Brownian ratchet model (Figure 1) shows, an increase in working filament density without clearance of links yields a rapid equilibration of a denser cortex with denser tethers that prevent edge motion. Hence, any mechanism that increases actin filament density can contribute productively to protrusion only after the deactivation of linkers. In line with this conjecture, canonical inputs to branched actin polymerization, such as soluble chemotactic or mechanical durotactic cues, amplify protrusion fluctuations but do not initiate them. This design enables cells to randomly sample their environment via small edge fluctuations, facilitating identification of the path of least resistance in complex microenvironments (Renkawitz et al., 2019), whereas the commitment to directed, persistent protrusion is made later via the amplification motif that ultimately guides directionality (Andrew and Insall, 2007; Neilson et al., 2011; Welf et al., 2012). Such a mechanism would function in the case that ezrin dephosphorylation was not regulated beyond general “front” and “back” signatures created by its kinases such as ROCK (Xu et al., 2003), which would bias ezrin phosphorylation to the cell rear. Thus, randomly distributed but small protrusion events would appear near the cell “front,” which would then be amplified via chemotactic or adhesive signaling in order to generate longer-lived, productive protrusions. In summary, our work complements the actin-centric views of protrusion regulation with a second key axis of regulation involving actin-membrane links. This insight might stimulate the investigation of the integrated mechano-chemical signaling networks with a fresh perspective.

STAR⋆METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will befulfilled by the Lead Contact, Erik Welf (Erik.Welf@UTsouthwestern.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

The general use software developed but our lab and used in this study is available at https://github.com/DanuserLab.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

U2OS cells were obtained from R. McIntosh (University of Colorado, Boulder CO). MV3 cells were obtained from Peter Friedl (MD Anderson Cancer Center, Houston TX). U2OS cells were cultured in McCoy’s Medium (Gibco) supplemented with 10% FBS and MV3 cells were cultured in DMEM (Gibco) supplemented with 10% fetal bovine serum (FBS; ThermoFisher). To obtain primary neurons, male and female embryonic day 18 (E18) primary cortical neurons were prepared from timed pregnant Sprague Dawley rats (Charles River Laboratories, Wilmington, MA). Embryonic cortices were harvested, neurons dissociated, and plated on 5 mm coverslips coated with poly-D-lysine. Neurons were cultured in completed Neurobasal medium (Gibco 21103049) supplemented with 2% B27 (Gibco 17504044), 1 mM glutamine (Gibco 25030081), and penicillin streptomycin (Gibco 15140148) at 37°C in a 5% CO₂ environment. Neurons were infected with purified and concentrated lentivirus after 4 days in vitro.

METHOD DETAILS

Computational Model

Our model describes the dynamics and mechanics of the protruding actin network at the lamellipodial leading edge. In the model, we consider the molecules in the immediate narrow vicinity of the leading edge, specifically – linear (along the edge) densities of polymerizing barbed ends, B, of ezrin-associated (linked) filaments, C, and of ezrin available for binding, Evolution of these densities is governed by the following processes: concentration of ezrin molecules not associated with actin is fluctuating around a stable equilibrium maintained by balances of transport processes in lamellipodial membrane and cytoplasm. The polymerizing filaments branch to nucleate new filaments, become capped and lag the leading edge, and finally bind and unbind from membrane-associated ezrin molecules. These binding and unbinding events are assumed to make polymerizing filaments tethered and vice versa, respectively. In the model, both the branching and unbinding rates increase with the protrusion velocity of the leading edge; all other rates are constants. Three stochastic differential equations account for the described actin dynamics:

$$\frac{\text{d}B}{\text{d}t}=\text{nucleation}-\text{capping}-\text{ezrin}\text{binding}+\text{unbinding}+\text{chemical}\text{noise}$$

$$\frac{\text{d}C}{\text{d}t}=\text{ezrin}\text{binding}-\text{unbinding}+\text{chemical}\text{noise}$$

$$\frac{\text{d}E}{\text{d}t}=\text{equilibriation}\text{to}\text{mean}\text{value}+\text{chemical}\text{noise}$$

The noise terms in the equations account for the random fluctuations of the densities due to limited numbers of molecules involved, stochasticity of the molecular events and Brownian movements. In order to close this system of equations, an expression for the protrusion velocity as a function of the polymerizing and tethered actin densities is needed and takes the form of

$$V=V_0\left(1-{\left(\frac{{\tau }_0+F_{tether}C}{F_{poly}B}\right)}^{\lambda }\right)$$

This velocity is dictated by a tug-of-war between the pushing polymerization forces and forces resisting protrusion. The polymerization force from growing filament barbed ends is taken to be proportional to the polymerizing filament density with microscopic polymerization force-per-filament F_poly The resistive force consists of membrane tension τ₀ and an elastic force from tethered filaments linking the lamellipodial actin network and the membrane, also taken to be proportional to the tethered filament density with force-per-filament F_tether. The shape of the force-velocity relation, dictated by parameter λ, arises from net contributions of microscopic forces [90].

Further details and model extensions to include space and other ezrin populations can be found in the Supplementary document.

Cell Culture and Reagents

U2OS cells were obtained from R. McIntosh (University of Colorado, Boulder CO). MV3 cells were obtained from Peter Friedl (MD Anderson Cancer Center, Houston TX). U2OS cells were cultured in McCoy’s Medium (Gibco) supplemented with 10% FBS and MV3 cells were cultured in DMEM (Gibco) supplemented with 10% fetal bovine serum (FBS; ThermoFisher). To obtain primary neurons, male and female embryonic day 18 (E18) primary cortical neurons were prepared from timed pregnant Sprague Dawley rats (Charles River Laboratories, Wilmington, MA). Embryonic cortices were harvested, neurons dissociated, and plated on 5 mm coverslips coated with poly-D-lysine. Neurons were cultured in completed Neurobasal medium (Gibco 21103049) supplemented with 2% B27 (Gibco 17504044), 1 mM glutamine (Gibco 25030081), and penicillin streptomycin (Gibco 15140148) at 37°C in a 5% CO₂ environment. Neurons were infected with purified and concentrated lentivirus after 4 days in vitro.

The GFP-ezrin constructs were acquired from Addgene (plasmids #20680 and #20681)(Hao et al., 2009) and cloned into the pLVX-puro vector (Clontech). U2OS and MV3 cells expressing GFP-ezrin were created by following the manufacturers instructions for virus preparation and cell infection. Cells were selected for expression by treatment with 10 μg/mL puromycin. The photoactivatable PRL3 construct was constructed by replacing the iSH2 domain of from the mCherry-CRY2-iSH2 (Addgene Plasmid #66839) with the PRL3 gene (obtained from Maja Khön, University of Freiburg, Germany)(Luján et al., 2016) as well as the mCherry gene with mRuby2 and cloned into the pLVX-neo vector (Clontech). The CIBN-CAAX plasmid was obtained from Addgene (Plasmid #79574) and cloned into the pLVX-puro vector. Cells expressing both the cry2-mRuby2-PRL3 and the CIBN-CAAX constructs were selected by treatment with 10 mg/mL puromycin and fluorescence-activated cell sorting. It is critical for the two-part cry2 photoactivation system that cells express sufficient concentration of the CIBN-CAAX construct or the cry2 construct will aggregate in the cytosol instead of being recruited to the membrane. Thus, the optimal ratio of CIBN:cry2 is >1; cells expressing insufficient CIBN-CAAX will not response to light. We also noted through the course of our experiments that cells will stop expressing one or both of these constructs if not kept constantly under selective pressure. Such a loss of expression will result in non-responsive cells.

The PA-Rac1 construct was obtained from Yi I. Wu (University of Connecticut Health Center, Farmington, CT). To image ezrin concentration without exposing cells to 488 nm light, we created an mRuby2-ezrin construct by replacing GFP in the pLVX-GFP-ezrin construct with mRuby2.

The tdTomato-CAAX membrane construct was obtained from the laboratory of Claire Waterman (NIH, Bethesda MD) and inserted into the pLVX-neo vector (Clontech). Cells expressing the membrane marker were selected using 1 mg/mL G418 (ThermoFisher). A U2OS cell line expressing an endogenously labeled Halo-Arp3 was generated by inserting the Halo tag into the Arp3 gene using CRISPR-Cas9. Cells were incubated with TMR halo ligand prior to imaging in accordance with the manufacturer’s instructions.

2D Imaging

U2OS and MV3 cells imaged in 2D were plated on glass coverslips coated with 10 mg/mL fibronectin and imaged on a Nikon EclipseTi-E inverted motorized microscope coupled to an Andor Diskovery TIRF/ Borealis widefield illuminator equipped with an additional 1.8× tube lens (yielding a final magnification of 108×). The microscope was equipped with an OKO lab custom built full body environmental chamber with temperature control and CO₂ stage incubator.

3D Sample Preparation

Collagen gels were created by mixing bovine collagen I (Advanced Biomatrix) with concentrated phosphate buffered saline (PBS) and water for a final concentration of 2 mg/mL collagen. UnpepsiThis collagen solution was then brought to pH 7 with 1N NaOH and mixed with cells just prior to incubation at 37°C to induce collagen polymerization. Cells were suspended using trypsin/EDTA (Gibco), centrifuged to remove media, and then mixed with collagen just prior to incubation at 37°C to initiate collagen polymerization. To image collagen fibers, a small amount of collagen was conjugated directly to AlexaFluor 568 dye and mixed with the collagen sample just prior to polymerization.

3D Cell Imaging

3D samples were imaged using either an axially swept light sheet microscope (Dean et al., 2015, 2016) or using our meSPIM microscope (Welf et al., 2016), both of which provide nearly isotropic, diffraction-limited 3D images. Samples were imaged in phenol red free DMEM containing 25mM HEPES (Thermo Fisher) with 10% FBS and antibiotic-antimycotic (Gibco), held at 37°C during imaging. For cells on coverslips imaged in 3D, the focused area of the light sheet was scanned parallel to the coverslip in order to increase imaging speed without sacrificing resolution (Dean et al., 2016). Images were collected using sCMOS cameras (Orca Flash4.0 v2, Hamamatsu) and microscopes were operated using custom Labview software. All software was developed using a 64-bit version of LabView 2016 equipped with the LabView Run-Time Engine, Vision Development Module, Vision Run-Time Module and all appropriate device drivers, including NI-RIO Drivers (National Instruments). Software communicated with the camera via the DCAM-API for the Active Silicon Firebird frame-grabber and delivered a series of deterministic TTL triggers with a field programmable gate array (PCIe 7852R, National Instruments). These triggers included analog outputs for control of mirror galvanometers, piezoelectric actuators, laser modulation and blanking, camera fire and external trigger. All images were saved in the OME-TIFF format. Some of the core functions and routines in the microscope control software are licensed under a material transfer agreement from Howard Hughes Medical Institute, Janelia Farm Research Campus.

3D Image Rendering and Analysis

3D image data was processed as described previously (Driscoll et al., 2019; Welf et al., 2016). Briefly, image data was segmented to create a surface represented as a 3D triangle mesh, using either a manually selected intensity threshold or using Ilastik (Sommer et al., 2011). The triangle meshes shown in Figures 1A–1C were rendered in ChimeraX (Goddard et al., 2018). Colored triangle meshes were exported from Matlab as Collada .dae files using custom-written code and were rendered using full lighting mode. To measure the fluorescence intensity local to each mesh face, we used the raw, non-deconvolved, fluorescence image. At each mesh face, we used a kd-tree to measure the average pixel intensity within the cell and within a sampling radius of the mesh face. To correct for surface curvature dependent artifacts, we depth normalized³³ the image prior to measuring intensity localization by normalizing each pixel by the average pixel intensity at that distance interior to the cell surface. Prior to analysis, we also normalized each cell’s surface intensity localization to a mean of one.

Photoactivation

Photoactivation of subcellular regions was performed using 488 nm light at 10% power via the FRAP module of a Zeiss LSM780 outfitted with temperature and CO₂ control. The estimate power mRuby2-ezrin and mCherry-PRL3 were imaged using 561 nm light so as to not activate either the light sensitive domain of each photoactivatable construct.

Because of the appearance of membrane ruffles and large changes in image intensity due to photoactivation, cry2-mRuby2-PRL3 photoactivation was quantified using a tailored analytical pipeline that differs from the standard procedures applied to cell morphodynamics analyses in our lab (see below). First, images of mRuby2-PRL3 were segmented using k-means segmentation with k=3. The group with the lowest intensity was set to background, and the other two groups were set to foreground. Holes in the foreground were then filled and the detected cell edge was smoothed via dilation using a circular structuring element with a radius of 2 pixels. The mean of the nonzero values of protruded area, measured every 20 frames, was calculated for each cell before and during photoactivation. The change in protrusion was calculated as the difference between the mean protruded area during photoactivation and before photoactivation. The change in intensity of the foreground image due to photoactivation was calculated similarly, except that the ratio of intensity was calculated due to nonzero values for the unstimulated condition.

The effect of photoactivation of PA-Rac was measured using our standard edge detection and windowing program, available at https://github.com/DanuserLab. The mean velocity of all sampling windows in the region of photoactivation was calculated for each cell. The ratio of the mean velocity during and before photoactivation (light/dark) was then calculated for each cell to quantify the effect of acute Rac1 activation. The control experiments shown in Figures 4 and 6 rely on photostimulation of cells not expressing photoresponsive constructs. Because of the laboratory shutdown enforced due to COVID-19 we were unable to perform separate control experiments for both PA-Rac and cry2-mRuby2-PRL3. Therefore, the same set of cells expressing only mRuby2-ezrin were used for both sets of control experiments, but they were analyzed using the different analytical pipelines used for the different experiments. In both cases, the conclusion is taken from these control experiments is that light stimulation does not cause protrusion in the absence of a photoactivation construct.

For the bulk cell photoactivation experiment, cells were stimulated using an LED array (BTF lighting, Amazon) set to blue light flashing mode for 5 minutes while inside of an incubator set at 37°C with 5% CO₂. Cells were then immediately lysed in the dark on ice. Cells for the “dark” condition were covered with aluminum foil to prevent any photoactivation and kept in the dark at all times.

Western Blotting

Cells were lysed with 1:1 dilution of 2xJS buffer (100mM HEPES ph7.5, 300mM NaCl, 10mM EGTA, 3mM MgCl2, 2% glycerol, 2% triton-100) and a 3:100 dilution of HALT phosphatase-protease cocktail (Thermo Scientific #1861281). 10 ug of protein was calculated using Pierce BCA Protein Assay Kit (ThermoFisher #23225) and loaded onto a 10% polyacrylamide gel with Laemmli sample buffer (BioRad #1610747) with fresh 2-mercaptoethanol (Fisher #BP176) ran through a 10% gel and transferred onto a PVDF Transfer Membrane (Thermo Scientific #88518). Membrane was blocked for 1 hour in 5% BSA (Equitech-Bio Inc #190524). Probed with primary antibody P-Ezrin(Thr567) (Cell Signaling #3149S), ezrin (Abcam #4069), moesin (ab169789), radixin (ab50238) and β-Actin (Sigma #A1978). Probed with goat anti-mouse (ThermoFisher #G21040) or goat anti-rabbit (ThermoFisher #G21234) secondary antibody conjugated with horseradish peroxidase. Secondary antibodies were detected through enhanced chemiluminescence (100 mM Tris pH 8.5, 1.2 mM luminol, 2.5 mM p-coumaric acid, and 0.04% hydrogen peroxide on a G:BOX (Syngene) equipped with a Synoptics 4.2-megapixel camera and controlled with Genesys software (Syngene).

To quantify band intensity, bands were manually identified using ImageJ software and the mean intensity value was normalized by the mean band intensity for a loading control (either total ezrin or actin). If necessary, blot images were inverted prior to analysis by subtracting the band dark value from the image saturation value (255).

Analysis of Temporal Relationships between Protrusion and GFP-ezrin Intensity

We performed several experiments to confirm that our observation of ezrin depletion before protrusion was not an artifact. To determine if the newly protruding region of lamellipodium is simply thinner than the established cortical region, we performed 3D light sheet microscopy of cells adhering to glass coverslips. Optical reslicing of this 3D data to show the profile of a cell during lamellipodial protrusion confirms that, within the limitation of the diffraction limit of light imaging, the newly protruding lamellipodium does not appear to be substantially thinner than the established lamellipodium (Figure S1). To confirm this result quantitatively and to exclude the possibility that a lamellipodial protrusion somehow restricts access of fluorescent markers from entering a protrusion, we analyzed the relationship between protrusion and intensity of a freely diffusing fluorophore in the cell’s cytosol. This analysis shows that the intensity of a cytosolic fluorophore in the second layer shows no relationship with protrusion onset or maximum velocity (Figure S6). Thus, we conclude that the reduction in ezrin is not due to a thinner protrusion or restricted access of a fluorophore to a protrusion. Finally, to eliminate any inaccuracies in the identification of the cell’s edge during protrusion, we performed image segmentation and edge velocity measurement on images of a cell membrane marker (tdTomato membrane) instead of GFP-ezrin. Linescans of a protrusion clearly show the cell edge movement via the tdTomato membrane signal, whereas the GFP-ezrin signal is reduced in the protrusion, although it quickly reaches similar intensity to the non-motile areas after protrusion (Figure S7). The GFP-ezrin intensity measurements were aligned to windows determined based on image masks of the tdTomato membrane images, so GFP-ezrin intensity measurements at the cell edge were not biased by the concentration of GFP-ezrin.

Time Series Analysis

The software used for this analysis is available at https://github.com/DanuserLab. To study dynamic subcellular activities relative to edge motion, we computationally tracked the cell boundary movement over time and subsequently defined a cell-shape invariant coordinate system allowing registration of movement and signaling. The cell boundaries were segmented using intensity thresholding using the tdTomato-membrane so that possible reductions in GFP-ezrin at the cell edge would not result in an inaccurate cell edge measurement. To calculate locally the displacement of the cell edge we morphed the segmented cell outlines between consecutive time points using the morphodynamic profiling algorithm previously described (Ma et al., 2018).

Upon definition of the cell edge motion, the segmented cell masks were partitioned into sampling windows of size 8×4 pixels (∼1 mm × 0.5 μm) using contour lines and ridges in the Euclidean distance transform map to the cell edge. One of the windows within the outermost layer at the first time point was set to be the origin. The location was propagated through time frames using the information of edge displacements calculated as above.

To identify the edge motion events, we first smoothed the edge velocity map by representing the motion time series of an individual window by a smoothing spline, computed with a Matlab function csaps() and manually chosen smoothing parameters. We identified the time points and locations where the smoothed velocities are positive (negative) as a protrusion (retraction) phases. Protrusion/retraction periods shorter than 25 seconds were excluded. Within each sampling window, the beginning time points of protrusion/retraction phases was then detected as the protrusion/retraction onsets. Within each protrusion/retraction period, the time points with the maximum/minimum smoothed velocities were also detected. To capture the local dynamics of ezrin intensity around the edge motion events, we first normalized time courses of ezrin intensity in each window by subtracting its mean and dividing by its standard deviation. We then locally sampled the normalized activities within ±40 sec before and after the motion events. Additional information about the computation was previously described(Azoitei et al., 2019)

Hidden Markov Modeling

To identify the temporal behaviors of edge velocity maps, we implement the hidden Markov modeling to the velocity map data, computed with the R package ‘depmixS4’ and the functions within (Visser and Speekenbrink, 2010). The modeling works with an input of pre-determined number of states and time series data which output the hidden state time series determined by the average and variance of the data within each state. The seed is initialized prior to model fitting by the function set.seed() for consistent output.

To have uniform criteria of state selection among different cells, we concatenate all the velocity time series into a single long vector with missing values connected. The data is saved as a depmix object and computed using the fit() function without setting initial transition probability. The package also supports multivariate time series computation that seems appropriate for our data. However, velocity data that is outside the range of 5 standard deviations is imputed as a NaN (Not a number) which give us time series with missing data. To deal with missing values within windows, we decided to consider the whole data as a single vector. The model computation is iterated until there is no significant change in likelihood.

The HMM was computed with increasing number of states until the minimum proportion of a single state reached 5 %. For the case of 12 WT cells and 6 TD cells, 8 states were chosen which gave good interpretation of the states by their average velocity. This method provides an interpretable clustering of time series data superior to Gaussian mixture modeling (GMM). The advantage of the HMM over the GMM is that the state isn’t strictly determined by a single time point but its previous data point. This gives a much smoother state selection that well represents the temporal dynamics of edge velocity maps.

For the temporal behaviors of ezrin & Arp2/3 localization, the Markov state selection was dominated by low frequency signals mostly representing the subcellular intensity level. Given that our interest was the sudden increase or decrease of signals related to the velocity dynamics, we implemented a low frequency normalization technique that adjusts the width of the temporal autocorrelation of the ezrin intensity signal to the width of the temporal autocorrelation of the velocity fluctuations. Using the fact that the full cycle of edge velocity is 40 frames (80 seconds), we subtract the median time series of a 60 frame moving window from the raw ezrin time series. This method removes variations in the signals with a quasi-periodicity longer than 120 seconds, which are unrelated to variations associated with the protrusion/retraction cycles. After this low frequency normalization, the hidden Markov model was computed for the concatenated time series from 5 cells. The signals were classified into 4 states ordered by the average intensity levels. We further combine the top 2 and bottom 2 states as high and low activity states. This was due to the fact that the HMM modeling with 2 states were mainly driven by the local variance of the activities, not the average intensity. This problem disappeared after choosing more than 3 states. To account for differential ezrin intensity values in different cells, the GFP-ezrin intensity for each cell was normalized to fall between 0 and 1. The values shown in Figure 4E represent the mean values over all windows in all cells measured.

Statistical Comparisons

In our experience, the greatest source of variation in cell edge fluctuations arises from cell-cell variability. Therefore, statistical comparisons between cells expressing wild type and mutant ezrin are performed on a per-cell basis, where the mean of each measurement for each cell represents one data point.

U2OS Cells

Protrusion initiation frequency was analyzed by counting the total protrusion events per cell as classified by HMM velocity states with mean greater than zero. Events were counted per window and then a mean (protrusions/window) was calculated for each cell. To avoid influence of frequent spurious events, only protrusions longer than 25 seconds were included in this analysis. We were not able to identify an appropriate probability distribution function to model the single cell distribution of protrusion initiation events per window, so we used a two sample t-test with equal variances to compare protrusion initiation event frequency between cells expressing WT and TD ezrin on a per cell basis. A Wilcoxan rank sum test of this comparison yields a significance of p = 0.0182.

A probability distribution function that fits the velocity data for each cell could not be found, therefore cells were compared via a t-test of the mean protrusion velocities measured for each cell. These differences were also significant according to a Wilcoxan rank sum test (p = 0.0245). To exclude the effect of rare but numerically more influential protrusion velocity values, we excluded velocity values greater than 20 nm/s from this analysis. The excluded velocity measurements accounted for less than 20% of all measurements across all cells.

For the comparisons between Arp2/3 and ezrin levels, the statistical tests were again performed on a cell-by-cell basis. For each condition, the Poisson ratio of protrusion events/total measurements windows was calculated per cell. T-tests on the resulting mean values produced p-values <0.01 for all comparisons shown in Figure 5C. A Wilcoxan rank sum test for these same comparisons produced p-values < 0.05. For the PA-Rac1 experiment, the Wilcoxan rank sum test yielded p = 0.0079.

MV3 Cells

Protrusion initiation frequency and duration was quantified by identifying protrusion events as classified by HMM velocity states with mean greater than zero. For protrusion frequency, events were counted per window and then a mean (protrusions/window) was calculated for each cell. The MV3 exhibited more spurious fluctuations than the U2OS cells, so we excluded protrusions shorter than 5 frames or longer than 25 frames and only included protrusions with speeds greater than 10 nm/s.

A non-parametric Wilcoxan rank sum test for DMSO vs NSC yielded the following p values: p (velocity) = 0.0522 and p (frequency) = 0.0649.

Estimating the Effect of Ectopic Expression of Mutant T567D Ezrin

Combining the definition of the ezrin-actin dissociation constant (Equations 1) and the ezrin mass balance (2):

$$K_D=\frac{[E][A]}{[EA]}$$ (Equation 1)

$$\left[E_{total}\right]=[E]+[EA]$$ (Equation 2)

we find a relation for the concentration of bound ezrin (Equation 3)

$$[EA]=\frac{\left[E_{total}\right][A]}{\left(K_D+[A]\right)}$$ (Equation 3)

which when substituted into the definition of the bound ezrin fraction (Equations 4) gives a relation between the ezrin bound fraction and the dissociation constant (5).

$$f_b=\frac{[EA]}{\left[E_{total}\right]}=\frac{[A]}{\left(K_D+[A]\right)}$$ (Equation 4)

$$K_D=\frac{[A]}{f_b}-[A]=[A]\left(1/f_b-1\right)$$ (Equation 5)

Considering the ratio of binding constants for wild type and mutant ezrin and using the fractional binding of WT and TD ezrin from Fritzsche et al., 2014 ($f_b^{WT}=0.1$; $f_b^{TD}=0.6$), we find (Equation 6):

$$\frac{K_D^{WT}}{K_D^{TD}}=\frac{\left(1/f_b^{WT}-1\right)}{\left(1/f_b^{TD}-1\right)}=13.5$$ (Equation 6)

The fraction of the TD ezrin bound to actin, relative to the total bound ezrin, is expressed as:

$$\frac{\left[E_{TD}\right][A]/K_D^{TD}}{\left[E_{WT}\right][A]/K_D^{WT}+\left[E_{TD}\right][A]/K_D^{TD}}=\frac{\left[E_{TD}\right]}{\left[E_{WT}\right]K_D^{TD}/K_D^{WT}+\left[E_{TD}\right]}$$ (Equation 7)

We plot the fraction of bound mutant ezrin as a function of the ratio between endogeneous ezrin and ectopically expressed mutant ezrin (Figure S2). We can see from this curve that even at a low expression of mutant ezrin relative to endogeneous (i.e. 0.25 ratio or 1:4 TD;WT), most (i.e. 77%) of the bound ezrin is the T567D mutant exhibiting higher affinity and thus reduced unbinding. Higher expression of T567D ezrin relative to wild type only increases the fraction of bound ezrin. At expression ratio 1:1 more than 90% of the bound ezrin is of the mutant form. Thus, we conclude that despite the presence of wild type ezrin, ectopic overexpression of mutant ezrin has the intended effect of increasing actin-membrane attachment.

QUANTIFICATION AND STATISTICAL ANALYSIS

In our experience, the greatest source of variation in cell edge fluctuations arises from cell-cell variability. Therefore, statistical comparisons between cells expressing wild type and mutant ezrin are performed on a per cell basis, where the mean of each measurement for each cell represents one data point. The number of cells and p-value for each comparison presented in the main text is given in the figure legend.

U2OS Cells

Protrusion initiation frequency was analyzed by counting the total protrusion events per cell as classified by HMM velocity states with mean greater than zero. Events were counted per window and then a mean (protrusions/window) was calculated for each cell. To avoid influence of frequent spurious events, only protrusions longer than 25 seconds were included in this analysis. We were not able to identify an appropriate probability distribution function to model the single cell distribution of protrusion initiation events per window, so we used a two sample t-test with equal variances to compare protrusion initiation event frequency between cells expressing WT and TD ezrin on a per cell basis. A Wilcoxan rank sum test of this comparison yields a significance of p = 0.0182.

A probability distribution function that fits the velocity data for each cell could not be found, therefore cells were compared via a t-test of the mean protrusion velocities measured for each cell. These differences were also significant according to a Wilcoxan rank sum test (p = 0.0245). To exclude the effect of rare but numerically more influential protrusion velocity values, we excluded velocity values greater than 20 nm/s from this analysis. The excluded velocity measurements accounted for less than 20% of all measurements across all cells.

For the comparisons between Arp2/3 and ezrin levels, the statistical tests were again performed on a cell-by-cell basis. For each condition, the Poisson ratio of protrusion events/total measurements windows was calculated per cell. T-tests on the resulting mean values produced p-values <0.01 for all comparisons shown in Figure 5C. A Wilcoxan rank sum test for these same comparisons produced p-values < 0.05.

For the PA-Rac1 experiment, the Wilcoxan rank sum test yielded p = 0.0079.

MV3 Cells

Protrusion initiation frequency and duration was quantified by identifying protrusion events as classified by HMM velocity states with mean greater than zero. For protrusion frequency, events were counted per window and then a mean (protrusions/window) was calculated for each cell. The MV3 exhibited more spurious fluctuations than the U2OS cells, so we excluded protrusions shorter than 5 frames or longer than 25 frames and only included protrusions with speeds greater than 10 nm/s.

A non-parametric Wilcoxan rank sum test for DMSO vs NSC yielded the following p values: p (velocity) = 0.0522 and p (frequency) = 0.0649.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
P-Ezrin(Thr567)	Cell Signaling	3149S; RRID: AB_823497
ezrin	Abcam	4069; RRID: AB_304261
moesin	Abcam	ab169789
radixin	Abcam	ab50238; RRID: AB_882260
β-Actin	Sigma	A1978; RRID: AB_476692
goat anti-mouse HRP	ThermoFisher	G21040; RRID: AB_2536527
goat anti-rabbit HRP	ThermoFisher	G21234; RRID: AB_2536530
Chemicals, Peptides, and Recombinant Proteins
McCoy’s Medium	Gibco	16600108
Neurobasal medium	Gibco	21103049
B27	Gibco	17504044
glutamine	Gibco	25030081
penicillin streptomycin	Gibco	15140148
fetal bovine serum	Gibco	16000044
DMEM	Gibco	12430054
puromycin	Gibco	A1113802
G418	ThermoFisher	10131027
trypsin/EDTA	Gibco	15400054
Pepsinized bovine collagen I	Advanced Biomatrix	5005
Unpepsinized bovine collagen I	Advanced Biomatrix	5026
phenol red free DMEM containing 25mM HEPES	Gibco	21063029
Alexa Fluor™ 568 NHS Ester	ThermoFisher	A20103
Laemmli sample buffer	BioRad	1610747
2-mercaptoethanol	Fisher	BP176
PVDF Transfer Membrane	Thermo Scientific	88518
Bovine Serum Albumin	Equitech-Bio	190524
Experimental Models: Cell Lines
Human Osteosarcoma U2OS	Laboratory of R. McIntosh, University of Colorado, Boulder CO	N/A
Human Melanoma MV3	Laboratory of Peter Friedl, MD Anderson Houston TX	N/A
Experimental Models: Organisms/Strains
Sprague Dawley rats	Charles River Laboratories, Wilmington, MA	Strain Code 001
Oligonucleotides
Arp3 1gRNA forward caccgttggagtcatgtcgtaaaat	Integrated DNA Technologies	N/A
Arp3 1gRNA reverse aaacattttacgacatgactccaac	Integrated DNA Technologies	N/A
Arp3 2gRNA forward caccgggattgtgacgacaaatgct	Integrated DNA Technologies	N/A
Arp3 2gRNA reverse aaacagcatttgtcgtcacaatccc	Integrated DNA Technologies	N/A
Recombinant DNA
pLVX vector	Clontech	632183
PRL3	Maja Khön, University of Freiburg, Germany	N/A
CIBN-CAAX	Addgene	79574
GFP-ezrin	Addgene	20680
GFP-ezrinT567D	Addgene	20681
mCherry-CRY2-iSH2	Addgene	66839
PA-Rac1	Yi I. Wu, University of Connecticut Health Center, Farmington, CT	N/A
tdTomato-CAAX	Laboratory of Claire Waterman (NIH, Bethesda MD)	N/A
Software and Algorithms
u-Shape3D	3D analytical software, Matlab platform	https://github.com/DanuserLab
Windowing-Protrusion	Dynamic protrusion analysis software, Matlab platform	https://github.com/DanuserLab
depmixS4	Hidden Markov Model fitting software, R platform	https://cran.r-project.org/web/packages/depmixS4/index.html
ImageJ		http://fiji.sc/
Other
LED array	BTF lighting, Amazon.com	N/A

Highlights.

• Actin and pressure-driven protrusions are triggered by actin-membrane detachment

• Increased actin polymerization is not sufficient to initiate protrusion

• Increased actin-membrane attachment reduces protrusion

• Stimulated decreases in actin-membrane attachment induce protrusion