Abstract
The purpose of this study is to compare the effect of the different physical factors on low-density lipoproteins (LDL) accumulation from flowing blood to the arterial wall of the left coronary arteries. The three-dimensional (3D) computational model of the left coronary arterial tree is reconstructed from a patient-specific computed tomography angiography (CTA) image. The endothelium of the coronary artery is represented by a shear stress dependent three-pore model. Fluid–structure interaction () based numerical method is used to study the LDL transport from vascular lumen into the arterial wall. The results show that the high elastic property of the arterial wall decreases the complexity of the local flow field in the coronary bifurcation system. The places of high levels of LDL uptake coincide with the regions of low wall shear stress. In addition, hypertension promotes LDL uptake from flowing blood in the arterial wall, while the thickened arterial wall decreases this process. The present computer strategy combining the methods of coronary CTA image 3D reconstruction, simulation, and three-pore modeling was illustrated to be effective on the simulation of the distribution and the uptake of LDL. This may have great potential for the early prediction of the local atherosclerosis lesion in the human left coronary artery.
Subject terms: Biomedical engineering, Computational biology and bioinformatics
Introduction
According to the report from the American Heart Association (AHA), coronary atherosclerosis accounts for over 30% of cardiovascular diseases1. Previous studies suggested that atherosclerosis lesion regions usually held local complex hemodynamic forces, such as vortex and oscillatory shear2. Hemodynamic studies found that the blood flow is always complex around the arterial bifurcations where atherosclerosis lesions usually occur3. Many pieces of evidence suggested that the initiation and progression of the atherosclerotic disease involves a significant accumulation of low-density lipoproteins (LDL) in the arterial wall4,5. Due to the high clinical incidence of coronary atherosclerosis, it is of great clinical significance to study the distribution of hemodynamic parameters and the accumulation of LDL in the coronary artery.
Previous studies revealed that atherosclerotic plaque predisposed area coincides with the regions of high LDL concentration distribution6,7. However, concentration distribution alone cannot explain the focal accumulation of LDL within the arterial wall. Endothelium is a major barrier of the LDL transport from the artery lumen into the vessel wall8. There are two pathways for LDL via the endothelium: (1) vesicles absorb LDL from plasma by receptor-mediated endocytosis; (2) LDL directly pass through endothelium by leaky junctions9. Early experimental studies have shown that more than 90% of LDL transport into the arterial wall through leaky junctions while only less than 10% of LDL flux via vesicular pathway10. However, the leaky junctions-based pathway is associated with endothelial cells in the state of mitosis or apoptosis11. Researches showed that the fraction of leaky junction on endothelium is influenced by the shear stress on the luminal surface12.
The arterial wall included multi-layers in physiologically. It was widely known that the distribution of the flow filed in arteries is co-regulated by all layers of the wall. Moreover, the LDL transport in the flowing blood is controlled by the convection–diffusion equation. To study the LDL transport to the arterial wall, previous researchers proposed many models for the representation of the multi-layer arterial wall, such as the four-layer model and the single-layered model13–17. However, these studies were based on the CAD-generated models that were unphysiological. In the current work, we want to go further than the existing literature on predicting the distribution and the uptake of LDL in the coronary arterial wall. To predict the LDL accumulation in the arterial wall, we introduced a three-pore model to represent the endothelium11,18. This model is fully taking account of the contribution of the vesicular pathway, normal junctions, and leaky junctions to the transport of LDL from lumen to the arterial wall. According to the three-pore model, LDL transport was greatly governed by the local wall shear stress ()12, therefore, it was of great clinical significance to figure out which factors may be the key cause of disturbing the blood flow. Moreover, the numerical model was generated from a patient-specific CTA image, which made the study model closer to physiological conditions. Complex vascular geometric structure and pulsatile could lead to a spatial and temporal alterations of blood flow in the human arterial system19. This made difficult to measure in vivo. Fortunately, fluid–structure interactions () technique is capable of capturing arterial wall move and flow change with high time and spatial resolution. In this study, two-way fully coupled simulations were carried out to capture the real-time changes of the intravascular flow field. The numerical simulations were performed with ANSYS 14.0 software. Hemodynamic parameters such as time-averaged wall shear stress (), oscillatory shear index (), relative residence time () and time-averaged wall shear stress gradient () were analyzed in the present study20–22.
Methods
Reconstruction of left coronary artery models
The CTA image used in this study came from a patient by medical examination in the Guangdong General Hospital. The voxel size of the coronary CTA image was 0.5 × 0.5 × 0.5 mm. This study was approved by the Research Ethics Committee of the Guangdong General Hospital, Guangdong Academy of Medical Sciences and conformed to the principles outlined in the Declaration of Helsinki.
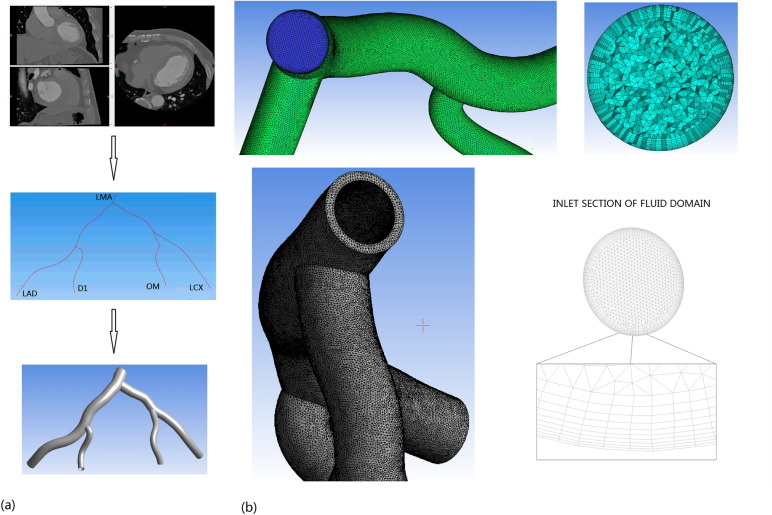
Many good results were analyzed with the use of Computer-Aided Design (CAD)-generated arteries in the previous studies23,24. However, these geometric models deviated from the physiological characteristics to a certain extent. In this study, the 3D fluid domain, as shown in Fig. 1a, was generated from the CTA image of a patient-specific left coronary artery. The first step was to extract and refine the centerline of the human left coronary arteries with the use of MIMICS software. The centerlines were formed by a series of center points that are located at the center of the cross-sectional plane of the 3D coronary artery. Then proceed as follows, dividing along the centerline to obtain circle borders of the human left coronary arteries on the vertical plane of the centerline, sweeping the circle borders, guided by the centerlines, to obtain the 3D model of the human left coronary artery. Lastly, we meshed the reconstructed model with the use of ANSYS ICEM-CFD software.
Figure 1.
Reconstruction of 3D human left coronary artery. (a) Reconstructed human left coronary artery from the original CT coronary data of a 54-year-old male patient. LMA left main coronary artery, LAD left anterior descending artery, LCX left circumflex artery, D1 first diagonal branch of the LAD, OM left obtuse marginal branch. (b) Meshes of blood-phase & arterial wall of human left coronary artery.
A typical structure of an arterial wall includes six layers. These layers are glycocalyx, endothelium, intima, internal elastic lamina, media, and adventitia, respectively. To simplify the numerical model in this study, the arterial wall was regarded as a single-layer with constant thickness. In our present study, the coronary arterial wall was given the thicknesses of and for the normal and thickened wall cases, respectively25.
Fluid and solid mesh was generated in ANSYS ICEM-CFD and ANSYS WORKBENCH-MESH, respectively. The mesh independence was considered achieved when the variation of , , and were less than 3% between two successive simulations (see Supplementary materials). The fluid mesh consisted of 2,474,927 elements with 10 prismatic layers near the wall, and the solid mesh for the arterial wall thickness of 0.53 mm and 0.77 mm contained 61,432 elements and 79,252 elements, respectively (Fig. 1b). The pulsatile transient simulations were carried out for three full cardiac cycles with the uniform time step of 0.01 s. The data for analysis were obtained at the third cardiac cycle.
Governing equations
It was well known that blood flow is a non-Newtonian fluid in physical, especially for the blood flow in micro-vessels. Many numerical studies on LDL transport problems were based on non-Newtonian assumption by previous researchers24,26. Moreover, previous studies suggested that the shear-thinning and viscoelastic of blood are essential factors that affect the blood flow under various flow rates27,28. The non-Newtonian models such as sPTT model, Giesekus model, and Carreau model can obtain relatively accurate results than using Newtonian model27, however, they are not convenient to study the effect of a specific viscosity on the flow. Hence, to study the effect of different viscosity on the LDL uptake, the blood flow here is assumption as homogeneous and incompressible blood with Newtonian rheology, the fluid dynamics in the artery lumen can be described by the Navier–Stokes equation. The governing equations of mass, momentum, and species were as follows,
| 1 |
| 2 |
| 3 |
where and are the fluid velocity vector and pressure, () and ( and for normal and hyper-viscosity cases, respectively) are the blood density and viscosity, is the fluid domain body force (in our present study, is zero), is the LDL concentration, and is the free diffusivity coefficient of LDL which could be set as 29.
The mechanism of the LDL transport into the vessel wall is in large measure determined by the endothelium. In this study, a three-pore model was introduced to describe LDL uptake on the left coronary arterial wall (see Supplementary materials), which was taking account of the contribution of the vesicular pathway, normal junctions, and leaky junctions as well as employing the local to obtain the total LDL mass flux11,14,30,31.
The arterial wall was considered as an elastic homogeneous material with a density of , a Poisson’s ratio of , and an isotropic Young’s modulus (E) of 32. The conservation equation of the solid part can be derived from Newton's second law of motion. The elastic-dynamic equation can be represented by
| 4 |
where is the density of arterial wall, is the acceleration within the solid region, is the Cauchy stress tensor, and is the solid domain body force.
Boundary conditions and computation procedures
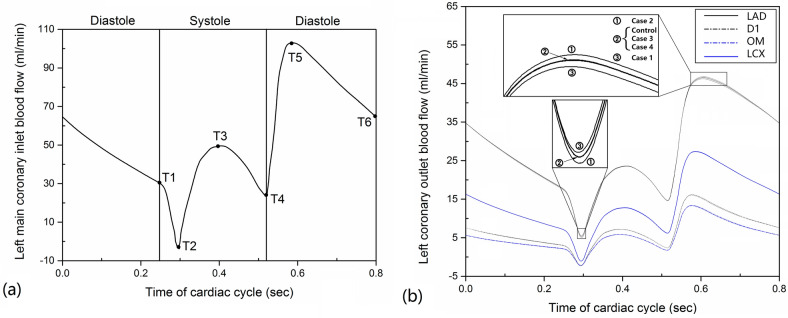
A pulsatile flat inlet flow profile in the left main coronary artery (LMA) was set based on a previous study (Fig. 2a)33. Pressure-outlet boundary conditions were used at the four inferior ends of the fluid domain, and non-slip boundary condition was specified at the luminal wall. Fully constrained boundary conditions were applied on the edge of the LMA, left anterior descending artery (LAD), first diagonal branch of the LAD (D1), left circumflex artery (LCX) and left obtuse marginal branch (OM) to give stability to the structural calculation. and were applied at the wall for normal and hypertensive cases, respectively13,33,34. A constant LDL concentration profile equal to , corresponding to the physiological LDL concentration in whole blood (bulk fluid concentration)13, was prescribed at the LMA inflow section. At each outflow section of the left coronary artery, were applied. At the luminal surface, the boundary conditions of LDL lumen-to-wall transfer were referenced to previous studies6,7,21.
Figure 2.
Pulsatile blood flow in human left coronary arteries. (a) A pulsatile inlet flow profile of the LMA. (b) Pulsatile outlet flow profiles of four coronary branch ends for the five simulation cases. Inserts are the pulsatile outlet flow profiles of the LAD. Case 1, Case 2, Case 3, and Case 4 respectively represent the condition of rigid wall, blood viscosity, blood pressure, wall thickness. Control represent the healthy condition.
To study the effect of the different factors on the LDL transport via endothelium, five cases were performed. The Control case represented a healthy individual. To study the effect of the elastic property of the arterial wall, a Case with a rigid wall was studied. The numerical simulations were performed with ANSYS 14.0 software. The details of five numerical calculations were as follows.
Control: , ,
Case 1: , ,
Case 2: , ,
Case 3: , ,
Case 4: , ,
Hemodynamic parameters
The characteristic time of endothelial cell response to shear stress in terms of mitosis or apoptosis was much longer than that of shear oscillation35. Therefore, the following time-averaged hemodynamic parameters were used to characterizing the response of endothelial cells to the blood flow36.
| 5 |
| 6 |
| 7 |
| 8 |
where T is the duration of the cardiac cycle. is the WSS vector which is defined as the scalar dot product of the unit normal vector to a surface and the viscous stress tensor37. , , and , are the partial derivatives with respect to the , and coordinates, respectively. represented the time-averaged magnitude of the WSS during the cardiac cycle(s). If is less than 1 Pa, intimal thickening occurs38. The OSI is employed to describe the oscillatory nature of the WSS throughout the cardiac cycle; and the RRT is included the effects OSI and , that is employed to identify regions in which high particle residence time occur37,38.
Ethics approval
This study was approved by the Research Ethics Committee of the Guangdong General Hospital, Guangdong Academy of Medical Sciences, and was performed per the Declaration of Helsinki.
Informed consent
The need of informed consent was waived by the Research Ethics Committee of the Guangdong General Hospital, Guangdong Academy of Medical Sciences.
Results
The change of blood flow flux with the cardiac cycle
For all the cases, LAD has the largest flow flux over all the time, followed by LCX, D1, and OM, respectively (Fig. 2b). Moreover, there is a deviation of flow rate among the five cases during the cardiac cycles, especially at the periods of early-systole and early-diastole. This suggested that the blood flow flux at the periods of early-systole and early-diastole are easily disturbed by external conditions. In detail, at the period of early-systole, Case 1 shows the highest blood flow rate in the arterial ends of LAD while Case 2 indicates the smallest flow rate (see “insert views” in Fig. 2b). The flow rate among Control and Case 3 and Case 4 have no significant difference. However, at the period of early-diastole, the situations of flow rate are totally reversed (see “insert views” in Fig. 2b), at which Case 2 shows the highest blood flow rate.
The streamline profiles at the different periods during the cardiac cycle
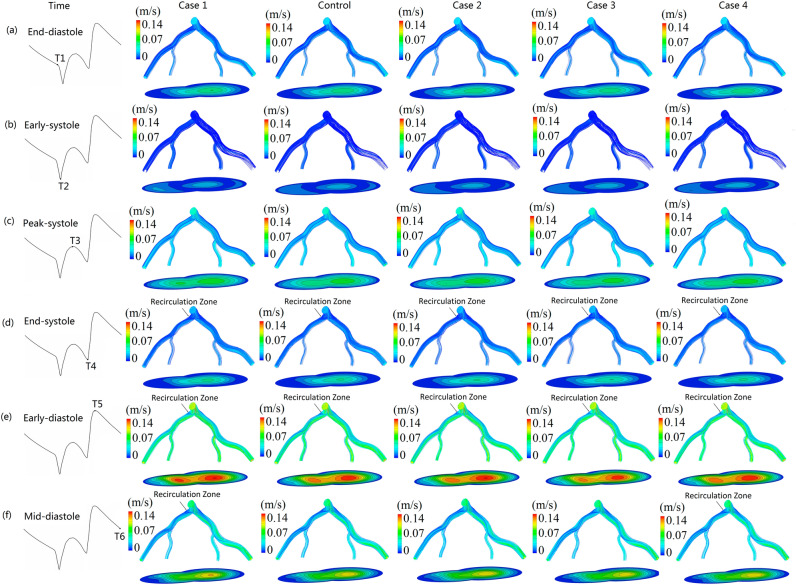
Figure 3 illustrates velocity profiles during the cardiac cycle for the five simulations. The flow patterns at the six different periods are significant difference from each other. Precisely, the coronary system keeps the smallest velocity at the period of early-systole while it holds the largest velocity at the period of early-diastole. At the period of early-diastole, strong secondary flow and recirculation zone at bifurcation regions can be observed. At the period of mid-diastole, the size of recirculation zone at bifurcation regions are different among the five cases (Fig. 3f). In detail, Case 1 has the largest recirculation zone in the bifurcation regions, followed by Case 4. However, there is no clear recirculation zone appearing in the bifurcation regions for the simulations of Case 2, Case 3, and Control. This suggested that rigid and thickened arterial hold the most complex flow at the bifurcation regions. As the elasticity of vessel decreased when the arterial wall thickness increased39, consequently, the thickened wall of the coronary artery will have lower elastic property when compared with non-thickened ones. In other words, superior elasticity of the arterial wall could decrease the complexity of the local flow field in the coronary bifurcation system.
Figure 3.
Streamlines and velocity profiles during the cardiac cycle for the five simulation cases. The marked points T1–T6 (a–f), respectively denote end-diastole, early-systole, peak-systole, end-systole, early-diastole, mid-diastole.
The distribution of hemodynamic parameters on the luminal wall
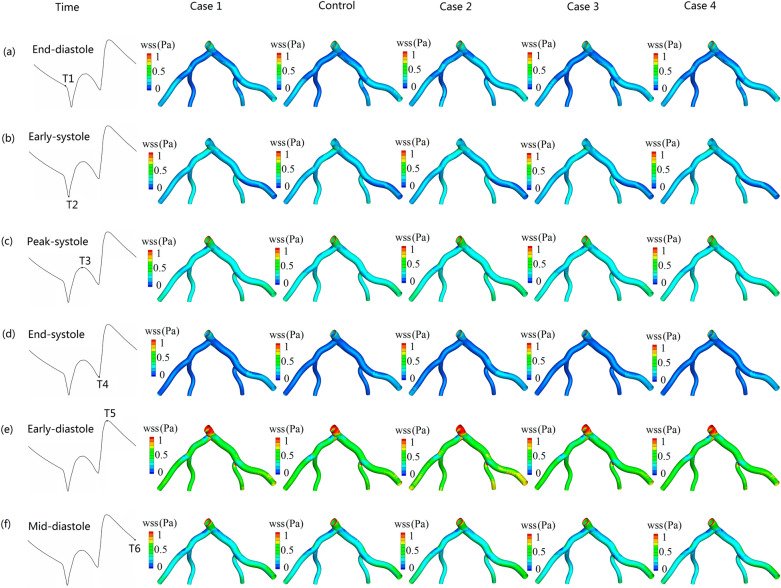
Figure 4 shows the distributions during the cardiac cycle for the five simulations. The results show that the at the deceleration period of cardiac cycle is lower than that at the acceleration period of cardiac cycle, especially at the period of end-deceleration. For all the simulations, at the period of end-systole, the luminal surface has the lowest , followed by the period of end-diastole. However, at the period of early-diastole, the luminal surface has the highest .
Figure 4.
Wall shear stress distributions during the cardiac cycle for the five simulations. (a–f), respectively, represent the period of end-diastole, early-systole, peak-systole, end-systole, early-diastole, mid-diastole.
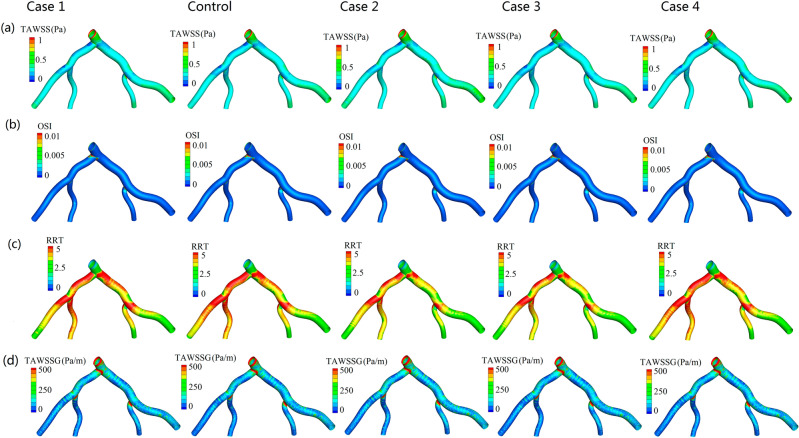
Figure 5a–d respectively displays the distribution of time-averaged hemodynamic parameters of , , and for the five cases. The distribution of these time-averaged hemodynamic parameters for all the simulation conditions are similar among the five cases. The of Case 2 is slightly higher than that of the other four cases (Fig. 5a). The regions with low , high are near the vascular bifurcations (Fig. 5a,b). Moreover, the in upstream and outside of LCX is relatively lower when it is compared with the downstream and inner wall. Results show that high- regions on the arterial wall are mainly located at the low- regions (Fig. 5a,c). Large areas of low are located at the downstream of four branch arteries (Fig. 5d). Extremely high can be easily found in the regions of vascular bifurcation, such as the bifurcation of LAD and LCX.
Figure 5.
Wall shear stress-based hemodynamic indicators distributions for the five simulations. (a) The distribution of time-averaged wall shear stress. (b) The distribution of oscillatory shear index. (c) The distribution of relative residence time. (d) The distribution of time-averaged wall shear stress gradient. time-averaged wall shear stress, oscillatory shear index, relative residence time, time-averaged wall shear stress gradient.
The distribution of three-pore model related indicators on the luminal wall
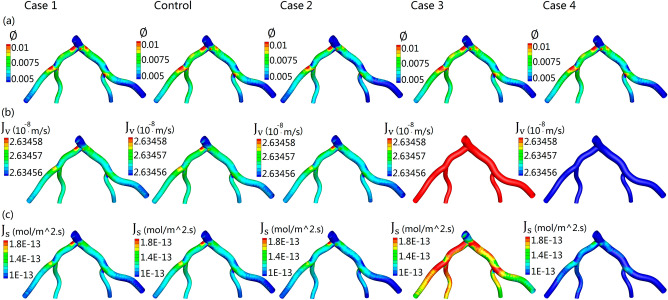
Figure 6a showes the fraction of leaky junctions () distribution on endothelium for the five simulation cases. The distribution of on the arterial wall is similar among the five cases. The regions of high consistent with the places of low regions (Figs. 5a, 6a). Figure 6b,c respectively shows the fluid volume fluxes and LDL mass fluxes through the endothelium for the five simulation cases. Higher fluid volume flux () regions are mainly located at the outer wall of LAD and LCX where the was relatively low (Figs. 5a, 6b). The values of for Case 3 are significantly higher than that of the other four cases, while Case 4 had the lowest among the five cases (Fig. 6b). Moreover, the value of on the LCX and OM is relatively higher than that on the LAD and D1. The highest value occurs at bifurcations where the LMA stem branches into LAD and LCX, the value at which is as high as . Low regions are mainly located at inner side of twisting arteries, the lowest value is under . According to the three pore-model, the value of into the arterial wall is not only determined by volume fluxes, but also by the concentration of LDL on the near wall. Moreover, the LDL transport in the bloodstream is calculated by the convection–diffusion equation (Eq. 3). As the distribution of all the hemodynamic parameters (TAWSS, OSI, RRT, TAWWSG) for the five different cases is similar from each other (Fig. 5a–d), hence, the distribution of LDL on the luminal wall would be also similar too. Nevertheless, LDL concentration profiles would be changed very much at the different places in the same model of the arterial wall surfaces. Figure 6c show the distribution of LDL mass flux () through the endothelium. Case 3 has the highest while Case 4 has the lowest among the five cases. The regions with high value of are always occurred at LCX and low value regions are mainly located at the downstream of LAD and LCX and the upstream of LMA. The highest value of are mainly located at the recirculation zones where the is usually very low. Overall, the distribution trend of is similar with , but the absolute values are not completely the same between them. In addition, although the color-coded maps of didn't appear to show much difference among the five different cases, and are still showing significant differences among the five different cases, especially case 3 (increased blood pressure) and case 4 (increased wall thickness).
Figure 6.
Three-pore model related indicators for the five simulations. (a) The distribution of the fraction of leaky junctions on endothelium () of human left coronary arteries. (b) The distribution of total plasma volume flux () through the endothelium. (c) The distribution of total mass flux of LDL ().
The distribution of the percentage difference of the and on the luminal wall
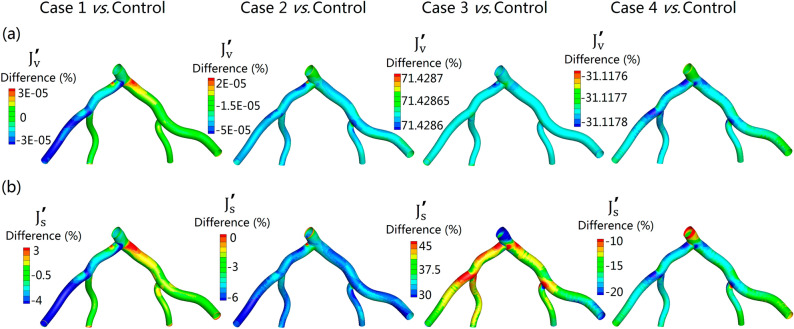
Figure 7a,b respectively shows the percentage difference of () and () between Case (1, 2, 3, 4) and Control case. The relatively high values of between rigid and elastic models (Case 1 vs. Control) are located at the regions of the outer wall of the bifurcation (from LMA into LAD and LCX) (slightly higher than 0.00003%). Moreover, all the of Case 1 vs. Control and Case 2 vs. Control in most regions are significant small (less than 0.00005%). Therefore, the value of between Case 1 and Case 2 and Control can be neglected. However, between Case 3 and Control is over 70% and the average value of between Case 4 and Control is over 30% (Fig. 7a). This phenomenon is similar to the value of , although the values between them are not completely the same (Fig. 7b). This suggested hypertension increased the plasma fluid and LDL mass flux through the endothelium, while the thickened arterial wall decreases this process.
Figure 7.
Comparison of the three-pore model related indicators for the five simulations. (a,b) respectively represent the percentage difference of () and () between different experimental groups and Control simulation. (a) , (b) . Where Case 1 vs. Control: the distribution of the percentage difference between Case 1 with rigid wall and Control. Case 2 vs. Control: the distribution of the percentage difference between Case 2 with increased blood viscosity and Control. Case 3 vs. Control: the distribution of the percentage difference between Case 3 with hypertension and Control. Case 4 vs. Control: the distribution of the percentage difference between Case 4 with thickened wall and Control.
Discussion
This paper applied an method to study the influence of different physical factors on the LDL uptake from flowing blood to the arterial wall in the left coronary artery. The results revealed that: (1) High elastic property of the arterial wall can decrease the complexity of the local flow field in the coronary bifurcation system. (2) The regions of high LDL uptake are located in the regions of low wall shear stress. (3) Hypertension can promote LDL uptake in the arterial wall, quite the contrary, thickened arterial wall can decrease the uptake of LDL.
The important feature of atherosclerosis is the narrowing of the arteries. It can block the blood flowing in the vessel. Atherosclerosis is characterized by patchy intimal plaques that encroach on the lumen of medium-sized and large arteries; the plaques contain lipids, inflammatory cells, smooth muscle cells, and connective tissue. As we know, risk factors of atherosclerosis include dyslipidemia, LDL, diabetes, cigarette smoking, family history, sedentary lifestyle, obesity, and hypertension40. There was much evidence suggesting that the initiation and progression of the atherosclerotic disease involved a significant accumulation of LDL in the arterial wall5. Moreover, a large number of LDL uptake is the key factor leading to the accumulation of LDL. Therefore, early accumulation of LDL could be the most important reason for the intimal thickening, which is the first step of the arterial narrowing (initiation of intimal thickening). Although our present study did not directly predict intimal thickening, it still can be effective in predicting the distribution and uptakes of LDL in the arterial wall. Hence, the present results may partially predict the intimal thickening according to the amounts of LDL uptakes in the coronary artery.
Previous studies showed that vascular geometric structure, such as the branches, curvatures, and bifurcations have a significant effect on the local flow field distribution41–44. Our recent research also confirms that complex flow, such as strong secondary flow and recirculation flow, are easily discovered around the bifurcation regions. In addition, the blood flow at the wide-angle bifurcations, such as LMA stem branches into LAD and LCX, are more complex when compared with the narrow-angle bifurcations (e.g. LAD branches into the D1 and the LCX branches into the OM) (Figs. 3, 4, 5). Our present study further indicates that in addition to the influence of vascular geometric structure on the blood flow field, other factors, such as the pulsatile and the elasticity of the arterial wall, also have much effect on the blood flow field (Figs. 2, 3, 4). It is shown that the flow patterns at different periods during the cardiac cycles are significantly different. The results also show that rigid wall condition leads to the largest recirculation zone and the most complex streamlines at the bifurcation regions when compared to the condition of the vascular wall with elastic properties (Fig. 3). Moreover, when flowing blood flows in the wall-thickened coronary artery, the flow field is also complex than that of the un-thickened ones. This indicates that the effect of the rigid wall and the thickened wall on the flow field are very similar. Study by Bastida et al. showed that thickened arterial wall has lower elastic property when compared with thinner arterial wall39. This suggested that the higher elasticity of arterial wall can decrease the complexity of the local flow profiles. The dysfunction of the endothelium led to atherogenesis, this process is stimulated by the complex hemodynamic forces12. Therefore, the elasticity of human blood vessels may play a self-protection role in preventing vascular atherosclerotic lesions.
For all the simulations, the regions of high blood plasma flux coincide with the regions of high LDL flux and the regions of low , high , high , and high (Figs. 5, 6). Other previous studies also indicated that LDL accumulation increased with lower wall shear stress26,45. Studies by John et al. suggested that the transport processes of LDL are determined by both blood flow and endothelium46. It was showed that the fluid mechanics may be influential when mass transfer coefficient is much smaller than the surface reaction rate coefficient (the process was termed “fluid-phase-limited”), conversely, luminal wall could be influential when mass transfer coefficient is greater than the surface reaction rate coefficient (the process was termed “wall-limited”)46. Previous studies show that blood plasma flux can not only through leaky junctions, but also through normal junctions46,47. However, LDL particles are too large to pass through normal junctions11, which means that the effect of convection effect of blood plasma transmural flow on LDL accumulation are largely affected by the percentage of leaky junctions, not normal junctions. There are two main ways for LDL particles transport through the endothelial wall, the portion of LDL transport via vesicular transcytosis mechanism is less than 10%, whereas the portion of LDL transport through leaky junctions mechanism is over 90%35. This suggested that the LDL transport into the arterial wall is largely affected by the number of leaky junctions. According to the three-pore model, the fraction of leaky junctions on endothelium is a function of local 11. The regions of low consistent with the places of a higher number of leaky junctions (Figs. 4, 5a, 6a). Hence, in the low regions, the transmural resistance on the endothelium to flow is decreased considerably33. This leads to an increase in the flux of blood plasma in those low regions of the coronary wall. Due to the convection effect of blood plasma in the leaky junctions, the increased plasma flux, in turn, leads to increased transportation of LDL particles from the lumen into the arterial wall (Fig. 6b,c).
On the other hand, increased transmural pressure also leads to an increased filtration velocity through leaky junctions, consequently, resulting in an increased convective flux of LDL through the endothelium. These results are consistent with previous numerical findings13,26,48. There are many reasons for this phenomenon. Firstly, according to the principle of fluid dynamics, higher blood pressure is usually accompanied by lower flow velocity, hence leads to lower wall shear stress. The effect of low wall shear stress on the LDL uptake has been demonstrated above. On the other hand, studies suggested that the increased transmural pressure could induce arterial wall distension and stretch, which leads to an increased number of mitosis and apoptosis49. This phenomenon will result in an increased number of leaky junctions, therefore, leads to an increase of endothelial diffusive permeability50,51. Moreover, pressure-driven convective flow at higher transmural pressure also enhances LDL uptake13. It is well accepted that the early atherogenesis tends to be hallmarked by an abnormally high accumulation of LDL7,13. Our results confirm that plasma flux and LDL mass flux of hypertension case is significantly higher than that of the control individual (Fig. 7). This suggested that that hypertension may increase the susceptibility to atherosclerosis by increasing the accumulation of LDL on the endothelium. Furthermore, as the blood pressure in the proximal end of coronary is usually greater than that in the distal end, therefore, the uptake of LDL is relatively high in the proximal end (Fig. 6). This gives us a hypothesis that the near heart arteries could be more susceptible to atherosclerosis. Therefore, it may partially be explained why atherosclerosis easily happened in large arteries, such as LMA and aorta.
Unlike the effect of blood pressure, the wall thickness played an opposite role on the uptake of LDL in coronary. The results in our recent studies show that thickened wall can act to inhibit LDL entry into the arterial wall. This may indicate that the earlier formation rate of atherosclerotic plaque is relatively faster. As the atherosclerotic plaque grew, and over time, the growth rate will become slower in the later period of plaque formation. This finding is consistent with the study by Liu et al. that the atherosclerotic plaque grows at a decreasing rate in the progression process52. Moreover, although high blood viscosity condition increases the on the arterial surface, it played a minor role in the effect of LDL uptake (Figs. 5a, 6c). This may because blood viscosity may affect the LDL transport only in the vessel lumen, but the uptake of LDL in the arterial wall could be mainly dominated by the surface passages of the endothelium53.
Limitations: All the simulations of the present study are based on a flat inflow boundary condition, and the ends of the artery branches are prescribed as constant pressures. This may not perfectly reproduce the pulse wave propagation. However, it should be pointed out that our method for the boundary conditions setting are still reasonable. It can help us to predict reasonable results on the distribution trend because the present boundary conditions set could only affect the absolute values, but not the trend. Furthermore, the arterial wall in our present study is regarded as a sing-layer with a constant thickness. The distribution of vascular wall thickness may be different along the luminal wall of the coronary arteries under the physiological conditions. However, it is unrealistic for us to build a model with different wall thicknesses along the vessel because the patient-specific CTA image used for generating the computational models is from a patient by medical examination in the hospital. There is no accurate information about arterial wall thickness, we can only obtain the contour of the blood vessel wall from the CTA image. Therefore, in this study, the parameter data of wall thickness are from the previously published paper. Another limitation of the present study is that all the simulations are based on a Newtonian fluid assumption with a constant viscosity. The shear-thinning and viscoelastic properties of blood can affect the blood flow under various flow rates. Nevertheless, this study can be convenient for us to quantitatively study the effect of different viscosities on the LDL accumulation.
Conclusions
By using the numerical method of technique for studying the LDL uptake in human left coronary arteries, we can know that high elastic property of the arterial wall can decrease the complexity of the local flow field in the coronary bifurcation system. This may suggest that the elastic property of the arterial wall is good for preventing atherosclerotic disease. Moreover, we can also know that the places of high levels of LDL uptake coincided with the regions of low wall shear stress; the thickened arterial wall can decrease the uptake of LDL; the present study revealed that hypertension significantly promoted LDL accumulating in the arterial wall. This study found that hypertension may play the chief culprit role in atherosclerotic lesions. More importantly, as the places of atherosclerosis lesion usually consistent with the regions with high LDL uptake, hence the present computer strategy has a great potential for the prediction of the local atherosclerosis lesion.
Supplementary Information
Acknowledgements
This work was supported by the National Natural Science Foundation of Guangdong Province [Grant No. 2015A030313659 (Y. Wu)], Union of National Natural Science Foundation of China -Guangdong Province [Grant No. U1401255 (J. Zhuang)], the Key Project of Natural Science Foundation of Guangdong Province [Grant No. 2019B151520071 (Y. Wu)], the Key Project of Natural Science Foundation of Guangdong Province [Grant Nos. 2017B030311010 & 2019B1515120071 (H. Huang)], the Science and Technology Program of Guangzhou [Grant No. 201510010190 (J. Zhuang)]. Guangdong Peak Project [Grant No. DFJH201802 (J. Zhuang)]. We thank Prof. Meiping Huang (Guangdong Provincial People's Hospital) provided the original CTA imaging data for this study.
Author contributions
Conceptualization, X.C. and Y.W.; methodology, X.C.; validation, X.C., J.Z., H.H. and Y.W.; data curation, X.C.; writing—original draft preparation, X.C.; writing—review and editing, J.Z., H.H. and Y.W.; funding acquisition, J.Z., and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of Guangdong Province [Grant No. 2015A030313659 (Y. Wu)], Union of National Natural Science Foundation of China -Guangdong Province [Grant No. U1401255 (J. Zhuang)], the Key Project of Natural Science Foundation of Guangdong Province [Grant No. 2019B151520071 (Y. Wu)], the Key Project of Natural Science Foundation of Guangdong Province [Grant Nos. 2017B030311010 & 2019B1515120071 (H. Huang)], the Science and Technology Program of Guangzhou [Grant No. 201510010190 (J. Zhuang)]. Guangdong Peak Project [Grant No. DFJH201802 (J. Zhuang)].
Data availability
The datasets supporting the conclusions of this article were included within the main paper.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-021-84155-3.
References
- 1.Benjamin EJ, et al. Heart disease and stroke statistics-2019 update: A report from the American Heart association. Circulation. 2019;139:e1–e473. doi: 10.1161/CIR.0000000000000659. [DOI] [PubMed] [Google Scholar]
- 2.Nerem RM. Hemodynamics and the vascular endothelium. J Biomech Eng. 1993;115:510–514. doi: 10.1115/1.2895532. [DOI] [PubMed] [Google Scholar]
- 3.Stankovic G, et al. Atherosclerosis and coronary artery bifurcation lesions: Anatomy and flow characteristics. Vojnosanit. Pregl. 2017;74:161–166. doi: 10.2298/VSP150809139S. [DOI] [Google Scholar]
- 4.Babiak J, Rudel LL. Lipoproteins and atherosclerosis. Bailliere's Clin. Endocrinol. Metab. 1987;1:515–550. doi: 10.1016/S0950-351X(87)80022-8. [DOI] [PubMed] [Google Scholar]
- 5.Wadhera RK, Steen DL, Khan I, Giugliano RP, Foody JM. A review of low-density lipoprotein cholesterol, treatment strategies, and its impact on cardiovascular disease morbidity and mortality. J. Clin. Lipidol. 2016;10:472–489. doi: 10.1016/j.jacl.2015.11.010. [DOI] [PubMed] [Google Scholar]
- 6.Liu X, Fan Y, Deng X, Zhan F. Effect of non-Newtonian and pulsatile blood flow on mass transport in the human aorta. J. Biomech. 2011;44:1123–1131. doi: 10.1016/j.jbiomech.2011.01.024. [DOI] [PubMed] [Google Scholar]
- 7.De Nisco G, et al. What is needed to make low-density lipoprotein transport in human aorta computational models suitable to explore links to atherosclerosis? Impact of initial and inflow boundary conditions. J. Biomech. 2018;68:33–42. doi: 10.1016/j.jbiomech.2017.12.009. [DOI] [PubMed] [Google Scholar]
- 8.Mundi S, et al. Endothelial permeability, LDL deposition, and cardiovascular risk factors—a review. Cardiovasc. Res. 2017;114:35–52. doi: 10.1093/cvr/cvx226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dabagh M, Jalali P, Tarbell JM. The transport of LDL across the deformable arterial wall: The effect of endothelial cell turnover and intimal deformation under hypertension. Am. J. Physiol. Heart Circ. Physiol. 2009;297:H983–996. doi: 10.1152/ajpheart.00324.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cancel LM, Fitting A, Tarbell JM. In vitro study of LDL transport under pressurized (convective) conditions. Am. J. Physiol. Heart Circ. Physiol. 2007;293:H126–132. doi: 10.1152/ajpheart.01188.2006. [DOI] [PubMed] [Google Scholar]
- 11.Olgac U, Kurtcuoglu V, Poulikakos D. Computational modeling of coupled blood-wall mass transport of LDL: Effects of local wall shear stress. Am. J. Physiol. Heart Circ. Physiol. 2008;294:H909–919. doi: 10.1152/ajpheart.01082.2007. [DOI] [PubMed] [Google Scholar]
- 12.Kim S, Giddens DP. Mass transport of low density lipoprotein in reconstructed hemodynamic environments of human carotid arteries: The role of volume and solute flux through the endothelium. J. Biomech. Eng. 2015;137:041007–0410017. doi: 10.1115/1.4028969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yang N, Vafai K. Modeling of low-density lipoprotein (LDL) transport in the artery—effects of hypertension. Int. J. Heat Mass Transf. 2006;49:850–867. doi: 10.1016/j.ijheatmasstransfer.2005.09.019. [DOI] [Google Scholar]
- 14.Chung S, Vafai K. Effect of the fluid-structure interactions on low-density lipoprotein transport within a multi-layered arterial wall. J. Biomech. 2012;45:371–381. doi: 10.1016/j.jbiomech.2011.10.002. [DOI] [PubMed] [Google Scholar]
- 15.Sun N, Wood NB, Hughes AD, Thom SA, Yun XuX. Effects of transmural pressure and wall shear stress on LDL accumulation in the arterial wall: A numerical study using a multilayered model. Am. J. Physiol. Heart Circ. Physiol. 2007;292:H3148–3157. doi: 10.1152/ajpheart.01281.2006. [DOI] [PubMed] [Google Scholar]
- 16.Iasiello M, Vafai K, Andreozzi A, Bianco N. Hypo and hyper thermia effects on LDL deposition in a curved artery. Comput. Thermal. 2018;11:2. [Google Scholar]
- 17.Sun N, Wood NB, Hughes AD, Thom SA, Xu XY. Fluid-wall modelling of mass transfer in an axisymmetric stenosis: Effects of shear-dependent transport properties. Ann. Biomed. Eng. 2006;34:1119–1128. doi: 10.1007/s10439-006-9144-2. [DOI] [PubMed] [Google Scholar]
- 18.Tarbell JM. Shear stress and the endothelial transport barrier. Cardiovasc. Res. 2010;87:320–330. doi: 10.1093/cvr/cvq146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tyfa Z, et al. Numerical simulations of the pulsatile blood flow in the different types of arterial fenestrations: Comparable analysis of multiple vascular geometries. Biocybern. Biomed. Eng. 2018;38:228–242. doi: 10.1016/j.bbe.2018.01.004. [DOI] [Google Scholar]
- 20.Wong KK, et al. Computational medical imaging and hemodynamics framework for functional analysis and assessment of cardiovascular structures. Biomed. Eng. Online. 2017;16:35. doi: 10.1186/s12938-017-0326-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li X, et al. Numerical simulation of haemodynamics and low-density lipoprotein transport in the rabbit aorta and their correlation with atherosclerotic plaque thickness. J. R. Soc. Interface. 2017 doi: 10.1098/rsif.2017.0140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rikhtegar F, et al. Choosing the optimal wall shear parameter for the prediction of plaque location-A patient-specific computational study in human left coronary arteries. Atherosclerosis. 2012;221:432–437. doi: 10.1016/j.atherosclerosis.2012.01.018. [DOI] [PubMed] [Google Scholar]
- 23.Qi N, et al. Investigation of the optimal collagen fibre orientation in human iliac arteries. J. Mech. Behav. Biomed. Mater. 2015;52:108–119. doi: 10.1016/j.jmbbm.2015.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Iasiello M, Vafai K, Andreozzi A, Bianco N. Analysis of non-Newtonian effects within an aorta-iliac bifurcation region. J Biomech. 2017;64:153–163. doi: 10.1016/j.jbiomech.2017.09.042. [DOI] [PubMed] [Google Scholar]
- 25.de Groot E, et al. Measurement of arterial wall thickness as a surrogate marker for atherosclerosis. Circulation. 2004;109:33–38. doi: 10.1161/01.CIR.0000131516.65699.ba. [DOI] [PubMed] [Google Scholar]
- 26.Iasiello M, Vafai K, Andreozzi A, Bianco N. Analysis of non-Newtonian effects on low-density lipoprotein accumulation in an artery. J. Biomech. 2016;49:1437–1446. doi: 10.1016/j.jbiomech.2016.03.017. [DOI] [PubMed] [Google Scholar]
- 27.Pinto SIS, Romano E, António CC, Sousa LC, Castro CF. The impact of non-linear viscoelastic property of blood in right coronary arteries hemodynamics—A numerical implementation. Int. J. Non-Linear Mech. 2020;123:103477. doi: 10.1016/j.ijnonlinmec.2020.103477. [DOI] [Google Scholar]
- 28.Bodnár T, Sequeira A, Prosi M. On the shear-thinning and viscoelastic effects of blood flow under various flow rates. Appl. Math. Comput. 2011;217:5055–5067. doi: 10.1016/j.amc.2010.07.054. [DOI] [Google Scholar]
- 29.Wada S, Karino T. Theoretical prediction of low-density lipoproteins concentration at the luminal surface of an artery with a multiple bend. Ann. Biomed. Eng. 2002;30:778–791. doi: 10.1114/1.1495868. [DOI] [PubMed] [Google Scholar]
- 30.Jesionek, K. & Kostur, M. The giant low-density lipoproteins (LDL) accumulation in the multi-layer artery wall model. (2014).
- 31.Chung S, Vafai K. Mechanobiology of low-density lipoprotein transport within an arterial wall–impact of hyperthermia and coupling effects. J. Biomech. 2014;47:137–147. doi: 10.1016/j.jbiomech.2013.09.030. [DOI] [PubMed] [Google Scholar]
- 32.Elkenani H, Al-Bahkali E, Souli M. Numerical investigation of pulse wave propagation in arteries using fluid structure interaction capabilities. Comput. Math. Methods Med. 2017;2017:4198095. doi: 10.1155/2017/4198095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Olgac U, Poulikakos D, Saur SC, Alkadhi H, Kurtcuoglu V. Patient-specific three-dimensional simulation of LDL accumulation in a human left coronary artery in its healthy and atherosclerotic states. Am. J. Physiol. Heart Circ. Physiol. 2009;296:H1969–1982. doi: 10.1152/ajpheart.01182.2008. [DOI] [PubMed] [Google Scholar]
- 34.Ai L, Vafai K. A coupling model for macromolecule transport in a stenosed arterial wall. Int. J. Heat Mass Transf. 2006;49:1568–1591. doi: 10.1016/j.ijheatmasstransfer.2005.10.041. [DOI] [Google Scholar]
- 35.Cancel LM, Tarbell JM. The role of mitosis in LDL transport through cultured endothelial cell monolayers. Am. J. Physiol. Heart Circ. Physiol. 2011;300:H769–776. doi: 10.1152/ajpheart.00445.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chen X, Zhuang J, Wu Y. The effect of Womersley number and particle radius on the accumulation of lipoproteins in the human aorta. Comput. Methods Biomech. Biomed. Eng. 2020;23:571–584. doi: 10.1080/10255842.2020.1752681. [DOI] [PubMed] [Google Scholar]
- 37.Mazzitelli R, Boyle F, Murphy E, Renzulli A, Fragomeni G. Numerical prediction of the effect of aortic left ventricular assist device outflow-graft anastomosis location. Biocybern. Biomed. Eng. 2016;36:327–343. doi: 10.1016/j.bbe.2016.01.005. [DOI] [Google Scholar]
- 38.Caruso MV, et al. A computational evaluation of sedentary lifestyle effects on carotid hemodynamics and atherosclerotic events incidence. Acta Bioeng. Biomech. 2017;19:42–52. [PubMed] [Google Scholar]
- 39.Bastida S, Eguiazábal J, Gaztelumendi M, Nazábal J. On the thickness dependence of the modulus of elasticity of polymers. Polymer Test. 1998;17:139–145. doi: 10.1016/S0142-9418(97)00042-1. [DOI] [Google Scholar]
- 40.White J, et al. Association of lipid fractions with risks for coronary artery disease and diabetes. JAMA Cardiol. 2016;1:692–699. doi: 10.1001/jamacardio.2016.1884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Moayeri MS, Zendehbudi GR. Effects of elastic property of the wall on flow characteristics through arterial stenoses. J. Biomech. 2003;36:525–535. doi: 10.1016/s0021-9290(02)00421-9. [DOI] [PubMed] [Google Scholar]
- 42.Kabinejadian F, Ghista DN. Compliant model of a coupled sequential coronary arterial bypass graft: Effects of vessel wall elasticity and non-Newtonian rheology on blood flow regime and hemodynamic parameters distribution. Med. Eng. Phys. 2012;34:860–872. doi: 10.1016/j.medengphy.2011.10.001. [DOI] [PubMed] [Google Scholar]
- 43.Boesen ME, Singh D, Menon BK, Frayne R. A systematic literature review of the effect of carotid atherosclerosis on local vessel stiffness and elasticity. Atherosclerosis. 2015;243:211–222. doi: 10.1016/j.atherosclerosis.2015.09.008. [DOI] [PubMed] [Google Scholar]
- 44.Chaichana T, Sun Z, Jewkes J. Computation of hemodynamics in the left coronary artery with variable angulations. J. Biomech. 2011;44:1869–1878. doi: 10.1016/j.jbiomech.2011.04.033. [DOI] [PubMed] [Google Scholar]
- 45.Nematollahi A, Shirani E, Mirzaee I, Sadeghi MR. Numerical simulation of LDL particles mass transport in human carotid artery under steady state conditions. Sci. Iran. 2012;19:519–524. doi: 10.1016/j.scient.2012.03.005. [DOI] [Google Scholar]
- 46.Tarbell JM. Mass transport in arteries and the localization of atherosclerosis. Annu. Rev. Biomed. Eng. 2003;5:79–118. doi: 10.1146/annurev.bioeng.5.040202.121529. [DOI] [PubMed] [Google Scholar]
- 47.Ogunrinade O, Kameya GT, Truskey GA. Effect of fluid shear stress on the permeability of the arterial endothelium. Ann. Biomed. Eng. 2002;30:430–446. doi: 10.1114/1.1467924. [DOI] [PubMed] [Google Scholar]
- 48.Iasiello M, Vafai K, Andreozzi A, Bianco N. Low-density lipoprotein transport through an arterial wall under hyperthermia and hypertension conditions—an analytical solution. J. Biomech. 2016;49:193–204. doi: 10.1016/j.jbiomech.2015.12.015. [DOI] [PubMed] [Google Scholar]
- 49.Lawrence AR, Gooch KJ. Transmural pressure and axial loading interactively regulate arterial remodeling ex vivo. Am. J. Physiol. Heart Circ. Physiol. 2009;297:H475–484. doi: 10.1152/ajpheart.00972.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Meyer G, Merval R, Tedgui A. Effects of pressure-induced stretch and convection on low-density lipoprotein and albumin uptake in the rabbit aortic wall. Circ. Res. 1996;79:532–540. doi: 10.1161/01.RES.79.3.532. [DOI] [PubMed] [Google Scholar]
- 51.Wu CH, et al. Transendothelial macromolecular transport in the aorta of spontaneously hypertensive rats. Hypertension. 1990;16:154–161. doi: 10.1161/01.HYP.16.2.154. [DOI] [PubMed] [Google Scholar]
- 52.Liu B, Tang D. Computer simulations of atherosclerotic plaque growth in coronary arteries. Mol. Cell. Biomech. MCB. 2010;7:193–202. [PMC free article] [PubMed] [Google Scholar]
- 53.Caro CG, Nerem RM. Transport of 14C-4-cholesterol between serum and wall in the perfused dog common carotid artery. Circ. Res. 1973;32:187–205. doi: 10.1161/01.RES.32.2.187. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets supporting the conclusions of this article were included within the main paper.