Effort, reward, and vigor in decision-making and motor control

Abstract

Decisions depend on the reward at stake and the effort required. However, these same variables influence the vigor of the ensuing movement, suggesting that factors that affect evaluation of action also influence performance of the selected action. Here, we describe a mathematical framework that links decision-making with motor control. Each action has a utility that combines the reward at stake with its effort requirements, both discounted as a hyperbolic function of time. We suggest that effort is related to the metabolic energy expended to produce that movement. This framework makes wide- ranging predictions, accounting for choices that birds make in walking vs. flying, choices that people make in reaching and force production, and the curious fact that pedestrians walk faster in certain cities. We suggest that decision-making and motor control share a common utility in which the expected rewards and the energetic costs are discounted as a function of time.

“Satisfaction lies in the effort, not in the attainment, full effort is full victory.”

Mahatma Ghandi

Introduction

There are two, often separately considered puzzles regarding the question of how the brain controls behavior. The first puzzle is with regard to which action to perform: should one reach for the coffee, or the donut? The second puzzle is with regard to how to perform that action: should one reach slowly, or quickly?

The first puzzle has been studied in the field of decision making using a framework in which a utility is assigned to each potential action. This utility depends on the reward at stake, and the effort that may be required to perform that action. The action that is chosen is often the one that has the highest utility. The second puzzle has been studied in the field of motor control using a framework in which a cost is assigned to each potential sequence of motor commands. This cost is computed via an accumulation of the (squared) motor commands during the movement. The motor commands that are chosen, i.e., the speed of the movement and its detailed trajectory, are the ones that minimize this cost. In a sense, decision making has been concerned with the question of what to do, whereas motor control has been concerned with the question of how to perform the selected movement.

It seems, however, that the two puzzles are related. For example, suppose you are at the airport awaiting arrival of a friend. As you scan the arriving passengers, you decide which one is your destination, and then walk to greet them. The speed with which you walk will likely be higher if the arriving passenger is your child. That is, both the decision of which movement to perform, and the ensuing movement speed, are influenced by the purpose of the movement: a movement that is associated with a high utility is not only preferred, but it is also performed faster ^{1, 2}.

Similarly, the effort involved in executing an action affects both the process of decision making, as well as the speed of the ensuing movement. For example, when people are given the option of reaching in one of two directions, they choose the direction that has the lower effective mass ³, choosing the movement that requires less effort. Curiously, they also perform that movement with high velocity ⁴, despite the fact that moving slower would require less effort.

These results suggest that while the utility of an action depends on the reward at stake and the required effort (dictating the decision of which movement to perform), the same variables also influence how the brain performs the selected action. Indeed, in principle the utility of an action depends on its effort requirements, but the effort requirements cannot be estimated unless we also know the details of how that action will be performed. What is needed is a unified framework in which we can understand both the decision that the brain makes as to which action to perform, and the details of the movement that ensues following that decision.

Here, we approach this problem by noting that through control of vigor, i.e., how fast we move, the brain determines how much effort it is willing to expend to acquire a rewarding state. We consider a variety of data in which people and other animals naturally vary vigor of their movements, ranging from classic motor control experiments in primates, to decision making in rats and birds, to geographical data from how fast people walk in various cities. For example, primates naturally reach faster in some directions, and slower in other directions. If we increase the inter-trial interval between movements, the vigor of their movements decreases. Birds choose to walk to acquire a certain amount of food, but will fly when the food volume increases. People walk faster in some cities, but cities in which people walk faster are also cities in which they do other actions more rapidly. Remarkably, vigor varies geographically. Why?

In all these data, animals are choosing what to do, but they are also choosing the effort that they are willing to expend to perform that action. We suggest that both aspects of behavior are critical clues that help unmask the processes that are shared between decision-making and motor-control. Our main result is to show that a single mathematical formulation of action, a utility that describes the goodness of the movement via effort, reward, and time, predicts both the decision that animals make (e.g., whether to reach in one direction or another, whether to walk or to fly), as well as the vigor of the movements that follow (how fast to reach, how fast to walk).

Results

Let us assume that the purpose of any voluntary movement is to change the state of the body to one that is more valuable. This value is determined by two factors: the reward we expect to acquire when we complete the movement, and the effort we will spend in executing that movement. The former serves as a gain, and the latter serves as a loss. Together, these two elements form a utility, i.e., a goodness, that might describe which movement to perform, as well as how to perform that movement.

For example, suppose that we wish to reach to pick up a piece of food. The food has value α >0, implying that there exists a scale with which one can compare the value of one food with another. This value is not constant, but changes as a function of time: it is better to receive reward sooner rather than later. That is, time discounts reward such that it is preferable to have food soon, rather than wait and receive it later. Psychologists and economists have used decision making to quantify the shape of the reward temporal discount function. In a typical experiment, the subject decides whether to receive small reward α_s immediately, or large reward α_L after delay T. The delay T is manipulated until it becomes equally likely for the subject to choose α_s and α_L. The decisions that people and other animals make suggest that time discounts reward as a hyperbolic function ^{5, 6}:

$${\alpha }_s=\frac{{\alpha }_L}{1+\gamma T}$$ (1)

The temporal discount factor γ determines how rapidly reward is discounted by time. The larger values of γ produce faster discounting, indicating a preference to take the immediate, less valuable reward α_s, and a reluctance to wait for the larger reward α_L.

Although hyperbolic temporal discount function of reward has been inferred in tasks where people and other animals make decisions between small immediate rewards and large delayed rewards, Shadmehr et al. ⁷ hypothesized that such a temporal discount function may also be relevant to control of movements. The idea was to view duration of a movement as an implicit delay in the acquisition of reward, and the act of moving fast or slow as a decision between acquisition of a large reward soon in exchange for payment of large effort, or acquisition of smaller, discounted reward later, in exchange for payment of small effort. Let us assume that in control of movements, as well as in decision-making, the brain assigns a value α to the goal state, and discounts it hyperbolically as a function of movement duration T. Importantly, we will assume that the parameters are identical in decision-making and motor-control.

Generating a movement involves expenditure of effort, which depends on the duration of the movement. We represent effort with function U(T), and write the utility of the movement as the sum of reward and effort:

$$J=\frac{\alpha }{1+\gamma T}+U(T)$$ (2)

The central question is with regard to how effort should be represented. Movements carry a natural cost via the metabolic energy it takes to produce them. Ralston ⁸ estimated the rate of metabolic energy expenditure ė during walking and found that this quantity increased as a quadratic function of average speed E[ẋ] (where E is the expected value operator):

$$\stackrel{.}{e}=a+cE[\stackrel{.}{x}{]}^2$$ (3)

In the above expression, ė is the rate of energy consumed per unit of mass (J/min/Kg). The term a is a bias, reflecting the energy consumption rate at rest. Therefore, the energy that is specific to making a movement (i.e., energy during moving with respect to rest) is:

$${\stackrel{.}{e}}_m=cE[\stackrel{.}{x}{]}^2$$ (4)

Average velocity is related to duration of the movement T and distance d via E[ẋ] = d/T. Therefore, the total movement-related energy expended as a function of duration and distance is:

$$e_m=c\frac{d^2}{T}$$ (5)

As a result, we find that the energy consumed to make a movement is inversely related to duration T, and therefore the energy required to make a movement of given amplitude per unit of mass becomes smaller as the duration of that movement increases.

Importantly, Eq. (5) is based on experimental observations made during walking. To determine whether a similar relation exists in other movements, we measured the rate of metabolic energy expenditure as subjects made 10cm and 20cm reaching movements of five different durations (very slow to very fast). We found that Eq. (5) did an excellent job of predicting the change in energy required as a function of distance and time (Fig. 1A). These results demonstrated that in both reaching and walking, the metabolic energy was inversely related to the duration of the movement.

Figure 1.

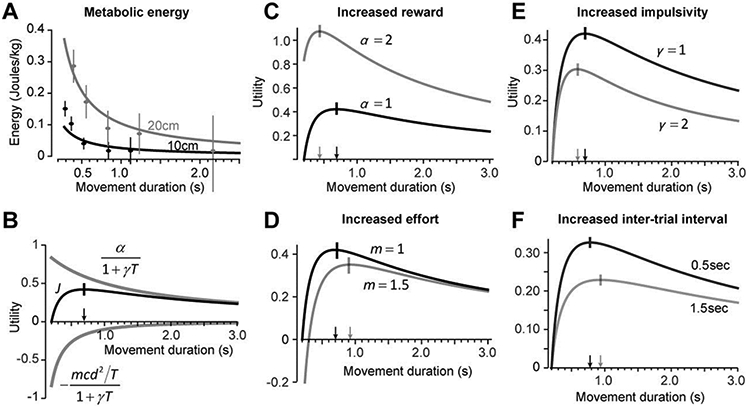
The effects of reward, effort, and time on decision-making and movement vigor. A. Metabolic energy expended during reaching as a function of reach duration for different distances. The data were fit to Eq. (5) to provide an estimate of parameter c. Error bars are SEM. B. The gray curves are the temporally discounted reward and metabolic cost of the movement, plotted as a function of movement duration, for a constant amplitude movement (Eq. 7). The black curve is the utility, which is the sum of the temporally discounted reward and metabolic cost. Increased movement duration T reduces both reward and effort, but has a greater effect on effort. As a consequence, the utility has a peak, corresponding to the duration of movement that maximizes the discounted sum of reward and effort. The small vertical line and the arrow indicate the movement duration that maximizes the utility. C. With increased reward, the utility of the movement increases for all durations. In addition, the optimal duration shifts to a smaller value. As a result, a stimulus that promises greater reward not only carries a greater utility, but also produces movements that have greater velocity (reduced duration). D. The effort of the movement is increased by increasing the mass of the limb. This decreases the utility of the movement for all durations, but also shifts the optimal duration to a larger value, thereby decreasing the velocity of the resulting movement. E. The effect of increased rate of temporal discounting. Increasing the rate of temporal discounting decreases the utility of the movement for all durations, but also shifts the optimal duration to a smaller value, thereby increasing movement velocity. F. The effect of increased inter-trial interval. Increased inter-trial interval decreases the utility of the movement for all durations, but shifts the optimal duration to a larger value, thereby decreasing movement velocity. Therefore, while increased inter-trial interval and rate of temporal discounting both decrease utility of the movement, the former decreases movement vigor, while the later increases it.

If the body part that we are moving has mass m, according to Eq. (5) the energy consumed during a movement of duration T is mcd²/T. If we assume that effort of a movement is proportional to the energy required to make that movement, and further assume that like reward, effort is discounted with time, we arrive at the following representation of effort:

$$U(T)=-\frac{mc{d}^2∕T}{1+\gamma T}$$ (6)

We now incorporate reward and effort into a single function that describes the utility of the movement:

$$J=\frac{\alpha -mc{d}^2∕T}{1+\gamma T}$$ (7)

The utility J, as well as the reward and effort components of this equation, are plotted in Fig. 1B. A fast movement has a small duration T, resulting in small discounting of reward (upper gray line), but will require larger effort (lower gray line). A slow movement has a long duration T, resulting in small effort, but will produce large discounting of reward. However, because metabolic cost becomes smaller with increased duration, the reward component of the utility declines at a slower rate as a function of T than the effort component. As a result, utility will generally have a peak, identifying the optimum movement duration. To find this duration, we take derivative of Eq. (7) with respect to T and after setting it to zero, find the optimum movement duration T* (arrow in Fig. 1A):

$$T^{\ast }=\frac{cm{d}^2+\sqrt{c^2{m}^2{d}^4+\alpha cm{d}^2{\gamma }^{-1}}}{\alpha }$$ (8)

Together, Eqs. (7) and (8) make a number of predictions.

As reward value α increases, the utility of the movement increases, and the duration of the resulting movement decreases (illustrated in Fig. 1C). This predicts that animals should not only prefer stimuli that promise greater reward, but also move with greater speed toward the more rewarding stimuli. The former has been demonstrated in numerous decision making tasks ⁹, and the later has been demonstrated in saccadic eye movements of monkeys ¹ and humans ², as well as reaching movements¹⁰.

As the effort requirements of the movement increases, for example by moving a larger mass m, the utility of the movement decreases, and the duration of the resulting movement increases (illustrated in Fig. 1D). This predicts that animals should not only prefer to move toward stimuli that require lower effort, but move with greater speed toward those stimuli.

As time is discounted more steeply via a larger γ, the utility of the movement decreases, and the duration of the resulting movement also decreases (illustrated in Fig. 1E). This predicts that individuals that are more impulsive (have a larger γ), should not only prefer the more immediate reward, but also move faster than those who are more patient. This has been shown in decision making patterns of healthy individuals and the velocity with which they move their eyes ¹¹.

Finally, if movements are separated by an inter-trial interval, effectively increasing the time to acquisition of reward, the result is a decrement in the utility of the movements, as well as an increase in the duration of the ensuing movements (illustrated in Fig. 1F). Let us examine these ideas in some detail.

Inter-movement interval and movement vigor

In the laboratory we often control the rate of movements through manipulation of the inter-movement interval. For example, we may have the subject wait a period of time q before displaying the ‘go’ signal. This alters the time to acquisition of reward by extending it from movement period T to T + q. In such a setting the movement utility becomes:

$$J=\frac{\alpha -mc{d}^2∕T}{1+\gamma (T+q)}$$ (9)

If we solve for the optimum movement duration T*, we find the following:

$$T^{\ast }=\frac{cm{d}^2+\sqrt{c^2{m}^2{d}^4+\alpha cm{d}^2\left({\gamma }^{-1}+q\right)}}{\alpha }$$ (10)

The above expression predicts that as inter-movement interval q increases, movement duration will increase (Fig. 1F), coinciding with reduced movement velocity. This is consistent with the findings of Haith et al. ¹².

We chose to discount reward and effort hyperbolically. In Supplementary Materials we consider the possibility that time discounts reward and effort exponentially, an approach commonly employed in reinforcement learning. We find that such form of discounting has trouble accounting for the fact that increased inter-trial interval reduces movement vigor.

Mass of the arm and movement vigor

The movement utility in Eq. (7) makes the further prediction that as the effort associated with making a movement increases, duration should decrease (Fig. 1D). A simple way to alter effort is via mass of the limb (Fig. 2A). The human arm has a mass distribution that resembles a heavy object when it moves in some directions (major axis of the inertia ellipse, e.g., 135°), and a light object when it moves in other directions (minor axis of this ellipse, e.g., 45°). Gordon et al. ⁴ asked their subjects to place their hand on a horizontal digitizing tablet and make a “single, quick, and uncorrected movement” to a target at 10cm. The subjects had no time constraints on their movements. They chose to reach with a peak velocity that was around 60 cm/s for some directions, but only 30 cm/s for other directions (dots, Fig. 2B). That is, there was a two-fold increase in the preferred movement speed simply due to a change in the direction of the movement.

Figure 2.

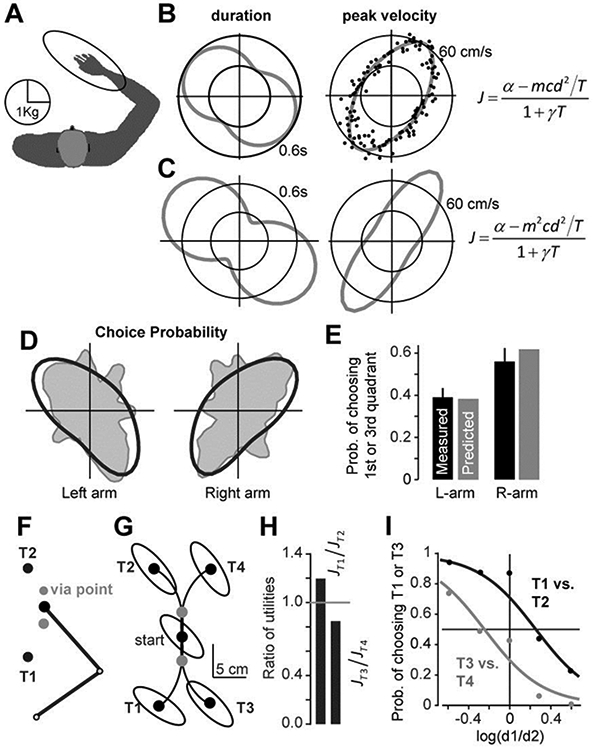
A single utility accounts for the decision of which movement to make, as well as the speed of the ensuing movement. A. The configuration of the arm at the start position and the associated mass matrix M(θ). In this configuration the greatest mass is associated movements to targets aligned with the forearm, and is 3 times the mass in the perpendicular direction. B. Subjects were instructed to reach to a target at 10cm with no time constraints. The resulting peak velocity as a function of direction is plotted as dots (data from Gordon et al. ⁴). The gray curve shows predictions of the utility function (Eq. 7). C. Predicted peak velocity and duration for an alternate utility in which effort depended quadratically on mass. D. Subjects performed an out-and-back movement, but were free to choose the reach direction (no target provided). The gray region shows the probability distribution of the observed choices (Wang and Dounskaia ¹⁵). The black curve is the prediction of Eq. (7). E. Probability of choosing to reach toward 1^st or 3^rd quadrant (measured data from Wang and Dounskaia ¹⁵, predicted data from Eq. (7)). F. Subjects were presented with two targets ³ and chose to reach to one of the targets, moving their hand through a via-point. G. The effective mass of the arm at the start position and at each of the various targets. H. The ratio of the utilities for targets T1 and T2, and targets T3 and T4, when all targets are 11cm from the start point. I. The probability of choosing target T1 (or target T3), as a function of the log of the ratio of the distances for targets T1 and T2 (or targets T3 and T4). The data points are from Cos et al. (2011). The curves are probabilities computed from the differences in utilities of the two targets.

Let us use the movement utility of Eq. (7) to consider these observations. According to our theory, the effort associated with reaching is specified by the metabolic data in (Fig. 1A), which sets c = 2.6 J.sec/Kg/m². We used the inertial properties of the arm (parameters from ¹³), to estimate the effective mass of the hand as a function of direction of reach (see Supplementary Materials), resulting in quantity m(θ), where θ is direction of reach (Fig. 2A). Using Eq. (8) we computed the expected duration of each reach (Fig. 2B) by estimating the only free parameter α (γ is set to 1). The resulting peak velocity had a direction-dependent pattern: the velocity was largest for the directions for which the effective mass was smallest (ellipse, Fig. 2B). This illustrated that the direction-dependent speed of the reaching movements could be accounted for by a utility in which effort was objectively measured via the metabolic cost of the movement.

We can consider a number of alternate models. In optimal control models, effort typically scales with the square of the mass (rather than linearly, as in Eq. 5). In such a case, for a movement of duration T, effort may be described as follows:

$$U(T)=-\frac{m^{2}c{d}^2∕T}{1+\gamma T}$$ (11)

In this scenario the resulting peak velocity has a direction-dependent pattern (Fig. 2C), but the resulting velocities are a poor match to the observed data: the predicted velocities are larger than observed in the directions of low mass, and lower than observed in the directions of high mass. A similar mismatch is observed if we assume that movement speed is chosen to be proportional to mass.

If our framework is useful, then it should not only be able to account for movement vigor as a function of mass, but also account for decision-making associated with those movements. For example, Fig. 1D demonstrates that as mass increases, utility declines for all durations. This means that if one is given the option of making a movement of constant amplitude with mass m₁ vs. mass m₂, where m₂>m₁, the utility of the movement with the smaller mass will be larger, and therefore one should prefer to make the movement with the smaller mass. Importantly, the difference in the utilities should predict the probability of choosing one action over another.

Without changing parameter values (i.e., nothing to fit), we tested this prediction in two experiments. In the first experiment, subjects were instructed to make a 15cm out-and-back movement to any direction, but they were not provided with a target. Rather, they were given the freedom to choose their own movement direction ^{14, 15}. The choices described a probability distribution as shown for the left and right arms in Fig. 2D (gray region). Our theory predicted these probabilities via the utility as a function of direction: the directions for which utility is higher should be performed more frequently. While keeping parameter values unchanged from the simulations shown in Fig. 2B, we used Eq. (7) to predict the choices (Fig. 2D, black curve). A key prediction was with regard to probability of choosing to reach to quadrants 1 or 3. With nothing to fit, the model accounted for the measured data (Fig. 2E).

In a different experiment, subjects were given two targets, and asked to make a decision as to which target they preferred to reach ³. The critical aspect was that a via-point was placed between the start position and the target, thereby constraining the reach trajectory (Fig. 2F). This made it so that part of the trajectory was aligned with the major or minor axis of the effective mass of the arm. For example, consider a trial in which the options were targets T1 and T2, each placed at a distance of 11cm from the start location (left panel of Fig. 2G). The authors found that subjects generally preferred to reach toward T1. Now consider a trial in which the option was between targets T3 and T4, each placed at 11cm from the start location (right panel of Fig. 2G). In this case, the subjects preferred to reach toward T4. That is, in one case they preferred to reach for a target that was toward them (T1), and in another case they preferred to reach for a target that was away from them (T4). Let us consider these data in the framework of movement utility.

Although the reach distance is the same for targets T1 and T2 (both at 11cm), approaching T2 from the via-point requires moving the hand along the major axis of the mass ellipse, whereas approaching T1 from the via-point requires moving the hand along the minor axis. Because the effective mass of the arm is higher along the trajectory toward T2, its utility is lower. As a consequence, people should prefer to reach toward T1. Similarly, when the trial requires choosing between T3 and T4, the effective mass is lower for T4, implying that its utility is higher. Therefore, people should prefer to reach toward T4.

Keeping the parameter values unchanged from above simulations (nothing to fit), we used Eq. (8) to predict the duration of the reaching movements to each target, and then used Eq. (7) to predict the utility of each action. The resulting ratio of the utilities for targets T1 and T2, represented as J_T1/J_T2, and targets T3 and T4, represented as J_T3/J_T4 are shown in Fig. 2H. Target T1 had a utility that was 1.25 times the utility of target T2, and a similar ratio existed between targets T4 and T3. Indeed, when the two targets were equally distant from the start point, the subjects chose target T1 on around 80% of the trials, and target T4 around 70% of the trials (Fig. 2I).

To model the choice of targets T1 and T3 as a function of movement distance, we used a logistic function:

$${\text{Pr}}_{{}_{T1}}=\frac{1}{1+\text{exp}(-k(J_{{}_{T1}}-J_{{}_{T2}}))}$$ (12)

Here, k is a free parameter representing noise in the decision making process and was fixed to the same value in all simulations. Figure 2I illustrates the fit of the function to the data for the probability of choosing target T1 over target T2, and target T3 over target T4. As the distance to target T1 and T3 increases, the preference shifts to target T2 and T4. Although the distance between the targets is identical, the choice curves for the two pairs of targets do not overlap.

In summary, the same utility that described the vigor of movements as a function of movement direction (Fig. 2A-C), also described the choices that people made when they were free to reach in any direction (Fig. 2D-E), or in one of two directions at various distances (Fig. 2F-I). Therefore, if we define utility of movements as the temporally discounted sum of gain and loss associated completion of the movement, where loss is defined as the metabolic cost of performing that movement, then we may account for both movement vigor and movement choice across various experiments.

To walk or to fly: the interplay between reward and effort

The theory that we have described has an important shortcoming. Although we used an objective measure of metabolic cost to define effort, we did not have a way to objectively estimate the value of reward α at stake. Fortunately, there are experimental data for which this variable is exactly known. Let us examine these data within the framework of the proposed utility.

Bautista et al. ¹⁶ trained wild-caught starlings to sit on a central perch and make a decision as to walk (low effort) or fly (high effort) to obtain a food reward. The value of reward α was objectively estimated as the caloric content of the food. Flying required a greater metabolic rate c_f than walking c_w (about 15 times as much), and therefore demanded greater effort. In a typical experiment, the birds were trained to choose between making a flying trip (to the reward site and then back to the start perch) to receive reward α, or a walking trip to receive the same reward. For a fixed number of flying trips, the number of walking trips was incremented until a preference reversal was observed, indicating an indifference point. The number of flights was then increased and the process was repeated until a few indifference points were measured. As a result, the total time and effort required to obtain a reward were increased simultaneously by increasing the number of required trips. The results are shown in Fig. 3A. On average, the utility of making 3 round trip flights was about equal to making 9 round trip walks, but the utility of making 9 round trip flights was about 40 round trip walks. Given the metabolic costs of walking and flying, and the reward value of the food at stake, can we understand the decisions that the birds made within the framework of movement utility?

Figure 3.

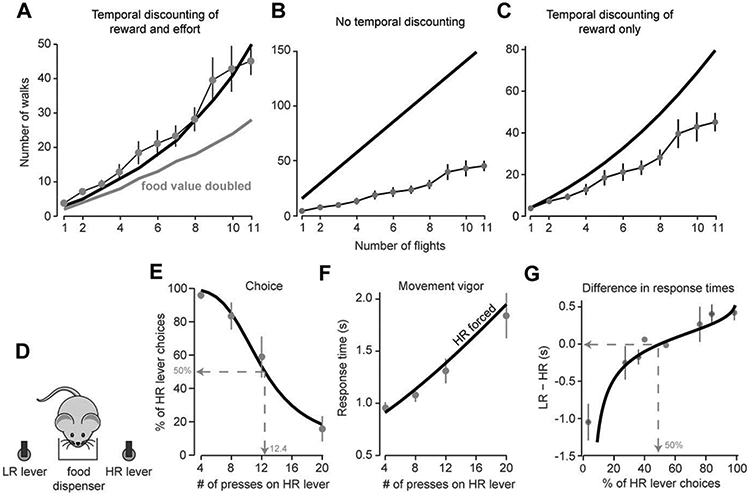
Top panel: decision-making in birds in an experiment in which the objective values of reward, and the metabolic cost of the movements, are both known. A. Birds chose between flying n_f number of times, and walking n_w number of times, to receive a reward. The data points represent the indifference values, computed from the choices that the animals made ¹⁶. The solid curve is the predicted indifference curve for the utility function in which both reward and metabolic cost were discounted by duration of the movements. The gray curve is the predicted indifference if the food value were doubled (the animals would we willing to fly more often). B. Predictions of a utility in which neither reward nor metabolic costs are discounted by duration of the movement. C. Predictions of a utility in which only reward is discounted by duration of the movement. Bottom panel: Decision-making in rats in an experiment in which they chose between the low-reward (LR) lever (4 presses would produce 2 pellets of food), or high-reward (HR) lever (a variable number of presses would produce 4 pellets of food). D. Schematic of the experimental setup. In choice trials, both options were available. In forced trials, only one option was available. E. Data points are the percent of choice trials in which the animals chose the HR lever, plotted as a function of the number of presses that were required on that lever (data from Walton et al. ⁹). The curve is the probability of choosing the HR option computed via the difference in the utilities of the two options. F. Response times in the forced trials in which only the HR lever was available. The points are measured data and the curve is the duration predicted by Eq. (16). G. The difference in response times in the force trials between the HR and LR options. The points are measured data and the curve is the difference in duration predicted by the model.

Using the measured metabolic costs and durations of travel, we can calculate the utility of each option (see Methods) and then compute indifference points (points where the utilities of two options are the same). The only free parameter in the model is γ. The indifference points for a candidate value of γ = 0.03 are plotted with the thick line in Fig. 3A. The model’s performance appears to be a reasonable match with the decisions that the birds made. The model also predicts that if the caloric value of the food was doubled, the birds would choose to fly much more frequently.

To test alternate formulations of the utility functions, let us consider a utility in which neither reward nor effort are temporally discounted and a utility in which only reward is temporally discounted, but not effort. In these scenarios, we have:

$$J=\alpha -e_m$$ (13)

$$J=\frac{\alpha }{1+\gamma T}-e_m$$ (14)

Eq. (13) has no free parameters and Eq. (14) has one free parameter. We find that the predictions of both these alternative utilities are grossly inconsistent with the data (Figs. 3B and 3C).

In summary, we find that in a task in which there are objective measures of reward and effort via caloric value of each variable, birds choose to make movements that are consistent with a utility in which reward and effort act as gains and losses that combine additively, but are discounted as a function of time.

Decision making and movement vigor

Our claim is that a single utility may account for both the decision that the animal makes as to what action to perform, and the vigor of the movement that follows. Let us examine this claim with data that systematically altered effort requirements of the task, and measured both the resulting decisions and the ensuing movements.

In a typical lever-pressing task ¹⁷, a rat chooses between a reference option consisting of low reward for a relatively low number of lever presses, and a high-reward that requires a greater number of presses. The effort requirement scales with the number of presses, and reward is increased by increasing the amount of food (i.e. two vs. four pellets). When the required number of lever presses for both the low and high reward options is low, rats prefer the high reward option ⁹. However, as the number of lever presses required for obtaining the high reward increases, rats switch their preference to the low reward/low effort option. When rewards are matched, they choose the less effortful option, and combinations of options could be found for which the animal would be indifferent ¹⁸. Therefore the utility of an option can be finely controlled with either reward or effort.

An example of such an experiment is one performed by Walton et al. ⁹. Rats were placed in a chamber that contained two retractable levers on either side of a food tray into which the pellets of food were dispensed (Fig. 3D). One lever was identified as the low reward (LR) option, releasing 2 pellets after 4 lever presses. The other lever was the high reward (HR) option, releasing 4 pellets after a variable number of presses. In the first session the HR option required 4 presses, but this requirement increased to 8, 12, and 20 presses in subsequent sessions. In sessions in which the HR lever required 4 presses, the rat chose it rather than the LR lever (Fig. 3E, the LR lever always required 4 presses). In subsequent sessions, as the number of presses required for the HR lever increased, the rats chose the HR lever less frequently. The authors made an interesting observation: in sessions in which the HR effort requirement was low, the response time on HR forced trials was low (Fig. 3F). However, in sessions in which the HR effort requirement was high, the response time on HR forced trials was high. That is, if the animal was forced to choose a high effort option, it performed that task with low vigor. In fact, it seemed that the difference between the LR and HR forced response times (Fig. 3G) mirrored the animal’s choice performance (Fig. 3E).

These experiments quantified not only the choice that the animal made, but also the vigor with which the animal performed that choice. Let us examine these data within the movement utility framework. The utility of an option that involves n lever presses, each with duration t, in exchange for reward α is:

$$J=\frac{\alpha -nc∕t}{1+\gamma nt}$$ (15)

If the animal is to perform n lever presses, how fast should each lever-press be? To answer this question, we find the lever press duration that maximizes that above utility:

$$t^{\ast }=\frac{cn+\sqrt{\alpha c{\gamma }^{-1}+c^2{n}^2}}{\alpha }$$ (16)

The above expression illustrates that the duration of a single lever press should decrease as reward value α associated with that action increases. It also indicates that the duration will increase as the number of lever presses n required to get reward increases. So the animal should express lower vigor as the required number of lever presses increases.

We can represent the two options with their utilities J_H and J_L, where J_H is the utility of pressing the HR bar n times to get reward α_H, and J_L is the utility of pressing the LR bar 4 times to get reward α_L. One should choose the option that has higher utility. We compute the quantity J_H − J_L by inserting Eq. (16) into Eq. (15) and arrive at the utility for each option as a function of number of lever presses n and reward α. If we set γ = 1, c = 1, and α_H = rα_L, we can compute J_H − J_L as a function of n :

$$J_{{}_H}-J_{{}_L}=a+\frac{r^2\sqrt{r+n^2}}{\left(n+\sqrt{r+n^2}\right)\left(r+n^2+n\sqrt{r+n^2}\right)}$$ (17)

This illustrates that as the reward ratio r = α_H/α_L increases, the relative utility of the HR lever increases. Furthermore, as the number of lever presses increases, the utility of HR lever decreases. So the animal should choose the HR option more frequently as the reward associated with it increases, or the number of lever presses associated with it decreases. We can use a logistic function to represent the probability of choosing the HR option:

$${\text{Pr}}_{{}_{HR}}=\frac{1}{1+\text{exp}(-k(J_{{}_H}-J_{{}_L}))}$$ (18)

The fit of the above function to the choices that the rats made is illustrated in Fig. 3E. As the number of lever presses n required for the HR option increased, the animal was less likely to choose that option. While keeping model parameters fixed, we use these equations to predict the vigor with which each option was executed. Eq. (16) predicted that duration of each lever press should increase quasi-linearly with increased number of lever presses. The model predictions closely matched the observed data (Fig. 3F).

Walton et al. ⁹ also noted that as the probability of choosing the HR lever increased, so did the difference in the response times for pressing the LR and HR levers (Fig. 3G). Importantly, when the animals were indifferent to the available options (choosing the HR option at 50% probability), the vigor with which they executed the movements was also similar between the two options. This is shown by the fact that at 50% probability of choosing the HR lever the difference between the response times of the LR and HR options is zero (Fig. 3G). Our framework accounts for this by noting that the utility of each option not only describes the probability of it being chosen, but also the vigor with which that movement is performed. When the two utilities are equal, so is the vigor (gray line, Fig. 3G). As the utility of the HR lever increases, so does its vigor, making the difference in the response times between LR and HR positive.

In summary, these experiments controlled effort and reward and measured both the decision that was made and the movement that followed. The animals preferred the high reward option when the effort required was low, but switched to the low reward option when the required effort increased. However, the vigor with which they performed these actions depended on the amount of reward at stake, and the effort required for obtaining that reward. The movement utility appeared consistent with both the decision-making process, and the motor-control process.

Metabolic cost of force

In the movement utility function a critical element is the representation of effort. Thus far we have relied on the finding that the rate of energy consumption grows as a quadratic function of movement speed ⁸, allowing us to compare movements of various amplitude and speeds. Let us now consider a more general situation in which effort must be assigned to force production.

Earlier we showed that for movements of constant amplitude the total energy consumed varied inversely with duration (Eq. 5). We can also show that for movements of constant amplitude the sum of forces produced throughout the movement (i.e. the force-time integral) also varies inversely with duration (Figure S1). This leads to the conjecture that in general, the energy consumed during a movement of duration T varies linearly with the force-time integral:

$$e\left(f(t)\right)=a_1\underset{0}{\overset{T}{\int }}\mid f(t)\mid dt+a_2$$ (19)

To test the validity of this conjecture, consider an experiment in which human subjects were engaged in an isometric task while the experimenters measured the metabolic cost of force production. Russ et al. ¹⁹ used spectroscopy to estimate concentration of ATP per gram of muscle in the human gastrocnemius. They electrically stimulated the muscle with trains of 20Hz or 80Hz pulses and measured the resulting forces (Fig. 4A) and energy consumption (dots in Fig. 4B). As stimulation duration increased, the energy also increased, but at a higher rate for the 80Hz stimulation than 20Hz.

Figure 4.

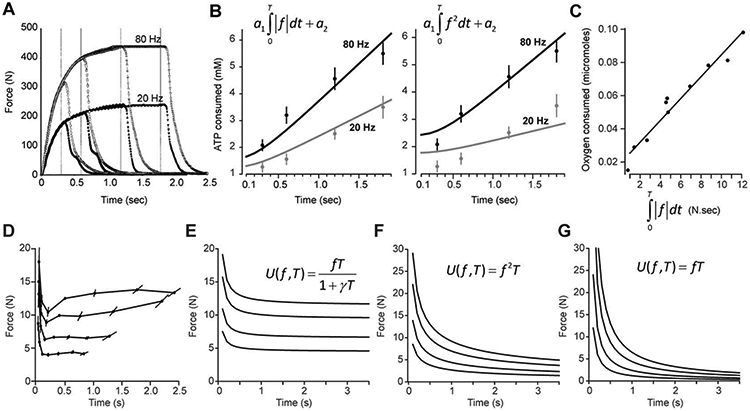
Top panel: Metabolic energy consumed during isometric contraction grows linearly with the force-time integral. A. The measured force during electrical stimulation of the human gastrocnemius muscle at 20 or 80Hz (data from Russ et al. ⁵³). The 20Hz stimulation produced a force that increased with a time constant of around 0.25sec, reaching a plateau of approximately 230N. The 80Hz stimulation produced a force that had a similar time constant, but reached a plateau of approximately 430N. B. Metabolic energy expended by the muscle as measured via consumption of ATP. The data points are from Russ et al. (2002). In the left subplot, the curves depict a model where metabolic costs grow linearly with the force-time integral. In the right subplot, the curves depict a model where metabolic costs grow with the squared force-time integral. The fit with the force-time integral has about half of the prediction errors as in the squared force-time integral. C. Oxygen consumed during electrical stimulation of a frog muscle plotted as a function of the force-time integral. Data from Kushmerick and Paul ²⁰. Bottom panel: Utility of producing isometric forces of various magnitudes and durations as assayed by the choices that they make in a decision-making task. D. Subjects produced a given force for a given amount of time, and then another force for another period of time, and then asked to choose which they preferred. The data points represent indifference curves ²⁴, where the line connects the force-time pairs that were judged to be equally effortful. For example, the participants perceived holding a force of 13N for 2.5s subjectively equal to 13N for 1.0s, and 18N for 0.1s. The surprising result is that for durations of greater than 0.5 seconds, force held for a short amount of time was judged to be approximately equal in effort to the same force magnitude held for a longer amount of time. E. The indifference curves predicted by an effort cost in which the metabolic cost of force production (force-time integral) is discounted by a hyperbolic function of time. The function reaches a plateau as duration of the force production increase. F. The indifference curves predicted by an effort cost that depends on the integral of the squared force (as is typical in optimal control models). The function goes to zero with increased duration. G. The indifference curves predicted by an effort cost that does not temporally discount the force-time integral. The function goes to zero with increased duration.

The forces produced by stimulation intensity i (Fig. 4A) can be written as:

$$f=k_i\left(1-\text{exp}(-t∕\tau )\right)$$ (20)

The force-time integral is:

$$\int f(t)dt=k_i\left(\tau \text{exp}(-t∕\tau )+t\right)$$ (21)

We note that the force-time integral for small durations of stimulation (t is small) depends on a nonlinear term (the exponential), but as time increases, the integral becomes a linear function of time, increasing as duration of force increases. If the total energy consumed varies linearly with the force-time integral, then as stimulation duration increases the energy consumed should grow linearly with the duration of stimulation. To check for this, we estimate k_i for the two stimulation intensities using the data in Fig. 4A, and then fitted Eq. (19) to the data points in Fig. 4B. In this approach we had two unknown parameters, a₁ and a₂. The resulting metabolic cost function had to explain energy consumption for both 80Hz and 20Hz stimulations simultaneously. The results are shown by the two lines in Fig. 4B (left subplot), which appear to be a reasonable match to the measured data.

An alternative measure of effort is one employed in optimal control theory, where force production carries a cost that depends on the integral of the squared force. This approach produced a mean squared error that was twice as large as the model in which force was raised to the power of one (Fig. 4B, right subplot). Therefore, energy consumption in the intact human muscle was better predicted by the force-time integral than by the force-squared time integral.

Energetic cost of force production has been estimated in other paradigms. Kushmerick and Paul ²⁰ electrically stimulated a frog muscle for various durations and measured the resulting oxygen consumption. An analysis of their data suggests that oxygen consumption grows linearly with the force-time integral (Fig. 4C). Taylor et al. ²¹ quantified the effect of increasing load on the metabolic cost of running in animals of various sizes, ranging from rats to humans to horses. They observed a near-linear increase in metabolic cost with added mass, in animals of all sizes. Lloyd and Zachs ²² had individuals run on a treadmill while a horizontal force pulled against them with a harness. They found that the metabolic rate ė increased proportionally with force, as would be predicted by our model. Gottschall and Kram ²³ revisited this paradigm during walking and also found that as the force that the subjects had to pull against increased, ė associated with the force production increased proportionally.

Taken together, it appears that a reasonable estimate of the metabolic cost of force is the force-time integral. This estimate is consistent with two ideas: 1) for movements of inertial objects along paths of constant amplitude but differing velocity, both the total energy expenditure and the force-time integral are inversely proportional to duration, and 2) for isometric tasks, as duration of force production increases the total energy expenditure is a linear function of the force-time integral.

Utility of effort

A critical aspect of our theory is that in computing the utility of a movement, both reward and effort are discounted by time. That is, while the energetic cost of an action may be the force-time integral, the utility of this act is the temporally discounted energetic cost. Let us show that this makes a surprising prediction regarding perception of effort. Consider the simple task of producing an isometric force f(t) for duration T in order to acquire reward α. The utility of this action is

$$J(f(t))=\frac{\alpha -c}{1+\gamma T}\left(a_1\underset{0}{\overset{T}{\int }}\mid f(t)\mid dt+a_2\right)$$ (22)

If we use the variable U to represent effort, effort is simply the temporally discounted force-time integral:

$$U(f(t))=-\frac{c}{1+\gamma T}\left(a_1\underset{0}{\overset{T}{\int }}\mid f(t)\mid dt+a_2\right)$$ (23)

Consider the case where f(t) is a constant force F. In that case effort is:

$$U=-\frac{c}{1+\gamma T}(a_{1}FT+a_2)$$ (24)

Note that as T increases, effort does not continue to grow, but approaches an asymptote. This makes the unexpected prediction that as duration of force production increases, subjects will become increasingly indifferent to duration.

Kording et al. ²⁴ asked volunteers to hold a force f₁ for period T₁, and then force f₂ for period T₂, and then choose which of the two forces they would like to experience again, under the instruction that “they should choose the force-time pair that they judged to be less effortful”. By increasing f₂, the authors determined the indifference point. For example, they found that if f₁ = 6 N was held for duration T₁ = 0.3 s, this effort was subjectively equal to holding f₂ = 9 N for duration T₂ = 0.1 s. This makes sense, as it demonstrates that people find the effort associated with holding a large force for a short time equal to a smaller force held for a longer time. However, the authors also found that as duration T₂ increased, the force that the subjects found equivalent did not go to zero, but rather plateaued (Fig. 4D). This is a puzzling result, but one that is predicted (see Methods) if effort is represented as the temporally discounted metabolic cost (Fig. 4E).

The idea that effort is discounted by time (as in the above presentation) differs sharply from current models in motor control where effort is often the undiscounted sum of squared forces that are produced during the duration of the task. That is, effort accumulates, usually as a quadratic function of force, $U\left(f(t)\right)=-c\underset{0}{\overset{T}{\int }}{f}^2(t)dt$. In this formulation of effort, as T₂ → ∞, then f₂ → 0, as shown by the indifference curves in Fig. 4F. However, this is inconsistent with the choices that the people made. Indeed, this inconsistency remains whether forces are quadratically penalized or not (as shown for a utility that depends only on time-integral of force, Fig. 4G).

In summary, a consequence of temporal discounting of effort is that the utility of generating a force for a given duration does not grow as a function of duration, but approaches an asymptote. If this is true, then as duration of force production increases, subjects should become increasingly indifferent to duration. Surprisingly, this prediction is in agreement with decisions that people made in an isometric force production task, suggesting that the perception of effort is the temporally discounting force-time integral.

The value of time

Consider a thought experiment in which a large predator observes a single prey, an unsuspecting rabbit. If the predator lives in an environment with gazelles nearby (but not available), it is likely to spent only a small amount of time attacking the rabbit and consuming it, because the time spent on the rabbit is taking valuable time away that could be used to attack gazelles. However, if the predator lives in an environment where there are usually only mice available, the predator is likely to spend a longer amount of time attacking the rabbit and consuming it, as the time spent on the rabbit is not taking valuable time away from other activities. Similarly, imagine a child reaching for a piece of candy. Suppose in one case she is reaching for this candy at home, where this is the only candy around, while in another case she is reaching for the same candy while visiting a home during Halloween, during which time other candies are available next door. The key idea is that the vigor of the movement depends not only on the available reward, but also on the value of time. Time is more valuable in some environments (gazelles, Halloween), than others.

We can define the value of time objectively via the expected utility rate: the expected utility of all actions in the environment, divided by the total time spent performing them. Its effect on movement vigor can be explained with the concept of an opportunity cost ²⁵. In an environment with a high utility rate (Halloween), the opportunity cost is high (time is very valuable). If we were to move slowly, or in the extreme, do nothing at all, we would be missing out on the reward we could have obtained during that time. As a result, a rich environment encourages faster movements because the cost of moving more vigorously is offset by the opportunity to obtain other rewarding options.

We formulated this idea by including a term representing the opportunity cost in the movement utility. The opportunity cost is the cost incurred for the time spent doing a given task of duration T. Let us define it as follows:

$$O(T)=E\left[\stackrel{.}{J}\right]T$$ (25)

In the above expression, $E\left[\stackrel{.}{J}\right]$ is the expected utility rate, or roughly speaking, the value of time. The opportunity cost will increase with the expected utility of the options in the environment, yet decrease with increased vigor. Thus, an environment with a high rate of expected utility (Halloween) should result in more vigorous movement. As a result, we modified the movement utility equation to incorporate a term representing the opportunity cost:

$$J=\frac{\alpha -mc{d}^2∕T}{1+\gamma T}-E\left[\stackrel{.}{J}\right]T$$ (26)

In Fig. 5A, we have plotted the model’s prediction regarding the time it takes for a person of m=90Kg to walk a distance of d=15m as a function of the expected utility rate. To produce this figure, we set α and γ in Eq. (26) equal to 1, used the measured metabolic cost of walking ⁸ to set the parameter c, and then solved for T as a function of $E\left[\stackrel{.}{J}\right]$. As the expected utility rate increased, the duration to walk 15m decreased, even though the reward value α was kept constant.

Figure 5.

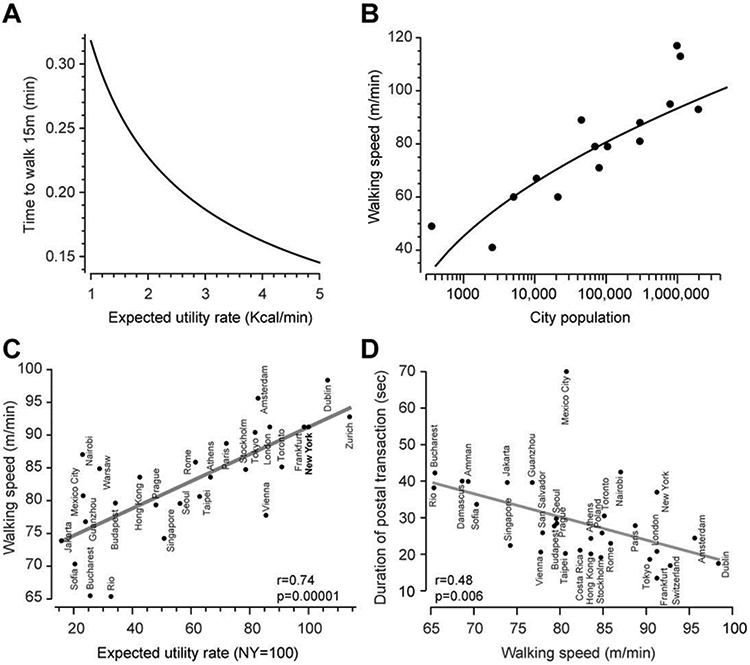
Increased value of time coincides with increased movement vigor. A. Optimum movement duration to walk 15m. The duration was computed by maximizing the utility function of Eq. (26). In the simulation, the term c is computed for a 90Kg person to walk a distance of 15m from measure data (see Methods), and the terms α and γ are set to 1. The plot shows the optimal duration as a function of expected utility rate $E\left[\stackrel{.}{J}\right]$. B. Average walking speed of pedestrians as measured in 15 cities and villages around the world. Data are from ²⁶. The curve was computed by finding the duration T that maximized the utility in Eq. (26), where the term c is computed for a 90Kg person to walk a distance of 15m (see Methods), the terms α and γ are set to 1, and the expected utility rate is a logarithmic function of the population of the city. C. Increasing expected utility rate coincides with increased walking speed. Expected utility rate is the average hourly net income for inhabitant of each city, normalized to the local purchasing power of that income, and represented with respect to the hourly net income of people in New York. The economic data are from ²⁸. The walking speed data are from ²⁷. D. Walking speed as measured in 31 cities around the world, as well as the duration of time it took to complete a postal transaction. Data from ²⁷.

Our framework provides a new way to consider an important puzzle: why do people walk faster in some cities? Between 1972 and 1974, Marc and Helen Bornstein visited cities around the world and measured the natural walking speed of pedestrians on a distance of 15m in “functionally parallel sites” like downtown or commercial areas ²⁶. They found that the walking speed increased roughly with the population of the city (Fig. 5B). To interpret their data, they suggested that “crowding has been thought to motivate … avoidance behaviors that reduce tension”, and therefore “increased walking speeds serve to minimize environmental stimulation.”

Our theory provides a very different explanation. We used the measured metabolic cost of walking ⁸ to set the parameter c in Eq. (26), set the other two parameters α and γ both equal to 1, and then found the one remaining parameter, the expected utility rate. We found that if the expected utility rate was to increase logarithmically as a function of population, the speed of walking would increase as observed in the data (Fig. 5B). Therefore, the theory suggested that walking speed was higher in large cities (as compared to small villages) because cities generally represented environments in which the value of time was greater.

If differences in walking speed across cities are indeed due to differences in the value of time, then the expected utility rate of each city should positively correlate with the walking speed of the inhabitants of that city. We tested this prediction directly. For walking speed we used data from observations in n=27 cities ²⁷. We estimated the expected utility rate for each city via the average hourly wage of its inhabitants, normalized to the cost of living in that city ²⁸. As the theory had predicted, the expected utility rate was an excellent predictor of walking speed (Fig. 5C, r=0.74, p=0.000012). That is, people whose time was more valuable walked faster.

Our theory made a further prediction: in an environment where people have a high expected utility rate, any goal-directed action will be performed faster. That is, when time is valuable, there is nothing special about walking, all actions will be affected. Levine and Norenzayan ²⁷ measured the time it took postal workers to complete a simple task for various cities around the world. They selected a few random post offices in each city, and went there to buy a stamp. They handed a note to the postal clerk along with a bill, and measured how long it took to complete the transaction. The cities in which people walked faster, postal workers completed the transaction faster (Fig. 5D, r=0.48, p=0.006).

To our knowledge, no laboratory-based experiment has directly tested the implications of an opportunity cost (see Supplementary Materials). In Supplementary Materials we suggest a specific experiment and provide the predictions that can test the validity of the theory.

In summary, movement vigor is not simply related to the effort and reward associated with the action, but also depends on the value of time for the individual performing that action. The value of time can be represented as the expected utility rate. We estimated this utility rate via the average hourly income for various cities around the world and found that 55% of the variance in the reported natural walking speeds of people was accounted for by differences in expected utility rates.

Discussion

The decisions people and other animals make regarding which action to perform appear to be related to the vigor of the movements that follow. We presented a framework with which to consider the problems of decision-making and motor control under a common rubric.

In our framework, each potential action was represented via a utility that combined the reward at stake with the effort requirements of the task, both discounted as a hyperbolic function of the duration of time it took to complete the task. The critical assumption of our model was to represent effort via the metabolic energy expended to produce the movement. This energetic representation described a parameterization of effort as a function of movement duration, mass of the limb, distance, and force, which we confirmed experimentally in reaching movements. The resulting model made predictions regarding how these variables would affect decision-making and motor control. We found that the framework provided insights into the following observations:

1. Subjects not only preferred the more rewarding stimulus, but also moved with greater vigor toward that stimulus (Fig. 1B) ^{1, 2}.

2. Subjects preferred to reach to the stimuli that required transport of a smaller mass ³, but did so with a higher vigor than when they were forced to make the same amplitude movement with a larger mass ⁴.

3. Subjects were willing to perform actions that required greater effort, but only in exchange for greater reward ⁹. However, they moved with less vigor when they were forced to perform the less preferable action (Fig. 3F).

4. Increasing the duration that subjects had to wait before making a movement (inter-movement interval) reduced the vigor of the ensuing movement ¹².

5. In a task in which there were objective measures of reward and effort via their caloric values, subjects chose actions which were consistent with a utility in which reward and effort were both discounted by the duration of the action ¹⁶.

6. As the duration of generating an isometric force increased, the perception of effort did not continue to increase, but rather reached a plateau ²⁴.

7. Natural walking speed, and well as the speed of performing other actions, varied with the city in which people lived ²⁷. That is, vigor appeared to vary geographically.

These results appeared consistent with a utility in which reward and effort were both discounted by time, and effort was an objective measure of the metabolic cost of the action.

Comparison to other models of motor control

The idea that movements are generated to maximize a utility (or minimize a cost) is a common feature of many models of motor control. However, in these models motor commands often carry a cost that accumulates with the squared force, resulting in a sum that is not discounted as a function of duration ^29-32. We found that both of these assumptions appeared inconsistent with certain behavioral data. For example, such a cost could not account for choices that people made in an isometric force task (Fig. 4F), or the velocity of movements that they chose to produce as a function of direction (Fig. 2C).

Here, we advanced these earlier models by linking motor costs with the energetic costs of producing that movement. The available data suggested that for constant amplitude movements, the energetic cost varied hyperbolically with movement duration, and in general, could be approximated as a linear function of the force-time integral. We therefore represented utility of an action as the sum of reward at stake, minus the metabolic cost of that action. However, we made the critical assumption that the time associated with performing the action discounted both the metabolic cost as well as the expected reward. These ideas proved useful in accounting for behaviors of birds in a flying vs. walking task (Fig. 3A), and people in an isometric force production task (Fig. 4D).

However, an important idea missing in our model but prominent in other models is the fact that motor commands not only carry a metabolic cost, but also affect consequences of the movement: large forces produce greater variability ³³. If acquisition of reward requires precision of action (e.g., reaching and placing the hand in a goal region), then in addition to generating metabolic cost, the motor commands affect probability of success. In this more realistic scenario the reward term in the utility function (α) should be modulated by a probability function that depends on the variability induced by the signal-dependent noise in the motor commands. The standard tools of optimal control could then be used to maximize this utility and produce a feedback control law to generate realistic movements ³⁴. In this framework, the same utility would form the basis of comparing potential actions, and the basis for producing the movement for the chosen action.

Comparison to other models of decision making

The formalism that we employed aimed to describe control of movements at a level that could predict the details of the ensuing action. This formalism is similar to that introduced by Rigoux and Guigon ³⁵, who proposed a reward-based optimal control model in which a utility function determined both the decision and the duration of the ensuing movement. In their approach, time discounted reward and effort, but did so exponentially, and effort was related to the time integral of the quadratic force. Here, our work advanced this previous approach in two ways. First, we found that hyperbolic but not exponential temporal discounting was consistent with the observation that changes in inter-trial intervals produced changes in movement vigor ¹². Second, we found that the force-time integral, but not a quadratic cost of force, was consistent with both the energetic cost of force production in muscles, and the perception of effort in the intact organism.

In our model we considered the background state of the animal (value of time) via an opportunity cost that depended on the expected utility rate. Niv et al. ²⁵ had suggested this idea by incorporating in the utility function a term representing average net reward rate that depended on the past history of rewards. We showed that in a rich environment where the expected utility rate was high, movements were generally faster because the time it took to perform any action took valuable time away from performing other rewarding actions. We used this formalism to consider natural walking speed of people in various cities. Our insight was to use objective data regarding hourly income of city inhabitants to estimate expected utility rates. We found that the theory could account for 55% of the variance in geographic distribution of vigor, suggesting that cities where people walked faster were inhabited by individuals who on average had a value of time. This idea appeared consistent with the observation that environments that encouraged faster walking also encouraged high vigor in other movements.

Neural basis of decision-making with reward and effort

The utility function that we have considered may provide insights into the neural basis of decision making and motor control. Salamone et al. ³⁶ studied decision making in a task where rats could eat a low quality food for little effort, or get access to a high quality food for a larger effort. The authors found that injection of dopamine antagonists in the nucleus accumbens, a structure in the ventral striatum, shifted preferences toward choices that were less effortful. Later work demonstrated that whereas animals under high levels of dopamine tended to select the energetically costly action ^{37, 38}, dopamine depletion in this structure coincided with decisions that exhibited increased sensitivity to effort ^{17, 39}. Together, these results suggest that the ability of dopamine to interact with cells in the striatum is critical to the process of decision-making with reward and effort.

In the striatum, dopamine interacts with medium spiny neurons (MSNs) that have distinct receptors. MSNs with D1-type receptors project via the direct pathway of the basal ganglia, whereas MSNs with D2-type receptors project via the indirect pathway. Bilateral activation of MSNs in the indirect pathway reduces movement vigor, whereas stimulation of MSNs in the direct pathway increases movement vigor ⁴⁰. This led Hwang ⁴¹ to propose that the indirect pathway of the basal ganglia is involved in computing effort costs, whereas the direct pathway is involved in computing the expected reward. In this framework, the utility of action may be computed via the convergence of the direct and indirect pathways at the substantia nigra pars reticulata (for control of saccades), or the internal segment of globus pallidus (for control of reaching).

The model proposed here implies a strong coupling between the neural circuits responsible for generating an action and the circuits involved in the process of deciding between actions. This aligns well with the hypothesis that the decision-making process involves sensorimotor areas, where each potential movement is represented simultaneously and competes against other potential movements ⁴². This would be in contrast to a goods-based model, where the decision process takes place in the space reserved for abstract representation of value and is then funneled to the sensorimotor areas for movement selection.

Limitations

When people train to reach in a force field in which a straight trajectory requires more force than a curved trajectory, they choose the straight trajectory, despite the fact that this trajectory requires greater energetic cost ⁴³ (but see Izawa et al. (2008), and Huang et al. ⁴⁴). This example illustrates an instance in which the brain chooses an action that entails greater effort, despite availability of a lower effort option. No framework that we know of can account for this curious result. We speculate that a straight-trajectory may represent a habitual reaction to presentation of a target, over-riding the usual processes that may be available for evaluation of available options.

In our model we did not consider how the evidence related to the decision is integrated over time ⁴⁵. Such decisions consider the problem of when to stop gathering information and thereby commit to a choice (i.e. the speed-accuracy tradeoff). A recent study demonstrated that the speed of this decision process is also related to movement characteristics ⁴⁶. When subjects increased the urgency with which they make a decision, (i.e. decision speed) they increased the vigor with which the ensuing movement was made. However, effort may also play a role in decision duration, as the animal could spend more effort at each time step, thereby improving the quality of the accumulated information ⁴⁷. Our contribution to this line of modeling is to suggest that effort is related to the metabolic cost of action, and discounted as a function of the duration of that action.

In summary, we presented a framework in which the value of an action was determined by the reward at stake minus the effort expended during the movement, all discounted by time. When we represented effort via the metabolic cost of action, the results unmasked a pattern of decision-making and motor-control that appeared consistent with a process of maximizing a common utility.

Methods

Here we start with a description of the experiment in which we measured metabolic cost of reaching as a function of duration and distance. The results of this experiment confirmed that in reaching, similar to walking, the rate of energetic cost decayed hyperbolically with the duration of movement. Next we describe the simulations that we performed to produce the subsequent results.

EXPERIMENT: Metabolic cost of reaching

To quantify the relation between energetic cost and duration and distance in reaching movements, we measured metabolic rate via expired gas analysis as subjects made reaching movement of different distances and durations.

Subjects

Twelve young adults (mean +/− s.d. age 24.2 +/− 4.4 yrs, 6 females, 6 males) with no physical injuries or known pathologies participated in this study. All subjects were right-handed and recruited from the University of Colorado Boulder student body. The University of Colorado Institutional Review Board approved the study protocol and all subjects gave informed consent.

Task

Seated subjects grasped the handle of a robotic arm (Interactive Motion Technologies, Shoulder-Elbow Robot 2) to move a circular cursor from a home circle to a target circle at five pre-determined reaching speeds. The cursor, home circle, and target circle were displayed on a vertically mounted computer screen at the subject’s eye-level. The five speeds are referred to as Very Slow, Slow, Medium, Fast, and Very Fast. We tested two reach distances of 10cm and 20cm, with 8 subjects per reach distance. On odd numbered trials, reaches started ~15 cm in front of the chest area with the arm in a flexed position. The reach involved extending the arm out anteriorly to the target in front of them. On even numbered trials, the reach started at the previous target location with the arm in an extended position and involved flexing the arm back towards the center target. Thus, each subsequent home circle was the previous trial’s target circle. Subjects wore bilateral shoulder straps and a lap belt to limit torso movement. A cradle attached to the robot handle supported the right forearm against gravity and restricted wrist movement.

A training bar that moved with a velocity that corresponded to the minimum jerk trajectory was used to illustrate the desired reaching speed during a familiarization period at the beginning of each reaching block. Additionally, the target turned gray if the reach was too slow, green if the reach was too fast, and “exploded” as a flashing yellow ring if the reach was within ±50ms of the desired movement duration. A pleasant auditory tone was also used to signal that the subjects successfully hit the target within the desired time window. After reaching the target, subjects had 800ms to settle in the center ring of the home circle before the next target circle was displayed. Thus, the inter-trial time was fixed at 800ms for all speeds at each reach distance.

Metabolic Cost

We measured metabolic cost using expired gas analysis (ParvoMedics, TrueOne 2400). Subjects wore a nose clip and breathed in and out of a mouthpiece during the metabolic data collection. We measured the rates of oxygen consumption $({\stackrel{.}{V}}_{O2})$ and carbon dioxide production $({\stackrel{.}{V}}_{CO2})$ as subjects made reaching movements at the desired speeds. Data collections occurred early in the morning, after subjects had fasted overnight. We calibrated the metabolic system prior to each data collection using certified gas mixtures and with a range of flow rates using a 3 liter calibration syringe. All metabolic data were corrected with standard temperature and pressure, dry (STPD). Metabolic data were recorded approximately every 5 seconds (i.e. 5-second average in the ParvoMedics system).

Protocol

Subjects performed six 5-minute reaching blocks at each of the five fixed speeds (Very Slow, Slow, Medium, Fast, and Very Fast). The speeds for these five reaching blocks were randomized for each subject. Each 5-minute reaching block began with 20 practice trials during which no metabolic data was recorded. After the practice trials, subjects put the nose clip on, inserted the mouthpiece, and breathed for ~1 minute while sitting quietly. After this 1-minute breathing period, subjects performed N number of reaches, where N was chosen to last ~5 minutes. Thus, all subjects performed the same number of reaches for a given reaching speed and reach distance. In between reaching blocks, subjects rested for at least 5 minutes during which no metabolic data was recorded. If subjects were naïve to reaching with the robotic arm, we asked them to come in for a brief ~15 minute familiarization session the day prior to the data collection. The familiarization session involved short reaching blocks of 50 trials at relatively slow and fast speeds until the subject appeared to be comfortable with the robotic arm and the task.

Metabolic analysis

We defined movement onset as the time when the tangential velocity first exceeded a velocity threshold and movement end as the first time after the peak tangential velocity when the velocity was less than the velocity threshold. Only the trials performed during the last 3 minutes of each reaching block, corresponding to the steady-state metabolic data, were used in the calculations.

We only analyzed metabolic data with respiratory exchange ratio, $RER={\stackrel{.}{V}}_{CO2}∕{\stackrel{.}{V}}_{O2}$, values less than 1.0 and generally below 0.85, suggesting that oxidative metabolism was primarily involved ⁴⁸. Normal resting RER values range from 0.74 to 0.87, partly depending on diet and other factors ^{49, 50}.

We calculated the rate of metabolic energy expended to perform the task in terms of Joules per second, ė, using the measured rates (ml/s) of oxygen consumption, ${\stackrel{.}{V}}_{O2}$, and carbon dioxide production, ${\stackrel{.}{V}}_{CO2}$, in the Brockway equation ⁵¹ and normalized by body mass, yielding metabolic rate with units of J/s/kg.

$$\stackrel{.}{e}=16.58{\stackrel{.}{V}}_{O2}+4.51{\stackrel{.}{V}}_{CO2}$$ (M1)

We next parameterized the relation between a movement’s energetic cost and the duration and distance of the movement. As we were interested only in movement related changes, we focused on fitting the component of the data that changed with duration and distance and thus subtracted the bias representing steady-state metabolic rate. To obtain a movement’s energetic cost in units of J/Kg, we multiplied the metabolic rate in J/s/Kg for each movement duration and distance, by the movement duration. We then fit the metabolic cost data to Eq. (5), where c is the only free parameter. A value of c = 2.6 J.sec/Kg/m² provided the best fit to the data. We fixed c to this value in all simulations that involved reaching movements.

SIMULATIONS

In simulations shown in Fig. 1B-F, unless otherwise noted we used the following parameter values: α = 1, γ = 1, m = 1, c = 1, d = 1, q = 0.

Mass of the arm, movement vigor, and choice of the movement

To test the predictions of the movement utility in conditions where the mass of the limb was varied via the direction of the reach (Fig. 2), we considered an inertial model of the human arm that was composed of two segments, with the following properties:

$$\begin{gathered} d_1=0.33d_2=0.43\text{meters} \\ {m}_1=1.93m_2=1.52\text{kg} \\ {\lambda }_1=\frac{d_1}{2}{\lambda }_2=\frac{2d_2}{3}\text{meters} \\ {I}_1=0.014I_1=0.019{\text{kg m}}^2 \end{gathered}$$

In the above expressions, d_i is length of each segment, m is mass, λ is length from point of rotation of the segment to its center of mass, and I is the inertial of the segment, with the subscript 1 referring to the upper arm, and subscript 2 referring to the forearm and hand. To predict what the movement duration and velocity should be for each direction θ, we first computed the effective mass along that direction m(θ) by computing the length of the vector that resulted when an acceleration of 1 m/s² in the direction of movement was multiplied by the mass matrix M. The result was scalar value function m(θ), which was then used to compute the predicted duration for a reach in that direction (Eq. 8), with an amplitude of 10cm, that is, d = 0.1 (as shown in Fig. 2B). We then computed the peak velocity of the resulting movement using a minimum-jerk trajectory⁵². We used the c value determined experimentally, c = 2.6 J.sec/Kg/m², and set γ = 1. Therefore the only free parameter was α. We found that a value that provided a good fit to the data of Gordon et al. (1994) was α = 0.35. We kept this value constant for all other reaching simulations. As a result, we had no parameters to fit for the data shown in Fig. 2D-I.

To test the robustness of the model we considered an alternate formulation of the utility function in which effort grew with the square of the mass, as is the case in most optimal control models. Effort was described as follows:

$$U(T)=-\frac{m^{2}c{d}^2∕T}{1+\gamma T}$$ (M2)

The resulting movement utility took the form:

$$J=\frac{\alpha -m^{2}c{d}^2∕T}{1+\gamma T}$$ (M3)

For this representation of movement utility, the optimum movement duration T^* is:

$$T^{\ast }=\frac{c{m}^2{d}^2+md\sqrt{c^2{m}^2{d}^2+\alpha cm{\gamma }^{-1}}}{\alpha }$$ (M4)

We computed the optimal duration using the above expression (shown in Fig. 2C), and then used a minimum-jerk trajectory of amplitude 10cm to compute the velocity of the resulting movement. We again found that the resulting peak velocity had a direction-dependent pattern. However, the resulting pattern of velocities was a poor match to the observed data: the predicted velocities were larger than observed in the directions of low mass, and lower than observed in the directions of high mass (Fig. 2B vs. Fig. 2C).

The tested the predictions of the utility function by considering the choices that people made when they were free to choose their own movement direction. In this experiment, the right and left arms were placed in a given configuration and the subjects were asked to make an out-and-back reaching movement to a circle of 15cm radius, but to a direction of their choice ¹⁵. The resulting probability distribution of the directions that they chose is shown in Fig. 2D (gray region). To see whether our theory could account for the data, we kept all parameters unchanged from the simulations shown in Fig. 2B. Therefore, we had no free parameters to fit these data.

We first computed the effective mass for the left and right arms for the out-and-back movement by using the mass at the start point and each possible turn-around point about a circle of 15cm radius. We then used this effective mass in Eq. (8) to predict the duration of each 30cm movement, and then used that duration in Eq. (9) to predict the utility of that movement. The kidney-shaped black curve in Fig. 2D is the resulting utility function. In Fig. 2E, the sum of utilities for quadrants 1 and 3 is compared to the fractions of trials that the subjects chose to reach to those quadrants.

Our formulation of utility function was further tested by considering the choices that people made when they were given the option of reaching to one of two possible targets (Fig. 2F). The idea was that for each target, the effective mass of the movement described the utility for that movement, and the difference in the utilities associated with the two targets should describe the probability of choosing one target over another. We kept the parameters that we had found in Fig. 2B unchanged. This produced a utility function with nothing to fit. To compute the effective mass for the reach to a given target, we computed the effective mass at the start and end points and averaged the two. To compute the probability of choosing a target, we used a logistic function in which the probability was a function of the difference in the utility of each target. In the logistic function, the only free parameter was k, which we found to be 32 for the data in Fig. 2I.

To walk or to fly

The utility function depended on reward, a variable that was not easy to measure in the reaching experiments. We therefore considered a task in which some of the key variables were objectively known. In the task where starlings decided between flying and walking to a reward (Fig. 3 top panel), the caloric content of the reward was known, α = 1.3x10³, as was the metabolic rate associated with walking, perching, and flying: c_w = 2, c_p = 1.09, and c_f = 32. Time spent in each act was also known: t_w = 0.5, t_p = 1.25, and t_f = 1.1 sec. The utility function took the following:

$$J=\frac{\alpha -e_m}{1+\gamma T}$$ (M5)

Here, T is total travel time, e is total metabolic cost of the movements, and γ is a temporal discounting factor. The variable T represents the time the bird spent performing three different activities: moving, perching, and handling the food. The movement time t_w is the time the birds spent walking in a one-way trip (or time spent flying, represented as t_f). In addition to walking or flying, the animals spent time perching in between walking or flying one-way trips (t_pw and t_pf, respectively), and there was additional time spent handling the reward (t_h) before they consumed it. If the animal chose to walk n_w times to acquire reward α, the travel time is:

$$T_{{}_w}\left(n_{{}_w}\right)=2n_{{}_w}\left(t_{{}_w}+t_{{}_{pw}}\right)+t_{{}_h}$$ (M6)

Bautista et al. ¹⁶ estimated the metabolic rate during perching c_p from previous recordings and assumed that the metabolic rate of handling c_h was the same. Thus the total energetic cost for making n_w walking trips is:

$$e_{{}_w}\left(n_{{}_w}\right)=2n_{{}_w}\left(c_{{}_w}{t}_{{}_w}+c_{{}_p}{t}_{{}_{pw}}\right)+c_{{}_p}{t}_{{}_h}$$ (M7)

Combining the above equations, we find the utility for the choice of taking n_w walking trips:

$$J_{{}_w}\left(n_{{}_w}\right)=\frac{\alpha -\left(2n_{{}_w}\left(c_{{}_w}{t}_{{}_w}+c_{{}_p}{t}_{{}_{pw}}\right)+c_{{}_p}{t}_{{}_h}\right)}{1+\gamma \left(2n_{{}_w}\left(t_{{}_w}+t_{{}_{pw}}\right)+t_{{}_h}\right)}$$ (M8)

We can similarly define the utility for flying, J_f.

The indifference point n_w is found by setting J_w (n_w) = J_f (n_f) and solving for n_w. The only unknown parameter was γ, which we found to be 0.03 to produce the fit shown in Fig. 3A. There were no free parameters for the data shown in Fig. 3B, and the only free parameter for the plot in Fig. 3C was γ, which we found to be 0.007. We found that the mean-squared error was an order of magnitude larger if the utility function did not temporally discount effort.

Lever-pressing for reward

To consider decision-making and vigor within the same paradigm, we examined an experiment in which rats chose between two levers, each baited with an amount of food (Fig. 3 bottom panel). A trial began with a light cue, instructing the rat to poke its nose into the food tray to activate the levers. Four out of every six trials were choice trials: both levers were activated and once the rat pressed one lever, the other retracted to prevent change of mind. The remaining two trials were forced trials (one for each option), where only one lever was activated. In both choice and forced trials, once a lever was selected, it retracted only after the effort requirement was completed. To prevent the frequency of reinforcement from influencing the rats’ actions, the inter-trial-interval was set to 60s minus the amount of time it took to complete the lever-pressing requirement.

The closed form solution in Eq. (16) predicted that regardless of parameter values, the vigor of the movement as assayed with its duration varied quasi-linearly with the number of lever presses required for obtaining reward, which we found to be in reasonable agreement with the data (Fig. 3E). The fit to the actually observed durations produced a metabolic rate of c = 0.168 and temporal discount rate of γ = 0.08. To fit the choices that the animals made, we used a logistic function that depended on the difference in the utility of the two options, with parameter k = 3.

Walton et al. (2006) found that when animals were indifferent to the available options, the vigor with which they executed the movements was also similar. We can consider this fact by noting that the utility of each option not only describes the probability of it being chosen, but also the vigor with which that movement is performed. To illustrate this point, we computed the number of HR lever presses for which the duration of lever press for the HR option, represented as $t_H^{{}^{\ast }}$, is the same as the LR option, $t_H^{{}^{\ast }}=t_L^{{}^{\ast }}$. We used $n_H^{{}^{\ast }}$ to represent this indifference number of lever presses for the condition that the LR lever produces 2 pellets of food, and the HR lever produces 4 pellets. We found the following relationship:

$$n_{{}_H}^{{}^{\ast }}=\frac{3n_{{}_L}}{2}+\frac{\sqrt{c\left(2+c\gamma n_{{}_L}^2\right)}}{2c}$$ (M9)

The indifference point in the above expression was calculated by setting the vigor of the two movements equal, but it also predicts the indifference point in the two options: using the same parameters as before, $n_H^{{}^{\ast }}$ is 12.4 presses, not very different from the indifference point observed in the experimental data (~13 presses, Fig. 3G).

Metabolic cost of force production and perception of force

To derive a relationship between energy expenditure and force production, we considered movements of constant amplitude but differing accelerations and found that the force-time integral of such movements (under the assumption of moving an inertial object) scaled linearly with movement duration. This was realized if the energy consumed varied linearly with the force-time integral, but not if energy varied with the squared force. To test whether energy consumption actually varied linearly with force-time integral, we considered data from an experiment in which energy consumption was estimated via the change in ATP concentration (or alternatively, oxygen uptake) during the electrical stimulation of an isometric muscle (Fig. 4). We modeled the actual forces produced by the muscle, computed its integral, and then fitted Eq. (9) to the measured data, with the results shown in Fig. 4B (left panel). We found that this model produced a mean-squared error that was about half as large as those produced if we had assumed that energy was related to the integral of the squared force :

$$e\left(f(t)\right)=a_1\underset{0}{\overset{T}{\int }}{f}^2(t)dt+a_2$$ (M10)

The results are shown in the right subplot of Fig. 4B. Other experimental data provided further evidence for this conjecture (Fig. 4C).

Using the metabolic cost of isometric force production we computed perception of effort, resulting in indifference curves for the utility of effort. We considered the utility of holding force f₁ for duration T₁, which is approximately $\frac{c{T}_1{f}_1}{1+\gamma T_1}$ (we are ignoring the bias term a₂). According to this measure of effort, the force f₂ that would produce the same effort is:

$$\begin{gathered} f_2=\frac{T_1(1+\gamma T_2)f_1}{T_2(1+\gamma T_1)} \\ =\frac{T_1{f}_1}{T_2(1+\gamma T_1)}+\frac{\gamma T_1{f}_1}{(1+\gamma T_1)} \end{gathered}$$ (M11)

The above expression demonstrates that as T₂ → ∞, then $f_2\to \frac{\gamma T_1{f}_1}{(1+\gamma T_1)}$. That is, the utility predicts that as T₂ increases, the force f₂ associated with this duration will not go to zero, but asymptote to a non-zero value that grows larger as f₁ increases (Fig. 4E).

In current models of movement control, effort is often the undiscounted sum of squared forces that are produced during the duration of the task. That is, effort accumulates, usually as a quadratic function of force, so that the cost of producing force f(t) is:

$$U\left(f(t)\right)=-c\underset{0}{\overset{T}{\int }}{f}^2(t)dt$$ (M12)

If the effort associated with generating force does not include a temporal discount, as in the above expression, then the cost of holding force f₁ for duration T₁ is $c{f}_1^2{T}_1$. According to this cost, the force f₂ that would be an equivalent amount of effort is:

$$f_2=\sqrt{\frac{f_1^2{T}_1}{T_2}}$$ (M13)

The above expression predicts that as T₂ → ∞, then f₂ → 0, as shown by the indifference curves in Fig. 4F. However, this is inconsistent with the choices that the subjects made. Indeed, this inconsistency remains whether forces are quadratically penalized or not (as shown for a utility that depends only on time-integral of force, Fig. 4G).

Walking speed and the value of time

To consider the value of time, we incorporated an opportunity cost in the utility function. This opportunity cost represented the expected rate of utility (or rate of reward) over the period for which the movement would be performed. To find the optimal movement duration, we differentiated J with respect to movement duration and found the following expression:

$$\frac{dJ}{dT}=\frac{mc{d}^2\left(1+2\gamma T\right)∕T^2-\gamma \alpha }{(1+\gamma T{)}^2}-E\left[\stackrel{.}{J}\right]$$ (M14)

To find the optimal duration of a movement, we set the above expression equal to zero and solved for T to find a fourth order polynomial. The root of this polynomial under the assumption that all parameter values are positive was a single real expression for optimal duration T^*.

We used the idea of opportunity cost to consider the fact that pedestrians walk faster in cities as compared to towns. To approach the problem, we began with data from ⁸ who had estimated the metabolic cost of walking as a function of speed. He estimated c = 0.0053 cal.min/kg/m². In the utility function, we set m = 90 kg, reflecting the average mass of an adult, and d = 15 m, reflecting the distance over which the walking speed was measured by Bornstein and Bornstein (1976). We set the remaining parameters α and γ to 1, and then solved for T such that we maximized the utility. Once we found the optimum duration T^*, we found the optimum speed of walking by the ratio of the distance to duration: d/T^*. To fit the measured data, we modeled expected utility rate $E\left[\stackrel{.}{J}\right]$ as a logarithmic function of city population:

$$E\left[\stackrel{.}{J}\right]=b_1{\log }_{10}p-b_0$$ (M15)

In the above equation, p is the population of the city, b₁ is a scaling parameter (reflecting how fast utility rate grows as a function of population), and b₀ is a bias (reflecting the minimum utility rate regardless of city’s population). The parameters b₀ and b₁ were the only free parameters in the model.

If differences in walking speed across cities are due to between-city differences in the value of time for its inhabitants, then independent of population, the expected utility rate of each city should predict the walking speed of the inhabitants of that city. We tested this prediction directly. For walking speed we used data from observations in n=27 cities ²⁷. We estimated the expected utility rate for each of these cities via the average hourly wage of its inhabitants, normalized to the cost of living in that city ²⁸. The cost of living was calculated based on a basket of goods containing 154 items. The same basket of goods was used for all cities. The result was an estimate of expected utility rate as dollars per hour, normalized to the local cost of living. The expected utility rate for the inhabitants of the city of New York was set to 100 and the data for all other cities was represented with respect to New York (Domestic Purchasing Power, page 10 of ²⁸). We used linear regression to quantify the relation between walking speed and expected utility rate, and the relation between walking speed and the speed of a postal transaction.