State-dependent sequential allostery exhibited by chaperonin TRiC/CCT revealed by network analysis of Cryo-EM maps

Abstract

The eukaryotic chaperonin TRiC/CCT plays a major role in assisting the folding of many proteins through an ATP-driven allosteric cycle. Recent structures elucidated by cryo-electron microscopy provide a broad view of the conformations visited at various stages of the chaperonin cycle, including a sequential activation of its subunits in response to nucleotide binding. But we lack a thorough mechanistic understanding of the structure-based dynamics and communication properties that underlie the TRiC/CCT machinery. In this study, we present a computational methodology based on elastic network models adapted to cryo-EM density maps to gain a deeper understanding of the structure-encoded allosteric dynamics of this hexadecameric machine. We have analysed several structures of the chaperonin resolved in different states toward mapping its conformational landscape. Our study indicates that the overall architecture intrinsically favours cooperative movements that comply with the structural variabilities observed in experiments. Furthermore, the individual subunits CCT1-CCT8 exhibit state-dependent sequential events at different states of the allosteric cycle. For example, in the ATP-bound state, subunits CCT5 and CCT4 selectively initiate the lid closure motions favoured by the overall architecture; whereas in the apo form of the heteromer, the subunit CCT7 exhibits the highest predisposition to structural change. The changes then propagate through parallel fluxes of allosteric signals to neighbours on both rings. The predicted state-dependent mechanisms of sequential activation provide new insights into TRiC/CCT intra- and inter-ring signal transduction events.

1. Introduction

1.1. Cryo-EM revolution is accompanied by advances in molecular modelling and computations

Cryogenic electron microscopy (cryo-EM) has found increasingly more use in structural biology in recent years as a maturing tool to characterize not only a single structure but the ensemble of conformations, often relevant to biological function, especially for supramolecular assemblies (Callaway, 2020; Nogales, 2016). Thanks to radically new technological advances experienced by this technique in recent years in both microscope hardware and image processing software, termed the resolution revolution, cryo-EM is now capable of capturing information about biomolecular structure in multiple states to near-atomic resolution (Cheng, 2018; Mitra, 2019; Nogales, 2016).

Cryo-EM data on macromolecules consists of a large number of 2D projections of “particles” in an unknown range of orientations and conformations trapped in a thin layer of vitreous ice after plunge freezing (Mitra, 2019). 3D structures are recovered by maximum likelihood image analysis methods to assign orientations to each particle and reconstruct 3D structural information (Cossio and Hummer, 2018; Scheres et al., 2007; Vilas et al., 2018). While methods are emerging for initial model reconstructions (Elmlund et al., 2013; Gomez-Blanco et al., 2019; Lyumkis et al., 2013; Punjani et al., 2017; Xie et al., 2020) and dealing with continuous heterogeneity (Maji et al., 2020; Sorzano et al., 2019), 3D reconstruction is usually achieved by alignment to a reference structure and aided by classification (Cossio and Hummer, 2018; Vilas et al., 2018). The result is a number of electron density maps corresponding to class averages, which can be found in the EM Data Bank (EMDB) or EM Data Resource (Lawson et al., 2016, 2020). Density maps are then analysed further to better understand the underlying structure and structural variability of the protein or complex being studied. This is usually done by building or fitting and refining atomic models to match the density map (Alnabati and Kihara, 2019; Kim et al., 2020; Malhotra et al., 2019; Miyashita and Tama, 2018; Nicholls et al., 2018).

Fitting of existing x-ray crystallographic, nuclear magnetic resonance (NMR), and/or integrative modelling data on the components of a complex structure or assembly resolved by cryo-EM is especially important for low-to-intermediate resolution cryo-EM maps while ab initio modelling may be carried out at higher resolutions (~4 Å or better) (DiMaio and Chiu, 2016; Joseph et al., 2017; Koukos and Bonvin, 2020; Leelananda and Lindert, 2020; Nicholls et al., 2018). Given the conformational variability of these components, flexible fitting methods have been developed, which use the collective modes of motion predicted by normal mode analysis (NMA) (e.g. NMFF (Tama et al., 2004a; Tama et al., 2004b), NORMA (Suhre et al., 2006) and other tools; see below), or the conformational changes sampled in molecular dynamics (MD) simulations (e.g. MDFF (Trabuco et al., 2008)). Similar approaches are used in replica simulation frameworks for fitting ensembles of structures and inferring dynamics from cryo-EM maps (Bonomi et al., 2018; Bonomi and Vendruscolo, 2019; Miyashita et al., 2017). Accelerated by enhanced sampling schemes (Abrams and Bussi, 2013; Bernardi et al., 2015; Harpole and Delemotte, 2018) and/or dedicated hardware such as the Anton supercomputers (Shaw et al., 2009, 2014), MD simulations are also used for exploring the microseconds to milliseconds dynamics of proteins (Dror et al., 2012; Hollingsworth and Dror, 2018).

However, conducting MD simulations of supramolecular systems at atomic detail is still extremely expensive, both in terms of computing time and memory (Hollingsworth and Dror, 2018). MD simulations suffer from inaccuracies in sampling the conformational space, especially the cooperative changes in structure that are often functional. MD simulations are also sensitive to force field parameters, especially over the long timescales needed to observe biologically relevant events (Bottaro and Lindorff-Larsen, 2018). It is thus desirable to develop physically inspired models and methods that lend themselves to efficient analytical solutions for large data analyses and cooperative/global motions of molecular machines, albeit at low resolution, rather than detailed atomic models that provide precise information but on limited length and time scales.

1.2. Insights into the allosteric dynamics of cryo-EM structures can be gained upon representing their electron density maps by elastic network models

Elastic network models (ENMs) combined with normal mode analysis (NMA) provide a robust framework for efficiently determining collective motions of biological relevance (Bahar et al., 2010a, 2010b; Doruker et al., 2012), as shown for biomolecular systems at multiple scales, from single proteins to supramolecular assemblies (Atilgan et al., 2001; Bahar et al., 2010b; Eyal et al., 2015), and more recently the chromatin (Sauerwald et al., 2017; Zhang et al., 2020a). These models allow for analytical derivations of the spectrum of normal modes of motion, uniquely encoded by the architecture. Each normal mode is characterized by a vibrational frequency and mode shape (i.e. movements of all nodes/residues of the network/structure along each mode). In particular, the global modes or softest modes at the lowest frequency end of the spectrum robustly enable the predisposition of the structure to cooperative changes relevant to function (Bahar et al., 2010b; Zheng et al., 2006). These properties have led to the development of many flexible fitting algorithms using NMA (Costa et al., 2020; Hinsen et al., 2005; Lopez-Blanco and Chacon, 2013; Matsumoto and Ishida, 2009; Miyashita and Tama, 2018; Suhre et al., 2006; Tama et al., 2004a; Velazquez-Muriel and Carazo, 2007; Zheng and Tekpinar, 2014) as well as hybrid methods that utilize ENMs for modelling mechanisms of action, allosteric signalling and evolution (Krieger et al., 2020).

While ENM NMA emerged as an efficient tool for investigating the dynamics of large systems where high resolution atomic models may be lacking, such as those characterised by cryo-EM, a barrier has been that electron density maps could not be readily converted into a network model. Among approaches developed to address this issue, the topology representing network (TRN) method (Martinetz and Schulten, 1994; Ming et al., 2002a) and the closely related quantized elastic deformational model (Martinetz and Schulten, 1994; Ming et al., 2002a) have shown good performance and robustness (Beuron et al., 2003; Chacon et al., 2003; Kong et al., 2003; Ming et al., 2002b) as has the approximation-accuracy control method (Jonic and Sorzano, 2016).

In the present study, we adopt and extend the TRN method to generate a coarse-grained (CG) representation of cryo-EM density maps amenable to ENM analysis at large scale. We also developed (i) a new implementation of adaptive ANM (Yang et al., 2009c), enabling easier access to this method for calculating conformational transitions; (ii) an extension of topology preserving techniques, Spectral Clustering (Lee and Verleysen, 2007; Ma and Fu, 2012) and Self-Organizing Maps (SOM) (Kohonen, 2001) for identification of dynamical domains related to subunits; and (iii) a residue-agnostic nearest neighbour method for aligning CG and atomic models.

We integrated our method into the ProDy API, a widely used Python interface for protein dynamics analyses (Bakan et al., 2011, 2014), thus enabling its automated use for the broader community. ProDy features a wide range of tools for identifying functional sites and mechanisms and building ensembles of related structures. The integration of our new TRN-based pipeline into ProDy allows one to use various ENMs such as the Gaussian network model (GNM) (Bahar et al., 1997), the anisotropic network model (ANM) (Atilgan et al., 2001; Eyal et al., 2015), distance-dependent ENMs (Hinsen, 1998, 2008; Hinsen and Kneller, 1999; Hinsen et al., 2000; Riccardi et al., 2009; Yang et al., 2009a), the rotation and translation of blocks (RTB) model (Tama et al., 2000), and the reduced Hessian framework for modelling environment effects (Hinsen et al., 2000; Ming and Wall, 2005; Zheng and Brooks, 2005) including membrane environment (Lezon and Bahar, 2012).

1.3. The mammalian chaperonin TRiC/CCT is a cryo-EM-resolved allosteric machine that requires multiscale mode analysis

We applied our approach to the chaperonin CCT (also known as TRiC), a molecular machine of critical importance for ensuring correct folding of about 10% of eukaryotic proteins. CCT has been implicated in a number of diseases including cancer, Huntington’s, Alzheimer’s and Parkinson’s diseases (Jin et al., 2019b), and hence extensively studied, thus providing a wealth of structural and functional data for assessing the significance of our predictions. It is also of sufficiently large size to demonstrate the utility of our new CG methodology, which is still amenable to all-atom ANM analysis, for multiscale methodology. Finally, the availability of structural data at atomic level for CCT, as well as the rapidly growing data on this system, will serve as a testbed for our methodology.

TRiC/CCT, like the bacterial chaperonin GroEL, is composed of two oligomeric rings, stacked back-to-back against each other. However, CCT rings are hetero-octameric with pairwise sequence identities of 20–35% between the subunits (see Fig. S1A), while GroEL rings are homo-heptameric. Furthermore, CCT subunits in a given structure exhibit large structural heterogeneity (more than 6 Å root-mean-square deviation (RMSD) in their coordinates; Fig. S1B), resulting in asynchronous movements between the subunits. Previous studies indeed suggested that each subunit has different ATP binding affinities and hydrolysis capabilities (Amit et al., 2010; Reissmann et al., 2012). Yet, CCT chaperonin activity requires coordinated conformational changes across the eight subunits in a given ring as well as inter-ring couplings, driven by ATP binding and hydrolysis (Cong et al., 2012; Meyer et al., 2003; Reissmann et al., 2012; Skjaerven et al., 2015) for enabling ring closure and formation of a chamber enclosing the substrate. So, instead of moving concertedly, typical of the MWC model for allostery (Changeux, 2012), the conformational changes of CCT subunits are sequential (Gruber and Horovitz, 2016; Gruber et al., 2017; Jin et al., 2019a; Rivenzon-Segal et al., 2005), characterized by the KNF model (Bai et al., 2010; Duke et al., 2001; Koshland et al., 1966).

The allosteric cycle of CCT (Cong et al., 2012) comprises five main conformational states (Fig. 1A–B), whose interconversions are regulated by ATP binding and hydrolysis. The set of structures enclosed in the green box includes the apo and ATP-bound CCT (e.g., PDB models 4a0o, 5gw4, 6ks7 and 4a0v). These transition to more closed structures upon ATP hydrolysis including an asymmetric conformer (purple; PDB model 4a0w) and fully closed structures (yellow; including PDB model 3iyg). Phosphate release leads to the opening of the chaperonin (PDB model 4a13). Recent studies have expanded this structural repertoire considerably (see Fig. 1B–C) but the basic conformational features remain largely unchanged.

Fig. 1. The allosteric cycle of the eukaryotic chaperonin CCT and conformational states visited during the cycle.

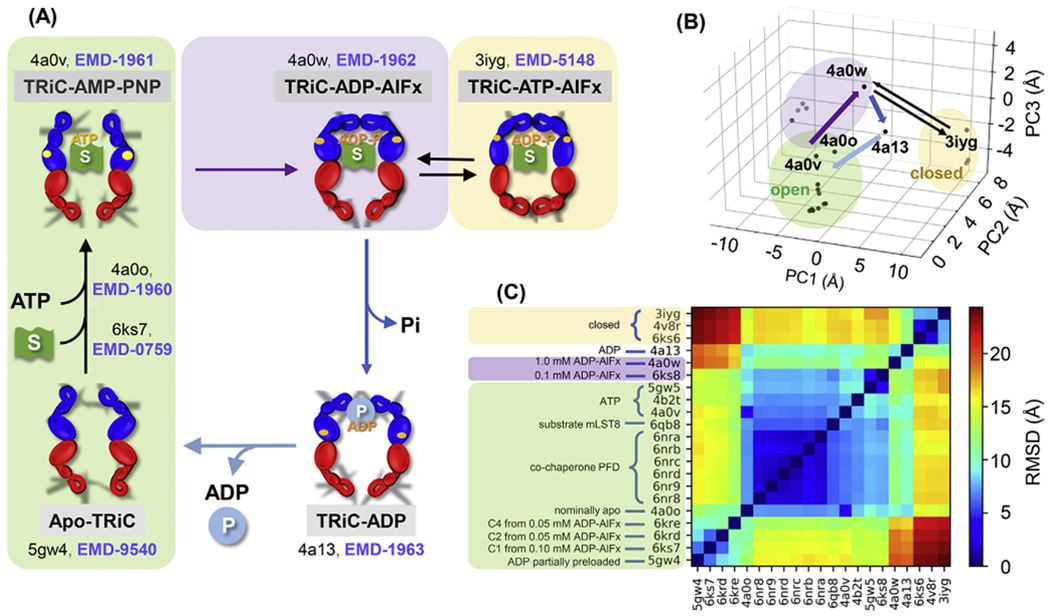
(A) Major conformational transitions triggered by ATP and substrate (S; green flag) binding and ATP hydrolysis (upper part). The upper left conformation represents the ATP-bound form as AMP-PNP (PDB: 4a0v) and ATP-γ-S (PDB: 4b2t) are non-hydrolysable ATP analogues. ATP hydrolysis is accompanied by ring closure (upper right); treatment with ADP-AlFx and ATP-AlFx (containing various aluminium fluorides) generates analogues corresponding to different stages in the hydrolysis process. Then phosphate release leads to ring opening again in the presence of the remaining ADP (lower right). This is followed by release of ADP and folded product (P; blue sphere), returning the heteromeric structure to the apo state (lower left). PDB and EMDB IDs are labelled for key resolved states. An ensemble of intermediate structures has been resolved for the ATP binding transition (including PDB: 6ks7) (Jin et al., 2019a). (B) Projection of all known structures onto the first three principal components (PC1-PC3) deduced from the principal component analysis (PCA) of the known conformers (each represented by a dot). The purple, dark blue and light blue arrows show the primary pathway between structures with at least one ring open, and the thin black equilibrium arrows display the passages between the kinetically trapped, fully closed conformations. (C) RMSDs between all pairs of structures shown in B. Green, yellow and purple shaded regions refer to conformers in open, closed and intermediate states in all panels.

In the present study, with the help of NMA and a Markovian stochastic model, both hinging on the ENM representation, we will dissect the space of motions accessible to CCT and identify the dominant mechanisms of structural changes (presented in several movies) at various stages of the allosteric cycle. We will show that the functional changes in structure such as lid closure/opening are favoured by ANM modes intrinsically accessible to the 3D architecture. Our study further shows that each intermediate passage during the allosteric cycle is initiated in a state-dependent manner by different subunits, pointing to the complexity of the overall machinery of this eukaryotic chaperonin. Finally, combination of these results with ANM analysis for full-atomic structures will provide a multiscale view of the intrinsic dynamics of the individual modules (subunits and their domains) and how these are exploited in the global chaperoning machinery.

2. Methods

2.1. Topology representing network (TRN) algorithm

The original TRN algorithm has been outlined earlier (Martinetz and Schulten, 1994), and successfully applied to cryo-EM density maps (Beuron et al., 2003; Chacon et al., 2003; Kong et al., 2003; Ming et al., 2002b). In this study, we modify the algorithm, as described below, in order to learn a CG representation of the structure from its cryo-EM density map.

The cryo-EM density map can be considered as an array of N real numbers, ρ = [ρ₁, ρ₂, …, ρ_N], each associated with a 3D coordinate r_i = [x_i, y_i, z_i], indicating the density at the designated position. To reduce noise and remove negative densities, we first set any density that is lower than a threshold (e.g., 1.0 used in this study) to be 0. This essentially gives us a discrete probability distribution function for each voxel at r_i:

$$P({\mathit{r}}_i)={\rho }_i/\sum _j{\rho }_j$$ (1)

Suppose we use M nodes to represent the density map, whose initial coordinates are r_m(0) with 0 ≤ m ≤ M are sampled from P(r_i). The following adaptation steps are iteratively applied to refine the positions of the nodes: (1) sample r from the distribution P(r_i); (2) determine the distance of each one of the node positions r_m to r and sort these distances into a ranking k_m, such that the closest one to r has rank k = 0, and the farthest, k = M − 1; and (3) update the coordinates of all m nodes following

$${\mathit{r}}_m(t+1)={\mathit{r}}_m(t)=\epsilon e^{-k_m∕\lambda }(\mathit{r}-{\mathit{r}}_m(t))$$ (2)

where t is the number of adaptation steps already applied, ε is the step size, and λ is a parameter effectively controlling the number of updated nodes. Intuitively, the closest node is dragged towards r_i with the distance εr_i − r_m(t), and others are dragged towards r_i in the same manner with the distance penalized based on their ranking using the exponential term. With decreasing λ, e^−k_m/λ goes to zero, and effectively no node other than the closest is moved. Both ε and λ are computed adaptively during the iterations as follows:

$$\lambda (t)={\lambda }_0{\left(\frac{{\lambda }_f}{{\lambda }_0}\right)}^{t∕t_f}$$ (3)

$$\epsilon (t)={\epsilon }_0{\left(\frac{{\epsilon }_f}{{\epsilon }_0}\right)}^{t∕t_f}$$ (4)

so that λ and ε starts with λ₀ and ε₀, and as t→t_f, λ and ε go to λ_f and ε_f, respectively. In this study, we used the following parameters (Martinetz and Schulten, 1994): λ₀ = 0.2M, λ_f = 0.01, ε₀ = 0.3, ε_f = 0.05, t_f = 200M, M = 3000 for EMD-1961 (~1/3 of CCT residues).

Nodes corresponding to unidentified densities in the centre of the CCT chamber (Cong et al., 2012) were removed, resulting in a refined model with M = 2,908 nodes. The network connectivity is defined as described below. The algorithm is implemented and incorporated into the ProDy API.

2.2. ENM-based analyses

In general, an ENM represents the structure as a bead-and-spring model where the bead positions are identified with those of α-carbons (C^α), and elastic springs connect pairs of beads within a cut-off distance characteristic of the range of inter-residue coordination. In the application to cryo-EM data, we used the TRN nodes to build the network. NMA and Markovian analyses were performed using methods previously implemented within ProDy (Bakan et al., 2011). For ClustENM, we used a procedure similar to that previously introduced (Kurkcuoglu et al., 2016). We upgraded the adaptive ANM (aANM) (Yang et al., 2009c) to improve the efficiency of sampling the space between pairs of conformers, also implemented in ProDy.

In order to compare the mode spectra predicted by the TRN representation of electron density maps and corresponding all-atomic models in the PDB, we aligned the TRN against the atomic models using a nearest neighbour approach where each TRN bead was matched with the nearest α-carbon; and we treated the non-aligned nodes as the environment of the aligned system using the reduced model framework (Hinsen et al., 2000; Ming and Wall, 2005; Zheng and Brooks, 2005). See Supplementary Methods for details.

2.3. Subunit identification by spectral clustering

Spectral Clustering (SC) is based on the graph Laplacian, which encodes the connectivity between data points. The eigenvector corresponding to the first nonzero eigenvalue of the Laplacian, also called Fiedler vector, and a set of consecutive eigenvectors partition the Laplacian in such a way that it becomes a block diagonal, each block representing a principal subspace associated with a different cluster (Fiedler, 1989; Jianbo and Malik, 2000; Ng et al., 2001). Here we used a Gaussian kernel constructed by a pairwise distance matrix with a soft cut-off of 10 Å, which ensures full connectivity. Using SC, we organized the graph into 8 clusters, each containing two CCT subunits. A second round of SC subdivided each cluster into four, each containing the equatorial and apical domains of the subunit pairs. Sub-clusters of the same subunit were then combined which led to 16 clusters corresponding to the 16 subunits. We compared the results from SC with those from Self-Organizing Maps (SOM) plus k-means (Fig. S2). We defined the “ground truth” by mapping beads to the nearest α-carbons in the corresponding all-atom model (PDB: 4a0v).

3. Results

3.1. TRN representation of electron density maps coupled with ANM provides an effective description of the CCT architecture and equilibrium dynamics

As schematically depicted in Fig. 2A, the subunits are designated as a₁ to a₈ in one of the rings (termed cis or upper ring), and a₁’ to a₈’ in the other (trans or lower), using the nomenclature introduced in cryo-EM studies (Cong et al., 2012; Zang et al., 2016). Supplementary Table S1 lists alternative nomenclature/identifications adopted in different studies, as reference. In the current study, we use either the identifiers a₁-a₈ and a₁’-a₈’ for the respective cis and trans rings, or the corresponding subunit numbers CCT 2, 4, 1, 3, 6, 8, 7, 5 (same in both rings), identified recently (Kalisman et al., 2013; Leitner et al., 2012; Wang et al., 2018; Zang et al., 2018), or both names (a₁/CCT2, a₂/CCT4, …, a₈’/CCT5) for clarity.

Fig. 2. Model for ATP-bound CCT generated using the Topology Representing Network (TRN) and Spectral Clustering (SC) guided by ANM.

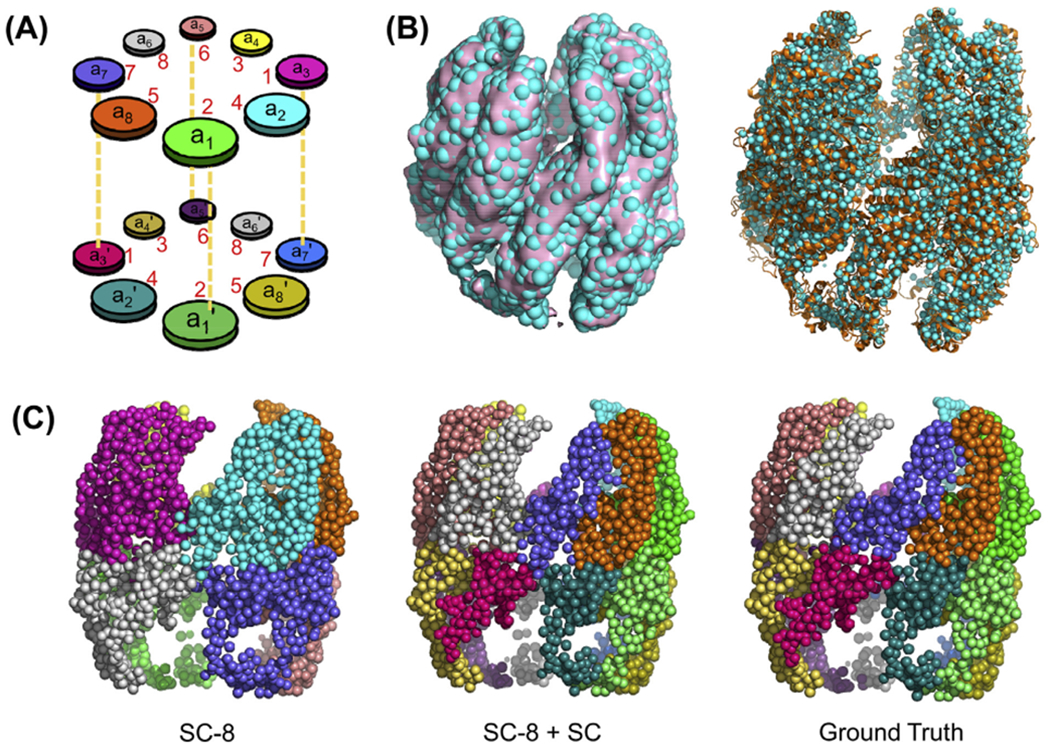
(A) Diagram depicting the nomenclature of subunits in the two hetero-octameric rings. The pairs of subunits a_k and a_k’ belonging to the respective upper and lower rings are sequentially identical; the pairs (a₁, a₁’) and (a₅, a₅’) are vertically stacked against each other while the remaining subunits are arranged in a two-fold symmetric way. Numbers in red correspond to the biological subunit numbers without the CCT prefix. (B) Superposition of the refined network of 2,908 nodes (cyan, spheres) with either the electron density map (EMD-1961; pink surface; left) or the corresponding all-atom model (right; PDB: 4a0v; orange ribbon). (C) Decomposition of the structure into clusters using spectral clustering, starting with eight clusters (SC-8, left). Subdivision of each cluster obtained from SC-8 into two subunits using Spectral Clustering (SC-8 + SC) yields the middle diagram. The right diagram represents the ground truth where beads are grouped into subunits by mapping them to the nearest α-carbons in the atomic structure (PDB: 4a0v). Corresponding SOM + k-means results are shown in Fig. S2A. The clusters are coloured as in panel A.

The algorithm assigns a network of N nodes to a probability distribution based on the EM density map voxels as described in Section 2.1. Information on connectivity is included in the original algorithm, but, in our adaptation, we use the ANM to derive the Hessian H that also accounts for the stiffness of inter-node couplings (Atilgan et al., 2001; Bahar et al., 2017).

Structural superposition of the TRN beads and the original density map (Fig. 2B left) as well as the all-atom structure deposited in the PDB (Fig. 2B right) (Cong et al., 2012) verified that a network of about M = 3,000 nodes adequately represented the density data for CCT-AMP-PNP and provided a good description of overall architecture. A few nodes that protrude with respect to the density maps, often located at highly sparse, peripheral positions with elongated shapes, could be attributed to artefacts from averaging of flexible/disordered substrates, termini and apical loops with variable occupancies and conformations (Cong et al., 2012). Such nodes were removed from the model as their large swinging motions could obscure the cooperative motions of the multimer, a phenomenon known as the tip effect (Lu et al., 2006). The refined network had M = 2,908 nodes.

The level of granularity adopted here for the TRN is comparable to that of recent cryo-EM structure analyses (Sorzano et al., 2019; Vilas et al., 2018). On the other hand, it is lower than that of conventional single-node-per-residue ANM, which would contain more than 8,000 nodes based on 16 subunits of >500 residues each. Previous work demonstrated that the ANM is scalable, i.e. one can retain the accuracy of the results even with 1-2 orders of magnitude fewer nodes provided that the cut-off distance for defining the network connectivity and corresponding Hessian is suitably rescaled (Doruker et al., 2002). This feature was borne out by previous application to bacterial chaperonin GroEL, which showed that soft-partitioning of the structure into 10²-10³ nodes (clusters of spatially neighbouring residues) almost invariably retained GroEL global dynamics and allosteric signalling properties otherwise described by a full-residue (~8,000 nodes) model (Chennubhotla and Bahar, 2006). Based on these considerations, in order to adapt the TRN algorithm to the ANM analysis of cryo-EM data, we rescaled the cut-off distance using the relationship between the network model granularity and the optimal cut-off distance (Doruker et al., 2002). This led to a TRN cut-off distance of 20 Å, as opposed to 12–15 Å in the conventional ANM (Fig. S3A).

The TRN representation is agnostic to chain connectivity, or to the identity of the individual subunits. As the network contains intertwined domains which may not lend itself to identification of subunits by standard clustering methods, we adopted two topology-based methods, namely, spectral clustering (SC; implemented in scikit-learn (Pedregosa et al., 2011)), and Self-Organizing Maps (SOM; implemented in NeuPy (Shevchuk, 2015)) for identifying subunit boundaries. As shown in Fig. 2C, SC organized the CCT nodes into four well-defined clusters in each ring in the first step. We then used a multi-step procedure guided by the following features: (i) CCT-ATP subunits are spatially grouped in pairs (Cong et al., 2012), (ii) subunits also move in pairs as observed in the ANM analysis (see Section 3.2), and (iii) intermediate and equatorial domains of neighbouring subunits are tightly connected. Our multistep procedure led to 16 clusters that closely approximated the 16 subunits of EMD-1961 (Fig. 2C, middle).

The SOM method generated similar clusters, in support of SC results, but a few clusters contained disjoint nodes (see red arrow in Fig. S2A), so we adhered to SC results. Besides, SC partitions the beads based on the eigenvectors of the graph Laplacian, which bears close resemblance to the Gaussian Network Model (GNM) (Bahar et al., 1997) mode decomposition. The SC result is therefore conceptually rational and consistent with the ENM framework. Finally, either algorithm, SC or SOM, was verified to yield an accuracy of ~90% upon comparison of the identified partitioning (of nodes into subunits) to that obtained by mapping the nodes to the nearest α-carbon atoms in the deposited all-atom structure (ground truth in Fig. 2C, right).

Overall, this analysis showed that topology-based hierarchical (multi-step) clustering guided by ANM dynamics accurately discerned the subunits. Tight packing of equatorial domains of neighbouring subunits made this a nontrivial process. Since our method is guided by ANM dynamics and SC effectively groups nodes with similar motions together, the generated clusters are dynamics-based domains, which may not necessarily coincide with protomers. However, they are functionally important, and therefore, such a partitioning of the structure is useful. Furthermore, successively smaller domains can be identified by a multistep approach.

Two additional tests were performed for assessing the use of TRN for modelling CCT equilibrium dynamics. First, we evaluated the GNM-predicted mean-square fluctuations (MSFs) of residues for CCT bound to an ATP-analogue, TRiC-AMP-PNP (EMD-1961), using its TRN model. Comparison to x-ray crystallographic B factors observed for CCT bound to another ATP analogue (ATP-γ-S; PDB: 2xsm) (Munoz et al., 2011) showed a good level of agreement despite the low resolution (5.5 Å) of the x-ray structure and the use of electron density maps for constructing the TRN (Fig. S4). Second, we compared the global mode spectra predicted for the TRN representation of TRiC-AMP-PNP, with that computed using the GNM and ANM for its all-atomic model (PDB: 4a0v), which yielded reasonable agreement (Fig. S5). These results confirmed that the TRN provides an adequate framework for analysing the collective dynamics of CCT.

3.2. The architecture of ATP-analogue-bound CCT favours pairwise couplings between intra-ring neighbours and en bloc motions of selected subunits

To explore the machinery of CCT on a global scale, we analysed as a first step the softest 20 non-zero modes accessible to TRiC-AMP-PNP modelled above. The soft modes usually facilitate, if not drive, the collective rearrangements (of all subunits) relevant to biological function (Bahar et al., 2017); therefore it is of interest to determine which particular subunits exhibit a high predisposition to undergo a lid closure (e.g. passage to TRiC-ADP-AlFx in Fig. 1) accompanying ATP hydrolysis.

The mean-square fluctuations (MSFs) of the subunits and the cross-correlations (or covariance) driven by these softest modes are presented in Fig. 3. The surface in panel A is colour-coded by MSFs; the regions undergoing the smallest motions are in blue, and intermediate and higher mobility regions in green and orange, respectively. The equatorial domains are highly stable and closely coupled between the two rings, while the apical domains exhibit the highest mobility consistent with previous computations (Chacon et al., 2003) and experiments (Cong et al., 2012).

Fig. 3. Global dynamics of TRiC-AMP-PNP.

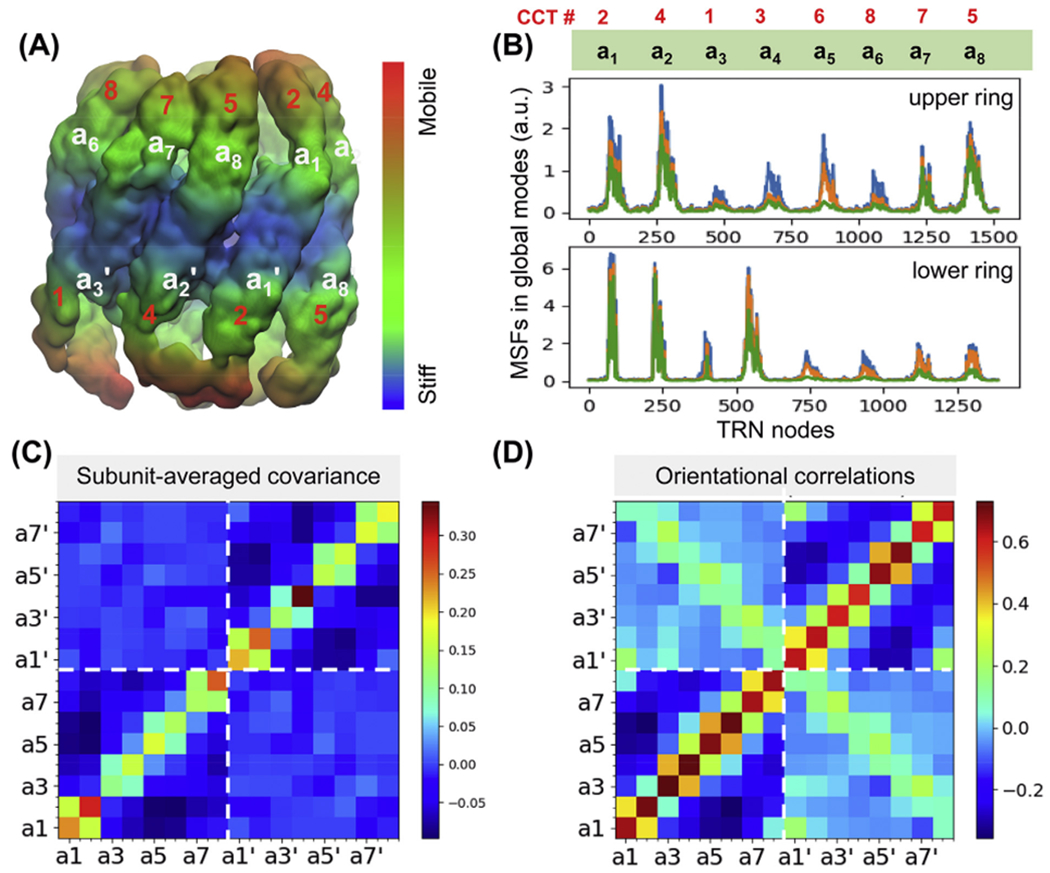
(A) Results from ANM analysis of the TRN (based on EMD-1961), displaying the architecture colour-coded by the MSFs of nodes (in surface representation; blue: most rigid; orange: most mobile) in the softest 20 modes. (B) MSFs of the subunits as driven by the subsets of 5 (green), 10 (orange) and 20 (blue) softest modes. Note the high mobility of subunits a₁, a₂ and a₈ in the upper ring, and those of a₁’, a₂’ and a₄’ in the lower ring. Two sets of labels are listed in panels A and B: a₁-a₈ (or a₁’-a₈’ for the lower panel) and corresponding biological subunit names CCT1-8 (in red). (C) Covariance between the global motions of the subunits based on the softest 20 modes. Strong coupling between pairs of adjacent subunits on a given ring are seen. (D) Orientational correlations between the global movements of the subunits (same as covariance but normalized with respect to MSFs).

Fig. 3B shows the subunits that exhibit the highest tendency to move in the ATP analogue-bound structure driven by the softest 5 (green), 10 (orange) and 20 (blue) modes (see details for modes 1–5 in Fig. S6). In principle the peaks in the slowest modes would indicate the subunits that undergo the earliest movements. Here CCT5, CCT4 and CCT2 in the cis ring (upper panel), and CCT4, CCT2 and CCT3 in the trans ring (lower panel) exhibit the highest peaks. The trans ring is less constrained than the cis ring (compare the ordinate values in the two panels), which could be attributed to stabilization induced upon ATP analogue or substrate binding to the upper ring subunits.

We have also verified that the MSFs and cross-correlations driven by the global modes were insensitive to the inter-node distance-dependency of the spring constants in the ENM. As shown in Figs. S3B–C, conventional ANM (with uniform spring constant for all pairs closer than 15 Å), the ENM with force constant exponentially decaying with distance (Hinsen, 1998), and a parameter-free ANM where the spring constant scales inversely with the distance squared (Yang et al., 2009a) yielded comparable results to those with uniform spring constant for all pairs closer than 20 Å. The major difference was a few excessively high peaks predicted by parameter-free ANM, which signals the possible underestimation of inter-node couplings at specific loci in the latter.

The covariance maps in Fig. 3C–D provide information on the level of coherence/coupling between nodes within individual subunits (diagonal elements) and across subunits (off-diagonal). The lower-left and upper-right quadrants correspond to the intra-ring correlations for the upper and lower rings, respectively; and off-diagonal quadrants display the inter-ring correlations. The boundary between the two rings is shown by the white dashed lines. Dark red and dark blue entries refer to the strongest correlations (large movements in the same direction, usually intra-subunit) and anticorrelations (large movements in opposite directions, intersubunit). Subunits a₂/CCT4, a₈/CCT5 and a₁/CCT2 exhibit the largest and most coherent (en bloc) movements in the upper ring; as do subunits a₄’/CCT3, a₂’/CCT4, and a₁’/CCT2 in the lower ring consistent with their distinctive mobilities in panel B. A closer look at the diagonal 2 × 2 blocks indicates that the subunits tend to move in pairs. This feature is observed in both upper and lower rings, suggesting that such couplings are not associated with nucleotide binding, but with the asymmetric hetero-octameric nature of the rings.

The covariance map in Fig. 3C reflects both the sizes of subunit motions and their relative orientations (correlation cosines). Further examination of purely orientational correlations (upon normalization with respect to subunit-averaged MSFs; see Supplemental Methods) in Fig. 3D confirms the strong coupling between sequential pairs (a₁, a₂), (a₃, a₄), (a₅, a₆), (a₇, a₈) in the cis ring, and their counterparts in the trans ring. We note the motions of each pair are anticorrelated with respect to others in the same ring, and especially the pairs at the opposite face (dark blue regions in the lower left quadrant). Similar anticorrelations can be discerned in the lower ring (upper right quadrant). Therein, the pair a₅’ and a₆’ is distinguished by a strong coupling. Finally, the light green-yellow diagonal along the inter-ring quadrants shows the couplings between neighbouring subunits across the rings. Calculations confirmed the reproducibility of this map using either uniform or distance-dependent (exponential) spring constants, but not with parameter-free ANM (Fig. S3C).

3.3. Differential mobilities of the subunits in the ATP-bound form reveals the predisposition of CCT4 and CCT5 to enable functional changes

By definition, the collective modes of motions predicted by the ANM describe the thermal fluctuations accessible to an equilibrium structure under physiological conditions (Atilgan et al., 2001; Bahar et al., 2010b). They also underlie the adaptability of the structure to changes induced by intermolecular interactions (Haliloglu and Bahar, 2015; Zhang et al., 2020b). Perturbations caused by any energy input, for example ATP hydrolysis, would “push” the equilibrium structure away from its energy minimum along the most easily accessible modes, starting from mode 1, 2, etc. The individual modes represent axes of overall reconfiguration away from the equilibrium state in the multidimensional conformational space, and many structural changes are indeed effectuated by a combination of selected modes (Meireles et al., 2011). Among the accessible modes, those requiring a lower energy ascent (lower frequency or smaller uphill curvature along the energy landscape) will be naturally preferred in response to perturbations, e.g. ATP binding or hydrolysis. These soft modes naturally show more significant movements than the ones with higher frequency, in response to the same amount of energy allocated to each mode as dictated by the equipartition law. Figs. 3B and S6C show that subunits a₂/CCT4, a₈/CCT5 and a₁/CCT2 in the upper ring and a₁’, a₂’ and a₄’ (CCT2, CCT4 and CCT3) in the lower ring are predisposed to exhibit the largest movements in the softest modes. As such, these subunits are suggested to be most readily adaptable to subsequent structural changes that the ATP-bound state will undergo, i.e. those taking place upon ATP hydrolysis, if not driving the changes that facilitate hydrolysis. We also note that subunit a₄’ is distinguished by a large en bloc movement (Fig. 3C); and adjacent pairs in each ring tend to move in tandem (Fig. 3C–D).

3.4. Conformers along the allosteric cycle exhibit state-dependent dynamics manifested by differential sequences of subunit motions in soft modes

The results in Subsections 3.2–3.3 are uniquely defined by the architecture of CCT bound to non-hydrolysable ATP analogues. Computations performed for TRiC/CCT structures in different states along the allosteric cycle revealed, on the other hand, the high mobility of other subunits, in a state-dependent manner. Fig. 4 displays the results for three additional conformers visited at different stages of the allosteric cycle: (A) TRiC resolved (Zang et al., 2016) in a nucleotide-partially-preloaded (NPP) state equivalent to the apo state (green shaded in Fig. 1), (B) another newly resolved structure at relatively low (0.1 mM) ADP-AlFx level, called conformation 1 (Jin et al., 2019a), representative of an intermediate during ATP binding; and (C) the TRiC structure at 1 mM ADP-AlFx (Cong et al., 2012) which may be viewed as an intermediate stabilized during hydrolysis (purple shaded in Fig. 1). The plots on the right display the subunit displacements driven by the softest modes of motion. Peaks therein indicate the subunits with highest propensity to undergo conformational changes, like Fig. 3B for the ATP-analogue-bound TRiC (except for displaying the results here for the two rings by consecutive residue numbers indicated by the respective blue and grey bars along the upper abscissa).

Fig. 4. Different conformational states of TRiC visited during its allosteric cycle and corresponding mobility profiles.

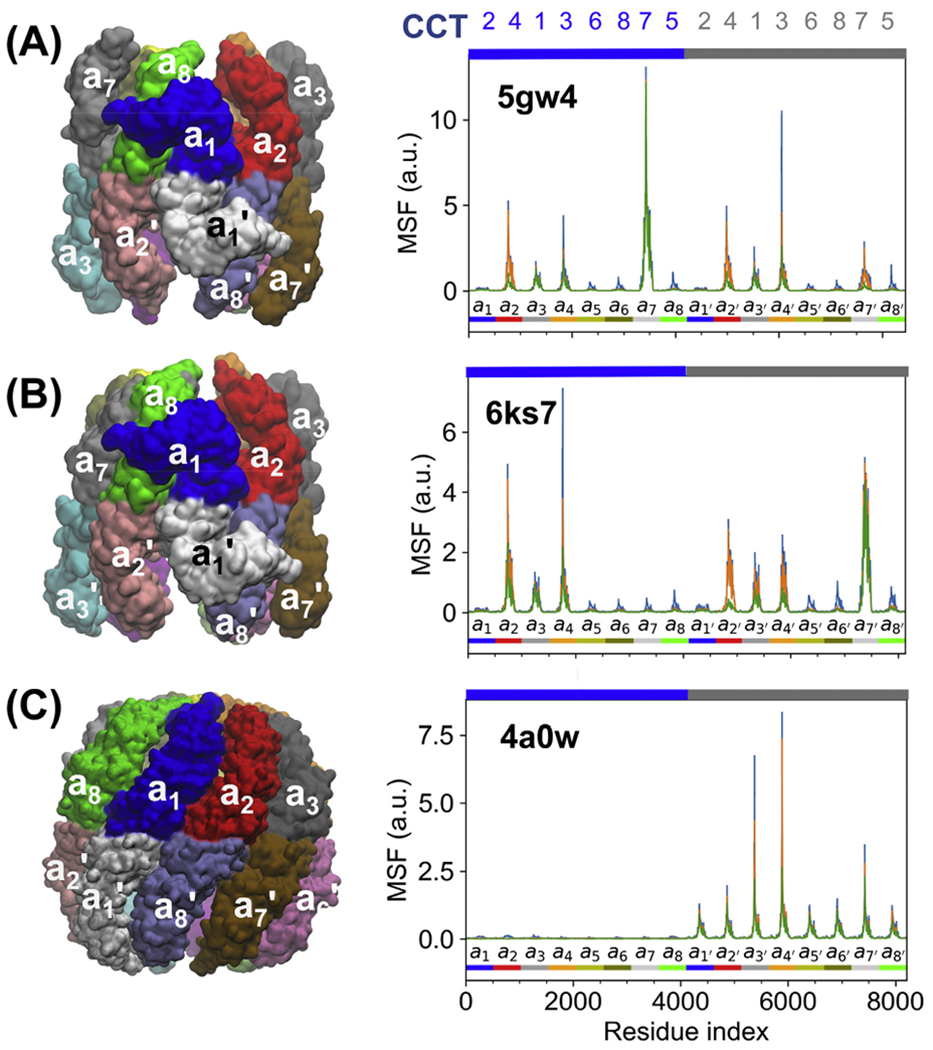
Panels A and B display results for intermediate structures between apo and ATP-bound forms, namely (A) ADP partially preloaded form (PDB: 5gw4) and (B) Conformation 1 at 0.1 mM ADP-AlFx concentration (PDB: 6ks7). Panel C shows TRiC at 1 mM ADP-AlFx (an intermediate stabilized during hydrolysis; PDB: 4a0w). The MSF curves on the right display the movements driven by 5 (green), 10 (orange), and 20 (blue) ANM modes. Labels along the upper abscissa indicate the subunit numbers (CCT1-8). The colour code along the lower abscissa indicates the consecutive subunits, with the colour scheme matching the upper ring on the left.

Based on the mobility profiles driven by the softest modes, we conclude that the ability of subunits to readily undergo large-scale movements driven by these modes depends on the conformational state. Mainly, the subunits that are predicted to move first are: CCT7 (cis/upper ring) in (A); subunits CCT7 (trans), followed by CCT4 (cis) and CCT3 (cis) in (B); and CCT3 (trans) followed by CCT1 (trans) in (C).

Complemented by the results presented in Fig. 3 for the ATP analogue-bound state, which is an intermediate state between conformers (B) and (C), the present analysis shows that as the overall eukaryotic chaperonin proceeds from apo to ATP-bound, and then to ADP-bound state, different subunits exhibit a high propensity to undergo conformational rearrangements. Subunits CCT6, CCT8 and CCT3 reportedly bind nucleotides at low concentrations (Jin et al., 2019a). The former two subunits (as well as CCT2 and 5) are highly stable in the low nucleotide concentration conformers (A) and (B) in Fig. 4; they practically do not move in the soft modes; but CCT3 retains some intrinsic flexibility. Our analysis suggests that the initial conformational change toward the ATP-bound state is facilitated by consecutive motions of CCT7 (both rings), and then CCT3 and CCT4 (both rings) (Fig. 4A–B); the conformational changes accompanying the early stages of hydrolysis in ATP-bound TRiC are mainly undergone by CCT5, CCT4 and CCT2 in the cis ring, and CCT2 and CCT4 in the trans ring (Fig. 3B), followed by the concerted motions of CCT3 and CCT1 (trans) that ensure the trans ring closure/opening near the completion of hydrolysis (Fig. 4C).

3.5. Soft modes define pre-existing conformational paths that comply with the allosteric transitions of CCT

The above analysis provided information on specific subunits that are distinguished by their high conformational mobility/adaptability at various stages of the chaperonin cycle. We now examine the mechanisms of their motions.

Collective motions of ATP-analogue-bound TRiC.

We first focus on the softest ten modes intrinsically favoured in this state, toward gaining mechanistic insights into ATP-regulated events. These modes induce distributed motions across the subunits. Due to the heteromeric nature of the rings, they depart from perfect symmetry. Yet, we discern movements reminiscent of cylindrical symmetry, such as radial breathing, biaxial stretching/contraction across the circular cross-section, or overall rolling movements of subunits within rings, schematically depicted in Fig. 5A–C. For example, mode 6 induces a concerted opening/closing or bending of the eight apical domains that approximates a breathing motion when viewed from the top, but the circular symmetry is broken due to the heterogeneity of the subunits (Fig. 5D and Movie 1A).

Fig. 5. Schematic description of symmetric or antisymmetric movements approximated by CCT-ATP (EMD-1961).

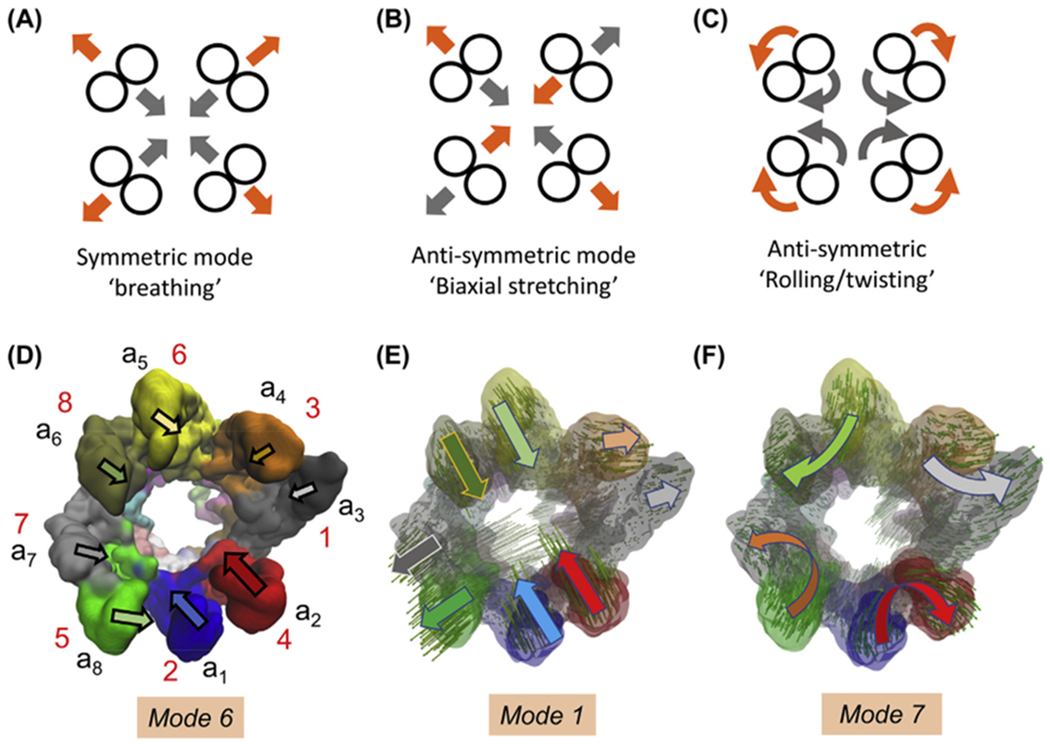
(A-C) Symmetric and anti-symmetric movements for circularly symmetric shapes. Note that grey and orange arrows indicate the opposite direction movements undergone by the subunits in those modes, i.e. the motions alternate between symmetric expansion and compression in A, stretching and contraction along orthogonal directions in B, and opposite direction rotations in C. The latter two are double degenerate in a circularly symmetric structure. (D) Mode 6 approximates the symmetric breathing mode, although it is deformed due to the heterogeneity of the subunits. The arrows display the approximate orientation and size of the motions of individual subunits in the upper ring (labelled). See also Movie 1A. (E) Mode 1 is reminiscent of anti-symmetric stretching depicted in (B); mode 2 shows similar features. (E) Modes 7 (and 8, not shown) approximate anti-symmetric rolling/twisting illustrated in (C).

The most cooperative modes, modes 1 and 2, tend to deform the circular cross-section into an ellipse by bringing closer together the pairs of subunits (a₁/CCT2, a₂/CCT4) and (a₅/CCT6, a₆/CCT8) that are oppositely located on the ring, while (a₇/CCT5, a₈/CCT7) and (a₃/CCT1, a₄/CCT3) splay apart, and vice versa (see Fig. 5E and Movie 2A). Modes 7 and 8 exhibit a concerted rolling of subunit pairs (Fig. 5F and Movie 2B). The latter two modes have similar frequencies (Fig. S2B), as do the pairs of modes 3–4 (Movie 1C), and 9–10 (Movie 2C), suggesting that they are almost doubly-degenerate by virtue of the close-to-cylindrical symmetry of the architecture (Na and Song, 2016). Such complementary modes may play essential roles in enabling functional transitions, similar to those observed in the cylindrically symmetric bacterial chaperonin GroEL and icosahedral viral capsids (Chennubhotla et al., 2005; Rader et al., 2005; Yang et al., 2009c).

Movies 1B–C illustrate the motions driven by modes 4 and 5. Both modes are distinguished by large coupled movements of a₁ and a₂ to enable the closure/opening of the upper ring by bending of the apical domains. In mode 5, their motion is accompanied by in-phase opening/closing of the adjacent pair a₈-a₇, while other subunits are practically rigid. In mode 4, on the other hand, the two pairs undergo out-of-phase opening/closure, accompanied by alternating anticorrelated movements of a₄ and a₆ with respect to both pairs. Fig. S6A depicts the subunit movements in mode 4, and Fig. S6B those in mode 5. Figs. S6C–D display the contributions of modes 1–5 to global movements and orientational crosscorrelations, respectively. Fig. S6C suggests a sequential mechanism in the ATP-bound form wherein lid closure, presumably driven by an ATP-affinity gradient-induced power stroke (Cong et al., 2012; Reissmann et al., 2012), is initiated by the movements of a₂, a₈ and a₁ (modes 1–2) succeeded by a₇ (modes 4–5). Notably, mode 5 plays a major role in driving the displacements of a₈ and a₇.

Transitions are enabled by movements along soft modes.

To test if these soft modes intrinsically accessible to the upper ring facilitate, if not enable, the transition toward the ADP-bound form where the upper ring is closed, we performed an adaptive ANM (aANM) analysis (Yang et al., 2009c) using the 1 mM ADP-AlFx-bound, hydrolysis-state CCT (PDB: 4a0w) as target structure (Fig. 6A and Movie 3). This approach generated a sequence of conformers whose RMSD from the target gradually decreased at each cycle (Fig. 6A–B). Larger decreases took place at earlier cycles that recruited global modes, supporting their dominant role in enabling this transition. The generated sequence of conformers is shown by the purple dots in the conformational landscape in Fig. 6B.

Fig. 6. Transitions between open and closed ring forms are enabled by soft modes.

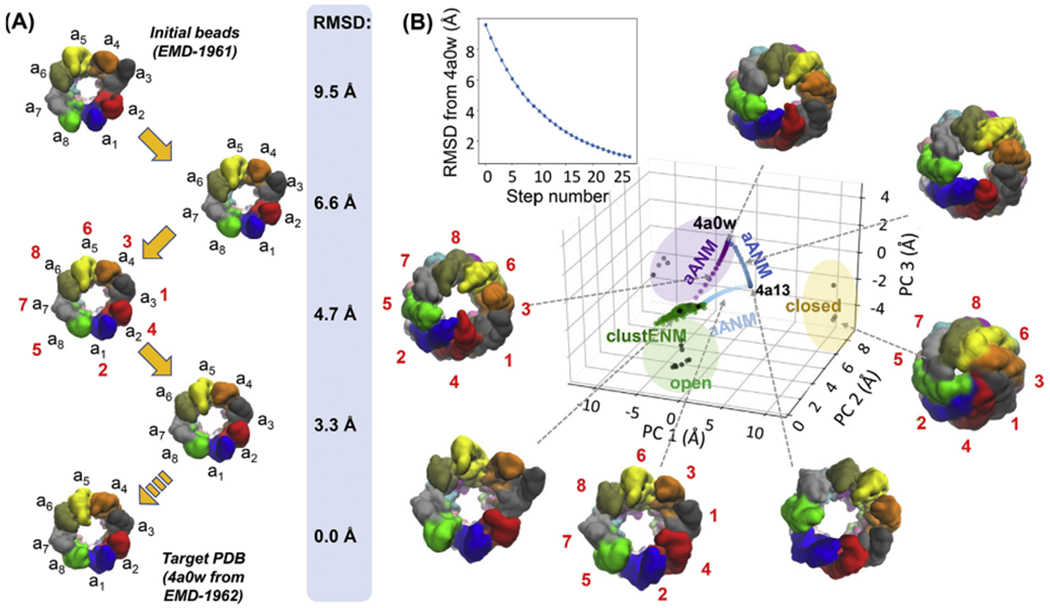
(A) The snapshots depict a path from the fully open (EMD-1961) ATP analogue-bound CCT to the asymmetric closed (EMD-1962) hydrolysis transition state analogue-bound form of CCT, driven by collective motions along soft mode coordinates. See corresponding movie, Movie S4, in the Supplementary Material. The conformational changes are generated using adaptive ANM (aANM). The conformation is shown after every 4 steps up until step 12 (4th structure), which reaches an RMSD of 3.6 Å (as compared to the original RMSD from target of 9.5 Å), as well as the target structure. (B) Comparison of aANM and ClustENM conformers with experimental structures via projection of generated conformers onto the 3D subspace defined by experimental structures in Fig. 1C (main panel). The upper plot shows the decrease in RMSD with respect to the target structure (PDB: 4a0w; inset). Three aANM runs are shown in purple, dark blue and light blue, and ClustENM conformers are green.

We also repeated the aANM analysis for the remaining core transitions of the functional cycle (light blue and dark blue arrows in Fig. 1C; same colour dots in Fig. 6B) using the all-atom models (PDB: 4a0w, 4a13 and 4a0o) and confirmed that all these transitions were also largely driven by global modes (Fig. 6B).

To explore the conformational space in an unbiased way, we employed the ClustENM approach (Kurkcuoglu et al., 2016) described in Methods subsection 2.2. We observed that the ATP analogue-bound structure explored a region in the vicinity of the starting point on a thin plane in the principal component space similar to that sampled during aANM (Fig. 6B). This confirms that the aANM transitions are intrinsically accessible to the TRN derived from the ATP analogue-bound state. Further, the apo state lies within the ClustENM-sampled region, revealing that there is an easily accessible (via soft modes) path intrinsically favoured by the overall architecture between the apo and ATP-bound conformers.

3.6. TRiC trans ring closure is enabled by collective bending of the apical domains intrinsically accessible to individual subunits

Finally, toward exploring the ability of the hydrolysis transition state analogue-bound structure (1.0 mM ADP-AlFx-bound CCT; PDB: 4a0w) to sample the symmetrically closed structures (PDB: 3iyg, 4v8r and 6ks6; yellow-shaded region in Fig. 1), we examined the ANM-predicted soft modes intrinsically accessible to the this asymmetric conformer. Movies 4–6 display the softest three modes. In all three cases, consistent with the suppressed mobility of the cis ring seen in Fig. 4C, the cis ring subunits retained their closed form with minimal change in conformation; whereas the trans ring subunits undergo highly cooperative motions. These motions are enabled by hinge-bending at their intermediate domain, which allows for the apical domains to come into close proximity. Modes 1–2 induce an alternating biaxial stretching/extension in the apical domains located at diametrically opposed ends of the ring when viewed from the bottom (Movies 4 and 5); whereas mode 3 induces a highly symmetric motion where all apical domains concertedly close and open the ring (Movie 6). The apical and equatorial domains act as the “lid” and “stave” for the complex.

We further analysed the intrinsic dynamics of the subunits, which enables the bending of the apical domains. ANM analysis for an isolated subunit showed that subunit bending that cooperatively enables the closure of the octameric ring is the softest mode (mode 1) favoured by the inter-residue contact topology of the subunit. This movement is mediated by a set of hinge residues in the intermediate domain (e.g. L169-V171 and 1347-A357 in subunit a₁ (CCT2); see Fig. 7A). The second softest mode induces an overall torsion, mediated by several residues acting as anchors (labelled in Fig. 7B), which is also observed in structural studies (Cong et al., 2012; Jin et al., 2019a). Movies 7A and B display the motions of the subunit, modelled as a TRN, along these two modes. Finally, the inter-residue cross-correlation map for the subunit reveals the critical role of the intermediate domain hinge residues which divide the subunit into two blocks (equatorial and apical domains) that undergo anticorrelated motions (Fig. 7C).

Fig. 7. Intrinsic dynamics of a single subunit in CCT-ATP.

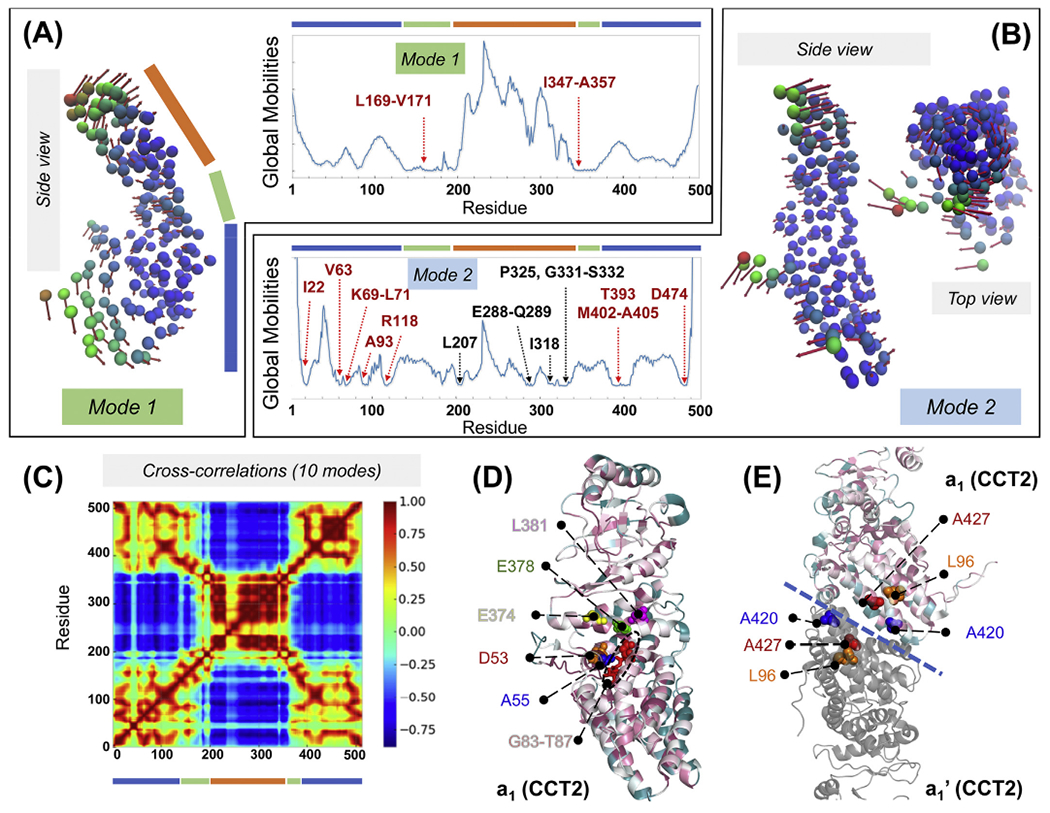
(A, B) ANM modes 1 and 2 of subunit a₁ from the TRN model of TRiC-AMP-PNP. Nodes are colour-coded based on their mobility. Side view arrows on the left show the movements in mode 1, and side and top views on the right show the movements in mode 2. Corresponding mobility profiles are shown in the middle two panels. Note that the intermediate domain (indicated by the green bar) exhibits minimal movements consistent with its hinge role. (C) Intrasubunit cross-correlations computed for subunit a₁ using the GNM, coloured from highly anticorrelated (dark blue) to highly correlated (dark red). Domains are indicated by blue, green and orange bars. (D) Cartoon representation of subunit a₁ (PDB: 4a0v), colour-coded by conservation scores from 1 (white) to 9 (purple; most conserved) predicted by Consurf (Ashkenazy et al., 2016). Potential functional sites predicted by DynOmics are labelled. Red sticks represent the ATP-binding/hydrolysis motif GDGTT, which consists of fully conserved residues G83-T87 (red sticks). (E) The transverse dimer of subunits a₁ and a₁’ with a₁ subunit coloured by conservation score. Potential functional sites predicted by DynOmics with conservation scores ≥ 7 (L96, A420 and A427) are shown by spheres. The blue dashed line indicates inter-ring interface.

In order to gain further insights into the biological significance of specific residues, we focused on the subunit a₁ in TRiC-AMP-PNP, and checked whether the hinge and functional sites predicted by ProDy (Bakan et al., 2011, 2014) and DynOmics (Li et al., 2017), respectively, were evolutionarily conserved. The hinge residues (V171, Q368, D371-E374, H378) in the softest GNM mode indeed had conservation scores ≥ 7 evaluated by the ConSurf server (Ashkenazy et al., 2016). As to the functional residues predicted by DynOmics using the slowest two modes from the PCA_NEST algorithm (Yang et al., 2009b), D53, A55, D84, E374, H378 and L381 were found to be conserved and are shown as spheres in Fig. 7D. Specifically, D84 participates in a highly conserved ATP-binding/hydrolysis motif, GDGTT, next to the equatorial domain. This motif is known to be crucial for the function of both bacterial (GroEL) and mammalian (CCT) chaperonins (Kabir et al., 2011). Thus, binding of ATP at this region would clearly impact the motions of the apical domain relative to the equatorial domain.

Overall, this analysis shows that the closure of the trans ring of the ADP-bound chaperonin is favoured by its overall architecture, enabled by the intrinsic dynamics of the individual subunits. While several structural changes along the allosteric cycle evolve by sequential, highly asymmetrical motions, it is interesting to note that this particular step simultaneously engages all eight subunits in the ring, at least at its initiation (driven by the slowest modes).

Further analysis of the coupled dynamics of the transverse dimer of subunits a₁ and a₁’, presented in Movies 8 and 9, showed that the apical domains gain greater relative mobility, especially at the protrusion helices, when the equatorial domains are constrained by inter-ring contacts. Such large motions have been noted by comparing the subunit conformations in the open (ATP-free) and closed (ATP-bound) forms (Skjaerven et al., 2015). The “bending” and “twisting” modes are preserved and even amplified at the apical domains upon complexation of the equatorial domains, mediated by highly conserved residues, L96, A420 and A427, at the dimeric interface (Movies 8–9 and Fig. 7E).

3.7. Markovian modelling of information flow between subunits reveals the differential rate of signal transfer across subunits and two fluxes of signal flow

Network modelling permits us to evaluate the hitting time, H(j, i), a quantitative measure of the efficiency of signal propagation across subunits in supramolecular systems, based on a Markovian stochastics model (Chennubhotla and Bahar, 2007). H(j, i) is the expected number of steps required to transmit a signal from node i to node j, averaged over all possible connections/paths. It is asymmetric, i.e. H(j, i) is not necessarily equal to H(i, j). Node i serves as broadcaster of signal/perturbation, and j as receiver. We evaluated the subunit-averaged hitting times, $\overline{H}(b,a)$ between each pair of subunits a and b (see Supplementary Methods) for the 16 CCT subunits in the ATP analogue-bound state, presented in Fig. 8A. The map is colour-coded from blue (fast communication, short hitting time) to red (slow communication, long hitting time). Rows indicate the ability/efficiency of subunits to receive signals; columns indicate their ability to send signals. Diagonal elements refer to the communication within subunits, which are always much faster than those between subunits (off-diagonal elements). We also see that the hitting times between neighbouring subunits (blue blocks near the diagonal) are shorter than those between non-neighbouring subunits. The diagonal from top left to bottom right (secondary diagonal) corresponds to inter-ring neighbours. Certain subunits (e.g. a₁/CCT2 and a₂/CCT4) exhibit low signal-receiving rates from their neighbours. In contrast, a₈/CCT5 is distinguished by its highly efficient communication with a₇/CCT7. Likewise, a₃/CCT1 communicates efficiently with a₄/CCT3.

Fig. 8. Intersubunit signal propagation behaviour of TRiC/CCT in the presence of ATP analogues.

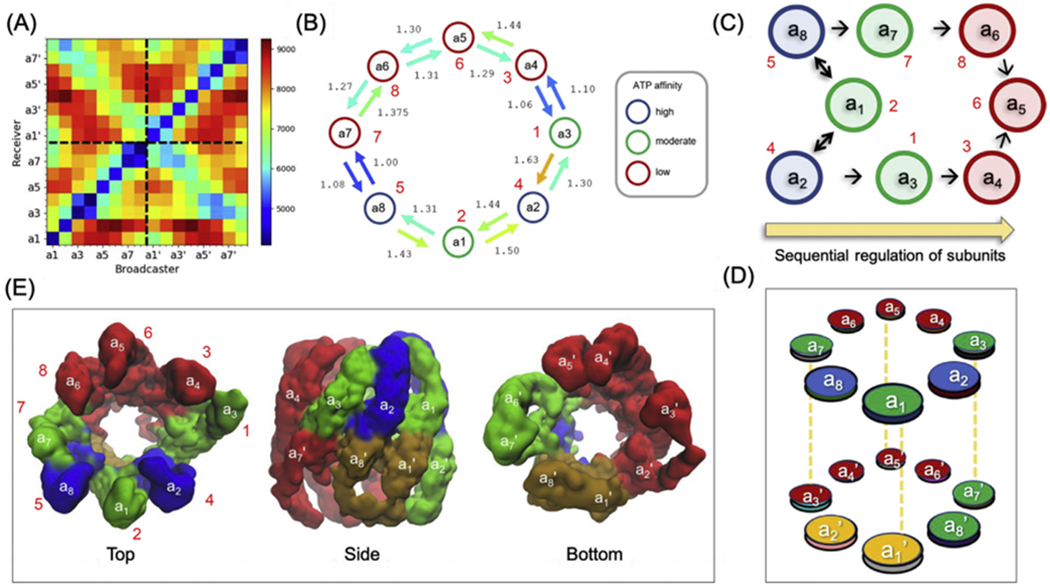
(A) Efficiency of information flow between subunits, represented by the subunit-averaged hitting time matrix. Each entry represents the hitting time from a broadcaster (horizontal axis) to a receiver (vertical axis), colour-coded from blue (fast communication) to red (slow communication). (B) Diagram illustrating the subunit-averaged hitting time between neighbouring subunits in the upper ring. Arrows are coloured based on the hitting times in the matrix shown in (A). Circles stand for the eight subunits, coloured according to their ATP affinities (Reissmann et al., 2012). The numbers are the hitting times relative to the fastest communication event $\overline{H}(a_7,a_8)$. (C) Sequence of events deduced from combined ANM and Markovian stochastics analysis. In dark blue are the subunits that initiate ATP-regulated events, first communicated to subunits in green, followed by subunits in red. Note that the time evolution (indicated by the arrow from left to right) conforms to ATP-binding affinities observed experimentally. Double headed arrows are shown for pairs with comparable hitting times in both directions. (D) Information flow across the entire chaperonin, colour-coded by the sequence of events. Subunits a₇’ and a₈’ are the first responders to a₂. The subunits a₁’ and a₂’ coloured yellow show an intermediate behaviour. (E) Top, side and bottom views of the structure colour-coded by the sequence of events depicted in panel D.

The emerging scheme of intra-ring allosteric signal transduction is depicted in Fig. 8B. The subunits (circles) are colour-coded by their experimentally observed propensity to bind and presumably hydrolyse ATP (see Discussion). The signal transduction efficiencies between neighbouring subunits are indicated by colour-coded arrows. These results, combined with intrinsic mobilities described in Fig. 3, lead to the following picture for possible time evolution of ATP-regulated signal transduction events across the upper ring subunits. The most adaptable/mobile subunits a₈/CCT5 and a₂/CCT4, followed by a₁/CCT2, are likely to lead the succession of events based on their intrinsic high mobility (see e.g. Fig. 3B or the diagonal elements of the covariance matrix in Fig. 3C). CCT5 and CCT4 are most likely to transduce signals to their neighbours a₇/CCT7 and a₄/CCT3, which in turn propagate the signals to a₆/CCT8 and a₅/CCT6. The sequence of parallel events is described by the scheme in Fig. 8C. Subunits are depicted by circles colour-coded by ATP-binding affinity and arrows indicate preferred information flow directions. Subunits with higher ATP-binding affinity appear to lead the process, the flow of information taking place from high- to low-affinity subunits.

The above analysis describes the flow of information within the cis ring. Of interest is to observe how information flows in the transverse direction, i.e. between rings. The latter can be inferred from the elements around the secondary diagonal in Fig. 8A. The blue (fastest signalling) entries in the upper left quadrant show that a₈’ immediately receives signals from a₂, consistent with their juxtaposition; and a₁’ receives from a₁, and a₂’ from a₈. Notably, these inter-ring signals are even faster than those, intra-ring, between a₁ and a₂, attesting to the close coupling between the two rings. These findings are depicted in Fig. 8D–E where subunits are coloured based on relatively fast (green), moderate (orange) and slow (red) transfer of information.

Finally, we note that the Markovian diffusion of allosteric signals revealed here is specific to the ATP-bound state, and in line with the state-dependent dynamics reported above (see Fig. 4), state-dependent signalling mechanisms operate at different stages of the chaperonin cycle, as illustrated in Fig. S7. For example, TRiC in the NPP state (Zang et al., 2016) (approximating an apo state) is distinguished by a remarkable communication between CCT3, CCT6 and CCT8 (Fig. S7A), which could explain their simultaneous preloading. As to the next structure in the cycle (represented by PDB model 6ks7 in Fig. S7B), it is interesting to distinguish that the communication between the low affinity half of the ring (CCT5-CCT8) is much faster than that occurring in the other half (composed of CCT1-CCT4) consistent with the propagation of nucleotide loading to moderate affinity subunits CCT1 and CCT7, and completion of the response of high-affinity subunits (Jin et al., 2019a).

Overall, this analysis again shows the state-dependency of allosteric signalling events at various stages of the chaperonin cycle, and reconciles several experimental observations that, at first sight, might seem contradictory.

4. Discussion and conclusion

The present study has been carried out with two major goals: one methodological and the other biological, enabled by the wealth of structural data collected in recent years on eukaryotic chaperonin TRiC/CCT depicted in Fig. 1. We present both aspects below.

4.1. A computational pipeline for automated evaluation of conformational dynamics from electron density maps

First, we developed and generalized a computational methodology for modelling the structure and dynamics of cryo-EM resolved systems. Structural studies of supramolecular dynamics are limited in their ability to gain insights into the mechanistic basis of allosteric events as a result of (i) limitations in cryo-EM data and their interpretation (Cianfrocco and Kellogg, 2020; Herzik et al., 2019; Sorzano et al., 2019), (ii) approximations in the structure fitting algorithms applied to their outputs (Cianfrocco and Kellogg, 2020; Kim et al., 2020; Malhotra et al., 2019), and (iii) sampling and force field inaccuracies in full-atomic simulations (Bottaro and Lindorff-Larsen, 2018). Hence, we adopted a low-resolution model (ENM/TRN) along with analytical approaches rooted in statistical mechanical and spectral graph theoretical methods, which enabled efficient analysis of global dynamics.

Our computational pipeline comprises three main steps: generation of a pseudoatomic structure from cryo-EM density maps via TRN, identification of subunits or domains via multistep spectral clustering, and analyses of the TRN using ENM-based methods. The pipeline has been implemented in the ProDy API, enabling users to take advantage of a wide range of tools developed for ENMs (Fuglebakk et al., 2012; Lopez-Blanco and Chacon, 2016; Tobi and Bahar, 2005; Zheng et al., 2009), including the prediction of the signature dynamics of protein families (Mikulska-Ruminska et al., 2019; Zhang et al., 2019). The ProDy API permits us (i) to reconcile physics-based theories of polymer statistical mechanics and machine learning algorithms of spectral graph theory for inferring signalling properties (Chennubhotla and Bahar, 2007); (ii) evaluate sensors and effectors of allosteric signals using perturbation-response theory (Atilgan and Atilgan, 2009; Atilgan et al., 2010; General et al., 2014); (iii) bridge between sequence conservation/coevolution and structural dynamics (Liu and Bahar, 2012); and (iv) visualize molecular motions through an interactive GUI, normal mode wizard NMWiz, that interoperates with VMD (Humphrey et al., 1996).

In principle, the pipeline can be applied to any cryo-EM density maps. The availability of the new tools developed here through our GitHub repository (https://github.com/prody/ProDy) enables application to a wide range of biological systems. The methodology is most beneficial for maps of large, dynamic biomolecular complexes at low resolution. Since ENM methods depend mostly on the overall architecture and are highly robust to small differences in atomic positions, TRN/ENM generates mode shapes comparable to those of ENM based on full-atomic models. The availability of all-atom models for CCT helped us test and validate this feature (see Figs. 2 and S5).

However, the accuracy of the current method is limited by that of electron density maps. For example, highly mobile regions such as the apical loops of TRiC/CCT can be missing in the resolved cryo-EM density maps and consequently, the structure and dynamics of those regions cannot be accurately modelled. However, because of their high flexibility/adaptability it is unlikely that these regions would alter the global dynamics. Another limitation is the lack of sequence information. Dynamical domains identified with spectral clustering (shown in Fig. 2) group residues with similar dynamics together but these are not necessarily sequentially contiguous segments. Yet, the overall variability in the 3D shape of the examined system is insensitive to chain connectivity, as bonded and non-bonded neighbours are not distinguished in the neighbour representation. As such, even without knowledge of the sequence, one can still understand the structure-encoded dynamics, and subunitor domain-averaged matrices and animations.

4.2. New insights into the conformational space and signalling mechanisms of the supramolecular machine TRiC/CCT

CCT is known to undergo sequential rather than all-or-none changes in the conformations of the subunits in each ring (Kafri and Horovitz, 2003; Reissmann et al., 2012; Rivenzon-Segal et al., 2005). The functional and dynamic asymmetry of this 16-meric machine (Gestaut et al., 2019; Jin et al., 2019a), originates from the sequence and structure heterogeneities of its subunits (see Fig. S1). Our study further revealed that the sequence of these events depends on the ‘state’ temporarily stabilized during the allosteric cycle of the chaperonin. The sequence of conformational changes undergone by the NPP state, for example, is different from that of the ATP-bound form, which is also different from the hydrolysis transition state, as delineated in Figs. 3–4.

Likewise, the different states exhibit different communication patterns between subunits (Fig. 8 and S7), as predicted by our Markovian stochastics model. Particular subunits exhibited higher propensity to initiate motions and signalling, reconciling previous structural, functional and kinetic studies (Amit et al., 2010; Gestaut et al., 2019; Gruber et al., 2017; Kabir et al., 2011; Kalisman et al., 2013; Leitner et al., 2012). Overall a functional division of the ring into two halves was apparent: one (containing a₁/CCT2, a₂/CCT4 and a₈/CCT5) with high ATP-binding affinity and early hydrolysis capabilities and the other (containing a₄/CCT3, a₅/CCT6 and a₆/CCT8) involved in binding substrate proteins.

In the case of the unbound or NPP state resolved under nominally nucleotide-free conditions (PDB: 5gw4) (Zang et al., 2016), the first subunit predicted to undergo a conformational change in the cis ring conformation is a₇ (Fig. 4A); whereas Fig. 4C reveals mobilities in selected trans ring subunits in perfect accord with the observations made at slight levels (0.1 mM) of ATP analogue (Jin et al., 2019a). Furthermore, our Markovian stochastics analysis demonstrated a high cooperativity and efficient communication between subunits a₄, a₅, and a₆ (CCT3, CCT6 and CCT8) (Fig. S7A) in this partially preloaded state, and this is also in agreement with the experimentally observed pre-loaded state of these subunits.

TRiC resolved at a slightly higher concentration of ATP analogue (Jin et al., 2019a), on the other hand, exhibits a distinctive peak in the trans ring subunit a₇’/CCT7 (Fig. 4B), also consistent with the propensity of this subunit to move after the cis ring subunit a₇ in the cryo-EM ensemble resolved at this ADP-AlFx level (Jin et al., 2019a). The structure in which subunit a₇ has moved from its NPP state position (PDB: 6ks7) exhibits a remarkable communication between subunits a₅/CCT6, a₆/CCT8, a₇/CCT7 and a₈/CCT5 (Fig. S7B), i.e. the original group of closely communicating subunits now expands to include subunits a₈ and a₇, prior to transitioning to the fully ATP (analogue)-bound state.

With regard to ATP hydrolysis, a number of studies proposed that the closure events stimulated by ATP-binding and hydrolysis start on the high ATP-binding affinity subunits a₂/CCT4 and a₈/CCT5 (Jin et al., 2019a; Reissmann et al., 2012; Rivenzon-Segal et al., 2005; Yamamoto et al., 2017). Notably, our current analysis also points to these two subunits as the most malleable/adaptable ones in the pre-hydrolysis ATP analogue-bound structure (see the green curves in Fig. 3B), succeeded by a₁/CCT2 and then a₇/CCT7. These are not necessarily the subunits that bind nucleotide first in the abovementioned studies, but they lead the hydrolysis process, enabled by the topology of contacts assumed in the ATP-bound form. Their high mobility in the global modes accessible to the ATP-bound state enable, if not drive, the movements that accompany the hydrolysis of ATP molecules.

Our Markovian information diffusion analysis (Fig. 8) suggested that the initial movements of CCT4/a₂ and CCT5/a₈ would propagate in both directions through two fast-communicating interfaces (a₃/a₄ and a₇/a₈; Fig. 8B) toward the low ATP affinity subunits. A recent study of hydrolysis kinetics (Gruber et al., 2017) indicates, however, that hydrolysis events start with the subunits that have shown first nucleotide binding behaviour, i.e. CCT3/a₄, CCT6/a₅ and CCT8/a₆, and that there are two conformational waves emanating from these subunits, clockwise and counterclockwise. This type of behaviour is plausible given that a₄/CCT3, a₅/CCT6 and a₆/CCT8 may have bound nucleotide earlier, and if the successive steps of allosteric changes from NPP (PDB: 5gw4) (Zang et al., 2016), to 0.1 mM ADP-AlFx-bound (PDB: 6ks7) (Jin et al., 2019a), and to fully loaded (1 mM) TRiC-ADP-AlFx (PDB: 4a0v) (Cong et al., 2012) (i.e. successive steps including the transitions within the green box of Fig. 1A–B and passage to TRiC-ADP-AlFx in purple box) are considered. When the individual steps are dissected and the propensity of the state TRiC-AMP-PNP per se is examined, however, our analysis reveals a signal feedback from a₂/CCT4 and a₈/CCT5 to a₄/CCT3, a₅/CCT6 and a₆/CCT8, via soft modes of motions (see Movies S1 and S2). Soft modes indeed enable the transition from ATP (analogue)-bound to ADP (analogue)-bound state as illustrated in Fig. 6 and Movie S3.

Next, we examined the intrinsic dynamics of the hydrolysis transition state. Our study also provides insights into motions in the trans ring presumably facilitating (Fig. 3B, lower panel) or succeeding (Fig. 4C) ATP hydrolysis. The hydrolysis intermediate structure (PDB: 4a0w) exhibits a relatively more ordered or symmetric organization of the subunits compared to that in the apo or partially preloaded states. This suggests that the closure of the protein folding chamber may also involve more symmetrically distributed movements. Our analysis indeed reveals the coupled involvement of all trans ring subunits in the softest modes (Movies 4–6) and in particular a highly cooperative mode (mode 3, Movie 6) that enables chamber closure by the collective bending of the apical domains of all subunits a₁’-a₈’ in the trans ring. This is in contrast to other states where movements of the subunits occurred in a sequential manner. This analysis thus reveals that the ‘order’ induced in the hydrolysis transition state may drive cooperative movements close to all-or-none in nature at the beginning of this particular step of the allosteric cycle. We note that the trans ring subunits a₃’/CCT3 and a₄’/CCT1 are distinguished by their higher mobilities after the deployment of these initial, uniformly distributed movements (high modes in the orange and blue curves in Fig. 4C).

In order to understand how the intrinsic movements of individual subunits assist in the global machinery, we looked at the softest modes predicted by the GNM for an isolated subunit, a₁/CCT2, of TRiC/CCT. Our analysis revealed that the apical domain’s bending ability is encoded in the 3D topology of the individual subunits (see also Movies 7–9) – a phenomenon also observed earlier in GroEL (Yang et al., 2009c) and emphasized in a recent review (Zhang et al., 2020b). The importance of the predicted hinge sites was underscored by their high evolutionary conservation. At the same time, the hinge sites were located next to (and partially coincide with) the highly conserved ATP binding/hydrolysis motif GDGTT near the equatorial domain. The close proximity of this motif to the hinge centre attests to the mechanochemical nature of ATP-regulated chaperonin activity. Further examination of the transverse dimers showed how the stabilization of the equatorial domains as anchors enhanced the mobility of the apical domains.

Although the focus of this study was on the intrinsically accessible mechanism of CCT structural change triggered before and upon ATP binding and hydrolysis, the mechanism of substrate loading is equally important for understanding how the CCT structure/dynamics is coupled to substrate folding, and release. Based on the structures, one possible scheme is that, ATP binding stabilizes a particular conformation of the lid (storing elastic energy for later), which helps unfolded and misfolded substrates bind to the apical domain of the low ATP affinity sides of the upper ring (Cuellar et al., 2019; Leitner et al., 2012; Llorca et al., 1999). Substrate binding then triggers ATP hydrolysis and consequently lid closure in one ring, which releases the elastic energy and facilitates substrate folding by destabilizing the metastable misfolded state. The correctly folded substrate has relatively weaker binding affinity to CCT and is released after lid opening. The sequential firing of ATP molecules might be important for using the ATP energy efficiently, as it might cause less energy dissipation directly as heat and give time for the polypeptide to search and relax within the conformation space – annealing. More experimental and computational data and studies are needed to clarify these aspects of the chaperoning process.

The present computations are exclusively based on the overall network topology representative of electron density maps; no information on sequence properties or chemical interactions is included. The observed mechanisms of events, many in line with experimental observations, reveal that the mechanical properties of the chaperonin have been tailored to comply with its chemical character and allosteric function, presumably optimized by evolution.

Abbreviations:

ANM

anisotropic network model

aANM

adaptive ANM

AlFx

aluminium fluoride with an unknown oxidation state x

CCT

chaperonin-containing TCP-1

cryo-EM

cryogenic electron microscopy

EMDB

electron microscopy data bank

ENM

elastic network model

GNM

Gaussian network model

MD simulations

molecular dynamics simulations

MSF

mean-square fluctuation

NMA

normal mode analysis

NPP

nucleotide partially preloaded

RMSD

root-mean-square deviation

SC

spectral clustering

SOM

self-organizing maps

TRiC

TCP-1 ring complex

TRN

topology-representing network