Estimation and inference for semi-competing risks based on data from a nested case-control study

Abstract

In semi-competing risks, the occurrence of some non-terminal event is subject to a terminal event, usually death. While existing methods for semi-competing risks data analysis assume complete information on all relevant covariates, data on at least one covariate are often not readily available in practice. In this setting, for standard univariate time-to-event analyses, researchers may choose from several strategies for sub-sampling patients on whom to collect complete data, including the nested case-control study design. Here, we consider a semi-competing risks analysis through the reuse of data from an existing nested case-control study for which risk sets were formed based on either the non-terminal or the terminal event. Additionally, we introduce the supplemented nested case-control design in which detailed data are collected on additional events of the other type. We propose estimation with respect to a frailty illness-death model through maximum weighted likelihood, specifying the baseline hazard functions either parametrically or semi-parametrically via B-splines. Two standard error estimators are proposed: (i) a computationally simple sandwich estimator and (ii) an estimator based on a perturbation resampling procedure. We derive the asymptotic properties of the proposed methods and evaluate their small-sample properties via simulation. The designs/methods are illustrated with an investigation of risk factors for acute graft-versus-host disease among N = 8838 patients undergoing hematopoietic stem cell transplantation, for which death is a significant competing risk.

1. Introduction

Acute graft-versus-host disease (aGVHD) is a complication experienced by about 50% of patients who undergo hematopoietic stem cell transplantation (HSCT) for leukemia.¹ An important challenge for studies of aGVHD following HSCT is high mortality; in data from the Center for International Blood and Marrow Transplant Research (CIBMTR), 15.1% of N = 8838 patients who underwent HSCT between 1999 and 2011 died within 100 days. It is therefore appropriate to frame this study as a problem of semi-competing risks,² in which scientific interest lies with some non-terminal event (e.g. aGVHD), the occurrence of which is subject to a terminal event (e.g. death). The terminal event is thus a competing risk for the non-terminal event, but not vice-versa. Although less familiar than competing risks, semi-competing risks arises in a broad range of applications including cancer,³ diabetes,⁴ cardiovascular disease,⁵ and Alzheimer’s disease.⁶

Let T₁ and T₂ be the time to the non-terminal and terminal events, respectively. In semi-competing risks, the joint distribution of (T₁, T₂) has restricted support since patients cannot experience a non-terminal event after a terminal event has occurred. As such, dependence between the two events must be explicitly acknowledged even if primary scientific interest lies in the non-terminal event.⁷ Various methods for semi-competing risks have emerged over the last 15 years.^8,9 Here, we focus on a class of methods that frames the data as having arisen from the so-called illness-death model.¹⁰

In all methods in the literature to date, complete data on all relevant risk factor covariates is presumed to be readily available, but this often will not be the case in practice. In large cohort studies, blood or saliva may be routinely collected on all participants but biomarkers not initially evaluated on everyone. In registry, claims, or electronic health records-based studies key covariates (e.g. current smoking status) may not be routinely recorded and require either manual chart review or additional data collection efforts. In these settings, if researchers are to learn about estimands of interest (such as the associations encoded in an illness-death model), they require a cost-efficient means of obtaining information on the otherwise-missing covariates for at least a sub-sample of patients. Towards this, researchers have a wide variety of study designs at their disposal. One design for time-to-event outcomes is the nested case-control (NCC) design.¹³ Typically, NCC designs are implemented by identifying all cases (i.e. those who experienced the event) and then selecting a random sample of non-cases from each risk set defined by each case. Estimation and inference are then performed with respect to a univariate Cox model for the time-to-event outcome that was the basis of the design.^14,15

In this study, we suppose that an NCC study has been conducted, but that the analysis is to proceed using an illness-death model (in lieu of a univariate model). Specifically, we propose a statistical framework for estimation and inference with respect to an illness-death model for semi-competing risks data arising from an existing NCC study, into which patients were selected based on either the non-terminal or terminal event, but not both. We refer to the event used to form risk sets as the index event, and the other as the non-index event. Throughout, it is assumed that information on both events is available for all individuals selected into the study. In addition, we introduce the supplemented NCC design (SNCC design) in which otherwise-missing covariates are also collected on cases of the non-index event in the original NCC study. We perform estimation via maximum weighted likelihood with respect to a frailty illness-death model, permitting baseline hazard functions to be specified parametrically as well as semi-parametrically via B-splines. For standard error estimation, we propose a sandwich estimator and a perturbation resampling-based procedure. We derive asymptotic properties of this estimator and evaluate its small-sample characteristics through a simulation study. The methods are illustrated with the aforementioned CIBMTR data.

2. The illness-death model for semi-competing risks

A central premise of this setting is that, given complete data on all covariates, the scientific question would be addressed via the fit of an illness-death model specified by three intensity or hazard functions: λ₁ (t₁), the hazard of the non-terminal event (implicitly in the absence of the terminal event); λ₂(t₂), the hazard of the terminal event conditional on the non-terminal event not having occurred; and λ₃(t₂|t₁), the hazard of the terminal event conditional on the non-terminal event having occurred at time t₁ (see Figure A.1 in Online Appendix A).

In practice, analysts need to specify models for these three hazard functions. Here, following Xu et al.¹¹ and Lee et al.,³ we focus on Cox model specifications of the form

$${\lambda }_1\left(t_1|\gamma \right)=\gamma {\lambda }_{01}\left(t_1\right)\exp \left({{\mathit{\beta }}_1}^{\prime }{\mathbf{X}}_1\right)$$ (1)

$${\lambda }_2\left(t_2|\gamma \right)=\gamma {\lambda }_{02}\left(t_2\right)\exp \left({{\mathit{\beta }}_2}^{\prime }{X}_2\right)$$ (2)

$${\lambda }_3\left(t_2|t_1,\gamma \right)=\gamma {\lambda }_{03}\left(t_2|t_1\right)\exp \left({{\mathit{\beta }}_3}^{\prime }{X}_3\right)$$ (3)

with X_g a vector of transition-specific covariates, g ∈ {1, 2, 3}, and γ a shared patient-specific frailty. Note, for simplicity, we omit a patient-specific index in the notation but do introduce it when we discuss estimation and inference (see below). Analogous to random effects in generalized linear mixed models (GLMMs), γ serves to account for residual within-patient dependence between the two events that is not accounted for by the covariates in the three models.⁷ Furthermore, analogous to a “random intercepts” GLMM, the vast majority of the illness-death model literature assumes that the frailties arise from some parametric distribution with mean 1.0 and variance θ, although some work has been done on more flexible specifications.¹⁶ While analysts are free to choose any such distribution, Gamma (θ⁻¹, θ⁻¹) is most commonly adopted (as in this study), since it produces a closed-form expression for the marginalized likelihood (Online Appendix A.2).

2.1. Specification of the baseline hazard function

Towards specification of the baseline hazard functions in expressions (1) to (3), one useful option in small-sample settings is to adopt a parametric specification, such as a Weibull (ϕ_g1, ϕ_g2) distribution for which λ₀(t) = ϕ_g1ϕ_g2t^ϕ_g1−1. A second option is to adopt a flexible specification via, say, B-splines. Specifically, one could define $\text{log}{\lambda }_{0g}(t)={\sum }_{k=1}^{K_g}{B}_{\mathit{gk}}(t){\varphi }_{\mathit{gk}}$ where K_g is the number of B-spline basis functions with B_gk(·) the kth such function, and ϕ_g ≡ (ϕ_g1, …, ϕ_gKg)^′ is a (K_g × 1) vector of coefficients (see Online Appendix A.4). Note, by modeling logλ_0g(t), rather than λ_0g(t) directly, we avoid the need to introduce constraints on ϕ_g that ensure positivity.^17,18 Finally, since λ₀₃(t₂|t₁) is a function of two continuous variables, it may be difficult to specify parametrically or estimate non-parametrically. In practice, this is typically resolved by adopting either a Markov specification, where λ₃(t₂|t₁, γ) ≡ λ₃(t₂, γ), or a semi-Markov specification, where λ₃(t₂|t₁, γ) ≡ λ₃(t₂ − t₁, γ).¹¹

3. NCC designs for semi-competing risks

Given an i.i.d. sample of size N from the population of interest, with complete data on all elements of X = (X₁, X₂, X₃), estimation and inference for the illness-death model given by equations (1) to (3) are well established in both the frequentist^10,11 and Bayesian paradigms.^3,12,19 Here, we propose analyses under an NCC design in which complete data on X are not available.

3.1. The NCC design

The NCC study design is a frequently used, cost-efficient outcome-dependent sampling design for univariate time-to-event outcomes.¹³ Within the univariate setting, the design first identifies all patients who experience the index event. For each such “case,” m “controls” are randomly sampled without replacement from the risk set formed at the time of the event. The otherwise-unavailable covariate data are then ascertained for the case and each selected control. Since the sampling of controls across different risk sets is independent, the same patient may be sampled as a control for more than one case and/or become a case after having been previously selected as a control.

Typically, data arising from an NCC design are analyzed using univariate time-to-event models, with estimation and inference via a modification of the usual partial likelihood¹⁴ or inverse probability weighting (IPW).¹⁵ In some settings, interest may lie with a non-index event; to that end, recent work permits the reuse of controls from the original NCC design to estimate components of a univariate model for the non-index event via IPW.^20,21 Here, we suppose that scientific interest lies with an illness-death model, of the form given by equations (1) to (3). With this in mind, we consider settings where the data from the NCC design are to be re-used for estimation and inference with respect to the illness-death model, with the index event being either the non-terminal or the terminal event. Throughout, we assume that, in addition to information on the otherwise-unavailable covariates, information on the non-index event is available on all individuals selected by the design through the end of follow-up.

3.2. The SNCC design

The NCC design is most commonly used when the index event is rare, with all patients who experienced the event being “selected” along with a sub-sample of those who did not. As applied to the semi-competing risks context, this implies that all patients who experience the index event will be in the NCC sub-sample. This, however, is not guaranteed for those patients who only experience the non-index event. In the aGVHD context, for example, consider an NCC study with the index event being death. While patients who experienced both aGVHD and death are guaranteed to be in the sub-sample (and therefore have complete data), patients who experienced aGVHD but were censored prior to death are not guaranteed to be in the sub-sample. Depending on the event rates and who was selected in the risk sets formed by the index event, estimation and inference may be difficult and/or inefficient for certain transitions. To mitigate this, we propose that the NCC study be post hoc supplemented by sampling additional patients who did not experience the index event but did experience the non-index event. As with the patients already selected, covariate information on these patients would be retrospectively ascertained. We refer to this novel design as an SNCC design. In the remainder of this study, for ease of exposition, we label standard (i.e. unsupplemented) NCC designs based on the non-terminal event and the terminal event as NT-NCC and T-NCC designs, respectively. Analogously, we label SNCC designs based on the non-terminal event and the terminal event as NT-SNCC and T-SNCC designs, respectively.

4. Maximum weighted likelihood for the illness-death model

Towards estimation and inference for the illness-death model, we develop a strategy based on IPW; the methods will be implemented in an upcoming version of the SemiCompRisks R package. Note, since the presence of a frailty term links the estimation of all parameters, a partial likelihood-based strategy is not feasible. For simplicity, we adopt a semi-Markov specification for the baseline hazard functions; details for the Markov specification are provided in Online Appendix A.2.

4.1. Estimation and inference given complete data

Let Y_i = (Y_i1, δ_i1, Y_i2, δ_i2) denote the observed outcome data for individual i, where Y_i1 = min(T_i1, T_i2, C_i), with C_i denoting the right-censoring time, δ_i1 = I{T_i1 ≤ min(T_i2, C_i)}, Y_i2 = min(T_i2, C_i), and δ_i2 = I{T_i2 ≤ C_i}. C_i is assumed to be independent of (Y_i1, Y_i2) conditional on the covariates in the model. Let ξ = (θ, β₁, β₂, β₃, ϕ) denote the collection of unknown parameters from models (1) to (3), where ϕ = (ϕ₁, ϕ₂, ϕ₃) indexes the specification of the three baseline hazard functions. Adopting γ ~ Gamma (θ⁻¹, θ⁻¹), detailed arguments in Online Appendix A.2 show that the (integrated) observed data likelihood for individual i are

$${\mathcal{L}}_i\left(\xi \right)={\lambda }_1^{\ast }{\left(y_{i1}\right)}^{{\delta }_{i1}}{\lambda }_2^{\ast }{\left(y_{i1}\right)}^{\left(1-{\delta }_{i1}\right){\delta }_{i2}}{\lambda }_3^{\ast }{\left(y_{i2}-y_{i1}\right)}^{{\delta }_{i1}{\delta }_{i2}}{\left(1+\theta \right)}^{{\delta }_{i1}{\delta }_{i2}}\times {\left[1+\theta \left\{{\Lambda }_1^{\ast }\left(y_{i1}\right)+{\Lambda }_2^{\ast }\left(y_{i1}\right)+{\Lambda }_3^{\ast }\left(y_{i2}-y_{i1}\right)\right\}\right]}^{-\left(\frac{1}{\theta }+{\delta }_{i1}+{\delta }_{i2}\right)},$$

where ${\lambda }_g^{*}(t)$ is defined so that ${\lambda }_g(t)=\gamma {\lambda }_g^{*}(t)$, and ${\Lambda }_g^{*}(t)={\int }_0^t{\lambda }_g^{*}(s)\partial s$.

Given complete data, $\mathcal{D}=\{{\mathbf{Y}}_i,{\mathbf{X}}_i;i=1,\dots ,N\}$, one could proceed via the log-likelihood: $\ell (\xi )={\sum }_{i=1}^N\text{log}{\mathcal{L}}_i(\xi )={\sum }_{i=1}^N{\ell }_i(\xi )$. See Online Appendix A.3 for the corresponding score functions when the baseline hazard functions are parameterized using a Weibull distribution. If the log-baseline hazard functions are specified using B-splines, analysts may choose to induce smoothness by applying a penalty on the second derivatives,¹⁷ that is, basing estimation and inference on a penalized log-likelihood ${\ell }^p(\xi )=\ell (\xi )-\mathcal{P}({\kappa }_1,{\kappa }_2,{\kappa }_3,\xi )$, where $\mathcal{P}({\kappa }_1,{\kappa }_2,{\kappa }_3,\xi )={\sum }_{g=1}^3{\kappa }_g\int (\log {\lambda }_{0g}{)}^{″2}(u)\mathit{du}$. See Online Appendices A.4 and A.5 for the score functions corresponding to ℓ(ξ) and ℓ^p(ξ), and a cross-validation procedure for selecting {κ₁, κ₂, κ₃}.

4.2. Estimation and inference given data from an NCC or SNCC design

Suppose now that complete data are only available on a sub-sample of patients selected via an unsupplemented NCC design, ${\mathcal{D}}_{\mathrm{NCC}}$. If the index event is non-terminal, let $Y_i^{*}=Y_{i1}$, while if it is terminal, let $Y_i^{*}=Y_{i2}$. For either event type, let ${\delta }_i^{*}$ be an indicator of whether individual i was observed to experience the index event. Then, define ${\mathcal{R}}_i=\{j:Y_j^{*}\ge Y_i^{*}\}$ as the risk set formed at the observed event time if ${\delta }_i^{*}=1$. Furthermore, let R_0ij be a binary variable indicating whether individual i was selected as a control from ${\mathcal{R}}_j$. Following Samuelsen¹⁵ and Cai and Zheng,²² ${\mathcal{D}}_{\mathrm{NCC}}$ consists of all individuals for whom R_i = 1, where $R_i={\delta }_i^{*}+(1-{\delta }_i^{*})R_{0i}$ and $R_{0i}=1-{\prod }_{j:i\in {\mathcal{R}}_j}(1-{\delta }_j^{*}{R}_{0\mathit{ij}})$ is an indicator that the individual was selected as a control from at least one of the risk sets formed by the observed index events. Furthermore, the corresponding probability of being selected by the NCC design over the course of the observed follow-up period is ${\pi }_i=P(R_i=1;{\mathcal{D}}_{\mathrm{NCC}})={\delta }_i^{*}+(1-{\delta }_i^{*}){\pi }_{0i}$ where

$${\pi }_{0i}=1-\prod _{j:i\in {\mathcal{R}}_j}\left\{1-{\delta }_j^{\ast }\left(\frac{m}{\Vert {\mathcal{R}}_j\Vert -1}\right)\right\}.$$ (4)

An estimate of ξ, denoted $\widehat{\xi }$, can be obtained via maximization of ${\ell }^w(\xi )={\sum }_{i=1}^N{R}_i{\pi }_i^{-1}{\ell }_i(\xi )$ or ${\ell }^{\mathit{wp}}(\xi )={\ell }^w(\xi )-\mathcal{P}({\kappa }_1,{\kappa }_2,{\kappa }_3,\xi )$. Note, in the univariate time-to-event context, Samuelsen¹⁵ refers to ℓ^w(ξ) as the log pseudo-likelihood.

Now suppose that ${\mathcal{D}}_{\mathrm{NCC}}$ was supplemented with all cases of the non-index type who were not selected at the outset. Building on the notation above, let ${\mathcal{D}}_{\mathrm{SNCC}}$ denote the sub-sample of patients selected by the SNCC design, consisting of individuals for whom R_i = 1, where $R_i={\delta }_i^m+(1-{\delta }_i^m)R_{0i}$, with ${\delta }_i^m=\text{max}({\delta }_{i1},{\delta }_{i2})$ and R_0i defined as above. Furthermore, the corresponding probability of being selected by the SNCC design over the course of the observed follow-up period is ${\pi }_i=P(R_i=1;{\mathcal{D}}_{\mathrm{SNCC}})={\delta }_i^m+(1-{\delta }_i^m){\pi }_{0i}$ where π_0i is as defined above.

4.3. Asymptotics and standard error estimation

Here, we summarize the asymptotic properties of the proposed maximum weighted likelihood estimator and propose two estimators of the asymptotic standard error. Since the primary focus of this study is valid estimation and inference from an NCC or SNCC design, we focus the presentation here on unpenalized estimation (i.e. when κ_g = 0 for g ∈ {1, 2, 3}); analogous arguments regarding penalized likelihood estimation are given in Online Appendix B.2.

Let ${\mathcal{U}}^w(\xi )={\sum }_{i=1}^N{\mathbf{U}}_i^w(\xi )={\sum }_{i=1}^N{}_{}{R}_i{\pi }_i^{-1}{\mathbf{U}}_i(\xi )$ denote the score functions corresponding to ℓ^w(ξ), with U_i(ξ) = ∂ℓ_i(ξ)/∂ξ. Assuming the model is correctly specified, it is straightforward to show that $E_{\mathbf{Y},\mathbf{R}}[{\mathcal{U}}^w(\xi )]=E_{\mathbf{Y}}[\mathcal{U}(\xi )]=\mathbf{0}$ (Online Appendix B.1). Since solutions of unbiased estimating equations are asymptotically linear and asymptotically linear estimators have a unique influence function, then assuming suitable regularity conditions,²³ we have that $\sqrt{N}(\widehat{\xi }-{\xi }_0){\to }_d\mathrm{Normal}(\mathit{0},{\mathit{J}}^{-1}\mathbf{\Gamma }{\mathit{J}}^{-1})$, where ξ₀ is the true parameter value, J = E_Y,R[∂U^w(ξ)/∂ξ]|_ξ=ξ0 and Γ = Var_Y,R[U^w(ξ)]|_ξ=ξ0.

In practice, given suitable plug-in estimators, the asymptotic variance of $\widehat{\xi }$ can be estimated by $\widehat{\mathrm{Var}}[\widehat{\xi }]=N^{-1}{\widehat{\mathit{J}}}^{-1}\widehat{\Gamma }{\widehat{\mathit{J}}}^{-1}$. Towards this, following the arguments above, note that

$$\begin{gathered} E_{\mathbf{Y},\mathbf{R}}\left[\frac{\partial }{\partial \xi }{\mathcal{U}}^w\left(\xi \right)\right]=E_{\mathbf{Y}}\left[E_{\mathbf{R}|\mathbf{Y}}\left[\frac{\partial }{\partial \xi }\sum _{i=1}^N{R}_i{\pi }_i^{-1}{\mathbf{U}}_i\left(\xi \right)\right]\right] \\ =E_{\mathbf{Y}}\left[\frac{\partial }{\partial \xi }\mathcal{U}\left(\xi \right)\right], \end{gathered}$$

and that

$$\begin{gathered} {\mathrm{Var}}_{\mathbf{Y},\mathbf{R}}\left[{\mathcal{U}}^w\left(\xi \right)\right]={\mathrm{Var}}_{\mathbf{Y}}\left[E_{\mathbf{R}|\mathbf{Y}}\left[\sum _{i=1}^N{R}_i{\pi }_i^{-1}{\mathbf{U}}_i\left(\xi \right)\right]\right]+E_{\mathbf{Y}}\left[{\mathrm{Var}}_{\mathbf{R}|\mathbf{Y}}\left[\sum _{i=1}^N{R}_i{\pi }_i^{-1}{\mathbf{U}}_i\left(\xi \right)\right]\right] \\ ={\mathrm{Var}}_{\mathbf{Y}}\left[\mathcal{U}\left(\xi \right)\right]+E_{\mathbf{Y}}\left[\sum _{i=1}^N\sum _{j=1}^N\frac{\mathrm{Cov}\left[R_i,R_j\right]}{{\pi }_{ij}}{\mathbf{U}}_i\left(\xi \right){\mathbf{U}}_j{\left(\xi \right)}^T\right] \end{gathered}$$

where π_ij = P(R_i = 1, R_j = 1) is the joint probability that individuals i and j are selected by the NCC design at some pointy during the observed follow-up period. Hence, one can write $\widehat{\mathrm{Var}}[\widehat{\xi }]={\widehat{\mathrm{Var}}}_I[\widehat{\xi }]+{\widehat{\mathrm{Var}}}_{\mathit{II}}[\widehat{\xi }]=N^{-1}{\widehat{\mathit{J}}}^{-1}{\widehat{\mathbf{\Gamma }}}_I{\widehat{\mathit{J}}}^{-1}+N^{-1}{\widehat{\mathit{J}}}^{-1}{\widehat{\mathbf{\Gamma }}}_{\mathit{II}}{\widehat{\mathit{J}}}^{-1}$, where the first component estimates the sandwich variance of the complete data estimator (i.e. for the full cohort) and the second is an additional term that is due to the design. One option that avoids the calculation of all Cov[R_i, R_j] is to use a plug-in estimator that ignores the design component,²⁴ specifically $\widetilde{\mathrm{Var}}[\widehat{\xi }]=N^{-1}{\widehat{\mathit{J}}}^{-1}{\widehat{\mathbf{\Gamma }}}_I{\widehat{\mathit{J}}}^{-1}$ where

$$\widehat{\mathit{J}}=\frac{1}{N}\sum _{i=1}^N\frac{\partial }{\partial \xi }{\mathbf{U}}_i^w(\widehat{\xi }),{\widehat{\mathbf{\Gamma }}}_I=\frac{1}{N}\sum _{i=1}^N{\mathbf{U}}_i^w(\widehat{\xi }){\mathbf{U}}_i^w{(\widehat{\xi })}^T.$$

Note, since the sampling indicators for two individuals (i.e. R_i and R_j) are negatively correlated if they are members of the same risk set, $\widetilde{\mathrm{Var}}[\tilde{\xi }]$ may be expected to yield standard error estimates that are too large and thus conservative, particularly when risk sets are small.

As an alternative to the sandwich estimator, $\widetilde{\mathrm{Var}}[\widehat{\xi }]$, we propose an estimator based on a perturbation resampling procedure under NCC designs for estimators that minimize some generic loss function.²² This method recovers the impact of the negative correlation among the sampling indicators on variance estimation by exploiting the relationship between exact weights under sampling without replacement and estimated weights under sampling with replacement. First, generate $\mathcal{I}=\{{\mathcal{I}}_{\mathit{ab}}:a,b=1,\dots ,N\}$ as N² random draws from a distribution with $E[{\mathcal{I}}_{\mathit{ab}}]=\mathrm{Var}[{\mathcal{I}}_{\mathit{ab}}]=1.0$ (e.g. Exponential (1)). Let S be an indicator of whether the NCC design is supplemented. Then, set

$$R_i^{\ast }=\left\{{\delta }_i^{\ast }(1-S)+{\delta }_i^{m}S\right\}{\mathcal{I}}_{ii}+[1-\left\{{\delta }_i^{\ast }(1-S)+{\delta }_i^{m}S\right\}]\times \left\{1-\prod _{l:i\in {\mathcal{R}}_l}(1-{\delta }_l^{\ast }{R}_{0il}{\mathcal{I}}_{il})\right\}$$

and

$${\pi }_i^{\ast }=\left\{{\delta }_i^{\ast }(1-S)+{\delta }_i^{m}S\right\}+[1-\left\{{\delta }_i^{\ast }(1-S)+{\delta }_i^{m}S\right\}]\times \left\{1-\exp \left(-\sum _{l:i\in {\mathcal{R}}_l}{\delta }_l^{\ast }\frac{{\Sigma }_{k\in {\mathcal{R}}_l}{R}_{0kl}{\mathcal{I}}_{kl}}{\Vert {\mathcal{R}}_l\Vert -1}\right)\right\}$$

for each $i\in {\mathcal{D}}_{\mathrm{NCC}}$ or $i\in {\mathcal{D}}_{\mathrm{SNCC}}$, as appropriate. If case s is selected in the supplementation step, then $R_s^{*}={\mathcal{I}}_{\mathit{ss}}$ and ${\widehat{\pi }}_s^{*}=1$, but R_0is = 0 for all patients i ≠ s. Then, compute all perturbed weights $w_i^{*}=R_i^{*}/{\pi }_i^{*}$ and let ${\widehat{\xi }}^{(1)}$ be the solution to: ${\mathbf{U}}^{w*}(\xi )={\sum }_{i=1}^N{R}_i{w}_i^{*}{\mathbf{U}}_i(\xi )=\mathbf{0}$. These steps are repeated B times to give $\{{\widehat{\xi }}^{(b)},b=1,\dots ,B\}$, which approximates the sampling distribution of $\widehat{\xi }$. Thus, an estimate of $\mathrm{Var}[\widehat{\xi }]$ is the (empirical) variance of the ${\widehat{\xi }}^{(b)}$.

5. Simulations

We conducted a series of simulation studies to evaluate the small-sample operating characteristics of the proposed methods. In each simulation, 10,000 “full cohorts” of size N = 10,000 were initially generated. From these, data that would be observed from a given NCC design were generated by mimicking the appropriate selection procedure.

5.1. Setup

For each of the 10,000 full cohorts, we randomly generated N = 10,000 covariate vectors X = (X_A, X_B, X_C), with X_A (the covariate of interest) a Bernoulli random variable with P(X_A = 1) = expit(−1.25 + 1.25X_B), and X_B and X_C both independent Bernoulli (0.5) random variables. Given X, semi-competing risks outcome data were generated under models (1) to (3) using the simID() function in the SemiCompRisks package in R. Table 2 in Online Appendix C provides the true values of the regression coefficients used in all simulations. For the baseline hazard functions λ_0g(·) for g ∈ {1, 2, 3}, we considered two primary scenarios based on underlying Weibull distributions; Table 3 and Figure 2 in Online Appendix C provide the parameter values and corresponding baseline survivor functions. In Scenario 1, the parameters were chosen such that, on average, 22.2% of patients experienced the non-terminal event, 21.5% experienced the terminal event, and 11.7% experienced both events, following independent censoring from a Uniform (50, 60) distribution. In Scenario 2, the event rates were approximately half of those in Scenario 1, in line with the observed event rates in the CIBMTR data. We considered θ = 1 and θ = 3 for the variance of the subject-specific frailties.

As we elaborate upon below, the proposed methods exhibited (relatively) poor performance when the data arise from the NT-NCC design. We examined performance for this design under two additional scenarios: Scenario 3 in which the event rates were approximately double those of Scenario 1, and Scenario 4 in which the event rates were approximately the same as in Scenario 1 but the terminal events occurred later in time.

For each full cohort, we generated four NCC data sets by mimicking the NCC sampling scheme using the nonterminal event as the index event and, separately, the terminal event as the index event, considering m = 1 and m = 3 controls per case. For each resulting data set, we mimicked a SNCC design that included all non-index cases who were not originally selected. Thus, eight NCC data sets were generated for each full cohort.

5.2. Analyses

For each of the full cohorts and NCC data sets, we obtained maximum likelihood and maximum weighted likelihood estimates of the unknown parameters, adopting a Weibull specification for the baseline hazards. Additionally, for Scenario 1, unpenalized maximum likelihood and maximum weighted likelihood estimates were also obtained based on a B-spline specification for the log-baseline hazard functions with K_g = 6. Throughout, we computed both proposed standard error estimators. For the conservative sandwich estimator, the derivatives in $\widehat{\mathit{J}}$ were computed numerically. For the perturbation resampling-based estimator, we set B = 500; because of the computational burden involved, we only evaluated the perturbation resampling-based estimator for the first 2000 simulation iterations for the Weibull specification of the baseline hazards.

To avoid a small number of iterations having an unduly large impact on the results, we removed all iterations whose exponentiated estimates of logθ were > 6 median absolute deviation (MAD) from the median estimate,²⁵ rarely excluding more than 1% of iterations. Online Appendix D provides a table illustrating the number of iterations removed for all outputs in Tables 1 to 4. This rule was also applied within each perturbation estimate of the standard error. Additionally, in Scenario 2 for m = 1, there was some instability in the estimation of β_A2 for the NT-NCC design; 289 iterations were removed whose estimates for that parameter were >6 MAD from the median estimate.

Table 1.

Results for β_A1, β_A2, β_A3, and θ under simulation Scenario 1 with θ = 1 and Weibull specifications for the baseline hazard functions, based on 10,000 simulated data sets.

	m = 1							m = 3
Parameter/design	Percentage bias	Standard error			Coverage		Rel Unc	Percentage bias	Standard error			Coverage		Rel Unc
		Emp	CS	PR	CS	PR			Emp	CS	PR	CS	PR
βA1
NT unsupp.	1.7	0.092	0.085	0.092	0.92	0.96	1.69	1.3	0.069	0.065	0.070	0.93	0.95	1.27
NT supp.	0.1	0.070	0.070	0.070	0.95	0.95	1.30	0.1	0.059	0.058	0.059	0.95	0.95	1.08
T unsupp.	−0.2	0.088	0.087	0.087	0.95	0.95	1.63	0.1	0.065	0.064	0.063	0.95	0.94	1.20
T supp.	0.1	0.071	0.071	0.072	0.95	0.95	1.32	0.1	0.059	0.059	0.060	0.95	0.94	1.09
βA2
NT unsupp.	5.4	0.470	0.408	0.396	0.93	0.91	4.66	1.6	0.303	0.268	0.253	0.93	0.93	3.01
NT supp.	0.6	0.111	0.110	0.110	0.95	0.95	1.10	0.5	0.103	0.103	0.103	0.95	0.96	1.02
T unsupp.	0.8	0.114	0.113	0.113	0.95	0.95	1.13	0.6	0.104	0.104	0.104	0.95	0.95	1.03
T supp	0.5	0.111	0.111	0.111	0.95	0.95	1.10	0.5	0.104	0.103	0.104	0.95	0.95	1.03
βA3
NT unsupp.	−2.7	0.084	0.086	0.087	0.95	0.95	1.10	−1.7	0.079	0.080	0.081	0.95	0.96	1.04
NT supp.	−0.2	0.076	0.077	0.077	0.95	0.95	1.00	−0.2	0.076	0.077	0.077	0.95	0.96	1.00
T unsupp.	−0.4	0.119	0.118	0.115	0.95	0.94	1.57	−0.3	0.089	0.089	0.085	0.95	0.93	1.18
T supp.	−0.2	0.076	0.077	0.077	0.95	0.95	1.00	−0.2	0.076	0.077	0.077	0.95	0.96	1.00
θ
NT unsupp.	23.6	0.482	0.289	0.530	0.65	0.88	2.51	16.3	0.344	0.239	0.321	0.73	0.87	1.79
NT supp.	0.3	0.199	0.211	0.214	0.94	0.96	1.04	0.8	0.194	0.203	0.208	0.94	0.96	1.01
T unsupp.	−3.9	0.295	0.290	0.303	0.93	0.92	1.54	0.2	0.212	0.224	0.221	0.94	0.94	1.11
T supp.	0.2	0.200	0.213	0.214	0.95	0.95	1.04	0.8	0.194	0.203	0.210	0.94	0.96	1.01

Note: Percentage bias, empirical standard errors (Emp), standard error estimates, and coverage for Wald-based 95% confidence intervals (CS: conservative sandwich estimator; PR: perturbation resampling estimator) are shown, for four designs that vary by the index event (NT: non-terminal; T: terminal) and whether the supplementation of non-index cases was used. Relative uncertainty is also shown, defined as the ratio of the (empirical) standard error for estimates based on a given NCC design to that of the estimates from an analysis of the full cohort.

Table 4.

Results for β_A1, β_A2, β_A3, and θ for an unsupplemented NCC design with the non-terminal event as the index event, under Scenarios 1 to 4 with m = 1, θ = 1, and based on 10,000 simulated data sets.

Parameter/simulation scenario	Percentage bias	Standard error		Cov	Rel Unc
		Emp	CS	CS
βA1
1: Original	1.7	0.092	0.085	0.92	1.69
2: Lower event rates	2.6	0.135	0.132	0.94	1.87
3: Higher event rates	1.0	0.069	0.063	0.94	1.61
4: Later event times	0.6	0.078	0.073	0.92	1.47
βA2
1: Original	5.4	0.470	0.408	0.93	4.66
2: Lower event rates	15.2	0.836	0.740	0.95	6.10
3: Higher event rates	0.8	0.276	0.236	0.93	3.81
4: Later event times	3.7	0.357	0.329	0.94	3.32
βA3
1: Original	−2.7	0.084	0.086	0.95	1.10
2: Lower event rates	−5.0	0.128	0.130	0.94	1.19
3: Higher event rates	−0.9	0.064	0.063	0.95	1.14
4: Later event times	−1.2	0.077	0.077	0.95	1.02
θ = 1
1: Original	23.6	0.482	0.289	0.65	2.51
2: Lower event rates	73.8	1.419	1.400	0.56	2.98
3: Higher event rates	8.4	0.131	0.100	0.69	2.10
4: Later event times	5.5	0.369	0.347	0.81	1.92

Note: Percentage bias, empirical standard errors (Emp), standard error estimates, and coverage for Wald-based 95% confidence intervals based on the conservative sandwich estimator (CS) are shown. Relative uncertainty is also shown, defined as the ratio of the (empirical) standard error for estimates based on a given NCC design to that of the estimates from an analysis of the full cohort.

5.3. Results: Point and standard error estimation

Tables 1 to 3 and Figure 1 present select results for Scenarios 1 and 2 under θ = 1; comprehensive results for all parameters and for when θ = 3 are provided in Online Appendix D. We see that point estimates are generally unbiased for each of the NT-SNCC, T-NCC, and T-SNCC designs. Table 1 shows that the standard error estimators are both generally close to the empirical standard error and yield 95% confidence intervals (CIs) with close to nominal coverage. That the sandwich standard error estimator performs well is as expected; the risk sets from which the controls are selected are relatively large, so that negative correlation among sampling indicators would be expected to have little impact. Results for the perturbation resampling estimator under the remaining scenarios can be found in Online Appendix D. Comparing Tables 1 and 2, we see that, for Scenario 1 at least, the adoption of a B-spline for the log-baseline hazard functions did not adversely introduce any systematic small-sample bias in either the point or standard error estimates. Figure 1 shows that the spline-based model also performs well in estimating the baseline survival functions.

Table 3.

Results for β_A1, β_A2, β_A3, and θ under simulation Scenario 2 with θ = 1 and Weibull specifications for the baseline hazard functions, based on 10,000 simulated data sets.

	m = 1					m = 3
Parameter/design	Percentage bias	Standard error		Cov	Rel Unc	Percentage bias	Standard error		Cov	Rel Unc
		Emp	CS	CS			Emp	CS	CS
βA1
NT unsupp.	2.6	0.135	0.132	0.94	1.87	1.9	0.097	0.095	0.95	1.34
NT supp.	0.2	0.100	0.099	0.95	1.38	0.2	0.081	0.081	0.95	1.12
T unsupp.	−0.5	0.146	0.145	0.95	2.03	−0.2	0.100	0.100	0.95	1.38
T supp.	0.4	0.103	0.099	0.94	1.41	0.3	0.081	0.081	0.95	1.12
βA2
NT unsupp.	15.2	0.836	0.740	0.95	6.10	7.2	0.530	0.460	0.93	3.85
NT supp.	0.7	0.153	0.154	0.95	1.11	0.5	0.143	0.142	0.95	1.04
T unsupp.	1.4	0.155	0.156	0.95	1.13	0.9	0.143	0.143	0.95	1.04
T supp.	0.7	0.156	0.154	0.95	1.12	0.6	0.143	0.143	0.95	1.03
βA3
NT unsupp.	−5.0	0.128	0.130	0.94	1.19	−3.2	0.115	0.116	0.94	1.07
NT supp.	−1.4	0.108	0.107	0.95	1.00	−1.2	0.108	0.107	0.95	1.00
T unsupp.	−3.5	0.211	0.201	0.93	1.96	−2.0	0.147	0.145	0.94	1.36
T supp.	−1.4	0.110	0.107	0.94	1.00	−1.5	0.109	0.107	0.94	1.00
θ
NT unsupp.	73.8	1.419	1.400	0.56	2.98	45.7	0.968	0.581	0.64	2.04
NT supp.	−0.6	0.491	0.470	0.89	1.03	0.7	0.484	0.516	0.88	1.02
T unsupp.	−19.5	0.698	0.506	0.85	1.47	−6.8	0.575	0.701	0.88	1.21
T supp.	0.6	0.496	0.470	0.88	1.04	0.7	0.489	0.462	0.89	1.02

Note: Percentage bias, empirical standard errors (Emp), standard error estimates, and coverage for Wald-based 95% confidence intervals using the conservative sandwich estimator (CS) are shown, for four designs that vary by the index event (NT: non-terminal; T: terminal) and whether the supplementation of non-index cases was used. Relative uncertainty is also shown, defined as the ratio of the (empirical) standard error for estimates based on a given NCC design to that of the estimates from an analysis of the full cohort.

Figure 1.

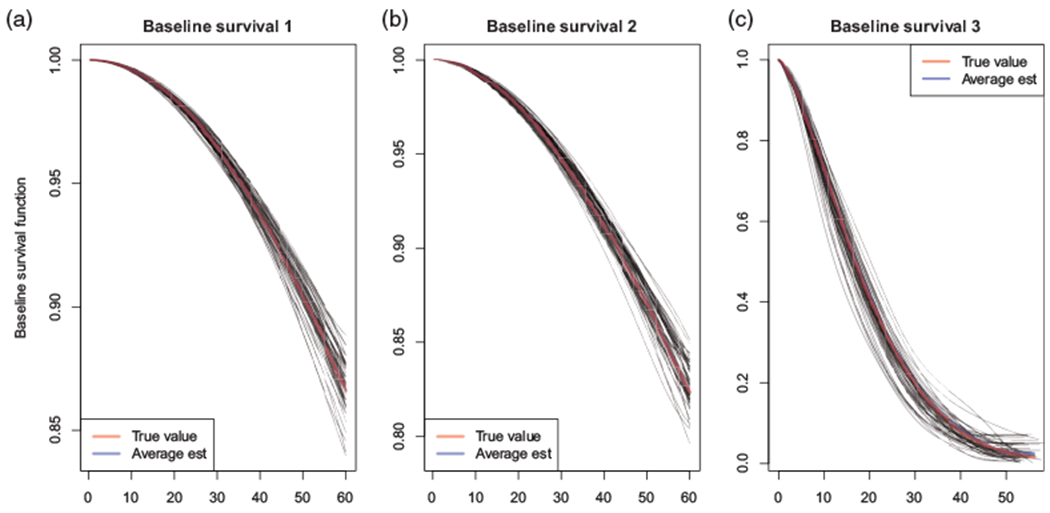
Estimates of the baseline survivor functions under simulation Scenario 1 with θ = 1, based on 10,000 simulated data sets, fitting the spline-based model. The true Weibull baseline survival function (red) and the average spline-based estimate (blue) are overlaid with results from the first 50 runs of the simulation (gray). (a) Baseline survival 1, (b) Baseline survival 2, and (c) Baseline survival 3.

Table 2.

Results for β_A1, β_A2, β_A3, and θ under simulation Scenario 1 with θ = 1 and B-spline specifications for the log-baseline hazard functions (with K_g = 6), based on 10,000 simulated data sets.

	m = 1					m = 3
Parameter/design	Percentage bias	Standard error		Cov	Rel Unc	Percentage bias	Standard error		Cov	Rel Unc
		Emp	CS	CS			Emp	CS	CS
βA1
NT unsupp.	0.9	0.092	0.090	0.94	1.61	0.8	0.068	0.068	0.95	1.20
NT supp.	0.2	0.071	0.071	0.95	1.25	0.2	0.061	0.060	0.95	1.07
T unsupp.	−0.2	0.087	0.087	0.95	1.54	0.1	0.066	0.066	0.95	1.16
T supp.	0.2	0.073	0.073	0.95	1.29	0.2	0.061	0.061	0.94	1.07
βA2
NT unsupp.	7.2	0.463	0.413	0.93	4.56	2.8	0.295	0.267	0.93	2.90
NT supp.	0.5	0.111	0.111	0.95	1.09	0.4	0.104	0.104	0.95	1.02
T unsupp.	1.0	0.115	0.115	0.95	1.13	0.5	0.105	0.105	0.95	1.03
T supp.	0.5	0.112	0.112	0.95	1.11	0.4	0.104	0.104	0.95	1.02
βA3
NT unsupp.	−1.9	0.082	0.087	0.95	1.08	−0.9	0.078	0.080	0.96	1.02
NT supp.	−0.5	0.077	0.077	0.95	1.00	−0.5	0.077	0.077	0.95	1.00
T unsupp.	−0.8	0.119	0.118	0.95	1.56	−0.8	0.090	0.090	0.95	1.17
T supp.	−0.5	0.077	0.077	0.95	1.00	−0.5	0.077	0.077	0.95	1.00
θ
NT unsupp.	10.1	0.528	0.440	0.86	1.91	7.2	0.369	0.353	0.89	1.34
NT supp.	0.1	0.298	0.307	0.92	1.08	1.1	0.282	0.291	0.92	1.02
T unsupp.	−6.3	0.403	0.551	0.91	1.46	−0.2	0.315	0.348	0.92	1.14
T supp.	0.0	0.298	0.310	0.92	1.08	0.9	0.285	0.293	0.92	1.03

Note: Percentage bias, empirical standard errors (Emp), standard error estimates, and coverage for Wald-based 95% confidence intervals using the conservative sandwich estimator (CS) are shown, for four designs that vary by the index event (NT: non-terminal; T: terminal) and whether the supplementation of non-index cases was used. Relative uncertainty is also shown, defined as the ratio of the (empirical) standard error for estimates based on a given NCC design to that of the estimates from an analysis of the full cohort.

For the NT-NCC design, the performance of the point and standard error estimators is sub-optimal, particularly for θ. We note that IPW estimation is known to be unstable when some individuals who have low probabilities of selection are nonetheless selected and, therefore, have large weights.²⁶ In the context of an NT-NCC design, all individuals who experience the non-terminal event will have weight 1.0; it is individuals who did not and are therefore eligible to be selected as controls, who will have weight > 1.0. From expression (4), potential controls will have a low probability of selection if they are members of few risk sets, which can happen if they have short observed follow-up times (either due to censoring or experiencing the terminal event) and/or the nonterminal event rate is low. Table 4 presents results for the NT-NCC design under Scenarios 3 and 4, indicating that the non-terminal event rate and the timing of the events play an important role in the extent of small-sample bias and coverage of 95% CIs. Moreover, the results suggest caution may be needed if θ is of central scientific interest and yet information is solely available from an NT-NCC design. We note that under each of the other three designs (i.e. the NT-SNCC, T-NCC, and T-SNCC designs), individuals who experience the terminal event are guaranteed to be selected and therefore have a weight of 1.0. As confirmed in Tables 1 to 3, these designs are less likely to suffer from the phenomena explored in Table 4.

5.4. Results: Relative uncertainty

Tables 1 to 3 also report on relative uncertainty, defined as the ratio of the (empirical) standard error for estimates based on a given NCC design to that of the estimates from an analysis of the full cohort (i.e. the relative widths of the respective 95% CIs). Note that the NCC design plays an important and distinct role across the parameters. For example, of the three regression parameters, β_A2 is estimated with comparable efficiency across the NT-SNCC, T-NCC, and T-SNCC designs (with relative uncertainty ranging from 1.10 to 1.13). This is because all individuals who experience the terminal event only, a group that is critical to estimation of parameters for the second transition in the illness-death model, are guaranteed to be selected. In contrast, β_A2 is estimated inefficiently under the NT-NCC design because individuals who transition directly to the terminal event are not guaranteed to be selected if the risk sets are being formed on the basis of the non-terminal event. This imbalance also factors into the suboptimal estimation of θ, which in turn affects the quality of the estimation of all other parameters in the NT-NCC design—this may explain why β_A1 is estimated somewhat less efficiently under the NT-NCC design than under the T-NCC design. The same patterns hold for the relative uncertainty of estimates using the spline specification of the baseline hazards, shown in Table 2.

Comparing the two unsupplemented designs, we see that the T-NCC design yields more efficient estimators than the NT-NCC design, with the exception of β_A3. This is because individuals who experience the non-terminal event but are censored prior to experiencing the terminal event are not guaranteed to contribute, in contrast to the design where the non-terminal event is taken as the index event. Throughout, supplementation improves relative uncertainty, regardless of which event is the index event, for all parameters in all settings.

6. Application: aGVHD

6.1. Background and data

Data were extracted from the CIBMTR databases for patients who underwent first allogeneic human leukocyte antigen (HLA)-identical sibling or unrelated donor HSCT between January 1999 and December 2011. From these data, we conceive of a hypothetical study of the association between aGVHD prophylaxis regimen and grade III or IV aGVHD within 100 days of transplantation.¹ To maintain a comparable time scale for aGVHD and death, follow-up was administratively censored at 100 days. For simplicity, we restrict our attention to a sub-sample of N = 8838 patients with complete data on key covariates and who underwent one of five aGVHD prophylaxis treatments (Table E.1 of the Online Appendix). Among these patients, 5.1% were diagnosed with aGVHD and died within 100 days, 10.0% died within 100 days without a diagnosis of aGVHD, 12.6% were diagnosed with aGVHD but did not die within 100 days, and 72.4% did not experience either event (Table E.1 of the Online Appendix).

6.2. Design and analysis

For the hypothetical study, we suppose that only basic clinical information (sex, age, and diagnosis) is readily available, and that chart review is required for all other factors needed for the analysis. Towards this, we mimicked two NCC studies: one based on aGVHD within 100 days as the index event and the second based on death within 100 days. In both studies, we selected all cases who experienced the index event and m = 1 control from each risk set. For the first study, based on aGVHD, the total sample size was 2840; for the second, based on death, the total sample size was 2427. Finally, we supplemented both studies to mimic the SNCC design. For example, in the second study, we additionally selected all those patients among the 12.6% who experienced aGVHD but did not die and were not selected as controls. Following supplementation, the total sample sizes were 3391 and 3598, respectively.

For each hazard (1) to (3), we adopted a B-spline with K_g = 6 for the log-baseline hazard functions and adjusted for sex, HLA compatibility, age, African-American race, Karnofsky score, diagnosis, disease stage, year of treatment, graft type, conditioning intensity, whether in-vivo T-cell depletion was performed, and aGVHD prophylaxis. For each NCC and SNCC data set, we fit the model using the unpenalized weighted likelihood estimator. To serve as a “gold standard,” we analyzed the full cohort (i.e. all N = 8838 patients). Finally, in addition to hazard ratio (HR) estimates, we report Wald-based 95% CIs using both proposed standard error estimators.

6.3. Results

Figure 2 and Table 5 summarize the results. Figure 2(a) shows that the estimates of the baseline survivor function for aGVHD induced by the B-spline-based estimates of logλ₀₁(·) from the four designs correspond closely to that of the full cohort analysis. From Figure 2(b), the estimates of the baseline survivor function for death without aGVHD generally correspond, with the one exception being that based on the NT-NCC design. From Figure 2(c), the estimators based on the NT-NCC and T-NCC designs also overestimate mortality following aGVHD. In each case, however, the supplementation resolves the overestimation.

Figure 2.

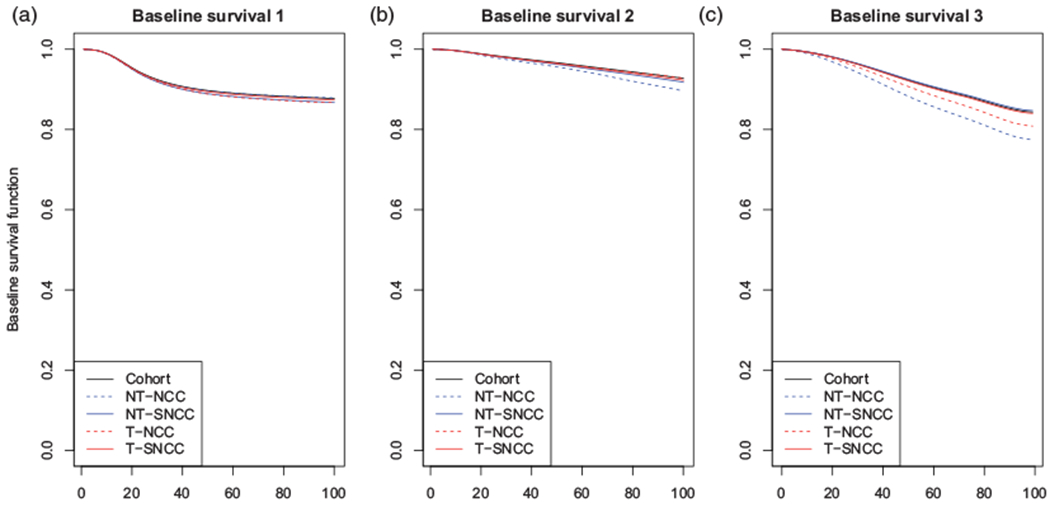
Estimates of the baseline survivor functions from the weighted illness-death model fits for the four NCC/SNCC studies based on the CIBMTR data as well as the cohort data. In each case, the underlying log-baseline hazard function was specified via a B-spline with K_g = 6. NCC: nested case-control; SNCC: supplemental NCC; NT: non-terminal; T: terminal. (a) Baseline survival 1, (b) Baseline survival 2, and (c) Baseline survival 3.

Table 5.

HR estimates of the association between aGVHD prophylaxis and risk of aGVHD, based on fitting the illness-death model to the full CIBMTR data as well as four unmatched nested case-control designs.

	Tac/MTX	Tac	CsA/MTX	CsA	Ex vivo TCD
Full cohort (N = 8838)
HR	1.00	1.31	1.08	1.69	0.64
95% CI		(1.13, 1.52)	(0.93, 1.25)	(1.37, 2.09)	(0.47, 0.87)
NCC based on aGVHD
Unsupplemented (NT-NCC) (N = 2840)
HR	1.00	1.20	1.17	1.66	0.59
CS 95% CI		(0.94, 1.55)	(0.88, 1.57)	(1.14, 2.41)	(0.36, 0.96)
PR 95% CI		(0.95, 1.52)	(0.91, 1.52)	(1.17, 2.36)	(0.38, 0.92)
Supplemented (NT-SNCC) (N = 3598)
HR	1.00	1.21	1.08	1.76	0.63
CS 95% CI		(0.98, 1.49)	(0.89, 1.32)	(1.32, 2.34)	(0.43, 0.94)
PR 95% CI		(0.99, 1.48)	(0.88, 1.32)	(1.34, 2.31)	(0.43, 0.93)
NCC based on death
Unsupplemented (T-NCC) (N = 2427)
HR	1.00	1.32	1.29	1.56	0.49
CS 95% CI		(0.91, 1.92)	(0.90, 1.85)	(0.98, 2.50)	(0.23, 1.01)
PR 95% CI		(0.93, 1.88)	(0.92, 1.79)	(0.99, 2.45)	(0.23, 1.01)
Supplemented (T-SNCC) (N = 3391)
HR	1.00	1.30	1.04	1.74	0.52
CS 95% CI		(1.04, 1.61)	(0.83, 1.29)	(1.28, 2.37)	(0.34, 0.79)
PR 95% CI		(1.04, 1.61)	(0.84, 1.28)	(1.28, 2.37)	(0.35, 0.76)

Note: 95% CIs based on the CS estimate of the standard error and the PR-based estimator are also shown. HR: hazard ratio; CI: confidence interval; CS: conservative sandwich; PR: perturbation resampling; NCC: nested case-control; SNCC: supplemental NCC; NT: non-terminal; T: terminal; aGVHD: acute graft-versus-host disease; MTX: methotrexate; TCD: T-cell depletion; Tac: tacrolimus; CsA: cyclosporin A.

Table 5 presents results regarding the association between aGVHD prophylaxis and risk of aGVHD (see Table E.2 of the Online Appendix for complete results). From the top row, we find that ex vivo T-cell depletion (TCD)/CD34⁺ selection is associated with a lower risk of aGVHD when compared to the referent regimen of tacrolimus/methotrexate (Tac/MTX) (HR: 0.64, 95% CI: 0.47, 0.87), while Tac alone (HR: 1.31, 95% CI: 1.13, 1.52) and cyclosporin A (CsA) alone (HR: 1.69, 95% CI: 1.37, 2.09) are associated with an increased risk. From the remainder of the table, despite only being based on 27% to 41% of the cohort, the HR point estimates generally align with those from the full cohort. As anticipated, estimates from the SNCC designs are generally closer to the full cohort estimates than those from the unsupplemented NCC designs. Finally, supplementation leads to efficiency gains over analyses of the corresponding unsupplemented NCC studies. For example, while the point estimates for the Tac HR are similar, the width of the 95% CI under the T-SNCC design is approximately half of the one under the T-NCC design.

7. Discussion

This work is, to the best of our knowledge, the first to consider the simultaneous analysis of multiple outcomes based on data from an NCC study. While the proposed framework provides researchers with a valid approach to estimation and inference for the illness-death model, there are many opportunities for further work. For example, motivated by the potential for efficiency gains, some authors have proposed to truncate the weights used in IPW estimators at the expense of slight bias.²⁶ This may serve as a strategy for improving the stability of estimation when selected controls with high weights are present, particularly for the NT-NCC design. A second direction could be the development of more efficient estimation through survey sampling techniques, such as calibration, that permit the use of data available on the whole cohort.²⁷ Third, while time-varying covariates cannot be used in this scheme unless investigators have access to their complete trajectories, since IPW breaks the matching within risk sets that typically occurs in an NCC study,¹⁵ an extension permitting time-varying covariates would be valuable. Finally, it would be of interest to explore strategies for the optimal choice of K_g and κ when using B-splines.

Although the results regarding relative uncertainty in Tables 1 to 4 speak to the inherent loss of information when one only has complete data on a sub-sample, a thorough evaluation of statistical power/efficiency will help researchers tailor designs to their own goals. Indeed, many interesting design considerations could be explored. For example, our results demonstrate that supplementation of a standard NCC design yields numerous meaningful benefits, particularly when the index event is the non-terminal event. As such, it seems clear that supplementation should be undertaken when possible. Additional design considerations include the relative impact on the statistical power/efficiency of matching schemes in the original NCC design as well as the potential interplay between matching and subsequent supplementation.

Furthermore, the NCC design is typically employed for settings where the outcome of interest is rare, such that all index cases are “selected.” When the outcome is neither rare nor common (as in the aGVHD data) or when resources are severely limited, researchers may be interested in only selecting a sub-sample of the index and non-index cases. To the best of our knowledge, this has not even been considered for NCC designs in the usual univariate time-to-event setting. Finally, while this study focuses on the re-use of an NCC study for a semi-competing risks analysis, one important extension to our work is the design of NCC studies in which the pre-specified objective is a semi-competing risks analysis. Aside from designating only one of the two events as the index event, other options are available—for instance, defining the index event as the composite endpoint formed by aGVHD and death.

The illness-death model specified in equations (1) to (3) involves a shared patient-specific frailty that is assumed to arise from some distribution with mean 1.0 and variance θ. Although, as previously indicated, analysts are free to choose any such distribution, we have focused on a Gamma(θ⁻¹, θ⁻¹) distribution in part because this is consistent with much of the literature and because it simplifies calculation of the marginal likelihood. Despite this practical benefit, the appropriateness of any given choice needs to be queried. Towards this, although it is beyond the scope of this study, future work should consider the extent to which misspecification of the distribution may result in bias, possibly following in the steps of the rich literature on the choice of random effects distributions in GLMMs.^28,29 Furthermore, there are likely opportunities to develop graphical and numerical techniques to assess the adequacy of a given choice by building on existing work for standard multivariate failure time settings.³⁰