Abstract
For decades one has strived to synthesize a compound with the longest covalent C−C bond applying predominantly steric hindrance and/or strain to achieve this goal. On the other hand electronic effects have been added to the repertoire, such as realized in the electron deficient ethane radical cation in its D form. Recently, negative hyperconjugation effects occurring in diamino-o-carborane analogs such as di-N,N-dimethylamino-o-carborane have been held responsible for their long C−C bonds. In this work we systematically analyzed CC bonding in a diverse set of 53 molecules including clamped bonds, highly sterically strained complexes such as diamondoid dimers, electron deficient species, and di-N,N-dimethylamino-o-carborane to cover the whole spectrum of possibilities for elongating a covalent C−C bond to the limit. As a quantitative intrinsic bond strength measure, we utilized local vibrational CC stretching force constants (CC) and related bond strength orders BSO n(CC), computed at the B97X-D/aug-cc-pVTZ level of theory. Our systematic study quantifies for the first time that whereas steric hindrance and/or strain definitely elongate a C−C bond, electronic effects can lead to even longer and weaker C−C bonds. Within our set of molecules the electron deficient ethane radical cation, in D symmetry, acquires the longest C−C bond with a length of 1.935 Å followed by di-N,N-dimethylamino-o-carborane with a bond length of 1.930 Å. However, the C−C bond in di-N,N-dimethylamino-o-carborane is the weakest with a BSO n value of 0.209 compared to 0.286 for the ethane radical cation; another example that the longer bond is not always the weaker bond. Based on our findings we provide new guidelines for the general characterization of CC bonds based on local vibrational CC stretching force constants and for future design of compounds with long C−C bonds.
Keywords: longest CC bonds, vibrational spectroscopy, local mode theory, local mode force constants, steric versus electronic effects
1. Introduction
Carbon-carbon single bonds are essential to organic chemistry and form the framework for many materials and life forms, e.g., serving as fundamental connectors in genes and proteins. The typical length of a C(sp3)−C(sp3) bond is around 1.54 Å [1]. However, it may exceed this standard value considerably, which has led to a competition of pushing the CC bonds to their limits by finding the best strategy for synthesizing the longest but still intact CC bond [2,3,4,5,6,7]. Whereas the question of the practical use of such ultra-long C−C bonds is still open, the study of these extreme cases including novel CC bonding situations such as e.g., the recently established CC tetrel bonding [8,9,10] strongly contributes to enriching our understanding of the CC bond and the concept of the chemical bond in general [11,12,13]. Besides long C−C bonds other elongated bonding situations are also of interest, notably long OO bonds and dative bonding. Interestingly, spectroscopic analysis of gas phase HOON has revealed that the O−O bond surpasses a length of 1.91 Å (1.9149 ±0.0005 Å) but is relatively stable than previously thought [14]. Also, computational analysis of H2O6, conducted at the CCSD(T)/cc-pVTZ level of theory, has shown the molecule to have an unusually long central O−O bond at a length of 1.91 Å (≈1.902 Å) [15]. Dative bonding within BN systems involves the substitution of two C atoms with boron and nitrogen atoms; in contrast to carbon analogs, longer and weaker bonds result for dative bonds. For instance, the B−N single bond of NB ethylamine, evaluated at the CC2/TZVPP level of theory, shows to be the strongest dative B−N bond and is 0.08 Å greater than the usual C(sp3)−C(sp3) bond length [16].
Increasing the exchange (steric) repulsion via bulky substituents has long been known to lengthen interatomic distances. In an alkane, one way to increase the bond length between two carbons is to replace hydrogens with alkyl groups [17,18,19,20,21,22,23,24]. The central C−C bond of 2,2,3,3-tetramethylbutane [25] was one of the first investigated in this regard, and many related studies followed [20,21,23,24,26]. Schreiner and co-workers [27] constructed dumbell-shaped molecules consisting of a central C-C bar holding on each end three-dimensional diamond-like alkanes (so-called diamondoids). The outer surfaces of these diamondoids are capped by hydrogens, the van der Waals attraction between the hydrogens on either side of the central bond holds these molecules together. Meanwhile, the repulsive forces of each diamondoid on either side of the central C−C bridge are sufficient enough to stretch the bond by more than 0.2 Å compared to the typical C−C bond length of an alkane. The enforcement of a cage-topology clamped bonds, involving the bridging atoms, is another way to lengthen a covalent bond [28,29]. Some extensively investigated examples regarding clamped bonds are bi(anthracene-9,10-dimethylene) [30] and acenaphthene-5,6-diyl bis(diphenylmethylium), both being sensitive to light, heat, and pressure [31]. Moret and co-workers discussed the formation of exceptionally weak C−C bonds by metal-templated pinacol coupling, where metal coordination is the key stabilizing factor [32]. A different strategy has been based on the fact that the loss of bonding electrons or bonding electron density leads to weaker and longer bonds as a consequence of electron deficient bonding. The D symmetrical ethane radical cation is a classic example with calculated C−C bond lengths of 1.915 Å or more, depending on the level of theory used [33,34,35]. A series of diamino-o-carboranes have been synthesized with inner-cluster C−C bond lengths between 1.990 Å [4] and 1.931 Å [5] for which negative hyperconjugation between the nitrogen lone pairs and the (C−C) orbital has been held primarily responsible for causing CC bond elongation [3]. Recently, Mandal et al. demonstrated in a B3PW91-D3/cc-pVTZ study how fine tuning of negative hyperconjugation effects can result in even longer C−C bonds as in the case of amino oxide-o-carborane and di-N,N-dimethylamino-o-carborane [12].
In contrast to the vast number of experimental and theoretical studies, the relationship between CC bond elongation and the intrinsic strength of the CC bond is not well established, mainly caused by the lack of a reliable intrinsic bond strength measure which is required to systematically quantify the CC bond strength in these systems. Although bond dissociation energies (BDE)s and bond dissociation enthalpies (BDH)s play a fundamental role in determining chemical reactivity and selectivity [36,37,38] their use as bond strength measures is questionable. BDEs/BDHs are reaction parameters that include all changes taking place during the dissociation process. Accordingly, they include any (de)stabilization effects of the fragments to be formed, reflecting the energy needed for bond breaking, but also containing energy contributions due to geometry relaxation and electron density reorganization in the dissociation fragments. Therefore, the BDE/BDH is generally not a suitable measure for the intrinsic strength of a chemical bond and its use may lead to misjudgments, as documented in the literature [8,39,40,41,42,43,44,45]. Also the bond length is not always a qualified bond strength descriptor [46,47]. A handful of cases have been reported illustrating that a shorter bond is not always a stronger bond [48,49,50,51,52].
In this situation the local vibrational mode analysis (LMA), originally introduced by Konkoli and Cremer [53,54,55,56,57], offers an attractive alternative by providing local vibrational stretching force constants () as an ideal measure of the intrinsic strength of a bond and/or weak chemical interaction [58] including ultra long C−C bonds [11].
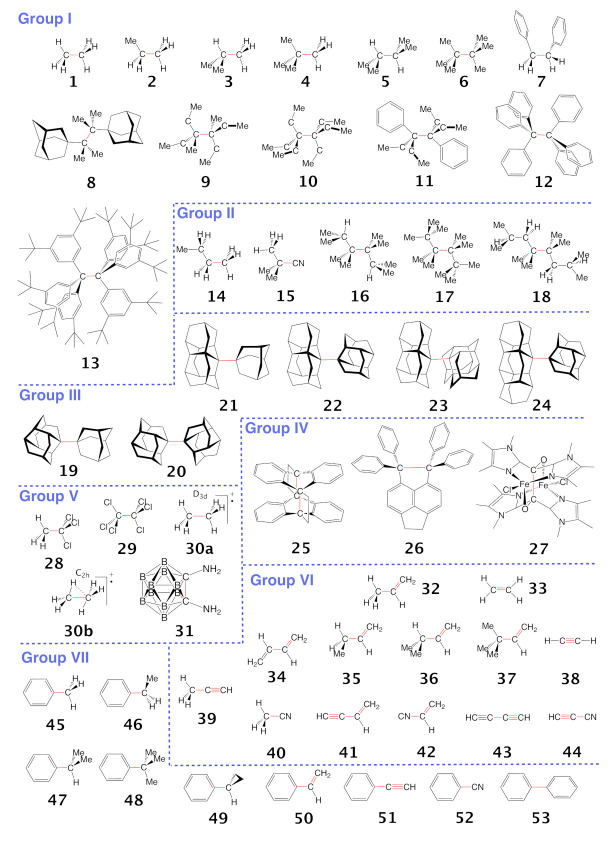
We applied in this work LMA supported by natural bond orbital [59] and electron density [60,61] analyses to a diverse set of 53 molecules shown in Figure 1, possessing long C−C bonds representing distinct bonding scenarios to systematically assess the effect and interplay of steric, strain, and electronic factors leading to CC bond weakening. Molecules 1–53 are categorized into seven groups Group I–Group VII and targeted CC bonds are indicated by red coloration. The C−C bonds of Group I molecules (1–13) and Group II molecules (14–18) are exposed to increasing steric repulsion as the bulkiness of substituents increases. Group III molecules (19–24) represent different diamondoid configurations. Group IV molecules (25–27) represent both strained and clamped C−C bonds. Molecules 28–31 of Group V reflect electronic effects on the C−C bond. Group VI molecules (32–44) and Group VII molecules (45–53) contain conjugated C−C bonds and CC double and triple bonds used as reference.
Figure 1.
Molecules 1–53 investigated in this work, categorized in Groups I–VII. Targeted CC single, double, and triple bonds are shown in red.
2. Computational Methods
Equilibrium geometries and vibrational frequencies for all molecules were derived using the B97X-D functional [62,63] in combination with Dunning’s aug-cc-pVTZ basis set [64]. The B97X-D functional was chosen as it has proven to reliably describe weak (long-range) intermolecular interactions covering the diverse range of molecules considered [62,65,66,67]. The aug-cc-pVTZ basis set was applied as the augmented diffuse basis functions describe long range effects [68,69]. All DFT calculations were performed with the Gaussian 16 Rev. program package [70]. Geometry optimizations were conducted with an ultra fine grid integration and tight convergence criteria. BDHs were calculated for the target molecules using the Gaussian-4 (G4) composite method [71,72,73,74]. G4 is known for providing BDH values which are comparable to experimental results. Further, to verify the accuracy of the chosen methods, calculated C−C bond lengths and BDHs were compared with their experimental counterparts.
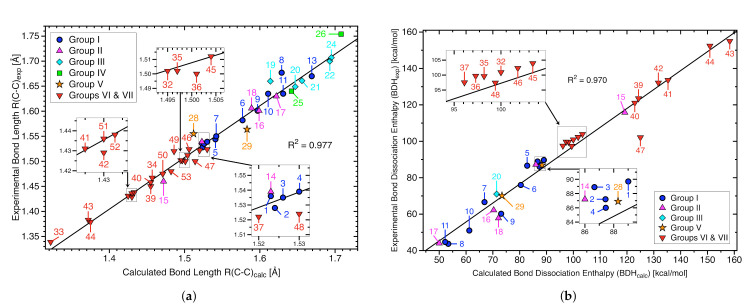
Considering the diversity of C−C bonds investigated in this work the agreement between calculated and experimental C−C bond lengths (Figure 2a, = 0.977) and calculated and experimental BDH values (Figure 2b, = 0.970) is satisfactory. It has to be noted that the experimental bond lengths were obtained by different techniques, at different temperatures, and in different environments leading to variations up to 0.035 Å. A comprehensive compilation of experimental bond lengths is provided in the Supporting Information, Table S1. This data includes electron diffraction, x-ray diffraction, microwave spectroscopy, and infrared spectroscopy data. A comprehensive summary of experimental BDH values are compiled in the Supporting Information, Table S2.
Figure 2.
(a) Comparison between calculated and experimental C−C bond lengths for Group I–Group VII molecules (for available experimental bond lengths). The solid black line indicates a linear fit for the targeted C−C bonds; (b) corresponding correlation between BDH and BDH (for available experimental dissociation energies).
Second order perturbation stabilization energies (), due to charge transfer events (i.e., orbital interactions), were retrieved via natural bond orbital (NBO) analysis through the application of the NBO6 program [75,76]. Electron densities () and energy densities () at CC bond critical points were determined with the AIMAll package [77]. The nature of the CC bonds was characterized following the Cremer-Kraka criterion, which implies that covalent bonding is characterized by a negative energy density, i.e., < 0 whereas electrostatic interactions are indicated by positive energy density values, i.e., > 0 [78,79,80]. Following geometry optimization and normal mode analysis, LMA was employed to quantify the intrinsic strength of the targeted CC bonds utilizing the LModeA software [58,81]. A comprehensive discussion of the underlying theory of LMA is provided in Reference [58], therefore in the following only a summary of the essential features are given.
Vibrational spectroscopy offers detailed information on the electronic structure of a molecule and its chemical bonds as encoded in the normal vibrational modes, ready to be deciphered. However, normal vibrational modes in a polyatomic molecule tend to couple, therefore they cannot be directly used to derive an intrinsic bond strength measure [82,83]. There are two coupling mechanisms between normal vibrational modes, mass coupling and electronic coupling. The electronic coupling can be eliminated via the Wilson GF-matrix formalism [82,83,84,85], i.e., by solving the secular equation of vibrational spectroscopy, which is a standard procedure in all quantum chemistry package calculating normal vibrational frequencies and corresponding normal modes. The vibrational secular equation expressed in terms of ) internal coordinates ; (: number of translations and rotations; 6 for nonlinear and 5 for linear molecules) is given by [82]
| (1) |
is the force constant matrix expressed in terms of internal coordinates , G is the Wilson G matrix [82], also called the “inverse kinetic energy” matrix. The eigenvector matrix D is comprised of vibrational eigenvectors d ( = 1,...,) and the diagonal matrix contains the vibrational eigenvalues ( = 4, c = constant for the speed of light and = harmonic vibrational frequencies of the normal mode vectors expressed in cm). Solving Equation (1) the diagonal normal force constant matrix = is obtained,
| (2) |
where is a vector that collects normal coordinates [86]. It is important to note that the diagonalization of the force constant matrix , i.e., transforming to normal coordinates [87,88,89] eliminates the off-diagonal coupling force constant matrix elements and in this way the electronic coupling [82]. However, it does not eliminate the kinematic (mass) coupling which often has been overlooked. Konkoli and Cremer solved this problem by introducing a mass-decoupled analogue of the Wilson equation [53,54,55,56] resulting in local vibrational modes () that are free from any mode-mode coupling
| (3) |
where represents the local mode vector that is affiliated with the n-th internal coordinate describing the local mode n. To each local mode a a local mode force constant can be assigned
| (4) |
and a local vibrational frequency
| (5) |
where corresponds to a diagonal element of the Wilson G matrix.
There is a 1:1 relationship between the normal vibrational modes and each complete, non-redundant set of local vibrational modes via an adiabatic connection scheme (ACS) [90], which can be considered as the most important milestone of the local mode theory; (i) it proves the physical relevance of local vibrational modes and (ii) it forms the basis for the decomposition of each normal mode into local mode contributions, providing a new comprehensive way to analyze vibrational spectra [58]. Any normal vibrational mode can be decomposed into local mode contributions [55,57] leading to a detailed analysis of the vibrational spectrum and a wealth of information about structure and bonding [91,92].
Local mode force constants, contrary to normal mode force constants are independent of the choice of the coordinates used to describe the molecule in question [90,93,94]. They are sensitive to differences in the electronic structure (e.g., caused by changing a substituent), and because they are, in contrast to frequencies, independent of the atomic masses, they capture pure electronic effects. In their landmark paper, Zou and Cremer [95] provided the important proof that the local stretching force constant (AB) reflects the intrinsic strength of the bond/interaction between two atoms A and B being described by an internal coordinate . Replacing the calculated vibrational frequencies in Equation (5) with measured fundamental frequencies leads to experimentally based local mode force constants [57] including anharmonicity effects not being captured by calculated harmonic force constants [91,96]. This important feature opens LMA to the experimental vibrational spectroscopists. For the comparison of larger sets of values, the use of a relative bond strength order BSO n is more convenient. Both are connected according to the generalized Badger rule derived by Cremer, Kraka, and co-workers [39,93] via the following power relationship:
| (6) |
(For simplification, in the reminder of the manuscript represents i.e., = .) The constants a and b are calculated from values of two reference compounds with known BSO n values and the requirement that for a zero force constant the corresponding BSO n value is zero. For the CC bonds investigated in this work, ethane (1) and ethene (33) were used as references with assigned BSO n values of 1.0 and 2.0, respectively [48]. The b97xd/aug-cc-pVTZ model chemistry utilized in this work leads to a = 0.3135 and b = 0.8062, approximately.
3. Results and Discussion
Table 1 summarizes the calculated CC bond distances (R), experimental CC bond distances (R), calculated bond dissociation enthalpies (BDH), experimentally determined bond dissociation enthalpies (BDH), local stretching force constants (), local mode vibrational frequencies (), bond strength orders (BSO n), electron densities (), and energy densities (H) for the targeted CC bonds of molecules 1–53. Figure 3a shows the BSO n values and local stretching force constants for all targeted CC bonds of molecules 1–53 and Figure 3b exhibits the corresponding values for the targeted C−C bonds.
Table 1.
Summary of geometry, calculated bond distances (), experimental bond distances (), calculated bond dissociation enthalpies (BDH), experimental calculated bond dissociation enthalpies (BDH), vibrational spectroscopy data, electron densities (), and energy densities () of targeted CC bonds for molecules 1–53 .
| # | sym | bond | BDH | BDH | BSO n | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | D3d | C−C | 1.523 | 1.536 [97] | 89.0 | 89.7 [98] | 4.216 | 1092 | 1.000 | 1.659 | −1.431 |
| 2 | C2v | C−C | 1.524 | 1.528 [99] | 87.4 | 87.2 [98] | 4.160 | 1085 | 0.989 | 1.671 | −1.443 |
| 3 | C3v | C−C | 1.526 | 1.535 [100] | 86.7 | 88.9 [98] | 4.092 | 1076 | 0.976 | 1.675 | −1.442 |
| 4 | T | C−C | 1.530 | 1.539 [26] | 87.5 | 86.0 [98] | 3.997 | 1063 | 0.958 | 1.669 | −1.423 |
| 5 | C2h | C−C | 1.541 | 1.544 [25] | 82.8 | 86.6 [98] | 3.786 | 1035 | 0.917 | 1.645 | −1.369 |
| 6 | D3 | C−C | 1.577 | 1.582 [25] | 80.4 | 76.0 [98] | 3.229 | 956 | 0.807 | 1.544 | −1.181 |
| 7 | C2 | C−C | 1.542 | 1.550 [101] | 66.9 | 66.6 [98] | 3.675 | 1020 | 0.895 | 1.601 | −1.322 |
| 8 | C2 | C−C | 1.629 | 1.677 [18] | 53.4 | 43.7 [102] | 2.414 | 826 | 0.639 | 1.387 | −1.925 |
| 9 | C1 | C−C | 1.597 | 1.601 [103] | 73.1 | 60.2 [104] | 2.888 | 904 | 0.737 | 1.481 | −1.079 |
| 10 | C2 | C−C | 1.611 | 1.635 [103] | 61.2 | 51.0 [104] | 2.693 | 873 | 0.697 | 1.443 | −1.016 |
| 11 | C2 | C−C | 1.631 | 1.635 [105] | 52.2 | 44.7 [105] | 2.290 | 805 | 0.611 | 1.371 | −1.918 |
| 12 | D2 | C−C | 1.699 | - | 16.6 | - | 1.518 | 678 | 0.439 | 1.188 | −1.663 |
| 13 | S6 | C−C | 1.669 | 1.670 [106] | 33.9 | - | 1.919 | 737 | 0.526 | 1.275 | −1.830 |
| 14 | C2h | C−C | 1.523 | 1.539 [26] | 86.0 | 87.2 [98] | 4.177 | 1087 | 0.993 | 1.672 | −1.447 |
| 15 | C3v | C−CN | 1.472 | 1.460 [107] | 119.2 | 115.8 [98] | 4.432 | 1120 | 1.041 | 1.787 | −1.852 |
| C−C | 1.535 | - | - | - | 3.915 | 1052 | 0.942 | 1.644 | −1.388 | ||
| 16 | C2 | C−C | 1.599 | 1.601 [103] | 70.3 | 62.2 [106] | 2.853 | 898 | 0.730 | 1.477 | −1.070 |
| 17 | C2 | C−C | 1.622 | 1.630 [18] | 50.0 | 44.0 [106] | 2.509 | 842 | 0.658 | 1.410 | −1.965 |
| 18 | C2 | C−C | 1.589 | 1.606 [103] | 72.1 | 57.8 [106] | 3.050 | 929 | 0.770 | 1.506 | −1.119 |
| 19 | C1 | C−C | 1.614 | 1.660 [19] | 78.6 | - | 2.792 | 889 | 0.717 | 1.427 | −1.996 |
| 20 | C1 | C−C | 1.647 | 1.647 [18] | 71.4 | ≈ 71 [18] | 2.401 | 824 | 0.635 | 1.331 | −1.855 |
| 21 | C1 | C−C | 1.656 | 1.659 [18] | 64.3 | - | 2.245 | 797 | 0.602 | 1.310 | −1.824 |
| 22 | C1 | C−C | 1.693 | 1.704 [18] | - | - | 1.874 | 728 | 0.521 | 1.218 | −1.694 |
| 23 | C1 | C−C | 1.787 | - | - | - | 1.142 | 568 | 0.351 | 1.014 | −1.465 |
| 24 | C1 | C−C | 1.695 | 1.707 [18] | - | - | 1.861 | 726 | 0.519 | 1.211 | −1.687 |
| 25 | D2h | C−C | 1.642 | 1.640 [108] | - | - | 2.411 | 826 | 0.637 | 1.317 | −1.857 |
| 26 | C1 | C−C | 1.708 | 1.754 [31] | - | - | 1.788 | 711 | 0.502 | 1.153 | −1.620 |
| 27 | C2h | C−C | 1.651 | - | - | - | 1.591 | 671 | 0.456 | 1.347 | −1.876 |
| 28 | C3v | C−C | 1.512 | 1.516 [109] | 86.9 | 88.3 [98] | 4.154 | 1084 | 0.988 | 1.747 | −1.615 |
| 29 | D3d | C−C | 1.583 | 1.564 [110] | 73.4 | 70.1 [98] | 2.944 | 913 | 0.749 | 1.575 | −1.181 |
| 30a | D3d | C−C | 1.935 | - | 41.2 | - | 0.894 | 503 | 0.286 | 0.523 | −1.194 |
| 30b | C2h | C−C | 1.591 | - | 42.7 | - | 0.971 | 524 | 0.306 | 1.272 | −1.929 |
| 31 | C2v | C−C | 1.930 | - | - | - | 0.604 | 413 | 0.209 | 0.742 | −1.242 |
| 32 | Cs | C−C | 1.495 | 1.501 [99] | 100.0 | 100.9 [98] | 4.575 | 1138 | 1.068 | 1.770 | −1.637 |
| C=C | 1.324 | 1.336 [99] | - | - | 9.821 | 1667 | 1.997 | 2.444 | −1.197 | ||
| 33 | D2h | C=C | 1.322 | 1.339 [97] | 173.9 | 172.2 [98] | 9.961 | 1679 | 2.000 | 2.449 | −1.214 |
| 34 | C2h | C−C | 1.457 | 1.467 [111] | - | 116.0 [98] | 5.119 | 1203 | 1.169 | 1.920 | −1.934 |
| C=C | 1.329 | 1.349 [111] | - | - | 9.537 | 1642 | 1.931 | 2.426 | −1.145 | ||
| 35 | C1 | C−C | 1.497 | 1.502 [112] | 98.2 | 99.6 [98] | 4.484 | 1126 | 1.051 | 1.776 | −1.639 |
| C=C | 1.324 | 1.340 [112] | - | - | 9.804 | 1665 | 1.975 | 2.443 | −1.195 | ||
| 36 | Cs | C−C | 1.501 | 1.500 [113] | 97.3 | 99.7 [98] | 4.382 | 1113 | 1.032 | 1.775 | −1.628 |
| C=C | 1.324 | 1.341 [113] | - | - | 9.811 | 1666 | 1.976 | 2.443 | −1.198 | ||
| 37 | Cs | C−C | 1.520 | 1.522 [103] | 96.1 | 97.5 [98] | 4.179 | 1087 | 0.993 | 1.749 | −1.573 |
| C=C | 1.324 | - | - | - | 9.765 | 1662 | 1.968 | 2.438 | −1.188 | ||
| 38 | D∞h | C≡C | 1.194 | 1.208 [97] | 228.1 | 229.9 [98] | 17.777 | 2243 | 3.190 | 2.894 | −1.700 |
| 39 | C3v | C−C | 1.455 | 1.450 [26] | 124.3 | 123.5 [98] | 5.254 | 1219 | 1.194 | 1.844 | −1.895 |
| C≡C | 1.196 | 1.207 [26] | - | - | 17.515 | 2226 | 3.153 | 2.862 | −1.742 | ||
| 40 | C3v | C−C | 1.455 | 1.458 [99] | 122.9 | 121.1 [98] | 5.141 | 1206 | 1.173 | 1.828 | −1.931 |
| 41 | Cs | C−C | 1.425 | 1.431 [26] | 135.3 | 133.6 [98] | 5.777 | 1278 | 1.289 | 1.974 | −1.151 |
| C=C | 1.329 | - | - | - | 9.564 | 1645 | 1.936 | 2.418 | −1.137 | ||
| C≡C | 1.199 | - | - | - | 17.264 | 2210 | 3.116 | 2.860 | −1.699 | ||
| 42 | Cs | C−C | 1.430 | 1.429 [114] | 131.7 | 132.1 [98] | 5.582 | 1256 | 1.254 | 1.938 | −1.141 |
| C=C | 1.327 | 1.339 [114] | - | - | 9.645 | 1656 | 1.957 | 2.428 | −1.166 | ||
| 43 | D∞h | C−C | 1.372 | 1.383 [26] | 158.3 | 155.0 [98] | 7.406 | 1447 | 1.575 | 2.142 | −1.517 |
| C≡C | 1.199 | 1.209 [115] | - | - | 17.160 | 2203 | 3.101 | 2.858 | −1.684 | ||
| 44 | C∞v | C−C | 1.375 | 1.379 [116] | 150.9 | 152.4 [98] | 7.348 | 1442 | 1.565 | 2.122 | −1.491 |
| C≡C | 1.196 | 1.204 [116] | - | - | 17.470 | 2223 | 3.146 | 2.878 | −1.708 | ||
| 45 | Cs | C−C | 1.504 | 1.512 [117] | 103.4 | 103.9 [98] | 4.528 | 1132 | 1.059 | 1.745 | −1.581 |
| 46 | Cs | C−C | 1.506 | 1.524 [118] | 101.8 | 102.3 [98] | 4.446 | 1121 | 1.044 | 1.751 | −1.585 |
| 47 | Cs | C−C | 1.514 | 1.500 [119] | 125.0 | 102.1 [98] | 4.274 | 1100 | 1.011 | 1.732 | −1.540 |
| 48 | Cs | C−C | 1.530 | 1.524 [120] | 99.4 | 97.4 [98] | 3.966 | 1059 | 0.952 | 1.681 | −1.439 |
| 49 | Cs | C−C | 1.486 | 1.520 [121] | - | 111.9 [122] | 4.751 | 1159 | 1.101 | 1.815 | −1.708 |
| 50 | Cs | C−C | 1.471 | 1.475 [123] | - | 116.9 [98] | 4.919 | 1180 | 1.132 | 1.868 | −1.820 |
| C=C | 1.327 | - | - | - | 9.549 | 1644 | 1.933 | 2.427 | −1.154 | ||
| 51 | C2v | C−C | 1.430 | 1.436 [124] | - | 140.7 [98] | 5.750 | 1275 | 1.284 | 1.961 | −1.112 |
| C≡C | 1.198 | - | - | - | 17.286 | 2211 | 3.119 | 2.860 | −1.707 | ||
| 52 | C2v | C−C | 1.433 | 1.438 [124] | - | 132.7 [98] | 5.569 | 1255 | 1.252 | 1.929 | −1.116 |
| 53 | D2 | C−C | 1.482 | 1.480 [125] | - | 118.0 [98] | 4.850 | 1171 | 1.120 | 1.840 | −1.752 |
a Calculated and experimentally determined CC bond distances R(CC) in Å. CC local stretching force constants (ka) in mdyn/Å, local vibrational mode frequencies (ωa) in cm−1, and bond strength order represented by BSO n values. Calculated and experimentally determined bond dissociation enthalpies (BDH) in kcal/mol. More detailed information on the experimental values is provided in the Supporting Information, Tables S1 and S2. The electron density at the CC bond critical point rb in e/Å3 and the energy density at the CC bond critical point Hb in Hartree/Å3. Calculated BDH values were computed with G4 and all other values were calculated with ωB97X-D/aug-cc-pVTZ. “-” no data available. The numbers within the table correspond to the molecules shown in Figure 1.
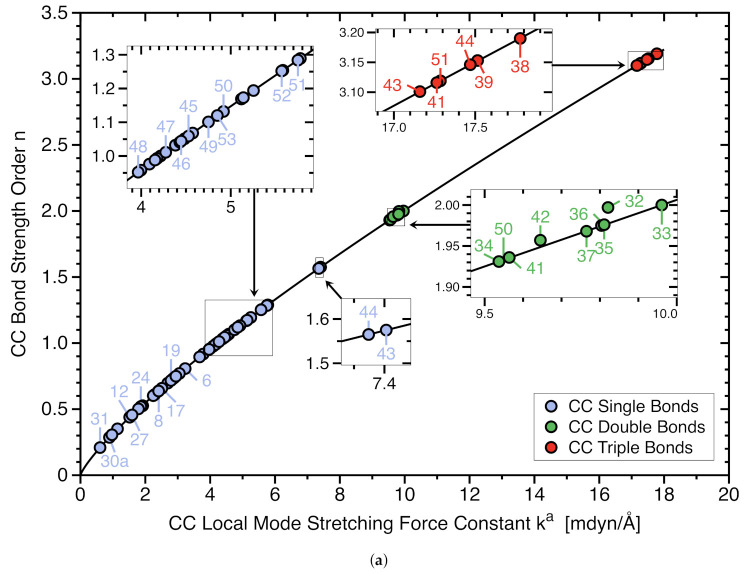
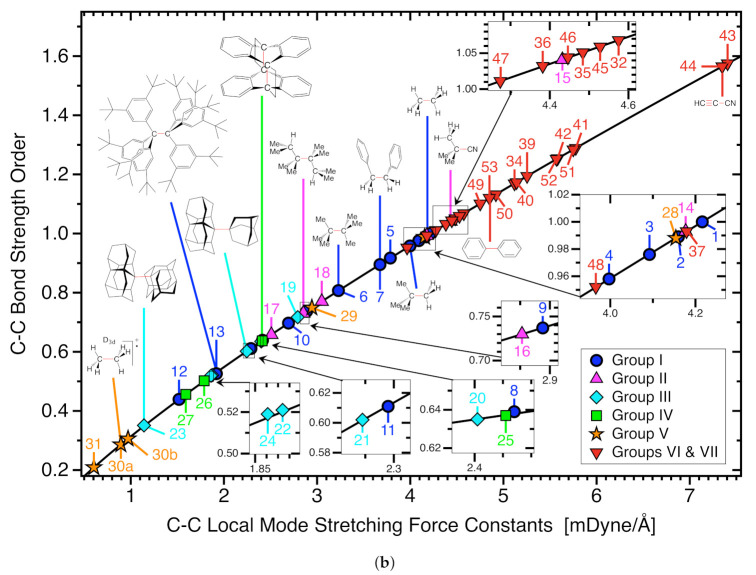
Figure 3.
(a) BSO n values of all targeted CC single, double, and triple bonds for Group I–Group VII molecules, obtained with the power relationship BSO n = 0.3135 () utilizing local mode stretching force constants (CC). Calculated at the B97X-D/aug-cc-pVTZ level of theory. See text and Equation (6) for the derivation of the power relationship; (b) corresponding power relationship for all C−C bonds.
As depicted in Figure 3a the CC single bonds of our set of 53 molecules show the largest variation in bond strength (BSO n(C−C) values from to 0.21 to 1.58) reflecting the diversity of our test set whereas as expected, the variation of the bond strength of the double bonds (BSO n(C=C) values from 1.93 to 2.00), and that for the triple bonds is relatively small (BSO n(C≡C) values from 3.10 to 3.15), in line with the fact that is more difficult to modulate a CC double and triple bond than a CC single bond. The gap between single and double bonds (0.35 BSO n units) is smaller than that between double and triple bonds (1.10 BSO n units), confirming that the power relationship is in compliance with general organic chemistry rules.
The focus in Figure 3b is on CC single bonds. As expected, BSO n values larger than one (ethane, 1) are found for Group VI and VII members with conjugated C−C bonds. 1,3-butadiyne 43 and cyanoethyne 44 have the strongest C−C bonds with BSO n values of 1.575 and 1.565, respectively. The middle range (BSO n values between 0.5 and 1) representatives of Group I - Group V are found, revealing that different scenarios can lead to CC bond elongation. On the low end of the bond strength spectrum (BSO n values > 0.5) the diiron(II) bis(1-methyl-4,5-dimethylimidazolyl)pinacolate bis-chlorido complex 27 (BSO n = 0.456, weakest C−C bond within Group IV), hexaphenylethane 12 (BSO n = 0.439, weakest C−C bond within Group I), 2-(2-triamantyl)triamantane 23 (BSO n = 0.351, weakest C−C bond within Group III) are located. The overall weakest C−C bonds are found for Group V members representing electron deficient bonding; ethane radical cation D3d 30a (BSO n = 0.286) and C2h 30b (BSO n = 0.306) and di-N,N-dimethylamino-o-carborane 31 (BSO n = 0.209). It has to be noted that whereas 31 has the weakest C−C bond, 30a has the longest C−C bond of 1.935 Å compared with the R(C−C) of 1.930 Å for 31.
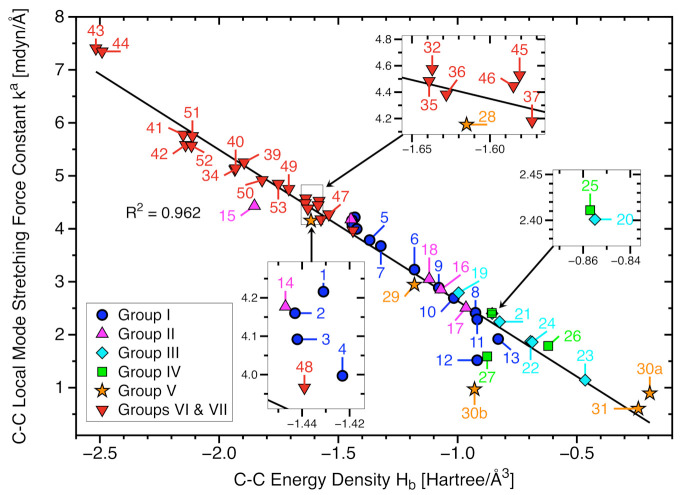
Figure 4 confirms that all targeted C−C bonds of our set of 53 molecules, including the weakest such as 30a and 31, are covalent in nature according to the Cremer-Kraka criterion of covalent bonding, i.e., all values are smaller than zero (see also Table 1). The correlation between the local stretching force constants of targeted C−C bonds and the corresponding energy density is moderate ( = 0.962), reflecting that the local force constant picks up the electronic environment of a bond whereas reflects the electronic structure just at a single point, i.e., the bond critical points r. [58]. Nevertheless, a general trend can be visualized; the C−C bond strength decreases alongside a decrease in covalent character.
Figure 4.
Local mode stretching force constants (C−C) versus energy density for all C−C bonds (Groups I through VII). B97X-D/aug-cc-pVTZ level of theory.
3.1. Bond Dissociation Enthalpies and Bond Lengths as Bond Strength Measure
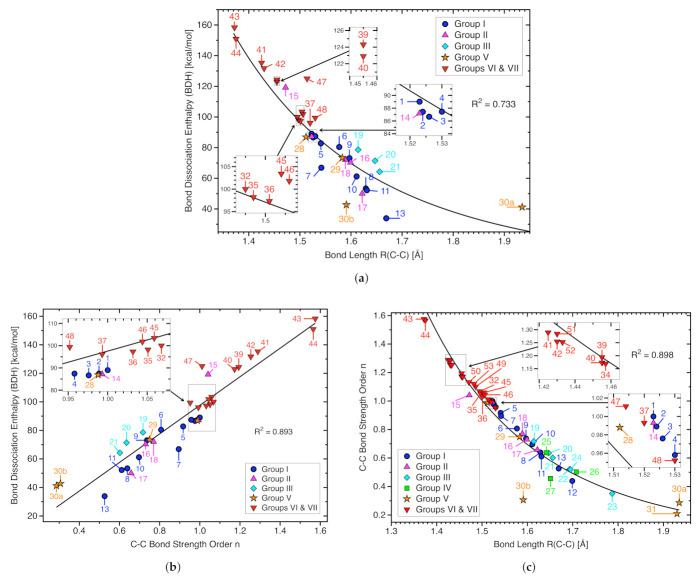
Zavitsas [103] reported a linear relationship between CC bond lengths and bond dissociation energies (BDE)s for strained and unstrained compounds, which predicts a maximum C−C bond length of 1.75 Å. However, this simple relationship fails for C−C bonds in more complex situations, such as for compounds with extraordinary ring strain or steric congestion [19,51,126]. In Figure 5 the corresponding calculated BDH and R(C−C) values for our set of 53 molecules are compared. In contrast to Zavitsas, we find a qualitative exponential relationship ( = 0.733) with several outliers such as sterically crowed molecules 7 and 13 in line with previous observations [19,51,126] and the ethane radical cations 30a and 30b. In particular 30b with a bridging hydrogen bond situation falls off the curve.
Figure 5.
(a) Correlation between calculated bond dissociation enthalpies and calculated C−C bond lengths. BDH values calculated with the composite G4 method and R(C−C) values at the B97X-D/aug-cc-pVTZ level of theory; (b) correlation between and BSO n(C−C). values were obtained using G4 and BSO n(C−C) values calculated at the B97X-D/aug-cc-pVTZ level of theory; (c) Relationship between BSO n(C−C) and R(C−C) calculated at the B97X-D/aug-cc-pVTZ level of theory.
In Figure 5b values are correlated with the C−C bond strength orders BSO n(C−C). Although there is some trend that the BDH value increases with increasing C−C bond strength, the overall correlation is moderate (R = 0.893), showing that the BDH is not a good measure for the intrinsic strength of the CC bond because it includes the overall effects of bond breakage, as discussed in the introduction. This concerns in particular crowded molecules with larger possibilities for geometry and electron density reorganization of the fragments such as 7, 13, and 15. Figure 5c correlates BSO n(C−C) values with calculated C−C bond lengths. Again there is some trend that shorter C−C bonds are stronger bonds (R = 0.898). However there are also some outliers, such as the organometallic compound 27 and the ethane radical cation 30b representing the special case of hydrogen bridging. This clearly shows that a comprehensive discussion of the intrinsic CC bond strength is better based on local vibrational modes and corresponding bond strength orders, which is pursued in the following sections focusing on trends within the individual groups.
3.2. C−C Bonds of Group I
The central C−C bonds of Group I molecules (1–13) are subjected to increasing levels of steric congestion as substituent bulkiness is incremented from 1 to 13. The C−C bond lengths for molecules 1–11 and 13 range between 1.523 Å to 1.669 Å, where the shortest C−C bond length is exhibited by ethane (1). The C−C bond lengths mentioned above are consistent with experimentally derived values (See Table 1 and Figure 2a). As the methylation of ethane proceeds from 1 to 6 the elongation of the C−C bond progresses from 1.523 (1) to 1.577 mdyn/Å (5) alongside bond weakening depicted by decreases in BSO n values from 1.000 (1) to 0.807 mdyn/Å (6) (See Figure 3). The overall stabilization energy values (), due to the hyperconjugation (i.e., charge transfer) predominately occurring from (C−H) →(C−C), reveal increasing hyperconjugation as the methylation of ethane proceeds from 1 to 6 ( = 0.00 (1), 3.73 (2), 7.74 (3), 13.29 (4), 14.84 (5), 28.14 kcal/mol (6)). Further, the orbital occupancy (e) of the central (C−C) orbital of molecules 1–6 decreases as the methylation proceeds (1.997 to 1.960 e) while the occupancy of the (C−C) orbital steadily increases (0.00 to 0.05 e). Thus, the target C−C bonds of 1–6 increase and decrease in length and strength due to increasing hyperconjugation between (C−H) and (C−C), the increase in hyperconjugation is responsible for the parallel relationship between the decrease of (C−C) electron occupancy and increase of (C−C) electron occupancy.
The C−C bond lengths for molecules 5 and 7 are virtually the same with BSO n values of 0.917 ( = 3.786 mdyn/Å) and 0.895 ( = 3.675 mdyn/Å). It is noted that the gauche configuration for 1,2-diphenylethane (7) results in the most stable rotational isomer (by 1.10 kcal/mol); this result indicates the presence of -stacking which may contribute towards the shortening of the central C−C bond. Moreover, the central C−C bond of 7 is longer than that of 5 as the steric repulsion between the two phenyl groups of 7 outweighs that which occurs between the four methyl groups of system 5. The C−C bond of 6, in comparison to that of 5 and 7, is forced to a greater distance due to the steric crowding of the six methyl groups (See Table 1). Further, the electron density value () at the C−C bond critical point of 6 is less than that of both 5 and 7 while the of 5 is greater than that of 6 and 7 ( = 1.645 (5), 1.544 (6), 1.601 e/Å (7)). The C−C bond of molecule 6 is longer and weaker than that of 5 and 7 as a result of weaker covalent bond character indicated by a less negative energy density value at the C−C bond critical point ( = −1.369 (5),−1.181 (6), −1.322 h/Å (7)), the decrease in the covalent bond character is reflected from a smaller (C−C) occupancy (1.963 (5), 1.960 (6), and 1.974 e (7)) together with a larger (C−C) occupancy (0.028 (5), 0.050 (6), and 0.021 e (7)).
Targeted C−C bonds within molecules 8–13 range in length between values of 1.597 and 1.699 Å as BSO n measures fluctuate amidst values of 0.439 and 0.737, where the C−C bond length elongates as the bond strength decreases. The repulsive forces between the adamantane groups of 8 enable the C−C bond length to become longer in contrast to molecules 9 and 10, where methyl and/or only ethyl groups are present; the repulsive forces between substituents of 9 and 10 do not exceed that occurring between the adamantane groups of 8 as reflected by the shorter C−C bond length values for 9 and 10 (R = 1.629 (8), 1.597 (9), 1.611 Å (10)). The steric repulsion between the phenyl and ethyl substiuents of 11 is greater than that occurring between adamantane substituents of 8 as indicated by from the longer C−C bond length for 11 (R = 1.631 Å). The electron density values of 8–13 decrease in parallel to C−C bond lengthening and weakening (see Table 1) as well as the magnitude of corresponding energy density values, these results shows that longer and weaker C−C bonds concur as C−C covalent bond character diminishes (see Table 1 and Figure 2b).
Molecules 12 and 13 involve complete phenylation of ethane, in the case of 13 methyl groups replace two hydrogen atoms on every phenyl group, increasing steric crowding even further. In contrast to 13, which has been synthesized and characterized [106,127], 12 has not been isolated so far being in line with the small calculated BDH value of 16.6 kcal/mol compared to that of 13 (BDH = 33.9 kcal/mol). It seems counter-intuitive that for the less crowded hexaphenylethane 12 a longer C−C bond is found than for the hexakis-(3,5-di-tert-butylphenyl)ethane 13, R = 1.699 versus 1.669 Å and that 13 is more stable. Schreiner et al. [127] attribute the stabilization of the more crowed compound to London dispersion through the increasing polarizability of alkyl substituents and the fact that conformationally more flexible hydrocarbon substituents introduce large unfavorable entropy contributions which help to stabilize these extraordinary bonding situations. This clearly shows that steric crowding, although being a key factor for CC bond elongation, strongly depends on the bonding environment. As a consequence, the introduction of even more sterically demanding substituents, such as adamantyl groups, could even lead to a further reduction of the central C−C bond length instead of the desired elongation.
3.3. C−C Bonds of Group II
Molecules 14–18 obtain C−C bond lengths ranging between values of 1.472–1.787 Å where BSO n values vary between 0.604–0.993. The di-methylation of ethane in a trans configuration (14) results in a slightly shorter bond than that of the mono-methylated equivalent (2) (See Table 1). Molecule 14 obtains a slightly shorter and stronger than 2 due to a slightly greater bond covalent character ( = −1.443 (2), −1.447 (14) Hartree/Å) attributed to the larger amount of allocated electron density at the C−C bond critical point (See Table 1). Comparing the C−C bond lengths within systems 4 (2-methylpropane) to 15 (2-cyano-2-methylpropane) reveals that the the replacement of three hydrogen atoms with a nitrogen atom causes the C−C bond to shorten from 1.530 to 1.472 Å, both bond length values being in good agreement with experimental results (See Table 1). The nitrogen atom of 15 results in C−C charge values of −1.160 and +0.295 e, where the positive charge value is that of the carbon atom directly linked to the nitrogen atom (See Figure S1, Supporting Information). Because NBO C−C charges for 4 reflect repulsion between C−C atoms, unlike 15 where the charges denote attraction between CC atoms, the results reveal that the inductive through bond effect of nitrogen results in a the polarization of the C−C bond; the polarization of this bond causes the C−C bond to shorten further due to attractive forces between the carbon atoms. As a result of the attractive forces between carbon atoms of C−C within 15, with respect to that of 4, a larger covalent bond character results ( = −1.423 (4), −1.852 Hartree/Å (15)). Moreover, the C−C bond of 15 obtains a greater value of electron density at the C−C bond critical point in contrast to 4 (See Table 1). The enhancement of the covalent bond character for C−C bond of 15 causes the CC bond of 15 to be stronger than that of 4 (BSO n: 0.958 (4), 1.787 (15)).
The application of 4 methyl and 2 isopropyl groups (16) and 4 methyl and 2 tert-butyl groups (17) increases steric strain in contrast to the other systems of Group II, the increase in strain is reflected from longer C−C bond lengths of 1.599 (16) and 1.622 Å(17) which are the longest C−C bonds observed for Group II. Further, extending the carbon chain from six to eight carbons for a system with 4 methyl and 2 isopropyl groups, as represented by molecules 17 (2,2,3,3,4,4,5,5-octamethylhexane) and 18 (2,4,4,5,5,7-hexamethyloctane), results in a decrease of strain between functional groups (R(C−C) = 1.622 (17), 1.589 Å (18)). In general, C−C electron density values of 14–18 decrease alongside C−C bond elongation and weakening (see Table 1); as the electron density values decrease the energy density values at the C−C bond critical point become less negative. Thus, as for Group I, the C−C bonds for Group II molecules become weaker and longer as bond covalency decreases (See Table 1 and Figure 2b).
3.4. C−C Bonds of Group III
Fokin, Schreiner, and others [27,128,129] synthesized, characterized, and computationally investigated a series of homo and heterodimeric diamondoid compounds connected by exceptionally long C−C bonds. These adamantyl dimers are exposed to the inherent conflict of repulsion between the two extremely bulky groups only held together a single C−C bond. Despite the exceptionally long central bond C−C, these compounds are found to have exceptional stability, persisting at temperatures greater than 200 C which is primarily attributed to attractive London dispersion forces between these units caused by weak interactions between the hydrogen atoms on the cages on either side of the molecule [52,128,129]. Furthermore, the radical fragments resulting from homolytic cleavage are only capable of little geometry relaxation and rehybridization qualifying them as perfect test cases for exploring bond length bond dissociation energy relationships and challenging Zavitsas’ empirical relationship [103]. We included 1-(1-adamantyl)diamantane, 1-(1-diamantyl)diamantane, 2-(1-adamantyl)triamantane, 2-(1-diamantyl)triamantane, 2-(2-triamantyl)triamantane, and 2-(1-diamantyl)[121]tetramantane molecules (19–24) in this work, calculated with a larger basis set than previously published. Our model chemistry reproduces computational results well with one exception, compound 23, a theoretical compound with a record C−C bond length of 1.830 Å, which has evaded synthesis so far. However, the previously reported molecule 23 turns out to be a transition state of first order at our level of theory. There exists a more stable rotational isomer with a C−C length of 1.787 Å , which is −17.8 kcal/mol lower in energy, see Table 1. Although the C−C bond lengths of this isomer is 0.043 Å longer than that of the transition state, it still remains the longest C−C bond found for this group.
The calculated C−C bond lengths for complexes 19–22 and 24, ranging from 1.614 to 1.695 Å , are in good agreement with the experimental values, deviations range between 0.002–0.014 Å (see Figure 2b). As the sizes of interacting groups take up more space steric strain increases and is counterbalanced by increasing the C−C bond lengths as to maintain molecular stability. As C−C bonds of Group III molecules (19–24) become longer they become weaker as reflected by the local mode force constants which reduce from 2.792 mdyn/Å (molecule 19) to 1.142 mdyn/Å (molecule 23) and the corresponding BSO n values of 0.717 for 19 and 0.351 for 23. The weakening of the C−C bonds is in line with progressive bond destabilization observed via the values ranging from −0.996 Hartree/Å for 19 to −0.465 Hartree/Å for 23. It has to be noted that the strained adamantyl dimer 23 outperforms the strained hexaphenylethane 12 of Group I in terms of a longer C−C bond (R = 1.787 versus 1.699 Å ) and weaker C−C bond (BSO n = 0.351 versus 0.439). Overall these two groups show similar CC bond elongation effects as depicted in Figure 3b, outperforming Group II members.
3.5. C−C Bonds of Group IV
The members of this group are bianthracene-9,1-dimethylene, molecule 25, 1,1,2,2-tetraarylpyracene, molecule 26 in which one of the aliphatic five-membered rings (5MR)s annealed to a naphthalene chromophore is substituted by four bukly phenyl groups, and the diiron(II) bis(1-methyl-4,5-dimethylimidazolyl)pinacolate bis-chlorido complex, molecule 27. They represent a situation where the central C−C bond can no longer freely expand to counterbalance steric crowding because it is “clamped” in the molecular framework. Despite this obvious restriction, molecules 25–27 compete well with their Group I and Group III counterparts, as shown in Figure 3b. It also has to be noted that homolytic C−C bond breakage in these systems is hampered by the fact that the two fragments cannot easily separate, potentially leading to recombination. Therefore, it has been suggested that the bonded and non-bonded states in these systems are seamlessly connected in terms of the interatomic C−C distances [7].
Molecule 25 has a calculated C−C bond length of 1.642 Å. The result agrees well with the experimental value of 1.640 Å, obtained by Dougherty et al. [108], as well as a previously calculated value of 1.645 Å [30]. For 26, the calculated C−C length (1.708 Å) is much shorter than the experimental value of 1.754 Å, which was obtained via low temperature X-ray crystallography [7,31]. As discussed by the authors, this discrepancy could result from a triplet diradical with a considerably larger CC bond distance (3 Å) being in thermal equilibrium with the closed shell structure in the crystal at higher temperatures.
In line with the bond lengths the C−C bond of 25 is somewhat stronger than that of 26, as reflected by the BSO n values of 0.637 and 0.502, respectively. The NBO charges of the C atoms composing the C−C bond in 26 are slightly larger than those of C atoms composing the C−C bonds in 25 (−0.185 e versus −0.044 e respectively, see Figure S1, Supporting Information) leading to larger repulsive forces between C−C atoms in 26 adding to the larger steric congestion caused by the four phenyl substituents. Furthermore, the molecular framework of 26 allows the two carbon atoms to separate more than it is possible in 25 by widening the CCC bond angles at the C−C base of the substituted 5MR to 109.3 compared to 106.9 in the unsubstituted 5MR with a much smaller effect on CCC angle opposite to base, 116.3 compared to 116.0 for the unsubstituted 5MR. In line with observed bond length trends are the energy density values for 25 and 26 suggesting that the C−C bond of 26 is less covalent bond nature than the corresponding C−C bond of 25; ( = −0.620 Hartree/Å for 26 and −1.857 Hartree/Å for 25). These two examples clearly show the impact of the molecular framework on CC bond elongation.
Molecule 27 complements the group with organometallic compounds. As recently reported, Fe and Zn templated pinacol-type coupling leads to dinuclear metal complexes with ultra long central C−C bonds (R > 1.7 Å) being clamped by the organometallic framework [32,130]. For the diiron(II) bis(1-methyl-4,5-diphenylimidazolyl)pinacolate bis-chlorido complex a central C−C bond length of 1.730 Å was confirmed by both Xray structure and DFT calculations [32], which is much longer than a usual pinacolate type C−C [131]. It has been suggested that metal coordination contributes to stabilizing the weak C−C bond in the obtained cage structure. In order to make the calculations more feasible we simplified the complex by replacing the eight phenyl groups with methyl groups leading to the corresponding bis(1,4,5-trimethylimidazolyl)pinacolate complex 27, see Figure 1. This resulted in a stable molecule, with a C−C bond length of 1.651 Å, in close agreement with the C−C bond length of the protonated pinacolate compound discussed by Folkersma et al. [32]. The relatively large positive charge of 0.210 e (see Figure S1, Supporting Information) assists in pushing the two carbon atoms apart. We find a BSO n value of 0.456, identifying the targeted C−C bond in 27 as the weakest in Group IV showing the strong potential of organometallic frameworks hosting ultra long C−C bonds.
3.6. C−C Bonds of Group V
The overall theme of Group V systems is CC bond elongation via electron deficient bonding. Molecules 28–29 were chosen to evaluate if electron withdrawing halogen substituents can lead to CC bond elongation. 30 exploits a more drastic option, i.e., electron removal leading to a radical cation, and molecule 31 combines the clamped CC situation with negative hyperconjugative effects.
To evaluate electron withdrawing effects on the C−C bond length chlorinated ethane molecules 28 and 29 were investigated. For 28 we find a C−C bond that is 0.011 Å shorter than the corresponding C−C bond in 1. This value is in perfect agreement with the experimental value supporting the empirical rule of Sugie et al. [109], which suggests that addition of Cl atoms shortens generally a C−C bond. As reflected by the NBO charges of 28 (−0.638 e for the CH3 carbon versus −0.099 e for the CCl3 carbon as compared to −0.585 e for the carbon atoms of 1, see Figure S1, Supporting Information) chlorination of one methyl group leads to a polar C−C bond. However, although being shorter, the resulting C−C bond becomes weaker as reflected by a value of 4.154 mdyn/Å compared to 4.216 mdyn/Å for 1, whereas the value of −1.615 Hartree/Å compared to −1.431 Hartree/Å for 1 is in line with bond shortening. It is important to note that the local mode force constant as a second order property is a sensitive bond strength measure picking up subtile second order effects which are not shown in the energy density evaluated just at the bond critical point which describes the covalent character, whereas includes counterbalancing steric repulsion effects or C−C bond weakening via delocalization of charge from the Cl lone pair into the (C−C, i.e., the so-called negative hyperconjugation effect [132,133], or intramolecular halogen-halogen dispersion interaction [134]. Further details on the systematic chlorination of 1, including calculations with a DFT functional designed for the description of dispersion effects, is included in the Supporting Information. Full chlorination of ethane, as realized in hexachloroethane 29, results in C−C bond lengthening of 0.06 Å compared to 1, revoking Sugie’s rule [109]. The steric congestion of the six Cl atoms overrides the electron withdrawing effects showing that electronic effects may not always cooperate with steric effects. Therefore, a case by case investigation is necessary and the local mode force constant can serve as a helpful guide.
The next Group V representative is the ethane radical cation in which one electron is removed from 1 either out of the outer valence shell of the C−C or the C−H orbitals resulting in a diborane-like isomer of C symmetry, molecule 30b which is slightly lower in energy of 0.3 kcal/mol than a second isomer 30a with D symmetry [33,135,136]. In line with experimental data, we find that the C−C bond length of 1.591 Å is still close to that in 1. This is caused by H-bridge bonding, as revealed by the small C-C-H angles of 83.1 of the in-plane H-atoms. This leads to a unique CC bonding situation which is reflected by the fact that in most graphs shown in this work 30b appears as outlier as for example in Figure 4. In contrast, 30a yields an ultra-long bond of 1.935 Å, the longest C−C bond found for all molecules investigated in this work as also reflected by the smallest of value of −0.194 Hartree/Å. Intrigued by the strong bond lengthening effect of electron removal we also tested if this can be further increased by invoking steric strain. Therefore, we investigated potential radical cationic forms of 21 and 26. Upon removal of an electron, the diamondoid system 21 dissociates into two fragments. In the clamped radical cation 26, the single electron is delocalized over the entire molecule resulting in an increase of the C−C bond length from 1.708 Å to 1.709 Å , which cannot be considered meaningful. This example clearly shows that CC bond lengthening effects result from a complex interplay of electronic and steric effects and are not necessarily additive.
Di-N,N-dimethylamino-o-carborane, molecule 31 represents an interesting case for a clamped C−C bond which is, in addition, exposed to negative hyperconjucation. Li, Müller at al. synthesized a series of 1,2-diamino-o-carboranes with exceptionally long C−C bonds ranging between 1.627 and 1.931 Å depending on the amino substituents [5]. The longest C−C bond of 1.931 Å was found for the diphenyl compound. As a major factor for the CC bond elongation negative hyperconjucation between the nitrogen lone pair and the C−C orbitals was identified [5]. Recently, Mandal et al. calculated an even longer C−C bond of 2.011 Å using a B3PW91-D3/cc-pVTZ model chemistry [12] which seems to overshoot the C−C bond length [137]. We find a C−C bond length for 31 of 1.930 Å, slightly shorter by 0.005 Å than the C−C bond in the ethane cation 30a and in good agreement with the experimental data of Li, Müller at al. [5]. It is interesting to note that obviously two different effects, namely electron removal in 30a and a clamped C−C bond exposed to negative hyperconguation in 31 leads to a comparable CC bond elongations. However, this is not true for the bond strength as reflected by the local mode force constants ( = 0.894 mdyn/Å and BSO n = 0.286 for 31 compared with 0.604 mdyn/Å and BSO n = 0.209 for 30a) qualifying the C−C bond in 31 as the weakest of all molecules investigated in this work.
3.7. CC Reference Bonds, Group VI and VII
Group VI and VII members comprise a series of molecules with hyperconjugated C−C bonds making them shorter and stronger as well as double and triple reference bonds. These molecules are included in order to validate the applicability of (C−C) as a bond strength measure stretching from long to short C−C bonds. The C−C bonds in Group VI are in conjugation with a vinyl group and an alkyne (molecules 32, 34–37) or a cyano group (molecules 39–44). Group VII C−C bonds, molecules 45–53, are in conjugation with a phenyl group (see Figure 1).
The C−C bond lengths of Group VI and Group VII molecules (32–52) range from 1.372 to 1.530 Å, where the shortest and longest C−C bond lengths are reflected by molecules 43 and 48. The C−C bond lengths for molecules of Groups VI and Group VII fall in line with experimentally determined measures (See Table 1 and Figure 2a). The BSO n(C−C) values Group VI and Group VII molecules (32–52) range from 0.952 to 1.575, where the weakest and strongest C−C bonds belong to molecules 43 and 48. The shorter C−C bond of 43 obtains the largest value of energy density allocated at the C−C bond critical point region with regard to the targeted C−C bonds of molecules composing Groups VI and VII (See Table 1). Moreover, the C−C bond of molecule 43 is shorter and stronger than all other targeted C−C bonds for molecules of Groups VI and VII as 43 possesses the largest covalent C−C bond character (See Table 1). System 48 involves a trimethylated carbon attached to a carbon atom of a phenyl group, due to the presence of three methyl groups, which take up the most space out of all other systems of Groups VI and VII, the steric strain between the groups increases greatly in contrast to the other systems of Groups VI and VII. The increase in steric strain within 48 is mirrored by the elongation of the C−C bond, which enables 48 to possess the longest C−C bond for Groups VI and VII. Moreover, the C−C electron density and energy density at the C−C bond critical point is the smallest and the least negative (See Table 1). Thus, the longest and weakest C−C bond of Groups VI and VII, belonging to 48, is due to 48 having the smallest C−C bond covalency as reflected by the least negative value of the energy density H for these groups (See Table 1).
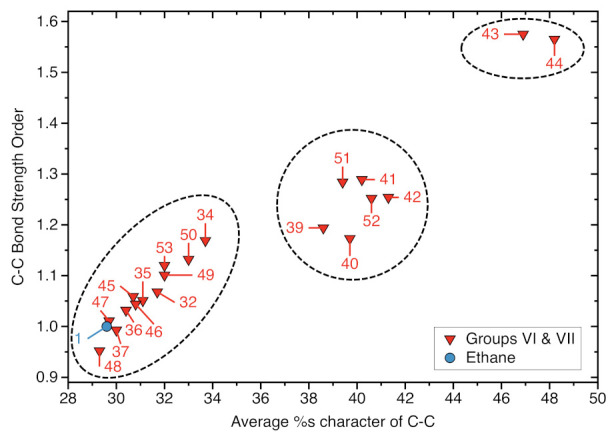
A well-accepted concept in organic chemistry relates the length and the strength of a CC bond to its s-character, resulting from the type of hybridization. The more s character, the shorter and stronger the bond [138]. The average % s-character of a C−C single bond with two sp hybridized C atoms is 29.6, that of a C=C bond with two sp hybridized C atoms is 40.7, and that of a C≡C triple bond 52.3 in line with decreasing bond length and increasing bond strength in this order. Although this is a simplified picture, we see an interesting trend between the average %s character of the two C atoms forming the targeted bond and the local mode force constant as depicted in Figure 6 and Table 2 As the average % s character of the targeted C−C bond increases the C−C bond strength increases, adding to the model quantity % s character a physical relevance.
Figure 6.
Average % s-character the targeted C−C bonds of ethane (1), Group VI, and Group VII molecules determined from the NBO analysis versus the corresponding BSO n(C−C) values. B97X-D/aug-cc-pVTZ level of theory.
Table 2.
% s-character of the C atoms C1 and C2 forming the targeted C−C bond in Group VI and Group VII molecules determined from the NBO analysis .
| # | % s (C1) | % s (C2) | Sum of % s Character | Av. of % s Character |
|---|---|---|---|---|
| 1 | 29.6 (sp) | 29.6 (sp) | 59.2 | 29.6 |
| 33 | 40.7 (sp) | 40.7 (sp) | 81.4 | 40.7 |
| 38 | 52.3 (sp) | 52.3 (sp) | 104.6 | 52.3 |
| 32 | 30.2 (sp) | 33.2 (sp) | 63.4 | 31.7 |
| 34 | 33.7 (sp) | 33.7 (sp) | 67.4 | 33.7 |
| 35 | 28.8 (sp) | 33.4 (sp) | 62.2 | 31.1 |
| 36 | 27.2 (sp) | 33.7 (sp) | 60.8 | 30.4 |
| 37 | 25.6 (sp) | 34.4 (sp) | 60.0 | 30.0 |
| 39 | 29.5 (sp) | 47.7 (sp) | 77.1 | 38.6 |
| 40 | 26.8 (sp) | 52.4 (sp) | 79.3 | 39.7 |
| 41 | 47.9 (sp) | 32.5 (sp) | 80.4 | 40.2 |
| 42 | 52.2 (sp) | 30.3 (sp) | 82.5 | 41.3 |
| 43 | 46.9 (sp) | 46.9 (sp) | 93.8 | 46.9 |
| 44 | 45.7 (sp) | 50.7 (sp) | 96.4 | 48.2 |
| 45 | 31.1 (sp) | 30.3 (sp) | 61.4 | 30.7 |
| 46 | 31.5 (sp) | 30.0 (sp) | 61.5 | 30.8 |
| 47 | 31.9 (sp) | 27.5 (sp) | 59.4 | 29.7 |
| 48 | 32.5 (sp) | 26.0 (sp) | 58.5 | 29.3 |
| 49 | 31.7 (sp) | 32.3 (sp) | 64.0 | 32.0 |
| 50 | 32.0 (sp) | 34.0 (sp) | 66.0 | 33.0 |
| 51 | 30.6 (sp) | 48.0 (sp) | 78.7 | 39.4 |
| 52 | 28.6 (sp) | 52.5 (sp) | 81.1 | 40.6 |
| 53 | 32.0 (sp) | 32.0 (sp) | 64.0 | 32.0 |
C1 and C2 are numbered according to Figure 1, e.g., in 39 C1 is the methyl carbon and C2 is the alkyne carbon atom. The hybridization of the carbon atom is given in parenthesis. The s-character percentages are based upon B97X-D/aug-cc-pVTZ calculations.
Furthermore, we observe a pattern with three clusters; the first cluster ranging from 28 to 35 average %s character involves systems where one of the targeted C atoms is bonded to a hydrogen and or methyl substituents and the other C atom bonded to a vinyl or only phenyl substituent (See Figure 6). The second cluster, where the average %s character of the C−C bond ranges from 37 to 43 %, includes systems in which one of the targeted C atoms is connected to an alkyne or cyano group (See Figure 6). The third cluster features systems 43 and 44 with the largest average %s characters of 46.9 % for 43 and 48.2 % 44, respectively. In 43 both bond targeted C atoms are conjugation with an alkyne group and in 44 one of the targeted C atoms is conjugated with an alkyne and the other with a cyano group. Work is in progress to explore this further.
4. Conclusions and Outlook
In this work we investigated a diverse set of 53 molecules with ultra long C−C bonds including C−C bonds in a highly sterically strained situation, i.e., clamped C−C bonds, crowded bonding environment as found for diamondoid dimers, and electron deficient C−C bonds caused by electron removal, electron withdrawing substituents, or negative hyperconjugation as discussed for di-N,N-dimethylamino-o-carborane (organized in Groups I-V) to elucidate the wide spectrum of possibilities for elongating a covalent C−C bond. For comparison, we included also some C−C bonds within conjugated and hyperconjucated systems, which generally leads to shorter bonds, as well as a number of double and triple bonds (Groups VI and VII).
Vibrational spectroscopy provides a comprehensive overview of a molecule’s electronic structure and its local environment (e.g., the strength of intermolecular interactions) as concealed within the normal vibrational modes. We utilized local mode force constants, derived from local mode analysis, as a quantitative measure to assess the strength of these long C−C bonds. The local mode analysis was complemented with NBO analysis and electron density analysis where the covalent character of each ultra long C−C bond was confirmed via the energy density taken at the bond critical point r. This has led to the following findings:
Although steric crowding/strain increases the C−C bond length electronic effects can lead to even longer and weaker CC bonds. The overall weakest C−C bonds are found within Group V where electron deficient bonding is represented by the ethane radical cation in D3d (30a) (BSO n = 0.286) and C2h (30b) (BSO n = 0.306) symmetry and di-N,N-dimethylamino-o-carborane (31) (BSO n = 0.209). However, whereas 31 has the weakest C−C bond, 30a has the longest C−C bond at a value of 1.935 Å compared to the C−C length of 1.930 Å for 31, confirming previous findings that the longer bond is not always the weaker bond.
A gap beyond 0.1 Å is present between the two longest C−C bonds (30a and 31) and the other CC bonds within this study. This gap is due to the C−C bonds within molecules 30a and 31 being governed by electronic effects. The C−C bond of 30a is heavily affected by its electron deficient nature while the CC bond length of system 31 is influenced by negative hyperconjugation effects.
The covalent character of all C−C bonds has been verified via the negative energy density values taken at the bond critical point r. In most cases is in line with the or BSO n values, reflecting that stronger bonds have more covalent character. However, we also found some exceptions such as the chlorinated ethanes (28 and 29). The results demonstrate that the local mode force constant is a sensitive bond strength measure that considers subtle second order effects that are not considered for the energy density evaluated just at the bond critical point which describes the covalent character, whereas includes counterbalancing steric repulsion effects or C−C bond weakening via delocalization of charge from the Cl lone pair into the (C−C), i.e., the so-called negative hyperconjugation effect, or intramolecular halogen-halogen dispersion interaction.
Although there is some trend that the BDH value increases with increasing C−C bond strength, the overall correlation is moderate (R = 0.893), revealing that the BDH is an inadequate measure for the intrinsic strength of the CC bond as BDH includes the overall effects of bond breakage. Such concerns in particular crowded molecules with greater possibilities for geometry and electron density reorganization of the fragments such as molecules 7, 13, and 15.
We found an interesting relationship between the %s-character and the strength of the C−C bond as expressed via the local mode force constant. As the average %s-character of the targeted C−C bond increases the C−C bond strength increases which adds to the %s-character model quantity a physical relevance.
Overall, this study shows that the local stretching vibrational force constant is the perfect tool for comprehending the nature of CC bond elongation which, as shown in this work, is often a result of a complex interplay of steric/strain and electronic effects that sometimes add to the weakening but also may work in a counterbalancing fashion. The local mode force constants can quickly be calculated after a routine frequency calculation and therefore, can provide important guidance for the synthesis of a compound with a C−C bond of a particular strength. Work is in progress to investigate long CC bonds in nanotubes and crystals under pressure at ambient temperature [139,140,141,142,143].
Acknowledgments
This work was financially supported by the National Science Foundation, Grant CHE 1152357. We thank SMU for providing computational resources.
Supplementary Materials
The following are available online, Figure S1: Scheme of molecules 1-53 with atomic charges from the natural bond orbital (NBO) analysis. Table S1: Provides a summarized compilation of experimental bond lengths of the targeted compounds, references are listed. Table S2: Lists experimental bond dissociation enthalpies (BDH) values, references are cited. Table S3: Provides IUPAC nomenclature for systems. Table S4: Summarizes the calculated bond distances R(CC) in Å, local mode force constants k (CC) in mdyn/Å, energy densities H at the bond critical point r in Hartree/Å and NBO charges in electrons for the CC bonds of fluorinated and chlorinated ethane at different levels of theory. The optimized coordinates of molecules 1–53, obtained at the B97X-D/aug-cc-pVTZ level of theory, are provided at the end of the SI.
Author Contributions
Conceptualization, E.K.; methodology, E.K.; formal analysis, A.A.A.D., A.H., R.K.; investigation, A.A.A.D., A.H. and R.K.; data curation, A.A.A.D., A.H., R.K. and M.F.; writing—original draft preparation, A.A.A.D. and E.K.; writing—review and editing, A.A.A.D., M.F. and E.K.; visualization, A.H. and M.F.; supervision, E.K.; project administration, E.K.; funding acquisition, E.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science Foundation grant number CHE 1152357.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Bell J.A. Chemistry: A Project of the American Chemical Society. W H Freeman & CO; New York, NY, USA: 2004. [Google Scholar]
- 2.Howes L. The Fight Over the Longest Carbon-Carbon Bond is Redefining What a Bond Is. C&E News. 2019;97:1–8. [Google Scholar]
- 3.Mandal N., Datta A. Molecular Designs for Expanding the Limits of Ultralong C–C Bonds and Ultrashort H···H Non-bonded Contacts. Chem. Commun. 2020;56:15377–15386. doi: 10.1039/D0CC06690G. [DOI] [PubMed] [Google Scholar]
- 4.Wu Y., Zhang J., Xie Z. How Long a C–C Bond Can Be? An Example of Extraordinary Long C–C Single Bond in 1,2-Diarylamino-o-carborane. Chin. Chem. Lett. 2019;30:1530–1532. doi: 10.1016/j.cclet.2019.04.034. [DOI] [Google Scholar]
- 5.Li J., Pang R., Li Z., Xiao G., Müller T. Exceptionally Long C–C Single Bonds in Diamino-o-carborane as Induced by Negative Hyperconjugation. Angew. Chem. Int. Ed. 2019;58:1397–1401. doi: 10.1002/anie.201812555. [DOI] [PubMed] [Google Scholar]
- 6.Shimajiri T., Suzuki T., Ishigaki Y. Flexible C−C Bonds: Reversible Expansion, Contraction, Formation, and Scission of Extremely Elongated Single Bonds. Angew. Chem. Int. Ed. 2020;59:22252–22257. doi: 10.1002/anie.202010615. [DOI] [PubMed] [Google Scholar]
- 7.Ishigaki Y., Shimajiri T., Takeda T., Katoono R., Suzuki T. Longest C−C Single Bond among Neutral Hydrocarbons with a Bond Length beyond 1.8 Å. Chem. Commun. 2018;4:795–806. doi: 10.1016/j.chempr.2018.01.011. [DOI] [Google Scholar]
- 8.Sethio D., Oliveira V., Kraka E. Quantitative Assessment of Tetrel Bonding Utilizing Vibrational Spectroscopy. Molecules. 2018;23:2763. doi: 10.3390/molecules23112763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Del Bene J., Alkorta I., Elguero J. Carbenes as Electron-Pair Doners to CO2 for C...C Tetrel Bonds and C–C Covalent Bonds. J. Phys. Chem. A. 2017;121:4039–4047. doi: 10.1021/acs.jpca.7b03405. [DOI] [PubMed] [Google Scholar]
- 10.Del Bene J., Alkorta I., Elguero J. Carbon-Carbon Bonding Between Nitrogen Heterocyclic Carbenes and CO2. J. Phys. Chem. A. 2017;121:8136–8146. doi: 10.1021/acs.jpca.7b08393. [DOI] [PubMed] [Google Scholar]
- 11.Humason A., Zou W., Cremer D. 11,11-Dimethyl-1,6-methano[10]annulene-An Annulene with an Ultralong CC Bond or a Fluxional Molecule? J. Phys. Chem. A. 2014;119:1666–1682. doi: 10.1021/jp5082966. [DOI] [PubMed] [Google Scholar]
- 12.Mandal N., Pal A.K., Gain P., Zohaib A., Datta A. Transition-State-like Planar Structures for Amine Inversion with Ultralong C–C Bonds in Diamino-o-carborane and Diamino-o-dodecahedron. J. Am. Chem. Soc. 2020;142:5331–5337. doi: 10.1021/jacs.0c00181. [DOI] [PubMed] [Google Scholar]
- 13.Allinger N.L., Lii J.H., Schaefer H.F., III Molecular Mechanics (MM4) Studies on Unusually Long Carbon-Carbon Bond Distances in Hydrocarbons. J. Chem. Theory Comput. 2012;12:2774–2778. doi: 10.1021/acs.jctc.5b00926. [DOI] [PubMed] [Google Scholar]
- 14.Crabtree K.N., Talipov M.R., Martinez O., O’Connor G.D., Khursan S.L., McCarthy M.C. Detection and Structure of HOON: Microwave Spectroscopy Reveals an O−O Bond Exceeding 1.9 Å. Science. 2013;342:1354–1357. doi: 10.1126/science.1244180. [DOI] [PubMed] [Google Scholar]
- 15.Denis P.A., Huelmo C.P. New Trends Along Hydrogen Polyoxides: Unusually Long Oxygen–Oxygen bonds in H2O6 and H2O7. Mol. Phys. 2014;112:3047–3056. doi: 10.1080/00268976.2014.928385. [DOI] [Google Scholar]
- 16.Pupim C.F., Catão A.J.L., López-Castillo A. Boron–Nitrogen Dative Bond. J. Mol. Model. 2018;24:283. doi: 10.1007/s00894-018-3810-9. [DOI] [PubMed] [Google Scholar]
- 17.Suzuki T., Uchimura Y., Ishigaki Y., Takeda T., Katoono R., Kawai H., Fujiwara K., Nagaki A., Yoshida J. Nonadditive Substituent Effects on Expanding Prestrained C–C Bond in Crystal: X-ray Analyses on Unsymmetrically Substituted Tetraarylpyracenes Prepared by a Flow Microreactor Method. Chem. Lett. 2012;41:541–543. doi: 10.1246/cl.2012.541. [DOI] [Google Scholar]
- 18.Schreiner P.R., Chernish L.V., Gunchenko P.A., Tikhonchuk E.Y., Hausmann H., Serafin M., Schlecht S., Dahl J.E.P., Carlson R.M.K., Fokin A.A. Overcoming Lability of Extremely Long Alkane Carbon-Carbon Bonds Through Dispersion Forces. Nature. 2011;477:308–311. doi: 10.1038/nature10367. [DOI] [PubMed] [Google Scholar]
- 19.Grimme S., Schreiner P.R. Steric Crowding Can Stabilize a Labile Molecule: Solving the Hexaphenylethane Riddle. Angew. Chem. Int. Ed. 2011;50:12639–12642. doi: 10.1002/anie.201103615. [DOI] [PubMed] [Google Scholar]
- 20.Suzuki T., Takeda T., Kawai H., Fujiwara K. Ultralong C–C Bonds in Hexaphenylethane Derivatives. Pure Appl. Chem. 2008;80:547–553. doi: 10.1351/pac200880030547. [DOI] [Google Scholar]
- 21.Tanaka K., Takamoto N., Tezuka Y., Kato M., Toda F. Preparation and Structural Study of Naphtho- and Anthrocyclobutene Derivatives Which Have Extremely Long C–C bonds. Tetrahedron. 2001;57:3761–3767. doi: 10.1016/S0040-4020(01)00249-6. [DOI] [Google Scholar]
- 22.De Silva K.M.N., Goodman J.M. What Is the Smallest Saturated Acyclic Alkane that Cannot Be Made? J. Chem. Inf. Model. 2005;45:81–87. doi: 10.1021/ci0497657. [DOI] [PubMed] [Google Scholar]
- 23.Kawai H., Takeda T., Fujiwara K., Wakeshima M., Hinatsu Y., Suzuki T. Ultralong Carbon-Carbon Bonds in Dispirobis(10-methylacridan) Derivatives with an Acenaphthene, Pyracene, or Dihydropyracylene Skeleton. Chem. Eur. J. 2008;14:5780–5793. doi: 10.1002/chem.200702028. [DOI] [PubMed] [Google Scholar]
- 24.Kaupp G., Boy J. Overlong C–C Single Bonds. Angew. Chem. Int. Ed. 1997;36:48–49. doi: 10.1002/anie.199700481. [DOI] [Google Scholar]
- 25.Bartell L., Boates T. Structure of the Strained Molecules Hexamethylethane and 1,1,2,2-Tetramethylethane by Gas-Phase Electron Diffraction. J. Mol. Struct. 1976;32:379–392. doi: 10.1016/0022-2860(76)85015-6. [DOI] [Google Scholar]
- 26.Szabo Z., Thege I. Some Empirical Correlations on Chemical Bonds. Acta Chem. Acad. Sci. Hung. 1975;86:127–145. [Google Scholar]
- 27.Fokin A., Chernish L., Gunchenko P., Tikhonchuk E., Hausmann H., Serafin M., Dahl J., Carlson R., Schreiner P. Stable Alkanes Containing Very Long Carbon-Carbon Bonds. J. Am. Chem. Soc. 2012;134:13641–13650. doi: 10.1021/ja302258q. [DOI] [PubMed] [Google Scholar]
- 28.Plitzko K., Rapko B., Gollas B., Wehrle G., Weakley T., Pierce D.T., Geiger W.E., Haddon R.C., Boekelheide V. Bis(η6-hexamethylbenzene)(η6,η6-[2n]cyclophane)diruthenium- (II,II) Complexes and Their Two-Electron Reduction to [2n]Cyclophane Derivatives Having Two Cyclohexadienyl Anion Decks Joined by an Extremely Long Carbon-Carbon Bond. J. Am. Chem. Soc. 1990;112:6545–6556. doi: 10.1021/ja00174a015. [DOI] [Google Scholar]
- 29.Komatsu K., Nishinaga T., Takeuchi K., Lindner H.J., Richter J. A Polycyclic Pentamer of Bicyclo[2.2.2]octene. A Hydrocarbon Molecule with a Long C–C Single Bond Connecting Two Cofacially Disposed Cyclopentadiene Rings. J. Org. Chem. 1994;59:7322–7328. doi: 10.1021/jo00103a024. [DOI] [Google Scholar]
- 30.Slepetz B., Kertesz M. Volume Change during Thermal [4+4] Cycloaddition of [2.2] (9,10)Anthracenophane. J. Am. Chem. Soc. 2013;135:13720–13727. doi: 10.1021/ja402485j. [DOI] [PubMed] [Google Scholar]
- 31.Takeda T., Kawai H., Herges R., Mucke E., Sawai Y., Murakoshi K., Fujiwara K., Suzuki T. Negligible Diradical Character for the Ultralong C–C Bond in 1,1,2,2-Tetraarylpyracene Derivatives at Room Temperature. Tetrahedron Lett. 2009;59:3693–3697. doi: 10.1016/j.tetlet.2009.03.202. [DOI] [Google Scholar]
- 32.Folkertsma E., Benthem S., Witteman L., van Slagnaat C.A.M.R., ad Lutz M., Klein Gebbink R., Moret M.E. Formation of Exceptionally Weak C–C Bonds by Metal-Templated Pinacole Coupling. Dalton Tans. 2017;46:6177–6182. doi: 10.1039/C7DT01130J. [DOI] [PubMed] [Google Scholar]
- 33.Jacovella U., Stein C., Grütter M., Freitag L., Lauzin C., Reiher M., Merkt F. Structure and Dynamics of the Radical Cation of Ethane Arising from the Jahn-Teller and Pseudo-Jahn-Teller Effects. Phys. Chem. Chem. Phys. 2018;20:1072–1081. doi: 10.1039/C7CP06907C. [DOI] [PubMed] [Google Scholar]
- 34.Eriksson L.A., Lunell S. Theoretical Study of Deuterated Ethane Cations. J. Phys. Chem. 1993;97:12215–12219. doi: 10.1021/j100149a020. [DOI] [Google Scholar]
- 35.Bellville D.J., Bauld N.L. Elongated (One-Electron) Carbon-Carbon Bond in σ and n Organic Cation Radicals. J. Am. Chem. Soc. 1982;104:5700–5702. doi: 10.1021/ja00385a025. [DOI] [Google Scholar]
- 36.Luo Y.R. Comprehensive Handbook of Chemical Bond Energies. Taylor and Francis; Boca Raton, FL, USA: 2007. [Google Scholar]
- 37.Morse M.D. Predissociation Measurements of Bond Dissociation Energies. Acc. Chem. Res. 2018;52:119–126. doi: 10.1021/acs.accounts.8b00526. [DOI] [PubMed] [Google Scholar]
- 38.St. John P.C., Guan Y., Kim Y., Kim S., Paton R.S. Prediction of Organic Homolytic Bond Dissociation Enthalpies at Near Chemical Accuracy with Sub-Second Computational Cost. Nat. Commun. 2020;11:2328. doi: 10.1038/s41467-020-16201-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cremer D., Kraka E. From Molecular Vibrations to Bonding, Chemical Reactions, and Reaction Mechanism. Curr. Org. Chem. 2010;14:1524–1560. doi: 10.2174/138527210793563233. [DOI] [Google Scholar]
- 40.Kalescky R., Kraka E., Cremer D. Are Carbon-Halogen Double and Triple Bonds Possible? Int. J. Quant. Chem. 2014;114:1060–1072. doi: 10.1002/qua.24626. [DOI] [Google Scholar]
- 41.Kalescky R., Zou W., Kraka E., Cremer D. Quantitative Assessment of the Multiplicity of Carbon-Halogen Bonds: Carbenium and Halonium Ions with F, Cl, Br, and I. J. Phys. Chem. A. 2014;118:1948–1963. doi: 10.1021/jp4120628. [DOI] [PubMed] [Google Scholar]
- 42.Oliveira V., Kraka E., Cremer D. Quantitative Assessment of Halogen Bonding Utilizing Vibrational Spectroscopy. Inorg. Chem. 2016;56:488–502. doi: 10.1021/acs.inorgchem.6b02358. [DOI] [PubMed] [Google Scholar]
- 43.Setiawan D., Sethio D., Cremer D., Kraka E. From Strong to Weak NF Bonds: On the Design of a New Class of Fluorinating Agents. Phys. Chem. Chem. Phys. 2018;20:23913–23927. doi: 10.1039/C8CP03843K. [DOI] [PubMed] [Google Scholar]
- 44.Krapp A., Bickelhaupt F.M., Frenking G. Orbital Overlap and Chemical Bonding. Chem. Eur. J. 2006;12:9196–9216. doi: 10.1002/chem.200600564. [DOI] [PubMed] [Google Scholar]
- 45.Zhao L., Hermann M., Schwarz W.H.E., Frenking G. The Lewis Electron-Pair Bonding Model: Modern Energy Decomposition Analysis. Nat. Rev. Chem. 2019;3:48–63. doi: 10.1038/s41570-018-0060-4. [DOI] [Google Scholar]
- 46.Zhao L., Pan S., Holzmann N., Schwerdtfeger P., Frenking G. Chemical Bonding and Bonding Models of Main-Group Compounds. Chem. Rev. 2019;119:8781–8845. doi: 10.1021/acs.chemrev.8b00722. [DOI] [PubMed] [Google Scholar]
- 47.Gavezzotti A. Comparing the Strength of Covalent Bonds, Intermolecular Hydrogen Bonds and Other Intermolecular Interactions for Organic Molecules: X-ray Diffraction Data and Quantum Chemical Calculations. New J. Chem. 2016;40:6848–6853. doi: 10.1039/C6NJ01087C. [DOI] [Google Scholar]
- 48.Kalescky R., Kraka E., Cremer D. Identification of the Strongest Bonds in Chemistry. J. Phys. Chem. A. 2013;117:8981–8995. doi: 10.1021/jp406200w. [DOI] [PubMed] [Google Scholar]
- 49.Kraka E., Cremer D. Weaker Bonds with Shorter Bond Lengths. Rev. Proc. Quim. 2012;6:39–42. doi: 10.19142/rpq.v6i11.153. [DOI] [Google Scholar]
- 50.Cremer D., Wu A., Larsson A., Kraka E. Some Thoughts about Bonds with Bond Lengths, and Force Constants. J. Mol. Model. 2000;6:396–412. doi: 10.1007/PL00010739. [DOI] [Google Scholar]
- 51.Kaupp M., Metz B., Stoll H. Breakdown of Bond Length-Bond Strength Correlation: A Case Study. Angew. Chem. Int. Ed. 2000;39:4607–4609. doi: 10.1002/1521-3773(20001215)39:24<4607::AID-ANIE4607>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
- 52.Kaupp M., Danovich D., Shaik S. Chemistry is About Energy and its Changes: A Critique of Bond-Length/Bond-Strength Correlations. Coord. Chem. Rev. 2017;344:355–362. doi: 10.1016/j.ccr.2017.03.002. [DOI] [Google Scholar]
- 53.Konkoli Z., Cremer D. A New Way of Analyzing Vibrational Spectra. I. Derivation of Adiabatic Internal Modes. Int. J. Quant. Chem. 1998;67:1–9. doi: 10.1002/(SICI)1097-461X(1998)67:1<1::AID-QUA1>3.0.CO;2-Z. [DOI] [Google Scholar]
- 54.Konkoli Z., Larsson J.A., Cremer D. A New Way of Analyzing Vibrational Spectra. II. Comparison of Internal Mode Frequencies. Int. J. Quant. Chem. 1998;67:11–27. doi: 10.1002/(SICI)1097-461X(1998)67:1<11::AID-QUA2>3.0.CO;2-1. [DOI] [Google Scholar]
- 55.Konkoli Z., Cremer D. A New Way of Analyzing Vibrational Spectra. III. Characterization of Normal Vibrational Modes in terms of Internal Vibrational Modes. Int. J. Quant. Chem. 1998;67:29–40. doi: 10.1002/(SICI)1097-461X(1998)67:1<29::AID-QUA3>3.0.CO;2-0. [DOI] [Google Scholar]
- 56.Konkoli Z., Larsson J.A., Cremer D. A New Way of Analyzing Vibrational Spectra. IV. Application and Testing of Adiabatic Modes within the Concept of the Characterization of Normal Modes. Int. J. Quant. Chem. 1998;67:41–55. doi: 10.1002/(SICI)1097-461X(1998)67:1<41::AID-QUA4>3.0.CO;2-Z. [DOI] [Google Scholar]
- 57.Cremer D., Larsson J.A., Kraka E. New Developments in the Analysis of Vibrational Spectra on the Use of Adiabatic Internal Vibrational Modes. In: Parkanyi C., editor. Theoretical and Computational Chemistry. Elsevier; Amsterdam, The Netherlands: 1998. pp. 259–327. [Google Scholar]
- 58.Kraka E., Zou W., Tao Y. Decoding Chemical Information from Vibrational Spectroscopy Data: Local Vibrational Mode Theory. WIREs Comput. Mol. Sci. 2020;10:1480. doi: 10.1002/wcms.1480. [DOI] [Google Scholar]
- 59.Weinhold F., Landis C.R., Glendening E.D. What is NBO Analysis and How is it Useful? Int. Rev. Phys. Chem. 2016;35:39–440. doi: 10.1080/0144235X.2016.1192262. [DOI] [Google Scholar]
- 60.Bader R.F.W. Atoms in Molecules: A Quantum Theory (International Series of Monographs on Chemistry) Clarendon Press; Oxford, UK: 1994. [Google Scholar]
- 61.Popelier P.L. Atoms in Molecules: An Introduction. Prentice Hall; Upper Saddle River, NJ, USA: 2000. [Google Scholar]
- 62.Chai J.D., Head-Gordon M. Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008;10:6615–6620. doi: 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- 63.Chai J.D., Head-Gordon M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. J. Chem. Phys. 2008;128:084106/1–084106/15. doi: 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
- 64.Dunning T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989;90:1007–1023. doi: 10.1063/1.456153. [DOI] [Google Scholar]
- 65.Sato T., Nakai H. Density Functional Method Including Weak Interactions: Dispersion Coefficients Based On the Local Response Approximation. J. Chem. Phys. 2009;131:224104/1–224104/12. doi: 10.1063/1.3269802. [DOI] [PubMed] [Google Scholar]
- 66.Athar M., Das S., Jha P.C., Jha A.M. Conformational Equilibrium Study of Calix[4]tetrolarenes Using Density Functional Theory (DFT) and Molecular Dynamics Simulations. Supramol. Chem. 2018;30:982–993. doi: 10.1080/10610278.2018.1517876. [DOI] [Google Scholar]
- 67.Hachim M.E., Sadik K., Byadi S., Aboulmouhajir A. Electronic Investigation and Spectroscopic Analysis Using DFT With the Long-Range Dispersion Correction On the Six lowest Conformers of 2.2.3-Trimethyl Pentane. J. Mol. Model. 2020;26:1–16. doi: 10.1007/s00894-020-04430-4. [DOI] [PubMed] [Google Scholar]
- 68.Pople J.A., Head-Gordon M., Raghavachari K. Quadratic Configuration Interaction. A General Technique for Determining Electron Correlation Energies. J. Chem. Phys. 1987;87:5968–5975. doi: 10.1063/1.453520. [DOI] [Google Scholar]
- 69.Kendall R.A., Dunning T.H., Harrison R.J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992;96:6796–6806. doi: 10.1063/1.462569. [DOI] [Google Scholar]
- 70.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Petersson G.A., Nakatsuji H., et al. Gaussian 16 Revision B.01. Gaussian Inc.; Wallingford, CT, USA: 2016. [Google Scholar]
- 71.Chan B., Radom L. BDE261: A Comprehensive Set of High-Level Theoretical Bond Dissociation Enthalpies. J. Chem. Phys. A. 2012;116:4975–4986. doi: 10.1021/jp302542z. [DOI] [PubMed] [Google Scholar]
- 72.Curtiss L., Redfern P., Raghavachari K. Gaussian-4 Theory Using Reduced Order Perturbation Theory. J. Chem. Phys. 2007;127:124105/1–124105/8. doi: 10.1063/1.2770701. [DOI] [PubMed] [Google Scholar]
- 73.Curtiss L., Redfern P., Raghavachari K. Gaussian-4 Theory. J. Chem. Phys. 2007;126:084108/1–084108/12. doi: 10.1063/1.2436888. [DOI] [PubMed] [Google Scholar]
- 74.Pople J., Head-Gordon M., Fox D., Raghavachari K., Curtiss L. Gaussian-1 Theory: A General Procedure for Prediction of Molecular Energies. J. Chem. Phys. 1989;90:5622–5629. doi: 10.1063/1.456415. [DOI] [Google Scholar]
- 75.Reed A.E., Curtiss L.A., Weinhold F. Intermolecular Interactions From a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988;88:899–926. doi: 10.1021/cr00088a005. [DOI] [Google Scholar]
- 76.Weinhold F., Landis C.R. Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective. Cambridge University Press; Cambridge, UK: 2005. [Google Scholar]
- 77.Keith T.A. AIMAll (Version 12.06.03) TK Gristmill Software; Overland Park, KS, USA: 2012. [Google Scholar]
- 78.Cremer D., Kraka E. Chemical Bonds without Bonding Electron Density? Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem. Int. Ed. 1984;23:627–628. doi: 10.1002/anie.198406271. [DOI] [Google Scholar]
- 79.Cremer D., Kraka E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy. Croat. Chem. Acta. 1984;57:1259–1281. [Google Scholar]
- 80.Kraka E., Cremer D. Chemical Implication of Local Features of the Electron Density Distribution. In: Maksic Z.B., editor. Theoretical Models of Chemical Bonding. The Concept of the Chemical Bond. Volume 2. Springer; Heidelberg, Germany: 1990. pp. 453–542. [Google Scholar]
- 81.Zou W., Tao Y., Freindorf M., Makos M., Verma N., Kraka E. Local Vibrational Mode Analysis (LModeA) Computational and Theoretical Chemistry Group (CATCO), Southern Methodist University; Dallas, TX, USA: 2020. [Google Scholar]
- 82.Wilson E.B., Decius J.C., Cross P.C. Molecular Vibrations. The Theory of Infrared and Raman Vibrational Spectra. McGraw-Hill; New York, NY, USA: 1955. [Google Scholar]
- 83.Woodward L.A. Introduction to the Theory of Molecular Vibrations and Vibrational Spectroscopy. Oxford University Press; Oxford, UK: 1972. [Google Scholar]
- 84.Wilson E.B., Jr. A method of obtaining the expanded secular equation for the vibration frequencies of a molecule. J. Chem. Phys. 1939;7:1047. doi: 10.1063/1.1750363. [DOI] [Google Scholar]
- 85.Califano S. Vibrational States. Wiley; London, UK: 1976. [Google Scholar]
- 86.Groner P. Normal Coordinate Analysis. John Wiley; New York, NY, USA: 2006. [Google Scholar]
- 87.Kelley J.D., Leventhal J.J. Problems in Classical and Quantum Mechanics. Springer; Berlin/Heidelberg, Germany: 2017. Normal Modes and Coordinates; pp. 95–117. [Google Scholar]
- 88.Neto N. Tensor Formalism in Anharmonic Calculations. Chem. Phys. 1984;91:89. doi: 10.1016/0022-2860(86)80349-0. [DOI] [Google Scholar]
- 89.Stare J. First-Principle Calculation of Reduced Masses in Vibrational Analysis Using Generalized Internal Coordinates: Some Crucial Aspects and Examples. J. Chem. Inf. Model. 2007;47:840–850. doi: 10.1021/ci6005245. [DOI] [PubMed] [Google Scholar]
- 90.Zou W., Kalescky R., Kraka E., Cremer D. Relating Normal Vibrational Modes to Local Vibrational Modes with the Help of an Adiabatic Connection Scheme. J. Chem. Phys. 2012;137:084114. doi: 10.1063/1.4747339. [DOI] [PubMed] [Google Scholar]
- 91.Kalescky R., Kraka E., Cremer D. Local Vibrational Modes of the Formic Acid Dimer-The Strength of the Double H-Bond. Mol. Phys. 2013;111:1497–1510. doi: 10.1080/00268976.2013.796070. [DOI] [Google Scholar]
- 92.Kalescky R., Kraka E., Cremer D. New Approach to Tolman’s Electronic Parameter Based on Local Vibrational Modes. Inorg. Chem. 2013;53:478–495. doi: 10.1021/ic4024663. [DOI] [PubMed] [Google Scholar]
- 93.Kraka E., Larsson J.A., Cremer D. Generalization of the Badger Rule Based on the Use of Adiabatic Vibrational Modes. In: Grunenberg J., editor. Computational Spectroscopy. Wiley; New York, NY, USA: 2010. pp. 105–149. [Google Scholar]
- 94.Zou W., Cremer D. Properties of Local Vibrational Modes: The Infrared Intensity. Theor. Chem. Acc. 2014;133:1451–1466. doi: 10.1007/s00214-014-1451-3. [DOI] [Google Scholar]
- 95.Zou W., Cremer D. C2 in a Box: Determining its Intrinsic Bond Strength for the X1Σ+g Ground State. Chem. Eur. J. 2016;22:4087–4097. doi: 10.1002/chem.201503750. [DOI] [PubMed] [Google Scholar]
- 96.Kalescky R., Zou W., Kraka E., Cremer D. Local Vibrational Modes of the Water Dimer-Comparison of Theory and Experiment. Chem. Phys. Lett. 2012;554:243–247. doi: 10.1016/j.cplett.2012.10.047. [DOI] [Google Scholar]
- 97.Gunnelin K., Glans P., Rubensson J.E., Såthe C., Nordgren J., Li Y., Gelḿukhanov F., Ågren H. Bond-Length-Dependent Core Hole Localization Observed in Simple Hydrocarbonds. Phys. Rev. Lett. 1999;83:1315–1318. doi: 10.1103/PhysRevLett.83.1315. [DOI] [Google Scholar]
- 98.Afeefy H., Liebman J., Stein S. In NIST Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 69. [(accessed on 19 October 2020)];2001 Available online: http:webbook.nist.gov/
- 99.Martin J., Fernandez M., Tortajada J. Application of Wiberg Indices to Geometry Optimization. C–C Distances. J. Mol. Struct. 1988;175:203–208. doi: 10.1016/S0022-2860(98)80076-8. [DOI] [Google Scholar]
- 100.Hilderbrandt R., Wieser J. The Zero Point Average Structure of Isobutane as Determined by Electron Diffraction and Microwave Spectroscopy. J. Mol. Struct. 1973;15:27–36. doi: 10.1016/0022-2860(73)87004-8. [DOI] [Google Scholar]
- 101.Shen Q. The Molecular Structure of 1,2-Diphenylethane as Determined by Gas-Phase Electron Diffraction. J. Mol. Struct. 1998;471:57–61. doi: 10.1016/S0022-2860(98)00392-5. [DOI] [Google Scholar]
- 102.Flamm-ter M., Beckhaus H.D., Peters K., von Schnering H.G., Rüchardt C. 2,3-Di-1-adamantyl-2,3-dimethylbutane; Long Bonds and Low Thermal Stability. Chem. Ber. 1985;113:4665–4671. [Google Scholar]
- 103.Zavitsas A.A. The Relation between Bond Lengths and Dissociation Energies of Carbon-Carbon Bonds. J. Phys. Chem. A. 2003;107:897–898. doi: 10.1021/jp0269367. [DOI] [Google Scholar]
- 104.Winiker R., Beckhaus H.D., Rüchardt C. Thermische Stabilität, Spannungsenthalpie und Struktur Symmetrisch Hexaalkylierter Ethane. Chem. Ber. 1980;113:3456–3476. doi: 10.1002/cber.19801131105. [DOI] [Google Scholar]
- 105.Kratt G., Beckhaus H.D., Lindner H., Rüchardt C. Thermolabile Kohlenwasserstoffe, XX. Synthese, Struktur und Spannung Symmetrischer Tetraalkyldiarylethane. Chem. Ber. 1983;116:3235–3263. doi: 10.1002/cber.19831160921. [DOI] [Google Scholar]
- 106.Kahr B., Van Engen D., Mislow K. Length of the Ethane Bond in Hexaphenylethane and its Derivatives. J. Am. Chem. Soc. 1986;108:8305–8307. doi: 10.1021/ja00286a053. [DOI] [Google Scholar]
- 107.Livingston R., Ramachandra Rao C. The Molecular Structure of Pivalonitrile Electron Diffraction. J. Am. Chem. Soc. 1958;81:3584–3586. doi: 10.1021/ja01523a026. [DOI] [Google Scholar]
- 108.Dougherty D., Choi C., Kaupp G., Buda A., Rudziński J., Osawa E. Effects of Substituents on the Length of Central C(sp3)-C(sp3) Bond in Anthracene Photodimers and Related Molecules. J. Chem. Soc. Perkin Trans. 2. 1986;7:1063–1070. doi: 10.1039/P29860001063. [DOI] [Google Scholar]
- 109.Sugie M., Kato M., Matsumura C., Takeo H. Microwave Spectra and Molecular Structures of 1,2-Dichloroethane, 1,1-Dichloroethane and 1,1,1-Trichloroethane. J. Mol. Struct. 1997;413–414:487–494. doi: 10.1016/S0022-2860(97)00166-X. [DOI] [Google Scholar]
- 110.Almenningen A., Andersen B., Trætteberg M. An Electron Diffraction Investigation of the Molecular Structure of Hexachloroethane in the Vapour Phase. Acta Chem. Scand. 1964;18:603–611. doi: 10.3891/acta.chem.scand.18-0603. [DOI] [Google Scholar]
- 111.Bock C., Panchenko Y. An Ab Initio Structural Investigation of 1,3-Butadiene, Isoprene and 2,3-Dimethyl-1,3-butadiene Rotamers. J. Mol. Struct. THEOCHEM. 1989;187:69–82. doi: 10.1016/0166-1280(89)85150-4. [DOI] [Google Scholar]
- 112.VanHemelrijk D., Van den Enden L., Geise H., Sellers H.L., Schäfer L. Structure Determination of 1-Butene by Gas Electron Diffraction, Microwave Spectroscopy, Molecular Mechanics, and Molecular Orbital Constrained Electron Diffraction. J. Am. Chem. Soc. 1980;102:2189–2195. doi: 10.1021/ja00527a007. [DOI] [Google Scholar]
- 113.Guirgis G., Zheng C., Gounev T., Durig J. Conformational Stability, Ab Initio Calculaitons, and ro structural Parameters of 3-Methyl-1-butene and Dimethylvinylsilane. J. Mol. Struct. 2003;651–653:771–780. doi: 10.1016/S0022-2860(03)00123-6. [DOI] [Google Scholar]
- 114.Kraśnicki A., Zbigniew K., Drouin B., Pearson J. Terahertz Spectroscopy of Isotopic Acrylonitrile. J. Mol. Spectrosc. 2011;1006:20–27. doi: 10.1016/j.molstruc.2011.05.050. [DOI] [Google Scholar]
- 115.Thorwirth C., Harding M.E., Muders D., Gauss J. The Empirical Equilibrium Structure of Diacetylene. J. Mol. Spect. 2008;251:220–223. doi: 10.1016/j.jms.2008.02.020. [DOI] [Google Scholar]
- 116.Kang L., Novick S. The Microwave Spectra of the Weakly Bound Complex Between Carbon Monoxide and Cyanoacetylene, OC H-C≡C–C≡N. J. Mol. Spectrosc. 2012;276–277:10–13. doi: 10.1016/j.jms.2012.06.001. [DOI] [Google Scholar]
- 117.Amir-Ebrahimi V., Choplin A. Microwave Spectrum of the 13C-Ring-Monosubstituted Toluenes and Structure of Toluene. J. Mol. Spectrosc. 1982;89:42–52. doi: 10.1016/0022-2852(81)90158-2. [DOI] [Google Scholar]
- 118.Scharfenberg P., Rozsondai B., Hargittai I. Conformation and Structure of Ethylbenzene in the Vapour Phase. Z. Naturforsch. 1980;35a:431–436. doi: 10.1515/zna-1980-0414. [DOI] [Google Scholar]
- 119.Vilkov L., Sadova N., Mochalov S. The Structure of Cumene and Phenylcyclobutane Molecules, as Studied by Means of Electron Diffraction Patterns. Dokl. Akad. Nauk SSSR. 1968;179:896–899. [Google Scholar]
- 120.Campanelli A., Ramondo F., Domenicano A., Hargittai I. Molecular Structure and Conformation of Tert-Butylbenzene: A Concert. Study Gas-Phase Electron Diffr. Theor. Calc. J. Phys. Chem. 1994;98:11046–11052. doi: 10.1021/j100094a011. [DOI] [Google Scholar]
- 121.Shen Q., Wells C., Trætteberg M., Bohn R., Willis A., Knee J. Molecular Structure and Conformation of Cyclopropylbenzene as Determined by Ab Initio Molecular Orbital Calculations, Pulsed Jet Fourier Transform Microwave Spectroscopic, and Gas-Phase Electron Diffraction Investigations. J. Org. Chem. 2001;66:5840–5845. doi: 10.1021/jo010293u. [DOI] [PubMed] [Google Scholar]
- 122.Lide D. Structure of the Isobutane Molecule; Change of Dipole Moment on Isotopic Substitution. J. Chem. Phys. 1960;33:1519–1522. doi: 10.1063/1.1731435. [DOI] [Google Scholar]
- 123.Cochran J., Hagen K., Paulen G., Shen Q., Tom S., Trætteberg M., Wells C. On the Planarity of Styrene and its Derivatives: The Molecular Structures of Styrene and (Z)-β-Bromostyrene as Determined by Ab Initio Calculations and Gas-Phase Electron Diffraction. J. Mol. Spectrosc. 1997;413–414:313–326. doi: 10.1016/S0022-2860(97)00071-9. [DOI] [Google Scholar]
- 124.Rudolph H., Demaison J., Császár A. Accurate Determination of the Deformation of the Benzene Ring Upon Substitution: Equilibrium Structures of Benzonitrile and Phenylacetylene. J. Chem. Phys. A. 2013;117:12969–12982. doi: 10.1021/jp408208s. [DOI] [PubMed] [Google Scholar]
- 125.Karle I., Brockway L. The Structures of Biphenyl, O-Terphenyl Tetraphenylene. J. Am. Chem. Soc. 1942;66:1974–1979. doi: 10.1021/ja01239a057. [DOI] [Google Scholar]
- 126.Isea R. What is the maximum stretching for a C–C single bond? J. Mol. Struct. 2001;540:131–138. doi: 10.1016/S0166-1280(00)00721-1. [DOI] [Google Scholar]
- 127.Rösel S., Balestrieri C., Schreiner P.R. Sizing the Role of London Dispersion in the Dissociation of All-meta Tert-Butyl Hexaphenylethane. Chem. Sci. 2017;8:405–410. doi: 10.1039/C6SC02727J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Fokin A.A., Zhuk T.S., Blomeyer S., Perez C., .Chernish L.V., Pashenko A.E., Antony J., Vishnevskiy Y.V., Berger R.J.F., Grimme S., et al. Intramolecular London Dispersion Interaction Effects on Gas-Phase and Solid-State Structures of Diamondoid Dimers. J. Am. Chem. Soc. 2017;139:16696–16707. doi: 10.1021/jacs.7b07884. [DOI] [PubMed] [Google Scholar]
- 129.Wagner J., Schreiner P. London Dispersion in Molecular Chemistry—Reconsidering Steric Effects. Angew. Chem. Int. Ed. 2015;54:12274–12296. doi: 10.1002/anie.201503476. [DOI] [PubMed] [Google Scholar]
- 130.Folkertsma E., Benthem S.H., Jastrzebski J.T., Lutz M., Moret M.E., Gebbink R.J.K. 1,2-Addition of Diethylzinc to a Bis(Imidazolyl)ketone Ligand. Eur. J. Inorg. Chem. 2018;2018:1167–1175. doi: 10.1002/ejic.201701363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Qiu Z., Pham H.D.M., Li J., Li C.C., Castillo-Pazos D.J., Khaliullin R.Z., Li C.J. Light-enabled metal-free pinacol coupling by hydrazine. Chem. Sci. 2019;10:10937–10943. doi: 10.1039/C9SC03737C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Schneider W.F., T Nance B.I., Wallington T.J. Bond Strength Trends in Halogenated Methanols: Evidence for Negative Hyperconjugation? J. Am. Chem. Soc. 1995;117:478–485. doi: 10.1021/ja00106a055. [DOI] [Google Scholar]
- 133.Wiberg K.B., Rablen P.R. Origin of the Stability of Carbon Tetrafluoride: Negative Hyperconjugation Reexamined. J. Am. Chem. Soc. 1993;115:614–625. doi: 10.1021/ja00055a034. [DOI] [Google Scholar]
- 134.Johansson M.P., Swart M. Intramolecular halogen–halogen bonds? Phys. Chem. Chem. Phys. 2013;15:614–625. doi: 10.1039/c3cp50962a. [DOI] [PubMed] [Google Scholar]
- 135.Lunell S., Huang M.B. Theoretical Confirmation of the E.S.R. Spectrum of the Ethane Cation. J. Chem. Soc. Chem. Commun. 1989;15:1031–1033. doi: 10.1039/c39890001031. [DOI] [Google Scholar]
- 136.Huang M.B., Lunell S. Equilibrium Structure and Hyperfine Parameters of the Ethane Cation. Chem. Phys. 1990;147:85–90. doi: 10.1016/0301-0104(90)85023-P. [DOI] [Google Scholar]
- 137.Tsuzuki S., Uchimaru T. Accuracy of Intermolecular Interaction Energies, Particularly Those of Hetero-atom Containing Molecules Obtained by DFT Calculations with Grimme’s D2, D3 and D3BJ Dispersion Corrections. Phys. Chem. Chem. Phys. 2020;22:11543–11553. doi: 10.1039/D0CP03679J. [DOI] [PubMed] [Google Scholar]
- 138.Klein D. Organic Chemistry. Wiley; Hoboken, NJ, USA: 2015. [Google Scholar]
- 139.Bakowicz J., Turowska-Tyrk I. Structural Transformations in Crystals Induced by Radiation and Pressure. Part 10. The Crystallographic Picture of Photochemical Behaviour of bi(anthracene-9,10-dimethylene) under High Pressure. Crystals. 2020;10:1031. doi: 10.3390/cryst10111031. [DOI] [Google Scholar]
- 140.Wang D., Yan Y., Zhou D., Liu Y. Evolution of Crystal and Electronic Structures of Magnesium Dicarbide at High Pressure. Nature Sci. Rep. 2020;5:17815/1–17815/8. doi: 10.1038/srep17815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Neves W.Q., Alencar R.S., Ferreira R.S., Torres-Dias A.C., Andrade N.F., San-Miguel A., Kim Y.A., Endo M., Kim D.W., Muramatsu H., et al. Effects of Pressure on the Structural and Electronic Properties of Linear Carbon Chains Encapsulated in Double Wall Carbon Nanotubes. Carbon. 2018;133:446–456. doi: 10.1016/j.carbon.2018.01.084. [DOI] [Google Scholar]
- 142.Chen M., Christmann A.M., Muniz A.R., Ramasubramaniam A., Maroudas D. Molecular-Dynamics Analysis of Nanoindentation of Graphene Nanomeshes: Implications for 2D Mechanical Metamaterials. ACS Appl. Nano Mater. 2020;3:3613–3624. doi: 10.1021/acsanm.0c00327. [DOI] [Google Scholar]
- 143.Rojas W.Y., Winter A.D., Grote J., Kim S.S., Naik R.R., Williams A.D., Weiland C., Principe E., Fischer D.A., Banerjee S., et al. Strain and Bond Length Dynamics upon Growth and Transfer of Graphene by NEXAFS Spectroscopy from First-Principles and Experiment. Langmuir. 2018;34:1783–1794. doi: 10.1021/acs.langmuir.7b03260. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data presented in this study are available in Supplementary Materials.