A Deterministic Ratchet for Sub-micrometer (Bio)particle Separation

Abstract

Resolving the heterogeneity of particle populations by size is important when the particle size is a signature of abnormal biological properties leading to disease. Accessing size heterogeneity in the sub-micrometer regime is particularly important to resolve populations of sub-cellular species or diagnostically relevant bioparticles. Here, we demonstrate a ratchet migration mechanism capable of separating sub-μm sized species by size and apply it to biological particles. The phenomenon is based on a deterministic ratchet effect, is realized in a microfluidic device and exhibits fast migration allowing separation in tens of seconds. We characterized this phenomenon extensively with the aid of a numerical model allowing to predict the speed and resolution of this method. We further demonstrate the deterministic ratchet migration with two sub-μm sized beads as model system experimentally as well as size-heterogeneous mouse liver mitochondria and liposomes as model system for other organelles. We demonstrate excellent agreement between experimentally observed migration and the numerical model.

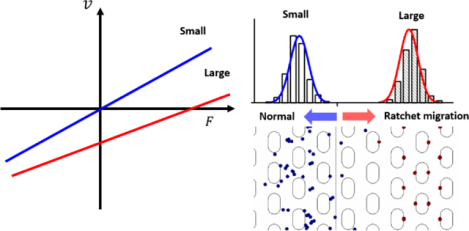
Graphical Abstract

INTRODUCTION

The vast complexity of biological particles requires efficient strategies for separation and fractionation in order to study variations of biomolecular signatures qualitatively and quantitatively. Bioparticles span a large size range comprising several orders of magnitude from a few hundred nm to several tens of micrometers. Typically, mammalian cells have extensions of several tens of micrometers, whereas their sub-cellular organelles are mostly sub-μm sized. The latter are crucial for many cell functions, such as cell metabolism or energy generation and their malfunction can give rise to disease. Other bioparticles such as exosomes comprise ~50–100 nm sized entities, are excreted from cells and thus found in body fluids. The analysis of such small bioparticles is extremely important for diagnostic purposes. Fractionation and separation techniques for such sub-μm bioparticles are, however, scarce limiting fundamental bioanalytical studies and diagnostic applications. Here, we demonstrate a novel approach for fractionation of sub-μm-sized particles, including organelles, based on a unique deterministic ratchet migration mechanism.

An intrinsic problem in organelle analysis is the complexity of cell lysate from which they need to be recovered. Ultracentrifugation approaches are suitable for separating into specific organelle fractions, such as in differential centrifugation¹ or density gradient centrifugation². Other approaches are based on biomarkers, allowing extraction strategies based on binding to suitable affinity reagents often bound to a solid support such as beads³. However, this approach is limited by the selectivity of the affinity reagents and the availability of a biomarker on the target bioparticle⁴. In addition, in some cases, the biological malfunction may be associated with the size of the bioparticles requiring effective methods for separation of subpopulations by size to further study the underlying biomolecular causes of malfunction⁵. This is apparent for mitochondria and lipid droplets, where abnormally sized or giant organelles indicate malfunction of cells. They have been attributed to playing a role in diseases such as amyotrophic lateral sclerosis⁶ and atrophy⁷, lesions⁸, acute lymphocytic leukemia⁹, Huntington’s disease¹⁰, paraganglioma¹¹ and kidney nephrotic syndrome¹².

Methods, allowing fractionation of organelles by size are limited and only a few approaches based on free flow fractionation^13,14 or continuous sorting in a microdevice¹⁵ have been demonstrated previously. Ratchet migration mechanisms have demonstrated to induce size selective transport^16,17. Such migration mechanisms typically involve an asymmetric structure, a periodic driving force for particles and a stochastic element such as Brownian motion¹⁸. The interplay of these ‘ingredients’ allows transport at zero applied force, size-selective transport and under selected conditions steering of differently sized particles into opposite directions. Ratchet devices have been used for fast transport of particles^19,20 and have shown to induce separation in periodic systems with broken spatial symmetry^21,22, or with symmetrical post arrays when combined with hydrodynamic flow²³. However, applications for biological particles are often limited to objects of similar size to whole cells, not allowing the application for sub-μm sized particles, such as organelles.

Designing ratchet devices for sub-μm particles typically requires designing nm-sized features to restrict particle migration into a specific direction and induce a ratchet-like migration. However, combining ratchet concepts with additional trapping forces, such as for example dielectrophoresis (DEP), can lead to deterministic ratchet transport¹⁵, as recently shown for μm-sized latex beads²⁴. Such concepts can in principle also be applied to bioparticles, but the complexity of the structural design elements inducing ratchet migration and the interplay of the underlying dielectrophoretic forces require detailed analysis of the involved size selectivity, which has not been addressed comprehensively.

Dielectrophoresis (DEP) refers to the migration of polarizable particles in a non-uniform electric field²⁵. The DEP force scales with the particle size to the third power as well as the electric field gradient, thus providing a tunable parameter for size-based separation of μm- and sub-μm sized particles. Recently, DEP has been used to induce ratchet migration as a tool for trapping and patterning colloidal particles²⁶ and for analyzing particles differing in their electrical properties²⁷. Gorre-Tallini presented a Brownian ratchet employing dielectrophoretic potential barriers for latex particles²⁸. In a variation of this concept, the same authors designed a shifted ratchet, in which electrode based DEP could be employed to induce differential particle transport for μm-sized latex beads²⁸.

Here, we present a DEP-based ratchet migration mechanism in a non-linear, yet symmetrical post array applying the separation capabilities of particle ratchets in the sub-μm size range and demonstrate the application for organelles. This novel size-selective migration was studied for 0.28 μm and 0.87 μm polystyrene beads employing insulator-based dielectrophoresis. A numerical model adapted to the electrokinetic and dielectrophoretic properties of the polystyrene beads was developed in very good agreement with the experimentally observed ratchet mechanism. The numerical model further allowed to study the separation quality dependent on driving parameters for sufficiently large particle numbers revealing baseline resolution in one driving period corresponding to 10 seconds. In addition, the DEP-based ratchet migration was demonstrated for mouse hepatic mitochondria and resulted in good agreement with the numerical model. Our work is critical to further develop ratchet-based migration for the separation of sub-μm sized bioparticles including organelles.

EXPERIMENTAL SECTION

Materials and Chemicals

0.28- (FP-0262–2) and 0.87-μm-diameter (FP-0852–2) polystyrene beads exhibiting negative surface charges were purchased from Spherotech (Lake Forest, IL, USA). SYLGARD^® 184 silicone elastomer kit for polydimethylsiloxane (PDMS) was purchased from Dow Corning Corporation (Midland, MI, USA). 4-(2-hydroxyethyl)piperazine-1-ethanesulfonic acid (HEPES), poly(ethylene glycol)-block-poly(propylene glycol)-block-poly(ethylene glycol) (brand name Pluronic^® F108), potassium hydroxide (KOH), potassium chloride (KCl), potassium phosphate dibasic anhydrous (K₂HPO₄), magnesium chloride (MgCl₂), dimethyl sulfoxide (DMSO), Phosphatidylcholine (PC), phosphatidylethanolamine (PE), phosphatidylserine (PS), cholesterol and sucrose were purchased from Sigma-Aldrich (St. Louis, MO, USA). Deionized (DI) water was obtained from a Synergy purification system (Millipore, USA). Fisherbrand^® Plain Microscope glass slides (75 × 50 × 1.0 mm; USA), DiD (1,1’-Dioctadecyl-3,3,3’,3’-Tetramethylindodicarbocyanine Perchlorate) and DiO (3,3’-Dioctadecyloxacarbocyanine Perchlorate) were purchased from Thermo Fisher Scientific Inc. (Waltham, MA, USA). Gold-Seal coverslips were purchased from Electron Microscopy Sciences (48 × 60 mm, No. 1; Hatfield, PA, USA). Platinum wire was purchased from Alfa Aesar (Ward Hill, MA, USA). Extruder kits were purchased from Avanti Polar Lipids (Alabaster, AL).

Microchip fabrication

A silicon master wafer patterned with the inverse of the microfluidic structures was fabricated by photolithography as described before²⁹. The master wafer was employed for elastomer molding using soft lithography. Briefly, the PDMS silicone elastomer base and curing agent were mixed at a 10:1 ratio (w/w), poured onto the master wafer, degassed under vacuum, and cured in an oven for at least 4 h at 80 °C. The PDMS mold was then peeled off from the master wafer resulting in channels with a depth of 10 μm, and 2-mm-diameter reservoirs were manually punched at the channel ends. The PDMS mold was then cleaned with isopropanol and distilled water and was dried in a stream of nitrogen. A glass slide was cleaned, dried and then spin-coated at 1300 rpm for 30 seconds with PDMS pre-polymer similarly prepared as the PDMS mold. Subsequently, the PDMS-coated glass was placed in an oven for at least 4 hours at 80 °C resulting in an approximately 20 μm thick PDMS layer. In order to minimize the PDMS autofluorecence³⁰, the PDMS mold containing the microchannel and the PDMS-coated glass were exposed to UV light for 1 hour. Then they were treated with oxygen plasma (PDC-001; Harrick Plasma, Ithaca, NY, USA) at high RF for 1 min and assembled to form a sealed microchannel. The microfluidic channel was 1 cm long and contained an array of posts (see Figure 1(a)).

Figure 1.

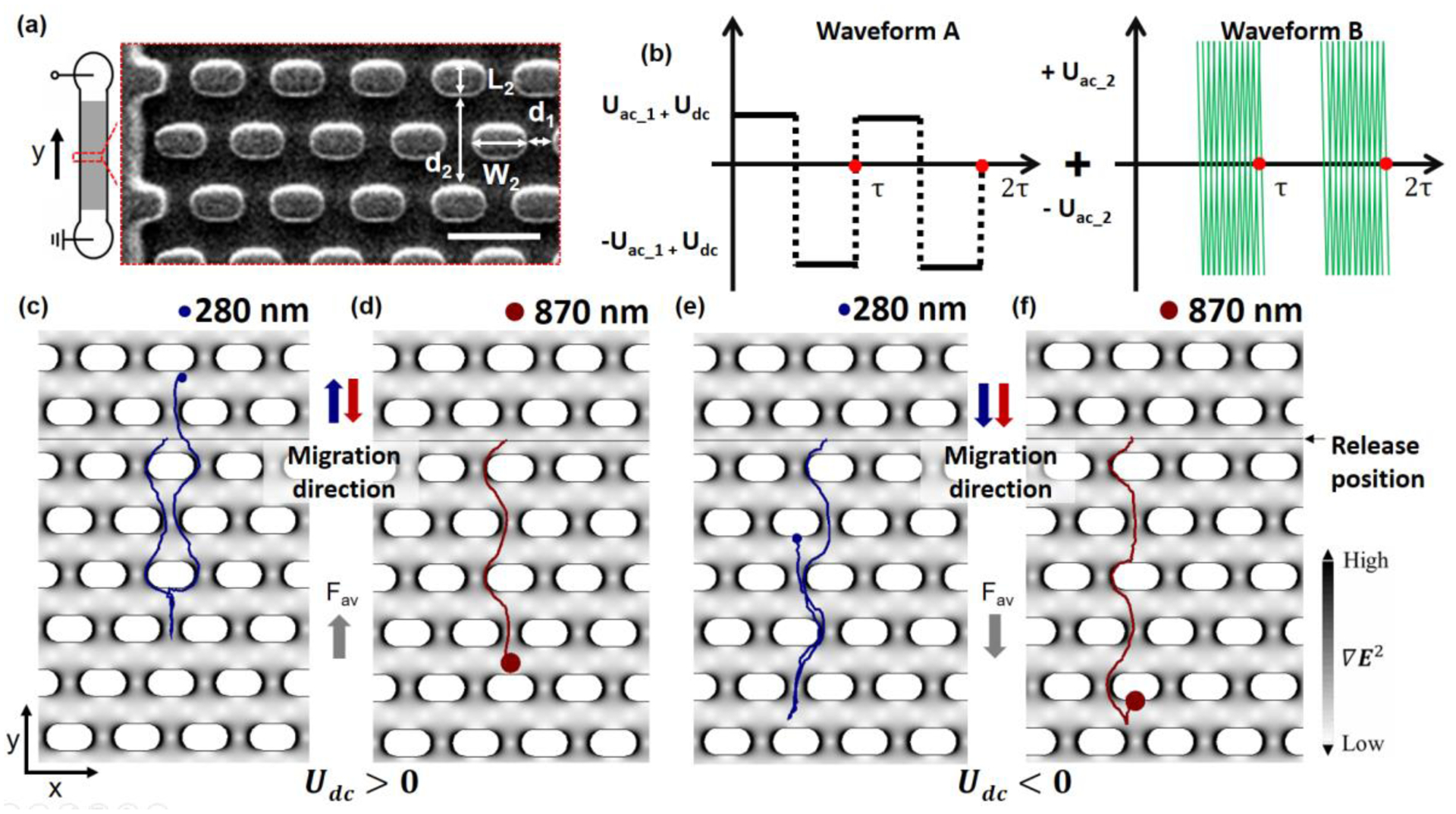
(a) The top view of the 1-cm long channel with the shaded area (gray) indicating the post array region. The enlargement shows a partial view of the PDMS post region (SEM image). The width of fluidic channel is 285 μm and the post array details are indicated with the white arrows (post length L₂ = 17 μm, post width W₂ = 10 μm, horizontal gap size d₁ = 8 μm and row spacing d₂ = 20 μm). Electrodes are immersed into the reservoirs (2 mm diameter) to apply potentials across the microchannel. Scale bar in the SEm image of (a) is 30 μm. b) Waveform A switches periodically between ±U_{ac_1} with a DC potential offset, U_dc, giving rise to a biased voltage (here for U_dc >0). Waveform A is superimposed with a high frequency sinusoidal signal of amplitude U_{ac_2} and frequency f. τ indicates the length of each complete period, and two periods are depicted here. (c-f) show images of trajectories obtained from the numerical model for small and large beads. (c-d) depict the case positive offset (U_dc =10 V) and (e-f) for negative U_dc (U_dc =−10V) after one driving period with U_{ac_1}= 50, U_{ac_2}= 800 V (with f=30 kHz) and τ=10 s. Trajectories are shown for a 0.87 μm (red) and a 0.28 μm (blue) particle and the distribution of the electric field gradient is shown in gray scale in (c-f). The electric field is applied along the y-direction. Particles were released at t = 0 from the release line (black horizontal line) in (c-f).

Fluidic operations

All the experiments were performed using the microfluidic device schematically shown in Figure 1(a). After assembly, each channel was filled with solution A (1 mM F108, 10 mM HEPES, pH adjusted to 7.4 by KOH, sterile-filtered to 0.2 μm) by capillarity immediately and the chip was placed in a humid environment overnight (16 – 24 hours) to coat all surfaces with F108. Solution B (250 mM sucrose in solution A, pH 7.4, 0.03 S/m, sterile-filtered to 0.2 μm) was used to prepare the mitochondria or the polystyrene bead suspension (see also below) and to rinse the channel for three times right before use. A low conductivity buffer (0.03 S/m) was employed to minimize Joule heating effects.³¹ A 0.5-cm-thick PDMS holder was employed to increase reservoir volume and provide stability for the electrodes on top of the assembled device. The prepared bead or mitochondrial suspension was added to an inlet reservoir and solution B to another reservoir. Mineral oil was added on top of the liquid layer in both reservoirs to prevent evaporation. Pt electrodes attached to the reservoirs were connected via micro-clamps (LabSmith, Livermore, CA, USA) to an AC power supply from a high voltage amplifier (AMT-3B20, Matsusada Precision Inc.) driven through a Multifunction DAQ card (USB X Series, National Instruments, TX, USA) programmed by LabVIEW 2014 (version 14.0, National Instruments).

Preparation of bead, mitochondrial and liposome suspensions

The bead suspension was prepared by diluting 1 μL original bead suspension from the manufacturer in 100 μL solution B. Then, the beads were rinsed for three times by repeating a procedure of 1 min vortex, centrifugation at 10000g for 5 min, removing the supernatant and resuspension of the pellet in 100 μL solution B. After rinsing, the bead suspension was sonicated for 1 hour.

The mitochondrial samples were prepared from the liver of a four-week old male C57BL/6 mouse. All mice were housed in a designated clean facility and treated in accordance with protocols approved by the Institutional Animal Care and Use Committee at the University of Minnesota. In general, once the mitochondrial samples were prepared according to the procedures described previously²⁴, they were flash-frozen in a liquid nitrogen Dewar. Then, the mitochondrial samples were shipped from the University of Minnesota to Arizona State University on dry ice and stored in a nitrogen Dewar flask when received.

One day prior to the experiment, a vial of the mitochondrial sample was transferred to a −80°C freezer. At the time of experimentation, 1 mM MitoTracker Green (Life Technologies, USA) stock solution in DMSO was thawed to room temperature, diluted by solution C (100 mM sucrose, 125 mM KCl, 10 mM HEPES, 2 mM K₂HPO₄, 5 mM MgCl₂, pH adjusted to 7.4 by KOH, sterile-filtered to 0.2 μm) and added to mitochondria sample to reach a final concentration of 800 nM MitoTracker Green. The mitochondrial suspension was incubated at 37 °C with gentle shaking (160 rpm) for 15 min and then centrifuged (10000g) for 10 min followed by removal of the supernatant. The resulting pellet was resuspended gently in solution B followed by a 5-min centrifugation (10000g) step. After removing the supernatant, the resulting mitochondrial pellet was re-suspended in solution B.

The liposome samples were prepared based on a previous study³². Phospholipid stock solutions containing 0.012 M of PS, 0.013 M of PE, 0.0129M of PC, and 0.025M of cholesterol were dissolved in chloroform. Their molar ratio was 47.3:2.3:42.9:7.5 respectively in a two separate 20-mL of glass vial. Each glass vial contained a total volume of 1mL phospholipids stock solution. The solvent was evaporated overnight under a stream of nitrogen at room temperature and vacuum to remove trace of organic solvent. After all solvent was evaporated, 1mL of solution A containing lipophilic tracers (DiO and DiD) were added to each vial. One vial contained red fluorophore (DiD) and the other vial contained green fluorophore (DiO). The suspensions were vortexed for 1 min and placed at 4 °C for 2 h. DiD labeled liposomes were forced through a polycarbonate filter (pore diameter 200-nm) to yield uniform small liposome fraction via extrusion. After five times washing by spinning at 13800g for 5 min, the suspension was re-dispersed in solution A. After the particle preparation, the size, surface charge and electrophoretic mobility of the particles were measured using a Nanosight NS300 and Zetasizer Nano ZS system (both from Malvern Instruments, UK), see supporting information for details.

Detection and data analysis

Fluorescence images were acquired with an inverted microscope (IX71, Olympus, Center Valley, PA, USA) equipped with a 100 W mercury burner (U-RFL-T, Olympus, Center Valley, PA, USA) and fluorescence filter set (for mitochondria and 0.87-μm beads: exciter ET470/40, dichroic T495LP, emitter ET525/50, Semrock, USA; for 0.28-μm beads: exciter 607/36, emitter 670/39). The migration of mitochondria in the microchannel was visualized by a 60× (UPLSAPO60×W, water immersion, NA = 1.20) objective and the bead migration was visualized by the 60× objective or a 40× (LUCPlanFLN, NA = 0.60) objective. Images were captured by a CCD camera (QuantEM:512SC, Photometrics, Tucson, AZ, USA) and Micro-Manager software (version 1.4.7, Vale Lab, UCSF, CA, USA). The obtained videos for mitochondria or beads were then processed by ImageJ software (version 1.49, NIH). For each data point in the ratchet velocity profile for beads (Figure 3) or mitochondria (Figure 4), 20 individual trajectories of beads or mitochondria per microchannel in a complete period at the specific driving conditions were evaluated using the Manual Tracking plugin³³. The experiment was repeated in three channels for beads and mitochondria, respectively.

Figure 3.

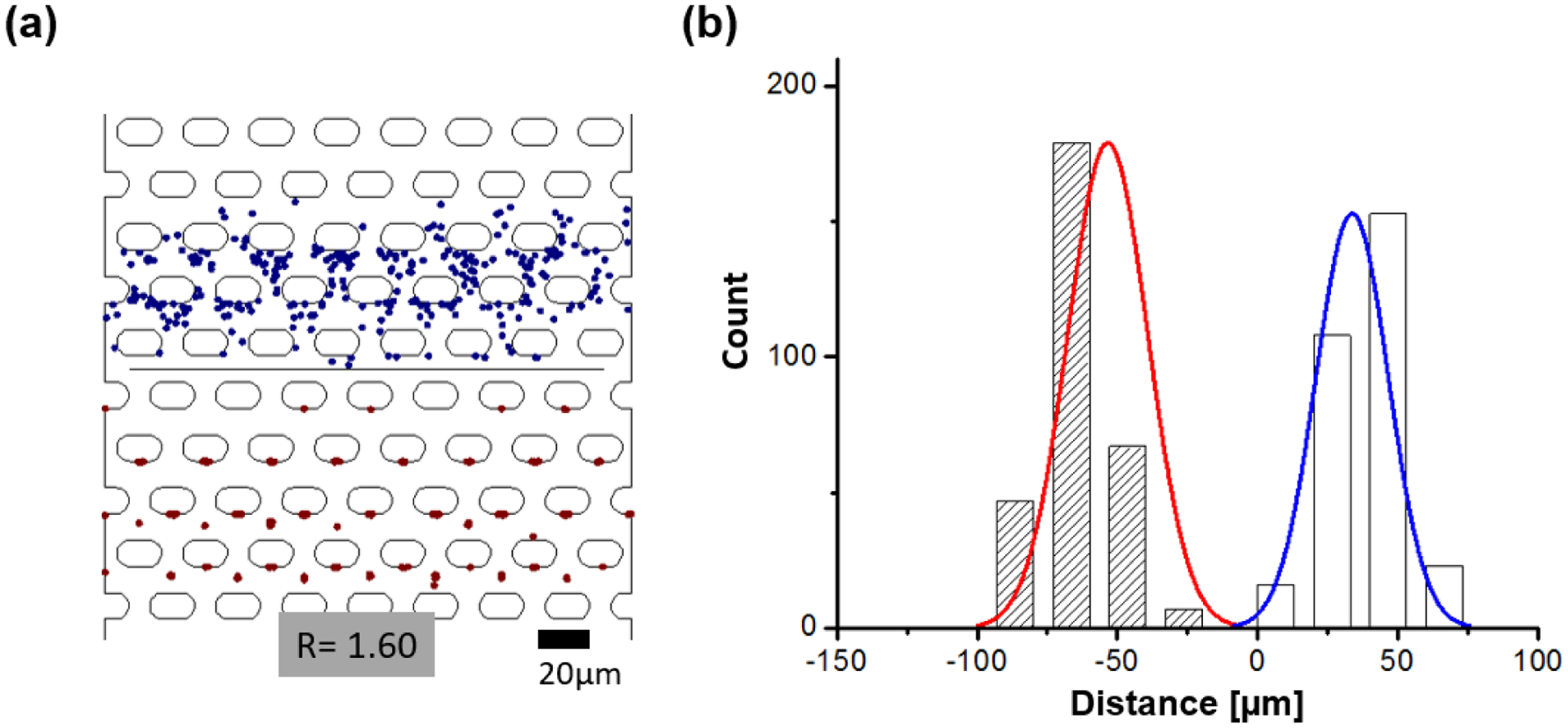
a) Snapshot image of particle end positions after one complete period (10s) as obtained from the numerical model 0.28 μm particles are represented with blue dots and 0.87 μm particles in red). Particles are subject to one driving period at U_{ac_1}= 50 V, U_dc = 10 V and U_{ac_2}= 800 V at a frequency of 30 kHz. Particles were released at t = 0 from the release line (black horizontal line) in the middle of the channel section. b) Histogram and Gaussian fit of the particle end positions (N = 300). The red curve indicates the Gaussian fir for the 0.87 μm and the blue curve for the 0.28 μm particles. The resultant resolution is 1.60. The distance in μm on the x-axis indicates the particle migration distance from the particle release line in the numerical model.

Figure 4.

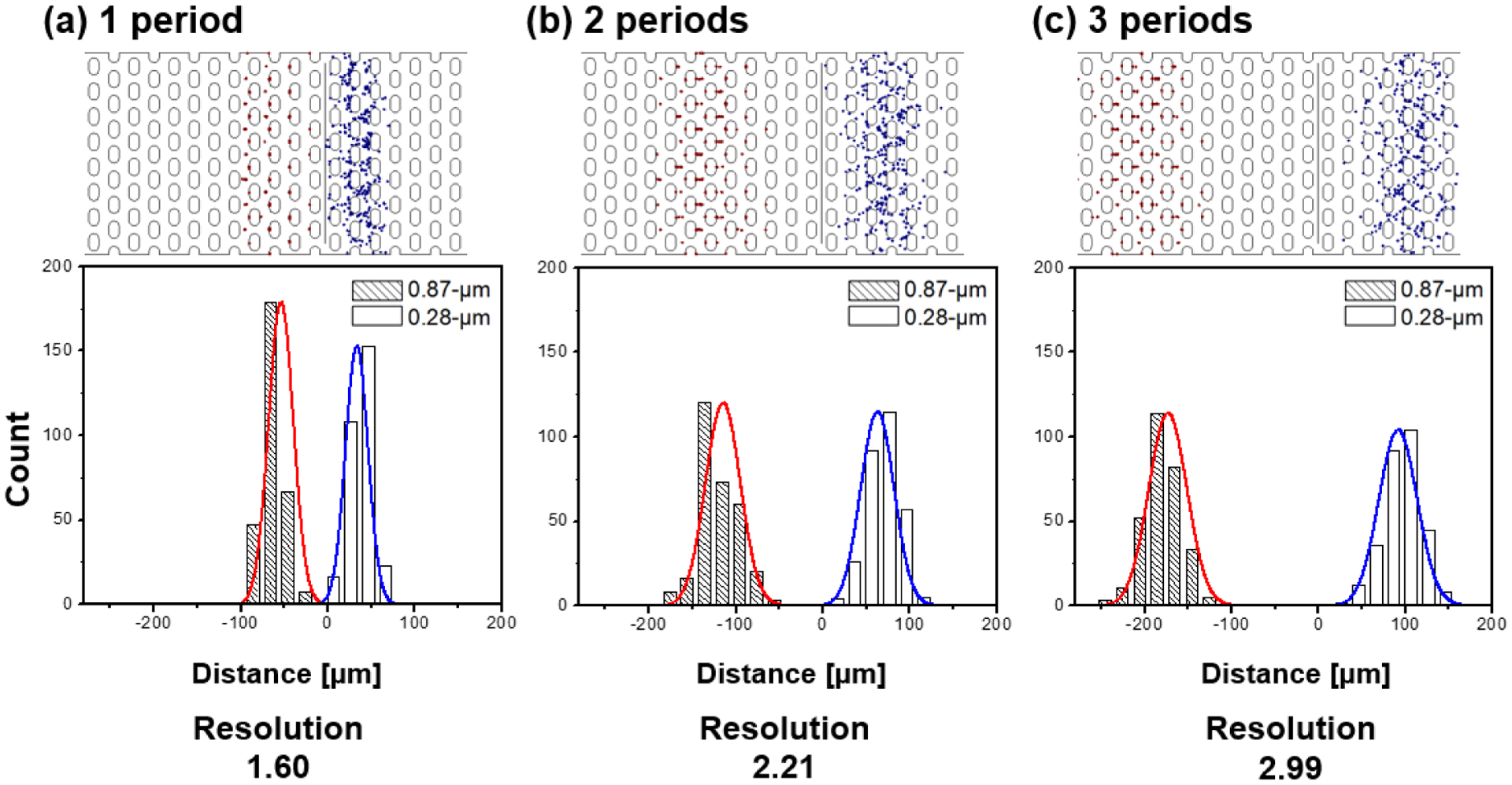
Histogram and Gaussian fit are shown for the 0.87 μm(red) and 0.28 μm(blue) beads comparing the resolution at the end of multiple periods (n = 1,2,3). 300 particles are studied at U_{ac_1}= 50 V, U_dc = 10 V and U_{ac_2}= 800 V at f = 30 kHz (τ = 10 s) in the numerical study. The resultant resolution values are (a) 1.60, (b) 2.21 and (c) 2.99, respectively. The distance in μm on the x-axis indicates the particle migration distance from the particle release line in the numerical model.

Numerical Modeling

Numerical modeling was performed using COMSOL Multiphysics 5.3 according to a model previously described²⁴ by Luo et al. and as specified in the supporting information. Briefly, the model was adapted to reflect the AC waveform employed in this manuscript as shown in Figure 1b and particle properties including the zeta potential and electrophoretic mobility as determined experimentally with the current monitoring method (see details in the supporting information)^34,35. The non-linear spatially periodic structure was re-drawn in the model. The electric field in the post array was calculated for an 800 μm long section with potentials applied at the extremities of the device section in accordance with previous works^36–38. The potentials were adapted to match the overall experimentally applied electric field, E, to the actual channel section in the model.

The static study result of the Electric Current module was combined with a rectangle and an analytic function, resulting in a tunable alternating current electric field with a complex waveform represented schematically in Figure 1b and described with equation 1. The result was then coupled with a time-dependent study using the Creeping Flow module. Finally, the particle trajectories were solved for individual particles considering the DEP force (F_dep), the drag force (F_D) and the Brownian force (F_B) with the Particle Tracing for Fluid Flow module according to:

$$\frac{m_{p}v}{\Delta t}=F_D+F_{dep}+F_B$$

where, v is the particle velocity, m_p is the particle mass and Δt is the time step. To reflect the electrophoretic force acting on the particles, the electrophoretic mobility was included in the drag force (F_D) as velocity component. For the detailed equations and parameters used, see the supporting information. The particle trajectory was then visualized by solving the instant velocity of a particle time-dependently as previously shown by Luo et al.²⁴. The mitochondria were considered spherical reflecting their shape after tissue isolation and suspended in buffer solution³⁹.

The waveform used to induce migration via applying an electric potential across the entire channel with waveform g(t) is defined as follows:

$$g\left(t\right)=\underset{\text{Waveform}\text{A}}{\underbrace{\left\{-U_{a{c}_{-}1}\times sgn\left[\mathit{\text{sin}}\left(\frac{2\pi }{\tau }t\right)\right]+U_{dc}\right\}}}+\underset{\text{Waveform}\text{B}}{\underbrace{\left\{U_{a{c}_{-}2}\times \frac{1}{2}\left\{sgn\left[\mathit{\text{sin}}\left(\frac{2\pi }{\tau }t\right)\right]-1\right\}\times \mathit{\text{sin}}(2\pi ft)\right\}}}$$ eq. 1

Here, t is the time, τ is the period of waveform A and B, and U_dc corresponds to the magnitude of the DC offset voltage. U_{ac_1} and U_{ac_2} denote the amplitudes for the low frequency and high frequency AC waveforms respectively. The frequency of waveform B is denoted f. In the numerical model, the dielectrophoretic force is included via the size-selective particle trapping induced by the magnitude of U_{ac_2}. The results obtained from this model are shown in Figure 2–6 and discussed in detail in the Results and Discussion section.

Figure 2.

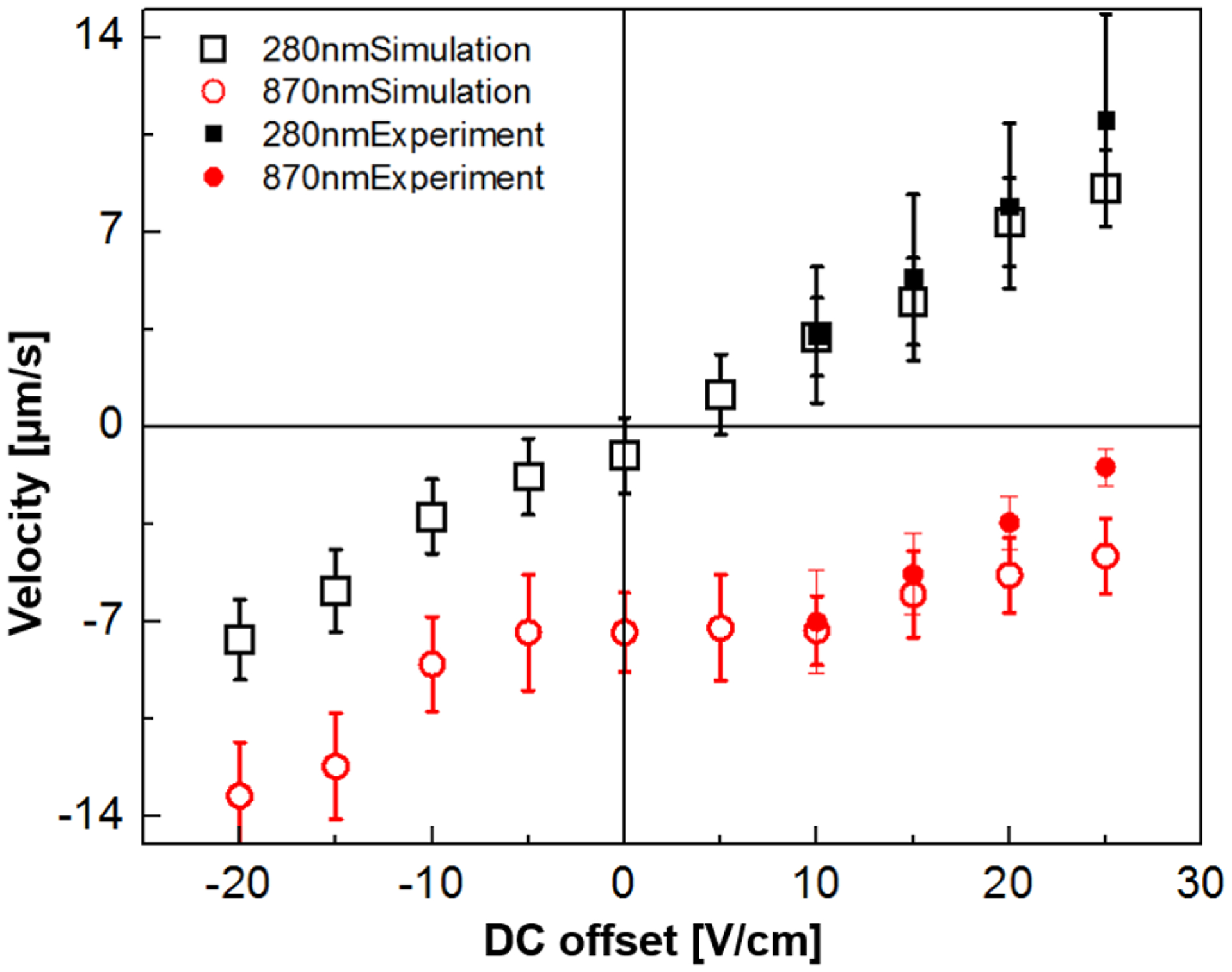
Velocity variations of 0.28- and 0.87-μm-diameter polystyrene beads (empty symbols for numerical modeling results and solid symbols for experimental data) along the microchannel constriction at various U_dc. The magnitude of the U_{ac_1} (τ=10s) and U_{ac_2} (f=30 kHz) were maintained at 50 V and 800 V, respectively. The error bars indicate the standard deviation of average velocity obtained at each U_dc by tracking 60 or 300 individual trajectories from the experimental or the simulation results, respectively. At the applied U_dc conditions from 0 to + 30 V in both the experiment and the numerical modeling, the average velocities of 0.87 μm particles were in the opposite direction to the applied U_dc, showing apparent ratchet migration, whereas 0.28 μm particles showed the normal response with positive migration velocities according to the sign and magnitude of U_dc.

Figure 6.

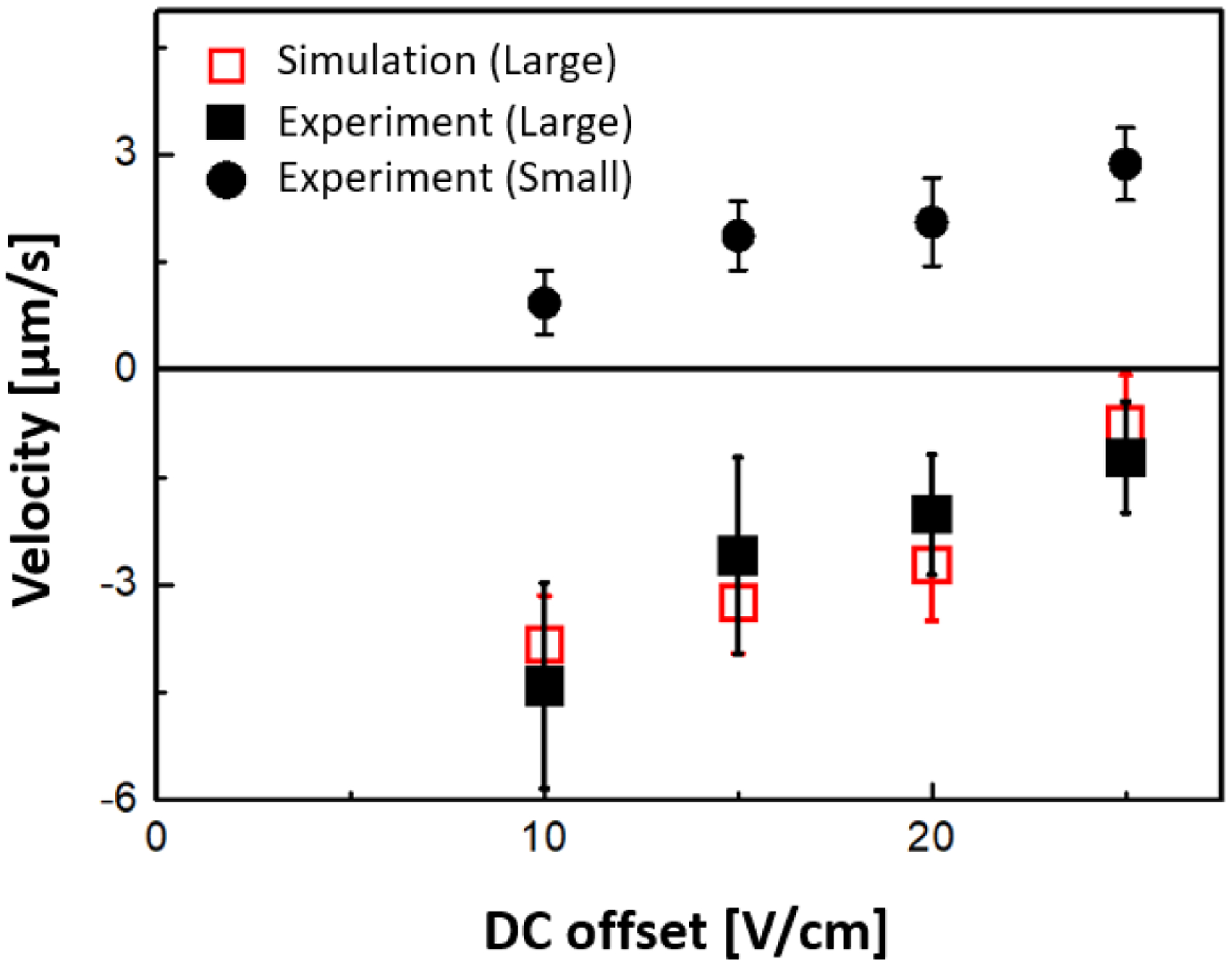
Experimental and simulation results of velocity vs. U_dc for the isolated mouse hepatic mitochondria. The error bars indicate the standard deviation of average velocity obtained at each U_dc by tracking individual trajectories (10 particles for the small mitochondria and 60 particles for large mitochondria) from the experimental results, respectively. Here, U_{ac_1} = 35 V for U_dc = 25 V, U_{ac_1} = 40 V for U_dc = 20 V, U_{ac_1} = 45 V for U_dc = 15 V, and U_{ac_1} = 50 V for U_dc = 10 V were applied for one complete period with U_{ac_2} of 800 V and f = 30 kHz to induce DEP-based ratchet migration. At these experimental conditions, the average migration velocities of large mitochondria (black square) were negative demonstrating the ratchet mechanism and the average migration velocities of small mitochondria (black circles) were positive showing the normal migration. Red open squares indicate simulation results for 650 nm sized organelles (300 particles for large mitochondria were simulated).

A useful parameter to describe separation problems is the resolution, R. According to Giddings, R is defined as⁴⁰:

$$R=\frac{1.18\left(d_1-d_2\right)}{W_1+W_2}$$ eq. 2

where d₁ and d₂ refer to the average distance from the initial position and W₁ and W₂ are the full widths at half maximum of Gaussian fits of the position distribution. R was obtained for both particle number and period variation by extracting the location of particle sizes after each period from the resulting end coordinates in the COMSOL model. The corresponding positions were represented in a histogram by splitting the data into bins of equal size with Origin software (OriginLab Corp., Northampton, MA, USA). Then, a Gaussian curve was fitted to the histogram and the resolution (eq.2) was calculated from the full width at half maximum for each Gaussian.

RESULTS AND DISCUSSION

Description of ratchet device and migration mechanism

To demonstrate the novel DEP-based ratchet for sub-μm sized particles, a device as depicted in Figure 1a was employed. This device geometry was chosen to induce the ratchet mechanisms for particles exhibiting negative DEP, such as polystyrene beads or mitochondria²⁴. The microchannel contained a periodic array of micro-posts as depicted in Figure 1a. All rows had a constant distance with a period of 20 μm whereas each second row was shifted in the x-direction by 12.5 μm compared to the previous row. This creates a symmetric structure to which an asymmetric periodic electrical potential was applied to induce migration. The array of posts induces an inhomogeneous electric field, allowing DEP trapping of beads according to insulator-based dielectrophoresis. The migration mechanism thus is composed of a combination of the particles’ intrinsic electrokinetic migration, DEP migration and trapping components. We note that the Brownian motion does not contribute to the actual migration mechanism, but the variance of the particle velocities. This was tested independently modeling the migration with and without the Brownian force applied (data not shown). We thus classify this migration as deterministic.

The applied potentials are shown in a depictive scheme in Figure 1(b) and described in equation 1 (see numerical modeling section). Initially, periodic driving forces consisting of a square wave potential with amplitude U_{ac_1} is induced, to which a DC offset (U_dc) is added. The periodic driving is generated from the electric potential described in Waveform A of Figure 1(b). Considering this waveform only, electrokinetic migration is induced with opposing directions in the two half periods of waveform A (as long as |U_dc|<|U_{ac_1}|). In addition, an AC component of higher frequency with waveform B is overlaid in the second half period of waveform A inducing DEP. (Note that the amplitudes of waveform A are too small to induce DEP trapping, as determined experimentally for the employed particles.) Therefore, if DEP forces are large enough, particle trapping occurs in the second half driving period. The resulting migration of particles for U_dc > 0 results in two paths:

1. In path one (blue), particles are too small to induce DEP trapping. Thus, in one entire driving period, the small particle (blue) migrates in one direction first (first half driving period of waveform A), but reverses direction in the second half period (second half driving period of waveform A). The particle ceases migration just below the starting point (see Figure 1c).

2. A larger particle (red), starting at the same position as the blue particle, migrates similarly to the smaller particle in the first half driving period. However, in the second half driving period of waveform A, DEP trapping is induced due to waveform B. As a result, the larger particle is trapped and migration is stalled. DEP trapping occurs at positions near the posts where the electric field gradient is smallest, thus the trapping behavior originates due to nDEP. Correspondingly, the resulting trapping positions are at the flat side of the posts where the electric field are lowest (see Figure 1d).

The resulting migration direction of a particle over one entire driving period thus depends critically on the size of the particle and the induced DEP trapping force in the second half driving period. In the U_dc > 0, the smaller particles migrate in the opposite direction compared to the larger particles, as can be observed from the positions of the particles after one full driving period (Figure 1c–d). Overall, the smaller particles follow the average applied force in the “normal” direction, whereas the larger particles show a ratchet effect i.e. migration in the opposite direction.

For U_dc < 0, however, the two differently sized particles migrate overall into the same direction and show “normal” migration. This can be explained through the detailed migration in the first and second half driving periods of U_{ac_1}. Both particles respond to the applied potential with a migration in the same direction in the first half period of waveform A (Figure 1 e–f). The larger particles are trapped in the second half period (whereas their response to the first half period is almost identical to that of the smaller particles). The migration of the larger particles is thus primarily governed by the sum of U_{ac_1} and U_dc in the first half driving period (Figure 1f). The smaller particles are not trapped in the second half period and migrate in the opposite direction towards the release position. Since the absolute value of U_{ac_1} and U_dc now is smaller but opposite in sign (than in the first half driving period), the smaller particles cannot migrate fully to the release position (Figure 1e). Overall, they also show “normal” migration behavior, but of smaller velocity than compared with the larger particles. As a result, both particles migrate into the same direction overall.

Numerical model and experimental results

Figure 2 provides a summary of the above-described migration mechanism for the small and large particle species and compares experimental with numerical modeling data. The model parameters are described in the Numerical Modeling section and in the supporting information. According to the model results (see Figure 2), the ratchet signature was apparent for 0.87 μm diameter particles, whereas 0.28 μm diameter particles exhibited normal migration behavior. For positive U_dc, the larger particles show negative velocities, whereas smaller particles show positive velocities. The larger particles thus migrate in opposite directions compared to the smaller particles. This situation is advantageous for a separation or fractionation approach based on size, since the particles are spatially separated and can easily be collected. For negative U_dc, both particles migrated in the same direction, however, the larger particle somewhat slower, due to the induced DEP forces. In the following discussion, we will focus on the situation of positive U_dc, since largest differences in the migration velocities have been observed in this regime.

To investigate the ratchet migration experimentally, electrical driving parameters matching the numerical model were tested. The recorded migration velocities are shown in Figure 2 (filled symbols). The observed ratchet migration matches the numerical results in the occurrence of the ratchet migration for the 0.87 μm particles and the normal migration for the smaller 0.28 μm particles. It is apparent that the migration velocities as quantified from the numerical study match experimentally observed values in excellent agreement for large U_dc. Only at larger offsets, the experimentally observed values start to deviate. This discrepancy could be attributed to an overestimation of the dielectrophoretic trapping component. However, μ_dep is more difficult to be accessed experimentally through a direct measurement. We thus estimated μ_dep, based on known dielectric properties of polystyrene beads and measured medium conductivity (see details in the Supplementary Information). We note that μ_dep may change if other polarization mechanisms such as surface conductivity^41,42 contribute to the DEP behavior of beads which were not considered here. In addition, other sources such as slight differences in the post geometries between experiments and modelled geometry could also attribute to the differences in the migration velocities between model and experiment.

We further note that the ratchet mechanism was only observed for amplitudes of U_{ac_1} between 30 and 50 V (see Supplementary Information – Figure S-2). In this range, the migration velocities were independent of the applied amplitude of U_{ac_1}. We believe that the increase in U_dc is counteracted by the change in the amplitude of U_{ac_1}. In addition, the ratchet mechanism and necessary iDEP trapping were independent of the applied frequency and amplitude of waveform B, as long as trapping was induced. The here observed trapping regime matches previous observations for iDEP trapping of similarly sized beads¹⁵.

Resolution of Ratchet Separation Mechanism

To employ the novel DEP-based ratchet mechanism for separation applications, parameters describing the separation quality are important to assess. We have therefore employed the framework of the numerical modeling in conjunction with particle tracing analysis to investigate the separation resolution R of the DEP-based ratchet mechanism. For this purpose, the particle positions were analyzed for N = 40, 100, 300 and 500 particles after n periods (with n = 0,1,2,…) of length τ. From the resulting particle positions, R can be obtained.

Figure 3 shows the image of particle positions for driving conditions of U_{ac_1} = 50 V, U_dc= 10 V and U_{ac_1} = 800 V at f = 30 kHz. Depicted is the case of 300 particles for both small (0.28 μm) and large (0.87 μm) particle diameters. The model allows to construct histograms of particle positions as shown in Figure 3b which can be fit with a Gaussian to calculate R according to eq. 2. We investigated particle numbers from 40 up to 500 particles (see Figure S-3 for histograms and fits) but could show that the resolution does not change significantly when >100 particles are modelled. Videos showing particle migration and separation with the numerical model are also available in the Supplementary Information.

The numerical model allows retrieving additional information on the parameters influencing the separation resolution. Table 1 shows R depending on U_dc. In all cases, the resolution is satisfying for a separation experiment. In addition, we can access the influence of the number of periods employed, as shown in Figure 4. Up to three periods were tested, and not surprisingly, the separation resolution increased from 1.60 to 2.99. The supplementary video S-3 shows the results for 3 periods exemplarily.

Table 1:

R obtained at U_{ac_1} = 50 V and U_{ac_2} = 800 V at f = 30 kHz.

Udc [V]	R
0	1.04
5	1.24
10	1.60
15	1.79
20	1.91

Beyond studying two particle species, we have extended our study for four particle size species. Figure 5(a) shows the positions of three differently-sized particles for U_{ac_1} = 50 V, U_dc= 10 V and U_{ac_2} = 800 V at f = 30 kHz (τ = 10 s) after 4 driving periods. The simulation was carried out with 300 particles each for 0.87 (red), 0.52 (green), 0.28 μm (cyan) polystyrene beads with a period length of 40 s and n = 4. Histograms of the resulting particle location were constructed for the three different particle species and fit with a Gaussian, as shown in Figure 5(a). We find, that particles with sizes above 0.52 μm showed ratchet migration behavior (0.87μm and 0.52μm) and those below showed normal migration. Interestingly, the species with 0.52μm and 0.28μm are well resolved (R=2.19) indicating that the applied conditions allow to separate particles with 240nm size difference. We also note, that the 0.28 μm particles and 0.16 μm particles can be resolved with baseline resolution for U_{ac_2} = 1400 V as shown in Figure 5(b). The represented ratchet migration thus allows for separating sub-μm species.

Figure 5.

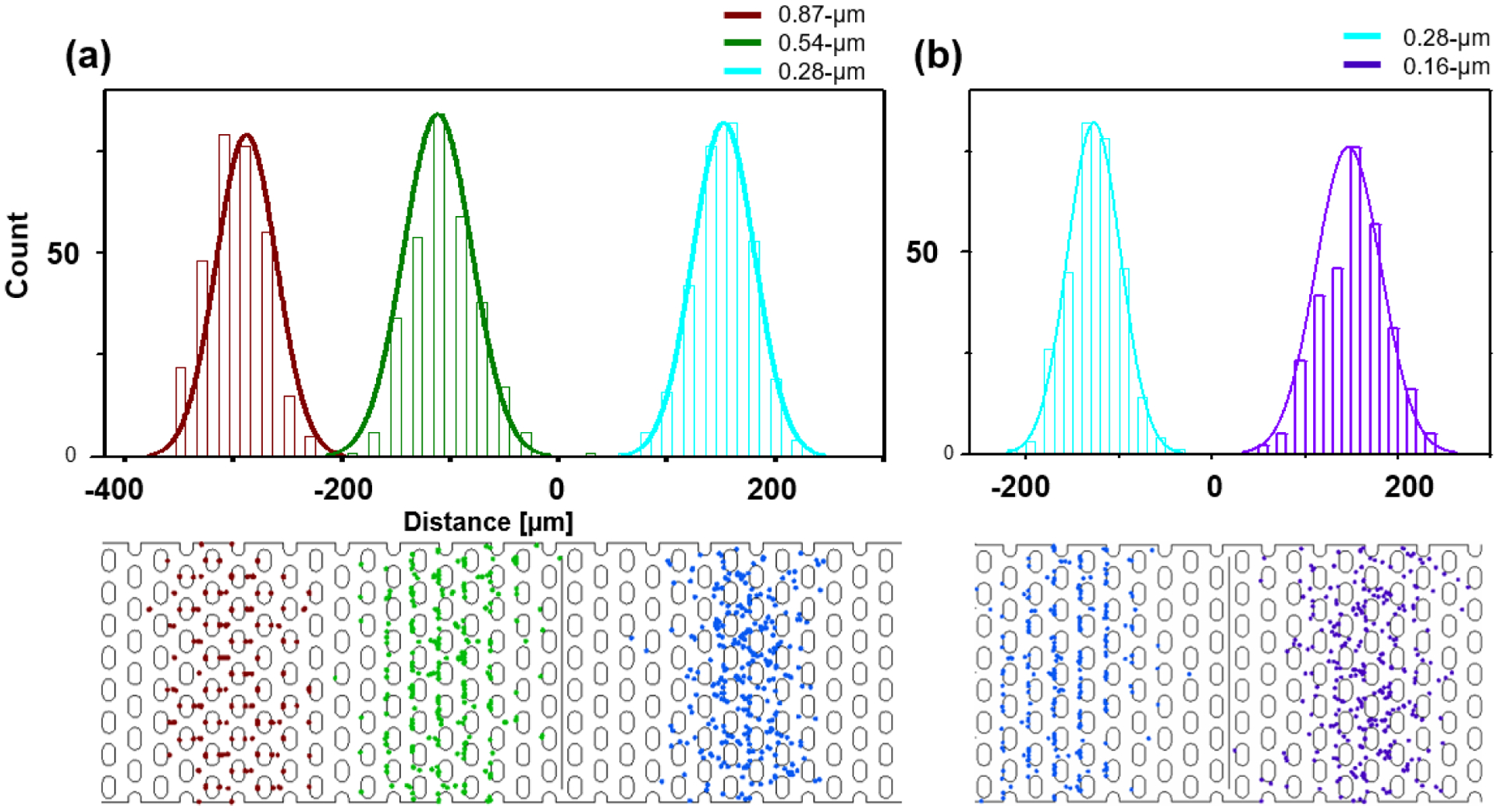
Top: Histogram and Gaussian fit for particle positions at the end of 4 periods. Sizes are 0.87 (red), 0.52 (green), 0.28 (cyan), and 0.16 (purple) beads. B) Corresponding image of the channel section with particle positions at the end of 4 periods. (a) 300 particles per size are studied at U_{ac_1}= 50 V, U_dc = 10 V, (a) U_{ac_2}= 800 V at f = 30 kHz (τ = 10 s) with the numerical model. All three particles can be separated with baseline resolution. B) With U_{ac_2} = 1400 V but otherwise same conditions as (a), 0.28μm and 0.18 μm particles can be separated with baseline resolution. Note: The dots are not reflective of particle size and are adjusted for visualization. The distance in μm on the x-axis indicates the particle migration distance from the particle release line in the numerical model.

In addition, we tested the minimum particle size for which a ratchet migration mechanism could be induced. For that purpose, we varied the amplitude of U_{ac_2}. As shown in Table 2, by increasing the applied potential, smaller particles begin to demonstrate ratchet migration at higher applied potentials. By increasing the amplitude of U_{ac_2}, we note that the ratchet migration can be induced for particles down to 0.28 μm in size. We attribute this to stronger DEP trapping with higher potentials. This is in accordance with previous reports in the literature demonstrating that sub-μm species and even biomolecules can be trapped with dielectrophoretic forces^43–45.

Table 2:

Migration behavior obtained at U_{ac_1} = 50 V with various conditions ofU_{ac_2} at f = 30 kHz. 300 particles are studied at each bead size. Positive (+) signs represent normal migration and negative (−) signs represent ratchet migration, respectively.

Amplitude of Uac_2	Size of Particles(μm) and migration behaviors
V/cm	0.87	0.52	0.28	0.16	0.08
1400	−	−	−	+	+
1000	−	−	+	+	+
900	−	−	+	+	+
850	−	−	+	+	+

Ratchet Mechanism for Liposome and Mitochondria

The ratchet mechanism was also investigated for isolated mouse hepatic mitochondria. In our previous study¹⁵, the dielectrophoretic trapping properties of mitochondria under iDEP conditions were investigated, and similar parameters were used here to find the regimes of ratchet migration for mitochondria. The size distribution of the isolated hepatic mitochondria ranged from 300nm to 700nm as verified by dynamic light scattering (see supplementary information, Figure S-4). As shown in Figure 6, the ratchet migration is apparent for large mitochondria since the resultant migration velocity is negative. For data analysis, we analyzed organelles that were trapped during the second half driving period, similarly to the model study with beads. These mitochondria showed the highest fluorescence intensities and were thus counted as large mitochondria (see supplementary movie 4). Importantly, the analysis of trajectories of small mitochondria (with fluorescence intensities just barely allowing tracking analysis) not trapped in the second half driving period reveals positive migration velocities, thus a normal migration effect. According to Figure S-4, we attribute large mitochondria to such of size above 600 nm. We thus conclude, that the ratchet effect can be induced for large mitochondria in a size-heterogeneous sample and that mitochondria of different size can be steered into different directions taking advantage of the coexistence of normal and ratchet-like migration for the small and large species, respectively.

The ratchet mechanism also offers a speed advantage over other related mechanisms. The maximum velocity of mitochondria undergoing ratchet migration in this work amounts in ~5 μm/s, which is two orders of magnitude larger than reported for absolute negative mobility migration⁴⁶ and is up to two times larger in magnitude to ratchet approaches with micrometer-sized particles²². This also holds for the sub-μm sized beads employed in this study, as described above. Thus, the deterministic ratchet mechanism described here induces significantly larger migration velocities, which is a highly desirable feature in the design of fast separation of particles and organelles.

The experimentally obtained migration velocities for mitochondria are also compared to the numerical model, in which parameters are employed matching experimentally measured electrophoretic mobilities for mitochondria. The supplementary information lists the parameters used for mitochondria. The obtained ratchet migration velocities are in excellent agreement with experimental values within measurement errors. We thus conclude that the model adequately reflects the migration of the larger mitochondria population in the sample with a size above 600nm.

Furthermore, we have applied the ratchet migration mechanism to liposomes labeled with lipophilic dye molecules. A smaller liposome fraction was prepared via an extrusion method rendering liposomes < 0.2 μm labelled with a red fluorophore. Accordingly, a larger size fraction with liposomes >0.3μm was prepared containing a green fluorophore. Figure 7a summarizes the average migration velocities for the two liposome species for variations in U_dc. The size of liposomes as measured by nanoparticle tracking analysis are shown in Figure 7b. Small liposomes (red) showed two major distributions at 102.9 ± 16.7 nm and 177.2 ± 39.5 nm. The size of large liposome (green) resulted in two major distributions with a mean of 338.9 ± 21.5 nm and of 639.5 ± 38.3 nm. As apparent from Figure 7a, when the driving conditions of U_{ac_1} = 30 V with U_{ac_2} of 800 V with f = 25 kHz were applied for one complete period, the small liposomes showed normal migration whereas the large liposomes showed ratchet migration behavior. Figure 7 thus demonstrates that the developed separation mechanism can be applied for sub-μm particles such as liposomes, which serve as model for biological species consistent of membranes such as other organelles.

Figure 7.

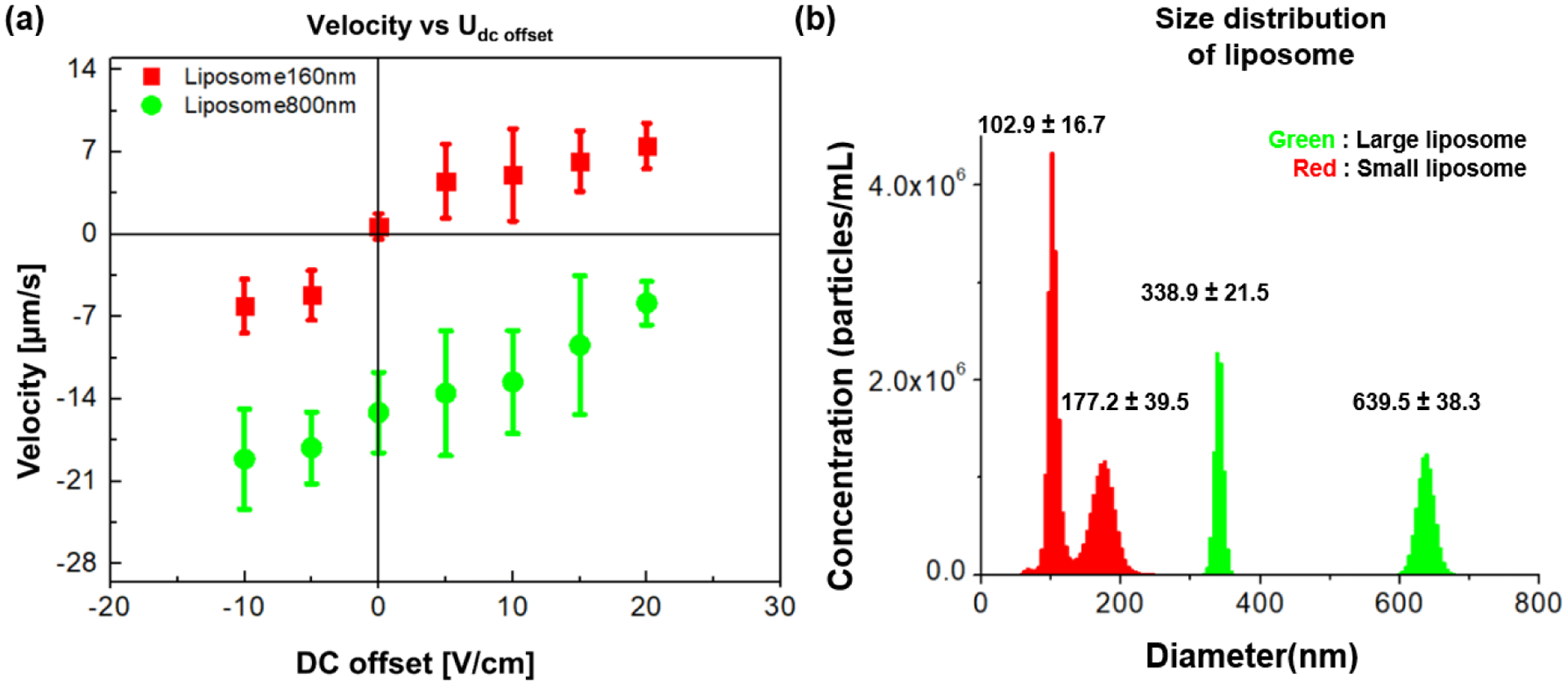
Ratchet migration observed for liposomes (a) Experimental results of migration velocity vs. U_dc. The error bars indicate the standard deviation obtained by tracking 60 individual liposome trajectories. U_{ac_1} was 30V and U_{ac_2} was 800 V with f = 25 kHz. The large liposome species in green (average size 640 ± 40 nm, diameter, green) show the ratchet migration mechanism and small liposome in red (average size 177 ± 40 nm and 102.9± 16.7nm, diameter, red) exhibited normal migration. (b) Particle size distribution of liposomes in HEPES-sucrose buffer solution determined by a Nanoparticle Tracking Analysis demonstrate an average size of 340 ± 20 nm and 640 ± 40 nm diameter for larger liposomes (green) and an average size of 177 ± 40 and 102 ± 20 nm diameter for the smaller liposomes (red).

Overall, we demonstrate that large mitochondria and liposomes show a ratchet-like migration mechanism similarly to the numerical and experimental study for sub-micrometer sized beads, whereas small mitochondria and liposomes showed normal migration. Compared to cumbersome ultracentrifugation methods⁴⁷, our ratchet approach is highly selective to sub-μm particle sizes and allows tuning of the size range via the applied driving conditions. In addition, our methods allows separations in the time scales of one minute, an improved speed over field-flow-fractionation techniques¹⁴ and ultracentrifugation methods. Moreover, our method does not require any affinity capturing using magnetic beads⁴⁸ or immobilized affinity agents for specific screening and separation of organelles³. The numerical model and the experiments with mitochondria and liposomes show that the ratchet migration mechanism can be applied to sub-μm particles with tunable selectivity and that it gives access to separations down to ~200 nm sized particles suitable for typical organelle sizes or even smaller bioparticles such as exosomes. Therefore, the demonstrated migration mechanism has a large potential as a tool for the separation of organelle subpopulations.

CONCLUSION

In this work, a deterministic DEP-based ratchet separation was realized in a non-linear microfluidic post array to explore this migration mechanism for organelle separations. It was demonstrated experimentally with sub-μm particles polystyrene particles, mitochondria and liposomes. The migration mechanism was reproduced with a numerical model, capturing the experimentally observed migration directions and absolute velocities in excellent agreement. The numerical model could be employed as a predictive tool for separation parameters, as demonstrated with particle species varying from 0.08 μm to 0.87 μm. Employing decreasing particle sizes, the numerical model demonstrated, that the ratchet effect can be induced down to 0.28 μm particles for polystyrene beads. Furthermore, a binary mixture of 0.28 μm and 0.16 μm particles could be separated with excellent separation resolution after only one driving period. We also showed that the separation resolution can be increased by increasing the number of driving periods. Moreover, the deterministic ratchet mechanism could be demonstrated experimentally with large mitochondria, whereas small organelles showed normal migration. In addition, we could experimentally demonstrate the coexistance of normal and ratchet migration for two sub-μm sized liposome samples. We further note, that the here presented iDEP-based ratchet approach can be readily realized with standard photolithographic and soft lithographic techniques and allows the adjustment of the DEP trapping forces through the variation of the externally applied potentials. It is thus envisioned that the investigated driving conditions can be adapted to a wide range of separation problems in which size selectivity is required, such as in the fractionation of organelles and their subpopulations, in nanotechnology-based applications or as fractionation method for protein nanocrystals.

Supplementary Material

Video S-1

Video S-1.mov : Simulation result showing polystyrene beads migration behavior under the positive U_dc offset

Video S-2

Video S-2.mov : Simulation result showing polystyrene beads migration behavior under the negative U_dc offset

Video S-4

Video S-4.mov : Video showing the ratchet behavior of mouse liver mitochondria experimentally

Video S-3

Video S-3.mov : Simulation result showing the ratchet behavior of 0.87 μm beads and the normal behavior of 0.28 μm beads polystyrene beads