Integrating Family-Based and Mendelian Randomization Designs

Abstract

Most Mendelian randomization (MR) studies published in the literature to date have involved analyses of unrelated, putatively independent sets of individuals. However, estimates obtained from these sorts of studies are subject to a range of biases including dynastic effects, assortative mating, residual population stratification, and horizontal pleiotropy. The inclusion of related individuals in MR studies can help control for and, in some cases, estimate the effect of these biases on causal parameters. In this review, we discuss these biases, how they can affect MR studies, and describe three sorts of family-based study designs that can be used to control for them. We conclude that including family information from related individuals is not only possible given the world's existing twin, birth, and large-scale population-based cohorts, but likely to reap rich rewards in understanding the etiology of complex traits and diseases in the near future.

Mendelian randomization (MR) is a method commonly used in epidemiology that uses genetic markers to investigate possible causal relationships between exposures and outcomes. The majority of MR studies to date have investigated putative causal relationships between exposures and outcomes using unrelated individuals. However, information contained within family-based designs can be useful for a number of purposes including estimation of the causal effect of maternal exposures on offspring outcomes, controlling for biases induced by unmodeled dynastic effects, assortative mating and population stratification, and mitigating the effects of horizontal pleiotropy induced by genetic confounding (i.e., the genetic marker, or one in linkage disequilibrium [LD] with it, influencing both the exposure and the outcome through different pathways). The purpose of this paper is to discuss these biases and review some of the family-based designs that can be used to control for and, in some cases, estimate them. Specifically, we will review three sorts of family-based MR studies: (1) MR studies employing within-family tests of association in sib pairs and/or parent–offspring trios to estimate causal effects that are potentially more robust to effects from dynastic effects, assortative mating, and population stratification; (2) MR studies of mothers and their offspring to estimate the causal effect of maternal exposures on offspring outcomes; and (3) the MR direction of the causation model (MR-DOC), which uses an extension of the classical twin design to control for potential confounding by horizontal pleiotropy.

MR STUDIES EMPLOYING WITHIN-FAMILY TESTS OF ASSOCIATION

In addition to horizontal pleiotropy, which has received wide attention in the literature (Bowden et al. 2018), causal estimates from MR studies can also be biased by dynastic effects, assortative mating, and residual population stratification. We discuss each of these potential sources of bias in turn before describing some family-based methods to overcome them.

Dynastic Effects

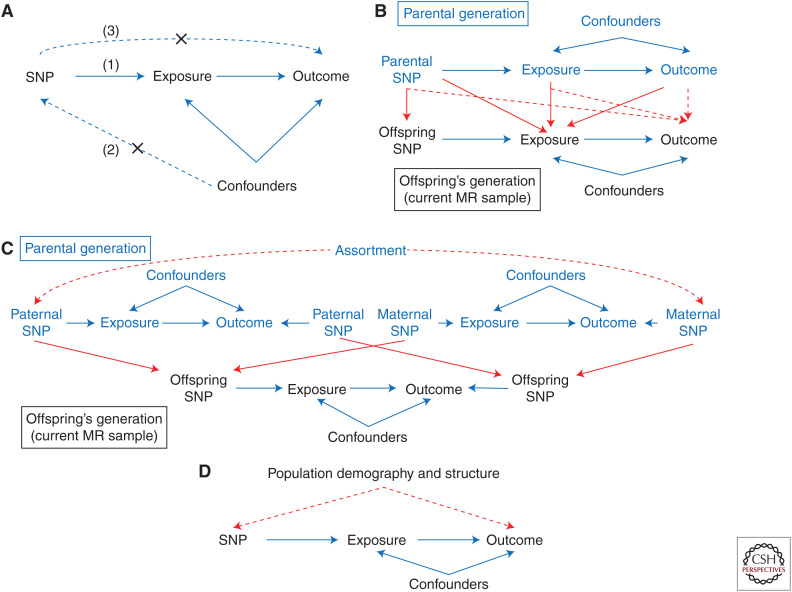
Dynastic effects, also known as genetic nurture effects, occur when the expression of parental genotype in the parents’ phenotype directly affects their offspring's outcomes (Brumpton et al. 2019). These effects can lead to biased estimates of the single-nucleotide polymorphism (SNP)-outcome associations in the offspring (Fig. 1B; Davies et al. 2019). To see why, consider an MR study that is investigating the effects of an exposure, for example, educational attainment, on an outcome on body mass index (BMI). Assume also that parental educational attainment affects offspring BMI (e.g., perhaps more educated parents encourage their offspring to maintain a healthy BMI). This study could use genetic variants associated with educational attainment to estimate the effects of education on BMI in one generation. However, the genotypes of the offspring will be correlated with that of their parents, and if the effects of education are estimated using samples of unrelated individuals, the effect of parental education on offspring's BMI will be ignored and mistakenly attributed to the offspring's educational attainment. Another example of potential dynastic effects are maternal intrauterine effects. Maternal effects such as these create backdoor paths from offspring's genotype to mother's genotype to offspring's outcomes, which are not mediated by the offspring's exposure and can bias MR studies using unrelated individuals. In some situations, however, it is the causal effect of the parents’ environment/behavior/trait on the offspring outcome that is actually of interest (e.g., the causal effect of maternal alcohol consumption during pregnancy on offspring health outcomes); in a later section, we will show how family-based designs can be utilized to partition genetic effects into parental and offspring components and subsequently estimate the causal effect of maternal exposures on offspring outcomes in MR studies.

Figure 1.

Genetic variants are valid instrumental variables for Mendelian randomization (MR) if they satisfy three core assumptions: (1) they associate with the exposure of interest, (2) there are no confounders of the genetic marker–outcome association, and (3) the genetic variants only affect the outcome via the exposure of interest. These core assumptions are depicted in A. (A–D) The solid blue arrows represent relationships within an individual (e.g., the effects of offspring single-nucleotide polymorphisms [SNPs] on offspring exposure). The red lines represent the effects of relationships between individuals (e.g., the direct effects of parents’ phenotypes on their children). Dynastic effects, shown in B, refer to any effect of parental genotype on the offspring outcome that is not mediated via the offspring exposure. These effects are indicated by the dashed red lines in B. Dynastic effects violate the second core assumption for a valid genetic instrument by opening a path from offspring SNPs to offspring outcome that is not due to the offspring exposure. Cross-trait assortative mating, as shown in C, induces associations between SNPs related to the exposure and the outcome in the parental generation (indicated by dashed red lines). If the parents assort on the exposure and the outcome (e.g., more educated females tending to mate with taller men, as indicated by the dashed red arrow in C), then this will induce correlation between exposure-related SNPs and the outcome in the offspring generation that is not mediated by the offspring exposure (i.e., outcome ← offspring SNP ← maternal SNP—assortment—paternal SNP → offspring SNP → exposure). Therefore, assortative mating can bias MR estimates of the causal effect. Finally, population structure and demography can also open a path from SNP to outcome, which is not mediated via the exposure of interest, and introduce bias, as shown in D. (Figure based on data in Brumpton et al. 2019.)

Assortative Mating

Humans do not mate at random, rather they select partners partly based on characteristics similar to their own, a phenomenon referred to as assortative mating. For example, mothers and fathers tend to be more similar to each other in terms of height, BMI, and education than would be expected by chance (Robinson et al. 2017). Assortment can occur on a single phenotype, for example, if more educated mothers on average have offspring with more educated fathers, or cross-trait, for example, where more educated mothers on average have offspring with taller fathers. Cross-trait assortative mating can cause bias in MR studies because it can induce associations between SNPs used as instruments for the offspring's exposure and their outcomes. This bias occurs because assortative mating induces associations between parents’ genotypes for the exposure and outcome, which opens a path from offspring genotype to offspring outcome via parents’ genotype and not the exposure of interest (Fig. 1C; Hartwig et al. 2018). Perhaps less intuitively, assortment on a single phenotype can also bias the results of MR analyses if the trait undergoing assortment is genetically correlated with (or causes) the exposure and outcome under investigation (Hartwig et al. 2018). The reason is because this sort of assortment results in correlations between variants associated with the exposure in one parent and variants underlying the outcome in the other parent. This means that when the variants are transmitted from the parents to their offspring, a backdoor path potentially opens between any markers used to proxy the exposure in the offspring and the offspring outcome.

Residual Population Stratification

Population differences can induce noncausal associations between genetic variants and traits or diseases (Fig. 1D). If these noncausal associations are between an SNP and an outcome of interest for MR analyses, then the MR analysis will be biased away from the true causal effect of the exposure. For example, consider genetic variation associated with lactase persistence. There are substantial regional differences in the frequency of genetic variation related to lactase persistence (e.g., the SNP rs4988235) across Europe (Plantinga et al. 2012). If there are also regional differences in prevalence of disease or the mean value of an outcome (for example, prevalence of coronary heart disease), then an MR study of the effect of consuming dairy products on coronary heart disease may mistakenly conclude that there is a causal effect. Historically, residual population stratification has been dealt with in two ways, first by restricting analyses to a single ancestrally homogenous population (historically, most frequently European populations), and second by adjusting for ancestry informative principal components derived from, for example, genome-wide SNP data. However, while residual population stratification does not appear to be a major issue in smaller genetic studies (Mathieson and McVean 2012), there is increasing evidence that in larger samples, principal components may not completely control for fine-scale structure nor all the regional differences between samples (Haworth et al. 2019). In other words, residual population stratification can confound SNP-outcome associations and lead to spurious conclusions in large-scale MR studies.

Controlling for Bias Using Within-Families Estimators

Dynastic effects, assortative mating, and residual population stratification result in biased estimates of the SNP-phenotype associations. If biased SNP-phenotype associations are used in MR analyses, then the estimated causal effect may also be biased. The direction and magnitude of these biases is dependent on the specific context and application. It is possible for the bias in the SNP-exposure and SNP-outcome associations to be of similar magnitude, resulting in little bias in the estimated causal effect. However, the direction and size of a bias in the estimated causal effect may not be intuitive. For example, if the SNP-exposure association is biased downward (i.e., underestimated), and the SNP-outcome association is estimated without bias, then this will overestimate the causal effect via Wald-type estimators (i.e., because if the denominator in the Wald ratio is lower, the Wald ratio itself will be higher).

Do these biases exist and are they of consequence for MR studies? One way we can obtain information on the extent of the problem is by estimating the association between untransmitted parental alleles and offspring phenotypes (Bates et al. 2018). For example, Kong et al. (2018) estimated these associations using samples of families from Iceland. They found that untransmitted allelic variants that were associated with parental educational attainment were also associated with offspring educational attainment, offspring age at first child, high-density lipoprotein (HDL) cholesterol, BMI, fasting glucose, height, cigarettes per day, and a composite health measure. These results suggest that accounting for dynastic effects is likely to be important for valid MR studies, at least for some phenotypes of interest like educational attainment (Davies et al. 2019). Transgenerational genome-wide association studies (GWAS) (Evans et al. 2019; Warrington et al. 2019) and G-REML approaches that estimate the proportion of variance in offspring phenotypes explained by parental genetic effects (Eaves et al. 2014; Qiao et al. 2020) will likely provide further indications as to the existence of dynastic effects, their magnitude, and how important they are likely to be for MR studies.

The potential sources of bias discussed above (i.e., residual population stratification, dynastic effects, and assortative mating) can be controlled for by applying within-family tests of association to datasets of related individuals including sibling pairs and parent–offspring trios. Genetic differences between sibling pairs from the same family are primarily due to chance events that occur at conception. As a result, these differences are independent of population stratification. Likewise, siblings from the same family share the same parents. This has two implications. First, differences in genotype between siblings from the same family will be independent of assortative mating. Second, the effects of parents on their offspring (dynastic effects) are likely to be similar across siblings. Thus, the difference in genotypes between siblings from the same family is also likely to be independent of many dynastic effects. Similarly, conditional on parental genotype, the genotypes inherited by offspring are stochastic. Therefore, if genotyped parent–offspring trios where the offspring has been phenotyped are available, then performing tests of genetic association controlling for parental genotype may also control for population stratification, dynastic effects, and assortative mating. To see why, consider the directed acyclic graphs (DAGs) shown in Figure 1 (Fig. 1B, dynastic effects; Fig. 1C, assortative mating; Fig. 1D, population stratification). In each case, controlling for parental genotype will block the alternative paths from offspring genotype to offspring outcome.

If sibling data are available, then we can use either difference, within-family, or family-fixed effects estimators to perform MR analyses (Brumpton et al. 2019). Difference estimators estimate the association between the difference in genotype and the difference in phenotype across siblings. Multiple sibling pairs from each family can be included in difference estimates by calculating all differences between all sibling pairs and clustering standard errors by family. Within-family estimators estimate the association between genotype and phenotype controlling for the mean family outcome. Family-fixed effect estimators include an indicator variable for family and cluster standard errors by family. If the sample is restricted to pairs of siblings (i.e., exactly two siblings per family), then the difference and family-fixed effects estimators are identical. These estimators can be used with single-sample designs, for example, by allowing for family-fixed effects and clustering standard errors by family. Alternatively, these estimators can be used in a two-sample MR setting in which the SNP-exposure and SNP-outcome associations are estimated allowing for a familial effect (e.g., using the difference, within-family, or family-fixed effects mentioned above) in separate samples of siblings.

If data on parent–offspring trios are available, then preliminary work suggests that estimates of the SNP-exposure and SNP-outcome associations conditional on the parental genotype may be unbiased by many of the complicating factors we have discussed above (researchers would ideally want to condition both the SNP-exposure and SNP-outcome associations on parental genotypes). This would certainly be the case for many forms of dynastic effects. Hartwig et al. (2018) showed via simulation and illustrated via DAGs that the inclusion of parental genotypes should control for any biases in causal estimates introduced by assortative mating. While no studies have specifically investigated whether including parental genotypes in the model also guards against bias induced by population stratification in MR studies, this may well be the case; however, this assertion will need to be confirmed by future work (obviously, ancestry informative principal components can also be included in the model). Inclusion of parental genotypes in the design also has the additional advantage of permitting explicit estimation of parental genetic effects on offspring phenotypes if these quantities are of interest (e.g., for estimating the causal effect of parental phenotypes on offspring outcomes) and may be more powerful than just utilizing, for example, sibling pairs. Multiple siblings can also be included in the design if appropriate adjustments are made to standard errors.

Most software packages can implement family-fixed effects for one-sample MR. However, a downside to this approach is that power is limited to the sibling pairs or parent–offspring trios available with both the exposure and outcome measured. In contrast, two-sample MR estimates SNP-exposure and SNP-outcome associations using separate samples. An advantage of two-sample MR is that the exposure and the outcome do not need to be measured in the same sample, and two-sample MR can use summary data from GWAS studies, subject to assumptions. If a GWAS has been run using within-family estimators (either the difference or sibling-fixed effect method above, or the trio method adjusting for parental genotype), then the SNP-phenotype summary data can be used in downstream MR analyses. These analyses can include sensitivity analyses and estimators that are robust to other forms of bias that can occur in MR studies, such as MR-Egger, weighted median, and weighted modal estimators that potentially overcome horizontal pleiotropy (Bowden et al. 2015, 2016; Hartwig et al. 2017) or multivariable MR (Sanderson et al. 2019).

Power of Within-Families Estimators

The power of sibling or trio models for a given sample and effect size is substantially lower than MR analyses using samples of unrelated individuals (Sham et al. 2000). As a result, the standard errors of within-family tests of association are larger and consequently the results are less precise. Furthermore, across the world there are far fewer cohorts containing siblings and parent–offspring trios than samples of unrelated individuals. Thus, sample sizes for within-family analyses are typically far smaller than GWAS of unrelated individuals. This limited power can be mitigated by selecting variants as instruments using large GWAS of unrelated individuals and then estimating the SNP-exposure and SNP-outcome associations for MR using available samples of siblings or trios.

Limitations

In addition to limited power and precision, these within-family methods may still be affected by a number of sources of bias. For example, sample selection bias, in which individuals are selected into a study on the basis of factors related to both their exposure and outcome, may induce spurious associations between genotype, exposure, and outcome. Selection bias will be particularly problematic if the selection effects differ across sibling genotypes and these differences relate to differences in outcomes between siblings (Munafò et al. 2018). Within-family effects, for example, effects of one sibling on the other sibling, may also induce bias in the estimated causal effects. Finally, differential measurement error in the outcome between siblings can result in further bias, for example, if a sibling that inherited more education-associated alleles was less likely to misreport their disease status.

MENDELIAN RANDOMIZATION STUDIES OF MATERNAL EXPOSURES AND OFFSPRING OUTCOMES

There is growing interest in using MR to estimate the causal effect of maternal environmental exposures on their offspring's outcomes. In large part, this interest is driven by the fact that randomized controlled trials (RCTs) are often neither ethically nor practically feasible in this context. For example, poor maternal nutrition during pregnancy has been hypothesized to lead to intrauterine growth restriction and increased risk of cardiometabolic disease in offspring later in life through developmental compensations (Schulz 2010). However, this hypothesis is difficult to test by an RCT as it is obviously inappropriate to randomize pregnant mothers to receive poor nutrition, in addition to the practical difficulties and expenses associated with waiting decades before their offspring begin to develop signs of cardiometabolic disease. In these, and other situations, MR studies may offer a valuable, practical, ethical, and cost-effective alternative to estimating the causal effect of maternal influences on their offspring.

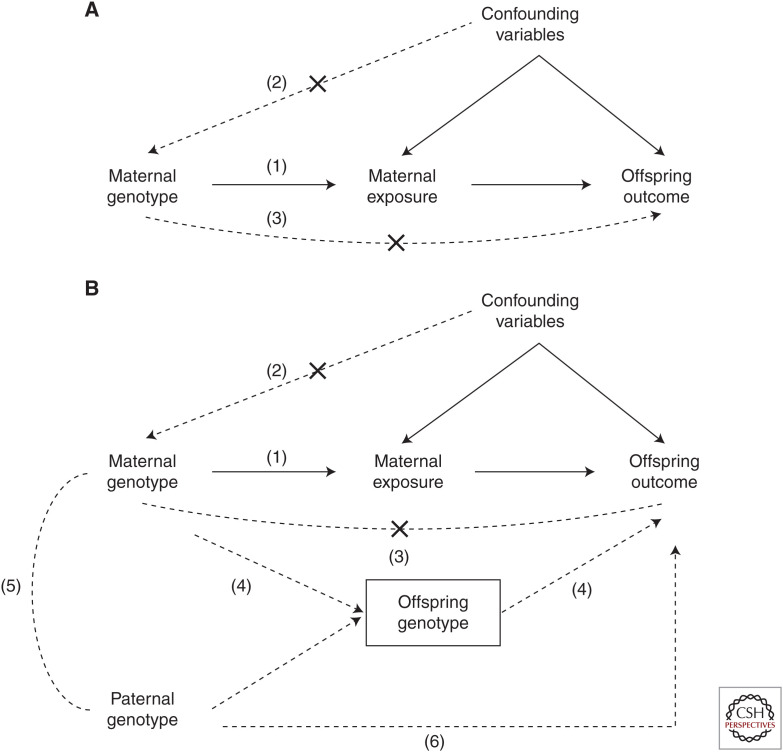
MR studies of mothers and their offspring proceed along similar lines as ordinary MR studies of unrelated individuals (Fig. 2A). However, as shown in Figure 2B, maternal genotype is correlated with offspring genotype, which can potentially influence the offspring outcome by pathways other than through the maternal exposure. This additional pathway from maternal genetic variant to offspring outcome violates one of the three core assumptions of MR—that genetic variants are only potentially associated with the outcome through the exposure of interest. Thus, it is important to block this pathway to provide unbiased estimates of the causal effect of the maternal exposure on the offspring outcome.

Figure 2.

Directed acyclic graphs showing the three core assumptions underlying Mendelian randomization (MR). (A,B) Assumption (1) requires that maternal genetic variants must be robustly associated with the maternal exposure of interest. Assumption (2) requires that the genetic variants are uncorrelated with confounders of the maternal exposure–offspring outcome relationship. Assumption (3) requires that the genetic variants are only potentially associated with the offspring outcome through the maternal exposure of interest. Offspring genetic variants violate assumption (3), as they permit a path to the offspring outcome that is not mediated by the maternal exposure (4). However, conditioning on offspring variants (as indicated by a box around the offspring single-nucleotide polymorphism [SNP]), blocks path (4). Conditioning on offspring genotype induces a correlation between maternal and paternal genotypes (5). This may produce biased estimates of the causal effect (collider bias) if markers at the same loci (or loci in linkage disequilibrium with them) also exert paternal genetic effects on the offspring phenotype (6). This possibility can be prevented by conditioning on paternal genotype as well as offspring genotype in the analysis. (Figure based on data in Evans et al. 2019.)

The most intuitive way of blocking this path is by conditioning on offspring genotype by including it as a covariate in the MR analysis (Lawlor et al. 2017). For example, Tyrrell et al. (2016) used this strategy to show that high blood pressure in mothers during pregnancy is likely to be causal for reduced birth weight in their offspring. However, this strategy requires genotype information on both mothers and their offspring, and as there is a paucity of cohorts around the world that contain this sort of information, these MR studies are likely to be small and underpowered to evaluate many effects of interest. An additional complication is that because offspring genotypes are a product of paternal genotypes, conditioning on offspring genotype will induce a negative correlation between maternal and paternal genotypes. This may in turn bias estimates of maternal and offspring genetic effects if the markers used in the MR analysis (or ones correlated with them) exert effects on the offspring when present in the father (i.e., paternal genetic effects). If paternal genotypes are available, they can also be included as covariates in the statistical model, which should ameliorate this potential complication.

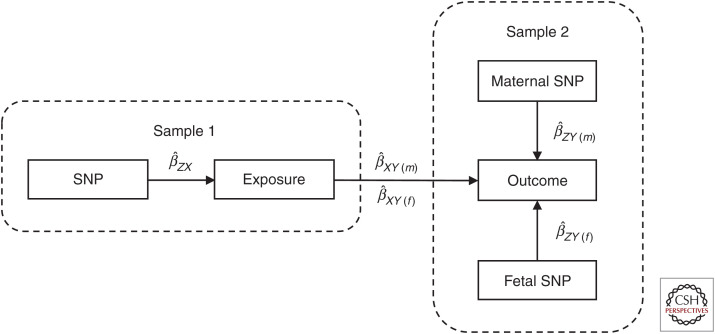
Recently, we have proposed increasing the power of maternal offspring MR studies by using a two-sample strategy (Evans et al. 2019). The basic idea is to first generate estimates of the maternal SNP-offspring outcome association conditional on offspring genotype. These estimates can then be combined with (potentially independent) estimates of the maternal SNP-exposure association to obtain estimates of the causal effect, similar to what is done in traditional two-sample MR studies (Fig. 3). The advantage of this strategy is that both estimates (but especially estimates of the conditional maternal SNP-offspring outcome association) can be obtained in vastly increased numbers of individuals using a number of different family-based designs, not just genotyped mother–offspring pairs.

Figure 3.

Two-sample Mendelian randomization study testing the causal effect of a maternal exposure on an offspring outcome. Estimates of the single-nucleotide polymorphism (SNP)-exposure association $({\widehat{\text{β}}}_{ZX})$ are calculated in the first sample of unrelated individuals. The association between these same SNPs and the offspring outcome is then estimated in the second sample of individuals, except in this case, the genetic association is partitioned into maternal $({\widehat{\text{β}}}_{ZY(m)})$ and offspring $({\widehat{\text{β}}}_{ZY(f)})$ genetic effects on the outcome (see Fig. 4 for how these can be estimated using structural equation modeling). These estimates are then combined to yield estimates of the causal effect of the maternal exposure on the offspring outcome $({\widehat{\text{β}}}_{XY(m)}={\widehat{\text{β}}}_{ZY(m)}/{\widehat{\text{β}}}_{ZX})$, and the causal effect of the exposure in the offspring on their own outcome $({\widehat{\text{β}}}_{XY(f)}={\widehat{\text{β}}}_{ZY(f)}/{\widehat{\text{β}}}_{ZX})$. It is important to realize that under this model, the same SNP-exposure association is being used to index both maternal and fetal exposures. While this may be appropriate in some circumstances (e.g., examining the effect of maternal and offspring IQ on offspring obesity in teenagers), it may not make sense for other exposures of interest (e.g., SNPs that index maternal smoking cannot index fetal smoking in utero). Investigators therefore need to think carefully about whether estimates of the offspring causal effect make sense in the particular context in which they are derived.

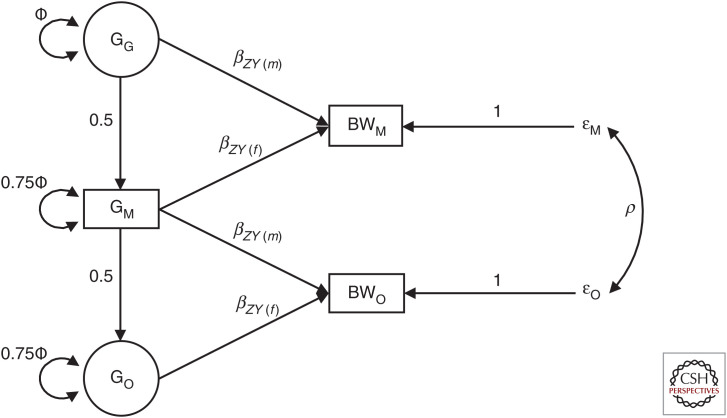
For example, within the context of a large genetic study of birth weight, Warrington et al. showed how an SEM approach could be used to estimate the association between maternal SNPs and offspring outcomes conditional on offspring genotype (Warrington et al. 2018). Mothers in the UK Biobank (Sudlow et al. 2015) report both their own birth weight and the birth weight of their first offspring. Warrington et al. showed how an SEM can be fitted to these data to estimate both the association between maternal genotype and offspring phenotype conditional on offspring genotype (termed the “maternal genetic effect”), and the association between offspring genotype and offspring phenotype conditional on maternal genotype (termed the “offspring genetic effect” or the “fetal genetic effect”) (Fig. 4). The authors showed how the approach yielded unbiased estimates of maternal and fetal genetic effects on birth weight, gave similar answers to traditional conditional association analyses of genotyped mother–offspring pairs, and had low sensitivity to random measurement error (Warrington et al. 2018). Indeed, one of the main advantages of SEM is that the approach is flexible in that an arbitrary number of different study designs and pedigree structures can be easily incorporated into the analysis (for example, genotyped mother–offspring duos, genotyped individuals reporting their own and their offspring's phenotype, genotyped singleton individuals, etc.). Most importantly though, the method is flexible enough to include both individual level genotype data and summary level GWAS results, meaning that potentially huge numbers of individuals can be incorporated into the analysis leading to large gains in power (Moen et al. 2019). The resulting estimates can then be used in two-sample MR studies of maternal exposures and offspring outcomes as described above. For an application of fitting SEMs and using the results in two-sample MR studies of maternal exposures and offspring outcomes, see a recent study of birth weight where these methods are used to confirm that high maternal blood pressure is likely to be causal for low offspring birth weight, and high maternal blood glucose is likely to be causal for increased offspring birth weight (Warrington et al. 2019).

Figure 4.

Structural equation modeling (SEM) used for the analysis of birth weight in Warrington et al. (2018). The squares represent observed variables in the analysis, in this particular case, the birth weight of the individual (BW_M), the birth weight of her first offspring (BW_O), and the genotype of the mother (G_M). The circles represent latent variables in the analysis, that is, the genotype of the individual's mother (G_G) and the genotype of the individual's offspring (G_O). The total variance of the latent genotypes for the individual's mother (G_G) and offspring (G_O) and for the observed single-nucleotide polymorphism (SNP) variable is set equal to the estimated parameter Φ, that is, variance (G_G) = Φ, variance (G_M) = 0.75Φ + 0.25Φ, and variance (G_O) = 0.75Φ + 0.25Φ as can be confirmed by path analysis. The β_ZY(m) and β_ZY(f) path coefficients refer to maternal and offspring genetic effects on birth weight, respectively (i.e., the association between maternal genotype and offspring birth weight conditional on offspring genotype, and the association between the offspring genotype and offspring birth weight conditional on maternal genotype). The residual error terms for the birth weight of the individual and their offspring are represented by ɛ_M and ɛ_O, respectively, and the variance of both of these terms is estimated in the SEM. The covariance between residual genetic and environmental sources of variation on birth weight is given by ρ. (Figure adapted from Warrington et al. 2018 with permission from the authors.)

MR studies aimed at assessing the causal effect of maternal exposures on offspring outcomes carry with them a number of additional assumptions that need to be borne in mind. The first is the absence of paternal genetic effects on the offspring outcome at the same (or correlated) markers that are used as putative instruments in the analysis. This may be a reasonable assumption for some perinatal traits where the father's phenotype has limited impact on the offspring, but probably not for many other offspring traits of interest. Since paternal genotypes are also correlated with offspring genotype, the presence of paternal genetic effects on the offspring outcome will bias estimates of the maternal and offspring genetic effects, unless paternal genotype is included in the model. The effect of the paternal genotype can be modeled, for example, by analyzing genotyped parent offspring trios, or extending the SEM (Fig. 4) to include paternal genotypes. This latter approach could be advantageous if the sample consists of a mixture of maternal–child pairs and father–offspring pairs for example.

A second assumption is that the estimate of the SNP-exposure association is specific to and reflects the particular time period under study. As individuals’ genetic variants are present from conception, the causal estimates from MR studies are often thought to reflect life-long exposures to the environmental factor of interest. This can be problematic if the focus is on a particular period of the life course, such as the period of pregnancy to assess an intrauterine exposure. Indeed, in this particular instance, estimating paternal genetic effects can be a useful negative control (Gage et al. 2016), as one would expect to see evidence of a causal association in mothers but not fathers if the causal effect is mediated by the intrauterine environment.

Third, a complication to bear in mind is that under this model, the same SNP-exposure association is being used to index both maternal and fetal exposures. While this may be appropriate in some circumstances (e.g., examining the effect of maternal and offspring IQ on offspring obesity in teenagers), it may not make sense for other exposures of interest (e.g., SNPs that index maternal smoking cannot index fetal smoking in utero). Investigators therefore need to think carefully about whether estimates of the offspring causal effect make sense in the particular context in which they are derived.

Last, and particularly relevant for two-sample MR studies of maternal exposures and offspring outcomes, the assumption is made that estimates of the SNP-exposure association utilized in the calculation are representative of those in the particular population of interest. For example, genetic instruments are typically identified in GWAS performed in the general population (i.e., healthy men and women). Most two-sample MR studies extract SNP-exposure statistics from publicly available summary results data published from these studies. However, it is possible that these SNPs (and the magnitude and direction of their associations with the exposure) are different from what is observed in, for example, pregnant women. The field as a whole would benefit from large, well-powered studies investigating whether this is actually the case across a range of different exposures of interest and whether such an assumption is justified.

Finally, we note that although we have focused our discussion on estimating the causal effects of maternal exposures on their offspring's outcomes, many of the methods we have discussed and the issues we have raised are also relevant for studying the causal effect of paternal influences on offspring outcomes. As the size and number of cohorts with genotyped father offspring pairs grows, it will be interesting to use MR methods in this context as well.

MENDELIAN RANDOMIZATION DIRECTION OF CAUSATION MODEL

The MR-DOC method is an attempt to fuse MR principles with the DOC twin model from biometric genetics (Evans et al. 2002). The original DOC twin model uses monozygotic (MZ) twin pairs (who are genetically identical) and dizygotic (DZ) pairs (who on average share half their genes identical by descent) to estimate the causal effect of one variable on another. The basic idea is that the effect of one variable on the other produces different expectations for the MZ and DZ cross-twin, cross-trait covariances depending on the DOC, for example, whether variable one causes variable two, or vice versa, or the variables reciprocally cause each other. Using these differences, causal parameters can be estimated through SEM (Heath et al. 1993).

The original DOC twin model formulation has a number of serious limitations. First, it is susceptible to measurement error, which can be partially overcome by including multiple indicator variables in the model (Gillespie et al. 2003). Second, it has low statistical power in that the model tends to work best when the two traits under investigation have radically different etiologies (for example, one trait is highly genetic, whereas variation in the other trait is mostly due to common environmental factors) (Duffy and Martin 1994). Finally, and perhaps most importantly (and not always appreciated), the model makes the strong assumption that the only source of covariation between the two traits is due to the causal effect of one trait on the other. In other words, the DOC model assumes that latent (genetic or environmental) confounding does not contribute to covariation between the traits, vastly limiting its utility (Rasmussen et al. 2019).

In 2018, Minică et al. extended the DOC model to include an additional component due to a polygenic risk score (PGS) (Fig. 5; Minică et al. 2018). In this MR-DOC model, the phenotypic variance and covariance between an observed exposure variable (X) and an outcome variable (Y) is decomposed into latent additive genetic (A), common environmental (C), and unique environmental sources of variation (E) (indicated by circles) as in the traditional DOC model. These latent factors are assumed to have zero mean and unit variance. However, the model also includes an additional observed variable, a PGS designed to proxy the exposure variable X. In equation form, the model is:

$$X_{ij}=a_X{A}_{X_{ij}}+c_X{C}_{X_{ij}}+e_X{E}_{X_{ij}}+b_1\mathrm{PG}{\mathrm{S}}_{ij},$$

$$Y_{ij}=a_Y{A}_{Y_{ij}}+c_Y{C}_{Y_{ij}}+e_Y{E}_{Y_{ij}}+g_1{X}_{ij}+b_2\mathrm{PG}{\mathrm{S}}_{ij},$$

where subscript i represents the twin pair and j twin one or twin two. The coefficients a, c, and e represent path coefficients linking latent additive genetic, common environmental, and unique environmental factors to the observed exposure (X) and outcome (Y), b₁ and b₂ represent the direct effect of the PGS on the exposure and outcome, respectively, and, finally, g₁ represents the causal effect of the exposure on the outcome. The model makes the usual assumptions regarding random mating, absence of gene–environment interaction, gene–environment covariance, etc. The model can be fit and parameters estimated using full information maximum likelihood in, for example, the software package OpenMx (Neale et al. 2016).

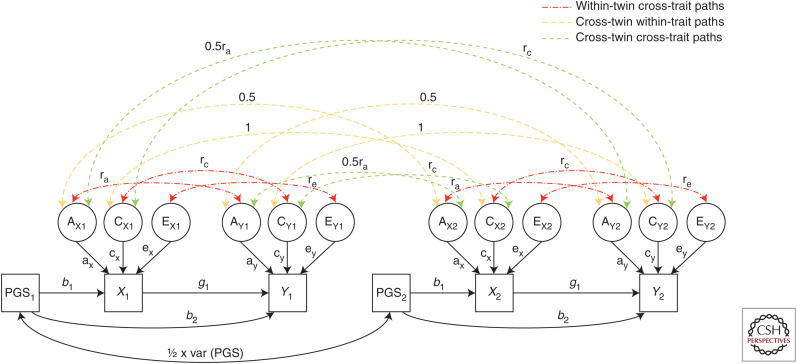
Figure 5.

The Mendelian randomization direction of the causation model (MR-DOC) illustrated as a path diagram for dizygotic (DZ) twins. Phenotypic variation and covariation between a polygenic risk score (PGS) and two observed phenotypes (X and Y) for twin one and twin two are decomposed into latent additive genetic (A), common environmental (C), and unique environmental (E) sources of variation (all latent variables are assumed to have mean zero and variance one). To assist with explication, correlational paths that contribute to within-twin, cross-trait covariances are displayed in red (dot dashes), correlational paths that contribute to cross-twin, within-trait covariances are shown in orange (long dashes), and correlational paths that contribute to cross-twin, cross-trait covariances are presented in green (short dashes). There are 13 potentially free parameters to be estimated in this model including the variance of the PGS [var(PGS)], the additive genetic, common environmental, and unique environmental path coefficients for variable X (a_x, c_x, e_x) and variable Y (a_y, c_y, e_y), the additive genetic, common environmental, and unique environmental correlations between variable X and Y (r_a, r_c, r_e), the direct effect of the PGS on variable X (b₁) and variable Y due to pleiotropy (b₂), and the causal effect of variable X on variable Y (g₁). The covariance among the PGSs is equal to half the variance of the polygenic scores. For the model to be identified, some parameters must be constrained (e.g., r_e = 0), which may not be an accurate reflection of reality. The path model for monozygotic (MZ) twins is similar except the cross-twin, same-trait correlation between latent additive genetic sources of variation is set to one, the cross-twin, cross-trait correlation between latent additive genetic sources of variation is set to r_a, and the covariance among the PGSs is equal to the variance of the PGSs. If there is no horizontal pleiotropy (i.e., b₂ = 0), then both MR-DOC and standard MR analyses (i.e., MR using two-stage least squares, Wald ratio, etc.) should give unbiased estimates of the causal effect (g₁). In contrast, if b₂ ≠ 0, then standard MR analyses will be biased, whereas MR-DOC will produce unbiased estimates of g₁ (assuming r_e = 0). (Figure based on data in Minică et al. 2018.)

The potential advantage of the MR-DOC model over traditional MR formulations is that the pleiotropic effect of the PRS (b₂) can be estimated from the data. However, for the model to be identified (i.e., all the paths to be estimated uniquely) the model requires additional assumptions (Minică et al. 2018). One way of ensuring model identification is to assume that the cross-trait unique environmental correlation is set to zero (r_e). This assumption is equivalent to the (strong) assumption of the absence of confounding in the data through unique environmental factors. In other words, the model permits confounding through genetic but not unique environmental sources of variation. It remains to be seen how realistic this constraint is in real-life situations (Rasmussen et al. 2019).

Another strategy that permits model identification while still allowing estimation of the causal effect (g) and genetic pleiotropy (b₂) is to fix r_E to a range of values and investigate the sensitivity of the model and estimates of the causal effect. Alternatively, the model could be modified to freely estimate r_E while fixing the genetic correlation (r_G) to a value consistent with those obtained from an orthogonal data source (e.g., from estimates of the genetic correlation from LD score regression [Bulik-Sullivan et al. 2015], G-REML [Yang et al. 2010], or IBD-based methods [Visscher et al. 2006]). However, our preliminary work investigating this interesting possibility has suggested that estimates of the causal effect are exquisitely sensitive to the choice of r_G and so this possibility may not be practical (data not shown).

MR-DOC is a relatively recent addition to the growing arsenal of MR methods designed to detect and/or correct for the effect of pleiotropic instruments. It will be interesting to see how the method performs on real data (particularly in instances where we are reasonably certain of the true DOC), and how it compares to existing MR methods. We suspect that the main impediments to its widespread adoption will be the fact that epidemiologists tend to be unfamiliar with the methods used for its implementation, and of course the necessity for having large numbers of genotyped MZ and DZ twins available for analysis. Indeed, it may be that those more familiar with the intricacies of SEM like behavior geneticists and twin modelers may need to take the lead in evaluating whether this interesting method is likely to produce gains in understanding trait etiology relative to other MR approaches.

CONCLUSIONS

Most MR studies conducted to date have involved analyses of independent unrelated individuals. However, these sorts of studies are subject to a range of biases including dynastic effects, assortative mating, residual population stratification, and horizontal pleiotropy. MR designs capitalizing on the additional information contained within related individuals such as twin pairs, sibling pairs, mother–offspring pairs, and parent–offspring trios, offer the ability to control for many of these biases and in some cases estimate the magnitude of their effects directly. The availability of genotyped twin studies, population-based birth cohorts of parents and their children, as well as large-scale biobanks containing related individuals will provide an opportunity to fit many of the models described in this chapter and quantify the effects of biases that may contaminate MR studies of unrelated individuals.