Localized end-of-outbreak determination for coronavirus disease 2019 (COVID-19): examples from clusters in Japan

Abstract

Objectives

End-of-outbreak declarations are an important component of outbreak response because they indicate that public health and social interventions may be relaxed or lapsed. Our study aimed to assess end-of-outbreak probabilities for clusters of coronavirus disease 2019 (COVID-19) cases detected during the first wave of the COVID-19 pandemic in Japan.

Methods

A statistical model for end-of-outbreak determination, which accounted for reporting delays for new cases, was computed. Four clusters, representing different social contexts and time points during the first wave of the epidemic, were selected and their end-of-outbreak probabilities were evaluated.

Results

The speed of end-of-outbreak determination was most closely tied to outbreak size. Notably, accounting underascertainment of cases led to later end-of-outbreak determinations. In addition, end-of-outbreak determination was closely related to estimates of case dispersionk and the effective reproduction number $R_{\text{e}}$. Increasing local transmission ($R_{\text{e}}>1$) leads to greater uncertainty in the probability estimates.

Conclusions

When public health measures are effective, lower$R_{\text{e}}$ (less transmission on average) and larger k (lower risk of superspreading) will be in effect, and end-of-outbreak determinations can be declared with greater confidence. The application of end-of-outbreak probabilities can help distinguish between local extinction and low levels of transmission, and communicating these end-of-outbreak probabilities can help inform public health decision making with regard to the appropriate use of resources.

Introduction

The coronavirus disease 2019 (COVID-19) pandemic has been the most fatal and disruptive biological disaster in recent history. As of 24 February 2021, COVID-19 had been diagnosed in over 113 million people and associated with more than 2.5 million deaths. Travel restrictions, school closures, cancellation of public events, and other public health and social measures implemented to curb disease transmission have deeply affected lives and livelihoods worldwide. In the midst of the disaster, mathematical modeling has served prominently in informing pandemic response as outbreaks have erupted and grown (Anderson et al., 2020, Ferguson et al., 2020), but the field can also provide insight into the transmission dynamics of outbreaks as they come to an end (Thompson et al., 2019, Lee and Nishiura, 2019). Control of COVID-19 has proven difficult, and timely, localized information regarding which outbreaks are growing and which are likely to end is needed to inform control measures. Here, we explain a method to estimate end-of-outbreak probabilities at localized levels, allowing for evidence-based decision making around the scaling-back of public health and social response measures in real time. Our study demonstrates the applicability of this method in relation to clusters of cases, using several examples from Japan.

Early research into the transmission dynamics of COVID-19 indicated that spread of the causal virus, severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), was highly overdispersed (Endo et al., 2020, Lloyd-Smith et al., 2005). The degree of overdispersion is quantified by the dispersion parameter $k$, which describes the variance in the distribution of the number of secondary cases infected by a typical primary case. Lower values of k represent greater variance and thereby a propensity towards superspreading — the phenomenon by which some infected individuals transmit a pathogen to large numbers of secondary cases, while most do not infect others (Lloyd-Smith et al., 2005). Larger values of k indicate less dispersion, and a Poisson distribution is obtained as a special case of the negative binomial distribution as $k\to \infty$ (Lloyd-Smith, 2007). During the pandemic, $k$ for COVID-19 has been reported in the range of 0.1–0.6 (Endo et al., 2020, Bi et al., 2020, Riou and Althaus, 2020, Tariq et al., 2020), indicating that most secondary infections are caused by a small fraction of primary cases, and therefore that superspreading events can fuel disease transmission.

In Japan, the propensity of COVID-19 towards superspreading was addressed by including the prevention, detection, and suppression of clusters — groups of cases linked by a common place and time — as a key component of the national response (Japan National COVID-19 Cluster Taskforce, 2020). Additional public health and social measures took into consideration commonalities in transmission settings between clusters (Furuse et al., 2020) — most prominently in the form of a nationwide messaging campaign encouraging residents to avoid the ‘three Cs’: closed spaces with poor ventilation, crowded places, and close-contact situations (Japan National COVID-19 Cluster Taskforce, 2020, Prime Minister’s Office of Japan and Ministry of Health Labour and Welfare, 2021). Although Japan had reported relatively low levels of epidemic growth and fatalities during the first 6 months of the pandemic compared with other developed nations in Europe and North America, it faced a resurgence of cases during the summer months.

Current World Health Organization (WHO) guidance focuses on assigning levels of risk based on epidemiological, health-system, and surveillance criteria from trends and other descriptive data to inform the loosening and re-tightening of response activities (World Health Organization (WHO), 2020a). The guidance indicates that an outbreak can be considered controlled if the effective reproduction number $R_{\text{e}}$ — the average number of secondary cases produced per primary case in the presence of interventions and immune individuals in a given time period — is maintained below the threshold value of 1 for at least 2 weeks. While this distinguishes well between epidemic growth and decline, this method of surveillance does not differentiate between whether an outbreak will end entirely or will continue as stuttering chains of transmission (i.e. $0<R_{\text{e}}<1$) before potentially resurging ($R_e>1$) (Blumberg and Lloyd-smith, 2013). Other COVID-19 guidance that addresses end-of-outbreak declarations relates to the incubation period-based guidelines used for other directly transmittable diseases, such as measles and Ebola virus disease. For those diseases, two times the maximum incubation period — the time from infection to symptom onset — since the last possible date of exposure to a source of infection within the outbreak is used to determine the time until the end of an outbreak can be declared (Public Health Agency of Canada, 2020, World Health Organization (WHO), 2020b). Despite widespread use, this method has previously been proven flawed, and is particularly vulnerable when local surveillance systems are weak (Thompson et al., 2019, Lee and Nishiura, 2017).

An alternative, statistically based method is to leverage parameters that describe transmission dynamics underlying the epidemic curve, in order to estimate the probability that one or more cases will be reported going forward in time (Nishiura et al., 2016). This more rigorous basis for end-of-outbreak determination can also be adjusted to account for additional factors, such as case underascertainment and changing transmission dynamics. Including this statistical analysis adds to the information available to politicians and public health officials when making decisions regarding response needs. Here, we present examples of where this method was used to assess end-of-outbreak probabilities for clusters in Japan during the first wave of the pandemic.

Methods

Data collection and cluster selection

Epidemiological data were collected from the official case reports published online by reporting jurisdictions (prefectures and some cities) within Japan. In some instances, the data were supplemented and additionally verified using information from press briefings from the reporting jurisdictions. The collected data included date of onset, date of report, and linkage information used to support the grouping of cases into clusters. A dataset, including dates and cluster information, is included in the supplementary materials.

For this study, four clusters representing different social contexts and time points during the epidemic were selected. The first cluster occurred early in the pandemic in Aichi Prefecture, with the first case reported on February 14, 2020 (Ministry of Health Labour and Welfare (MHLW), 2020). This involved chains of transmission related to fitness gym use and social contact between cases. The second cluster was identified in Kyoto Prefecture in March, and was initiated by importation of cases exposed to SARS-CoV-2 in Europe. Subsequent domestic transmission occurred during a series of events attended by university students and other contacts. The third and fourth clusters were linked to nosocomial transmission in a medical facility and a senior care facility in Hokkaido Prefecture, with cases reported during April and May, respectively. Clusters included all secondary cases arising from chains of transmission linking back to the original sources of common exposure.

Statistical model

In the model used, each cluster is given by the epidemic curve represented at the time of report t, with onset dates $t_i\le t$ for an epidemiologically defined group of cases $i=\{1,\dots ,M\}$. The probability that one or more new cases $X(t)$ will be reported on day $t$ is written as follows: (Nishiura et al., 2016)

$$\text{P}\text{r}\text{o}\text{b}\left(X\left(t\right)>0\right)=1-{\prod }_{i=1}^M\sum _{y=0}^{\infty }{p}_y{\left[F\left(t-t_i\right)\right]}^y$$ (1)

where $p_y$ is the probability that y secondary cases arise from a given primary case i, following a negative binomial distribution with the mean $R_{\text{e}}$ and variance $R_{\text{e}}(1+\frac{R_{\text{e}}}{k})$, with k the dispersion parameter.

The function $F\left(.\right)$ defines the cumulative distribution function (CDF) of the serial interval f, which is backprojected using the time delay from illness onset to report $h$, and defined by the convolution:

$$F\left(t-t_i\right)=\sum _{s=2}^{t-t_i}\sum _{\tau =1}^{s-1}f\left(s-\tau \right)h\left(\tau \right)$$ (2)

Outbreak extinction is determined once the estimate for the probability of observing one or more additional cases $\text{P}\text{r}\text{o}\text{b}\left(X\left(t\right)>0\right)$ becomes lower than a given threshold. The day the probability estimate drops below the threshold is, in effect, the day the outbreak would be declared over. Selection of a threshold value depends on whether the goal is to minimize the observation period (higher threshold) or minimize the risk that undetected cases may exist and become detected following the end of outbreak declaration (lower threshold). In this study, we examined a 5% threshold, which translates to a 5% risk that the end-of-outbreak declaration would be preemptive, and case(s) would be detected following the declaration (Lee and Nishiura, 2019).

Missing dates of illness onset

For some cases, the date of onset was unavailable. Either the case did not give permission for disclosure, the information was not collected, or the case was asymptomatic at the time of detection and did not later report symptoms. The latter scenario can therefore represent either presymptomatic cases with no follow-up reports or cases who were completely asymptomatic until recovery.

We approached the missing dates of illness onset in two ways. First, we excluded cases with no reported onset date and calculated the probability of new cases based solely on the existing epidemic curve of illness onsets, hereafter referred to as the ‘reported’ dataset. Second, we sampled the reporting delays and subtracted their values from the known report dates for all cases with no available date of illness onset to obtain a proxy onset date, hereafter referred to as the ‘imputed’ dataset.

Underascertainment of cases

Despite efforts to obtain high-quality surveillance data through contact tracing and testing, it is still likely that cases remain underascertained. Previous reports have suggested 9.2–44.4% case ascertainment, using data on Japanese evacuees from the original epicenter of Wuhan, China and laboratory testing conducted in Japan during January and February 2020, respectively (Nishiura et al., 2020a, Omori et al., 2020). For clusters with relatively stable and captive populations (e.g. medical centers and senior homes), ascertainment is likely to be higher due to intensive contact tracing on a focused population, although as chains of transmission move away from the common exposure setting, ascertainment will approach that of the general population. Clusters based on social contact linked to > 1 common exposure setting (e.g. multiple restaurants, gyms, or other venues) are more likely to have lower levels of case ascertainment; however, in Japan it is expected that ascertainment for cases related to a cluster would be higher than for the general population due to targeted case finding.

To address likely case underascertainment, we sampled from a binomial distribution with probability of success $p=1-q$, where $q$ was the ascertainment rate. We assumed that underascertained cases could only exist within one serial interval (i.e. 5 days (Nishiura et al., 2020b)) from the date of onset of the last reported case because the contact tracing team was unlikely to miss cases from two consecutive generations. A number of unreported cases $u_{\tau }$ at day $\tau$ can be then inferred, using the following observational model:

$$i_{\tau }\sim \text{B}\text{i}\text{n}\text{o}\text{m}\text{i}\text{a}\text{l}\left(\text{s}\text{i}\text{z}\text{e}=u_{\tau }+i_{\tau },\text{p}\text{r}\text{o}\text{b}=p\right)0\le u_{\tau }\le U,\tau \le \text{max}\left(t_i\right)+5$$ (3)

where $U$ is a maximally possible number of unreported cases, which was assigned to 50 in our simulations.

Parameter selection and statistical analysis

The model was applied using data on the epidemic curves for individual clusters, accounting for missing dates of onset and varying levels of case ascertainment, as described previously. The applied parameter values are shown in Table 1 . $R_{\text{e}}$ was explicitly varied between 0.5, 1.5, and 3, although an estimate of the local time-varying effective reproduction number ($R_{\text{t}}$) would be a sensible option when conducting analyses in real time. Otherwise, we accounted for parameter uncertainties via resampling. Estimates for $k$ were drawn from a positive half-normal distribution using mean and SD values from published studies (Bi et al., 2020, Tariq et al., 2020, Zhang et al., 2020). Other distributions were also resampled from their empirical distributions. The serial interval distribution was previously reported by Nishiura et al. (Nishiura et al., 2020b), and the reporting delay was estimated from all cases reported in Japan through to the end of May, using doubly interval-censored methods described elsewhere (Nishiura et al., 2020b, Linton et al., 2020). The reporting delay was estimated from cases reported through to the end of May, to coincide with the time interval during which cases for the four clusters were reported. Analysis was implemented using R 4.0.3 and CmdStan 2.26.1 (R Development Core Team, 2019). Reproducible code for this study is available on GitHub at https://github.com/nlinton/covid19_eoo.

Table 1.

Parameters used in the statistical model.

Description	Distribution	Examined values	References
Offspring distribution	Negative binomial	Re: 0.5, 1.5, 3.0 k (SD): 0.11 (0.05), 0.25 (0.19), 0.58 (0.26)	Park et al. (2020) and Bi et al. (2020); Tariq et al. (2020); Zhang et al. (2020)
Serial interval	Weibull	Mean: 4.8 (SD: 2.3)	Nishiura et al. (2020b)
Reporting delay	Gamma	Mean: 7.2 (SD: 4.7)	Estimated

R_e: effective reproduction number; k: overdispersion parameter; SD: standard deviation.

Ethical considerations

Our study analyzed publicly available data, which had already been de-identified upon press release. The study was approved by the Medical Ethics Board of the Graduate School of Medicine, Kyoto University (R2673).

Results

Characteristics of the four clusters are shown in Table 2 . The Aichi fitness gyms cluster had the smallest number of cases (n = 40) while the Hokkaido senior care facility cluster was the largest (n = 94). The average age was lowest for the Kyoto cluster, which was associated with parties attended primarily by university students, while the average age was highest for the senior care facility cluster. Three-quarters of the Hokkaido cancer center cluster were female, while the female-to-male ratio for the gyms and university-related parties cluster were nearly evenly split between males and females. The proportion of cases with no reported date of onset ranged from 2.5% for the Aichi gyms cluster to 46.5% for the Kyoto university-related parties cluster. The time between first onset and last onset within each cluster ranged from 22 to 43 days.

Table 2.

Descriptive information regarding the four case clusters.

Characteristics	Fitness gyms	University parties	Senior care	Cancer center
Source of index case infection	Imported	Imported	Domestic	Domestic
Number of cases	40	72	94	92
Age in years,a mean (range)	59 (20–80)	30 (0–70)	72 (20–100)	50 (20–80)
Female (%)	19 (47.5)	33 (45.8)	71 (75.5)	62 (67.4)
Date of onset not reported (%)	1 (2.5)	33 (45.8)	34 (36.2)	24 (26.1)
First to last onset	35 days	22 days	35 days	43 days

^aAges were reported in deciles. Source of index case infection ‘imported’ indicates that the index case(s) for the cluster reported international travel and were likely infected while abroad.

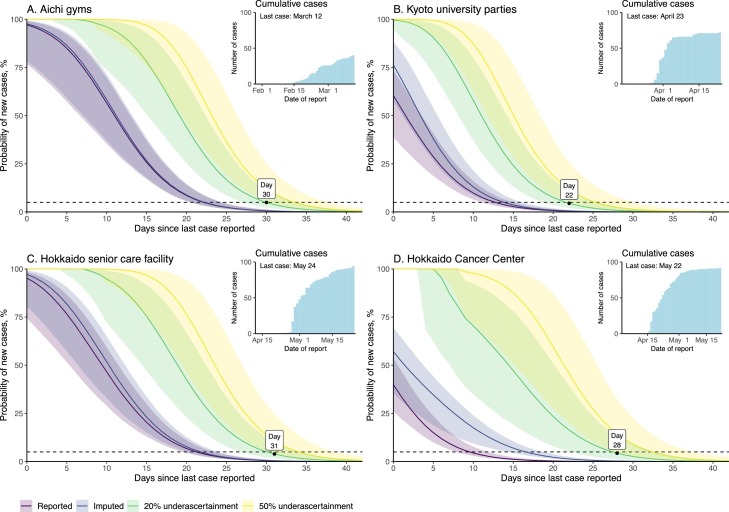
The delay from onset to prefecture report date for cases reported between when the first case was detected in January and May 31, 2020 was estimated at 7.2 days (95% credible interval [CrI]: 7.1–7.3 days), using the best-fit gamma distribution (Table S1 and Figure S1). Figure 1 depicts the probability distributions for observing additional cases by cluster, varyingly accounting for asymptomatic cases and missing dates of onset (imputed dataset) and underascertainment of cases.

Figure 1.

End-of-outbreak probabilities for four coronavirus disease 2019 (COVID-19) case clusters in Japan.

Each subfigure begins on the last date of onset within the cluster. All plots assume $R_{\text{e}}=0.5$ and $k$ = 0.25. Lines are median values and shaded areas are 95% credible intervals (CrI) for the datasets. Purple represents the datasets including only reported dates of onset; indigo represents the datasets including imputed dates of onset; yellow represents the datasets accounting for 20% underascertainment of cases; green represents the datasets accounting for 50% underascertainment of cases. The horizontal line represents the threshold for 5% probability of failure of the model. Cumulative case counts over time for each cluster are shown in the inset figures.

Table 2 presents the estimated observation period in days for each cluster, based on the varying parameter values. End-of-outbreak determination was most closely tied with the size of the outbreak. The datasets with more cases (accounting for missing onsets and underascertainment of cases) reached the proscribed probability thresholds at later dates compared with the datasets based on the original epidemic curve (the reported dataset). Studies on Ebola virus disease likewise found that lower ascertainment of cases indicated that more time is needed to be sufficiently certain that the end of an outbreak is declared appropriately (Thompson et al., 2019, Lee and Nishiura, 2019). Moreover, a larger $R_{\text{e}}$ consistently resulted in slightly longer observation periods compared with smaller $R_{\text{e}}$ values (Table 3 and Figures S2.1–2.4). The CrIs were widest for combinations of large $R_{\text{e}}$ and small $k$, indicating greater uncertainty over whether the outbreak had truly ended. The probabilities for some of the upper 95% CrIs never dropped below the threshold values within the 42-day periods examined.

Table 3.

Length of the observation period in days from last date of report of a case to estimated end of transmission for four coronavirus disease 2019 (COVID-19) case clusters in Japan.

Cluster			A	B	C	D
Parameters	Re	k	Probability threshold (5%)
Reported onsets	0.5	0.11	23	13	22		10
		0.25	23	13	22		10
		0.58	23	13	22		10
	1.5	0.11	27	17	26		14
		0.25	27	17	26		14
		0.58	27	17	26		14
	3.0	0.11	29	20	29		17
		0.25	29	20	28		17
		0.58	29	20	28		17
Imputed onsets	0.5	0.11	23	14	22		17
		0.25	23	14	22		17
		0.58	23	14	22		17
	1.5	0.11	27	18	26		21
		0.25	27	18	26		21
		0.58	27	18	26		22
	3.0	0.11	30	21	29		24
		0.25	29	21	29		24
		0.58	29	21	29		24
20% ascertainment	0.5	0.11	30	22	30		28
		0.25	30	22	30		28
		0.58	30	22	31		28
	1.5	0.11	35	27	35		33
		0.25	35	26	35		32
		0.58	34	26	35		32
	3.0	0.11	–	–	–		–
		0.25	38	29	38		35
		0.58	37	29	37		34

Cluster A: fitness gyms cluster; Cluster B: university parties cluster; Cluster C: senior care facility; Cluster D: cancer center cluster. Observation days are reported relative to the last date of report of a case in the cluster (day 0). Cells with ‘– ‘did not reach the proscribed threshold probability within the 42-day period analyzed.

Discussion

As guidance continues to be developed for COVID-19 responses, it is important to incorporate insights from statistical modeling for declining phases of the pandemic (Thompson et al., 2020). In this regard, localized, end-of-outbreak declarations are a valuable component of outbreak responses because they indicate that public health interventions may be relaxed or lapsed. Statistical models that can provide insight into levels of certainty of the decline of an outbreak are useful for dynamically optimizing the timing of such declarations.

Our application of a transmission characteristic-based statistical model to COVID-19 clusters found that confidence in end-of-outbreak determination was most closely tied to estimates of $R_{\text{e}}$ and, which in turn reflected local levels of control. If public health measures are effective, we would expect to see lower $R_{\text{e}}$ (less transmission on average) and larger $k$ (lower risk of superspreading due to measures targeted to prevent superspreading events), and have more confidence in declaring the end of the outbreak. When considering end-of-outbreak scenarios we would generally anticipate $R_{\text{e}}<1$. However, if no or lax public health interventions are implemented, $R_{\text{e}}$ may be > 1. Under these circumstances, there is less certainty as the end-of-outbreak probabilities approach zero (see supplementary figures). Under some assumptions of $R_{\text{e}}$ and $k$, we estimated that end-of-outbreak declarations could be made before 28 days (two times the approximate maximum incubation period for COVID-19) (Public Health Agency of Canada, 2020, Linton et al., 2020) had passed from the date of last reporting of any case (which was often the same day the case was isolated). Using these estimates would potentially allow for earlier end-of-outbreak declarations, leading to saved resources.

Parameters such as reporting delay and serial interval can also vary throughout the epidemic. When surveillance is heightened the reporting delay may be shorter than when surveillance systems are overwhelmed. Similarly, nonpharmaceutical interventions, such as contact tracing, isolation, and physical distancing, change contact patterns and limit the time during which an infectious case may be in contact with susceptible individuals, shortening the serial interval (Ali et al., 2020). Although these possible variations were not accounted for in this study, they can be incorporated if deemed to be of value to inform decisions regarding the continuation of public health and social response measures.

The size and scale of the epidemic curves used in our analyses depended on case, cluster, and outbreak definitions, as well as case ascertainment by the surveillance system. When a cluster definition is limited to cases linked directly to a location or activity (e.g. a hospital or an event) then the cluster size will be smaller than if the cluster includes all secondary infections of household members and other contacts not directly related to the transmission event(s) that defined the cluster. Likewise, when the cases are limited to those whose samples test positive (i.e. via polymerase chain reaction [PCR] or antigen testing) the scope and scale of the epidemic curve will be smaller than if other probable cases were included in the outbreak case definition. The clusters reported here include original cluster cases as well as all subsequent cases in chains of transmission reported by local public health jurisdictions. It is possible that some cases associated with the cluster were missed or incorrectly attributed; however, we repeatedly reviewed the data to minimize these possibilities. Our analyses accounting for possible underascertainment of cases likewise showed that, when accounting for missed cases, the observation period before reaching our 5% threshold was extended.

Up to the end of May 2020, only PCR-positive cases were included in the case definition for COVID-19 cases in Japan. Infected individuals may not have been tested if they were never suspected of being a case or did not meet testing criteria (Ministry of Health Labour and Welfare (MHLW), 2021). In addition, PCR sensitivity is less than perfect, reducing to around 70% more than 1 week after symptom onset (Miller et al., 2020), so some infected individuals may have received a false negative test result if their viral load at the time they were tested was insufficient to trigger a positive result. Sequentially repeated PCR testing in Japan for persons with persistent symptoms and/or new onset of symptoms after initially being tested while asymptomatic has identified cases that were initially PCR negative but epidemiologically linked to other cases, as has been seen elsewhere (Ai et al., 2020).

Importation of cases is not accounted for in this method. Defining outbreaks based on the epidemiological linkage of cases to at least one common source of exposure (i.e. clusters) necessarily precludes inclusion of new sources of infection (i.e. importation). A new case linked to, for example, a physical location that was a common source of exposure for cases in a cluster may represent an importation event rather than a continuation of the outbreak/cluster, unless there is clear epidemiological link (e.g. close contact or physical proximity during a given timeframe) between the newly detected case and the cluster. When applying this method to outbreaks defined by a geographic region with free-flow borders to other regions with active transmission — as was the cases for prefectures in Japan during the first wave of the pandemic — importation of one or more cases before the outbreak would simply add to the existing epidemic curve and feed into the end-of-outbreak probability calculations. Likewise, exportation of cases is not accounted for in this method, because any case epidemiologically linked to the cluster is included, regardless of the geographic boundaries within Japan. However, possible exportation across international borders is not accounted for. Even when considering clusters, if local public health jurisdictions minimize publicly shared information (as was seen in later stages of the pandemic), some links may be missed.

Lastly, further analyses describing transmissivity of the virus are needed to improve understanding of the most plausible range for these critical values. In addition, when more information is available regarding the different transmission routes of COVID-19 (i.e. airborne, droplet spread, or contact with contaminated fomites) the model could potentially be updated to account for differences in these routes, as was previously done for modeling the flare-ups of Ebola virus disease due to sexual transmission from male survivors (Lee and Nishiura, 2019).

Other methods for statistical end-of-outbreak determination have recently been proposed, and provide alternative options for examining cases using geographically based outbreak definitions (Parag et al., 2020, Hart et al., 2019). The focus of this study on clusters may be different from typical geographically based analyses, but we believe that focusing on this scale can be meaningful to decision makers dealing with individual clusters, such as officials for the involved local health jurisdictions (i.e. cities and prefectures) as well as the facilities (hospitals, senior homes, gyms, schools, etc.) where cases have been identified.

In summary, this study incorporated a reporting delay distribution into a model for end-of-outbreak probability estimation, and applied this method to clusters in the COVID-19 epidemic in Japan. In doing so, it provides estimates of the probability that the outbreak will continue in real time. Communicating these probabilities can inform public health decision making regarding the appropriate use of resources when transmission has declined for a given outbreak.

Conflict of interest

The authors have no conflicts of interest to disclose.

Funding

NML received a Japanese Ministry of Education, Culture, Sports, Science, and Technology (MEXT) graduate scholarship. HN received funding from a Health and Labor Sciences ResearchGrant (19HA1003, 20CA2024, and 20HA2007), the Japan Agency for Medical Research and Development (AMED; JP19fk0108104 andJP20fk0108140), the Japan Society for the Promotion of Science (JSPS) KAKENHI (17H04701), the Inamori Foundation, and the Japan Science and Technology Agency (JST) CREST program (JPMJCR1413). The funders were not involved in the collection, analysis, or interpretation of the data, the writing of the manuscript, or the decision to submit for publication.

Appendix A. Supplementary data

The following is Supplementary data to this article: