Abstract
Several independent datasets suggest blood type A is over-represented and type O under-represented among COVID-19 patients. However, blood group antigens appear not to be conventional susceptibility factors in that they do not affect disease severity, and the relative risk to non-O individuals is attenuated when population prevalence is high. Here, I model a scenario in which ABO transfusion incompatibility reduces the chance of a patient transmitting the virus to an incompatible recipient – thus in Western populations type A and AB individuals are “super-recipients” while type O individuals are “super-spreaders”. This results in an offset in the timing of the epidemic among individuals of different blood types, and an increased relative risk to type A/AB patients that is most pronounced during early stages of the epidemic. However, once the majority of any given population is infected, the relative risk to each blood type approaches unity. Published data on COVID-19 prevalence from regions in the early stages of the SARS-CoV-2 epidemic suggests that if this model holds true, ABO incompatibility reduces virus transmissibility by at least 60 %. Exploring the implications of this model for vaccination strategies shows that paradoxically, targeted vaccination of either high-susceptibility type A/AB or “super-spreader” type O individuals is less effective than random vaccination at blocking community spread of the virus. Instead, the key is to maintain blood type diversity among the remaining susceptible individuals. Given the good agreement between this model and observational data on disease prevalence, the underlying biochemistry urgently requires experimental investigation.
Keywords: SARS-CoV-2, Enveloped virus, Glycoprotein, ABO blood group, Modelling
1. Introduction
Multiple recent published studies and preprints have suggested that the prevalence of COVID-19 disease varies by blood type, with type A being relatively susceptible and type O being less susceptible. Initial reports from China were followed by confirmation in the US and Europe (Zhao et al., 2020; Zietz and Tatonetti, 2020; Kolin et al., 2021; Ellinghaus et al., 2020; Gérard et al., 2020), and have now been substantiated across the globe (reviewed in (le Pendu et al., 2021)). Although some studies report an association with disease severity, this is not consistently observed, with the case fatality ratio (CFR) and the probability of progressing to intensive care appearing independent of blood type in other studies (e.g. (Dzik et al., 2020)). Consistent with this, the most recent data (release r5) from the Covid-19 Host Genetics Initiative (The COVID-19 Host Genetics Initiative, 2020) indicates that the ABO gene is the most significant region genome-wide for SARS-CoV-2 infection rate, yet has no detectable association with disease severity when comparing hospitalized and non-hospitalized COVID-19 patients. Similarly, an association with disease incidence, but not severity, is seen in data from home genetics tests carried out by 23andMe and AncestryDNA (Anon., 2021a; Roberts et al., 2021). However, despite the strong worldwide association between ABO blood group and infection risk, a recent study of 1769 crewmembers from the French Navy nuclear aircraft carrier Charles de Gaulle conclusively demonstrates that in this scenario, with an overall attack rate of 75.8 %, there was no correlation between blood type and incidence of infection (Boudin et al., 2020). These conflicting observations require explanation.
Here, I investigate the behaviour of “ABO-interference”: a model of epidemic spread in which the transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2, the causal agent of COVID-19) is dependent on the ABO blood type compatibility between an infected individual and the susceptible people they encounter. Mechanistically, this models a scenario in which infectious virions acquire the glycosylation pattern and hence the ABO antigen status of their current host. This in turn allows shed virions to be “rejected” by incompatible recipients, blocking the initial infective step. This immediately explains the lack of correlation with disease severity, since once an infection is established, virions produced within the new host are necessarily self-compatible and able to spread freely between cells.
The plausibility of this hypothesis has already been established by work on HIV (Neil et al., 2005; Arendrup et al., 1991), and was also previously proposed for the 2003 epidemic of SARS (Cheng et al., 2005; Guillon et al., 2008), for measles (Preece et al., 2002), and indeed for enveloped viruses in general (Seymour et al., 2004; Cooling, 2015). Modelling of the proposed evolutionary interaction between virus transmission and host ABO antigens provides a convincing explanation for the worldwide distribution of A, B and O alleles at this locus (Seymour et al., 2004) (see also Discussion). SARS-CoV-2 has an outer lipid membrane containing spike, membrane and envelope (S, M and E) proteins, all of which are exposed to immune recognition and any or all of which may be glycosylated. Structural studies show that S is heavily glycosylated, including fucosylated glycans that may potentially bear ABO determinants (Cooling, 2015; Watanabe et al., 2020), and in vitro studies show that spike protein does indeed acquire ABO determinants when produced in cells expressing the relevant glycosyltransferases (Deleers et al., 2020). The glycosylation status of the M and E proteins has not yet been characterised, nor the glycosylation status of the membrane lipids. Cell-cell adhesion experiments using engineered CHO cells expressing S and an ACE2-expressing cell line show that anti-A antibodies can block spike-mediated adhesion, but only when the S-expressing cells also express the A glycosyltransferase (Guillon et al., 2008). This study also showed via modelling that ABO-interference can reduce the progress of an epidemic dependent on the magnitude of the block to transmission and the local population structure. However, despite the mechanistic plausibility of this hypothesis and the preliminary data from the SARS epidemic, there has as yet been no detailed modelling exploring the implications of ABO-interference for the relative susceptibility of individuals with different blood types at different stages of the epidemic, or for vaccination strategies.
In this analysis, I develop an extended SIR (Susceptible, Infected, Recovered) epidemiological model which allows for a partial or total block to virus transmission from an infected patient to an incompatible recipient, and explore the implications of this model for epidemic progression and for vaccination strategies. Strikingly, I find that this model is able to reconcile all the observations to date. ABO-interference does indeed lead to significant differences in disease incidence between different blood types, but only when the overall population prevalence is low.
2. Results
2.1. Modelling ABO-interference with virus transmission
The simplest of all epidemic models assumes a homogeneously mixing population divided into susceptible, infectious and recovered groups or “compartments”. This yields three variables S, I and R, which respectively represent the proportion of the population with each status. Such a model is completely described by two parameters β and ν, representing the rate constants for infection and recovery respectively. The duration of the infectious period d is given by 1 / ν. All simulations presented here are based on d = 7 days, and none of the results presented are sensitive to this parameter. R0 is given by the product β.d (or equivalently ) and represents the basic reproduction number, i.e. the mean number of individuals infected by a typical infectious individual during their illness, in the context of a completely susceptible population (Jones, 2007).
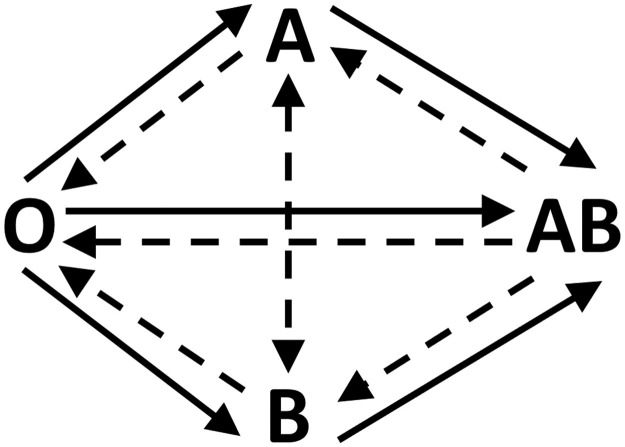
To this model I add a further parameter ρ where 0 ≤ ρ < 100 %, representing the relative probability of cross-type infection (Fig. 1 , see Methods for full details). In this extended model, R0 is not a well-defined quantity since even in a fully susceptible population the current effective R value, denoted R(t), depends on ρ and on the blood type distributions in both S and I. Below, I use Rmax to indicate the maximal possible value of R(t). This will be observed when the population is fully susceptible and transmission is unimpeded, i.e. when ρ = 100 % or all currently infected individuals are type O.
Fig. 1.
Illustration of the transmission model. Full arrows represent unimpeded transmission (infection rate = β) and dashed arrows represent impeded transmission (infection rate = ρ ⋅ β).
2.2. A quasi steady state is obtained when all blood types are infected
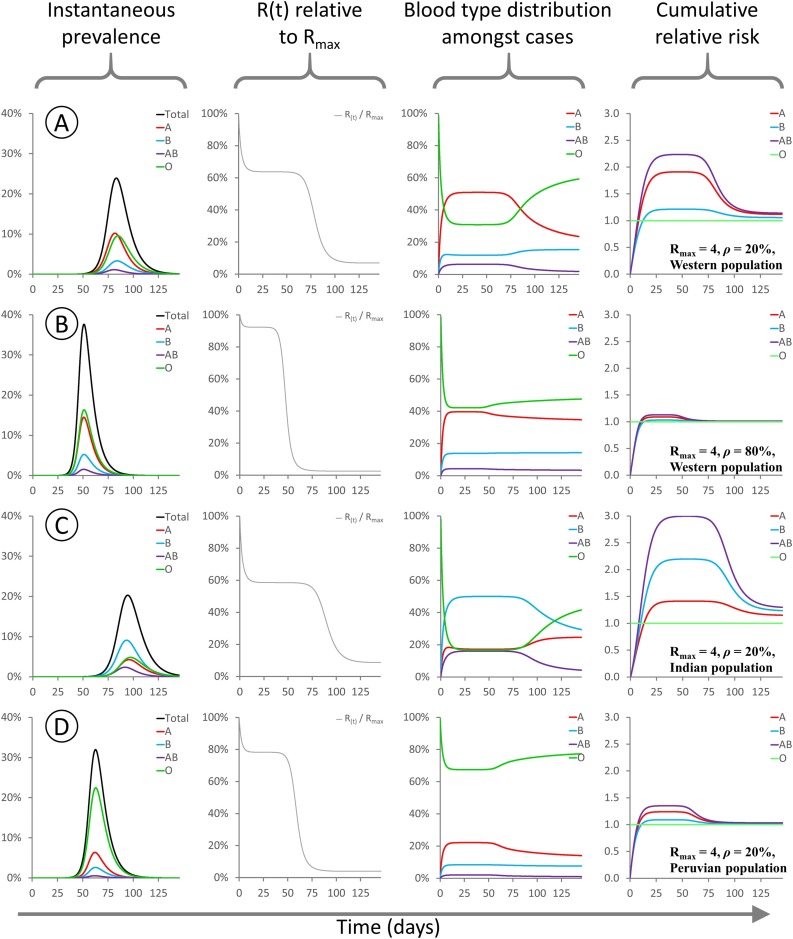
If ρ = 0 and the index case is non-O, then it is impossible for the epidemic to enter the O sub-population. Since this is not the case in the real world, this scenario is not explored further here. Fig. 2 illustrates the progress of simulated epidemics occurring under varying values of ρ and different population blood group distributions. In row 2A, I analyse an epidemic with Rmax = 4 and ρ = 20 %, occurring within a typical Western population with a high frequency of each of types O and A, and lower frequencies of types B and AB. Since ρ = 20 % represents a substantial block to transmission, the transmission rate R(t) during initial stages of the epidemic is depressed by around 1/3 compared to an unmitigated epidemic. In the early stages of the epidemic, the relative risk is highest for types A and AB, and since AB is rare at the population level, the majority of infections are type A individuals. Conversely, type O is relatively protected during early stages of the epidemic. By the later stages of the epidemic the pool of susceptible A, B and AB individuals has become depleted and thus type O cases predominate. In terms of cumulative cases, type AB (as the universal recipient) is at highest relative risk, and type O (as the most restrictive recipient) at lowest relative risk, however the magnitude of the difference is starkly different depending on whether the epidemic is in the late or early phase.
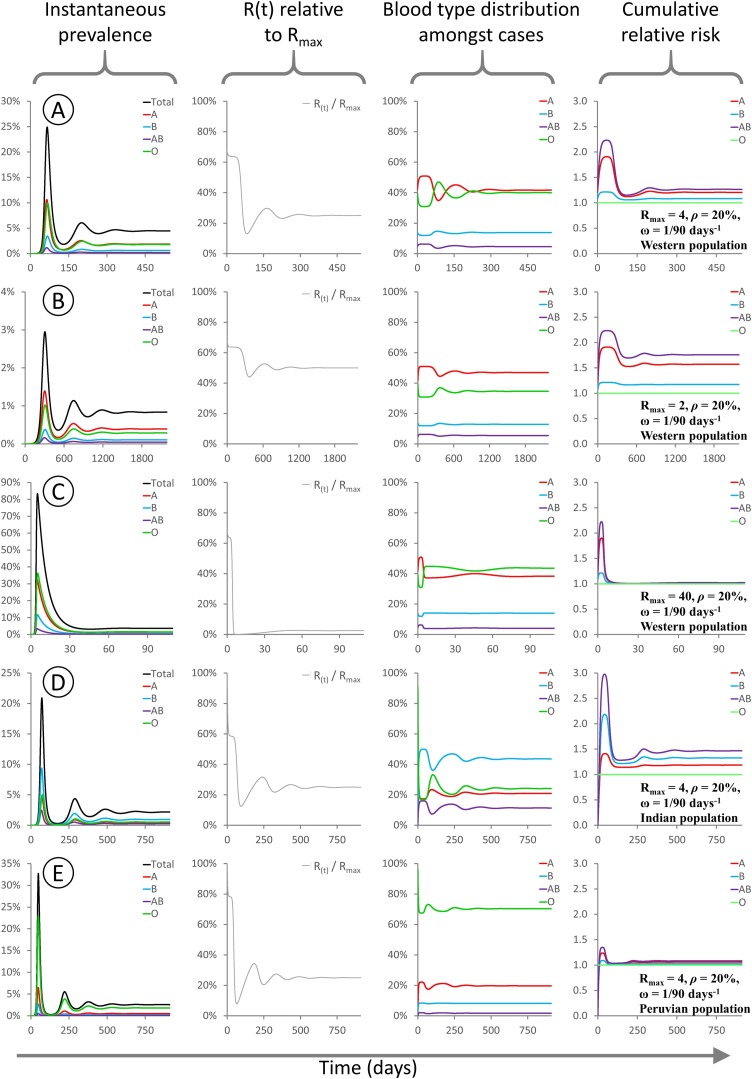
Fig. 2.
These panels show the evolution of various modelled parameters for epidemics initialised under different conditions. For all epidemics Rmax = 4 and the model is initialized with type O index cases comprising 1/1,000,000 of the population. Since type O transmits freely to all recipients, R(t) = Rmax at time t = 0.
A: Rmax = 4, ρ = 20 %, “Western” population blood type distribution, 38 % A / 14 % B / 4 % AB / 44 % O.
B: Rmax = 4, ρ = 80 %, “Western” population blood type distribution as above.
C: Rmax = 4, ρ = 20 %, “Indian” population blood type distribution, 21.4 % A / 39.9 % B / 9.4 % AB / 29.3 % O (Cooling, 2015).
D: Rmax = 4, ρ = 20 %, “Peruvian” population blood type distribution, 18.9 % A / 8.1 % B / 1.6 % AB / 71.4 % O (Watanabe et al., 2020).
For all sub-panels, X axis denotes days. Y axes: (first column) proportion of the population infected; (second column) R(t) as a fraction of Rmax; (third column) distribution of blood types among currently infected individuals; (fourth column) cumulative risk of infection for each blood type relative to type O.
In row 2B, I analyse an epidemic with Rmax = 4 and ρ = 80 %, occurring within the same Western population. The same general pattern is observed, however the level of suppression of R(t) is less pronounced, and the overall difference in risk between the blood groups is greatly attenuated, due to the higher level of cross-type transmission. Rows 2C and 2D illustrate epidemics with Rmax = 4 and ρ = 20 %, occurring within populations with blood type distributions typical of India or Peru, respectively. In the “Indian” model epidemic, the degree of R(t) suppression is similar to that seen in a Western population, but type B individuals are at higher risk than type A. In the “Peruvian” model epidemic, the high frequency of type O (universal transmitter) in the population means that R(t) is barely suppressed even though cross-type transmission is greatly restricted.
Importantly, whenever infection is present among individuals with all four blood types (i.e. there is at least one type O index case, or ρ > 0), the blood type distribution among infected people rapidly converges upon a new equilibrium that is significantly skewed relative to the initial population distribution. This equilibration process causes R(t) to also settle on an equilibrium value during the early stages of the epidemic, hereafter called Rsteady. This is a rapid process, with R(t) reaching Rsteady within a few serial intervals: in these simulations this equates to ∼0.1 % of the population being infected. Therefore, in real-world epidemics subject to ABO-interference, estimates of R0 based on population statistics are likely to actually measure Rsteady and thus underestimate the true value of Rmax.
2.3. Estimating ρ for SARS-CoV-2
During the early steady state described above, Rsteady is a consistent multiple of Rmax, indicating that ABO-interference suppresses the epidemic with equal efficiency regardless of both the underlying infectiousness of the pathogen and any effect of non-pharmaceutical interventions on R(t). Similarly, the relative risk to each blood type is also dependent only on ρ and the background population blood type distribution, and independent of Rmax (Supplementary Fig. 1). Thus, regardless of whether the epidemic in any given region is progressing quickly or slowly, the relative risk to each blood type is predictable from the population blood type frequencies and the value of ρ. Conversely, so long as total seroprevalence is low and the epidemic lies within the steady-state region of the curve, measurement of the relative risk for different blood types allows estimation of ρ.
Table 1 shows data compiled from a range of published studies that have reported ABO frequencies amongst infected SARS-CoV-2 patients and controls (Zhao et al., 2020; Zietz and Tatonetti, 2020; Ellinghaus et al., 2020) during the early stages of the first wave of the worldwide pandemic. These collectively cover epidemics in two regions of China, three regions of Spain, and one region each of Italy and the United States. For each data set, I used the control blood type distribution to predict the expected steady state distribution among infected patients for different values of ρ, and thus the expected case frequencies for each study, dependent upon sample size. A chi-square goodness-of-fit test was then used to compare the observed case frequencies to the model-based expectations. A low p value indicates that the observed case frequencies are incompatible with the model prediction, and thus the corresponding value of ρ is unlikely. Conversely, a higher p value indicates that the corresponding value of ρ is compatible with the observed data. Notably, for all data sets the chi-square peak p value lies between ρ = 20 % and ρ = 55 % despite the different underlying blood type frequencies and relative risk ratios in each country, indicating that in all regions of the world, the most plausible estimate of ρ lies in this range. For the Italian and Spanish study, data was also provided for area-matched control data from blood donors (Ellinghaus et al., 2020): using these instead of the internal control data does not affect the result.
Table 1.
Observed case and control numbers are taken from references Zhao et al. (2020), Zietz and Tatonetti (2020), Ellinghaus et al. (2020). The Italian and Spanish data sets provided both internal and external controls. For each area, the control blood group frequencies were used to calculate expected case numbers for each blood group in each study, for varying values of ρ. Calculating the chi-square goodness of fit between the predicted case numbers and observed numbers allows region-specific estimation of ρ. The orange highlight indicates the most plausible value of ρ for each study, while the yellow highlight indicates all values with p > 0.05 after Bonferroni multiple testing correction.
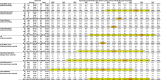 |
Several caveats apply to this analysis. Firstly, poor demographic matching between cases and controls may distort the results. This is apparent in the Spanish sample from (Ellinghaus et al., 2020), where the distribution of cases and controls was uneven between contributing hospitals. Thus, for the aggregate sample, all values of ρ have a low chi-square p value indicating a poor fit between model and data. In this case, using locally matched blood donor samples results in a better fit without altering the overall findings (Table 1 and Supplementary Fig. 2).
Secondly, the “steady state” only holds during the early stages of the epidemic, and the relative risk approaches unity once the majority of the population is infected as in the case of the Charles de Gaulle study (Boudin et al., 2020)). Even in the countries analysed here, in which overall prevalence was low at the time of study, the local prevalence in “hotspots” is much higher (Percivalle et al., 2020). Infected individuals will by definition originate preferentially from hotspot regions. In such areas, the epidemic may have progressed beyond the steady state region of the epidemic curve, reducing the degree of blood type skewing among the infected population and partially masking the effects of ABO-interference on virus transmission. In this case, in order to generate the observed changes in blood type frequency, then the degree of ABO-interference must be even more pronounced. i.e. the estimate of ∼40 % is a maximum bound, and the true frequency of cross-type transmission may be even lower.
Thirdly, the SIR model assumes that population mixing and opportunities for transmission are independent of blood type. This is unlikely to be the case since blood relatives living together are both more likely to infect each other and more likely to share a blood type. This effect will also tend to mask the effect of ABO-interference. This effect will be most pronounced in areas with relatively segregated ethnic communities, as for example in the New York sample where black and white Americans have differing blood type distributions and social mixing is also likely to be uneven.
Fourthly, when there is nosocomial spread within a hospital, an increase in frequency of one blood type among infected patients will lead to a decrease in frequency of that blood type in the remaining uninfected hospital patients. This will exaggerate the effects of ABO-interference if uninfected hospitalised patients are used as controls.
Since the majority of these effects will tend to oppose the effects of ABO-interference and thus bias the estimate of ρ upwards, the central estimate of ∼40 % represents a best-guess upper bound for ρ. Intriguingly, previous data from direct contact tracing (Guillon et al., 2008) imply ρ = 47.7 % for the 2003 hospital outbreak of SARS in Hong Kong, suggesting that values around this range may be a feature of coronavirus infections in general.
2.4. Is targeting by blood type a useful vaccination strategy?
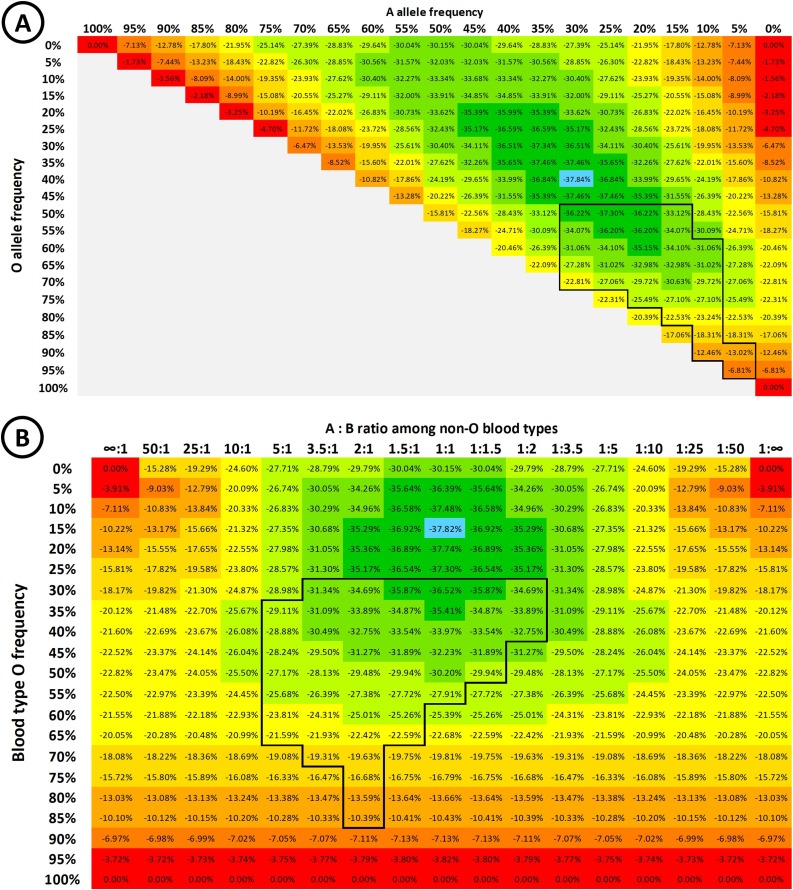
Initial preprints noting the increased risk to type A individuals have proposed that these may require additional surveillance and priority for protection. However, ABO-interference with virus transmission presents a unique and striking scenario that has not previously been modelled in detail, in which those most prone to infection are those least likely to pass it on, and vice versa. This raises the question as to whether it is more important to vaccinate the most susceptible individuals, or the most infectious individuals. Fig. 3 A shows (, i.e. the degree to which R0 is suppressed by ABO-interference, across the full spectrum of potential ABO allele frequencies for ρ = 30 %. ABO-interference suppresses transmission most efficiently when the allele frequency ratio is approximately 40 % O / 30 % A / 30 % B alleles. Translating allele frequencies to blood type frequencies yields Fig. 3B. Thus, ABO-interference suppresses transmission most efficiently when type O individuals make up 15 % of the population and type A / type B individuals are present in equal proportions. This is however not the case for any existing human populations, since O is the most common blood type worldwide (see Discussion). A similar shape heat map is obtained for values of ρ = 20 % and ρ = 90 % (not shown). Amongst actual populations worldwide, the effect of ABO-interference in lowering R(t) is likely to be most pronounced within East and Southeast Asian countries, where type O is only moderate frequency, and A and B are more evenly balanced.
Fig. 3.
A: Heat map showing , i.e. the degree of suppression of R0 during the early “steady state” portion of an epidemic with ρ = 30 %, according to the population ABO allele frequencies. B allele frequency = (100 % - O% - A%). B: Heat map showing the degree of suppression of R0 during the early stages of the epidemic, according to the background population blood type frequencies. In both heat maps, ABO allele frequencies are assumed to be in Hardy-Weinberg equilibrium – i.e. allele frequencies are not changing from generation to generation, there is no net selection or gene flow, and that mating is random with respect to genotype. The colour gradient from red to green indicates the degree of suppression in 5 % increments, with the blue highlight indicating maximal suppression of virus transmission. The boxed areas of the plots indicate allele / blood type frequencies that are typically observed in human populations (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article).
From the standpoint of vaccination strategy, vaccinating type O individuals effectively moves the population upwards in Fig. 3B, while vaccinating type A or B moves the population right or left respectively. In principle, an optimal vaccination strategy will cause the distribution among susceptible individuals to move “down” the gradient towards more effective suppression of the epidemic. Conversely, the vaccination strategy must also be careful not to disrupt the intrinsic protection afforded by ABO-interference. To illustrate this, consider a population with 50 % type A and 50 % type O individuals, similar to Māori and some Polynesian populations where the type B frequency is very low (Edinur et al., 2013). In general, the predicted herd immunity threshold is , so in the absence of ABO-interference the threshold for an epidemic with an Rmax of 3 is 66.7 %. In such a population, if ρ = 30 % then Rsteady = 2.32, ald the risk for type A individuals is 1.82 times higher than type O individuals, and type O individuals are 1.54 times as infectious as type A individuals.
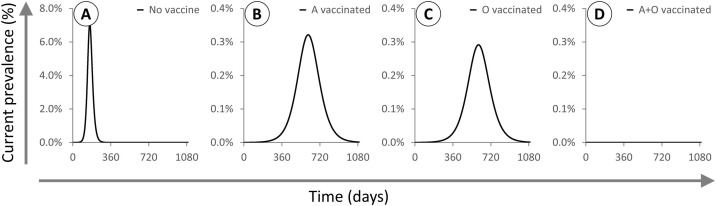
A well-intentioned strategy to reduce infection might prioritise vaccinating type O “super-spreaders” before type A. However, once all type O individuals have been immunised, the protective effect of ABO-interference is abolished since the remaining susceptible population is now exclusively type A, and an infected type A individual can freely transmit to any remaining susceptible individual. Herd immunity will therefore only be attained when the full 66.7 % of the population is vaccinated. The same applies in reverse if the more vulnerable type A individuals are instead prioritised for vaccination. However, vaccinating both blood types equally produces herd immunity when 56.9 % of the population is vaccinated, consistent with Rsteady in this population. This effect is further magnified if transmission is brought down by other means, for example non-pharmaceutical interventions including social distancing. For the same population and same value of ρ = 30 %, if Rmax = 2 then Rsteady = 1.55. In this case the herd immunity threshold is 50 % of the population if preferentially vaccinating either type O or type A, but only 35.4 % if vaccinating individuals at random [Fig. 4 ].
Fig. 4.
X axis: days. Y axis: proportion of the population infected (note different scale used for panel A). All epidemics are based on a population with 50 % A / 50 % O individuals and initialised at t = 0 with type O index cases and 1/1,000,000 of the population infected. Rmax = 2 and ρ = 30 % for all epidemics modelled. A: No vaccination. B: 35.4 % of the population vaccinated at t = 0, all type A. C: 35.4 % of the population vaccinated at t = 0, all type O. D: 35.4 % of the population vaccinated at t = 0, half type A and half type O. Vaccinating O is slightly more effective than vaccinating A, but vaccinating both types leads to herd immunity at a lower threshold.
2.5. The effect of waning immunity for a virus subject to ABO-interference
At present it is unknown whether SARS-CoV-2 leads to long-lasting immunity. The four other endemic human coronaviruses do not confer lasting immunity, and repeat infection is common. In an SIR model, when immunity is allowed to wane over time, then population spread of the virus can resume once the population level of immunity falls below the herd immunity threshold. Over time this leads to damped oscillatory behaviour, with recurrent pulses of infection converging on a final steady state. In this final steady state, by definition R(t) = 1 and there is steady sustained transmission with overall infection levels neither growing nor shrinking [Fig. 5 ]. The final population disease burden depends on the duration of immunity, with a shorter immune duration leading to a higher population-wide average prevalence. In the endemic state, with waning immunity and recurrent infection, the relative risk to each blood type should be interpreted as a difference in the frequency of infection: e.g. if type A has a relative risk of 1.1 compared to type O, it means type A individuals are 10 % more likely to suffer an infection within any given time period.
Fig. 5.
These panels show the evolution of various modelled parameters for epidemics involving waning immunity. Waning immunity is described by a parameter ω representing the rate of loss of immunity (see Methods for details). For all epidemics ρ = 20 %, and the model is initialized with type O index cases comprising 1/1,000,000 of the population. Since type O transmits freely to all recipients, R(t) = Rmax at time t = 0.
A: Rmax = 4, ρ = 20 %, ω = 1/90 days−1, “Western” population blood type distribution, 38 % A / 14 % B / 4 % AB / 44 % O.
B: Rmax = 2, ρ = 20 %, ω = 1/90 days−1, “Western” population blood type distribution as above.
C: Rmax = 40, ρ = 20 %, ω = 1/90 days−1, “Western” population blood type distribution as above. D: Rmax = 4, ρ = 20 %, ω = 1/90 days−1, “Indian” population blood type distribution, 21.4 % A / 39.9 % B / 9.4 % AB / 29.3 % O (Chandra and Gupta, 2012).
E: Rmax = 4, ρ = 20 %, ω = 1/90 days−1, “Peruvian” population blood type distribution, 18.9 % A / 8.1 % B / 1.6 % AB / 71.4 % O (Anon., 2021b).
For all sub-panels, X axis denotes days. Y axes: (first column) proportion of the population infected; (second column) R(t) as a fraction of Rmax; (third column) distribution of blood types among currently infected individuals; (fourth column) cumulative risk of infection for each blood type relative to type O. The relative risks to different blood types during the final steady state depend on Rmax (compare A,B,C) and on the background blood type distribution (compare A,D,E). The final case burden depends on all of Rmax, ω, ρ and the background blood type distribution.
Intriguingly, while the relative risk to different blood groups during disease emergence is independent of Rmax (see Supplementary Fig. 1), the final steady state for an endemic disease with waning immunity is independent of ω but does depend on Rmax (compare 5A, B, C). When Rmax is high, the relative risk at equilibrium for all blood types is close to unity. When Rmax is low, then the relative risk at equilibrium for all blood types is similar to that seen during disease emergence. Intuitively, this follows from the fact that for a highly contagious disease with a high Rmax, everyone will become infected as soon as their immunity wears off, irrespective of blood type. For a less contagious disease with a low Rmax, then there is more scope for differential susceptibility to play a part in how frequently individuals become infected.
3. Discussion
3.1. The biological interpretation of the parameter ρ
In this model, ρ represents the relative probability of virus transmission between an infected individual and an ABO-incompatible target individual. Mechanistically, this will encompass at least three sources of variability: (a) the extent to which the infected individual deposits ABO antigen on the surface of the virions produced, (b) the extent to which the target individual carries anti-A or anti-B antibodies, and (c) the ability of these antibodies to access the incoming virions and prevent infection.
Of these, (a) will depend not only on the host’s ABO genotype, but also on their Secretor (Se) status (Watkins, 1980). “Non-secretor” individuals are homozygous for null mutations in the FUT2 gene. In these individuals, ABO antigen is expressed exclusively in red blood cells and the vascular endothelium and is not present in other cell types. Conversely, in “secretor” individuals with at least one functional FUT2 allele, ABO antigens will be present on many different types of epithelial cells including the lining of the respiratory and digestive tracts. In the context of the ABO-interference model described here, non-secretor individuals will still form anti-A and anti-B antibodies, and thus exhibit disease susceptibility according to their ABO blood type. However, they are unlikely to deposit A or B determinants on virions produced in lung cells, and so will transmit the virus freely, as if they were type O. Since around 20 % of individuals in Western countries are non-secretors (Nordgren et al., 2016), and the estimated value of ρ is ∼40 % (see above), then non-secretor individuals likely account for around half the observed cross-type transmission.
Factors (b) and (c) are related and I shall consider them together. While titres vary, virtually all individuals carry at least some antibodies to non-self ABO glycans. These are generally acquired in the first few years of life following exposure to microbial surface glycans similar to A or B determinants (Cooling, 2015). Anti-A and anti-B antibodies are typically IgM and IgA subtypes, however IgG can also be seen in patients following heterologous transfusion and systemic exposure to antigen. This has implications for factor (c) in that secretory IgA is the predominant antibody type found in mucosal secretions, along with smaller amounts of secreted IgM (Cerutti et al., 2011). While the level of anti-ABO antibody in respiratory secretions has not been well studied, it is plausible that some amounts of both IgA and IgM may be present. These will not however be able to trigger complement-mediated inactivation of virus particles as the full complement cascade requires serum and is not present in the case of mucosal immunity. Anti-A/B antibodies may however block virus entry directly if the AB determinants are borne on the virus spike glycoprotein, as previously shown (Guillon et al., 2008; Preece et al., 2002; Deleers et al., 2020). Alternatively, IgA and IgM may agglutinate virus particles and trap them in the mucus barrier layer.
3.2. Implications of the estimated level of ABO-interference for public health strategy
If ABO-interference is the cause of the widely observed bias in SARS-CoV-2 infection rates among different blood types, then this model allows us to conclude that ABO incompatibility reduces SARS-CoV-2 transmission by at least 60 % and potentially more. This implies that the apparent R0 for most of the largest epidemics around the world has already been suppressed by at least ∼25 %, and that Rmax is likely to be substantially higher than the actually-measured Rsteady. However, it is key to appreciate that no blood type is necessarily high- or low-risk: rather the nature of any protection is entirely context dependent. The presence of a diverse mix of blood types within any given community (i.e. within the pool of individuals that freely mix and may transmit the virus to each other) confers significant protection. Conversely, communities with limited blood type diversity have little or no inherent protection and will suffer disproportionately from SARS-CoV-2 infection. Herd immunisation threshold estimates derived from current data may therefore substantially underestimate the level of vaccination required to protect vulnerable communities such as Native populations in both North and South America. In these, the type O frequency approaches 100 % (Ottensooser and Pasqualin, 1949), thus the true infectious potential of SARS-CoV-2 will be unmasked and the local R0 will tend towards Rmax.
This heterogeneity in transmissibility means that in general, the risk to non-O and in particular type AB individuals in most countries will be higher than risk to type O individuals, while type O individuals are more infectious than non-O individuals. This may contribute to the marked overdispersion in transmission frequency for SARS-CoV-2 (Endo et al., 2020), and help explain why a small subset of patients are responsible for the majority of transmission events. If other polymorphic surface glycans (e.g. Lewis and P antigens) behave similarly, this will further magnify the differences between “super-spreaders” and “super-recipients”.
Paradoxically, however, although in this model both disease vulnerability and infectiousness vary substantially between different blood types, it is important not to simplistically target vaccination on this basis. Rather, once a vaccine is available, care should be taken not to inadvertently destroy the existing blood type frequency structure that provides population-wise disease resistance, by ensuring good vaccine uptake among all communities. There is a danger that the growing public perception that “type O = low risk” will lead type O individuals to neglect or even refuse vaccination. If this tendency is not monitored and compensated for, it may disproportionately reduce the efficacy of public vaccination programs. Other types of blood-type-aware non-pharmaceutical interventions are not modelled here. If protective equipment is in limited supply, it may for example be appropriate for hospitals and care facilities to emphasise source control measures for type O “super-spreaders”, and recipient protection measures for type A and AB “super-recipients”. More sophisticated agent-based approaches will be needed to model this possibility (Ferguson et al., 2020)
3.3. Implications of this model for evolution of the ABO polymorphism
Irrespective of the detailed epidemiology of any disease, at the individual level type O alleles are always selectively favoured under this model, while type A and B alleles are subject to frequency-dependent selection. This predicts that - as seen across the globe - type O will have the highest allele frequency, while A and B alleles will be at lower frequency and more nearly similar to each other. Extending the SIR model to cover the case of waning immunity shows that the elevated risk to non-O blood types remains present even for endemic rather than epidemic disease, and thus long-term population morbidity and mortality from diseases subject to ABO-interference may be one factor affecting ABO allele population frequency, as previously modelled by Seymour et al. (Seymour et al., 2004).
Evolutionarily, this model provides an interesting case where individual and group advantages differ, since while O is always individually favoured, population-level disease resistance is optimised at relatively low type O frequencies. This tension between individual and group optima leads to a “tragedy of the commons” in which selection drives O alleles to a higher frequency than the group optimum and leaves the resulting population more vulnerable to disease. Seymour et al. show that there must necessarily also be some countervailing selection pressure to prevent fixation of type O – they attribute this to a concomitant “arms race” with bacterial pathogens that use ABO antigens as adhesins and thus provide a constant balancing selection in favour of rare blood groups (Seymour et al., 2004). The net result is thus a contest between the bacterial interactions (which generally favour equal frequencies of all blood groups) and virus interactions (which always favour type O).
However, under this model it is not clear why type A and type B are not globally more equal in frequency. A recent preprint (Souilmi et al., 2021) may shed light on this debate, providing genetic evidence for past coronavirus-driven selective sweeps occurring specifically within East Asian populations. As well as indicating that coronavirus emergence in this region has been a recurrent threat over thousands of years, this regionally-contained selective pressure provides a plausible basis for the more balanced A:B frequencies found in these regions. More generally, it is likely that ABO frequency in the population will be locally determined by their interactions with the pathogens most prevalent in each region over evolutionary time scales.
3.4. ABO-interference and seasonal coronaviruses with waning immunity
For seasonal endemic coronaviruses, if these are subject to ABO-interference, this model predicts that that (in Western populations) type A and AB individuals should be more susceptible to infection, and type O less susceptible, but to a less pronounced degree than for SARS-CoV-2. It will therefore be interesting to determine whether non-O blood types are indeed more likely to suffer more frequent repeat endemic coronavirus infections. More speculatively, given the emerging evidence that COVID-19 is a multisystemic infection with particular impact on clotting pathways (Levi et al., 2020), could it be possible that the endemic coronaviruses may also have some effect on the likelihood of thrombosis? In addition to the known effect of ABO blood type on von Willebrand factor (vWF) levels (Franchini and Lippi, 2016), this could be an additional pro-thrombotic risk factor for non-O blood types.
3.5. Key observations and new experiments needed to test this model
In testing this model, the key experiment will be to directly determine whether A or B antigens are present on the virus envelope in in vivo infections, and whether A- or B-specific antisera can neutralise virus harvested from patients with the appropriate blood types. However, there are at least five other testable predictions from this model that may be addressable using existing epidemiological data:
-
(i)
in countries with high type B frequency such as India, type B individuals should be at higher risk than type A individuals. This prediction has already been substantiated by two studies published during review of this modelling work (Rahim et al., 2020; Padhi et al., 2020)
-
(ii)
in studies of super-spreading events, the index cases should be disproportionately type O individuals and/or non-secretor individuals.
-
(iii)
Direct contact-tracing data should in general follow the blood transfusion rules. For in-family tracing, transmission between blood relatives - being more likely to share a blood type - may be more common than transmission between spouses, though this will be substantially confounded by age and behavioural effects.
-
(iv)
In hotspot areas, once the overall case frequency exceeds approximately 20 %, the relative risks will begin to decline, as the epidemic proceeds through the type O population in a delayed manner. Longitudinal studies will be needed to address this, however this factor may explain the lack of any blood type correlation with susceptibility in high prevalence scenarios such as the Charles de Gaulle study (Boudin et al., 2020).
-
(v)
In communities with high type O frequency, Rsteady will be higher, the doubling time shorter and the relative risk to non-O blood types reduced when compared to otherwise similar communities with lower type O frequency. Similarly, communities with a highly skewed A:B ratio will have a higher Rsteady and a shorter doubling time than communities with more nearly equal numbers of A and B individuals. This latter prediction has already been supported by two recent preprints (Liu et al., 2020; Miotto et al., 2020)
4. Materials and methods
4.1. An SIR model of ABO-interference with virus transmission
A standard SIR model of infection divides the population into three compartments, Susceptible, Infectious, Recovered, representing the proportion of individuals in the population with each status, and thus S + I + R = 1. These compartments are linked by three differential equations:
The parameters β and ν represent the rate constants for infection and recovery, and their reciprocals 1 / β and 1 / ν represent the average time required for one infectious individual to transmit to one susceptible individual, and the average duration of the infectious period. The ratio β / ν represents the basic reproductive number R0. The parameter ω represents the rate constant for loss of immunity, and thus transfer from the R compartment back to S. Its reciprocal 1 / ω represents the average duration of immunity following recovery. In the analyses presented here, I extend this model by splitting each of S, I and R into four subcompartments representing the four ABO blood types. These are then linked by a set of twelve equations:
These equations were implemented as a Microsoft Excel spreadsheet (Supplementary Data File 1). In this model R0 is not a well-defined quantity since even in a fully susceptible population the current effective R value, denoted R(t), depends on ρ and on the blood type distributions in both S and I. In this paper, I use Rmax to indicate the ratio β / ν, i.e. the R0 that would be observed in the absence of any ABO-interference. This is the maximal possible value of R(t), and would be observed if ρ = 100 %, or if all currently infected individuals are type O. For the work presented here, all epidemics were initiated by transferring 1/1,000,000 of the population from S to I at time t = 0. This for example represents an initial importation of ∼9 infected index cases into a city the size of London. Varying these boundary conditions from 1/10,000 to 1/100,000,000 has no effect other than accelerating or retarding the initial progress of the epidemic (not shown). All index cases were assumed to be of blood type O. For all analyses except that presented in Fig. 5, immunity was assumed to be permanent and thus ω = 0.
CRediT authorship contribution statement
Peter J.I. Ellis: Conceptualization, Methodology, Software, Formal analysis, Investigation, Writing - original draft, Writing - review & editing, Project administration, Supervision, Resources.
Declaration of Competing Interest
The authors report no declarations of interest.
Acknowledgments
I would like to thank Dr Rupert Beale, Dr Jeremy Rossman, Dr Mike Clark and Mr C.F. Helix for helpful discussions. My position is funded by the UK Higher Education Funding Council for England (HEFCE), and my laboratory work is funded by the Leverhulme Trust (RPG-2019-414 194) and the Eastern Academic Research Consortium. I have no competing interests to declare. All data and code used in the analysis are available in the manuscript and supplementary materials.
Footnotes
Supplementary material related to this article can be found, in the online version, at doi:https://doi.org/10.1016/j.epidem.2021.100446.
Appendix A. Supplementary data
The following are Supplementary data to this article:
References
- https://blog.23andme.com/23andme-research/blood-type-and-covid-19/.
- Retrieved July 3, 2020, from https://rhnegativoperu.com/donaciones-de-sangre/porcentajes-grupo-sanguineo/.
- Arendrup M., Hansen J.E., Clausen H., Nielsen C., Mathiesen L.R., Nielsen J.O. Antibody to histo-blood group A antigen neutralizes HIV produced by lymphocytes from blood group A donors but not from blood group B or O donors. AIDS. 1991;5(4):441–444. doi: 10.1097/00002030-199104000-00014. Apr. [DOI] [PubMed] [Google Scholar]
- Boudin L., Janvier F., Bylicki O., Dutasta F. ABO blood groups are not associated with risk of acquiring the SARS-CoV-2 infection in young adults. Haematologica. 2020 doi: 10.3324/haematol.2020.265066. Jul 23:haematol.2020.265066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerutti A., Chen K., Chorny A. Immunoglobulin responses at the mucosal interface. Annu. Rev. Immunol. 2011;29:273–293. doi: 10.1146/annurev-immunol-031210-101317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandra T., Gupta A. Frequency of ABO and rhesus blood groups in blood donors. Asian J. Transfus. Sci. 2012;6(1):52–53. doi: 10.4103/0973-6247.95057. Jan. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y., Cheng G., Chui C.H., Lau F.Y., Chan P.K., Ng M.H., Sung J.J., Wong R.S. ABO blood group and susceptibility to severe acute respiratory syndrome. JAMA. 2005;293(12):1450–1451. doi: 10.1001/jama.293.12.1450-c. Mar 23. [DOI] [PubMed] [Google Scholar]
- Cooling L. Blood groups in infection and host susceptibility. Clin. Microbiol. Rev. 2015;28(3):801–870. doi: 10.1128/CMR.00109-14. Jul. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deleers M., Breiman A., Daubie V., Maggetto C., Barreau I., Besse T., Clémenceau B., Ruvoën-Clouet N., Fils J.F., Maillart E., Doyen V., Mahadeb B., Jani J.C., Van der Linden P., Cannie M.M., Hayef N., Corazza F., Le Pendu J., El Kenz H. Covid-19 and blood groups: ABO antibody levels may also matter. Int. J. Infect. Dis. 2020;104:242–249. doi: 10.1016/j.ijid.2020.12.025. Dec 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dzik S., Eliason K., Morris E.B., Kaufman R.M., North C.M. COVID-19 and ABO blood groups. Transfusion. 2020 doi: 10.1111/trf.15946. Jun 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edinur H.A., Dunn P.P., Lea R.A., Chambers G.K. Molecular approaches to transfusion medicine in Polynesians and Maori in New Zealand. Int. J. Immunogenet. 2013;40(6):460–470. doi: 10.1111/iji.12073. Dec. [DOI] [PubMed] [Google Scholar]
- Ellinghaus D., Degenhardt F., Bujanda L. Genomewide association study of severe Covid-19 with respiratory failure. N. Engl. J. Med. 2020 doi: 10.1056/NEJMoa2020283. Jun 17:NEJMoa2020283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endo A., Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group, Abbott S. Estimating the overdispersion in COVID-19 transmission using outbreak sizes outside China. Wellcome Open Res. 2020;5:67. doi: 10.12688/wellcomeopenres.15842.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson N., Laydon D., Nedjati Gilani G. 2020. Report 9: Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID19 Mortality and Healthcare Demand. March 27, 2020 ( https://spiral.imperial.ac.uk:8443/handle/10044/1/77482). Preprint. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franchini M., Lippi G. Relative risks of thrombosis and bleeding in different ABO blood groups. Semin. Thromb. Hemost. 2016;42(2):112–117. doi: 10.1055/s-0035-1564832. Mar. [DOI] [PubMed] [Google Scholar]
- Gérard C., Maggipinto G., Minon J.M. COVID-19 and ABO blood group: another viewpoint. Br. J. Haematol. 2020 doi: 10.1111/bjh.16884. May 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillon P., Clément M., Sébille V., Rivain J.G., Chou C.F., Ruvoën-Clouet N., Le Pendu J. Inhibition of the interaction between the SARS-CoV spike protein and its cellular receptor by anti-histo-blood group antibodies. Glycobiology. 2008;18(12):1085–1093. doi: 10.1093/glycob/cwn093. Dec. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones J.H. Stanford University; Stanford: 2007. Notes on R0.https://web.stanford.edu/jhj1/teachingdocs/Jones-on-R0.pdf Retrieved July 3, 2020, from. [Google Scholar]
- Kolin D., Kulm S., Elemento O. Clinical and Genetic Characteristics of Covid-19 Patients from UK Biobank. (https://www.medrxiv.org/content/10.1101/2020.05.05.20075507v1). Preprint. [DOI] [PMC free article] [PubMed]
- le Pendu J., Breiman A., Rocher J., Dion M., Ruvoën-Clouet N. ABO blood types and COVID-19: spurious, anecdotal, or truly important relationships? A reasoned review of available data. Viruses. 2021;13(2):160. doi: 10.3390/v13020160. Jan 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levi M., Thachil J., Iba T., Levy J.H. Coagulation abnormalities and thrombosis in patients with COVID-19. Lancet Haematol. 2020;7(6):e438–e440. doi: 10.1016/S2352-3026(20)30145-9. Jun. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Steinacker J.M., Haeussinger L., Dinse-Lambracht A. 2020. Association Between Epidemic Dynamics of Covid-19 Infection and ABO Blood Group Types. July 15, 2020 ( https://www.medrxiv.org/content/10.1101/2020.07.12.20152074v1). Preprint. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miotto M., Di Rienzo L., Gosti G., Milanetti E., Ruocco G. 2020. Does Blood Type Affect the COVID-19 Infection Pattern? July 13, 2020 ( https://arxiv.org/abs/2007.06296). Preprint. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neil S.J., McKnight A., Gustafsson K., Weiss R.A. HIV-1 incorporates ABO histo-blood group antigens that sensitize virions to complement-mediated inactivation. Blood. 2005;105(12):4693–4699. doi: 10.1182/blood-2004-11-4267. Jun 15. [DOI] [PubMed] [Google Scholar]
- Nordgren J., Sharma S., Kambhampati A., Lopman B., Svensson L. Innate resistance and susceptibility to norovirus infection. PLoS Pathog. 2016;12(4) doi: 10.1371/journal.ppat.1005385. Apr 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ottensooser F., Pasqualin R. Blood types of Brazilian Indians (Matto grosso) Am. J. Hum. Genet. 1949;1(2):141–155. Dec. [PMC free article] [PubMed] [Google Scholar]
- Padhi S., Suvankar S., Dash D., Panda V.K., Pati A., Panigrahi J., Panda A.K. ABO blood group system is associated with COVID-19 mortality: an epidemiological investigation in the Indian population. Transfus. Clin. Biol. 2020;27(4):253–258. doi: 10.1016/j.tracli.2020.08.009. Nov. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Percivalle E., Cambiè G., Cassaniti I. Prevalence of SARS-CoV-2 specific neutralising antibodies in blood donors from the Lodi Red Zone in Lombardy, Italy, as at 06 April 2020. Euro Surveill. 2020;25(24) doi: 10.2807/1560-7917.ES.2020.25.24.2001031. Jun. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preece A.F., Strahan K.M., Devitt J., Yamamoto F., Gustafsson K. Expression of ABO or related antigenic carbohydrates on viral envelopes leads to neutralization in the presence of serum containing specific natural antibodies and complement. Blood. 2002;99(7):2477–2482. doi: 10.1182/blood.v99.7.2477. Apr 1. [DOI] [PubMed] [Google Scholar]
- Rahim F., Amin S., Bahadur S., Noor M., Mahmood A., Gul H. ABO / Rh-D blood types and susceptibility to Corona Virus Disease-19 in Peshawar, Pakistan. Pak. J. Med. Sci. 2020;37(1) doi: 10.12669/pjms.37.1.3655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genevieve H.L. Roberts, Danny S. Park, Marie V. Coignet, Shannon R. McCurdy, Spencer C. Knight, Raghavendran Partha, Brooke Rhead, Miao Zhang, Nathan Berkowitz, AncestryDNA Science Team, Asher K. Haug Baltzell, Harendra Guturu, Ahna R. Girshick, Kristin A. Rand, Eurie L. Hong, Catherine A. Ball. AncestryDNA COVID-19 Host Genetic Study Identifies Three Novel Loci. (https://www.medrxiv.org/content/10.1101/2020.10.06.20205864v1). Preprint.
- Seymour R.M., Allan M.J., Pomiankowski A., Gustafsson K. Evolution of the human ABO polymorphism by two complementary selective pressures. Proc. Biol. Sci. 2004;271(1543):1065–1072. doi: 10.1098/rspb.2004.2674. May 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yassine Souilmi, M. Elise Lauterbur, Ray Tobler, Christian D. Huber, Angad S. Johar, David Enard. An ancient viral epidemic involving host coronavirus interacting genes more than 20,000 years ago in East Asia. (https://www.biorxiv.org/content/10.1101/2020.11.16.385401v2). Preprint.
- The COVID-19 Host Genetics Initiative The COVID-19 Host Genetics Initiative, a global initiative to elucidate the role of host genetic factors in susceptibility and severity of the SARS-CoV-2 virus pandemic. Eur. J. Hum. Genet. 2020;28:715–718. doi: 10.1038/s41431-020-0636-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe Y., Allen J.D., Wrapp D., McLellan J.S., Crispin M. Site-specific analysis of the SARS-CoV-2 glycan shield. Science. 2020 doi: 10.1126/science.abb9983. May 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watkins W.M. Biochemistry and Genetics of the ABO, Lewis, and P blood group systems. Adv. Hum. Genet. 1980;10 doi: 10.1007/978-1-4615-8288-5_1. 1-136, 379-85. [DOI] [PubMed] [Google Scholar]
- Zhao J., Yang Y., Huang H. 2020. Relationship Between the ABO Blood Group and the COVID-19 Susceptibility. March 27, 2020 ( https://www.medrxiv.org/content/10.1101/2020.03.11.20031096v2). Preprint. [Google Scholar]
- Zietz M., Tatonetti N.P. 2020. Testing the Association between Blood Type and COVID-19 Infection, Intubation, and Death. April 11, 2020 ( https://www.medrxiv.org/content/10.1101/2020.04.08.20058073v1). Preprint. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.