Abstract
Motivated by the importance of understanding various competing mechanisms to the current-induced spin-orbit torque on magnetization in complex magnets, we develop a theory of current-induced spin-orbital coupled dynamics in magnetic heterostructures. The theory describes angular momentum transfer between different degrees of freedom in solids, e.g., the electron orbital and spin, the crystal lattice, and the magnetic order parameter. Based on the continuity equations for the spin and orbital angular momenta, we derive equations of motion that relate spin and orbital current fluxes and torques describing the transfer of angular momentum between different degrees of freedom, achieved in a steady state under an applied external electric field. We then propose a classification scheme for the mechanisms of the current-induced torque in magnetic bilayers. We evaluate the sources of torque using density functional theory, effectively capturing the impact of the electronic structure on these quantities. We apply our formalism to two different magnetic bilayers, Fe/W(110) and Ni/W(110), which are chosen such that the orbital and spin Hall effects in W have opposite sign and the resulting spin- and orbital-mediated torques can compete with each other. We find that while the spin torque arising from the spin Hall effect of W is the dominant mechanism of the current-induced torque in Fe/W(110), the dominant mechanism in Ni/W(110) is the orbital torque originating in the orbital Hall effect of the non-magnetic substrate. Thus the effective spin Hall angles for the total torque are negative and positive in the two systems. Our prediction can be experimentally identified in moderately clean samples, where intrinsic contributions dominate. This clearly demonstrates that our formalism is ideal for studying the angular momentum transfer dynamics in spin-orbit coupled systems as it goes beyond the “spin current picture” by naturally incorporating the spin and orbital degrees of freedom on an equal footing. Our calculations reveal that, in addition to the spin and orbital torque, other contributions such as the interfacial torque and self-induced anomalous torque within the ferromagnet are not negligible in both material systems.
I. INTRODUCTION
Spin-orbit coupling plays a central role in a plethora of phenomena occurring in magnetic multilayers [1]. Current-induced spin-orbit torque is one of the most important examples, and is a workhorse in the field of spintronics [2, 3]. In contrast to spin-transfer torque in spin valve structures, a device utilizing spin-orbit torque does not require an extra ferromagnetic layer to create spin polarized current. Instead, nonequilibrium spin currents and spin densities are generated in nonmagnetic materials due to spin-orbit coupling. The magnitude of spin-obit torque can be sufficient to induce magnetic switching, as demonstrated in magnetic bilayers consisting of a nonmagnet and a ferromagnet [4–8]. Spin-orbit torque also enables fast current-induced magnetic domain wall motion [9–12]. Several microscopic mechanisms of current-induced spin-orbit torque have been proposed. However, quantification of the individual contributions is challenging both theoretically and experimentally. Moreover, our understanding of the phenomenon based on the properties of the electronic structure is rather unsatisfactory yet.
In this work, we examine the fundamental physical nature of spin-orbit torque in view of angular momentum exchange between different interacting degrees of freedom in solids. The possible channels for angular momentum transfer among these degrees of freedom are schematically shown in Fig. 1. It is conceptually important to separate (i) angular momentum carried by a conduction electron, encoded in its orbital and spin parts of the wave function, (ii) mechanical angular momentum of the lattice, and (iii) spin angular momentum encoded into the local magnetic moment emerging as a result of magnetic ordering. While spin-orbit coupling mediates an angular momentum transfer between spin and orbital degrees of the electron, the crystal field potential leads to an orbital angular momentum transfer between the electron and the lattice, while the exchange interaction enables spin transfer between the conduction electron’s spin and local magnetic moment. In its most elemental definition, the spin-orbit torque is understood as an angular momentum flow from the surrounding lattice to the local magnetic moment – a process which is mediated by spin-orbit entangled electrons.
FIG. 1.
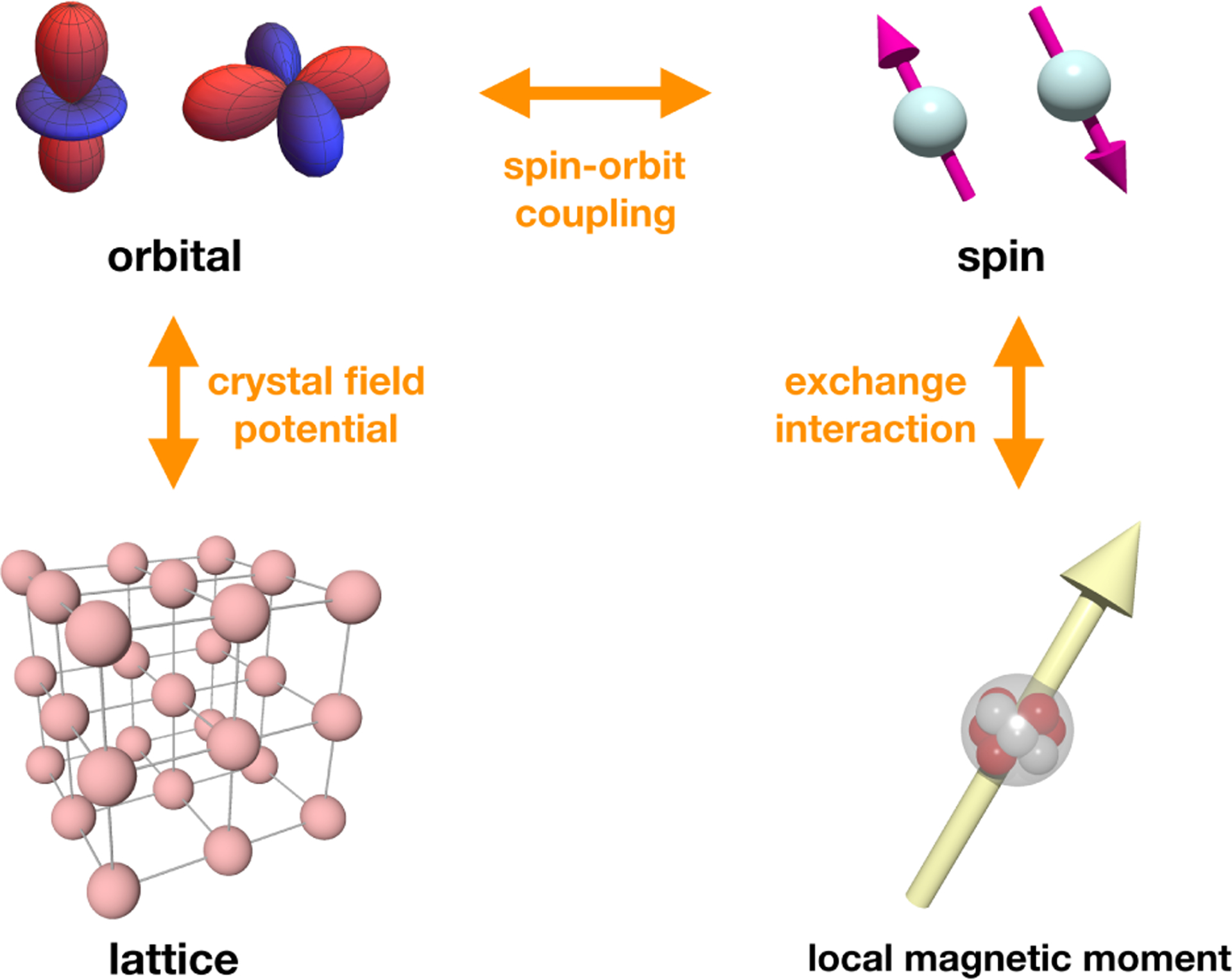
Interactions between angular-momentum-carrying degrees of freedom in solids: spin and orbital of the electron, the crystal lattice, and the local magnetic moment. Orange arrows indicate microscopic interactions by which angular momentum is exchanged: the spin-orbit coupling for interaction between the spin and orbital momenta of an electron, crystal field potential for the interaction between the lattice and the orbital angular momentum of the electron, and exchange interaction for the interaction between the local magnetic moment and the spin of the electron.
Depending on the specifics of a particular angular momentum exchange transfer channel, which takes place in different parts of the solid, e.g., in the bulk or at the interface, we can understand various competing mechanisms in non-uniform magnetic heterostructures in an unified manner. Here, we choose to consider a nonmagnet/ferromagnet bilayer geometry, which is most widely studied in experiments. In this case we can classify the current-induced torque into four different mechanisms (Fig. 2). The classification is based on two independent criteria: (1) the spatial origin of the spin-orbit interaction, and (2) the spatial origin of the current responsible for the angular momentum generation, which is absorbed by the magnetization.
FIG. 2.

Classification of the mechanisms of the current-induced torque. The row represents the origin of spin-orbit coupling (SOC) in either the nonmagnet (NM) or in the ferromagnet (FM). The column represents the locality of the torque: i.e., whether the torque acting on the FM originates from the electrical current flowing in the NM (nonlocal) or in the FM itself (local). The red arrows represent the spin, and the blue arrows represent the orbital angular momentum. The local magnetic moment is represented with a big yellow arrow.
The spin Hall effect arising from the nonmagnet is considered to be one of the main mechanisms for generating a torque on the magnetization of the ferromagnet (upper left panel in Fig. 2) [5, 6]. The spin Hall conductivity of the nonmagnet is often assumed to be a bulk property, and the spin injection and resulting torque generation on the local magnetic moment is explained by the theory of the spin-transfer torque [13, 14]. We denote this contribution due to spin injection from the nonmagnet as a spin torque. As a competing mechanism, the spin-orbit coupling at the nonmagnet/ferromagnet interface has been intensively investigated [15–23]. Since the Rashba-type interfacial states are formed at the nonmagnet/ferromagnet interface due to broken inversion symmetry [24–26], scattering of electrons from the interface leads to finite spin density and current [22, 23], which interacts with and exerts a torque on the local magnetic moments of the ferromagnet (upper right panel in Fig. 2). We denote this contribution as interfacial torque. We remark that the our definition of the interfacial torque is restricted rather than general. For example, our definition neglects an effect of the current flowing in the nonmagnet in the proximity of the interface. The definition agrees with the picture that spin-orbit effects in the ferromagnet originate in the proximity-induced spin-orbit coupling from the nonmagnet.
While the role of spin-orbit coupling in the ferromagnet has been considered to be negligible as compared to that of the spin-orbit coupling in the nonmagnet, which usually comprises heavy atomic species, it has been found that spin-orbit coupling in the ferromagnet can induce a sizable amount of self-induced torque by the generation of the intrinsic spin current, e.g., via the spin Hall effect [27–29]. The corresponding torque contribution is called the anomalous torque in analogy to the anomalous Hall effect in ferromagnets [28]. When inversion symmetry is present in a stand-alone ferromagnet, the net anomalous torque sums to zero. However, in the nonmagnet/ferromagnet bilayer, where the inversion symmetry is broken at the interface, the anomalous torque may exert a finite torque (lower right panel in Fig. 2), comparable to the spin torque and interfacial torque. The above mechanisms (spin torque, interfacial torque, and anomalous torque) arise from spin-dependent scattering in the bulk or at the interface, and rely on the concept of spin current or spin density.
Recently, a mechanism of the torque generation based on orbital angular momentum injection has been proposed [30]. This mechanism is fundamentally different from the other mechanisms in that it requires the consideration of the orbital part of the electron’s angular momentum, rather than its spin. Called the orbital torque (lower left panel of Fig. 2), the orbital angular momentum generated from the nonmagnet, e.g. by the orbital Hall effect [31–34], is transferred to the local magnetic moment, which is mediated by the spin-orbit coupling in the ferromagnet. We remark that the orbital Hall effect can be gigantic [31, 32] and its mechanism is independent of the spin-orbit coupling [33, 34].
Manifestly, all of the above mentioned mechanisms predict same symmetry of the current-induced torque, which greatly complicates the analysis of the experiments. Since previous theoretical models have been developed assuming a restricted setup and evaluated only specific contributions to the torque [22, 27], it is difficult to compare magnitudes of different contributions directly. On the other hand, first-principles approaches often evaluate the total torque from linear response theory [35–40], which also makes it difficult to assess contributions by different mechanisms quantitatively. Thus, it is necessary to develop a unified theory within which different mechanisms of the current-induced torque are classified and can be separately evaluated for a given system. This would bridge the gap between the theoretical pictures set up by models and first-principles calculations of real materials. The main difficulty here lies in the nonlocality of magnetoelectric coupling [41, 42] and different sources of the spin-orbit coupling.
The orbital torque mechanism [30] is highly nonlocal in nature, with the orbital current converted into spin current in the ferromagnet. In view of the existing analysis based on the spin current, the orbital torque mechanism appears abnormal as the spin current seems to emerge out of nowhere, while in fact it originates in the orbital current. This implies that tracing only the spin current inevitably fails to describe the orbital torque. In general, spin is not conserved in the presence of spin-orbit coupling, and the spin current does not directly correspond to the spin accumulation or torque on the local magnetic moment [43]. However, it is important to realize that the angular momentum of the spin is not simply lost. Instead, it is transferred to other degrees of freedom. Therefore, in our theory, we track not only the flow of spin but also the flow of orbital angular momentum, as well as their interactions with other degrees of freedom in solids, such as the crystal lattice and local magnetic moment. Detailed analysis of the transfer of angular momentum between these channels provides a long-sought insight into the microscopic nature of different competing mechanisms of current-induced torque.
Recent theories imply that the current-induced dynamics and spin transport in the presence of spin-orbit coupling originate in the orbital degrees of freedom [32, 33]. For example, while the orbital Hall effect occurs regardless of the spin-orbit coupling, the spin Hall effect is a consequence of the orbital Hall effect by virtue of the spin-orbit coupling [33]. Depending on the correlation (or relative orientation) between the spin and orbital angular momentum, the relative sign of the orbital Hall effect and spin Hall effect may be the same or opposite, following Hund’s rule behavior [32, 33]. In this sense, the orbital Hall effect can be considered as a precursor to the spin Hall effect. Another example is a Rashba-type state, which is responsible for the interfacial torque generation. It is well known that the Rashba state originates in a chiral orbital angular momentum texture [44–46]. Such an orbital Rashba effect persists even in the absence of spin-orbit coupling, which induces current-induced orbital dynamics and transport [47, 48]. Through spin-orbit coupling, the orbital Rashba state couples to the spin and the spin texture emerges, thus leading to spin dynamics.
In general, such a hierarchy is expected to be a rather universal feature. The reason is the following: in the microscopic Hamiltonian of the electrons in solids, the spin cannot interact with an external electric field unless the spin-orbit coupling is present. On the other hand, the orbital degree of freedom, originating in the real-space charge distribution, directly couples to an external electric field (see Fig. 1). Hence, under the perturbation by an external electric field, the orbital dynamics is expected to occur prior to the spin dynamics regardless of the spin-orbit coupling, and the spin dynamics becomes correlated with the orbital dynamics due to the spin-orbit coupling. We emphasize that the precedence of orbital-related phenomena to spin-related phenomena is a fundamental concept in orbitronics.
An exception to this picture is a noncollinear magnet, where orbital angular momentum is associated with the spin chirality [49–51] or density of topological charge [51, 52]. Here, spin and orbital momenta may interact even without relativistic spin-orbit coupling [53]. Although such chiral or topological orbital angular momentum exhibits exotic dynamic phenomena associated with complex spin structures [54, 55], we leave this case to future work.
The manuscript is organized as follows. In Sec. II, we develop a theoretical formalism that describes angular momentum transfer between the spin and the orbital angular momentum of the electron, lattice, and local magnetic moment in steady state under an external electric field. This formalism is based on the continuity equations for the spin and orbital angular momentum of the electron, which was outlined in Ref. [56]. In Sec. III, we present the result of first-principles calculation on two real material systems: Fe/W(110) and Ni/W(110), which are carefully chosen with the expectation that the spin torque and orbital torque have an opposite sign in these bilayers. We show that the current-induced torque is dominated by spin torque and orbital torque contributions in Fe/W(110) and Ni/W(110), respectively, which leads to opposite effective spin Hall angles for these systems. This peculiar result is due to a positive sign of the orbital Hall conductivity in W and pronounced spin-orbit correlation in Ni. In Sec. IV, we further discuss the disentangling of the various mechanisms of current-induced torque and comment on several issues of orbital transport and dynamics. This includes similarity and difference between the orbital current and spin current, and implications on experiments. Finally, Sec. V summarizes and concludes the paper.
II. THEORETICAL FORMALISM
A. Overview
In this section, we start from the effective single-particle Hamiltonian to separately define the spin-orbit coupling, the crystal field potential, and the exchange interaction, which is adapted for the density functional theory framework (Sec. II B). Then we derive the continuity equations for the spin and orbital angular momentum in Sec. II C. In the continuity equations, rates for the changes of the spin and orbital angular momentum are captured by the influxes of the spin and orbital angular momentum as well as torques describing the angular momentum transfer between different degrees of freedom. To evaluate individual contributions appearing in the continuity equations under an external electric field, we consider interband and intraband contributions within the Kubo formula (Sec. II D). However, we point out that the interband contribution does not satisfy the stationary condition in the steady state (Sec. II E). To resolve this problem, we propose a balance-type equation that describe a relation between the interband and intraband contributions in the steady state, which we call the interband-intraband correspondence. The application of the interband-intraband correspondence to the continuity equations of the spin and orbital angular momentum leads to the equations of motion (Sec. II F), which is the main result of this section.
B. Effective Single-Particle Hamiltonian
Within the effective single-particle description, such as the Kohn-Sham treatment within the density functional theory, the general electronic Hamiltonian in a solid is formally written as
| (1) |
where Ψ(r) and Ψ†(r) are electron annihilation and creation field operators in the second quantization representation, respectively. Here, p = −iℏ∇r is the momentum operator, ℏ is the reduced Plank constant, and m0 is the electron mass. The effective single-particle potential Veff(r) can be divided into the spin-orbit coupling VSO(r), the exchange interaction VXC(r), and the crystal field potential VCF(r):
| (2) |
We define VCF(r) such that it is independent of the spin. The spin-orbit coupling and exchange interaction are explicitly written as
| (3) |
| (4) |
respectively. Here, σ is the vector of the Pauli matrices representing the spin, β = ℏ/4m2c2 with the speed of light c, μB is the Bohr magneton, and ΩXC(r) is an effective magnetic field caused by the exchange interaction. We construct VSO(r) by neglecting VXC(r) as an approximation. Note that the degrees of freedom of the lattice and the local magnetic moment are implicitly included in this description, entering as coordinates in the respective potentials VXC(r) and VCF(r). In the evaluation of operators we use symmetrized representations such that the hermiticity is kept in the numerical implementation. However, we present non-symmetrized forms throughout the paper for notational brevity.
C. Continuity Equations for Spin and Orbital Angular Momenta
The continuity equations for spin and orbital angular momentum have been introduced by Haney and Stiles in Ref. [56]. Here, we derive the expression adapted for the first-principles calculation based on the density functional theory, starting from the general single particle Hamiltonian [Eqs. (1) and (2)]. In the Heisenberg picture (indicated by the hat symbol below), we define the orbital angular momentum and spin density operators as
| (5a) |
| (5b) |
While the spin S is represented by the vector of the Pauli matrices S = (ℏ/2)σ, evaluation of the orbital angular momentum is nontrivial in periodic solids because the position r is ill-defined under periodic boundary conditions. Nonetheless, we can calculate the orbital angular momentum with respect to the atomic spheres called muffin tins centered at the positions of the atoms:
| (6a) |
| (6b) |
Here, Θ(x) is the Heaviside step function, μ is the index of an atom in the unit cell whose center is located at τμ, rμ = r − τμ is the displacement from the atom center, and Rμ is the radius of the muffin tin. This method is called atom-centered approximation, and it gives a reliable result when orbital currents are associated with partially occupied d or f shells, which are localized around atomic centers. Thus, the usage of the atom-centered approximation is justified in magnetic bilayers consisting of transition metal elements, Fe/W(110) and Ni/W(110), which are in the focus of our study. Under the atom-centered approximation, the size of the region in real space which gives rise to the orbital angular moment is smaller than that of a wave packet, thus the orbital can be treated as an internal degree of freedom, similar to the spin (see Sec. IV B for the discussion). However, the atom-centered approximation neglects contributions from nonlocal currents, e.g., in Chern insulators and noncollinear magnets [57], and ultimately one should resort to the modern theory of orbital magnetization [58–60].
For the orbital angular momentum and spin densities defined in Eq. (5), we can derive continuity equations from the Heisenberg equations of motion. These are formally written as
| (7a) |
| (7b) |
where α = x, y, z. Here,
| (8a) |
| (8b) |
are orbital and spin current operators, respectively, where
| (9) |
is the velocity operator ( and act on the left and on the right, respectively), and
| (10a) |
| (10b) |
are torque operators for the orbital angular momentum and spin, respectively.
The appearance of the torques in Eq. (7) signals the fact that the orbital angular momentum and spin are not conserved. This implies that the angular momentum is transferred from the electron to other degrees of freedom as described in Fig. 1. The electrons exchange orbital angular momentum with the lattice and with the electron’s spin via the crystal field potential VCF(r) and spin-orbit potential VSO(r), respectively. Thus, the torque acting on the orbital angular momentum of the electron is decomposed as
| (11) |
where
| (12) |
| (13) |
We denote as the crystal field torque and as the spin-orbital torque. Note that we included the effect of VXC(r) in the definition of the crystal field torque, as it contains non-spherical component in general. On the other hand, the electron exchanges the spin angular momentum with the local magnetic moment and the electron’s orbital angular momentum via VXC(r) and VSO(r), respectively. Thus, the torque acting on the electron’s spin can be decomposed as
| (14) |
where
| (15) |
| (16) |
We denote as the exchange torque and as the spin-orbital torque. Note that and differ, and we specify them as the spin-orbital torques acting on the orbital and spin, respectively.
We have a few remarks on the different torques and their definitions. In the absence of the spin-orbit coupling, the spin-orbital torques vanish. Thus in a steady state, where , Eq. (7b) becomes . Here, 〈⋯〉 represents expectation value in the steady state. This implies that the spin current divergence is absorbed by the local magnetic moment. Thus, this corresponds to the spin-transfer torque in the absence of the spin-orbit coupling. If we consider the opposite situation where the spin current flux is absent, occurring e.g. in atomically thin magnetic films, where the spin current effect can be neglected along the perpendicular direction to the film plane, Eq. (7b) becomes . Thus, the exchange torque amounts to the spin-orbital torque. This is related to the widely used terminology, spin-orbit torque [15]. However, in our terminology, the net torque acting on the local magnetic moment is the exchange torque, which may differ from the spin-orbital torque due to the presence of the spin current flux. In general, both the spin current flux and spin-orbital torque contribute to the exchange torque.
We obtain additional insight from explicitly evaluating the torques in a simplified situation. Let us first consider the exchange torque. By using Eqs. (4) and (15), the exchange torque can be written as
| (17) |
in general. Thus, it describes a precession of the spin with respect to the direction of the exchange field. On the other hand, by using Eqs. (3) and (16), the spin-orbital torque acting on the spin is formally written as
| (18) |
Since it depends on the spatial gradient of VCF(r), the dominant contribution to it is concentrated near the atom centers, where VCF(r) is almost spherical. Thus, within the muffin tins, we can approximately write ∇rVCF(r) ≈ Σμ Θ(Rμ − rμ)[∂VCF(rμ)/∂rμ]. Within this approximation
| (19) |
Thus, the spin-orbital torque becomes
| (20) |
where
| (21) |
is the strength of the spin-orbit coupling for the μ-th atom. Therefore, Eq. (20) indicates that the spin-orbital torque describes a mutual precession between the orbital angular momentum and the spin. That is,
| (22) |
While it is approximately true in most systems, we keep superscripts S and L separately, because and differ in general due to nonspherical contributions to the VSO(r) although it is small.
Meanwhile, the crystal field torque cannot be expressed in simple terms. In general, it describes an angular momentum transfer between the lattice and the electronic orbital angular momentum. It originates due to the breaking of the continuous rotation symmetry by the crystal field, which differentiates specific directions depending on the structure of the crystal, and leads to various anisotropic effects.
D. Kubo Formula: Interband and Intraband Responses
The current-induced torque corresponds to the response of the exchange torque to an electric field, [Eqs. (15) and (17)]. One of the most widely used approaches for its calculation is linear response theory, where often interband and intraband contributions are evaluated separately. The interband contribution originates in the change of a given state by a coherent superposition of the eigenstates for a given k: in response to an external electric field the periodic part of the Bloch state |unk〉 changes as
| (23) |
where
| (24) |
Here, e > 0 is the absolute value of the charge of the electron, k is the crystal momentum, Enk is the energy eigen-value for the periodic part of the n-th Bloch state |unk〉. The infinitesimally small number η > 0 arises from the causality relation. That is, in describing time-evolution of the state, the electric field is adiabatically turned on from t = −∞ to t = 0 by the vector potential such that . As a result, the interband response of an observable is given by
| (25) |
where fnk is the Fermi-Dirac distribution function for the state |unk〉. By combining Eqs. (24) and (25) and manipulating the dummy indices n and m, we arrive at
| (26) |
Here, we define in k-space. The interband contribution in Eq. (26) is also known as the intrinsic contribution since it depends only on the electronic structure, the eigenstates and their energy eigenvalues in the ground state.
On the other hand, the intraband response arises due to a shift of the Fermi surface by disorder scattering. The leading contribution arises from the change of the occupation function:
| (27) |
which is also referred to as Boltzmann-like contribution. Here, is the shift of the Fermi surface caused by the electric field , and τ is the momentum relaxation time. Up to linear order in Δk,
| (28) |
where . Thus, the intraband contribution is written as
| (29) |
Note that it is described by a single phenomenological parameter τ, which is assumed to be state-independent. As τ increases, i.e., as the resistivity decreases, the intraband contribution linearly increases. In general, the momentum relaxation time depends on the particular state in the electronic structure. In ferromagnets, for example, it is known that the momentum relaxation times of the majority and minority electrons are different, which plays an important role in understanding various magnetotransport effects [61]. However, within the approach that we pursue here, as given by Eq. (29), we do not consider these effects.
E. Stationary Condition in the Steady State
A serious problem of the linear response described by Eqs. (26) and (29) is that the stationary condition is not satisfied. That is,
| (30) |
where . Thus, the continuity equations (7) are not satisfied if one naively evaluates the sum of the interband and intraband contributions. This discrepancy is due to the inconsistent treatment of disorder scattering, which is only taken into account by the Fermi surface shift within the relaxation time approximation. In general, the effect of disorder scattering enters the equation via the self-energy correction and vertex correction. It is known that a consistent treatment of the self-energy and vertex corrections up to the same order as the perturbation (which is a disorder potential in this case) ensures that the continuity equation satisfied. This is known as the Ward identity [62]. However, such treatment is computationally demanding, and it requires us to assume a specific model of the disorder potential.
Instead, we propose a remedy by finding a nontrivial relation between the interband and intraband contributions. This allows us to evaluate the response functions given by Eqs. (26) and (29) and retain the stationary condition. We find that the following relation holds:
| (31) |
as long as the operator does not have k-dependence. The proof is presented in Appendix A. A physical interpretation of Eq. (31) is the following. The right hand side of the equation describes intrinsic pumping of , which depends only on the electronic structure. The left hand side of the equation is related to a relaxation process, which tend to suppress deviations from the equilibrium value of . In the steady state, the intrinsic pumping and the relaxation rates are equal, thus is determined by the relaxation rate τ. Therefore, Eq. (31) describes a balance between a tendency to increase by the intrinsic process and a relaxation rate by the extrinsic process. For the spin operator, Eq. (31) holds precisely since it does not have k-dependence. On the other hand, the orbital angular momentum operator [Eq. (6)] depends on k since it contains momentum operator p, which turns into e−ik·rpeik·r = p + ℏk in the k-space representation. However, the k-dependence of the local orbital momentum is usually very small within the atom-centered approximation as it is usually dominated by a k-independent contribution, i.e., L(k) ≈ L(0). In Secs. III D and III E, we verify that Eq. (31) is satisfied for the orbital angular momentum with high precision, which implies that the k = 0 contribution in L(k) dominates and determines overall behavior of the orbital angular momentum operator within the atom-centered approximation.
Meanwhile, the intraband contribution alone satisfies the steady state condition:
| (32) |
A proof of the stationary condition for the intraband contribution is given in Appendix B. Note that for the intraband contribution, the stationary condition does not rely on k-dependence of , which is in contrast to the interband-intraband correspondence [Eq. (31)]. Equations (31) and (32) are used to derive the equations of motion below.
F. Steady State Equations of Motion for Spin and Orbital Angular Momenta
By applying the interband-intraband correspondence [Eq. (31)] to the continuity equations [Eq. (7)], we arrive at the following equations:
| (33a) |
| (33b) |
Note that that the time dependence no longer appears since the equations describe the steady state. Also, the hat symbol for the Heisenberg picture is removed. Equation (33) relates the current fluxes and torques of the intrinsic origin to the intraband accumulation of the orbital angular momentum and spin. Application of Eq. (32) leads to constraints between intraband contributions for the current fluxes and torques of the orbital angular momentum and the spin:
| (34a) |
| (34b) |
The above equations constitute equations of motion for the spin and orbital angular momenta, which are coupled by the spin-orbit coupling, in the steady state reached after an external electric field has been applied. This is one of the main results of our work. Previous theories on the current-induced torque have focused on evaluating linear response of the exchange torque [Eq. (15)] [35–39, 63, 64]. In contrast, Eqs. (33) and (34) enable one to identify individual microscopic mechanisms responsible for current-induced torque, as we illustrate next.
III. FIRST-PRINCIPLES CALCULATIONS
In this section we apply the formalism presented in the previous section to two specific systems: W/Fe and W/Ni bilayers. Before presenting an in-depth analysis of these systems based on the formalism presented in the previous section, it is useful to begin with an overview of the systems’ behavior. The angular momentum flows that we calculate for the two systems are illustrated schematically in Fig. 3. For the W/Fe system, the flux of orbital angular momentum into the ferromagnetic layer is mostly transferred to a torque on the lattice, while the flux of spin angular momentum is mostly transferred to a torque on the magnetization. This behavior is emblematic of the conventional spin Hall effect combined with spin transfer picture of spin-orbit torque in bilayer systems. The W/Ni system exhibits qualitatively different behavior: the orbital angular momentum flux entering the ferromagnetic layer contributes substantially to the torque on the magnetization, indeed a magnitude which exceeds the contribution from the spin current flux. In this case, the more prominent spin-orbit coupling in Ni enables a flow of angular momentum from orbital to spin degrees of freedom. The distinction between W/Fe and W/Ni is evident by a different sign of the current-induced torque on the magnetization in the two systems (equivalently, a different sign of the effective spin Hall effect). In the following sections we begin with a description of the key differences in the electronic structure of the two systems which underlie the difference in their magnetic response. We then briefly discuss the symmetry constraints on the systems, and finally present an in-depth analysis of the terms entering the conservation of angular momentum in Eq. (33).
FIG. 3.
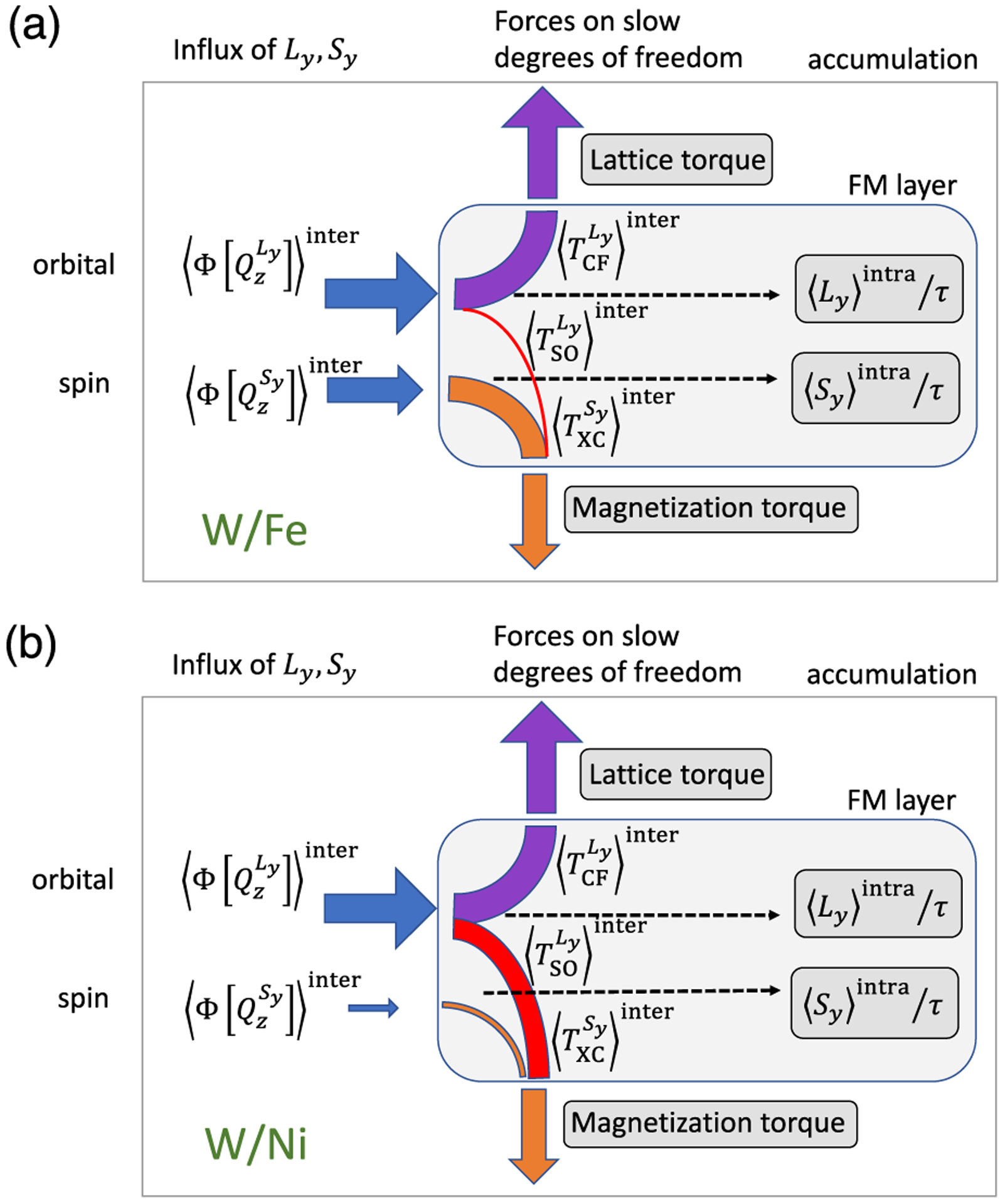
Schematics of the angular momentum flow in (a) W/Fe and (b) W/Ni. We note that (a) in W/Fe a torque on the magnetization is mostly coming from the spin current influx. (b) On the other hand, in W/Ni, there is a significant contribution of the spin-orbital torque to the magnetization torque.
A. Motivation for Choice of Material Systems
One of the main motivations in choosing a material system is to find a system with dominant orbital torque behavior, which has been elusive since the first theoretical prediction [30], and compare it with a conventional system where the spin torque is dominant. To do this, consider a case in which the signs of the orbital torque and spin torque are opposite. The sign of the net torque acting on the local magnetic moment will vary depending on whether the orbital torque is larger than the spin torque, or vice versa. This implies that when the orbital torque is dominant over the spin torque, the sign of the torque acting on the local moment can be opposite to that expected from the spin torque mechanism only. This situation can be realized either (1) when the spin Hall effect and orbital Hall effect in the nonmagnet have opposite signs and the spin-orbit correlation in the ferromagnet is positive or (2) when the spin Hall effect and orbital Hall effect in the nonmagnet have same sign and the spin-orbit correlation in the ferromagnet is negative. The spin-orbit correlation in the ferromagnet is important in the orbital torque mechanism because the injected orbital angular momentum in the ferromagnet first couples to the spin and then exerts a torque on the local magnetic moment. For typical 3d ferromagnets, such as Fe, Co, and Ni, the spin-orbit correlation is expected to be positive as d shells are more than half-filled, which tends to align the orbital and spin angular momenta along the same direction. Thus, we aim to achieve the case (1), which is schematically illustrated in Fig. 4. As the directions of the orbital Hall effect and spin Hall effect are opposite, the angular momentum transfers (represented as the rotation of the arrows in the ferromagnet in Fig. 4) are also opposite.
FIG. 4.
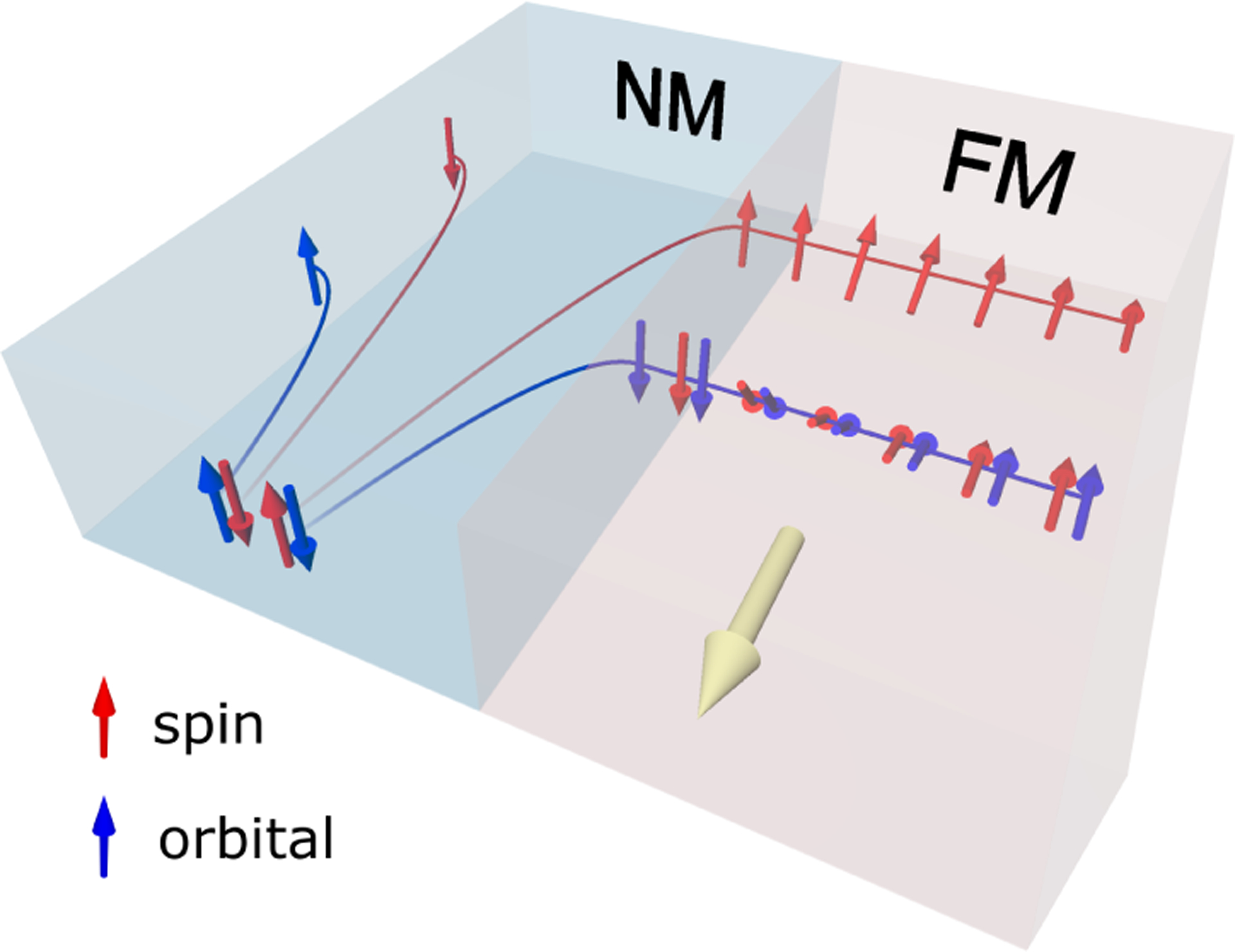
Competition between the orbital torque and the spin torque when the directions of the orbital Hall effect and spin Hall effect are opposite in the nonmagnet (NM). In the ferromagnet (FM), rotations of the angular momentum represent angular momentum transfer to the local magnetic moment by dephasing, whose directions are opposite for the spin injection and orbital injection.
One of the key features of the orbital torque mechanism is that it relies on the spin-orbit coupling of the ferromagnet, thus the orbital torque depends on the choice of the ferromagnet. Although the spin-orbit coupling strength is similar for typical 3d ferromagnets such as Fe, Co, and Ni, the resulting effect of spin-orbit coupling depends on details of the electronic structure, such as the band structure, band filling, magnitude of the exchange splitting, etc. This explains a noticeable difference of the spin Hall conductivities of Fe and Ni: and [27]. Thus, even among 3d ferromagnets the effective spin-orbit coupling strength – which incorporates not only the spin-orbit coupling itself but also electronic structure effects – can vary significantly. We expect that the effective spin-orbit coupling strength is much stronger in Ni than in Fe, and we show this by explicit calculations below.
Therefore, we consider nonmagnet/ferromagnet bilayers where the nonmagnet exhibits an opposite sign of the orbital Hall effect and spin Hall effect, while the ferromagnet is varied such that the strength of effective spin-orbit coupling is controlled. These criteria lead us to the choice of Fe/W and Ni/W bilayers. For W, the orbital Hall conductivity is by an order of magnitude larger than the spin Hall conductivity, with opposite sign [31]. A reason for choosing Fe and Ni as ferromagnets is the expectation that the orbital-to-spin conversion efficiency of the orbital torque mechanism is much larger in Ni than it is in Fe. Moreover, both materials can be grown epitaxially along the [110] direction of the body-centered cubic (bcc) structure. We denote these systems as Fe/W(110) and Ni/W(110), respectively. Meanwhile, Fe/W(110) has been previously studied for the anisotropic Dzyaloshinskii-Moriya interactions for stabilizing the anti-Skyrmion [65].
Figures 5(a) and 5(b) respectively display side and top views of the ferromagnet/W(110) structure, where the ferromagnet = Fe or Ni. We consider 8 layers of W and 2 layers of the ferromagnet. We denote the magnetic atom closest to the interface as Fe1 and Ni1, while the magnetic atom at the surface of the slab is marked as Fe2 and Ni2. For the bcc(110) stack of the W layers, we assume that the film follows the bulk lattice parameters of the bcc W, whose lattice constant is a = 6.028a0 in the cubic unit cell convention, where a0 is the Bohr radius. As a result, the distance between√ the neighboring layers of W is . The in-plane unit cell is of a rectangular shape, whose length along the [001] and [] directions are a = 6.028a0 and , respectively. The layer distances between W-ferromagnet and ferromagnet-ferromagnet were optimized in order to minimize the total energy: dW–Fe = 3.825a0 and dFe–Fe = 3.296a0 for Fe/W(110), and dW–Ni = 3.607a0 and dNi–Ni = 3.301a0 for Ni/W(110). We assume that the local magnetic moment is oriented along the direction of , where is defined as the direction of [110]. The details of first-principles calculation are given in Appendix C.
FIG. 5.
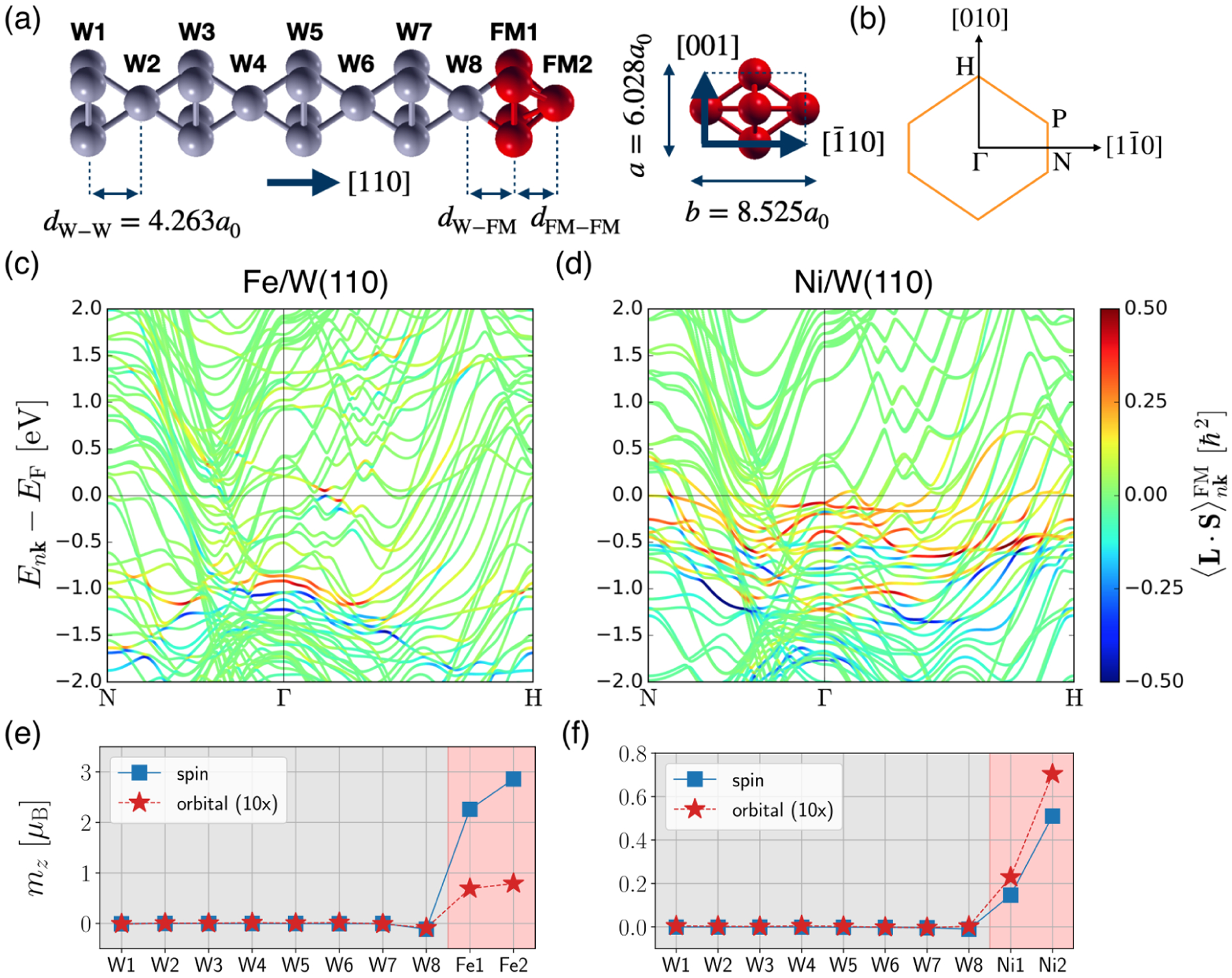
(a) Crystal structure of ferromagnet (FM)/W(110), where FM = Fe or Ni. Side and top views are displayed on the left and right, respectively. (b) First Brillouin zone and high symmetry points of bcc(110) film. Electronic energy dispersion Enk and the spin-orbit correlation in the ferromagnet for (c) Fe/W(110) and (d) Ni/W(110), which are represented by the line and color map, respectively. Note that is much more pronounced in Ni compared to Fe near the Fermi energy EF. Layer-resolved plots of the spin (blue squares) and orbital (red stars) moments for (e) Fe/W(110) and (f) Ni/W(110). Comparing Fe/W(110) and Ni/W(110), the spin moment in Fe is much larger than that in Ni, but the relative ratio of the orbital moment over the spin moment is much larger in Ni. This implies that the orbital degree of freedom is not frozen in Ni/W(110), while it is quenched in Fe/W(110).
B. Spin-Orbit Correlation and Orbital Quenching
The calculated electronic band structures of Fe/W(110) and Ni/W(110) are shown in Figs. 5(c) and 5(d), respectively. On top of each energy band Enk, the spin-orbit correlation in the ferromagnet is shown in color, which is defined as
| (35) |
Here, |ψnk〉 is the Bloch state of band n at k-point k, and Pz is the projection operator onto a layer whose index is z. It can be seen that near the Fermi energy EF, the spin-orbit correlation is negligible in Fe/W(110). The hotspot of this quantity is located about 1.0 eV below the Fermi energy, whose effect is negligible in the steady state transport. On the other hand, in Ni/W(110) the spin-orbit correlation is much more pronounced for states near the Fermi energy. The positive sign of this correlation tends to align the orbital angular momentum and the spin in the same direction.
The difference in the spin-orbit correlation directly affects the orbital moment of the ferromagnet in equilibrium. In Figs. 5(e) and 5(f), spin and orbital magnetic moments are plotted in each layer for Fe/W(110) and Ni/W(110), respectively. Blue square symbols and red star symbols respectively indicate the spin and orbital moments. For Fe/W(110) [Fig. 5(e)], the magnitude of the spin moment is large: +2.259 μB and +2.856 μB for Fe1 and Fe2, respectively. On the other hand, the orbital moments of Fe1 and Fe2 are small: +0.069 μB and +0.079 μB, respectively. The ratio of the orbital moment over the spin moment is 3.06 % and 2.76 % for Fe1 and Fe2, respectively, which is fairly small. Thus, the orbital magnetism is strongly quenched in Fe. This implies that even though the orbital angular momentum may be injected into Fe, i.e., by the orbital Hall effect of W, it is likely that most of the orbital angular momentum is relaxed to the lattice through the crystal field torque [Eq. (12)] instead of being transferred to the angular momentum of the spin through the spin-orbital torque [Eq. (13)]. Therefore, in Fe/W(110), it is expected that the orbital torque mechanism is not significant and the spin torque mechanism will be dominant, in accordance with common expectation. Meanwhile, we find proximity magnetism in W8 by the hybridization with Fe, where the spin and orbital moments are −0.114 μB and −0.009 μB, respectively.
In contrast to Fe/W(110), Ni atoms in Ni/W(110) exhibit much smaller spin moment but relatively large orbital moment. The spin moments are +0.146 μB, +0.510 μB and the orbital moments are +0.023 μB, +0.070 μB for Ni1 and Ni2, respectively. Remarkably, the ratio of the orbital moment over the spin moment is 15.64 % and 13.80 % for Ni1 and Ni2, respectively. Thus, the orbital moment is far from being quenched in Ni. Such electronic structure, which is prone to the formation of the orbital angular momentum, promotes the mechanism where an orbital Hall effect-induced orbital angular momentum can efficiently couple to the spin, resulting in the torque on the local magnetic moment. Therefore, at this point we expect that the orbital torque can be significantly larger than the spin torque in Ni/W(110), leading to the opposite effective spin Hall angle when compared to the Fe/W(110) bilayer.
C. Symmetry Constraints
Before presenting the results of first-principles calculations, we consider symmetry constraints on the electric response of the system. We define , , and , and apply an external electric field along the direction. We consider a situation when , for which the symmetry analysis reveals that only the y component is nonzero in Eq. (33). On the other hand, for the equations of motion of the intraband contribution [Eq. (34)], the x component is the only non-zero component. Thus, we present the result for α = y and β = x in Eqs. (33) and (34), respectively. Details of the symmetry analysis are given in Appendix D. The current-induced torque on the local magnetic moment is given by
| (36a) |
| (36b) |
We further decompose Tm into dampinglike (TDL) and fieldlike (TFL) components:
| (37) |
By comparing Eqs. (36b) and (37), we have
| (38a) |
| (38b) |
Below, we present the analysis for Ly and Sy components of quantities from Eqs. (33a) and (33b), respectively, which is closely related to that of the dampinglike torque. The analysis for Lx and Sx from Eqs. (34a) and (34b) is presented in the Appendix E. In order to perform the decomposition of the computed quantities into contributions coming from each atomic layer, we adopt the tight-binding representation of the equations of motion, as explained in detail in Appendix F. In the tight-binding representation, we denote orbital and spin current influxes, which correspond to the first terms in the right hand side of Eqs. (7a) and (7b), as and , respectively.
D. Fe/W(110)
In Fig. 6(a), spatial profiles of individual terms appearing in Eq. (33a) are shown for Ly. Note that the current influx and torque have the same dimension, thus we omit the labels for the current influx in the y-axes. We find that (blue squares) is negative near W1 and positive at W8, which corresponds to a positive sign of the orbital Hall conductivity. In concurrence with , (purple diamonds) appears in the opposite sign. However, (red stars) is much smaller than and . This means that most of the the orbital current influx is absorbed by the lattice. Meanwhile, the sum of and the total torque (cyan crosses), which corresponds to the right hand side of Eq. (33a), matches 〈Ly〉intra/τ (black dashed line), which corresponds to the left hand side of Eq. (33a). This confirms the validity of the equation of motion Eq. (33a). Slight deviations are due to a finite η parameter assumed in the calculation of the interband responses by Eq. (26) (Appendix C) and k-dependence of the orbital angular momentum operator (Appendix A).
FIG. 6.
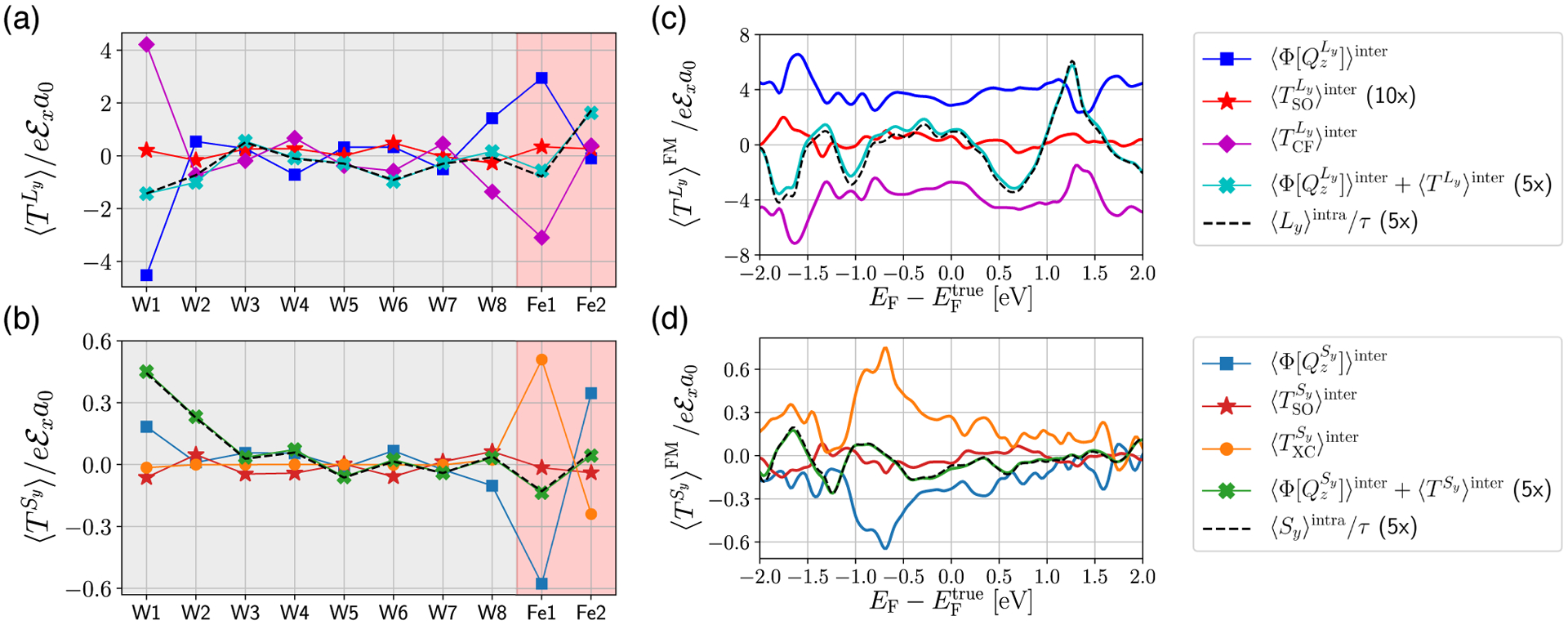
Electric response (per unit cell) of Ly and Sy current influxes – and and various torques – , , , and – arising from the interband processes and accumulation, and arising from the intraband processes (divided by τ) in Fe/W(110). Spatial profiles for (a) orbital and (b) spin quantities at the true Fermi energy . Fermi energy dependence for (c) orbital and (d) spin quantities, summed over the ferromagnet layers (Fe1 and Fe2). Note that the sum of the interband responses of the orbital/spin current influx and the total torque ( and for orbital and spin, respectively) matches with the intraband response of the orbital/spin accumulation divided by τ.
Analogously, spatial profiles of the individual terms appearing in Eq. (33b), related to the spin degree of freedom, are displayed in Fig. 6(b). We remark that the responses related to spin are an order of magnitude smaller than those related to the orbital channel in Fig. 6(a). This is natural since the spin dynamics is caused by the orbital dynamics that occurs first. From the sign of (light blue squares), which is positive near W1 and negative near W8, we conclude that the sign of the spin Hall conductivity is negative. In Fe layers, (orange circles) is sizable, where the exchange interaction is dominant. The overall positive sign of in Fe layers corresponds to a negative sign of the effective spin Hall angle. We observe a strong correlation between and . This implies that the spin current influx is mostly transferred to the local magnetic moment, which agrees with the spin torque mechanism. Meanwhile, (dark red stars) is much smaller, but not negligible. The sum of and the total torque on the spin (green crosses), the right hand side of Eq. (33b), corresponds to 〈Sy〉intra/τ on the left hand side (black dashed line).
A pronounced value of near the Fe layers, compared to its value at W1, may seem anomalous [Fig. 6(b)]. However, it can be understood by looking at 〈Sy〉intra, which exhibits a much more pronounced magnitude in W1 and W2, as compared to its value in Fe1 and Fe2. That is, in Fe1 and Fe2, the spin current is efficiently absorbed by the ferromagnet instead of inducing the spin accumulation. The situation is opposite in W1 and W2, where such spin current absorption is not possible, and the spin current simply results in spin accumulation. A similar behavior, where the spin current is strongly enhanced near the ferromagnet interface, has been also predicted in Co/Pt [36] and Py/Pt [66].
To understand the predicted behavior in terms of the electronic structure, we present the Fermi energy dependence of the computed quantities in Figs. 6(c) and 6(d) for spin and orbital channels, respectively, where a superscript FM means that it is summed over Fe1 and Fe2 layers. To arrive at these plots, we intentionally varied the Fermi energy EF from −2 eV to +2 eV with respect to the true Fermi energy , assuming that the potential [Eq. (2)] remains invariant when EF changes. For the orbital channel [Eq. (33a) and Fig. 6(c)], we observe that (blue solid line) and (purple solid line) tend to cancel each other. Meanwhile, (red solid line) is smaller than the rest of the contributions. Thus, most of the orbital angular momentum is transferred to the lattice instead of the spin. We find that the equation of motion [Eq. (33a)] is valid over the whole range of EF, where the sum of and (cyan solid line) corresponds to 〈Ly〉intra/τ (black dashed line). The Fermi energy properties for the spin channel [Eq. (33b)] are shown in Fig. 6(d). Here, a strong correlation between (light blue solid line) and (orange solid line) can be observed. We thus conclude that the spin torque mechanism is dominant over the whole range of EF. At the same time, (dark red solid line) is suppressed, which implies that the contribution to the current-induced torque caused by the spin-orbit coupling in the ferromagnet, i.e., the orbital torque and anomalous torque mechanisms, is negligible.
In order to clarify the microscopic mechanism of the current-induced torque better, we intentionally switch on and off the spin-orbit coupling in Fe or W atoms. When spin-orbit coupling is on in W and off in Fe [Fig. 7(a)], the Fermi energy dependence of (light blue solid line) perfectly matches that of with reversed sign (orange solid line), which supports the spin torque mechanism. On the other hand, (dark red solid line) is essentially zero due to the absence of spin-orbit coupling in Fe. Meanwhile, when spin-orbit coupling is off in W and on in Fe [Fig. 7(b)], all the responses become very small. Thus, any contribution arising from the spin-orbit coupling of the ferromagnet (orbital torque or anomalous torque) is negligible.
FIG. 7.
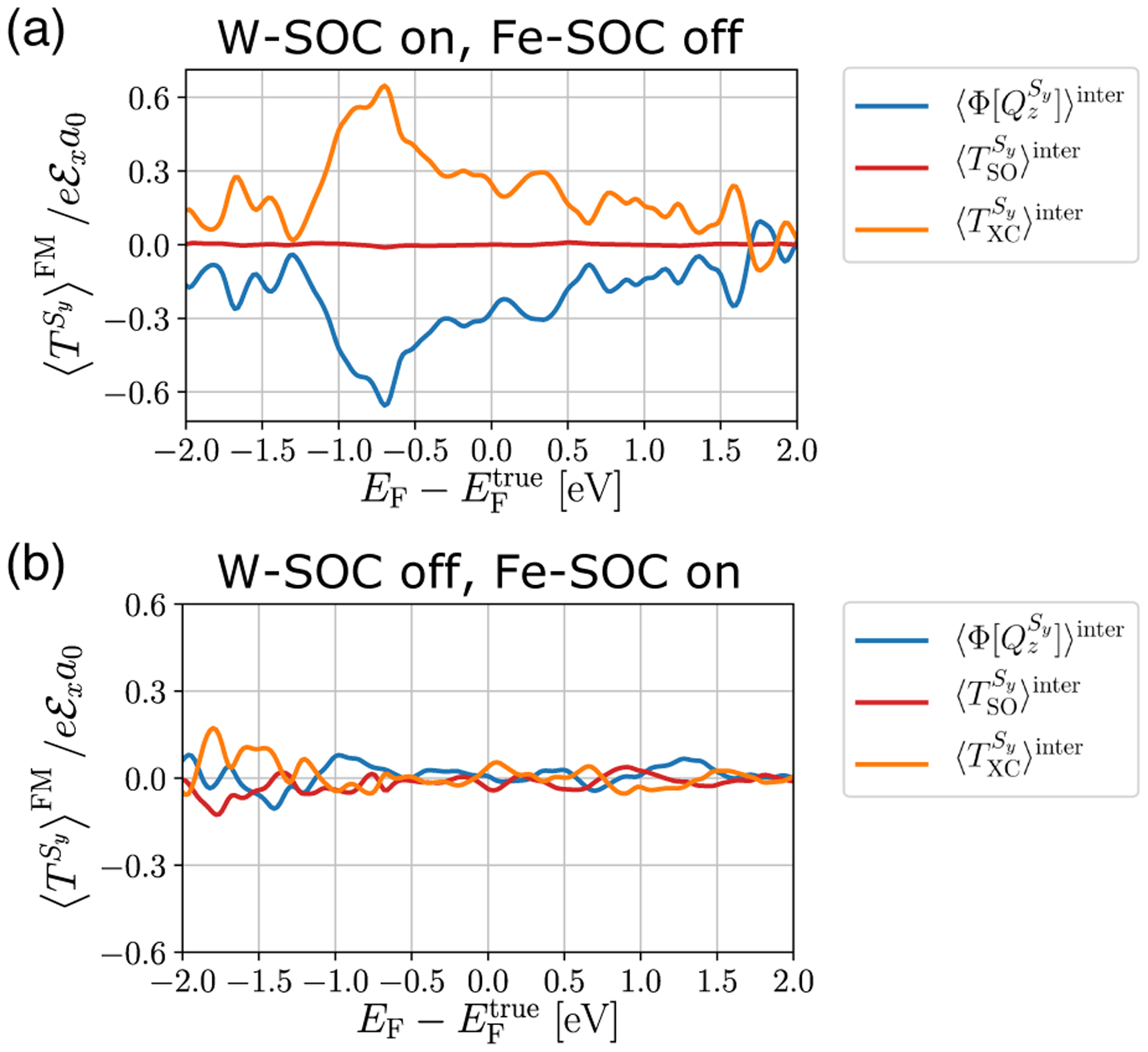
Fermi energy dependence of interband responses (per unit cell) of the spin current influx (light blue solid line), spin-orbital torque (dark red solid line), and exchange torque (orange solid line), which are summed over the Fe layers in Fe/W(110). (a) The result when spin-orbit coupling is on in W and off in Fe, and (b) the result when spin-orbit coupling is off in W and on in Fe.
E. Ni/W(110)
In Figs. 8(a) and 8(b) we show the plots of layer-resolved individual terms appearing in the equation of motion [Eq. (33)] for the y component of the orbital and spin parts, respectively, in Ni/W(110). In Fig. 8(a), we find that the orbital Hall conductivity is positive in sign according to (blue squares). As in the case of Fe/W(110), and (purple diamonds) are only different in sign, implying that the orbital angular momentum is transferred to the lattice. Thus, (red stars) is much smaller. These features are similar to those we found in Fe/W(110). The interband-intraband correspondence between 〈Ly〉intra/τ (black dashed line) and the sum of and total torque (cyan crosses) is also preserved.
FIG. 8.
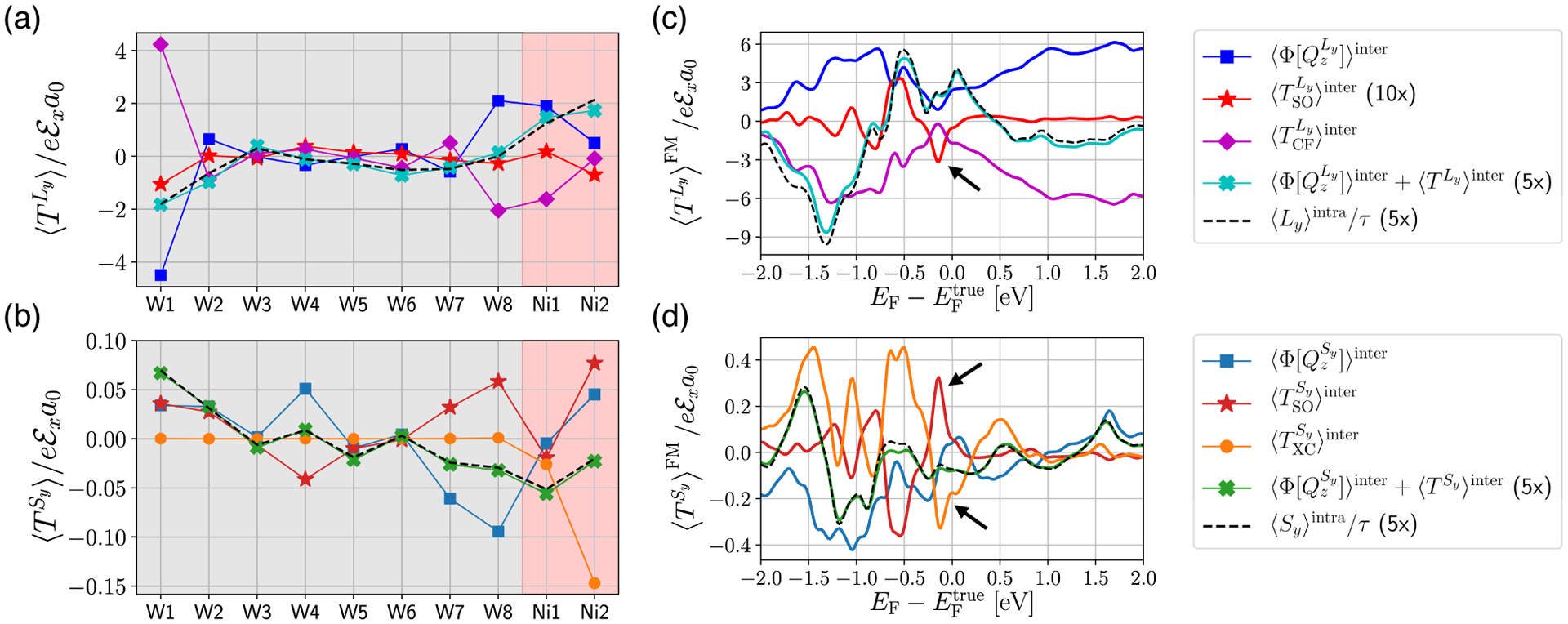
Electric response (per unit cell) of Ly and Sy current influxes – and – and various torques – , , , and – arising from the interband processes and accumulation, and arising from the intraband processes (divided by τ) in Ni/W(110). Spatial profiles for (a) orbital and (b) spin quantities at the true Fermi energy . Fermi energy dependence for (c) orbital and (d) spin quantities, summed over the ferromagnet layers (Ni1 and Ni2). Note that the sum of the interband responses of the orbital/spin current influx and the total torque ( and for orbital and spin, respectively) matches with the intraband response of the orbital/spin accumulation divided by τ.
On the other hand, as shown in Fig. 8(b), spatial profiles of spin quantitites are significantly different from those of Fe/W(110). First, we notice that (light blue squares) does not exhibit a close correlation with (orange circles). Moreover, the sign of is negative. This means positive effective spin Hall angle in Ni/W(110), which is opposite to the negative sign of the spin Hall conductivity in W. This is in contrast to the common interpretation that the spin Hall angle is a property of the nonmagnet, regardless of the ferromagnet. Second, (dark red stars) is comparable to the rest of the contributions, indicating the importance of spin-orbit coupling in Ni. Meanwhile, the interband-intraband correspondence stands with high precision (green crosses for the sum of and , and a black dashed line for 〈Sy〉intra/τ).
The Fermi energy dependence of the computed quantities, shown in Figs. 8(c) and 8(d) for orbital and spin channels respectively, provides a detailed information on the overall trend. Although and have opposite sign, their magnitudes differ and we find that is very pronounced near the Fermi energy, with corresponding peak indicated with a black arrow [Fig. 8(c)]. Since the response of the spin quantities is an order of magnitude smaller than that for the orbital channel, the pronounced spin-orbital torque, which is still much smaller than and , can have a significant effect on the dynamics of spin. In concurrence with the increase of , is significantly decreased near the Fermi energy. This implies that a channel for the orbital angular momentum transfer to the lattice is suppressed.
As a result, the response of spin in Ni/W(110) exhibits a much more rich and complicated behavior when compared to Fe/W(110) [Fig. 8(d)]. We first notice that the correlation between (light blue solid line) and (orange yellow solid line) is no longer present. Moreover, with the negative drop of , corresponding to the positive sign of the effective spin Hall angle, there is an associated positive peak from (dark red solid line), which is indicated with a black arrow. This indicates that the spin is transferred from the orbital rather than spin current influx. Therefore, the orbital angular momentum is responsible for the current-induced torque in Ni/W(110). Meanwhile, the interband-intraband correspondence (green solid line for the sum of and and black dashed line for 〈Sy〉intra/τ) is satisfied.
As we have done for Fe/W(110), we switch on and off the spin-orbit coupling separately for W and Ni atoms in Ni/W(110) as well, showing the results in Fig. 9. In Fig. 9(a), the Fermi energy dependence of , , and is shown when the spin-orbit coupling of W is on and the spin-orbit coupling of Ni is off. First of all, we find that is positive at the Fermi energy, which is opposite to the full-spin-orbit coupling case [Fig. 8(d)]. In this case, we find a strong correlation between and . Thus, the negative sign of the effective spin Hall angle is caused by the spin injection from the spin Hall effect of W. However, such correlation is not as perfect as in the case of Fe/W(110) [Fig. 7(a)]. We attribute such difference to an interfacial mechanism, where the torque is generated regardless of the spin current. Meanwhile, is negligible since the spin-orbit coupling of Ni is off.
FIG. 9.
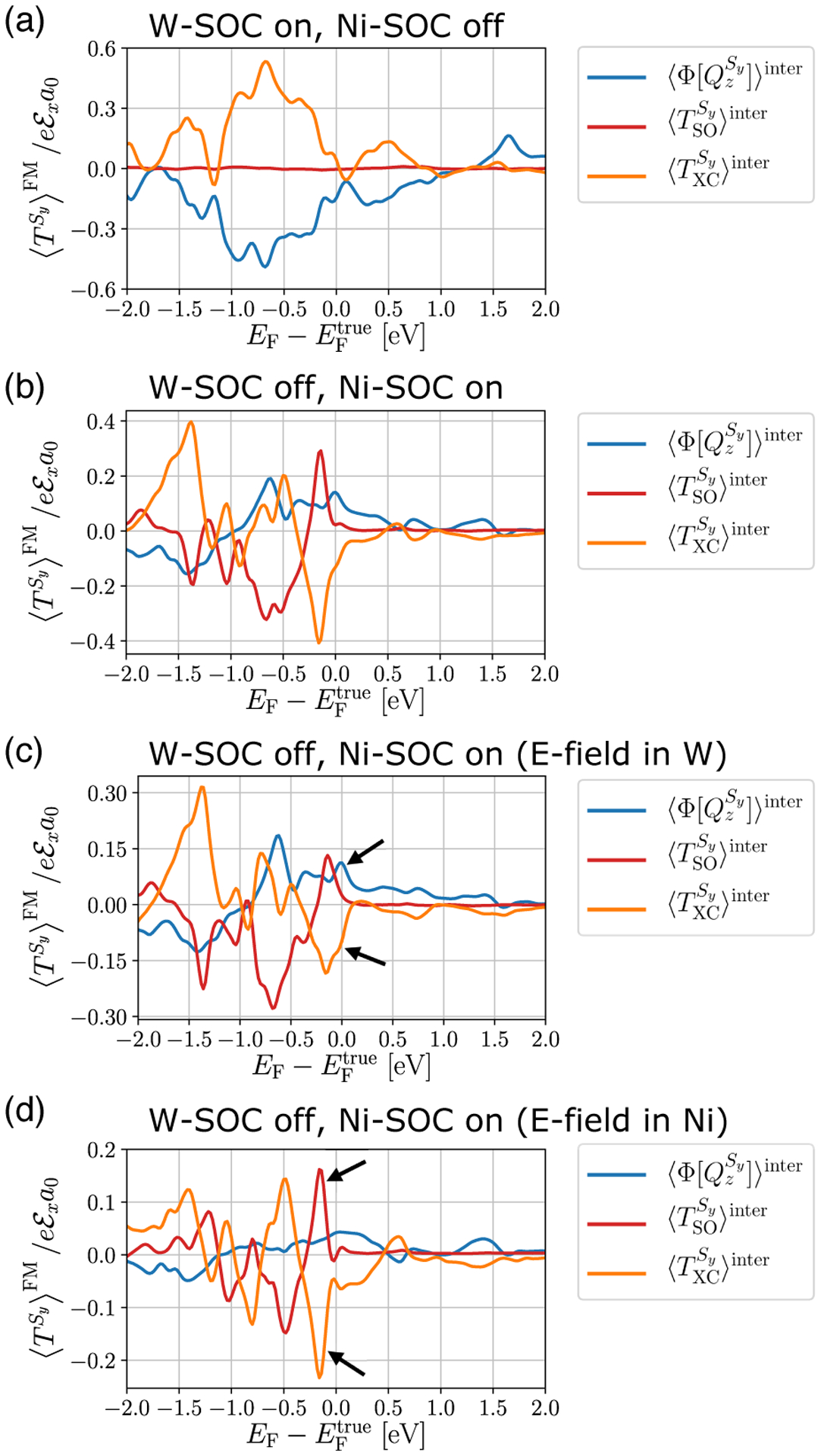
Fermi energy dependence of interband responses (per unit cell) of the spin current influx (light blue solid line), spin-orbital torque (dark red solid line), and exchange torque (orange solid line), which are summed over the Ni layers in Ni/W(110), for the case when (a) the spin-orbit coupling is on in W and off in Ni, and (b) the spin-orbit coupling is off in W and on in Ni. Both (c) and (d) show the results when the spin-orbit coupling is off in W and on in Ni, and the external electric field is applied only in (c) W and (d) Ni layers.
As shown in Fig. 9(b), when the spin-orbit coupling is off in W and on in Ni, nontrivial features show up in , , and , which is in contrast to Fe/W(110) [Fig. 7(b)]. This is due to nontrivial spin-orbit correlation of Ni shown in Fig. 5(d). Moreover, is negative at the Fermi energy. We find that nontrivial peak features [black arrows in Fig. 8(d)] are reproduced in this calculation. Thus, we confirm that the latter peaks originate in the spin-orbit coupling of Ni. To further clarify the microscopic mechanisms, we apply the external electric field in W only [Fig. 9(c)] or Ni only [Fig. 9(d)] when the spin-orbit coupling of the W is off and the spin-orbit coupling of Ni is on, which correspond to the orbital torque and the anomalous torque contributions, respectively (more details can be found in the Appendix C). In both cases, exhibits a negative drop near , which is correlated with a positive peak of . This implies that for both cases the angular momentum transfer from the orbital channel to the spin channel is crucial. The difference is that for the orbital torque mechanism, Fig. 9(c), exhibits a positive peak at the Fermi energy (marked with a black arrow), which comes from the conversion of the orbital current into the spin current by the spin-orbit coupling of Ni. We find that it is correlated with a shoulder feature of at the Fermi energy (marked with a black arrow). Such peak of implies that in the orbital torque mechanism, there are two different microscopic channels for the orbital-to-spin conversion: one for the spin converted from the orbital angular momentum via , and the other for the conversion of the orbital current into the spin current followed by the spin-transfer torque. Meanwhile, in Fig. 9(d), which corresponds to the anomalous torque mechanism, is not very pronounced, and only the peak of is observed (indicated with a black arrow). The negative sign of (positive sign of the effective spin Hall angle) is due to a positive sign of the spin Hall conductivity in Ni. We note that, as expected, for the anomalous torque mechanism, the orbital-to-spin conversion via is crucial since it originates in the spin-orbit coupling of the ferromagnet. Therefore, we conclude that in Ni/W(110) the orbital torque and anomalous torque are the first and the second dominant mechanisms for the torque generation on the local magnetic moment.
IV. DISCUSSION
A. Disentangling Different Microscopic Mechanisms
In Sec. III, we found that the spin torque provides the dominant contribution to the current-induced torque in Fe/W(110) according to the correlation between the exchange torque and the spin current influx from W, which is reflected in the negative effective spin Hall angle [Fig. 7(a)]. In Ni/W(110), on the other hand, the orbital torque is found to be the most dominant contribution. The evidence for the orbital torque is provided by pronounced peaks in the spin-orbital torque and the spin current influx that suggests a positive effective spin Hall angle, associated with the exchange torque [Fig. 9(c)]. However, we also observed that the anomalous torque can be associated with the spin-orbital torque [Fig. 9(d)] because the self-induced spin accumulation in the ferromagnet results from the current-induced orbital angular momentum. A crucial difference between the orbital torque and anomalous torque is that while the orbital torque is due to an electrical current flowing in the nonmagnet, the anomalous torque is due to an electrical current passing through the ferromagnet. In this respect, only the orbital torque is important for memory applications where the ferromagnetic layer must be patterned to form a physically separate memory cell, whereas both orbital torque and anomalous torque are important for applications based on magnetic textures (i.e., domain walls and Skyrmions) for which such patterning is not necessary.
We can disentangle each of the contributions in the current-induced torque of Fe/W(110) and Ni/W(110), according to the classification scheme outlined in Fig. 2. The different contributions to the current-induced torque can be disentangled by modifying the system parameters “by hand” in the calculation. To distinguish between local and nonlocal contributions to the torque, the electric field is selectively applied to only the ferromagnetic or nonmagnetic layer, respectively. We note, however, that this is an approximate measure since an electric current may flow in the ferromagnet(nonmagnet) although an electric field is applied only to the nonmagnet (ferromagnet) layer, as the electronic wave functions are delocalized across the film. For determining the spin-orbit coupling origin (nonmagnet versus ferromagnet), we do not simply turn on and off the spin-orbit coupling because it causes significant change of the band structure. Instead, we change the sign of the the spin-orbit coupling in the relevant layer, which changes the sign of its contribution. For example, we rely on the property that the sign of the orbital torque and anomalous torque should become opposite after flipping the sign of spin-orbit coupling in the ferromagnet, while the spin torque and interfacial torque remain invariant. By computing the torque under different system configurations, the four contributions to the current-induced torque can be determined, as illustrated in Fig. 2 and described in detail in Appendix G. We note that the sum of spin torque, orbital torque, interfacial torque, and anomalous torque equals the net torque when the electric field applied to the entire system with the actual spin-orbit coupling strength of each atom. Although this classification scheme relies on computational handles with no experimental counterpart, it provides a systematic basis for physically interpreting the results of calculations, which in turn enables the development of intuition about materials and system designs.
In Figs. 10(a) and 10(b) we show the decomposition of the total dampinglike torque in Fe/W(110) and Ni/W(110), respectively, into separate contributions. In Fe/W(110), the spin torque is the most dominant contribution. However, our analysis reveals that the interfacial torque is not negligible, accounting for about 35 % of the spin torque. Overall, the spin torque and interfacial torque are larger than the orbital torque and anomalous torque, implying that the spin-orbit coupling in W is more important than that in Fe. In Ni/W(110), on the other hand, the orbital torque is the most dominant contribution. The second largest contribution is the anomalous torque, which is comparable to a half of the orbital torque. The magnitude of the interfacial torque is not much smaller, reaching as much as 37 % of the magnitude of the orbital torque. Overall, the orbital torque and anomalous torque are dominant over the spin torque and interfacial torque in Ni/W(110). This suggests that the spin-orbit coupling in Ni is more important than the spin-orbit coupling in W in this system, in contrast to an intuitive expectation that spin-orbit coupling in 3d ferromagnets plays a minor role as compared to the spin-orbit coupling of the heavy element. These results are consistent with our analysis of the results presented in Figs. 7 and 9.
FIG. 10.
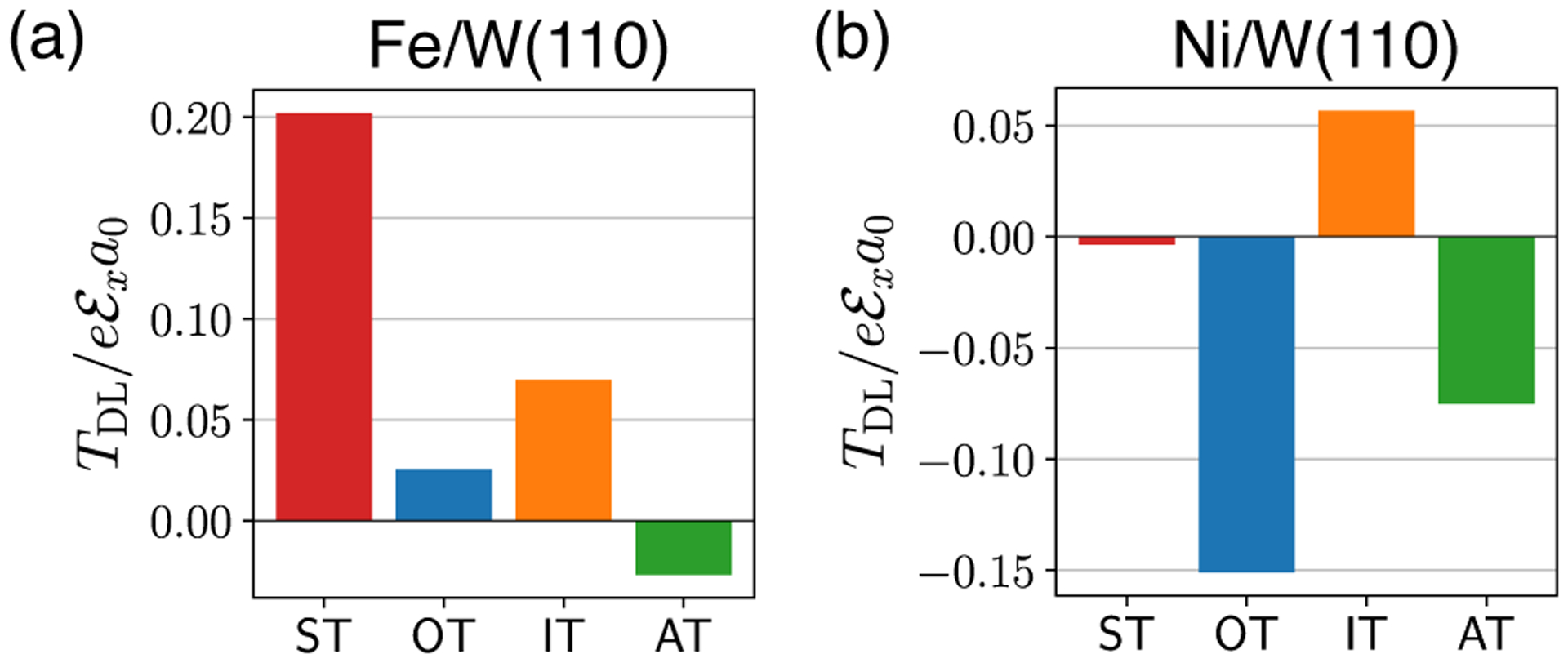
Disentanglement of the dampinglike torque into the spin torque (ST), orbital torque (OT), interfacial torque (IT), and anomalous torque (AT) in (a) Fe/W(11) and (b) Ni/W(110). Note that the ST and OT are the most dominant mechanisms in Fe/W(110) and Ni/W(110), respectively. We note that the IT and AT are not negligible neither in Fe/W(110) nor in Ni/W(110).
B. Orbital Current versus Spin Current
Although the orbital current [Eq. (8a)] and the spin current [Eq. (8b)] are defined in a similar way, there are differences in their numerical treatment. While the spin and its current can be locally defined everywhere in space, the orbital angular momentum is evaluated within the muffin-tin by the atom-centered approximation. This leads to a conceptual problem in defining the orbital current: The orbital current evaluated in the interstitial region becomes zero although its value is finite inside the muffin-tin. Heuristically, the orbital angular momentum is encoded in a vorticity of the phase of a wave function, which exists not only in the muffin-tin but also in the interstitial region. It is the vorticity of the wave function that is transported through the interstitial region. On the other hand, the orbital current “influx” into the muffin-tin does not suffer from such problem because orbital angular momentum and velocity can be calculated on the boundary of the muffin-tin. Therefore, we have evaluated orbital current influx into the muffin-tin instead of calculating the orbital current itself throughout the manuscript.
As the atom-centered approximation neglects the contribution from interstitial region, the crystal field torque in our calculation [Eq. (12)] only describes angular momentum transfer from the orbital to the lattice within the muffin-tin, which is mostly concentrated near the surfaces and the interface [Figs. 6(a) and 8(a)]. In general, we expect that nonspherical component of the potential is more pronounced in the interstitial region, which provides another channel for angular momentum transfer from the electronic orbital to the lattice. However, as the d character electronic wave function of a transition metal is localized inside the muffin-tin, we expect that additional contribution to the crystal field torque from the interstitial region is small.
C. Experiments and Materials
Although the effective spin Hall angle measured in experiments is the sum of all contributions to the torque on the local magnetic moment, it has been assumed that it is a property of the nonmagnet in nonmagnet/ferromagnet bilayers, which can be incorrect. For example, we have shown that the current-induced torque depends on the choice of the ferromagnet in ferromagnet/W(110), where ferromagnet is Fe or Ni. In this case, it is due to an opposite sign of the orbital Hall effect and spin Hall effect in W, and the resulting orbital-to-spin conversion efficiencies are different for Fe and Ni. As a result, even the sign of the effective spin Hall angle changes: from negative for Fe/W(110) to positive for Ni/W(110). We believe that such change-of-sign behavior can be directly measured in experiment. More concretely, we suggest performing a spin-orbit torque experiment on an FeNi alloy in order to observe change of the effective spin Hall angle as the alloying ratio varies, with the effective spin Hall angle turning to zero at a certain critical concentration.
We speculate that this behavior would be observed in other systems where the orbital Hall effect competes with the spin Hall effect. For example, among 5d elements, Hf, Ta, and Re exhibit gigantic orbital Hall conductivity, whose sign is opposite to that of the spin Hall conductivity [32]. Such behavior holds in general for groups 4–7 among transition metals. For 3d elements, such as Ti, V, Cr, and Mn, the spin Hall conductivity is much smaller than that of 5d elements, while the orbital Hall conductivity is almost as large as in 5d elements [34]. Thus, the orbital torque contribution is expected to be more pronounced than the spin torque contribution when the nominally nonmagnetic substrate is made of 3d elements, as compared to the systems where the nonmagnet is made of 5d elements. Therefore, alloying not only the ferromagnet but also the nonmagnet provides a useful knob for observing competing mechanisms of the current-induced torque.
The layer thickness dependence of the spin-orbit torque has been measured in Ta/CoFeB/MgO [67] and Hf/CoFeB/MgO [68], where the sign of the current-induced torque was found to change when the thickness of Ta or Hf was as small as ≈ 1 nm to 2 nm. The origin of the sign change has been attributed to the competition between the bulk and interfacial mechanisms, which correspond to the spin torque and interfacial torque mechanisms in our terminology. Recently, such behavior has also been observed in a similar system Zr/CoFeB/MgO [69], where a 4d element Zr was used instead of a 5d element. Due to a negligible spin Hall conductivity of Zr as compared to the orbital Hall conductivity, it has been proposed that the sign change occurs due to a competition between the spin torque and orbital torque [69], instead of the competition between the spin torque and interfacial torque. Detailed investigation of these systems by our method may reveal the origin of the sign change.
Another widely-studied system in spintronics is a Pt-based magnetic heterostructure. Due to a large spin Hall conductivity of Pt [70], the spin torque is assumed to be the most dominant mechanism of the torque in Pt-based systems [5]. In Co/Pt, however, theoretical analysis revealed that the interfacial spin-orbit coupling contributes significantly to the fieldlike torque [19, 71]. On the other hand, the dampinglike torque is attributed to the spin torque mechanism [35, 71], which is also supported by experiments [72]. Hayashi et al. compared Ni/Pt and Fe/Pt bilayers, finding that the current-induced torque strongly depends on the choice of the ferromagnet [73]. According to their interpretation, while the bulk effect is dominant in Ni/Pt, a pronounced interface effect in Fe/Pt not only leads to fieldlike torque but also suppresses the spin current injection from Pt, which leads to a distinct ferromagnet dependence of the torque [73]. A similar conclusion has also been drawn in an experiment by Zhu et al., where the interfacial spin-orbit coupling has been varied by choosing different samples and annealing conditions [74]. Further investigation of the exact mechanism in these systems by theory is required.
For the study of the interplay between the spin and orbital degrees of freedom transition metal oxides may present a very fruitful playground. In transition metal oxides, a strong entaglement of the spin, orbital, and charge degrees of freedom has been intensively studied in the past [75–77]. For example, magnetic properties of transition metal oxides are heavily affected by the orbital physics not only via the effect of spin-orbit coupling but also because of the anisotropic exchange interactions caused by the shape of participating orbitals [75]. However, most studies on the transition metal oxides have focused on their ground state properties, such as various competing magnetic phases. We expect that the investigation of the spin-orbital entangled dynamics would provide crucial insights into understanding the complex physics of transition metal oxides.
V. CONCLUSION
Motivated by various proposed mechanisms of the current-induced torques, which are challenging to disentangle both theoretically and experimentally, we developed a theory of current-induced spin-orbital coupled dynamics in magnetic heterostructures, which tracks the transfer of the angular momentum between different degrees of freedom in solids: spin and orbital of the electron, lattice, and local magnetic moment. By adopting the continuity equations for the orbital and spin angular momentum [Eq. (7)], we derived equations for the angular momentum dynamics in the steady state reached when an external electric field is applied, which provide relations between interband and intraband contributions to the current influx, torques, and accumulation of the spin and orbital angular momentum [Eqs. (33) and (34)]. We remark that this formalism can be generally applicable to various schemes of calculation such as k · p method and tight-binding model, as well as density functional theory. The only requirement is that each term in the Hamiltonian is separately defined as in Eqs. (1) and (2).
This formalism is particularly useful for the detailed study of the microscopic mechanisms of the current-induced torque. In this work we implemented this formalism in first principles calculations to investigate the spin-orbit torque origins in Fe/W(110) and Ni/W(110) bilayers. In Fe/W(110), we observe a strong correlation between the spin current influx and the exchange torque, which is a key characteristic of the spin torque mechanism. On the other hand, such correlation is not observed in Ni/W(110). Instead, we observe a pronounced correlation between the exchange torque and the spin-orbital torque, indicating the transfer of angular momentum from the orbital to the spin channel. Moreover, the spin current influx exhibits a sign opposite to that of the spin Hall effect in W. This leads us to a conclusion that the orbital torque is dominant in Ni/W(110). Considering that our calculations capture contributions driven by electronic structure – i.e. the intrinsic-type of contributions – our prediction is expected to be observed in experiments when the sample is in a “moderately clean” regime of the resistivity. Although the calculations presented here do not capture disorder-driven contributions such as side jump and skew-scattering, our theoretical approach and predictions can play a guiding role for further advances in this area, in analogy to the theoretical developments around the anomalous and spin Hall effects [78, 79]. Consistent treatment of the disorder scattering effects such as side jump and skew-scattering remains to be investigated, but this goes beyond the scope of this work.
We further proposed a classification scheme of the different mechanisms of current-induced torque based on the criteria of whether the scattering source is in the nonmagnet-spin-orbit coupling or the ferromagnet-spin-orbit coupling, and whether the torque response is of local or nonlocal nature (Fig. 2). This analysis also confirms that the spin torque and orbital torque are the most dominant mechanisms in Fe/W(110) and Ni/W(110), respectively. However, we also find that the other contributions, interfacial torque and anomalous torque, are not negligible as well. Our formalism enables an analysis of the angular momentum transport and transfer dynamics in detail, which clearly goes beyond the “spin current picture”. Since it treats the spin and orbital degrees of freedom on an equal footing, it is ideal for systematically studying the spin-orbital coupled dynamics in complex magnetic heterostructures.
ACKNOWLEDGMENTS
D.G. thanks insightful comments from discussions with Gustav Bihlmayer, Filipe Souza Mendes Guimarães, Mathias Kläui, OukJae Lee, Kyung-Whan Kim, and Daegeun Jo. K.-J. L., J.-P. H., and Y. M. acknowledge discussions with Mark D. Stiles. J.-P. H., and Y. M. additionally acknowledge discussions with Jairo Sinova. We thank Mark D. Stiles and Matthew Pufall for carefully reading the manuscript and providing insightful comments. We gratefully acknowledge the Jülich Supercomputing Centre for providing computational resources under project jiff40. D.G. and H.-W. Lee were supported by SSTF (Grant No.BA-1501-07). F.X. acknowledges support under the Cooperative Research Agreement between the University of Maryland and the National Institute of Standards and Technology Physical Measurement Laboratory, Award 70NANB14H209, through the University of Maryland. We also acknowledge funding under SPP 2137 “Skyrmionics” (project MO 1731/7-1) and TRR 173 - 268565370 (project A11) of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation).
Appendix A: Interband-Intraband Correspondence
Here we provide a proof of Eq. (31). We assume that the operator does not have position dependence, which leads to . From Eqs. (29), the left hand side of Eq. (31) is written as
| (A1) |
where we used
| (A2) |
Application of integration by parts to the first term in Eq. (A1) leads to
| (A3) |
It can be rewritten as
| (A4) |
By using identities
| (A5) |
and
| (A6) |
for n ≠ m, we have
| (A7a) |
| (A7b) |
| (A7c) |
This proves Eq. (31). In case when k-dependent, the deviation is given by
| (A8) |
such that
| (A9) |
holds even when k-dependent.
Appendix B: Stationary Condition of the Intraband Contribution
For a proof of Eq. (32), we apply Eq. (29) to :
| (B1) |
Because
| (B2) |
for any Hermitian operator , we have
| (B3) |
Appendix C: Computational Method
First-principles calculation consists of three steps. The first step is calculation of the electronic structure from the density functional theory. In this step, we obtain Bloch states and their energy eigenvalues. The second step is to obtain maximally-localized Wannier functions (MLWFs) starting from the Bloch states obtained in the first step. Once the MLWFs are found, matrix elements of all relevant operators (Hamiltonian, position, spin, and orbital) are expressed within the basis set of the MLWFs. Thus, a tight-binding model is obtained. The last step is evaluation of the interband and intraband responses of the individual terms in the equations of motion [Eqs. (33) and (34)] by solving the tight-binding model obtained from the second step.
The electronic structure of ferromagnet/W(110) (ferromagnet=Fe or Ni), whose lattice structure is shown in Fig. 5, is calculated self-consistently in the film mode of the fullpotential linearized augmented plane wave method [80] from the code FLEUR [81]. We use Perdew-Burke-Ernzerhof exchange-correlation functional within the generalized gradient approximation [82]. Muffin-tin radii of the ferromagnet and W atoms are set to 2.1a0 and 2.5a0, respectively, where a0 is the Bohr radius. The plane wave cutoff is set to . The Monkhorst-Pack k-mesh of 24 × 24 are sampled from the first Brillouin zone. The spin-orbit coupling is treated self-consistently within the second variation scheme. The layer distances dFM−FM and dW−FM are optimized such that the total energy is minimized. The optimized values for Fe/W(110) are dW−Fe = 3.825a0 and dFe−Fe = 3.296a0, and those for Ni/W(110) are dW−Ni = 3.607a0 and dNi−Ni = 3.301a0.
In order to obtain MLWFs, we initially project the Bloch states onto dxy, dyz, dzx, and sp3d2 trial orbitals for each atom, and minimize their spreads using the code WANNIER90 [83]. We obtain in total 180 MLWFs out of 360 Bloch states, that is, 18 MLWFs for each atom. For the disentanglement of the inner and outer spaces, we set the frozen window as 2 eV above the Fermi energy. The Hamiltonian, position, spin, and orbital operators, which are evaluated beforehand within the Bloch basis, are then transformed to the basis of MLWFs, and the tight-binding model is obtained.
Individual terms appearing in the equations of motion [Eqs. (33) and (34)] are evaluated using Eqs. (26) and (29) for interband and intraband contributions, respectively. The integration is performed over interpolated k-mesh of 240 × 240. For the interband contributions, we set η = 25 meV for convergence, which describes broadening of the spectral weight by disorders. In the intraband contribution, we set the momentum relaxation time as τ = ℏ/2Γ with Γ = 25 meV, which corresponds to τ = 1.26 × 10−14 s. We set the temperature in the Fermi-Dirac distribution function as room temperature T = 300 K. For the application of an external electric field specifically onto ferromagnet or W layers, we replaced vx in Eq. (26) by
| (C1a) |
| (C1b) |
where Pz is the projection onto the MLWFs located in a layer whose index is z. We confirm that the 18 MLWFs are well localized in each layer. Note that Eq. (C1) is defined such that
| (C2) |
Appendix D: Symmetry Analysis
In Sec. III C, we state that only y and x components are nonzero in Eqs. (33) and (34), respectively. Here, we prove this by symmetry argument. Two important symmetries present in ferromagnet/W(110), where the magnetization is pointing the z direction, are and symmetries. Here, is the time-reversal operator and is the mirror reflection operator along the direction of x(y). Since all the terms appearing in the same equation should transform in the same way, we consider only the response of a torque operator
| (D1) |
for a general angular momentum operator J, which can be either orbital and spin origin. To find symmetry constraints on the interband [Eq. (26)] and intraband [Eq. (29)] responses, we first investigate how matrix elements of vx and TJ transform. We define and as Hilbert space representations of and , respectively. Note that transforms vx and TJ as
| (D2) |
and
| (D3) |
respectively. On the other hand, and symmetries transform vx and TJ as
| (D4a) |
| (D4b) |
and
| (D5a) |
| (D5b) |
| (D5c) |
| (D5d) |
| (D5e) |
| (D5f) |
As a result, and symmetries transform vx and TJ as
| (D6a) |
| (D6b) |
and
| (D7a) |
| (D7b) |
| (D7c) |
| (D7d) |
| (D7e) |
| (D7f) |
where . Note that and commute each other.
We remark that and are anti-unitary and unitary operators, respectively. Thus, is anti-unitary. For an arbitrary anti-unitary operator Θ, a matrix element of an operator satisfies
| (D8) |
Thus, combining this result with Eqs. (D6) and (D7) provides constraints on the interband [Eq. (26)] and intraband [Eq. (29)] contributions.
As an illustration, let us demonstrate that both interband and intraband contributions vanishes for . We consider symmetry at first. By this, matrix elements of vx and transform as
| (D9) |
and
| (D10) |
where k′ = (+kx, −ky, −kz). On the other hand, symmetry gives
| (D11) |
and
| (D12) |
where k″ = (−kx, +ky, −kz).
A constraint for the interband contribution for [Eq. (26)] is given by symmetry:
| (D13a) |
| (D13b) |
| (D13c) |
| (D13d) |
in the limit η → 0+. Thus, is forbidden by symmetry. In Eq. (D13a), we used the fact that the linear response can also be written in terms of the transformed states. Note that we use the Bloch state representation instead of their periodic parts. For the intraband contribution, we have the following constraint by symmetry:
| (D14a) |
| (D14b) |
| (D14c) |
Therefore, both interband and intraband responses for vanishes by the symmetries. By the procedure for different components of the torque, we arrive at the conclusion that the presence of and symmetries allows only and to be nonzero.
Appendix E: Intraband Response
In Fig. 11, intraband contributions appearing in Eq. (34) are plotted for each layer of Fe/W(110). We confirm that the sum of the current influx and torques vanishes for the intraband contributions, respectively for the orbital and spin, which confirms Eq. (34). For the orbital [Fig. 11(a)], we find that tends to cancel with and is small. Meanwhile, for the spin, not only and but also are of comparable magnitudes, which is distinct from the interband response [Fig. 6(b)]. However, near the Fe layers, is small, and tends to cancel with . We attribute this behavior to small spin-orbit correlation in Fe [Fig. 5(c)], and quenching of the orbital moment. Fermi energy dependence plots in Fig. 11 also show the cancellation behaviors between the the orbital current influx and crystal field torque, and between the spin current influx and and the exchange torque. Although the spin-orbital torque is not particularly small in general, only near the true Fermi energy it is suppressed. Therefore, the fieldlike torque originates in the spin current injection (spin torque mechanism).
FIG. 11.
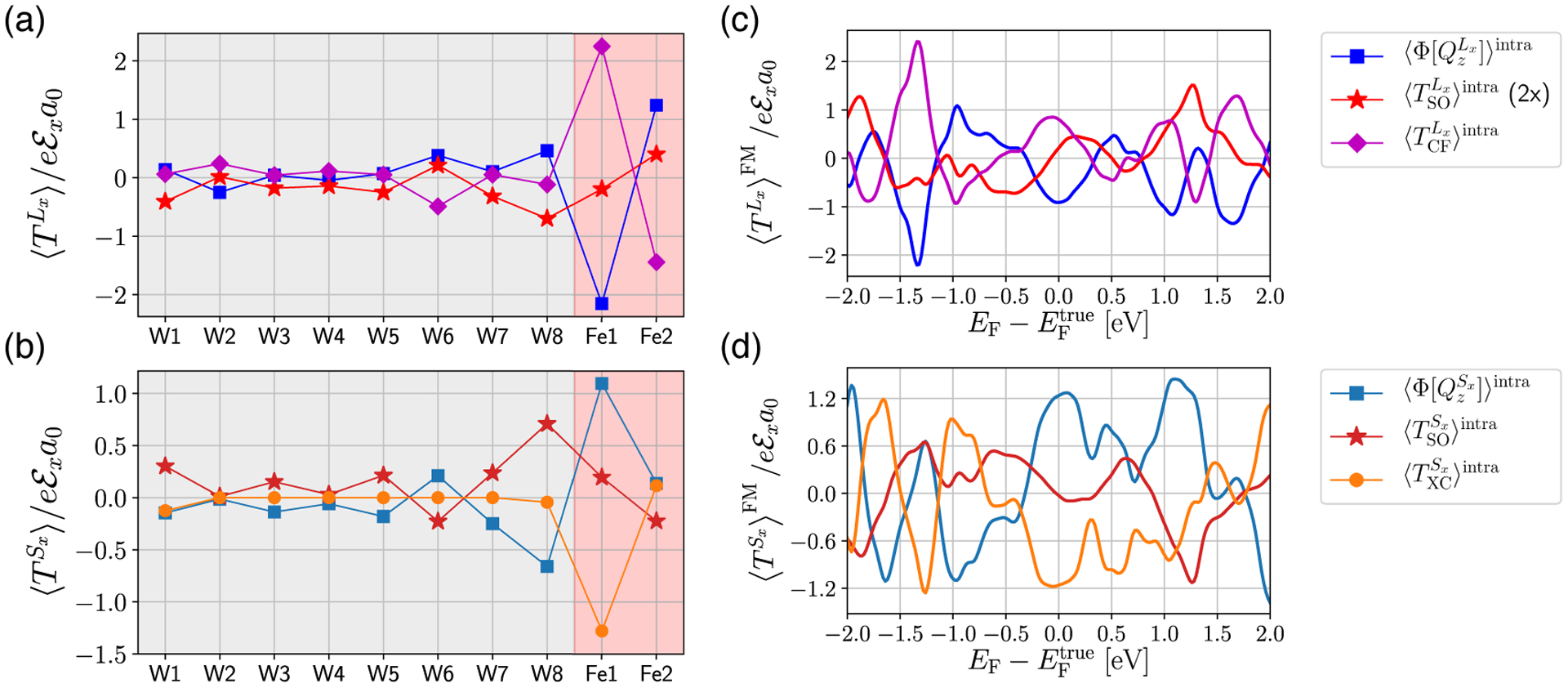
Electric response of current influxes − and – and various torques − , , , and – arising from the intraband process in Fe/W(110). Spatial profiles for (a) the orbital and (b) the spin at true Fermi energy . Fermi energy dependences for (c) the orbital and (d) the spin, which are summed over the ferromagnet layers (Fe1 and Fe2).
In Ni/W(110), for the orbital, and cancel each other, with small magnitude of [Fig. 12(a)]. For the spin, on the other hand, as well as , contributes to , in comparable magnitudes [Fig. 12(b)]. This is due to pronounced spin-orbit correlation of Ni at the Fermi energy [Fig. 5(d)]. The Fermi energy dependence plots in Figs. 12(c) and 12(d) also show that the spin-orbital torque is nonnegligible at the Fermi energy. Therefore, in Ni/W(110), the fieldlike torque is a combined effect of the spin injection and the spin-orbit coupling. Such behavior has also been observed in Pt/Co [71].
FIG. 12.
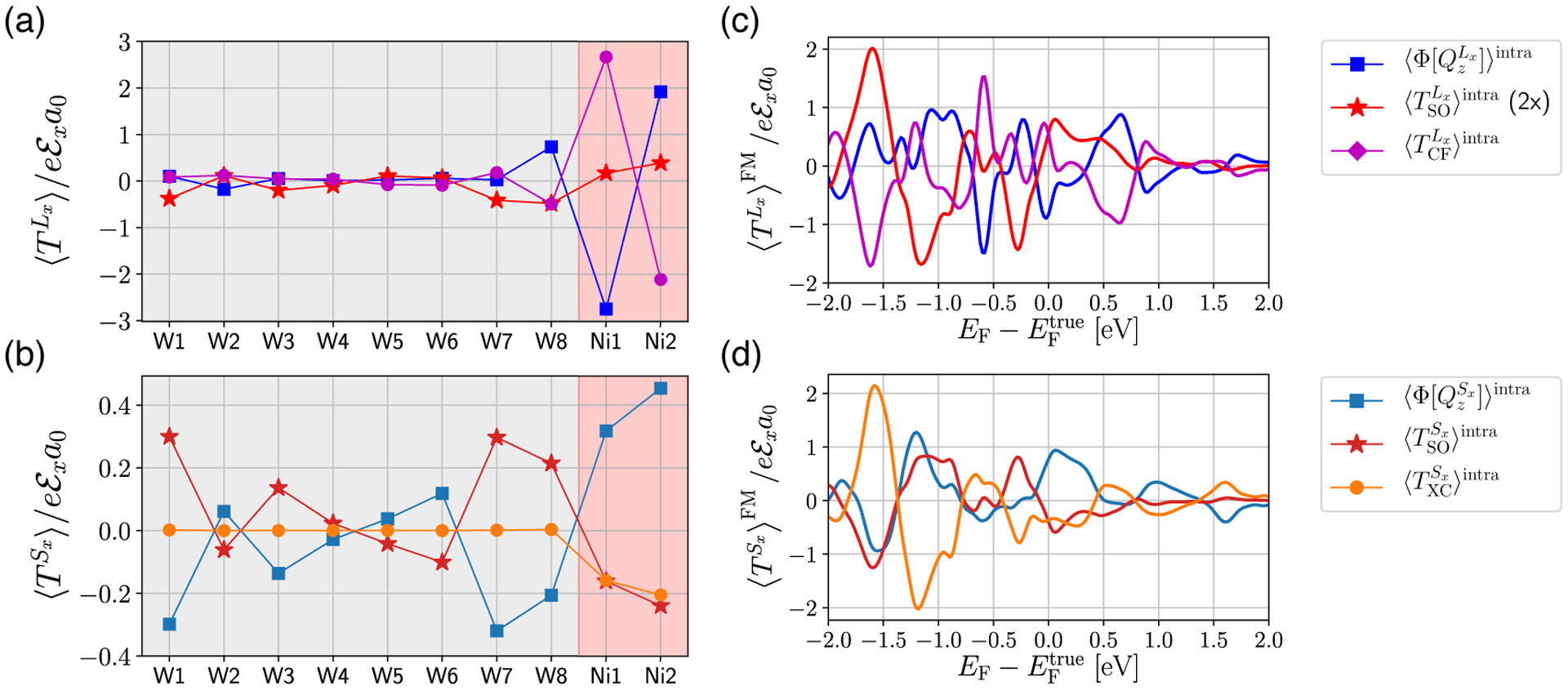
Electric response of current influxes – and – and various torques – , , , and – arising from the intraband process in Ni/W(110). Spatial profiles for (a) the orbital and (b) the spin at true Fermi energy . Fermi energy dependences for (c) the orbital and (d) the spin, which are summed over the ferromagnet layers (Ni1 and Ni2).
To clarify microscopic mechanisms of different origins, we disentangle the fieldlike torque into the spin torque, orbital torque, interfacial torque, and interfacial torque, analogously to Fig. 10. For Fe/W(110) [Fig. 13(a)], we find that the spin torque is the most dominant contribution, as expected. On the other hand, for Ni/W(110) [Fig. 13(b)], not only the spin torque but also the anomalous torque significantly contributes. This is due to pronounced spin-orbit correlation in Ni. Meanwhile, we also find that the interfacial torque is not negligible.
Appendix F: Tight-binding Representation of the Continuity Equation
Here, we derive a tight-binding representation of the current influx and torque appearing in the continuity equation [Eq. (7)]. To do this, we first define Pz as a projection operator onto a set of MLWFs located near a layer whose index is z. Then, for the spin operator S, we define
| (F1) |
as the spin operator at z, such that
| (F2) |
The Heisenberg equation of motion for S(z) is written as
| (F3a) |
| (F3b) |
| (F3c) |
| (F3d) |
We define local torque operator at z by
| (F4a) |
| (F4b) |
where
| (F5) |
is the total torque operator, and we define
| (F6) |
the spin current influx at z.
FIG. 13.
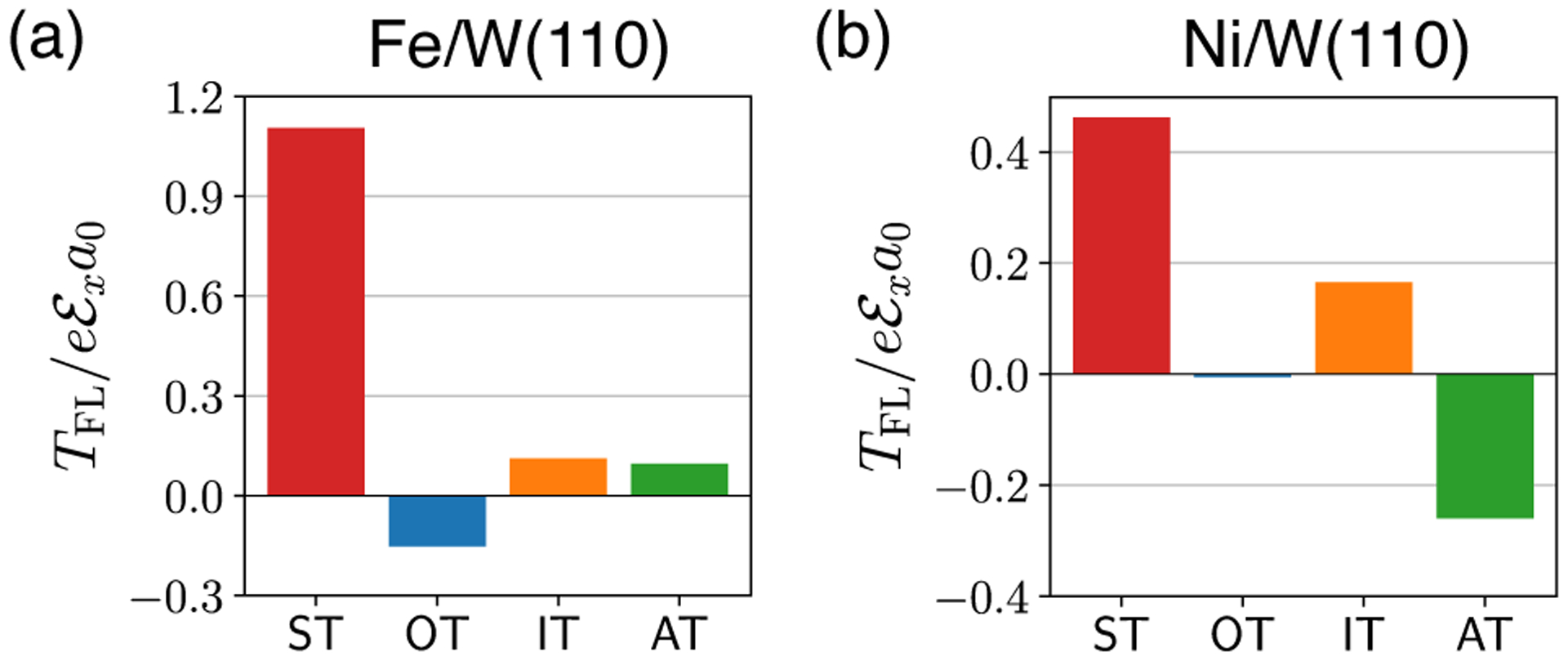
Disentanglement of the fieldlike torque into the spin torque (ST), orbital torque (OT), interfacial torque (IT), and anomalous torque (AT) in (a) Fe/W(11) and (b) Ni/W(110). In both systems, the ST is most dominant mechanism. We note that the AT is not negligible in Ni/W(110).
Although Φ[jS](z) may not seem intuitive, it corresponds to an usual definition of the spin current influx. To demonstrate this point, we consider the case where P = |r〉 〈r| and , where |r〉 is an eigenket for the position operator r. Then Φ[jS] becomes
| (F7) |
Thus, a matrix element between states ϕ and ψ is written as
| (F8a) |
| (F8b) |
where
| (F9) |
From Eq. (F9), we find that this is consistent with usual definition of the spin current jS = S⊗(p/m0). Therefore, Eq. (F6) can be understood as an operator of the spin current influx to the subspace defined by the projection Pz.
Appendix G: Disentangling Different Contributions of the Current-Induced Torque
To disentangle different contributions of the torque (Figs. 10 and 13), we utilize a property that upon changing the sign of the spin-orbit coupling constant in the ferromagnet the orbital torque and anomalous torque flip their signs while the signs of the spin torque and interfacial torque remains invariant. That is, the total exchange torque is decomposed as the sum of the contribution driven by the spin-orbit coupling in the nonmagnet and the contribution driven by the spin-orbit coupling in the ferromagnet:
| (G1) |
In an auxiliary system where the sign of the spin-orbit coupling is flipped in the ferromagnet atoms, the exchange torque becomes
| (G2) |
Thus, the nonmagnet-spin-orbit coupling contribution is written as
| (G3) |
and the ferromagnet-spin-orbit coupling contribution is written as
| (G4) |
Then, by applying the electric field only in the nonmagnet or ferromagnet layers by Eq. (C1), we can separately evaluate the spin torque, orbital torque, anomalous torque, and interfacial torque.
References
- [1].Hellman Frances, Hoffmann Axel, Tserkovnyak Yaroslav, Beach Geoffrey S. D., Fullerton Eric E., Leighton Chris, MacDonald Allan H., Ralph Daniel C., Arena Dario A., Dürr Hermann A., Fischer Peter, Grollier Julie, Heremans Joseph P., Jungwirth Tomas, Kimel Alexey V., Koopmans Bert, Krivorotov Ilya N., May Steven J., Petford-Long Amanda K., Rondinelli James M., Samarth Nitin, Schuller Ivan K., Slavin Andrei N., Stiles Mark D., Tchernyshyov Oleg, Thiaville André, and Zink Barry L., “Interface-induced phenomena in magnetism,” Rev. Mod. Phys 89, 025006 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Gambardella Pietro and Miron Ioan Mihai, “Current-induced spin-orbit torques,” Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 369, 3175–3197 (2011). [DOI] [PubMed] [Google Scholar]
- [3].Manchon A, Železný J, Miron IM, Jungwirth T, Sinova J, Thiaville A, Garello K, and Gambardella P, “Current-induced spin-orbit torques in ferromagnetic and antiferromagnetic systems,” Rev. Mod. Phys 91, 035004 (2019). [Google Scholar]
- [4].Miron Ioan Mihai, Garello Kevin, Gaudin Gilles, Zermatten Pierre-Jean, Costache Marius V., Auffret Stéphane, Bandiera Sébastien, Rodmacq Bernard, Schuhl Alain, and Gambardella Pietro, “Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection,” Nature (London) 476, 189 (2011). [DOI] [PubMed] [Google Scholar]
- [5].Liu Luqiao, Lee OJ, Gudmundsen TJ, Ralph DC, and Buhrman RA, “Current-Induced Switching of Perpendicularly Magnetized Magnetic Layers Using Spin Torque from the Spin Hall Effect,” Phys. Rev. Lett 109, 096602 (2012). [DOI] [PubMed] [Google Scholar]
- [6].Liu Luqiao, Pai Chi-Feng, Li Y, Tseng HW, Ralph DC, and Buhrman RA, “Spin-Torque Switching with the Giant Spin Hall Effect of Tantalum,” Science 336, 555–558 (2012). [DOI] [PubMed] [Google Scholar]
- [7].Yu Guoqiang, Upadhyaya Pramey, Fan Yabin, Alzate Juan G., Jiang Wanjun, Wong Kin L., Takei So, Bender Scott A., Chang Li-Te, Jiang Ying, Lang Murong, Tang Jianshi, Wang Yong, Tserkovnyak Yaroslav, Amiri Pedram Khalili, and Wang Kang L., “Switching of perpendicular magnetization by spin-orbit torques in the absence of external magnetic fields,” Nat. Nanotechnol 9, 548 (2014). [DOI] [PubMed] [Google Scholar]
- [8].Baumgartner Manuel, Garello Kevin, Mendil Johannes, Avci Can Onur, Grimaldi Eva, Murer Christoph, Feng Junxiao, Gabureac Mihai, Stamm Christian, Acremann Yves, Finizio Simone, Wintz Sebastian, Raabe Jörg, and Gambardella Pietro, “Spatially and time-resolved magnetization dynamics driven by spin-orbit torques,” Nature Nanotechnology 12, 980–986 (2017). [DOI] [PubMed] [Google Scholar]
- [9].Miron Ioan Mihai, Moore Thomas, Szambolics Helga, Buda-Prejbeanu Liliana Daniela, Auffret Stéphane, Rodmacq Bernard, Pizzini Stefania, Vogel Jan, Bonfim Marlio, Schuhl Alain, and Gaudin Gilles, “Fast current-induced domain-wall motion controlled by the Rashba effect,” Mat. Mater 10, 419 (2011). [DOI] [PubMed] [Google Scholar]
- [10].Ryu Kwang-Su, Thomas Luc, Yang See-Hun, and Parkin Stuart, “Chiral spin torque at magnetic domain walls,” Nat. Nanotechnol 8, 527 (2013). [DOI] [PubMed] [Google Scholar]
- [11].Emori Satoru, Bauer Uwe, Ahn Sung-Min, Martinez Eduardo, and Beach Geoffrey S. D., “Current-driven dynamics of chiral ferromagnetic domain walls,” Nat. Mater 12, 611 (2013). [DOI] [PubMed] [Google Scholar]
- [12].Martinez Eduardo, Emori Satoru, and Beach Geoffrey S. D., “Current-driven domain wall motion along high perpendicular anisotropy multilayers: The role of the Rashba field, the spin Hall effect, and the Dzyaloshinskii-Moriya interaction,” Appl. Phys. Lett 103, 072406 (2013). [Google Scholar]
- [13].Stiles MD and Zangwill A, “Anatomy of spin-transfer torque,” Phys. Rev. B 66, 014407 (2002). [Google Scholar]
- [14].Ralph DC and Stiles MD, “Spin transfer torques,” Journal of Magnetism and Magnetic Materials 320, 1190 – 1216 (2008). [Google Scholar]
- [15].Manchon A and Zhang S, “Theory of spin torque due to spin-orbit coupling,” Phys. Rev. B 79, 094422 (2009). [Google Scholar]
- [16].Garate Ion and MacDonald AH, “Influence of a transport current on magnetic anisotropy in gyrotropic ferromagnets,” Phys. Rev. B 80, 134403 (2009). [Google Scholar]
- [17].Kim Kyoung-Whan, Seo Soo-Man, Ryu Jisu, Lee Kyung-Jin, and Lee Hyun-Woo, “Magnetization dynamics induced by in-plane currents in ultrathin magnetic nanostructures with Rashba spin-orbit coupling,” Phys. Rev. B 85, 180404(R) (2012). [Google Scholar]
- [18].Haney Paul M., Lee Hyun-Woo, Lee Kyung-Jin, Manchon Aurélien, and Stiles MD, “Current induced torques and interfacial spin-orbit coupling: Semiclassical modeling,” Phys. Rev. B 87, 174411 (2013). [Google Scholar]
- [19].Haney Paul M., Lee Hyun-Woo, Lee Kyung-Jin, Manchon Aurélien, and Stiles MD, “Current-induced torques and interfacial spin-orbit coupling,” Phys. Rev. B 88, 214417 (2013). [Google Scholar]
- [20].Amin VP and Stiles MD, “Spin transport at interfaces with spin-orbit coupling: Formalism,” Phys. Rev. B 94, 104419 (2016). [Google Scholar]
- [21].Amin VP and Stiles MD, “Spin transport at interfaces with spin-orbit coupling: Phenomenology,” Phys. Rev. B 94, 104420 (2016). [Google Scholar]
- [22].Kim Kyoung-Whan, Lee Kyung-Jin, Sinova Jairo, Lee Hyun-Woo, and Stiles MD, “Spin-orbit torques from interfacial spin-orbit coupling for various interfaces,” Phys. Rev. B 96, 104438 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Amin VP, Zemen J, and Stiles MD, “Interface-Generated Spin Currents,” Phys. Rev. Lett 121, 136805 (2018). [DOI] [PubMed] [Google Scholar]
- [24].Rashba E, “Properties of semiconductors with an extremum loop. 1. cyclotron and combinational resonance in a magnetic field perpendicular to the plane of the loop.” Sov. Phys. Solid State 2, 1109–1122 (1960). [Google Scholar]
- [25].Manchon A, Koo HC, Nitta J, Frolov SM, and Duine RA, “New perspectives for Rashba spin-orbit coupling,” Nat. Mater 14, 871 (2015). [DOI] [PubMed] [Google Scholar]
- [26].Bercioux Dario and Lucignano Procolo, “Quantum transport in Rashba spin–orbit materials: a review,” Reports on Progress in Physics 78, 106001 (2015). [DOI] [PubMed] [Google Scholar]
- [27].Amin VP, Li Junwen, Stiles MD, and Haney PM, “Intrinsic spin currents in ferromagnets,” Phys. Rev. B 99, 220405(R) (2019). [Google Scholar]
- [28].Wang Wenrui, Wang Tao, Amin Vivek P., Wang Yang, Radhakrishnan Anil, Davidson Angie, Allen Shane R., Silva TJ, Ohldag Hendrik, Balzar Davor, Zink Barry L., Haney Paul M., Xiao John Q., Cahill David G., Lorenz Virginia O., and Fan Xin, “Anomalous spin-orbit torques in magnetic single-layer films,” Nature Nanotechnology 14, 819–824 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Davidson Angie, Amin Vivek P., Aljuaid Wafa S., Haney Paul M., and Fan Xin, “Perspectives of electrically generated spin currents in ferromagnetic materials,” Physics Letters A 384, 126228 (2020). [Google Scholar]
- [30].Go Dongwook and Lee Hyun-Woo, “Orbital torque: Torque generation by orbital current injection,” Phys. Rev. Research 2, 013177 (2020). [Google Scholar]
- [31].Tanaka T, Kontani H, Naito M, Naito T, Hirashima DS, Yamada K, and Inoue J, “Intrinsic spin Hall effect and orbital Hall effect in 4d and 5d transition metals,” Phys. Rev. B 77, 165117 (2008). [Google Scholar]
- [32].Kontani H, Tanaka T, Hirashima DS, Yamada K, and Inoue J, “Giant Orbital Hall Effect in Transition Metals: Origin of Large Spin and Anomalous Hall Effects,” Phys. Rev. Lett 102, 016601 (2009). [DOI] [PubMed] [Google Scholar]
- [33].Go Dongwook, Jo Daegeun, Kim Changyoung, and Lee Hyun-Woo, “Intrinsic Spin and Orbital Hall Effects from Orbital Texture,” Phys. Rev. Lett 121, 086602 (2018). [DOI] [PubMed] [Google Scholar]
- [34].Jo Daegeun, Go Dongwook, and Lee Hyun-Woo, “Gigantic intrinsic orbital hall effects in weakly spin-orbit coupled metals,” Phys. Rev. B 98, 214405 (2018). [Google Scholar]
- [35].Freimuth Frank, Blügel Stefan, and Mokrousov Yuriy, “Spin-orbit torques in Co/Pt(111) and Mn/W(001) magnetic bilayers from first principles,” Phys. Rev. B 90, 174423 (2014). [Google Scholar]
- [36].Freimuth Frank, Blügel Stefan, and Mokrousov Yuriy, “Direct and inverse spin-orbit torques,” Phys. Rev. B 92, 064415 (2015). [Google Scholar]
- [37].Géranton Guillaume, Freimuth Frank, Blügel Stefan, and Mokrousov Yuriy, “Spin-orbit torques in L10 – FePt/Pt thin films driven by electrical and thermal currents,” Phys. Rev. B 91, 014417 (2015). [Google Scholar]
- [38].Mahfouzi Farzad and Kioussis Nicholas, “First-principles study of the angular dependence of the spin-orbit torque in Pt/Co and Pd/Co bilayers,” Phys. Rev. B 97, 224426 (2018). [Google Scholar]
- [39].Belashchenko KD, Kovalev Alexey A., and Schilfgaarde M. van, “First-principles calculation of spin-orbit torque in a Co/Pt bilayer,” Phys. Rev. Materials 3, 011401 (2019). [Google Scholar]
- [40].Guimarães Filipe S. M., Bouaziz Juba, dos Santos Dias Manuel, and Lounis Samir, “Spin-orbit torques and their associated effective fields from gigahertz to terahertz,” Communications Physics 3, 19 (2020). [Google Scholar]
- [41].Valenzuela SO and Tinkham M, “Direct electronic measurement of the spin Hall effect,” Nature 442, 176–179 (2006). [DOI] [PubMed] [Google Scholar]
- [42].Kimura T, Otani Y, Sato T, Takahashi S, and Maekawa S, “Room-Temperature Reversible Spin Hall Effect,” Phys. Rev. Lett 98, 156601 (2007). [DOI] [PubMed] [Google Scholar]
- [43].Chen Hua, Niu Qian, and MacDonald Allan H., “Spin Hall effects without spin currents in magnetic insulators,” (2018), arXiv:1803.01294. [Google Scholar]
- [44].Park Seung Ryong, Kim Choong H., Yu Jaejun, Han Jung Hoon, and Kim Changyoung, “Orbital-Angular-Momentum Based Origin of Rashba-Type Surface Band Splitting,” Phys. Rev. Lett 107, 156803 (2011). [DOI] [PubMed] [Google Scholar]
- [45].Park Jin-Hong, Kim Choong H., Lee Hyun-Woo, and Han Jung Hoon, “Orbital chirality and rashba interaction in magnetic bands,” Phys. Rev. B 87, 041301(R) (2013). [Google Scholar]
- [46].Go Dongwook, Hanke Jan-Philipp, Buhl Patrick M., Freimuth Frank, Bihlmayer Gustav, Lee Hyun-Woo, Mokrousov Yuriy, and Blügel Stefan, “Toward surface orbitronics: giant orbital magnetism from the orbital rashba effect at the surface of sp-metals,” Scientific Reports 7, 46742 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Salemi Leandro, Berritta Marco, Nandy Ashis K., and Oppeneer Peter M., “Orbitally dominated rashba-edelstein effect in noncentrosymmetric antiferromagnets,” Nature Communications 10, 5381 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Canonico Luis M., Cysne Tarik P., Molina-Sanchez Alejandro, Muniz RB, and Rappoport Tatiana G., “Orbital Hall insulating phase in transition metal dichalcogenide monolayers,” Phys. Rev. B 101, 161409(R) (2020). [Google Scholar]
- [49].Hoffmann M, Weischenberg J, Dupé B, Freimuth F, Ferriani P, Mokrousov Y, and Heinze S, “Topological orbital magnetization and emergent Hall effect of an atomic-scale spin lattice at a surface,” Phys. Rev. B 92, 020401(R) (2015). [Google Scholar]
- [50].Hanke Jan-Philipp, Freimuth Frank, Blügel Stefan, and Mokrousov Yuriy, “Prototypical topological orbital ferromagnet γ-FeMn,” Scientific Reports 7, 41078 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Lux Fabian R., Freimuth Frank, Blügel Stefan, and Mokrousov Yuriy, “Engineering chiral and topological orbital magnetism of domain walls and skyrmions,” Communications Physics 1, 60 (2018). [Google Scholar]
- [52].dos Santos Dias Manuel, Bouaziz Juba, Bouhas-soune Mohammed, Blügel Stefan, and Lounis Samir, “Chirality-driven orbital magnetic moments as a new probe for topological magnetic structures,” Nature Communications 7, 13613 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Grytsiuk S, Hanke J-P, Hoffmann M, Bouaziz J, Gomonay O, Bihlmayer G, Lounis S, Mokrousov Y, and Blügel S, “Topological-chiral magnetic interactions driven by emergent orbital magnetism,” Nature Communications 11, 511 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Li chuan Zhang Fabian R. Lux, Hanke Jan-Philipp, Buhl Patrick M., Grytsiuk Sergii, Stefan Blügel, and Yuriy Mokrousov, “Orbital Nernst Effect of Magnons,” (2019), arXiv:1910.03317. [Google Scholar]
- [55].Kipp J, Samanta K, Lux FR, Merte M, Hanke JP, Redies M, Freimuth F, Blügel S, Ležaić M, and Mokrousov Y, “The chiral hall effect in canted ferromagnets and antiferromagnets,” (2020), arXiv:2007.01529. [Google Scholar]
- [56].Haney Paul M. and Stiles MD, “Current-Induced Torques in the Presence of Spin-Orbit Coupling,” Phys. Rev. Lett 105, 126602 (2010). [DOI] [PubMed] [Google Scholar]
- [57].Hanke J-P, Freimuth F, Nandy AK, Zhang H, Blügel S, and Mokrousov Y, “Role of Berry phase theory for describing orbital magnetism: From magnetic heterostructures to topological orbital ferromagnets,” Phys. Rev. B 94, 121114(R) (2016). [Google Scholar]
- [58].Thonhauser T, Ceresoli Davide, Vanderbilt David, and Resta R, “Orbital Magnetization in Periodic Insulators,” Phys. Rev. Lett 95, 137205 (2005). [DOI] [PubMed] [Google Scholar]
- [59].Ceresoli Davide, Thonhauser T, Vanderbilt David, and Resta R, “Orbital magnetization in crystalline solids: Multiband insulators, Chern insulators, and metals,” Phys. Rev. B 74, 024408 (2006). [Google Scholar]
- [60].Shi Junren, Vignale G, Xiao Di, and Niu Qian, “Quantum Theory of Orbital Magnetization and Its Generalization to Interacting Systems,” Phys. Rev. Lett 99, 197202 (2007). [DOI] [PubMed] [Google Scholar]
- [61].Mathon J, “Phenomenological theory of giant magnetoresistance,” in Spin Electronics, edited by Ziese Michael and Thornton Martin J. (Springer Berlin Heidelberg, Berlin, Heidelberg, 2001) pp. 71–88. [Google Scholar]
- [62].Mahan Gerald D., “dc conductivities,” in Many-Particle Physics (Springer US, Boston, MA, 2000) pp. 499–577. [Google Scholar]
- [63].Ghosh S and Manchon A, “Spin-orbit torque in a three-dimensional topological insulator–ferromagnet heterostructure: Crossover between bulk and surface transport,” Phys. Rev. B 97, 134402 (2018). [Google Scholar]
- [64].Manchon G, Ghosh S, Barreteau C, and Manchon A, “Semi-realistic tight-binding model for spin-orbit torques,” (2020), arXiv:2002.05533. [Google Scholar]
- [65].Hoffmann Markus, Zimmermann Bernd, Müller Gideon P., Schürhoff Daniel, Kiselev Nikolai S., Melcher Christof, and Blügel Stefan, “Antiskyrmions stabilized at interfaces by anisotropic Dzyaloshinskii-Moriya interactions,” Nature Communications 8, 308 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Wang Lei, Wesselink RJH, Liu Yi, Yuan Zhe, Xia Ke, and Kelly Paul J., “Giant Room Temperature Interface Spin Hall and Inverse Spin Hall Effects,” Phys. Rev. Lett 116, 196602 (2016). [DOI] [PubMed] [Google Scholar]
- [67].Kim Junyeon, Sinha Jaivardhan, Hayashi Masamitsu, Yamanouchi Michihiko, Fukami Shunsuke, Suzuki Tetsuhiro, Mitani Seiji, and Ohno Hideo, “Layer thickness dependence of the current-induced effective field vector in Ta/CoFeB/MgO,” Nature Materials 12, 240–245 (2013). [DOI] [PubMed] [Google Scholar]
- [68].Ramaswamy Rajagopalan, Qiu Xuepeng, Dutta Tanmay, Pollard Shawn David, and Yang Hyunsoo, “Hf thickness dependence of spin-orbit torques in Hf/CoFeB/MgO heterostructures,” Applied Physics Letters 108, 202406 (2016). [Google Scholar]
- [69].Zheng ZC, Guo QX, Jo D, Go D, Wang LH, Chen HC, Yin W, Wang XM, Yu GH, He W, Lee H-W, Teng J, and Zhu T, “Magnetization switching driven by current-induced torque from weakly spin-orbit coupled Zr,” Phys. Rev. Research 2, 013127 (2020). [Google Scholar]
- [70].Guo GY, Murakami S, Chen T-W, and Nagaosa N, “Intrinsic Spin Hall Effect in Platinum: First-Principles Calculations,” Phys. Rev. Lett 100, 096401 (2008). [DOI] [PubMed] [Google Scholar]
- [71].Mahfouzi Farzad, Mishra Rahul, Chang Po-Hao, Yang Hyunsoo, and Kioussis Nicholas, “Microscopic origin of spin-orbit torque in ferromagnetic heterostructures: A first-principles approach,” Phys. Rev. B 101, 060405(R) (2020). [Google Scholar]
- [72].Fan Xin, Celik Halise, Wu Jun, Ni Chaoying, Lee Kyung-Jin, Lorenz Virginia O., and Xiao John Q., “Quantifying interface and bulk contributions to spin-orbit torque in magnetic bilayers,” Nature Communications 5, 3042 (2014). [DOI] [PubMed] [Google Scholar]
- [73].Hayashi Hiroki, Musha Akira, Sakimura Hiroto, and Ando Kazuya, “Spin-orbit torques originating from bulk and interface in Pt-based structures,” (2020), arXiv:2003.07271. [Google Scholar]
- [74].Zhu Lijun, Ralph DC, and Buhrman RA, “Spin-Orbit Torques in Heavy-Metal–Ferromagnet Bilayers with Varying Strengths of Interfacial Spin-Orbit Coupling,” Phys. Rev. Lett 122, 077201 (2019). [DOI] [PubMed] [Google Scholar]
- [75].Tokura Y and Nagaosa N, “Orbital physics in transition-metal oxides,” Science 288, 462–468 (2000). [DOI] [PubMed] [Google Scholar]
- [76].Mochizuki Masahito and Imada Masatoshi, “Orbital physics in the perovskite ti oxides,” New Journal of Physics 6, 154–154 (2004). [Google Scholar]
- [77].Oleś Andrzej M, “Fingerprints of spin–orbital entanglement in transition metal oxides,” Journal of Physics: Condensed Matter 24, 313201 (2012). [DOI] [PubMed] [Google Scholar]
- [78].Nagaosa Naoto, Sinova Jairo, Onoda Shigeki, MacDonald AH, and Ong NP, “Anomalous Hall effect,” Rev. Mod. Phys 82, 1539–1592 (2010). [Google Scholar]
- [79].Sinova Jairo, Valenzuela Sergio O., Wunderlich J, Back CH, and Jungwirth T, “Spin hall effects,” Rev. Mod. Phys 87, 1213–1260 (2015). [Google Scholar]
- [80].Wimmer E, Krakauer H, Weinert M, and Freeman AJ, “Full-potential self-consistent linearized-augmented-plane-wave method for calculating the electronic structure of molecules and surfaces: O2 molecule,” Phys. Rev. B 24, 864–875 (1981). [Google Scholar]
- [81]. https://www.flapw.de.
- [82].Perdew John P., Burke Kieron, and Ernzerhof Matthias, “Generalized Gradient Approximation Made Simple,” Phys. Rev. Lett 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- [83].Pizzi Giovanni, Vitale Valerio, Arita Ryotaro, Stefan Blügel Frank Freimuth, Guillaume Géranton Marco Gibertini, Gresch Dominik, Johnson Charles, Koretsune Takashi, Julen Ibañez-Azpiroz Hyungjun Lee, Lihm Jae-Mo, Marchand Daniel, Marrazzo Antimo, Mokrousov Yuriy, Mustafa Jamal I, Nohara Yoshiro, Nomura Yusuke, Paulatto Lorenzo, Samuel Poncé Thomas Ponweiser, Qiao Junfeng, Thöle Florian, Tsirkin Stepan S, Wierzbowska Małgorzata, Marzari Nicola, Vanderbilt David, Souza Ivo, Mostofi Arash A, and Yates Jonathan R, “Wannier90 as a community code: new features and applications,” Journal of Physics: Condensed Matter 32, 165902 (2020). [DOI] [PubMed] [Google Scholar]


