Effect of heterotopic ossification after bryan-cervical disc arthroplasty on adjacent level range of motion: A finite element study

Abstract

Background

Quantitative bone re-modelling theories suggest that bones adapt to mechanical loading conditions. Follow-up studies have shown that total disc replacement (TDR) modifies stress patterns in the bones, leading to heterotopic ossification (HO). Although there are a few studies on HO using finite element models (FEM), its effect on the adjacent levels and change in range of motion (ROM) have not been adequately investigated. This study interfaces the HO using bone re-modelling algorithm with a finite element solution and investigates the subsequent changes in segmental ROM.

Methods

A FEM of the human cervical spine (C3–C7) was developed for this study, with material properties obtained from literature. The motion of the segments in the sagittal, frontal and transverse planes under combined loading conditions of 1 Nm moment and 73.6 N compression were validated against experimental corridors. The natural disc between the C5–C6 segment was replaced with the Bryan artificial cervical disc, and changes in sagittal ROM were compared before and after HO. The process of HO was simulated using a bone remodelling algorithm using strain energy density (SED) as the mechanical stimuli.

Results and conclusion

Our study demonstrates the feasibility of using SED calculations from the flexion-extension loading conditions for prediction of HO after ADR. The current findings suggest that the nature of trabecular stresses, and the subsequent rate and location of HO formation could differ based on the geometric design and nature of constraint for different artificial discs. The Bryan disc significantly reduced ROM at the implanted level in flexion. However, in extension, ROM increased at the implanted level and decreased slightly at the adjacent levels. After HO, ROM drastically reduced at the implanted level in both extension and flexion, and showed a minor increase in the adjacent levels, indicating that biomechanical behavior of high-grade HO is similar to a fused segment, thereby reducing the intended and initial motion preservation.

1. Introduction

Biomechanical studies have shown that anterior cervical discectomy and fusion (ACDF) might be responsible for enhancing adjacent level degeneration due to increased internal stress responses.¹ Cervical total disc replacement (TDR) is generally considered to be a better surgical solution to treat cervical disc disease over ACDF.² TDR is claimed to provide better clinical outcomes because of theoretical advantages such as motion preservation, restoration of segmental lordosis and prevention of adjacent level degeneration.³ While TDR provides acceptable long-term results, occurrence of abnormal bone growth or heterotopic ossification (HO) have been frequently observed in patients in follow-up studies.⁴ Despite its rarity, there have been cases where Bryan disc-assisted cervical arthroplasty has caused excessive fusion due to HO formation.⁵ A review and a meta-analysis study found 38% incidences of HO within two days of cervical TDR and up to 54% in a ten-year follow up. The occurrence of HO limits the ROM at the index segment and affects the clinical outcomes of the cervical TDR.⁶

HO is an adaptive bone-remodelling process where bone growth occurs outside the skeletal system. It is defined as ectopic lamellar bone formation in soft tissues and is often recognised as a complication after major orthopaedic surgeries.⁷ Cases of HO have been reported in multiple regions of the body including hip, knees and spinal joints due to musculoskeletal trauma and spinal cord injury.⁸ Several factors such as age, sex, bone dust and stress at the interface of the bone and implant are thought to contribute to HO formation. Studies assert that increase in ROM of the implanted segment and over-correction of segmental height during surgery is another factor.⁹ While early mathematical models using ‘Wolff’s Law’ have attempted to quantitatively describe the bone-remodelling process based on mechanical stimuli,10, 28 the exact nature and cause of HO largely remains to be understood.

The bone adaptation process based on strain energy density (SED) has been the fundamental quantitative basis behind multiple computer simulation studies.^11,12 The regions of bone formation and resorption predicted by these simulations are in-line with anatomical observations.^13,14 Ganbat et al. (2016) was the first to use a 3D FE model to study the formation of HO after TDR in the C5–C6 motion segment for different physiological loading conditions.⁸ Park and Jin (2019) investigated the biomechanical influences of extragraft bone formation and bridging after ACDF in the motion segment.¹⁵ However, the impact of geometric design on high grade HO at the implanted level and subsequent adjacent level after TDR has not been adequately studied. The objective of this study is to i) illustrate the feasibility of using strain energy density calculations with FE analysis for predicting HO through the sagittal plane loading modes ii) investigate the formation of HO with respect to volume, location, and effect on ROM in the adjacent levels after Bryan-assisted cervical disc arthroplasty.

2. Methods

A previously validated 3D osteoligamentous model of the human cervical spine was used for this study.16, 17, 18 The model consists of four segments (C3–C7) meshed with hexahedral elements, and the material properties for all the components were obtained from existing literature. The model contains both trabecular bone and cortical bone, apart from the intervertebral disc and soft tissues. The major ligaments were modelled as tension-only truss elements (i.e., anterior longitudinal ligament (ALL), posterior longitudinal ligament (PLL), capsular ligaments (CL), ligamentum flavum (LF), and interspinous ligaments (ISL). The intervertebral disc comprised of two components: annulus fibrosus and the nucleus pulposus. Linear elastic properties were used to characterize the disc properties. The annulus ground and fibre definitions that make up the annulus were modelled as detailed in a recent finite element study.¹⁹ The material properties [Table 1] used in the study and their references have been given in Table 1.

Table 1.

Material properties and their references.

Component	Element Type	Constitutive Model	Properties (Elastic Modulus in Mpa)	Reference
Cortical Bone	Hexahedral solid	Linear Elastic	E = 10,000, μ = 0.3	Song (2014)20
Trabecular Bone	Hexahedral solid	Linear Elastic	E = 100, μ = 0.3	Song (2014)20
Annulus Ground	Hexahedral solid	Linear Elastic	E = 2.5, μ = 0.45	Kleinburger (1993)21
Nucleus Pulposus	Hexahedral solid	Linear Elastic	E = 1, μ = 0.49	Zhang (2006)22
Endplate	Quadrilateral shell	Linear Elastic	E = 500, μ = 0.4	Song (2014)20
Facet Cartilage	Quadrilateral shell	Linear Elastic	E = 10, μ = 0.3	Yamada (1970)23
ALL	Truss	Linear Elastic	E = 30, μ = 0.3	Zhang (2006)22
PLL	Truss	Linear Elastic	E = 20, μ = 0.3	Zhang (2006)22
CL	Truss	Linear Elastic	E = 10, μ = 0.3	Ganbat (2016)8
ISL	Truss	Linear Elastic	E = 10, μ = 0.3	Zhang (2006)22
LF	Truss	Linear Elastic	E = 10, μ = 0.3	Zhang (2006)22

The number of layers in the posterior and anterior region were four layers (total in 8) and eight layers (total in 16) respectively. A bilateral gap at the uncovertebral clefts was formed due to the discontinuous ring of fibres. There was a total of 60,670 elements in the model, and the number of elements for the annulus fibres were 2060, 1970, 2060, 2130 from C3–C4 to C6–C7 respectively. The fibres were defined using shell elements with directional fibres embedded in the ground substance. The fibres in the anterior annulus region were defined in a crisscross manner, while fibres in the posterior region were defined in the vertical direction. The nucleus pulposus was modelled to be almost incompressible in its behavior, to simulate its fluid-like nature.

An external moment of 1.0 Nm and a compressive load of 73.6 N was applied at the superior endplate of C3 vertebra.^8,24 The moment was applied in the sagittal plane, and the ROM in flex-extension was validated against other finite element models and experimental corridors.^19,22,25 ABAQUS (Simulia, Providence, RI, USA) software was used to conduct the analysis and a Python code was used to automate the process of calculating the ROM based on nodal data extracted from the workspace. The deformed and undeformed coordinates were used to visualize physiological planes and the angle between them was calculated.

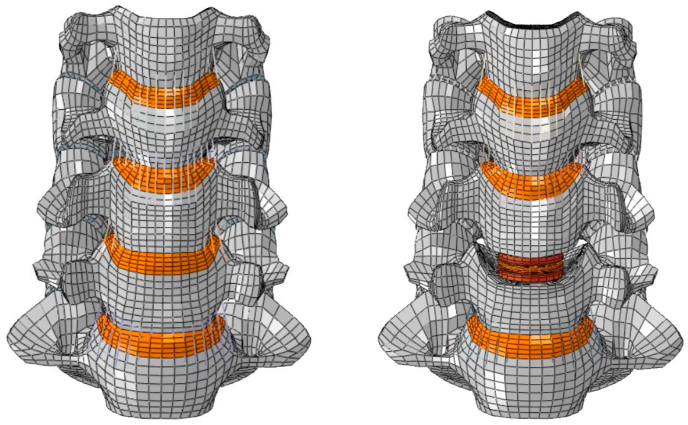
The intervertebral disc at C5–C6 was removed and Bryan (Medtronic Sofamor Danek, Memphis, TN, USA) cervical disc was inserted to simulate TDR. Similar to surgical discectomy, ALL, PLL and the endplates were removed at the implanted level. The Bryan disc model consisted of upper and lower titanium endplates connected by a polyurethane membrane containing a saline-lubricated polyurethane core.¹⁹ A frictionless surface-to-surface contact was assigned between the disc endplate and inner core, and tied contact was used to define the interaction between the bone-implant interface. The intact spine FEM and the ADR model have been shown in Fig. 1.

Fig. 1.

FE models of Intact and Bryan-ADR at C5–C6.

The grade of HO formation is classified based on the degree of severity and its location, and it may occur along both the anterior and posterior edges of the implanted vertebra.²⁵ Potential regions of HO were thus defined completely around the Bryan artificial disc to ensure that any grade of HO formation could be adequately captured. Based on previous studies, it is assumed that the density and Young’s modulus of HO bone is in-between the trabecular and cortical bone.⁸ The initial bone density of the HO region is taken to be 0.73 g/cm³. Some earlier studies have also used the cortical bone density for the HO region, implying that HO bone is cortical bone.^11,12,27 The quantitative relationship between Young’s modulus and the density of bone is given by E = 3790ρ³.²⁷ By substituting the initial density of 0.73 g/cm3 to this relationship, we get the Young’s modulus of HO bone to be 1474 MPa. Poisson’s ratio was set to 0.3 for both the cortical and cancellous bones.

SED is considered to be the stimulating factor for the bone remodelling algorithm that was integrated with the FE model.⁸ A Fortran code was successfully compiled and linked with ABAQUS to execute the iterative procedure. The change in bone density with respect to time is given as a function of the bone resorption rate coefficient B_r, bone formation rate coefficient B_f, SED value S, homeostatic SED value K and threshold value of the lazy zone s as follows:

$$\frac{d\rho }{dt}=\{\begin{array}{c}{B}_r\left(S-K\left(1+s\right)\right),S\ge K\left(1+s\right)\\ 0,K\left(1-s\right)\le S\le K\left(1+s\right)\\ B_f\left(S-K\left(1-s\right)\right),S\le K\left(1-s\right)\end{array}$$

The lazy zone is defined to be a region where no change in bone density occurs, for SED values falling between the limits and . The initial values for the parameters were taken from earlier studies where HO was studied on the cervical spine after TDR with Prodisc-C.⁸

The time unit is taken to be for days in a month, SED value J/g, threshold level of the lazy zone , the remodelling rate coefficient (g/cm³)²/(MPa × time unit), and . The SED value K is chosen to approximate the cyclic loading conditions under which HO is formed.

The iterative process calculates the SED at each step and automatically identifies if elements in the potential HO zone are involved in formation or resorption. The iterative procedure was repeated 20 times to allow adequate time before bone formation, as clinical studies indicate that HO occurs months or even years after the procedure. Bone formation under sagittal loading conditions were studied, and the ROM was compared before and after HO. The volume of HO bone formed was also measured.

3. Results and discussions

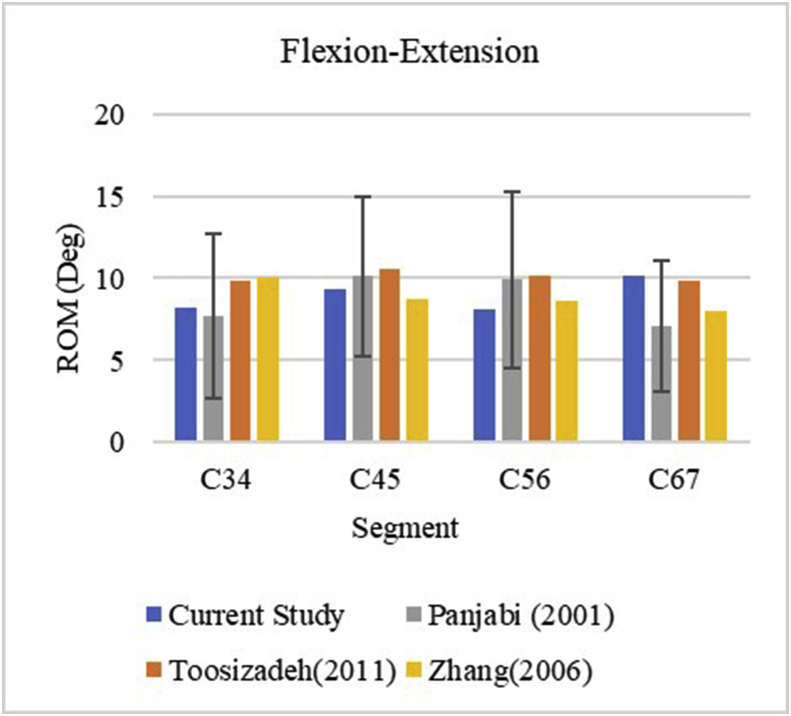
The motion of the intact cervical spine was validated against an experimental study, as well as with other FE models.^22,24,25 The comparisons are plotted below in Fig. 1. ROM for all the motion segments fell within experimental corridors in flexion-extension. The C5–C6 segment appeared to be stiffer compared to other studies, but the ROM was well within the corridor, as shown in Fig. 2. The intact model was considered validated at this point and was further used to simulate Bryan-assisted TDR and HO formation.

Fig. 2.

ROM corridors for flex-extension.

There was impaired motion at the implanted level in flexion, but increased ROM at the C3–C4 and C4–C5 levels. In extension, ROM was decreased at all levels but increased at the implanted level. This trend agrees with a recent FE study on artificial discs that compared the ROM of Bryan disc with the intact spine.¹⁹ This hypermobility observed in extension after cervical disc replacement has been an object of study, and may lead to degeneration of adjacent levels.⁹ The changes in motion at the implanted and index levels may change the alignment of the spine, leading to a change in the directional stresses along the artificial disc. This induces bone formation according to various bone remodelling theories, though they have to be studied further.^13,14

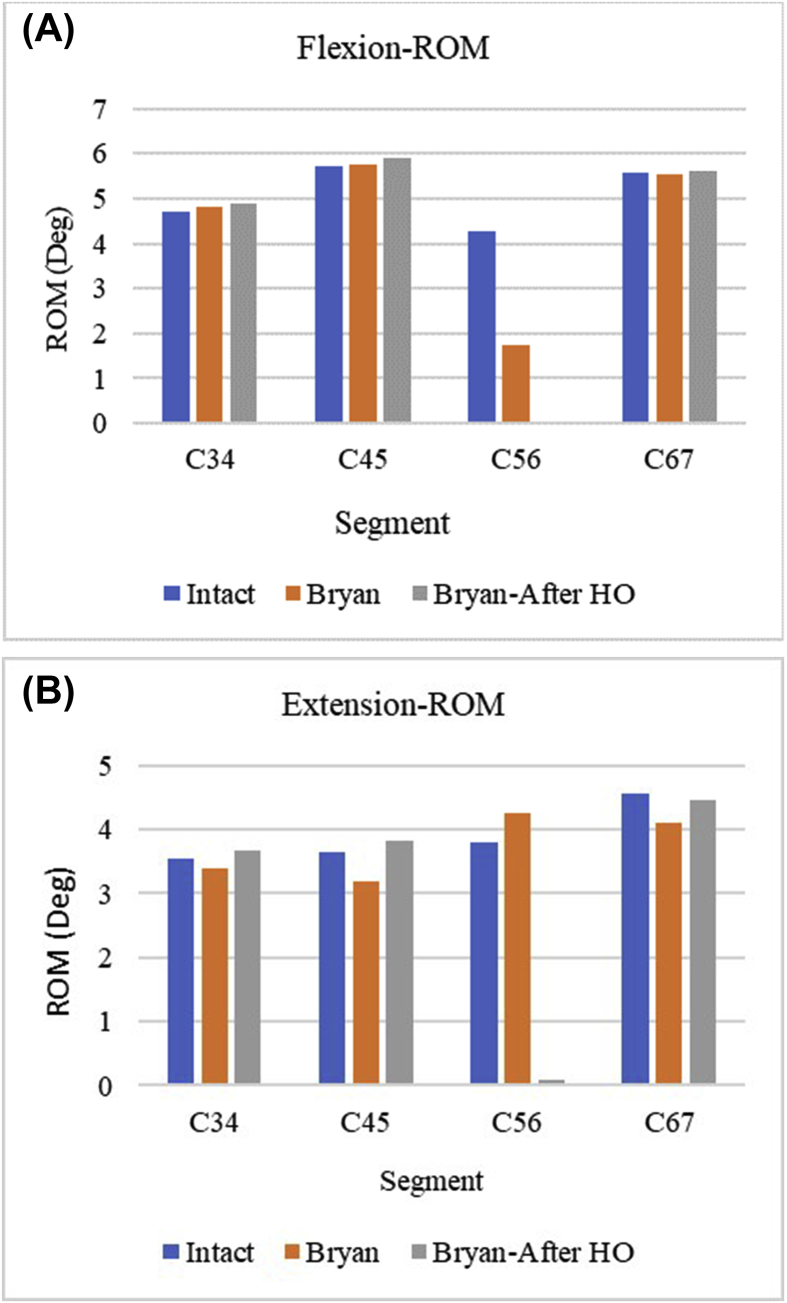
For the same loading conditions, ROM was compared with the intact spine before and after HO formation. There was very minimal motion at the implanted level after HO, and ROM showed significant increase at the adjacent levels in both flexion and extension as shown in Fig. 3. This trend is generally observed in ACDF, indicating that the effects of excessive HO formation are similar to fusion. This observation is supported by clinical studies where it is shown that the advantages of cervical disc replacement over fusion is potentially lost after 1 year of surgery.²⁶

Fig. 3.

ROM comparison before and after HO.

The increase in adjacent level ROM after HO in flexion was found to be 2.2%, 2.3% and 1.2% for the C3–C4, C4–C5 and C6–C7 levels respectively. The behavior at the implanted level was identical to that observed in fusion in both flexion and extension. Extension exhibited higher percentage increase in adjacent level ROM than flexion. There was an increase of 8.5%, 19.9% and 8.2% at the C3–C4, C4–C5 and C6–C7 levels respectively.

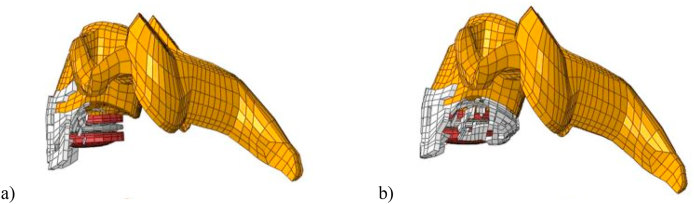
The volume of HO bone was also measured after the analysis. Extension displayed a markedly higher amount of HO when compared to flexion, volume of bone being 428.35 mm³ and 334.94 mm³ respectively. The location of the ossification along the edges of the vertebrae and its obstructive growth over the disc suggests that this is Grade 4 HO as shown in Fig. 4.

Fig. 4.

Regions of HO in a) Flexion and b) Extension shown in white.

A similar study conducted on the Prodisc-C showed a higher volume of HO formation than what is obtained in our study.⁸ This could be due to the application of a lower load, which in turn decreases the stress values observed in the trabecular bone. Another key difference is the higher number of motion segments included in this study, which results in decreased trabecular stresses due to distribution of load across the vertebrae. While the difference in disc geometries will likely play a role in the nature of stresses, the exact effect of this cannot be ascertained without further studies comparing the discs under similar loading parameters.

A clinical study conducted on 170 patients found that patients with Bryan arthroplasty had the least percentage of HO formation after a mean follow-up duration of 19.9 months, but it was also the only disc to report Grade 4 HO.²⁹ The Mobi-C and ProDisc-C reported significantly higher percentage of patients with HO, which could possibly be linked to their difference in design.

Researchers have compared the biomechanical behavior of different artificial discs and their effect on the range of motion, intradiscal pressure and facet force at the implanted and adjacent levels.¹⁹ The Bryan disc is an unconstrained one-piece design, and it has been concluded that it behaves differently to other discs that are semi-constrained or multi-piece with respect to the range of motion and intradiscal pressure. Therefore, it is naturally expected that other artificial discs induce varying stress patterns in the trabecular bone, leading to dissimilar rates of HO formation and volume of new bone formed. The various rate modelling constants and threshold values used in the bone-remodelling algorithm can sufficiently compensate for alternative designs such as single piece or multi-piece build, and an optimisation study to obtain clinically accurate results is a study for the future.

The current formulations of HO account for biomechanical factors such as stress and SED, however other factors may also be responsible for its causation. Although the current study has compared the ROM before and after HO, this is usually case-specific in patients. Clinical studies have shown that some patients do not exhibit signs of HO at all, while some patients display Grade 1or Grade 2 HO after the same follow-up period. The various rate constants used to model the phenomena can be suitably adjusted to simulate any of the different grades of HO. The unit of time can also be suitably adjusted to accommodate different follow-up durations.

4. Conclusions

Finite element models provide multiple advantages in areas of study where the possibilities of in-vivo tests are limited. They are also invaluable in obtaining datasets like stress and strain which are not directly obtainable via X-rays. Despite these advantages, the use of finite element models to study and understand HO of the cervical spine is still relatively new. Our study shows that integrating SED calculations with FE analysis can be useful for prediction of HO after ADR using the flexion-extension, sagittal plane loading modes.

This study also extends the possibilities for studying HO in other clinical cases such as bi-level TDR surgeries. As more and more clinical and biomechanical factors influencing HO come to light, appropriate modifications could be made to the underlying assumptions in the algorithm. More finite element studies into the nature of HO, and the likelihood of different prostheses reducing or increasing its possibility should be conducted to improve surgical outcomes in the long run. The formation of HO may negate the primary purpose of motion preservation of the TDR at the index level, and also affect the adjacent level(s) under physiological loadings. The current findings suggest that the nature of trabecular stresses with the subsequent rate and location of HO formation could differ based on the geometric design and nature of constraint for different artificial discs The present study mainly focused on the Bryan artificial disc, conducting similar finite element studies on other artificial discs in the future may shed some light on the impact of constrained, semi-constrained or unconstrained design on the rate and nature of HO formation.

Declaration of competing interest

The authors do not have any conflict of interest.