Climate control on terrestrial biospheric carbon turnover

Significance

Terrestrial organic-carbon reservoirs (vegetation, soils) currently consume more than a third of anthropogenic carbon emitted to the atmosphere, but the response of this “terrestrial sink” to future climate change is widely debated. Rivers export organic carbon sourced over their watersheds, offering an opportunity to assess controls on land carbon cycling on broad spatial scales. Using radiocarbon ages of biomolecular tracer compounds exported by rivers, we show that temperature and precipitation exert primary controls on biospheric-carbon turnover within river basins. These findings reveal large-scale climate control on soil carbon stocks, and they provide a framework to quantify responses of terrestrial organic-carbon reservoirs to past and future change.

Abstract

Terrestrial vegetation and soils hold three times more carbon than the atmosphere. Much debate concerns how anthropogenic activity will perturb these surface reservoirs, potentially exacerbating ongoing changes to the climate system. Uncertainties specifically persist in extrapolating point-source observations to ecosystem-scale budgets and fluxes, which require consideration of vertical and lateral processes on multiple temporal and spatial scales. To explore controls on organic carbon (OC) turnover at the river basin scale, we present radiocarbon (¹⁴C) ages on two groups of molecular tracers of plant-derived carbon—leaf-wax lipids and lignin phenols—from a globally distributed suite of rivers. We find significant negative relationships between the ¹⁴C age of these biomarkers and mean annual temperature and precipitation. Moreover, riverine biospheric-carbon ages scale proportionally with basin-wide soil carbon turnover times and soil ¹⁴C ages, implicating OC cycling within soils as a primary control on exported biomarker ages and revealing a broad distribution of soil OC reactivities. The ubiquitous occurrence of a long-lived soil OC pool suggests soil OC is globally vulnerable to perturbations by future temperature and precipitation increase. Scaling of riverine biospheric-carbon ages with soil OC turnover shows the former can constrain the sensitivity of carbon dynamics to environmental controls on broad spatial scales. Extracting this information from fluvially dominated sedimentary sequences may inform past variations in soil OC turnover in response to anthropogenic and/or climate perturbations. In turn, monitoring riverine OC composition may help detect future climate-change–induced perturbations of soil OC turnover and stocks.

Terrestrial biospheric carbon residing in vegetation and soils may moderate or exacerbate ongoing buildup of atmospheric greenhouse gases on timescales that are of direct relevance to humankind (1). Much current debate surrounds the response and potential contributions of terrestrial ecosystems to climate change, with large uncertainties concerning the magnitude—and even the sign—of change in response to different environmental forcing factors such as temperature and hydrology (2, 3). Because of their large organic carbon (OC) stocks and potential to stabilize carbon on a range of timescales, soils are thought to regulate overall terrestrial ecosystem carbon storage (4, 5). Globally, soil carbon turnover time (τ_soil) (i.e., the ratio of soil carbon stock to input flux) is estimated via remote sensing approaches (4, 5) and Earth-system models (3) that are calibrated using numerous observational and experimental studies investigating controls on soil OC turnover in a range of ecosystems and soil types (6, 7). However, findings from such studies are often relevant only to a specific experiment, plot, or environment, thus hindering extrapolation and regional validation of remote sensing and model products (8, 9).

One major reason for this limitation is our lack of constraints regarding the importance of erosion and lateral transport, despite a growing realization that these processes are pervasive on diverse landscapes (10) and link terrestrial and aquatic components of the carbon cycle (11). Investigations of lateral transport of terrestrial biospheric carbon have thus far focused on small spatial scales (e.g., hillslopes), which do not fully encompass heterogeneous landscape mosaics (10, 12, 13) and cannot be readily extrapolated to assess processes relevant at the ecosystem or biome scale. In particular, there is a paucity of information on how carbon turnover observed at individual plots relates to landscape- and basin-scale biospheric carbon dynamics. Depending on the mode of carbon turnover, mobilization, and transport, lateral processes can either export freshly synthesized carbon (e.g., via surface runoff) or exhume carbon stocks sequestered in deeper soils and wetlands (14, 15); the relative importance of these processes likely exerts a strong influence on carbon stocks and dynamics but is currently underrepresented in large-scale models. Given that climate change, as well as direct anthropogenic perturbations (e.g., land-use practices), may potentially modify and amplify such carbon fluxes and trajectories (3), establishing the underlying drivers and pacing of carbon cycling on appropriate spatial and temporal scales is of key importance.

Insight into the factors that control ecosystem-scale carbon turnover times can be determined using the ¹⁴C activity (reported as age in ¹⁴C years) of OC laterally exported by rivers. Rivers integrate processes within their watersheds, thus enabling investigation of biogeochemical processes at the basin scale, facilitating observational extrapolation, and linking terrestrial and marine realms. Fluvial systems form the major conduit that transfers OC from the continents to the ocean, exporting a combined ∼4.5 × 10¹⁴ g of dissolved organic carbon (DOC) and particulate organic carbon (POC) annually (16, 17). The majority of this OC exported by rivers is in dissolved form, but much of this is rapidly mineralized (16). Although POC is also subject to extensive degradation (16) and riverine POC export is estimated to account for less than 0.2% of net primary production (NPP, 17), the export of terrestrial biospheric POC and its subsequent burial in marine sediments is important in modulating atmospheric CO₂ on a range of timescales (18) and provides some of the most continuous and long-term records of past climate and carbon-cycle dynamics on the continents.

Prior studies have examined the nature and magnitude of carbon transfer via rivers to the ocean (ref. 17 and references therein) and have shown that soil OC represents a dominant component of the terrestrial POC exported by many fluvial systems (19, 20). Strong contrasts in POC yield (i.e., carbon flux per unit catchment area) and composition relate to geomorphic and climatic factors influencing mobilization and retention of OC within drainage basins, as well as the proportions and fluxes of biospheric versus rock-derived (“petrogenic”) carbon inputs (14, 21). Bulk OC radiocarbon measurements in both particulate and dissolved phases reveal a wide variety of ¹⁴C ages (22); however, interpretations in terms of biospheric-carbon dynamics are confounded by diverse OC contributions (e.g., petrogenic OC; ref. 17 and references therein) and secondary overprinting (within-river autotrophy and heterotrophy) (22). Moreover, for most modern river systems, anthropogenic activities influence ¹⁴C ages through the introduction of organic contaminants that may be either relatively modern (e.g., domestic sewage) or fossil (e.g., petroleum or petrochemical contamination) in age (23).

These interferences can be obviated by determining ages of organic compounds unique to vascular land-plant biomass (24). To explore controls on the age of terrestrial biospheric carbon exported from river basins, here we compile previously reported (n = 95) and report additional (n = 28) ¹⁴C age measurements of source-specific “biomarker” tracer compounds measured on 36 fluvial systems representing diverse watersheds and collectively accounting for ∼42, 29, and 20% of the global riverine water, sediment, and POC discharge, respectively (Fig. 1 and SI Appendix, Fig. S1 and Tables S1 and S2) (17). We focus on two well-established classes of terrestrial higher plant biomarkers—plant-wax lipids (25) and lignin-derived phenols (26). Because of their hydrophobic nature, plant waxes reside in the particulate phase—particularly via association with mineral surfaces (27)—and persist in soils and downstream environments (24). The abundances, distributions, and stable isotopic compositions (¹³C/¹²C, reported as δ¹³C) of these compounds preserved in sedimentary and soil sequences carry information on past vegetation inputs, plant productivity, and environmental conditions (24). We specifically analyze n-alkanoic acids (“fatty” acids [FAs]) since n-alkanes can be influenced by contributions from bedrock- or fossil-fuel–derived sources that impact corresponding ¹⁴C ages (19). Lignin imparts structural support for the plant; phenolic monomers liberated by chemical hydrolysis of this biopolymer and its corresponding residues in soils and sediments carry information on plant and tissue type and extent of degradation (ref. 26 and references therein). Assessments of lignin stability and turnover in soils vary (7); however, like plant waxes, lignin signatures are present in fluvial sediments and deposits (15). We therefore treat measured ¹⁴C ages of these two biomarker classes as independent yet complementary estimates of the mean age of fluvially exported biospheric OC.

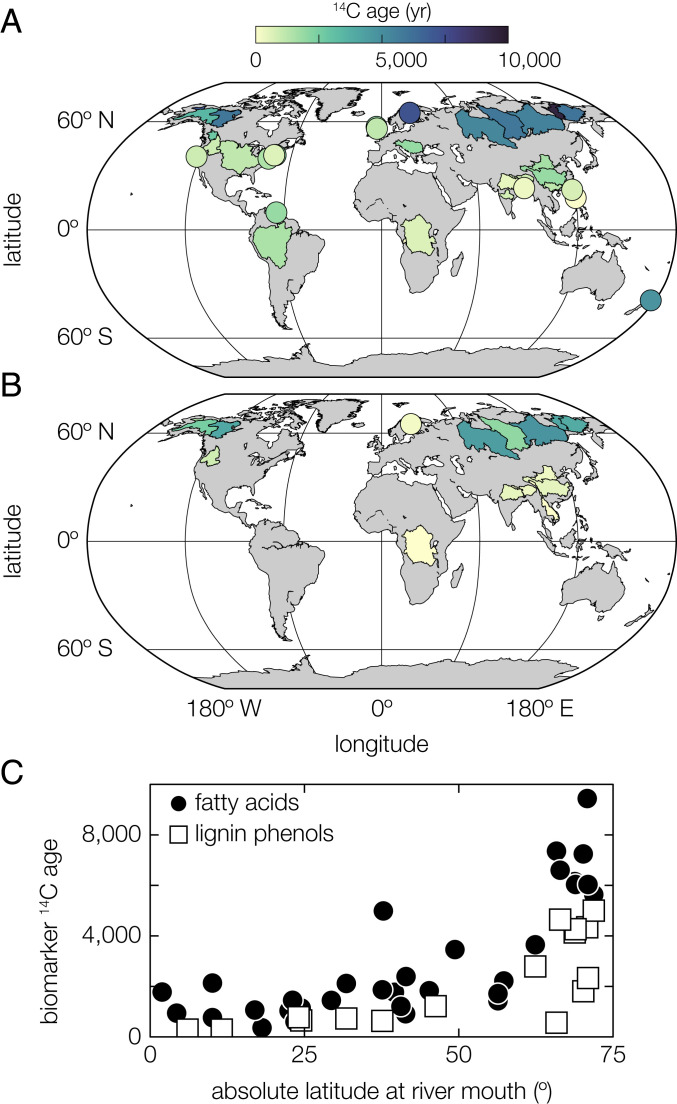
Fig. 1.

Riverine biomarker ¹⁴C ages. The catchment areas of all rivers analyzed in this study are color coded by (A) plant-wax fatty-acid and (B) lignin-phenol ¹⁴C ages (SI Appendix, Table S1). Rivers with catchment areas smaller than 30,000 km² are shown as colored circles for clarity. The legend above (A) applies to both panels. (C) Biomarker ages as a function of the absolute latitude at the river mouth, showing both fatty acids (black circles) and lignin phenols (white squares).

Results and Discussion

Relationships with Basin Properties.

We examined ¹⁴C and, in selected cases, δ¹³C variations in bulk OC, lignin phenols, and fatty acids from fluvial sediment samples (Materials and Methods and SI Appendix, Tables S1 and S2). Bulk OC ¹⁴C ages and δ¹³C values in the investigated rivers encompass much of the variability that has been observed in riverine POC worldwide (SI Appendix, Fig. S2) (22), indicating that our sample set accurately captures global trends. Bulk POC ages range from modern to almost 11,000 ¹⁴C y in our sample set (n = 43), whereas biomarker ages range from above modern (reflecting incorporation of nuclear-bomb–derived ¹⁴C) to more than 10,000 ¹⁴C y for fatty acids (n = 44) and from above modern to almost 5,000 ¹⁴C y for lignin phenols (n = 16) (SI Appendix, Tables S1 and S2). Observed age offsets between fatty acids and lignin phenols collected from the same river basins may reflect differences in their degree of mineral stabilization (28) and/or pathways of mobilization (15).

To identify key parameters governing bulk OC and biomarker ¹⁴C ages and δ¹³C values, we performed an ordinary least squares (OLS) multivariate linear regression (MLR) using a suite of climatic, geomorphic, and anthropogenic properties as control variables (Materials and Methods; SI Appendix, Table S3). This approach implicitly treats results calculated using modern datasets as representative of control variable values over the timescales of biomarker ¹⁴C ages (i.e., centuries to millennia). Because this assumption does not strictly hold for all control variables (e.g., anthropogenic land use), correlations calculated herein may deviate from steady-state results. Many control variables are spatially resolved and must be averaged across each river basin. However, it has been shown that fluvially exported POC and, in particular, biomarker isotope signatures exhibit a downstream bias and do not represent a uniformly integrated basin signal (29). We therefore weight spatial values by a factor—the e-folding distance—that decays exponentially with upstream flow distance from each sampling location (Materials and Methods). We choose as the optimal e-folding distance the value that maximizes the fraction of total bulk OC and biomarker isotope variance that is explained by our MLR analysis (average adjusted r² = 0.72; SI Appendix, Fig. S3). This optimal value of ∼500 km agrees with previous estimates of biomarker spatial integration in large river basins (29, 30). For all statistical analyses, spatially resolved control variables are thus weighted by upstream flow distance with an e-folding distance of 500 km when calculating catchment averages (SI Appendix, Table S3). For all bulk and biomarker isotope measurements, MLR-predicted values show no bias (measured versus predicted slopes are always statistically identical to unity) and explain the majority of observed sample variance (measured versus predicted adjusted r² always ≥ 0.35 and typically ≥ 0.64; SI Appendix, Fig. S4), indicating the robustness of the chosen control variables.

Catchment-weighted geomorphic characteristics such as basin area, relief (mean basin slope), and relative floodplain extent showed no significant relationship with biomarker age (SI Appendix, Table S4). Instead, FA and lignin-phenol ¹⁴C ages are significantly correlated with climate variables—chiefly, catchment-weighted mean annual temperature (MAT) and precipitation (MAP) (Fig. 2A and SI Appendix, Table S4). Globally, biomarker ¹⁴C ages decrease (become younger) with increasing MAT and MAP; this phenomenon manifests as a relationship between biomarker ¹⁴C age and latitude because of the strong covariation of the latter with climate (Fig. 1C). A significant, albeit weaker, positive correlation is also observed between biomarker ¹⁴C ages and the fraction of catchment area that is impacted by anthropogenic land use (i.e., agriculture and urbanization; Fig. 2A and SI Appendix, Table S4), suggesting such perturbations might mobilize old OC that would otherwise be stable under natural conditions. However, directly ascribing land-use–change impacts on biomarker ¹⁴C ages is challenging since the extent of anthropogenically perturbed area additionally exhibits strong covariance with climate variables, particularly MAT and MAP. Finally, lignin-phenol and, to a lesser extent, plant-wax fatty-acid ¹⁴C ages display a significant negative correlation with runoff (Fig. 2). While other variables—for example, soil properties such as clay content (31, 32)—may contribute to these relationships, their strength implies that climate constitutes the dominant direct or indirect driver of biospheric-carbon ages. Bulk OC ¹⁴C ages display systematically weaker correlations with the set of tested control variables (e.g., MAT and MAP), as well as with latitude (SI Appendix, Fig. S5), reflecting the influence of additional OC sources (e.g., petrogenic carbon, in situ aquatic productivity) on bulk OC isotopic signatures.

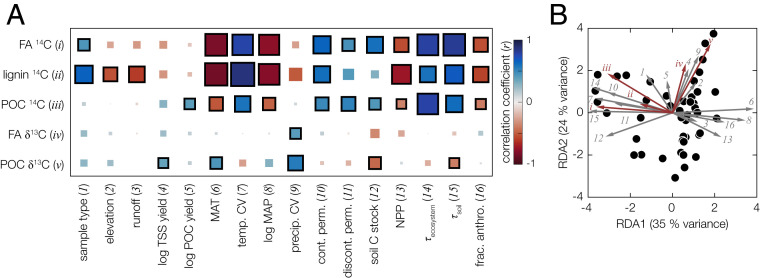
Fig. 2.

Multivariate statistical analysis. (A) Matrix of Pearson correlation coefficients (r values) between environmental control variables (x-axis) and POC and biomarker ¹⁴C and δ¹³C responses (y-axis) (SI Appendix, Table S4). Box sizes and colors correspond to the strength of the correlation (sizes: magnitude only; colors: magnitude and sign). Correlations that are significant at the P = 0.05 level are outlined with a thick, black border. “Sample type” refers to the following: suspended sediment, bank/bedload sediment, or shelf-deposit sediment. (B) RDA triplot showing the RDA1 and RDA2 canonical axes (SI Appendix, Table S5); labels show the percent of total sample variance explained by each axis. Environmental control variable loadings are plotted as gray arrows, POC and biomarker ¹⁴C and δ¹³C response variable loadings are plotted as red arrows, and individual sample scores are plotted as black circles. Environmental and response variable loadings are scaled for visual clarity. Numbers and roman numerals correspond to control and response variables, respectively, as listed in (A). Only control variables that are statistically significantly correlated with at least one response variable are included in the analysis (SI Appendix, Table S4). TSS, total suspended sediment; POC, particulate organic carbon; CV, coefficient of variation; cont. perm., continuous permafrost cover; discont. perm., discontinuous permafrost cover; MAP, mean annual precipitation; NPP, net primary production.

To further assess underlying natural variables controlling bulk POC and biomarker isotope compositions, we additionally performed a redundancy analysis (RDA) (Materials and Methods). The results show that two orthogonal axes explain a combined 57% of the total sample variance (Fig. 2B and SI Appendix, Table S5). The first axis (RDA1) loads closely with catchment-weighted MAT, MAP, and associated highly correlated variables (e.g., permafrost cover, land use), whereas the second axis (RDA2) loads closely with precipitation seasonality (coefficient of variability). All ¹⁴C metrics, particularly fatty-acid ¹⁴C age, load almost exclusively onto RDA1, indicating that they are controlled most strongly by MAT and MAP (and/or all highly correlated variables). In contrast, δ¹³C values of fatty acids and bulk POC, broadly reflecting biome structure within the basin (25), load almost exclusively on RDA2, revealing that they are controlled most strongly by precipitation seasonality (and/or all highly correlated variables). Specifically, lower δ¹³C values correspond to lower seasonal variation in precipitation, as observed in other regional studies (e.g., 33).

Relationships with τ_soil and Mean Age.

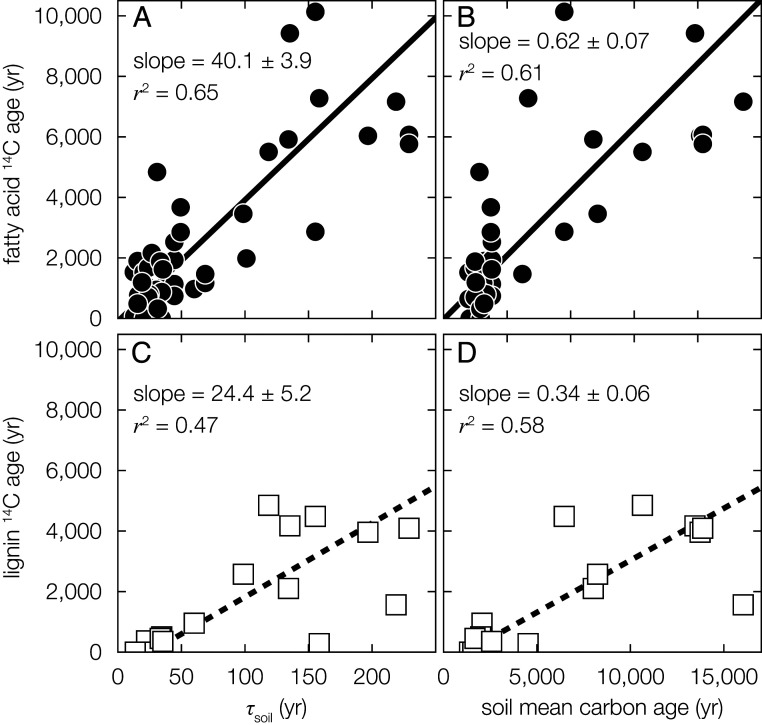
Plant-wax fatty-acid and, to a lesser extent, lignin-phenol ¹⁴C ages display positive relationships with catchment-weighted τ_soil estimated from remote-sensing–derived soil carbon stocks and NPP (Fig. 3 A and C). These linear relationships imply the age of fluvially exported biospheric OC reflects soil carbon turnover at the basin scale, the latter being controlled by MAT and MAP (4, 5). Still, fatty-acid and lignin-phenol ¹⁴C ages are on average 43.6- and 16.6-fold greater than the corresponding τ_soil. To further probe these relationships, we additionally considered recent spatially resolved estimates of soil ¹⁴C ages (34). Biomarker ¹⁴C ages display similar positive relationships with catchment-weighted soil ¹⁴C ages integrated from 0 to 100 cm depth, further demonstrating the strong imprint of soil OC aging processes on fluvial biomarker radiocarbon ages (Fig. 3 B and D, Materials and Methods, and SI Appendix, Table S4). Unlike τ_soil, however, fatty-acid and lignin-phenol ¹⁴C ages are on average 2.5- and 5.0-fold lower than corresponding soil ¹⁴C ages, suggesting that lateral transport processes do not fully capture older, deeper soil horizons. This interpretation is supported by correlations between biomarker ¹⁴C ages and catchment-weighted soil ¹⁴C ages integrated from 0 to 30 cm depth, in which biomarkers display similar or slightly older ¹⁴C ages than corresponding soils, and integrated from 30 to 100 cm depth, in which soils display significantly older ¹⁴C ages than corresponding biomarkers (SI Appendix, Fig. S6).

Fig. 3.

Relationships between τ_soil, soil mean carbon age, and biomarker ¹⁴C age. (A and B) Plant-wax fatty-acid and (C and D) lignin-phenol ¹⁴C ages as a function of weighted-catchment τ_soil (Left, ref. 5), and soil mean carbon age (0 to 100 cm, Right, ref. 34). Solid and dashed black lines are reduced major-axis regression lines; reported values are the corresponding reduced major-axis regression slopes and r² values (Materials and Methods). Uncertainty (±1σ) is always smaller than marker points.

Nonetheless, the observed discrepancy between biomarker ¹⁴C ages and τ_soil contrasts with the much closer agreement between biomarker ¹⁴C ages and soil mean carbon age, regardless of soil integration depth (Fig. 3 and SI Appendix, Fig. S6). This offset between both biomarker ¹⁴C ages and catchment-weighted soil ¹⁴C ages on one hand and τ_soil on the other hand likely reflects the fundamental principles governing organic matter degradation and aging. Natural organic matter is compositionally heterogenous, with age heterogeneity evident even within individual compound populations (20, 35). Complex interplay between environmental properties and chemical composition results in widely variable OC degradation rates (36). We therefore attribute discrepancies between riverine biospheric-carbon age and τ_soil to a heavy-tailed distribution of OC degradation, as has been hypothesized previously (37). Assuming degradation rate constants follow a lognormal distribution with given variance (38), the ratio between mean age and turnover time is proportional to the natural exponential function of the variance (39). Accepting that mean ages can be approximated using ¹⁴C ages (Materials and Methods), the biomarker ¹⁴C age versus τ_soil slopes (Fig. 3 A and C) provide estimates of the globally averaged ratio between mean age and turnover time. These ratios correspond to lognormal degradation rate-constant variances of 3.6 ± 0.7 using fatty acids (μ ± 1σ, n = 44) and 2.7 ± 0.8 using lignin phenols (μ ± 1σ, n = 16), consistent with experimentally determined plant OC degradation rate-constant variances of ∼1.0 to 4.0 (38, 39).

The scaling of biomarker ¹⁴C ages (and soil mean carbon age) with ecosystem turnover time reveals the heterogenous nature of organic matter and the associated wide distribution of OC degradation rates. This is particularly relevant in the context of potential soil OC destabilization upon increases in temperature and precipitation since OC pools characterized by low decay rates (i.e., long turnover) are proportionally more vulnerable to destabilization. Specifically, the theory of temperature-dependent activation energies predicts that turnover of long-lived OC pools (characterized by low decay rates) will increase proportionally more than that of short-lived OC pools (characterized by high decay rates) for a given increase in temperature or precipitation (40). As such, the prevalence of wide OC degradation rate distributions observed here implies that some fraction of the global soil OC reservoir is characterized by low decay rates and is thus susceptible to destabilization upon increases in temperature and precipitation—a positive climate feedback.

Interpreting Exported Carbon Ages.

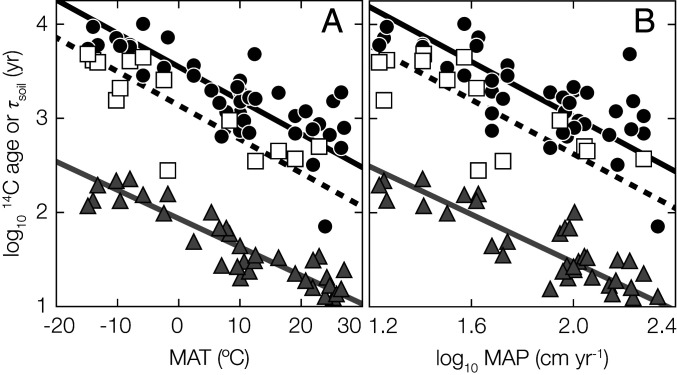
Lignin-phenol ¹⁴C ages, fatty-acid ¹⁴C ages, and τ_soil all exhibit significant negative power-law relationships with MAT and the logarithm of MAP (Fig. 4). For both fatty acids and lignin phenols, this implies a ∼0.4 order-of-magnitude decrease in mean age for each 10-degree increase in MAT. Interestingly, this power-law exponent is statistically identical for τ_soil and both biomarker classes despite differences in their absolute ¹⁴C ages and the fact that they likely reflect different biospheric-carbon provenance, transport pathways, and/or degradation rates within the drainage basin (15). Meanwhile, sediment yield does not appear to correlate with either τ_soil or the ages of biospheric OC exported by rivers (SI Appendix, Fig. S7). This contrasts with biospheric OC yield (i.e., the annual riverine flux of biospheric OC normalized to catchment area), which is primarily controlled by erosion rates (17), suggesting a decoupling between biospheric OC yield and age. Soil carbon turnover is primarily driven by respiration flux, which is linked to climate variables (4), whereas the comparatively minor riverine biospheric OC export flux is controlled by geomorphic properties such as catchment slope and runoff (14).

Fig. 4.

Environmental controls on τ_soil and biomarker ¹⁴C ages. Logarithmic plant-wax fatty-acid ¹⁴C ages (black circles), lignin-phenol ¹⁴C ages (white squares), and catchment τ_soil [gray triangles (5)] as functions of (A) MAT and (B) logarithmic MAP (SI Appendix, Tables S1 and S3). Solid black, dashed black, and gray lines are fatty-acid–, lignin-phenol–, and τ_soil-reduced major-axis regression lines. Relationship slopes and r² values are as follows: (A) fatty-acid ¹⁴C ages: slope = −0.036 ± 0.004, r² = 0.62; lignin-phenol ¹⁴C ages: slope = −0.036 ± 0.006, r² = 0.67; and τ_soil: slope = −0.030 ± 0.002, r² = 0.83. (B) Fatty-acid ¹⁴C ages: slope = −1.46 ± 0.17, r² = 0.55; lignin-phenol ¹⁴C ages: slope = −1.44 ± 0.30, r² = 0.56; and τ_soil: slope = −1.13 ± 0.11, r² = 0.72. Uncertainty (±1σ) is always smaller than marker points.

Overall, our observations suggest that the age of vascular plant biomarkers exported by rivers echo organic-matter dynamics at the basin scale and are primarily controlled by τ_soil. This implies that basin-scale information on the latter can be gleaned from ¹⁴C investigations of biospheric-carbon components exported by rivers and that past changes in ecosystem dynamics in response to climate and anthropogenic forcing can be deduced using sedimentary archives (41), although additional preaged carbon sources such as permafrost or peat deposits must be carefully considered (16). Furthermore, this study provides a global assessment and mechanistic understanding of biospheric-carbon age in modern river basins, thus contextualizing any observed future perturbations in biospheric-carbon turnover. Ongoing temperature increases and accompanying changes to the hydrological cycle are likely to influence ecosystem turnover times and vulnerability of previously stable carbon stocks. Potential shifts in the balance of degradation versus lateral transport of these carbon stocks may influence the distribution of carbon in Earth’s active reservoirs. In-depth investigations of carbon dynamics in river basins are needed to assess the large-scale impact of environmental change on terrestrial ecosystems and the manner and efficiency by which rivers act as carbon “conveyors” or “reactors” (42).

Materials and Methods

Sample Selection.

Rationale for selection of river systems.

We focus on 36 globally distributed river systems that collectively account for one-third of the global exorheic land surface and for 42, 29, and 20% of the global riverine water, sediment, and POC discharge, respectively (SI Appendix, Table S5). The majority of these rivers have been the subject of prior in-depth biogeochemical studies. The 36 rivers included in this study nearly cover the full range of intrinsic basin properties (e.g., catchment area, latitude, relief, physical erosion rate, discharge, and POC flux) and are evenly distributed across the continuum of geomorphic characteristics (SI Appendix, Fig. S1). This ensures that our results are not biased toward any particular set of basin properties.

Rationale for focus on POC as opposed to DOC.

We focus on organic matter that is associated with fluvial, fluvially derived, or fluvially influenced sediments either transported as suspended particles or recently deposited near the terminus of the river system. The translocation and sequestration of POC in marine sediments is considered to influence atmospheric CO₂ over millennial and longer timescales, whereas DOC is efficiently remineralized in coastal waters (16, 18). This POC leaves a legacy of terrestrial carbon fixation that can be traced in the sediment record and can be used to reconstruct continental carbon cycling over a wide range of timescales. Diagnostic biomarkers of higher plant productivity (including lignin and plant-leaf waxes) reside in the particulate fraction because of their physiological role (e.g., structural polymers) or their hydrophobic nature (e.g., lipids), enabling biospheric carbon to be directly traced from plant source to sedimentary sink.

Sample Congruency.

We consider potential complications and variability that may arise from heterogeneities within the overall sample suite. Because these measurements result from field and analytical work that span a range of sampling dates, modes of collection, and settings, we assess potential biases that may be introduced. Specifically, the samples have been collected over a period spanning more than three decades, during which the atmospheric ¹⁴C signature, and hence the ¹⁴C content of coeval produced biomass, has changed significantly (43). Samples have also been collected in differing locations with respect to the terminus of the river under different flow conditions (e.g., high discharge events versus low flow conditions) and also span a range of sample types (e.g., suspended sediments, river flood deposits, offshore depocenters, etc.). Our statistical analysis did not identify any obvious biases related to the heterogenous nature of the sample set. Still, below we discuss the influence of a set of individual parameters in the context of the overall observed variability and trends.

Sample type.

Our sample set includes suspended sediments, bed sediments, recently deposited bank deposits (i.e., flood deposits), and floodplain sediments, as well as fluvially dominated coastal sediments collected at or close to the river terminus. In general, biospheric OC tends to be concentrated in the finer grain-size fractions, likely reducing potential impact from sorting processes. Moreover, where possible, poorly sorted bed and bank/flank sediments were presieved to concentrate finer-grained (<63 μm) material, as well as to exclude coarse-grained detritus that may have been locally introduced (e.g., from riverbank erosion) to the river. Nevertheless, given potential differences in grain size distribution and associated hydrodynamic characteristics, it is important to assess associated variability in ¹⁴C characteristics. In the Yellow River, for example, plant-wax ¹⁴C ages have been found to vary among grain-size fractions of suspended sediments (44). For systems for which more than one sample type is available (i.e., Brahmaputra, Danube, Ganges, and Mississippi), a comparison of ¹⁴C characteristics reveals no systematic offsets between sample type. In the Danube River, vertical water-column profiles of plant-wax δ¹³C and ¹⁴C ages showed no systematic trend with depth (45), suggesting plant waxes are relatively homogenous within the water column and rather insensitive to hydrodynamic sorting. This likely results from the association of plant-wax compounds with mineral surfaces (especially clay minerals) and the uniform distribution of fine-grain clays in the water column (46, 47). We nonetheless include sample type in the statistical analysis since it is significantly correlated with lignin ¹⁴C age (Fig. 2).

Seasonal and interannual variability.

Most rivers included in this study exhibit large seasonal variations in water and sediment discharge, which has been linked to variations in the composition of POC (29, 48). Our sampling generally does not capture seasonal variations in the ¹⁴C age of biomarkers. The limited number of investigations of temporal variability in rivers does not reveal marked seasonal variations in biomarker ¹⁴C age [e.g., plant waxes in the Yellow River (49); lignin phenols in the Mekong River (50)]. Furthermore, in many cases, the samples investigated in this study were collected during or shortly following maximum discharge, which accounts for much of the annual sediment and POC load. As such, we argue that overall, our sampling is not affected by a strong seasonal bias. Interannual variability of riverine sediment load and bulk POC composition has been reported for several river systems (51, 52). Our dataset includes samples collected over different years for several river systems (Brahmaputra, Danube, Ganges, Yangtze, and Yellow River). Compared to the observed overall range of variability, none of these rivers shows large interannual variations in fatty-acid ¹⁴C ages. This suggest that interannual variations are not a significant driver of the observed trends in biomarker ¹⁴C ages.

Sample collection date.

Samples have been collected between 1976 and 2016, a period of time over which atmospheric ¹⁴C, and hence freshly produced terrestrial plant organic matter, has exhibited a marked decline in response to the redistribution of “bomb ¹⁴C” (from above-ground thermonuclear weapons testing in the late 1950s and early 1960s) in the earth’s surface carbon reservoirs (43, 53). Recently synthesized biospheric carbon then transmits this bomb ¹⁴C signal through river basins, inducing time-variable deviations from natural ¹⁴C levels. We have examined this potential influence on observed signals for selected river systems in two different ways: 1) through comparison of data from samples from the same river system but collected at different times over the last few decades; and 2) through analysis of rapidly accumulating and well-dated fluvially influenced sedimentary sequences with well-defined chronologies that span a time interval encompassing the bomb spike (20, 35). Although the influence of the bomb ¹⁴C spike clearly manifests itself in plant-wax fatty acids, the induced variability is small relative to the overall ¹⁴C variability observed within the global dataset presented in this study. These muted changes in plant-wax fatty-acid ¹⁴C ages require the presence of at least two different aged populations—one reflecting rapid (i.e., within years to decades) transfer of these tracer molecules from biological source to sedimentary sink and a second, substantially preaged (i.e., hundreds to several thousand years) component that implies substantial retention prior to export and deposition. In both of the above studies, model results suggest that the majority (49 to 83%) of the plant-wax signal derives from a preaged pool that likely corresponds to a mineral-bound soil OC component. Hence, sensitivity to bomb ¹⁴C is relatively small, and the date of sampling does not impart a large bias on our results.

Anthropogenic influences.

A key consideration in any study of modern rivers is the extent to which modern observations of fluvial-sediment flux and composition have been impacted by anthropogenic activity, both within the catchment area (e.g., land-use change) and on the hydrological network (e.g., damming, channelization, etc.). As a proxy for anthropogenic influences, here we include in our statistical analysis the fraction of each river basin that is impacted by anthropogenic land-use change (i.e., agriculture and urbanization) (SI Appendix, Table S3). This approach implicitly assumes the following: 1) Land use is an accurate proxy for all anthropogenic disturbances, and 2) modern land-use change extent is representative of perturbations over the timescale of biomarker ¹⁴C ages (i.e., centuries to millennia). Neither of these assumptions is strictly true in all studied river basins. For example, several of the rivers included in the current study are greatly impacted by recent human activity, particularly since the industrial era (e.g., Yellow, Yangtze, and Danube) (49, 51). In contrast, other fluvial systems have been subject to human modification over millennia (e.g., Godavari) (54). Nonetheless, our statistical correlation results indicate that biomarker ¹⁴C ages are more strongly controlled by climate as opposed to anthropogenic variables (SI Appendix, Table S4), suggesting that differences in the type and duration of anthropogenic disturbance likely impart only a small impact on resulting biomarker ¹⁴C ages.

Sample Collection and Processing.

Sample collection.

Samples include suspended sediments obtained via filtration of river water, riverbed sediments sampled via a grab or bedload sampler, recently deposited river flank and floodplain sediments, and fluvially influenced coastal sediments deposited proximal to the mouth of the river. For river flank, floodplain, and coastal sediments, emphasis was placed on sampling deposits where fine-grained sediments accumulate, such as quiescent areas characterized by weak river and coastal currents.

Sample processing and analysis procedures vary somewhat between field campaigns. Detailed procedures are provided in previous publications and are briefly summarized below. In general, exposed or slightly submerged riverbank/flood-deposit sediments were collected using a shovel, whereas riverbed samples used a bedload sampler (55), and suspended river samples were obtained by large-volume filtration (typically 100 L) over either polyethersulfone membrane filters or precombusted glass fiber filters (48, 55). Samples were then stored, refrigerated, or frozen before freeze-drying in the laboratory. For selected samples (mostly floodplain materials), the sediment was wet sieved to <63 μm to remove large fragments that may have been directly introduced (e.g., via riverbank erosion). The <63-μm fraction is also considered to more closely resemble the riverine suspended load owing to its overall smaller grain size compared to deposited sediments (45, 56, 57).

Sample aliquots were processed for the content, stable carbon isotopic composition, and radiocarbon content of bulk OC. Carbonates were removed using the acid-fumigation method (58) prior to bulk OC analysis. OC content and stable isotope composition were measured via elemental analyzer–isotope ratio mass spectrometry (IRMS). Bulk OC radiocarbon analysis was performed either at the National Ocean Science Accelerated Mass Spectrometry (NOSAMS) facility (Woods Hole Oceanographic Inst. [WHOI]) or at the Laboratory of Ion Beam Physics (LIP) using established procedures (59–61).

Plant-wax lipids were extracted from freeze-dried sample aliquots using a mixture of dichloromethane and methanol. The lipid extract was subsequently treated to obtain a fatty-acid fraction, and the latter was derivatized to obtain fatty-acid methyl esters (FAMEs). The FAMEs were further purified via column chromatography and ultimately isolated by preparative capillary gas chromatography (62). Isolated compounds were subsequently analyzed by accelerator mass spectrometry (AMS) (¹⁴C contents) and gas chromatography (GC)-IRMS (δ¹³C). Resulting ¹⁴C data are corrected for any derivative carbon as well as methodological and instrumental blanks (see below) and reported using the fraction modern (Fm) notation and as radiocarbon ages (63). We report abundance-weighted average ¹⁴C compositions of long-chain FA homologs in the 24 to 32 carbon number range. In some cases, sample availability and/or technical issues led to averaging over a subset of homologs within this carbon number range. For coastal sediments that may have additional sources of midchain FA homologs (e.g., ref. 35), we used corresponding δ¹³C values from GC-IRMS to select homologs that are exclusively derived from terrestrial vascular plants.

Lignin-derived phenols were recovered by alkaline oxidative hydrolysis (CuO oxidation) of freeze-dried or solvent-extracted sediments (64). Resulting hydrolysis products were then purified via high-performance liquid chromatography (50, 64) and subsequently measured for ¹⁴C content by AMS.

Biomarker ¹⁴C data corrections.

Compound-specific radiocarbon data were corrected using mass-balance equations for procedural blanks and, in the case of fatty acids, for the addition of derivative carbon during methylation with methanol with a known ¹⁴C composition. Procedural blanks varied depending on the instrumental set up used (e.g., at WHOI versus at ETH) and the measurement date, as these methods have been continuously refined over the course of this study. Overall, procedural blanks were in the range of 1 to 2 µg C, with compositions intermediate between modern and dead. Details of blank assessments and corrections can be found in Santos et al. (65), French et al. (20), Haghipour et al. (66), and Feng et al. (64). The uncertainty related to blank corrections varies from sample to sample, primarily according to sample size and ¹⁴C age. Overall, these uncertainties remain below 0.05 Fm units and are therefore small compared to the variability observed across our entire dataset.

Geospatial Analysis.

All geospatial analyses were performed in ArcGIS version 10 (ESRI Corporation). River basin outlines were calculated either upstream of each sampling point (for suspended-sediment and bank-sediment samples) or at the river mouth (for shelf-deposit samples), and environmental control variables were calculated using the following data sources: 1) Elevation, slope, and floodplain fractional area (here defined as area with slope less than 1% rise) were calculated using the United States Geological Survey (USGS) GTOPO30 digital elevation model with 30-arc-second resolution [1 km at the equator (67)]. 2) Catchment-averaged MAT, temperature seasonal coefficient of variability (TCV), MAP, and precipitation seasonal coefficient of variability (PCV) were calculated from the raster data set of New et al. (68) with 10’ resolution. 3) τ_soil and NPP were calculated from the raster data set of Bloom et al. (5) with 1° resolution. 4) Total ecosystem carbon turnover time (ecosystem τ) and soil carbon stocks were calculated from the raster data set of Carvalhais et al. (4) with 0.5° resolution. 5) Anthropogenic land-use fractional area was calculated as the sum of “croplands,” “urban and built-up,” and “cropland/natural vegetation mosaic” pixels (International Geosphere Biosphere Program classification) extracted from the USGS Global Land Cover Characterization raster data set version 2.0 with 30-arc-second resolution [1 km at the equator (69)]. 6) Soil carbon ¹⁴C ages (0 to 30 cm, 30 to 100 cm, and 0 to 100 cm depth integrated) were calculated from the raster data set of Shi et al. (34) with 0.5° resolution.

All other environmental control variables were compiled from the literature (15, 17, 70). When comparing biomarker ¹⁴C ages and soil turnover times, we implicitly assume that the soil turnover times determined using estimates of soil C stocks and NPP are representative of the average turnover time over the timescales reflected in the biomarker ¹⁴C ages (centuries to millennia). While short-term small variations in NPP have likely occurred over these timescales and regional-scale climate variability during the late Holocene locally impacted soil carbon stocks (71), this relatively quiescent time interval is unlikely to have seen large, globally coherent variations in soil carbon stocks. As such, temporal variations in τ_soil are unlikely to contribute significantly to the systematic difference observed between τ_soil and biomarker ¹⁴C ages (i.e., since plant-wax fatty-acid and lignin-phenol ¹⁴C ages are on average 43.6- and 16.6-fold greater, respectively, than corresponding τ_soil).

For spatially resolved control variables (i.e., elevation, slope, floodplain fraction, MAT, TCV, MAP, PCV, τ_soil, NPP, ecosystem τ, and soil C stocks), weighting factors were calculated using hydrologically conditioned versions of the GTOPO30 digital elevation model [i.e., Hydro1k and HydroSHEDS (72, 73)]. Hydrologic distance upstream of each sampling location was calculated using the “Flow Length” feature in ArcGIS and was weighted as an exponential decay following

$$w\hspace{0.17em}=\hspace{0.17em}{e}^{-kl},$$ [1]

where w is the weighting factor (ranging from 0 to 1), l is the upstream distance, and k is the reciprocal of the prescribed e-folding distance. All spatially resolved control variables were taken as the weighted-catchment averages.

Statistical Analyses.

Multiple linear regression.

Regression analyses were performed using the Numpy and Scipy packages in Python version 3.5; all analysis code is provided in Dataset S1. To determine the strength of relationships between environmental control variables and biomarker and POC response variables, OLS MLR was performed following standard practices (74). In summary, all data were first “whitened” by subtracting the mean and dividing by the SD for each variable in order to facilitate comparisons between variables with differing units and ranges. The regression parameter matrix, B, was then calculated as

$$\mathbf{B}={\left({\mathbf{X}}^T\mathbf{X}\right)}^{-1}{\mathbf{X}}^T\mathbf{Y},$$ [2]

where X is the whitened matrix of environmental control variables, and Y is the whitened matrix of biomarker and POC response variables. The matrix of MLR-predicted response variable best estimates, Ŷ, was then calculated as

$$\hat{\mathrm{Y}}=\mathbf{X}\mathbf{B},$$ [3]

and the matrix of residuals was calculated as

$${\mathbf{Y}}_r=\mathbf{Y}-\hat{\mathrm{Y}}.$$ [4]

The matrix of correlation strengths between X and Y, termed S_XY, was then calculated following

$${\mathbf{S}}_{\mathbf{X}\mathbf{Y}}=\frac{1}{n}{\mathbf{X}}^T\mathbf{Y},$$ [5]

where n is the number of samples in the data set, and correlation P values were calculated individually for each control and response variable pair using standard OLS methods (74). Reported MLR r² values are the square of the diagonal elements of S_XY. The optimal e-folding k value was calculated using an inverse approach by repeating Eqs. 1–5 and choosing the value that maximizes the average resulting r² value (SI Appendix, Fig. S3). Because scatterplot variables presented in this study generally contain uncertainty in both x and y variables (e.g., Figs. 3 and 4), predictive relationships were calculated using reduced major-axis regression (75). Note that some environmental control variables, and particularly biomarker response variables, contained missing data entries; missing data were ignored when performing statistical calculations by utilizing Numpy “masked” arrays (reference Dataset S1 for details).

Finally, we test if and how averaging all samples of a given sample type (i.e., suspended sediment, bedload sediment, or shelf/slope sediment) within a given river basin impacts the results of our statistical analysis. We repeated Eqs. 1–5 using either “catchment averaged” or “all reported samples” as the response variable dataset (i.e., SI Appendix, Tables S1 and S2, respectively). Resulting correlation coefficients exhibit only small differences and are largely independent of our choice of response variable dataset (SI Appendix, Fig. S8). We therefore use the catchment averaged dataset for all subsequent calculations as this avoids potential biases that could arise because of uneven sampling density between river basins.

Redundancy analysis.

To extract the canonical axes and to determine the loadings of each sample, environmental control variable, and biomarker and POC response variable onto each canonical axis, RDA was performed following Legendre and Legendre (76) using the Numpy and Scipy packages in Python version 3.5. All analysis code is provided in Dataset S1. RDA is a canonical extension of MLR that transforms all control variables into orthogonal (linearly uncorrelated) axes and determines the fraction of sample variance explained by each orthogonal axis; it is ideally suited for situations with highly correlated control variables, as is the case here (76). Heuristically, RDA extracts the principal components of response variables as predicted by control variables; that is, it calculates the amount of variance within the response variables that can be explained by the set of control variables and maps all variables onto a set of underlying orthogonal axes. Briefly, RDA involves independently performing principal component analyses on Ŷ, the matrix of MLR-predicted response variables, and on Y_r, the matrix of residuals. Analogous to Eq. 5, the correlation matrix between MLR-predicted response variables is first calculated as

$${\mathbf{S}}_{\hat{\mathrm{Y}}\hat{\mathrm{Y}}}=\frac{1}{n}{\hat{\mathrm{Y}}}^T\hat{\mathrm{Y}}.$$ [6]

Then, the following eigenvalue problem is solved:

$$\left({\mathbf{S}}_{\hat{\mathrm{Y}}\hat{\mathrm{Y}}}-{\text{λ}}_j\mathbf{I}\right)u_j=0,$$ [7]

where λ_j is the jth canonical eigenvalue, u_j is the jth canonical eigenvector, and I is the identity matrix; the response variable loadings onto the jth canonical axis (termed “species scores”) are thus the entries of u_j. Eqs. 6 and 7 are then repeated using Y_r instead of Ŷ to calculate the noncanonical eigenvalues and eigenvectors. The percentage of response variable variance explained by each axis is calculated as λ_j divided by the sum of all (canonical plus noncanonical) eigenvalues. Finally, constrained sample loadings (“constrained site scores”) onto each canonical axis, termed Z, are calculated as

$$\mathbf{Z}=\hat{\mathrm{Y}}\mathbf{U},$$ [8]

and control variable loadings (“constraining variable scores”) onto each canonical axis, termed C, are calculated as

$$\mathbf{C}=\mathbf{B}\mathbf{U},$$ [9]

where U is the column-wise matrix of u_j eigenvectors. Species scores, constrained site scores, and constraining variable scores for any two canonical axes can then be plotted as in Fig. 2B; the angles between species scores and constraining variable scores thus represent the strength of their linear correlation. Reference Dataset S1 for further details and analyses.

Data Availability

All study data are included in the article and/or supporting information.