Competitive binding of independent extension and retraction motors explains the quantitative dynamics of type IV pili

Significance

Many bacteria use the extension and retraction of external protein filaments called type IV pili (TFP) as arm-like tentacles to grab a surface and pull forward or catch and internalize DNA. We here propose and test a model for how the dynamics of TFP and the switch between phases of extension and retraction are coordinated. This model quantitatively predicts all the observed TFP behaviors and important features such as pilus length and the pilus production rate accurately. It further yields insights into the molecular details of how the dedicated extension and retraction motors interact with the pilus machine. These results advance our understanding how TFP operate and how their dynamics give rise to biological function.

Abstract

Type IV pili (TFP) function through cycles of extension and retraction. The coordination of these cycles remains mysterious due to a lack of quantitative measurements of multiple features of TFP dynamics. Here, we fluorescently label TFP in the pathogen Pseudomonas aeruginosa and track full extension and retraction cycles of individual filaments. Polymerization and depolymerization dynamics are stochastic; TFP are made at random times and extend, pause, and retract for random lengths of time. TFP can also pause for extended periods between two extension or two retraction events in both wild-type cells and a slowly retracting PilT mutant. We developed a biophysical model based on the stochastic binding of two dedicated extension and retraction motors to the same pilus machine that predicts the observed features of the data with no free parameters. We show that only a model in which both motors stochastically bind and unbind to the pilus machine independent of the piliation state of the machine quantitatively explains the experimentally observed pilus production rate. In experimental support of this model, we show that the abundance of the retraction motor dictates the pilus production rate and that PilT is bound to pilus machines even in their unpiliated state. Together, the strong quantitative agreement of our model with a variety of experiments suggests that the entire repetitive cycle of pilus extension and retraction is coordinated by the competition of stochastic motor binding to the pilus machine, and that the retraction motor is the major throttle for pilus production.

Type IV pili (TFP) are amazing molecular machines that extend and retract extracellular polymers used for many biological functions (1–3). TFP have emerged to be of particular interest in the opportunistic human pathogen Pseudomonas aeruginosa, as they promote surface motility, colonization, biofilm formation, and surface sensing (4–11). In P. aeruginosa, the semiflexible polymers of TFP are based on the major pilin (PilA) subunits whose extension is mediated by the PilB molecular motor and whose retraction is mediated by the PilT motor (2, 3). The structures of TFP and the components that build them have been well characterized by static methods such as electron microscopy (12). However, the behaviors mediated by TFP rely on their dynamics, and no quantitative model has been proposed to date to explain how cycles of extension and retraction are controlled. For example, even after decades of research by many groups, fundamental questions like whether there is a molecular ruler that sets TFP length or whether pilus extension/retraction are triggered or stochastic have remained unanswered.

The major hurdle to describing TFP dynamics is the lack of large-scale quantitative data on multiple features of TFP extension and retraction dynamics that are needed for formulating and testing a biophysical model. For example, TFP were first imaged by electron microscopy, but this method can only be performed on fixed or frozen cells such that dynamics are lost (13–17). Optical tweezers, atomic force microscopy, micropillar assay, and traction force microscopy are techniques to measure pilus retraction forces and also yield information about retraction dynamics but in an indirect way and only for pilus retraction (4, 18–23). A recent study used interferometric imaging to directly image pili in living cells, but this technique generates a strong halo around the cell that overshadows any pili that are shorter than ∼3 microns (24). Despite the limitations of these approaches, they have led to several competing models for how the switch between TFP extension and retraction is controlled. A cryogenic electron microscopy (cryo-EM) study did not observe motors at the base of unpiliated structures, suggesting that the motors do not remain bound after TFP retraction (12). Meanwhile, an interferometry study focusing on the longest subpopulation of TFP suggested that TFP retraction is triggered by surface association (24). Importantly, the lack of data following the dynamics of the entire TFP population previously limited the ability to directly test these models.

Here, we addressed the above limitations by fluorescently labeling the TFP of P. aeruginosa directly and using high temporal resolution imaging to quantify multiple features of their dynamics for thousands of pili across several genetic backgrounds. Fluorescent labeling of TFP was first achieved with nonspecific labeling of extracellular proteins (25). This approach has powerful potential, but we struggled to implement it. Importantly, the only study that applied the nonspecific TFP labeling approach to P. aeruginosa reported the extension and retraction velocities of <60 individual pili from <30 individual cells and did not measure additional parameters such as pilus length, extension/retraction times, and pausing (25). Thus, there is still a need for additional approaches to provide data and analysis on P. aeruginosa TFP dynamics. Recently, TFP from Caulobacter crescentus and Vibrio cholerae were directly labeled by introducing a reactive cysteine residue into the pilin sequence (26–28). Here, we apply this approach to P. aeruginosa and use it to analyze thousands of pili and perform direct quantitative analysis of full TFP extension and retraction cycles of individual pili. We use these data to develop and test quantitative models for the behaviors we observe. We show that TFP production rate, length, and dynamics can be fully explained by the mutually exclusive stochastic binding of the extension and retraction motors and that this stochasticity persists in the presence or absence of surface association.

Results

Quantifying TFP Dynamics Reveals that TFP Labeling Is Not Perturbative and that P. aeruginosa Makes Mostly Short Pili that Are Highly Dynamic.

We fluorescently labeled the major protein of the P. aeruginosa pilus fiber (PilA) by introducing a cysteine point mutation, A86C, that we then labeled with the thiol-reactive maleimide dye Alexa488-mal (Fig. 1 A and B and SI Appendix, Fig. S1) (26). Analogous mutations have been shown to preserve TFP function and dynamics in C. Cresentus and V. cholera (26–28). Nevertheless, to confirm that neither this mutation nor the presence of the dye disrupt TFP function, we analyzed twitching motility. Using a standard stab agar twitch assay, we showed that the PilA-A86C mutant twitches at levels close to wild type (WT) on the population level, and that this result does not change in the presence of the Alexa488-mal dye (SI Appendix, Fig. S1A). We also examined individual cells confined between a 0.5% agarose pad and a coverslip and found that cells in this condition twitch actively (Movie S1), indicating that the PilA-A86C mutation is functional. We used this configuration for all our experiments unless stated otherwise.

Fig. 1.

The quantitative measurement of pilus dynamics using Alexa488 coupled to thiol-reactive maleimide and the PilA-A86C Cysteine knock-in mutant on an agarose pad. (A) The movie frames showing the extension and retraction of a long pilus (white arrow, L_p = 5 μm). (Scale bar, 2 μm.) (B) The movie frames showing the typical extension and retraction of several short pili (white arrows, L_p ≤ 1 μm). (Scale bar, 2 μm.) (C) The comparison of the fraction of cells in a single image that have at least one pilus when analyzed in just a single frame (static) or a movie (dynamic) of 30 s in length. The boxes represent the median and 25%/75% quantiles. (D) The distribution of pilus production rate per cell (markers) and exponential fit (line). The error bars are the SD obtained by bootstrapping. (E) The distribution of the maximum extension lengths of individual pili. The error bars are the SD obtained by bootstrapping. Gray shaded area: 95% CI from model simulation for comparison (MCS, see below and Materials and Methods). No significant difference between the distributions of the simulations and experiments (P > 0.05) was found. (F) The pilus extension and retraction velocity. The boxes represent the median and 25%/75% quantiles.

The fluorescent TFP labeling strategy resulted in bright images of dynamic pili with high contrast (Fig. 1 A and B and Movies S2–S5) and low unspecific background (SI Appendix, Fig. S1B). Having established that we can label TFP without disrupting their function, we first counted the number of pili that individual cells make in a single snapshot (Fig. 1C). These results confirmed previous reports that used electron microscopy to show that only a minority of cells (<25%) are piliated at any given time (13, 17, 29), thereby supporting our conclusion that TFP labeling is not perturbative. However, when we then imaged single cells for a period of ∼30 s, we found that >80% of cells formed at least one pilus in this time period (Fig. 1C). We quantified the rate of pilus production R_p in individual cells and found a very broad distribution between 0 and 35 pili-per-minute, with a characteristic rate R_C = 8 min⁻¹ for a typical cell (Fig. 1D). Here, we refer to a typical cell as a cell with a pilus production rate R_P = R_C such that the amplitude of the respective exponential probability density exp(−R_P/R_C) drops to exp(−1) ∼ 0.37. Thus, whereas static imaging suggested that pili are only made by a small subpopulation of P. aeruginosa cells and that these cells only make few pili (1 to 2 on average) (13, 17, 29), our dynamic imaging suggests that nearly all P. aeruginosa cells make many (typically 8 min⁻¹) short-lived highly dynamic pili.

To further quantify TFP behavior we measured the distribution of pilus lengths (Fig. 1E). We found that the pilus length (L_p) also exhibits a wide distribution between 0.3 (limited by optical resolution) and 8 μm, with a characteristic length for a typical pilus of 0.8 μm. We note that this result agrees with results from electron microscopy that showed that Pseudomonas makes many short pili (<1 μm) (14) but differs from the only other study that quantified the pilus length of live Pseudomonas cells, which observed only pili longer than 3 μm (24). However, the interferometric imaging technique used in that live-cell study could not detect pili shorter than the halo produced by the cell itself (2 to 3 μm). Together, these results indicate that most P. aeruginosa extend short, short-lived pili.

The ability to directly label pili also enabled us to analyze the extension and retraction dynamics of individual pili. A typical pilus had an average extension velocity ± SD of v_ext = (361 ± 182) nm/s and an average retraction velocity of v_ret = (644 ± 290) nm/s (Fig. 1F). These rates are in agreement with the previous study that measured extension and retraction velocities in P. aeruginosa using nonspecific labeling (25), further validating that our measurements accurately reflect the dynamics of wild-type P. aeruginosa TFP.

TFP Extension and Retraction Dynamics Are Unaffected by the Presence of a Surface.

To understand the mechanisms that control pilus dynamics and the biophysical basis for our findings we next sought to understand how the switch between TFP extension and retraction is coordinated. A hypothesis that has recently gained increased interest is that TFP retraction is triggered by mechanical contact of the pilus tip with a surface (12, 24). To test this model, we compared the TFP dynamics of cells in two different conditions: cells confined between agarose and a coverslip (surface associated) and cells prevented from contacting a surface by holding them 5 μm above the coverslip using an optical trap (30) (liquid trapped) (Fig. 2A). In addition to holding the bacteria away from the surface, the line-scanning optical trap (31, 32) orients the cells with the microscope focal plane, which allowed us to observe pilus dynamics on both cell poles. We note that the force the optical trap imparts on the entire cell body was chosen as low as possible to prevent the cell body from drifting away due to Brownian motion. The mechanical influence of the trap on the pili is therefore negligible.

Fig. 2.

Pilus retraction does not require mechanical stimulation. (A) A schematic of surface-contact–free (“liquid-trapped”) assay: single cells are held about 5 μm above the surface and aligned with the focal plane by line-scanning optical tweezers. (B) The image sequence of an individual pilus extending and retracting without surface contact (also see Movie S10). (C) A time trace of pilus length for seven individual pili (roman numerals) extending and retracting from the same pole of the same cell without surface contact. (D) The fraction of retracting pili for cells with and without surface contact. (E) The dwell times between stop of extension and start of retraction of individual pili for cells with and without surface contact. (F) The maximum length of individual pili for cells with and without surface contact. (E and F) No significant difference between the distribution of the simulations and experiments (P > 0.05) was found. See Materials and Methods for details of the statistical testing. (See SI Appendix, Table S4 for sample sizes and number of replicates).

As show in Movies S6 and S7, individual cells with labeled pili confined between 0.5% agarose and the coverslip can twitch, which means that their TFP are in mechanical contact with the environment. Similarly, we observed frequent TFP extension and retraction for liquid-trapped cells (Fig. 2 B and C and Movies S8–S10), indicating that loss of surface contact does not completely abolish pilus retraction. If the surface-triggered model is true, the dynamics of TFP for cells with and without surface contact should be quantitatively different. For example, if mechanical contact of the pilus tip with a surface triggers pilus retraction, then we expect to see fewer retracting TFP for liquid-trapped cells compared to surface-associated cells. Surprisingly, the fractions of all pili that had been made during the experiment and also retracted are 95% for liquid-trapped cells and 93% for surface-associated cells and are therefore indistinguishable (Fig. 2D). It is possible that we did not observe a difference in the fraction of retracting pili because surface association accelerates the timing between extension and retraction, in which case TFP would retract eventually even without a mechanical trigger signal. To test this hypothesis, we quantified the time each TFP dwells between when the extension comes to a halt and the retraction starts. If the contact with a surface stimulates pilus retraction, the distribution of dwell times should be shorter for surface-associated cells. However, the distributions of dwell times for both conditions were indistinguishable from each other (Fig. 2E). Similarly, the distributions of TFP length were indistinguishable in both conditions (Fig. 2F), indicating that surface contact also does not stop TFP extension. While it is possible that many of the pili in our analysis are not directly surface bound, even if only a fraction of pili of surface-associated cells were in contact with the surface we would still expect to see a change in the distribution relative to liquid-trapped cells without surface contact. We therefore conclude that the dynamics of the switch between pilus extension and retraction of most pili are indistinguishable whether or not a surface is present.

A Stochastic Model of Motor Binding Predicts that Pilus Extension and Retraction Can Be Discontinuous.

In light of our result that TFP dynamics are unaffected by the presence of a surface, we considered other mechanisms that could explain the switch between extension and retraction. A recent cryo-EM study suggested that only one type of motor, extension or retraction, is bound to the pilus machine at any given time (12). This indicates that both motors must compete for the binding to the machine. Furthermore, the distributions of the maximum pilus length and the rate of pilus production are exponential in shape (Fig. 1 D and E), suggesting that stochastic protein binding and unbinding might govern pilus dynamics (see Materials and Methods). We thus formulated a quantitative model in which pilus extension and retraction are governed by the stochastic binding of an extension or retraction motor to the pilus base in a mutually exclusive manner. We note that the only assumptions of this model are that each motor has a finite probability to bind the unbound pilus machine, and that no more than one motor can be bound at a given time (Fig. 3A).

Fig. 3.

Competitive substrate binding model predicts rare multistep extension and retraction events with short intervening stalls. (A) The model schematic. The extension motor (Ext, purple) and retraction motor (Ret, green) bind with probability P(Ext, on) and P(Ret, on), respectively. (I) and (II) denote, respectively, unpiliated and piliated pilus machine without bound extension or retraction motor. (B) A time trace of pilus length for a typical pilus extension/retraction event: extension time T_ext, dwell time T_d, and retraction time T_ret. (C) A time trace of pilus length for a discontinuous extension event. (D) A time trace of pilus length for a discontinuous retraction event. B–D Also see SI Appendix, Fig. S2 and Movies S3–S5. (E) A Histogram of extension times of individual pili. (F) A Histogram of dwell times between stop of pilus extension and start of the subsequent pilus retraction. (G) A Histogram of the time individual pili spent retracting (full retractions are limited by the length of pili). (E–G) The error bars are the SD obtained by bootstrapping. The shaded areas are 95% CIs from model simulations (MCS, see SI Appendix, Materials and Methods). No significant difference between simulations and experiments (P > 0.05) was found. See SI Appendix, Materials and Methods for details of the statistical testing. (See SI Appendix, Table S4 for sample sizes and number of replicates).

Interestingly, if binding of the motors to the machine is stochastic, we would expect to see a subset of pili where two extension motors subsequently bind to the same pilus machine, resulting in two subsequent extension events. Similarly, if unbinding of the motors is stochastic, we would expect to see a subset of pili where the retraction motor unbinds before the pilus is fully retracted followed by a second retraction motor binding to fully retract the pilus. In both cases, pilus extension or retraction would appear discontinuous. Intrigued by this prediction of the model, we analyzed the entire extension–retraction cycle of individual pili by tracing the tips of pili relative to the cell body over time and defining periods of extension, dwelling, and retraction (see Materials and Methods and SI Appendix, Fig. S2). A typical pilus extends for about T_ext = 2 s, then dwells for less than T_d = 1 s, and finally retracts all the way back (Fig. 3B and Movie S3). In 15 out of 196 dwell events, an extension event was followed by another extension (Fig. 3C and Movie S4). Similarly, in 11 out of 127 retraction events, the pilus stalled during the retraction, resulting in another dwell event followed by continued retraction as shown in Fig. 3D and Movie S5.

To test if these observed discontinuous extension and retraction events represent “normal” events as predicted by the model with similar properties as continuous events, we compared continuous and discontinuous events. A stochastic motor binding/unbinding model would predict that the longer a pilus is in length, the longer its retraction should take and thus the more likely the retraction is to be discontinuous. Consistent with this prediction, pili that displayed a discontinuous retraction event were significantly longer than those with continuous retraction (SI Appendix, Fig. S3E). Specifically, the probability to observe a discontinuous retraction event for a pilus that is shorter than 1 μm was significantly lower than that for a pilus that is larger than 1 μm (SI Appendix, Fig. S4A). Next, we compared the distributions of pilus lengths, dwell times, and extension and retraction velocities from pili with continuous or discontinuous extension and retractions. We found no significant difference between continuous and discontinuous events except for the expected increase in the length of discontinuously retracted pili (SI Appendix, Fig. S3).

This suggests that the discontinuous extension and retraction events are normal events that occur in pairs. Further, discontinuous extensions are followed by normal retractions, and discontinuous retractions are preceded by normal extensions. Such intermittent dwell events, resulting in discontinuous extension and retraction, have been observed indirectly by measuring the dynamics of Neisseria gonorrhoeae TFP under tension attached to an optically trapped bead (33). However, TFP dwelling has not been previously reported in P. aeruginosa and thus represents a largely unappreciated feature of TFP behavior that highlights the importance of carefully quantifying pilus dynamics.

Estimating the Binding and Unbinding Rates of the Extension and Retraction Motors.

Encouraged by the fact that the stochastic model predicted previously unappreciated features of pilus dynamics, we next sought to determine the parameters of the model that would allow us to make quantitative predictions to test the model experimentally. This stochastic model for TFP dynamics includes six independent parameters: the extension and retraction velocity of the pili (v_ext and v_ret), the binding and unbinding rates of the extension motors (k_ext,on and k_ext,off), and the binding and unbinding rates of the retraction motors (k_ret,on and k_ret,off). The extension and retraction velocities were directly measured (Fig. 1F). In the following, we show how each of the other rates can be estimated from our data (see Fig. 3 and Materials and Methods for details). We then used our model to make quantitative predictions that we validated experimentally.

The duration of each pilus extension event is equal to how quickly the extension motor becomes unbound. Thus, the unbinding rate of the extension motor can be derived from the characteristic unbinding time τ_ext by 1/k_ext,off = τ_ext,off = τ_ext. We directly measured the distribution of pilus extension times (Fig. 3E), which had an exponential shape (indicative of stochastic unbinding of the extension motor) and a characteristic time of 1.6 s (τ_ext, Fig. 3 A and B), indicating that $k_{ext,off}^{-1}={1.6}_{-0.2}^{+0.5}$ s.

The relationship between the unbinding rate of the retraction motor and the duration of retraction events is more complicated. For the majority of retraction events, the pilus becomes fully retracted so we cannot tell when the retraction motor becomes unbound. We do, however, observe a number of discontinuous retraction events that are interrupted by a dwell period, suggesting that the retraction motor became unbound during these events. We observed such events with a probability of 11 discontinuous retractions out of 127 total events (9%). These events represent the short-time tail of the distribution of unbinding times. To account for all retraction events, we used a maximum-likelihood approach to find the characteristic time constant of unbinding that best accounts for the full distribution of both complete and discontinuous retraction events. We note that the only assumption in this approach is that the retraction unbinding times are exponentially distributed, which is consistent with all our other pilus measurements. As detailed in the Materials and Methods and SI Appendix, Fig. S5, this maximum-likelihood approach estimated the unbinding rate of the retraction motor as $k_{ret,off}^{-1}={9.1}_{-3.8}^{+9.7}$ s.

The dwell periods T_d that follow every extension event allowed us to estimate the binding rates of both extension and retraction motors. The time to the next extension or retraction event is set by the binding of the next motor to that pilus, such that τ_dwell = 1/(k_ext,on + k_ret,on). We measured a characteristic dwell time of ${\tau }_{dwell}={0.35}_{-0.05}^{+0.25}$ s from the distribution of all dwells (Fig. 3F). The exponential shape of the distribution of dwell times is again indicative of stochastic protein binding. The ratio of the binding rates of the extension and retraction motors sets the fraction of postdwell events that are extensions versus retractions. As described above, postdwell, we observed 15 secondary extensions and 181 retractions, suggesting k_ext,on/k_ret,on = 15/181. Combining these values and taking into account the finite experimental time resolution that limits our ability to detect short dwell periods (see Materials and Methods and SI Appendix, Fig. S6), we estimate $k_{ext,on}^{-1}={2.4}_{-0.3}^{+1.8}$ s and $k_{ret,on}^{-1}={0.40}_{-0.05}^{+0.30}$ s.

To further validate our model and parameters, we sought to use the model to predict the ratio of discontinuous to full retractions. We simulated cycles of extension and retraction of individual pili using the Monte Carlo method by drawing random samples from the model’s distributions of extension and retraction times and velocities (referred to as MCS, see Materials and Methods). From those numbers, we calculated the expected length of each pilus and determined if its retraction time was enough to fully retract it (i.e., if the retraction gave rise to a discontinuous or full retraction). We compared our simulated distribution of discontinuous retractions (Fig. 3D, yellow dashed) and full retractions (Fig. 3D, yellow) to our experimental findings (markers) and found good agreement (P > 0.05). As yet further validation, we analyzed an independent set of data that was not used to estimate the model’s parameters and found that the resulting pilus lengths agreed well (P > 0.05) with our model’s simulated results (Fig. 1E). Together, these findings suggest that discontinuous pilus extension and retraction events can be used to derive the underlying features of all extension and retraction events and that our stochastic model quantitatively captures these features.

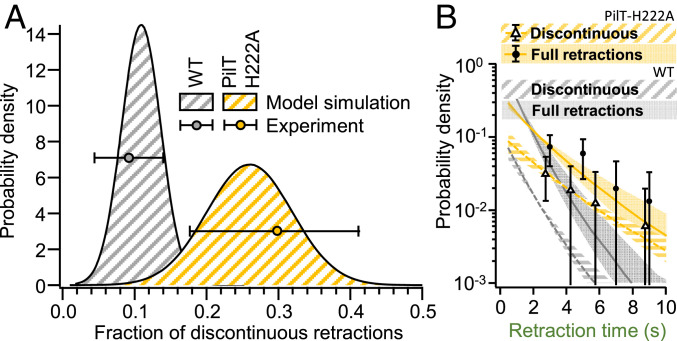
The Effect of a Retraction Motor Mutant on Discontinuous Retractions Is Accurately Predicted by the Stochastic TFP Model.

To further support our model, we used a genetic approach to test one of its predictions. The model suggested that if TFP extension and retraction velocities are independent of motor binding rates, a mutant that reduces retraction velocity should show more discontinuous retraction events because TFP need more time to complete a full retraction. To test this prediction, we analyzed pilus dynamics in a point mutant (PilT-H222A) in the ATPase activity of the PilT retraction motor that affects pilus retraction velocity (34). Since we expressed this mutant ectopically at a different locus on the chromosome under a tetracycline-inducible promoter (Ptet::pilT-H222A) in a background where the native copy of PilT has been deactivated by a transposon insertion (PilT::Tn5) (35), we first verified that pili in the PilT::Tn5 mutant do not retract. We then identified expression levels of PilT-H222A that resulted in WT-like pilus behavior with respect to pilus extension velocity, all four binding/unbinding rates, and the properties of the discontinuous retraction events (SI Appendix, Figs. S3 and S7–S9). Despite its similarity to WT in most regards, at this induction level PilT-H222A pili retracted three times slower compared to WT (as predicted for a mutant with an impaired retraction motor). We then measured the fraction of discontinuous retractions of PilT-H222A pili, and indeed found that they increased about threefold relative to WT (Fig. 4A). We also performed a simulation in which we reduced v_ret threefold but left all the other parameters unchanged and observed good agreement (P > 0.05) with the experimental observation for the fraction of discontinuous retraction events. Similarly, the distributions of retraction times (the time a pilus spent retracting until it either dwelled or was fully retracted) between the simulation and our experimental results with WT and PilT-H222A are indistinguishable (P > 0.05) (Fig. 4B). We note that the distribution of retraction times does change between WT and PilT-H222A in both experiments and simulations because the slower retraction takes more time, providing a larger window during which the motor can disengage. These results further support that discontinuous events are a normal part of TFP dynamics and show that the discontinuous pilus retraction can be explained quantitatively by the stochastic binding and unbinding of the pilus motors.

Fig. 4.

The increase of the fraction of discontinuous retractions for the slowly retracting mutant PilT-H222A is accurately predicted by the model. (A) The fraction of discontinuous retractions increases about threefold from WT to PilT-H222A. The shaded areas indicate distributions of the fraction of discontinuous retraction events obtained by simulation. The markers indicate the experimentally obtained fraction of discontinuous retractions with SD obtained by bootstrapping. No significant difference between simulations and experiments (P > 0.05) was found. (B) The distribution of retraction times of individual pili for PilT-H222A (yellow = model prediction, markers = experimental data) and WT (gray) for comparison. The error bars are the SD obtained by bootstrapping. The shaded areas are 95% CIs from model simulation ([MCS], see Materials and Methods). No significant difference between simulations and experiments (P > 0.05) was found. (See SI Appendix, Table S4 for sample sizes and number of replicates).

The Switch between Extension and Retraction Is Governed by the Stochastic Binding and Unbinding of Both Motors.

We next sought to use our quantitative framework to determine how TFP switch between extension and retraction. Based on our observations and recent cryo-EM and interferometric imaging data, we tested three competing models (12, 24). One hypothesis is that both the binding and unbinding of the retraction motor are purely stochastic and independent of the presence of the pilus itself (Model 1: the stochastic model). A second possibility is that the retraction motor can only bind to the machine if a pilus is present but unbinds in a stochastic manner whether or not the pilus has fully retracted (Model 2: the pilus-dependent model). A third possibility is that the retraction motor both only binds if a pilus is present and unbinds as soon as the pilus is fully retracted (Model 3: the pilus-sensing model). These three models make different predictions for the TFP production rate. Due to the rapid on rate and slow dissociation rate of the retraction motor compared to the extension motor, Model 1 predicts that the pilus machine is occupied by the retraction motor most of the time. Because the extension and retraction motors compete for binding to the pilus machinery, this suggests that the rate of pilus production is primarily limited by the retraction motor. In Models 2 and 3, the retraction motor does not bind the unpiliated machine, and thus the extension motor can bind more frequently, resulting in more pilus extension events compared to Model 1. Furthermore, since the retraction motor unbinds after the pilus is fully retracted in Model 3, we would expect to see the largest number of pili in this model.

To differentiate between these different behaviors of the retraction motor, we again used the Monte Carlo method (see Materials and Methods) to simulate cycles of the stochastic binding and unbinding of the extension and retraction motors using each of the three models (Fig. 5A). We counted the number of pilus extension events per pilus machine in a 60-s time window in the simulation and found that, for the simple stochastic model (Model 1), the pilus production rate was approximately exponentially distributed with typically one pilus event per minute (Fig. 5C). The simulations for Models 2 and 3 were distinctively different from those of Model 1 as both Models 2 and 3 displayed a more Gaussian distribution peaking between 3 pili per minute (Model 2) and 6 pili per minute (Model 3).

Fig. 5.

Comparison of the pilus production rate predicted by different models for the switch between extension and restriction. (A) An example of Monte Carlo simulation for binding and unbinding of the extension and retraction motor showing a single pilus extension event. Note that the retraction motor stays attached after the pilus is retracted fully. (B) The maximum projection of 60 superresolved movie frames recorded at 1 Hz frame rate showing directions of all pili that have been extended by the cell. The roman numerals label individual pilus machines. The thick, transparent curve represents the line scan area used to analyze pili. (C) A distribution of the pilus production rate per machine. The experimental data are shown as black markers with error bars. The Monte Carlo simulations are shown for the stochastic model (Model 1, gray), the pilus-dependent model (Model 2, pink), and the pilus-sensing model (Model 3, blue). The error bars are the SD obtained by bootstrapping. The shaded areas are 95% CIs from model simulation (MCS, see Materials and Methods), and bold lines are their means. (See SI Appendix, Table S4 for sample sizes and number of replicates).

To experimentally differentiate the three hypotheses, we measured the pilus production rates of individual pilus machines and compared these results to the simulated distributions from the three models. Measuring the pilus production rate of individual machines is experimentally challenging because a pilus machine is only 15 to 20 nm in diameter and neighboring complexes can be closer together than the conventional optical resolution limit (12). To tackle this problem, we used live-cell super-resolution microscopy and looked at maximum projections of entire movie stacks (Fig. 5B and Movie S11). Due to the strong curvature at the poles, pili originating from close-by machines (roman numerals in Fig. 5B) emanate at different angles and can be more easily distinguished. We thus analyzed changes in intensity along a line just outside the cell circumference (transparent curve, Fig. 5B) in a kymograph (SI Appendix, Fig. S10B). By assigning each pilus extension event to the machine from which it emanated, we were able to count the frequency of pilus extension events per individual machine (SI Appendix, Fig. S10C). We found that pilus extension frequency was exponentially distributed with an average of roughly one pilus extension event per minute. Qualitatively, these data agreed well with the simple stochastic model (Model 1) but were incompatible with both Models 2 and 3 since these distributions have a different shape (Fig. 5C).

The only deviation between our Model 1 simulation and the experimental results is for production rates ≥ 4 pili ⋅ min⁻¹. We suggest that this small deviation can be attributed to the finite imaging resolution. This resolution limit makes it difficult to distinguish if two short pili emanate from the same machine or from two nearby complexes, which in turn leads to a systematic overestimation of pilus extension frequency. Nevertheless, we quantitatively tested if this deviation is statistically significant and performed Kolmogorov-Smirnov tests that compare the simulations for each model using the mean binding/unbinding rates and their lower and upper bounds separately to the experimental data. Model 1 has P < 0.05 for the mean binding/unbinding rates, P < 0.001 for the lower bound of these rates, and P > 0.05 for their upper bounds. Models 2 and 3 yield P > 0.05 for all combinations of the rates. This confirms the qualitative result that Model 1 can best explain the experimental data and further indicates that our estimates for the binding and unbinding rates of the motors might be slightly higher than the actual binding and unbinding rates. Together, our findings support the conclusion that the switch between pilus extension and retraction is stochastic and that the rate of pilus production is limited by the slow unbinding step of the retraction motor.

PilT Is Limiting for Pilus Production but Not Pilus Length.

A prediction of our stochastic competitive binding model is that changing the levels of the retraction motor should change the probability of the extension motor binding but should not affect the rate at which the extension motor unbinds. The probability of the extension motor binding determines the frequency with which pili extend while the duration of the extension motor remaining bound determines pilus length. We thus sought to test our model’s prediction by overexpressing the PilT retraction motor and measuring its effect on pilus production rate and pilus length. Specifically, we made an arabinose-inducible PilT strain (Pbad::pilT) on a high copy number plasmid to overexpress PilT. Induction of PilT with more than 0.003% Arabinose resulted in a significant decrease in pilus production (Fig. 6A), and expression of PilT with 0.1% Arabinose resulted in a strong loss of pilus production with fewer than 20% of cells still making pili. In contrast to the strong effect of PilT overexpression on pilus production rate, the maximum length of the pili produced did not change throughout the entire range of induction levels (Fig. 6B). This result confirms that PilT is a limiting factor for pilus production in P. aeruginosa and supports our model in which the relative concentration of the retraction and extension motors changes their effective binding rates without disrupting their unbinding-dependent behavior.

Fig. 6.

Overexpression of the retraction motor PilT limits pilus production but not pilus length. (A) The fraction of cells that make pili and (B) the maximum length of individual pili as a function of arabinose induction. PilT was induced ectopically from a high-copy number plasmid under control of the arabinose promoter Pbad. The native copy of PilT was inactivated by a transposon insertion. The boxplots represent the median and 25%/75% quantiles. (ns): not significant, P > 0.05. (***) P < 0.001. See Materials and Methods for details of the statistical testing. (See SI Appendix, Table S4 for sample sizes and number of replicates).

PilT Binds to Active Pilus Machines Even in the Absence of Pili.

Our results suggest that PilT both remains bound to the pilus machine after retraction is complete and can stochastically bind to naïve machines, such that PilT should often be bound to machines that lack extended pili. To test this prediction, we made a fluorescent fusion to the retraction motor (mRuby3-PilT) and correlated the localization of PilT with pilus activity. After establishing that this mutant is functional (SI Appendix, Fig. S1), we first confirmed previous reports (17, 36) that PilT localizes to the poles of most cells by analyzing single images with long exposure times (10 s) (Fig. 7A). We then acquired time lapse movies (45 s long) of pilus activity together with PilT fluorescence at a higher frame rate (every 1 s) to measure the correlation between pilus activity and PilT localization. P. aeruginosa has mainly unipolar pili (SI Appendix, Fig. S1 and ref. 17) and we first checked if PilT only localizes to piliated poles or if it also localizes to unpiliated poles. We used maximum projections of all pilus frames of a given movie to distinguish between active poles that make pili and inactive poles that do not make pili (Fig. 7 B and C). To measure PilT localization, we integrated all PilT frames to one image and compared the intensity of PilT at the pole to the average intensity of the cytoplasm (Fig. 7 B and C). As expected, we found that, in this 45-s window, many poles never extended pili (Fig. 7 A and B). Quantifying PilT fluorescence at these inactive poles revealed that most inactive poles (86%) do not localize PilT and display PilT fluorescence intensity that is indistinguishable from cytoplasmic fluorescence (Fig. 7D). The remaining 14% of inactive poles that had an elevated PilT fluorescence could be poles where there was a pilus that we did not detect, either because it was too short to be resolved or it extended and retracted between two subsequent frames of pilus activity.

Fig. 7.

PilT localizes to poles with active pilus dynamics even in the absence of pili. (A) N-terminally tagged mRuby3-PilT localizes to most poles of P. aeruginosa. An overlay of phase image and red fluorescence channel (mRuby3). (B) Simultaneous imaging of PilT localization (Left, integrated projection) and pilus activity (Right, maximum projection) shows that active poles with pili (filled triangle) localize PilT while inactive poles without pili (open triangle) do not. (C) The quantification of PilT localization using a line scan through the long axis of the cell. (D) The relative brightness of the cell pole with respect to the cytoplasm for active and inactive poles, comparing only times when no pilus is present at the active pole. The boxplots represent the median and 25%/75% quantiles. (E) The C-terminally tagged PilO-Cherry localizes to the poles of P. aeruginosa. (F) An overlay of PilO localization (red) and pilus activity (green, maximum projection). The white arrows point to extended pili. (G) The fraction of poles that localize PilO and that make dynamic pili. The boxplots represent the median and 25%/75% quantiles. (H) The consecutive time-lapse images (every 1 s) of PilT (red) and pilus activity (green). PilT localized (red arrow) to the piliated pole immediately before the pilus started retracting (between frame two and three) and remained bound after the pilus was fully retracted (frames five and six). The color channels were acquired sequentially: first green, then red. (All scale bars are 2 μm.) (See SI Appendix, Table S4 for sample sizes and number of replicates).

The simplest explanation for why poles would have neither pili nor PilT localization is that there are no pilus machines at inactive poles. To test this hypothesis, we made a fluorescent fusion to PilO (PilO-mCherry, Fig. 7E), a structural protein of the pilus machine (2). PilO is an essential TFP protein, and its localization to immobile spots on the pole indicates that it is incorporated into a larger structure, most likely representing an intact TFP machine. We thus interpreted the presence of PilO foci as a fully assembled pilus machine. After validating that this mutant is functional (SI Appendix, Fig. S1), we analyzed the fraction of poles with PilO fluorescence (Fig. 7 E and F) and the fraction of poles with pilus activity (Fig. 7F). Our results show that 96% of poles have PilO, suggesting that almost all poles have pilus machines (Fig. 7G). In contrast, only about two thirds of poles make pili (Fig. 7G). Thus, many poles have inactive pilus machines and PilT appears to specifically bind to poles with active pilus machines.

To assess if PilT binds to active poles only when pili are present, we focused on “active” poles that produced pili at some point during the 45-s observation window (Fig. 7 B and C). Correlating changes in PilT fluorescence at active poles to the extension and retraction of individual pili revealed many cases (SI Appendix, Fig. S11) where polar PilT fluorescence increased (Fig. 7H, frame two) immediately prior to the start of a pilus retraction event (Fig. 7H, frame three). This is consistent with PilT’s known role in initiating retraction. In addition, we often observed that polar PilT fluorescence persisted (Fig. 7H, frames five and six) well after the pilus was fully retracted (Fig. 7H, frame five). Interpreting changes in polar PilT localization is complicated by the fact that most active poles have more than one active pilus machine (SI Appendix, Fig. S10). Thus, an observed change in PilT fluorescence could be due to a binding/unbinding event of PilT to the machine that has an active pilus or to another machine that currently does not have a pilus. To circumvent this complication, we analyzed polar PilT fluorescence intensity during phases where there was no pilus present for a period of at least 10 s. We integrated the PilT intensity of all images during this period and compared the intensity at the poles to the cytoplasmic intensity. We found that 80% of active poles had significantly elevated polar PilT fluorescence even in these periods during which they had no pilus (Fig. 7D). These results support our hypothesis that PilT exhibits significant binding to pilus machines that lack pili.

Discussion

Here, we fluorescently labeled the TFP of P. aeruginosa and quantified the extension and retraction cycles of individual pili. In addition to demonstrating that labeling does not affect twitching, our findings agree well with the previously available data on P. aeruginosa TFP (13, 14, 24, 25). Importantly, our findings also enable us to reconcile these previous reports. For example, both we and early electron microscopy studies (14) find a broad distribution of TFP lengths with many short pili (<1 μm), suggesting that the recent creative use of interferometry to measure dynamics of unlabeled pili in live cells was limited in its ability to detect short pili by the 2- to 3-μm halo surrounding the cell body (24). Meanwhile, the study of P. aeruginosa TFP by nonspecific labeling (25) did not quantify pilus length distributions, event times, or dwelling but did report similar TFP extension and retraction rates to those we quantify here. Importantly, while our data agree with previous results, they fundamentally alter the previous interpretation that only a small fraction of cells make pili, and that piliated cells typically only make 1 to 2 pili (13, 14, 17, 24). In contrast to that conception, our ability to detect short pili and to detect pili over an extended period of time revealed that TFP are highly prevalent and dynamic: a typical cell makes a new pilus every 5 to 10 s and retracts each pilus rapidly.

To explain the observed pilus behaviors, we propose a model that is minimal in its nature and relies only on the presence of extension and retraction motors and their competitive, stochastic interactions with the pilus machine. The exponential shapes of the distributions of all pilus properties that are governed by the binding or unbinding of the motors (such as pilus length, extension time, retraction time, and dwell time) support the stochastic nature of the interactions of the motors with the pilus machine. The model predicted the existence of discontinuous extension and retraction events, which we experimentally confirmed. Such dwell events have also been observed in N. gonorrhoeae TFP under high pulling forces using laser tweezers (33). We note that our model also predicts the existence of a secondary extension that follows a discontinuous retraction. As outlined in SI Appendix, Fig. S12, these events are expected to occur in only ∼0.5% of cells and are thus very rare and hard to detect. To support that the discontinuous events are normal events and to support the model itself, we verified that the distributions of pilus length, dwell time, and extension and retraction velocity are indistinguishable from regular, continuous events. The fraction of discontinuous events changed in a PilT point mutation that only affected the pilus retraction velocity in a way that was accurately predicted by the model. In addition, PilT overexpression, which affects extension motor binding but not unbinding, resulted in a strong decrease of pilus activity but not pilus length, in agreement with the model and similar experiments in Neisseria (33). By comparing different molecular models for the switch between extension and retraction, we further show that the stochastic model accurately predicts the experimentally verified pilus production rate of individual pilus machines. Together, these results demonstrate that there is strong quantitative agreement between our simulations and experiments, showing that the stochastic binding and unbinding of extension and retraction motors is sufficient to quantitatively explain all TFP dynamics, and that these behaviors are not altered by the presence of a surface.

A nonintuitive conclusion from our stochastic competition model is that the major throttle of pilus extension is the low unbinding rate of the retraction motor that causes PilT to persist after pilus retraction completes and therefore limit extension motor binding. We support this result by directly demonstrating that PilT localizes to active pilus machines even after pilus retraction is complete. We also show that, while almost all cell poles show PilO localization and thus likely have fully assembled pilus machines, many of these machines do not actively make pili or bind PilT. The existence of such inactive pilus machines that cannot bind motors could explain why a cryo-EM study of many Myxococcus xanthus pilus machines averaged together did not observe retraction motors on unpiliated machines (12). Another possibility is that TFP dynamics differ across species, though we note that our P. aeruginosa findings are consistent with simulations of twitching in N. gonorrhoeae (37–39). We also note that, because several pilus machines could be present within the diffraction-limited resolution of our measurements, future super-resolution methods will be required to directly link polar motor dynamics obtained by fluorescence microscopy to the binding and unbinding rates of individual motors obtained by measuring pilus extension and retraction. Future structural studies in P. aeruginosa and TFP dynamics measurements in M. xanthus should also help understand these differences.

Previous studies have invoked complicated force sensors and fast coordination between motor elements to explain TFP dynamics (12, 24). However, our findings indicate that such elaborations are not necessary to explain basic pilus behaviors. Nevertheless, our results do not exclude the possibility that surface contact is sensed actively by pilus retraction leading to subsequent biochemical signaling that changes protein synthesis or transcription (5, 27, 40). While the presence of a surface does not alter TFP dynamics directly, surface sensing could still be mediated by TFP through biochemical changes in the pilus machine that do not affect the binding or unbinding rates but are sensed by auxiliary modules like PilJ. Competitive binding could then be regulated by accessory factors that alter the base rates of binding and unbinding of the extension and retraction motors. The titration of PilT suggests that cells can control pilus production by altering pilus motor levels transcriptionally or posttranscriptionally. In P. aeruginosa, PilB and PilT are in different operons, which could facilitate the control of their relative expression levels. In M. xanthus, the Frz system orchestrates oscillations in the direction of twitching motility (41, 42). The interaction of the small Ras-like GTPase MglA-GTP with the tetratricopeptide repeat domain–containing protein SgmX promotes TFP formation at the leading cell pole, while the cognate GTPase-activating protein MglB converts MglA-GTP to MglA-GDP and thus directly inhibits TFP formation at the lagging cell pole (43, 44). This suggests that the Frz/Mgl/Sgm system directly regulates pilus dynamics on the motor level. Similarly, in P. aeruginosa, the Pil-Chp two-component system regulates pilus behaviors, both through biochemical interaction of the two response regulators PilG and PilH with the pilus machine and by transcriptional modification using the cAMP-dependent transcriptional regulator Vfr (40, 45–47). The second messenger c-di-GMP has also been shown to interact directly with the extension motor and other components of the TFP machine (48–50), thereby representing another interesting candidate for the regulation of the binding and unbinding rates of TFP (51). This suggests that while TFP motor protein binding itself is stochastic, additional factors can activate and/or deactivate individual pilus machines like a master switch by promoting or inhibiting motor binding. This explains our result that pili themselves are predominantly unipolar while assembled pilus machine (indicated by the presence of PilO) can be found at both poles.

We also note that our model abstracts the extension and retraction motors. In P. aeruginosa, PilB is the only known extension motor, PilT is considered the primary retraction motor, and PilU has been shown to affect retraction (24, 52). Our analysis confirms that PilU is not needed for retraction (SI Appendix, Fig. S11) and that PilT overexpression is limiting for pilus production (Fig. 6). Nevertheless, recent studies also suggest that these motors may have more complicated interactions (52, 53), and in the future our model could help tease apart the specific contributions of different mutants to the extension and retraction cycle.

Our findings show that while most P. aeruginosa make many pili, these cells have tuned the affinities and rates of the extension and retraction motors to generate short pili that are rapidly and fully retracted. However, this also prevents individual pilus machines from rapidly extending new pili after a retraction event, such that frequent pilus extension requires the presence of multiple pilus machines. We suggest that tuning the pilus parameters to increase retraction events benefits P. aeruginosa by enhancing surface interactions such as the displacement required for twitching motility. Frequent pilus retraction also allows planktonic cells to efficiently sample the environment for the presence of a surface. Once a pilus is bound and retracts under load, subsequent downstream signaling may activate transcriptional programs associated with a surface-bound lifestyle (5, 11, 27, 40, 54). Similarly, tuning the parameters to ensure that most pili are fully retracted enhances pilus subunit recycling to the membrane, thereby enhancing the rate of new pilus production. Thus, our findings support the hypothesis that P. aeruginosa has evolved to maximize its pilus budget for interaction with surfaces. In the future, it will be interesting to see how regulatory elements such as the Pil-Chp two-component system or second-messenger–mediated modifications can alter the base rates described here (40, 48–50). Further, it is likely that other species with other physiological demands and constraints modulate the kinetics of motor binding to change pilus length, number, and dynamics to achieve other functions, like cell–cell interactions or DNA uptake.

Materials and Methods

Strains and Growth Conditions.

Information on cloning, plasmids, and primers used in this study can be found in the SI Appendix, Materials and Methods and Tables S1–S3.

P. aeruginosa PAO1 was grown in liquid lysogeny broth (LB) Miller (Difco) and Cysteine-free EZ rich defined medium (Teknova) (55) in a floor shaker, on LB Miller agar (1.5% Bacto Agar), on Vogel-Bonner minimal medium (VBMM) agar (200 mg/l MgSO₄ 7H2O, 2 g/l citric acid, 10 g/l K₂HPO₄, 3.5 g/l NaNH₄HPO₄ 4 H₂O, and 1.5% agar), and on no-salt LB (NSLB) agar (10 g/l tryptone, 5 g/l yeast extract, and 1.5% agar) at 30 °C (for cloning, see below) or at 37 °C. Escherichia coli S17 was grown in liquid LB Miller (Difco) in a floor shaker and on LB Miller agar (1.5% Bacto Agar) at 30 °C (for cloning, see below) or at 37 °C. Antibiotics were used at the following concentrations: 200 μg/mL carbenicillin in liquid (300 μg/mL on plates) or 10 μg/mL gentamycin in liquid (30 μg/mL on plates) or 10 μg/mL anhydrotetracycline in liquid for Pseudomonas, and 100 μg/mL carbenicillin in liquid (100 μg/mL on plates) or 30 μg/mL gentamycin in liquid (30 μg/mL on plates) for E. coli.

Sample Preparation and Imaging.

Technical information on the microscopes can be found in the SI Appendix.

For imaging of pilus dynamics, cells were grown overnight in EZ rich medium at 37 °C, diluted 1:1,000 into fresh EZ rich, and grown to mid log phase (optical density = 0.4). EZ rich medium has a low background fluorescence, and the absence of free Cysteine improves the labeling efficiency with the maleimide dye while assuring rich growth conditions. 1 mg of Alexa488 maleimide (Fisher A10254) was suspended in 400 μL dimethyl sulfoxide, aliquoted, and stored at −20 °C. Freeze–thaw cycles were avoided as they degrade efficiency of pilus labeling. Dye was added 1:100 to 180 μL of culture and incubated for 45 min at 37 °C in the dark. Cells were washed twice gently in EZ rich by pelleting at 6,000 revolutions per minute for 30 s in a conventional tabletop centrifuge and concentrated to 20 μL. For optical trapping experiments in liquid, a tunnel slide was made by placing a regular coverslip on a microscope slide, separated by double-sided sticky tape at each side of the coverslip. Cells were flushed in by capillary forces using a pipette, and ends were sealed with Valap to prevent evaporation and flow of liquid. WT cells have flagella and typically swim out of the optical trap. To prevent cells from leaving the trap, we used a flagella knockout ΔfliC for all quantitative experiments after confirming qualitatively that flagellated WT cells still make and retract pili when trapped. For all other experiments, 0.5% agarose pads were made by melting 1.0% agarose in water. Agarose was cooled down to 60 °C and mixed 50:50 with double-concentrated EZ rich at 60 °C. Then, 1 μL of labeled cell culture was spotted on each pad, and the pad was transferred to a number 1.5 glass-bottom Petri dish (Mattek). All experiments were performed at 37 °C on 3 different microscopes as described in the SI Appendix, Materials and Methods.

Data Availability

All data supporting this study are available within the article and SI Appendix.