Significance
The kinetic assessment of catalytic reactions is essential to the design and application of thermochemical processes useful in petrochemical synthesis, energy conversion, and environmental remediation. We demonstrate that the ubiquitously used Langmuir–Hinshelwood formalism is incomplete and fails to correctly describe even simple catalytic reactions (e.g., A + A → A2). An accurate kinetic description requires explicit rate equations for multisite configurations (e.g., A*–A* pairs) to account for the nonrandom clustering/isolation of surface species. We rigorously describe clustering/isolation phenomena by derivation of coverage-dependent stoichiometric coefficients, which capture the distinct influence each elementary step exerts on each catalytic site ensemble—thereby overcoming limitations of the mean-field (i.e., Hinshelwood) assumption in describing reactions of mobile Langmuirian adsorbates on catalytic surfaces.
Keywords: catalytic site ensembles, surface diffusion, coverage-dependent rates
Abstract
We demonstrate that the Langmuir–Hinshelwood formalism is an incomplete kinetic description and, in particular, that the Hinshelwood assumption (i.e., that adsorbates are randomly distributed on the surface) is inappropriate even in catalytic reactions as simple as A + A → A2. The Hinshelwood assumption results in miscounting of site pairs (e.g., A*–A*) and, consequently, in erroneous rates, reaction orders, and identification of rate-determining steps. The clustering and isolation of surface species unnoticed by the Langmuir–Hinshelwood model is rigorously accounted for by derivation of higher-order rate terms containing statistical factors specific to each site ensemble. Ensemble-specific statistical rate terms arise irrespective of and couple with lateral adsorbate interactions, are distinct for each elementary step including surface diffusion events (e.g., A* + * → * + A*), and provide physical insight obscured by the nonanalytical nature of the kinetic Monte Carlo (kMC) method—with which the higher-order formalism quantitatively agrees. The limitations of the Langmuir–Hinshelwood model are attributed to the incorrect assertion that the rate of an elementary step is the same with respect to each site ensemble. In actuality, each elementary step—including adsorbate diffusion—traverses through each ensemble with unique rate, reversibility, and kinetic-relevance to the overall reaction rate. Explicit kinetic description of ensemble-specific paths is key to the improvements of the higher-order formalism; enables quantification of ensemble-specific rate, reversibility, and degree of rate control of surface diffusion; and reveals that a single elementary step can, counter intuitively, be both equilibrated and rate determining.
The Langmuir model of adsorption, used ubiquitously in the study of fluid physics (1–3), environmental remediation (4–7), separations (8, 9), heterogeneous catalysis (10–12), and other fields (13, 14), describes the adsorption and desorption of fluid-phase species on solid surfaces under the following conditions: 1) the adsorbent is a perfect, flat two-dimensional (2D) lattice; 2) each adsorption site can be occupied by at most one occupant; and 3) the surface is energetically uniform, and adsorbates have no energetic interactions. We refer to this as the system being thermodynamically ideal.
With the above assumptions, the specific rate, r, of reversible adsorption of a gas-phase species A(g), which occupies a single site as surface species a, is
| [1] |
where θo and θa are, respectively, the fractional surface coverages of vacant sites and a-occupied sites, kdes is the rate constant of desorption, and kads is the product of the rate constant of adsorption and the thermodynamic activity (ideally, partial pressure) of A(g). Catalytic reactions of Langmuirian adsorbates are commonly described by the Langmuir–Hinshelwood theory (12), which, in addition to the conditions of Langmuirian adsorption, assumes the following: 4) adsorbates are randomly distributed on the surface (i.e., there are no spatial correlations between sites). We refer to this as the system being combinatorially ideal.
The Hinshelwood assumption permits simple mathematical description of a surface reaction between neighboring adsorbates. Consider, for example, the reaction between two a surface species. The general rate expression for such an elementary step is
| [2] |
where kr is the rate constant of the reaction, z is the coordination number of the 2D lattice, and θaa is the fraction of pairs of sites which contain two a species (15, 16). The rate expression in Eq. 2 can be simplified in terms of only single-site coverages by use of the Hinshelwood assumption (12), giving
| [3] |
The Hinshelwood assumption reduces coverages of site configurations of any size to a product of coverages of all constituent single-site occupants. In other words, the mean-field metric
| [4] |
is taken to be unity for all pairs of site occupants i and j per the Hinshelwood assumption. Similarly, θijk is assumed equal to θiθjθk, and so on.
The veracity of the Hinshelwood assumption is contingent on a sufficiently randomizing process—namely, arbitrarily fast surface diffusion—to achieve a uniform adsorbate distribution. Kinetic Monte Carlo (kMC) studies of CO oxidation (15), CO2 hydrogenation (17), CO methanation (18), and NO oxidation and NO2 reduction (19) have recognized the shortcomings of the Hinshelwood assumption and demonstrated surface diffusion in catalytic systems is often insufficiently fast to validate the Langmuir–Hinshelwood formalism even in the absence of lateral interactions—evinced by mean-field metrics, which deviate from unity by factors ≳100× (15, 18) and significantly miscalculated rates and reaction orders (15, 17–19). These deficiencies arise because multisite requirements of elementary steps induce clustering (μij > 1) and isolation (μij < 1) of surface species to which the Hinshelwood assumption is ignorant; each site ensemble uniquely combinatorially couples to the sorptive/reactive/diffusive configuration of each elementary step and therefore requires unique rate terms to capture the propensity of each step to engender islanding or partitioning of surface species which constitute the considered ensemble.
In this work, we develop an analytical formalism which derives higher-order rate terms necessary to describe dynamics of ensembles of any size and shape. The Langmuir–Hinshelwood formalism is the 0th-order variant of the presented mathematical framework (i.e., retains only terms of the 0th order) and consequently can only reliably describe catalytic sequences consisting of exclusively single-site elementary steps—thereby prohibiting quantitative description of surface diffusion events which inherently require two sites (e.g., ao ⇌ oa). The first-order treatment retains terms of the 0th and first order, enabling quantitative description of combinatorial nonidealities that are neglected by the Hinshelwood assumption and are necessary to generally describe catalytic reactions of mobile Langmuirian adsorbates. Closed-form first-order rate expressions permit calculation of ensemble-specific degrees of rate control and reaction orders inaccessible to kMC simulation; the kMC method does accurately predict adsorbate clustering/isolation and the kinetic consequences thereof. However, in doing so stochastically, it is unable to identify compendious rate terms responsible for these phenomena.
Combinatorial Nonidealities in Langmuirian Adsorption
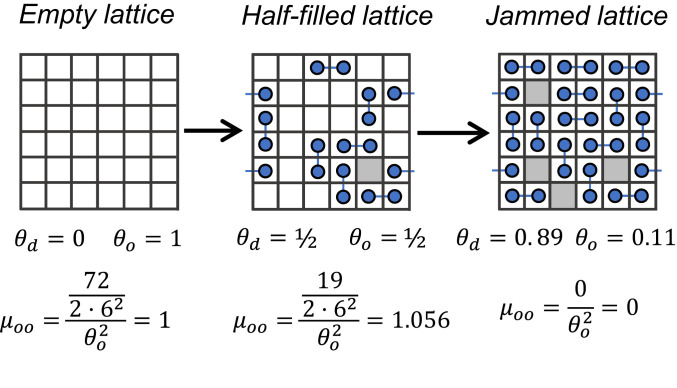
We introduce the general mathematical framework used to describe catalysis of Langmuirian adsorbates through the simplest example of a combinatorially nonideal rate process—irreversible adsorption of unreactive, immobile dimers, dd, on a 2D square lattice (20–23). Consider the filling of the lattice starting from an empty state, depicted in Scheme 1. As dimers randomly adsorb on the surface, some fraction of vacant sites, o, will become irreversibly isolated (e.g., the gray site in the half-filled lattice in Scheme 1). Therefore, at saturation, the population of vacant pairs will be zero, but the coverage of isolated vacant sites will be finite (i.e., μoo = 0). The unfilled, saturated lattice is said to be in a “jammed” state, and the saturation coverage is referred to as the dimer jamming limit for a 2D square lattice (20–23). The Langmuir–Hinshelwood formalism is unable to reproduce jamming phenomena such as these because the fraction of site pairs available for adsorption is always taken to be , which cannot be zero when θo is nonzero (i.e., μoo is assumed to be unity, which is inaccurate). The inability to capture jamming behavior exemplifies the limitations of the Langmuir–Hinshelwood model to describe combinatorially nonideal dynamics of thermodynamically ideal adsorbates.
Scheme 1.
Jamming of adsorbing dimers on a 2D square lattice. Snapshots of irreversible adsorption of unreactive dimers (blue circles connected by blue lines) on a 6 × 6 square lattice with periodic boundary conditions. Bonds extending outside the lattice (blue lines) indicate dimers adsorbed on either side of the periodic boundary. Gray squares indicate isolated vacant sites.
Hierarchical Rate Equations
The complete analytical description of catalysis of Langmuirian adsorbates generalizes formalisms for jamming phenomena (20–24) to include desorption, surface reaction, and surface diffusion processes by construction of an infinite set of hierarchical rate equations which describe time evolution of coverages of all possible site configurations of any size (21, 22). By hierarchical, we mean to say that the rate equations for populations of configurations containing n sites is dependent on populations of configurations of containing n + 1 sites, thereby generating an unending list of rate equations considering ever larger configurations of sites. The hierarchical nature of the rate equations confers a complete description of combinatorially nonideal catalysis which we regard as the analytical analog to the kMC method; however, completeness must be sacrificed to make the analytical pen and paper model tractable. The infinite hierarchy of rate equations demands a consistent truncation scheme to yield a finite, solvable set of coupled rate equations. In the following, we first explicate the hierarchical nature of catalytic rate equations and then introduce and provide an example of the first-order truncation procedure—which we regard as having the optimum balance of completeness and simplicity (25).
We continue the example of irreversible dimer adsorption on a square lattice to demonstrate the hierarchical nature of rate equations. We derive the rate equation describing the time evolution of vacant site pairs, oo, during dimer adsorption with the aid of Scheme 2, which illustrates all configurations which annihilate oo site pairs. The adsorption rate equation for oo is
| [5] |
where kdd,ads is the product of the rate constant of adsorption and the thermodynamic activity of the fluid-phase species adsorbing as dd. The first term enclosed in parenthesis in Eq. 5 accounts for the annihilation of oo for every adsorption event—as shown in the first row of Scheme 2. The last two terms in Eq. 5 account for annihilation of an additional oo pair if the adsorption center is neighbored by another vacant site at any of the six nearest neighbor positions per the second and third rows of Scheme 2. From inspection of Eq. 5, we see that the population, or probability, of the two-site configuration oo is dependent on populations of three-site configurations. Furthermore, rate equations for three-site configurations, for example ooo, are functions of populations of four-site configurations, for example,
| [6] |
and the rate equations for four-site configurations are functions of populations of five-site configurations, and so on, ad infinitum. Therefore, the complete analytical description of irreversible dimer adsorption, or any rate process involving Langmuirian adsorbates, requires an infinite hierarchy of rate equations—capable of capturing combinatorial nonidealities involving site ensembles of arbitrary size and shape. The complete, infinite set of equations is made finite and solvable by introduction of a mathematically consistent truncation procedure—formally detailed in the work of Nord and Evans (21, 22, 26). The truncation procedure operates directly on conditional probabilities and is described in the following.
Scheme 2.
Elimination of oo pairs by D2(g) adsorption (D2(g) + oo → dd). d monomers are shown by filled red circles. Gray squares indicate lattice sites that host adsorption. Blue and green squares indicate sites that are the nearest neighbors to the adsorption center.
Conditional Probabilities and Truncation of Hierarchical Rate Equations
Consider the conditional probability, χ, that a particular conditioned site is vacant, o, provided the neighboring conditioning site, ϕ, is known to be vacant. We distinguish ϕ from o since the site indicated by ϕ is vacant with 100% probability. The described conditional probability is written as χoϕ and is given by
| [7] |
Similarly, conditional probabilities of three-site configurations, such as χoϕϕ, are given by
| [8] |
and other such examples provided in SI Appendix, section S0. The order of the truncation procedure is the number of lattice vectors from the conditioned site (e.g., o) within which conditioning sites (e.g., ϕ) are retained (21–24). Therefore, the 0th-order truncation scheme only explicitly considers configurations of one site and is simply that of the Langmuir–Hinshelwood treatment. For example,
| [9] |
The first-order procedure truncates all conditioning sites except nearest neighbors to the conditioned site. For example, in a first-order truncation scheme, χoϕϕϕϕ truncates to χoϕ. Therefore, the first-order scheme only explicitly considers probabilities of configurations with two sites or fewer; probabilities of configurations with three or more sites are reduced to products and quotients of probabilities of one- and two-site configurations (SI Appendix, section S0 further details the first-order truncation procedure). The first-order scheme is consequently an incomplete improvement of the Langmuir–Hinshelwood model and is ignorant to spatial correlations between next-nearest neighbors and beyond—which requires retention of >first-order terms. Truncation schemes of order greater than one, however, introduce significant mathematical complexity which we regard insufficiently remunerative for processes occurring on one or two sites (24, 25). For example, first-order calculations for jamming limits of dimers (θd = 0.8889) on square lattices are in nearly quantitative agreement with third- (θd = 0.9064) and fourth-order predictions (θd = 0.9068) despite only considering configurations of two sites or fewer and using >100 fewer equations (21). To our knowledge, a scheme of order greater than one has not been used for cases other than reactions on one-dimensional lattices and the calculation of jamming coverages (23–25, 27–29).
First-Order Model of Catalysis of Mobile Langmuirian Surface Species
This work hereinafter is dedicated to the construction and evaluation of first-order rate equations which may be generally applied to any catalytic reaction of mobile Langmuirian surface species (see SI Appendix, sections S0–S8 for detailed derivations). To explicate the execution of the first-order truncation scheme, we return to the dimer jamming example. We simplify Eq. 5 by first rewriting in terms of conditional probabilities
| [10] |
and then truncating conditioning sites to within one lattice vector of the conditioned site,
| [11] |
which, collecting terms, gives
| [12] |
The construction of Eq. 12 explicates the provenance of coverage-dependent stoichiometric coefficients which characterize the first order formalism and are absent in the Langmuir–Hinshelwood formalism. Rate equations for all multisite ensembles require consideration of populations of configurations larger than that on which the rate event occurs, resulting in new coverage-dependent rate terms derived from truncation of conditional probabilities specific to each site configuration. For example, the stoichiometric coefficient 1 + 6θoo/θo in Eq. 12 is derived from truncation of three-site conditional probabilities (Eqs. 10 and 11) and accounts for adsorbate proximity effects unique to θoo; in the Langmuir–Hinshelwood model, θoo is simply taken to be θo2, and the rate equation for vacant sites, dθo/dt = −4kdd,adsθo2, features no consideration of the proximity effects which engender isolation of o-sites characteristic of jamming phenomena.
The first-order model of irreversible dimer adsorption is completed by use of site balances, detailed in Eqs. 14 and 15 to follow, and by coupling Eq. 12 with the rate equation for θo,
| [13] |
where the factor of “4” accounts for the coordination number of the square lattice. By comparison, the second-order treatment requires independent rate equations for populations of seven configurations, —each in terms of truncated conditional probabilities of configurations with as many as six sites (20).
Through a procedure analogous to derivation of Eq. 12, first-order rate equations may be constructed for any rate process involving mobile Langmuirian adsorbates—which we present generally for all one- and two-site sorption, reaction, and diffusion steps in SI Appendix, sections S0–S9. SI Appendix, Tables S1–S4 respectively provide the general first-order rate equations for monomer and homogeneous dimer sorption and heterogeneous two-site events (e.g., surface reactions such as NH2* + H* → NH3(g) + ** and N* + H* → NH* + *). SI Appendix, Table S5 reports the first-order rate equations for adsorbate surface diffusion (e.g., N* + * → * + N*), which is a two-site process that does not affect single-site coverages, and, consequently, cannot be described by the Langmuir–Hinshelwood formalism. The first-order formalism explicitly describes surface diffusion of each adsorbate by incorporation of unique rate terms for each multisite ensemble—thereby accounting for the propensity of each diffusion event to ally isolated (disperse clustered) surface species.
SI Appendix, Tables S1–S5 are derived in detail in SI Appendix, sections S1–S8 and are found in SI Appendix, section S9. From SI Appendix, Tables S1–S5, the reader may construct a first-order model for any catalytic system of mobile Langmuirian adsorbates in which all elementary steps involve at most two sites. Case studies to follow will tabulate full first-order microkinetic models for particular reaction systems.
The rate equations in the first-order model are constrained by overall and component site balances, respectively,
| [14] |
and
| [15] |
where indices i and j for site occupants include vacant sites, o. We refer to time derivatives of Eqs. 14 and 15 as rate balances,
| [16] |
and
| [17] |
SI Appendix, Tables S1–S5 demonstrate that rate balances in Eqs. 16 and 17 hold for rate equations for all one- and two-site rate processes in the first-order truncation scheme.
The first-order rate equations listed in SI Appendix, Tables S1–S5, in conjunction with site (Eqs. 14 and 15) and rate (Eqs. 16 and 17) balances, constitute a kinetic description distinct to, yet in agreement with, kMC simulations; the ensemble specificity of first-order rate terms is absent in kMC algorithms. The two methods nonetheless predict quantitatively similar results because of their respective analytical and computational capacity to explicitly count site-pair populations.
Degree of Rate Control, Reaction Order, and Reversibility
We assess the kinetic descriptions of the Langmuir–Hinshelwood, first-order, and kMC methods by comparison of degrees of rate control, reaction orders, and reversibilities. We note here that rate constants in definitions of kinetic descriptors in this section are intrinsic rate constants and do not include activities of fluid-phase species.
The kinetic degree of rate control, XRC,i, of the transition state shared by steps i and −i, TS,i, is given by
| [18] |
where ki is the forward rate constant of step i, Ki is the equilibrium constant of step i, and is the standard free energy of the transition state in step i (30–37). The degree of rate control for a kinetically irrelevant step is zero, and the sum of all XRC,i is unity. Therefore, if there exists a single rate-determining step (rds), XRC,rds = 1 and XRC,i≠rds = 0.
The reaction order of species j, given by
| [19] |
is the fractional change in turnover rate per fractional change in the thermodynamic activity (ideally, partial pressure) of species j, aj.
The reversibility of elementary step i in a fluid-phase reaction or in the Langmuir–Hinshelwood model is
| [20] |
In a model of order greater than zero, however, the stoichiometric coefficient in the rate equation of step i for each species j is coverage dependent and distinct (e.g., dθoo/dt = −kdd,adsθoo × [1 + 6θoo/θo] for dimer adsorption). Therefore, there is not a single rate expression assignable to step i or −i. We therefore define a reversibility of step i for each site configuration j retained by the truncation scheme
| [21] |
Distinct zi,[j] calculable in higher-order truncation schemes provide physical insight obscured by the Langmuir–Hinshelwood formalism, which only considers single-site configurations. Indeed, single-site configurations in schemes of any truncation order always have numeric, coverage-independent stoichiometric coefficients which confer identical reversibilities for all single-site configurations j1, since r-i,[j1] and ri,[j1] are proportional to rates of the fundamental rate process (e.g., for dimer adsorption, dθo/dt = −4kdd,adsθoo). We therefore equivalently refer to all zi,[j1] as zi since the definition of zi in Eq. 20 is equal to zi,[j1] for all j1.
Ensemble-specific coverage-dependent stoichiometric coefficients also demand definition of ensemble-specific rate constants ki,[j], sensitivities si,[j], and degrees of rate control XRC,i,[j] for each step i and ensemble j. We define reaction sensitivities, si, derive si,[j] and XRC,i,[j], and discuss the relationship between si,[j] and zi,[j] in SI Appendix, section S10.
Results and Discussion
In the following, we present three case studies of catalytic reaction systems which exemplify the limitations of the Langmuir–Hinshelwood formalism and demonstrate the insight provided by the first-order model. Case studies one to three respectively illustrate that 1) Langmuir–Hinshelwood description of simple catalytic reactions (i.e., A + A → A2) of immobile, thermodynamically ideal adsorbates is inappropriate even if adsorption is equilibrated and the surface is essentially bare; 2) the inaccuracies of the Hinshelwood assumption persist with moderate rates of kinetically relevant surface diffusion and, as expected, are rectified if diffusion is equilibrated with respect to all site ensembles; and 3) the Langmuir–Hinshelwood formalism miscalculates degrees of rate control in the industrially relevant ammonia synthesis reaction on Ru(0001) step sites because of an ignorance to islanding of N* species which must be scavenged by kinetically relevant N* surface hydrogenation and diffusion.
Case Study One: Bimolecular Catalytic Reaction A + A → A2 with Immobile Adsorbates.
Let us return to the catalytic system presented in the introduction and summarized in Table 1.
Table 1.
Bimolecular catalytic reaction
| # | Step | Rate constants |
| 1 | kads* | |
| −1 | kdes | |
| 2 | kr |
kads is the product of the rate constant of adsorption and the thermodynamic activity (ideally, partial pressure) of A(g).
Table 2 compares 0th-order and first-order rate equations which describe the A + A → A2 reaction summarized in Table 1. The rate equation for each elementary step with respect to each site configuration is the product of the corresponding entry in the row labeled “Rate” and the corresponding entry in the ensemble-labeled row. For example, (dθaa/dt)des = −2θaa/θa × kdesθa in the first-order formalism. In the Langmuir–Hinshelwood formalism, coverages of site pairs are set by the condition μij = 1 and therefore do not have unique rate equations or stoichiometric coefficients. The results to follow demonstrate that the inability of the Langmuir–Hinshelwood formalism to identify rate terms unique to each multisite ensemble results in miscalculated rates and reaction orders and misinterpretation of quasi-equilibrated A(g) adsorption.
Table 2.
Rate equations in the 0th and first order
| Langmuir–Hinshelwood | First order | |||||
| Step | Adsorption | Desorption | Reaction | Adsorption | Desorption | Reaction |
| Rate | ||||||
| Ensemble-specific stoichiometric coefficients | ||||||
| 1 | −1 | −4 | 1 | −1 | −4 | |
| −1 | 1 | 4 | −1 | 1 | 4 | |
| No explicit rate equations. | ||||||
Rate equations for each ensemble and each elementary step are constructed by product of the fundamental rate of the step (e.g., kadsθo for A(g) adsorption) and the corresponding ensemble-specific stoichiometric coefficient (e.g., 2θao/θo for aa for A(g) adsorption in the first order). The Langmuir–Hinshelwood model is unable to describe dynamics of multisite ensembles, and therefore entries for aa, ao, and oo are absent.
In the Langmuir–Hinshelwood model, description of the A + A → A2 reaction requires summation and solution of sorption and surface reaction rate equations for one of θo and θa—the other is algebraically fixed by overall site balance θo + θa = 1. We choose θa; using Table 2,
| [22] |
The first-order formulation explicitly describes rate equations for five-site configurations {a, o, aa, ao, and oo} and is constrained by one overall site balance (θo + θa = 1) and two component site balances (θoo + θao = θo and θaa + θao = θa). Therefore, we require summation and solution of sorption and surface reaction rate equations for the 5 − 3 = 2 independent ensembles; we choose aa and ao. Using Table 2, the rate equations for aa and ao are
| [23] |
and
| [24] |
Eqs. 22 to 24 explicate the distinct rate terms which characterize the 0th and first order, namely, the coverage-dependent ensemble-specific stoichiometric coefficients required for Eqs. 23 and 24, which explicitly treat dynamics of multisite ensembles.
The steady-state rates and coverages for the 0th- and first-order models are solved in MATLAB, starting from a clean surface and forward integrating until all coverages are time invariant. Results from the analytical models are compared to those of kMC simulations averaged over at least 20 simulations.
Fig. 1 shows rates, coverages, and mean-field metrics calculated by the Langmuir–Hinshelwood, first-order, and kMC methods for kdes = 1 and kr = 50. All three models predict near identical rates and coverages for kads ≥ 10 since μaa ∼1 is consistent with the Hinshelwood assumption. Mean-field metrics calculated by the first-order model and kMC simulation agree for all kads and slightly exceed unity for kads = 50 to 100 because of a small clustering of aa pairs resultant from irreversibility of A(g) adsorption and a balance in rate control of adsorption and reaction—the combination of which limits the desorption process aa → ao. For kads ≤ 10, μaa deviates significantly from unity and asymptotically approaches ∼0.038 as kads → 0 and θa → 0.
Fig. 1.
(A) Rate of A2(g) formation and fractional coverage of aa pairs (θaa = r/4kr) calculated by the Langmuir–Hinshelwood (LH), first-order, and kMC methods and by closed-form, QE rate expressions per the LH (Eq. 25) and first-order (Eq. 27) formalisms. (B) Fractional coverage of a species, θa, calculated by the LH, first-order, and kMC methods. (C) Mean-field metric μaa calculated by the LH, first-order, and kMC methods. Calculations are of the reaction network in Table 1 with rate constants kdes = 1, kr = 50.
In the 0th-order scheme, the inappropriate assumption that θaa = θa2 both increasingly overestimates the coverage of rapidly scavenged aa pairs as kr/kads → ∞ and underestimates θa in the regime of large |dμaa/dkads|, which engenders accumulation of a because of the scarcity of a neighbors with which to react. The coverage of a calculated by the three models converges for kads ≤ 10−4 because of equilibration of A(g) adsorption (Fig. 2A), which algebraically fixes θa = Kads(1 + Kads)−1 where Kads = kads/kdes.
Fig. 2.
(A) A(g) reaction order and reversibility of A(g) adsorption (ΨA, zads) calculated by the Langmuir–Hinshelwood (LH), first-order, and kMC methods. (B) Degrees of rate control of adsorption and surface reaction (XRC,ads, XRC,r) calculated by the LH, first-order, and kMC methods. Calculations are of the reaction network in Table 1 with rate constants kdes = 1, kr = 50. kMC error bars are the standard error of the mean (SEM) and are only shown if larger than the corresponding symbol.
The Langmuir–Hinshelwood overestimation of r = 4krθaa by ∼25× in the low a coverage regime (θa ∼ Kads < 10−3) and agreement with the first order in the moderate to high a coverage regime (θa ≳ 0.1) differentiates the catalytic consequences of ensemble site effects (i.e., combinatorial nonidealities) and lateral adsorbate interactions (i.e., thermodynamic nonidealities). Adsorbate interactions are most consequential on high-coverage surfaces in which preponderant adsorbate–adsorbate pairs induce significant changes to elementary step activation energy barriers—as we show in SI Appendix, section S11 (38, 39). Contrarily, combinatorial nonidealities manifest profoundly on essentially bare surfaces because disparate elementary steps rates and ensemble site requirements tend to engender nonrandom distribution in low-coverage species which have greater configurational flexibility than high-coverage species (e.g., μoo = θooθo−2 ∼ 1 × 1−2 = 1 for θa < 10−3 and μaa = θaaθa−2 ∼ 1 × 1−2 = 1 for θa ∼ 1 in this case study). Lateral interactions, of course, may be incorporated as an additional consideration in first-order descriptions of catalytic reactions proceeding through site ensembles; however, these thermodynamic nonidealities are a distinct, superimposed phenomena which only exacerbate existing combinatorial nonidealities inherent to ensemble site catalysis (SI Appendix, section S11).
Fig. 2 shows reaction orders, degrees of rate control, and reversibilities calculated by analytical and kMC treatments. Reaction orders and degrees of rate control of the three methods are in agreement for kads ≥ 10, the same conditions for which rates and coverages agree. The Langmuir–Hinshelwood model underestimates the reaction order in A(g), ΨA, by as much as 0.68 in the same regime wherein θa is underestimated because the Hinshelwood assumption is ignorant to the extent of A(g) adsorption required to replenish aa pairs for reaction. The consequences of neglecting site partitioning effects are manifest in the degrees of rate control calculated by the 0th-order model compared to the first-order and kMC methods. As kads → 0 and μaa → 0.038, the isolation of a species, undetected in the 0th order, results in rate-determining adsorption of A(g) or XRC,r ∼0 and XRC,ads ∼1 (Fig. 2B).
The adsorption of A(g) equilibrates (i.e., zads → 1 in Fig. 2A) for kads ≲ 10−3 in all three models, enabling accurate application of the quasi-equilibrium (QE) approximation. Conjunction of quasi-equilibrated adsorption and θa << 1 (Fig. 1B) enables derivation of a simple closed-form Langmuir–Hinshelwood rate expression,
| [25] |
which agrees with the full Langmuir–Hinshelwood microkinetic model for kads < 10−3 (Fig. 1A). In the first-order model, however, application of the QE approximation for A(g) adsorption and recognition of θa << 1 yields a distinct closed-form rate expression,
| [26] |
which we derive in detail in SI Appendix, section S12. Eqs. 25 and 26 are identical if kr/2kdes << 1; however, since kr/2kdes = 25 >> 1 in this case study, Eq. 26 simplifies to
| [27] |
which agrees with the full first-order microkinetic model for kads < 10−1 (Fig. 1A) and remarkably does not contain the rate constant of surface reaction. Inspection of Eqs. 25 and 27 makes clear the disparate rate-determining steps identified by the Langmuir–Hinshelwood and first-order models, respectively. In Eq. 25 (Eq. 27), kr (kads) is the sole intrinsic rate constant and is linearly proportional to rate. Thus, the Langmuir–Hinshelwood and first-order models respectively identify surface reaction and A(g) adsorption as rate-determining steps for kads < 10−3 (Fig. 2B). We regard this result to be highly counter intuitive; prevailing kinetic understanding of chemical reactions suggests quasi-equilibrated steps cannot be rate determining and, conversely, are kinetically irrelevant. The ostensible paradox of a rate-determining, equilibrated step is resolved by inspection of ensemble-specific adsorption reversibilities identifiable in the first-order model but impossible to calculate in the Langmuir–Hinshelwood model.
The ensemble-specific adsorption reversibilities of aa, ao, and oo are the ratios of respective desorption and adsorption rates in Table 2,
| [28] |
| [29] |
and
| [30] |
and are shown in Fig. 3.
Fig. 3.
First-order– and kMC-calculated A(g) adsorption reversibility for aa (A), ao, and oo (B) site ensembles. kMC-calculated zads, [ao] and zads, [oo] are within error and are therefore shown with a single symbol. Calculations are of the reaction network in Table 1 with rate constants kdes = 1, kr = 50.
Fig. 3 demonstrates that, although A(g) adsorption for a, o, ao, and oo is equilibrated for kads ≤ 10−3 in the first-order model, the adsorption process for aa is nearly irreversible (i.e., zads,[aa] = 0.038 as shown in Fig. 3A). The irreversibility of adsorption for aa pairs is resultant from isolation of a species for kads = 10−6 − 10−1. In fact, we find that as kads → 0, zads,[aa] → μaa. This equality becomes apparent from evaluation of Eq. 28, taking note that zads = μao = 1 for kads ≤ 10−4. Substituting coverages of site pairs with mean-field metrics in Eq. 28 gives
| [31] |
as kads → 0. The irreversibility of adsorption for the aa ensemble is therefore a direct consequence of the scarcity of aa pairs imperceptible in the Langmuir–Hinshelwood model and resolves the conundrum of a rate-determining, equilibrated step. The Langmuir–Hinshelwood model incorrectly asserts that the QE of an elementary step, with respect to single-site configurations (i.e., zads,[j1] = zads = 1), guarantees the step is entirely equilibrated with respect to all site ensembles (40). In actuality, as the first-order model and kMC method correctly identify, each ensemble is described by a unique reversibility, and only in the case that the reversibility, with respect to each ensemble, is unity can a step be identified as entirely quasi-equilibrated and, thus, kinetically irrelevant. In this example, A(g) adsorption is equilibrated with respect to all site ensembles except the reactive configuration aa, thereby allowing A(g) adsorption to be both equilibrated, in the sense that zads = 1, and rate determining.
From this case study, we conclude that quasi-equilibrated adsorption is insufficient to guarantee validity of the Hinshelwood assumption. Mean-field metrics which deviate from unity by ∼25× even for zads = 1 demonstrate that the QE condition cannot ensure use of the Langmuir–Hinshelwood formalism is appropriate; the Hinshelwood assumption is accurate only if all adsorption steps are entirely equilibrated (i.e., zads,[j] = 1 for all site ensembles j)—as is guaranteed in the case of arbitrarily fast surface diffusion (40). In the following, we introduce surface diffusion of a surface species to the A + A → A2 reaction to demonstrate that the Langmuir–Hinshelwood model remains inaccurate for moderate diffusion rates and agrees exactly with the first-order and kMC methods if characteristic diffusion rates far exceed those of sorption and reaction steps, as expected.
Case Study Two: Bimolecular Catalytic Reaction A + A → A2 with Adsorbate Surface Diffusion.
Adsorbate surface diffusion rates in catalytic surface reactions has been proposed as a kinetically relevant consideration in CO oxidation (15, 36, 41) and methanation (18), ammonia decomposition (42), and NO reduction (43). Analytical description of surface diffusion steps requires >0th-order formalisms, which contain explicit rate equations for multisite ensembles. To assess the importance of surface diffusion rates in determining rates, reaction orders, and degrees of rate control, we introduce diffusion of a species to the 2A(g) → A2(g) reaction (Table 3).
Table 3.
Bimolecular catalytic reaction with surface diffusion
| # | Step | Rate constants |
| 1 | kads* | |
| −1 | kdes | |
| 2 | kr | |
| 3 | kdiff |
kads is the product of the rate constant of adsorption and the thermodynamic activity of A(g).
Table 4 compares 0th- and first-order rate equations for a diffusion. Since surface diffusion does not change the total coverage of any site occupants, the Langmuir–Hinshelwood model contains no explicit description of surface reaction; rather, the Hinshelwood assumption implicitly assumes surface diffusion of all species is arbitrarily fast, ensuring θij = θiθj. The first-order formalism is completed by addition of diffusion rate equations listed in Table 4 to those for sorption and reaction listed in Table 2.
Table 4.
Diffusion rate equations in the 0th and first order
| Langmuir–Hinshelwood | First order | |
| Step | Diffusion (ao → oa) | |
| Rate | ||
| Ensemble-specific stoichiometric coefficients | ||
| 0 | 0 | |
| 0 | 0 | |
| No explicit rate equations. |
||
The rate equation for surface diffusion with respect to each site configuration is the product of the corresponding entry in the row labeled “Rate” and the corresponding entry in the ensemble-labeled row. For example, (dθaa/dt)diff = 6(θao/θo − θaa/θa) × kdiffθao in the first order. The Langmuir–Hinshelwood model is unable to describe dynamics of multisite ensembles, and therefore entries for aa, ao, and oo are absent.
Fig. 4 shows rates, coverages, reaction orders, mean-field metrics, and degrees of rate control calculated by the first-order and kMC methods as a function of kdiff with kdes = 1 and kr = 50, identically to Case Study One, and with kads = 10−2—at which condition the first-order and Langmuir–Hinshelwood models disagree significantly in the absence of surface diffusion (Figs. 1–3). All kinetic descriptors calculated for kdiff = 0 (kdiff ≥ 103) agree with first-order and kMC (Langmuir–Hinshelwood) results in the previous case study.
Fig. 4.
(A) Rate of A2(g) formation and fractional coverage of aa pairs (θaa = r/4kr) calculated by the first-order and kMC methods. (B) A(g) reaction order and mean-field metric of aa pairs (ΨA, μaa) calculated by the first-order and kMC methods. (C) Degrees of rate control of adsorption, surface reaction, and surface diffusion calculated by the first-order and kMC methods. Calculations are of the reaction network in Table 3 with rate constants kads = 10−2, kdes = 1, and kr = 50. kMC error bars are the SEM and are only shown if larger than the corresponding symbol.
Fig. 4A demonstrates that r = 4krθaa is a strong function of kdiff; larger diffusion rates ally previously isolated a species, thereby increasing the coverage of aa pairs and the rate of their self-annihilation. A2(g) formation rates asymptotically approach the Langmuir–Hinshelwood limit as kdiff → ∞ randomizes the surfaces to effect μaa → 1 (Fig. 4B). The sigmoidal increase of θaa and μaa as a function of kdiff demonstrates that surface diffusion only exerts significant rate control when kdiff is similar in magnitude to rate constants for sorption and reaction (Fig. 4C). Indeed, the degree of rate control of surface diffusion reaches a maximum value of ∼0.4 for kdiff ∼ kdes because A(g) desorption is the only other mode of surface relaxation capable of randomizing the surface and increasing μaa—evinced by agreement of Eqs. 25 and 26 for kdes >> kr even if adsorbates are immobile.
In the same regime that surface diffusion is kinetically relevant, the reaction order in A(g), ΨA, and the rate control of A(g) adsorption, XRC,ads, decrease since A(g) adsorption is no longer the only process actively generating aa pairs. Similarly to all other kinetic descriptors, ΨA and XRC,ads plateau as XRC,diff → 0 for sufficiently large kdiff. The waning influence of surface diffusion for kdiff ≳ kr is qualitatively attributed to diffusion rates being “infinitely fast” (15, 36)—a condition which we contend requires quantitative evaluation. To this end, we derive ensemble-specific reversibilities for surface diffusion, which, just as for any other elementary step, must all equal unity to affirm the infinitely fast nature of diffusion relative to all other steps.
The two-site diffusion rate equations listed in Table 4 and derived in SI Appendix, section S8 proffer a means to define ensemble-specific reversibilities of surface diffusion based on the microscopically reversible elementary diffusion steps which create and consume multisite ensembles. For example, the diffusion events which consume/produce aa pairs are all of the form
| [32] |
save for configurational variance. The elementary steps which produce and consume aa pairs are therefore the microscopic reverse of one another and occur with reversibility,
| [33] |
which explicitly demonstrates that all a-relevant mean-field metrics must be unity for surface diffusion to be equilibrated with respect to aa pairs. We note that μaa and μao cannot be equal unless both are unity because component site balance constrains μaaθa + μaoθo = 1.
Eq. 33 provides a rigorous metric by which to evaluate the fidelity of surface diffusion to randomize the distribution of aa pairs. Indeed, diffusion is only considered arbitrarily fast, or “entirely” equilibrated, in the case that zdiff,[j] = 1 for all site ensembles j (40). The diffusion reversibilities for the remaining ensembles oo and ao are the respective ratios of ensemble-specific elementary step consumption and production rates and are functions of mean-field metrics,
| [34] |
| [35] |
as we derive in SI Appendix, section S13. Eqs. 33 to 35 effectively quantify the rapidity of surface diffusion and tend to unity as the adsorbate distribution randomizes with increasing kdiff, as shown in Fig. 5.
Fig. 5.
Surface diffusion reversibilities for aa, oo, and ao ensembles calculated by the first-order and kMC methods. Calculations are of the reaction network in Table 3 with rate constants kads = 10−2, kdes = 1, and kr = 50. kMC error bars are the SEM and are only shown if larger than the corresponding symbol.
The scarcity of aa pairs for kdiff ≲ 1 is manifested in zdiff,[aa], which is the only diffusion reversibility not equal to unity and quantifies the increase in diffusion rate necessary to achieve a random surface. The reversibility of diffusion with respect to aa pairs, zdiff,[aa], therefore provides a compendious metric to evaluate the kinetic significance of surface diffusion; other kinetic descriptors, such as the degree of rate control, fail to recognize potential of increase in kdiff to unite isolated a species and enhance A2(g) formation rate (i.e., XRC,diff ∼0 for kdiff < 10−2). The ensemble specificity conferred by the first-order model is key to identifying synoptic kinetic descriptors such as zdiff,[aa] and is necessary to capture combinatorial nonidealities conferred by elementary step ensemble site requirements.
The kinetic influence of thermodynamic nonidealities (e.g., adsorbate lateral interactions) may also be readily described by the first-order formalism and is profoundly affected by surface diffusion rates and reversibilities—as we intend to detail in a subsequent study; until such time, SI Appendix, section S11 discusses and contains a simple demonstration of incorporating lateral interactions and surface diffusion in the first-order formalism. Briefly, explicit rate equations for multisite ensembles prove critical for describing lateral interactions and provide an alternative to the heuristic use of linear coverage-dependent activation energy relations in microkinetic models. We stress that adsorbate interactions are an additional nonideal phenomenon distinct to combinatorial nonidealities; are most relevant in high-coverage regimes, antithetically to clustering/isolation phenomena on bare surfaces described herein; and only exacerbate the inadequacies of the Langmuir–Hinshelwood model we redress by explicit counting of site-pair populations in the first-order formalism.
Case Study Three: Ammonia Synthesis on Ru (0001) Step Sites.
The two case studies examined heretofore, although simple, typify the inadequacies of the Langmuir–Hinshelwood model and demonstrate the capacity of first-order terms to accurately describe kinetic consequences of site ensembles—as evidenced by quantitative agreement with kMC-calculated rates, selectivities, reaction orders, and degrees of rate control. We further demonstrate the critical significance of combinatorial nonidealities in catalysis of mobile Langmuirian adsorbates by examination of the industrially relevant ammonia synthesis reaction (Table 5) using density-functional theory (DFT)-calculated pre-exponential factors and activation energies reported by Logadóttir and Nørskov for reaction and sorption steps (44) and DFT-calculated (42, 45, 46) and experimentally measured (46–48) activation energies for surface diffusion of all adsorbed species. Pre-exponential factors for diffusion are calculated to be similar to those for sorption and reaction and are within an order of magnitude of experimentally determined (46–48) and previously calculated (42, 45, 46) values. All kinetic parameters are tabulated in SI Appendix, section S14.
Table 5.
Ammonia synthesis on Ru (0001) step sites
| # | Step | Rate constants* |
| 1 | k1, k–1 | |
| 2 | k2, k–2 | |
| 3 | k3, k–3 | |
| 4 | k4, k–4 | |
| 5 | k5, k–5 | |
| 6 | k6, k–6 |
Rate constants for ammonia synthesis are intrinsic rate constants and do not include activities of fluid-phase species. Diffusion steps can be found in SI Appendix, Table S14.1.
Fig. 6 shows select mean-field metrics, elementary step rates, and degrees of rate control calculated by the 0th- and first-order description at industrially practiced NH3 synthesis conditions: 200 bar, 20% N2/60% H2/20% NH3, 623 K to 823 K. The well-known difficulty of activating N–N triple bonds results in very low coverages of N* (θN* = 10−6 − 10−5) and surface saturation by H adatoms (θH* = 0.93 to 0.99), as shown in SI Appendix, Fig. S14.1A. Similar to θa << 1 enabling μaa << 1 in Case Studies One and Two, the very low coverages of N* permit significant nonrandomness in the distribution of N*–N* and N*–NH* pairs; Fig. 6A shows θN*–N* (θN*–NH*) is 105 (102) times greater than (θN*θNH*)—demonstrating that surface diffusion can be kinetically relevant even on covered surfaces (θ* = 0.006 to 0.08). Mean-field metrics μN*–j* for j* ≠ {N*, NH*} are near unity and identical, however, because N* and NH* are the only two sites which experience significant isolation or clustering; surface diffusion rates are sufficient to randomize the distribution of all other adsorbed species.
Fig. 6.
(A) Mean-field metrics μN*-j* calculated by the first-order model. All μN*-j* = 1 by definition in the Langmuir–Hinshelwood (LH) model. (B) Directional elementary step rates r-1 and r2 calculated by the LH and first-order models. (C) Degrees of rate control calculated by the LH and first-order models. XRC only shown if |XRC| > 10−2. XRC,1 = 1 in the LH model, and therefore no other XRC are shown. Calculations are of the reaction network in Table 5 at 200 bar total pressure with composition 20% N2/60% H2/20% NH3.
The significant clustering of N*–N* pairs results from the disparate combinatorially ideal rates of recombinative N2(g) desorption and N* hydrogenation—the only two steps besides N* surface diffusion that can annihilate N*–N* pairs (Fig. 6B). On a random, uniform surface (i.e., in the Langmuir–Hinshelwood model), the rate of N* hydrogenation, r2, is 104 to 106 times faster than N2(g) desorption, r-1, because of the high coverage of H* (θH*/θN* ∼105) and k2 ∼ k-1. Quantitatively accounting for surface diffusion, however, the relative rapidity of N* hydrogenation results in an accumulation of N*–N* pairs because annihilation by recombinative desorption or diffusion is prohibitively slow—thereby enhancing the N2(g) desorption rate relative to that on a uniform surface (Fig. 6B).
In essence, if surface diffusion is not arbitrarily fast, the surface must counter balance disparate production and consumption rates by clustering slowly consumed species (e.g., μN*–N* = 103.5 to 105) and isolating rapidly consumed species (e.g., μaa = 0.038 in Case Study One). The enhancement to r-1 because of N*–N* clustering effects orders of magnitude increase to the reversibility of N2(g) adsorption (SI Appendix, Fig. S14.1B) and consequently decreases the kinetic degree of rate control XRC,1, which is equal to unity in the Langmuir–Hinshelwood model (Fig. 6C), which incorrectly assumes N* and NH* diffusion to be infinitely fast. In the first-order model, rate control shifts to N* hydrogenation and surface diffusion, both of which bear a kinetic burden to scavenge congregated N* and initiate the rapid hydrogenation cascade from NH* to NH3*.
Conclusion
The analytical kinetic description of mobile Langmuirian adsorbates by use of the Hinshelwood assumption is generally inappropriate and, as we demonstrate heretofore, results in erroneous interpretation of QE, calculation of rates and reaction orders, and identification of rate-determining steps. We present a higher-order kinetic theory, which, by derivation of multisite ensemble-specific rate terms, faithfully describes any catalytic surface reaction of mobile, thermodynamically ideal adsorbates proceeding through two sites or fewer. The concepts we establish in derivation of first-order rate equations are robust to the inclusion of lateral adsorbate interactions and to retention of ≥second-order terms to describe catalytic reactions proceeding through three or more sites.
Consequences of ensemble site requirements analytically described in this work are purported to be significant in catalytic reactions, including alkane dehydrogenation and hydrogenolysis (49–52), alkene hydrogenation (53, 54) and epoxidation (55, 56), and NO decomposition (57, 58)—all of which have been largely analyzed in the context of the Langmuir–Hinshelwood formalism. We contend accurate kinetic interpretation and microkinetic modeling of catalytic surface reactions such as these must quantitatively account for, or rationalize neglect of, combinatorial nonidealities—especially if surface diffusion is not known to be facile and/or constituent elementary steps require large site ensembles.
Materials and Methods
All calculations were performed using the MATLAB code detailed in SI Appendix and found at the link https://github.com/neilrazdan/RazdanBhan-SiteEnsembles or by communication with the authors. Briefly, kMC simulations were performed on periodic 2D square lattices with time incremented in accordance with Poisson statistics for calculation of steady-state coverages and ensemble-specific rates. Steady-state kinetic descriptors of Langmuir–Hinshelwood and first-order formalisms were calculated using stiff ordinary differential equation solvers ode23s or ode15s in MATLAB.
Supplementary Material
Acknowledgments
We thank Dr. Andrew Hwang for careful proofing, Dr. Brandon L. Foley for helpful discussion, Dr. Linh Bui for insightful technical advice, and the reviewers for their valuable comments. This work was funded by the US Department of Energy, Office of Basic Energy Science, Catalysis Science Program (Award DE-SC00019028).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2019055118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix.
References
- 1.Le N. T. P., White C., Reese J. M., Myong R. S., Langmuir-Maxwell and Langmuir-Smoluchowski boundary conditions for thermal gas flow simulations in hypersonic aerodynamics. Int. J. Heat Mass Transf. 55, 5032–5043 (2012). [Google Scholar]
- 2.Myong R. S., Gaseous slip models based on the Langmuir adsorption isotherm. Phys. Fluids 16, 104 (2004). [Google Scholar]
- 3.Singh H., Javadpour F., Langmuir slip-Langmuir sorption permeability model of shale. Fuel 164, 28–37 (2016). [Google Scholar]
- 4.Manohar D. M., Krishnan K. A., Anirudhan T. S., Removal of mercury(II) from aqueous solutions and chlor-alkali industry wastewater using 2-mercaptobenzimidazole-clay. Water Res. 36, 1609–1619 (2002). [DOI] [PubMed] [Google Scholar]
- 5.Wu Y., Zhang S., Guo X., Huang H., Adsorption of chromium(III) on lignin. Bioresour. Technol. 99, 7709–7715 (2008). [DOI] [PubMed] [Google Scholar]
- 6.Syers J. K., Browman M. G., Smillie G. W., Corey R. B., Phosphate sorption by soils evaluated by the Langmuir adsorption equation. Soil Sci. Soc. Am. J. 37, 358–363 (1973). [Google Scholar]
- 7.Mittal A., Kurup L., Mittal J., Freundlich and Langmuir adsorption isotherms and kinetics for the removal of Tartrazine from aqueous solutions using hen feathers. J. Hazard. Mater. 146, 243–248 (2007). [DOI] [PubMed] [Google Scholar]
- 8.Zhang P., Wang L., Extended Langmuir equation for correlating multilayer adsorption equilibrium data. Separ. Purif. Tech. 70, 367–371 (2010). [Google Scholar]
- 9.Forssén P., Samuelsson J., Fornstedt T., Relative importance of column and adsorption parameters on the productivity in preparative liquid chromatography II: Investigation of separation systems with competitive Langmuir adsorption isotherms. J. Chromatogr. A 1347, 72–79 (2014). [DOI] [PubMed] [Google Scholar]
- 10.Boudart M., Djéga-Mariadassou G., “Kinetics of Overall Reactions” in Kinetics of Heterogenous Catalytic Reactions, Prausnitz J. M., Brewer L., Eds. (Princeton University Press, ed. 1, 1984), pp. 78–90. [Google Scholar]
- 11.Taylor H. S., A theory of the catalytic surface. Proc. R. Soc. Lond. 108, 105–111 (1925). [Google Scholar]
- 12.Hinshelwood C. N., Kinetics of Chemical Change in Gaseous Systems (Oxford University Press, 1926). [Google Scholar]
- 13.Park J. J., et al., Langmuir adsorption study of the interaction of CdSe/ZnS quantum dots with model substrates: Influence of substrate surface chemistry and pH. Langmuir 25, 443–450 (2009). [DOI] [PubMed] [Google Scholar]
- 14.Belton G. R., Langmuir adsorption, the gibbs isotherm, and interfacial kinetics in liquid metal systems. Metall. Mater. Trans. B 7, 35–42 (1976). [Google Scholar]
- 15.Temel B., Meskine H., Reuter K., Scheffler M., Metiu H., Does phenomenological kinetics provide an adequate description of heterogeneous catalytic reactions? J. Chem. Phys. 126, 204711 (2007). [DOI] [PubMed] [Google Scholar]
- 16.Davis M. E., Davis R. J, “Heterogeneous catalysis” in Fundamentals of Chemical Reaction Engineering, Glandt E. D., Klein M. T., Edgar T. F., Eds. (Springer-Verlag, 2003), pp. 133–183. [Google Scholar]
- 17.Hong Q.-J., Liu Z.-P., Mechanism of CO2 hydrogenation over Cu/ZrO2 (212) interface from first-principles kinetics Monte Carlo simulations. Surf. Sci. 604, 1869–1876 (2010). [Google Scholar]
- 18.Andersen M., Plaisance C. P., Reuter K., Assessment of mean-field microkinetic models for CO methanation on stepped metal surfaces using accelerated kinetic Monte Carlo. J. Chem. Phys. 147, 152705 (2017). [DOI] [PubMed] [Google Scholar]
- 19.Pineda M., Stamatakis M., Beyond mean-field approximations for accurate and computationally efficient models of on-lattice chemical kinetics. J. Chem. Phys. 147, 024105 (2017). [DOI] [PubMed] [Google Scholar]
- 20.Vette K. J., Orent T. W., Hoffman D. K., Hansen R. S., Kinetic model for dissociative adsorption of a diatomic gas. J. Chem. Phys. 60, 4854–4861 (1974). [Google Scholar]
- 21.Nord R. S., Evans J. W., Irreversible immobile random adsorption of dimers, trimers, ... on 2D lattices. J. Chem. Phys. 82, 2795–2810 (1985). [Google Scholar]
- 22.Evans J. W., Nord R. S., Competitive irreversible random one-, two-, three-, ... point adsorption on two-dimensional lattices. Phys. Rev. B Condens. Matter 31, 1759–1769 (1985). [DOI] [PubMed] [Google Scholar]
- 23.Evans J. W., Burgess D. R., Hoffman D. K., Irreversible random and cooperative processes on lattices: Exact and approximate hierarchy truncation and solution. J. Chem. Phys. 79, 5011–5022 (1983). [Google Scholar]
- 24.Evans J. W., Random and cooperative sequential adsorption. Rev. Mod. Phys. 65, 1281–1329 (1993). [Google Scholar]
- 25.Meng B., Weinberg W. H., Evans J. W., Transitions in the kinetics and steady states of irreversible A+BC surface-reaction models. Phys. Rev. E 48, 3577–3588 (1993). [DOI] [PubMed] [Google Scholar]
- 26.Evans J. W., Nord R. S., Random dimer filling of lattices: Three-dimensional application to free radical recombination kinetics. J. Stat. Phys. 38, 681–705 (1985). [Google Scholar]
- 27.Evans J. W., Hoffman D. K., Burgess D. R., Competing irreversible cooperative adsorption on polymer chains. J. Chem. Phys. 80, 936–943 (1984). [Google Scholar]
- 28.Zhong D., Ben-Avraham D., Muñoz M. A., Mean-field solution of the parity-conserving kinetic phase transition in one dimension. Eur. Phys. J. B 35, 505–511 (2003). [Google Scholar]
- 29.Hinrichsen H., Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 49, 815–958 (2000). [Google Scholar]
- 30.Stegelmann C., Andreasen A., Campbell C. T., Degree of rate control: How much the energies of intermediates and transition states control rates. J. Am. Chem. Soc. 131, 8077–8082 (2009). [DOI] [PubMed] [Google Scholar]
- 31.Campbell C. T., Finding the rate-determining step in a mechanism comparing DeDonder relations with the “degree of rate control”. J. Catal. 204, 520–524 (2001). [Google Scholar]
- 32.Foley B. L., Bhan A., Degree of rate control and De Donder relations-An interpretation based on transition state theory. J. Catal. 384, 231–251 (2020). [Google Scholar]
- 33.Dumesic J. A., Analyses of reaction schemes using De Donder relations. J. Catal. 185, 496–505 (1999). [Google Scholar]
- 34.Mao Z., Campbell C. T., The degree of rate control of catalyst-bound intermediates in catalytic reaction mechanisms: Relationship to site coverage. J. Catal. 381, 53–62 (2020). [Google Scholar]
- 35.Cortright R. D., Dumesic J. A., Kinetics of heterogeneous catalytic reactions: Analysis of reaction schemes. Adv. Catal. 46, 161–264 (2001). [Google Scholar]
- 36.Meskine H., Matera S., Scheffler M., Reuter K., Metiu H., Examination of the concept of degree of rate control by first-principles kinetic Monte Carlo simulations. Surf. Sci. 603, 1724–1730 (2009). [Google Scholar]
- 37.Foley B. L., Bhan A., Thermodynamically consistent forward and reverse degrees of rate control in reversible reactions. J. Catal. 389, 566–577 (2020). [Google Scholar]
- 38.Zhdanov V. P., Effect of the lateral interaction of adsorbed molecules on preexponential factor of the desorption rate constant. Surf. Sci. Lett. 111, L662–L666 (1981). [Google Scholar]
- 39.Zhdanov V. P., Lattice-gas model for description of the adsorbed molecules of two kinds. Surf. Sci. 111, 63–79 (1981). [Google Scholar]
- 40.Lewis G. N., A new principle of equilibrium. Proc. Natl. Acad. Sci. U.S.A. 11, 179–183 (1925). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Matera S., Meskine H., Reuter K., Adlayer inhomogeneity without lateral interactions: Rationalizing correlation effects in CO oxidation at RuO2(110) with first-principles kinetic Monte Carlo. J. Chem. Phys. 134, 064713 (2011). [DOI] [PubMed] [Google Scholar]
- 42.Mortensen H., Diekhöner L., Baurichter A., Jensen E., Luntz A. C., Dynamics of ammonia decomposition on Ru(0001). J. Chem. Phys. 113, 6882 (2000). [Google Scholar]
- 43.Avalos L. A., Bustos V., Uñac R., Zaera F., Zgrablich G., Dynamic Monte Carlo simulation of the NO + CO reaction on Rh(111). J. Phys. Chem. B 110, 24964–24971 (2006). [DOI] [PubMed] [Google Scholar]
- 44.Logadóttir Á., Nørskov J. K., Ammonia synthesis over a Ru(0001) surface studied by density functional calculations. J. Catal. 220, 273–279 (2003). [Google Scholar]
- 45.Hammer B., Adsorption, diffusion, and dissociation of NO, N and O on flat and stepped Ru(0001). Surf. Sci. 459, 323–348 (2000). [Google Scholar]
- 46.Truong T. N., Truhlar D. G., Chelikowsky J. R., Chou M. Y., A new ab initio potential energy surface for H on Ru(0001) and its use for variational transition state theory and semiclassical tunneling calculations of the surface diffusion of H and D. J. Phys. Chem. 94, 1973–1981 (1990). [Google Scholar]
- 47.Farbman I., Rosenzweig Z., Asscher M., Diffusion of ammonia on Re(001). Faraday Discuss. 96, 307–316 (1993). [Google Scholar]
- 48.Zambelli T., Trost J., Wintterlin J., Ertl G., Diffusion and atomic hopping of N atoms on Ru(0001) studied by scanning tunneling microscopy. Phys. Rev. Lett. 76, 795–798 (1996). [DOI] [PubMed] [Google Scholar]
- 49.Flaherty D. W., Iglesia E., Transition-state enthalpy and entropy effects on reactivity and selectivity in hydrogenolysis of n-alkanes. J. Am. Chem. Soc. 135, 18586–18599 (2013). [DOI] [PubMed] [Google Scholar]
- 50.Frennet A., Adsorption site of alkanes and associated hydrogen pressure effects. Catal. Today 12, 131–137 (1992). [Google Scholar]
- 51.Bond G. C., Cunningham R. H., Alkane transformations on supported platinum catalysts 4. Kinetics of hydrogenolysis of ethane, propane, and n-butane on Pt/Al2O3 (EUROPT-3) and PtRe/Al2O3 (EUROPT-4). J. Catal. 166, 172–185 (1997). [Google Scholar]
- 52.Sullivan M. M., Bhan A., Effects of oxygen coverage on rates and selectivity of propane-CO2 reactions on molybdenum carbide. J. Catal. 357, 195–205 (2018). [Google Scholar]
- 53.Cortright R. D., Goddard S. A., Rekoske J. E., Dumesic J. A., Kinetic study of ethylene hydrogenation. J. Catal. 127, 342–353 (1991). [Google Scholar]
- 54.McLeod A. S., Gladden L. F., Monte Carlo simulation of kinetic discontinuities in hydrocarbon hydrogenation reactions. Catal. Lett. 43, 189–194 (1997). [Google Scholar]
- 55.Stegelmann C., Schiødt N. C., Campbell C. T., Stoltze P., Microkinetic modeling of ethylene oxidation over silver. J. Catal. 221, 630–649 (2004). [Google Scholar]
- 56.Campbell C. T., Koel B. E., Chlorine promotion of selective ethylene oxidation over Ag(110): Kinetics and mechanism. J. Catal. 92, 272–283 (1985). [Google Scholar]
- 57.Alas S. J., Vicente L., TPD study of NO decomposition on Rh(111) by dynamic Monte Carlo simulation. Surf. Sci. 604, 957–964 (2010). [Google Scholar]
- 58.Makeev A. G., Slinko M. M., Mathematic modelling of the peculiarities of NO decomposition on Rh(111). Surf. Sci. 359, L467–L472 (1996). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix.