Emergence of diauxie as an optimal growth strategy under resource allocation constraints in cellular metabolism

Significance

When several sugars are at its disposition, the bacterium Escherichia coli consumes them in a specific order—a behavior called diauxie. We developed a framework combining dynamic methods and models of metabolism and gene expression to show that diauxie and its associated lag in cell growth can be explained simply as an optimal behavior under constraints on the protein amount and renewal in a cell. We validate our model by reproducing experimental results and successfully predict a diauxic behavior on a growth medium containing two types of sugar, glucose and lactose. Finally, we claim that the regulation mechanism inducing diauxie (the lac operon) is a control system to implement growth optimality at the cellular level.

Abstract

Diauxie, or the sequential consumption of carbohydrates in bacteria such as Escherichia coli, has been hypothesized to be an evolutionary strategy which allows the organism to maximize its instantaneous specific growth—giving the bacterium a competitive advantage. Currently, the computational techniques used in industrial biotechnology fall short of explaining the intracellular dynamics underlying diauxic behavior. In particular, the understanding of the proteome dynamics in diauxie can be improved. We developed a robust iterative dynamic method based on expression- and thermodynamically enabled flux models to simulate the kinetic evolution of carbohydrate consumption and cellular growth. With minimal modeling assumptions, we couple kinetic uptakes, gene expression, and metabolic networks, at the genome scale, to produce dynamic simulations of cell cultures. The method successfully predicts the preferential uptake of glucose over lactose in E. coli cultures grown on a mixture of carbohydrates, a manifestation of diauxie. The simulated cellular states also show the reprogramming in the content of the proteome in response to fluctuations in the availability of carbon sources, and it captures the associated time lag during the diauxie phenotype. Our models suggest that the diauxic behavior of cells is the result of the evolutionary objective of maximization of the specific growth of the cell. We propose that genetic regulatory networks, such as the lac operon in E. coli, are the biological implementation of a robust control system to ensure optimal growth.

In his pioneering work on the growth of bacterial cultures, the French biologist Jacques Monod (1) observed that the growth of Escherichia coli in a mixture of carbohydrates followed two distinct exponential curves separated by a plateau—a phenomenon he called diauxie. Hypothesized to allow optimal growth of the culture (2), this cellular behavior corresponds to the sequential consumption of sugars: one sugar is preferentially consumed, and the second is only consumed after depletion of the first. Although current optimality-based computational models can predict diauxie, these lack a detailed description of the protein dynamics during the phenomenon (3). Diauxie is an evolved, complex behavior, and its occurrence is controlled by the regulation network of the lac operon in E. coli (4, 5). The emergence of such a control mechanism is the product of evolutionary pressure, and being able to fully elucidate its raison d’être in terms of cell physiology is an important milestone to understand and better engineer the intracellular dynamics of bacterial growth. There is thus a need for a formulation describing diauxie at the proteome level.

Genome-scale models of metabolism (GEMs) combine constraint-based modeling and optimization techniques to study cell cultures (6–8). A key method for studying GEMs is flux balance analysis (FBA) (9), which formulates a linear optimization problem that employs stochiometric constraints through the mass conservation of metabolites given their synthesis and degradation reactions. Under the typical steady-state and growth rate maximization assumptions, FBA models predict the simultaneous consumption of two or more carbon sources to achieve the maximum possible growth (3). However, this contradicts Monod’s observation of distinct, sequential phases of carbon consumption and suggests that diauxie does not come from stoichiometric constraints.

To account for diauxie beyond stoichiometric modeling, we looked into other biological features. Because a cell has a physiological constraint on the total amount of enzymes it can house, which we will call a proteome allocation constraint, it is likely that the cell will preferentially distribute its limited catalytic capacity toward pathways that utilize the most efficient substrate/enzyme combination (2, 10, 11). Therefore, models that account for proteome limitation in cells may be able to account for diauxie. Toward this end, the role of protein limitation in diauxie was demonstrated by Beg et al. (12) with their formulation of flux balance analysis with molecular crowding (FBAwMC). Their method correctly predicts the uptake order of five different carbon sources in a batch reactor, using a proteome allocation constraint. In a push toward more global models, models of metabolism and expression (ME models) (13, 14) include proteome allocation but also gene expression mechanisms, a modeling paradigm that is ideal for studying diauxie at the proteome level. ME models also fully describe the requirements of enzyme synthesis, degradation, and dilution effects, as well as messenger RNA (mRNA) and enzyme concentrations.

Since diauxie is also a time-dependent phenomenon, we chose to complement ME models with a dynamic modeling approach. Dynamic flux balance analysis (dFBA) (15) is a generalization of FBA for modeling cell cultures in time-dependent environments. In its original static optimization approach formulation, the time is discretized into time steps, and an FBA problem is solved at each step. At each iteration, kinetic laws and the FBA solution are used to update the boundary fluxes, extracellular concentrations, and cell concentration, based on the amount of substrate consumed, by-products secreted, and biomass produced by the cells. We expected that the combination of a dFBA and ME models would yield a formulation that can describe diauxie at the proteome level.

However, we identified three major challenges in the conception of dynamic ME models. First, while dFBA studies of metabolic networks can be solved by common linear solvers, ME models are nonlinear by nature and significantly more complex. The species and reactions introduced and considerations of the interactions between enzyme expression and metabolism result in nonlinear problems that are often one to two orders of magnitude bigger in terms of constraints and variables than the corresponding linear (d-)FBA problem. The increase in complexity is compounded when iteratively solving an optimization problem. As a result, combining ME models and dynamic studies brings along difficulties that arise from the high computational cost of solving multiple times, with different conditions, these large, nonlinear problems. Second, the use of iterative methods presents the additional challenge of alternative solutions, which can span several physiologies. It is thus necessary to find, for each time step, a suitable representative solution that will be used to integrate the system. This also poses the problem of finding a set of initial conditions for the system. Third, the current state-of-the-art models present limitations at the proteome level. Lloyd et al. (16) developed an efficient ME model for E. coli, and Yang et al. (17) used it to formulate a dynamic analysis framework (dynamic ME) similar to dFBA. However, the assumptions introduced to alleviate the computational complexity of their model limit some aspects of the modeling capabilities of their method. To improve the capacity of our models to generalize, we sought a formulation relying on less stringent assumptions, which allowed us to capture more biological features. We provide in SI Appendix, Note S1 a detailed list of items in which dETFL (dynamic Expression and Thermodynamics-enabled Flux models) differs from dynamic ME and a list of elements we believe our method addresses better. In particular, dynamic ME forces a strict coupling between enzyme concentrations and fluxes. However, a change in the growth conditions will trigger a change in the proteome allocation to adapt to a new metabolic state or lag phase. During that time, it is expected that some previously active enzymes will not be able to carry flux in the new conditions. Therefore, enzyme flux and concentration will decouple, unless the enzyme composition of the proteome changes at the same rate as the environment. As a result, this previous method cannot simulate lag phase during glucose depletion and proteome reallocation. dETFL does not use such coupling between enzyme concentrations and reaction rates, which allowed the prediction of a lag phase in our simulations.

Both dynamic models and models including gene expression mechanisms are important components in the development of successful predictive biology (18). We propose a dynamic method that tackles the challenges mentioned above and models diauxie at the proteome level. To this effect, we used our recently published framework for ME models, ETFL (19). The formulation of ETFL permits the inclusion of thermodynamics constraints in expression models, as well as the ability to describe the growth-dependent allocation of resources. ETFL is faster than previous ME model formulations thanks to the use of standard mixed integer linear programming (MILP) solvers (19). We herein leverage ETFL for dynamic analysis, in a method called dETFL. It includes a method based on Chebyshev centering to robustly select a representative solution from the feasible space at each time step. The representative solution captures phenotypic and genotypic differences between cells precultured in different media. The ETFL method, on which dETFL is built, does not need dedicated quadprecision solvers, unlike previous ME model formulations (13, 14, 16, 17, 20). It also does not use strict equality coupling between flux rates and enzyme concentration, unlike the previous state-of-the-art ME model methods (16, 17). This strict coupling was instrumental in improving the solving performance of these formulations at the cost of reducing the predictive capacity of the methods, in particular with respect to the prediction of the lag phase (discussion is in SI Appendix, Note S1). Instead, (d-)ETFL relies on a combination of scaling methods and MILP formulation, which allows models to be solved efficiently. As a result, whole-proteome reconfiguration during sugar consumption can be simulated with reasonable solving times, which enabled the modeling of the lag phase in diauxie.

Herein, we model the emergence and dynamics of diauxie arising at the proteome level. We first propose a small conceptual model of a cell, with a limited in proteome, and demonstrate its ability to predict diauxie under a minimal set of assumptions. Using the dETFL method, we subsequently show these assumptions hold in E. coli and reproduce experimental results of bacterial growth. Finally, we apply the dETFL framework to the growth of E. coli in a glucose/lactose mixture in a batch reactor and demonstrate that it robustly predicts diauxie. In particular, we capture the preferential consumption of glucose over lactose, the emergence of a time delay when the cell changes substrate, the proteome origin of this delay, and differential behavior depending on preculture conditions. This dynamic formulation of ME models is able simulate at the genome-scale evolution of the proteome in diauxic conditions, including the time lag it induces and the effect of preculture conditions. Overall, dETFL offers a method to robustly survey intracellular dynamics of cellular physiology under changing environmental conditions.

Results

Conceptual Model for the Emergence of the Diauxie Phenotype from Proteome Limitation.

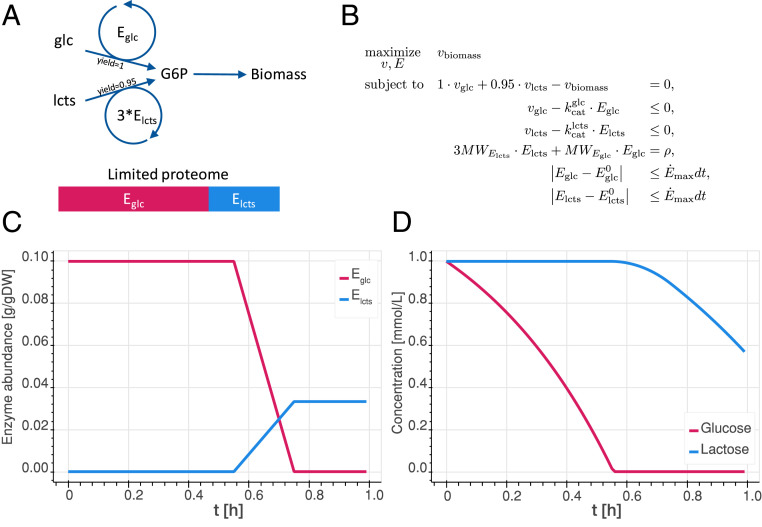
We designed a simplified conceptual model to illustrate diauxie from proteome limitations, as described in Fig. 1A. The model includes both glucose and lactose as substrates, and it is a simplified version of the E. coli metabolism based on four considerations.

Fig. 1.

(A) Conceptual model used for the preliminary analysis, where “glc” stands for glucose and “lcts” stands for lactose. The catalytic efficiencies of the enzymes are assumed to be the same. Three enzymes are assumed to be necessary to produce the intermediate metabolite G6P from lactose, and only one enzyme is required from glucose. (B) Optimization problem used to represent the model. $v$ are fluxes, $E$ are enzyme concentrations, $E^0$ are reference values, $MW$ are molecular weights, $\rho$ is the mass fraction of the cell occupied by the enzymes we consider, ${Ė}_{max}$ is the maximal variation of enzyme concentration over time, and $dt$ is the integration interval. (C) Enzyme content over time for the conceptual model growing on a mixed substrates. (D) Changes in sugar content of the batch reactor over time.

Consideration 1:

The biomass carbon yield on glucose is slightly higher than that of lactose (21).

Consideration 2:

Glucose and lactose are taken up and converge to a common intermediate metabolite, glucose 6-phosphate (G6P). Glucose is transformed into G6P by a glucokinase. The lactose pathway (Leloir pathway) splits the lactose, a disaccharide, into its glucose and galactose subunits. The galactose is then converted to G6P by a series of enzymes.

Consideration 3:

The Leloir pathway requires one enzyme to split the lactose into glucose and galactose, four enzymes to convert galactose into glucose-1-phosphate (22, 23), and one to convert glucose-1-phosphate into G6P; this bring the total to six enzymes needed for the synthesis of two G6P, which is equivalent to three enzymes per G6P.

Consideration 4:

The molecular mass of the each of the enzymes in the lactose pathway is around 60 to 90 kDa (24), which is heavier than the 33-kDa glucokinase (Uniprot identification A7ZPJ8).

Based on these considerations, we devised a conceptual model of glucose and lactose metabolism for E. coli. The model accounts for the consumption of the two substrates, which both synthesize an intermediate metabolite that is then used to make biomass. We thus made five modeling assumptions.

Assumption 1.

Glucose has a slightly higher carbon yield than lactose—based on Consideration 1.

Assumption 2.

The glucose metabolism leading to the intermediate G6P is summarized in a single step, modeled by a single enzyme—based on Consideration 2. The same is done for the lactose metabolism, resulting in two modeling enzymes summarizing these two pathways.

Assumption 3.

The molecular weights of the enzymes are the same, and three times more enzymes are required for lactose metabolism than for glucose metabolism—based on Consideration 3.

Assumption 4.

The catalytic activities of the two enzymes synthesizing G6P are similar.

Assumption 5.

The variation of enzyme concentrations reaches a maximum at each time step.

Assumption 6.

The total enzyme amount in the cell is limited.

The mathematical formulation of the problem (Fig. 1B) involves one mass balance, one conservation equation of the total enzymes, two inequalities that constrain the metabolism for glucose and lactose as a function of the corresponding enzymes concentrations, and two enzyme variation constraints.

Due to total enzyme conservation, the two maximum activity constraints are not independent. This constraint is similar to that found in other approaches accounting for proteome allocation such as FBAwMC (12).

The conceptual model is able to predict diauxic behavior in our system. The model shows the preferential consumption of glucose over lactose (Fig. 1D), controlled by a switch in the proteome composition over time (Fig. 1C). The diauxic phenomenon is due to the fact that the system will invest all of the (limited) enzyme resources into the metabolism of glucose, which is both the highest yielding substrate (Consideration 1 and Assumption 1) and the one with the fewest enzyme requirements (Consideration 3 and Assumption 3). As the glucose is depleted, the uptake flux is reduced, and the system gradually allocates part of its proteome for enzymes needed for lactose metabolism. This gradual proteome reallocation corresponds to the observed lag phase in an experimental system. While this conceptual model lacks catabolite repression mechanisms, it can still describe diauxie phenomenon from only the proteome capacity constraint.

The lack of proteome limitation and enzyme catalytic constraints is why the original FBA approach fails to predict diauxie, which leads to the simultaneous utilization of both sugar substrates. However, another important constraint to accurately describe the lag phase is the limitations on the rate of change in enzyme concentrations, without which the proteome switch would occur instantaneously (SI Appendix, Fig. S1). Indeed, physiologically, a cell needs time to adapt its proteome. However, steady-state methods lack a memory process, and subsequent optimization as conditions change will just yield unrelated physiologies. The constraints on the rate of change of enzyme concentrations represent the catalytic limitation of the cell to break down old enzymes and synthesize new ones better adapted to the new conditions. They add a memory to the optimization process, constraining the new physiology depending on the previous state of the cell.

The conceptual model also allows for the study of the conditions under which the system switches to lactose as a carbon source and the identification of parameters responsible for this behavior. If we note, for glucose and lactose, respectively, the specific growth rates on each substrate $v_{biomass}^{\mathrm{g}\mathrm{l}\mathrm{c}},v_{biomass}^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}$, the carbon yields $Y_{\mathrm{g}\mathrm{l}\mathrm{c}},Y_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}$, and the catalytic rate constants $k_{\mathrm{c}\mathrm{a}\mathrm{t}}^{\mathrm{g}\mathrm{l}\mathrm{c}},k_{\mathrm{c}\mathrm{a}\mathrm{t}}^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}$ of enzymes at concentrations $E_{\mathrm{g}\mathrm{l}\mathrm{c}},E_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}$, then the preferred carbon source will change to lactose if and only if

$$v_{biomass}^{\mathrm{g}\mathrm{l}\mathrm{c}}<v_{biomass}^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}},$$ [1]

$$Y_{\mathrm{g}\mathrm{l}\mathrm{c}}\cdot v_{\mathrm{g}\mathrm{l}\mathrm{c}}^{max}<Y_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}\cdot v_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}^{max},$$ [2]

$$Y_{\mathrm{g}\mathrm{l}\mathrm{c}}\cdot k_{\mathrm{c}\mathrm{a}\mathrm{t}}^{\mathrm{g}\mathrm{l}\mathrm{c}}\cdot E_{\mathrm{g}\mathrm{l}\mathrm{c}}^{max}<Y_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}\cdot k_{\mathrm{c}\mathrm{a}\mathrm{t}}^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}\cdot E_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}^{max}.$$ [3]

If the amount of available enzymes is represented by $\rho$, as a fraction of the total cell mass (in grams per grams of dried cells [${\mathrm{g}.\mathrm{g}\mathrm{D}\mathrm{W}}^{-1}$]), and assuming different molecular weights ${MW}_E$, the proteome limitation constraint will be written

$${MW}_{E_{\mathrm{g}\mathrm{l}\mathrm{c}}}\cdot E_{\mathrm{g}\mathrm{l}\mathrm{c}}+3{MW}_{E_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}}\cdot E_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}=\rho .$$ [4]

The maximal achievable values for the enzyme concentrations will be $E_{\mathrm{g}\mathrm{l}\mathrm{c}}^{max}=\rho /{MW}_{E_{\mathrm{g}\mathrm{l}\mathrm{c}}}$ and $E_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}^{max}=\rho /\left(3{MW}_{E_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}}\right)$. Replacing these values in Eq. 3 directly gives the condition

$$\frac{Y_{\mathrm{g}\mathrm{l}\mathrm{c}}}{Y_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}}<\frac{k_{\mathrm{c}\mathrm{a}\mathrm{t}}^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}}{k_{\mathrm{c}\mathrm{a}\mathrm{t}}^{\mathrm{g}\mathrm{l}\mathrm{c}}}\cdot \frac{{MW}_{E_{\mathrm{g}\mathrm{l}\mathrm{c}}}}{3\cdot {MW}_{E_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}}}.$$ [5]

In our conceptual model, ${MW}_{E_{\mathrm{g}\mathrm{l}\mathrm{c}}}={MW}_{E_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}}$, and we can simplify Eq. 5:

$$3\cdot \frac{Y_{\mathrm{g}\mathrm{l}\mathrm{c}}}{Y_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}}<\frac{k_{\mathrm{c}\mathrm{a}\mathrm{t}}^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}}{k_{\mathrm{c}\mathrm{a}\mathrm{t}}^{\mathrm{g}\mathrm{l}\mathrm{c}}}.$$ [6]

This expression identifies the boundary in the parameter space that separates the preferential use of glucose vs. lactose.

In this section, we showed that a constraint symbolizing proteome limitation was sufficient to induce a diauxic behavior of the cell, thus validating the hypothesis that catalytic limitation is at the origin of diauxie (2, 10, 11). These calculations can be generalized for a more realistic model by accounting for the molecular weight of the enzymes and setting an adequate proteome fraction allocated to carbon metabolism. In particular, Wang et al. (11) propose an in-depth analysis of the optimal protein allocation for a broad range of carbon sources, connected to the central carbon metabolism at different levels. In practice, in our model, the catalytic efficiencies of the glycolytic enzymes are also higher than those of the Leloir pathway (Assumption 3 and SI Appendix, Table S1), and the Leloir pathway enzymes are heavier (Consideration 4 and Assumption 4), which favors glucose consumption even more. Additionally, we did not consider the synthesis cost of the enzymes used to carry the fluxes in each pathway. Taking such property into account would also strengthen the preference toward glucose, as fewer enzymes are needed for its metabolism.

Diauxie in Genome-Scale ME Models with Thermodynamic Constraints.

Going beyond a conceptual model, we next used dETFL to model diauxie in an ME model of E. coli. dETFL is built on top of the existing ETFL formulation (summarized in SI Appendix, Note S1) using additional rate-of-change constraints (detailed in Materials and Methods) and the robust selection of reference solution at each time step using a method based on the Chebyshev center of polytopes (detailed in Materials and Methods). This method allowed us to study metabolic switches in response to a changing environment, under the aspect for intracellular enzyme and mRNA concentrations. To do this, we studied how ME models can describe diauxie in experiments where E. coli is grown in two different conditions. First, we investigated the growth of E. coli on glucose. In this experiment, the cells exhibit overflow metabolism, or the secretion of acetate, even under aerobic conditions. Experimentally, the bacterium reutilizes the secreted acetate after glucose depletion, a form of diauxic behavior. This type of study was also used as the first proof of concept for dFBA (15). Thus, we first validated the dETFL model by demonstrating its ability to model a first diauxic phenotype: overflow metabolism and acetate secretion in the presence of excess glucose, followed by acetate reutilization on glucose depletion. Second, we reproduced Jacques Monod’s experiment of the diauxic growth of E. coli in an oxygenated batch reactor (1) with a limited carbon supply made of a mixture of glucose and lactose. We aimed at reproducing the results shown in the conceptual model on a model of a real organism and characterizing the intracellular dynamics underlying the glucose/lactose diauxic behavior.

To conduct these studies, we used the E. coli model published by Salvy and Hatzimanikatis (19) that is based on the genome-scale model by Orth et al. (25) (iJO1366) and was assembled using ETFL. This model is significantly bigger than the conceptual model studied in the previous section, with 5,295 species, 8,061 reactions, and 578 enzymes. A summary of the model is available in Table 1.

Table 1.

Properties of the vETFL model generated from iJO1366

Property	Value
Growth upper bound $\overline{\mu }$	$3.5h^{-1}$
No. of bins $N$	128
Resolution $\frac{\overline{\mu }}{N}$	$0.027h^{-1}$
No. of constraints	69,323
No. of variables	50,010
No. of species	5,295
Metabolites	1,806
Enzymes	578
Peptides	1,433
mRNAs	1,433
tRNAs	21 $\times 2$
rRNAs	3
No. of reactions	8,061
Metabolic	1,840
Transport	733
Exchange flux	330
Transcription	1,433
Translation	1,433
Complexation	578
Degradation	2,011
No. of metabolites ${\mathrm{\Delta }}_{f}G\prime o$	1,737
No. of reactions ${\mathrm{\Delta }}_{r}G\prime o$	1,787
Metabolites ${\mathrm{\Delta }}_{f}G\prime o$, %	93.9
Reactions ${\mathrm{\Delta }}_{r}G\prime o$, %	69.5

rRNA, ribosomal RNA; tRNA, tranfer RNA.

For the integration of the dynamic method, it is important to choose a time step that respects the quasisteady-state assumptions on which the FBA and ETFL frameworks depend (19). We used a time step of $0.05\hspace{0.17em}\mathrm{h}=3\hspace{0.17em}\mathrm{m}\mathrm{i}\mathrm{n}$ for the numerical integration, as this is around 10 times smaller than a typical doubling time for E. coli and efficiently balances the integration approximation and solving time.

Diauxic growth on glucose and acetate.

We compared the accuracy of our computational modeling of diauxie with experimental findings. Specifically, we studied the diauxic growth of E. coli on glucose in batch reactors using experimental data published in Varma and Palsson (6) and Enjalbert et al. (26). Previously, Varma and Palsson (6) used their data to validate a stoichiometric model of E. coli in quasisteady state, whereas the data from Enjalbert et al. (26) were used to validate a population-based approach of dFBA by Succurro et al. (27).

To reproduce the results of these two batch growth experiments, we applied constraints to the uptake of glucose and oxygen in the dETFL model (Materials and Methods). The initial uptake rate of glucose is set to $15\hspace{0.17em}\text{mmol}\cdot {\text{gDW}}^{-1}\cdot {\text{h}}^{-1}$. This value is characteristic of a typical physiology for E. coli growing on glucose with excess oxygen (6, 15, 25, 27).

We also set the initial concentrations of cells, glucose, and acetate to values matching the experimental data. Oxygen transfer was considered free (no kinetic law on uptake) in a first approximation, as done by Succurro et al. (27).

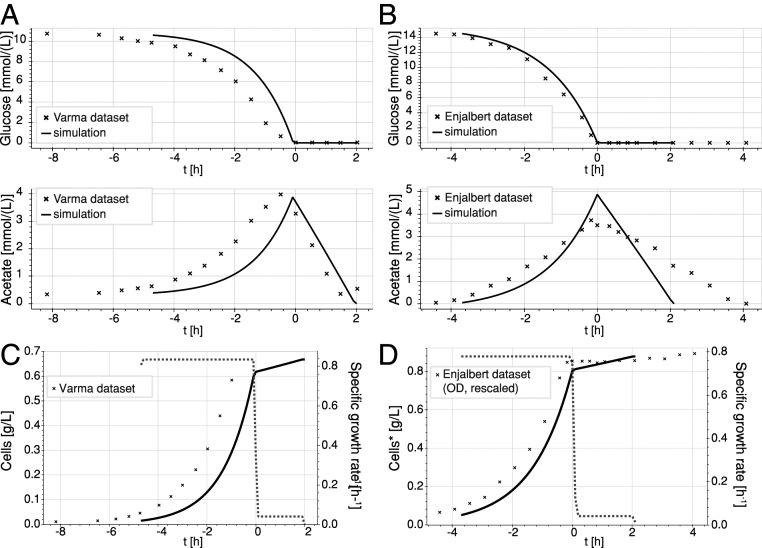
Our simulations agreed with the published experimental data. The temporal evolution of the glucose and acetate concentrations in the simulated batch reactor agreed with both the Varma and Palsson (6) and the Enjalbert et al. (26) datasets, as shown in Fig. 2 A and B, respectively. The cell concentration and specific growth rate also follow a similar trend (Fig. 2 C and D). Both of the simulations predict a first phase where the bacteria grow steadily on glucose, which is sustained until glucose is depleted in the medium. During that time, acetate is steadily secreted by the cell, due to the overflow metabolism. When extracellular glucose is depleted, the residual acetate is consumed by the cell. We observe a sharp drop in the cell growth rate, and the simulation ends when no acetate is left in the medium.

Fig. 2.

Comparison of simulated and experimental data of glucose depletion over time [Varma and Palsson (6) and Enjalbert et al. (26)]. Simulated data are represented by solid lines; experimental data are represented by crosses. (A) Temporal evolution of the simulated extracellular concentrations of glucose and acetate (solid lines) vs. experimental data [Varma and Palsson (6) dataset; crosses]. (B) Temporal evolution of the simulated (solid lines) extracellular concentrations of glucose and acetate (solid lines) vs. experimental data [Enjalbert et al. (26) dataset; crosses]. (C) Cell concentration (solid line) and growth rate (dashed line) over time: simulation and Varma and Palsson (6) dataset (crosses). (D) Cell concentration (solid line) and growth rate (dashed line) over time: simulation and Enjalbert et al. (26) dataset (crosses). *Experimental values were in optical density (OD) and were linearly scaled to represent cell concentrations.

We achieved these simulated curves with no fitting. The results are the predictions of dETFL—given only the starting point of the simulation and then, time shifting the curves based on the time of glucose depletion to account for experimental lag phases. The discrepancy between the simulation and the experiment data points can be attributed to several factors. First, several simulation parameters, including the maximal uptake rates for glucose, oxygen, and acetate and the acetate maximal secretion rates, are reported with a 50% variability between the Varma and Palsson (6) and Succurro et al. (27) studies. We chose a common set of parameters that showed good qualitative agreement with both datasets. Changing these parameters can alter the quantitative behavior of the model, but the models always show the same two phases. Second, variability in the experimental setup, including the E. coli strain, can also account for the difference in the reported glucose uptake rate by their respective authors. ME models and ETFL in particular can account for the strain variability if the genetic differences (gene knockouts, enzyme activities, enzyme overexpression) are known. Finally, Biselli et al. (28) recently showed that biomass composition and (non–)growth-associated maintenance are parameters that depend on preculture conditions, for which no data were available.

Overall, these results show that the dETFL framework for ME models is able to reproduce experimental measurements of glucose uptake, acetate secretion, and biomass production in glucose–acetate diauxic growth. Our findings validate the dETFL framework as a modeling method to study the batch growth of single organisms or communities on multiple substrates and suggest its utility for investigating diauxie in mixed substrate media.

Diauxic growth on glucose and lactose.

Diauxic experiments show that, on a mixed medium of glucose/lactose, E. coli will preferentially consume glucose first and then lactose (29, 30). Modeling the diauxic growth of E. coli with dETFL should capture the lag phases and proteomic reconfiguration that are caused by the shift to a new carbon source. Therefore, this is an ideal system to challenge the ability of ME models to describe the dynamic reorganization of the bacterial proteome. dFBA will always predict simultaneous uptake of both carbon sources since it includes no term associated with the proteomic cost of their uptake. In contrast, ME models describe the synthesis of enzymes and their contribution to the overall proteome. As a result, ME models capture the competitive allocation of the proteome to the transport of different carbon sources.

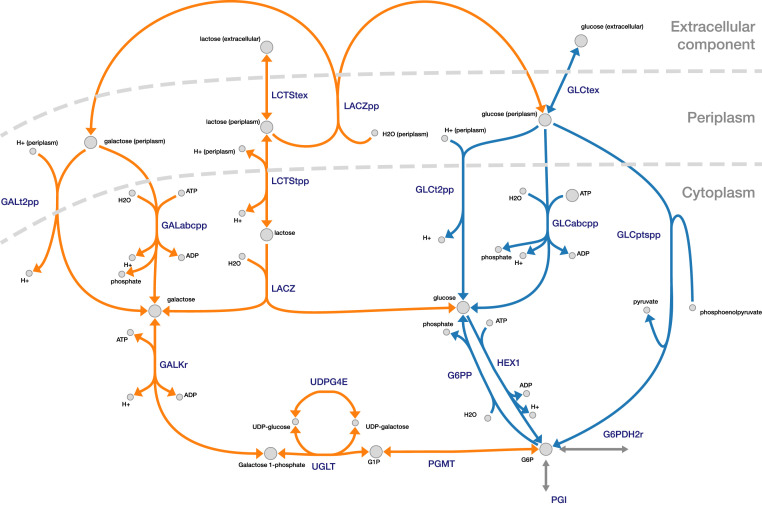
For reference, the pathways related to the glucose and lactose metabolism to G6P are summarized in Fig. 3. The figure highlights the multiple additional steps involved in the lactose pathway to form G6P, compared with the shorter glucose pathway.

Fig. 3.

Possible uptake routes for glucose (blue) and lactose (orange) toward G6P. The splitting of lactose by LACZ can be done either intracellularly or in the periplasm. Routes toward the main central carbon metabolism are in gray. The figure was made using Escher (31).

To initialize the model for the simulation of diauxic growth, we first simulate the preculturing in glucose by running the model with the same standard physiology as before, with an uptake rate of $15\hspace{0.17em}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{g}\mathrm{D}\mathrm{W}}^{-1}\cdot {\mathrm{h}}^{-1}$ for glucose and no lactose initially present. The model is subsequently run with these initial conditions on a mixture of glucose and lactose at the physiologically relevant concentrations of 1 and $2\hspace{0.17em}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{L}}^{-1}$, respectively. The cell concentration is set at $0.05\hspace{0.17em}\mathrm{g}\cdot {\mathrm{L}}^{-1}$. After this initialization step, we ran the simulation according to the method detailed before.

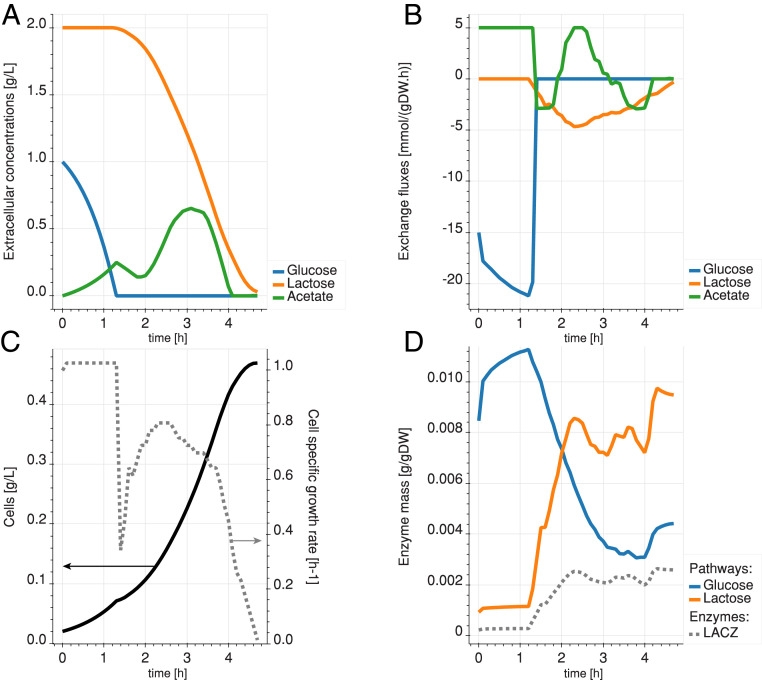
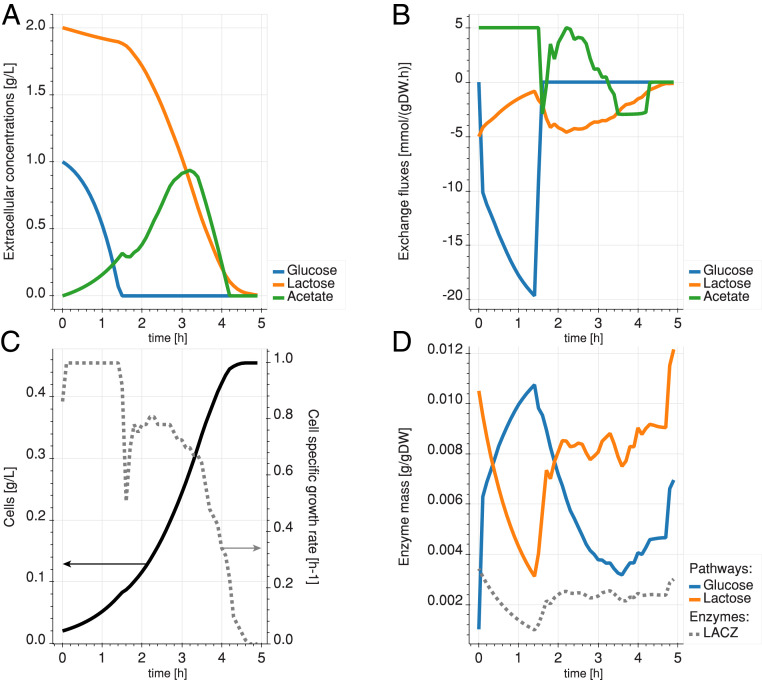
The time evolution of the extracellular metabolite concentrations, cellular exchange fluxes, specific growth rate, and total biomass of the culture exhibit four phases (Fig. 4). We observe a first phase similar to the previous experiment, where glucose is taken up at a rapid rate until its depletion, with the simultaneous production of acetate through overflow metabolism (Fig. 4 A and B). During this phase, the growth rate is steady and high (Fig. 4C). Relative to glucose, lactose is taken up at lower rates (Fig. 4A). In the second phase, the specific growth rate decreases sharply, while the proteome reallocates its enzymes for lactose metabolism. We also observe a drop in acetate secretion during the proteome switch and short period of acetate reconsumption. This is the lag phase, where acetate is used as a carbon source, while the proteome is reconfigured to metabolize lactose. Indeed, since glucose has been depleted and few lactose-metabolizing enzymes are available, acetate is the next best-available carbon source for the cell to operate. Direct acetate consumption is possible because acetate transport is mostly diffusive in E. coli (32) and involves pathways that were already active in the cell. The proteome reconfiguration shows a reduction of the total mass of enzymes that convert glucose into G6P and an increase in the total mass of enzymes responsible for the conversion of lactose to G6P (Fig. 4D). The third phase is characterized by a peak in lactose uptake and cell growth, followed by a decline as lactose becomes scarce. In the fourth phase, when lactose becomes scarce, the residual acetate is being taken up instead of secreted. Since it happens after lactose uptake falls below a low threshold, it indicates that lactose consumption is preferred to that of acetate. More details on the time-dependent enzyme concentrations of the glucose and Leloir pathways can be found in SI Appendix, Figs. S2 and S3, respectively.

Fig. 4.

Diauxic simulation with glucose-only preculture. (A) Temporal evolution of the extracellular concentrations of glucose (blue), lactose (orange), and acetate (green). (B) Exchange rates of the cell. Positive exchange rates mean production, and negative exchange rates mean consumption. (C) Cell concentration (solid line) and growth rate (dashed line) of the culture over time. (D) Mass of enzymes allocated to the transformation of glucose (blue) and lactose (orange) in G6P. The dashed gray line shows the levels of $\beta$-galactosidase (LACZ) enzyme (in the Leloir pathway).

We next sought to assess the robustness of our diauxie prediction and to determine whether the delayed utilization of lactose was an artifact of the initial conditions used in the simulation. We conducted a simulation that included a preculture wherein the E. coli model initially only had access to lactose, with an uptake rate of $5\hspace{0.17em}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{g}\mathrm{D}\mathrm{W}}^{-1}\cdot {\mathrm{h}}^{-1}$. Following this preculture, we ran the simulation with identical initial conditions to previous experiments in terms of glucose, lactose, and cell concentrations.

Over the course of this simulation, we observed the same four phases: 1) preferred glucose consumption, 2) proteome switch with acetate uptake, 3) lactose consumption, and 4) acetate reutilization. Initially, glucose is taken up at a significantly smaller rate than that of the glucose preculture. The glucose uptake rate then gradually increases until glucose depletion (Fig. 5 A and B). Comparatively, the lactose uptake rate stays low, while the glucose uptake rate increases during the first phase of the experiment. The evolution of the growth rate is similar to that of the previous experiment (Fig. 5C). Although the model was precultured in lactose, the total amount of enzymes transforming lactose decreases while glucose is available (Fig. 5D). We observe a delay, close to the cell doubling time, for initiating the utilization of glucose compared with the glucose preculture experiment. We attribute this delay to proteome switch from a proteome optimized for lactose consumption to a proteome optimized for glucose consumption in this phase. In the second phase, after glucose depletion, we also observe acetate reutilization, while the enzymes needed for lactose conversion to G6P are resynthesized. In the third phase, the proteome shifts again to accommodate lactose consumption. As a result, the lactose uptake rate increases. In the final phase, acetate reutilization initiates again under scarce conditions. More details on the time-dependent enzyme concentrations of the glucose and Leloir pathways can be found in SI Appendix, Figs. S4 and S5, respectively.

Fig. 5.

Diauxic simulation with lactose-only preculture. (A) Temporal evolution of the extracellular concentrations of glucose (blue), lactose (orange), and acetate (green). (B) Exchange rates of the cell. Positive exchange rates mean production, and negative exchange rates mean consumption. (C) Cell concentration (solid line) and growth rate (dashed line) of the culture over time. (D) Mass of enzymes allocated to the transformation of glucose (blue) and lactose (orange) in G6P. The dashed gray line shows the levels of $\beta$-galactosidase (LACZ) enzyme (in the lactose pathway).

These simulations show strong qualitative agreement with the experimental data for both the glucose and the lactose precultured conditions. In particular, Kremling et al. (30) showed a similar evolution of extracellular concentrations with a two-phase consumption of sugars. Although their work reports diauxic growth of a different E. coli strain, we report in SI Appendix, Fig. S6 the comparison between our simulated E. coli K-12 and their experimental measurements, which shows strong qualitative agreement. Additionally, we observe a dip in the specific growth rate, close to a generation time, when the substrate being consumed changes. This additional time needed to reach a new maximal growth rate is what is observed empirically as a lag phase. Here, we see it can be interpreted as the proteome switch time, the result of the cost of rearranging the proteome allocation to adapt to new culture conditions. This lag phase is not predicted by the previous state of the art in dynamic ME models, dynamic ME (17). These simulations also demonstrated that intracellular LACZ enzyme levels increase when lactose is the sole substrate left and decrease when glucose is consumed—even after a lactose preculture (Figs. 4D and 5D). These agreements were achieved without adjusting any of the parameters or settings of the original ME model. However, a key element for the consistency between the model simulations and the cellular state is a robust accounting of the intracellular states (mRNA species, enzymes, and fluxes) between consecutive time steps. This has been made possible by the use of the Chebyshev centering of the cellular states in the dETFL formulation as detailed in Materials and Methods.

Our results strongly suggest that diauxie in E. coli is an optimal growth behavior. Our conceptual study suggests it is the consequence of the maximization of the cell-specific growth rate under the constraint of a limited proteome. This optimal behavior of privileging glucose consumption over lactose does not come from the preculturing step but instead, from the optimality of the system itself under the constraint of proteome allocation for sugar consumption. We performed additional studies and demonstrated that this behavior is not due to differences in enzyme catalytic efficiencies between the two pathways, as switching the $k_{\mathrm{c}\mathrm{a}\mathrm{t}}$ values does not change the trend (SI Appendix, Fig. S7). Finally, we showed that the lag time observed in experiments is determined by the proteome reallocation and quantitatively predicted changes in the amount of enzyme for each pathway.

Discussion

We devised both a conceptual model and a dynamic ME model that reproduce a diauxic behavior in E. coli, a phenomenon that cannot be captured with current state-of-the-art models. From simulation, we determined that the preferential consumption of glucose over lactose in E. coli is a combined effect of its limited proteome size, enzyme properties, and substrate yield. Our model demonstrates, at the proteome level, the mechanisms of the proteome switch between conditions and provides a method to resolve the intracellular dynamics of bacterial growth. In agreement with experimental observations, our model predicts a diauxic behavior on a medium of mixed sugars.

In our simulations, we observed lag phases concurrent with proteome switching. The co-occurrence of the proteome reallocation and acetate reutilization suggests secreted acetate can work as an energy reserve and help the cell adapt to changing environmental conditions. The dETFL model was also able to capture different dynamic trajectories in cell fates that were dependent on the preculture conditions.

The preferential consumption of one carbon source vs. the other is the result of an optimal trajectory of the system under the constraints of mass balance, resource allocation, and thermodynamics. These constraints are directly connected to the chemistry of the metabolic pathways in bacteria. Our conceptual model suggests that the diauxic phenomenon might be controlled through the engineering of three aspects: 1) the specific activity of enzymes ($k_{\mathrm{c}\mathrm{a}\mathrm{t}}$), 2) the molecular weight of the enzymes, and 3) the number of steps involved in the substrate metabolism. The molecular weight and activity of enzymes can be altered through protein engineering, and alternative chemistries from heterologous pathways provide avenues for modifying substrate metabolism (33).

While dETFL does not account for catabolite repression, it can quantitatively describe the behavior of a cell operating under the influence of the lac operon. Our results imply that the genetic circuits responsible for catabolite repression are evolved as a controller to implement robust dynamic control of the optimal growth. In this regard, the catabolite repression through the lac operon observed in wild-type E. coli can be considered as a control system that ensures optimal growth of the organism. Under the selective pressure of evolution, the system might have evolved the lac operon to preferentially metabolize glucose in mixtures of sugars as it guaranteed an evolutionary advantage (faster growth) compared with substrate coutilization (5).

As an approach, dETFL avoids the pitfalls of simplifying modeling assumptions used in the current state-of-the-art computational models of metabolism and gene expression. Because of this, dETFL is a dynamic ME model formulation that can model lag phase and gradual proteome reconfiguration. However, despite these innovative findings, there are still drawbacks to dynamic constraint-based models that need refinement. For example, finding a good representative solution at each time step is extremely important. Here, we used the Chebyshev ball approach, as it is a single linear problem that is computationally simpler than other methods such as variability analysis or sampling. While we have reduced the computational burden of ME models enough to efficiently perform iterative solving, there are opportunities to further alleviate the computational cost of simulations. Directions to explore include fixing the integer variables of subproblems to reduce the nonpolynomial hardness of the model and using quadratic programming, for instance, to perform an ellipsoid approximation of the enzyme solution space. Additionally, systematically reduced models, where less important parts of metabolic machinery are omitted, can also be used to reduce the complexity of the simulations (34, 35). With a reduced computational cost of simulations, exciting research targets are also within reach, such as the dynamic effects of gene knockouts or drug-induced changes in cell physiology.

The computational formulations developed herein also offer opportunities to test other hypotheses that explain diauxie. Succurro et al. (27) postulated the existence of two subpopulations of E. coli where one obligately consumes glucose, while the other consumes acetate. Although the study of communities including thermodynamics-enabled ME models is, for now, a computational challenge, cross-testing the hypothesis we present in this paper with a similar community-based context would certainly yield important insights on the respective role of proteome limitation and substrate competition in the emergence of diauxic behavior.

The inhibitory effect of glucose on certain parts of the metabolism is multiple, and includes catabolite repression, transient repression, and inducer exclusion (36). Moreover, more complex regulation mechanisms are found in natural environments. For example, it has been shown that, on its natural marine substate, the bacterium Pseudoalteromonas haloplanktis evolved regulation mechanisms allowing simultaneous diauxie and substrate coutilization (37). Such high-order behavior might also have its origin in an optimal growth program, and finding the biochemical constraints responsible for it would yield valuable insight on the optimal growth of organisms on complex media. In general, elucidating the emergence of regulation mechanisms in the context of evolutionary pressure will considerably increase our understanding and ability to engineer regulation systems, which are ubiquitous in biology from wild-type E. coli to cancer cells. dETFL is an important step forward in this direction. Its use to uncover the optimality principles guiding the emergence of cellular regulatory control systems is key to a better understanding and ultimately, mastery of metabolic engineering, be it applied to industrial hosts or the development of cell-based therapies.

Materials and Methods

Rate of Change of Fluxes.

One of the important points in the original formulation of dFBA is that the rate at which intracellular fluxes change is constrained. In the dFBA formulation, one imposed constraint is

$$v\left(x,t+\mathrm{\Delta }t\right)-v\left(x,t\right)\le {\dot{v}}^{max}\cdot \mathrm{\Delta }t,$$ [7]

where ${\dot{v}}^{max}\cdot \mathrm{\Delta }t$ is defined as the maximum change of flux between two time points. However, the relationship between flux and enzyme concentration, as well as the dynamic mass balance, can be expressed in the following way (19):

$$v\left(x,t\right)\le k_{\mathrm{c}\mathrm{a}\mathrm{t}}E,$$ [8]

$$\frac{dE}{dt}=v^{\mathrm{s}\mathrm{y}\mathrm{n}}-v^{\mathrm{d}\mathrm{e}\mathrm{g}}-v^{\mathrm{d}\mathrm{i}\mathrm{l}},$$ [9]

with all of the rates strictly positive. From this, it directly follows that

$${\dot{v}}^{\mathrm{m}\mathrm{a}\mathrm{x}}=k_{\mathrm{c}\mathrm{a}\mathrm{t}}{Ė}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$ [10]

$$-v^{\mathrm{d}\mathrm{e}\mathrm{g}}-v^{\mathrm{d}\mathrm{i}\mathrm{l}}\le {Ė}^{\mathrm{m}\mathrm{a}\mathrm{x}}\le v^{\mathrm{s}\mathrm{y}\mathrm{n}},$$ [11]

where we can rewrite ${Ė}^{max}$ in two components, one strictly positive and the other strictly negative: ${Ė}^{max}={Ė}_{+}^{max}-{Ė}_{-}^{max}$. Using expression relationships from ETFL, it is hence possible to bound the maximal rate change of fluxes in a fashion that is compatible with linear programming:

$${Ė}_{-}^{max}\le v^{\mathrm{deg}}+v^{\mathrm{d}\mathrm{i}\mathrm{l}},$$ [12]

$${Ė}_{+}^{max}\le v^{\mathrm{s}\mathrm{y}\mathrm{n}}.$$ [13]

These two constraints represent the limitation in the decrease (dilution and degradation) and increase (synthesis) of the enzyme concentration, respectively. We can rewrite these in terms of dETFL variables:

$$0\le E_j^{t_{i+1}}-E_j^{t_i}\le v_j^{\mathrm{s}\mathrm{y}\mathrm{n}}\cdot \mathrm{\Delta }t,$$ [dEP_j]

$$0\le E_j^{t_i}-E_j^{t_{i+1}}\le \left(v_j^{\mathrm{deg}}+v_j^{\mathrm{d}\mathrm{i}\mathrm{l}}\right)\cdot \mathrm{\Delta }t.$$ [dEN_j]

Variability in the Estimation of Macromolecule Concentrations.

A key element in ETFL is that macromolecule concentrations are an explicit variable in the optimization problem. In dETFL, these concentrations are important because they will constrain the feasible space for the calculation of next time step.

The formulation of ETFL relies on the approximation of the growth rate of the organism by a piecewise-constant function in the dilution term of the mass balances of macromolecules. This, in turn, allows the linearization of the bilinear term in the mass balances. However, this approximation has an error, which is given by the resolution $\eta$ of the discretization. Given $\overline{\mu }$ the maximum growth rate of the model and $N$ the number of discretization points, the resolution of ETFL is given by $\eta =\frac{\overline{\mu }}{N}$. We can easily obtain the resolution of the estimation of a macromolecule concentration from this quantity.

The mass balance of a macromolecule $X$ at concentration $\left[X\right]$ under steady-state assumption is written in ETFL:

$$\frac{d\left[X\right]}{dt}=v^{\mathrm{s}\mathrm{y}\mathrm{n}}-v^{\mathrm{deg}}-v^{\mathrm{d}\mathrm{i}\mathrm{l}},$$ [14]

$$=v^{\mathrm{s}\mathrm{y}\mathrm{n}}-k_{\mathrm{deg}}\cdot \left[X\right]-\mu \cdot \left[X\right],$$ [15]

$$=0,$$ [16]

where $v^{\mathrm{s}\mathrm{y}\mathrm{n}}$, $v^{\mathrm{deg}}$, and $v^{\mathrm{d}\mathrm{i}\mathrm{l}}$ are the synthesis, degradation, and dilution rates, respectively, of the macromolecule; $mu$ is the growth rate; and $k_{\mathrm{deg}}$ is the degradation rate constant of the macromolecule. In ETFL, $\mu$ is approximated by $\hat{\mu }=p\eta$, with $p\in \left\{0..N\right\}$. $\eta$ is the resolution of this approximation, which means at all times:

$$\mu \in \left[\hat{\mu }-\frac{\eta }{2},\hat{\mu }-\frac{\eta }{2}\right].$$ [17]

From Eq. 15, and the relationship given in ref. 17, we can rewrite

$$\left[X\right]\hspace{0.17em}=\frac{v^{\mathrm{s}\mathrm{y}\mathrm{n}}}{k_{\mathrm{d}\mathrm{e}\mathrm{g}}+\mu }$$ [18]

$$\frac{v^{\mathrm{s}\mathrm{y}\mathrm{n}}}{k_{\mathrm{d}\mathrm{e}\mathrm{g}}+\hat{\mu }+\frac{\eta }{2}}\le \left[X\right]\le \frac{v^{\mathrm{s}\mathrm{y}\mathrm{n}}}{k_{\mathrm{d}\mathrm{e}\mathrm{g}}+\hat{\mu }-\frac{\eta }{2}}.$$ [19]

We use this expression to represent the uncertainty on the macromolecules concentrations at the previous time step, which is then used to constraint the current time step.

Backward Euler Integration Scheme.

At each time step, we operate an integration of the model between two time points. To this effect, using a robust integration scheme is necessary to guarantee a solution quality that is as good as possible. We chose to use a backward (implicit) Euler integration scheme given its ability to handle stiff problems (38). Usually, a drawback of implicit schemes is that they require us to solve an implicit equation to define the state of the system at each time step. In contrast, explicit methods simply require us to apply a defined set of calculations (e.g., a linearized state function) to the current state. In our case, however, there is little cost associated with using an implicit method rather than the explicit Euler method since we already need to solve a whole MILP problem to compute the solution to the dETFL problem at each time step.

In this context, we can rewrite Eqs. ${dEP}_j$ and ${dEN}_j$ in their Euler form:

$$0\le E_j\left(t_{i+1}\right)-E_j\left(t_i\right)\le v_j^{\mathrm{s}\mathrm{y}\mathrm{n}}\left(t_{i+1}\right)\cdot \mathrm{\Delta }t,$$ [dEP_j]

$$0\le E_j\left(t_i\right)-E_j\left(t_{i+1}\right)\le \left(v_j^{\mathrm{deg}}\left(t_{i+1}\right)+v_j^{\mathrm{d}\mathrm{i}\mathrm{l}}\left(t_{i+1}\right)\right)\cdot \mathrm{\Delta }t,$$ [dEN_j]

where $E_j$ is the concentration of a given enzyme at the previous time step and $E_j\left(t_{i+1}\right)$, $v_j^{\mathrm{deg}}\left(t_{i+1}\right)$, $v_j^{\mathrm{deg}}\left(t_{i+1}\right)$, and $v_j^{\mathrm{d}\mathrm{i}\mathrm{l}}\left(t_{i+1}\right)$ are variables of the dETFL problem in the next time step. $E_j\left(t_i\right)$ is a variable constrained around the value of the previous solution, as explained in the previous section.

Chebyshev Center.

One important issue when dealing with both (mixed integer) linear optimization and iterative solving is the multiplicity of solutions. Indeed, the optimality principle in LP only guarantees a unique global optimum value for the objective but not a unique optimal solution for the variables. In fact, at each time point, there is most often a (piecewise) continuum of solutions (including flux values, macromolecule concentrations …) that can satisfy a maximal growth rate while describing different physiologies. For example, two optimal states, using different pathways with a similar enzyme cost, will yield different proteomes and associated fluxes. In addition, due to the constraints applied on the rate of change of macromolecule concentrations, in each subsequent time point, the proteome, transcriptome, and flux values will be dependent on all of the previous solutions. Because of these two factors, each realization of the integration procedure might yield different results.

An additional issue is that simplex-based solvers tend to give sparse and extremal results (corners of the explored simplex), which do not represent accurately the full extent of the considered solution space. Several methods can alleviate these issues, all based on finding a good representative of the solution space. One first solution is to use as observation the mean of the variability analysis, rather than a single optimal solution. This, however, requires $\mathcal{O}\left(2n\right)$ optimizations to be carried out. Another way would be to sample the feasible space, but the sheer size of dETFL models makes sampling impractical. SI Appendix, Fig. S8 shows a two-dimensional example of the difference between these three approaches. The method we chose is to try to find the maximally inscribed sphere in the solution space. The center of this sphere, called the Chebyshev center, can be found by optimizing a single linear problem if the solution space is a polytope (39). It is the case in dETFL, as the problem is defined with linear inequality constraints.

In the case of a polyhedron defined by inequalities of the form $a_i^{\top }x\le b_i,x\in {\mathbb{R}}_{+}^n$, finding the Chebyshev center of the solution space amounts to solving the following optimization problem:

$$\begin{array}{cc}\hfill & \underset{r,x}{maximize}\hspace{1em}r\hfill \\ \hfill & \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\hspace{0.17em}\mathrm{t}\mathrm{o}\hspace{1em}{a}_i^{\top }x+{‖a_i‖}_{2}r\le b_i\hfill \end{array}.$$ [20]

This is similar to adding a common slack to all inequalities and maximizing its size, which maximizes the distance of the solution to the inequality constraints. However, not all variables and constraints need to be considered in the definition and inscribing of this sphere. In particular, we are interested in a representative solution for macromolecule concentrations, which only play a role in a limited set of constraints. To this effect, we define ${\mathcal{I}}_c$ and ${\mathcal{J}}_c$ as the set of inequality constraints and variables, respectively, with respect to which the Chebyshev center will be calculated. Let us also denote $\mathcal{E}$ the set of equality constraints of the problem; $a_i,c_i$ the left-hand side of the inequality and equality constraints, respectively; and $b_i,d_i$ their right-hand side, respectively. From there, we can define the modified centering problem:

$$\begin{array}{cc}\hfill \underset{r,x}{maximize}\hspace{1em}& r\hfill \\ \hfill \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\hspace{0.17em}\mathrm{t}\mathrm{o}\hspace{1em}& \hspace{1em}\hspace{1em}\mu =\mu *,\hfill \\ \hfill & a_i^{\top }x+{‖{\mathbb{1}}_{{\mathcal{J}}_c}○a_i‖}_{2}r\le b_i,\hspace{1em}\forall i\in {\mathcal{I}}_c\hfill \\ \hfill & a_i^{\top }x\le b_i,\hspace{1em}\forall i\notin {\mathcal{I}}_c\hfill \\ \hfill & c_k^{\top }x=d_k,\hspace{1em}\forall k\in \mathcal{E},\hfill \end{array}$$ [21]

where $\mu *$ is the maximal growth rate calculated at this time step, $r$ is the radius of the Chebyshev ball, $x$ is the column vector of all of the other variables of the ETFL problem, ${\mathbb{1}}_{{\mathcal{J}}_c}$ has for $j$th element zero if $j\in {\mathcal{J}}_c$ and else one, and $○$ denotes the elementwise product between two vectors. Thus, ${‖{\mathbb{1}}_{{\mathcal{J}}_c}○a_i‖}_2$ is the norm of the projection of the constraint vector onto ${\mathcal{J}}_c$. We show an example illustration in three dimensions in SI Appendix, Fig. S9.

For enzymes, for example, it is akin to making the model produce more enzymes than necessary to carry the fluxes while respecting the total proteome constraint. By maximizing the radius of the sphere inscribed in the solution space, at maximal growth rate, we are effectively choosing a representative solution of the maximal growth rate feasible space. We then use this solution as a reference point for the next computation step.

We chose the Chebyshev center as a representative solution for its advantages in computational complexity, as well as its low-bias physiological implications. Indeed, the Chebyshev center can be interpreted as the solution that produces a similar amount of excess enzyme for all enzymes. The choice of such a low-bias objective was also important to show the spontaneous emergence of diauxie under the most limited set of assumptions. It is also possible to choose a reference solution with more bias, as can be the case when qualitative biological knowledge is available. Methods that allow this include lexicographic optimization and minimization of adjustment methods, as described in Salvy and Hatzimanikatis (19).

All simulations in this paper perform Chebyshev centering on enzyme variables at each time step.

Initial Conditions.

Since dETFL is an iterative method, it is necessary to set an initial reference point (initial conditions) from which the dynamic analysis will integrate over time. The initial solution is set up as follows: 1) set typical uptake fluxes for carbon sources and oxygen, 2) perform a growth maximization using ETFL, 3) fix the growth to the optimum, and 4) find the Chebyshev center of the solution space.

The solution reported by the latter optimization problem is then used as a starting solution for the dETFL analysis.

Extracellular Concentrations.

At each time step, extracellular concentrations are updated following a standard Euler scheme, similarly to what is done in Mahadevan et al. (15). The extracellular concentrations of glucose, lactose, and acetate follow a system of ordinary differential equations:

$$\frac{d\left[Glc\right]}{dt}=v_{\mathrm{g}\mathrm{l}\mathrm{c}}\hspace{0.17em}\cdot X,$$ [22]

$$\frac{d\left[Ac\right]}{dt}=v_{\mathrm{a}\mathrm{c}}\hspace{0.17em}\cdot X,$$ [23]

$$\frac{d\left[Lcts\right]}{dt}=v_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}\hspace{0.17em}\cdot X.$$ [24]

We linearize this system into the following forward Euler scheme:

$${\left[Glc\right]}_{t+1}={\left[Glc\right]}_t\hspace{0.17em}+v_{\mathrm{g}\mathrm{l}\mathrm{c}}\hspace{0.17em}\cdot X\cdot \mathrm{\Delta }t,$$ [25]

$${\left[Ac\right]}_{t+1}={\left[Ac\right]}_t\hspace{0.17em}+v_{\mathrm{a}\mathrm{c}}\hspace{0.17em}\cdot X\cdot \mathrm{\Delta }t,$$ [26]

$${\left[Lcts\right]}_{t+1}={\left[Lcts\right]}_t\hspace{0.17em}+v_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}\hspace{0.17em}\cdot X\cdot \mathrm{\Delta }t.$$ [27]

We use these linearized equations to update the extracellular medium after the solution to each time step has been computed.

Model.

The model used is the vETFL model of iJO1366, presented in the original ETFL publication (19). Fifteen additional enzymes were added to the model to properly account for the protein cost of transporting glucose, lactose, and galactose from periplasm to the cytoplasm. A simplified metabolic map of the glucose, lactose, and galactose pathways to G6P is shown in Fig. 3.

Kinetic Information.

The Michaelis–Menten parameter $K_M^{\mathrm{g}\mathrm{l}\mathrm{c}}=0.015\hspace{0.17em}\mathrm{m}\mathrm{M}$ for glucose was taken from the original dFBA paper (15). The $K_M^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}=1.3\hspace{0.17em}\mathrm{m}\mathrm{M}$ for lactose was obtained from a study by Olsen and Brooker (40) on the specificity of lactose permeases. Details on the added enzymes are available in SI Appendix, Table S1. The Michaelis–Menten parameter $V_{max}^{\mathrm{g}\mathrm{l}\mathrm{c}}=15\hspace{0.17em}\mathrm{m}\mathrm{M}$ was used similarly to previous work (15).

Because of uncertainty in the values found in the literature, $V_{max}^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}$ was directly computed from the catalytic rate constants of enzymes consuming periplasmic lactose (LACZpp, LCTStpp, LCTS3ipp). Since ETFL gives access to enzyme concentrations, we can rewrite the expression of $V_{max}^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}$ using catalytic rate constants $k_{\mathrm{c}\mathrm{a}\mathrm{t}}^j$:

$$V_{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}^{max}=\sum _{j\in \mathcal{L}}{k}_{\mathrm{c}\mathrm{a}\mathrm{t}}^j\cdot \left[E_j\right],$$ [28]

where $\mathcal{L}$ is the set of periplasmic enzymes consuming lactose. Taking this into account allows us to replace the parameter $V_{max}^{\mathrm{l}\mathrm{c}\mathrm{t}\mathrm{s}}$ by an explicit internal variable.

Acetate transport is assumed to be mostly diffusive (32); its secretion rate was bounded at $5\hspace{0.17em}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{g}\mathrm{D}\mathrm{W}}^{-1}\cdot {\mathrm{h}}^{-1}$ and its uptake to $3\hspace{0.17em}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{g}\mathrm{D}\mathrm{W}}^{-1}\cdot {\mathrm{h}}^{-1}$. Oxygen is assumed to be nonlimiting and is given a maximal uptake rate of $15\hspace{0.17em}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{l}\cdot {\mathrm{g}\mathrm{D}\mathrm{W}}^{-1}\cdot {\mathrm{h}}^{-1}$. These values are of the same order of magnitude as in previous studies (6, 15, 27).

Implementation.

The code has been implemented as a plug-in to pyTFA (41), a Python implementation of the thermodynamics-based flux analysis method, and ETFL (19), an implementation of ME models accounting for expression, resource allocation, and thermodynamics. It uses COBRApy (42) and Optlang (43) as a back end to ensure compatibility with several open-source (GLPK, scipy) as well as commercial (CPLEX, Gurobi) solvers. The code is freely available under the APACHE 2.0 license at https://github.com/EPFL-LCSB/etfl and https://gitlab.com/EPFL-LCSB/etfl under the folder ./work/detfl.

Data Availability

Code data have been deposited in GitHub (https://github.com/EPFL-LCSB/etfl).