Ferromagnetic liquid droplets with adjustable magnetic properties

Significance

Structured functional liquids combine mechanical versatility of fluids with solid-state properties, such as ferromagnetism, and offer a route to synthesize and control magnetic liquids for adaptive liquid robotics. Studies on these intriguing materials are only in their nascent state, and a profound understanding of the physical state is still lacking. We use hydrodynamics experiments to probe how the magnetization of ferromagnetic liquid droplets, governed by the assembly and jamming of magnetic nanoparticles at liquid–liquid interfaces, and their response to external stimuli can be tuned by chemical, structural, and magnetic means. Our results highlight the leading role of structural short-range order on magnetic properties, which provide a path toward nano-patterning structured liquids.

Abstract

The assembly and jamming of magnetic nanoparticles (NPs) at liquid–liquid interfaces is a versatile platform to endow structured liquid droplets with a magnetization, i.e., producing ferromagnetic liquid droplets (FMLDs). Here, we use hydrodynamics experiments to probe how the magnetization of FMLDs and their response to external stimuli can be tuned by chemical, structural, and magnetic means. The remanent magnetization stems from magnetic NPs jammed at the liquid–liquid interface and dispersed NPs magneto-statically coupled to the interface. FMLDs form even at low concentrations of magnetic NPs when mixing nonmagnetic and magnetic NPs, since the underlying magnetic dipole-driven clustering of magnetic NP-surfactants at the interface produces local magnetic properties, similar to those found with pure magnetic NP solutions. While the net magnetization is smaller, such a clustering of NPs may enable structured liquids with heterogeneous surfaces.

Liquid–liquid interfaces act as traps to molecular surfactants (1, 2), polyelectrolytes (3, 4), biomaterials (5), and microparticles/nanoparticles (NPs) (6, 7) that reduce the interfacial energy (6) and endow the interface with their inherent properties. This functionalization enables novel magnetic (8–10), optical (11–13), electric response (14, 15), and bio-inspired (16) materials. The particles jammed at the interface provide the system with high stability against deformation and coalescence, which is relevant for applications like encapsulation for drug delivery and fluidic reactors (17, 18). Hard and soft colloidal suspensions exhibit a concentration-dependent glass formation; the solution reaches a glassy state when the concentration of colloids is sufficiently high to retard the long-range movement of single particles (19–23). Ramsden and Gotch (24) found that suspensions dissolved in solution can coagulate at the surface to form a solid-like layer that stabilizes a nonequilibrium shape of the droplets. Herzig et al. (19) used the jamming of a monolayer of colloidal particles at the interface of liquids undergoing spinodal phase separation to arrest the system in a bicontinuous liquid state called “bijels.” The enabling rigidity is imparted by the interfacial jamming of a monolayer of NPs, which can locally unjam in the presence of an external force, allowing the structured liquids to be reconfigured (15). To maintain a nonequilibrium shape of the liquids, the binding energy of NPs to the interface must be sufficiently high to resist the compressive force that occurs when the liquids attempt to return to their spherical, equilibrium shape. To this end, Russell and coworkers (15) developed the concept of NP-surfactants that form at the interface between two immiscible liquids, where the functionalized NPs are dispersed in one liquid, and ligands, having a complementary functionality, are dissolved in the second liquid. Ligands anchor to the surface of the NPs at the interface to form the NP-surfactants, where the binding energy of the NP-surfactants to the interface is orders of magnitude larger than that for NPs. Applying an external electric field deforms a water droplet containing NPs in an oil containing polymeric ligands into an ellipsoid. This structural transformation generates more interfacial area and promotes the assembly of more NP-surfactants at the interface. Upon removal of the field, the NP-surfactants jam, locking in the nonequilibrium ellipsoidal shape. The NP-surfactants are screened from the electrostatic repulsion between the NPs that favor dense packing (25–27). The absorbed polymer ligands on the surface of the NPs can further enhance the capillary force between NPs (28).

Recently, we found that the interfacial assembly and jamming of paramagnetic iron oxide (${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$) NPs at the interface between an aqueous phase containing functionalized NPs and a toluene solution with functionalized ligands with complementary functionality transformed the original ferrofluid droplets into ferromagnetic liquid droplets (FMLDs) (9) by restricting the translational and rotational degrees of freedom of the NPs and enhancing coupling strength associated with the magnetic dipole interactions between adjacent NPs by increasing their packing density (29, 30). The latter is accomplished by reducing the spatial separation between electrostatically repulsive NPs through electrostatic screening near the interface. Simultaneously, the jammed NP-surfactants endow the droplet with a high elastic modulus that resists droplet deformation and indefinitely locks in the shape of the droplet. Unlike solid permanent magnets, where magnetism originates from exchange-coupled rigid and immobile atoms, the assembly of the magnetic NP-surfactants is dynamic and reversible. Magnetic properties are dominated by a structural liquid-to-glass transition, which generates a two-dimensional (2D) layer of NPs on the curved interface and produces a remanent magnetization of the droplet (9, 10). Studies on these intriguing materials are only in their nascent state, and a full understanding of the NP assembly and resulting magnetization of the droplet in the presence and absence of an external magnetic field is still lacking. In this context, a more detailed study of the assembly and jamming process in reference to the influence of NP concentration, nature of ligands and NPs, pH, and droplet size is needed.

Examining the kinetics of the formation, assembly, and jamming of magnetic NP-surfactant assemblies is critical to understand and control both the magnetic and mechanical properties of the FMLDs, linked via structural short-range order of magnetic NP-surfactants, and to provide insight into the reversible transformation of the ferrofluid droplets into FMLDs. Depending on chemical properties that promote or impede electrostatics-driven NP migration to the interface, the timescale of the magnetic NP-surfactants formation is on the order of minutes, rendering the intrinsic timescales of NP magnetization switching (femtoseconds) irrelevant. However, since the magnetic NPs possess translational and rotational degrees of freedom in the liquid state prior to jamming, their structural arrangement is impacted by magnetic dipole interactions between adjacent NPs and an external magnetic field. In this sense, the magnetization of individual NPs can be pictured as a macro-spin influenced by its surroundings via magneto-static interactions. Dynamics and assembly of magnetic NPs at liquid–air and liquid–liquid interfaces can be quite sophisticated and tuned by alternating magnetic fields, previously demonstrated with unjammed magnetic particles and clusters (31–33). The combination of the hydrodynamic fluid flowing around the magnetic particles and the external periodic magnetic field alters the dynamic self-assembly and mobility of the magnetic particles at the interface. Long chains (32–34) and lattices (35) form in alternating in-plane magnetic fields, where the balance between viscous and magnetic torque, and magnetic attraction and hydrodynamic repulsion govern the stability and mechanical response of the dynamically stable and ordered structures. In contrast, dense packing of jammed magnetic particles inhibits the mobility of individual particles, producing a remanent magnetization of the entire droplet. Generating a magnetization configuration that preserves both direction and magnitude of the remanent magnetization, tunable magnetic properties, and shape reconfigurability make FMLDs appealing for applications in adaptive/responsive magnetic systems, biomimetic robotic systems, and liquid actuators (36–38).

Here, we study the magnetic-field-induced rotational and translational motion of microliter FMLDs ($\approx 5\times 10^{10}$ NPs) to probe the jamming of magnetic and nonmagnetic NPs and their influence on magnetic properties of the structured liquid. The relationship between structural and magnetic short-range order of magnetic NP-surfactants (Fig. 1A) and net magnetization of the FMLD is investigated by analyzing the mechanical response in terms of velocity and angular frequency to stationary and a rotating magnetic field as a function of angular velocity of the magnet [$\left(1\sim 50\right)$ Hz], droplet volumes [$\left(0.2\sim 20\right)\hspace{0.17em}\mathrm{\mu }$L], pH, NP concentration, and time. An analytical description of the hydrodynamics and micromagnetic simulations of a significantly smaller FMLD are used to interpret the findings. Our analysis is based on the assumption of an increased net magnetization of the FMLD with increasing jamming due to the densification of the surfactant layer and an enhanced coupling of the dispersed particles to the interface driven by magneto-static interaction. The latter stems from magnetic dipole fields emanating into the droplet from irregularly shaped NPs randomly oriented at the liquid–liquid interface. The experiments reveal a volume/surface area-dependent layer thickness (magnetization), which is attributed to an interfacial multilayer formation in the form of magnetic NPs magneto-statically coupled to the magnetic NP-surfactants or dispersed specimens amplifying the magnetic susceptibility in the vicinity of the droplet surface. The corresponding enhancement of the magnetic torque on the droplet and the angular frequency of droplet rotation are accessible by optical means. Electrostatic repulsion between charged NPs is stronger at higher pH, due to the deprotonation of the carboxyl group, which increases the separation distance and weakens the coupling strength associated with magnetic dipole interaction. Despite short-range order being affected by magneto-static forces, the electrostatic interaction dominates the assembly and enables chemical control in the present experiments.

Fig. 1.

FMLDs constructed by iron oxide NPs jammed at liquid–liquid interfaces. (A) Illustration based on micromagnetic simulations of short-range-ordered NPs (left) and corresponding macro spins (right) forming a 2D curved surface with a remanent magnetization. Color and arrow of the right side of the droplet indicate an in-surface magnetization vector. (B) Size distribution of the ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH NPs with a mean diameter of $\left(29.6\pm 2.8\right)$ nm determined from Gaussian fitting. (C) Short-range order of dried ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH NPs on silicon nitride nanomembranes visualized with full-field transmission electron microscopy. (Scale bar: 80 nm.) (D) Radial distribution (dist.) function of NP assemblies similar to that displayed in C corroborates dense packing and short-range ordering. First and second peaks appear at 37.6 and 71.2 nm, respectively. (E) In situ atomic force microscopy image of iron oxide NPs jammed at a liquid–liquid interface measured after a 25-min incubation time. (Scale bar: 200 nm.) (F) Temporal evolution of interfacial (interf.) tension of aqueous ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH NP dispersions (1 g/L) introduced to solutions of POSS-${\mathrm{N}\mathrm{H}}_2$ in toluene (1 g/L), displaying the interfacial activity of magnetic NP-surfactants at different pH.

The interface of two immiscible liquids, e.g., water and oil, is inherently negatively charged due to the absorption of hydroxyl ions (39). We use negatively charged carboxylic acid-functionalized iron oxide magnetic NPs (${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH) dispersed in water, which are repelled from the interface. The overall thickness of the organic layers, i.e., one monolayer of oleic acid and one monolayer of amphiphilic polymer, is uniformly $\approx 4$ nm. The NP diameter totals $\left(29.6\pm 2.8\right)$ nm with an inorganic magnetic core of $\approx 22$ nm. The statistical distribution of particle shape and size (Fig. 1B) amplifies the glassy state with short-range order (Fig. 1 C and D). The latter is quantified in terms of the radial distribution function of dried specimens similar to those depicted in Fig. 1C. First, second, and third peaks appear at multiples of the mean particle diameter plus $\approx 8$ nm (depending on pH), indicating dense packing and short-range order. Whereas these statistics are derived from transmission electron microscopy (TEM) images of dried magnetic NP-surfactants, due to challenges with imaging magnetic NP-surfactant layers in their liquid state, as evident from the inferior image quality of atomic force microscopy (AFM), a similar distribution and behavior are expected and, to some extent, supported by experiments (Fig. 1E). The electrostatic repulsion is adjusted by varying pH and adding polyhedral oligomeric silsesquioxane (POSS) molecules to the oil phase, which assemble at the water/oil interface due to their high interfacial activity. These measures promote the formation and assembly of NP-surfactants at the interface (Fig. 1E), causing an immediate reduction in the interfacial tension (Fig. 1F). The jammed NP-surfactant layers are densely packed with a sizable degree of structural disorder (Fig. 1 C–E) and transform the iron oxide NPs into ferromagnetic NP-surfactants split into magnetic domains near remanence (Fig. 1A).

Hydrodynamics Experiments

Previously, we used conventional methods, including vibrating sample magnetometry and magneto-optical Kerr effect magnetometry, to assess magnetic properties and distinguish between jammed (FMLD) and unjammed (ferrofluid) droplets (9). These static characterization tools, which rely on magnetic saturation, are typically slow in data acquisition and can influence the assembly and jamming of the magnetic NPs. They are relatively insensitive to small changes of structural short-range order affecting the magnetization of the FMLDs, owing to varying particle separation (magneto-static coupling strength) and number of nearest neighbors (spin frustration). A different perspective can be obtained by magnetic-field-driven hydrodynamics experiments, which focus on the mechanical response, in terms of rotational and translational motion under the influence of an external magnetic field. This approach is surprisingly sensitive to the formation of a ferromagnetic surfactant layer and experimentally feasible when dealing with microliter droplets that are visible under an optical microscope (Fig. 2). An NP concentration of 1 g/L translates into $\approx 5\times 10^{10}$ NPs dispersed in a 1-$\mathrm{\mu }$L droplet. Generally, a nonvanishing angular frequency is induced by a locked-in net magnetization of the FMLD that persists at remanence and even in the presence of an external driving field ($<20$ mT/${\mu }_0$). This requirement is essential to physically steer the FMLD with a magnetic field and prevent switching of the magnetization of individual magnetic NP-surfactants. Consequently, analyzing the temporal evolution of the angular frequency reveals information about the jamming process, i.e., partial, local jamming or complete jamming, and the formation of surfactant layers with various densities and thicknesses. The rotation of the droplet is monitored with an optical microscope from the point of droplet formation ($t=0$ s), and quantified in terms of angular frequency, derived from a time sequence of images (Movie S1) by autocorrelation.

Fig. 2.

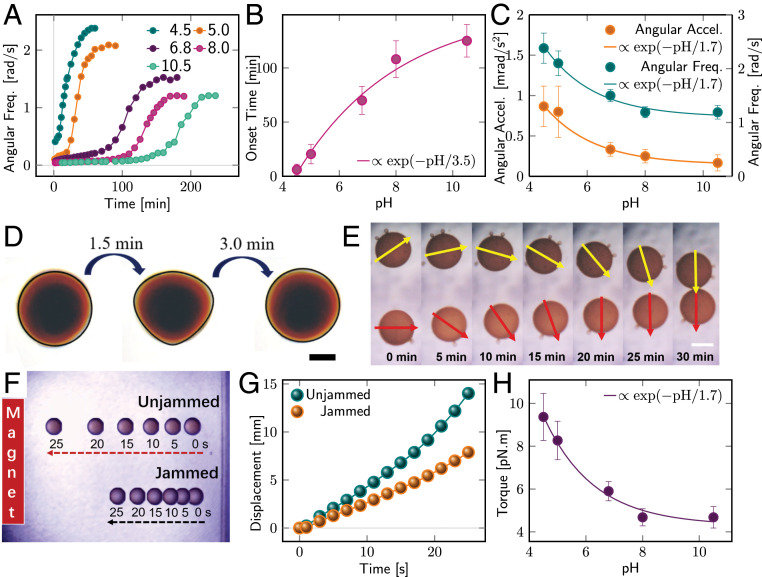
Magnetic-field-driven motion of FMLDs. (A) Temporal evolution of the droplet’s angular frequency (freq.) at different pH under the influence of an external magnetic field rotating at a constant driving frequency of 5 Hz. The concentrations of ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH NPs and POSS-${\mathrm{N}\mathrm{H}}_2$ are both 1 g/L; droplet volume is 1 $\mathrm{\mu }$L. (B and C) Onset time (B) and angular acceleration (accel.) and equilibrium angular frequency (C) retrieved from A. The onset time is determined from the extrapolation of the flank; the angular acceleration represents the slope of the flank. Both quantities are described by an exponential decay. (D) Structural deformation during FMLD formation in the presence of a rotating magnetic field indicating partial, local jamming near onset time. The FMLD is formed at a pH of 5 after 25 min. (Scale bar: 0.5 mm.) (E) Image series of two FMLDs approaching each other at remanence in the oil phase. Concentrations of ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH NPs and POSS-${\mathrm{N}\mathrm{H}}_2$ are 0.5 and 10 g/L, respectively. The remanent magnetizations are indicated by arrows. (Scale bar: 1 mm.) (F and G) Magnetic field gradient-induced linear motion of ferromagnetic liquid (jammed) and paramagnetic ferrofluid (unjammed) droplets revealing different velocities and acceleration. (H) Equilibrium torque on FMLD as a function of pH showing the same trend as angular acceleration and frequency in C.

The unjammed droplet has a very small angular frequency and acceleration, since the density of NP-surfactants at the interface is insufficient to cause a close packing of NPs and a sizable magnetic dipole coupling (Fig. 2A). In fact, the NPs are likely randomly positioned at the interface with rotational and translational degrees of freedom similar to their dispersed counterparts, which can lead to a rotation of the interface area of the droplet, despite remaining a paramagnetic ferrofluid (Movie S2). The formation of NP-surfactants and corresponding interfacial jamming layer is slowed down at high pH, due to weaker electrostatic screening and stronger repulsion. The latter originates from a promoted deprotonation of carboxyl groups decorating the jammed NPs and a reduced absorption of positive charged ligands to the interface. During this time, the droplet slowly rotates as a result of local aggregations (Movie S3). While individual rotating NPs barely induce any movement, the microsized aggregates with a net magnetization experience a magnetic torque, triggering a rotation of the surrounding liquid, and eventually the entire droplet due to friction (Fig. 2A). At this stage, the remanent magnetization of the droplet is negligible, owing to quasi-free motion of randomly distributed aggregates. The surface coverage of aggregation (areal density of NP-surfactant) grows with time, which increases the degree of jamming and the remanent magnetization. Experimentally, we observed the transition from unjammed to partially and completely jammed interfaces in the form of the structural deformation of the initial and final spherical droplet in the presence of a rotating magnetic field (Fig. 2D) due to spatial variations in rigidity, magnetization, and magnetic in-surface anisotropy driven by magnetic dipole interactions within the magnetic NP-surfactant layer (10).

The point in time, at which the critical density of NP-surfactant for a complete interfacial jamming is reached, is referred to as onset time and depends on pH and electrostatic screening (Fig. 2B). Further in-surface rearrangements of the NP-surfactant compress the assembly and open up space for more NP-surfactants to form and assemble at the interface. The closer packing enhances the magnetic dipole interaction, magnetic in-surface anisotropy, magnetization, and corresponding angular frequency. The equilibrium angular frequency is, to a first approximation, proportional to the magnetization and indirectly proportional to pH, due to weaker electrostatic screening and slightly larger NP separation that significantly reduce magnetic dipole interactions and stability at high pH. A similar dependence reveals the maximal angular acceleration arising from the jamming process itself, which shows the same exponential decay with pH ($1.7\pm 0.3$ vs. $1.7\pm 0.6$) as the equilibrium angular frequency (Fig. 2C). The restriction to single-particle mobility affects both structural properties, i.e., liquid to glass transition, and magnetic characteristics of the jammed NPs that, according to micromagnetic simulations of droplets with a diameter of 200 nm, show a magnetic short-range order on a scale of 5 to 10 NPs visible in the magnetic domain formation (Fig. 1A) and spatial spin–spin correlation functions (10). While we do not expect a significant change with increasing droplet size, the magnetic ordering and emergent net magnetization will strongly depend on the intrinsic properties of the NPs, i.e., magneto-crystalline and shape anisotropy, temperature, and chemical parameters defining particle separation and enabling chemical control by pH. Despite lacking proof of magnetic short-range order, ultimately requiring magnetic imaging or scattering experiments, the resulting net magnetization of FMLDs is evident from a reorientation of approaching FMLDs due to capillary and magnetic dipole forces (Fig. 2E). The existence of a net magnetization impedes translational motion driven by a magnetic field gradient compared with ferrofluids with otherwise the same properties (Fig. 2 F and G). The difference in acceleration and, hence, velocity and displacement is directly proportional to the number of NPs whose magnetization aligns along the direction of the magnetic field.

Mathematically, the hydrodynamics experiments can be described as a coupled nonlinear system for the angular displacements $\phi$ (shell) and ${\phi }_c$ (core), where the rotating magnetic field exerts a magnetic torque on the rigid shell, i.e., ferromagnetic NP-surfactant layer, that experiences friction on either side:

$$\begin{array}{ll}\hfill J_s\ddot{\phi }\left(t\right)& ={\mu }_0{\mu }_{r}M{H}_0\sin \left({\omega }_{0}t-\phi \left(t\right)\right)\hfill \\ \hfill & -8\pi \eta r^3\dot{\phi }\left(t\right)-8\pi {\eta }_c{r}_{in}^3\left[\dot{\phi }\left(t\right)-{\dot{\phi }}_c\left(t\right)\right],\hfill \\ \hfill J_c{\ddot{\phi }}_c\left(t\right)& =-8\pi {\eta }_c{r}_{in}^3\left[\dot{\phi }\left(t\right)-{\dot{\phi }}_c\left(t\right)\right].\hfill \end{array}$$ [1]

Here, $r$ and $r_{in}\left(t\right)=\left(r-\mathrm{\Delta }r\cdot t\right)$ represent the outer and inner radius of the droplet shell, respectively. The latter may monotonically increase with time due to magneto-static interactions between dispersed and jammed NPs after the dispersed specimens are magnetized and propelled toward the interface by the magnetic field gradient. The moments of inertia of the interfacial surfactant layer and water droplet containing the dispersed NPs are defined as $J_s=\frac{2}{3}\left(\frac{4}{3}\pi {\rho }_{NP}\left[r^3-r_{in}^3\right]\right)r^2$ and $J_c=\frac{2}{3}\left(\frac{4}{3}\pi {\rho }_{water}{r}_{in}^3\right)r_{in}^2$, respectively. The viscosity of the water and oil phases are chosen as $\eta =0.89$ g/(m$\cdot$s) and ${\eta }_c=0.656$ g/(m$\cdot$s), respectively. Assuming an ideal spherical droplet with homogeneous surfactant density, and related homogeneous friction and magnetization, leaves the inner droplet radius $r_{in}$ as the only free parameter. All other parameters are experimentally determined. The magnetization $M$ is the renormalized volume-saturation magnetization of the surfactant layer (shell), dependent on the inner radius $r_{in}$ and approximated as a homogeneous distribution of macro-spins (closely packed NPs) that possess a saturation magnetization of 300 kA/m. The renormalization coefficient ($0.28\pm 0.01$ at pH of 5), retrieved from experimental and micromagnetic $M\left(H\right)$ hysteresis loops, considers the smaller magnetization in the presence of the driving field. To some extent, this takes into account the modified magnetic permeability ${\mu }_r$ of dispersed NPs enhancing the magnetic induction of the external magnetic field near the interface. Both the water and oil phases exert a viscosity-related damping that linearly depends on the angular frequency, which causes, for insufficient magnetic torques, a desynchronized rotation. The direction and amplitude of torque and angular acceleration vary periodically (Fig. 3 A and B; SI Appendix, Fig. S1), as they depend on the relative angle between the external magnetic field ($H_0=20$ mT/${\mu }_0$), rotating at a constant frequency of ${\omega }_0/2\pi$ = 5 Hz, and net magnetization of the FMLD. This leads to a sizable reduction of the experimentally accessible, time-averaged angular frequency. This is observed in both experiment (Fig. 3C) and numerical modeling (Fig. 3B) (10). In fact, the hydrodynamic angular frequency of all investigated FMLDs is at least one order of magnitude lower than the driving frequency ${\omega }_0$. Lowering friction, i.e., reducing droplet size or viscosity, or driving frequency can compensate for a low magnetization. This trend is experimentally observed for ${\omega }_0/2\pi$ ranging from 1 to 50 Hz (Fig. 3C) and microliter droplets with volumes ranging from 0.2 to 20 $\mathrm{\mu }$L (Fig. 3D). In a first approximation, the magnetic torque on the net magnetization of the FMLD can be derived from the equilibrium angular frequency, considering the balance between magnetic torque and friction with the surrounding oil. Aside from neglecting contributions originating from NP switching (taking place on the picosecond time scale), which effectively reduces the magnetization the torque is acting on, it assumes no acceleration or synchronized rotation of the shell and core, which is valid for very small accelerations or if the angular frequency equals the driving frequency. While for constant droplet volumes, the equilibrium magnetic torque resembles the angular frequency (Fig. 2H), it is an interesting measure to quantify the magnetization of FMLDs with varying volumes and friction (Fig. 3E).

Fig. 3.

Size and frequency dependence of field-driven FMLD rotation. (A) Temporal evolution of experimental angular frequency (freq.) for two different time constants revealing periodic changes in both sign and strength of angular acceleration and a substantially smaller value than the driving frequency. (B) Simulated angular frequency of a rotating FMLD whose magnetic torque is insufficient to ensure synchronized rotation due to friction. (C) Equilibrium angular frequency for different FMLD volumes and different driving frequency showcasing effect of desynchronization. (D) Temporal evolution of the angular frequency as a function of droplet volume at a constant driving frequency of 5 Hz. The concentrations of ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH NPs and POSS-${\mathrm{N}\mathrm{H}}_2$ are both 1 g/L. (E) Equilibrium torque on the FMLD. (F) Comparison between experimental and modeled angular frequency. Magneto-static interaction of dispersed and jammed NPs triggers the formation of a surfactant multilayer, which is reflected in simulations by a radius-dependent layer thickness h.

The equilibrium angular frequency exponentially decreases with the droplet radius both in experiment (Fig. 3C) and simulations. This is particularly prominent for small driving frequencies where the rotational motion is closer to synchronization. Furthermore, larger droplets take longer to accelerate and reach steady state, owing to prolonged NP absorption to and jamming at the interface, and the larger drag force in the form of friction by fluids inside and outside the droplet. Considering structural and magnetic short-range order in reference to more than 1 billion NPs jammed at the interface, changing dimensions of microliter droplets are unlikely to affect domain formation, propagation, or pinning. Calculating the magnetic torque applied to the droplet yields an exponential dependence on the radius (Fig. 3E), which indicates a radius-dependent surfactant-layer thickness and magnetization. The latter is quantified by correlation with hydrodynamics simulations, using Eq. 1, and varying the layer thickness (Fig. 3F). The magnetization is presumed to be locked, i.e., does not rotate with the driving magnetic field. Although we have no means to corroborate or refute this presumption in our experiments, a significant contribution is unlikely to be the cause of the radius dependence of the angular frequency, since small FMLDs are expected to suffer less than larger ones. Our experiments show the opposite trend. While the modeling of a constant layer thickness, i.e., surfactant monolayer, deviates significantly from the experimental data for small droplets, a layer thickness linear in the droplet radius shows good agreement between experimental and numerical data. Although the droplet volume varies over two orders of magnitude (0.2 to 20 $\mathrm{\mu }$L), the corresponding radius (0.4 to 1.7 mm) remains constant with respect to the size of NPs ($\sim 10$ nm) and short-range order. This radius dependence suggests an important role of the surface-to-volume ratio in the form of available NPs dispersed in solution.

The FMLD can be approximated as an ensemble of a ferrofluid core and a jammed ferromagnetic shell. Iron oxide NPs jammed at the liquid–liquid interface become ferromagnetic by the stabilizing magnetic dipole interactions between adjacent NPs. The remaining dispersed NPs can contribute to the magnetic torque in the form of either an effective magnetic susceptibility enhancing the magnetic induction or a thicker ferromagnetic surfactant layer. For the NP concentration of 1 g/L and a droplet volume of 1 $\mathrm{\mu }$L, the maximal thickness of the magnetic NP-surfactant layer is seven monolayers; the susceptibility enhancing dispersed NP near the interface may reach up to 1 $\mu$m. For perfect spherical NPs without magneto-crystalline or shape anisotropy, the surfactant layer would exhibit an in-surface magnetic anisotropy with magnetization and, to a great extent, magnetic stray fields confined to the interface (Fig. 1A) (10). A more realistic picture is the random distribution of NP shape, size, and crystal axes orientation (Fig. 1C). This leads to localized stray fields emanating from the interface that attract dispersed iron oxide NPs to the interface. The net magnetization pushes more dispersed NPs to the interface driven by magneto-static interaction. As a result, the assembly is governed by the NP properties and local short-range order, as well as the available number of dispersed NPs (SI Appendix, Fig. S2). The aforementioned hydrodynamics modeling and discussions referred to this assembly as a surfactant multilayer. We stress that this terminology is motivated by magnetic properties and does not infer mechanical jamming of all layers from a chemical point of view. The capacity of the FMLD to form magnetic surfactant multilayers is highly dependent on the ligand functionalization (10), which is in support of the current interpretation of a magnetic stray field-induced assembly.

The construction of FMLDs requires NP jamming and the formation of a surfactant layer with a magnetization. This can be achieved with either iron oxide NPs or mixtures of magnetic and nonmagnetic NPs. The latter is illustrated in the example of carboxylic acid-functionalized silicon oxide (${\mathrm{S}\mathrm{i}\mathrm{O}}_2$-COOH) and ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH NPs, which have diameters of 15 and 22 nm, respectively. Adding smaller ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ NPs benefits a denser packing and enhanced jamming of NPs (SI Appendix, Fig. S4) since both NPs can form NP-surfactants with ligands at the interface (SI Appendix, Fig. S3). The magnetization and, hence, the angular frequency decreases with increasing concentration of silica NPs (Fig. 4A). A comparison with hydrodynamics simulations, considering a homogeneous magnetization scaled by the iron oxide NP concentration, shows a much weaker decay than predicted, which becomes prominent for iron oxide NP concentrations below 80% (Fig. 4B). This discrepancy is attributed to a clustering of iron oxide NPs (Fig. 4 B, Inset) during the jamming process which possess, due to short-range ordering, similar magnetic properties, e.g., magnetization and coercivity, as a jammed interface with only iron oxide NPs. For comparison, a homogeneous distribution of magnetic and nonmagnetic NP-surfactants would render the jammed surfactant layer paramagnetic due to negligible magnetic dipole interactions (40). The heterogeneous NP distribution makes a quantitative analysis of magnetic properties based on analytics nearly impossible and requires molecular-dynamic and micromagnetic simulations to establish the link between structural microscopic and magnetic macroscopic properties.

Fig. 4.

Mechanical response of heterogeneous FMLDs synthesized from a mixture of magnetic ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$ and nonmagnetic ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ NPs. (A) Angular frequency (freq.) of 1-$\mathrm{\mu }$L droplets as a function of time for different magnetic NP concentrations. The total NP concentration is 1 g/L; 20% equals 0.2 g/L ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$ NPs; pH of the aqueous phase is 5; the droplets form at $t=0$ s. (B) Comparison between experiment and numerical modeling of the angular frequency, assuming a homogeneous distribution of NPs. B, Inset shows the droplet with dark dots indicating clustering of iron oxide NPs. (Scale bar: 0.1 mm.)

Conclusion

We synthesized FMLDs and investigated their mechanical response to a rotating magnetic field as a function of numerous chemical and structural parameters to assess their magnetic properties. Independent of the exact interaction between magnetic NPs with different pH, jamming was a prerequisite for the formation of FMLDs and corresponding rotation. Large pH impeded the formation of a jammed layer and caused smaller magnetizations, owing to weaker electrostatic screening and weaker stabilizing magnetic dipole interactions. The thermally stable magnetization configuration of the NP-surfactant layer consolidated a net magnetization that is expected to exert a magnetic force on the dispersed magnetic NPs. The latter can couple the dispersed NPs to the interface and lead to surfactant multilayers from the perspective of magnetic properties. As a result, the magnetic properties of the droplet depended on the total number of NPs inside the droplet and, for a given particle concentration, on the droplet volume. This translates into an equilibrium angular frequency that scales with the radius and a smaller linear velocity compared to unjammed droplets. The time-averaged angular frequency of all investigated samples was significantly smaller than the driving frequency and decreased with the driving frequency, due to desynchronization and periodically fluctuating angular acceleration. The magnetic properties of FMLDs were further altered by jamming mixtures of iron oxide and nonmagnetic NPs at the liquid interface. Low concentrations of iron oxide NPs exceeded the magnetization extrapolated from high concentrations, due to high interfacial activity and proclivity to form clusters with magnetizations similar to pure magnetic NP solutions. Our findings demonstrate that a heterogeneous patterning of multifunctional NP-surfactant layers is possible without impairing functionality. The latter may be achieved by selective assembly of NPs in the presence of magnetic fields perpendicular to the interface, similar to domain formations in ferrofluids (41).

Materials and Methods

Synthesis of NP Dispersions.

To prepare the solutions for forming FMLDs, we use two immiscible liquids, i.e., water and oil, whose interface is inherently negatively charged, due to the absorption of hydroxyl ions (39). Adding negatively charged carboxyl NPs, such as iron oxide magnetic NPs (${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH; Ocean Nanotech) and silicon dioxide NPs (${\mathrm{S}\mathrm{i}\mathrm{O}}_2$-COOH; Microsphere-Nanosphere), to the water phase causes an automatic repulsion from the interface and a homogeneous dispersion. The water solubility is provided by an amphiphilic polymer coating with a carboxylic acid group and a zeta potential ranging from $-35$ to $-15$ mV. The overall thickness of the organic layers, i.e., one monolayer of oleic acid and one monolayer of amphiphilic polymer, is $\approx 4$ nm. The inorganic magnetic core is 22 nm in diameter; the silicon dioxide core is 15 nm in diameter. We dissolve PSS-[3-(2-aminoethyl)amino]propyl-heptaisobutyl substituted POSS (POSS-${\mathrm{N}\mathrm{H}}_2$; Sigma-Aldrich) ligands in the oil (toluene or ${\mathrm{C}\mathrm{C}\mathrm{l}}_4$) phase. The POSS molecules are very interfacial active, assemble at the water/oil interface, and cause a marked reduction in the interfacial tension. A concentration of 1 g/L is used for both ${\mathrm{F}\mathrm{e}}_3{\mathrm{O}}_4$-COOH and POSS-${\mathrm{N}\mathrm{H}}_2$. Lower NP concentrations are obtained by the addition of deionized water. The pH of the dispersions is adjusted by using 1.0 M NaOH or HCl and measured with a pH meter (Mettler Toledo Electrode Kit EL20 Edu Ph Benc). The toluene 99.9% and ${\mathrm{C}\mathrm{C}\mathrm{l}}_4\hspace{0.17em}\gtrsim 99.5\%$ were both purchased from Sigma-Aldrich. The amine groups are protonated and positively charged for $\mathrm{p}\mathrm{H}<p{K}_a\left(\approx 11\right)$. The POSS molecules initially form a monolayer at the water–oil interface, changing the charge of the interface from negative to positive. By Brownian motion, the functionalized NPs diffuse to the interface and interact with the assembled POSS, anchoring the POSS to the NP surface. The number of POSS molecules that anchor to the surface self-regulate to minimize the interfacial energy of each NP. The number of POSS molecules anchored to the NP surface increase with decreasing pH, due to the degree of protonation of the carboxy and amino functionalities. The reduction in the interfacial tension resulting from the formation and assembly of the NP-surfactants at the interface is measured by pendant drop tensiometry (Krüss DSA30).

Data Availability

All study data are included in the article and/or supporting information.